Как нарисовать правильный треугольник вписанный в окружность
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5.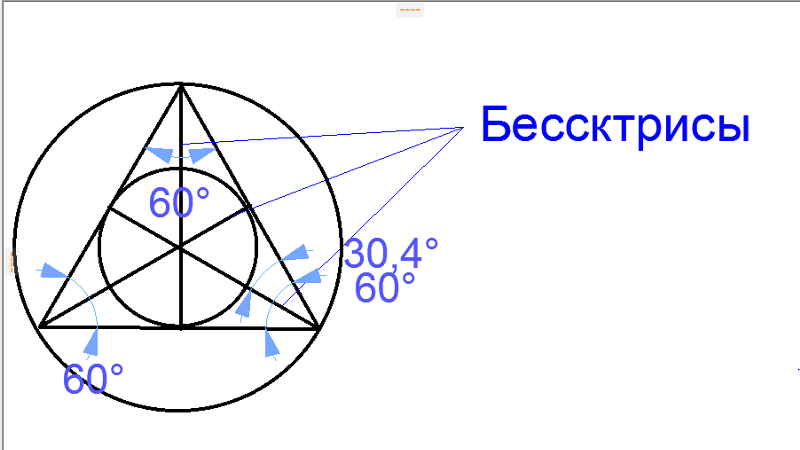 Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг.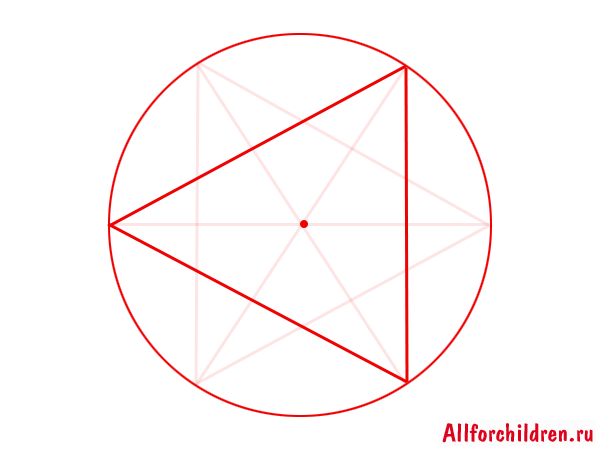 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Деление окружности на равные части и построение правильных вписанных многоугольников можно выполнить как циркулем, так и с помощью угольников и рейсшины.
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис.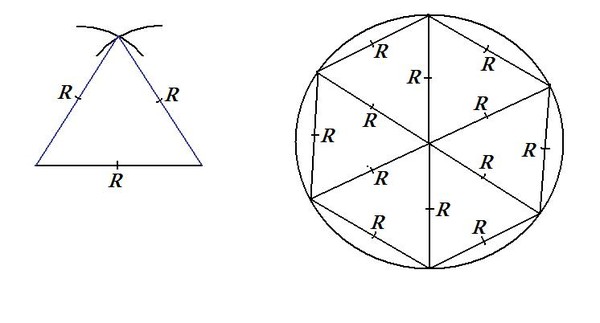 115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 115, в).
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.
При делении окружности циркулем на три равные части из любой точки окружности, например из точки Л пересечения центровых линий с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку Л. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным радиусу данной окружности, получают точки 2 и 3.
Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку Л. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным радиусу данной окружности, получают точки 2 и 3.
При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис. 117, в).
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.
При построении двенадцатиугольника с помощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.
119 и 120.
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 122.
Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /5 длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4. Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, начиная построение из точки /, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник (рис. 123, б).
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.
Из любой точки окружности, например точки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).
Сначала окружность делится на семь равных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).
СОПРЯЖЕНИЯ
Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.
На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхности. На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
Плавный переход одной цилиндрической поверхности в другую может являться цилиндрической поверхностью (рис. 127, а). На чертеже эти цилиндрические поверхности изображены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окружности в другую осуществляется дугой окружности заданного радиуса.
На рис. 126, а и 127, а рассмотрены простейшие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображаются различными сочетаниями прямых, окружностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет одно — плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Задачи на сопряжения условно можно разделить на три группы.
Первая группа задачвключает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.
Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.
Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O1, О2и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т.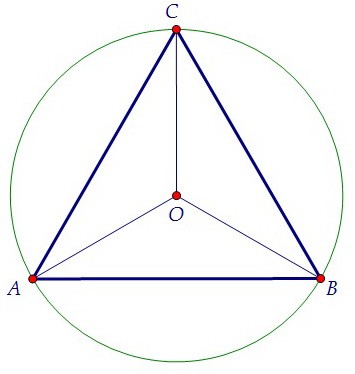 е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окружность.
Задача аналогична предыдущей, но дополнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.
129, б), который определяет величину прямолинейного участка.
Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют перпендикуляр, на котором откладывают радиус R заданной окружности, и находят центр окружности (точку О). При обводке сначала от точки касания проводится дуга заданного радиуса, а потом — прямая.
Из сказанного следует:
1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;
Не нашли то, что искали? Воспользуйтесь поиском:
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую.
 Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник. - Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
Построение правильных многоугольников — Техническое черчение
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника.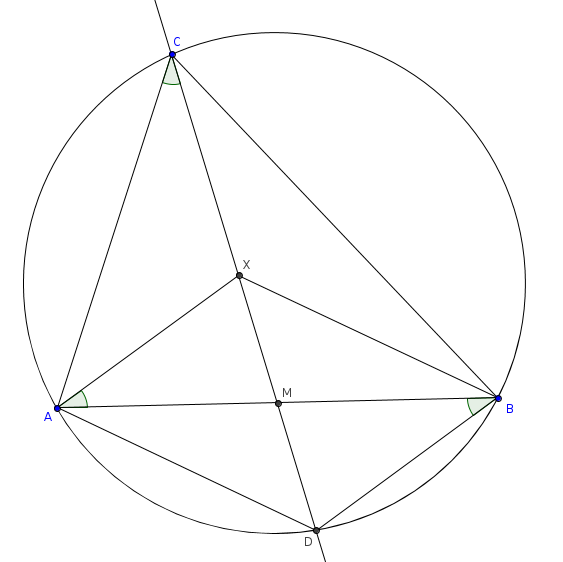 Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
|
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника. |
длина сторон, сумма углов.
 Описанный тупоугольный треугольник Как рисуется остроугольный треугольник
Описанный тупоугольный треугольник Как рисуется остроугольный треугольникКак начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.

- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
- Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
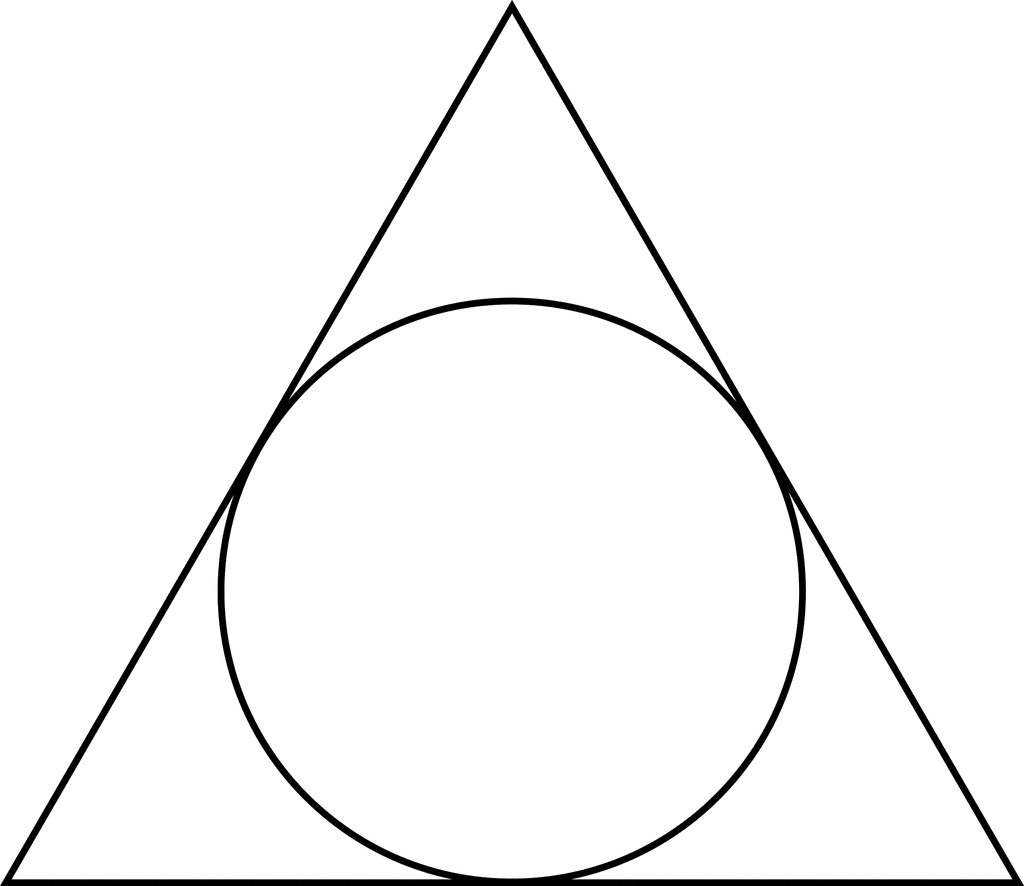
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
Разбираемся с понятиями
В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о. Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Правильное начертание
Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.
Основные линии
Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.
Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.
Так, биссектрисы делят угол пополам, а противоположную сторону — на отрезки, которые пропорциональны прилегающим сторонам.
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Серединный перпендикуляр — это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.
Работа с окружностями
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.
Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.
Вписанные треугольники
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.
Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.
Описанные треугольники
Также довольно часто приходится работать со вписанными окружностями.![]() По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p — это полупериметр треугольника, c, v, b — его стороны.
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Инструкция
Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.
В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.
Аналогичным способом поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.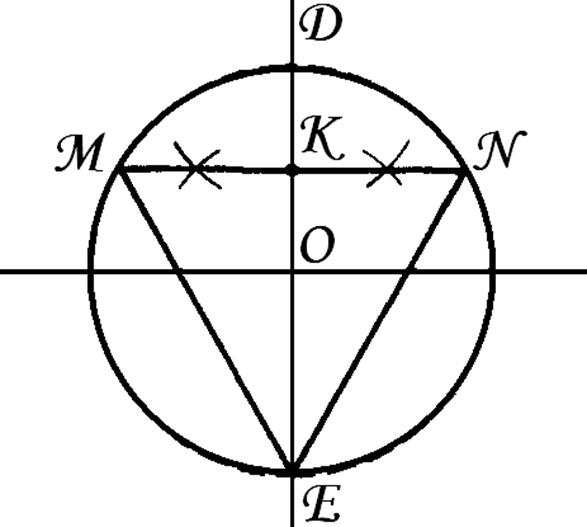
В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.
Получив все три вершины, соедините их прямыми линиями с помощью любой ровной поверхности (лучше линейки). Треугольник ABC построен.
Если окружность касается всех трех сторон данного треугольника, а её центр находится внутри треугольника, то ее называют вписанной в треугольник.
Вам понадобится
- линейка, циркуль
Инструкция
Из вершин треугольника (стороны противоположной делимому углу) циркулем проводят дуги окружности произвольного радиуса до пересечения их между собой;
Точку пересечения дуг по линейке соединяют с вершиной делимого угла;
Тоже самое проделывают с любым другим углом;
Радиусом вписанной в треугольник окружности будет отношение площади треугольника и его полупериметра: r=S/p , где S — площадь треугольника, а p=(a+b+c)/2 — полупериметр треугольника.
Радиус вписанной в треугольник окружности равноудален от всех сторон треугольника.
Источники:
- http://www.alleng.ru/d/math/math52.htm
Рассмотрим задачу построения треугольника при условии, что известны три его стороны или одна сторона и два угла.
Вам понадобится
- — циркуль
- — линейка
- — транспортир
Инструкция
Допустим, даны три стороны : a, b и с. Пользуясь , несложно с такими сторонами. Для начала выберем самую длинную из этих сторон, пусть это будет сторона с, и начертим ее. Затем установим раствор циркуля на величину другой стороны, стороны a, и начертим циркулем окружность радиуса a с центром на одном из концов стороны c. Теперь установим раствор циркуля на величину стороны b и начертим окружность с центром на другом конце стороны c. Радиус этой окружности равен b. Соединим точку пересечения окружностей с центрами и получим треугольник с искомыми сторонами.
Чтобы начертить треугольник с заданной стороной и двумя прилегающими углами, возьмите транспортир.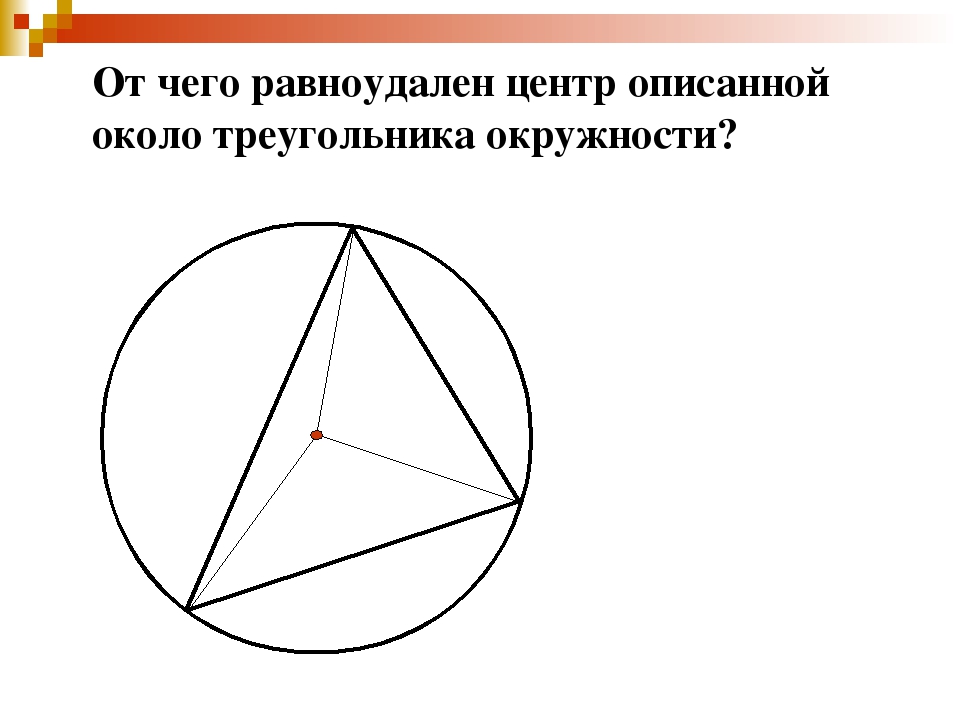 Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.
Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.
Видео по теме
Обратите внимание
Для сторон треугольника справедливо следующее утверждение: сумма длин двух любых сторон должна быть больше третьей. Если это не выполняется, то построить такой треугольник невозможно.
Окружности в шаге 1 пересекаются в двух точках. Можно выбрать любую, треугольники будут равными.
Правильный треугольник — тот, у которого все стороны обладают одинаковой длиной. Исходя из этого определения, построение подобной разновидности треугольника является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
С помощью линейки соединить отмеченные на листке точки последовательно, друг за другом так, как это показано на рисунке 2.
Обратите внимание
В правильном (равностороннем) треугольнике все углы равны 60 градусам.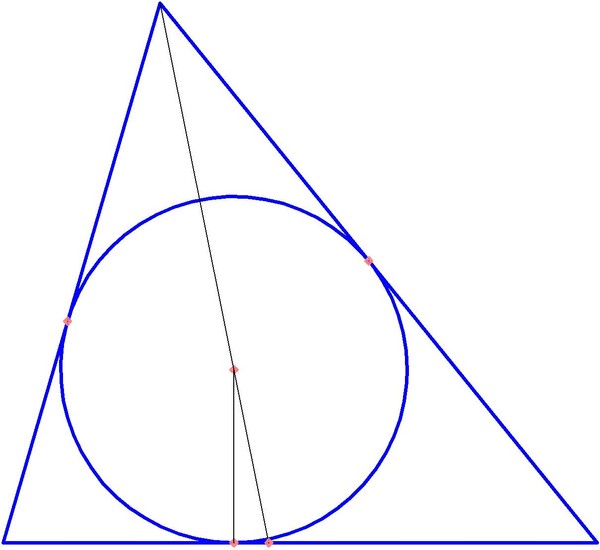
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это означает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Любой правильный треугольник является равнобедренным, в то время как обратное утверждение не верно.
У любого равностороннего треугольника одинаковы не только стороны, но и углы, каждый из которых равен 60 градусам. Однако чертеж такого треугольника, построенный при помощи транспортира, не будет обладать высокой точностью. Поэтому для построения данной фигуры лучше воспользоваться циркулем.
Вам понадобится
- Карандаш, линейка, циркуль
Инструкция
Затем возьмите циркуль, установите его в из концов (будущей вершине треугольника) и проведите окружность с радиусом, равным длине этого отрезка. Можно не проводить окружность целиком, а начертить лишь ее четверть, от противоположного края отрезка.
Теперь переставьте циркуль в другой конец отрезка и снова начертите окружность того же радиуса. Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.
Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.
Чтобы закончить построение, снова возьмите линейку с карандашом и соедините точку пересечения двух окружностей с обоими концами отрезка. Вы получите треугольник, все три стороны которого абсолютно равны, – это можно будет легко проверить с помощью линейки.
Видео по теме
Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.
Вам понадобится
- Линейка, циркуль.
Инструкция
С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С.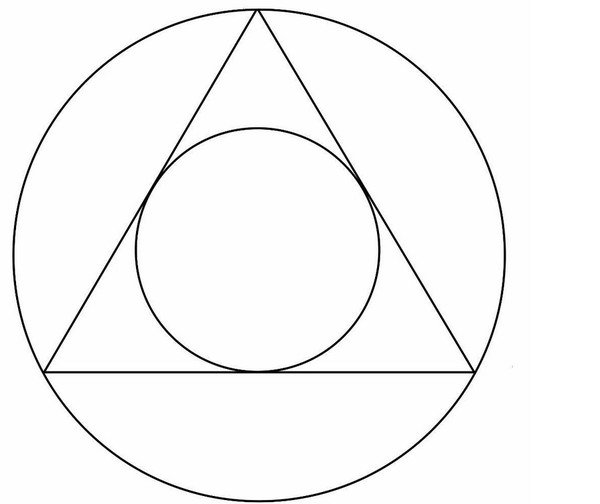 Это будет третьей вершиной треугольника.
Это будет третьей вершиной треугольника.
Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.
Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.
Не сдвигая линейки после построения отрезка ОК, приложите перпендикулярно к ней еще одну линейку. Проведите прямую m пересекающую отрезок ОК в середине.
С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.
Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки.
Обратите внимание
Убедиться в том, что треугольник правильный можете с помощью транспортира, измерив углы.
Полезный совет
Равносторонний треугольник так же можно начертить на листе в клетку с помощью одной линейки. Вместо другой линейки используйте перпендикулярные линии.
Вместо другой линейки используйте перпендикулярные линии.
Источники:
- Классификация треугольников. Равносторонние треугольники
- Что такое треугольник
- построение правильного треугольника
Вписанным называется такой треугольник, все вершины которого находятся на окружности. Построить его можно, если знать хотя бы одну сторону и угол. Окружность называется описанной, и она будет единственной для данного треугольника.
Вам понадобится
- — окружность;
- — сторона и угол треугольника;
- — лист бумаги;
- — циркуль;
- — линейка;
- — транспортир;
- — калькулятор.
Инструкция
От точки А с помощью транспортира отложите заданный угол. Продолжите сторону угла до пересечения с окружностью и поставьте точку С. Соедините точки В и С. У вас получился треугольник АВС. Он может быть любого типа. Центр окружности у остроугольного треугольника него, у тупоугольного — вне, а у прямоугольного — на гипотенузе. Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.
Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.
Значительно чаще приходится иметь дело с обратным построением, когда задан треугольник и надо вокруг него описать окружность. Вычислите его радиус. Сделать это можно по нескольким формулам, в зависимости от того, что вам дано. Радиус можно найти, например, по стороне и синусу противолежащего угла. В этом случае он равен длине стороны, разделенной на удвоенный синус противолежащего угла. То есть R=a/2sinCAB. Можно его выразить и через произведение сторон, в этом случае R=abc/√(a+b+c)(a+b-c)(a+c-b)(b+c-a).
Определите центр окружности. Разделите все стороны пополам и проведите серединам перпендикуляры. Точка их пересечения и будет центром окружности. Начертите ее так, чтобы она пересекла все вершины углов.
Две короткие стороны прямоугольного треугольника, которые принято называть катетами, по определению должны быть перпендикулярны между собой. Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.
Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.
Вам понадобится
- Бумага, карандаш, линейка, транспортир, циркуль, угольник.
Как нарисовать шестиугольник в круге
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.
Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.
В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.
Способ вычерчивания шестиугольника циркулем, линейкой
Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.
Метод выглядит следующим образом:
Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- циркулем вычерчивается окружность — радиус является размером стороны;
- по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
- находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
- находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.
Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.
Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.
Способ вычерчивания шестиугольника без циркуля
Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.
Способ построения выглядит следующим образом:
Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
- на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
- операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
- разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
- уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
- строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
- контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком
Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.
Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.
Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.
В последнем случае удобнее несколько изменить технологию:
- после вычерчивания центрального отрезка по нему выравнивается рейсшина;
- инструмент откатывается вниз на произвольную величину;
- короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
- скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.
Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.
Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.
Как построить треугольник с помощью циркуля. Как построить треугольник с помощью циркуля Как построить треугольник помощью циркуля
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №34 с углубленным изучением отдельных предметов
МАН, физико-математическая секция
«Геометрические построения с помощью циркуля и линейки»
Выполнила: ученица 7 «А» класса
Батищева Виктория
Руководитель: Колтовская В.В.
Воронеж, 2013
3. Построение угла равного данному.
Проведем произвольную окружность с центром в вершине А данного угла (рис.3). Пусть В и С — точки пересечения окружности со сторонами угла. Радиусом АВ проведем окружность с центром в точке О-начальной точке данной полупрямой. Точку пересечения этой окружности с данной полупрямой обозначим С 1 . Опишем окружность с центром С 1 и Рис.3
радиусом ВС. Точка В 1 пересечения построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.
6. Построение перпендикулярных прямых.
Проводим окружность с произвольным радиусом r с центром в точке O рис.6. Окружность пересекает прямую в точках A и B. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей. Точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.
Искомая прямая проходит через точки С и О.
Рис.6
1. Задача Брахмагупты
Построить вписанный четырехугольник по четырем его сторонам. Одно из решений использует окружность Аполлония. Решим задачу Аполлония, используя аналогию между трехокружником и треугольником. Как мы находим окружность, вписанную в треугольник: строим точку пересечения биссектрис, опускаем из нее перпендикуляры на стороны треугольника, основания перпендикуляров (точки пересечения перпендикуляра со стороной, на которую он опущен) и дают нам три точки, лежащие на искомой окружности. Проводим окружность через эти три точки – решение готово. Точно также мы поступим с задачей Аполлония.
2. Задача Аполлония
Построить с помощью циркуля и линейки окружность, касающуюся трех данных окружностей. По легенде, задача сформулирована Аполлонием Пергским примерно в 220 г. до н. э. в книге «Касания», которая была потеряна, но была восстановлена в 1600 г. Франсуа Виетом, «галльским Аполлонием», как его называли современники.
Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
П
равильный (или равносторонний ) треугольник — это
правильный многоугольник
с тремя сторонами, первый из правильных многоугольников. Все
стороны
правильного
треугольника
равны между собой, а все
углы
равны 60°.
Чтобы построить равносторонний треугольник нужно разделить окружность на 3 равные части. Для этого необходимо провести дугу радиусом R этой окружности лишь из одного конца диаметра, получим первое и второе деление. Третье деление находится на противоположном конце диаметра. Соединив эти точки, получим равносторонний треугольник.
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения через деление окружности на 6 частей. Используем равенство сторон правильного шестиугольника радиусу описанной окружности. Из противоположных концов одного из диаметров окружности описываем дуги радиусом R. Точки пересечения этих дуг с заданной окружностью разделят её на 6 равных частей. Последовательно соединив найденные точки, получают правильный шестиугольник.
Построение правильного пятиугольника.
П
равильный пятиугольник может быть
построен с помощью циркуля и линейки, или вписыванием его в заданную
окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом
в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O . (Это зелёная окружность на схеме справа).
Выберите на окружности точку A , которая будет одной из вершин пятиугольника. Постройте прямую через O и A .
Постройте прямую перпендикулярно прямой OA , проходящую через точку O . Обозначьте одно её пересечение с окружностью, как точку B .
Постройте точку C посередине между O и B .
C через точку A . Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D .
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F .
Проведите окружность с центром в E через точку A G .
Проведите окружность с центром в F через точку A . Обозначьте её другое пересечение с первоначальной окружностью как точку H .
Постройте правильный пятиугольник AEGHF .
Следующие три задачи на построение были поставлены ещё в античности:
Трисекция угла — разбить произвольный угол на три равные части.
Иначе говоря, необходимо построить трисектрисы угла — лучи, делящие угол на три равные части. П. Л. Ванцель доказал в 1837 году, что задача разрешима только тогда, когда например, трисекция осуществима для углов α = 360°/n при условии, что целое число n не делится на 3. Тем не менее, в прессе время от времени публикуются (неверные) способы осуществления трисекции угла циркулем и линейкой.
Удвоение куба — классическая античная задача на построение циркулем и линейкой ребра куба, объём которого вдвое больше объёма заданного куба.
В современных обозначениях, задача сводится к решению уравнения . Всё сводится к проблеме построения отрезка длиной . П. Ванцель доказал в 1837 году, что эта задача не может быть решена с помощью циркуля и линейки.
Квадратура круга — задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу .
Как известно, с помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины π. Таким образом, неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа π, которая была доказана в 1882 году Линдеманом.
Другая известная неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис .
Причём эта задача остаётся неразрешимой даже при наличии трисектора.
Только в XIX веке было доказано, что все три задачи неразрешимы при использовании только циркуля и линейки. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.
Когда-то в построение правильных многоугольников вкладывали мистический смысл.
Так, пифагорейцы, последователи религиозно-философского учения, основанного Пифагором, и жившие в древней Греции (V I-I V вв. до н. э.), приняли в качестве знака своего союза звездчатый многоугольник, образованный диагоналями правильного пятиугольника.
Правила строгого геометрического построения некоторых правильных многоугольников изложены в книге «Начала» древнегреческого математика Евклида, жившего в III в. до н.э. Для выполнения этих построений Евклид предлагал пользоваться только линейкой и циркулем, который в то время был без шарнирного устройства соединения ножек (такое ограничение в инструментах было непреложным требованием античной математики).
Правильные многоугольники нашли широкое применение и в античной астрономии. Если Евклида построение этих фигур интересовало с точки зрения математики, то для древнегреческого астронома Клавдия Птолемея (около 90 — 160 г. н. э.) оно оказалось необходимым как вспомогательное средство при решении астрономических задач. Так, в 1-й книге «Альмагесты» вся десятая глава посвящена построению правильных пяти- и десятиугольников.
Однако помимо чисто научных трудов, построение правильных многоугольников было неотъемлемой частью книг для строителей, ремесленников, художников. Умение изображать эти фигуры издавна требовалось и в архитектуре, и в ювелирном деле, и в изобразительном искусстве.
В «Десяти книгах о зодчестве» римского архитектора Витрувия (жившего примерно в 63 -14 гг. до н. э.) говорится, что городские стены должны иметь в плане вид правильного многоугольника, а башни крепости «следует делать круглыми или многоугольными, ибо четырехугольник скорее разрушается осадными орудиями».
Планировка городов очень интересовала Витрувия, который считал, что нужно спланировать улицы так, чтобы вдоль них не дули основные ветры. Предполагалось, что таких ветров восемь и что они дуют в определенных направлениях.
В эпоху Возрождения построение правильных многоугольников, и в частности пятиугольника, представляло не простую математическую игру, а являлось необходимой предпосылкой для построения крепостей.
Правильный шестиугольник явился предметом специального исследования великого немецкого астронома и математика Иоганна Кеплера (1571-1630), о котором он рассказывает в своей книге «Новогодний подарок, или о шестиугольных снежинках». Рассуждал о причинах того, почему снежинки имеют шестиугольную форму, он отмечает, в частности, следующее: «…плоскость можно покрыть без зазоров лишь следующими фигурами: равносторонними треугольниками, квадратами и правильными шестиугольниками. Среди этих фигур правильный шестиугольник покрывает наибольшую площадь»
0дним из наиболее известных ученых, занимавшихся геометрическими построениями, был великий немецкий художник и математик Альбрехт Дюрер (1471 -1528), который посвятил им значительную часть своей книги «Руководства…». Он предложил правила построения правильных многоугольников с 3. 4, 5… 16-ю сторонами. Методы деления окружности, предложенные Дюрером, не универсальны, в каждом конкретном случае используется индивидуальный прием.
Дюрер применял методы построения правильных многоугольников в художественной практике, например, при создании разного рода орнаментов и узоров для паркета. Наброски таких узоров были сделаны им во время поездки в Нидерланды, где паркетные полы встречались во многих домах.
Дюрер составлял орнаменты из правильных многоугольников, которые соединены в кольца (кольца из шести равносторонних треугольников, четырех четырехугольников, трех или шести шестиугольников, четырнадцати семиугольников, четырех восьмиугольников).
Итак, геометрические построения — это способ решения задачи, при котором ответ получают графическим путем. Построения выполняют чертежными инструментами при максимальной точности и аккуратности работы, так как от этого зависит правильность решения.
Благодаря этой работе я познакомилась с историей возникновения циркуля, подробнее познакомилась с правилами выполнения геометрических построений, получила новые знания и применила их на практике.
Решение задач на построение циркулем и линейкой – полезное времяпровождение, позволяющее по-новому посмотреть на известные свойства геометрических фигур и их элементов.
В данной работе рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями с помощью циркуля и линейки. Рассмотрены основные задачи и даны их решения. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.
Таким образом, цель работы достигнута, поставленные задачи выполнены.
1. Какая фигура называется треугольником?
2. Какие виды треугольников вы знаете?
3. В чем заключается неравенство треугольника?
4. Известны стороны равнобедренного треугольника
6 см и 8 см. Чему равна третья сторона треугольника?
5. Существуют ли треугольники со сторонами
10 см; 15 см; 30 см?
6. Существуют ли треугольники со сторонами
11 см; 5 см; 6 см?
элементам сводится к решению трех
основных задач
1 задача — построение треугольника по двум
сторонам и углу между ними.
2 задача — построение треугольника по двум
углам и стороне между ними.
3 задача -построение треугольника по трем
сторонам.Задача 1
Построение треугольника по двум сторонам и углу
между нимиДано: отрезки
a
а
b
угол hp
b
h
p
Построить:
ABC по
двум сторонам и углу
между нимиАлгоритм построения
b
1. Проведем прямую d.
a
2. Отложим на ней с помощью
циркуля отрезок АВ, равный
M
отрезку a.
h
3. Построим угол ВАМ, равный
данному углу hp.
C
4. На луче АМ отложим отрезок
p
АС, равный отрезку b.
5. Проведём отрезок BC.
6. Построенный треугольник
АВС – искомый.
А
В
dЗадача 2
Построение треугольника по стороне и двум
прилежащим к ней угламДано: отрезок
a
h
p
m
n
а
угол hp
угол mn,
Построить:
ABC по
двум углам и сторонеАлгоритм построения
1. Проведем прямую d.
2. Отложим на ней с помощью
циркуля отрезок АВ, равный
отрезку a.
3. Построим угол ВАМ, равный
данному углу hp.
4. Построим угол АВК, равный
данному углу mn.
5. Точку пересечения
лучей АМ и ВК обозначим С
6. Построенный треугольник
d
АВС – искомый.
m
n
p
М
K
С
А
a
В
10.
Задача 3Построение треугольника по трем сторонам
11.
Дано: отрезок аотрезок b
отрезок c
a
b
с
Построить:
ABC по
трем сторонам
12.
Алгоритм построения1. Проведем прямую а.
a
2. Отложим на ней с помощью
циркуля отрезок АВ, равный
отрезку а.
3. Построим окружность с
центром А и радиусом равным b.
4. Построим окружность с
центром В и радиусом равным c.
5. Одну из точек пересечения
этих окружностей обозначим
А
точкой С.
6. Проведём отрезки АС и ВС.
7. Построенный треугольник
АВС – искомый.
b
с
С
а
В
13.
Всегда ли, данная задачабудет иметь решение?
Задача 3 не всегда имеет
решение.
Если какой-нибудь из
отрезков больше или равен
сумме двух других отрезков,
то треугольник построить
будет не возможно.
b
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
- Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Помогите! Внучке задали. С помощью циркуля построить правильный треугольник. и получил лучший ответ
Ответ от КИНОголик[гуру]
Сначала постройте отрезок длиной равной длине будущего треугольника.
Затем растворите циркуль на длину этого отрезка и, поставив конец циркуля в начало отрезка, проведите окружность.
Поставьте циркуль в другой конец отрезка и проведите еще одну окружность.
Окружности пересекутся в двух точках — над и под отрезком. Соединив концы отрезка с одной из этих точек, вы получите правильный (равносторонний треугольник).
Ответ от Гриша Колосов [новичек]
спс
Ответ от Александр Жидайкин [новичек]
Окружность разделить на 4 равных части. В самую нижнюю точку поставить ножку циркуля и провести вторую окружность, этого же радиуса. Получили две точки пересечения-это две точки треугольника. Третья точка находится в самой верхней точки первой окружности. Соединяем, получаем)
рисунок 61 в помощь
Ответ от Дед07 [гуру]
Начертите окружность. На окружности обозначьте точку (пусть А) . От этой точки по окружности в обе стороны отмерьте по 2 радиуса. Соедините полученные 3 точки
Ответ от *АпЕлЬсИнКа* [гуру]
ru.wikibooks.org/wiki/…/Построение_правильного_треугольника
Ответ от Елена яковлева [гуру]
Начертите окружность и тем же радиусом разделите её на 6 частей (поставьте 6 точек), затем соедините три точки (через одну) прямыми.
Ответ от Антип [гуру]
1) На прямой циркулем отметить отрезок произвольной длины
2) из одного конца отрезка циркулем, открытым на длину отмеченного отрезка, нарисовать дугу (достаточно длинную)
3) из другого конца отрезка сделать то же самое
4) дуги пересекутся
5) точку пересечения соединить с концами отрезка
6) вот и получился равносторонний треугольник — правильный
Ответ от Вега [гуру]
начертили окружность, потом ставите иглу на окружность и делаете две засечки на линиях, потом переставляете циркуль так, чтобы на засечке поставить карандаш, а иглу перенести дальше и сделать следующую засечку…вот и соедините все три засечки… получится правильный треугольник..
Ответ от Ђатьяна Егорова [гуру]
На прямой откладываете отрезок определенным раствором циркуля и этим же раствором с обеих концов проводите дуги. Эти дуги пересекутся. Это третья вершина вашего треугольника.
Ответ от 3 ответа [гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Помогите! Внучке задали. С помощью циркуля построить правильный треугольник.
Вписанный и описанный треугольник — материалы для подготовки к ЕГЭ по Математике
Вписанный треугольник — треугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг треугольника.
Очевидно, расстояние от центра описанной окружности до каждой из вершин треугольника одинаково и равно радиусу этой окружности.
Вокруг любого треугольника можно описать окружность, причем только одну.
Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.
В любой треугольник можно вписать окружность, причем только одну.
Попробуйте сами описать окружность вокруг треугольника и вписать окружность в треугольник.
Как вы думаете, почему центр вписанной окружности — это точка пересечения биссектрис треугольника, а центр описанной окружности — точка пересечения серединных перпендикуляров к его сторонам?
В задачах ЕГЭ чаще всего встречаются вписанные и описанные правильные треугольники.
Есть и другие задачи. Для их решения вам понадобятся еще две формулы площади треугольника, а также теорема синусов.
Вот еще две формулы для площади.
Площадь треугольника равна половине произведения его периметра на радиус вписанной окружности.
,
где — полупериметр,
— радиус окружности, вписанной в треугольник.
Есть и еще одна формула, применяемая в основном в задачах части :
где — стороны треугольника, — радиус описанной окружности.
Для любого треугольника верна теорема синусов:
Ты нашел то, что искал? Поделись с друзьями!
. Радиус окружности, вписанной в равнобедренный прямоугольный треугольник, равен . Найдите гипотенузу c этого треугольника. В ответе укажите .
Треугольник прямоугольный и равнобедренный. Значит, его катеты одинаковы. Пусть каждый катет равен . Тогда гипотенуза равна .
Запишем площадь треугольника АВС двумя способами:
Приравняв эти выражения, получим, что . Поскольку , получаем, что . Тогда .
В ответ запишем .
Ответ: .
. Сторона АС треугольника АВС с тупым углом В равна радиусу описанной около него окружности. Найдите угол В. Ответ дайте в градусах.
По теореме синусов,
Получаем, что . Угол — тупой. Значит, он равен .
Ответ: .
. Боковые стороны равнобедренного треугольника равны , основание равно . Найдите радиус описанной окружности этого треугольника.
Углы треугольника не даны. Что ж, выразим его площадь двумя разными способами.
, где — высота треугольника. Ее найти несложно — ведь в равнобедренном треугольнике высота является также и медианой, то есть делит сторону пополам. По теореме Пифагора найдем . Тогда .
Задачи на вписанные и описанные треугольники особенно необходимы тем, кто нацелен на решения задания .
Как нарисовать треугольник на листе чтобы вырезать. Как нарисовать несуществующий объемный треугольник поэтапно. Построение остроугольного треугольника
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии — это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
- Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы — необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта — расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект — должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу — это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
- Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Сегодня мы расскажем вам, как легко прослыть художником среди своих друзей или показать девушке, какой ты весь разносторонний (о, они это любят!). Итак начнем!
Нам понадобится: 50 грамм для храбрости, 2 карандаша (один жесткий, другой мягкий), лист бумаги, линейка и ластик. Да начнется магия!
Шаг 1.
Рисуем обычный треугольник – он не должен являть собой венец геометрической мысли: просто соедини три линии.
Шаг 2.
Теперь нарисуй внутри линии, прямо как у нас. Старайся сделаить их одной ширины, ты ж не рукожоп, как мы!
Шаг 3.
Нарисовал? Молодец! Теперь нарисуй еще, как мы показали. Мы знаем, ты устал, но скоро все закончится.
Шаг 4.
Спили вершины треугольника как на рисунке.
Шаг 5.
Теперь обведи все линии, которые выделили мы, жирным карандашом, пером или гелевой ручкой. Или маркером. Или фломастером. Может надо бутерброд забацать?
Шаг 6.
Сотри все ненужное. Мы близко к цели, видишь?
Шаг 7.
Тут мы обратились к богам Олимпа и они нарисовали нам тени. Ты рисуй сам.
Шаг 8.
Теперь можно вырезать наше творение лезвием или ножницами и ломать хрупкие разумы своих друзей. Этот треугольник входит в число фигур, которые геометрически не имеют право на существование или по по-другому “несуществующие фигуры”.
Надеемся, тебе понравилось, ибо мы старались и крали этот урок рисования несуществующего треугольника поэтапно. И теперь тебе лучше нарисовать героев
- карандаш,
- стерка,
- лист бумаги,
- пошаговая интсрукция.
- сперва изобразить треугольник,
- затем все его грани, начиная с внешней,
- заштриховать участки свето-тени, чтобы придать объем фигуре,
- при необходимости разукрасить объект.
Нарисуем треугольник 3D с оптической иллюзией поэтапно.
Сначала рисуем обыкновенный равносторонний треугольник карандашом. Внутри него, параллельно каждой из сторон, проводим по линии на равном расстоянии так, что внутри треугольника получается еще один треугольник.
Вновь проводим параллельные линии, отступив на то же расстояние и рисуя еще один меньший треугольник внутри первых двух.
Жирно проводим контур по периметру сторон большого треугольника, обводя его стороны, но срезая острые углы.
Проводим еще один контур из двух прямых, повторяющих одну сторону среднего и одну сторону меньшего треугольников внутри большого, как показано на рисунке.
Проводим еще по контуру, — две прямые, повторяя стороны треугольников, как на рисунке.
И еще раз делаем те же действия, с другими сторонами, — обводим жирным контуром две прямые, как на рисунке.
Лишние линии убираем. Вот получился 3D треугольник, пока не закрашенный.
Заштриховываем стороны треугольника, придавая изображению объемность. Рисунок готов, треугольник 3D иллюзия .
Посмотрим видео, как рисовать оптическую иллюзию треугольник 3D.
Нарисовать треугольную иллюзию несложно, особенно если есть пошаговая инструкция. Понадобится карандаш, бумага и желательно линейка, с ней будет аккуратнее рисунок. По шагам повторить все действия, а потом затенить с помощью растушевки нужные места.
Как нарисовать треугольник … Да, при этом не простой, а очень сложный с множеством треугольников внутри. Чтобы все его грани проглядывались, а на бумаге он выглядел реалистичным и четким.
Для этого нам потребуется:
Процесс рисования:
Получается необычайная фигура с множеством завихрений. Смотрится немного завораживающе, так как разум пытается продлить все линии и уловить суть.
Видео-инструкция, как нарисовать треугольник на бумаге:
Треугольник Пенроуза или невозможные фигуры. Был придуман в 1953 году художником Оскаром Реутерсвардом. Первый треугольник был сделан из кубиков.
Уникальность этого объекта в том, что посмотрев на прямые палки под определнным углом можно четко увидеть треугольник. Как например вот на этом памятнике.
Как построить (нарисовать) равносторонний треугольник
Содержание
- Построить равносторонний треугольник
- Как нарисовать равносторонний треугольник с помощью циркуля
- Как построить равносторонний треугольник, вписанный в круг
- Постройте равносторонний треугольник, вписанный в круг Доказательство
- Как нарисовать равносторонний треугольник
- Нарисуйте доказательство равностороннего треугольника
Построить равносторонний треугольник
Равносторонние треугольники легко построить с помощью циркуля, линейки и карандаша, потому что внутренние углы 60 ° можно найти, используя только радиус круга вокруг треугольника (описанный круг).
Предположим, вам дана длина одной стороны требуемого равностороннего треугольника. Вы должны построить две одинаковые стороны, которые каким-то образом образуют три внутренних угла в 60 °.
Вот сегмент CE:
[вставить чертеж линейного сегмента CE]
- Поместите иглу циркуля для рисования в точку C, затем отрегулируйте рычаг карандаша так, чтобы он касался точки E.
- Поверните дугу вверх, образуя легкую строительную линию.
- Не регулируя компас, переместите стрелку в точку E.
- Поверните дугу вверх от точки C, образуя еще одну легкую строительную линию. [вставить чертеж, показывающий дуги поворота компаса для этих точек]
- В месте пересечения двух дуг находится точка третьей вершины равностороннего треугольника. Назовите это точкой A. Используйте линейку, чтобы соединить точки A и C, точки A и E. У вас есть равносторонний треугольник ACE!
Как нарисовать равносторонний треугольник с помощью компаса
Точки C и E — центры конгруэнтных окружностей с радиусами, равными CE.Длины AC и CE являются радиусами окружности C. Длины AE и CE также являются радиусами окружности E. По переходному свойству:
Три совпадающие стороны означают, что треугольник должен быть равносторонним.
Как построить равносторонний треугольник, вписанный в круг
Предположим, вам дан круг, а не сторона. Предположим, вас попросили построить внутри этого круга равносторонний треугольник:
[вставить чертеж круга S]
Вы знаете только центральную точку, точку S, но из нее вы можете скопировать радиус (расстояние от центра, точки S, до самой окружности).
- Настройте циркуль для рисования и установите радиус.
- Сделайте отметку на круге в любом месте. Установите игольную консоль в эту точку.
- Не меняя циркуля, поверните две небольшие дуги выше и ниже точки окружности, чтобы дуги пересекали окружность.
- Переместите стрелку циркуля для рисования на одну из этих дуг.
- Снова поверните циркуль, чтобы образовать небольшую дугу на окружности.
- Повторите это еще два раза, чтобы создать шесть точек на окружности (исходная точка плюс шесть маленьких дуг, пересекающих ее).
- Используйте линейку, чтобы соединить все остальные точки на окружности. То есть нарисуйте линейные сегменты, скажем, от вашей первой точки на окружности до третьей точки и еще один линейный сегмент от третьей точки до пятой точки. Еще одна линия, от пятой точки обратно к исходной точке, и вот она. Вы вписали в круг равносторонний треугольник!
[вставьте рисунок, показывающий это, или анимируйте конструкцию трех сторон]
Постройте равносторонний треугольник, вписанный в круг Доказательство
Представьте, что этот равносторонний треугольник состоит из трех меньших равнобедренных треугольников, имеющих точку S как общую вершину.Это означает, что каждый из трех треугольников имеет центральный угол (в точке S) 120 °, полученный путем деления полных 360 ° круга на 3 (количество центральных углов).
Каждый из этих меньших равнобедренных треугольников имеет две вершины на окружности, и каждый имеет одинаковые стороны с другими треугольниками. Таким образом, две из трех сторон треугольников совпадают.
Если две стороны равнобедренного треугольника совпадают, то третья сторона также определяется теоремой стороны-угла-стороны.
Как нарисовать равносторонний треугольник
Этот метод позволяет вам контролировать размер вашего равностороннего треугольника, потому что вы строите его с нуля.
- Настройте циркуль для рисования, чтобы нарисовать круг; назовем его Circle E.
- Используйте линейку, чтобы установить диаметр (отрезок прямой, проходящий через центральную точку E с конечными точками на самой окружности). Обозначьте конечные точки Точки B и R. [вставьте рисунок или анимацию, показывающую эти шаги]
- Не мешая компасу, опустите стрелку в точку R и сделайте еще один полный круг. Там, где новый круг пересекает старый в двух точках выше и ниже диаметра BR, обозначьте эти точки A и S.
- Соедините точку B с точкой A, точку A с точкой S и точку A с точкой B. МЕДВЕДЬ замечает, что вы построили равносторонний треугольник!
Нарисуйте доказательство равностороннего треугольника
Вы можете доказать, что треугольник равносторонний, используя свои знания о том, что любой угол, вписанный в полукруг, является прямым углом, что дает вам прямые углы ∠BAR и ∠BSR, что создает два конгруэнтных прямоугольных треугольника △ BAR и △ BSR, имеющих общую гипотенузу BR .
Таким образом, AB ≅ BS (соответствующие стороны равнобедренных треугольников), что означает, что △ BAS равнобедренный.Это делает BAS и ∠BSA конгруэнтными (углы основания равнобедренного треугольника совпадают). Мы знаем, что ∠ABS составляет 60 °, оставляя два оставшихся угла в сумме равными 120 °, так что каждый из них составляет 60 °. Все три внутренних угла △ BAS равны, что делает его равносторонним треугольником.
Следующий урок:
Как построить биссектрису угла
Иллюстративная математика
Задача
Предположим, нам дан круг радиуса $ r $. Цель этой задачи — построить равносторонний треугольник, три вершины которого лежат на окружности.Предположим, что $ \ overline {AB} $ — диаметр окружности. Нарисуйте круг с центром $ A $ и радиусом $ r $ и обозначьте две точки пересечения кругов $ P $ и $ Q $, как показано ниже:
- Докажите, что $ m (\ angle ABP) = 30 $ и $ m (\ angle ABQ) = 30 $.
- Покажи это $ \ треугольник PBQ $ — это равносторонний треугольник, вписанный в данную окружность.
Комментарий IM
Построение равностороннего треугольника, вписанного в круг, требует творческого подхода и хорошего знания геометрии и / или тригонометрии.Подход, принятый в данном решении, использует тот факт, что $ \ sin {30} = \ frac {1} {2} $. Следовательно, чтобы построить угол в 30 градусов, достаточно уметь построить прямоугольный треугольник, гипотенуза которого в два раза больше длины катета. Студентам необходимо знать, что $ \ angle APB $ правильный, поскольку он вписан в круг с одним лучом по диаметру круга. Отношение $ (2: 1) $ для гипотенузы к катету определяется с использованием диаметра окружности для гипотенузы и радиуса конгруэнтной окружности для катета.
Эта задача реализует многие важные идеи из геометрии, включая тригонометрические отношения, важные факты о треугольниках и отражения, если учащиеся предпочитают рассматривать $ \ треугольник ABQ $ как отражение $ \ треугольника ABP $ относительно $ \ overleftrightarrow {AB} $. В результате рекомендуется выполнять эту задачу относительно поздно в учебной программе по геометрии. Он также может быть дан в открытой форме, то есть с просьбой создать вписанный равносторонний треугольник внутри данного круга без предложения подхода или изображения.Альтернативный метод начинается с того, что если $ O $ — центр исходной окружности, то $ \ треугольник AOP $ равносторонний (все три стороны являются радиусами конгруэнтных окружностей). Мы можем продолжать рисовать круги с центрами $ P $ и $ Q $, и каждый раз мы получаем еще один равносторонний треугольник. Конечным результатом будет правильный шестиугольник, вписанный в круг: соединение всех остальных вершин этого шестиугольника дает равносторонний треугольник, вписанный в круг. Вариант этого аргумента, сфокусированный только на шестиугольнике, представлен в http: // www.illustrativemat Mathematics.org/illustrations/786.
Работа над этой задачей может развить навыки, связанные с MP1, понимать проблемы и настойчиво их решать, а также MP3, создавать жизнеспособные аргументы и критиковать рассуждения других. В первом случае аргумент сложен и требует объединения нескольких абстрактных аргументов, которые необходимо связать с построением желаемого равностороннего треугольника. Из-за своей сложности он идеально подходит для групповой работы, чтобы учащиеся могли объединить свои сильные стороны и навыки.
Планшет Геометра
ОПРЕДЕЛЕНИЯ:
- Key означает Key Curriculum Press, Inc., 1150 65th Street, Emeryville, CA 94608, США. Программное обеспечение
- означает компьютерную программу Geometer Sketchpad версии 5, полученную вами из любого источника.
- Документация означает печатные или электронные справочные материалы и другие печатные или электронные материалы, сопровождающие Программное обеспечение.
- Продукт означает Программное обеспечение и Документацию.
- Использование означает установку, использование, доступ, отображение, запуск или иное взаимодействие с Продуктом. Лицензия
- означает лицензию на одного пользователя, лицензию для учебного заведения / учебного заведения, студенческую лицензию, студенческую лицензию на 1 год или любую другую лицензию, которая время от времени определяется ключом.
- Лицензиат означает физическое или юридическое лицо, получившее Лицензию на законных основаниях и имеющее законную возможность Использовать Продукт в соответствии с условиями этой Лицензии, или любое физическое лицо, которое использует Продукт в рамках Лицензии с ограниченным предварительным просмотром.
- Название лицензии означает имя, данное Лицензии Лицензиатом или Ключом с целью идентификации Лицензии, обычно это название учебного заведения или учреждения или имя отдельного Лицензиата, если Лицензиат не выберет другое идентифицирующее имя.
- Администратор лицензии означает лицо, назначенное Лицензиатом для администрирования Лицензии от имени Лицензиата. Код авторизации
- означает уникальный код, предоставленный Лицензиату вместе с Лицензией и позволяющий использовать Программное обеспечение в соответствии с условиями Лицензии.
- Preview Mode означает ограниченное и ограниченное по времени состояние Программного обеспечения до регистрации Программного обеспечения с помощью кода авторизации, необходимого для использования по лицензии.
- Лицензия на ограниченный просмотр означает лицензию на использование Программного обеспечения в режиме предварительного просмотра.
- Подтверждение заказа или Подтверждение лицензии означает распечатанную или электронную копию счета-фактуры или записи подтверждения счета, полученную Лицензиатом от Key или от одного из авторизованных образовательных дилеров или дистрибьюторов Key, или любое другое печатное или электронное подтверждение Лицензии, полученное Лицензиатом от Ключ или отображается Программным обеспечением при регистрации.
- Срок действия лицензии означает период времени, связанный с Лицензией, если таковая имеется.
ПРЕДОСТАВЛЕНИЕ ЛИЦЕНЗИИ
Ключпредоставляет Лицензиату ограниченную неисключительную лицензию на Использование Продукта на одном или нескольких компьютерах Лицензиата в соответствии с условиями, изложенными ниже. Если будет установлено, что Лицензиат нарушил эти условия использования, Key может аннулировать Лицензию Лицензиата и расторгнуть настоящее Соглашение. Все остальные права прямо принадлежат Key.
- Однопользовательские лицензии: Лицензиат с однопользовательской лицензией может использовать Продукт максимум на трех персональных компьютерах при условии, что одновременно используется только одна копия Продукта.
- Лицензии для учебного заведения / учреждения: Лицензиат с лицензией для учебного заведения / учреждения может использовать Программное обеспечение или разрешить Использование Программного обеспечения на количестве физических или виртуальных компьютеров, как указано в Подтверждении заказа или Подтверждении лицензии. Использование инструктором на персональном или домашнем компьютере считается одним из случаев использования согласно школьной / институциональной лицензии.
- Студенческие лицензии: Студенческий лицензиат со студенческой лицензией может использовать Продукт максимум на трех личных или семейных компьютерах при условии, что одновременно используется только одна копия Продукта. Учащийся, получивший Продукт и / или код авторизации от школы или учебного заведения для использования Программного обеспечения на личном или семейном компьютере, считается Лицензиатом и должен соблюдать условия Студенческой лицензии. Пользователь Студенческой лицензии должен быть студентом образовательного учреждения на момент покупки или получения лицензии.
Срок действия лицензии: Если Лицензия имеет Срок действия или если Подтверждение заказа или Подтверждение лицензии указывает Срок действия лицензии, Лицензиат может использовать Программное обеспечение в течение указанного Срока действия лицензии, начинающегося в день выдачи лицензии (дата, на которую Код авторизации был сгенерирован). Использование Программного обеспечения вне Срока действия лицензии или вмешательство в программное обеспечение с целью его использования вне Срока действия лицензии является нарушением настоящего Соглашения.
ПРЕДОСТАВЛЕНИЕ ОГРАНИЧЕННОЙ ЛИЦЕНЗИИ НА ПРЕДВАРИТЕЛЬНЫЙ ПРОСМОТР: Key предоставляет каждому человеку, устанавливающему Продукт на компьютер, ограниченную неисключительную лицензию на Использование Продукта в режиме предварительного просмотра на компьютере, на котором он установлен.
ПРОВЕРКА ЛИЦЕНЗИИ: Лицензиат должен зарегистрировать Продукт на компьютере с действующим именем лицензии и кодом авторизации, чтобы разблокировать полный набор функций Продукта. При запуске Продукт может связываться через Интернет с сервером лицензий, поддерживаемым Key, с целью проверки лицензии. Это сообщение содержит название лицензии и код авторизации, связанные с лицензией, а также соответствующую информацию о компьютерах, на которых зарегистрирована и используется лицензия.Чтобы помочь администраторам лицензий в устранении проблем с регистрацией, если они возникнут, в случае лицензий для учебных заведений / учебных заведений и специальных лицензий обмен данными включает адрес управления доступом к среде (MAC) каждого компьютера, другую информацию, относящуюся к компьютеру, и адрес Интернет-протокола (IP). Чтобы защитить конфиденциальность лицензиатов с однопользовательской лицензией или студенческой лицензией, вся информация, идентифицирующая конкретный компьютер, на котором используется Sketchpad, шифруется таким образом, чтобы создать уникальную подпись, обеспечивая при этом конфиденциальность.Key будет использовать эту информацию только для проверки действительности Лицензии, помощи Лицензиатам в решении технических проблем и для улучшения Продукта. Эта информация не будет передана сторонам, кроме назначенного Лицензиатом Администратора лицензий и лиц, отвечающих за обслуживание Продукта, а также проверку и администрирование Лицензий на продукт.
ОГРАНИЧЕНИЯ НА ИСПОЛЬЗОВАНИЕ: Продукт лицензируется как единый продукт, и его составные части не могут быть разделены для использования на большем количестве компьютеров, чем указано в Лицензии и / или как указано в Подтверждении заказа или Подтверждении лицензии.Права, предоставляемые по настоящему Соглашению, являются личными для Лицензиата. Ни Продукт, ни права, предоставленные по настоящему Соглашению, не могут быть перепроданы, сублицензированы, назначены, сданы в аренду, одолжены или сданы в аренду, за вознаграждение или иным образом, кроме как предварительно утвержденными Ключевыми торговыми посредниками или в соответствии с условиями настоящего Соглашения. Название лицензии и код авторизации, связанные с лицензией, не могут публиковаться для публичного доступа и использования, включая, помимо прочего, веб-сайты в Интернете. Продукт не должен использоваться в рамках соглашения о таймшеринге или сервисном бюро.Продукт нельзя модифицировать, реконструировать, декомпилировать или разбирать. Обозначения прав собственности, содержащиеся на Продукте и в нем, нельзя удалять или скрывать.
ПЕРЕДАЧА ИСПОЛЬЗОВАНИЯ ШКОЛАМИ: школы или образовательные учреждения, которые приобретают либо лицензию школы / учреждения, либо студенческую лицензию на домашнее использование, могут передать или продать сублицензию на такой Продукт для использования преподавателем или студентом, зарегистрированным в школе или образовательное учреждение. Для целей данной Лицензии такой преподаватель или студент считается Лицензиатом при соблюдении всех условий использования Продукта в качестве первоначального Лицензиата.
ПРЕДСТАВЛЕНИЯ ЛИЦЕНЗИАТА: Лицензиат заявляет, что он получил все необходимое согласие и полномочия для импорта и использования Продукта в юрисдикции, в которой Лицензиат намеревается использовать Продукт.
ПРАВА НА ИНТЕЛЛЕКТУАЛЬНУЮ СОБСТВЕННОСТЬ: Ключевые и / или правообладатели, указанные в Продукте, являются владельцами и сохраняют за собой право собственности на все права собственности и интеллектуальной собственности на Продукт, включая авторские права, коммерческую тайну, товарные знаки и защищенные ноу-хау. законами США и Канады об авторском праве, а также положениями международных договоров.Копирование Продукта, кроме случаев, явно указанных в данном документе, представляет собой нарушение прав правообладателей на интеллектуальную собственность. Лицензиат признает вышесказанное и соглашается с тем, что он не имеет никаких прав, титулов или интересов в отношении Продукта, за исключением случаев, специально указанных в настоящем документе, и что Лицензиат не имеет прав на какие-либо товарные знаки, определенные как принадлежащие правообладателям.
ПОДДЕРЖКА: Key может предоставлять Лицензиату услуги поддержки, связанные с Продуктом («Услуги поддержки»).Использование Служб поддержки регулируется политиками и программами Key, описанными в справочном руководстве по программному обеспечению пользователя, в онлайн-документации и / или в других материалах, предоставленных Key. Любое дополнительное программное обеспечение, предоставленное Лицензиату в рамках Услуг поддержки, считается частью Продукта и регулируется положениями настоящего Соглашения. В случае, если Лицензиат предоставляет Key техническую информацию в связи с предоставлением Услуг поддержки, Key может использовать эту информацию в своих деловых целях, включая поддержку и разработку продукта.
ПРЕКРАЩЕНИЕ: Без ущерба для каких-либо других прав, Key может прекратить действие настоящего Соглашения, если Лицензиат не соблюдает условия настоящего Соглашения. В таком случае Лицензиат соглашается удалить все копии Продукта со всех компьютеров, на которых они были установлены, и уничтожить все такие копии.
ОГРАНИЧЕННАЯ ГАРАНТИЯ: ПРОДУКТ ПРЕДОСТАВЛЯЕТСЯ «КАК ЕСТЬ», БЕЗ КАКИХ-ЛИБО ГАРАНТИЙ, ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ, ВКЛЮЧАЯ, НЕ ОГРАНИЧЕННАЯ, ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ ТОВАРНОЙ ЦЕННОСТИ, ПРИГОДНОСТИ ДЛЯ КОНКРЕТНОЙ ЦЕЛИ, НАРУШЕНИЯ, НАЗВАНИЯ И ПРАВИЛА ПРОДУКТ, И ПРЕДОСТАВЛЕНИЕ ИЛИ ОТСУТСТВИЕ УСЛУГ ПОДДЕРЖКИ.В НЕКОТОРЫХ ЮРИСДИКЦИЯХ НЕ ДОПУСКАЕТСЯ ИСКЛЮЧЕНИЕ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ, ПОЭТОМУ ВЫШЕУКАЗАННОЕ ИСКЛЮЧЕНИЕ МОЖЕТ НЕ ОТНОСИТЬСЯ К ВАМ.
ОГРАНИЧЕНИЕ ОТВЕТСТВЕННОСТИ: В СЛУЧАЕ ИСКЛЮЧЕНИЯ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ НЕ ПРИМЕНЯЕТСЯ, И В СЛУЧАЕ НАРУШЕНИЯ ТАКИХ ГАРАНТИЙ КЛЮЧЕВЫЕ И ЕГО ДИЛЕРЫ И ДИЛЛИБЬЮТОРЫ БУДУТ ПОЛНОСТЬЮ ОТВЕТСТВЕННОСТЬЮ И ИСКЛЮЧИТЕЛЬНЫМ УСЛУГОМ ЗАЩИТЫ A) ВОЗВРАТ УПЛАЧЕННОЙ ЦЕНЫ, ЕСЛИ ЕСТЬ ЕСТЬ; ИЛИ (B) РЕМОНТ ИЛИ ЗАМЕНА ИЗДЕЛИЯ, ВОЗВРАЩЕННОГО НА КЛЮЧ С ЧЕТОЙ ПОКУПКИ.В МАКСИМАЛЬНОЙ СТЕПЕНИ, РАЗРЕШЕННОЙ ДЕЙСТВУЮЩИМ ЗАКОНОДАТЕЛЬСТВОМ, НИ ПРИ КАКИХ ОБСТОЯТЕЛЬСТВАХ KEY ИЛИ ЕГО ПОСТАВЩИКИ НЕ НЕСЕТ ОТВЕТСТВЕННОСТИ ЗА ЛЮБЫЕ ОСОБЫЕ, СЛУЧАЙНЫЕ, КОСВЕННЫЕ ИЛИ КОСВЕННЫЕ УБЫТКИ (ВКЛЮЧАЯ БЕЗ ОГРАНИЧЕНИЙ, УБЫТКИ ОТ ПОТЕРИ ДЕЛОВОЙ ИНФОРМАЦИИ, ПОТЕРЯ ДЕЛОВОЙ ИНФОРМАЦИИ ИЛИ ЛЮБЫЕ ДРУГИЕ УБЫТКИ), ВЫЗВАННЫЕ ИСПОЛЬЗОВАНИЕМ ИЛИ НЕВОЗМОЖНОСТЬЮ ИСПОЛЬЗОВАТЬ ПРОДУКТ, ИЛИ ПРЕДОСТАВЛЕНИЕМ ИЛИ НЕОБХОДИМОМ ПРЕДОСТАВЛЕНИЯ УСЛУГ ПОДДЕРЖКИ, ДАЖЕ ЕСЛИ КЛЮЧ БЫЛ ПРЕДЪЯВЛЯЕТСЯ О ВОЗМОЖНОСТИ ТАКИХ УБЫТКОВ. Поскольку НЕКОТОРЫЕ ЮРИСДИКЦИИ НЕ ДОПУСКАЮТ ИСКЛЮЧЕНИЯ ИЛИ ОГРАНИЧЕНИЯ ОТВЕТСТВЕННОСТИ, ВЫШЕУКАЗАННОЕ ОГРАНИЧЕНИЕ МОЖЕТ НЕ ПРИМЕНЯТЬСЯ В ОПРЕДЕЛЕННЫХ ЮРИСДИКЦИЯХ.
ПОЛНОЕ СОГЛАШЕНИЕ: Лицензиат соглашается с тем, что настоящее Соглашение является полным и единственным заявлением соглашения между Лицензиатом, Key и дистрибьюторами и дилерами Key и заменяет все заявления, сделанные в отношении Продукта, и все другие соглашения (письменные или устные). ), относящиеся к предмету настоящего Соглашения.
ЧАСТИЧНАЯ НЕЗАКОННОСТЬ: Если какие-либо положения настоящего Соглашения будут истолкованы как незаконные или недействительные, это не повлияет на законность или действительность любого другого его положения, а незаконные или недействительные положения будут считаться перечеркнутыми и удаленными из него в той же степени. и действуют, как если бы они никогда не включались в настоящий документ, но все остальные положения остаются в полной силе.
ПРИМЕНИМОЕ ЗАКОНОДАТЕЛЬСТВО: Права и обязанности сторон по настоящему Соглашению не регулируются Конвенцией Организации Объединенных Наций о договорах международной купли-продажи товаров. Вместо этого, если это прямо не запрещено местным законодательством, права и обязанности сторон по настоящему Соглашению регулируются штатом Калифорния и применимыми законами Соединенных Штатов.
Key Curriculum Press 1150 65th Street Emeryville, CA 94608 Телефон: 510-595-7000 Факс: 510-595-7040 Интернет: www.keypress.com
Построение равностороннего треугольника. Евклид I. 1.
Содержание | Введение | Дом
П л а н е г о м е т р и я
Приключение в области языка и логики
на основе
Книга I. Предложение 1
Предложение 1
Формальные части предложения
Молчаливые предположения
ЛОГИЧЕСКАЯ ТЕОРИЯ ПЛОСКОЙ ГЕОМЕТРИИ состоит из первых принципов, за которыми следуют предложения, которые бывают двух видов: теоремы и проблемы.Теорема предлагает утверждение для доказательства. Проблема предлагает задачу, которую нужно выполнить.
Наше первое предложение — это проблема: на данной прямой AB нас попросят нарисовать равносторонний треугольник. Это не сложно.
Поместите конец циркуля в точку A; отрегулируйте циркуль так, чтобы карандаш оказался в точке B; и нарисуйте дугу. Затем с той же настройкой компаса поместите точку в точке B и нарисуйте дугу, позволяя ей пересекать первую точку в точке C.Проведя прямые CA, CB, треугольник будет равноугольным.
В формальном доказательстве ниже мы должны сделать три вещи:
1. Надо описать конструкцию.
| 2. | Затем мы должны доказать , что построенная нами фигура на самом деле является равносторонним треугольником; то есть, что он удовлетворяет определению единицы. |
| 3. | Мы должны санкционировать каждое утверждение конструкции и доказательства, цитируя первый принцип. Продолжая, мы подкрепим эти утверждения утверждениями, которые мы уже доказали. Это то, что в математике называется строгостью. |
Это и все формальные доказательства являются упражнениями в риторике, то есть искусстве использования языка как средства убеждения.
Чтобы свести к минимуму прокрутку, повторим цифры.
| 1. | По заданной прямой построить равносторонний треугольник. | |
| 2. | Пусть AB — заданная прямая; | |||
| 3. | нам требуется построить равносторонний треугольник на AB. | |||
| 4. | С центром A и радиусом AB начертите окружность BCD; | |||
| (Постулат 3) | ||||
| 5. | с центром B и радиусом BA, нарисуйте окружность ACE; | |||
| (Постулат 3) | ||||
| 6. | и от точки C, где круги пересекаются, | |||
| 7. | нарисуйте прямые CA и CB. | (Постулат 1) | ||
| 8. | Тогда, поскольку точка A является центром окружности BCD, | ||||||||||||||||||||||
| 9. | AC невероятно похож на AB. | (определение 16) | |||||||||||||||||||||
| 10. | А так как точка B является центром окружности ACE, | ||||||||||||||||||||||
| 11. | BC невероятно похож на AB. | ||||||||||||||||||||||
| 12. | Но мы показали, что CA также равно AB; | ||||||||||||||||||||||
| 13, | , следовательно, CA и CB равны AB. | ||||||||||||||||||||||
| 14. | И вещи, которые равны одному и тому же, равны друг другу; | ||||||||||||||||||||||
| (Аксиома 1) | |||||||||||||||||||||||
| 15. | , следовательно, CA равно CB. | ||||||||||||||||||||||
| 16. | Следовательно, три прямые CA, AB, BC равны одной | ||||||||||||||||||||||
| 17. | другой. | ||||||||||||||||||||||
| 18. | Следовательно, треугольник ABC равносторонний, | (определение 9) | |||||||||||||||||||||
| 19. | и мы построили его на данной прямой AB. | ||||||||||||||||||||||
| 20. | Это то, что от нас требовалось сделать. | ||||||||||||||||||||||
Это первое предложение не только показывает, как нарисовать эквивалентный треугольник. Это доказывает, что, поскольку мы можем построить , равносторонние треугольники существуют логически. См. Комментарий к определениям.
Ниже приводится руководство к риторике.
Формальные части предложения
Общее утверждение предложения называется его высказыванием.Формулировка этого предложения выделена курсивом в строке 1. В нем говорится о том, что дано и что мы должны заключить или сделать.
После изложения следует изложение, строка 2. Здесь мы применяем то, что дано к конкретной фигуре. Далее следует спецификация, строка 3. Здесь, в отношении этой цифры, мы конкретно указываем, что мы должны доказать или сделать.
Далее идет сама конструкция (строки с 4 по 7), а за ней следует доказательство (строки с 8 по 17).
Наконец, у нас есть закрытие. В заключении мы возвращаемся к высказыванию и подтверждаем то, что мы сделали или показали. Строки с 18 по 20 являются закрывающими.
Проблема, традиционно закрываемая латинским текстом Quod erat faciendum , буквально «Что должно было быть сделано», сокращенно Q.E.F. Теорема, завершенная с помощью Quod erat manifestrandum , которое должно было быть доказано, сокращенно Q.E.D. Скоро мы начнем использовать эти закрытия.
Это шесть формальных частей предложения.Стабильность, которую они имели более 2500 лет, проистекает из эстетики ясной демонстрации, которая принадлежит изучению риторики. («Скажите им, что вы собираетесь делать; сделайте это; скажите им, что вы это сделали».)
Цитаты из постулатов, определений и аксиом, которые мы поместили в крайнем правом углу, не были включены в Элементы . Однако вошло в обычай включать их в качестве руководства к рассуждениям. Мы надеемся, что они не будут отвлекать от изящества демонстраций Евклида; баланс, который нарушается сегодняшними доказательствами из двух столбцов.
Молчаливые предположения
Были ли вам понятны все части предложения? Если нет, то, как только вы поймете, вы можете найти свой собственный способ, более ясный способ выразить это.
Была ли демонстрация убедительной? То есть были ли аргументы действительными и были ли они основаны только на вещах, которые были ранее признаны? Ведь каждое сделанное нами утверждение должно принадлежать к какой-то логической категории. Это должно быть Определение, Постулат, Аксиома или предложение, которые мы уже установили.Это называется аксиоматическим методом.
Или были какие-то неявные предположения? (Слово , молчаливый, означает «не произнесено»; поэтому молчаливое предположение — это то, что явно не указано. Например, если a больше b , а b больше c , то молчаливое предположение может заключаться в том, что a больше, чем c .)
Были ли какие-то неявные предположения? Как насчет вывода, что два круга действительно пересекаются друг с другом в точке под названием C? (Строка 6.) Гарантирует ли это какой-либо постулат или аксиома? Если нет, можете ли вы предложить такой постулат?
(Такой постулат должен констатировать нечто чрезвычайно очевидное, и, следовательно, его будет тем труднее сформулировать. Он должен подразумевать, что, когда непрерывная линия существует по обе стороны от другой линии, то в какой-то момент она должна пересекать эту другая строка.)
При строгом рассмотрении любой логической науки делается попытка выявить все неявные предположения.Это означает, что каждое доказательство подвергается поисковому анализу. Мы этого делать не будем. В этот раз мы подняли вопрос о неявных предположениях и оставим его как есть, что не должно мешать студенту задавать вопросы.
Таким образом, математика не является статичным предметом, поскольку всегда будут люди, которые недовольны текущими методами, концепциями и доказательствами. Только поставив под сомнение то, что «очевидно» или что одобрено, наука может когда-либо проникнуть в то, что истинно.
Пожалуйста, «переверните» страницу и решите проблемы.
или
Перейти к следующему предложению.
Содержание | Введение | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Как нарисовать равносторонний треугольник по кругу »OrigamiTree.com
Поиск по ключевому слову
ДОБРО ПОЖАЛОВАТЬ!
Origami Tree предлагает БЕСПЛАТНЫЕ уроки ремесла на YouTube — дом для миллионов посетителей с ноября 2013 года.Копаться в архивах
Копаться в архивах Выберите месяц Апрель 2021 Сентябрь 2020 Октябрь 2019 Сентябрь 2019 Август 2019 Июль 2019 Июнь 2019 Май 2019 Апрель 2019 Март 2019 Февраль 2019 Январь 2019 Декабрь 2018 Ноябрь 2018 Октябрь 2018 Сентябрь 2018 Август 2018 Июль 2018 Июнь 2018 Май 2018 Апрель 2018 Март 2018 Февраль 2018 Январь 2018 Декабрь 2017 Ноябрь 2017 Октябрь 2017 Сентябрь 2017 Август 2017 Июль 2017 Июнь 2017 Май 2017 Апрель 2017 Март 2017 Февраль 2017 Январь 2017 Декабрь 2016 Ноябрь 2016 Октябрь 2016 Сентябрь 2016 Август 2016 Июль 2016 Июнь 2016 Май 2016 Апрель 2016 Март 2016 Февраль 2016 Январь 2016 Декабрь 2015 Ноябрь 2015 Октябрь 2015 Сентябрь 2015 Август 2015 Июль 2015 Июнь 2015 Май 2015 Апрель 2015 Март 2015 Февраль 2015 Январь 2015 Декабрь 2014 Ноябрь 2014 Октябрь 2014 Сентябрь 2014 Август 2014 Июль 2014 Июнь 2014 Май 2014 Апрель 2014 Март 2014 Февраль 2014 Январь 2014 Январь 2014 Декабрь 2013 Ноябрь 2013 Октябрь 201 3 июня 2013 г. март 2013 г. июнь 2011 г. декабрь 2010 г.Хотите помочь?
Поддержите продолжение бесплатных обучающих программ, сделав пожертвование сегодня!В этом уроке я покажу вам простой способ нарисовать треугольник внутри круга.С помощью этого метода вы можете построить равносторонний треугольник (все стороны треугольника равны) в данном круге. Вы можете выучить это для помощи в домашнем задании по геометрии / математике, или вы можете создать из них бумажный орнамент! Ага, верно! Вам понадобится циркуль, линейка, ручка или карандаш и лист бумаги.
Больше веселья!
Как сделать орнамент из бумаги (треугольник в единицах круга)
Нравится:
Нравится Загрузка…
Связанные 19 декабря 2016 г. в Back-to-School, Tips & Tricks. Теги: круг, геометрия, математика, орнамент, треугольникМогу ли я получить равносторонний треугольник внутри круга, сначала нарисовав случайный треугольник, сложив стороны треугольника и разделив на 3?
Вы спрашиваете, одинаковы ли суммы сторон всех вписанных в круг треугольников, разделенные на 3.Это то же самое, что сказать, что суммы сторон всех таких треугольников одинаковы, БЕЗ деления на 3. Это должно быть так, если то, что вы предложили, было верным.
Но это не так.
Начнем с равностороннего треугольника. Я знаю, что длина каждой стороны «вписанного» равностороннего треугольника в √3 раз больше радиуса круга, поэтому сумма сторон равна 3√3 r.
Чтобы увидеть, что это не то же самое, что сумма сторон любого вписанного треугольника, нарисуйте треугольник, подобный этому: Начните с точки, близкой к вершине круга (с точки зрения бумаги, на которой вы ее нарисовали на.Теперь нарисуйте одну сторону, которая ПОЧТИ диаметр круга. Он проходит чуть левее центра и пересекает точку почти точно напротив первой точки. Теперь нарисуйте другую сторону, которая также начинается от верхней точки, но проходит справа от центра и переходит в другую точку, почти точно противоположную первой точке. И, наконец, третья сторона треугольника соединяет две противоположные точки, которые вы создали, которые на самом деле очень близки друг к другу.
Теперь у вас есть треугольник с двумя длинными сторонами, почти равными диаметру круга, и одной короткой стороной, почти равной 0.Фактически, чем ближе вы сделаете две точки напротив исходной точки, тем ближе длинные стороны к диаметру (2r) и тем ближе короткая сторона к 0.
Итак, если вы сделаете две нижние точки ОЧЕНЬ ОЧЕНЬ близкими друг к другу, длины двух длинных сторон в сумме ОЧЕНЬ ОЧЕНЬ близки к d + d = 2r + 2r = 4r, а длина короткой стороны будет ОЧЕНЬ ОЧЕНЬ близкой к 0. Если вы сложите их, вы получите сумму сторон, которая ОЧЕНЬ ОЧЕНЬ близка к 4r. Это не может быть таким же, как 3√3 r.Это показывает, что сумма сторон любого вписанного случайного треугольника не обязательно будет такой же, как сумма сторон вписанного равностороннего треугольника.
И есть другие способы показать это, используя другой пример «случайных» треугольников.
Значит, ваша процедура не сработает.
Построение равносторонних треугольников, вписанных в круги Презентация PowerPoint, бесплатная онлайн-загрузка PPT Y7XRMD
Построение равносторонних треугольников, вписанных в окружности, на основе образовательных треугольников Уолча Треугольник — это многоугольник с тремя сторонами и тремя углами.Есть много типов треугольников, которые можно построить. Треугольники классифицируются на основе их угла и размеров сторон. Равносторонние треугольники — это треугольники, у которых все три стороны равны по длине.
Меры каждого угла равностороннего треугольника равна 60. 1.3.1: Построение равносторонних треугольники, вписанные в Кругах 2 Кругов Круга множество всех точек, которые находятся на одинаковом расстоянии от опорной точки, в центре. Набор точек образует двумерную кривую, равную 360.Кружки названы по их центру. Например, если круг имеет центральную точку G, значение
Кругназывается кругом G. 1.3.1: Построение равносторонних треугольников, вписанных в круги 3 круга, продолжение Диаметр круга — это прямая линия, проходящая через центр круга и соединяющая две точки на окружности. Это в два раза больше радиуса. Радиус круга — это отрезок прямой, который проходит от центра круга до
точка на окружности.Радиус круга равен половине его диаметра. В каждом круге 1,3.1: 360. Построение равносторонних треугольников, вписанных в круги 4 Вписывание фигур Вписать означает нарисовать фигуру внутри другой фигуры так, чтобы каждая вершина заключенной фигуры касалась внешней фигуры. Фигура, вписанная в круг, — это цифра
.нарисован внутри круга так, чтобы каждая вершина фигуры касалась круга. 1.3.1. Построение равносторонних треугольников, вписанных в окружности 5 Метод 1. Построение равностороннего треугольника, вписанного в окружность, с помощью циркуля 1.Чтобы построить равносторонний треугольник, вписанный в круг, сначала отметьте положение центральной точки круга. Обозначьте точку X. 2. Постройте круг с острием циркуля в центре. 3. Отметьте точку на окружности A. 4. Не меняя настройки компаса, поставьте острие
компаса на A и нарисуйте дугу, чтобы пересечь круг в двух точках. Обозначьте точки B и C. 5. Используйте линейку для построения. BC 6. Поместите острие циркуля в точку B.Раскройте компас до тех пор, пока он не расширится на. Нарисуйте BCточку D. другую дугу, пересекающую окружность. Этикетка 7. Используйте линейку для построения и. CD BD 1.3.1: Построение равносторонних треугольников, вписанных в окружности
6 Метод 2: Построение равностороннего треугольника, вписанного в круг, с помощью циркуля 1. Чтобы построить равносторонний треугольник, вписанный в круг, сначала отметьте положение центральной точки круга. Обозначьте точку X.2. Постройте круг с острием циркуля в центре. 3. Отметьте точку на окружности A. 4. Не меняя настройки компаса, поместите острие циркуля в точку A и нарисуйте дугу, чтобы пересечь окружность в одной точке. Обозначьте точку пересечения B. (продолжение) 5. Поместите острие циркуля в точку B и нарисуйте дугу, чтобы пересечь круг в одной точке. Обозначьте точку пересечения C.
6. Продолжайте движение по кругу, отмечая точки D, E и F.Убедитесь, что не изменили настройку компаса. 7. Используйте линейку, чтобы соединить A и C, C и E, а также E и A. 1.3.1: Построение равносторонних треугольников, вписанных в круги 7 Спасибо за просмотр! Г-жа Дамбревиль
.
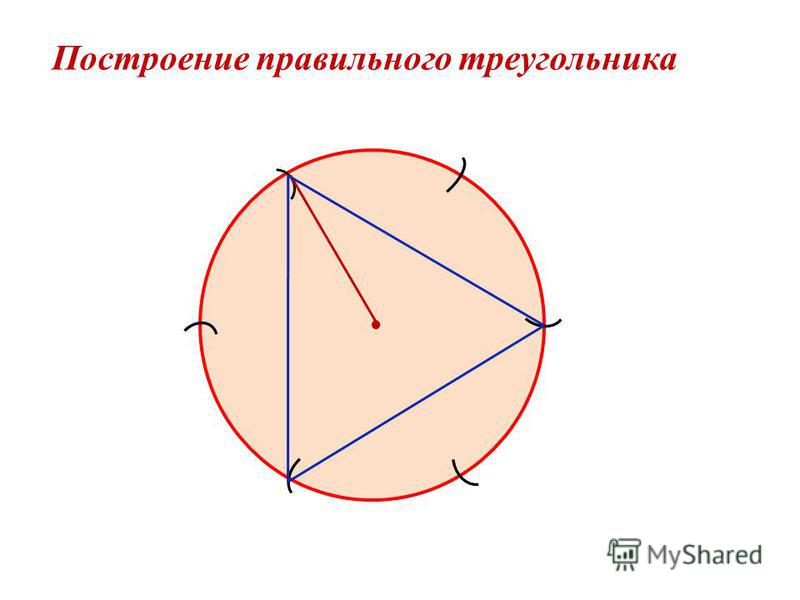 Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
 Простая техника, которая по душе и дошкольникам, и ребятам постарше.
Простая техника, которая по душе и дошкольникам, и ребятам постарше. Для того чтобы этого не случилось, необходимо следовать простым правилам:
Для того чтобы этого не случилось, необходимо следовать простым правилам:
 Оно имеет совершенно другие мотивы и цели. Для детей рисование – это игра. Научить ребенка рисовать означает развить его умение отражать жизненные впечатления в графической форме на листе бумаги, представляя предмет изображения в определенной форме, в цвете, в строении. Главное в обучении – не просто в развитии руки и подчинении ее задаче изображения, а в совместном движении руки и глаза.
Оно имеет совершенно другие мотивы и цели. Для детей рисование – это игра. Научить ребенка рисовать означает развить его умение отражать жизненные впечатления в графической форме на листе бумаги, представляя предмет изображения в определенной форме, в цвете, в строении. Главное в обучении – не просто в развитии руки и подчинении ее задаче изображения, а в совместном движении руки и глаза.
 Для рисования нужны следующие навыки:
Для рисования нужны следующие навыки: Для детей 6-7 лет рисование – это не только удовольствие, но и способ усовершенствовать свои творческие и интеллектуальные навыки.
Для детей 6-7 лет рисование – это не только удовольствие, но и способ усовершенствовать свои творческие и интеллектуальные навыки.

 Можно обсуждать определенные недостатки, не высказываясь негативно о рисунке в целом.
Можно обсуждать определенные недостатки, не высказываясь негативно о рисунке в целом. И будет считать, что его рисунок “неправильный”. Нужно показывать рисунки разных художников и говорить, что нарисовать собаку можно еще десятками способов.
И будет считать, что его рисунок “неправильный”. Нужно показывать рисунки разных художников и говорить, что нарисовать собаку можно еще десятками способов. 04.2021).
04.2021).  Рисунок, как деятельность, позволяет детям выразить в работах своё представление об окружающем мире, передать настроение в данную минуту, выразить отношение к окружающему миру через лист бумаги и краски. Поэтому овладение изобразительной деятельностью с раннего детства имеет для ребенка огромное значение: создать положительный эмоциональный настрой, что способствует развитию творчества, эстетического чувства, чувства образного представления и воображения, так же дошкольник получает возможность самостоятельно создать рисунок, показать его родителям и доставить им радость, получить поощрение.
Рисунок, как деятельность, позволяет детям выразить в работах своё представление об окружающем мире, передать настроение в данную минуту, выразить отношение к окружающему миру через лист бумаги и краски. Поэтому овладение изобразительной деятельностью с раннего детства имеет для ребенка огромное значение: создать положительный эмоциональный настрой, что способствует развитию творчества, эстетического чувства, чувства образного представления и воображения, так же дошкольник получает возможность самостоятельно создать рисунок, показать его родителям и доставить им радость, получить поощрение. Необходимо помнить о координации «рука — глаз», так как развитие мелких движений рук происходит под контролем зрения. Известно, что в головном мозге человека центры, отвечающие за речь и движение пальцев, располагаются очень близко друг к другу. Развивая мелкую моторику, мы активируем эти центры. В будущем эти навыки ребенку потребуются для использования двигательной деятельности, чтобы рисовать, писать, одеваться и так далее. Тем самым, можно сделать вывод о том, что развитие движений мышц при рисовании стимулирует зоны мозга, которые помогут ребёнку приобрести навыки, необходимые для полноценной жизни.
Необходимо помнить о координации «рука — глаз», так как развитие мелких движений рук происходит под контролем зрения. Известно, что в головном мозге человека центры, отвечающие за речь и движение пальцев, располагаются очень близко друг к другу. Развивая мелкую моторику, мы активируем эти центры. В будущем эти навыки ребенку потребуются для использования двигательной деятельности, чтобы рисовать, писать, одеваться и так далее. Тем самым, можно сделать вывод о том, что развитие движений мышц при рисовании стимулирует зоны мозга, которые помогут ребёнку приобрести навыки, необходимые для полноценной жизни.
 Акриловая живопись приобретает широкую популярность. Освоить вид акриловой живописи намного легче, чем акварельную технику либо масло. Картины, написанные акрилом, обладают особенным неповторимым очарованием.
Акриловая живопись приобретает широкую популярность. Освоить вид акриловой живописи намного легче, чем акварельную технику либо масло. Картины, написанные акрилом, обладают особенным неповторимым очарованием. Художественная студия Matita представляет вашему вниманию мастер-класс по рисованию акриловыми красками для начинающих.
Художественная студия Matita представляет вашему вниманию мастер-класс по рисованию акриловыми красками для начинающих. Она представляет собой особенный раствор, придающий дереву белый цвет.
Она представляет собой особенный раствор, придающий дереву белый цвет. Полотна, созданные красками на основе пластика, имеют интересную объемную структуру. Рисовать акрилом не сложнее, чем акварелью. При этом законченную картину не нужно обрабатывать фиксирующими составами — краски имеют высокую стойкость, не выцветают и не боятся воды.
Полотна, созданные красками на основе пластика, имеют интересную объемную структуру. Рисовать акрилом не сложнее, чем акварелью. При этом законченную картину не нужно обрабатывать фиксирующими составами — краски имеют высокую стойкость, не выцветают и не боятся воды. Она представляет собой специальную эмульсию с диоксидом титана, которая придает белизну. Наносится грунтовка на подготовленную доску в несколько слоев и сушится в течение суток.
Она представляет собой специальную эмульсию с диоксидом титана, которая придает белизну. Наносится грунтовка на подготовленную доску в несколько слоев и сушится в течение суток.
 Поэтому, рисование акриловыми красками на холсте будет правильным решением!
Поэтому, рисование акриловыми красками на холсте будет правильным решением!
 Важно тут выбрать хорошую кальку, которая после нескольких намоканий не начнет покрываться ворсом, который затем попадет в краски и на холст. По мнению некоторых художников, лучшая для этих целей калька находится в коробках конфет.
Важно тут выбрать хорошую кальку, которая после нескольких намоканий не начнет покрываться ворсом, который затем попадет в краски и на холст. По мнению некоторых художников, лучшая для этих целей калька находится в коробках конфет.
 Представьте себе визуально размер холста….
Представьте себе визуально размер холста…. Поэтому писать ими желательно в прочном фартуке или рабочем халате.
Поэтому писать ими желательно в прочном фартуке или рабочем халате.
 На какой поверхности вам нравится рисовать? Если вам нравится рисовать на холсте, то бумажный холст — отличная выбор для начала. Он не дорогой и имеет текстуру натянутого холста. Доска, дерево и фанера — тоже отлично подойдут.
На какой поверхности вам нравится рисовать? Если вам нравится рисовать на холсте, то бумажный холст — отличная выбор для начала. Он не дорогой и имеет текстуру натянутого холста. Доска, дерево и фанера — тоже отлично подойдут.  После того, как ваша картина будет завершена, дайте ей полностью высохнуть, прежде чем поместить ее в рамку. Для художника нет ничего хуже, запороть работу после создание шедевра. Вы не сможете сразу создавать шедевры, но с практикой вы начнете развивать навыки и уверенность в своей работе. Это замечательный процесс — наслаждайтесь им.
После того, как ваша картина будет завершена, дайте ей полностью высохнуть, прежде чем поместить ее в рамку. Для художника нет ничего хуже, запороть работу после создание шедевра. Вы не сможете сразу создавать шедевры, но с практикой вы начнете развивать навыки и уверенность в своей работе. Это замечательный процесс — наслаждайтесь им. 

 Учась рисовать, начинайте с темных оттенков, плавно переходя и к светлым тонам. Смешивайте краски на цветовом круге. Поэтапное рисование с детьми позволит получить на бумаге красивые изображения.
Учась рисовать, начинайте с темных оттенков, плавно переходя и к светлым тонам. Смешивайте краски на цветовом круге. Поэтапное рисование с детьми позволит получить на бумаге красивые изображения.  – Гомель, 2016. – Ч. 3. – С. 220-223.
– Гомель, 2016. – Ч. 3. – С. 220-223. ru
ru ЦЕЛИ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ
ЦЕЛИ И ЗАДАЧИ ОСВОЕНИЯ ДИСЦИПЛИНЫ 1. Общие положения
1. Общие положения Ф.И.О. педагога: Матерова Елена Геннадьевна. 2. Образование: Высшее специальное. В 1993 г. Нижневартовское педагогическое училище, по специальности «Преподавание в младших
Ф.И.О. педагога: Матерова Елена Геннадьевна. 2. Образование: Высшее специальное. В 1993 г. Нижневартовское педагогическое училище, по специальности «Преподавание в младших Сумей оказаться их солнышком, Сумей обогреть росточки (из авторской поэмы «Моя педагогическая философия») Б
Сумей оказаться их солнышком, Сумей обогреть росточки (из авторской поэмы «Моя педагогическая философия») Б McFaull, 560 So. 2d 1013
McFaull, 560 So. 2d 1013
 La.R.S. 13: 1722. Мы находим, что La.C.C.P. искусство. 10 (A) (5) не запрещает осуществление юрисдикции.
La.R.S. 13: 1722. Мы находим, что La.C.C.P. искусство. 10 (A) (5) не запрещает осуществление юрисдикции. Дополнительным элементом процедуры раздельного проживания является вопрос о временной опеке над несовершеннолетним в ожидании рассмотрения дела о раздельном проживании в соответствии с C.C. искусство. 146. Вопрос заключается в том, обладает ли Гражданский окружной суд округа Орлеан юрисдикцией определять опеку над ребенком.
Дополнительным элементом процедуры раздельного проживания является вопрос о временной опеке над несовершеннолетним в ожидании рассмотрения дела о раздельном проживании в соответствии с C.C. искусство. 146. Вопрос заключается в том, обладает ли Гражданский окружной суд округа Орлеан юрисдикцией определять опеку над ребенком. Это относится к настоящему делу, поскольку родственник проживает в Новом Орлеане, и он утверждал, что основание для отделения, отказа от него возникло здесь. Согласно C.C. искусство. 146 опека над несовершеннолетним является вспомогательной по отношению к производству о раздельном проживании. Следовательно, суд первой инстанции правомочен решать этот вопрос об опеке над ребенком, и суд ошибся, посчитав иначе.
Это относится к настоящему делу, поскольку родственник проживает в Новом Орлеане, и он утверждал, что основание для отделения, отказа от него возникло здесь. Согласно C.C. искусство. 146 опека над несовершеннолетним является вспомогательной по отношению к производству о раздельном проживании. Следовательно, суд первой инстанции правомочен решать этот вопрос об опеке над ребенком, и суд ошибся, посчитав иначе. Поступить иначе — значит оставить дело в подвешенном состоянии. Справедливость требует, чтобы у матери была возможность доказать, что опека над ней будет лучше для ребенка. Точно так же в наилучших интересах ребенка, чтобы суд расследовал положение ребенка, находящегося под опекой отца. Однако статут требует, чтобы критерий наилучших интересов для юрисдикционных целей в первую очередь зависел от того, имеют ли ребенок и хотя бы один участник значимую связь с государством и доступны ли существенные доказательства , касающиеся ребенка , в этом состоянии .
Поступить иначе — значит оставить дело в подвешенном состоянии. Справедливость требует, чтобы у матери была возможность доказать, что опека над ней будет лучше для ребенка. Точно так же в наилучших интересах ребенка, чтобы суд расследовал положение ребенка, находящегося под опекой отца. Однако статут требует, чтобы критерий наилучших интересов для юрисдикционных целей в первую очередь зависел от того, имеют ли ребенок и хотя бы один участник значимую связь с государством и доступны ли существенные доказательства , касающиеся ребенка , в этом состоянии . Оба родителя присутствуют здесь для дачи показаний, как и двенадцатилетний сводный брат ребенка, ребенок здесь, респонденту доступны современные технологии для передачи доказательств из Ленинграда, интерес Советского правительства к делу указывает на то, что ответчик может получить помощь из этого источника здесь доступны эксперты, а респондент представлен квалифицированным адвокатом.
Оба родителя присутствуют здесь для дачи показаний, как и двенадцатилетний сводный брат ребенка, ребенок здесь, респонденту доступны современные технологии для передачи доказательств из Ленинграда, интерес Советского правительства к делу указывает на то, что ответчик может получить помощь из этого источника здесь доступны эксперты, а респондент представлен квалифицированным адвокатом. 06.2020 58-е заседание Европейской группы исследований высокого давления (EHPRG 2020)
06.2020 58-е заседание Европейской группы исследований высокого давления (EHPRG 2020) 06.2020 Литологическое совещание ГЕОЛОГИЯ РИФОВ
06.2020 Литологическое совещание ГЕОЛОГИЯ РИФОВ Животных отбирали из эксперимента в камере CO 2 через 24 часа, 30 часов, 48 часов, 72 часа, 5 дней, 7 дней или 10 дней после операции (по 5–6 животных на каждый срок).
Животных отбирали из эксперимента в камере CO 2 через 24 часа, 30 часов, 48 часов, 72 часа, 5 дней, 7 дней или 10 дней после операции (по 5–6 животных на каждый срок).