Малюнок з геометричних фігур: ⬇ Скачать картинки D0 b3 d0 b5 d0 be d0 bc d0 b5 d1 82 d1 80 d0 b8 d1 87 d0 bd d1 96 d1 84 d1 96 d0 b3 d1 83 d1 80 d0 b8, стоковые фото D0 b3 d0 b5 d0 be d0 bc d0 b5 d1 82 d1 80 d0 b8 d1 87 d0 bd d1 96 d1 84 d1 96 d0 b3 d1 83 d1 80 d0 b8 в хорошем качестве
- Фігури з геометричних фігур. Картинки для дітей 2-3 років, дошкільнят, 1-2 клас. Шаблони для аплікацій у дитячому садку
- З якого віку можна починати вчити з дитиною геометричні фігури
- Вивчення геометричних фігур: назви, форма, колір, розмір
- Вивчення складних геометричних фігур за допомогою простих: користь занять для дітей
- Уроки нарисної геометрії для дітей
- Приклади і покрокові інструкції для створення аплікацій з геометричних фігур
- Відео про геометричні фігури
- Вчимося розрізняти і називати геометричні фігури – Освіта.UA
- Розмальовки Геометричні фігури
- Картинки тварин з геометричних фігур. Малювання геометричних тел Як намалювати 2 геометричні фігури
- Як намалювати овал самостійно швидко і красиво
- Добірка мультфільмів та ігор, що допоможуть першокласникам розрізняти геометричні фігури
- Домашні вправи для роботи з дітками з інтелектуальними порушеннями
- Геометрические фигуры Занятия по математике и STEM Идеи для детей
- Ранняя математика: знакомство с геометрией маленьким детям
- Что дети знают и что им нужно узнать о форме и пространстве
- Видео для детей, обучающие геометрии
- Симметрия для детей (3:48)
- Видео с песней Polygon (4:02)
- Они многоугольник Песня (3:18)
- Узнайте о двухмерных фигурах с поездом Чу-Чу — Часть 1 (9:35)
- Изучите трехмерные фигуры (геометрические тела) с помощью поезда Choo-Choo — Часть 2 (12:05)
- Двухмерные геометрические формы для лепки (6:12)
- Трехмерные фигуры с пластилином (9:06)
- Как легко рисовать треугольники с Евклидом (3:47)
- Песня о полигонах для детей Рэп-видео: геометрия, четырехугольники, шестиугольники и т. Д. (1:57)
- Песня о параллельных, перпендикулярных и пересекающихся линиях | NUMBEROCK (2:21)
- Песня в 3-х формах для детей | Трехмерное видео по NUMBEROCK (2:04)
- Колин Доддс — Геометрические преобразования (3:15)
- Песня Shapes: Shapes Rap / Chant — Песня формы робота (3:36)
- Песня о треугольниках ⋆ Типы треугольников для детей от NUMBEROCK (1:55)
- Другие ресурсы для обучения геометрии
- (PDF) Идеи детей младшего возраста о геометрических фигурах
- 16 забавных детских книжек о фигурах
- 7 игрушек с удивительной геометрией для детей
Фігури з геометричних фігур. Картинки для дітей 2-3 років, дошкільнят, 1-2 клас. Шаблони для аплікацій у дитячому садку
Фігури та кольори малюки починають вивчати з самого дитинства з допомогою різних методик, зокрема, через аплікації. Ці аплікації складаються з геометричних фігур, які дитина приклеює до картонній або паперовій основі.
З якого віку можна починати вчити з дитиною геометричні фігури
На думку вчених, навчати малюка слід з самого народження, при цьому його проводять у кілька етапів:
- Після народження малюк майже нічого не запам’ятовує, однак привчається дивитися на світ у всіх його аспектах. У цей час рекомендується розмовляти з немовлям, промовляючи кожну фігуру, читати невеликі дитячі вірші, співати пісні.
- Коли дитині виповниться 6 місяців, він постарається дізнатися про світ більше. Для цього він буде чіпати і покусувати предмети. Важливо підібрати правильні іграшки. Підійде набір м’яких квадратів, на яких намальовані квіти, метелики, пташки.
- Наступний етап починається тоді, коли малюк навчається говорити. Необхідно проговорювати всі назви фігур, починаючи з найпростіших (коло, трикутник, квадрат). Потім прийде черга трапеції, прямокутники і інших. На цьому етапі допоможе іграшкова пірамідка, пластмасові кубики, з яких будують вежу, і малювання.
Вивчення геометричних фігур з дитиною можна починати з самого раннього віку
Таким чином, навчання можна з народження дитини, використовуючи різні методики.
Вивчення геометричних фігур: назви, форма, колір, розмір
З віком дитина повинна дізнаватися все більше фігур і кольорів.
До 2 років необхідно знати:
- трикутник;
- квадрат;
- коло.
У цьому ж віці потрібно знати основні кольори:
- синій;
- червоний;
- жовтий;
- зелений;
- білий.
До 2 років дитина повинна знати основні геометричні фігури та кольори
Деякі діти в 2 роки знають дещо більше кольорів:
- оранжевий;
- фіолетовий;
- чорний;
- рожевий.

До 6 років дитина дізнається про більш складних, комбінованих кольорах і відтінках, знайомиться з складовими (складаються з основних) фігурами.
Діти навчаються через ігри, вони бувають різної складності, тому давати їх дитині рекомендується в такій послідовності:
- Намальовані на картоні кола, трикутники, квадрати різних розмірів і кольорів. Називайте зображення своїми іменами, промовляючи їх вголос.
- Намалювати на картоні тільки контури фігур, причому всі контури повинні бути різних кольорів, щоб малюк обводив їх відповідними кольорами, розфарбовував і промовляв назви вголос. У віці від 2 років слід починати порівнювати розміри.
Сортер з геометричними фігурами допомагає дітям у вивченні
- Вирізати фігури і розкласти на видних місцях в будинку, щоб малюк шукав малюнки. Кожен раз, коли дитина знаходить зображення, він повинен назвати наступні характеристики: фігуру, колір і розмір.
- Ігрові набори, призначені для вивчення вище перерахованого. Наприклад, пірамідка, гриби різних кольорів і розмірів на підставці, мозаїка та інші. Такі ігри розважать дитину, приверне його увагу.
- Пошук геометричних фігур в навколишньому світі. Наприклад, стіл – це прямокутник, шкатулка – квадрат, а м’ячик – коло. Рекомендується розглядати і більш складні форми: склянку – циліндр, а святковий ковпак – піраміда.
Розроблено безліч методик, призначених для вивчення фігур і кольорів. Вони розраховані для дітей різного віку, а також враховують їх улюблені заняття.
Вивчення складних геометричних фігур за допомогою простих: користь занять для дітей
Фігури з геометричних фігур, або складені фігури, простіше вивчати через прості форми. Необхідно вирізати кілька квадратів, кіл і трикутників і складати їх.
Приклади складання складних фігур:
- Трапеція: квадрат + 2 трикутника.
- Прямокутник: 2 і більше квадратів.
- Ромб: 2 рівних трикутника.

- Паралелограм: 2 квадрата + 2 рівних трикутника.
Дитина має бути повністю залучений в процес навчання, в іншому випадку навчання буде марним. Навчання в форматі гри – найкращий спосіб привернути увагу учня і зробити процес цікавим. Роблячи відкриття самостійно, малюк побажає продовжити навчання.
Уроки нарисної геометрії для дітей
Нарисна геометрія спрямована на розвиток просторового мислення. Дитина вчиться представляти складні об’ємні фігури, розкладаючи їх на прості і плоскі. Завдання передбачають не тільки вибір правильних відповідей, але і пояснення свого вибору і чому інші відповіді неправильні.
Домалювати фігуру за зразком
Закріпити урок допоможе малювання.
Що потрібно зробити:
- Показати дитині фігури, розповісти про них, навести приклади речей відповідної форми, які знаходяться в кімнаті.
- Роздрукувати бланки, на яких пунктирною лінією зображено недорисованные фігури (приклад бланка наведено вище).
- Завдання: продовжити пунктир, сказати, що зображення є колом, квадратом, прямокутником.
- Обговорити отримані результати.
Замість пунктирних ліній можуть бути і звичайні, але прерывающиеся. Це спрощений варіант вправи. Щоб ускладнити завдання, необхідно роздрукувати бланк, на якому частина фігури замальовано, але не повторює контури. Це заплутає малюка.
Крім домальовування, з’являється необхідність зафарбувати частину фігури.
Обведена фігури по точкам
Вправа по з’єднанню точок розвиває уяву, дозволяючи представити, які потрібно з’єднати точки, щоб вийшла задана фігура. Цей навик розвиває здатність до виконання завдань за зразком, що стане в нагоді в школі. Дитина повинен малювати олівцем, щоб він міг виправити помилки.
Як робити вправу:
- Роздрукувати бланки завдань.
- На кожному бланку зліва представлений зразок малюнка, а праворуч безліч точок, з яких потрібно скласти такий же малюнок.

- Дитина повинна помітити, що різні точки: є точки з хрестиками, чорні крапки і білі. Однакові точки з’єднувати не можна.
- Праворуч точок більше, ніж потрібно – деякі залишаться поза малюнка.
Пошук геометричних фігур на зображенні
Фігури з геометричних фігур привертають увагу дітей. Їм стає цікаво, як же розділити складний об’єкт на простий, а простий зібрати в складний. У цьому завдання пропонується знайти круги, квадрати, трикутники. В ускладненому варіанті додаються прямокутники, трапеції, овали і ромби.
Легкий малюнок «метелик» для дівчаток:
- Кола різних розмірів – тулуб.
- 2 пари однакових трикутників – нижні і верхні крила.
- По 2 штуки маленьких, середніх і великих кіл – прикраса крил.
У малюнку «дім» можна знайти:
- Квадрат – основна частина будинку.
- Прямокутник – двері.
- Два кола або овалу – вікна.
- Маленький круг – дверна ручка.
- Трикутник – дах.
Ускладнений малюнок «кораблик»:
- Трапеція – корпус корабля.
- 3 кола – вікна кают.
- 2 прямокутники різних розмірів – піднесення на палубі.
- Трикутники – вітрила.
Малюнок «робот»:
- Квадрат – тіло робота.
- 2 рівних прямокутника – ноги.
- 2 однакових рівносторонніх трикутника – ступні.
- 2 рівних ромба – кнопки на тілі робота.
- Довгий прямокутник – плечі.
- 2 кола, 2 прямокутника і 2 кола – руки.
- Невеликий квадрат – особа.
- 2 маленькі кола – очі.
- Трикутник – ніс.
- Тонкий прямокутник – рот.
- Трапеція (в довжині повинна бути більше квадрата особи) – капелюх.
Приклади малюнків розташовані по ступені складності (від легкого до складного).
Малювання геометричних фігур
Завдання розвиває просторове мислення, так як дитина повинен зафарбувати фігури так, щоб одна перекривала іншу.
Як проводити вправу:
- Намалювати на аркуші паперу пари коло-квадрат, трикутник, коло, квадрат-трикутник і інші так, щоб їх кінці перетиналися, перекриваючи один одного.
- Надати дитині аркуш і кольорові олівці.
- Попросити малюка розфарбувати фігури так, щоб одна з пари знаходилася зверху один одного, промовляючи вголос кольору.
Щоб полегшити завдання, необхідно заздалегідь показати дитині об’ємні фігури, дати йому можливість посувати їх і пограти.
Пазл з геометричних фігур: як скласти потрібні форми
Фігури з геометричних фігур не відразу зрозумілі дітям. Для спрощення навчання рекомендується збирати своєрідні «пазли».
Фігури з геометричних фігур допоможе дитині навчитися збирати гра в пазли
Як проводити перший варіант вправи:
- Роздрукувати бланки, на яких зверху намальовані прості фігури, а внизу кілька складних форм.
- Дитина повинна знайти, який з варіантів на нижній частині листа поєднує в собі всі перераховані форми на верхній частині аркуша.
- Також необхідно пояснити отримані відповіді.
Спочатку слід давати прості малюнки, в яких фігури з’єднуються без нахилу. Також форма може містити тільки квадрати або тільки трикутники.
Вправа розвиває фантазію і орієнтацію в площині фігур.
Групування простих фігур у складні
Це завдання назад попереднього.
Як виконувати вправу:
- Роздрукувати на картоні кілька кіл, квадратів, трикутників і трапецій, вирізати їх.
- Завдання дитини – скласти якомога більше різних форм, що складаються з перерахованих вище фігур.
- Щоб вивчити цифри, необхідно вважати кожен вид фігур.
Щоб ускладнити завдання, дитина має скласти певний малюнок (птицю, корабель).
Другий варіант виконання вправи:
- Показати дитині зафарбоване зображення і надати фігури, необхідні для складання цього малюнка.

- Задача полягає у складанні ідентичного зображення.
Цей варіант призначений для дітей від 6 років.
Приклади і покрокові інструкції для створення аплікацій з геометричних фігур
В залежності від віку дитини аплікації виконують по-різному:
- До 2,5 років діти не вміють вирізати, тому це робить дорослий. На розсуд дорослого, приклеювати паперові деталі до картону може дитина або дорослий сам. У другому випадку, слід радитися з малюком, куди саме приклеїти деталь.
- Від 2,5 до 5 років діти уміють вирізати ножицями, але роблять це нерівно, тому при необхідності слід виправляти нерівності.
- Від 5 років діти навчаються рівно різати, тому участь дорослого в процес створення аплікації мінімально.
З 2 до 5 років діти ще нерівно вирізають фігури і способн робити найпростіші аплікації
У маленькому віці малюк намагається спростити форму, яку бачить. Наприклад, хмари, схожі на кучері, спрощуються до овалу.
Для дітей 3-5 років
Залучити маленьких дітей можуть незвичайні картинки і процес їх створення. Аплікація «Їжачок» нестандартна, але проста у створенні. Як голок використовуються долоньки з коричневої або чорної папери.
Їх можна зробити двома способами:
- Прикласти долоню дитини до паперу з звороті аркуша і простим олівцем обвести. Вирізати долоньку по контуру.
- Розфарбувати долоньку малюка фарбою і прикласти до паперу. Обводити контури не слід. Вирізати деталь.
Знадобиться 4 долоньки.
Також знадобляться наступні деталі:
- «Човник», що складається з овалу і кривого трикутника. Ця деталь послужить тілом і носом їжачка.
- Невеликий круг – кінчик носа.
- Червоне півколо – рот.
- Білий півколо – частина ока.
- Маленький чорний коло – зіниця.
- Коло з підрізаними верхньою і нижньою частиною зеленого кольору – яблуко.

- Темно-зелені ромби – 2 аркуша яблука.
- Деталь, схожа на капсулу білого кольору – ніжка гриба.
- Коричневий півколо – капелюшок гриба.
- Чотири трапеції різних розмірів – ноги.
Деталі слід приклеювати в тій послідовності, в якій вони перелічені вище. При цьому 2 долоньки розташовані пальцями вгору, одна – по діагоналі, остання – вбік.
Кінець тіла розташовується біля останньої долоньки.
Аплікація «Об’ємна сонечко»:
- Половина чорного овалу – голова.
- Два червоних або рожевих кола – тіло. Круги потрібно зігнути навпіл: одну половину приклеїти до картону, другу залишити. Половину другого кола приклеїти поряд з першою так, щоб з приклеєною частини утворилося коло.
- Чорні круги – точки. Вони розташовуються як на приклеєних, так і на відступаючих частинах тіла.
- Покупні очі різного розміру.
- Вусики і кола на їх кінцях домалювати чорним фломастером.
Картина приваблює своїм обсягом. Дитина може пограти з виступаючими частинами божої корівки.
Як зробити аплікацію «квіткова галявина»:
- Розфарбувати картонний аркуш зеленою фарбою.
- Невеликий квадрат скласти 4 рази так, щоб вийшов квадрат меншого розміру. Обрізати 3 кута (крім кута згину). Розігнути лист.
- У центр одержані з квадрата пелюсток приклеїти коло контрастного кольору.
- Зробити кілька квіток.
- Приклеїти квіти на розфарбований аркуш картону.
Картина вийде багатобарвної, тому дитині стане цікаво розглянути квіти ближче.
Для учнів 1 класу
Першокласники здатні створювати більш складні аплікації, використовуючи нові матеріали.
Аплікація «Бузок»:
- Розфарбувати картонний аркуш акварельною фарбою. При бажанні, можна зробити плавний перехід від одного кольору до іншого (від червоного до фіолетового, від фіолетового до синього або синього до блідо-блакитного).

- Дати фону підсохнути.
- Вирізати прямокутник і круг для вази.
- Приклеїти до основи спочатку прямокутник, а коло – зверху нього.
- Вирізати з гофрованого паперу зеленого кольору 4 тонкі короткі смужки. Ці смужки будуть стеблами.
- Рівномірно приклеїти стебла до кінця вази.
- Вирізати з кольорового серветки 6 деталей овальної або яйцеподібної форми. Ці деталі допоможуть позначити межі суцвіть бузку.
- Приклеїти деталі поруч зі стеблами. Так як суцвіть більше, ніж стебел, необхідно співвіднести 4 суцвіття зі стеблами, а решта приклеїти по краях вази.
- Розрізати серветки на маленькі квадрати.
- Деякі квадрату зім’яти, решта спочатку порвати, а потім зім’яти.
- Змастити суцвіття клеєм, розподілити на ньому грудочки з серветок.
- Повторити пункти 9-11 для інших суцвіть.
- Вирізати 6 листів з гофрованого паперу: 4 приклеїти на стебла, інші – по краях.
- В деяких місцях об’ємних суцвіть нанести плями рожевого акварельної фарби.
Виконати аплікацію «Гусениця» під силу кожній дитині 7 років. Процес створення займає небагато часу, тому підійде, щоб зайняти дитину на невеликий період часу.
Як робити:
- Вирізати кілька різнокольорових кіл однакового розміру.
- Приклеїти на картон кола один за одним. При бажанні, розташувати кола з підйомами, ніби повзе гусениця.
- На першому колі намалювати усмішку, приклеїти очі і домалювати вії.
- Приклеїти ріжки – два трикутника.
Для дітей 2-4 класу
Фігури, вивчені дітьми до 11 років, дозволяють створювати складні і цікаві малюнки. Складання комбінацій з геометричних фігур та вирізання дрібних деталей розвиває дрібну моторику. Зокрема, цьому сприяє аплікація «Миші».
Деталі, необхідні для першої миші:
- Сірий півколо – тіло.
- 2 чорних кола різних розмірів – носа і очей.
- 2 однакових сірих кола – вуха.

- 2 відрізка чорної дроту – вуса.
- Відрізок товстої білої нитки – хвіст.
Спочатку слід приклеювати до основи одне вухо, потім тіло, яке трохи перекриває вухо, потім інші деталі.
Деталі, необхідні для другої миші:
- Сірий овал з загостреними кінцями – тіло.
- 2 сірих кола – вуха.
- 2 маленьких чорних кола – очі.
- Чорний коло більшого розміру – ніс.
- 2 відрізка чорної дроту – вуса.
- Відрізок товстої білої нитки – хвіст.
Шматок сиру – жовтий трикутник рівносторонній. Його необхідно скласти навпіл і склеїти. На подвійному трикутнику намалювати кола і вирізати з допомогою манікюрних ножиць. Нижню частину трикутника обрізати так, щоб трикутник виявився рівностороннім.
Як розташувати елементи на сторінці:
- Приклеїти сир так, щоб кут був направлений у верхню праву діагональ.
- Першу мишу приклеїти над сиром ближче до основи. Хвіст опустити вниз і вправо так, щоб він знаходився на сирі.
- Другу миша розташувати під сиром ближче до його кінця так, щоб ніс майже упирався в край сиру.
В якості фону може виступати не тільки однотонний картон, але і картон з незвичайним орнаментом (клітка сорочки або круги). Діти віком 8-10 років здатні комбінувати різні елементи, створюючи складні сюжети.
Щоб створити аплікацію «Космос», необхідно зробити наступні моделі ракет:
- Вирізати корпус ракети, який показаний на фото нижче.
- Вирізати 3 кола контрастного кольору однакового розміру.
- Вирізати 3 кола меншого розміру.
- В кожне коло з пункту 2 приклеїти по одному колу з пункту 3. Вийдуть вікна.
- Приклеїти вікна на корпус ракети.
Друга модель ракети:
- Вирізати корпус ракети з фото.
- Вирізати два кола різного розміру.
- Вставити в маленьке коло великою.

- Вирізати овал, розрізати його на 4 частини (2 частини – крила ракети).
- Приклеїти вікно і крила до корпусу ракети.
Необхідно зробити кілька ракет і приклеїти до аркуша так, щоб вони летіли в різних напрямках. Решту площа заповнити невеликими колами і зірками. У мультфільмах з хвоста ракет виривається вогонь або дим, який можна зобразити овалами або спіральної деталлю.
Геометрична аплікація «Транспорт»
Фігури з геометричних фігур складаються в повноцінні картини при їх правильному розподілі.
Нижче розглянуті аплікації різних видів транспорту. Аплікація «Поїзд» складається з вагонів двох типів: першого вагона та інших. Спочатку перераховані фігури, необхідні для першого вагона.
| Аплікація | Фігури, які використовуються в процесі створення аплікації | Частина транспорту, яку зображує постать | Особливості розташування |
| «Поїзд» | Прямокутник | Корпус | Півколо знаходиться зліва від прямокутника |
| Півколо | |||
| Великий і маленький прямокутники | Кабіна водія | Один з прямокутників — вікно | |
| Трикутник | Труба | Частина фігури перекривається прямокутником корпусу | |
| Трикутник меншого розміру | Ліхтар | Частково перекритий півколом корпуси | |
| Прямокутник | Основа для коліс | Клеїться під корпусом | |
| 3 кола | Колеса | Розташовуються під корпусом, кріпляться на прямокутник | |
| Коло більшого розміру | Колесо | Клеїться під кабіною водія, частково перекриваючи | |
| Тонкі прямокутники | Ланцюги, що з’єднують вагони | — | |
| Прямокутники | Вагони | — | |
| По 4 кола 1 вагон | |||
| «Автобус» | Великий прямокутник | Корпус | — |
| 2 кола | Колеса | Перекривають частину корпусу, розташовуються ближче до країв прямокутника | |
| 2 прямокутника | Двері | Розташовуються близько коліс | |
| 4 більш тонких прямокутника | Вікна дверей | На кожну двері 2 вікна | |
| 2 квадрата | Вікна на корпусі | Квадратні вікна розташовуються по краях дверей, а прямокутне вікно – між ними | |
| Прямокутник | |||
| «Корабель» | Трикутник з обрізаними краями | Основна частина корабля | — |
| 3 кола | Вікна | — | |
| Тонкий довгий прямокутник | Палиця, на яку кріпляться вітрила | Клеїться лівіше середини основного трикутника | |
| Трикутник | Вітрила | Клеяться з двох сторін від палиці | |
| Півколо | |||
| Квадрат | Прапор | Розташовується у верхній частині палиці | |
| Прямокутні трикутники | |||
| «Вантажівка» | 2 прямокутники різних розмірів | Кабіна водія і передня частина | Менший прямокутник кріпиться збоку від великого |
| Квадрат | Вікно | — | |
| Прямокутник | Кузов | — | |
| 2 кола | Колеса | Один коло розташований під кабіною водія, а другий – під кузовом. Частина кіл перекриває ту частину вантажівки, до якого кріпиться. Частина кіл перекриває ту частину вантажівки, до якого кріпиться. | |
| Трикутник | Вантаж | — |
Аплікації з геометричних фігур «Тварини»
Тварин можуть зобразити навіть найменші.
Аплікація «Мавпа» складається з наступних фігур:
- Овал – тіло.
- 4 тонких овалу – руки і ноги.
- Тонкий вигнутий циліндр – хвіст.
- Коло – особа.
- 4 кола (2 маленьких і 2 середніх) – вуха.
- Коло – ніс.
- 2 білих і 2 чорних кола – очі.
Аплікація «Ведмідь» складається з тих самих фігур, але в якості вух використовуються 2 півкола, а хвіст не видно.
Аплікація «Курча»:
- Вирізати 2 овалу і приклеїти на відстані один від одного. Ці овали стануть крилами.
- Вирізати жовтий овал – тіло майбутнього курчати. Приклеїти тіло між крилами так, щоб воно перекривало частина крил.
- Зверху приклеїти коло – особа курчати.
- Вирізати маленький помаранчевий коло. Всередину приклеїти ще більш маленький чорний коло.
- Склеєні кола приклеїти на обличчя збоку, ніби курча дивиться вправо або вліво.
- Вирізати 3 червоних трикутника.
- Один трикутник приклеїти збоку від особи поряд з оком – цей трикутник буде дзьобом.
- Інші трикутники приклеїти під тілом – це лапи птиці.
- Один прямокутний жовтий трикутник приклеїти з того боку, де розташований дзьоб. Цей трикутник – хвіст.
Щоб скласти повноцінну картину, необхідно додати траву, що складається з овалів різних розмірів і довжини, поруч з лапами курчати. Таким чином, птах ніби бігає по полю.
Аплікація слон складається з наступних деталей:
- Коло – тіло.
- Прямокутники – ноги.
- Напівкола – ступні.
- Тонкий трикутник – хвіст.
- Півколо більшого розміру – вухо.
- Невеликий круг – голова.
- Прямокутник – хобот.

- Білий і чорний кола – око.
Рекомендується дати дитині вибрати самостійно, яка тварина він хоче зобразити і як хоче це зробити.
Малюнки з геометричних фігур: завдання для дітей
Вивчивши геометричні фігури, дитині необхідно зрозуміти, як їх комбінувати в складні малюнки.
Фігури з геометричних фігур – перший етап вивчення. Другий етап – складання фігур на зображення навколишніх предметів.
Варіанти вправ на знання геометричних фігур:
- Роздрукувати бланк, на якому зображені різні предмети. Завдання дитини – назвати фігури, які він бачить у представлених предметах.
- Розділити його на 2 частини. У лівій частині намалювати за пари з двох однакових фігур. Вправа полягає в тому, що дитина повинна намалювати в правій частині фігури, які можна отримати з пар фігур зліва (2 прямокутних трикутника – прямокутник).
- Роздрукувати бланки, на яких зображені різні предмети (поїзд, корабель, ялинка з кульками). Завдання: порахувати кількість кожної з фігур на малюнках.
- Роздрукувати бланки, на яких намальовані картинки і задано певну кількість якої-небудь фігури. Необхідно знайти малюнок, на якому присутній вказану кількість заданої фігури.
Перераховані вище завдання допомагають дитині запам’ятати фігури і навчитися правильно рахувати. З геометричними фігурами дитина починає знайомитися з самого народження, дізнаючись все більше інформації про навколишній світ. Навчання рекомендується проводити у формі гри, складаючи з дитиною різні комбінації фігур.
Відео про геометричні фігури
Як зробити фігури з геометричних фігур — вироби для дітей у цьому відео:
Вчимося розрізняти і називати геометричні фігури – Освіта.UA
Найкращі практичні завдання, що допоможуть дітям вивчити назви й зовнішній вигляд геометричних фігур |
Проект «Розвиток дитини» пропонує батькам, вихователям та вчителям двадцять п’ять оригінальних практичних завдань, які допоможуть дітям вивчити назви й зовнішній вигляд геометричних фігур, розвинути просторове мислення й уважність та сприятимуть розвитку конструктивно-технічних здібностей.
Виконання запропонованих завдань спрямоване на створення підґрунтя для подальшого розвитку навичок конструювання, моделювання, здатності уявляти предмети в тривимірному просторі й аналізувати їхнє положення.
Вивчаємо фігури під час читання: овал, прямокутник. Це завдання допоможе дитині розвинути навички читання, закріпити знання про овал і прямокутник та частини мови. Дитині пропонується прочитати історію і позначити в тексті прикметники – овалами, власні назви – прямокутниками. Також потрібно порахувати й записати кількість фігур різних.
Шлях із фігур №1: коло, трикутник. Це завдання містить лабіринт, у якому лінії від зайчика та вовка мають привести до різних фігур. Дитині пропонується заповнити проміжки на шляху тварин відповідними фігурами, малюючи кола й трикутники за пунктирними лініями та самостійно.
Перетворюємо фігури на новорічні предмети або істот. Це завдання стане чудовою нагодою для розвитку фантазії вашої дитини, водночас допомагаючи закріпити знання про геометричні фігури. На сторінці розміщено 5 фігур. Дитині пропонується домалювати до кожної фігури певні елементи таким чином, щоб перетворити її на річ або істоту, що пов’язані з Новим роком.
Дитині пропонується домалювати до кожної фігури певні елементи таким чином, щоб перетворити її на річ або істоту, що пов’язані з Новим роком.
Уявляємо вигляд фігур зверху №1. Це завдання спрямовано на розвиток просторового мислення. Дитині пропонується розглянути фігуру з кубиків і уявити, як ця фігура виглядатиме, якщо дивитися на неї зверху. Виконуючи завдання, дитина розвиватиме уважність, дрібну моторику, здатність уявляти предмети в просторі.
Вибираємо об’ємну фігуру правильної форми №1. Це завдання допоможе розвинути просторове мислення й зорове сприйняття дитини. У ньому дитині пропонується розглянути 3 фігури з кубів, а також пронумеровані заглибини на полі. Потрібно визначити, яка з фігур до якої заглибини пасує, й поставити біля кожної фігури номер заглибини відповідної форми.
Веселі кубики №1. Це завдання містить три об’ємні фігури з кубів. Дитині пропонується перемалювати ці фігури по точках (за бажанням фігури можна розмалювати). Також потрібно порахувати кількість кубів у кожній фігурі й записати ці числа поряд.
Вивчаємо об’ємні фігури: куб. Це завдання допоможе дитині вивчити таку об’ємну фігуру, як куб. Воно містить підписаний малюнок куба й малюнки різноманітних предметів. Серед наявних малюнків дитині потрібно розмалювати ті, на яких зображено предмети, що мають форму куба.
Три куби: розвиваємо просторове мислення. Це завдання-розмальовка сприятиме розвитку геометричних уявлень і просторового мислення дитини. Воно містить чорно-білий малюнок, який дитині пропонується розмалювати, не залишаючи незафарбованих квадратиків.
Тренуємо просторову уяву. Це завдання допоможе дитині розвинути математичне й просторове мислення, увагу й кмітливість. Дитині пропонується розглянути 8 фігур з клітинок. Потрібно знайти в кожній фігурі запропоновану комбінацію клітинок і розмалювати повтори цієї комбінації різними кольорами (як у зразку).
З яких фігур можна скласти куб? Це завдання допоможе дитині розвинути математичне мислення, увагу й кмітливість, а також краще вивчити таке геометричне поняття, як куб. Виконуючи завдання, дитина розвиватиме логіко-математичні здібності, просторову уяву, пізнавальну активність, учитиметься моделювати математичні ігри.
Погляд зверху: розвиваємо просторове мислення. Це завдання-головоломка сприятиме розвитку геометричних уявлень і просторового мислення дитини. Воно містить малюнок піраміди, складеної з різних типів ліній. Дитині пропонується уявити, як буде виглядати ця фігура зверху й вибрати один з шести варіантів зовнішнього вигляду піраміди, поданих унизу сторінки.
Малюємо фігури, не відриваючи руки. Це завдання допоможе розвивати логіко-математичну компетентність дитини. На аркуші є шість фігур, що складаються з прямокутних і трикутних елементів. Дитині пропонується намалювати кожну зображену фігуру по клітинках, не відриваючи руки від паперу і не проводячи двічі по одній і тій самій лінії.
Малюємо та вивчаємо геометричні фігури. Це завдання допоможе дитині вивчити базові геометричні форми. На сторінці геометричні фігури та їхні контури розміщені хаотично. Задача дитини – назвати ці фігури, намалювати кожну з них за цілісним контуром, а потім за основними точками. Далі необхідно розмалювати три однакові фігури в однаковий колір.
Намалюй фігури по точках. У цьому завданні дитині пропонується намалювати двомірні геометричні фігури по точках, що позначають їх кути. Завдання може стати першим кроком до вивчення геометричних фігур. Крім того, завдання розвиватиме у дитини більш чітку координацію дрібних рухів та просторове сприйняття.
Скопіюй фігури №1: на 6 точок. Це завдання допоможе дитині розвинути зорово-моторну координацію, просторове мислення та дрібну моторику. Воно містить шість фігур-зразків (на 6 точок кожна). Дитині пропонується відтворити ці фігури за опорними точками.
Воно містить шість фігур-зразків (на 6 точок кожна). Дитині пропонується відтворити ці фігури за опорними точками.
Малювання геометричних фігур. Цей комплект завдань — перший крок до вивчення геометричних фігур. Завдання також сприяють здобуттю дитиною навичок дрібної моторики. У завданнях дитина кілька разів з’єднує пунктирні лінії для малювання різноманітних геометричних фігур, а потім самостійно малює відповідну фігуру у спеціально відведеному місці.
Геометричні фігури: вивчаємо трикутник. Це завдання сприятиме розвитку просторової уяви дитини та її творчого мислення, а також навчить розпізнавати таку геометричну фігуру, як трикутник. Дитині необхідно написати назву цієї фігури за пунктирними лініями, потім намалювати трикутник спочатку за пунктиром, а потім самостійно, виконати інші завдання.
Кросворд «Геометричні фігури». Цей ілюстрований кросворд пропонує дитині сімнадцять різних геометричних фігур, сім з яких плоскі, а десять – об’ємні (просторові). Вона має пригадати їх назви та вписати у відповідні клітинки.
Вивчаємо дванадцять просторових фігур. Це завдання допоможе дитині познайомитися з різними просторовими геометричними фігурами, запам’ятати їх назви та навчитись вирізняти з-поміж інших фігур за ключовими особливостями. Дитині треба з’єднати лінією кожну фігуру з її назвою.
Рахуємо фігури веселого конструктора №1. Завдання пропонує дитині порахувати, записати кількість геометричних фігур кожного виду та розмалювати їх. Також потрібно скласти й розв’язати відповідні приклади.
Кольори фігур: розмальовуємо квадрати. Ця розмальовка допоможе дитині закріпити знання про зовнішній вигляд і назву такої фігури, як квадрат, розвинути просторове мислення й зорове сприйняття. Виконуючи завдання комплекту, дитина навчиться краще уявляти розташування предметів у просторі, розвине дрібну моторику й увагу.
Головоломка «Кольорові фігури». Це завдання-головоломка допоможе дитині розвинути логіко-математичне мислення, увагу й кмітливість. Дитині пропонується розмалювати фігури, використовуючи лише чотири кольори. Фігури одного кольору не повинні перетинатися.
Головоломка «Скільки квадратів?» Це завдання-головоломка допоможе дитині розвинути логіко-математичне мислення, увагу й кмітливість. Дитині пропонується визначити й записати, скільки квадратів розміщено у кожному колі. Потрібно розмалювати видимий квадрат зеленим кольором, а частини прихованих квадратів – улюбленими кольорами, так, щоби було видно кількість фігур.
Круг, коло, куля: вчимося розрізняти площинні й об’ємні геометричні фігури. Завдання допоможе дитині закріпити знання про геометричні фігури круг, коло й кулю, сприятиме розвитку спостережливості, уваги, формуванню математичного мислення.
Кросворд у малюнках «Плоскі геометричні фігури». Це завдання-кросворд допоможе дитині навчитися розрізняти плоскі геометричні фігури, а також опанувати правопис їхніх назв, тренуючи при цьому пам’ять, увагу, логічне мислення й дрібну моторику. Дитині потрібно подивитися на малюнки геометричних фігур і вписати відповідні назви в клітинки кросворда.
Кожне завдання можна роздрукувати на звичайному або кольоровому принтері та використовувати необмежену кількість разів. Завантаження завдань для дітей доступне для користувачів сайту після швидкої реєстрації.
БІЛЬШЕ ЗАВДАНЬ
Освіта.ua
12.05.2020
Розмальовки Геометричні фігури
Розмальовки Геометричні фігури – це не просто можливість зайняти дитину малюванням, це простий і захоплюючий спосіб познайомити його з геометричними фігурами. Трикутники, ромби, квадрати, овали і трапеції представлені на малюнках цієї розмальовки, як у вигляді звичайних геометричних фігур, так і збудованих з них фігурок тварин і людей. Є тут і маленькі будиночки, що складаються з одного квадрата і трикутника, і прекрасні замки, і хитромудрі конструкції з овалів і ромбів, і прикрашені зірками башточки, і космічні кораблі, і багато іншого. Розфарбовуючи всі ці об’єкти, малюк навчитися розрізняти елементи геометричного достатку і відповідати на пов’язані з ним питання.
Є тут і маленькі будиночки, що складаються з одного квадрата і трикутника, і прекрасні замки, і хитромудрі конструкції з овалів і ромбів, і прикрашені зірками башточки, і космічні кораблі, і багато іншого. Розфарбовуючи всі ці об’єкти, малюк навчитися розрізняти елементи геометричного достатку і відповідати на пов’язані з ним питання.
Динозавр з геометричних фігур
Розфарбуй об’ємні геометричні фігури
Розфарбування Об’ємні геометричні фігури
Заєць з геометричних фігур
Будинок з геометричних фігур
Порахуй геометричні фігури
Розфарбування Геометричні фігури
Корабель з геометричних фігур
Об’ємні геометричні фігури
Божа корівка з геометричних фігур
Робот з геометричних фігур
Птиці з геометричних фігур
Веселі геометричні фігури
Обведи геометричні фігури
Катінка Геометричні фігури
Вовк з геометричних фігур
Малюнок Геометричні фігури
Ведмідь з геометричних фігур
Корабель з геометричних фігур
Кіт з геометричних фігур
Геометричні фігури по точках
Фігурки
Кораблтк
Геометричні фігури
Грають діти
Ракета
Політ у космос
Фігури
Замок
Зайчик
Фігури
Квітка
Всі фігури
Вивчення фігур
Коло і ромб
Геометричні фігури
Слоненя
Будиночок
Будиночок біля дерева
Будиночок
Назви
Картинки тварин з геометричних фігур. Малювання геометричних тел Як намалювати 2 геометричні фігури
Виявлення індивідуально-типологічних відмінностей.
Інструкція до тесту
«Вам потрібно намалювати фігуру людини, складену з 10 елементів, серед яких можуть бути трикутники, кола, квадрати. Ви можете збільшувати або зменшувати ці елементи (геометричні фігури) в розмірах, накладати один на одного в міру потреби. Важливо, щоб всі ці три елементи в зображенні людини були присутні, а сума загальної кількості використаних фігур дорівнювала десяти. Якщо при малюванні ви використовували більшу кількість фігур, то потрібно закреслити зайве, якщо ж вами використано фігур менше, ніж десять, необхідно домалювати відсутні. Виконайте малюнок по даній інструкції ».
Ви можете збільшувати або зменшувати ці елементи (геометричні фігури) в розмірах, накладати один на одного в міру потреби. Важливо, щоб всі ці три елементи в зображенні людини були присутні, а сума загальної кількості використаних фігур дорівнювала десяти. Якщо при малюванні ви використовували більшу кількість фігур, то потрібно закреслити зайве, якщо ж вами використано фігур менше, ніж десять, необхідно домалювати відсутні. Виконайте малюнок по даній інструкції ».
матеріал: Випробуваним пропонується три аркуша паперу розміром 10 × 10 см, кожен лист нумерується і підписується. На аркуші № 1 виконується перший пробний малюнок; далі, відповідно, на аркуші № 2 — другий, на аркуші № 3 — третій. Після виконання трьох малюнків дані обробляються. При порушенні інструкції матеріал не обробляється.
Обробка результатів тесту
Обробка даних проводиться таким чином: підраховується кількість витрачених в зображенні чоловічка трикутників, кіл і квадратів (по кожному малюнку окремо), і результат записується у вигляді тризначних чисел, де
- сотні позначають кількість трикутників,
- десятки — кількість кіл,
- одиниці -кількість квадратів.
Ці тризначні цифри становлять так звану «формулу малюнка», по якій відбувається віднесення малюють до відповідних типів і підтипів, які представлені в таблиці.
Інтерпретація результатів тесту
Інтерпретація тесту заснована на тому, що геометричні фігури, які використовуються в малюнках, розрізняються за семантикою. трикутник зазвичай відносять до «гострої», «наступальної» фігурі, пов’язаної з чоловічим началом. коло — фігура обтічна, більш співзвучна зі співчуттям, м’якістю, округлістю, жіночністю. З елементів квадратної форми будувати що-небудь легше, ніж з інших, тому квадрат, Прямокутник інтерпретуються як специфічно технічна конструктивна фігура, «технічний модуль».
типи особистості
I тип — « керівник». Зазвичай це люди, які мають схильність до керівної та організаторської діяльності. Орієнтовані на соціально-значущі норми поведінки, можуть володіти даром хороших оповідачів, які базуються на високому рівні мовного розвитку. Мають гарну адаптацією в соціальній сфері, Домінування над іншими утримують в певних межах.
Зазвичай це люди, які мають схильність до керівної та організаторської діяльності. Орієнтовані на соціально-значущі норми поведінки, можуть володіти даром хороших оповідачів, які базуються на високому рівні мовного розвитку. Мають гарну адаптацією в соціальній сфері, Домінування над іншими утримують в певних межах.
формули малюнків: 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640.
- найбільш жорстко домінування над іншими виражено у підтипів 901, 910, 802, 811, 820;
- ситуативно -у 703, 712, 721, 730;
- при впливі промовою на людей — вербальний керівник або «викладацький підтип» — 604, 613, 622, 631, 640.
Потрібно пам’ятати, що прояв даних якостей залежить від рівня психічного розвитку. При високому рівні розвитку індивідуальні риси розвинені, реалізовані, досить добре усвідомлюються. При низькому рівні розвитку можуть не виявлятися в професійної діяльності, А бути присутнім ситуативно, гірше, якщо неадекватно ситуацій. Це відноситься до всіх характеристикам.
II тип — « відповідальний виконавець»Володіє багатьма рисами типу« керівник », проте в прийнятті відповідальних рішень часто присутні коливання.
Даний тип людей більш орієнтований на «вміння робити справу», високий професіоналізм, Володіє високим почуттям відповідальності і вимогливості до себе та інших, високо цінує правоту, тобто характеризується підвищеною чутливістю до правдивості. Часто вони страждають соматичними захворюваннями нервового походження як наслідок перенапруги.
формули малюнків: 505, 514, 523, 532, 541, 550.
III тип — « тривожно-недовірливий»-Характеризується різноманітністю здібностей та обдарованості — від тонких ручних навичок до літературної обдарованості. Зазвичай людям даного типу тісно в рамках однієї професії, вони можуть поміняти її на абсолютно протилежну і несподівану, мати також хобі, яке по суті є другою професією. Фізично не переносять безлад і бруд. Зазвичай конфліктують через це з іншими людьми. Відрізняються підвищеною ранимою і часто сумніваються в собі. Потребують м’якому підбадьорювання.
Зазвичай конфліктують через це з іншими людьми. Відрізняються підвищеною ранимою і часто сумніваються в собі. Потребують м’якому підбадьорювання.
формули малюнків: 406, 415, 424, 433, 442, 451, 460.
- 415 — «поетичний підтип» — зазвичай особи, які мають таку формулу малюнка, мають поетичної обдарованістю;
- 424 — підтип людей, відомих по фразі: «Як це можна погано працювати? Я собі не уявляю, як це можна погано працювати ». Люди такого типу відрізняються особливою ретельністю в роботі.
IV тип — « вчений». Ці люди легко абстрагуються від реальності, мають «концептуальним розумом», відрізняються здатністю розробляти «на все» свої теорії. Зазвичай мають душевним рівновагою і раціонально продумують свою поведінку.
формули малюнків: 307, 316, 325, 334, 343, 352, 361, 370.
- 316 характеризується здібностями створювати теорії, переважно глобальні, або здійснювати велику і складну координаційну роботу;
- 325 — підтип, який характеризується великою захопленістю пізнання життя, здоров’я, біологічними дисциплінами, медициною.
Представники даного типу часто зустрічаються серед осіб, що займаються синтетичними видами мистецтва: кіно, цирк, театрально-видовищна режисура, мультиплікація і т.д.
V тип — « інтуїтивний». Люди цього типу володіють сильною чутливістю нервової системи, Високою її виснажуваністю.
Легше працюють на переключення від однієї діяльності до іншої, зазвичай виступають «адвокатами меншини», за яким стоять нові можливості. Мають підвищену чутливість до новизни. Альтруїстичні, часто проявляють турботу про інших, мають гарні ручними навичками і образним уявою, що дає можливість займатися технічними видами творчості.
Зазвичай виробляють свої норми моралі, мають внутрішнім самоконтролем, тобто воліють самоконтроль, негативно реагуючи на посягання, що стосуються їх волі.
формули малюнків: 208, 217, 226, 235, 244, 253, 262, 271, 280.
- 235 — часто зустрічається серед професійних психологів або осіб з підвищеним інтересом до психології людей;
- 244 — має здатність літературної творчості,
- 217 — має здатність до винахідницької діяльності;
- 226 — велика потреба в новизні, зазвичай ставить дуже високі критерії досягнень для себе.

VI тип — « винахідник, конструктор, художник». Часто зустрічається серед осіб з «технічної жилкою». Це люди, що володіють багатою уявою, просторовим баченням, часто займаються різними видами технічного, художнього та інтелектуального творчості. Найчастіше інтравертіровани, так само, як інтуїтивний тип, живуть власними моральними нормами, не сприймають ніяких впливів з боку, крім саме контролю.
Емоційні, одержимі своїми оригінальними ідеями.
формули малюнків: 109, 118, 127, 136, 145, 019, 028, 037, 046.
- 019 — зустрічається серед осіб, які добре володіють аудиторією;
- 118 — тип з найбільш сильно вираженими конструктивними можливостями і здатністю до винаходів.
VII тип — « емотивний». Мають підвищеним співпереживанням по відношенню до інших людей, важко переживають жорстокі кадри фільму, можуть надовго бути вибитими з колії і бути враженим від жорстоких подій. Болі і турботи інших людей знаходять у них участь, співпереживання і співчуття, на яке вони витрачають багато власної енергії, в результаті стає скрутної реалізація їх власних здібностей.
формули малюнків: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.
VIII тип — « нечутливий до переживань інших». Володіє протилежною тенденцією емотивної типу. Зазвичай не відчуває переживань інших людей або ставиться до них з неувагою і навіть посилює тиск на людей.
Якщо це хороший фахівець, то він може змусити інших робити те, що він вважає за потрібне. Іноді для нього характерна «черствість», яка виникає ситуативно, коли в силу будь-яких причин людина замикається в колі власних проблем.
формули малюнків: 901, 802, 703, 604, 505, 406, 307, 208, 109.
Вивчення і малювання геометричних тіл в навчальному академічному малюнку є основою для освоєння принципів і методів зображення більш складних форм.
навчання образотворчим мистецтвам вимагає суворого дотримання послідовності ускладнення навчальних завдань і багаторазових повторень для оволодіння технікою. Найбільш відповідною формою для засвоєння принципів побудови малюнка є геометричні тіла, Що мають в своїй основі ясні конструктивні будови. на простих геометричних тілах найлегше зрозуміти і засвоїти основи об’ємно-просторової конструкції, передачі форм в перспективному скороченні, закономірності світлотіней і пропорційні співвідношення.
Найбільш відповідною формою для засвоєння принципів побудови малюнка є геометричні тіла, Що мають в своїй основі ясні конструктивні будови. на простих геометричних тілах найлегше зрозуміти і засвоїти основи об’ємно-просторової конструкції, передачі форм в перспективному скороченні, закономірності світлотіней і пропорційні співвідношення.
Вправи з малювання простих геометричних тіл дозволяють не відволікатися на деталі, наявні в більш складних формах, таких, як архітектурні об’єкти і тіло людини, а цілком зосередитися на головному — образотворчої грамоти.
Правильно поняті і засвоєні закономірності при зображенні простих форм повинні сприяти більш усвідомленому підходу до малювання складних форм в подальшому.
Для того, щоб навчитися грамотно і правильно зображати форму предмета, необхідно усвідомити приховану від очей внутрішню структуру предмета — конструкцію. Під словом «конструкція» мається на увазі «будова», «структура», «план», тобто взаємне розташування частин предмета і їх співвідношення. Це важливо знати і розуміти при зображенні будь-яких форм. Чим складніше форма, тим більше і серйозніше доведеться вивчати внутрішню будову натурної моделі. Так, наприклад, при малюванні живої натури — голови або фігури людини, крім знання конструктивних особливостей неодмінно слід знати і пластичну анатомію. Тому без ясного розуміння будови форми і характеру предмета неможливо грамотно освоїти малюнок.
При зображенні просторових форм, крім знання закономірностей будови конструкції, необхідні знання про закони перспективи, пропорціях, світлотіні. Для правильного зображення натурної моделі необхідно привчити себе завжди аналізувати натуру, чітко уявляти її зовнішню і внутрішню будову. Підходити до роботи слід усвідомлено, з наукової точки зору. Тільки таке малювання буде сприяти успішному виконанню робіт по зображенню як простих, так і складних форм.
Малювання геометричних форм малодосвідчених малювальників здається на перший погляд досить легким.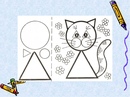 Але це далеко не так. Для впевненого оволодіння малюнком перш за все необхідно освоїти методи аналізу форм і принципи побудови простих тел. Будь-яка форма складається з плоских фігур: прямокутників, трикутників, ромбів, трапецій та інших багатокутників, які відмежовують її від навколишнього простору. Завдання полягає в тому, щоб правильно зрозуміти, як ці поверхні поєднуються між собою, утворюючи форму. Для правильного її зображення необхідно навчитися малювати такі фігури в перспективі, щоб без праці виділяти на площині об’ємні тіла, обмежені цими плоскими фігурами. Плоскі геометричні фігури є основою розуміння конструктивного побудови об’ємних тіл. Так, наприклад, квадрат дає уявлення про побудову куба, прямокутник — про побудову призми паралелепіпеда, трикутник — піраміди, трапеція — усіченого конуса, коло видається кулею, циліндром і конусом, а елліпсовідниє фігури — кулястими (яйцевидним) формами.
Але це далеко не так. Для впевненого оволодіння малюнком перш за все необхідно освоїти методи аналізу форм і принципи побудови простих тел. Будь-яка форма складається з плоских фігур: прямокутників, трикутників, ромбів, трапецій та інших багатокутників, які відмежовують її від навколишнього простору. Завдання полягає в тому, щоб правильно зрозуміти, як ці поверхні поєднуються між собою, утворюючи форму. Для правильного її зображення необхідно навчитися малювати такі фігури в перспективі, щоб без праці виділяти на площині об’ємні тіла, обмежені цими плоскими фігурами. Плоскі геометричні фігури є основою розуміння конструктивного побудови об’ємних тіл. Так, наприклад, квадрат дає уявлення про побудову куба, прямокутник — про побудову призми паралелепіпеда, трикутник — піраміди, трапеція — усіченого конуса, коло видається кулею, циліндром і конусом, а елліпсовідниє фігури — кулястими (яйцевидним) формами.
Всі предмети мають об’ємно-просторові характеристики: висоту, довжину і ширину. Для визначення і зображення їх на площині користуються точками і лініями. Точками визначаються характерні вузли конструкції предметів, ними встановлюється взаємне просторове розташування вузлів, що характеризує конструкцію форми в цілому.
Лінія є одним з основних образотворчих засобів. Лініями позначають контур предметів, що утворюють їх форму. Ними позначають висоту, довжину, ширину, конструктивні осі, допоміжні, що визначають простір лінії, лінії побудови і багато іншого.
Для ґрунтовного вивчення геометричні форми краще за все слід розглядати у вигляді прозорих каркасних моделей. Це дозволяє краще простежити, зрозуміти і засвоїти основи просторового побудови конструкцій і перспективного скорочення форм геометричних тел: куба, піраміди, циліндра, кулі, конуса і призми. Разом з тим, такий прийом в значній мірі полегшує побудова малюнка, в якому чітко простежуються всі просторові кути, ребра, грані тіла, незалежно від їх поворотів в просторі і в перспективному скороченні. Каркасні моделі дозволяють розвинути у художника-початківця об’ємно-просторове мислення, тим самим сприяючи правильному зображенню геометричної форми на площині паперу.
Каркасні моделі дозволяють розвинути у художника-початківця об’ємно-просторове мислення, тим самим сприяючи правильному зображенню геометричної форми на площині паперу.
Для ґрунтовного закріплення в свідомості художника об’ємно-просторового уявлення про будову цих форм було б найбільш ефективним виконати їх своїми руками. Моделі можна зробити без особливих зусиль з підручних матеріалів: звичайної гнучкої алюмінієвої, мідної або будь-який інший дроту, дерев’яних або пластмасових рейок. В подальшому, з метою засвоєння закономірностей світлотіні, можна буде виготовити моделі з паперу або тонкого картону. Для цього необхідно зробити заготовки — відповідні розгортки або окремо вирізані площини для склеювання. Не менш важливим є сам процес моделювання, який більше принесе користі для усвідомлення учнями сутності будови тієї чи іншої форми, ніж використання вже готової моделі. Для виготовлення каркасних і паперових моделей буде потрібно чимало часу, тому в цілях його економії не слід робити моделі великого розміру — достатньо, якщо їх габарити не будуть перевищувати трьох-п’яти сантиметрів.
Повертаючи виготовлену паперову модель під різними кутами до джерела світла, можна простежити за закономірностями світла і тіні. При цьому слід звернути увагу на зміну пропорційних відносин частин предмета, а також на перспективне скорочення форм. Наближаючи і віддаляючи модель від джерела світла, можна побачити, як змінюється контрастність освітлення на предмет. Так, наприклад, пр наближенні до джерела світла світло і тінь на формі набувають найбільшу контрастність, а в міру віддалення стають менш контрастними. Причому, прилеглі кути і грані будуть найбільш контрастними, а кути і грані, що знаходяться в просторової глибині, — менш контрастними. Але найголовніше на початковому етапі малювання — це вміння правильно відображати об’ємно-просторову конструкцію форм за допомогою точок і ліній на площині. Це є основним принципом в освоєнні малюнка простих геометричних форм, а також при подальшому вивченні більш складних форм і усвідомленому їх зображенні.
Як навчитися складати штрих за формою предмета- будемо вдосконалити свою майстерність володіння олівцем і вчитися створювати малюнок геометричних фігур, Створюючи їх обсяг. У нашому арсеналі є куб, куля, конус і циліндр.
Наша робота буде поділятися на дві частини. Перша частина-ми малюємо по- поданням. Можливо у вас є макети цих фігур, якщо немає, то тоді можете заглянути на сторінку як зробити макет геометричних фігур і, власне, зробити їх, але почнемо ми з вами з іншого. Ми почнемо з розуміння, аналізу форми спочатку без макетів. Ви можете спочатку їх створити і іноді поглядати на них при малюванні, але головне зараз-навчитися аналізувати, логічно мислити, вся ваша робота зараз полягає в тому, що-б думаючи, без натури, навчитися передавати форму цих основних фігур. Спочатку адже робота проходить в голові, а не перед очима. Вірно?
Друга частина-будемо малювати з натури, але так-же, як і в першому випадку, що не чіпляємося до натури сильно, а в першу чергу думаємо і аналізуємо самі, і тепер уже перевіряємо себе з тим, що нам показує натура.
Отже, перша частина. Можна малювати на форматі А3. Беремо ватман, олівець і малюємо фігуру, також не погано використовувати знання перспективи при побудові її. А потім починаєте «ложить» штрих за формою, виліплюючи обсяг фігури за допомогою свого розуму і олівця.
Ми вже знаємо, що світлотінь розподіляється по формі предмета, створюючи тональні градації, або зони. Поки візьмемо три основние- світло, півтінь і тінь. Обмежуємося лише фігурами, не використовуючи весь простір.
Давайте намалюємо куб. Уникаємо помилок. У мене на малюнку зліва сильно передана перспектива, надто, так не робіть. Тут досить зовсім небагато передати її, злегка спотворивши форму. Подивіться на малюнок справа. Бачите різницю між передньою стінкою і задньої? Цього достатньо. Не такі у нас великі розміри використовуються, що- б ми з малих форм перетворювали архітектуру.
Поговоримо про передачі світла. Світло, тінь і півтінь показані.
Але не забудьте про золотом правіле- світло віддаляючись за формою предмета темніє, тінь- світлішає. Дивіться: світло, віддаляючись в перспективу злегка втрачає свою яскравість, додайте туди трохи штріховочкі. А тепер півтінь і тінь, та-ж картина, але в зворотному порядку. Тінь віддаляючись слабшає, злегка світлішає. Але все одно, загальний тон тіні ніколи не буде світліше загального тону світла, і півтінь теж не виривається зі своїх тонових кордонів. Все на своєму місці.
Дивимося ще: як ми проводили навчання з першого нашого уроку, см. Основи малюнка, про те не забуваємо і зараз. Ближні до нас кути і грані виділяємо, робимо на них акценти. Ближня грань і кути у мене акцентовані, ніж та беруть основну увагу на себе, все інше плавно йде в простір. Але сильно тут цей простір не потрібно передавати, так як відстані у нас, в принципі, маленькі.
Зауваження: як визначити загальний тон- пріщурьте трохи очі. Різкість зменшиться і ви зможете побачити все в загальному. І ще не треба дивитися на роботу «влоб», частіше віддаляйте її від себе, розсіюйте зір, що не чіпляйтеся за деталі.
І далі інші фігури. Ці фігури, в загальному, у нас досить обтічні, заокруглени, так- що помічаємо наступне:
Припустимо, першим в ряду стоїть куля. Акцентом на ньому тут є тінь і найбільш сильна вона буде в тому місці, де куля наближений до нас найбільше. По краях у мене акцентів немає, так як там форма пішла в простір-враховуйте цей момент при малюванні обтічної форми.
Так-же справа йде і з циліндром і конусом. Там, де форма починає завертатися і йде в простір-акцент робити не варто. Але де і потрібно акцентувати форму, то там, де йде злам форми і там, де це буде ближче всього до наших очей.
Зверніть увагу на конус- нижня частина його до нас наближена більше, ніж верхівка. Значить, нижня частина його буде передана сильніше, а піднімаючись до верху слабее- дивіться на тінь, внизу вона сильніша, в той час як піднімаючись вгору вона втрачає свою активність.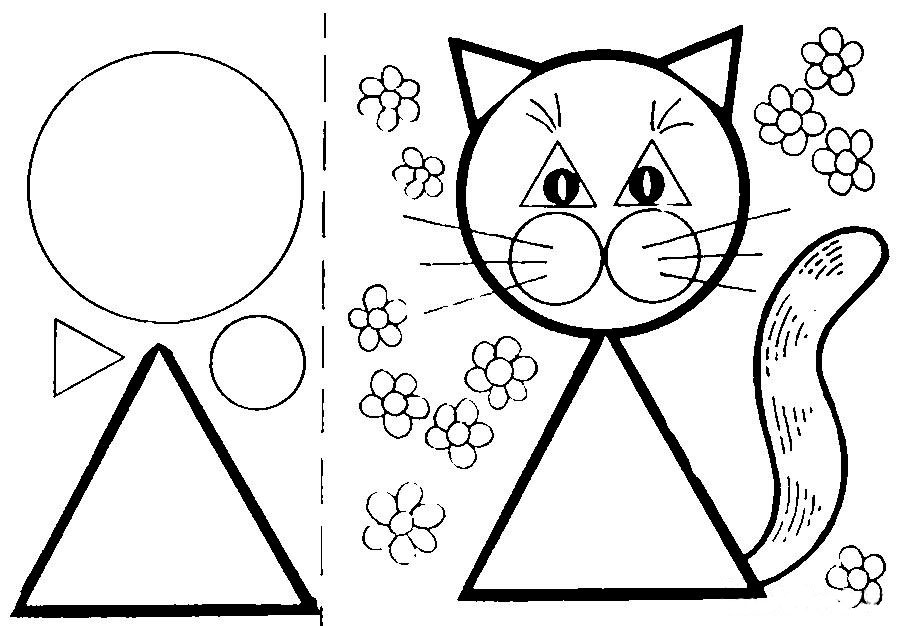 Не робіть її однаковою тональністю по всій висоті. Величини ці тут не величезні, але все одно існують, інакше умовне простір правильно не передати.
Не робіть її однаковою тональністю по всій висоті. Величини ці тут не величезні, але все одно існують, інакше умовне простір правильно не передати.
Зупиняю вашу увагу на штриховке. Це щось ні- на- є стовідсотковий штрих, який лягає по формі. Незважаючи на те, що він кілька одноманітний і нудний, але дуже корисний в плані навчання. Він вчить дисциплінованості, концентрації уваги, вчить робити рівні лінії і просто чистоті виконання. Рекомендую виконати цю роботу із застосуванням саме цього штриха, просто намагайтеся «виліплює» форму геометричної фігури, відчуйте руками і очима весь її обсяг і як її форма «живе» в просторі. Написано дивно, але намагаюся якомога соковитіше передати вам всю красу цієї вправи. А про штрихах, які повинні лягати за формою предмета і які ними не є ми з вами далі ще поговоримо.
І непережівайте, якщо щось не буде виходити. Ніхто не застрахований від помилок, а їх може бути багато і ідеального на світі не існує нічого. Але у кожного з нас є можливість спробувати ще раз, щоб зробити ще краще.
Як намалювати геометричні фігури
Як намалювати геометричні фігури-тепер спробуємо намалювати геометричні фігури з оточенням. Оповита їх повітрям, намалюємо в просторі. Беремо основні:
Першим у нас братова циліндр. Ставимо циліндр на предметну плоскость- стіл, освітлення ставимо так, що- б тінь від постаті падала красиво на предметну площину, не була ні сильно розтягнутої, ні маленькой- була гармонійною і підкреслювала обсяг фігури.
Натягніть папір на планшет, щоб створити чистий малюнок. Беріть планшет розміром 30-40, для такої роботи цілком достатньо.
Тепер нам потрібно закомпоновано наш циліндр в площині листа, знайдіть його гармонійне місце в просторі листа, враховуючи і тіні, обов’язково. Використовуйте для пошуку пропорцій окомір, підкріплюються його відчуттями лінійної перспективи.
Обов’язково передайте предметну площину. Фігура у нас не «плаває» в просторі, вона знаходиться на предметній площині!
При побудові фігури обов’язково показуйте і невидимі грані, показуйте як будівниц- лінії побудови. Це потрібно більше вам, ніж глядачеві. Розставляйте акценти там, де це потрібно, показуйте перетин площин. Не забувайте про перспективу. Якщо ви помітили, то нижня площину циліндра нам видно більше, ніж верхня, воно і правильно, тому що лінія горизонту (принаймні у мене, у вас може бути по-іншому), дає такий огляд.
Це потрібно більше вам, ніж глядачеві. Розставляйте акценти там, де це потрібно, показуйте перетин площин. Не забувайте про перспективу. Якщо ви помітили, то нижня площину циліндра нам видно більше, ніж верхня, воно і правильно, тому що лінія горизонту (принаймні у мене, у вас може бути по-іншому), дає такий огляд.
Подивіться як будується тінь- її можна правильно передати, використовуючи лінії побудов. Образно: від джерела світла йдуть промені, які поділяються на два види, одні-висвітлюють фігуру, зупиняються на ній, тому за фігурою далі світла не буде. А промені світла, які не потрапляють на фігуру йдуть далі, висвітлюючи все на своєму шляху. І цю межу ми з вами можемо показати. І ще: тінь, віддаляючись від фігури, буде мати тенденцію до деякого збільшення, це нагадує зворотний перспективу. Розумієте чому? Якщо направити промені навпаки, то лінії побудови тіні зійдуться в одній точке- точці, З якої йде світло.
Ось приблизно так у вас повинно вийти. Далі в принципі натура нам вже й не потрібна, так як все можна проаналізувати самостійно. Включити аналітичне мислення і логічно міркувати. Але, все-таки, давайте розбирати далі:
За фігурі видно, що світло падає з боку і зверху. Значить, верхня площина циліндра у нас буде освітлена найбільше, і світло так-же буде падати на предметну площину, так як вона теж як і площину ціліндра- горизонтальна. Вертикальні площині-стіна і обрив предметної площині, а так-же, сам обсяг циліндра будуть отримувати менше освітлення, так як падає основного світла вони не отримують.
Далі: предметну площину ми Чорна не делаем- кут предметної площині отримує в даному випадку достатньо світла, щось би тінь не була тут найактивнішою. Але виділити її-предметну площину все- таки потрібно. Це досягається за рахунок виділення кута предметної площині.
Далі: наша предметна площину отримує основне світло, але нам потрібно показати, що вона горизонтально розташована. І ми знаємо, що віддаляючись світло гасне, слабшає. Ось чим далі від нас предметна площину буде йти, то менше її світло буде-кладемо штрих таким чином.
Тепер треба розібратися з тією частиною циліндра, що буде перебувати в тіні. Циліндр у нас розташований вертикально до предметної площини, значить основне світло буде падати на горизонтальну його верхню площину. Все інше в тіні, за винятком тієї ділянки, де світло ковзає по формі, так як світло падає не точно зверху, а трохи зі сторони-цю ділянку у мене виділено найсвітлішим на вертикальній площині його. Загальна-же тінь циліндра активніше стіни, так як циліндр має активну власну тінь і сам до нас ближче, хоч стіна також розташована вертикально.
Стіна-же буде темніше предметної площині, тому як вона вертікальна- значить світла тут буде менше, і тому, що вона буде перебувати далі за все, буде на задньому плані. Кладемо штрих таким чином.
Падаюча тінь фігури буде найактивнішою, але вона так-же лежить на предметній площині, а тому- віддаляючись на ній буде трохи ставати слабкіше.
Ну і залишилося розставити акценти там, де це необхідно- злами форм, які будуть до нас розташовуватися бліже- будуть акцентовані.
Якщо по початку рука не слухається, важко тримати олівець і важко покладати штрих за формою, так і чітко визначити саму форму штрихом важко, то є можливість попрацювати так, як показано на малюнку зліва.
Легенько плануєте злами форми. То- є: припустимо, ви в курсі, як розподіляється світло за формою предмета. Ви знаєте, що цих зон п’ять: відблиск, світло, півтінь, тінь і рефлекс. Це все одно, але умовно. Щось би передати більш якісно обсяг фігури, ви можете намічати скільки завгодно зламів, і чим їх буде більше, тим обсяг фігури буде показаний м’якше. Візуально поділяєте фігуру на ці зони і кладіть звичайний прямий штришок, але так, що-б виліпити обсяг- використовуєте частоту стежка- штриха або силу натиску олівця.
Тут прошу вас не плутати два поняття: як розподіляється світло за формою предмета і як лягає штрих за формою предмета. У першому випадку у нас-5 зон, у другому-можемо намічати стільки зон, зламів форми, скільки вам буде потрібно. Але не чорний, все допоміжні лінії повинні бути малопомітними.
Але не чорний, все допоміжні лінії повинні бути малопомітними.
Зауваження: якщо ви могли помітити, подивившись на цей малюнок, то побачили, що з більш освітленої сторони конуса стіна на задньому плані темніше, а з іншого, менш освітленої сторони конуса- стіна світліше.
Справа в тому, що стіна однакова і там і там, але так вже бачить наше око. Для гостроти відчуття дійсності, для найкращого акценту світла і тіні, для гармонійного дотику нашим оком малюнка, та й врешті-решт, давайте зробимо нашому оку приємне! Нехай він бачить в малюнку те, що бачить в натурі. Це тільки легкий нюанс, який тільки збагатить наш малюнок, можна ненав’язливо передати.
Доповнення: дивіться як будується тінь у конуса.
Далі давайте зробимо малюнок кулі. Побудова ви можете побачити зліва. Зауважте, як будується тінь фігури. З падаючої ми вже розібралися, на кшталт: визначаємо за допомогою окоміру і підкріплює знаннями перспективи. Не забувайте, що тінь падає на предметну плоскость- це потрібно передати і розуміти.
А ось як справи йдуть з власною тінню? Цікаво, що якщо провести лінії від точки освітлення до центру кулі, через який проходить діаметр, який утворює коло тіні, то цей діаметр буде перпендикулярний лінії, проведеної до точки освітлення. Якщо це зрозуміти, то і як класти штрих по формі кулі, щоб показати власну тінь- зовсім не складно.
Тепер мені щось стало нудно малювати в одній манері і захотілося поекспериментувати. Подивіться на роботу справа. Як ви думаєте, вона виконана штрихуванням? Не схоже. Вона виконана тональним плямою з використанням олівців відмінності ступеня м’якості. Якщо ви візьмете олівці з цільним грифелем, без дерев’яної оправи, і будете просто набирати тон на папері, а не Штрихована, то у вас теж вийде такий ось малюнок.
А що ще, крім техніки виконання у нас не так? Світло на місці, тіні теж, значить-все в порядку.
Але все-таки розглянемо детальніше. Найяскравіший світло у нас буде на освітленій стороні кулі, на площині він буде не таким активним і буде слабшати з віддаленням від нас. Сама темна тінь буде падаюча, на зламі предметної площині буде світла трохи більше, але тим не менш, акцентуємо цю область.
Сама темна тінь буде падаюча, на зламі предметної площині буде світла трохи більше, але тим не менш, акцентуємо цю область.
Подивіться на власну тінь шара- я ставлю акцент на тій області його, яка буде ближче до нас, і загортаючись за формою, тінь буде втрачати активність. Пам’ятайте: шар-форма обтічна.
Стіна в півтіні, притому на задньому плані-ось нехай там ненав’язливо і залишається. Єдине-вона буде «грати» з об’ємом кулі. З боку світла стіна буде здаватися кілька темніше, з боку тені- світліше. Давайте і тут зробимо нашому оку приємне;)
Як навчитися складати штрих за формою предмета. штрихування
Ось тут ми плавно підійшли до того, про що вже говорили на самому початку цієї сторінки. Як лягає штрих за формою предмета і який штрих таким не є. Справа в тому, що у кожного художника, в процесі роботи або навчання виробляється свій певний стиль штриха. Звичайно, є канони, у різних історичних часів свої власні канони малювання і штриха, але зовсім не обов’язково їм дотримуватися. За бажанням. Я вважаю, якщо за допомогою штриха можна передати обсяг фігури і сам простір в листі, то абсолютно все одно, що з себе представляє цей штрих. Головне, що- б було грамотно все зроблено і красиво. За простому- Не робіть соломи, вчіться малювати красиво. До штриху це так- ж відноситься. На цій сторінці ми вчилися робити штрих, продовжимо ще трохи.
Ось наприклад ось так, як я малюю кубик, який у нас ще залишився намальований.
1. Визначаємо місце фігури в аркуші
2. Маємо фігуру на предметній площині і знаходимо його конструкцію і його тінь, не забуваючи враховувати перспективу
3. Визначаємо місце світла і тені- кладемо легкий штрих. Це дає нам можливість відразу визначитися з розподілом світла і тіні в нашому малюнку, розділити їх
Якщо ви подивіться на штрих, яким виконана робота, то він досить незвичайний, вірно? На уроках малюнка до такого штриху краще не вдаватися, що не лякайте вчителів, у них не такі сучасні прогресивні погляди, як у вас.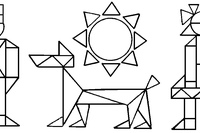 Але в своїх творчих роботах такий штрих застосовувати можна, чому б і ні? Адже малюнок зроблений за всіма законами. Передано простір в листі, показана форма предмета, передані основні тональні співвідношення в нашому малюнку. Але до цього ще ми додали штрих, який робить роботу цікавою і повітряної. Ну а далі знову, розбираємо малюнок, аналізуємо:
Але в своїх творчих роботах такий штрих застосовувати можна, чому б і ні? Адже малюнок зроблений за всіма законами. Передано простір в листі, показана форма предмета, передані основні тональні співвідношення в нашому малюнку. Але до цього ще ми додали штрих, який робить роботу цікавою і повітряної. Ну а далі знову, розбираємо малюнок, аналізуємо:
Давайте пройдемося по основним тональним відносин, для початку по тіням: найтемніша тінь- падаюча, далі йде власна тінь куба. Злам предметної площині займає третє місце, її ми виділяємо, але не чорним, так як там достатньо світла. І четвертая- стіна, на яку теж потрапляє світло, можна сказати, що стіна знаходиться в напівтіні, але далі все. Дивіться як грає півтінь стіни з формою куба: з боку освітленій частині куба стіна темніше, з боку тені- світлішає. Ці градації можуть бути дуже невелекий, але вони присутні.
Далі аналізуємо світло: найсвітліша і освітлена частина буде верхня площина куба, друга по светлоте- предметна площину, яка знаходиться перед нами горизонтально і йдучи в простір-втрачає світло.
На зламах форм робимо акценти. Ближні грані куба і кути виділяємо, це допоможе витягнути його з простору наперед.
І не забиваем- світло віддаляючись темніє, гасне, тінь віддаляючись втрачає свою активність і кілька світлішає, але враховуємо золоте правило: найтемніший півтон на світлі світліше найяснішого півтони в тіні.
На останок: якщо ви вирішите поекспериментувати зі штрихуванням. Так як і варіюється тональність світло тіні, яку ми передаємо в просторі листа, так і штрих може змінювати форму-пограйте з розміром штриха. Стіна виконана штрихом середнього стібка, досить статична. Куб виконаний дрібним і активним штришком, що надає кубу динаміку. А предметна площину виконана довгими стібками, досить тривіальними і малоцікавими. Так що, навіть штрих допомагає виявити в картині головна дійова особа-куб, який виконаний найбільш динамічним штрихом, який притягує увагу, на мій погляд. А як вам здається?
Попробуйде зробити щось своє, поекспериментуйте, тоді сама проста робота буде виконуватися із задоволенням, великою увагою і величезним інтересом. А коли ви сидите, виконуєте роботу, наприклад-намагаєтеся рівно покласти штрих за формою, та ще у вас і виходить, і при цьому починаєте помічати, що від концентрації вашої уваги завмирає дихання, ось в ці самі хвилини і відчуваєш всю предесть малюнка і отримуєш невимовне задоволення.
А коли ви сидите, виконуєте роботу, наприклад-намагаєтеся рівно покласти штрих за формою, та ще у вас і виходить, і при цьому починаєте помічати, що від концентрації вашої уваги завмирає дихання, ось в ці самі хвилини і відчуваєш всю предесть малюнка і отримуєш невимовне задоволення.
Веселі і барвисті завдання для дітей «Малюнки з геометричних фігур» є дуже зручним навчальним матеріалом для дітей дошкільного та молодшого шкільного віку по вивченню і запам’ятовування основних геометричних форм: трикутника, кола, овалу, квадрата, прямокутника і трапеції. Всі завдання призначені для самостійної роботи дитини під наглядом дорослих. Батько або педагог повинні правильно пояснити дитині, що він повинен зробити в кожному завданні.
1. Малюнки з геометричних фігур — Умови до виконання завдань:
Щоб почати виконувати завдання, скачайте у вкладеннях бланк, в якому ви знайдете 2 типу завдань: малюнки з геометричних фігур для розфарбовування і завдання для малювання фігур за допомогою логічного і образного мислення. Роздрукуйте завантажену сторінку на кольоровому принтері і дайте дитині разом з кольоровими олівцями або фломастерами.
- У першому завданні малюкові потрібно подумки з’єднати кожні дві частини представлених фігур в одну і намалювати отриману геометричну форму у відповідній клітці. Поясніть дитині, що деталі можна повертати в розумі в різні боки до тих пір, поки він не отримає потрібну комбінацію для складання фігури. Наприклад, два трикутника можна повернути так, щоб вийшов квадрат. Після цього квадрат потрібно намалювати в клітці поруч з трикутником. За таким же принципом необхідно зробити і інші малюнки.
- У другому завданні діти повинні правильно назвати фігури з яких складаються намальовані картинки. Потім ці картинки потрібно розфарбувати, використовуючи кольору поруч з геометричними фігурами. Кожну фігуру потрібно розфарбувати тільки в зазначений колір.
Щоб надати заняття більше енергії та ентузіазму — можна об’єднати кілька дітей в групу і надати їм виконання завдань на час. Та дитина, який перший виконає всі завдання без помилок, визнається переможцем. В якості призу можна повісити його роботу на стіну досягнень (така стіна обов’язково має бути присутня як вдома, так і в дитячому садку).
Та дитина, який перший виконає всі завдання без помилок, визнається переможцем. В якості призу можна повісити його роботу на стіну досягнень (така стіна обов’язково має бути присутня як вдома, так і в дитячому садку).
Завантажити завдання «Малюнки з геометричних фігур» ви можете у вкладеннях внизу сторінки.
2. Геометричні фігури в малюнках — 3 завдання-розмальовки:
Наступне заняття також приховує основні геометричні фігури в малюнках. Дитині потрібно знайти ці фігури, назвати їх, а потім розфарбувати таким чином, щоб кожній фігурі відповідав певний колір (керуючись інструкцією на бланку із завданням).
У другому завданні потрібно намалювати на всіх поверхах будь-які геометричні фігури, але при цьому необхідно дотримуватися умова: на кожному поверсі фігури повинні перебувати в різному порядку. Надалі можна це завдання видозмінити. Для цього досить накреслити на папері точно такий будиночок і попросити дитину заповнити його фігурами так, щоб в кожному під’їзді зустрічалися однакові фігури (під’їзд — вертикальний ряд квадратів).
У третьому завданні потрібно, керуючись стрілками, намалювати точно такі ж геометричні фігури всередині або зовні даних фігур.
Чи не квапте дитини і не підказуйте йому, поки він сам вас про це не попросить. Якщо у малюка щось вийшло неправильно — ви завжди можете роздрукувати ще один екземпляр навчального бланка із завданням.
Завантажити завдання «Геометричні фігури в малюнках» ви можете у вкладеннях внизу сторінки.
У цьому занятті дітям знову належить відшукати геометричні фігури серед малюнків. Після попередніх занять їм буде вже легше орієнтуватися в знайомих формах, так що, я думаю, обидва завдання не викличуть у них труднощів.
Друге завдання також дає можливість дитині повторити математичні знаки і засвоїти рахунок до десяти, так як йому знадобиться порахувати кількість фігур і поставити знаки «більше» «менше» між картинками.
Завантажити розмальовку «Смішні малюнки з фігур» ви можете у вкладеннях внизу сторінки.
Також вам будуть корисні і інші матеріали з вивчення геометричних фігур:
Тут ви з дитиною можете вивчити геометричні фігури і їх назви за допомогою веселих завдань в картинках.
Завдання ознайомлять дитину з основними фігурами геометрії — кругом, овалом, квадратом, прямокутником і трикутником. Тільки тут не занудне зазубрювання назв фігур, а своєрідна гра-розмальовка.
Як правило, геометрію починають вивчати, малюючи плоскі геометричні фігури. Сприйняття правильної геометричної форми неможливо без виведення її своїми руками на аркуші паперу.
Це заняття неабияк потішить ваших юних математиків. Адже тепер їм доведеться знаходити знайомі форми геометричних фігур серед безлічі картинок.
Накладання фігур один на одного — це заняття з геометрії для дошкільнят і молодших школярів. Сенс вправи полягає в розв’язуванні прикладів на додавання. Тільки це незвичайні приклади. Замість цифр тут потрібно складати геометричні фігури.
Це завдання складено у вигляді гри, в якій дитині слід змінювати властивості геометричних фігур: форму, колір або розмір.
Тут ви можете завантажити завдання в картинках, в яких представлений рахунок геометричних фігур для занять з математики.
У цьому завданні дитина познайомиться з таким поняттям, як креслення геометричних тел. По суті, це заняття є міні-урок з нарисної геометрії
Тут ми підготували для вас об’ємні геометричні фігури з паперу, які потрібно вирізати і склеїти. Куб, піраміди, ромб, конус, циліндр, шестигранник, роздрукувати їх на картоні (або кольоровому папері, а потім наклеїти на картон), а потім дати дитині для запам’ятовування.
Діти люблять розфарбовувати і обводити, тому дані завдання зроблять ваші заняття з навчання рахунку максимально ефективними.
І ще можете пограти в математичні ігри онлайн від лисеняти Бібуші:
У цієї розвиваючої онлайн грі дитині має бути визначено, що є зайвим серед 4 картинок. При цьому необхідно керуватися ознаками геометричних форм.
З даного уроку починається наша програма навчання малюнку. У цьому завданні розглядається тема малювання простих геометричних фігур.
Малювання геометричних фігур можна порівняти з вивченням алфавіту для того, хто освоює іноземна мова. Геометричні форми — перша стадія побудови об’єкта будь-якої складності. Це добре видно в комп’ютерному моделюванні, де побудова тривимірного космічного корабля починається з простого кубика. У малюнку все зображувані предмети завжди складаються або діляться на прості геометричні форми. Для навчання малюнку це означає рівно одне: навчившись правильно зображати геометричні фігури, навчитеся малювати все інше.
Побудова геометричних фігур.
Починати побудову потрібно з аналізу моделі, образно кажучи, проникнути вглиб конструкції на рівень вершин і ліній. Це означає, уявити геометричну фігуру у вигляді каркаса, що складається тільки з ліній і вершин (місце перетину ліній), шляхом уявного видалення площин. Важливим методологічним прийомом є зображення невидимих, але існуючих ліній. Закріплення такого підходу з перших уроків стане корисним прийомом для малювання складніших моделей.
Далі, під керівництвом педагога намітити на аркуші розташування ліній і вершин, легкими, плавними рухами, без натиску на олівець.
Положення малюнка на аркуші варто приділити окрему увагу з кількох причин:
- Знаходження центральної осі аркуша допоможе при подальшому побудові як відправний пункт для вертикальних ліній конструкції.
- Визначення лінії горизонту, для правильного зображення перспективи.
- Облік светотеневой моделювання, власні і падаючі тіні, щоб вони помістилися в просторі листа і врівноважували один одного.
Після нанесення основних конструктивних ліній слід детальне промальовування видимих \u200b\u200bребер предмета, у випадку з об’єктами обертання (куля, конус) це зовнішні краї форми.
За конструктивною частиною слід штриховая моделювання. На ми детально розбираємо правила і техніку нанесення штрихів на геометричні предмети.
На ми детально розбираємо правила і техніку нанесення штрихів на геометричні предмети.
Професійне навчання рисунку легко порівняти з уроками музики, де сухі правила і точні схеми в кінцевому підсумку призводять майбутнього композитора до творчим творам. Так і в малюнку закони побудови форм, правила перспективи, схеми розташування тіней допомагають художнику створювати унікальні шедеври.
Від чого досвідчені художники можуть швидко наносити складні малюнки, Не витрачаючи багато часу на розмітку, побудова? Тому що спочатку міцно завчили правила і канони, і тепер досить чітко уявляють будова будь-якої форми. Схематичний малюнок звільняє увагу автора від конструкції і зосереджує фокус на композиції, ідеї, образі свого творіння. Існує думка, що завчені схеми не дадуть художнику повністю розкритися.
Варто подивитися, з чого починали такі креативні майстри як Пікассо і Далі, щоб зрозуміти хибність даного судження. Але найкращою перевіркою стане навчання в нашій студії, де ви на практиці переконайтеся в плюсах академічного підходу.
Чекаємо Вас в нашій художній студії!
Як намалювати овал самостійно швидко і красиво
Овал — геометрична фігура, яка застосовується для відображення окремих частин предметів інтер’єру, малювання тварин і багато чого іншого. Багато хто цікавиться, як намалювати овал правильно від руки.
Як самостійно правильно намалювати овал
Щоб малюнок вийшов красивим і гармонійним, необхідно грамотно і точно промальовувати всі його елементи. Однак не кожен знає, як виконати еліпс від руки правильно і красиво.
Щоб зробити еліпс, необхідно взяти:
- альбомний аркуш;
- лінійку;
- олівець;
- ластик.
Спочатку необхідно посередині листа накреслити ромб, всі сторони якого будуть рівними, а протилежні сторони будуть паралельними. Ромб повинен бути таким, щоб у нього добре вписувався овал необхідного розміру. Потім в отриманий ромб необхідно вписати овал. Після цього ромб потрібно стерти олівцем.
Після цього ромб потрібно стерти олівцем.
Рівне і красиво малюємо овал
Щоб геометричні фігури виглядали відмінно, необхідно знати, як намалювати овал циркулем за кілька хвилин. Щоб виконати еліпс за допомогою циркуля, необхідно взяти:
- альбомний аркуш;
- олівець;
- циркуль;
- нитку;
- шпильки.
Щоб красиво промальовувати еліпс, необхідно спочатку провести дві прямі лінії, які будуть перпендикулярними. Вістря циркуля поставити в точку перетину двох ліній і потім накреслити коло.
Діаметр такої окружності буде відповідати ширині еліпса. Потім, залишивши циркуль на тому ж місці, необхідно накреслити коло трохи більшого розміру, щоб отримати довжину еліпса. Потім необхідно з’єднати два кола, стерши зайві лінії. Таким чином, вийде красивий і рівний овал, з якого потім можна малювати різних тварин і птахів. Знаючи, як намалювати овал від руки, можна робити дуже гарні і оригінальні малюнки без особливих зусиль.
Як намалювати морську свинку на основі овалу
Дуже цікаво виглядають малюнки тварин і птахів, намальовані з простих геометричних фігур. Багато хто цікавиться, що можна намалювати з овалу разом з дітьми.
За допомогою овалу можна швидко і красиво намалювати морську свинку. Щоб зробити малюнок, необхідно намалювати два овалу в горизонтальному положенні, один з яких буде трохи менше іншого.
Один овал повинен перетинатися з іншим, а потім зовнішні кути, що утворилися при перетині двох фігур, закрити лініями. Таким чином, вийде шия тварини. У центрі невеликого овалу потрібно намалювати точку, з якої потім вийде очей.
Після цього необхідно намалювати в верхній частині невеликого овалу маленькі вушка. Коли все буде готово, слід намалювати морську свинку лапки. При цьому варто враховувати те, що передні лапки повинні бути трохи коротше задніх і практично непомітні.
Коли все буде повністю промальовано, зайві лінії можна стерти, а потім необхідно розфарбувати морську свинку, зробивши тварина плямистим.
Знаючи, як намалювати овал, можна зробити на основі цієї геометричної фігури дуже красиві малюнки тварин і птахів.
Добірка мультфільмів та ігор, що допоможуть першокласникам розрізняти геометричні фігури
Протягом кожного навчального тижня НУШ засвоюється низка нових компетенцій. Учні, граючись, опановують нові знання та навички.
Упродовж 9 навчального тижня першокласники НУШ мають, поміж іншим, вивчити геометричні фігури та дізнатися про значення і користь онлайн-ігор.
Дидактичні ігри та вправи
Такий формат гри зручний тим, що не потребує використання мультимедійних пристроїв. Для того, щоб реалізувати один із запропонованих варіантів, вам знадобляться лише роздруківки з тематичними малюнками.
Вправа «Розпізнай фігури»
Принцип виконання: Запропонуйте учням розглянути малюнки та визначити, де і які геометричні фігури на ньому зображено.
Обладнання: Роздрукований малюнок.
Час виконання: 5 хв.
Приклад роздруківки для вправи «Розпізнай фігури» з ресурсу Pinterest
Вправа-казка «Майструємо геометричні фігури»
Принцип виконання: Вчитель читає казку, а учні мають змоделювати відповідні геометричні фігури, про які йде мова, використовуючи рахункові палички (сірники) та мотузочки.
Матеріали: Набори рахункових паличок, мотузочки (шнурки).
Час виконання: 10 хвилин.
Казка про братів
Жили-були два брати –Трикутник і Квадрат. Старший, був дуже добрим і життєрадісним, а ось молодший – незадоволеним і заздрісним (Запитайте у школярів, якої геометричної форми був старший брат, а якої – молодший).
Якось Трикутник каже старшому братові: «Ти такий великий, повніший та ширший за мене, в тебе більше сторін і кутів, в мене лише 3, а в тебе цілих 4 кути!». Старший брат лише знизав плечима: «Я таким народився!».
Настала ніч, і Трикутник вирішив позлодійкувати та повідрізати братові всі кути зі словами: «Ну що ж, спати лягав ти квадратом, а прокинешся без кутів!» (Вчитель уточнює у дітей, яку фігуру думав утворити таким чином Трикутник з квадрата?А діти мають викласти коло за допомогою паличок та мотузки).
Але на ранок молодший брат стояв без слів. Отакої! Тепер у брата вісім новеньких кутів! (учні складають восьмикутник, показують всі геометричні фігури та пояснюють, чим вони відрізняються одна від одної).
Гра «Подорож містом Геометричних Фігур»
Хід гри: Вчитель пропонує відправитись в уявну подорож до міста Геометричних Фігур, в якому діти познайомляться з машканцями та виконають кілька завдань (за основу взятий матеріал вчителя-дефектолога Фільченкової Лариси Іванівни).
Обладнання: Малюнки (місто фігур та казкова стежина), набори різнокольорових паперових фігурок (попередньо роздруковані та вирізані вчителем).
Час виконання: 15 хв.
1. «Чарівна стежина»
Учитель пропонує відправитись до міста Геометричних Фігур. Однак, щоб туди потрапити, треба знайти відповідну стежку із фігур певної форми. З яких фігур вона викладена? (трикутники). Учитель пропонує назвати їх колір українською та англійською мовами (зелений, green).
Стежка до міста Геометричних фігур
2. «Подорожуймо містом»
Ось і місто Геометричних Фігур. На чому тут можна подорожувати? (корабель, вантажний автомобіль, легковий автомобіль, потяг).
Учитель пропонує визначити, з яких геометричних фігур складається кожен вид транспорту, порахувати їх і назвати кольори українською та англійською мовами.
3. Жителі міста Геометричних Фігур
Учитель пропонує уважно поглянути на малюнок міста Геометричних ФІгур та знайти зображених там місцевих жителів, які зображено (пташку, кота, ведмедя). З яких геометричних фігур їх утворено? Якого вони кольору?
Запропонуйте школярам, використовуючи шаблони завчасно підготовлених геометричних фігур, створити казкових чоловічків, які б залюбки стали жителями уявного міста Геометричних Фігур.
Приклади чоловічків, яких можуть створити учні, використовуючи підготовлені геометричні фігури
Онлайн-ігри для вивчення геометричних фігур
З онлайн-іграми, як правило, переважна більшість школярів добре знайома вже до вступу в перший клас. Цей формат пізнання навколишнього світу надзвичайно подобається дітям. До того ж він може бути корисним інструментом, який варто використовувати для досягнення навчальних цілей!
Цей формат пізнання навколишнього світу надзвичайно подобається дітям. До того ж він може бути корисним інструментом, який варто використовувати для досягнення навчальних цілей!
Гра «Впізнай фігуру»
Принцип гри: Кожна гра складається з трьох етапів: власне демонстрації геометричної фігури; завдання, в якому потрібно на малюнку знайти всі фігури відповідної форми, та завдання, в якому необхідно знайти всі предмети, які мають подібну форму до певної геометричної фігури.
Завдання з гри «Впізнай фігуру», в якому необхідно позначити «пташкою» всі прямокутники
Добірка включає 6 простих і водночас цікавих для першачків онлайн-ігор:
Гра «Порахуй кути»
Принцип гри: На дисплеї окремо демонструються геометричні фігури (загалом 10). Учню необхідно порахувати, скільки кутів має кожна фігура, та обрати відповідний варіант серед запропонованих варіантів відповідей.
Приклад завдання з гри «Порахуй кути»
Перейти до гри можна, натиснувши сюди.
Гра «Танграм»
Танграм – надзвичайна гра-головоломка. Так, поєднавши відповідним чином всього 7 фігурок-танів, можна скласти практично будь-яку фігуру (так можна скласти будь-яку літеру абетки, тварин, цифри, силуети людей та ін.).
Принцип гри: Необхідно всередину білого контура вмістити всі 7 фігур таким чином, щоб вони не накладалися одна на одну.
Приклад завдання з гри «Танграм-мешканці морів»
На ресурсі можна знайти 5 ігр-танграмів, у кожній з яких пропонується скласти по 5 фігурок:
Така гра може стати надзвичайно захопливим заняттям як для школярів, так і для дорослих, адже вона розвиває логічне та креативне мислення.
Гра «Геометричні фігури у головоломці»
Ігрове поле складається з геометричних фігур – кружечків, квадратиків та восьмикутних зірок, розташованих по всій його поверхні. Поза ним розміщені фішки з комірками відповідної форми (кружечки, квадрати та зірки).
Принцип гри: Необхідно розмістити на ігровому полі всі фішки таким чином, щоб не залишилось пустих комірок.
Фішки можна повертати за допомогою стрілочок на клавіатурі, а переміщувати – за допомогою курсора мишки.
Інтерфейс онлайн-гри «Геометричні фігури у головоломці»
Перейти до гри можна, натиснувши сюди.
Мультфільми
Що люблять діти більше за все? Звісно, ігри та мультики! Тож пропонуємо кілька варіантів мультфільмів, які можна переглянути зі школярами під час вивчення геометричних фігур.
Мультфільм «Летючі геометрики»
Кожна з 10 геометричних фігур забула своє ім’я, вона лише пам’ятає свої ознаки. Визначте разом зі своїми першачками, хто з фігур яку має назву!
Мультфільм «Летючі геометрики»
Мультфільм «Веселі фігури»
Діти обожнюють розповіді, а якщо вони ще й анімовані, то це подвійна радість! Запропонуйте школярам разом переглянути короткий мультфільм, в якому представлено 5 історій про основні геометричні фігури.
Мультфільм «Веселі фігури»
Мультфільм «Урок – геометричні фігури»
Які предмети у побуті мають подібну до основних геометричних фігур форму? Про це ваші учні можуть дізнатися, переглянувши трихвилинний мультфільм.
Мультфільм «Урок – геометричні фігури»
Мультиплікаційна руханка
Руханка – це веселий спосіб активізувати увагу школярів під час уроку! А ця ігрова вправа дозволяє поспівати, потанцювати та згадати назви геометричних фігур українською і кольори англійською мовами.
Мультиплікаційна руханка
Анімована вправа для вивчення геометричних фігур англійською
Така мультиплікаційна вправа стане знахідкою для вчителів англійської! У відеоматеріалі по черзі представлено 12 геометричних фігур і до кожної з них подано зображення, написання та вимова їхніх назв англійською мовою.
Геометричні фігури англійською
Матеріали для вивчення геометричних фігур із Бібліотеки «На Урок»
Тема: Геометричні фігури. Гра «Хто більше»
Гра «Хто більше»
Автор: Шаповалова Світлана Володимирівна
Про матеріал: Презентація складається з 5 слайдів, на кожному з яких зображено по 2 малюнки, які утворені найпростішими геометричними фігурами. Завдання школярів – визначити, на якому малюнку «сховано» більше фігур.
Тема: Презентація «У замку Королеви Геометрії»
Автор: Шевчук Ольга Василівна
Про матеріал: У запропонованій презентації представлені декілька надзвичайно цікавих дидактичних ігор, за допомогою яких можна у невимушеній формі перевірити рівень опанування школярами навчального матеріалу з теми «Найпростіші геометричні фігури». Учитель пропонує різноманітні завдання – назвати фігури, знайти окремі фігури з-поміж інших, скласти геометричні фігури із сірників або з паперу, використовуючи техніки орігамі тощо.
Тема: Дидактичні ігри на уроках математики
Автор: Наумович Ірина Іванівна
Про матеріал: Збірки з 80 дидактичних ігор, серед яких є й ігри для вивчення геометричних фігур. Кожну гру можна використовувати на уроках та в позакласній роботі з учнями. Дібраний матеріал сприяє розвитку інтелектуальних здібностей дітей, формуванню інтересу до вивчення математики у першачків.
А які ігрові прийоми застосовуєте ви? Долучайтесь до спільноти проактивних учителів, додавайте матеріали до Бібліотеки освітнього проекту «На Урок». Діліться власним досвідом та ідеями цікавих уроків, а також використовуйте напрацювання колег з усієї України!ф
Домашні вправи для роботи з дітками з інтелектуальними порушеннями
Вправа «Назви 5 слів»
Мета: розвиток мислення, зосередженості, мовлення.
– Назви 5 імен хлопців. – Назви 5 імен дівчат.
– Назви 5 видів квітів. – Назви 5 видів дерев.
– Назви 5 видів фруктів/овочів.
Вправа «Злови слово»
Мета: розвиток концентрації, переключення уваги.
– Я зачитаю тобі слова, коли серед слів трапиться назва рослини, ти повинен плеснути в долоні – «зловити слово».
Варіанти слів: дорога, тигр, береза, літак, пшениця, троянда, змія, дуб, лялька, гриб, школа, шипшина, ромашка, рама, дім, машина, малина, тополя, потяг, мурашка, ваза, гвоздика, цвях, музей, гра, верба, горобець, каштан, пальма, намет, кіно, кенгуру, калина, хокей, місто, собака, волошка, глечик, молоко, тюльпан, гарбуз, ліс, ялинка, сосна, дорога, книга, музика, осика, балет, паркет, плющ, кульбаба.
Вправа «Запам’ятай і намалюй»
Мета: розвиток уваги, зосередженості, зорової пам’яті, удосконалення уміння працювати за інструкцією дорослого.
– На листку А4 намалюйте кілька геометричних фігур (коло, трикутник, чотирикутник, прямокутник, овал). Покажіть дитині:
– Розглянь уважно, які геометричні фігури зображені на листку паперу (5-8 фігур). Запам’ятай їх.
– Намалюй ті фігури, які ти запам’ятав.
Вправа «Намалюй по крапочках» ( дошкільний, молодший шкільний вік)
Мета: розвиток дрібної моторики руки, сприймання, довільної уваги.
– Обведи малюнок по крапочках. Яке зображення у тебе вийшло? (малюнки простих геометричних фігур, тварин, рослин).
Вправа «Штрихування» ( дошкільний, молодший шкільний вік)
Мета: розвиток дрібної моторики руки, сприймання, довільної уваги.
– На листку А4 намалюйте кілька геометричних фігур (коло, трикутник, чотирикутник, прямокутник, овал). Покажіть дитині:
– Назви, які фігури зображені на малюнку.
– Тобі потрібно заштрихувати ці фігури (горизонтальні/вертикальні, косі лінії).
Джерело: www.ircentr.space
Геометрические фигуры Занятия по математике и STEM Идеи для детей
Уберите листы и вместо этого поиграйте с математикой! Наше простое задание для детей с геометрическими фигурами легко выполнять дома или в математическом центре в школе. Это также делает потрясающий проект STEAM, включая немного искусства и дизайна. Учитесь, делая, создавая, открывая и исследуя с помощью простого и увлекательного упражнения по геометрии.
Это также делает потрясающий проект STEAM, включая немного искусства и дизайна. Учитесь, делая, создавая, открывая и исследуя с помощью простого и увлекательного упражнения по геометрии.
ПРОСТАЯ МАТЕМАТИКА С ГЕОМЕТРИЧЕСКИМИ ФОРМАМИ АКТИВНОСТЬ
G предназначен для геометрических фигур! В этом месяце мы изучаем практическую математику для серии A – Z STEM! Это задание по математике с геометрическими фигурами идеально подходит для игр в дошкольном и детском саду!
Вы можете вводить формы, такие как треугольники, квадраты, пятиугольники, восьмиугольники, трапеции и многое другое, сохраняя при этом легкость и игривость! Что такое STEM? Прочтите все о STEM здесь.
ГЕОМЕТРИЧЕСКИЕ ФОРМЫ ДЕЯТЕЛЬНОСТЬ ПОСТАВКИ
листов пенопласта {или плотной бумаги}
палочек для мороженого (используйте также разрезанные соломки!}
ножницы
магнитные числа {или любые числа}
НАСТРОЙКА ДЕЯТЕЛЬНОСТИ ГЕОМЕТРИЧЕСКИЕ ФОРМЫ
Я использовал наш пакет для печати фигур, чтобы предоставить различные формы для использования. Сначала я нарисовал их на листах пенопласта. Я сделал столько, сколько смог, чтобы у нас было много разнообразия и цветов! Кроме того, дети могут заполнять имена, считать стороны и записывать их на листах для печати!
Затем я разложил формы из пенопласта с помощью палочек для мороженого и магнитных чисел, чтобы получить приглашение поиграть и исследовать геометрические формы!
Геометрические фигуры — важный обучающий блок для маленьких детей.Изучение этих форм и их свойств, таких как углы и стороны, пригодится в будущем, особенно на уроках геометрии! Если у вас есть блоки с узорами, вы также можете добавить их в упражнение!
ЧТО ТАКОЕ ГЕОМЕТРИЧЕСКАЯ ФОРМА?
Геометрические формы, определенные в Википедии: «Многие двумерные геометрические формы могут быть определены набором точек или вершин и линий, соединяющих точки в замкнутой цепи, а также результирующими внутренними точками. Такие формы называются многоугольниками и включают треугольники, квадраты и пятиугольники ».
Такие формы называются многоугольниками и включают треугольники, квадраты и пятиугольники ».
НОЖНИЦЫ ДЛЯ ПЕЧЕНЬЯ И ПЕСОЧНОЕ ТЕСТО ПОДХОДЯТ ДЛЯ РАБОТЫ С ФОРМАМИ!
Легко развлечься математикой с домашним заданием с геометрическими фигурами. Наши дизайны разлетелись по столу. Мы много посчитали и выбрали формы внутри фигур.
Ему больше всего нравились шестиугольные геометрические формы, и он создавал узоры и узоры как из геометрических фигур из пеноматериала, так и из палочек для мороженого!
Геометрические формы — огромная часть нашей жизни! Они повсюду.Утром мы завершили нашу работу с геометрическими фигурами прогулкой по дому. В каждой комнате мы указали на разные формы.
Этот список примеров повседневных геометрических фигур, который я нашел, был очень полезен для меня, поскольку я мог извлекать некоторые предметы, о которых я даже не подумал бы показывать геометрические фигуры каждый день! Также обязательно ищите формы в сообществе.
РАЗВЛЕЧЕНИЯ И РУКИ НА ДЕТСКИЕ ГЕОМЕТРИЧЕСКИЕ ФОРМЫ ДЕЯТЕЛЬНОСТЬ ДЛЯ ДЕТЕЙ!
Играйте больше с математикой и числами.Щелкните по фотографиям.
Ранняя математика: знакомство с геометрией маленьким детям
Известный израильский художник Яаков Агам был расстроен. Он вошел в центр научных исследований в области образования и заявил: «Дети визуально безграмотны!» Исследователи в области образования работали с ним над дальнейшей разработкой и тестированием созданной им программы обучения визуальной грамотности на основе теории форм и того, как они сочетаются, чтобы создавать все, от букв алфавита до великих произведений искусства.
Несмотря на то, что программа «Агам» длительная и сложная, варианты занятий можно адаптировать для вашей работы с маленькими детьми. Далее следует несколько типов действий, которые можно повторять с разными формами.
Формирование знаний о формах
Начните с того, что помогите детям развить базовые знания о формах. Обозначьте все круги вокруг себя, например тарелки или крышки банок. Очень важно называть формы, которые дети видят в своем окружении.
Расширьте эти впечатления, проведя пальцем по объектам, пока вы говорите «круг», и говорите о том, как он продолжает изгибаться.Попросите детей сделать то же самое. Когда вы говорите о треугольниках, говорите о прямых сторонах и острых углах.
Анализ форм
Затем вовлеките детей в анализ предметов и картинок в их окружении, определяя их основные формы. Например, они могут:
- Найдите круги в книжках с картинками
- Отправляйтесь на «поиск фигур» и найдите все прямоугольники в классе
- Ищите фигуры, такие как треугольники или квадраты, которые вы спрятали вокруг комнаты
Когда вы рассказываете о формах, которых не так много в большинстве сред, таких как треугольники или ромбы (ромбы), вы можете делать копии из картона или плотной бумаги.(Сохраните их для последующих занятий.) Убедитесь, что вы делаете разные формы и размеры. Дети усваивают ограниченные представления о формах, если мы не показываем им множество примеров.
Поддержка визуальной памяти
Следующим шагом будет формирование у детей зрительной памяти картинок и форм. Например, покажите ребенку очень простую картинку, такую как рисунок, всего на две или три секунды. Затем накройте его и попросите ребенка описать его. По мере развития способностей ребенка переходите к более сложным картинкам.
Продолжайте играть в эту «флеш-игру» с вариациями. Например, на две секунды покажите ребенку один из трех очень простых рисунков. Затем смешайте все три и позвольте ребенку найти тот, который вы показали. Позже, когда вы поработаете с несколькими формами и комбинациями фигур, это может быть весело и сложно: ребенку, возможно, придется вспомнить, видел ли он треугольник внутри круга или круг внутри треугольника.
Объединение фигур
Как только вы поработали с несколькими фигурами, комбинируйте эти фигуры в своей деятельности.Например, после того, как вы изучили горизонтальные и вертикальные линии, изучите картинки с детьми, например городские сцены, и предложите им найти все горизонтальные и вертикальные линии, которые они смогут. Поговорите о вертикальных и горизонтальных линиях в вашем классе и о том, как они сочетаются, чтобы образовывать разные формы и предметы.
Воспроизведение форм и комбинаций фигур
После приобретения у детей знаний о формах и их сочетаниях, поощряйте их воспроизводить их.Например, покажите ребенку квадрат, сделанный вами из кубиков или ершиков для труб. Затем предложите ребенку скопировать форму.
Создание с помощью фигур
Дети должны использовать фигуры, с которыми вы работаете, для создания своих собственных рисунков и картинок. Вскоре после воспроизведения форм предложите детям изобретать собственные способы использования формы для создания конструкций с помощью приспособлений для чистки труб, зданий из блоков и картинок с помощью мелков.
Предоставьте детям комбинацию различных материалов, таких как маленькие кубики, средства для чистки труб и краски.Напомните детям об изученных вами формах. Затем дайте им возможность использовать материалы для создания форм по-своему. Разные материалы побуждают детей по-разному думать о своей фигуре. Чтобы сделать квадрат, вы должны выбрать правильное количество блоков (четыре одинаковых длины). Используя очистители для труб, вы должны согнуть их «в самый раз», чтобы получить квадратные углы.
Почему мы так уверены в том, что эти занятия принесут детям столько пользы? Вместе с разработчиками Agam мы провели обширное исследование программы.Дети показали прирост геометрических и пространственных навыков. Они показали явные преимущества в математике и готовности к письму. Они даже повысили свой IQ. Дети лучше подготовлены к школе — и к жизни, — когда они могут обдумывать и использовать инструменты, основанные на основных геометрических идеях.
Дети лучше подготовлены к школе — и к жизни, — когда они могут обдумывать и использовать инструменты, основанные на основных геометрических идеях.
http://teacher.scholastic.com/products/ect/creativemath.htm
Что дети знают и что им нужно узнать о форме и пространстве
Геометрия включает в себя два основных компонента. Один рассуждает о форме .Мы узнаем, например, что треугольники должны иметь три прямые стороны и три угла, но углы могут быть узкими или широкими, а треугольники могут быть высокими или короткими, красными или синими или наклоненными любым количеством способов. Второй компонент думает о пространстве . Мы узнаем, как объекты соотносятся друг с другом и с нами в пространстве: мяч находится на диване, диван находится под мячом, а мы находимся перед ними обоими.
Хотя дети точно воспринимают форму и пространство в своей повседневной среде, детям дошкольного возраста примерно от трех до пяти лет необходимо научиться думать по этим темам.Наша основная образовательная цель должна заключаться в том, чтобы способствовать пониманию базовой геометрии.
ФормаКонтекст и обзор
Восприятие предметов начинается вскоре после рождения. С самого раннего возраста и примерно до 18 месяцев младенцы могут легко видеть различия между общими объектами: они видят, что мать отличается от отца, а собака отличается от кошки. Младенцы могут различать типы предметов: они видят, что это тарелка, а это чашка, даже если они не знают названия каждого из них и не могут сформулировать ключевые различия между ними.Кроме того, младенцы могут идентифицировать предметы, даже когда они меняют местоположение: это мать, независимо от того, видим ли мы ее с той или иной стороны, или близко она или далеко, лежит или стоит, или частично или полностью видна.
К концу младенчества восприятие объектов относительно хорошо развито, и дети относительно легко ориентируются в повседневном мире. В то же время им еще предстоит многому научиться, особенно анализу форм, то есть пониманию их основных свойств.Выучить названия форм легко. Но анализировать их намного сложнее. Следовательно, основное внимание в раннем обучении геометрии должно быть сосредоточено на анализе и понимании.
В то же время им еще предстоит многому научиться, особенно анализу форм, то есть пониманию их основных свойств.Выучить названия форм легко. Но анализировать их намного сложнее. Следовательно, основное внимание в раннем обучении геометрии должно быть сосредоточено на анализе и понимании.
Раннее восприятие и идеи формы
Примерно в три-четыре года дети изучают несколько аспектов фигур, как двухмерных ( 2-D, ), так и твердых ( 3-D ). Следующие ниже иллюстрации в основном используют двумерные формы, но то же самое можно сказать и о твердых телах.
Восприятие различия и сходства
Маленькие дети могут легко различать (видеть или воспринимать различия) между разными формами. Например, если спросить, отличаются ли двухмерные фигуры на рис. 1, дети быстро согласятся, что это так.
Они также могут легко различать трехмерные формы, например, прямоугольную призму (например, книгу) и сферу (например, шар), или между сферой и кубом (например, блок с шестью квадратными гранями).
Ясно, что маленькие дети могут видеть различий между треугольниками и прямоугольниками, а также между книгами и шарами. Они могут даже знать названия треугольник и прямоугольник . Но в то же время они могут быть не в состоянии проанализировать основы своей дискриминации. Они могут ничего не знать о свойствах треугольников и прямоугольников. Они могут не понимать, например, что треугольник должен иметь три стороны, что это замкнутая фигура или что обе фигуры являются многоугольниками.
Короче говоря, способность различать означает только то, что дети видят , что формы выглядят по-другому. В то же время, дети могут не знать о них ничего важного. Нам нужно различать видение и мышление, восприятие и мысль.
А как насчет идеи того же ? Маленькие дети могут видеть, что два прямоугольника воспринимаются одинаково или идентичны ( конгруэнтно ). Они могли бы даже увидеть совпадение, если бы один из прямоугольников был немного наклонен в сторону (но не слишком сильно!).На рисунке 2 показан пример.
Они могли бы даже увидеть совпадение, если бы один из прямоугольников был немного наклонен в сторону (но не слишком сильно!).На рисунке 2 показан пример.
Определить сходство в смысле конгруэнтной формы не очень сложно для маленьких детей, которые хорошо воспринимают, по крайней мере, того, что находится на поверхности. Их восприятие в основном невербальное и прямое. Обратите внимание, что язык не важен для любого из этих суждений: дети (или животные) могут видеть, что формы идентичны, но не могут их назвать. Дети также могут давать формам неправильные имена, но при этом точно воспринимать сходство (и различие).Например, вы можете сказать, что стая «собак» — это то же самое, хотя вам следовало бы назвать их «слонами». Объекты видятся одинаковыми, как бы вы их ни называли.
На рис. 3 показано интересное усложнение. Иногда кажется, что дети не замечают четкой разницы. Например, трехлетний ребенок может сказать, что фигуры на рис. 3 одинаковы, потому что у них обоих «заостренные вершины».
Означает ли это, что ребенок не видит разницы между формами? Не обязательно.Ребенок, вероятно, видит различий, но думает, что , тем не менее, формы те же самые. Если взрослый спросит, разные ли формы вообще, ребенок может сказать, что у одной есть три стороны, а у других четыре, но они одинаковы, потому что у каждой есть «заостренный верх». Итак, ребенок видит различие восприятия, но думает, что формы одинаковы, потому что каждая из них имеет общую вершину наверху. На самом деле ребенок совершенно прав: хотя формы разные, они совпадают в описываемом им свойстве.Это одна из причин опросить детей, чтобы попытаться выявить мышление, лежащее в основе их открытых ответов. Ребенок может говорить «то же самое», но также понимать, что формы отличаются в другом отношении.
Классификация. Детям младшего возраста необходимо выйти за рамки восприятия одинаковости и различия. Они должны научиться классифицировать объекты, которые на похожи на (в отличие от конгруэнтных) в ключевых отношениях. Им нужно усвоить, что трехсторонние фигуры разного размера — это все треугольники; что несовместимые, но похожие четырехгранные фигуры одинаковой длины и прямых углов — все квадраты; что баскетбольные мячи и шары — это сферы; и что блоки разного цвета могут быть кубиками.
Им нужно усвоить, что трехсторонние фигуры разного размера — это все треугольники; что несовместимые, но похожие четырехгранные фигуры одинаковой длины и прямых углов — все квадраты; что баскетбольные мячи и шары — это сферы; и что блоки разного цвета могут быть кубиками.
Некоторые классификации легче для маленьких детей, чем другие. Например, они могут видеть, что все квадраты разных размеров идут вместе. Они могут идентифицировать прототипы, то есть стандартные обычные треугольники, подобные изображенным на рисунке 4, независимо от размера. Опять же, это можно сделать, не зная имен. Как бы ни назывались фигуры, одни идут вместе, а другие — нет.
Имена. Конечно, детям нужно выучить правильные имена. Имена полезны по-разному: они позволяют вам общаться с другими («Это треугольник.»), И они также отсылают вас к категории для анализа (« Это называется треугольником, и они тоже. Интересно, почему они одинаковы »). Имена фигур на английском языке немного странны, потому что многие из них происходят от греческого или латинского языков. Например, слово треугольник происходит от греческого слова «три угла». Напротив, китайские названия форм прозрачны. На китайском языке название прямоугольника переводится как «четырехгранная форма». Несмотря на это, геометрические имена детям выучить несложно. Дети дошкольного возраста знают тысячи имен, в том числе специальные имена, такие как Бронтозавр или эзотерические имена героев мультфильмов, игрушек или фигурок.Учитывая их способность усваивать речь, маленькие дети не должны испытывать особых трудностей в изучении таких имен, как прямоугольная призма или пятиугольник . Но взрослый всегда должен помнить, что имена, хотя и необходимы, носят поверхностный характер. Детям необходимо научиться понимать свойства фигур, а не только то, как их сортировать или называть.
Понимание . Понимание многогранно. Детям нужно научиться анализировать форм, определять их определяющие свойства, а говорить о них . Им нужно узнать, что делает треугольник треугольником и чем треугольник отличается от квадрата. Им нужно узнать, что квадрат — это подкласс прямоугольников.
Им нужно узнать, что делает треугольник треугольником и чем треугольник отличается от квадрата. Им нужно узнать, что квадрат — это подкласс прямоугольников.
Как упоминалось выше, дети могут легко научиться классифицировать прототипы форм. Они узнают, что равносторонний, равнобедренный и прямоугольный треугольники — это все треугольники. В то же время дети могут не знать, что длинный, тонкий, разносторонний треугольник, подобный изображенному на рисунке 5, также является законным членом семейства треугольников, и что все треугольники любого цвета могут быть маленькими или большими, наклоненными к вершине. сбоку или лежа на горизонтальном основании.Размер, цвет и ориентация не имеют значения, если цель состоит в том, чтобы идентифицировать фигуры одного типа.
Основная задача ребенка — получить четкие знания об определяющих свойствах форм. Дети должны понимать, что треугольник имеет одни определяющие свойства, а квадрат — другие, и что эти формы неизменны при изменении размера, ориентации и цвета. Им также необходимо уметь говорить о формах; чтобы объяснить, почему треугольник является треугольником, даже если он не является прототипом.
Ограниченное понимание детьми основных и второстепенных свойств может частично происходить из-за ограниченного набора форм, которые они видят. Дети часто сталкиваются с прототипами форм в книгах и игрушках. Если в книжке с картинками представлен треугольник, он, скорее всего, будет равносторонним или равнобедренным и редко разносторонним. Игрушки для сортировки по форме также включают в себя прототипы, в данном случае трехмерные, такие как равносторонняя треугольная призма.
Учитывая, что детям редко представляются непрототипные формы, взрослые должны показывать детям их и обучать их основным свойствам, объясняя причины, по которым одна фигура является треугольником, а другая — пятиугольником.Как и в других областях, взрослым необходимо помочь детям математизировать их знания форм, то есть развить явное понимание формальной математики. Детям необходимо научиться думать и открыто говорить о математических свойствах, таких как количество вершин и сторон, определяющих фигуру.
Детям необходимо научиться думать и открыто говорить о математических свойствах, таких как количество вершин и сторон, определяющих фигуру.
Составление и разложение фигур . Детям также необходимо изучить и узнать о том, как разбирать фигуры и использовать фигуры для создания других фигур. Например, если цель состоит в том, чтобы создать квадрат из двух треугольников, ребенок должен обратить внимание на внутренние углы и длину сторон треугольников.Состав и разложение способствуют анализу.
Дети могут изучать формы, используя несколько упражнений этого типа. Как показано на рисунке 6, дети могут составлять фигуры. Когда ребенок складывает два квадрата одинакового размера, выравнивая их ширину, получается длинный прямоугольник. Когда ребенок складывает два одинаковых полукруга вместе, выравнивая их диаметры, получается полный круг.
Дети тоже умеют раскладывать фигуры. Как показано на рисунке 7, когда ребенок делит прямоугольник по диагонали или разрезает равносторонний треугольник посередине, ребенок получает два прямоугольных треугольника.
Составление и разложение может быть очень интересным, независимо от того, являются ли фигуры физическими или компьютерной графикой, и занимается ли ребенок исследованием или решением проблемы, созданной взрослым.
КосмосКонтекст и обзор
Людям (и животным тоже) необходимы базовые концепции пространства, если они хотят адекватно функционировать в повседневном мире. По этой причине маленькие дети (даже младенцы) часто сами по себе начинают использовать или развивать базовые пространственные концепции, включая идеи о местоположении, относительном положении, симметрии и направлении.Некоторые пространственные навыки и идеи встроены в систему восприятия человека: даже младенцы демонстрируют, что могут различать близкое и далекое, когда они пытаются дотянуться до ближайшей из двух игрушек. Младенцы и дети ясельного возраста развивают эти способности, когда ползают или ходят, осознают свое окружение и думают о том, куда они идут. Они знают, где находятся в космосе и как перемещаться из одного места в другое. В знакомых местах, таких как дома и школы, они обычно знают, где находятся вещи и как добраться до того, что им нужно.Они узнают, что мяч находится близко к стулу, что кукла находится под стулом и что самый быстрый путь к стулу — это пройти под столом. Они учатся использовать слова для описания позиций, местоположений и направлений. Когда они становятся старше, они используют блоки и другие объекты для создания иногда красивой симметрии, такой как создание, показанное на рисунке 8.
Они знают, где находятся в космосе и как перемещаться из одного места в другое. В знакомых местах, таких как дома и школы, они обычно знают, где находятся вещи и как добраться до того, что им нужно.Они узнают, что мяч находится близко к стулу, что кукла находится под стулом и что самый быстрый путь к стулу — это пройти под столом. Они учатся использовать слова для описания позиций, местоположений и направлений. Когда они становятся старше, они используют блоки и другие объекты для создания иногда красивой симметрии, такой как создание, показанное на рисунке 8.
Хотя их повседневные пространственные идеи часто полезны (как в случае перемещения по знакомой среде), а иногда и удивительно мощны (как в случае сложных симметрий), маленьким детям еще есть чему поучиться, и им нужны взрослые, чтобы помочь им двигаться. вперед.Учителя и родители могут развивать и расширять то, что маленькие дети уже знают о космосе. Взрослые могут помочь маленьким детям математизировать их повседневные представления о пространстве. Это включает использование языка и различных представлений для описания и понимания пространственных идей.
Видео для детей, обучающие геометрии
Дети часто бывают очень наглядными, когда дело доходит до обучения, что делает включение видео в ваши уроки забавным и простым инструментом, отвечающим их визуальным потребностям. Особенно по математике! Ваши ученики могут не ожидать, что вы будете воспроизводить видео во время обучения математике, что придаст вашему уроку неожиданный поворот! Этот элемент неожиданности и застать их врасплох, поделившись различными видео, связанными с геометрией, — отличный способ полностью заинтересовать ваших маленьких учеников! Кроме того, математические видеоролики доставляют массу удовольствия и часто очень интерактивны.
В следующем списке видеороликов представлены разнообразные энергичные песни, отличная графика и простые объяснения по геометрии. Поскольку эти видео в совокупности затрагивают различные учебные классы и подтемы геометрии, у вас не должно возникнуть проблем с поиском идеального места в ваших инструкциях по математике для использования одного (или нескольких) из этих развлекательных и образовательных видео по геометрии.
Некоторым ученикам может быть трудно понять симметрию — но не тогда, когда вы им показываете это видео! Он предлагает идеальное введение в концепцию симметрии! Мне очень нравится, как это видео не только показывает и объясняет симметрию с точки зрения форм и рисунков, но и использует реальные объекты в качестве примеров.Это действительно помогает детям задуматься о симметрии, существующей в окружающем их мире! Несмотря на то, что в этом видео нет броской мелодии, привлекательная графика и невероятно четкое объяснение симметрии делают его отличным ресурсом для знакомства с концепцией базовой симметрии.
Симметрия для детей (3:48)
Ваши дети будут в восторге от изучения симметрии с этим веселым видео! В него входит веселая рок-н-ролльная песня, которая поможет вашим ученикам расширить свои знания о симметрии далеко за пределы основ! Используя яркие формы и красочную графику в сочетании с простыми текстовыми пояснениями и запоминающейся мелодией, песня и видео работают вместе, чтобы эффективно раскрыть множество различных аспектов симметрии. Это отличное видео для расширения этой концепции, поскольку в нем исследуются различные варианты симметрии, такие как двусторонняя и вращательная симметрия.
Это отличное видео для расширения этой концепции, поскольку в нем исследуются различные варианты симметрии, такие как двусторонняя и вращательная симметрия.
Видео с песней Polygon (4:02)
Ваши дети полностью поймут, что такое многоугольник, послушав запоминающуюся песню из этого видео. Определение многоугольника объясняется сразу же и продолжает показывать изображения различных многоугольников, а также объясняет, как они получили свои названия.Он четко исследует и обсуждает трех-, четырех-, пятиугольные формы вплоть до десятиугольника. После объяснения каждой формы видео принимает интерактивный оборот: зрителей просят нарисовать различные фигуры в воздухе, подпевая их видео. Вашим детям это понравится!
Они многоугольник Песня (3:18)
Эта очаровательная песня помогает ясно показать разницу между «скучным квадратом» и другими формами, такими как пятиугольники, шестиугольники, семиугольники, восьмиугольники, неугольники и десятиугольники. Хотя припев песни немного монотонен с текстами о скучном квадрате, он отлично показывает, сколько сторон имеет каждая форма и чем каждая из них отличается от квадрата. Слово многоугольник на самом деле не упоминается в этом видео, поэтому показ ролика №3 перед этим был бы отличным способом сначала представить многоугольники, а затем усилить их суть, продемонстрировав это.
Хотя припев песни немного монотонен с текстами о скучном квадрате, он отлично показывает, сколько сторон имеет каждая форма и чем каждая из них отличается от квадрата. Слово многоугольник на самом деле не упоминается в этом видео, поэтому показ ролика №3 перед этим был бы отличным способом сначала представить многоугольники, а затем усилить их суть, продемонстрировав это.
Узнайте о двухмерных фигурах с поездом Чу-Чу — Часть 1 (9:35)
Хотя это видео длиннее и не содержит никаких запоминающихся тематических песен, это действительно эффективный инструмент для обучения двухмерных фигур младшим школьникам.Красочно анимированный говорящий поезд поможет заинтересовать ваших маленьких учеников, а четкие и простые для понимания объяснения не оставят места для путаницы в отношении двумерных фигур. Если вас беспокоит длина видео, вы можете пропустить первую минуту видео — в основном это просто вступительная музыка. Яркая анимация и подробные объяснения различных характеристик двумерных форм гарантируют, что ваши ученики полностью усвоят эту базовую концепцию геометрии и получат от этого удовольствие! Им понравится интерактивный характер этого видео, поскольку говорящий поезд задает вопросы аудитории на протяжении всего видео.
Изучите трехмерные фигуры (геометрические тела) с помощью поезда Choo-Choo — Часть 2 (12:05)
Часть 2 серии видеороликов Choo-Choo Train основывается на предыдущем видеоролике, переходя от двухмерных к трехмерным фигурам. Тот же говорящий поезд из предыдущего видео поможет вашим ученикам понять различные трехмерные формы и то, что делает их трехмерными. Опять же, если вас беспокоит время, вы можете перейти к минуте 2:55, чтобы перейти к реальной сути видео, где полностью исследуются все трехмерные формы и каждая из них соотносится с двухмерной формой.Как и двухмерное видео, это видео предлагает интерактивный компонент, так как он задает вопросы зрителям, исследуя различные трехмерные формы — предлагая вам прекрасную возможность сделать паузу и обсудить концепции со своими учениками! (Убедитесь, что ваши дети понимают, что такое многоугольник, прежде чем смотреть видео, поскольку он относится к многоугольникам без подробного объяснения.)
Двухмерные геометрические формы для лепки (6:12)
https://www.youtube.com/watch?v=yXRv8RPHJjc
Хотя в этом видео нет слов, его все же невероятно полезно использовать в качестве наглядного примера создания двухмерных фигур.Выполнение упражнения, показанного в видео, с вашим классом было бы отличным способом предложить учащимся практический опыт формирования фигур. Вы также можете использовать это видео в качестве подсказки для вопросов в классе о геометрии или пространственных отношениях. Например, какую форму вы видите над пятиугольником и т. Д. Видео короткое, но все же ему удается ясно показать детям, как формировать двумерные формы, используя маленькие шарики из пластилина и зубочистки! Если вы собираетесь выполнить это задание со своим классом, используйте это видео в качестве введения или в качестве фона для вашего класса, пока ваши ученики создают различные формы для лепки.
Вы также можете использовать это видео в качестве подсказки для вопросов в классе о геометрии или пространственных отношениях. Например, какую форму вы видите над пятиугольником и т. Д. Видео короткое, но все же ему удается ясно показать детям, как формировать двумерные формы, используя маленькие шарики из пластилина и зубочистки! Если вы собираетесь выполнить это задание со своим классом, используйте это видео в качестве введения или в качестве фона для вашего класса, пока ваши ученики создают различные формы для лепки.
Трехмерные фигуры с пластилином (9:06)
https://www.youtube.com/watch?v=Fy5abut63Qk
Очень похоже на предыдущий, это еще одно видео без слов, которое просто показывает детям этапы создания трехмерных фигур с помощью Play Dough и зубочисток. Вы можете легко использовать это видео сразу же после предыдущего, чтобы по-настоящему подчеркнуть разницу между двухмерными и трехмерными формами для ваших учеников. Его также можно легко использовать в качестве введения к этому заданию или в качестве справочной информации, пока ваши ученики создают трехмерные фигурки из теста для лепки.Если вас беспокоит длина этого видео, вы можете легко перемотать некоторые этапы построения фигур, когда увидите, что ваши дети уловили концепцию.
Как легко рисовать треугольники с Евклидом (3:47)
Не обманывайте себя названием — это видео не только учит детей рисовать треугольник. Главный герой, древнегреческий математик Евклид, дает зрителям краткое введение в несколько различных геометрических тем, включая линии, углы и треугольники.Он предлагает объяснения взаимосвязи между линиями, различных видов линий и того, как они пересекаются или не пересекаются, и в конечном итоге связывает эти идеи, показывая нам, как нарисован треугольник, соединяя три точки тремя линиями, а затем образуя три угла. Детям понравится, как рассказчик иллюстрирует Евклида во время разговора, а его британский акцент — дополнительный бонус! Это видео о гораздо большем, чем просто рисование треугольников, является отличным дополнением к любому уроку геометрии о линиях, углах И треугольниках.
Главный герой, древнегреческий математик Евклид, дает зрителям краткое введение в несколько различных геометрических тем, включая линии, углы и треугольники.Он предлагает объяснения взаимосвязи между линиями, различных видов линий и того, как они пересекаются или не пересекаются, и в конечном итоге связывает эти идеи, показывая нам, как нарисован треугольник, соединяя три точки тремя линиями, а затем образуя три угла. Детям понравится, как рассказчик иллюстрирует Евклида во время разговора, а его британский акцент — дополнительный бонус! Это видео о гораздо большем, чем просто рисование треугольников, является отличным дополнением к любому уроку геометрии о линиях, углах И треугольниках.
Песня о полигонах для детей Рэп-видео: геометрия, четырехугольники, шестиугольники и т. Д. (1:57)
https://youtu.be/meaGjrKWGFQ
Ваши дети будут в восторге от запоминающегося ритма в этой рэп-песне, поскольку в ней подробно объясняются различные предварительные исправления форм и их влияние на количество сторон формы. В этом видео замечательно то, что во время воспроизведения песни изображения каждой обсуждаемой формы отображаются в реальных ситуациях. Например, на видео показан треугольник в парусе лодки и четырехугольник в двери дома.Это поможет вашим ученикам увидеть, что формы можно найти повсюду вокруг нас, а также послужит отличным введением в потенциальное занятие по поиску формы.
Песня о параллельных, перпендикулярных и пересекающихся линиях | NUMBEROCK (2:21)
Если вы рассказываете своим детям о различных типах линий и о том, как они взаимодействуют друг с другом, вы обязательно должны поделиться этим видео со своим классом! С запоминающимся ритмом, припевом, который вы не скоро забудете, и четкой графикой — это видео и песня помогут вашим детям в кратчайшие сроки понять концепцию геометрических линий! Припев побуждает зрителей поднимать руки вверх и формировать руками различные линии во время постукивания в видео. Повторение в этом видео действительно помогает донести мысль о параллельных, перпендикулярных и пересекающихся линиях в веселой и приятной форме!
Повторение в этом видео действительно помогает донести мысль о параллельных, перпендикулярных и пересекающихся линиях в веселой и приятной форме!
Песня в 3-х формах для детей | Трехмерное видео по NUMBEROCK (2:04)
Еще одно отличное видео от NUMBEROCK, эта живая рэп-песня отлично объясняет зрителям трехмерные формы. Если некоторые из ранее упомянутых видеороликов, посвященных трехмерным фигурам, кажутся вашим ученикам слишком юными, это будет большим успехом для детей старшего возраста — и даже для младших! Хор помогает напомнить учащимся о характеристиках трехмерных форм, в то время как остальная часть песни объясняет конкретные трехмерные формы и места, где зрители могут видеть эти формы в повседневной жизни.Ваши дети не только лучше поймут трехмерные формы после просмотра этого видео, но и будут напевать мелодию в течение нескольких дней, показывая трехмерные формы вокруг себя!
Колин Доддс — Геометрические преобразования (3:15)
Понимание различных способов перемещения или трансформации фигур кажется достаточно простым, но некоторым ученикам может быть сложно полностью понять их. Хотя в этом видео не самая впечатляющая графика, мелодия запоминается, а объяснения различных способов движения фигур очень легко понять.Хор повторяет ключевые термины, касающиеся геометрических преобразований, таких как поворот, перевод и отражение, и полностью объясняет, что означает каждый термин. Это видео может быть лучше для студентов старшего возраста, поскольку в нем вводится более сложный термин, мозаика, а также много текстовых отображений определений. По этой причине может быть полезно показать это видео учащимся, которые умеют читать, хотя это не обязательно для того, чтобы оно было эффективным.
Это видео может быть лучше для студентов старшего возраста, поскольку в нем вводится более сложный термин, мозаика, а также много текстовых отображений определений. По этой причине может быть полезно показать это видео учащимся, которые умеют читать, хотя это не обязательно для того, чтобы оно было эффективным.
Песня Shapes: Shapes Rap / Chant — Песня формы робота (3:36)
Прекрасное введение в основные формы, это видео сочетает в себе простой фоновый рисунок с простыми объяснениями различных форм, таких как круги, треугольники, четырехугольники, параллелограммы и т. Д.После демонстрации визуального представления каждой формы в видео используется простая анимация, чтобы показать, как на самом деле создается каждая форма, и четко указать, сколько у нее сторон. Хотя графика довольно проста и бит не получит Грэмми в ближайшее время, это видео предлагает очень простые для понимания объяснения и введение в основные формы. Идеально подходит для младших школьников!
Песня о треугольниках ⋆ Типы треугольников для детей от NUMBEROCK (1:55)
https: // youtu.be / JQUTVgT9RXY
Можете ли вы сказать, что я большой поклонник этих видео NUMBEROCK? Я думаю, что они действительно отличное дополнение к любому уроку геометрии, потому что все они содержат разные, но одинаково запоминающиеся ритмы и мелодии в сочетании с понятными объяснениями данной концепции. Мне также нравится, как все они показывают реальные примеры геометрических концепций и геометрических фигур. В этом конкретном видео отлично исследуются все виды треугольников — концепция, с которой, как я обнаружил, многие мои ученики испытывают затруднения.В песне не только объясняются и показаны примеры различных треугольников, но и подчеркиваются различные характеристики, которые отличают эти треугольники друг от друга. Быстро, запоминающе и по делу — это видео станет отличным дополнением к любому уроку геометрии треугольников.
Мне также нравится, как все они показывают реальные примеры геометрических концепций и геометрических фигур. В этом конкретном видео отлично исследуются все виды треугольников — концепция, с которой, как я обнаружил, многие мои ученики испытывают затруднения.В песне не только объясняются и показаны примеры различных треугольников, но и подчеркиваются различные характеристики, которые отличают эти треугольники друг от друга. Быстро, запоминающе и по делу — это видео станет отличным дополнением к любому уроку геометрии треугольников.
Другие ресурсы для обучения геометрии
Нельзя отрицать, что некоторые видео действительно могут дать вашим ученикам возможность познакомиться с различными математическими концепциями, если вы включите их в свои уроки математики, но давайте не будем забывать обо всех других замечательных ресурсах, которые также могут помочь обогатить ваши инструкции по математике! Включение следующих ресурсов по геометрии от Lucky Little Learners в ваши инструкции по математике определенно поможет повысить вовлеченность учащихся и углубить их понимание различных геометрических концепций! Ознакомьтесь со всеми этими невероятными продуктами, перейдя по ссылкам ниже.
Блокнот по интерактивной геометрии для 1 класса по математике
Блокнот по интерактивной геометрии для 2-го класса по математике
Набор интерактивных тетрадей по математике для 2-х классов: время, деньги, геометрия
Карты задач с QR-кодом Geometry
Карты задач на геометрию (без QR-кодов)
Гостевой пост Марго Кармайкл из Carmichael’s Class
«Четыре года преподавания в 4-м классе помогли мне стать учителем, который увлечен созданием класса, который увлекает и вдохновляет моих учеников, объединяет обучение на основе технологий, предлагает реальный опыт и способствует творчеству.Я вел очень разнообразные классы с большим количеством изучающих английский как иностранный язык, изучающих специальное образование и с проблемами поведения, что дало мне глубокое понимание важности индивидуального подхода к обучению для каждого ученика. Как учитель, я постоянно учусь и развиваюсь, но одна постоянная — всегда ставить учеников на первое место! »
Как учитель, я постоянно учусь и развиваюсь, но одна постоянная — всегда ставить учеников на первое место! »
Спасибо за регистрацию. Нажмите на ссылку ниже, чтобы подтвердить подписку, и вы уже в путь.
(PDF) Идеи детей младшего возраста о геометрических фигурах
484 ОБУЧЕНИЕ ДЕТЕЙ МАТЕМАТИКЕ
Не так уж и много изменений
Было удивительно, как маленькие дети узнают о
формах от дошкольного возраста до средней школы.Для примера
наши дошкольники правильно определили около 60 из
процентов треугольников. В большом исследовании
учеников начальной школы, выполняющих одно и то же задание, оценки
варьировались от 64 процентов для детсадовцев до 81
процентов для шестиклассников (Клементс и Баттиста
1992a). Аналогичным образом, оценки дошкольников составляли 54
процентов по прямоугольникам, а оценки учащихся начальной школы
вмятин варьировались от 63 до 68 процентов.
Хотя эти
группы разделяют примерно восемь лет, оценки за одни и те же задания увеличились лишь на
минимально. Возможно, мы могли бы делать лучше
преподавания геометрии каждый год.
Индивидуальные различия
могут быть значительными
Один из шестилетних детей в нашем исследовании случайно выбрал прямоугольник
гля и назвал его «заостренным». При сравнении
один из трехлетних детей превзошел
всех шестилетних в задаче прямоугольника.
Хорошие возможности учиться более важны, чем уровень развития
, когда речь идет о
детском обучении формам.
При наличии хороших возможностей
детей ставят и решают
интересных задач
Учительница в нашем исследовании предложила своим детсадовцам
придавать своим телам различные формы. Два мальчика
пытались сделать ромб. Они сели лицом друг к другу
и раздвинули ноги.Их стопы
касались друг друга, и они образовали очень хороший ромб.
Один из детей в круге предложил: «Если мы поместим
другого ребенка в середину, мы получим два треугольника
!» Сразу же дети вызвали в службу
vice мальчика по имени Рэй, потому что он был самым маленьким,
, и попросили его сжать середину. Мальчики
поставили свои собственные задачи по разложению фигур
и разработали свои собственные решения.
Компьютеры помогают раздвинуть границы
того, что дети могут делать с геометрическими фигурами. Для примера
дошкольница Тэмми работала с компьютерной программой
, которая представляла фиксированный набор из
фигур. Она наложила два перекрывающихся треугольника на один квадрат
и раскрасила выбранные части этой фигуры.
Этот процесс создал третий треугольник, которого в программе не существовало! Компьютеры также могут быть
мощными и гибкими манипуляторами (Clements and
McMillen 1996).Например, Митчелл хотел
сделать шестиугольники, используя треугольник с узором и блоком.
Он начал без компьютера и использовал метод пробного
и ошибок, считая стороны и проверяя
после добавления каждого треугольника. Однако, используя компьютерную программу
Shapes, он начал с планирования
(Сарама, Клементс и Вукелич, 1996). Сначала он
разместил два треугольника, перетащив их и поворачивая
с помощью токарного инструмента. Затем он сосчитал пальцем
вокруг центра неполного шестиугольника
, визуализируя остальные треугольники.»Ого!» он
объявил. «Еще четыре!» После размещения следующего
он сказал: «Еще три!» В то время как без компьютера
Митчеллу приходилось сравнивать каждое размещение
с физическим шестиугольником, его преднамеренные и
преднамеренные действия на компьютере привели его к формированию
мысленных образов. То есть он мысленно разбил шестиугольник в
и предсказал каждое расположение.
Что такое хитрость
для детей?
Различные настройки, разные
решений
Определенные настройки влияют на решения детей.В нашу первую настройку
мы включили очевидные непримеры,
, такие как круги, в группу треугольных форм
. Дети принимали больше типов треугольников
и более «заостренных» форм, не являющихся треугольниками.
Точно так же дети принимали больше овалов в виде кругов
, когда фигуры рисовались друг в друге. Таким образом,
то, что выбирают дети, сильно зависит от
фигур, которые они сравнивают.
Во втором варианте мы поместили деревянные фигурки
внутрь обруча.Дети были реже
замечали или заботились о том, были ли они «длинными» или
«вверх ногами». То есть отсутствие прямоугольной системы отсчета
влияло на то, какие формы принимались
. В третьем случае мы попросили детей
обосновать свой выбор. Они часто меняли свои решения
, обычно на правильные. Например,
одна пятилетняя девочка увеличила свой результат на 26 процентов —
центовых пункта, когда ее попросили объяснить свой выбор.
Ограниченное понимание свойств
Хотя разговоры о формах часто помогают, знания
детей часто имеют пределы. Четырехлетние —
детей часто говорят, что треугольники имеют «три
точек» или «три стороны». Половина из них никогда не знала, что такое «точка» или «сторона» (Клементс
1987). Например, ученика попросили встать на треугольник
из нескольких наклеенных на пол контуров
фигур.Студент сразу же поставил на треугольнике
и объяснил, что «у него три стороны
и три угла». Когда ее спросили, что она имела в виду под
три угла, она ответила: «Не знаю».
Чем могут помочь учителя
?
Результаты исследований, которые мы описали,
имеют большое значение для обучения геометрии.
16 забавных детских книжек о фигурах
Эти настольные книги и книжки с картинками помогут вашему дошкольнику узнать о формах, включая круги, квадраты, треугольники и другие геометрические фигуры. Кроме того, эти детские книги по математике очень интересны для чтения. Иногда бывают даже веселыми или трогательными.
Кроме того, эти детские книги по математике очень интересны для чтения. Иногда бывают даже веселыми или трогательными.
Понимание форм — это фундаментальный математический навык, а также важный навык визуальной идентификации.
Когда дети начнут учиться, вы можете искать формы в своем окружении. Говорите о том, что вы заметили. Затем сравните, в чем разница между объектами. Кроме того, полезно сортировать фигуры по группам — вы можете делать это даже с едой! Чем больше вы будете практиковать, обучая своих детей геометрическим объектам, тем лучше.Также сюда входят такие идеи, как создание собственных фигур из зубочисток, соломинок или палочек. Наконец, это помогает дошкольникам научиться петь такие песни и стишки, как эти из Детства 101.
16 забавных детских книг о фигурах
Фигуры Стэнли от Williambee
Яркие графические иллюстрации сразу привлекают внимание читателей. Каждый двухстраничный разворот содержит множество геометрических объектов, которые нужно найти. Очень мило!
Фургончик с едой Фрэнки
Эта настольная книга представляет собой веселое обучающее приключение для детей, которые изучают формы.Каждый день недели Фрэнки выполняет разные формы. Поднимите заслонки тарелок, чтобы увидеть, какие продукты могут заказать его клиенты. В понедельник это квадраты, в среду кружки, а по пятницам — сердечки и звезды. Какое вкусное введение в формы!
Mail Duck Эрика Сиротич
Mail Duck доставляет формы! Во-первых, треугольники к Трудам. Посмотрите на все треугольники, которые Труди получает по почте, и на все треугольники в ее доме в форме буквы А.Mail Duck продолжает доставлять формы другим своим друзьям-животным: Сесилу нравятся круги, Скауту нравятся квадраты, Омару нравятся овалы, Рози любит прямоугольники, а Гарри любит сердца. Тогда приготовьтесь к забавному сюрпризу в почтовом отделении. Симпатичный, с подробными, интересными иллюстрациями, которые можно заливать по мере чтения, — это восхитительный способ попрактиковаться в распознавании форм.
Симпатичный, с подробными, интересными иллюстрациями, которые можно заливать по мере чтения, — это восхитительный способ попрактиковаться в распознавании форм.
Круг, Треугольник, Слон Кендзи Оикава и Маюко Такеучи
Поучительно и глупо, вы увидите три объекта на странице.Сначала вы увидите геометрические фигуры, такие как круг, прямоугольник, треугольник. Но становится очень глупо, когда автор добавляет к повествованию лодку, слона или даже лимон.
Это «Книга форм» Кеннета Крейгеля
Книга начинается с простого введения трех основных форм. Затем он переходит в глупость, представляя эму, толкающего тележку с блинами с холма. Он продолжается таким же образом, вводя формы, а затем случайным образом вставляя что-то глупое (морская свинья, читающая книгу анекдотов о тук-тук трем глупым морским черепахам. Эта книга — от кругов до овалов и носорогов в реактивных ранцах — это восхитительное и глупое приключение, которое действительно может помочь детям изучить формы!
Изображение этой формы автор: Judith Nouvion
Посмотрите на точки на крыльях божьей коровки или на треугольник зеленой бабочки. Затем посмотрите на алмаз, сделанный дьявольским лучом. Хотя это небольшая настольная книга, это прекрасная дань уважения тому, что вы можете открыть для себя в природе.
Запутанный Энн Миранда, иллюстрированный Эриком Комстоком
Геометрическая книга о формах, дружбе и решении проблем, которая настолько мила, что я с трудом выношу.Одна за другой фигуры попадают в тренажерный зал в джунглях и не могут выбраться наружу. Какая форма их вытянет? Это весело, очаровательно, и у аллилуйи есть подходящие рифмы!
Помогите Лису и Быку найти пропавший носок Фокса. Во-первых, Фокс пытается точно описать свой носок — он синий, с точками, с большими точками. Затем Бык увлекается поисками носка. Помогите друзьям отсортировать и сопоставить в этой веселой, беззаботной истории об узорах, формах, сравнении и противопоставлении, а также идентификации объектов.И ты никогда не угадаешь, где Фокс находит свой носок!
Round Is a Tortilla: A Book of Shapes , Roseanne Greenfield Thong, иллюстрация Джона Парры
Мне очень нравится эта книга. Я так рада видеть книгу форм, которая выделяется из толпы и прославляет латинскую культуру. « Звезды для вечеринок, звезды для света, яркие цвета на улицах. Куда бы вы ни пошли, там так много форм. Сколько еще форм вы знаете? ”
Полумесяцы и остроконечные минареты: мусульманская книга форм Хен Кхана, иллюстрировано Мехрдохтом Амини
Я не могу понять, насколько удивительно искусство в этой книге.Пышные, богато окрашенные иллюстрации сразу же привлекли меня к этой прекрасной книге с мусульманской точки зрения. « Hexagon — это плитка, / жирная и яркая, / нарисованная аятом / я люблю повторять ». Узнайте о геометрических фигурах, таких как круги, квадраты и восьмиугольники, из повседневной жизни и архитектуры.
Фигуры мышей Эллен Столл Уолш
Моим детям нравились книги о мышах, в том числе этот рассказ о мышах, убегающих от кошки.Они решают спрятаться среди множества фигур, а затем им нужно использовать геометрические фигуры, чтобы обмануть подлую кошку. Как они это сделают?
Трапеция — не динозавр Сюзанна Моррис
Если вы любите забавные книги, которые забавны и доставляют удовольствие, вам понравится эта книжка с картинками. Эти фигуры играют в игру. Они принимают трапецию за динозавра (легкая ошибка) и не позволяют ему участвовать. Потому что, очевидно, в пьесе о космосе динозавр не играет роли.Формы уточняют свои качества (стороны, углы и т. Д.), Поэтому дети также узнают свойства каждой формы, но это так многозначительно, игриво, что это не похоже на урок. Я ЛЮБЛЮ эту книгу — не пропустите.
Цвета против форм Майк Болдт
Цвета показывают, насколько талантливы формы, смешивая желтый и синий, чтобы получить зеленый. Затем Фигуры показывают Цвета, как два треугольника образуют квадрат. Они спорят пока.. . восьмиугольник и красный цвет сталкиваются. Ого! Может, им вместе лучше? Глупая забава о силе сотрудничества!
Circle, Square, Moose Келли Бингхэм, иллюстрировано Полом О. Зелински
Лось доходит до своих обычных выходок, потому что Зебра, рассказчик, не может заставить Лося выйти из книги !! Но Zebra найдет решение, и они всегда будут хорошими друзьями, несмотря ни на что. Это ВЕСЕЛЫЕ и одна из наших любимых книг о формах.(Добавлен в мой БОЛЬШОЙ СПИСОК ЗАБАВНЫХ КНИГ ДЛЯ ДЕТЕЙ.)
Формы города Дайана Мюррей, иллюстрация Брайана Коллиера
Маленькая девочка находит различные формы вокруг города, включая квадрат, прямоугольник, треугольник, круг, овал, ромб и звезду. Используйте эту книгу, чтобы вдохновить вас на охоту за формами окружающей среды. Великолепные акварельные и коллажные иллюстрации.
Прекрасная паутина Уолтера Тим Хопгуд
Вода соткала из его паутины формы, пытаясь сделать прочную, непродуваемую паутину.Можете ли вы предсказать, какие формы выдержат силу ветра?
Задача для пикника Джонатана Литтона, иллюстрированная Магали Мансилла
Макс и Сьюзи идут в парк, чтобы решить связанный с математикой поиск сокровищ и подсказок. Например, « У какого воздушного змея самый длинный хвост?» Игнорируйте строки, чтобы не потерпеть неудачу. ”Сначала Макс и Сюзи сравнивают хвосты воздушных змеев разной формы. Круглый змей становится победителем и получает следующую подсказку.В конце концов, есть масса забавных математических задач, которые дети могут решать вместе с главными героями.
Круг и Квадрат разные, но на самом деле лучшие друзья. Пока не появится Треугольник. Дружба Circle и Square внезапно наполняется ревностью и обидой. Они так злятся, что тянут Треугольник в линию. Что они могут сделать? Очевидно, им нужно будет снова собрать треугольник. Повсюду язвительный юмор придает этому знакомому посланию забавный математический поворот.
Круглые ролики Барбар Каннинен, иллюстрации Сержа Блоха
Когда круг катится, он заходит в точку треугольника, разлетаясь на крошечные кусочки.Это вызывает цепную реакцию сталкивающихся фигур, пока Октагон не остановит их всех. Когда они научатся работать вместе, они смогут снова собрать кусочки круга. К счастью, Круг снова катится! В конце концов, мне нравится (без каламбура) круговой финал.
Треугольник Мак Барнетта и Джона Классена
Причудливый юмор! Треугольник покидает свой дом, чтобы сыграть на площади подлую шутку. Square преследует Triangle обратно к дому Triangle, где Square застревает в треугольном дверном проеме.Но не волнуйтесь. Вы увидите, что Квадрат быстро соображает …
Вам также может понравиться:
7 игрушек с удивительной геометрией для детей
Наша дочь, как и ваши дети, недавно закончила учебный год заочно. В этом году геометрия была важной частью математической программы. Поэтому, пока я поддерживал ее обучение дома, я исследовал несколько удивительных игрушек по геометрии, чтобы закрепить ее уроки. От геометрических головоломок, таких как танграммы, до геометрических фигур для построения и исследования, я был поражен изобилием геометрических игрушек на рынке!
Чтобы помочь вашим маленьким Эйнштейнам в их путешествии по геометрии, мы собрали лучшие геометрические игрушки для детей! Наши обзоры предоставят вам прекрасное представление о плюсах и минусах каждой из этих геометрических игрушек, а также некоторые отличные идеи для расширения их потенциала! И здесь есть что-то для всех, от дошкольников и не только.Так что вы обязательно найдете игрушки с идеальной геометрией, которые удовлетворят потребности вашего ребенка.
Ищете другие игрушки для обучения вашего ребенка? Также ознакомьтесь с нашими любимыми математическими и техническими STEM-игрушками!
Spring Into STEM участвует в программе Amazon Associates. Это означает, что мы получаем комиссию за соответствующие покупки. Ссылки, отмеченные *, являются партнерскими ссылками.
Эта геометрическая головоломка представляет собой забавный и познавательный способ познакомить маленьких детей с миром форм.Каждая из 20 головоломок двусторонняя, всего 40 головоломок, состоящих из двух частей. Младшие дети могут сопоставить изображения фигур с фотографиями повседневных предметов, а дети постарше могут сопоставить названия фигур, такие как «ромб» и «квадрат», соответствующим формам. У этого набора головоломок определенно есть возможность расти вместе с вашими детьми! И будет отличным дополнением к любому дошкольному учреждению или детскому саду.
Возраст : 3 и старше
Что нам в нем нравится : Если вы ищете отличную вводную игрушку STEM с геометрией, эта головоломка на основе форм от Trend Enterprises — отличное место для начала.Каждая головоломка состоит всего из 2 частей, и только правильные совпадения подходят друг другу. В совокупности эти функции позволят детям без проблем освоить формы и геометрию. Кроме того, каждая головоломка напечатана на толстом прочном картоне, что делает их относительно устойчивыми к жестким играм. И, как известно любому, кто имеет маленькие дети, прочность — это ключ к успеху!
Минусы : В то время как этот набор геометрической головоломки заставляет детей собирать 40 разных головоломок, на самом деле они будут исследовать только 10 различных форм.И хотя это может ограничить возможности обучения для детей старшего возраста, это, вероятно, подходит для самых маленьких. Избыток фигур, новые имена и изображения форм могут легко отпугнуть маленьких математиков. Таким образом, хотя детям старшего возраста может быстро надоесть, мы думаем, что дети младшего возраста получат достаточные вызовы, не будучи перегруженными.
Мы не смогли бы сделать наш обзор удивительных геометрических игрушек без классического набора головоломок танграм! Этот набор от Melissa & Doug включает 120 цветных и магнитных геометрических фигур, а также 6 двусторонних карточек с узорами.Узор легко вставляется в рамку магнитной доски, позволяя детям воспроизвести любую геометрическую картинку. Но они также могут использовать свое воображение и повеселиться, создавая мозаику в свободном стиле! Вы даже можете подобрать к этому набору книги по танграму. Нам нравятся «Загадка военачальника» Вирджинии Пилегард * и «Танграмы: 50 загадок» Р. Дж. Кларка *.
Возраст : 3 и старше
Что нам в нем нравится : Во многих наборах деревянных пазлов Мелиссы и Дуга нет футляра для переноски, поэтому мы были потрясены, увидев, что в этом наборе головоломок tangram он есть! Все можно аккуратно убрать, что снижает вероятность пропажи деталей.Нам также нравится, что геометрические плитки прикрепляются к доске магнитно. Посмотрим правде в глаза — дети все еще развивают мелкую моторику, и им достаточно легко толкать или толкать то, над чем они работают. Но оригинальная магнитная доска означает, что даже малейшее движение руки не помешает вашим детям создавать красивые мозаики!
Минусы : В то время как этот набор головоломок танграм поставляется с удобной сумкой для переноски, контейнер, в котором хранятся части танграма, не имеет крышки.Как вы понимаете, это означает, что они просто выливаются из нее в сумку. Но мы думаем, что это легко исправить. Либо выбросьте контейнер и просто примите тот факт, что ваши дети, вероятно, все равно не сложат их должным образом, либо возьмите пластиковый пакет, чтобы держать их подальше.
Погрузитесь в мир Osmo со стартовым комплектом Genius! Доступные в наборах, совместимых с iPad * и Amazon Fire *, ваши дети будут изучать геометрию, математику, правописание и даже немного физики! Оба набора включают подставку для планшета, отражатель камеры и различные игровые элементы (танграм, числа, игральные кости и буквы).Таблетки продаются отдельно.
Возраст : 5 и старше
Что нам в нем нравится : Мы рассматриваем Osmo не в первый раз, и уж точно не в последний! Нам (родителям и ребенку) это очень нравится. Я никогда не чувствую себя виноватым из-за экранного времени, когда у нас есть дочь, потому что она так много учится! (Ознакомьтесь с некоторыми другими нашими обзорами здесь и здесь, поскольку в этом посте мы в основном сосредоточены на игре tangram). Во время игры в танграм вашим детям будет предложено собрать различные мозаики, используя их 7 геометрических плиток.В зависимости от возраста вашего ребенка узоры будут отображать каждую плитку по мере необходимости или в виде силуэта. В последнем случае у детей возникнут проблемы с позиционированием плитки, что отлично подходит для развития пространственной осведомленности и навыков решения проблем! Если им нравятся головоломки, им понравится эта техническая игра с геометрией!
Минусы : Хотя вы можете получить доступ ко всем играм Osmo, которые включены в Genius Starter Kit, без настройки учетной записи, без нее функциональность определенно снижается.Это было определенно неприятно, когда мы впервые установили программу на планшет нашей дочери. Игра tangram также может быть немного привередливой, если плитки не в кадре или немного не на своем месте. Но на самом деле, после нескольких сеансов наша дочь научилась этому и никогда не оглядывалась назад!
Мы уверены, что вы слышали о Magna-Tiles, так что вы, вероятно, будете так же взволнованы, как и мы, узнав об этом новом (ишом) продукте от бренда! Magna-Qubix похожа на оригинальные магнитные геометрические фигуры, только в 3D! Этот строительный набор включает 85 красочных деталей, в том числе множество кубиков, призм и пирамид.Куски размером примерно 1 на 1 дюйм, с магнитами на каждом краю.
Возраст : 3 и старше
Что нам в нем нравится : Мы большие поклонники Magna-Tiles в нашем доме. Но наша первая жалоба заключается в том, что части могут легко схлопнуться друг о друга при построении трехмерных структур (привет, магнетизм!). Это вызвало множество эпизодов разочарования у нашей дочери, когда она была моложе. Нет ничего более досадного, чем когда ваша почти вся конструкция рухнет от рывка руки.Мы очень рады, что Magna-Tiles разработала Magna-Qubix! 3D-фигуры уже собраны, поэтому детям младшего возраста будет намного проще строить их без лишних хлопот! Но это не только для маленьких. Если ваши дети уже являются мастерами Magna-Tile, Magna-Qubix станет отличным дополнением к их существующей коллекции, поскольку все они совместимы! Кроме того, поскольку блоки являются магнитными, вы можете проявить гораздо больше творчества в своих проектах, чем с традиционным набором блоков.
Минусы : Имейте в виду, что формы скромные по размеру, примерно 1 дюйм на 1 дюйм каждая.Это довольно мало. Намного меньше, чем ваш средний набор зданий. Но размер деталей не должен подавлять творчество. Только подумайте об удивительных творениях LEGO, которые они создали! И хотя есть наборы с меньшим количеством деталей (как 19 *, так и 29 *), ваши дети, вероятно, не смогут построить так много с таким малым количеством деталей. По этой причине мы рекомендуем более крупный набор из 85 предметов, который мы рассматриваем здесь. Пусть дети проявят творческий подход!
Набор «Геометрические тела» из учебных материалов включает 14 уникальных трехмерных форм, включая призмы, пирамиды и кубы.Каждая форма полупрозрачна и оснащена съемным основанием. Детали изготовлены из прочного пластика, каждая форма имеет размер от 3 до 6 см. Вы также получите 4-страничное учебное пособие.
Возраст : 8 и старше
Что нам в ней нравится : Эта геометрическая игрушка намного больше, чем ваш средний набор строительных блоков. Он был создан с целью обучения, как и большинство STEM-игрушек от Learning Resources. Руководство по занятиям обучает базовой терминологии геометрии (например, вершина, грань и край), а также таким понятиям, как объем (вы также можете легко указать площадь и периметр).Основание каждой формы легко снимается, что позволяет детям наполнять их жидкостью и экспериментировать с измерением и сравнением объема.
Минусы : По нашему мнению, большим преимуществом этих форм является то, что вы можете заполнить их, чтобы продемонстрировать объем. Однако иногда основания могут выскочить при обращении с ними. Так что обращайтесь с ними осторожно, когда они наполнены! Никто не хочет, чтобы кругом было полно воды!
Эта деревянная геодоска от Coogam идеально подходит для детей всех возрастов! Сам геоборд прочный, выдерживает тяжелые игры.Он разработан с 64 закругленными штифтами, поэтому вам не нужно беспокоиться о том, что заостренные края ткнут мизинцы. В комплект также входят латексные ленты разных размеров и цветов и 35 карточек-головоломок (5 из которых пустые). Дети могут весело провести время, воссоздавая различные узоры или создавая свои собственные!
Возраст : 3 и старше
Что нам в нем нравится : Географические доски — отличный инструмент для студентов, изучающих геометрию. Завершение дизайна карточек — увлекательная задача, но возможности на этом не заканчиваются.Помимо создания собственных шаблонов, дети могут использовать геодоски, чтобы по-настоящему расширить свое понимание геометрии. Предложите ребенку создать цветок, используя только треугольники. Или кошка, использующая 5 уникальных геометрических фигур (например, квадрат, треугольник, прямоугольник, ромб и пятиугольник). Географические доски также идеально подходят для демонстрации геометрических преобразований (переводов, отражений и поворотов) и более сложных тем, таких как площадь и периметр.
Минусы : Наша основная жалоба на эту геоборду заключается в том, что карточки с дизайном не соответствуют рекламе на коробке.В отличие от шаблонов, которые показывают, что должны быть размещены полосы разного цвета, карты имеют случайные твердые формы, которые необходимо воссоздать. Но, честно говоря, детям, вероятно, в любом случае будет больше удовольствия создавать свои собственные проекты. Поэтому мы не видим в этом большой проблемы.
В то время как ваши дети, вероятно, не умирают, чтобы изучать геометрию на ходу, Tangoes Jr. — отличная путешествующая STEM-игрушка, которая поможет вашим детям занять и развлечься! В этот набор входит сумка для переноски размером на коленях с 12 двусторонними узорами, 7 формами танграма и буклет с дополнительными головоломками, которые нужно решить.Доска и пазл обладают магнитными свойствами, что делает их идеальными для автомобильных поездок и других путешествий. Карты и детали удобно убираются в сумку для переноски.
Возраст : 4 и старше
Что нам в нем нравится : Помимо того, что это изящная геометрическая игрушка, которую можно носить на ходу, нам нравится, что она может расти вместе с вашим ребенком. 120 уникальных заданий имеют 3 разных уровня сложности, от новичка до эксперта. Так что каждому ребенку в вашем доме, безусловно, есть чем заняться! Более простые головоломки имеют очертания формы, указанные на карточке, а более сложные — просто показывают контур всего рисунка.Вы должны выяснить, куда деваются детали! А из пазлов из прилагаемого буклета дети должны будут собрать их «вольным образом» на магнитной доске. Нет подсказки, которая могла бы указывать на размещение фигур. Это сложно, но представляет собой серьезную задачу для детей, решивших более простые головоломки. Хотя эта геометрическая игрушка классифицируется разработчиком как «дошкольная», мы думаем, что она понравится и детям старшего возраста.
Минусы : Как мы уже упоминали выше, 12 двусторонних карточек действий имеют 3 разных уровня сложности.Но это означает, что для начинающих существует всего 8 головоломок с очертаниями фигур.










