Рисунок объемный квадрат: Объемный квадрат рисунок карандашом. Как рисовать объемные фигуры и тела карандашом
- Объемный квадрат рисунок карандашом. Как рисовать объемные фигуры и тела карандашом
- Как поэтапно рисовать 3D треугольник
- Как научиться рисовать предметы в 3D: несколько простых техник, которые освоит даже ребенок | Lifestyle
- Математический кубизм в Paint 3D
- Как начертить объемный квадрат. Как построить правильный квадрат
- Как сделать фигуру объемной в word 2010?
- Как рисовать в Ворде
- Первые шаги
- Как вставить фигуру на лист
- Стили фигур
- Как вставить текст в фигуру Word
- Положение и обтекание фигур
- Взаимное расположение фигур
- Группировка фигур в Ворде
- Поворот и отражение фигур
- Изменение размеров фигуры
- Включение вкладки «Рисование»
- Средства рисования
- Рисование с помощью фигур
- Инструменты для рисования
- Урок 62. куб — Математика — 4 класс
- Что такое трехмерные формы?
- Трехмерные формы | SkillsYouNeed
- Трехмерные фигуры — Космические фигуры
- 3D-фигур — трехмерные формы | Определение, типы и многое другое
- геометрических фигур
- Опишите двумерные фигуры, полученные в результате нарезки трехмерных фигур: CCSS.Math.Content.7.G.A.3
Объемный квадрат рисунок карандашом. Как рисовать объемные фигуры и тела карандашом
Попробуем понять принцип взаимодействия квадрата и окружности на перспективном рисунке. Научиться проверять правильность квадрата, вписывая в него окружность.
Изобразите в перспективе горизонтальный и вертикальный квадраты. Проверьте правильность их изображения при помощи вписанных окружностей.
Прежде, чем приступать к выполнению этого задания, внимательно рассмотрите схему на рис. 2.8. Точки касания сторон квадрата к окружности (точки 1, 2, 3, 4) делят стороны квадрата пополам. Средние линии квадрата и его диагонали пересекаются в центре окружности. Противолежащие стороны квадрата и соответствующие им средние линии параллельны и расположены на равном расстоянии друг от друга. Рассмотрите также рис. 2.9. На примере окружности и квадрата во фронтальной перспективе хорошо видно, что центр эллипса и центр окружности — две разные точки. Диаметр окружности, являющийся малой осью эллипса, делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю — больше, дальний — меньше (по закону перспективного сокращения), а точка центра эллипса делит этот же диаметр — малую ось эллипса — ровно пополам.
Нарисовать квадрат в перспективе можно в разной последовательности, например, сначала изобразить одну прямую — сторону квадрата, а затем другую, ей перпендикулярную, отложить на этих прямых от точки их пересечения отрезки, равные стороне квадрата, а затем от полученных вершин достроить остальные стороны, сводя параллельные прямые в точки схода. Или иначе — сначала провести две параллельные прямые, а затем еще две, перпендикулярные двум первым. В любом случае эта задача кажется простой только на первый взгляд. На самом деле слишком много позиций (степень схождения параллельных сторон квадрата, их направления и размеры) рисовальщику приходится определять на основании своего личного опыта, а его, как известно, иногда бывает недостаточно. Именно поэтому правильность квадрата необходимо проверить, например, вписав в него окружность.
Горизонтальный квадрат. Нарисуйте горизонтальный квадрат по представлению (рис. 2.10). Найдите точки касания, для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода (рис. 2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис. 2.13). Проверьте симметричность полученного эллипса относительно его осей.
Вертикальный квадрат. При вертикальном положении квадрата точки 1, 2, 3, 4 найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис. 2.14).
Несколько сложнее определить направление осей эллипса. Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры.
На рисунках, иллюстрирующих последовательность вписывания окружности в горизонтальный и вертикальный квадраты, представлены идеальные ситуации. В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.
Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе. Именно поэтому современная методика предлагает не проверять и исправлять подобным образом уже нарисованные квадраты, а строить их, описывая вокруг окружности.
Хоть квадрат и прямоугольник это простейшие геометрические фигуры, но, чтобы их нарисовать в фотошопе, нужно приложить некоторые усилия и обладать базовыми знаниями. Новичок без должной подготовки, скорее всего, не справится с этой задачей.
В этой статье разберем 3 самых популярных способа как нарисовать прямоугольник или квадрат в фотошопе.
Но прежде, чем приступить к выбору способа рисования, нужно определиться с будущими параметрами. Прямоугольник/квадрат может быть:
- залит сплошным цветом или только с отрисовкой границ;
- произвольный или с точно заданными размерами;
- с возможностью в любое время менять его размеры без потери качества.

Способ 1. Инструмент произвольная фигура
В этом способе прямоугольник или квадрат будут нарисованы залитым сплошным цветом. Если вам нужна только граница, переходите к следующим двум способам.
На панели инструментов выберите инструмент . Дальше возможны два варианта развития событий:
Вариант 1. Квадрат или прямоугольник с дальнейшей возможностью изменять размеры без потери качества
Здесь, конечно, подразумевается использование векторной фигуры. Чтобы ее нарисовать нужно выбрать параметр Слой-фигура :
В дальнейшем вы можете без потери качества изменять размеры этой фигуры. Для этого используйте инструмент — Ctrl+T , и с помощью угловых маркеров изменяйте размер.
Для тех кто не знает : векторные фигуры состоят не из пикселей, а из специальные математических формул. Поэтому изменение размера — это не процесс растягивания/сжатия пикселей, а сложный математический пересчет, за счет чего не происходит никакой потери качества.
Вариант 2. Стандартный (растровый) квадрат/прямоугольник
Чтобы нарисовать сразу растровую фигуру используйте на панели параметров настройку Выполнить заливку пикселов . Но прежде чем начать ее рисовать — !
Но на самом деле можно рисовать сразу и векторный, а потом просто его. Тут уже выбирайте сами.
Как сделать прямоугольник квадратным
Обыкновенное правило с зажатой клавишей Shift с произвольными фигурами не работает. Поэтому нужно воспользоваться панелью параметров инструмента и выбрать настройку, чтобы фотошоп рисовал именно квадрат.
В этой же панели, обратите внимание, вы можете указать точный размер необходимого прямоугольника/квадрата или рисовать его по заранее определенным пропорциям.
По умолчанию размеры определяются пикселями. Если вы хотите изменить единицу измерения, сначала введите в поле какое-либо значение, а затем кликните по нему правой кнопкой мыши. Появится окно выбора единиц измерения. Доступно: пиксели, дюймы, сантиметры, миллиметры, пункты и пики.
Прямоугольник или квадрат со скругленными углами
Чтобы получить фигуру со скругленными углами, делайте все то же самое, что описано выше, но в самом начале выберите инструмент Прямоугольник со скругленными краями . На панели параметров инструмента нужно будет указать только радиус закругления.
Способ 2. Обводка выделенной области
Этот способ простой, как 5 копеек. выберите инструмент и нарисуйте прямоугольник пунктирной линией. Чтобы нарисовать квадрат удерживайте нажатой клавишу Shift .
Теперь нужно сделать обводку границ этой выделенной области. Для этого перейдите в Редактирование — Выполнить обводку .
Затем в новом окне настройте вид обводки: укажите толщину рамки, желаемый цвет и отметьте как будет проходить обводка:
- Внутри — значит рамка ляжет по внутренней стороне выделенной области;
- По центру — значит рамка разделится поровну на часть проходящую внутри выделения и на часть со внешней стороны;
- Снаружи — значит рамка будет огибать пунктир выделения.
Вот как может получиться:
На скриншоте выше я специально не убрал пунктирную линию, поскольку у вас она также не исчезнет. Чтобы окончательно от нее избавиться нажмите Ctrl+D .
В этом способе, чтобы нарисовать фигуру точного размера, нужно сперва на панели параметров инструмента указать Стиль — Заданный размер или Заданные пропорции. После этого станут активными поля, куда введите значения ширины и высоты в пикселях. Кликом правой кнопкой мыши по одному из этих полей вызовет меню изменения единиц измерения.
Способ 2.1 Закрашивание выделения
Самый банальный способ рисования прямоугольника — нарисовать рамку выделения (как описано выше) и просто закрасить ее любым цветом. Вот вам и прямоугольник или квадрат.
Способ 3. Модификация выделения
На самом деле этот способ мне меньше всего нравится из-за очевидного минуса — углы прямоугольника будут подрезанными, а сама граница рамки в состоянии и повлиять на эти факты не представляется возможным.
Итак, нужно вновь выбрать инструмент , нарисовать рамку будущего прямоугольника или квадрата (с клавишей Shift ), а затем отправляемся в меню Выделение и выбираем команду Модификация — Граница .
Появится новое окно, в котором, в нашем случае, мы указываем ширину границы прямоугольника. Допустим, укажу 7 пикселей. Получим такой результат:
А теперь нужно просто закрасить получившуюся рамку. Для этого подойдет . Здесь, кстати, можно подойти к вопросу более творчески и закрасить, например, разными цветами. Результат:
Останется только снять выделение — Ctrl+D . Думаю этот способ подходит только для своих редких специфических задач, поскольку растушевка и подрезанные углы только все портят.
Заметили ошибку в тексте — выделите ее и нажмите Ctrl + Enter . Спасибо!
Все предметы, которые нас окружают можно мысленно вписать в простые геометрические тела (куб, шар, конус, цилиндр, призма и др.). Изучая форму куба, мы узнаем, как нарисовать, к примеру, дом, потому что упрощенно дом рисуется с использованием тех же приемов что и куб. У него есть вершины, ребра и грани, как и у куба. Крыша дома – это многогранная призма.
Нарисуем куб с натуры, а затем будем использовать эти знания на наших для изображения более сложных предметов таких как дома и улицы.
Куб – геометрическое тело, образованное пересечением плоскостей. И, как всякий объемный предмет, при изображении на плоском листе он будет претерпевать изменения в соответствии с законами перспективы. На рисунке изображена линия горизонта это уровень плоскости зрения художника . На ней находятся точки схода параллельных линий. В нашем случае — это четыре горизонтальных линии, стремящихся в точку схода слева и четыре горизонтальных линии, стремящихся в точку схода справа.
Мы изображаем предметы в пространстве так, как их воспринимает наш глаз. (Чем дальше от зрителя, тем меньше выглядит предмет и т.д.)
Начало любой картины – это композиция. Легкими линиями намечаем наш предмет на листе. Сверху всегда должно быть чуть больше места от края, чем снизу. Интуитивно определите масштаб так, чтобы предмет не выглядел гигантским или слишком маленьким.
Легкими линиями намечаем наш предмет на листе. Сверху всегда должно быть чуть больше места от края, чем снизу. Интуитивно определите масштаб так, чтобы предмет не выглядел гигантским или слишком маленьким.
Расположите самое ближнее вертикальное ребро так, чтобы оно не совпадало с центром листа, проходящим через пересечение его диагоналей. Засечками отмечаем высоту, это самое высокое ребро в нашем изображении, так как оно ближе всех к зрителю. На глаз определяем угол наклона ребер лежащих на столе относительно горизонтали. Тренируйте зрительную память, запоминая угол. Взгляд переводите быстро то на куб, то на рисунок.
То же проделаем и с верхними ребрами. Как передавать пространство на листе нам объясняют основные законы линейной перспективы. Все параллельные линии сливаются к линии горизонта в одну точку. Поэтому, чтобы передать что ребро находится дальше от зрителя, мы изобразим его меньше и расположим выше . Таким образом, все ребра будут разной высоты.
При пересечении дальних горизонтальных ребер образовались вершины. Через них проходит самое дальнее, невидимое глазом, ребро. На начальном этапе изобразим куб прозрачным для понимания полной конструкции предмета.
Для того, чтобы узнать на сколько сократились боковые грани, воспользуемся методом визирования . При помощи этого метода происходит восприятие очертаний предмета, художник учится изображать предметы пропорциональными и в различных ракурсах.
Как он работает? Возьмите карандаш на вытянутой руке, прикройте один глаз, совместите карандаш и изображение ребра куба в пространстве. Верхний край карандаша должен совпадать с верхней вершиной ребра, а пальцем зажмите на карандаше точку, совпадающую с нижней вершиной. Не убирая палец с карандаша, разверните под прямым углом и измеряйте расстояние между двумя ребрами. Таким образом, мы увидим соотношение высоты и ширины одной грани. Запомните это соотношение и передайте его на рисунке. Этим методом можно измерять и изображать так же соотношение ребер.
После того, как закончены линейные построения, приступаем к воздушной перспективе , а значит к штриховке.
Основная задача художника передавать объемные формы предметов. У нашего кубика мы видим три грани, все они разные по тону. Левая грань самая темная — это собственная тень предмета. Благодаря отраженному свету от окружающих предметов или рефлексам, штриховку делаем немного светлее по мере удаления влево. Самое большое ребро делают контрастней, чем все остальные. Таким образом, показывают его приближенность на передний план.
Верхняя плоскость темнее , чем вертикальная справа. Свет по ней лишь скользит, образуя полутон. Обратите внимание, что чем ближе к источнику света, тем светлее будет тон. Штриховку можно наносить по диагонали. На ребре ластиком высветлим, чтобы передать блик.
Для работы над самой светлой гранью возьмем твердый карандаш Н или 2Н . Он не даст сделать тон слишком темным. Штриховку нанесем вертикальную, по направлению плоскости.
Падающие тени всегда темнее, чем собственная тень предмета. Ближнее ребро – это линия перехода света и тени. Из нее начинается падающая тень. Чем ближе к предмету, тем насыщеннее тон. Отраженный свет от куба создает рефлекс внутри тени и она немного высветляется.
Рисование простых геометрических тел часто используется на и позволяет начинающему художнику научиться изображать предметы в пространстве, применяя законы перспективного построения и воздушной перспективы.
Доброго времени суток, начинающий художник и постоянный посетитель блога .
Надеюсь, было достаточно сфер? Так что давайте перейдем к важному, чрезвычайно разностороннему кубу . Куб настолько универсален, что вы будете использовать его для отрисовки рамок, домов, зданий, мостов, самолетов, автомобилей, цветов и рыб…рыб?? Да, куб поможет вам нарисовать даже маленьких рыб в 3D, а также лицо, цветы, ну и все, о чем вы можете подумать или увидеть вокруг. Так что приступим.
Так что приступим.
1. Начните с новой страницы вашего блокнота, напишите номер урока и заголовок, дату, время, местонахождение. Нарисуйте две точки напротив друг друга.
2. Поместите ваш палец между точками, используя другую руку. Затем нарисуйте точку над и под пальцем, как показано на рисунке.
Не стесняйтесь делать записи в блокноте, цитаты, и заметки. Чем больше вы вкладываете своих собственных мыслей и идей в свою записную книжку, тем большее она имеет значение для вас, тем больше вы будете ее использовать. В своем альбоме я делаю записи, напоминания, заметки, списки и все остальные вещи, которые нельзя нарисовать. Мой альбом – это первое место, куда я смотрю, когда мне нужно вспомнить что-то.
3. Взгляните на точки, которые вы нарисовали. Две новых точки должны располагаться близко друг от друга. Мы будем рисовать трапецию (квадрат в перспективе).
4. Проведите первую линию.
5. Проведите следующую линию.
6. Затем третью.
7. Закончите трапецию. Это очень важная форма для практики. Потренируйтесь, нарисовав такую трапецию еще несколько раз. ПРЕДУПРЕЖДЕНИЕ: рисуйте две средние точки очень близко друг к другу. Если они будут слишком далеко, у вас получится «полноразмерный» квадрат. А наша цель – «сплющенный».
В таком ракурсе объект искажается, и создает иллюзию, что одна часть находится ближе к зрителю. Для наглядного примера, вытащите монетку из кармана. Посмотрите на нее прямо. Она представляет собой плоский круг. 2D круг, который имеет длину и ширину (в двух измерениях), но не имеет высоты. Поверхность находится на одинаковом расстоянии от глаз. Теперь слегка наклоните монетку. Форма изменилась на эллипс, который теперь имеет высоту. Теперь у монеты есть все три измерения: длина, ширина и высота. Наклонив монетку, вы сместили край монеты подальше от ваших глаз, вы получили эллипс (круг в перспективе).
В основном, рисование трехмерных объектов сводится к тому, чтобы исказить изображения на плоском двумерном листе бумаги, чтобы создать иллюзию существования глубины. Рисунок 3D искажает формы, чтобы обмануть зрение и заставить объекты казаться ближе или дальше.
Рисунок 3D искажает формы, чтобы обмануть зрение и заставить объекты казаться ближе или дальше.
Теперь давайте вернемся к моему предупреждению о рисовании двух точек посередине. Если ваши точки будут слишком далеко друг от друга, ваш квадрат будет выглядеть вот так:
Если ваша фигура выглядит так, то перерисуйте ее несколько раз, размещая средние точки ближе друг к другу, пока ваша фигура не станет такой:
Ладно, достаточно об искажении пока. Держите эту мысль в голове, она очень важна и каждый урок будет начинаться с этого.
8. Нарисуйте стороны куба, с помощью двух вертикальных линий. Вертикальные, прямые линии сверху вниз без наклона. Вот подсказка: используйте сторону своего блокнота. Если вертикальные линии соответствуют сторонам страницы, ваш рисунок не наклонен.
9. Используя боковые опорные линии, нарисуйте среднюю линию немного длиннее и ниже. Использование нарисованных линий позволяет правильно определить позицию для вашей следующей линии, это очень важно при создании 3D изображений.
10. С помощью верхней крайней правой линии трапеции, нарисуйте нижнюю правую сторону куба. Просто повторите ее быстрым движением руки, смотря на верхнюю линию. Не переживайте, если вы вышли за пределы объекта, вы сможете подкорректировать это позже. Я предпочитаю рисунки с большим количеством дополнительных линий и черточек, которые выглядят трехмерно, а не которые имеют суперчистые и четкие линии.
11. Теперь нарисуйте нижнюю левую сторону куба, ссылаясь на верхнюю линию. Направляющие! Направляющие! Направляющие! Я настоятельно рекомендую вам потренироваться в использовании направляющих линий.
12. Теперь самое интересное — переходим к теням. Определите положение вашего воображаемого источника света. Свой я размещу справа сверху. Заметьте! Я использую направляющие линии, чтобы правильно выстроить угол тени. Путем продления нижнего правого ребра, нарисуйте падающую тень. Неплохо выглядит, правда? Похоже, что куб действительно «сидит» на земле? Это переломный момент, когда рисунок приобретает трехмерность.
13. Закончите ваш первый 3D куб, заштриховав грань противоположную от освещения. Заметьте, что я совсем ее не стал растушевывать. Я растушевываю тени только на округлых поверхностях.
УРОК 4: ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Давайте возьмем то, что мы узнали в основах рисования 3D куба, и добавим некоторые детали.
Мы собираемся нарисовать три кубика. Начните с первого с двух опорных точек. Говоря в следующих уроках «опорные точки», я буду иметь в виду эти точки.
1. Положите указательный палец посередине между опорными точками. Эта потрясающая привычка, которую вы сейчас приобретаете, к концу тридцатого урока станет для вас второй натурой.
2. Соедините точки в трапецию. Эта отличная фигура для практики в вашем альбоме, если у вас есть минута или около того. Например, когда находитесь в очереди или пробке. Поэтому всегда носите с собой свой альбом и карандаш, кто знает, когда у вас появится свободная минутка для рисования!
3. Нарисуйте вертикальные боковые линии и среднюю линию куба. Среднюю линию рисуйте всегда длиннее и ниже, чтобы она казалась ближе.
4. Закончите рисовать куб, с помощью направляющих верхних линий.
6. Нарисуйте опорные точки в середине каждого ребра верхней грани куба.
7. Давайте начнем с первого. Давайте нарисуем на нем старомодный подарочный почтовый пакет, украшенный лентой, в котором мы получаем подарки от бабушки на Новый год. Проведите вертикальную линию вниз вблизи левой опорной точки, а затем по верхней грани к другой опорной точке.
8. Повторите это с другой стороны. Опорные точки помогают нарисовать линию внутри трапеции. Опорные точки являются чрезвычайно полезным инструментом в построении углов, как здесь. Мы часто будем пользоваться этими точками в последующих уроках (очень часто!).
9. Чтобы нарисовать такие линии в горизонтальном направлении, используйте опорные точки снова, только на середине вертикальных линий.
10. Проведите линии, соединяя опорные точки, используйте линии сверху как направляющие.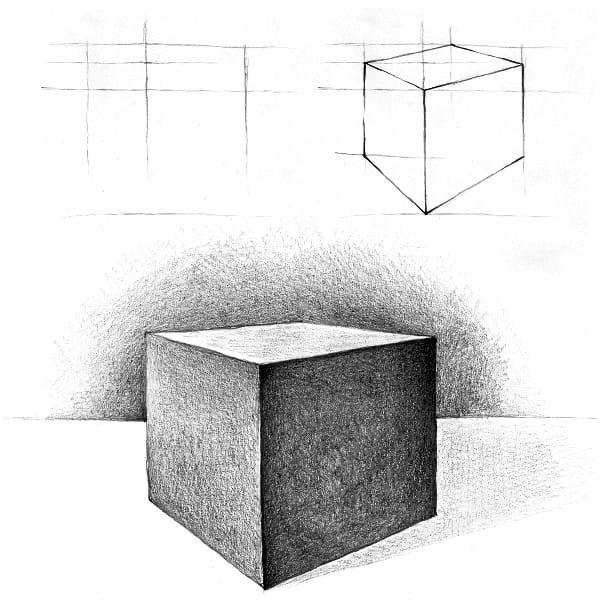
11. С помощью оберточной ленты вы можете закончить все три куба, представив их в виде посылки, игрального куба и подарка, завернутого в толстую ленту.
Еще одно хорошее задание для практики
Поместите любую коробку (обувную, из-под хлопьев или любую другую) на стол перед собой.
Присаживайтесь и разместитесь таким образом, чтобы вы могли увидеть верхнюю грань, похожую на трапецию, которую мы недавно рисовали.
Не паникуйте! Просто вспомните, что вы выучили в данном уроке, и пусть эти знания помогут вам нарисовать то, что видят ваши глаза. Взгляните, внимательно взгляните на тупые углы, затенения, падающую тень. Посмотрите, как надписи на коробке, также следуют за этими углами. Чем больше вы рисуете, тем больше вы буде те замечать множество увлекательных подробностей в реальном мире вокруг вас.
Делитесь вашими работами и получайте полезные советы в
Как поэтапно рисовать 3D треугольник
Сейчас 3D рисунки очень популярны. Люди восхищаются нарисованными от руки реалистичными изображениями, которые, кажется, могут в любую секунду ожить.
Создавать изображение в трехмерном пространстве только кажется трудно. Предлагаем освоить основы 3D искусства с нашей пошаговой инструкцией.
1
Основа
Нарисуйте квадрат средней величины. Если хотите, чтобы рисунок был больше, увеличьте основу.
2
Очертания
Внутри квадрата изобразите треугольник в плоском измерении. Нижняя сторона является частью квадрата.
3
Корректировка
Аккуратно стираем квадрат и оставляем только треугольник.
4
Углы
В верхнем углу фигуры рисуем маленький прямоугольник, чтобы он перекрывал угол. Его ширина равна ширине треугольника сверху.
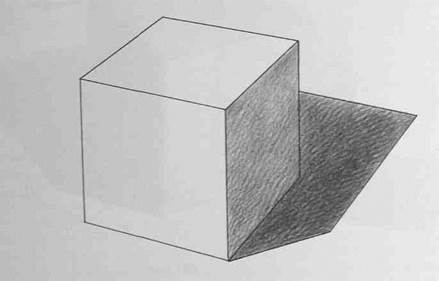
5
Корректировка
Прямоугольники аккуратно стираем, оставляя треугольник со срезанными углами.
7
Третье измерение
От верхней левой линии проводим еще одну вниз, будто изображая маленький треугольник. Еще одну горизонтальную часть изображаем справа.
Соединяем все последней линией, которая начинается от первой горизонтальной.
8
Раскрашиваем
Чтобы 3D треугольник выглядел более реалистично, нужно его правильно раскрасить. Можете использовать один цвет, как показано на рисунке, но внутренние детали сделать более темными.
Вы также можете раскрасить 3D фигуру в онлайн-режиме.
Выберите как хотите закрашивать.
9
Коллаж с этапами рисования 3D треугольника
Если вы увидели ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Как научиться рисовать предметы в 3D: несколько простых техник, которые освоит даже ребенок | Lifestyle
3D-рисунки — вид изображений, создающих иллюзию глубины. Благодаря особой технике, эти картинки кажутся буквально «живыми». Методика создания таких рисунков может показаться сложной. Но на самом деле рисование 3D-изображений — дело относительно простое. С помощью описанной ниже технологии вы сможете создавать такие иллюзии на основе самых разных объектов.
3D-коробка
Создание этого интересного изображения начините, нарисовав обычный квадрат. Если вы не художник и прямые линии от руки вам рисовать сложно, используйте линейку и карандаш. Чернилами квадрат-основу рисовать не нужно. Некоторые линии, чтобы получить 3D-фигуру, придется стереть.
Размеры нарисованный вами квадрат может иметь любые. Главное, чтобы он занимал не более четверти листа. На бумаге должно остаться место для остальных частей коробки. Этот первый квадрат в последующем будет служить лицевой частью куба.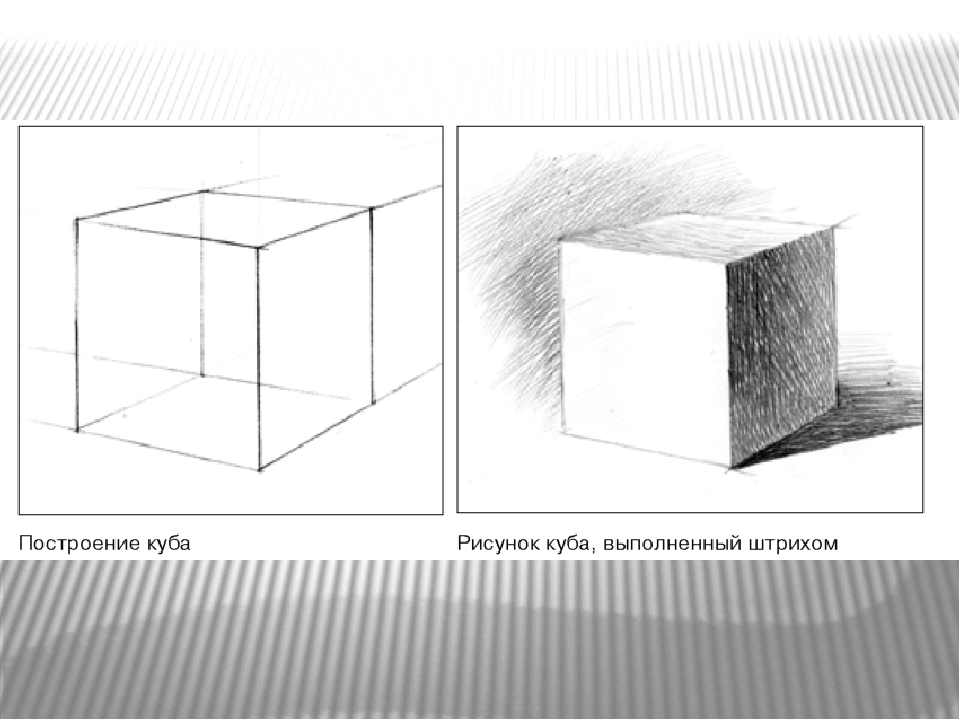
Нарисуйте второй квадрат, пересекающийся с первым. Расположите его немного правее и выше таким образом, чтобы наложение двух квадратов представляло собой также маленький квадрат. Стороны квадратов должны пересекаться по центру. В противном случае у вас получится не куб, а параллелепипед.
Соедините углы квадратов параллельно друг другу. Нарисованные вами линии создадут иллюзию нижней, верхней и боковой сторон куба.
Сотрите все лишнее, чтобы получить 3D-коробку. Эту операцию нужно выполнить только в том случае, если вы не хотите, чтобы ваш куб выглядел «прозрачным».
При желании раскрасьте стенки вашей коробки. Для того чтобы усилить эффект объема, используйте разные оттенки одного и того же цвета. Переднюю стенку сделайте более светлой. Для верхней грани куба, а также боковой используйте темные оттенки.
Другие фигуры
Пользуясь описанной выше технологией, вы можете нарисовать и другие объемные геометрические объекты. Это могут быть, к примеру, пирамида, цилиндр, параллелепипед и пр. Параллелепипед рисуется точно так же, как куб. Но два основных квадрата в данном случае нужно разнести дальше друг от друга. Для того чтобы получить 3D-цилиндр, нарисуйте овал, проведите две параллельные линии и соедините их дугой. Овал раскрасьте темным цветом. Для оставшейся части фигуры используйте более светлый оттенок.
Чтобы создать пирамиду, нарисуйте два треугольника и соедините их вершины прямой линией. Сотрите основание треугольников. Раскрасьте одну из граней пирамиды темным цветом, вторую — более светлым.
Сложные фигуры
Такие простые фигуры, конечно же, может нарисовать и школьник. Натренировав на них руку, можно приступить к созданию более сложных 3D-фигур. К примеру, попробуйте нарисовать объемные звезды или же даже какие-нибудь абстрактные объекты.
Трехмерная оптическая иллюзия
В данном случае сначала выберите объект, который вы хотите нарисовать. Это может быть что угодно. Но форму объект должен иметь четкую и простую. В этом случае создавать 3D-изображение вам будет легче. Например, вы можете нарисовать собственную руку, банан или, скажем, пончик.
В этом случае создавать 3D-изображение вам будет легче. Например, вы можете нарисовать собственную руку, банан или, скажем, пончик.
Положите вашу раскрытую ладонь левой руки на лист бумаги и обведите ее карандашом. Не нажимайте на карандаш слишком сильно. Как и в первом случае, некоторые части контура этого рисунка в последующем нужно будет стереть. Положите на левый край бумаги линейку.
Возьмите вторую линейку и прочертите поперек контура ручкой параллельные линии с шагом в несколько миллиметров. Чертите линии таким образом, чтобы они не заходили внутрь контура руки. Если рисовать вы умеете не слишком хорошо, сначала используйте карандаш, а затем обведите линии ручкой. Чернила на этом этапе можно использовать как одного цвета, так и нескольких. В районе пальцев линии располагайте чаще, внизу рисунка — реже. Нарисуйте дугообразные и волнистые линии внутри контура руки, соединяя ими прямые.
Добавьте немного теней по краю пальцев, косточек и ладоней. Используйте для этой цели мягкий карандаш.
Чтобы рисунок получился эффектным и реалистичным, сотрите контур, который рисовали на первом этапе (фото в самом верху страницы).
Использование перспективы
Если вы хотите нарисовать в 3D что-то, что находится перед вашими глазами в реальной жизни, предварительно внимательно изучите этот предмет или группу предметов. К примеру, поставьте на стол вазу с фруктами. Посмотрите, каким образом элементы вашей композиции связаны друг с другом. Сколько фруктов вы видите? Каким образом части фруктов, вазы и стола пересекаются друг с другом? Где находятся тени, а где на объекты попадает свет?
Для тренировки руки и глаз при создании сложных 3D-изображений художники рекомендуют использовать особую «слепую» технику.
Рисуйте контуры вашей картинки, глядя не на лист бумаги, а собственно на сам расположенный перед вами объект. Рука на бумаге при этом должна следовать за вашим взглядом.
Линия горизонта
Рисуя картинки, сюжет которых строится на больших расстояниях, начните с линии горизонта. Таким образом вы отметите для себя самую дальнюю часть будущей картинки. Чаще всего в 3D-рисунках горизонт располагают на расстоянии от 1/3 до 1/2 ширины листа от нижнего края. После того как горизонт будет отмечен, начните рисовать передний план под ним, а также небо и крупные объекты заднего плана — над ним.
Таким образом вы отметите для себя самую дальнюю часть будущей картинки. Чаще всего в 3D-рисунках горизонт располагают на расстоянии от 1/3 до 1/2 ширины листа от нижнего края. После того как горизонт будет отмечен, начните рисовать передний план под ним, а также небо и крупные объекты заднего плана — над ним.
Помимо горизонта, обязательно включите в рисунок точку перспективы. Расположите ее в любом месте на линии горизонта. Именно здесь в последующем будут сходиться все линии картинки.
Чтобы набить руку в рисовании 3D-картинок с большими расстояниями, художники рекомендуют на первых порах использовать кальку. К примеру, можно сфотографировать здания в городе в перспективе. Затем на фото нужно наложить кальку и обвести контуры домов.
Порядок работы
При создании картинок с перспективой сначала нарисуйте переднюю часть объекта. Далее прочертите от краев объекта линии к точке схода. При этом не рисуйте те части линий, которые пересекают «фасад». Начиная от точки схождения, укоротите линии до такой длины, чтобы у вас получился контур задней части фигуры. Соедините линии в вертикальной плоскости. В результате у вас должен получиться законченный контур вашей фигуры.
Светотень
Чтобы сделать ваши рисунки максимально реалистичными, грамотно используйте не только перспективу, но и светотень. Внимательно изучите находящийся перед вашими глазами объект. Посмотрите — с какой стороны на него падает свет и где на его поверхности располагаются тени.
Чаще всего тени находятся в углах объекта или там, где свет не отражается от его поверхности. Обычно художники раскрашивают 3D-объекты следующим образом:
- Определяют расположение источника света (его можно даже схематично изобразить на рисунке).
- Начинают закрашивать объект с форм, наиболее удаленных от источника света. При этом используют темные оттенки, оставляя светлыми лишь блики. Последние при этом располагают на той стороне, которая находится дальше всего от источника света.
 В полых объектах внутреннюю тень размещают ближе всего к источнику света.
В полых объектах внутреннюю тень размещают ближе всего к источнику света.
Далее определяют, куда будут падать отбрасываемые тени предметов. В данном случае можно использовать рассмотренный выше метод одноточечной перспективы. Чтобы смягчить переходы светотени, используйте бумажку, ластик или просто собственный палец. Границы более темных и светлых оттенков должны быть хорошо размытыми. Тогда 3D-изображение будет смотреться реалистичнее.
Штриховка
Светотень на объектах 3D-рисунков можно отображать не только методом сплошной заливки, но и штриховки. Чем ближе будут располагаться параллельные линии на таком рисунке, тем более глубокой будет смотреться тень.
Математический кубизм в Paint 3D
Занимательные задачи с кубиками традиционно используются на математических занятиях, конкурсах, олимпиадах. Представлены задания с кубиками и во всероссийских проверочных работах по математике для 5-6 классов (ВПР). Подобного рода задачи способствуют развитию пространственного воображения и служат пропедевтике изучения стереометрии. Головоломки с кубиками, несмотря на внешнюю лёгкость и занимательность, связаны с такими темами курса стереометрии старших классов, как:
- Взаимное расположение прямых в пространстве.
- Взаимное расположение плоскостей в пространстве.
- Многогранники. Элементы многогранников.
- Сечения.
- Комбинация тел в пространстве.
Предлагаю задействовать при решении головоломок с кубиками приложение Paint 3D. Это простейший графический редактор для создания и редактирования трехмерных и двухмерных объектов. Paint 3D входит в состав приложений операционной системы Windows 10. Работа в нём не требует специальных навыков и длительного освоения, подходит для работы с детьми разного возраста, начиная с начальных классов.
Рассмотрим примеры задач, направленных на развитие пространственного воображения и формирование умений исследовать геометрические тела с использованием Paint 3D.
Задача 1.
Нарисуйте кубик, который получится собрать из данной развёртки.
Указания к работе.
Нарисуйте куб. Команда Трёхмерные объекты → Куб. Чтобы получился не просто прямоугольный параллелепипед, а действительно куб с равными рёбрами, при рисовании удерживайте нажатой клавишу Shift.
Для просмотра объекта в объёмном виде используйте команду Трёхмерное представление. При выделении объекта вокруг него появляются маркеры для изменения размеров, перемещения и вращения по осям.
Раскрасьте грани куба в разные цвета соответственно данной развёртке. Применяйте инструмент Кисти → Заполнить. Чтобы окрасить определённую грань, а не сразу весь куб, укажите в Типе заливки параметр Боковая сторона.
Задача 2.
На гранях кубика изображены различные рисунки. На каждой грани свой рисунок: звезда, планета, сердечко, облако, радуга, солнышко.
На картинках кубик показан в трёх положениях.
Какой рисунок изображён напротив рисунка солнышко?
Указания к работе.
Нарисуйте кубик, применив команду Трёхмерные объекты → Куб. При рисовании удерживайте нажатой клавишу Shift.
Проанализируйте расположение рисунков на гранях кубика. Добавьте на грани нарисованного вами кубика рисунки, используя инструмент Наклейки. Наклейки размещаются на поверхности объекта и автоматически подстраиваются под его форму, «прилипая» к поверхности.
Задача 3.
1) Постройте конструкцию из кубиков.
2) Нарисуйте вид этой конструкции сверху.
Указания к работе.
Нарисуйте кубик, применив команду Трёхмерные объекты Куб. При рисовании удерживайте нажатой клавишу Shift.
Пересчитайте количество кубиков в заданной фигуре. Скопируйте кубики необходимое количество раз. Для копирования выделите объект, затем скопируйте его (сочетание клавиш Ctrl+C), затем вставьте (сочетание клавиш Ctrl+V). Те же операции можно сделать через контекстное меню. Щелчок правой кнопкой мышки по выделенному объекту, команды Копировать, Вставить.
Те же операции можно сделать через контекстное меню. Щелчок правой кнопкой мышки по выделенному объекту, команды Копировать, Вставить.
Раскрасьте кубики. К выделенному кубику примените команду Изменить цвет.
Выделите все кубики и примените команду Группировать. После группировки с полученной конструкцией можно работать как с единым объектом – вращать, перетаскивать, изменять размеры. Если возникнет необходимость разбить объект на отдельные элементы, то применяют команду Разгруппировать.
Представьте, как будет выглядеть данная конструкция, если посмотреть на неё сверху. Проверьте себя, развернув объект. Нарисуйте полученный вид сверху. Используйте команду Двумерные фигуры → Квадрат. Для рисования квадрата удерживайте нажатой клавишу Shift.
Раскрасьте квадраты, применяя инструмент Кисти.
Возможны различные варианты использования Paint 3D на уроках математики. Графический редактор может использовать учитель для подготовки наглядных и ярких дидактических материалов. Полезно провести практическую работу, когда ученики проводят исследование самостоятельно созданных ими стереометрических тел. Есть потенциал использования Paint 3D и для выполнения проектных работ по математике. Вместе с тем стоит понимать, что это средство рисования, а не система инженерной графики, что накладывает ряд ограничений и построение точных чертежей в Paint 3D невозможно. К аргументам за применение Paint 3D стоит отнести доступность освоения и повышенную познавательную активность учеников при создании объёмных конструкций.
О работе в Paint 3D.
Трёхмерная живопись
О 3D-моделировании в геометрии
Ваза в перспективе и шахматы во вращении
Стереометрия в стиле конструктивизма
Как начертить объемный квадрат. Как построить правильный квадрат
Все предметы и фигуры размещены в пространстве. Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.
Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.
Рисунок нужно воспринимать как пространство на бумаге, где существует плоскость и пропорции всех находящихся предметов, свет и тень, которая направляется по форме предмета.
Основные геометрические фигуры:
Двухмерные плоские фигуры
Трехмерные фигуры, у которых есть объем
Абсолютно все предметы в основе своего построения имеют эти фигуры.
Куб — фигура, основой которой является трехмерное изображение в пространственном соотношении листа. В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина . В самом кубе заложено понятие рисунка в целом.
Для начала понимания рисунка, мы поработаем именно с ним. При помощи образно-логических построений, мы с вами будем развивать мышление за счет аналитики формы . Для большего понимания и анализа рисунка есть несколько упражнений.
Упражнения
Садимся за мольберт, берем большой лист бумаги, можно недорогой, или вообще кусок обоев (в этом упражнении бумага особо значения не имеет) . Рисуем квадрат, естественно пытаемся сделать так, чтобы его стороны были ровными, а линии прямыми.
Итак, — мы видим обычный квадрат, совсем неинтересный и не впечатляющий, но это только в данный момент…
Делаем из квадрата куб карандашом: прорисовываем линии от граней примерно с углом 45 градусов . Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.
Чтобы нам чувствовать пространство, нужно придать рисунку плавности . То есть сделать так, чтобы нам было ясно, где передняя часть рисунка, а где задняя.
Сторону куба, находящуюся ближе к нам, нужно выделить, сделать четче и передать активнее. Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.
Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.
Вот таким способом мы передали пространство, чтобы добиться желаемого результата. Но это далеко не все. Сейчас важно правильно передать плавность, чтобы получить объемность в рисунке .
Представляем вашему вниманию небольшой видеоурок на тему оптических иллюзий.
Инструкция
Если есть возможность пользоваться измерительной линейкой и угольником, то задача до примитивности. Начните, например, с построения нижней стороны — поставьте точку А и начертите горизонтальный отрезок до точки В, отстоящей от А на расстояние заданной по условиям длины стороны. Затем по угольнику отмерьте то же расстояние вверх от точек А и В и поставьте точки D и С соответственно. После этого останется лишь соединить отрезками точки А и D, D и С, С и В.
Если в вашем распоряжении есть линейка и транспортир, то действовать можно так же, как и в предыдущем шаге. Постройте одну из сторон (АВ) квадрата, а затем приложите транспортир к проведенному отрезку так, чтобы его нулевая точка совпадала с точкой А. Поставьте вспомогательную отметку у транспортира, соответствующего 90°. На луче, исходящем из точки А через вспомогательную отметку, отложите длину отрезка АВ, поставьте точку D и соедините точки А и D. Затем проделайте такую-же операцию и точкой В, начертив сторону ВС. После этого соедините точки С и D и построение квадрата будет завершено.
Если в вашем распоряжении нет ни транспортира, ни , но есть циркуль, линейка и калькулятор, то и этого достаточно для построения квадрата с заданной длиной стороны. Если точные размеры квадрата не имеют значения, то можно обойтись и без калькулятора. Поставьте на листе точку в том месте, где хотите видеть одну из вершин квадрата (например, вершину А). Затем поставьте точку в противоположной ей вершине квадрата. Если длина стороны квадрата задана в условиях задачи, то расстояние между этими точками рассчитайте, исходя из теоремы Пифагора. Из нее вытекает, что нужная вам длина диагонали квадрата равна корню из удвоенного произведения длины стороны на саму себя. Посчитаете точное значение с помощью калькулятора или в уме и отложите полученное расстояние на циркуле. Проведите вспомогательный полукруг с центром в вершине А в направлении противоположной вершины С.
Из нее вытекает, что нужная вам длина диагонали квадрата равна корню из удвоенного произведения длины стороны на саму себя. Посчитаете точное значение с помощью калькулятора или в уме и отложите полученное расстояние на циркуле. Проведите вспомогательный полукруг с центром в вершине А в направлении противоположной вершины С.
Отметьте на проведенной дуге точку С и проведите такой же вспомогательный полукруг с центром в этой вершине, направленный в сторону точки А. Проведите две вспомогательные линии — одна должна проходить через точки А и С, а другая — через точки пересечения двух полукружий. Эти линии будут пересекаться под прямым углом в центре будущего квадрата. На линии, перпендикулярной диагонали АС, отложите в обе стороны от точки пересечения по половине рассчитанной длины диагонали и поставьте точки В и D. И, наконец, по четырем полученным точкам вершин начертите квадрат.
Хоть квадрат и прямоугольник это простейшие геометрические фигуры, но, чтобы их нарисовать в фотошопе, нужно приложить некоторые усилия и обладать базовыми знаниями. Новичок без должной подготовки, скорее всего, не справится с этой задачей.
В этой статье разберем 3 самых популярных способа как нарисовать прямоугольник или квадрат в фотошопе.
Но прежде, чем приступить к выбору способа рисования, нужно определиться с будущими параметрами. Прямоугольник/квадрат может быть:
- залит сплошным цветом или только с отрисовкой границ;
- произвольный или с точно заданными размерами;
- с возможностью в любое время менять его размеры без потери качества.
Способ 1. Инструмент произвольная фигура
В этом способе прямоугольник или квадрат будут нарисованы залитым сплошным цветом. Если вам нужна только граница, переходите к следующим двум способам.
На панели инструментов выберите инструмент . Дальше возможны два варианта развития событий:
Вариант 1. Квадрат или прямоугольник с дальнейшей возможностью изменять размеры без потери качества
Здесь, конечно, подразумевается использование векторной фигуры. Чтобы ее нарисовать нужно выбрать параметр Слой-фигура :
Чтобы ее нарисовать нужно выбрать параметр Слой-фигура :
В дальнейшем вы можете без потери качества изменять размеры этой фигуры. Для этого используйте инструмент — Ctrl+T , и с помощью угловых маркеров изменяйте размер.
Для тех кто не знает : векторные фигуры состоят не из пикселей, а из специальные математических формул. Поэтому изменение размера — это не процесс растягивания/сжатия пикселей, а сложный математический пересчет, за счет чего не происходит никакой потери качества.
Вариант 2. Стандартный (растровый) квадрат/прямоугольник
Чтобы нарисовать сразу растровую фигуру используйте на панели параметров настройку Выполнить заливку пикселов . Но прежде чем начать ее рисовать — !
Но на самом деле можно рисовать сразу и векторный, а потом просто его. Тут уже выбирайте сами.
Как сделать прямоугольник квадратным
Обыкновенное правило с зажатой клавишей Shift с произвольными фигурами не работает. Поэтому нужно воспользоваться панелью параметров инструмента и выбрать настройку, чтобы фотошоп рисовал именно квадрат.
В этой же панели, обратите внимание, вы можете указать точный размер необходимого прямоугольника/квадрата или рисовать его по заранее определенным пропорциям.
По умолчанию размеры определяются пикселями. Если вы хотите изменить единицу измерения, сначала введите в поле какое-либо значение, а затем кликните по нему правой кнопкой мыши. Появится окно выбора единиц измерения. Доступно: пиксели, дюймы, сантиметры, миллиметры, пункты и пики.
Прямоугольник или квадрат со скругленными углами
Чтобы получить фигуру со скругленными углами, делайте все то же самое, что описано выше, но в самом начале выберите инструмент Прямоугольник со скругленными краями . На панели параметров инструмента нужно будет указать только радиус закругления.
Способ 2. Обводка выделенной области
Этот способ простой, как 5 копеек. выберите инструмент и нарисуйте прямоугольник пунктирной линией. Чтобы нарисовать квадрат удерживайте нажатой клавишу Shift
.
Чтобы нарисовать квадрат удерживайте нажатой клавишу Shift
.
Теперь нужно сделать обводку границ этой выделенной области. Для этого перейдите в Редактирование — Выполнить обводку .
Затем в новом окне настройте вид обводки: укажите толщину рамки, желаемый цвет и отметьте как будет проходить обводка:
- Внутри — значит рамка ляжет по внутренней стороне выделенной области;
- По центру — значит рамка разделится поровну на часть проходящую внутри выделения и на часть со внешней стороны;
- Снаружи — значит рамка будет огибать пунктир выделения.
Вот как может получиться:
На скриншоте выше я специально не убрал пунктирную линию, поскольку у вас она также не исчезнет. Чтобы окончательно от нее избавиться нажмите Ctrl+D .
В этом способе, чтобы нарисовать фигуру точного размера, нужно сперва на панели параметров инструмента указать Стиль — Заданный размер или Заданные пропорции. После этого станут активными поля, куда введите значения ширины и высоты в пикселях. Кликом правой кнопкой мыши по одному из этих полей вызовет меню изменения единиц измерения.
Способ 2.1 Закрашивание выделения
Самый банальный способ рисования прямоугольника — нарисовать рамку выделения (как описано выше) и просто закрасить ее любым цветом. Вот вам и прямоугольник или квадрат.
Способ 3. Модификация выделения
На самом деле этот способ мне меньше всего нравится из-за очевидного минуса — углы прямоугольника будут подрезанными, а сама граница рамки в состоянии и повлиять на эти факты не представляется возможным.
Итак, нужно вновь выбрать инструмент , нарисовать рамку будущего прямоугольника или квадрата (с клавишей Shift ), а затем отправляемся в меню Выделение и выбираем команду Модификация — Граница .
Появится новое окно, в котором, в нашем случае, мы указываем ширину границы прямоугольника. Допустим, укажу 7 пикселей. Получим такой результат:
Допустим, укажу 7 пикселей. Получим такой результат:
А теперь нужно просто закрасить получившуюся рамку. Для этого подойдет . Здесь, кстати, можно подойти к вопросу более творчески и закрасить, например, разными цветами. Результат:
Останется только снять выделение — Ctrl+D . Думаю этот способ подходит только для своих редких специфических задач, поскольку растушевка и подрезанные углы только все портят.
Заметили ошибку в тексте — выделите ее и нажмите Ctrl + Enter . Спасибо!
Хотите узнать Как нарисовать квадрат карандашом поэтапно, сделайте несколько простых шагов.
Шаг 1. Первое, что вы собираетесь нужно сделать, это схватить линейку. Правитель не должен иметь никаких вмятин вдоль края если вы хотите, чтобы ваш сквер встать на свои места. В реальности вы должны начать с построения горизонтальной линии. Это так вы можете нарисовать свои очки равномерно друг с другом. Так что начните с рисования светом линии с помощью линейки. Как только горизонтальный, как нарисовано, добавить две точки, по одной на каждой стороне линии. Эти очки позволят вам нарисовать перпендикулярные линии, которые должны оказаться под углом 90 градусов.
Шаг 2. Сделать то же самое вы сделали в шаге один, но когда вы делаете ваши очки, обязательно пользоваться линейкой, так что в итоге вы получите идеально прямые линии.
Шаг 3. Это просто быстрая схема, показывающая вам, как квадрат на 90 градусов на каждой стороне.
Шаг 4. Начните рисовать ваш горизонтальной линии из точки А в точку Б для верхней и нижней частей квадратной формы.
Шаг 6. Вот ваш идеальный квадрат. Теперь вы можете использовать его как стройматериал для чего-то, что вам нужно сделать, или вы можете использовать то, что вы только что узнали другим способом, а.
Как сделать фигуру объемной в word 2010?
Как рисовать в Ворде
04.03.2017
Microsoft Office Word – это не только инструмент для создания и редактирования текстовых документов, но и чудесная программа для рисования. Тем не менее, создать шедевр в Ворде не получится. Но всё же, обычному обывателю будет достаточно стандартного набора функций. С помощью шаблонов возможно создать несложный рисунок.
Тем не менее, создать шедевр в Ворде не получится. Но всё же, обычному обывателю будет достаточно стандартного набора функций. С помощью шаблонов возможно создать несложный рисунок.
Первые шаги
- Для начала работы следует перейти на вкладку «Вставка», где можно найти необходимые инструменты для рисования, а точнее фигуры, из которых и будет состоять будущее изображение.
- Нажав на кнопку «Фигуры», пользователь получает доступ ко всем возможным фигурам для рисования.
- Из предложенных программой можно выбрать одну подходящую и начать процесс рисования. Кликнув по пиктограмме нужной геометрической фигуры, можно перенести её на лист с помощью левой кнопки мышки.
Также можно создать полотно, где тоже можно рисовать. Его преимуществом является то, что текст будет находиться только за его границами.
- Для того, чтобы создать новое полотно, перейдите на вкладку «Вставка» и нажав на кнопку «Фигуры», выберите опцию «Новое полотно».
- Далее можно подстроить готовое полотно под себя (увеличить размер, изменить заливку и так далее).
- Поворот
- Перемещение
- Изменение длинны, ширины или высоты объекта. Либо просто растяжение.
В результате проведения вышеописанных манипуляций получаем такой результат:
Для того, чтобы получившийся рисунок стал целым объектом, необходимо объединить все те фигуры, из которых собственно его и собрали.
- Сначала для этого необходимо выделить поочерёдно каждый элемент левой кнопкой мыши, удерживая клавишу Ctrl.
- Затем правой кнопкой мыши вызвать контекстное меню, в котором в пункте «Группировать»выбрать одноимённую опцию.
Изменение заливки фигур
По умолчанию, нарисованные фигуры имеют синий цвет заливки, поэтому при необходимости можно с лёгкостью заменить их цвет на подходящий. Для начала следует двойным щелчком левой кнопки мыши выбрать рисунок, и в открывшейся сверху вкладке в пункте «Заливка» выбрать нужный цвет. Готово.
Готово.
Изменение цвета контура рисунка
Это также несложная процедура, которая выполняется аналогично предыдущей. После того, как объект выбран, в пункте «Контур фигуры» выберите желаемый цвет.
Также в этом же меню можно подобрать толщину контура.
Возможно и изменение линий, которыми будет обведено изображение.
Изменения стиля фигуры
- Выбрав объект двойным нажатием ЛКМ, переходим на ту же самую вкладку, о которой было сказано в двух предыдущих пунктах.
- Слева от пунктов «Заливка» и «Контур» видим палитру всех предложенных стандартной библиотекой Ворда стилей оформления фигуры. Далее выбираем подходящий и готово.
Добавление эффектов
Почему бы не добавить чего-нибудь специфического для украшения созданного рисунка? Например, свечение, тень, отражение и многие другие. В этом случае будет использовано специальное меню, где можно подобрать спецэффекты по вкусу. Можно также поэкспериментировать с расширенными настройками. Они находятся снизу каждой группы эффектов.
Передний и задний план
При создании рисунка фигуры накладываются друг на друга. Например, как на картинке ниже:
То есть, для того, чтобы полумесяц переместить за тучи, необходимо кликнуть по нему ПКМ и выбрать пункт «На задний план». В случае, если его придётся переместить обратно, можно воспользоваться опцией «На передний план».
Что делать, если при перемещении текста передвигается фигура?
Эту проблему очень легко устранить. Достаточно нажатия правой кнопкой мыши по созданному рисунку. В меню «Обтекание текстом» выбрать опцию «Зафиксировать положение на странице». Вуаля!
Расширенные опции форматирования изображений
Желаете отредактировать созданное изображение более детально? Воспользуйтесь меню «Формат фигуры», которое вызывается кликом правой кнопки мыши.
«Формат фигуры» состоит из трёх вкладок:
- Заливка и границы;
- Эффекты;
- Макет и свойства.

А теперь о каждой вкладке подробнее.
Заливка и границы
В этой вкладке можно изменять заливку рисунка и линии, из которых он состоит.
Например, можно сделать узорную, текстурную либо любую другую заливку. Также можно изменить толщину линий и их прозрачность. К тому же, тут можно поэкспериментировать и с другими опциями.
Эффекты
Эта вкладка содержит в себе расширенные инструменты для подстройки спецэффектов. К примеру, здесь можно более точно отрегулировать прозрачность, размер, цвет. Также возможно добавить размытие и многие другие украшения.
Макет и свойства
Функции этой вкладки позволяют настроить положение текста, который обтекает рисунок, и позволяют установить размер полей в документе.
Рисование объёмных фигур
В Ворде возможно так же и создание трёхмерных изображений. Нарисовав обычную фигуру, перейдите в меню «Формат фигуры», где во вкладке «Эффекты» найдите подпункт «Формат объёмной фигуры». Затем внесите свои параметры.
Используя вышеприведённые инструкции, можно создать достаточно интересную композицию в Ворде. Надеемся, этот материал был для Вас полезным.
Расскажи друзьям в социальных сетях
Дата: 28 февраля 2018 Категория: Word Поделиться, добавить в закладки или статью
Здравствуйте, уважаемые читатели. Сегодня вставляем фигуры в Word. Для тех, кто не знает, фигуры — это векторные изображения, которые применяют для рисования различных конструкций в программе. Круги, треугольники, прямоугольники и т.п. Вы можете использовать одну фигуру, или объединить несколько. Все зависит от сложности конечного объекта.
В Ворде есть галерея предустановленных фигур, комбинируя которые, можно рисовать вполне рабочие схемы, которые, например, не получится сделать с помощью инструмента рисования схем SmartArt.
Как вставить фигуру на лист
Чтобы добавить фигуру в Word, кликните на ленте Вставка — Фигуры. Изучите открывшуюся галерею фигур и выберите ту, которая Вам нужна.
Кликните по миниатюре фигуры.Теперь можно ее вставлять на лист. Есть два способа вставки:
- Кликните мышью на листе в месте вставки. Объект будет вставлен в стандартном для него размере
- Растягивайте мышью фигуру на листе, пока не добьетесь нужного размера и соотношения сторон. Если при растягивании зажать Shift, программа будет соблюдать «правильные» соотношения сторон объекта
После выполнения такой последовательности, фигура появится на листе и займет то место, где Вы ее очертили. Но, похоже, это еще не то, что мы хотели получить. Как еще можно поработать с фигурами? Когда она вставлена и выделена, на ленте появляется вкладка Формат. Вот там и собран основной функционал по работе с фигурами. Некоторые из инструментов вкладки мы уже рассматривали в статье о стилизации картинок, потому коснусь их вскользь. А вот специальные возможности рассмотрим детальнее.
Стили фигур
Стили фигур практически идентичны стилям изображений, мы рассмотрели их в прошлом уроке. Но вкратце пробежимся по ним:
- Галерея стилей позволяет выбрать уже готовый макет фигуры для быстрой стилизации. Кликните на стрелке Вниз в блоке Формат — Стили фигур, чтобы выбрать один из готовых стилей. Кликните по подходящей миниатюре для применения.
- Заливка фигуры — изменить цвет и способ заливки объекта. Можно, например, сделать градиентную заливку, или текстуру. Нажмите на ленте Формат — Заливка фигуры, чтобы сделать соответствующие настройки
- Контур фигуры — позволяет изменить цвет, толщину, тип линии контура, добавить стрелки. Выполните на ленте Формат — Контур фигуры, сделайте свой выбор в соответствующих пунктах
- Эффекты фигуры — Добавляем к фигуре различные эффекты для придания объема: тень, отражение, подсветка, сглаживание и т.п.. Кликайте на ленте Формат — Эффекты фигуры,чтобы выбрать дополнительные эффекты
Как вставить текст в фигуру Word
Фигуры без текста практически лишены смысла. Потому, учимся добавлять надписи к ним. Для этого кликните правой кнопкой мыши по фигуре и выберите в контекстном меню Добавить текст. Внутри фигуры появится курсор, можете набирать текст.
Потому, учимся добавлять надписи к ним. Для этого кликните правой кнопкой мыши по фигуре и выберите в контекстном меню Добавить текст. Внутри фигуры появится курсор, можете набирать текст.
Форматирование текста фигуры
Когда к фигуре добавлен текст, можно с ним его дополнительно оформить. Кстати, здесь работают все возможности форматирования текста в Ворде, а не только специфические. На последних остановимся подробнее:
Положение и обтекание фигур
Как и с обычными картинками, Вы можете настраивать положение фигуры в тексте и способ ее обтекания текстом. Для этого на ленте кликаем Формат — Упорядочение — Положение и Формат — Упорядочение — Обтекание. На картинке для фигуры выбрано положение «сверху справа», а обтекание «по контуру».
Взаимное расположение фигур
Если на листе несколько фигур, при контакте одна другую могут перекрывать. Вот, как на рисунке звезда перекрывает ленту.
Но такое положение дел можно настраивать. Чтобы выдвинуть ленту на передний план, выделите ее и нажмите Формат — Упорядочение — Переместить вперед. Чтобы, наоборот, понизить уровень объекта относительно других — кликните Формат — Упорядочение — Переместить назад.
Чтобы выровнять на листе несколько фигур — выделите их все (зажмите Ctrl и кликайте мышью по ним), а потом нажмите Формат — Упорядочение — Выровнять объекты. Например, если выбрать в этом меню Выровнять по левому краю, Word выстроит фигуры так, чтобы их левые границы совпали. Но чаще всего выравнивают по нижнему краю, чтобы фигуры стали в ряд.
Так же, их можно Распределить по вертикали или Распределить по горизонтали. Программа расположит объекты так, чтобы между ними были одинаковые расстояния по вертикали и по горизонтали соответственно.
Группировка фигур в Ворде
Несколько фигур можно сгруппировать друг с другом, как будто они стали одним объектом. Для этого выделите нужные фигуры и нажмите Формат — Упорядочение — Группировать объекты — Группировать. Теперь эту конструкцию можно перемещать, изменять размеры, обтекание и т.д.
Теперь эту конструкцию можно перемещать, изменять размеры, обтекание и т.д.
Чтобы разгруппировать объекты — выделите эту группу и нажмите Формат — Упорядочение — Группировать объекты — Разгруппировать.
Поворот и отражение фигур
Как и обычные картинки, фигуры можно вращать и отражать. И делается это так же само. Выделяем объекты для поворота, жмем на ленте Формат — Упорядочение — Повернуть объекты. В раскрывшемся меню выбираем действие.
Если среди предложенных вариантов нет нужного — нажмите Другие параметры поворота и там выберите любой угол поворота в градусах. Или тяните мышью за маркер поворота.
Изменение размеров фигуры
Простейший способ изменить размер фигуры — выделить его и растягивать за белые маркеры в углах и на гранях рамки. Правда, иногда хочется задать точные размеры. Тогда найдите на ленте поля Формат — Размер — Высота фигуры и Ширина фигуры. Запишите в них те значения ширины и высоты, которые нужны.
Вот и все о работе с фигурами. Компонуя разные объекты и комбинируя их свойства, Вы можете создавать хорошие иллюстрации к своим документам. С их помощью можно создавать схемы, хотя для этого есть и отдельный, отличный инструмент — SmartArt. О нем я вскоре расскажу, а следующая статья будет о другом ноу-хау компании Майкрософт — надписях WordArt. Заходите, читайте, становитесь лучше!
Поделиться, добавить в закладки или статью
Довольно часто у нас под рукой нет никакого графического редактора, или просто нужно изобразить несложный рисунок в Word. Не все знают, что в Ворде можно рисовать, и в этой статье мы решили рассказать вам, как это делается.
Для того, чтобы начать рисование, запустим программу и создадим новый файл, либо можем сделать рисунок в уже существующем документе Word.
Для начала рисования в Ворде нам необходимо будет в верхнем меню выбрать Вкладку, и кликнуть на кнопку Фигуры. В развернутом списке выберете раздел «Новое полотно» так, как показано на рисунке ниже.
После нажатия в верхнем меню откроется панель инструментов для рисования в Ворд 2007 , а в теле документа область для рисования. Сразу отметим, что размеры области вы можете настроить сразу или потом.
Чтобы начать рисовать в Word 2007 и 2010 вы должны выбрать любой инструмент в открывшемся меню. А их там, ну очень много.
Вот так выглядит форма с готовыми шаблонами.
Соответственно, вы можете выбрать любой из них и сразу вставить в word документ, а не мучиться и рисовать самому. Это сэкономит значительное количество времени. Ну а уж если того, что вам нужно в стандартном расширении для рисования Ворда нет, то придется изображать это самим. Благо, все возможности для этого имеются.
Для рисования в Ворде есть и такие инструменты, чтобы создавать объемные фигуры, изменять их цвет, делать тень и так далее. Настроек очень много, и скорее всего, ваши нужды они полностью удовлетворят. Ну а если нет, то для рисования советуем использовать специальные программы. Ведь Word 2007 и 2010 предназначен немного для другого.
MS Word — это, в первую очередь, текстовый редактор, однако, рисовать в этой программе тоже можно. Таких возможностей и удобства в работе, как в специализированных программах, изначально предназначенных для рисования и работы с графикой, ждать от Ворда, конечно, не стоит. Тем не менее, для решения базовых задач стандартного набора инструментов будет достаточно.
Урок: Как нарисовать линию в Word
Прежде, чем рассмотреть то, как сделать рисунок в Ворде, следует отметить, что рисовать в данной программе можно двумя разными методами. Первый — вручную, подобно тому, как это происходит в Paint, правда, немного проще. Второй метод — рисование по шаблонам, то есть, с использованием шаблонных фигур. Обилия карандашей и кистей, цветовых палитр, маркеров и прочих инструментов в детище Майкрософт вы не найдете, но создать простой рисунок здесь все же вполне возможно.
Включение вкладки «Рисование»
В Microsoft Word есть набор средств для рисования, которые подобны таковым в стандартном Paint, интегрированном в Windows. Примечательно, что о существовании этих инструментов многие пользователи даже не догадываются. Все дело в том, что вкладка с ними по умолчанию не отображается на панели быстрого доступа программы. Следовательно, прежде, чем приступить к рисованию в Ворде, нам с вами предстоит эту вкладку отобразить.
Примечательно, что о существовании этих инструментов многие пользователи даже не догадываются. Все дело в том, что вкладка с ними по умолчанию не отображается на панели быстрого доступа программы. Следовательно, прежде, чем приступить к рисованию в Ворде, нам с вами предстоит эту вкладку отобразить.
1. Откройте меню «Файл» и перейдите в раздел «Параметры».
2. В открывшемся окне выберите пункт «Настроить ленту».
3. В разделе «Основные вкладки» установите галочку напротив пункта «Рисование».
4. Нажмите «ОК», чтобы внесенные вами изменения вступили в силу.
После закрытия окна «Параметры» на панели быстрого доступа в программе Microsoft Word появится вкладка «Рисование». Все инструменты и возможности этой вкладки мы рассмотрим ниже.
Средства рисования
Во вкладке «Рисование» в Ворде, вы можете видеть все те инструменты, с помощью которых можно рисовать в этой программе. Давайте подробно рассмотрим каждый из них.
Инструменты
В этой группе расположились три инструмента, без которых рисование попросту невозможно.
Выбрать: позволяет указать на уже нарисованный объект, расположенный на странице документа.
Рисовать пальцем: предназначен, в первую очередь, для сенсорных экранов, но может использоваться и на обычных. В таком случае вместо пальца будет использоваться указатель курсора — все как в Paint и других подобных программах.
Примечание: Если вам необходимо изменить цвет кисти, которой вы рисуете, сделать это можно в соседней группе инструментов — «Перья», нажав на кнопку «Цвет».
Ластик: этот инструмент позволяет стереть (удалить) объект или его часть.
Перья
В этой группе вы можете выбрать одно из множества доступных перьев, которые отличаются, в первую очередь, по типу линии. Нажав на кнопку «Больше», расположенную в правом нижнем углу окна со стилями, вы сможете увидеть предпросмотр каждого доступного пера.
Нажав на кнопку «Больше», расположенную в правом нижнем углу окна со стилями, вы сможете увидеть предпросмотр каждого доступного пера.
Рядом с окном стилей расположены инструменты «Цвет» и «Толщина», позволяющие выбрать цвет и толщину пера, соответственно.
Преобразовать
Инструменты, расположенные в этой группе, предназначены не совсем для рисования, а то и вовсе не для этих целей.
Редактирование от руки: позволяет выполнять редактирование документов с помощью пера. Используя этот инструмент, можно вручную обводить фрагменты текста, подчеркивать слова и фразы, указывать на ошибки, рисовать указательные стрелки и т.д.
Урок: Рецензирование текста в Word
Преобразовать в фигуры: сделав набросок какой-либо фигуры, вы можете преобразовать ее из рисунка в объект, который можно будет перемещать по странице, можно будет изменять его размер и выполнять все те манипуляции, которые применимы для других рисованых фигур.
Для преобразования наброска в фигуру (объект) необходимо просто указать на нарисованный элемент, воспользовавшись инструментом «Выбрать», а затем нажать кнопку «Преобразовать в фигуры».
Урок: Как сгруппировать фигуры в Ворде
Рукописный фрагмент в математическом выражении: мы уже писали о том, как добавлять математические формулы и уравнения в Word. С помощью данного инструмента группы «Преобразовать» вы можете вписать в эту формулу символ или знак, которого нет в стандартном наборе программы.
Урок: Вставка уравнений в Ворде
Воспроизведение
Нарисовав или написав что-то с помощью пера, вы можете включить визуальное воспроизведение этого процесса. Все, что для этого требуется, нажать кнопку «Воспроизведение рукописного ввода», расположенную в группе «Воспроизведение» на панели быстрого доступа.
Собственно, на этом можно было бы и закончить, так как мы с вами рассмотрели все инструменты и возможности вкладки «Рисование» программы Microsoft Word. Вот только рисовать в этом редакторе можно не только от руки, но и по шаблонам, то есть, используя для этого готовые фигуры и объекты.
С одной стороны такой подход может оказаться ограниченным в плане возможностей, с другой стороны — он предоставляет куда более широкий выбор средств для редактирования и оформления создаваемых рисунков. Более подробно о том, как в Ворде рисовать фигуры и рисовать с помощью фигур, читайте ниже.
Рисование с помощью фигур
Создать рисунок произвольной формы, со скруглениями, пестрыми цветами с плавными переходами, оттенками и прочими деталями этим методом практически невозможно. Правда, зачастую столь серьезный подход и не требуется. Проще говоря, не выдвигайте к Word высокие требования — это не графический редактор.
Урок: Как в Ворде нарисовать стрелку
Добавление области для рисования
1. Откройте документ, в котором нужно сделать рисунок, и перейдите во вкладку «Вставка».
2. В группе иллюстрации нажмите на кнопку «Фигуры».
3. В выпадающем меню с доступными фигурами выберите последний пункт: «Новое полотно».
4. На странице появится прямоугольная область, в которой и можно начать рисовать.
Если это необходимо, измените размеры поля для рисования. Для этого потяните в нужном направлении за один из маркеров, расположенных на его границе.
Инструменты для рисования
Сразу после добавления нового полотна на страницу, в документе откроется вкладка «Формат», в которой и будут находиться основные инструменты для рисования. Рассмотрим детально каждую из групп, представленных на панели быстрого доступа.
Вставка фигур
«Фигуры» — нажав на эту кнопку, вы увидите большой перечень фигур, которые можно добавить на страницу. Все они разделены по тематическим группам, название каждой из которых говорит само за себя. Здесь вы найдете:
Все они разделены по тематическим группам, название каждой из которых говорит само за себя. Здесь вы найдете:
- Линии;
- Прямоугольники;
- Основные фигуры;
- Фигурные стрелки;
- Фигуры для уравнений;
- Блок-схемы;
- Звезды;
- Выноски.
Выберите подходящий тип фигуры и нарисуйте ее, задав левым кликом мышки точку начала. Не отпуская кнопку, укажите конечную точку фигуры (если это прямая) или область, которую она должна занимать. После этого отпустите левую кнопку мышки.
«Изменить фигуру» — выбрав первый пункт в меню этой кнопки, вы можете, в буквальном смысле, изменить фигуру, то есть, вместо одной нарисовать другую. Второй пункт в меню этой кнопки — «Начать изменение узлов». Выбрав его, вы можете изменить узлы, то есть, точки привязки конкретных мест фигуры (в нашем примере это внешние и внутренние углы прямоугольника.
«Добавить надпись» — эта кнопка позволяет добавить текстовое поле и вписать в него текст. Поле добавляется в указанном вами месте, однако, при необходимости его можно свободно перемещать по странице. Рекомендуем предварительно сделать поле и его грани прозрачными. Более подробно о том, как работать с текстовым полем и что можно сделать с его помощью, вы можете прочесть в нашей статье.
Урок: Как в Word перевернуть текст
Стили фигур
С помощью инструментов данной группы вы можете изменить внешний вид нарисованной фигуры, ее стиль, текстуру.
Выбрав подходящий вариант, вы можете изменить цвет контура фигуры и цвет заливки.
Для этого выберите подходящие цвета в выпадающем меню кнопок «Заливка фигуры» и «Контур фигуры», которые расположены справа от окна с шаблонными стилями фигур.
Примечание: Если стандартные цвета вас не устраивают, вы можете изменить их с помощью параметра «Другие цвета».
Также, в качестве цвета заливки можно выбрать градиент или текстуру. В меню кнопки «Цвет контура» можно регулировать толщину линии.
«Эффекты фигуры» — это инструмент, с помощью которого можно еще больше изменить внешний вид фигуры, выбрав один из предложенных эффектов. В числе таковых:
- Тень;
- Отражение;
- Подсветка;
- Сглаживание;
- Рельеф;
- Поворот.
Примечание: Параметр «Поворот» доступен только для объемных фигур, некоторые эффекты из вышеперечисленных разделов тоже доступны только для фигур определенного типа.
Стили WordArt
Эффекты из данного раздела применяются исключительно к тексту, добавленнуму с помощью кнопки «Добавление надписи», расположенной в группе «Вставка фигуры».
Текст
Аналогично стилям WordArt, эффекты применяются исключительно к тексту.
Упорядочить
Инструменты этой группы предназначены для изменения положения фигуры, ее выравнивания, поворота и других подобных манипуляций.
Поворот фигуры выполняется точно так же, как и поворот рисунка — на шаблонное, строго заданное или произвольное значение. То есть, можно выбрать стандартный угол поворота, указать свой или просто повернуть фигуру, потянув за круговую стрелку, расположенную непосредственно над ней.
Урок: Как в Ворд повернуть рисунок
Кроме того, с помощью данного раздела можно наложить одну фигуру на другую, подобно тому, как это можно сделать с рисунками.
Урок: Как в Word наложить одну картинку на другую
В этом же разделе можно сделать обтекание фигуры текстом или сгруппировать две и более фигур.
Уроки по работе с Ворд:
Как сгруппировать фигуры
Обтекание картинки текстом
Примечание: Инструменты группы «Упорядочить» в случае работы с фигурами абсолютно идентичны таковыми при работе с рисунками, с их помощью можно выполнять ровно такие же манипуляции.
Размер
Возможность единого инструмента данной группы всего одна — изменение размера фигуры и поля, в котором она находиться. Здесь можно задать точное значение ширины и высоты в сантиметрах или изменить его пошагово с помощью стрелок.
Кроме того, размер поля, как и размер фигуры, можно менять вручную, используя для этого маркеры, расположенные по контуру их границ.
Урок: Как обрезать рисунок в Word
Примечание: Для выхода из режима рисования нажмите клавишу «ESC» или же кликните левой кнопкой мышки в пустом месте документа. Чтобы вернуться к редактированию и открыть вкладку «Формат», дважды кликните по рисунку/фигуре.
Вот, собственно, и все, из этой статьи вы узнали, как рисовать в Ворде. Не забывайте о том, что данная программа является в первую очередь текстовым редактором, поэтому не стоит возлагать на нее слишком серьезных задач. Используйте для таких целей профильный софт — графические редакторы.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Да Нет
Здравствуйте.
Довольно часто некоторые пользователи сталкиваются с простой, казалось бы задачей — нарисовать какую-нибудь простую фигуру в Word’e. Сделать это не сложно, по крайней мере, если вам не нужно ничего сверхъестественного. Даже больше скажу, в Word уже есть типовые стандартные рисунки, которые больше всего нужны пользователям: стрелки, прямоугольники, кружки, звездочки и пр. Используя эти простые, казалось бы фигуры, можно создать неплохую картинку!
И так…
Как рисовать в Word 2013
1) Первое что делаете — переходите в раздел «ВСТАВКА» (см. меню сверху, рядом с разделом «ФАЙЛ»).
меню сверху, рядом с разделом «ФАЙЛ»).
2) Далее, примерно по центру, выбираем опцию «Фигуры» — в открывшемся меню нужно выбрать в самом низу вкладку «Новое полотно».
3) В результате на листе Word появиться белый прямоугольник (стрелка №1 на картинке ниже), на котором можно начать рисовать. В своем примере я использую какую-нибудь стандартную фигуру (стрелка №2), и залью ее ярким фоном (стрелка №3). В принципе, даже таких простых инструментов хватит для того, чтобы нарисовать, например, домик…
4) Вот, кстати, результат.
5) Во втором шаге данной статьи мы создавали новое полотно. В принципе, можно этого и не делать. В случаях когда вам нужна небольшая картинка: просто стрелка или прямоугольник; можно сразу выбрать требуемую фигуру и расположить ее на листе. На скриншоте ниже показан вставленный треугольник на прямую на лист.
Оцените статью:
(2 голоса, среднее: 3 из 5)
Урок 62. куб — Математика — 4 класс
Математика, 4 класс
Урок № 62. Куб
Перечень вопросов, рассматриваемых в теме:
Что такое — куб?
Как распознавать и называть куб, его грани, ребра, вершины.?
Глоссарий по теме:
Куб — это многогранник, поверхность которого состоит из шести квадратов.
Грани куба – это стороны куба, которые представляют собой квадрат.
Ребра куба – это стороны граней куба.
Вершина куба— это точка, где сходятся три грани или точка, в которой сходятся три ребра куба.
Площадь фигуры – это часть плоскости, ограниченная замкнутой ломаной или кривой линией.
Периметр фигуры — это сумма длин всех сторон фигуры.
Основная и дополнительная литература по теме урока:
- Моро М.И., Бантова М.А. и др.
 Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 110
Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 110 - Математика: Рабочая тетрадь для 4 класса/ О.А. Рыдзе, К.А. Краснянская. – М.; СПб.: Просвещение, 2012. – с. 26-32
Теоретический материал для самостоятельного изучения
Подумайте, на какие две группы можно разделить фигуры?
Верно, на плоские и объемные.
Назовите плоские геометрические фигуры.
Верно, квадрат, треугольник, прямоугольник.
Объемные фигуры называются – геометрическими телами.
Вы видите геометрическое тело «шар» и геометрическое тело «куб».
Внимательно посмотрите и скажите, из какой фигуры состоит поверхность куба?
Верно, поверхность куба состоит из квадратов, их называют гранями куба.
Посчитайте, сколько граней у куба.
Правильно, у куба 6 граней.
Стороны граней (квадратов) называют ребрами куба.
Посчитайте, сколько ребер у куба?
Верно, у куба 12 ребер.
Вершины граней – это вершины куба.
Посчитайте, сколько вершин у куба.
Правильно, у куба 8 (восемь) вершин.
Таким образом, у куба 6 граней, 12 ребер, 8 вершин.
Для того чтобы изготовить модель куба необходимо построить развертку куба.
И какого бы куб ни был роста, сшить костюм для него очень просто. Для начала же, сделав разметку, изготовьте раскройку – развертку. Шесть квадратов! Нехитрое дело. Но расклеить их надо умело.
Куб в жизни человека.
Где можно встретить куб? Здания чаше всего имеют кубическую форму, так что можно просто выглянуть в окно, и вы сразу увидите куб.
Самая знаменитая игрушка-головоломка «кубик-рубик».
Кристаллы поваренной соли имеют форму куба.
Выполним несколько тренировочных заданий.
1. Найдите и напишите номер того куба, который сделан из данной развёртки.
Правильный вариант/варианты (или правильные комбинации вариантов): 4
2. Выберите правильное утверждение.
Выберите правильное утверждение.
а) площадь круга больше площади квадрата;
б) площадь круга меньше площади квадрата;
в) площади фигур равны.
Правильные варианты: б) площадь круга меньше площади квадрата.
Что такое трехмерные формы?
3-мерные игры
Объем с использованием юнит-кубовЕдиничный куб — это куб, имеющий объем или емкость 1 юнит. Вы можете подсчитать количество единичных кубиков, которые могут поместиться в твердое тело, чтобы определить его объем.
охватывает Common Core Curriculum 5.MD.5.aИграть сейчасПосмотреть все игры по геометрии >>Учитесь с помощью полной программы обучения математике K-5
Что такое трехмерные формы? В геометрии трехмерную фигуру можно определить как твердую фигуру или объект или форму, имеющую три измерения — длину, ширину и высоту.В отличие от двухмерных форм, трехмерные формы имеют толщину или глубину.
Учитесь с помощью полной программы обучения математике K-5
Атрибуты трехмерной фигуры — это грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.
Куб, прямоугольная призма, сфера, конус и цилиндр — это основные трехмерные формы, которые мы видим вокруг себя.
Мы видим кубик в кубике Рубика и игральную кость, прямоугольную призму в книге и коробке, сферу в глобусе и шаре, конус в морковке и рожок мороженого и цилиндр в ведре и бочка, вокруг нас.
Вот список трехмерных или трехмерных фигур с их названиями, изображениями и атрибутами.
| Название трехмерной формы : | Изображение 3D формы : | Атрибуты : |
| Куб | лиц — 6 Кромки — 12 вершин — 8 | |
| Прямоугольная призма или кубоид | лиц — 6 Кромки — 12 вершин — 8 | |
| Сфера | Изогнутая грань — 1 Кромки — 0 вершин — 0 | |
| Конус | Плоское лицо — 1 Изогнутая грань — 1 Кромки — 1 вершин — 1 | |
| Цилиндр | Плоское лицо — 2 Изогнутая грань — 1 Кромки — 2 вершин — 0 |
Интересные факты
|
Давайте споем!
3D-фигуры толстые, а не плоские.
Найди конус в шапке на день рождения!
Вы видите сферу в баскетбольном мяче,
И кубоид в таком высоком здании!
Вы видите куб в кости, которую вы бросаете,
И цилиндр в сияющем флагштоке!
Давай сделаем это!
Вместо того, чтобы показывать видео о трехмерных фигурах вашим детям и детским садам, попросите их понаблюдать за окружающими их предметами, в которых они могут найти трехмерные формы.
Вы можете также попросить их определить и отсортировать трехмерную форму и ее атрибуты.
Связанный математический словарь
Трехмерные формы | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. У трехмерной твердой формы тоже есть глубина. Трехмерные формы по своей природе имеют внутреннюю и внешнюю стороны, разделенные поверхностью.Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как твердые тела с прямыми сторонами, называемые многогранниками, которые основаны на многоугольниках, так и твердые тела с кривыми, такие как глобусы, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) — это твердые формы с прямыми сторонами. Многогранники основаны на многоугольниках, двухмерных плоских формах с прямыми линиями.
См. Нашу страницу Свойства полигонов для получения дополнительной информации о работе с полигонами.
Многогранники определяются как имеющие:
- Прямые кромки .
- Плоские стороны называются граней .
- углов, называемых вершинами .
Многогранники также часто определяются количеством ребер, граней и вершин, которые у них есть, а также тем, имеют ли их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (основанными на правильных многоугольниках) или неправильными (основанными на неправильных многоугольниках).Многогранники также могут быть вогнутыми или выпуклыми.
Как и многоугольники, многогранники могут быть правильными (основанными на правильных многоугольниках) или неправильными (основанными на неправильных многоугольниках).Многогранники также могут быть вогнутыми или выпуклыми.
Куб — один из самых простых и привычных многогранников. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
Пять правильных тел. — это особый класс многогранников, все грани которых идентичны, причем каждая грань представляет собой правильный многоугольник. Платоновы тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью гранями пятиугольника.
- Икосаэдр с двадцатью равносторонними треугольными гранями.
Каждый из этих правильных многогранников показан на диаграмме выше.
Что такое призма?
Призма — это любой многогранник, у которого есть два совпадающих конца и плоские стороны .Если вы разрежете призму в любом месте по ее длине, параллельно концу, ее поперечное сечение будет одинаковым — вы получите две призмы. Стороны призмы представляют собой параллелограммов — четырехугольные формы с двумя парами сторон равной длины.
Антипризмы похожи на обычные призмы, их концы совпадают. Однако стороны антипризм состоят из треугольников, а не параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с основанием многоугольника , который соединяется с вершиной (верхняя точка) прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, подобных тем, что строили древние египтяне, на самом деле они могут иметь любое основание многоугольника, правильное или неправильное. Кроме того, пирамида может иметь вершину в прямом центре ее основания, Правая пирамида , или может иметь вершину вне центра, когда это наклонная пирамида .
Более сложные многогранники
Есть еще много типов многогранников: симметричные и несимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано) представляет собой архимедово твердое тело с 14 гранями. 6 граней — правильные восьмиугольники, а остальные 8 — правильные (равносторонние) треугольники. У фигуры 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с закругленными или закругленными краями не являются многогранниками. Многогранники могут иметь только прямые стороны.
Многие из окружающих вас объектов будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными изогнутыми телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Общие трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца в форме круга или овала.Несмотря на то, что цилиндры похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
| Сфера в форме шара или земного шара представляет собой полностью круглый объект.Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | В форме кольца, шины или пончика, регулярный кольцевой тор образуется путем вращения меньшего круга вокруг большего круга. Существуют также более сложные формы торов. |
Площадь
На нашей странице «Расчет площади» объясняется, как рассчитать площадь двумерных фигур, и вам необходимо понимать эти основы, чтобы рассчитать площадь поверхности трехмерных фигур.
Для трехмерных форм мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двумерных форм для вычисления площади поверхности трехмерной формы, поскольку каждая грань или сторона фактически является двумерной формой.
Таким образом, вы прорабатываете площадь каждой грани, а затем складываете их вместе.
Как и в случае плоских форм, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и так далее.Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба — это площадь одной грани (длина х ширина), умноженная на 6, потому что все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно выполнить только одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба 10 × 10 см = 100 см 2 .Умножив на 6 количество граней куба, мы находим, что площадь поверхности этого куба равна 600 см 2 .
Другие правильные многогранники
Точно так же площадь поверхности других правильных многогранников (платоновых тел) можно вычислить, найдя площадь одной стороны и затем умножив ответ на общее количество сторон — см. Диаграмму основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22 см 2 , умножьте это на общее количество сторон (12), чтобы получить ответ 264 см 2 .
Пирамида
Для расчета площади поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Затем проработайте площадь одной стороны (треугольник). Измерьте ширину по основанию, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Затем вы можете либо разделить полученный ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножить на 4, чтобы получить площадь поверхности всех четырех сторон, либо просто умножьте площадь поверхности одного треугольника на 2.
Наконец, сложите площадь основания и стороны вместе, чтобы найти общую площадь поверхности пирамиды.
Чтобы вычислить площадь поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (боковая площадь), вам может потребоваться измерить стороны по отдельности.
Диаграммы сети
Геометрическая сеть — это двухмерный «узор» для трехмерного объекта. Сетки могут быть полезны при определении площади поверхности трехмерного объекта.На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды. Если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о сетевых диаграммах см. Нашу страницу 3D-фигуры и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два конца одинаковые и плоские стороны параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для обычной призмы (у которой все стороны одинаковые) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа (концы × стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги.Если отрезать сторону по длине и приплюснуть, получится прямоугольник. Поэтому вам нужно найти площадь двух кругов и прямоугольника.
Сначала проработайте область одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
Предполагая радиус 5 см, площадь одной из окружностей равна 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как есть два круга 157см 2
Площадь стороны цилиндра равна периметру окружности, умноженному на высоту цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4
Измерьте высоту цилиндра — в этом примере высота составляет 10 см. Площадь поверхности стороны 31,4 × 10 = 314см 2 .
Общую площадь поверхности можно определить, сложив вместе площадь кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
Длина наклона = 10 см
Конус
При расчете площади поверхности конуса необходимо использовать длину «склона», а также радиус основания.
Однако вычислить относительно просто:
Площадь круга у основания конуса равна π (пи) × радиус 2 .
В этом примере сумма равна 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь боковой части, наклонного участка, может быть найдена по следующей формуле:
π (пи) × радиус × длина уклона.
В нашем примере сумма равна 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к боковой области, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюйма
Сфера
Площадь поверхности сферы — это относительно простое разложение формулы для площади круга.
4 × π × радиус 2 .
Для сферы часто легче измерить диаметр — расстояние по сфере. Затем вы можете найти радиус, равный половине диаметра.
Диаметр стандартного теннисного мяча — 2.6 дюймов. Следовательно, радиус составляет 1,3 дюйма. Для формулы нам понадобится радиус в квадрате. 1,3 × 1,3 = 1,69.
Таким образом, площадь теннисного мяча составляет:
.4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площади поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На схеме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаковый для каждой детали.
Формула: площадь поверхности = (2πR) (2πr)
Для определения площади поверхности примера тора.
(2 × π × R) = (2 × 3.14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Умножьте два ответа вместе, чтобы найти общую площадь поверхности примера тора.
125,6 × 25,12 = 3155,072 см 2 .
Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел. Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Заполнение твердого тела: Том
Для трехмерных фигур вам также может потребоваться знать, какой объем у них .
Другими словами, если вы наполните их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
Трехмерные фигуры — Космические фигуры
В пространство, в котором мы живем, имеет три измерения: длину, ширину и высоту. Трехмерный геометрия, или геометрия пространства, используется для описания зданий, в которых мы живем и работы, инструменты, с которыми мы работаем, и объекты, которые мы создаем.Сначала мы посмотрите на некоторые типы многогранников. Многогранник — это трехмерная фигура гранями которого являются многоугольники. Его название происходит от греческого «поли». что означает «многие» и «хедра», что означает «лица».» Древние греки в 4 веке до н. Э. были блестящими геометрами. Они сделали важные открытия и, как следствие, получили названия объектов они обнаружили. Вот почему геометрические фигуры обычно носят греческие названия!
Мы можем связать некоторые многогранники — а также другие космические фигуры — к двумерному цифры, с которыми мы уже знакомы. Например, если вы переместите вертикальный прямоугольник по горизонтали через пространство, вы создадите прямоугольный или квадратный призма.
Если вы переедете вертикальный треугольник по горизонтали, вы создаете треугольную призму. Когда сделанная из стекла, призма этого типа разделяет солнечный свет на цвета Радуга.
А теперь давайте
посмотрите на некоторые космические фигуры, которые не являются многогранниками, но также связаны
знакомым двумерным фигурам. Что можно сделать из круга? Если
вы перемещаете центр круга по прямой, перпендикулярной
круг, вы получите цилиндр.Вы знаете эту форму — цилиндры
используется в качестве трубок, колонн, банок, музыкальных инструментов и во многих других областях.
Что можно сделать из круга? Если
вы перемещаете центр круга по прямой, перпендикулярной
круг, вы получите цилиндр.Вы знаете эту форму — цилиндры
используется в качестве трубок, колонн, банок, музыкальных инструментов и во многих других областях.
Банка с конусом может быть получен путем вращения прямоугольного треугольника вокруг одной из его ног. Это еще одна знакомая космическая фигура с множеством применений в реальном мире. Если вы любите мороженое, то наверняка знакомы хотя бы с одним из них!
Сфера создается, когда вы вращаете круг вокруг одного из его диаметров.Это один наших самых распространенных и знакомых форм — фактически, та самая планета, на которой мы живем это почти идеальная сфера! Все точки сферы находятся в такое же расстояние от его центра.
Есть многие другие космические фигуры — по сути, бесконечное число. У некоторых есть имена и некоторые нет. Вы когда-нибудь слышали о «ромбикосододекаэдре»? Некоторые утверждают, что это одна из самых привлекательных трехмерных фигур с равносторонними треугольники, квадраты и правильные пятиугольники для его поверхностей.Геометрия мир в себе, и мы просто касаемся поверхности этого мира. В этом разделе мы остановимся на наиболее распространенных космических фигурах.
назад наверх
3D-фигур — трехмерные формы | Определение, типы и многое другое
3D-формы — это не что иное, как твердые тела, состоящие из трех измерений, а именно длины, ширины и высоты. Буква «D» в «3D-фигурах» означает « размерный ».
Эти трехмерные формы занимают пространство и встречаются в нашей повседневной жизни.Мы прикасаемся к ним, чувствуем и используем их.
Давайте пройдемся по этому короткому уроку, чтобы узнать больше о трехмерных формах!
План урока Что такое 3D-фигуры? В математике мы изучаем трехмерные объекты в концепции твердых тел и пытаемся применить их в реальной жизни.
Теперь мы подробно рассмотрим каждую трехмерную фигуру.
3D-формы подразделяются на несколько категорий.
Некоторые из них имеют криволинейные поверхности; некоторые имеют форму пирамид или призм.
Определение трехмерных фигур
Трехмерные объекты, имеющие три измерения, а именно длину, ширину и высоту.
Давайте сначала узнаем о трехмерных формах с изогнутыми поверхностями на примерах.
Сфера- Он имеет форму шара и идеально симметричен.
- Каждая точка сферы находится на одинаковом расстоянии от центра.
- У него одна грань, без ребер и без вершин.
- Имеет одну изогнутую сторону.
- Форма остается неизменной от основания до верха.
- Это трехмерный объект с двумя одинаковыми концами круглой или овальной формы.
- Конус имеет круглое или овальное основание с вершиной (вершиной).
- Конус — это повернутый треугольник.
- В зависимости от того, как вершина совмещена с центром основания, образуется прямой или наклонный конус.
- Тор — это правильное кольцо, имеющее форму шины или бублика.

- Он образован вращением меньшего круга вокруг большего круга.
- У него нет ребер или вершин.
Теперь давайте узнаем о трехмерных формах, называемых пирамидами.
Пирамида- Пирамида — это многогранник с основанием многоугольника и вершиной с прямыми линиями.
- По совмещению вершины и центра основания их можно разделить на правильные и наклонные пирамиды.
- Пирамида с:
- Треугольное основание называется Тетраэдром
- Основание четырехугольника называется квадратной пирамидой
- Основание пятиугольника называется пятиугольной пирамидой
- Основание правильного шестиугольника называется шестиугольной пирамидой
Давайте узнаем о трехмерных формах, называемых призмами.
Призмы- Призмы — это твердые тела с одинаковыми концами многоугольника и плоскими сторонами параллелограмма.
- Он имеет одинаковое поперечное сечение по всей длине.
- Различные типы призм: треугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. Д.
- Призмы также широко подразделяются на обычные и наклонные призмы.
Далее, давайте узнаем о трехмерных формах с правильными многогранниками (Платоновы тела).
Многогранники / Платоновы тела- Всего пять многогранников.

- Тетраэдр с четырьмя равносторонне-треугольными гранями
- Октаэдр с восемью равносторонне-треугольными гранями
- Додекаэдр с двенадцатью гранями пятиугольника
- Икосаэдр с двадцатью равносторонне-треугольными гранями
- Куб с шестью квадратными гранями
- У них одинаковые грани правильных многоугольников.
- Рифма для запоминания трехмерных форм:
«Трехмерные формы толстые, а не плоские.
Найди конус в шапке на день рождения!
Вы видите сферу в баскетбольном мяче,
И кубоид в таком высоком здании!
Вы видите куб в кости, которую вы бросаете,
И цилиндр в сияющем флагштоке! » Перемещение пальцев по геометрическим телам поможет вам понять концепцию граней, ребер и вершин.
Где, радиус (r)
| Недвижимость | Площадь | Том |
|---|---|---|
|
Где, площадь основания (BA), периметр (P), высота (H)
| Недвижимость | Площадь | Том |
|---|---|---|
| \ (2 \ раз (BA) \) + \ (P \ times H \) | \ (BA \ раз H \) |
Если площадь основания (BA), высота периметра (P) (A) и высота наклона (SH)
| Недвижимость | \ (Поверхность \) \ (Площадь \) | Том |
|---|---|---|
| \ (B \: A \) + \ (\ frac {1} {2} \ times P \ times (SH) \) | \ (\ frac {1} {3} \ times BA \ times A \) |
Грани, кромки и вершины
Как упоминалось ранее, 3D-формы и объекты отличаются от 2D-форм и объектов из-за наличия трех измерений — длины, ширины и высоты.
В результате этих трех измерений эти объекты имеют грани, ребра и вершины.
Давайте разберемся с этими тремя подробнее.
Грани трехмерных фигур- Грань — это любая плоская поверхность твердого объекта.
- 3D-фигуры могут иметь несколько граней.
- Ребро — это отрезок линии на границе, соединяющий одну вершину (угловую точку) с другой.
- Они служат стыком двух лиц.
- Точка пересечения двух или более прямых называется вершиной.
- Это угол.
- Точка пересечения ребер обозначает вершины.
Например:
| Трехмерная форма | Лица | Кромки | вершины |
|---|---|---|---|
Сфера | 1 | 0 | 0 |
| Цилиндр | 2 | 2 | 0 |
| Конус | 2 | 2 | 1 |
| Куб | 6 | 12 | 8 |
| Прямоугольная призма | 6 | 12 | 8 |
Треугольная призма | 5 | 9 | 6 |
Пятиугольная призма | 7 | 15 | 10 |
Шестиугольная призма | 8 | 18 | 12 |
Квадратная пирамида | 5 | 8 | 5 |
Треугольная пирамида | 4 | 6 | 6 |
Пятиугольная пирамида | 6 | 10 | 6 |
Шестиугольная пирамида | 7 | 12 | 7 |
Как создавать трехмерные фигуры
Мы можем лучше понять трехмерные формы и их свойства , используя сети.
Двумерная форма, которую можно сложить в трехмерный объект, называется геометрической сеткой.
У твердого тела могут быть разные сети.
Проще говоря, сеть представляет собой развернутую форму трехмерной фигуры.
Давайте попрактикуемся в создании 3D-форм, используя моделирование, показанное ниже.
Переместите ползунок, чтобы увидеть, как сети превращаются в трехмерные фигуры.
В следующем моделировании показаны трехмерные формы с изогнутыми поверхностями.
Перемещайте ползунок и экран, чтобы исследовать вид под разными углами.
Следующая симуляция показывает, как создавать 3D-формы, обладающие свойствами правильного многогранника.
- Трехмерные объекты имеют 3 измерения, а именно длину, ширину и высоту.
- 3D-фигуры имеют грани, кромки и вершины.
- Изучение трехмерных тел поможет нам в повседневной жизни, поскольку большая часть нашей деятельности вращается и зависит от них.
Строитель хочет построить трехмерную сферу из цемента.3 \)
Найдите площадь поверхности кубоида длиной 3 дюйма, шириной 4 дюйма и высотой 5 дюймов.
Решение
При этом,
Длина куба = 3 дюйма
Ширина куба = 4 дюйма
Высота куба = 5 дюймов
Площадь кубоида
| \ (\ begin {align} 2 \ times (lb + bh + lh) \ end {align} \) |
\ (= 2 \ times (фунт + bh + lh) \)
\ (= 2 (3 \ раз 4 + 4 \ раз 5+ 3 \ раз 5 \))
\ (= 2 (12 + 20 + 15 \))
\ (= 2 (47) \)
\ (= 94 \: дюймы ^ 2 \)
| \ (\ следовательно \) Площадь поверхности кубоида = \ (94 \: дюймы ^ 2 \) |
Меган хочет пить молоко из стакана, имеющего форму цилиндра. 2 \ раз 15 \)
\ (V = \ pi (135) \)
\ (V = 424.3 \)
Определите правильный многогранник по изображениям, показанным ниже.
Решение
Правильные многогранники включают:
- Призмы
- Пирамиды
- Платоновы тела
Приведенные примеры многогранников должны подпадать под эти категории.
Таким образом, египетские пирамиды и кубик Рубика являются многогранниками.
| \ (\ следовательно \) Египетские пирамиды и кубик Рубика |
Приведите несколько примеров реальных объектов в форме ТОРУСА.
Решение
- Пончик
- Автомобильные шины
- Кольцо
- Плавательная трубка и т. Д.
Интерактивные вопросы
Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции Is 51 a Prime number.Математическое путешествие вокруг Is 51, простого числа начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах. Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.
О компании CuemathВ Cuemath наша команда математиков стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Как еще можно называть трехмерную фигуру?
В геометрии трехмерную форму также можно назвать твердым телом.
2. Какие объекты имеют трехмерную форму?
Объекты, которые являются трехмерными с определенными длиной, шириной и высотой, известны как 3D-фигуры.
Вот некоторые из распространенных примеров трехмерных фигур:
Игральные кости (куб)
Обувная коробка (прямоугольная или прямоугольная призма)
Рожок мороженого (рожок)
Глобус (сфера)
3. Каков объем трехмерной формы?
Объем 3D-фигур означает объем кубического пространства, заполненного внутри фигур.
Чтобы найти объем, нам нужны измерения трех измерений.
Издатель K12 Handhelds, Inc.
Лонг-Бич, Калифорния
www.k12handhelds.com
Телефон: 800-679-2226
Авторские права © 2005, K12 Handhelds, Inc. Лицензия CC-by,
Эта работа находится под лицензией Creative Commons Attribution 3.0 США.
Разработан совместно со школами округа Викомико.
Геометрия — это разновидность математики, которая изучает отношения между линиями, формами и трехмерными фигурами. Геометрия важна для многих работ. Строители используют геометрию, чтобы вычислить, сколько древесины и других материалов им нужно.Ученые используют геометрию для вычисления формул. Люди используют геометрию, чтобы выяснить, сколько ограждений купить или сколько краски им нужно, чтобы покрасить комнату.
Многоугольник — это замкнутая фигура или фигура с прямыми сторонами. Примеры многоугольников — квадраты и треугольники. Круг не является многоугольником, потому что у него нет прямых сторон.
Вот несколько типов полигонов:
Треугольник имеет три стороны.
У четырехугольника четыре стороны.
Это все четырехугольники.Квадрат — это четырехугольник с четырьмя прямыми углами и четырьмя сторонами одинаковой длины.
Прямоугольник — это четырехугольник с четырьмя прямыми углами и параллельными противоположными сторонами.
ПрямоугольникПараллелограмм — это четырехугольник, противоположные стороны которого параллельны и имеют одинаковую длину.
ПараллелограммРомб — это четырехугольник с четырьмя сторонами одинаковой длины.
РомбТрапеция — это четырехугольник, у которого только две стороны параллельны.
ТрапецияПятиугольник — это многоугольник с пятью сторонами.
ПентагонШестиугольник — это многоугольник с шестью сторонами.
ШестиугольникВосьмиугольник — это многоугольник с восемью сторонами.
ВосьмиугольникПериметр — это расстояние по внешней стороне фигуры. Добавление длины каждой стороны многоугольника даст вам периметр. Людям часто нужно знать периметр чего-либо. Например, если вы собираетесь купить ограждение, чтобы обойти свой двор, вам нужно знать периметр.
ПериметрПериметр этого прямоугольника составляет 12 футов. В этом можно убедиться, сложив длину всех сторон.
Периметр = 4 фута + 2 фута + 4 фута + 2 фута
БОНУС : Формула для расчета периметра прямоугольника:
Периметр = (2 x основание)) + (2 x высота)
Площадь фигуры — это пространство внутри фигуры. Поскольку площадь измеряет внутреннее пространство, она измеряется в квадратных единицах измерения, таких как квадратные дюймы или квадратные мили.Если вам нужно знать, сколько ковролина покупать для комнаты, вам нужно будет рассчитать площадь.
Площадь этого прямоугольника составляет 8 квадратных метров. Вы можете убедиться в этом, посчитав квадраты, заполняющие пространство.БОНУС : Формула для расчета площади четырехугольника:
Площадь = основание x высота
Преобразование — это изменение формы или способ отображения фигуры на другое пространство. Примеры преобразований — слайды, перевороты и повороты.
Слайд, или перевод, перемещает фигуру по линии. Форма перемещается, как если бы вы передвигали тарелку от одного человека к другому. Вот пример слайда:
На этом рисунке показан слайд в виде треугольника.Отражение или отражение — это способ перемещения фигуры по линии, создавая зеркальное отображение. Это все равно, что перевернуть блин. Вот пример переворота:
На этой картинке изображен перевернутый треугольник.Поворот или вращение — это вращение или вращение формы.Это похоже на то, как человек крутит колесо телеги. Вот пример поворота:
На этой картинке изображен поворот треугольника.Конгруэнтные формы имеют одинаковую форму и размер. Их можно было сдвинуть, перевернуть или повернуть, и тогда они были бы точно такими же. Это примеры конгруэнтных форм:
Эти формы совпадают. Их можно перемещать, чтобы они были точно такими же.Сходные формы имеют одинаковую форму, но могут быть разных размеров. Это примеры похожих форм:
Эти формы похожи.Они одинаковой формы, но разных размеров.Некоторые фигуры могут быть мозаичными. Тесселяция формы — это когда форма повторяется так, что она полностью покрывает поверхность, не оставляя места. Вот пример тесселяции:
МозаикаВы можете использовать программу «Тесселяция» на своем КПК для создания собственных мозаик.
Трехмерные фигуры — это фигуры в пространстве, имеющие длину, ширину и глубину. Это твердые объекты, такие как куб, сфера или пирамида.Иногда трехмерное обозначается аббревиатурой 3D. 3D-фильмы называются так потому, что объекты на экране кажутся выпрыгивающими, как трехмерные фигуры.
Стороны трехмерной фигуры — это ее плоские поверхности. Края встречаются там, где встречаются грани. Вершины — это углы или точки, где встречаются три или более поверхностей.
Вот несколько видов трехмерных фигур:
Куб — это трехмерная фигура с шестью одинаковыми квадратными гранями. Все стороны куба равны.Все грани квадратные. Примеры куба включают игральные кости и блок.
КубСфера — это круглая трехмерная фигура. Примеры сферы включают шар и землю.
Цилиндр — это трехмерная фигура с двумя плоскими круглыми гранями. Примеры цилиндров включают бревно и барабан.
ЦилиндрКонус — это трехмерная фигура с круглым плоским основанием и другой изогнутой поверхностью, которая поднимается вверх. Примером рожка является рожок для мороженого.
КонусПирамида — это трехмерная фигура с плоским основанием многоугольника и треугольными поверхностями, доходящими до точки. Древние египтяне построили в Египте знаменитые каменные пирамиды.
ПирамидаПризма — это трехмерная фигура с двумя гранями, которые являются параллельными многоугольниками, и другими гранями, которые являются параллелограммами. Прямоугольная призма состоит из двух параллельных прямоугольников. Треугольная призма состоит из двух параллельных треугольников. Пример прямоугольной призмы — коробка хлопьев.Стеклянная призма, которую вы можете использовать в науке для отклонения света, — это треугольная призма.
Это треугольная призма.Объем трехмерной фигуры — это объем кубического пространства внутри фигуры. Поскольку объем измеряет внутреннее пространство, он измеряется в кубических единицах измерения, например кубических дюймах или галлонах. Если вам нужно знать, сколько воды потребуется для наполнения бассейна, вам нужно будет рассчитать объем.
БОНУС : Формула для расчета объема прямоугольной призмы:
Объем = длина X ширина X глубина
площадь — количество места внутри замкнутой формы; количество квадратных единиц, необходимое для покрытия фигуры
основание — плоская поверхность, на которую может опираться трехмерная фигура.
закрытая фигура — фигура, которая начинается и заканчивается в одной точке и не имеет открытых промежутков
конус — трехмерная фигура с круглым плоским основанием и другой изогнутой поверхностью, доходящей до точки
конгруэнт — одинаковой формы и размера
куб — трехмерная фигура с шестью одинаковыми квадратными гранями
цилиндр — трехмерная фигура с двумя плоскими круглыми гранями
край — отрезок прямой, на котором встречаются две грани трехмерной фигуры.
грань — плоская сторона трехмерной фигуры
геометрия — область математики, изучающая отношения между линиями, фигурами и трехмерными фигурами
шестиугольник — многоугольник с шестью сторонами
линия симметрии — линия, по которой фигура может складываться так, чтобы обе стороны были одинаковыми
Показанная здесь красная линия — это линия симметрии этого треугольника.сетка — развертка, которую можно сложить, чтобы получилась объемная фигура
Это сеть куба.Если вырезать этот узор и сложить его вправо, получится тривосьмиугольник — многоугольник с восемью сторонами
открытая фигура — фигура, которая не начинается и не заканчивается в одной и той же точке.
Это открытая цифра. В нем есть пробел.параллель — линии, которые находятся на одинаковом расстоянии друг от друга и никогда не пересекаются с
параллелограмм — четырехугольник с параллельными противоположными сторонами одинаковой длины
пятиугольник — многоугольник с пятью сторонами
периметр — расстояние по внешней стороне объекта или формы
многоугольник — замкнутая фигура с прямыми сторонами
пирамида — трехмерная фигура с плоским основанием многоугольника и треугольными поверхностями, доходящими до точки
Каменные пирамиды в Египте были построены древними египтянами.четырехугольник — многоугольник с четырьмя сторонами
прямоугольник — четырехугольник, имеющий четыре прямых угла и противоположные стороны, параллельные
прямоугольная призма — трехмерная фигура с двумя гранями, которые являются параллельными прямоугольниками, и другими гранями, которые также являются прямоугольниками
отражение — флип; движение фигуры по линии, создающее зеркальное отображение
ромб — четырехугольник с четырьмя сторонами одинаковой длины
прямой угол — угол, равный 90 градусам
Это прямой угол.Он составляет ровно 90 градусов и составляет квадратный угол.поворот — поворот; поворот фигуры
сторона — линия, входящая в состав многоугольника
аналогичный — такой же формы, но, возможно, другого размера
сфера — круглая трехмерная фигура; мяч
квадрат — четырехугольник с четырьмя прямыми углами и четырьмя сторонами одинаковой длины
мозаика — повторяющиеся формы, которые покрывают плоскую поверхность, не перекрываясь и не оставляя зазоров
трехмерная фигура — фигура в пространстве, имеющая длину, ширину и глубину; это твердый объект
трансформация — изменение формы или способ отображения формы на другое пространство; примеры: перевод, отражение, вращение
перевод — слайд; переместить фигуру по линии
трапеция — четырехугольник только с двумя параллельными сторонами
треугольник — многоугольник с тремя сторонами
двумерная фигура — замкнутая фигура, имеющая длину и ширину; плоский объект
вершина — точка пересечения трех и более ребер трехмерной фигуры; форма множественного числа — вершины
Вершины этого куба обведены красным.volume — объем трехмерного пространства, занимаемого объектом
Вернуться наверхгеометрических фигур
геометрических фигур| АНАЛИЗ ФИГУР В 1, 2 или 3 РАЗМЕРАХ |
Что такое размер и сколько их?
Словарь определяет размер как «расширение в строке или в направлении », например, длина , ширина или высота .Большинство людей думают об измерении как то, что мы измеряем как , поэтому время соответствует этой категории. До недавнего времени нас учили, что мы живем в мире трех измерений — четырех, если считать время, — а кто не считает время? Но теперь физики говорят нам, что наш мир действительно имеет 27 измерений. Однако на этом уроке мы изучаем геометрических фигур из трех удобных измерений , в которых мы жили веками. Мы изучаем размеры, которые мы называем длиной, шириной и высотой или высотой .Мы также исследуем , количество точек , линии или ребер, и граней , которые составляют эти числа.
Одномерная фигура — это открытая плоскость фигура, которую можно измерить только ОДНОМ способом , например, длина или ширина , но не одновременно . Эти фигуры представляют собой линий, , некоторые из них прямые, другие изогнутые, но все они линейные.Они не замыкают форму. Мы измеряем одномерные фигуры с помощью линейных единиц , таких как дюймов, футов, ярдов, или миль . Когда вы измеряете свой рост, вы измеряете себя в одном измерении.
Двумерные фигуры могут быть измерены ДВУМЯ способами или направлениями, такими как длина И ширина . Это фигур на замкнутой плоскости квадратов, кругов или многоугольников любой формы и размера.Мы измеряем 2 аспекта двумерных фигур. Периметр или расстояние вокруг внешней стороны, выраженное в линейных единицах ; и область или пространство, ограниченное периметром, выраженным в квадратных единицах .
Периметр квадрата со сторонами 7 дюймов равен 4 × 7 или 28 дюймов .
Площадь того же квадрата равна 7 × 7 или 49 квадратных дюймов — записано дюйм² .
Трехмерные фигуры называются твердыми телами. Мы измеряем их в трех измерениях : длина , ширина и высота или высота. Мы используем линейных единиц для периметра , квадратных единиц, , для измерения поверхности , площадь и кубических единиц, , для измерения объема , или вместимости твердого тела.
Есть два типа трехмерных тел :
те , основанные на многоугольниках , и те , основанные на кругах .
В первую категорию входят призм всех форм.
Круговые тела включают цилиндров , конусов и сфер .
Многоугольные тела состоят из многоугольников граней , вершин или точек, где более чем пересекаются 2 стороны, и ребер 908 где две стороны встречаются .
Призма имеет 2 идентичных или совпадающих оснований в форме многоугольника .
Призма — это , названная по форме основания .
.
Подсчитаем вершины, края и грани
Хотя мы могли рисовать изображения трехмерного твердого тела и подсчитывать вершины, края и грани, есть способ получше.Мы разработали формул , чтобы найти эти числа по образцам, которые мы наблюдали при их подсчете.
Если твердое тело представляет собой куб , прямоугольную призму , треугольную призму или треугольную пирамиду :
Если нам известно число ЛИЦ (F) , то найдем число:
ВЕРШИНЫ (V): умножаем F на 2, затем вычитаем 4: V = 2 F — 4 = 2 ( F — 2)
КРАЯ (E) : умножаем F на 3, затем вычтите 6: E = 3 F — 6 = 3 ( F — 2)
Если мы знаем число КРАЙ (E) , чтобы найти количество:
ВЕРШИНЫ (V): умножаем E на 2, затем делим на 3: V = 2 E ÷ 3 = 2/3 E
ЛИЦА (F) : делим E на 3 , затем прибавляем 2: F = E ÷ 3 + 2
Для квадратной пирамиды с квадратным основанием и 4 треугольными гранями формулы следующие:
Если мы знаем количество ЛИЦ (F) , чтобы найти количество:
ВЕРШИНЫ (V): умножаем ( F -2) на 2, затем вычитаем 1: V = 2 ( F -2) — 1 = 2 F -5 =
КРАЯ (E) : умножаем ( F -2) на 3, затем вычитаем 1: E = 3 ( F -2) — 1 = 3 F -7
Если мы знаем количество КРАЙ (E) , чтобы найти количество:
ВЕРШИНЫ (V): умножаем ( E + 1) на 2, делим на 3, затем вычитаем 1: V = 2/3 ( E + 1) — 1.
ЛИЦ (F) : делим ( E + 1) на 3, затем прибавляем 2: F = ( E + 1) ÷ 3 + 2
| Цельный | Кол-во лиц | Кол-во вершин | Кол-во кромок |
| Куб | 6 | 8 | 12 |
| Прямоугольная призма | 6 | 8 | 12 |
| Треугольная призма | 5 | 6 | 9 |
| Треугольная пирамида | 4 | 4 | 6 |
| Формула | F | В = 2 ( Ф -2) | E = 3 ( F -2) |
| Формула | F = E ÷ 3 + 2 | В = 2/3 E | E |
| Квадратная пирамида | 5 | 5 | 8 |
| Формула | Ф | В = 2 ( Ф -2) — 1 | E = 3 ( F -2) — 1 |
| Формула | F = 1/3 ( E + 1) + 2 | В = 2/3 ( E + 1) — 1 | E |
.
Круглые тела
Эти тела основаны на окружностях. Бидоны, колонны на зданиях и резервуары для хранения жидкостей имеют цилиндрическую форму. Индикаторы объезда на шоссе и кубки Дикси у фонтана — это конусы, а планета, на которой мы живем, а также игрушки, которые мы подпрыгиваем, ударяем и бросаем, — это сферы.
.
Цилиндр имеет 2 плоские поверхности и 1 изогнутую поверхность.
Конус , , , , имеет 1 плоскую поверхность и 1 изогнутую поверхность.
Сфера имеет только изогнутые поверхности. Мы обычно называем Сферу шаром или глобусом.
.
Теперь возьмите карандаш, ластик и записную книжку, скопируйте вопросы,
выполните практические упражнения, а затем проверьте свою работу с решениями.
Если вы застряли, просмотрите примеры в уроке, а затем попробуйте еще раз.
.
Практика
1) Сопоставьте слова слева с описаниями справа.
| сфера | а) прямоугольная призма с 6 квадратными гранями. |
| фигура в открытой плоскости | б) 3 ( F -2) |
| прямоугольник | c) 1/3 (E + 1) + 2 |
| конус | г) 2-х мерная фигура с 4 сторонами и углами. |
| квадратная пирамида | e) можно измерить только одним способом. |
| куб | е) круглое твердое тело без плоских поверхностей. |
| формула для кромок | г) твердое тело круглой формы с одной плоской поверхностью. |
| формула для граней | з) трехмерное тело с 5 гранями. |
2)
.
Решения
1) Сопоставьте слова слева с описаниями справа.
| сфера | е) круглое твердое тело без плоских поверхностей. |
| фигура в открытой плоскости | e) можно измерить только одним способом. |
| прямоугольник | г) 2-х мерная фигура с 4 сторонами и углами. |
| конус | г) твердое тело круглой формы с одной плоской поверхностью. |
| квадратная пирамида | з) трехмерное тело с 5 гранями. |
| куб | а) прямоугольная призма с 6 квадратными гранями. |
| формула для кромок | b) 3 ( F -2) |
| формула для граней | c) 1/3 (E + 1) + 2 |
2)
a) Основание представляет собой прямоугольную призму с нет вершина — значит, у нее 6 — 1 = 5 граней .
b) Поскольку нет вершины , у него ½ числа вершин , поэтому он имеет 4 вершины на земле.Напомним, что вершина — это точка, в которой встречаются БОЛЕЕ 2 СТОРОН.
c) Крыша представляет собой треугольную призму без 1 прямоугольника , у нее нет дна — поэтому у нее 4 грани — 2 треугольника спереди и сзади и 2 прямоугольника — стороны крыши.
d) Крыша — это , прикрепленный к основанию, поэтому теряет 2 кромки спереди и сзади. Имеет 9-2 = 7 ребер .
.
( Primary MathRoom Index )
Опишите двумерные фигуры, полученные в результате нарезки трехмерных фигур: CCSS.Math.Content.7.G.A.3
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.

 В полых объектах внутреннюю тень размещают ближе всего к источнику света.
В полых объектах внутреннюю тень размещают ближе всего к источнику света.
 Также, в качестве цвета заливки можно выбрать градиент или текстуру. В меню кнопки «Цвет контура» можно регулировать толщину линии.
Также, в качестве цвета заливки можно выбрать градиент или текстуру. В меню кнопки «Цвет контура» можно регулировать толщину линии.
 Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 110
Математика 4 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 110

