Пространственные рисунки: D0 bf d1 80 d0 be d1 81 d1 82 d1 80 d0 b0 d0 bd d1 81 d1 82 d0 b2 d0 b5 d0 bd d0 bd d1 8b d0 b5 картинки, стоковые фото D0 bf d1 80 d0 be d1 81 d1 82 d1 80 d0 b0 d0 bd d1 81 d1 82 d0 b2 d0 b5 d0 bd d0 bd d1 8b d0 b5
- Моделирование пространственных отношений—ArcGIS Pro | Документация
- Определение пространственных взаимоотношений
- Обратное расстояние, обратное расстояние в квадрате (сопротивление)
- Диапазон расстояний (сфера влияния)
- Зона индифферентности
- Смежность полигонов (первого порядка)
- K ближайших соседей
- Триангуляция Делоне (естественная окрестность)
- Пространственно-временное окно
- Получение пространственных весов из файла (пространственные отношения, заданные пользователем)
- Выбор определения пространственных взаимоотношений: рекомендации
- Метод расстояния
- Собственный потенциал (поле, дающее интразональный вес)
- Стандартизация
- Диапазон расстояний или пороговое расстояние
- Количество соседей
- Файл матрицы весов
- Файл матрицы пространственных весов (.swm)
- Определение пространственных взаимоотношений
- Названы победители конкурса детских рисунков «Мои родители – строители!»
- Формы пространственного построения танца
- Пространственные фигуры — виды, изображения, свойства с примерами решения
- Декоративные пространственные решения | Статьи компании МДМ-Лайт
- Упражнение 9 Пространственные взаимосвязи | Основы геоинформатики: практикум в ArcGIS
- Введение
- Визуальный анализ векторных слоев
- Организация рабочего пространства
- Оверлей слоев методом пересечения
- Слияние результатов пересечения с целью получения показателя пространственной связи
- Подсчет суммарной площади каждой комбинации подтипа почв и типа рельефа
- Подсчет суммарной площади каждого подтипа почв
- Добавление нового поля для результирующих значений
- Соединение таблиц по названию подтипа почв
- Вычисление результирующих значений
- Контрольные вопросы
- Рисовать по клеточкам легкие картинки
- Пространственный рисунок, простое объяснение
- Пространственные чертежи | CIRCA Art Actuel
- Улучшение пространственных способностей с помощью инженерного рисования
- Пространственный поток: современные рисунки из коллекции Джоанн Гонсалес Хики — Грегори Алликарский художественный музей
- границ | Чему нас учат пространственные искажения в рисунках пациентов после повреждения правого полушария мозга относительно изображения пространства в искусстве?
- Hélio Oiticica — Пространственный рельеф и рисунки, 1955–59 — Выставки
- Чертеж — пространственное наложение
Моделирование пространственных отношений—ArcGIS Pro | Документация
В этом документе содержится дополнительная информация о параметрах инструментов, а также описываются основные термины и понятия, важные для анализа данных с помощью Инструментов пространственной статистики. Используйте этот документ как справочник, когда вам потребуется дополнительная информация о параметрах инструмента.
Определение пространственных взаимоотношений
Важное отличие между пространственной и традиционной (пространственной или непространственной) статистикой состоит в том, что пространственная статистика интегрирует пространство и пространственные отношения непосредственно в вычисления. Следовательно, многие инструменты из набора Пространственной статистики требуют, чтобы значение параметра Определение пространственных взаимоотношений было выбрано до выполнения анализа. Общая концептуальная модель (определение) включает обратное расстояние, время в пути, фиксированное расстояние, K ближайших соседей и смежность. Концептуальная модель определения пространственных взаимоотношений, которую вы используете, зависит от того, что именно вы измеряете. Если вы измеряете кластеризацию отдельных видов размножающихся семенами растений, вероятно, обратное расстояние подходит лучше всего. Однако, если вы оцениваете географическое распределение жителей пригородов, приезжающих на работу в город, время пути и стоимость пути будут лучше всего описывать пространственные отношения. Для некоторых видов анализа, пространство и время могут иметь меньшее значение, чем абстрактные концепции, такие как знакомство с чем-либо (чем более знакомо что-либо, тем большей функциональностью оно обладает) или пространственное взаимодействие (например, между Нью-Йорком и Лос-Анджелесом совершается значительно больше телефонных звонков, чем между Нью-Йорком и небольшим городом рядом с ним, таким как Пафкипси – можно предположить, что Лос-Анджелес и Нью-Йорк функционально ближе).
Концептуальная модель определения пространственных взаимоотношений, которую вы используете, зависит от того, что именно вы измеряете. Если вы измеряете кластеризацию отдельных видов размножающихся семенами растений, вероятно, обратное расстояние подходит лучше всего. Однако, если вы оцениваете географическое распределение жителей пригородов, приезжающих на работу в город, время пути и стоимость пути будут лучше всего описывать пространственные отношения. Для некоторых видов анализа, пространство и время могут иметь меньшее значение, чем абстрактные концепции, такие как знакомство с чем-либо (чем более знакомо что-либо, тем большей функциональностью оно обладает) или пространственное взаимодействие (например, между Нью-Йорком и Лос-Анджелесом совершается значительно больше телефонных звонков, чем между Нью-Йорком и небольшим городом рядом с ним, таким как Пафкипси – можно предположить, что Лос-Анджелес и Нью-Йорк функционально ближе).
Инструмент Пространственно ограниченная многовариантная кластеризация содержит параметр Пространственные ограничения, и хотя опции параметры аналогичны описанным для параметра Определение пространственных взаимоотношений, они используются по-разному. При наложении пространственного ограничения, только объекты с хотя бы одним соседом (что также определяется близостью, отношениями ближайшей окрестности или методами триангуляции) могут входить в одну группу. Дополнительные сведения и примеры см. в разделе Как работает инструмент Пространственно ограниченная многовариантная кластеризация.
При наложении пространственного ограничения, только объекты с хотя бы одним соседом (что также определяется близостью, отношениями ближайшей окрестности или методами триангуляции) могут входить в одну группу. Дополнительные сведения и примеры см. в разделе Как работает инструмент Пространственно ограниченная многовариантная кластеризация.
Опции параметра Определение пространственных взаимоотношений описываются ниже. Выбранные вами опции определяют взаимоотношения в окрестностях для инструментов, которые оценивают каждый пространственный объект в контексте окрестных объектов. К таким инструментам относятся Пространственная автокорреляция (глобальный индекс Морана I), Анализ горячих точек (Getis-Ord Gi*) и Анализ кластеров и выбросов (Anselin локальный индекс Морана I). Обратите внимание, что некоторые из этих опций доступны только, если вы используете инструмент Построить матрицу пространственных весов.
Обратное расстояние, обратное расстояние в квадрате (сопротивление)
При использовании опций обратного расстояния, концептуальная модель (определение) пространственных взаимоотношений зависит от сопротивления, или затухания в зависимости от расстояния. Все пространственные объекты воздействуют/влияют на другие пространственные объекты, но, с увеличением расстояния, это влияние снижается. В общем случае, если вы используете модель обратных расстояний, вам потребуется ввести значение Диапазон расстояний или пороговое расстояние для сокращения количества необходимых вычислений, особенно для больших наборов данных. Если эти значения не указаны, вычисляется пороговое значение по умолчанию. Вы можете ввести все объекты в ближайшую окрестность, задав значение 0 для параметра Диапазон расстояний или пороговое расстояние.
Все пространственные объекты воздействуют/влияют на другие пространственные объекты, но, с увеличением расстояния, это влияние снижается. В общем случае, если вы используете модель обратных расстояний, вам потребуется ввести значение Диапазон расстояний или пороговое расстояние для сокращения количества необходимых вычислений, особенно для больших наборов данных. Если эти значения не указаны, вычисляется пороговое значение по умолчанию. Вы можете ввести все объекты в ближайшую окрестность, задав значение 0 для параметра Диапазон расстояний или пороговое расстояние.
Обратное евклидово расстояние подходит для моделирования непрерывных данных, например изменений температуры. Обартное Манхэттенское расстояние лучше всего работает, если в анализе участвуют местоположения магазинов или других городских предприятий, в том случае, если данные дорожной сети недоступны. Концептуальная модель при использовании опции Обратные расстояния в квадрате не отличатся от модели, использующей Обратные расстояния, за исключением случаев, когда уклон острее, и влияния соседей спадают быстрее и только ближайший сосед оказывает наиболее значимое влияние на вычисления для данного объекта.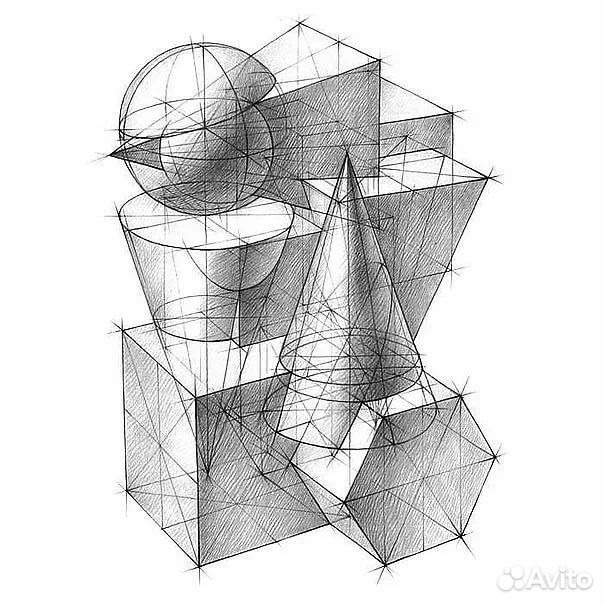
Диапазон расстояний (сфера влияния)
Для таких инструментов как Анализ горячих точек, Определение пространственных отношений выбирается по умолчанию. С помощью опции Полоса фиксированных расстояний вводится модель «сферы влияния» или «скользящего окна». Каждый пространственный объект анализируется в контексте окружающих его объектов, расположенных на расстоянии, заданном параметром Диапазон расстояний или пороговое расстояние. Соседи в пределах заданного расстояния имеют одинаковый вес. Пространственные объекты, находящиеся вне указанного расстояния, не оказывают влияния на вычисления (их вес принимается за 0). Используйте метод Полоса фиксированных расстояний, если вы хотите оценить статистические параметры данных при определенном (фиксированном) пространственном масштабе. Если вы изучаете закономерности ежедневных поездок в город из пригородов и знаете, что среднее расстояние поездки составляет 15 миль, вы можете использовать для анализа фиксированное расстояние в 15 миль.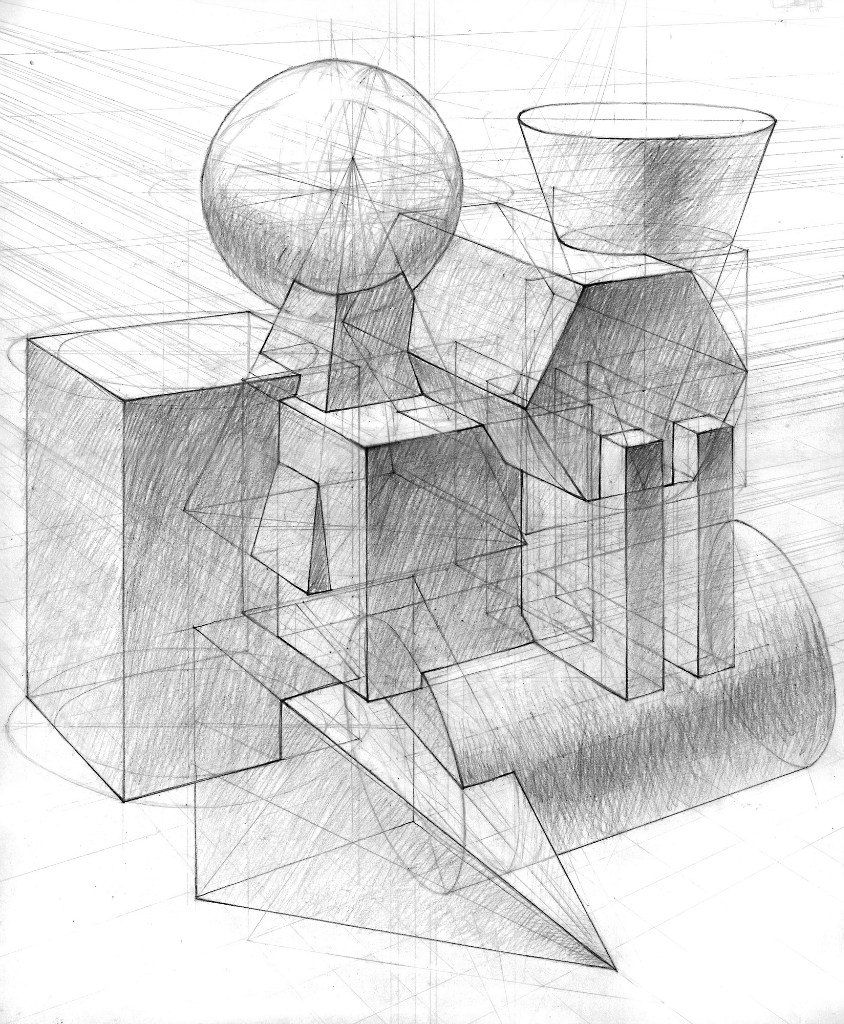 В разделе Выбор фиксированного расстояния приведены стратегии, которые помогут определить соответствующий вашему анализу масштаб.
В разделе Выбор фиксированного расстояния приведены стратегии, которые помогут определить соответствующий вашему анализу масштаб.
Зона индифферентности
Опция Зона индифферентности для параметра Определение пространственных отношений комбинирует модели Обратное расстояние и Диапазон фиксированных расстояний. Пространственные объекты, расположенные в пределах диапазона расстояний или порогового расстояния, включаются в анализ целевого пространственного объекта. После достижения критического расстояния, уровень влияния (вес) быстро уменьшается. Предположим, вы ищите работу и выбираете между офисами, расположенными на расстоянии 5 и 6 миль от дома. В этом случае, расстояние, скорее всего, не будет иметь для вас большого значения. Теперь, предположим, что один офис расположен в 5 милях от дома, а другой – в 20 милях. В этом случае, расстояние становится существенным и не может не учитываться при принятии решения. Используйте этот метод, если вы хотите иметь фиксированный масштаб анализа, но не хотите ограничиваться жесткими рамками окрестных объектов, включенных в вычисления для целевого объекта.
Смежность полигонов (первого порядка)
Для классов полигональных объектов можно выбрать опцию Только совпадающие ребра (которую иногда называют Rook’s Case) или Совпадающие ребра и углы (которую иногда называют Queen’s Case). В рамках метода Только совпадающие ребра полигоны, имеющие общее ребро (т. е. совпадающую границу), включаются в вычисления для целевого полигона. Полигоны, не имеющие общих ребер, исключаются из вычислений. В рамках метода Совпадающие ребра и углы полигоны, имеющие общее ребро или угол, включаются в вычисления для целевого полигона. Если часть двух полигонов пересекается, они считаются соседями и включатся в соответствующие вычисления. Используйте одну из этих концептуальных моделей смежности с объектами-полигонами в том случае, если вы моделируете распространение некоторых типов инфекционных заболеваний или работаете с непрерывными данными, представленными в виде полигонов.
K ближайших соседей
Отношения в окрестности можно также сконструировать так, что каждый пространственный объект будет доступен в пределах пространственного контекста, состоящего из заданного числа ближайших окрестностей. Если K (число окрестностей) равно 8, в вычисления для целевого пространственного объекта будут включены восемь ближайших окрестностей. В тех местах, где плотность пространственных объектов высока, пространственный контекст анализа будет меньше. Соответственно, если плотность объектов невелика, пространственный контекст анализа будет больше. Преимущество этой модели пространственных отношений состоит в том, что для каждого целевого объекта будет задано некоторое количество соседей, даже если плотность пространственных объектов в изучаемой области значительно различается. Этот метод можно применить, когда вы работаете с инструментом Построить матрицу пространственных весов. Опция Ближайшая окрестность K со значением 8 для параметра Количество соседей – это модель по умолчанию, используемая с инструментом Исследовательская регрессия для оценки невязок регрессии.
Если K (число окрестностей) равно 8, в вычисления для целевого пространственного объекта будут включены восемь ближайших окрестностей. В тех местах, где плотность пространственных объектов высока, пространственный контекст анализа будет меньше. Соответственно, если плотность объектов невелика, пространственный контекст анализа будет больше. Преимущество этой модели пространственных отношений состоит в том, что для каждого целевого объекта будет задано некоторое количество соседей, даже если плотность пространственных объектов в изучаемой области значительно различается. Этот метод можно применить, когда вы работаете с инструментом Построить матрицу пространственных весов. Опция Ближайшая окрестность K со значением 8 для параметра Количество соседей – это модель по умолчанию, используемая с инструментом Исследовательская регрессия для оценки невязок регрессии.
Триангуляция Делоне (естественная окрестность)
Опция Триангуляция Делоне создает окрестности методом построения треугольников Вороного по точечным объектам или по центроидам пространственных объектов, так, чтобы каждая точка/центроид становилась узлом (вершиной) треугольника. Узлы, соединенные ребрами треугольников, рассматриваются как окрестности. Использование триангуляции Делоне позволяет обеспечить для каждого пространственного объекта наличие хотя бы одной окрестности, даже если в данных присутствуют острова или плотность пространственных объектов меняется в широких пределах. Опцию DELAUNAY_TRIANGULATION не следует использовать для наборов данных с совпадающими объектами. Этот метод можно применить, когда вы работаете с инструментом Построить матрицу пространственных весов.
Узлы, соединенные ребрами треугольников, рассматриваются как окрестности. Использование триангуляции Делоне позволяет обеспечить для каждого пространственного объекта наличие хотя бы одной окрестности, даже если в данных присутствуют острова или плотность пространственных объектов меняется в широких пределах. Опцию DELAUNAY_TRIANGULATION не следует использовать для наборов данных с совпадающими объектами. Этот метод можно применить, когда вы работаете с инструментом Построить матрицу пространственных весов.
Пространственно-временное окно
С помощью этой опции можно определить отношения объектов как в пространственном (фиксированное расстояние), так и во временном (фиксированный интервал) окне. Эта опция доступна при создании файла матрицы пространственных весов с помощью инструмента Построить матрицу пространственных весов. При выборе опции Пространственно-временное окно также требуется указать Поле даты/времени, Тип интервала даты/времени (например, Часы, Дни или Месяцы) и Значение интервала даты/времени. Значение интервала – целое число. Если вы выбрали опцию Часы в качестве типа интервала и значение 3 как значение интервала, два объекта будут считаться соседями, если значения в поле Дата/Время расположены в пределах трех часов друг от друга. С такой моделью объекты будут соседями, если они расположены на определенном расстоянии и в пределах заданного временного интервала целевого объекта. В качестве примера можно выбрать опцию Пространственно-временное окно для параметра Определение пространственных взаимоотношений, если требуется создать файл матрицы пространственных весов для использования инструмента Анализ горячих точек, чтобы выявить горячие точки в пространстве-времени. Дополнительные сведения, в том числе о визуализации результатов, см. в разделе Пространственно-временной анализ. Имеются также другие возможности для визуализации в 3D пространственно-временного куба netCDF.
Значение интервала – целое число. Если вы выбрали опцию Часы в качестве типа интервала и значение 3 как значение интервала, два объекта будут считаться соседями, если значения в поле Дата/Время расположены в пределах трех часов друг от друга. С такой моделью объекты будут соседями, если они расположены на определенном расстоянии и в пределах заданного временного интервала целевого объекта. В качестве примера можно выбрать опцию Пространственно-временное окно для параметра Определение пространственных взаимоотношений, если требуется создать файл матрицы пространственных весов для использования инструмента Анализ горячих точек, чтобы выявить горячие точки в пространстве-времени. Дополнительные сведения, в том числе о визуализации результатов, см. в разделе Пространственно-временной анализ. Имеются также другие возможности для визуализации в 3D пространственно-временного куба netCDF.
Получение пространственных весов из файла (пространственные отношения, заданные пользователем)
Можно создать файл для хранения соседских отношений объектов с помощью инструмента Построить файл матрицы пространственных весов. Если пространственные отношения для ваших объектов заданы в таблице, можно использовать инструмент Построить матрицу пространственных весов для конвертации этой таблицы в файл матрицы пространственных весов (.swm). Определенные поля нужно включить в таблицу, чтобы использовать опцию Конвертировать таблицу для получения SWM-файла. Можно указать путь к форматированному текстовому ASCII-файлу, который задает пользовательское определение пространственных взаимоотношений (например, на основе пространственных взаимодействий).
Если пространственные отношения для ваших объектов заданы в таблице, можно использовать инструмент Построить матрицу пространственных весов для конвертации этой таблицы в файл матрицы пространственных весов (.swm). Определенные поля нужно включить в таблицу, чтобы использовать опцию Конвертировать таблицу для получения SWM-файла. Можно указать путь к форматированному текстовому ASCII-файлу, который задает пользовательское определение пространственных взаимоотношений (например, на основе пространственных взаимодействий).
Выбор определения пространственных взаимоотношений: рекомендации
Чем более точно вы сможете смоделировать взаимодействие пространственных объектов в пространстве, тем более точные результаты вы получите. Выбор параметра Определение пространственных взаимоотношений должен отражать внутренние отношения между пространственными объектами, которые вы анализируете. Иногда на выбор могут влиять характеристики имеющихся данных.
Методы обратно-взвешенного расстояния, (Обратное расстояние, Обратное расстояние в квадрате), например, лучше всего подходят для непрерывных данных или для моделирования процессов, в которых два объекта сближены в пространстве настолько, что с большей вероятностью оказывают влияние друг на друга. При такой пространственной модели, каждый объект является потенциальной окрестностью любого другого объекта, и, при использовании больших наборов данных, количество вычислений может стать значительным. Всегда следует пытаться включить значение Диапазон расстояний или пороговое расстояние при использовании модели обратно-взвешенного расстояния. Это особенно важно для больших наборов данных. Если вы оставите параметр Диапазон расстояний или пороговое расстояние пустым, пороговое расстояние будет вычислено автоматически, но оно может оказаться не вполне подходящим расстоянием для вашего анализа. По умолчанию пороговое расстояние равно минимальному расстоянию, которое гарантирует, что для каждого объекта имеется хотя бы одна окрестность.
При такой пространственной модели, каждый объект является потенциальной окрестностью любого другого объекта, и, при использовании больших наборов данных, количество вычислений может стать значительным. Всегда следует пытаться включить значение Диапазон расстояний или пороговое расстояние при использовании модели обратно-взвешенного расстояния. Это особенно важно для больших наборов данных. Если вы оставите параметр Диапазон расстояний или пороговое расстояние пустым, пороговое расстояние будет вычислено автоматически, но оно может оказаться не вполне подходящим расстоянием для вашего анализа. По умолчанию пороговое расстояние равно минимальному расстоянию, которое гарантирует, что для каждого объекта имеется хотя бы одна окрестность.
Метод Полоса фиксированных расстояний хорошо работает с точечными данными. Это опция по умолчанию, используемая инструментом Анализ горячих точек (Getis-Ord Gi*). Метод полосы фиксированных расстояний хорошо работает с полигональными данными, имеющими различные размеры полигонов (большие полигоны по краям изучаемой области и очень маленькие полигоны в центре изучаемой области, например), если вам требуется обеспечить согласованный масштаб анализа. В нижеследующем разделе Выбор значения полосы фиксированных расстояний приведены стратегии, которые помогут определить значение диапазона расстояний, подходящее для вашего анализа.
В нижеследующем разделе Выбор значения полосы фиксированных расстояний приведены стратегии, которые помогут определить значение диапазона расстояний, подходящее для вашего анализа.
Модель Зоны индифферентности хорошо работает при правильно подобранном фиксированном расстоянии, но слишком резкие границы отношений окрестностей мешают точному представлению данных. Имейте в виду, что в модели зоны индифферентности каждый пространственный объект рассматривается как окрестность другого объекта. Следовательно, эта опция не подходит для больших наборов данных, поскольку указанные значения Диапазона расстояний или порогового расстояния не ограничивают число окрестностей, а только определяют, где интенсивность пространственных отношений начинает снижаться.
Модель смежных полигонов (Только совпадающие ребра, Совпадающие ребра и углы) эффективна, когда полигоны имеют одинаковые размеры и однотипное распределение, а пространственные отношения являются функцией близости полигонов (если два полигона имеют общую границу, пространственное взаимодействие между ними возрастает).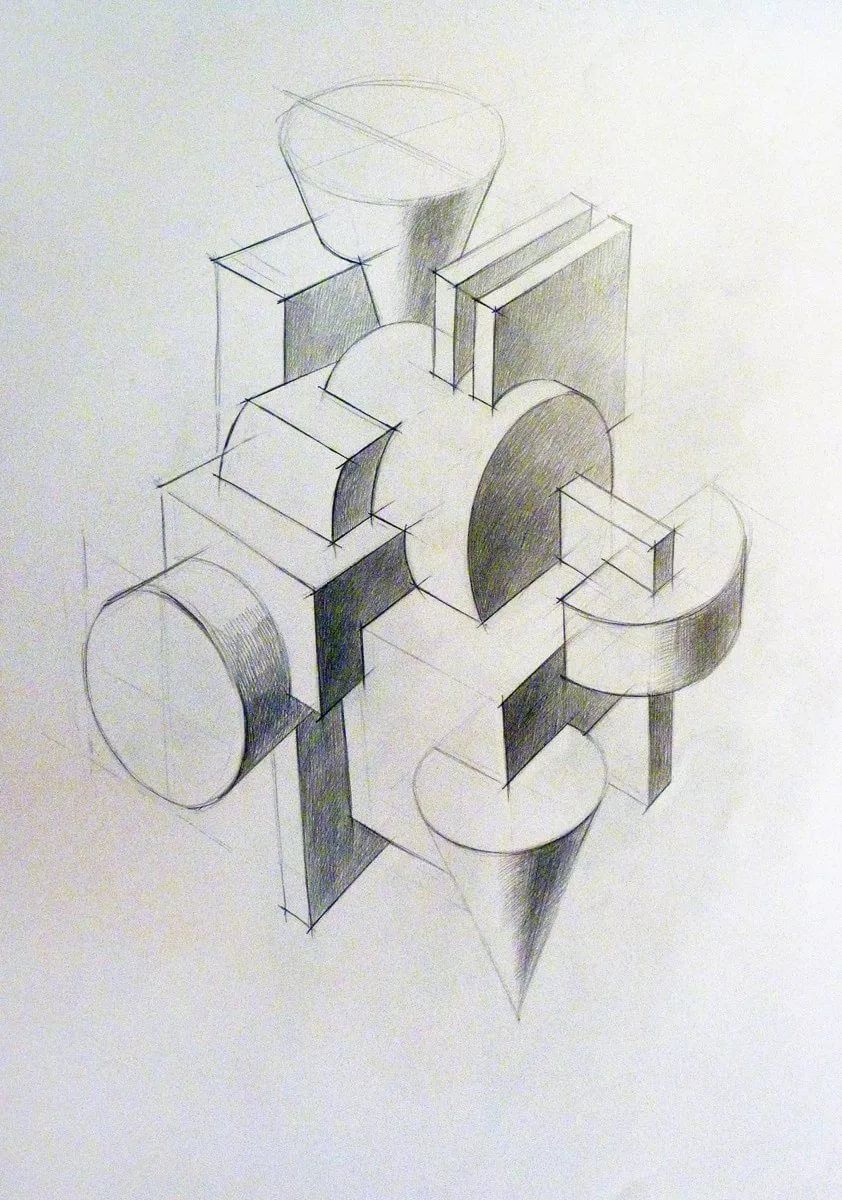 Если вы выбрали модель смежности полигонов, почти всегда потребуется выбрать нормализацию ряда (значений) для инструментов, которые имеют параметр Нормализация ряда.
Если вы выбрали модель смежности полигонов, почти всегда потребуется выбрать нормализацию ряда (значений) для инструментов, которые имеют параметр Нормализация ряда.
Опция K ближайших соседей (K nearest neighbors) эффективна, если вам необходимо задать минимальное количество окрестностей для анализа. Если значения, связанные с пространственными объектами, ассиметричны (не имеют нормального распределения), важно, чтобы каждый объект оценивался в контексте как минимум восьми (или около того) окрестностей. Если распределение данных в изучаемом районе неоднородно, т.е., некоторые пространственные объекты расположены очень далеко от всех остальных объектов, этот метод работает очень хорошо. Заметьте, однако, что пространственный контекст анализа меняется в зависимости от изменения плотности используемых пространственных объектов. Если фиксированный масштаб анализа имеет меньшее значение, чем фиксированное число окрестностей, можно использовать метод K ближайших соседей.
Некоторые аналитики рассматривают триангуляцию Делоне в качестве способа создания естественных окрестностей для набора пространственных объектов.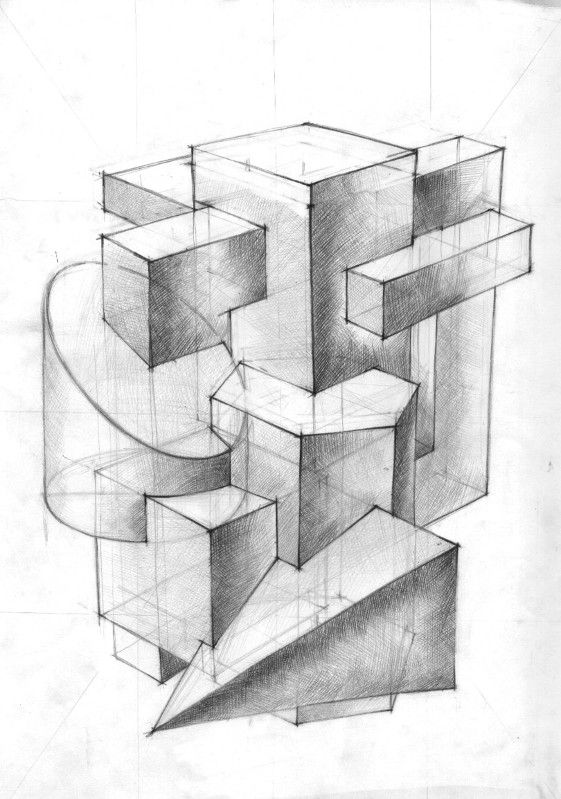 Этот метод является хорошим вариантом, если ваши данные содержат островные полигоны (изолированные полигоны, которые не имеют общих границ с другими полигонами), или в тех случаях, когда пространственные объекты распределены слишком неравномерно. Эту опцию не следует использовать для наборов данных с совпадающими объектами. Так же, как и метод K ближайших соседей, триангуляция Делоне обеспечивает для каждого пространственного объекта наличие минимум одной окрестности, при этом на основе распределения данных определяется количество окрестностей, которое может быть присвоено каждому объекту.
Этот метод является хорошим вариантом, если ваши данные содержат островные полигоны (изолированные полигоны, которые не имеют общих границ с другими полигонами), или в тех случаях, когда пространственные объекты распределены слишком неравномерно. Эту опцию не следует использовать для наборов данных с совпадающими объектами. Так же, как и метод K ближайших соседей, триангуляция Делоне обеспечивает для каждого пространственного объекта наличие минимум одной окрестности, при этом на основе распределения данных определяется количество окрестностей, которое может быть присвоено каждому объекту.
Опция Окно пространства-времени позволяет определить отношения объектов как с точки зрения пространственной, так и временной близости. Эта опция используется для определения горячих точек в пространстве-времени или формирования групп, членство в которых определяется близостью в пространстве и времени. Примеры пространственно-временного анализа, а также стратегии для эффективного отображения результатов такого анализа представлены в разделе Пространственно-временной анализ.
Для некоторых приложений пространственные взаимодействия лучше всего моделируются в терминах времени пути или расстояния пути. Если вы моделируете доступность до городских служб, например, или определяете «горячие точки» преступности, наилучшим выбором будет моделирование пространственных отношений в терминах сети. Используйте инструмент Построить матрицу пространственных весов для сети для того, чтобы создать файл матрицы весов (.swm) перед анализом. Выберите GET_SPATIAL_WEIGHTS_FROM_FILE значение для Определения пространственных взаимоотношений и укажите Файл матрицы весов, введя полный путь к созданному ранее файлу SWM.
Подсказка:
Многие организации сохраняют собственные сетевые наборы улиц, с которыми вы можете работать. В качестве альтернативы Street Map Premium for ArcGIS содержит предварительно построенные наборы сетевых данных в формате SDC, покрывающие Северную Америку, Латинскую Америку, Европу, Среднюю Восточную Африку, Японию, Австралию и Новую Зеландию. Эти наборы сетевых данных могут напрямую использоваться данным инструментом.
Эти наборы сетевых данных могут напрямую использоваться данным инструментом.
Если ни одна из опций параметра Определение пространственных взаимоотношений не подходит для вашего анализа, можно создать текстовый ASCII-файл или таблицу, содержащие необходимые вам отношения между пространственными объектами, и затем использовать их для построения файла матрицы пространственных весов. Если одна из указанных выше опций соответствует, но не идеально подходит для ваших целей, можно использовать инструмент Построить матрицу пространственных весов для создания базового SWM-файла, а затем изменить файл матрицы пространственных весов.
Метод расстояния
Многие инструменты из набора инструментов Пространственная статистика используют в вычислениях расстояние. Эти инструменты позволяют выбрать либо Евклидово, либо Манхэттоновское расстояние.
- Евклидово расстояние вычисляется по формуле
D = sq root [(x1–x2)**2. 0 + (y1–y2)**2.0]
0 + (y1–y2)**2.0]где (x1, y1) – координаты точки A, (x2, y2) – координаты точки B, а D – расстояние по прямой между точками A и B.
- Манхэттенское расстояние вычисляется по формуле
D = abs(x1–x2) + abs(y1–y2)где (x1, y1) – координаты точки A, (x2, y2) – координаты точки B, а D – сумма вертикальной и горизонтальной разности между точками A и B. Это расстояние, которое необходимо пройти, если возможность перемещения ограничена только направлениями север-юг и запад-восток. Этот метод дает более точные результаты, чем Евклидово расстояние, если путь ограничен дорожной сетью и если стоимость перемещения по уличной сети не доступна.
Когда ваши входные объекты не имеют проекции (т.е. когда координаты заданы в градусах, минутах и секундах), или когда в качестве выходной системы координат используется Географическая система координат, а также когда вы указываете путь выходного класса объектов к набору классов объектов, имеющему пространственную привязку Географической системы координат, расстояния будут рассчитываться с помощью хордовых измерений, а параметр Метод определения расстояния будет отключен. Измерения хордовых расстояний применяются постольку, поскольку они могут быть быстро вычислены и дают очень хорошие оценки истинных геодезических расстояний, по крайней мере для точек, расстояние между которыми в пределах порядка тридцати градусов. В основе хордовых расстояний лежит скорее сфероид, чем форма сплющенного у полюсов эллипсоида Земли. Если взять две любые точки на поверхности Земли, то хордовым расстоянием между ними будет длина прямой линии, проходящей через трехмерное тело Земли и соединяющей эти две точки. Хордовые расстояния выражаются в метрах.
Измерения хордовых расстояний применяются постольку, поскольку они могут быть быстро вычислены и дают очень хорошие оценки истинных геодезических расстояний, по крайней мере для точек, расстояние между которыми в пределах порядка тридцати градусов. В основе хордовых расстояний лежит скорее сфероид, чем форма сплющенного у полюсов эллипсоида Земли. Если взять две любые точки на поверхности Земли, то хордовым расстоянием между ними будет длина прямой линии, проходящей через трехмерное тело Земли и соединяющей эти две точки. Хордовые расстояния выражаются в метрах.
Внимание:
Следует обязательно производить проецирование ваших данных, если область исследования превышает 30 градусов. Хордовые расстояния не обеспечивают точных оценок геодезических расстояний, превышающих 30 градусов.
Собственный потенциал (поле, дающее интразональный вес)
Некоторые инструменты в наборе инструментов Пространственная статистика позволяют вычислить поле, представляющее вес, который используется для собственного потенциала. Собственный потенциал – это расстояние или вес между объектом и этим же объектом. Часто вес имеет значение 0, но в некоторых случаях может потребоваться определить другое фиксированное или изменяющееся для каждого объекта значение. Если ваша модель пространственных отношений основана на расстояниях в пределах или между переписными участками, то, например, вы можете решить смоделировать собственный потенциал, чтобы отразить средние расходы на путешествие с учетом размеров полигона:
Собственный потенциал – это расстояние или вес между объектом и этим же объектом. Часто вес имеет значение 0, но в некоторых случаях может потребоваться определить другое фиксированное или изменяющееся для каждого объекта значение. Если ваша модель пространственных отношений основана на расстояниях в пределах или между переписными участками, то, например, вы можете решить смоделировать собственный потенциал, чтобы отразить средние расходы на путешествие с учетом размеров полигона:
dii = 0.5*[(Ai / π)**0.5]где dii – транспортные расходы, связанные с внутризональным путешествием для полигонального объекта i, и Ai – область, связанная с полигональным объектом i.
Стандартизация
Нормализация ряда рекомендуется, независимо от того, распределены ли объекты потенциально предвзято в зависимости от дизайна примера или от установленной схемы агрегации. Когда выбирается нормализация ряда, каждый вес делится на его сумму весов ряда (сумму весов всех соседних объектов). Взвешивание с нормализацией весов ряда значений часто используется с фиксированным расстоянием до соседних окрестностей и практически всегда используется для соседей, основанных на полигональной смежности. Это для того, чтобы смягчить смещение из-за того, что объекты имеют разное количество соседей. Нормализация ряда масштабирует все веса так, что они варьируют между 0 и 1, создавая относительную, а не абсолютную схему взвешивания. В любом случае, когда вы работаете с полигональными объектами, представляющими административные границы, вы, вероятно, захотите выбрать опцию Нормализации ряда.
Взвешивание с нормализацией весов ряда значений часто используется с фиксированным расстоянием до соседних окрестностей и практически всегда используется для соседей, основанных на полигональной смежности. Это для того, чтобы смягчить смещение из-за того, что объекты имеют разное количество соседей. Нормализация ряда масштабирует все веса так, что они варьируют между 0 и 1, создавая относительную, а не абсолютную схему взвешивания. В любом случае, когда вы работаете с полигональными объектами, представляющими административные границы, вы, вероятно, захотите выбрать опцию Нормализации ряда.
Ниже приведены примеры:
- Предположим, что у вас есть полный набор всех инцидентов-правонарушений. В некоторых частях изучаемой территория представлено много точек, так как это места с высоким уровнем преступности. В других частях точек меньше, так как здесь уровень преступности низкий. Плотность точек очень хорошо отражает (представляет) то, что вы пытаетесь понять: пространственные закономерности преступлений.
 Возможно, вы не будете выполнять нормализацию ряда для пространственных весов.
Возможно, вы не будете выполнять нормализацию ряда для пространственных весов. - Предположим, вы взяли образцы почвы. По какой-то причине (погода была хорошая или вы были в месте без заборов, болот и горных вершин, которые нужно было преодолеть) у вас много образцов из определенных частей изучаемой территории и меньше образцов из других частей. Другими словами, плотность точек не является результатом тщательно спланированной произвольной выборки, из-за чего могло возникнуть собственное смещение. Кроме того, большое число точек необязательно является отражением пространственного распределения анализируемых данных. Чтобы минимизировать смещение, которое могло возникнуть в процессе получения образцов, необходимо выполнить нормализацию ряда пространственных весов. После выполнения нормализации ряда, тот факт, что у одного объекта два соседа, а другого их 18, не будет сильно влиять на результаты. Все веса в сумме будут давать 1.
- При агрегации данных вы придаете им определенную структуру.
 В редких случаях эта структура будет хорошим отражением анализируемых данных и исследуемого явления. Например: хотя полигоны переписи (как и районы переписи) сформированы на основе численности населения, даже если ваш анализ связан с вопросами численности, вам все равно придется нормализовать веса, так как эти полигоны представляют всего один из множества способов представления данных. Для полигональных данных нормализация ряда пространственных весов выполняется практически всегда.
В редких случаях эта структура будет хорошим отражением анализируемых данных и исследуемого явления. Например: хотя полигоны переписи (как и районы переписи) сформированы на основе численности населения, даже если ваш анализ связан с вопросами численности, вам все равно придется нормализовать веса, так как эти полигоны представляют всего один из множества способов представления данных. Для полигональных данных нормализация ряда пространственных весов выполняется практически всегда.
Диапазон расстояний или пороговое расстояние
Параметр Диапазон расстояний или пороговое расстояние позволяет установить масштаб анализа для большинства определений пространственных взаимоотношений (например, Обратное расстояние и Полоса фиксированных расстояний. Это положительное числовое значение, представляющее предельное расстояние. Объекты, расположенные за пределами указанного предельного расстояния, игнорируются в анализе для данного объекта. Однако для Зоны индифферентности влияние объектов, расположенных вне приведенного расстояния, сокращается в соответствие с близостью, в то время как расположенные в пределах порогового расстояния, рассматриваются в одинаковых условиях.
Выбор подходящего расстояния очень важен. Некоторые пространственные статистические показатели требуют для каждого объекта иметь как минимум одного соседа для того, чтобы анализ был надежный. Если значения, которое вы устанавливаете для параметра Диапазон расстояний или пороговое расстояние, слишком мало (и у некоторых объектов нет соседей), появится предупреждение и вам будет предложено увеличить расстояние. Инструмент Вычислить диапазон расстояний до числа соседних объектов позволяет оценить минимальное, среднее и максимальное расстояния для указанного количества соседей, и может помочь вам определить подходящий диапазон расстояний для анализа. См. также Выбор полосы фиксированных расстояний для дополнительных инструкций.
Когда значение не указано, рассчитывается пороговое расстояние по умолчанию. Приведенная ниже таблица демонстрирует, какие результаты выдают различные опции параметра Определение пространственных взаимоотношений для каждого из трех возможных типов (отрицательные значения не действительны):
| Обратное расстояние, обратное расстояние в квадрате | Полоса фиксированных расстояний, Зона индифферентности | Близость полигонов, Триангуляция Делоне, К ближайших соседей | |
|---|---|---|---|
0 | Пороговое и предельное значения не применяются; каждый объект – сосед для каждого другого объекта. | Неверно. Будет сгенерирована ошибка выполнения. | Игнорировано. |
пустой | Будет вычислено расстояние по умолчанию. Значение по умолчанию – это минимальное расстояние, которое гарантирует каждому объекту как минимум 1 соседа. | Будет вычислено расстояние по умолчанию. Значение по умолчанию – это минимальное расстояние, которое гарантирует каждому объекту как минимум 1 соседа. | Игнорировано. |
положительное число | Ненулевое, положительное значение будет использовано как предельное расстояние; соседские взаимосвязи будут только существовать среди объектов в пределах этой дистанции. | Для полосы фиксированных расстояний, только объекты в пределах этого указанного предельного расстояния будут соседями. Для зоны индифферентности, объекты в пределах указанного предельного расстояния будут соседями; объекты за пределами этого расстояния тоже будут соседями, но будут иметь все меньший и меньший вес/влияние по мере увеличения расстояния. | Игнорировано. |
Количество соседей
Укажите положительное целое число, чтобы представить количество соседей, которые должны быть включены в анализ. Когда для параметра Определение пространственных отношений выбрано значение K ближайших соседей, каждый объект будет оценен в контексте ближайших К соседей (где К – указанное количество соседей). Если при запуске инструмента Построить матрицу пространственных весов для Обратного расстояния или Фиксированного диапазона расстояний задать значение параметра Количество соседей, каждый объект будет гарантированно иметь как минимум К соседей. При расчете на основе примыкания полигонов, для любого объекта, для которого не указано Количество соседей, будут найдены соседние объекты на основании расчета близости по центроидам.
Файл матрицы весов
Некоторые инструменты позволяют вам определить пространственные отношения среди объектов, указывая путь к матрице пространственных весов. Пространственные веса – числа, которые отражают расстояние, время, или цену между объектами в базе данных. Файл матрицы пространственных весов можно создать с помощью инструмента Построить матрицу пространственных весов или использовать обычный ASCII-файл.
Пространственные веса – числа, которые отражают расстояние, время, или цену между объектами в базе данных. Файл матрицы пространственных весов можно создать с помощью инструмента Построить матрицу пространственных весов или использовать обычный ASCII-файл.
Когда файл матрицы пространственных весов – просто текстовый ASCII-файл, первая строка должна быть именем уникального поля ID. Это позволяет гибко использовать любое числовое поле из набора данных в качестве ID, при генерации файла; однако поле с ID должно быть целочисленным (длинным или коротким) и содержать уникальные значения для каждого объекта. После первой линии, файл пространственных весов должен быть форматирован в 3 колонки:
- От ID объекта
- К ID объекта
- Вес
Например, предположим, что у вас есть 3 АЗС. Поле, которое вы используете в качестве поля ID, называется StationID, а ID объектов – 1, 2 и 3. Вы хотите смоделировать пространственные отношения между этими тремя АЗС, используя время в пути в минутах. Вы можете создать ASCII-файл, который выглядит следующим образом:
Вы можете создать ASCII-файл, который выглядит следующим образом:
Обычно, когда веса представляют расстояние или время, они обращаются (например, 1/10, когда расстояние 10 миль или 10 минут) для того, чтобы ближайшие объекты имели больший вес, нежели удаленные. Заметьте из файла весов выше, что АЗС 1 в 10-ти минутах от АЗС 2. Заметьте также, что время в пути – несимметрично в этом примере (время в пути от АЗС 1 до АЗС 3 – 7 минут, но время в пути от АЗС 3 до АЗС 1 – только 6 минут). Заметьте, что вес между АЗС 1 и ей самой – 0, для АЗС 2 – пустое поле. Пустое поле означает 0.
Ручной ввод значений для матрицы пространственных весов – утомительная работа даже для маленьких наборов данных. Лучший подход – использовать инструмент Построить матрицу пространственных весов (Generate Spatial Weights Matrix) или быстро написать скрипт, чтобы выполнить эту задачу.
Файл матрицы пространственных весов (.swm)
Инструмент Построить матрицу пространственных весов создает файл матрицы пространственных весов (. swm), определяющий пространственные отношения между объектами в вашем наборе данных с учетом указанного параметра. Этот файл создается в двоичном формате, чтобы его нельзя было просматривать напрямую. Для просмотра или изменения отношений объектов в SWM-файле используйте инструмент Преобразовать матрицу пространственных весов в таблицу.
swm), определяющий пространственные отношения между объектами в вашем наборе данных с учетом указанного параметра. Этот файл создается в двоичном формате, чтобы его нельзя было просматривать напрямую. Для просмотра или изменения отношений объектов в SWM-файле используйте инструмент Преобразовать матрицу пространственных весов в таблицу.
Если пространственные отношения между объектами хранятся в таблице, можно использовать инструмент Построить матрицу пространственных весов для конвертации этой таблицы в файл .swm. В таблице должны присутствовать следующие поля:
| Имя поля | Описание |
|---|---|
<Уникальное имя поля ID> | Целое поле, которое существует во входящем классе объектов с уникальным ID для каждого объекта. |
NID | Целочисленное поле, содержащее ID соседних объектов. Это к ID объекта. |
WEIGHT | Это числовой вес, определяющий пространственные отношения между объектами: от объекта и к объекту. Большие значения отражают большие веса и более сильное влияние, или взаимодействие между двумя объектами. |
Разделение файлов матриц пространственных весов
Результатом работы инструмента Построить матрицу пространственных весов является файл SWM. Этот файл связывается с входным классом объектов, полем уникального ID и выходной системой координат при создании SWM-файла. Другие люди могут продублировать пространственные отношения, которые вы определяете для анализа, используя SWM-файл и тот же входной класс объектов или класс объектов, связывающий все или часть объектов с соответствующим полем Unique ID. В частности, если вы планируете предоставить SWM-файлы для совместной работы, попытайтесь избежать ситуации, когда ваша выходная система координат отличается от пространственной привязки, ассоциированной с входным классом объектов. Лучшая стратегия – перепроецировать Входной класс объектов, затем установить Выходную систему координат такую же, как и Входной класс объектов до создания файлов SWM.
Этот файл связывается с входным классом объектов, полем уникального ID и выходной системой координат при создании SWM-файла. Другие люди могут продублировать пространственные отношения, которые вы определяете для анализа, используя SWM-файл и тот же входной класс объектов или класс объектов, связывающий все или часть объектов с соответствующим полем Unique ID. В частности, если вы планируете предоставить SWM-файлы для совместной работы, попытайтесь избежать ситуации, когда ваша выходная система координат отличается от пространственной привязки, ассоциированной с входным классом объектов. Лучшая стратегия – перепроецировать Входной класс объектов, затем установить Выходную систему координат такую же, как и Входной класс объектов до создания файлов SWM.
Названы победители конкурса детских рисунков «Мои родители – строители!»
В историческом парке «Россия – моя история» в преддверье профессионального праздника – Дня строителя прошло награждение победителей конкурса детских рисунков «Мои родители – строители!»
С 2014 года конкурс традиционно проводится Союзом строительных объединений и организаций вместе с Группой «Эталон» и интернет-порталом «Кто строит. ру» при поддержке городского Правительства.
ру» при поддержке городского Правительства.
В этом году ребят и их родителей поздравили с победой заместитель председателя Комитета по строительству Константин Марков, заместитель директора парка «Россия – моя история» Анастасия Сулимовская, вице-президент РСС в СЗФО, исполнительный директор ССОО Олег Бритов и представитель Группы «Эталон» Диана Изотова.
Юным художникам вручили почетные грамоты и подарки. Специальный приз Комитета по строительству Санкт‑Петербурга достался Алексею Ляховичу за рисунок «Желтый самосвал», а специальный приз Союза строительных объединений и организаций и Группы «Эталон» – в этом году отдали Юлиане Болденковой, которая изобразила на своем рисунке всю семью – строительную династию.
Непосредственно тройка лидеров конкурса сложилась следующим образом:
- Третье место – у Екатерины Яковлевой (OOO «Сэтл Сити»)
- Второе место – Екатерина Ермакова (ПО «Баррикада»)
- Первое место – Родион Кулаков (ООО «ТехноКомСтрой»).

Также, в специальных номинациях били вручены почетные дипломы и памятные призы.
- Победитель в номинации «Быть строителем – здорово!» – Максим Шульгин (ООО «СПб — Гипрошахт»).
- Победитель в номинации «На стройке» – Марина Харитонова («УМ «Эталон», входит в Группу «Эталон»).
- Победитель в номинации «Портрет строителя» – Елизавета Искрова («Водоканал Санкт‑Петербурга»). Победитель в номинации «Город будущего» – Елизавета Григорьева («МегаМейд»)
- Победитель в номинации «Самая многоплановая композиция» – Елизавета Солдатова (СПб ГБУ «Управление строительными проектами)
- Победитель в номинации «Знаток строительной техники» – Милана Волкова (ЗАО «Управление №10 Метростроя»)
- Победитель в номинации «Знаток безопасности строительства» – Ирина Строкина (Спб ГБУ «Фонд капитального строительства и реконструкции»)
- Победитель в номинации «Моя мама – строитель» – Кира Рятте («Лидер Групп»)
- Победитель в номинации «Растем вместе!» – Вадим Семёнов («Метрострой»).

- Победитель в номинации «Приз зрительских симпатий» – Иван Белинский («ЛСР. Недвижимость – Северо-Запад»). Иван, также, стал обладателем специального приза от Союза строительных организаций Ленинградской области «ЛенОблСоюзСтрой», который вручил исполнительный директор Владимир Мозговой.
- Специальный приз от выставки «Ярмарка недвижимости» отдан Максиму Кондрашову (ПТО ФГУП «РСУ» Управления делами Президента РФ. Обособленное подразделение «Санкт‑Петербург»).
Дополнительная информация по телефону: 8 921 940-12-20, Рудакова Ольга – пресс-секретарь Комитета по строительству.
Формы пространственного построения танца
Формы пространственного
построения танца
Как известно композицию создает балетмейстер – сочинитель, создатель хореографического произведения. Этот может быть сочинения целого балета, отдельного танцевального номера, эпизода в пляске, дуэта, трио, квартета и т. д. каждая композиция включает в себя ряд танцевальных комбинаций, она должна основываться на определенном музыкальном материале и отражать все особенности музыки, строиться по законам драматургии и включать в себя экспозицию завязку, развитие, кульминацию и развязку. В композиции следует разрешать рисунок танца и хореографический текст. И именно о рисунке танца, а также о формах пространственного построения и пойдет речь в этой работе.
д. каждая композиция включает в себя ряд танцевальных комбинаций, она должна основываться на определенном музыкальном материале и отражать все особенности музыки, строиться по законам драматургии и включать в себя экспозицию завязку, развитие, кульминацию и развязку. В композиции следует разрешать рисунок танца и хореографический текст. И именно о рисунке танца, а также о формах пространственного построения и пойдет речь в этой работе.
Рисунок танца – это расположение и перемещение танцующих по сценической площадке. Если мы будем следить за танцующими, обращая внимание не на их движения, а лишь на перемещения по сценической площадке и зафиксируем эти передвижения на листе бумаги, то тем самым мы зафиксируем рисунок танца.
Рисунок танца, как и вся композиция, должен быть подчинен основной идеи хореографического произведения, эмоциональному состоянию героев, которое проявляется в их действиях и поступках. Следует сказать, что рисунок танца и танцевальный текст неразрывно связаны.
Рассмотрим каждый элемент пространственного строения танца отдельно, а затем попытаемся выяснить, как они взаимно действуют в хореографическом произведении.
Рисунок массового танца.
Рисунком массового танца можно считать всякое перемещение группы танцующих в организованном, фиксированном построении. Роль рисунка в хореографическом произведении чрезвычайно важна. Ясность содержаний, доходчивость и впечатление, которое танец производит на зрителей. По словам Н. В. Смирнова «Рисунок организует движение танцующих, систематизирует их. Различные построения и перестроения исполнителей в сценическом танце оказывают на зрителей определенное психическое воздействие».
Это не просто формальное перемещение исполнителей в организованном фиксированном построении. Рисунок массового танца – это динамическое поле чувств и взаимоотношений танцующих, определяющих суть выражаемого образа.
Определенными элементами рисунка массового танца являются:
Поле рисунка – то пространство, в пределах которого разворачивается действие танца. Оно позволяет судить о ходе взаимодействий и взаимоотношений танцующих. Например, все исполнители, держась за руки, двигаются по замкнутому кругу. А один из танцоров находится в стороне от общего круга и делает какое-то другое движение, казалось бы, он не участвует в коллективном взаимодействии, ни каким образом не связан с другими исполнителями. Но, поскольку он присутствует в поле рисунка, то естественно, его положение вносит свою интонационную пластическую лепту в общую картину взаимоотношений.
Вообще поле рисунка массового танца может иметь разные контуры, внешние очертания. Оно может быть простым и сложным, симметричным и ассиметричным, одноплановым и многоплановым, выражающее соответствующие чувства и настроения. Последовательность изменения контура поля имеет свою лампу развития, как в сторону нарастания активности сценического взаимодействия и взаимоотношения танцующих, так и в сторону спада.
Последовательность изменения контура поля имеет свою лампу развития, как в сторону нарастания активности сценического взаимодействия и взаимоотношения танцующих, так и в сторону спада.
Центр рисунка массового танца это узел взаимодействий и взаимоотношений танцующих. Это то в рисунке, что несет в себе основное содержание и проявляет это содержание. И это то в рисунке, на что в первую очередь нацелены действия и отношения исполнителей. То, что притягивает к себе внимание зрителей. Не случайно центр рисунка нередко называют точкой восприятия.
Секретом любого рисунка массового танца является смена его центра. Такая смена наполняет танец богатством содержания. «Читать» танцевальный рисунок – значит, в первую очередь увидеть и определить его центр, трактовать суть происходящих взаимодействий и взаимоотношений исполнителей. Например, в хороводе «Сударушка» Н.С. Надеждина строит выход девушек по диагонали с левого верхнего угла. На авансцене, почти у первой правой кулисы, каждая из сударушек поочередно выходит поклониться зрителям, а затем, обойдя кружок, снова становится в ряд. Это и есть центр данного диагонального рисунка. Балетмейстер как бы специально выделяет это место, в рисунке нацеливая на него внимание зрителей, получается «точка восприятия».
Это и есть центр данного диагонального рисунка. Балетмейстер как бы специально выделяет это место, в рисунке нацеливая на него внимание зрителей, получается «точка восприятия».
Особую значимость для выражения, а затем и для «зрительного прочтения» картины чувств и взаимоотношений танцующих, имеют такие элементы, как количество исполнителей рисунка танца, взаимосвязи между ними.
Особый вопрос, особая проблема – развитие разработка рисунка массового танца.
Танец – это искусство, в котором художественные образы создаются непрерывной сменой пространственного строения. Взаимодействие и взаимоотношения исполнителей в нем разворачиваются и развиваются не только в пространстве, но и во времени. И в этом смысле любой танцевальный рисунок является продолжением предыдущего действия и началом последующего.
Простая повторность – принцип, многократно повторяющихся фигур, рисунков, движений, пространственных переходов в танце. Именно через повторность, и только через нее, в сознании зрителей закрепляется хореографический образ.
Именно через повторность, и только через нее, в сознании зрителей закрепляется хореографический образ.
Повторность с изменением – в большинстве русских народных танцев часто повторяются отдельные рисунки, фигуры, но с некоторыми изменениями в конце. Например, в русских кадрилях, в парно-массовых танцах очень часто в одной фигуре «гуляют» (т.е. пляшут, импровизируют) молодцы, а затем эту же фигуру повторяют девушки. Они тоже пляшут, импровизируют. Но при этом начало фигуры у юношей и у девушек одинаковое, а окончание у тех и других разное.
Надо сказать, что все выше перечисленные принципы используются обычно в комплексе. Но, по всей видимости, могут встретиться отдельные примеры, в которых будет главенствовать какой-либо один из них.
Мизансцена:
(m: se en scene) с франц. как «постановка на сцене».
В хореографии мизансцену можно охарактеризовать как статичное расположение нескольких танцоров на сценической площадке, которое выявляет, отражает, показывает суть происходящих между ними взаимодействий и взаимоотношений.
Мизансцена не является доминирующим средством в хореографическом произведении. Статичные расположения танцоров по сценической площадке, как правило, является кратковременным явлением, и служат дальнейшим связующим звеном в танцевальном действии. Хотя, надо отметить, что в композиции любого танца используются мизансцены, позировки отдельных танцоров, исполняющие роль, если можно так выразиться «статичных движений».
Внутри групповой мизансцены у каждого отдельного исполнителя своя мизансцена тела, свое статичное положение.
Это своего рода жест, вытекающий из осмысленного и выразительно выполненного действия, но такой жест, в котором принимает участие все тело танцовщика. В наше время мизансцена тела становится все более изменчивой. Она может обогащаться стилистическими признаками народной хореографии; может наполняться признаками образного и очеловеченного подражания птице, сказочной ящерице; цветку, драгоценному камню; может пользоваться некоторыми приемами спорта, если это понадобится балетмейстеру по ходу сценического действия.
В танце встречаются различные мизансцены тела: (en face), в полуповорот по диагонали (epaulment), спиной и в профиль к зрителю. Положение epaulment тесно связано с понятием cro:sce, effacee, ecartee. Понятие cro:sce означает скрещенность линий в позе танцующего. Понятие effacee означает развернутое положение фигуры без скрещенных линий. Поза ecartee может быть как в положении epaulment cro:sce, так и в положении epaulment effacee.
План со спины и профиль в танцевальной мизансцене тела употребляются редко. Хотя профильный силуэт, если еще подсвеченный с заднего плана сцены, хорошо «читается» зрителем.
Обратимся теперь к танцевальной мизансцене как групповой расположение исполнителей на сценической площадке.
В хореографии немного произведений, в которых используется групповое мизансценирование как ведущее средство. Однако это не означает, что оно исчерпало свои возможности. Скорее наоборот. Танцевальная мизансцена таит в себе колоссальные изобразительные и выразительные возможности.
Мизансценирование нужно всегда интерпретировать с позиции развивающихся отношений между ними. Для того чтобы уметь «прочитывать» мизансцену, надо научиться разбирать ее структуру, знать слагаемые, из которых она состоит.
Как и в танцевальном рисунке, элементами мизансцены являются «поле», «центр», «количество лиц», «взаимосвязи между ними».
Поле мизансцены – пространство, в котором зафиксирован момент действий и взаимоотношений героев танца.
Центр мизансцены – это смысловой центр мизансцены, узел отображаемых взаимодействий, взаимоотношений ее героев, то, что главное в мизансцене, то, что в первую очередь привлекает внимание зрителей.
Количество лиц, занятых в мизансцене – важный элемент, определяющий мобильность мизансцены, ее зрелищность содержательность.
Взаимосвязи между лицами, занятыми в мизансцене – это самый сложный и самый ответственный элемент. Сложность его в реализации, а значит в предполагаемом зрительском «прочтении».
Сложность его в реализации, а значит в предполагаемом зрительском «прочтении».
Взаимосвязи между героями мизансцены материализуются в их пластике, поза, выражениях – словом во всем, что определяет понятие «мизансцена тела».
Пространственный переход.
Любое передвижение исполнителей от одного танцевального рисунка к другому, их перемещение от мизансцены к рисунку или к другой мизансцене, можно охарактеризовать как пространственный переход.
Данная характеристика определяет внешнюю сторону пространственного перехода. Внешняя сторона понятна. Это первое, что бросается в глаза зрителям. А что кроется за внешней стороной? Что происходит на самом деле при переходе исполнителей от рисунка к рисунку, от мизансцены к активному действию?
Возьмем, к примеру, хоровод «Березка» в постановке Н.С. Надеждиной. После выхода всех девушек, они идут парами, темп музыки замедляется, и встретившиеся пары склоняются, в поклоне начинается хоровод и следует первый переход: встретившиеся пары образуют пять кругов: четыре по углам, а один в центре. Второй переход, плавно переходящий в рисунок «Большой круг». Ведущие девушки в каждом кружочке выводят своих подруг на большой общий круг.
Второй переход, плавно переходящий в рисунок «Большой круг». Ведущие девушки в каждом кружочке выводят своих подруг на большой общий круг.
Как видно из описания, первый и второй переходы не равноценны. Первый длится в полтора раза меньше, чем второй. Первый является по существу переходом от мизансцены (поклон в начале) к танцевальному рисунку (пять кружков). Второй переход – это замена одного танцевального рисунка, другим рисунком. То есть в данном случае переход производит смену полей танцевальных рисунков.
Вместе с тем, в первом и втором переходах есть объединяющая их черта. Это то, что оба они меняют взаимосвязь девушек. Во втором переходе смена взаимоотношений танцующих.
Итак, сделаем вывод. При любом перестроении, будь то переход от рисунка к рисунку, от мизансцены к рисунку или другой мизансцене, меняется при этом поле, центр или количество лиц, главным остается одно, меняются взаимосвязи, взаимоотношения танцующих. И это заставляет видеть в пространственном переходе не просто технический прием изменения пространственного строения танца, а одно из немаловажных выразительных средств хореографического произведения.
И это заставляет видеть в пространственном переходе не просто технический прием изменения пространственного строения танца, а одно из немаловажных выразительных средств хореографического произведения.
Рисунок сольного танца.
Если «мизансцена тела» это статичное положение танцора, то «рисунок сольного танца» определяется как перемещение танцора на сценической площадке. То есть один танцор в статичном положении создает «мизансцену тела», а в движении – «рисунок сольного танца». Рисунок сольного танца характеризует передвижение каждого отдельного исполнителя, в отличие от рисунка массового танца. У каждого исполнителя может быть свой рисунок танца внутри массового танца.
По мнению Ж.Ж. Новерра, рисунок сольного танца вбирает в себя тончайшие оттенки взаимоотношений и является своеобразной партитурой действия каждого отдельного персонажа, героя, образа. Поэтому «повторение по два-три раза одних и тех же положений» недопустимо, т.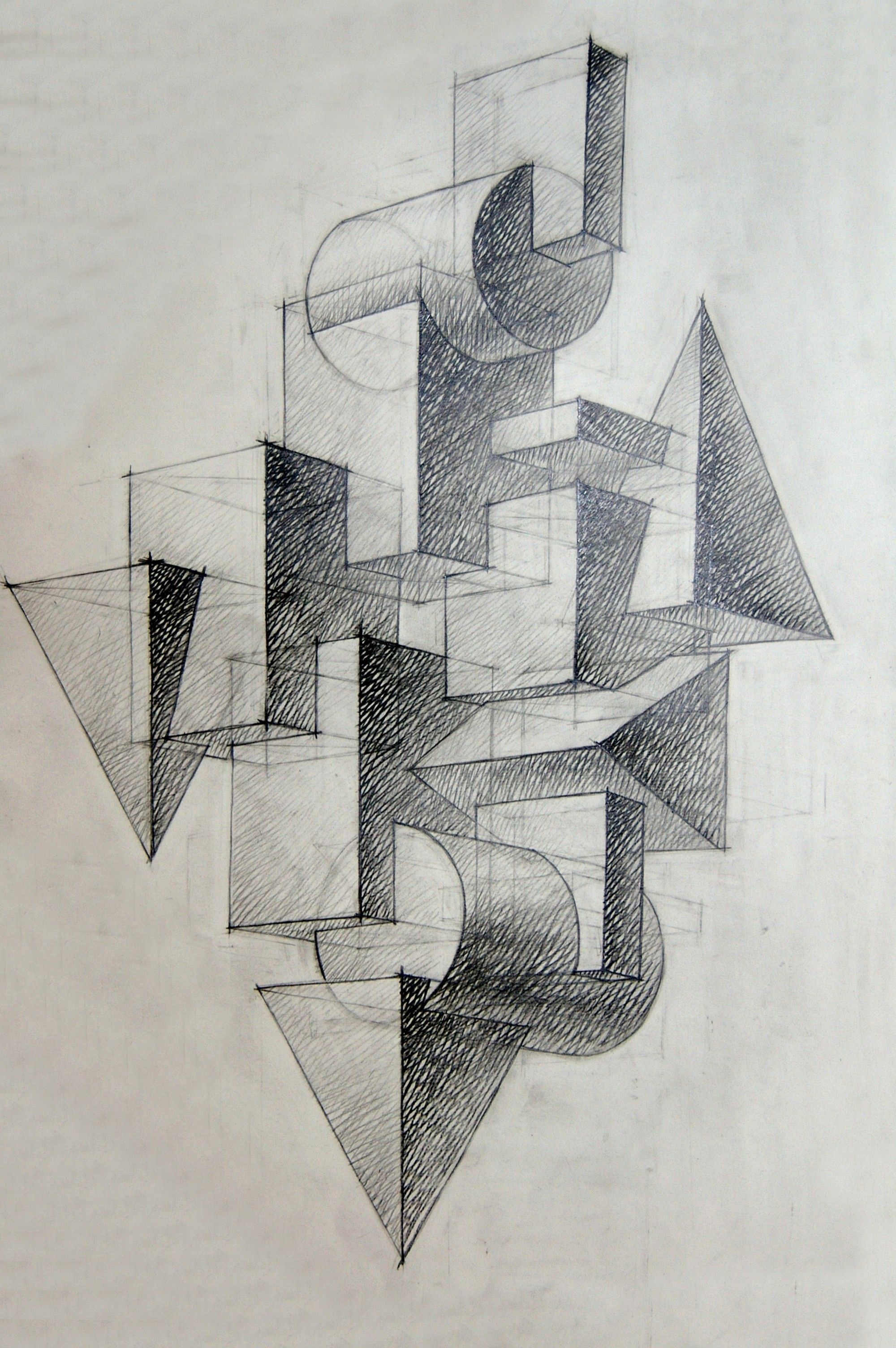 к. «подобный прием, лишь охлаждает действие».
к. «подобный прием, лишь охлаждает действие».
Многие балетмейстеры считают, что образ в танце создается исключительно за счет пластики и ритмике движений, мимике, мизансцен тела. И поэтому очень мало внимания уделяется рисунку сольного танца.
По словам О.Г. Тарасовой «Если рисунок пройден правильно, то он обладает такой самостоятельной образной выразительностью, что способен донести и характер, и смысл задуманного, даже если пластика еще не до конца разработана, сочинена. Если танец должен выразить образ гонимого ветром листа, оторвавшегося от дерева и стремящегося к нему, то не мелкие движения – трепет в руках или волнообразная координация корпуса – будут в первую очередь выражать этот смысл, а рисунок пространственных перемещений танцующего на планшете сцены, то удаляющегося, то приближающегося к воображаемому дереву.
Рисунок сольного танца определяется так же общим построением танцевального настроения. Здесь нельзя не согласиться с утверждением О. Г. Тарасовой, которая пишет: «Танец, выражающий ликование, и танец, выражающий печаль, скорбь».
Г. Тарасовой, которая пишет: «Танец, выражающий ликование, и танец, выражающий печаль, скорбь».
Рисунок фольклорного танца поражает своей связью с родной природой. Все те своеобразные черты: характер, пространства и т.д., течения и разливы рек, причудливые узоры цветов, красота лиственного леса на холмах и бесконечные степные дали – все это находит отражение в рисунках народных танцев. Эту народную традицию, передавать через рисунок массового танца продолжают в своем творчестве видные хореографы России.
При сочинении рисунка танца балетмейстер должен использовать все возможности, для того, чтобы добиться наибольшей выразительности, полнее раскрыть образ, характер, настроение героя. Рисунок танца должен развиваться логично, быть тесно связан с танцевальной лексикой, способствовать наиболее яркому выявлению на сцене танцевального текста.
Разнообразие и богатство рисунков танца никогда не должно быть самоцелью. Важно чтобы рисунок не отвлекал зрителя своей оригинальностью, а всей своей выразительностью способствовал пониманию основной идеи произведения, его образов.
Разнообразные узоры танцевальных рисунков доходчиво и зрелищно могут поведать о вещах людям, казалось бы, далеким от языка хореографического искусства.
В русских народных хороводах каждый танцевальный рисунок несет в себе определенную образную информацию. Например, спор, конфликт между противостоящими друг другу силами изображается линейными построениями. Классическим образом такого спорного действия, служит широко известный хоровод «А мы просо сеяли». В нем две группы танцующих под пение своих реплик поочередно, то наступают друг на друга, то отступают, выясняя отношения.
Однако если внимательно приглядеться к любому народному танцу, нетрудно заметить, что каждое построение и пространственное перемещение исполнителей в нем, выражает определенную идею, несет вполне конкретную обозначенность.
Сочиняя рисунок сольного танца, балетмейстер для каждого образа обязан находить свой индивидуальный пространственный рисунок. Все рисунки, должны составлять общую пространственную образную картину всей композиции в целом, которая должна восприниматься зрителем не только как живописная, но и как несущая, заключающая в себе образный смысл танца.
Все рисунки, должны составлять общую пространственную образную картину всей композиции в целом, которая должна восприниматься зрителем не только как живописная, но и как несущая, заключающая в себе образный смысл танца.
Образ
– как считает И.Г. Есаулов – это совокупность, неизбежных черт кого-либо или чего-либо, т.е. образ – некий символ.
Любой художник, режиссер или балетмейстер строит задачу средствами своего искусства, раскрыть перед зрителем образ, характер человека, создать атмосферу эпохи времени, о котором он рассказывает в своем произведении. Прежде чем начать сочинять, конкретные эпизоды, балетмейстер должен настолько влиться в представленный образ, чтобы научиться, не только думать его мыслями, но и разговаривать его языком.
Пространственные фигуры — виды, изображения, свойства с примерами решения
Пространственные фигуры:
Геометрические фигуры делятся на плоские и пространственные в зависимости от того, все или не все точки фигуры принадлежат одной плоскости.
Пространственные фигуры
Некоторые пространственные фигуры — призма (рис. 1), пирамида (рис. 2), цилиндр (рис. 3), конус (рис. 4), шар (рис. 5). Раздел геометрии, в котором изучаются плоские фигуры, называется планиметрией, а раздел, в котором изучаются пространственные фигуры, — стереометрией.
Ту или иную пространственную фигуру приходится изображать на плоскости листа в тетради или на плоскости доски. Соответствующий рисунок выполняют таким образом, чтобы он создавал то же впечатление, что и сама изображаемая фигура. При этом невидимые линии делают штриховыми.
На рисунке 6 изображены параллелограмм и треугольник которые пересекаются по отрезку Часть треугольника находится на параллелограммом часть — под ним. При этом часть четырёхугольника видна, а часть — не видна. Обращаем внимание на то, что точки и треугольника не принадлежат параллелограмму а значит, и его стороне
На рисунке 7 изображена треугольная пирамида которую пересекает плоскость по четырёхугольнику При этом у пирамиды невидимым является ребро а у сечения — его стороны и
Представление пространственной фигуры на рисунке называют изображением фигуры.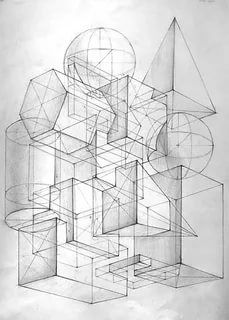
Важным классом пространственных фигур являются многогранники, под которыми понимают тела, ограниченные плоскими многоугольниками.
Эти многоугольники называются гранями многогранника, их вершины — вершинами многогранника, а стороны — рёбрами многогранника.
Отрезок, соединяющий две вершины многогранника, не принадлежащие одной грани, называется диагональю многогранника (рис. 8).
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой своей грани. На рисунке 9 изображён невыпуклый многогранник.
Б) Мы будем изучать простейшие выпуклые многогранники — призмы и пирамиды.
Призмой называется многогранник, две грани которого — равные угольники, а остальные граней — параллелограммы.
Равные грани-многоугольники призмы называют её основаниями, а остальные грани — боковыми гранями. Рёбра боковых граней, не принадлежащие основаниям, называются боковыми рёбрами (рис. 10).
Рёбра боковых граней, не принадлежащие основаниям, называются боковыми рёбрами (рис. 10).
В зависимости от количества сторон основания призмы отличают треугольную, четырёхугольную, пятиугольную и т. д. призмы. На рисунке 11 изображена шестиугольная призма.
Совокупность боковых граней призмы образуют боковую поверхность.
Площадь боковой поверхности призмы равна сумме площадей боковых граней.
Призмы разделяются на прямые и наклонные.
Прямая призма — призма, боковые грани которой являются прямоугольниками. Обычно, изображая прямую призму, её боковые рёбра проводят вертикально (рис. 12).
Призма прямая, если боковые рёбра перпендикулярны рёбрам основания призмы.
Призма наклонная, если боковые рёбра не перпендикулярны рёбрам основания призмы.
Прямая призма называется правильной, если её основания являются правильными многоугольниками.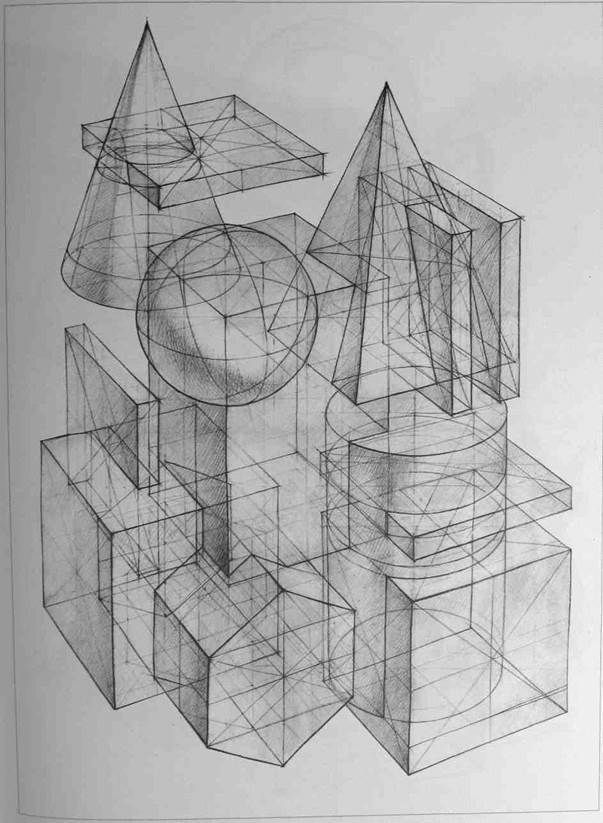
Призма, основаниями которой являются параллелограммы, называется параллелепипедом.
Параллелепипед, как и призма, может быть и прямым (рис. 13), и наклонным (рис. 14).
Прямой параллелепипед, основания которого являются прямоугольниками, называется прямоугольным параллелепипедом.
Все грани прямоугольного параллелепипеда являются прямоугольниками.
Три ребра прямоугольного параллелепипеда, сходящиеся в одной вершине, называются измерениями прямоугольного параллелепипеда.
Прямоугольный параллелепипед с равными измерениями называется кубом.
Все грани куба — равные друг другу квадраты.
В) Пирамидой называется многогранник, одна грань которого — многоугольник, а остальные являются треугольниками с общей вершиной.
На рисунке 15 изображена пирамида Многоугольник называют основанием пирамиды, треугольные грани — боковыми гранями, а общую вершину боковых граней — вершиной пирамиды. Обычно в записи обозначения пирамиды первая буква соответствует её вершине.
Обычно в записи обозначения пирамиды первая буква соответствует её вершине.
В зависимости от количества сторон основания пирамиды отличают треугольную, четырёхугольную, пятиугольную и т. д. пирамиды. Пирамида на рисунке 15 — пятиугольная, а на рисунке 16 — треугольная.
Пирамида, основание которой — правильный многоугольник, а отрезок, соединяющий её вершину с центром основания, перпендикулярен любой прямой, проведённой в плоскости основания через этот центр, называется правильной.
Высота боковой грани правильной пирамиды, опущенная из вершины пирамиды, называется апофемой пирамиды.
На рисунке 17 изображена правильная четырёхугольная пирамида отрезок — одна из её апофем.
Теорема 1. У правильной пирамиды равны её: а) боковые грани; б) апофемы.
Доказательство: Пусть — правильная пирамида и точка — центр её основания (рис. 18).
а) Поскольку треугольники и оба прямоугольные, имеют общий катет и равные катеты и то они равны. Поэтому равны и их гипотенузы и Аналогично доказывается, что другие боковые рёбра также равны
Поэтому равны и их гипотенузы и Аналогично доказывается, что другие боковые рёбра также равны
Боковые грани пирамиды — равнобедренные треугольники с равными боковыми сторонами. Основания этих треугольников также равны друг другу как стороны правильного многоугольника, который лежит в основании пирамиды. Поэтому боковые грани равны между собой по трём сторонам.
б) Поскольку боковые грани пирамиды равны между собой, то равны и их высоты, проведённые из вершины это значит, что все апофемы пирамиды равны.
Теорема 2. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра её основания и апофемы.
Доказательство: Пусть — правильная пирамида (см. рис. 18). Площадь её боковой поверхности состоит из площадей боковых граней, которые являются равными друг другу равнобедренными треугольниками с равными апофемами Поэтому
где — полупериметр основания пирамиды, — апофема пирамиды
Г) Ещё один класс пространственных фигур составляют тела вращения, к которым относятся цилиндр, конус, шар.
Цилиндром называется тело, полученное вращением прямоугольника вокруг одной из его сторон (рис. 19). При этом вращении одна сторона прямоугольника остаётся неподвижной, её называют осью цилиндра. Сторона, противолежащая оси, образует поверхность, которую называют боковой поверхностью цилиндра, а саму сторону — образующей цилиндра. Ещё две стороны прямоугольника при вращении образуют поверхности, которые являются равными кругами, эти круги называют основаниями цилиндра (рис. 20). На рисунке 21 дано изображение цилиндра.
Конусом называется тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов (рис. 22), который называют осью конуса. Второй катет описывает круг, который называют основанием конуса; неподвижную вершину треугольника, которая не принадлежит основанию, называют вершиной конуса. Гипотенуза при вращении образует поверхность, которую называют боковой поверхностью конуса, саму гипотенузу называют образующей конуса (рис. 23). На рисунке 24 дано изображение конуса.
23). На рисунке 24 дано изображение конуса.
Шаром называется тело, полученное вращением круга вокруг своего диаметра (рис. 25). При этом вращении окружность описывает поверхность, которую называют сферой (рис. 26). На рисунке 27 дано изображение шара.
Пример:
Найдите площадь боковой поверхности прямой четырёхугольной призмы, в основании которой лежит прямоугольник с измерениями 4 см и 5 см, а боковое ребро равно 6 см.
Решение:
Пусть — прямая призма; — прямоугольник, = 4 см, = 5 см, = 6 см (рис. 28).
— прямоугольники ( — прямая призма), поэтому
Ответ:
Боковая поверхность прямой призмы равна произведению периметра её основания и бокового ребра. Докажите это самостоятельно.
Пример:
Боковая поверхность правильной четырёхугольной пирамиды равна а её апофема — 12 см. Найдите площадь основания пирамиды.
Решение:
Пусть — правильная четырёхугольная пирамида; — апофема; = 12 см (рис.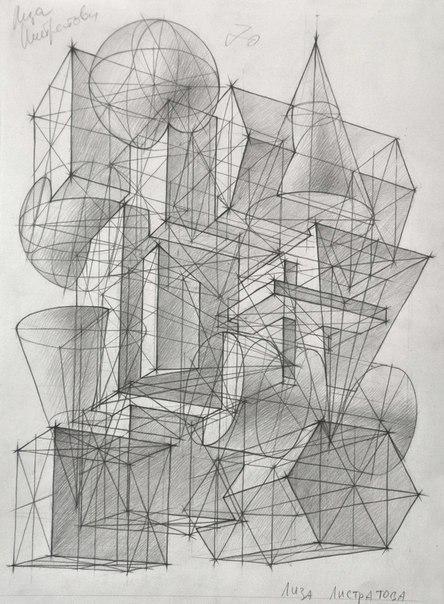 29).
29).
так как пирамида правильная, поэтому
Тогда так как — квадрат.
Ответ:
Площадь боковой поверхности пирамиды равна сумме площадей её боковых граней.
Пример:
Апофема правильной четырёхугольной пирамиды равна 30 см, а отрезок, соединяющий вершину пирамиды с центром основания, — 24 см. Найдите боковую поверхность пирамиды.
Решение:
Пусть — правильная четырёхугольная пирамида, — апофема, = 30 см, — центр основания = 24 см (см. рис. 29).
(см), так как (см), так как — квадрат, (см).
(см2),
так как пирамида правильная.
Ответ:
В правильной пирамиде отрезок, соединяющий центр основания пирамиды с основанием апофемы пирамиды, — радиус окружности, вписанной в основание пирамиды. Докажите это самостоятельно.
Пример:
Сторона основания правильной треугольной пирамиды равна см, а отрезок, который соединяет вершину пирамиды с центром основания, — 8 см.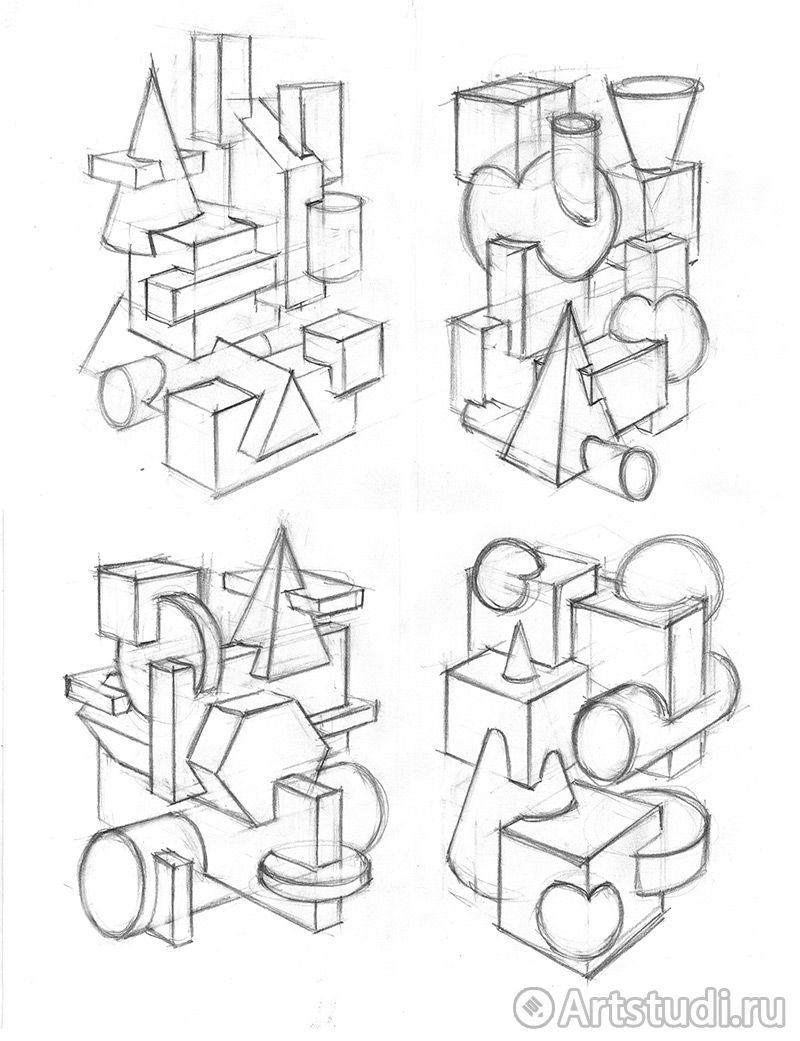 Найдите:
Найдите:
а) боковые рёбра пирамиды;
б) боковую поверхность пирамиды;
в) полную поверхность пирамиды.
Решение:
Пусть — правильная треугольная пирамида, см, — центр основания = 8 см (рис. 30).
a) (см), так как — радиус окружности, описанной около правильной треугольника
так как
так как — правильная треугольная пирамида.
б) Пусть — апофема. Тогда — середина (в и ).
(медиана, проведённая к основанию равнобедренного треугольника ), поэтому — радиус вписанной в окружности и (см).
(см), так как
(см),
так как — правильный.
В)
Ответ: а) см; б)
в)
Площадь полной поверхности пирамиды равна сумме площади боковой поверхности и площади основания
Изображение пространственных фигурЧтобы получить изображение призмы, достаточно построить многоугольник — основание призмы. Из вершин основания провести прямые, параллельные некоторой фиксированной прямой, и отложить на них одинаковые отрезки. Соединив концы этих отрезков, получим многоугольник — изображение другого основания призмы.
Соединив концы этих отрезков, получим многоугольник — изображение другого основания призмы.
Чтобы получить изображение пирамиды, достаточно построить изображение основания пирамиды, выбрать некоторую точку в качестве изображения вершины пирамиды и соединить её с вершинами многоугольника основания пирамиды.
Не каждый рисунок воспринимается нами как изображение реально существующей фигуры. Расхожее выражение «обман зрения» по сути является неверным. Глаза не могут обмануть нас, поскольку являются лишь промежуточным звеном между объектом и мозгом человека. Обман обычно возникает не из-за того, что мы видим, а из-за того, что неосознанно рассуждаем и непроизвольно ошибаемся.
Невозможные объекты представляют собой рисунки на двумерной плоскости, изображающие трёхмерные структуры, существование которых в реальном трёхмерном мире представляется невозможным. Классическим примером такой простой фигуры является невозможный треугольник Пенроуза (рис. 53). В этом треугольнике каждый угол сам по себе является возможным, но парадокс возникает тогда, когда мы рассматриваем его целиком. Стороны треугольника направлены одновременно и на зрителя, и от него, поэтому отдельные части треугольника не могут образовать реальный трёхмерный объект.
Стороны треугольника направлены одновременно и на зрителя, и от него, поэтому отдельные части треугольника не могут образовать реальный трёхмерный объект.
Наш мозг интерпретирует рисунок на плоскости как трёхмерную модель. Сознание задаёт «глубину», на которой находится каждая точка рисунка. Наши представления о реальном мире сталкиваются с противоречием, с определённой непоследовательностью, и приходится делать некоторые допущения: прямые двумерные линии интерпретируются как прямые трёхмерные линии; двумерные параллельные линии интерпретируются как трёхмерные параллельные линии; острые и тупые углы интерпретируются как прямые углы в перспективе; внешние линии рассматриваются как граница формы, которая крайне важна для восприятия определённого изображения.
Человеческое сознание сначала создаёт общий рисунок предмета, а затем анализирует его отдельные части. Каждый угол совместим с пространственной перспективой, но, соединившись, они образуют пространственный парадокс. Если закрыть любой из углов треугольника (рис. 54), то невозможность существования исчезает.
Если закрыть любой из углов треугольника (рис. 54), то невозможность существования исчезает.
Похожие фигуры явились источником вдохновения для многих творцов. График Маурицио Эшер создал ряд литографий (рис. 55), которые принесли ему известность художника-иллюзиониста.
Декоративные пространственные решения | Статьи компании МДМ-Лайт
Отдельным направлением нашей деятельности является производство декоративных и декоративно-функциональных осветительных решений на основе светотехнических полотен.
Световые потолки и стены, а также крупногабаритные светильники, изготавливаемые по этой технологии, сами по себе декоративны и самодостаточны, конечно, если знать, как их использовать.
World Class: декоративно-функциональные светильники. Ссылка на проект
Но особые декоративные свойства, индивидуальные свойства световым конструкциям придает дизайн: изменение формы, цвета, характера свечения, управление светом и использование светодинамических сценариев, нанесение графики или надписей, — все это возможно.
Рассмотрим основные возможности дизайна осветительного оборудования, изготовленного из светотехнического полотна.
На фото серия PENDO MAX
Цвет – один из важнейших инструментов, которым располагает дизайнер интерьеров. Осветительные системы из полотна предоставляют архитекторам и дизайнерам неограниченную палитру для творчества.
Говоря о цветных пространственных решениях, мы имеем ввиду декоративные, то есть без источника света (серия DECO) и декоративно-функциональные решения (цветные с источником света). На представленной выше визуализации можно увидеть, как сочетаются функциональные крупногабаритные светильники и такие же по форме декоративные элементы.
На фото реализация проекта освещения с PENDO MAX.
Поверхность полотна может иметь различные свойства: она может быть матовая, глянцевая или текстурированная.
Нанесение изображений непосредственно на световые натяжные конструкции (стены и потолки) – один из стремительно набирающих популярность трендов в дизайне интерьеров. Этот метод помогает воплощать любые идеи архитекторов в реальность.
На визуализации смелый потолок с принтом «под зебру».
Декоративные полотна – это не только яркие образы. Проявив фантазию легко найти элегантное решение, которое поможет подчеркнуть стиль интерьера или даже задать этот стиль.
Например, нанести на полотно авторский рисунок. Технология превращает поверхности помещения в холст художника и может быть рекомендована в качестве приема для дизайнерского интерьера, претендующего на оригинальность. Помимо индивидуального изображения на мембране этот вид световых конструкций дает возможность равномерной или точечной подсветки полотна (для выделения определенных зон рисунка).
Говоря о фирменном стиле, упомянем возможность нанесения надписей. А точнее логотипов. Стена за стойкой ресепшн, за барной стойкой или витрина магазина, не важно, световая стена с логотипом будет уместна всегда.
А точнее логотипов. Стена за стойкой ресепшн, за барной стойкой или витрина магазина, не важно, световая стена с логотипом будет уместна всегда.
Изображения на полотне крупногабаритного светильника могут стать изюминкой и офисных помещений. Они могут лаконично и ненавязчиво выразить стиль компании. Творческая атмосфера, создаваемая такими дизайнерскими решениями, несомненно, повлияет не только на комфорт сотрудников, работающих здесь, но и их мотивацию и результативность.
На фото проект освещения офиса LAMODA. Ссылка на проект.
Интересные перспективы открываются, если использовать диммированные светильники. К примеру, можно реализовать различные сценарии смены цветов и их насыщенности,причем управлять игрой света можно дистанционно – используя специальный пульт управления или сенсорную панель или создать автоматизированную систему. Возможности здесь безграничны – ротация цветов, ритм, мерцание, все что угодно,можно реализовать в соответствии с поставленными задачами.
На иллюстрации визуализация системы освещения ресторана со светильниками, декорированными принтами.
Источники света, светодиоды, могут быть разной мощности и цветовой температуры, могут управляться (диммироваться) по разным протоколам и менять цвет, если это RGB-светодиодные источники света (ленты или платы).
Сферы применения таких светильников, чаще всего, связаны с объектами досуга и культуры: торговыми центрами, кинотеатрами, развлекательными комплексами, а также с объектами сегмента HoReCa: ресторанами, кафе, барами,отелями и гостиницами.
Это понятно, ведь в этих сферах дизайнерам можно не ограничивать себя в идеях, как световые пространственные решения не ограничивают в реализации этих идей.
Несколько проектов с потолочными и настенными светехническими полотнами:
Другие материалы по теме:
Отправьте нам заявку и получите проект освещения бесплатно
Мы на выгодных условиях сотрудничаем с архитекторами и дизайнерами, сетевыми магазинами, строительными и девелоперскими компаниями, проектными организациями и дилерами. Свяжитесь с нами, и мы обсудим детали сотрудничества на особых условиях
Свяжитесь с нами, и мы обсудим детали сотрудничества на особых условиях
Спасибо, мы получили Ваше
обращение и перезвоним в
ближайшее время!
В рабочий день среднее время
ожидания не превышает 15 минут
Отправка заявки завершилась неудачей, пожалуйста, повторите попытку позднее
Понравилась статья? Поделитесь ей с друзьями!
Твитнуть
Поделиться
Плюсануть
Поделиться
Запинить
Теги: Осветительное оборудование, Освещение общественных пространств, Декоративное освещение
Упражнение 9 Пространственные взаимосвязи | Основы геоинформатики: практикум в ArcGIS
Скачать данные и файл отчета
Введение
Цель — научиться определять пространственную приуроченность двух явлений на основе процента взаимного покрытия их площадей (методом оверлея).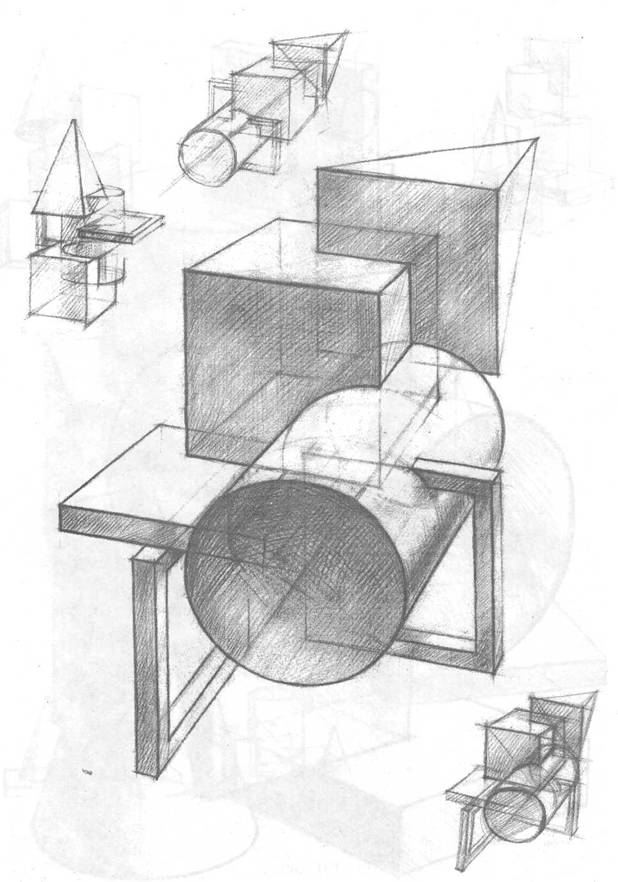
| Теоретическая подготовка | Оверлей пространственных объектов, геометрическое определение вероятности как отношения мер (площадей), соединение таблиц в реляционных базах данных, внешний и внутренний ключ соединения. |
| Практическая подготовка | Знание основных компонент интерфейса ArcGIS Desktop (каталог, таблица содержания, карта). Работы с базой пространственных данных. Настройка символики и подписей объектов. Владение базовыми ГИС-технологиями: пространственные и атрибутивные запросы, оверлей. |
| Исходные данные | База данных ГИС «Сатино». |
| Результат | Таблица взаимного покрытия площадей типов рельефа и подтипов почв. |
| Ключевые слова | Базовые технологии ГИС, оверлей, геометрическая вероятность. |
Контрольный лист
- Добавить на карту слои типов почв и рельефа, оформить их
- Произвести оверлей слоев
- Произвести слияние данных и соединение таблиц
- Подсчитать процент покрытия площадей
Аннотация
Задание посвящено знакомству с пространственным анализом на основе векторных данных. Векторная модель представляет объекты в виде отдельных геометрических фигур с набором атрибутов. Она является объектно-ориентированной и удобна для анализа формы, размеров объектов, их взаимной конфигурации в пространстве. Одним из широко используемых методов анализа на основе векторных данных является оверлей.
Векторная модель представляет объекты в виде отдельных геометрических фигур с набором атрибутов. Она является объектно-ориентированной и удобна для анализа формы, размеров объектов, их взаимной конфигурации в пространстве. Одним из широко используемых методов анализа на основе векторных данных является оверлей.
При оверлее происходит наложение двух или более слоев, в результате чего образуется их графическая композиция. Полученные участки наследуют атрибуты от каждого слоя. Эта операция базируется на стандартных отношениях множеств, таких как пересечение, объединение и симметрическая разность.
С помощью оверлея можно, например, установить, к каким генетическим типам рельефа приурочены различные типы и подтипы почв. В общем случае оверлей позволяет установить, какие комбинации объектов встречаются в пространстве. В задании предлагается исследовать методом оверлея взаимосвязь типов рельефа и типов и подтипов почв.
Визуальный анализ векторных слоев
В начало упражнения ⇡
В первую очередь при анализе данных следует провести их визуальную оценку, которая может натолкнуть на отыскание закономерностей во взаимном расположении объектов.
Скопируйте папку Ex10 из серверной директории в свой рабочий каталог с помощью Проводника.
Откройте ArcMap и в нем — окно Catalog.
Найдите базу геоданных Satino.gdb в своем каталоге Ex10 и перенесите на карту два тематических слоя: SoilTypes (Типы почв) и RelTypes (Типы рельефа) из группы Thematic.
Поместите слой Типы рельефа вниз таблицы содержания, откройте его свойства (двойным щелчком на названии) и перейдите на вкладку Symbology.
Выберите тип отображения Categories и в нем — режим Match to Symbols In a Style, который позволяет настроить символы в соответствии с заранее определенным стилем.
В качестве определяющего поля Value field выберите Тип рельефа. Далее нажмите кнопку Browse и выберите стиль Satino.style, лежащий в вашем каталоге Ex10.
 Нажмите кнопку Match symbols. Снимите флажок со строчки All other values. Окно свойств слоя должно принять вид, аналогичный представленному на рисунке. Нажмите ОК.
Нажмите кнопку Match symbols. Снимите флажок со строчки All other values. Окно свойств слоя должно принять вид, аналогичный представленному на рисунке. Нажмите ОК.Рис. 2. Настройка способа изображения в соответствии с предопределенным стилем
Настройте отображение слоя Типы почв в виде полигонов без заливки с ярко красной обводкой толщиной 1.5 пиксела. Чтобы сделать полигон без заливки, необходимо выбрать в меню Fill Color режим No Color. Нажмите ОК:
Рис. 3. Выбор режима отображения полигонов без заливки
Выберите инструмент идентификации и щелкните в пределах карты на любом полигоне.
Переведите инструмент идентификации в многослойный режим. Для этого в окне Identify раскройте верхний список Identify From и выберите пункт All layers. Попробуйте идентифицировать полигоны в разных участках карты, обращая внимания на информацию, которая отображается в окне идентификации.

Рис. 4. Переключение инструмента идентификации в многослойный режим
Проанализируйте совмещенное изображение границ типов почв и рельефа. Есть ли какие-то совпадения или подобия их рисунков в пределах речных долин, междуречий, малых эрозионных форм?
Теперь, когда данные исследованы визуально и путем идентификации, можно перейти к их анализу с помощью оверлея. Предварительно следует организовать рабочее пространство, чтобы результаты анализа хранились в структурированном виде и не смешивались с базовыми слоями.
Организация рабочего пространства
В начало упражнения ⇡
Поскольку в процессе оверлея будет создан новый слой (а затем еще и другие), возникает задача хранения вновь создаваемых данных. База геоданных Satino содержит базовые слои, и производные результаты лучше помещать в другое хранилище.
Сохраните документ карты в свой каталог Ex10 под именем Ex10_Оверлей.mxd
Откройте окно Catalog и обратите внимание на то, в нем наверху появился домашний каталог под именем Home — Фамилия/Ex10.
 . Раскройте его.
. Раскройте его.Домашний каталог — директория файловой системы, в которой хранится документ карты, с которым вы работаете в данный момент. Обычно в том же каталоге стараются хранить и сами данные (если они не берутся из внешней СУБД), чтобы избежать путаницы.
Щелкните правой кнопкой мыши по домашнему каталогу и выберите New > File Geodatabase для того, чтобы создать новую базу геоданных.
Назовите ее Ex10.gdb
Щелкните по Ex10.gdb правой кнопкой мыши и выберите пункт Make Default Geodatabase. Эта команда указывает программе, что все результаты обработки данных следует помещать в выбранную базу геоданных.
Оверлей слоев методом пересечения
В начало упражнения ⇡
Оверлей осуществляется в ArcGIS с помощью инструментов геообработки.
Геообработка (geoprocessing) в терминологии ArcGIS — это анализ и преобразование пространственных данных.
Доступ к инструментам геообработки осуществляется через окно ArcToolbox, где они сгруппированы по назначению. Некоторые наборы инструментов, такие как Spatial Analyst и 3D Analyst, являются дополнительными модулями ArcGIS, предназначенными для решения специализированного круга задач: растровый анализ, трехмерный анализ, сетевой анализ и т.д.
Откройте ArcToolbox с помощью красной кнопки на панели инструментов.
Раскройте группу инструментов Analysis Tools > Overlay. Здесь можно найти различные режимы оверлея.
Чем отличаются друг от друга режимы оверлея Intersect, Symmetrical Difference и Union?*
Запустите инструмент Intersect, который ищет геометрическое пересечение нескольких слоев. Изучите пояснительную иллюстрацию в правой части окна.
Перенесите из таблицы содержания в список Input features слой Типы почв, затем слой Типы рельефа
Обратите внимание на то, что система автоматически определила адрес и название выходного класса объектов в следующем виде:
D:/GIS/207/CAR/Петров/Ex10/Ex10. gdb/SoilTypes/Intersect
gdb/SoilTypes/IntersectЗамените SoilTypes_Intersect на SoilsRelief_Intersect, чтобы из названия было ясно, что с чем пересекается.
Параметр Join Attributes оставьте ALL. В этом режиме результат оверлея унаследует все поля из обоих слоев.
Диалог инструмента Intersect примет вид, аналогичный представленному на рисунке. Запустите вычисления, нажав кнопку ОК.
Рис. 5. Диалог инструмента Intersect
Дождитесь, пока в таблицу содержания добавится слой SoilsRelief_Intersect и переименуйте его в Комбинации почвы-рельеф. Для этого выделите слой в таблице содержания и нажмите F2 на клавиатуре, либо найдите пункт Rename в контекстном меню.
Поместите полученный оверлеем слой между слоями типов почв и рельефа, и настройте его отображение в виде полигона без заливки с черной обводкой толщиной 4 пиксела.
 Там, где границы совпадают с контурами типов рельефа, они будут черного цвета, а там где они совпадают с контурами типов почв, будет красная линия с черной обводкой.
Там, где границы совпадают с контурами типов рельефа, они будут черного цвета, а там где они совпадают с контурами типов почв, будет красная линия с черной обводкой.Раскройте атрибутивную таблицу слоя Комбинации почвы-рельеф.
Какие поля содержатся в атрибутивной таблице полученного слоя? Сравните его границы с границами двух исходных слоев.*
Слияние результатов пересечения с целью получения показателя пространственной связи
В начало упражнения ⇡
Поскольку каждый полигон в оверлейном слое содержит значение типа/подтипа почвы и типа рельефа, появляется возможность установить приуроченность типов и подтипов почв к определенным типам рельефа.
Чтобы подсчитать долю каждого типа рельефа в площади каждого подтипа почв, необходимо просуммировать площади каждой их уникальной комбинации. Например, дерново-карбонатные выщелоченные почвы (Д-в-к) на крутых эрозионных склонах встречаются в пределах Сатинского полигона в виде 6 разрозненных участков, имеющих некоторую суммарную площадь. Эта площадь, деленная на суммарную площадь почв подтипа Д-в-к даст вероятностный критерий приуроченности почв Д-в-к к крутым эрозионным склонам. То же самое касается остальных комбинаций подтипов почв и типов рельефа.
Эта площадь, деленная на суммарную площадь почв подтипа Д-в-к даст вероятностный критерий приуроченности почв Д-в-к к крутым эрозионным склонам. То же самое касается остальных комбинаций подтипов почв и типов рельефа.
С точки зрения рабочих процессов ГИС, операцию следует разбить на 5 шагов:
подсчет суммарной площади каждой комбинации подтипа почв и типа рельефа;
подсчет суммарной площади каждого подтипа почв;
добавление поля, в которое будет записана процентная доля;
соединение таблиц комбинаций и подтипов почв по названию подтипа почв;
деление площади комбинации на площадь подтипа почв и запись результата в соответствующее поле.
Объединение разрозненных объектов, обладающих одинаковым набором атрибутов, осуществляется с помощью операции слияния (Dissolve). Причем, если объекты примыкают друг к другу, граница между ними будет стерта, а если объекты разнесены в пространстве, на выходе получится сложный составной объект (Multipart feature), состоящий из нескольких полигонов.
Слияние — это один из методов генерализации.
Подсчет суммарной площади каждой комбинации подтипа почв и типа рельефа
В начало упражнения ⇡
Откройте в ArcToolbox инструмент геообработки Data Management Tools > Generalization > Dissolve. Изучите пояснительный рисунок в правой части окна интерфейса.
Выберите в качестве значения параметра Input Features слой Комбинации почвы-рельеф
В списке Dissolve Fields следует отметить поля SoilType, SoilSubtype и RelType, тем самым можно будет найти все уникальные комбинации подтипов почв и типов рельефа.
Поле SoilType необходимо отметить для того, чтобы в таблице результирующего слоя сохранилась информация о типах почв. Это не повлияет на сам результат, поскольку количество комбинаций типа и подтипа почв равно количеству самих подтипов.
Введите название выходного класса SoilsRelief_Intersect_Dissolve.
 Диалог инструмента Dissolve примет вид, аналогичный представленному на рисунке ниже.
Диалог инструмента Dissolve примет вид, аналогичный представленному на рисунке ниже.Рис. 6. Инструмент Dissolve, выполняющий слияние объектов по набору атрибутов
Остальные параметры оставьте по умолчанию и нажмите ОК.
После того как результат появится в таблице содержания, назовите полученный слой Слияние комбинаций почвы-рельеф.
Отключите этот слой в таблице содержания.
Подсчет суммарной площади каждого подтипа почв
В начало упражнения ⇡
Запустите инструмент Dissolve еще раз.
Выберите в качестве Input Features слой Типы почв.
В списке Dissolve fields выберите поля SoilType и SoilSubtype.
Введите название выходного класса SoilTypes_Dissolve.
Остальные параметры оставьте по умолчанию и нажмите ОК.

Назовите полученный слой Слияние подтипов почв. В данном слое в результате операции слияния каждый подтип почв будет представлен единственным объектом, а в его поле Shape_Area будет записана суммарная площадь данного подтипа
Отключите этот слой в таблице содержания.
Добавление нового поля для результирующих значений
В начало упражнения ⇡
Откройте таблицу слоя Слияние комбинаций почвы-рельеф.
Выберите в окне таблицы пункт меню Table Options > Add Field…
В диалоге введите название поля Percent.
Выберите тип поля Float (с плавающей точкой). Оставьте остальные параметры по умолчанию и нажмите ОК.
Соединение таблиц по названию подтипа почв
В начало упражнения ⇡
Для расчета пространственной взаимосвязи необходимо поделить площадь каждой комбинации на площадь соответствующего подтипа почв. Эти площади находятся сейчас в разных таблицах — Слияние подтипов почв и Слияние комбинаций почвы-рельеф. Их можно соединить по полю Подтип.
Эти площади находятся сейчас в разных таблицах — Слияние подтипов почв и Слияние комбинаций почвы-рельеф. Их можно соединить по полю Подтип.
Соединение таблиц (table join) — операция, в результате которой к одной таблице временно добавляются столбцы из другой таблицы. Чтобы установить соответствие между строками исходной и присоединяемой таблицы, необходимо иметь в каждой таблице поле с общими для них значениями. Например, это может быть числовой код объекта или, как в нашем случае, подтип почв.
Перейдите в контекстное меню слоя Слияние комбинаций почвы-рельеф и выполните команду Joins and Relates > Join. Внимательно изучите содержимое появившегося диалога.
Выберите Подтип в качестве поля 1, по которому будет делаться соединение:
Рис. 7. Диалог настройки соединения таблиц
Выберите Слияние подтипов почв в качестве присоединяемой таблицы 2.

Выберите Подтип в качестве поля, по которому будет присоединяться таблица Слияние подтипов почв.
Нажмите OK.
Что изменилось в атрибутивной таблице слоя Слияние комбинаций почвы-рельеф?
Вычисление результирующих значений
В начало упражнения ⇡
Откройте таблицу слоя Слияние комбинаций почвы-рельеф.
Щелкните правой кнопкой мыши на заголовке поля Percent, вызовите Field Calculator и введите туда указанное ниже выражение для подсчета процента площади. Вы можете просто набрать
100 *, а затем дважды щелкнуть по названию каждого поля в списке, чтобы не вписывать их вручную:100 * [SoilsRelief_Intersect_Dissolve.SHAPE_Area] / [SoilTypes_Dissolve.SHAPE_Area]Калькулятор поля (field calculator) используется для вычисления значений атрибутов.
 Вы можете, например, умножить значение одного поля на 100 и записать в другое, соединить несколько текстовых полей в одно предложение или просто скопировать значение одного поля в другое.
Вы можете, например, умножить значение одного поля на 100 и записать в другое, соединить несколько текстовых полей в одно предложение или просто скопировать значение одного поля в другое.Нажмите ОК. Посмотрите получившиеся значения в поле Percent.
Удалите соединение таблиц через контекстное меню слоя Слияние комбинаций почвы-рельеф командой Joins and Relates > Remove Joins > Remove All joins.
В атрибутивной таблице слоя Слияние комбинаций почвы-рельеф щелкните на любом поле правой кнопкой мыши и выберите команду Advanced Sorting.
Выберите в качестве первого поля Подтип и установите порядок сортировки Ascending (в сторону увеличения).
Выберите в качестве второго поля Percent и порядок сортировки Descending (в сторону уменьшения).
Растяните таблицу таким образом, чтобы хорошо было видно поле типа почв, поле подтипа почв, поле типа рельефа и поле Percent.

Нажмите ОК.
Отключите оба слоя слияния в таблице содержания.
Сохраните документ карты.
Получившаяся таблица отображает для каждого подтипа почвы типы рельефа в порядке уменьшения их доли в площади. Первая строка для каждого подтипа почвы устанавливает наиболее вероятный тип рельефа.
Какие почвы показывают наибольшую связь с определенным типом рельефа?
Отсортируйте таблицу только по убыванию значений в поле Percent (нажав дважды и еще раз дважды на нем) и выделите строки, в которых значение процента в поле Percent более 75.
Скомпонуйте окно приложения так, чтобы было видно целиком карту, а также выделенные в таблице строки, а также столбцы Тип, Подтип, Тип рельефа и поле Percent. Окно примет вид, аналогичный представленному на рисунке:
Рис. 8. Результаты оверлейного анализа
Снимок экрана №1 — Окно карты и результирующая таблица
Сохраните документ карты
Контрольные вопросы
В начало упражнения ⇡
Как с помощью оверлея можно получить показатель связи между двумя явлениями?
Если есть два полигона с совпадающими атрибутами, что произойдет с их площадью после выполнения операции Dissolve?
В чем суть операции соединения таблиц? Что должно быть в двух таблицах для их соединения?
Каким образом можно вычислить поле с использованием значения другого поля? Опишите последовательность действий.

Рисовать по клеточкам легкие картинки
Просмотров 12.3к. Обновлено
Рисовать по клеточкам картинки — значит поэтапно формировать пространственные представления и упражнять мелкомоторные навыки у детей.
Моторика и пространственные представления тесно связаны между собой: ведь даже для того, чтобы написать одну букву, ребенок должен мысленно ее увидеть, повернуть в пространстве и только после этого его мозг осуществляет целый комплекс действий, позволяющий связать руки с головой и написать нужный знак.
Сопровождение взрослым занятий по рисованию по клеточкам будет помогать ускоренному развитию ребенка: ведь то, что сегодня дошкольник сумеет сделать под руководством взрослого, завтра он сможет сделать и сам. Это именно то, что психологи называют «зоной ближайшего развития».
Рисовать по клеточкам животных
👉 Файл Рисовать по клеточкам картинки в формате PDF
Рисовать по клеточкам узоры и картинки
👉 Те же рисунки по клеточкам для рисования в формате PDF
Повтори рисунок по точкам
Необычное рисование картинки по точкам — задания, идеально дополняющие рисунки по клеточкам. Такие задания также развивают пространственное мышление, логику, мелкую моторику, математические способности.
Такие задания также развивают пространственное мышление, логику, мелкую моторику, математические способности.
👉 Задание Повтори рисунок по точкам в формате PDF
Зачем это нужно
Если ребенок сумеет выполнить все упражнения, то в школе ваш маленький ученик не будет писать зеркально буквы и цифры, не будет путать похожие буквы и цифры, будет понимать условия задач и видеть их решение, поймет разряды чисел и их значения, легко постигнет математические действия в столбик, соотношения чисел, понятия больше-меньше, ближе-дальше.
За все это главным образом отвечают пространственное воображение и мелкая моторика рук, развить которые можно, если рисовать по клеточкам.
Но список успехов, достигнутых благодаря развитому пространственному воображению далеко не ограничивается школьными. Здесь и умение правильно соблюдать дистанцию при общении, не задеть и не толкнуть другого в коллективных играх, успешность овладения всеми видами спорта, умение ориентироваться на местности.
Больше бесплатных заданий для раскрашивания и рисования по клеточкам ищите по тегу ПО КЛЕТОЧКАМ.
Пространственный рисунок, простое объяснение
Мы живем в трехмерном мире. И поэтому вам часто приходится обращать внимание на три измерения в графическом изображении, чтобы нарисовать мотив, который выглядит реалистично. Ибо всякий мотив обычно простирается в высоту, ширину и длину — в трех измерениях.
Если вы хотите изобразить это правильно, вы должны научиться правильно делать наброски и рисовать пространственно*. Основываясь на этом, вы сможете затем попрактиковаться в правильном рисовании в перспективе, чтобы правильно отображать трехмерные объекты.
Важное основное правило, если вы хотите рисовать пространственно: один и тот же объект всегда выглядит по-разному с разных ракурсов. Это происходит из-за формы и света/тени, которые описывают тело. Это относится как к неодушевленным предметам, так и к людям, животным или растениям.
Пример натюрморта с пространственным изображением
Укорочение перспективы
Перспективный ракурс — это эффект, который становится особенно отчетливым, когда мы смотрим прямо перед собой на объект, который простирается вдаль. Например, смотрим на вытянутую руку или ветку прямо спереди.
Например, смотрим на вытянутую руку или ветку прямо спереди.
Перспективный ракурс цилиндра с разных точек зрения
Рисунок ниже является еще одним хорошим примером перспективного ракурса. Здесь мы видим человека, раскинувшего руки в обе стороны. Наша точка зрения как наблюдателей сцены выбрана таким образом, что мы стоим почти в линию с вытянутыми руками. Таким образом, мы можем только догадываться о длине рук.Из-за этого нам как иллюстраторам довольно сложно реалистично нарисовать геометрию рук, включая одежду.
Пример перспективного ракурса
Моделью послужила следующая картина: Вечеря Господня в Эммаусе Караваджо
Графическая задача возникает из геометрической формы, которую принимают руки и рукава в этом ракурсе. Геометрия в данном контексте просто совершенно ненормальна, когда ее приходится рисовать. Причина: То, что нам нужно здесь нарисовать, противоречит нашему предубеждению, что руки, кисти и пальцы длинные и тонкие. Однако, с нашей точки зрения, эти части тела скорее принимают форму круга.
Однако, с нашей точки зрения, эти части тела скорее принимают форму круга.
Пример перспективного ракурса в натюрморте с зеленым луком
Кроме того, в этом ракурсе много «информации» сжато в очень малом пространстве. В нашем примере складки на рукаве сжаты до небольшой площади поверхности, которую мы можем видеть.
Ракурс перспективы также является эффектом, который можно легко изобразить с помощью техники перспективы точки схода.
Практика делает совершенным
Если вы хотите рисовать и раскрашивать пространство, вы найдете множество других советов и приемов на этом сайте. Некоторые из них также полезны для представления и рисования пейзажей и перспективного рисования. В разделе «Рисование пейзажей» вы найдете еще несколько уроков, посвященных тому, как рисовать в перспективе.
Пространственные чертежи | CIRCA Art Actuel
Пространственные рисунки представляет собой область крупномасштабных работ из дерева, которые изгибаются и изгибаются в, казалось бы, невозможных жестах.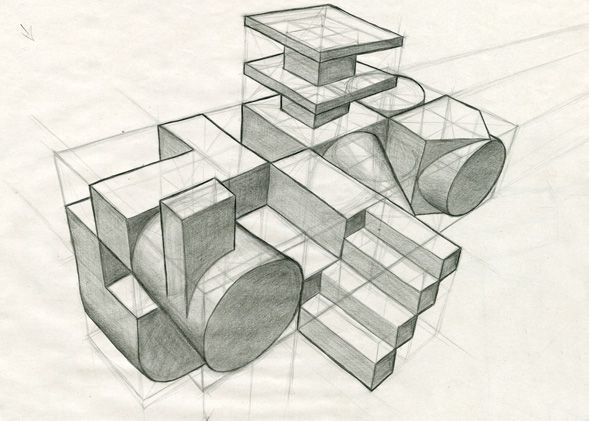 В то время как каждая автономная скульптура действует дискретно, большая собранная группа вызывает нечто более хореографическое. Линии каждого переходят друг в друга, и их связь с существующей архитектурой галереи используется либо как метод физической поддержки, либо задействована концептуальным образом. Домашние члены лиственных пород, которые делают эти необычные жесты, нуждаются в помощи, чтобы поддерживать навязанные им формы. Это объекты в процессе создания, визуально анимированные, как бы возникающие.Архитектура, механические вмешательства и включенные объекты — все намекает на временный характер оригинального жеста скульптуры и его зависимость от внешних сил. Эта сложность приоткрывает дверь к глубине практики и референтов в работе Эмили Хермант.
В то время как каждая автономная скульптура действует дискретно, большая собранная группа вызывает нечто более хореографическое. Линии каждого переходят друг в друга, и их связь с существующей архитектурой галереи используется либо как метод физической поддержки, либо задействована концептуальным образом. Домашние члены лиственных пород, которые делают эти необычные жесты, нуждаются в помощи, чтобы поддерживать навязанные им формы. Это объекты в процессе создания, визуально анимированные, как бы возникающие.Архитектура, механические вмешательства и включенные объекты — все намекает на временный характер оригинального жеста скульптуры и его зависимость от внешних сил. Эта сложность приоткрывает дверь к глубине практики и референтов в работе Эмили Хермант.
Простота форм приглашает к взаимодействию с минимализмом и формализмом. Американский минималист Роберт Моррис чаще всего упоминается в печатных обсуждениях ее работ из-за его утверждения о возможности формы быть найденной в процессе создания самой себя. Я бы предположил более прямую связь с пионером танца (и его бывшей возлюбленной) Ивонн Райнер с ее предложением артиста как деятеля — исполнителя задач — а также с поддерживающими перформансами Мирле Ладерманс Укелес, которые утверждали эти задачи не только как гендерный, но связанный с построением (политического) пространства и его потенциалом для более масштабных социальных изменений. Именно эта малоизвестная история имеет решающее значение для понимания того, как такой художник, как Хермант, обученный и воспитанный в текстильных традициях, приходит к такому производству.Хотя она утверждает, что ее практика по сути состоит из рисования, она глубоко укоренилась в возможном материальном проявлении. Ее обучение и привязанность отчасти опровергаются ее глубоким знанием материала — красный дуб, который она использует здесь, лучше всего понимать не как домашний строительный материал, а как целлюлозное волокно. Способность изменять древесину до такой степени возможна как благодаря ее корневому веществу, так и простым силам.
Я бы предположил более прямую связь с пионером танца (и его бывшей возлюбленной) Ивонн Райнер с ее предложением артиста как деятеля — исполнителя задач — а также с поддерживающими перформансами Мирле Ладерманс Укелес, которые утверждали эти задачи не только как гендерный, но связанный с построением (политического) пространства и его потенциалом для более масштабных социальных изменений. Именно эта малоизвестная история имеет решающее значение для понимания того, как такой художник, как Хермант, обученный и воспитанный в текстильных традициях, приходит к такому производству.Хотя она утверждает, что ее практика по сути состоит из рисования, она глубоко укоренилась в возможном материальном проявлении. Ее обучение и привязанность отчасти опровергаются ее глубоким знанием материала — красный дуб, который она использует здесь, лучше всего понимать не как домашний строительный материал, а как целлюлозное волокно. Способность изменять древесину до такой степени возможна как благодаря ее корневому веществу, так и простым силам.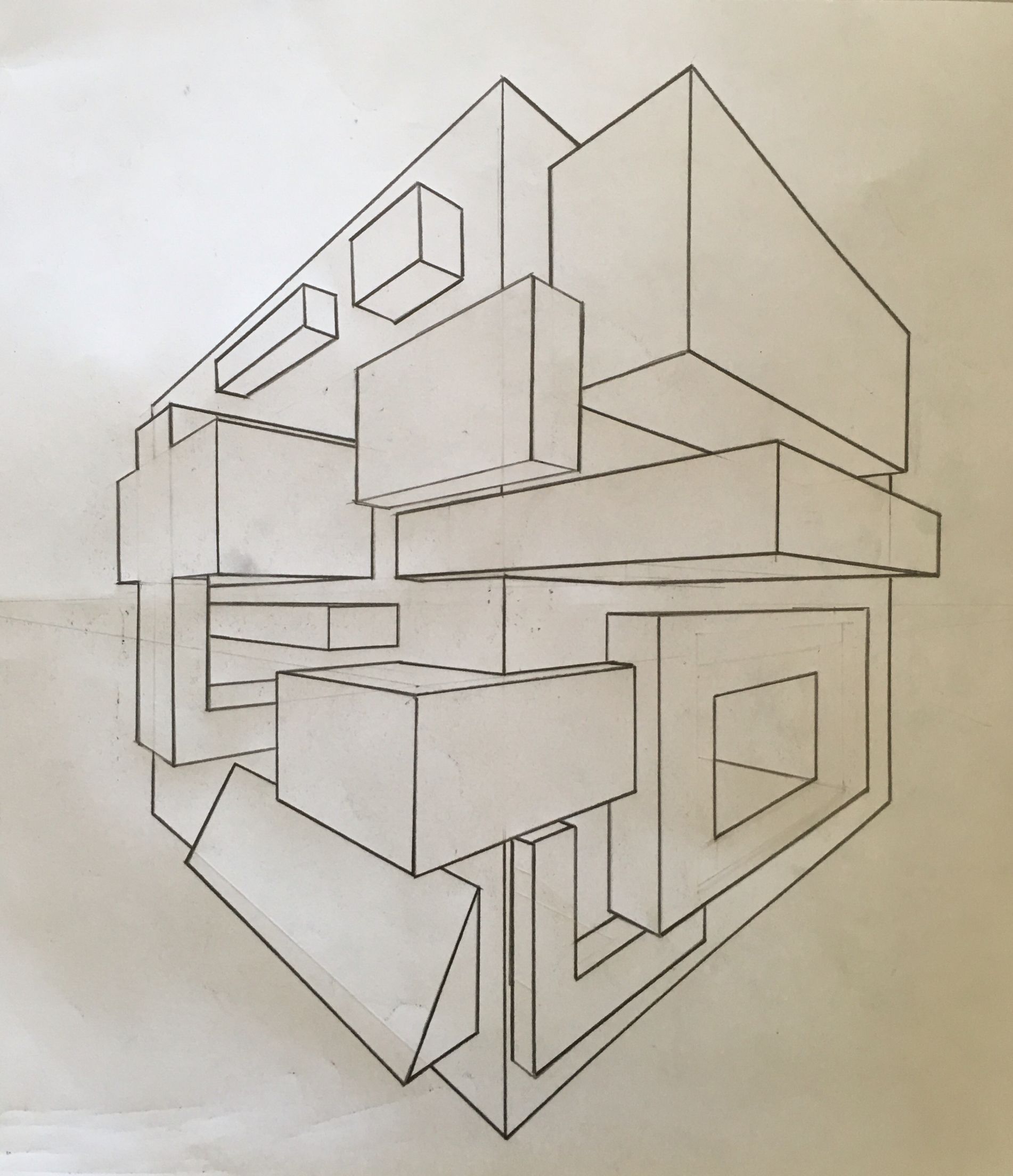 Тот факт, что Хермант использует существующий продукт для работы, а не сжимает или пропаривает древесину сама, показывает, что ее работа, по крайней мере частично, концептуальна.Ее задачи — воплощенное знание, дюшановский выбор и объединение материалов в пространстве.
Тот факт, что Хермант использует существующий продукт для работы, а не сжимает или пропаривает древесину сама, показывает, что ее работа, по крайней мере частично, концептуальна.Ее задачи — воплощенное знание, дюшановский выбор и объединение материалов в пространстве.
Эти методологии задействуют и объединяют неявные и потенциальные политические ассоциации каждой из их отдельных историй.
Формально произведение глубоко увлекательно, так как его поверхность переплетается со структурой, а отчасти потому, что его масштаб и манера поведения часто антропоморфны. Его производство колеблется между дискретными объектами формалистических и минималистских традиций и предположением о неадекватности этой истории, демонстрируемой их зависимостью от вмешательства повседневного объекта, чтобы остаться на месте.Я не могу не рассмотреть эту строчку из интервью 1968 года с Ивонн Райнер в связи со знаменитым высказыванием феминистки Одр Лорд, которая гласила: «Вы не можете разрушить дом хозяина, используя инструменты хозяина».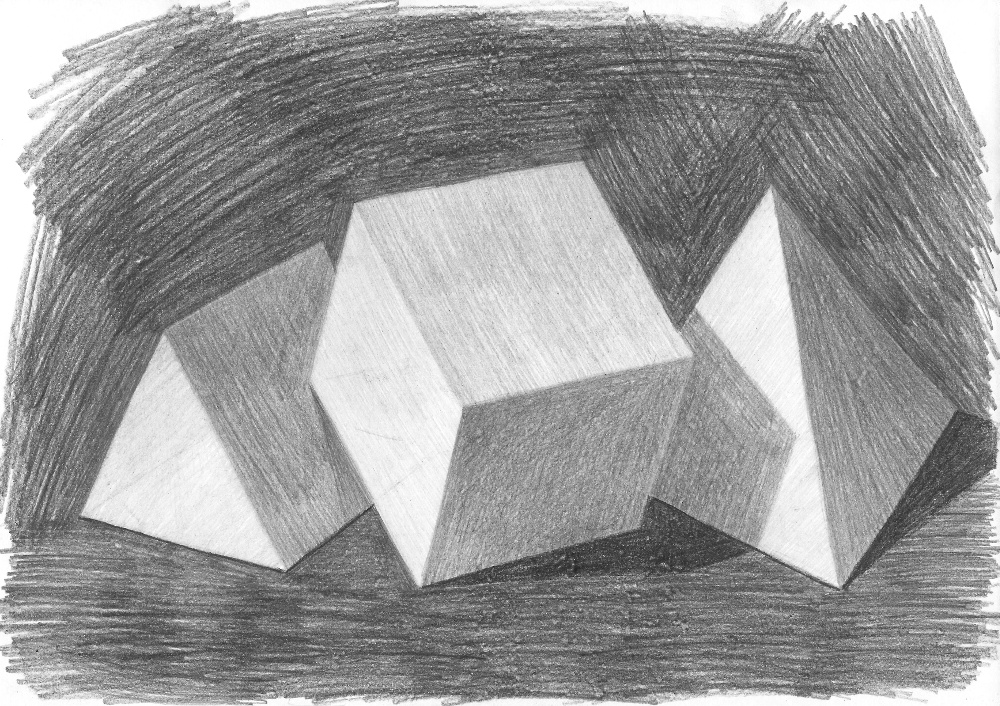 1 Райнер опроверг ее теорию, заявив: «Вы можете, если выставите инструменты». Я думаю, что проект Хермант состоит не в том, чтобы разобрать, а в том, чтобы усложнить, напрямую задействовать, а также вовлечь себя в долгую историю создания, а также встроить себя в более широкий канон. Это делается посредством столь же изящных и, казалось бы, невозможных жестов, посредством изображения становящихся форм, оно зарисовывается и предлагается, скрепляется опорными предметами, и подобно тому, как эти рисунки в пространстве обнажают орудия собственного изготовления, так и человек может пересмотреть только то, что строится.
1 Райнер опроверг ее теорию, заявив: «Вы можете, если выставите инструменты». Я думаю, что проект Хермант состоит не в том, чтобы разобрать, а в том, чтобы усложнить, напрямую задействовать, а также вовлечь себя в долгую историю создания, а также встроить себя в более широкий канон. Это делается посредством столь же изящных и, казалось бы, невозможных жестов, посредством изображения становящихся форм, оно зарисовывается и предлагается, скрепляется опорными предметами, и подобно тому, как эти рисунки в пространстве обнажают орудия собственного изготовления, так и человек может пересмотреть только то, что строится.
Джейк Мур
1 Идея Одре Лорд перефразирована Райнером в интервью, которое можно найти в: Yvonne Rainer Feelings Are Facts: A Life. (Кембридж, Массачусетс и Лондон: MIT Press, 2006). Оригинальная цитата: «Ибо инструменты хозяина никогда не разрушат дом хозяина. Они могут позволить нам временно победить его в его собственной игре, но они никогда не позволят нам осуществить подлинные изменения…» Встречается в исходном эссе Одре Лорд «Инструменты мастера никогда не разрушат дом мастера» в книге «Сестра Аутсайдер» (Трумансбург, Нью-Йорк: Crossing Press, The Crossing Press Feminist Series (1984)).
Эмили Хермант — междисциплинарный художник, чьи крупномасштабные скульптуры, инсталляции и рисунки исследуют темы общения, труда и гендера и проникнуты глубоким чувством воплощения. Хермант получила степень бакалавра искусств в Университете Конкордия в 2004 году и степень магистра иностранных дел в качестве попечителя за заслуги перед Школой Института искусств Чикаго в 2010 году. Ее работы выставлялись на национальном и международном уровнях, включая персональные выставки в Центре искусств Эванстона, Делавэрском центре. для современного искусства и Articule в Монреале; и групповые выставки в Университете Содружества Вирджинии, Миланском музее Триеннале в Италии и Музее искусств и дизайна в Нью-Йорке.Ее работы были рассмотрены в ArtSlant, Espace Sculpture, The Washington Post, Time Out Chicago и American Craft Magazine, и других. Эрман был удостоен грантов от Канадского совета по делам искусств, Совета искусств и литературы Квебека и Фонда Квебекских исследований в области общества и культуры, а также резиденций в ACRE, The Millay Colony for the Arts, The Vermont. Студио Центр и Студио ХХ. Хермант является приглашенным доцентом по программе «Волокна и материалы» на факультете студийного искусства в Университете Конкордия.
Студио Центр и Студио ХХ. Хермант является приглашенным доцентом по программе «Волокна и материалы» на факультете студийного искусства в Университете Конкордия.
Джейк Мур — художник, куратор и культурный деятель. Она имеет диплом по дизайну и строительству мебели Школы ремесел и дизайна Шеридан-колледжа, Оквилл, Онтарио, а также степень бакалавра искусств в области скульптуры и степень магистра искусств в области волокон и материалов Университета Конкордия в Монреале. Она широко выставлялась в Квебеке и Канаде, включая персональные выставки в парижской прачечной, галерее FOFA и Optica в Монреале, AXENÉO7 в Гатино, галерее Уолтера Филлипса в Банфе, Альберта, и на различных площадках в Виннипеге, Манитоба.
Улучшение пространственных способностей с помощью инженерного рисования
http://www.ex.ac.uk/cimt/ijmtl/ijabout.htm
International Journal of Mathematics Teaching and Learning
Апрель 2003 г.
суждения об идентичности пара стимулов (Pellegrino et al. , 1984). Действительно, стимул
, 1984). Действительно, стимул
вращается как целое тело.
Пространственная визуализация описывается как способность представлять вращения объектов или
их частей в трехмерном пространстве (Burnet & Lane, 1980) путем складывания и развертывания, например
(McGee, 1979).Манипуляции могут быть целостными, а также по частям
(Battista, Wheatley & Talsma, 1989), и движения должны быть воображаемыми (Clement &
Battista, 1992). Виды деятельности, используемые для измерения способности к пространственной визуализации, включают в себя
бланки, складывание бумаги и разработку поверхности (см. Приложение). Такие задачи часто требуют манипуляции, при которой происходит перемещение внутренних частей сложной конфигурации и/или складывание и развертывание плоских узоров (Pellegrino, et al., 1984). В кратком определении
пространственная визуализация — это умственная манипуляция и интеграция стимулов
, состоящих из более чем одной части или подвижных частей.
Как видно из определений, оба фактора связаны с некоторым умственным
манипулированием визуальными образами. Точно так же недавняя литература демонстрирует общее
согласие в том, что пространственная способность — это ментальное манипулирование объектами (Kovac, 1989) и их
частями в 2D и 3D пространстве.Тем не менее, тем не менее, различия между задачами 90 004 90 002, по-видимому, представляют собой два коррелирующих измерения производительности: скорость-мощность и сложность
(Pellegrino et al., 1984). В тестах на пространственные отношения от испытуемых требуется выполнить
заданий за определенное время (т.е. важна скорость), в то время как тесты на визуализацию относительно менее
ускорены (т.е. важна мощность). Задачи пространственных отношений, хотя и различаются по сложности среди
, включают менее сложные стимулы, чем задачи пространственной визуализации.Как видно из
, различия между факторами возникают на уровне задач с точки зрения сложности или
сложности и условий тестирования, таких как время. Поэтому можно сделать вывод, что
Поэтому можно сделать вывод, что
такое разделение зрительных способностей искусственно, а на самом деле оно одногранно. Таблица 1: Пространственные способности и их компоненты
Ассоциированный тест MGMP, Тест пространственной визуализации,
Тест первичных умственных способностей,
Minnesota Paper Form Board,
Тест дифференциальных способностей,
Французский справочный набор
Типовой тест
предмета 2D мысленное вращение, сравнение кубов,
3D мысленное вращение.Форма доска, складывание бумаги, поверхность
разработка, преобразование 2D-3D
Сложность Относительно простые задачи Относительно сложные задачи
Скорость-мощность Скорость важна Мощность важна
Пространственный поток: современные рисунки из коллекции Джоанн Гонсалес Хики — Грегори Алликарский художественный музей
Дата/Время
Дата (даты) — 29 мая 2018 г. — 23 сентября 2018 г.
10:00 — 18:00
Расположение
Музей искусств Грегори Алликара, Университетский центр искусств
Spatial Flux — выставка, организованная аспирантами факультета искусства и истории искусств Университета штата Колорадо. На выставке представлены работы на бумаге из коллекции Джоанн Гонсалес Хикки. Выставка исследует, как пространство создается и разрушается на двухмерной поверхности в процессе рисования или других методов создания меток. Spatial Flux стал возможен благодаря кураторской и учебной платформе, созданной вокруг коллекции Хики, известной как SYZYGY (syzygy-nyc.org).
На выставке представлены работы на бумаге из коллекции Джоанн Гонсалес Хикки. Выставка исследует, как пространство создается и разрушается на двухмерной поверхности в процессе рисования или других методов создания меток. Spatial Flux стал возможен благодаря кураторской и учебной платформе, созданной вокруг коллекции Хики, известной как SYZYGY (syzygy-nyc.org).
Этот проект щедро поддержан грантом от фонда Fort Collins Fort Fund города Форт-Коллинз и является частью серии резиденций критиков и художников, которая стала возможной благодаря FUNd в CSU.
Публикация
SPATIAL FLUX: Современные рисунки из коллекции Джоанн Гонсалес Хики
РЕЗИДЕНЦИЯ КРИТИКА И ХУДОЖНИКА
Пятница, 21 сентября 2018 г.
17:00
Театр танца | Университетский центр искусств
Стойка регистрации Учебный центр Роберта У. Хофферта
17:00 Танцевальные зарисовки: Атлас Джакони
В сотрудничестве с Эмили Морган и танцевальным факультетом CSU.
17:15 Мауро Джакони, artist talk
Работа Джакони связана со скульптурой, инсталляцией и, в основном, с рисунком, что служит сердцем всей его продукции и отправной точкой для создания пространственных вмешательств и образов, которые движутся через эстетику хаоса и процедурных исследований. . Архитектура, структура, память и окружающая среда — все это ключевые элементы в практике художника, которая фокусируется на предложении опыта, создающего напряжение между противоположными понятиями, такими как строительство и разрушение; рождение и смерть; заключение и свобода; глубина и поверхность; сон и пробуждение.
18:30 Приемная
границ | Чему нас учат пространственные искажения в рисунках пациентов после повреждения правого полушария мозга относительно изображения пространства в искусстве?
Введение
Одним из популярных различий во внутренних репрезентациях окружающего мира у людей является вербальное и зрительно-пространственное измерения (см. , например, Struiksma et al., 2009). Первый в основном зависит от левого полушария головного мозга, которое участвует в языковых процессах.Последнее в основном связано с активностью правого полушария головного мозга, которое играет важнейшую роль в пространственном познании, начиная от восприятия элементарных признаков, таких как расположение, цвет, ориентация линий или форма, до представления различных пространств (Девинский, 2009; Koch et al., 2013; Zaidel, 2013; Gainotti, 2014; за обзоры различных аспектов процессов, связанных с активностью правого полушария и нарушениями, вызванными поражением правого полушария). Однако эти два вида репрезентации тесно связаны: например, при чтении словесного описания природного пространства, как, например, описание леса Фонтенбло Гюставом Флобером (1821/1880) в его знаменитом романе « la vie». сентиментальный’ , мы можем спонтанно создать внутренний зрительный образ леса, что способствует усилению поэтического измерения повествования.Точно так же, глядя на картину маслом леса Фонтенбло, выполненную французским художником барбизонской школы Камилем Коро (1796/1875) в ту же эпоху, мы могли назвать и идентифицировать различные части пространства леса.
, например, Struiksma et al., 2009). Первый в основном зависит от левого полушария головного мозга, которое участвует в языковых процессах.Последнее в основном связано с активностью правого полушария головного мозга, которое играет важнейшую роль в пространственном познании, начиная от восприятия элементарных признаков, таких как расположение, цвет, ориентация линий или форма, до представления различных пространств (Девинский, 2009; Koch et al., 2013; Zaidel, 2013; Gainotti, 2014; за обзоры различных аспектов процессов, связанных с активностью правого полушария и нарушениями, вызванными поражением правого полушария). Однако эти два вида репрезентации тесно связаны: например, при чтении словесного описания природного пространства, как, например, описание леса Фонтенбло Гюставом Флобером (1821/1880) в его знаменитом романе « la vie». сентиментальный’ , мы можем спонтанно создать внутренний зрительный образ леса, что способствует усилению поэтического измерения повествования.Точно так же, глядя на картину маслом леса Фонтенбло, выполненную французским художником барбизонской школы Камилем Коро (1796/1875) в ту же эпоху, мы могли назвать и идентифицировать различные части пространства леса. изображение (см. рис. 1). Это различие между двумя типами эксплицитной пространственной репрезентации для восприятия — вербальной и зрительно-пространственной — также важно для клинического описания когнитивных нарушений, вызванных очаговым поражением головного мозга, особенно после повреждения правого полушария, где могут быть описаны различные нарушения.Эти недостатки проявляются в задачах рисования по памяти или по копии. Это могут быть пропуски, добавления или искажения частей объекта или всего объекта.
изображение (см. рис. 1). Это различие между двумя типами эксплицитной пространственной репрезентации для восприятия — вербальной и зрительно-пространственной — также важно для клинического описания когнитивных нарушений, вызванных очаговым поражением головного мозга, особенно после повреждения правого полушария, где могут быть описаны различные нарушения.Эти недостатки проявляются в задачах рисования по памяти или по копии. Это могут быть пропуски, добавления или искажения частей объекта или всего объекта.
РИСУНОК 1. Два типа эксплицитной (словесной и зрительно-пространственной) репрезентации пространства: пример леса Фонтенбло. Картина маслом La Forêt de Fontainebleau , автор Камиль Коро (1833 г.) — воспроизведена из Национальной галереи искусств, Вашингтон, округ Колумбия, с разрешения. Словесное описание (на французском и английском языках) Гюстава Флобера (1821/1880) в романе « la vie sentientale» 3ème partie chapitre III, стр. 483. «La diversité des arbres faisait un spectacle changeant. Les hêtres, à l’écorce blanche et lisse, entremêlaient leurs couronnes; des frênes courbaient mollement leurs glauques ramures; dans les cépées de charmes, des houx pareils à dubronse se hérissaient; puis venaient une file de minces bouleaux, inclinés dans des Attitudes élégiaques; et les pins, symétriques comme des tuyaux d’orgue, en se balançant continuellement, semblaient chanter». «Разнообразие деревьев представляло собой зрелище самого разнообразного характера.Буки с гладкой белой корой скручивались вершинами. Ясени мягко изгибали свои голубоватые ветви. В зарослях граба высились остролисты, жесткие, как бронза. Затем шел ряд тонких берез, склонившихся в элегических позах; и сосны, симметричные, как органные трубы, казалось, пели песню, покачиваясь взад и вперед».
«La diversité des arbres faisait un spectacle changeant. Les hêtres, à l’écorce blanche et lisse, entremêlaient leurs couronnes; des frênes courbaient mollement leurs glauques ramures; dans les cépées de charmes, des houx pareils à dubronse se hérissaient; puis venaient une file de minces bouleaux, inclinés dans des Attitudes élégiaques; et les pins, symétriques comme des tuyaux d’orgue, en se balançant continuellement, semblaient chanter». «Разнообразие деревьев представляло собой зрелище самого разнообразного характера.Буки с гладкой белой корой скручивались вершинами. Ясени мягко изгибали свои голубоватые ветви. В зарослях граба высились остролисты, жесткие, как бронза. Затем шел ряд тонких берез, склонившихся в элегических позах; и сосны, симметричные, как органные трубы, казалось, пели песню, покачиваясь взад и вперед».
Пространственное искажение после поражения правого полушария
Одна интересная особенность искажения информации касается восприятия размера (и объема) и средней линии (Milner and Harvey, 1995; Milner et al. , 1998). Эти искажения могут характеризоваться уменьшением размера, вплоть до полного опущения, левой части нарисованного объекта, что иллюстрируется предметно-центрированным (или аллоцентрическим) дефицитом левого пространственного игнорирования. Иногда наблюдается расширение правой стороны нарисованного объекта, когда также присутствуют продуктивные проявления с графическими персеверациями и/или гиперграфией (Rusconi et al., 2002; Ronchi et al., 2009). Эта размерная (и объемная) асимметрия может отражать сочетание двух основных расстройств синдрома одностороннего игнорирования: ипсильсионального смещения ориентации пространственного внимания и нарушения построения и/или исследования внутренних представлений о пространстве (Bisiach et al., 1994; Валлар, 1998 г.; Риччи и др., 2000, 2004; Роде и др., 2017).
, 1998). Эти искажения могут характеризоваться уменьшением размера, вплоть до полного опущения, левой части нарисованного объекта, что иллюстрируется предметно-центрированным (или аллоцентрическим) дефицитом левого пространственного игнорирования. Иногда наблюдается расширение правой стороны нарисованного объекта, когда также присутствуют продуктивные проявления с графическими персеверациями и/или гиперграфией (Rusconi et al., 2002; Ronchi et al., 2009). Эта размерная (и объемная) асимметрия может отражать сочетание двух основных расстройств синдрома одностороннего игнорирования: ипсильсионального смещения ориентации пространственного внимания и нарушения построения и/или исследования внутренних представлений о пространстве (Bisiach et al., 1994; Валлар, 1998 г.; Риччи и др., 2000, 2004; Роде и др., 2017).
В других случаях эта асимметрия размеров (и объема) может характеризоваться систематическим увеличением левой стороны объектов, нарисованных по памяти и по копии. Этот редко встречающийся дефицит наблюдается у пациентов с повреждением правого полушария, независимо от наличия одностороннего синдрома игнорирования, и получил название «гиперсхематии» (Rode et al. , 2006). В предыдущем исследовании мы сообщили о серии из 7 пациентов с повреждением правого полушария мозга, демонстрирующих это пространственное искажение для левого внеличностного пространства.Гиперсхематика может повлиять на рисование множества различных объектов, таких как ромашка, дерево, бабочка, человек, дом или сцена, объект целиком, а также некоторые его части (Роде и др., 2014). Гиперсхематия также может проявляться в трехмерных (моделирующих), зрительно-конструкционных задачах, усиливая в основном пространственный характер дефицита (Rode et al., 2008) (см. рис. 2, 3). Расстройство оставалось неизменным, когда пациентов просили рисовать с завязанными глазами (Rode et al., 2006). Гиперсхематия чаще всего контралатеральна поражению правого полушария, а что касается левого пространственного игнорирования (Ronchi et al., 2014). Больные не осознают наличие расстройства.
, 2006). В предыдущем исследовании мы сообщили о серии из 7 пациентов с повреждением правого полушария мозга, демонстрирующих это пространственное искажение для левого внеличностного пространства.Гиперсхематика может повлиять на рисование множества различных объектов, таких как ромашка, дерево, бабочка, человек, дом или сцена, объект целиком, а также некоторые его части (Роде и др., 2014). Гиперсхематия также может проявляться в трехмерных (моделирующих), зрительно-конструкционных задачах, усиливая в основном пространственный характер дефицита (Rode et al., 2008) (см. рис. 2, 3). Расстройство оставалось неизменным, когда пациентов просили рисовать с завязанными глазами (Rode et al., 2006). Гиперсхематия чаще всего контралатеральна поражению правого полушария, а что касается левого пространственного игнорирования (Ronchi et al., 2014). Больные не осознают наличие расстройства.
РИСУНОК 2. Асимметрия размеров (и объема) предметов в рисунках маргаритки (А) , гитары (В) и бабочки (С) и в лепке ромашки по памяти ( D) у пациентов с гиперсхематией слева (Rode et al. , 2014). Пациенты демонстрировали контралатеральное продуктивное поведение, характеризующееся систематическим левосторонним расширением рисунков и добавлением большего количества левосторонних деталей к нарисованному предмету, контралатеральному стороне поражения (маргаритке).
, 2014). Пациенты демонстрировали контралатеральное продуктивное поведение, характеризующееся систематическим левосторонним расширением рисунков и добавлением большего количества левосторонних деталей к нарисованному предмету, контралатеральному стороне поражения (маргаритке).
РИСУНОК 3. Асимметрия размеров (и объема) предметов на рисунках человека по памяти (А,Б) и при моделировании человека по памяти (С) у пациентов с гиперсхемией слева. У пациентов отмечалось левостороннее увеличение всех нарисованных или смоделированных частей тела: головы, рук, груди и ног.
Важно отметить, что когда пациентов попросили оценить две горизонтальные длины двух прямоугольников путем перцептивного сопоставления, сравнение результатов семи пациентов с левосторонней гиперсхемией и контрольной группы выявило только тенденцию к значимости.Однако анализ индивидуальных баллов пациентов показывает, что только у четырех из семи пациентов наблюдалось завышение оценок вправо; два пациента выступали в качестве контрольной группы участников с неврологическими нарушениями, а у одного пациента наблюдался противоположный паттерн, а именно переоценка влево. Нарушение перцептивной оценки латеральной протяженности не может объяснить гиперсхематию при рисовании, возможно, вместо этого это ассоциированный дефицит без прямой причинно-следственной связи с гиперсхематией.Наоборот, когда пациентов просили воспроизвести длину горизонтального сегмента (задача на удлинение линии), сравнение результатов семи пациентов и контрольной группы показало значительное чрезмерное удлинение линии влево, в то время как удлинение линии вправо было в пределах нормы (см. Рисунок 4).
Нарушение перцептивной оценки латеральной протяженности не может объяснить гиперсхематию при рисовании, возможно, вместо этого это ассоциированный дефицит без прямой причинно-следственной связи с гиперсхематией.Наоборот, когда пациентов просили воспроизвести длину горизонтального сегмента (задача на удлинение линии), сравнение результатов семи пациентов и контрольной группы показало значительное чрезмерное удлинение линии влево, в то время как удлинение линии вправо было в пределах нормы (см. Рисунок 4).
РИСУНОК 4. Задача расширения линии. Средние (SEM) LI семи пациентов с правым мозгом и шести участников контрольной группы для правых (R) и левых (L) расширенных линий (длина: 4, 6 и 8 см).Испытуемый должен был воспроизвести длину горизонтальной линии в двух условиях движения вправо и влево. В каждом случае конец линии был выровнен со средней сагиттальной плоскостью тела, и пациент воспроизводил воспринимаемую длину сегмента с расширением вправо или влево. Стимулы представляли собой двадцать четыре горизонтальные черные линии шириной 1 мм и восемь линий трех длин (4, 6 и 8 см). Длину отрезка, нарисованного каждым испытуемым в каждом испытании, измеряли с точностью до миллиметра.Для удлинения каждой линии влево был рассчитан следующий показатель индекса латеральности (LI): длина удлинения влево минус длина правосторонней линии/длина удлинения влево плюс длина правосторонней линии × 100. Для удлинения вправо Для каждого рисунка линии LI был равен: удлиненная длина вправо минус длина левосторонней линии/длина удлинения вправо плюс длина левосторонней линии × 100. Положительные/отрицательные значения LI указывают на чрезмерное/недостаточное удлинение. Средние значения LI были рассчитаны для двух направлений растяжения (вправо, влево) и для трех длин линии (4, 6 и 8 см).Все семь пациентов и шесть контрольных были протестированы. На рисунке показано, что 7 пациентов выполняют переразгибание влево на три длины линии (4, 6 и 8 см), в то время как показатели латеральности при разгибании вправо не отличаются от показателей контрольной группы.
Стимулы представляли собой двадцать четыре горизонтальные черные линии шириной 1 мм и восемь линий трех длин (4, 6 и 8 см). Длину отрезка, нарисованного каждым испытуемым в каждом испытании, измеряли с точностью до миллиметра.Для удлинения каждой линии влево был рассчитан следующий показатель индекса латеральности (LI): длина удлинения влево минус длина правосторонней линии/длина удлинения влево плюс длина правосторонней линии × 100. Для удлинения вправо Для каждого рисунка линии LI был равен: удлиненная длина вправо минус длина левосторонней линии/длина удлинения вправо плюс длина левосторонней линии × 100. Положительные/отрицательные значения LI указывают на чрезмерное/недостаточное удлинение. Средние значения LI были рассчитаны для двух направлений растяжения (вправо, влево) и для трех длин линии (4, 6 и 8 см).Все семь пациентов и шесть контрольных были протестированы. На рисунке показано, что 7 пациентов выполняют переразгибание влево на три длины линии (4, 6 и 8 см), в то время как показатели латеральности при разгибании вправо не отличаются от показателей контрольной группы.
Эти данные свидетельствуют о том, что гиперсхемия возникает, когда требуются операции (включая планирование и выполнение двигательных актов в левой части пространства). Более того, они предполагают, что это неспецифическое для модальности искажение пространственного представления может быть связано с латеральной анизометрией внутреннего представления пространства, а именно: пространственной среды с релаксацией влево (Rode et al., 2006, 2008). Эту релаксацию пространственного представления влево можно проиллюстрировать на этой картине маслом, сделанной пациентом с повреждением правого полушария (см. рис. 5, а также Rode et al., 2014).
РИСУНОК 5. Картина маслом на память о пациенте с повреждением правого мозга.
В более общем смысле, непропорциональное увеличение пространственного представления может также повлиять на телесное пространство. Первое описание дал французский отоларинголог Пьер Боннье (1905 г.) на основании клинического наблюдения за пациентами с вестибулярными расстройствами периферического происхождения (историческую справку см. в Vallar and Rode, 2009: см. также книгу Bonnier, 1905 г. «Le vertige»). ).Bonnier сообщил, что эти пациенты могут субъективно ощущать, что их тело или части тела непропорционально увеличены, и интерпретировал это расстройство как патологическое расширение пространственного представления тела или частей тела (гиперсхематия) (Vallar and Papagno, 2003). Эти ощущения также напоминают те, о которых сообщают пациенты с галлюцинациями макросоматогнозии или асоматогнозии, когда пациенты ссылаются на ощущение, что одна или несколько частей их тела непропорционально больше (Lhermitte and Tchehrazi, 1937; Frederiks, 1969; Denes, 1989) после пароксизмальных церебральных расстройств. такие как эпилепсия, мигрень и гипнагогические галлюцинации (Kew et al., 1998; Podoll and Robinson, 2002), соматосенсорная потеря после местной анестезии (Gandevia and Phegan, 1999; Paqueron et al., 2003) или поражение ствола мозга (Rode et al., 2012). Но, в отличие от гиперсхемации внеличностного пространства, пациенты всегда осознают свой дефицит, что предполагает различные лежащие в основе нейронные и функциональные механизмы и нервные процессы для нарушений, влияющих на представление о размере (и объеме) части внеличностного или личного пространства.
в Vallar and Rode, 2009: см. также книгу Bonnier, 1905 г. «Le vertige»). ).Bonnier сообщил, что эти пациенты могут субъективно ощущать, что их тело или части тела непропорционально увеличены, и интерпретировал это расстройство как патологическое расширение пространственного представления тела или частей тела (гиперсхематия) (Vallar and Papagno, 2003). Эти ощущения также напоминают те, о которых сообщают пациенты с галлюцинациями макросоматогнозии или асоматогнозии, когда пациенты ссылаются на ощущение, что одна или несколько частей их тела непропорционально больше (Lhermitte and Tchehrazi, 1937; Frederiks, 1969; Denes, 1989) после пароксизмальных церебральных расстройств. такие как эпилепсия, мигрень и гипнагогические галлюцинации (Kew et al., 1998; Podoll and Robinson, 2002), соматосенсорная потеря после местной анестезии (Gandevia and Phegan, 1999; Paqueron et al., 2003) или поражение ствола мозга (Rode et al., 2012). Но, в отличие от гиперсхемации внеличностного пространства, пациенты всегда осознают свой дефицит, что предполагает различные лежащие в основе нейронные и функциональные механизмы и нервные процессы для нарушений, влияющих на представление о размере (и объеме) части внеличностного или личного пространства. пространства.
пространства.
Пространственное искажение в живописи
Зрительно-пространственные способности правого полушария, особенно связанные с представлением размера (и объема) и срединной плоскости, играют решающую роль в процессах рисования и рисования у художников.Многие художники интересовались восприятием и изображением пространства от эпохи Возрождения до современности. В начале ХХ века (1907 г.) Жорж Брак и Пабло Пикассо создали новое художественное направление «кубизм», предложившее новый подход к восприятию и изображению пространства. Кубизм произвел революцию в живописи и скульптуре, а также повлиял на архитектуру, литературу и музыку. Их целью было деконструировать евклидово пространство и материализовать новые альтернативные представления.Это новое пространство кубистов характеризовалось заменой застывшей перспективы классических художников на подвижную перспективу. Открытие кубистов состояло в том, чтобы показать все объекты сразу со всех сторон, т. е. объединить несколько точек зрения (Paulhan, 1993).
Эта деконструкция пространства касалась симметрии размера (и объема) и представления средней линии плоскости. Это может быть проиллюстрировано картиной маслом под названием «Guitare et bouteille de marc sur une table» (Брак, 1930), которая представляет собой натюрморт, состоящий из нескольких предметов, размещенных на столе-пьедестале.В дополнение к удалению всех последовательных перспектив форма изображаемых объектов асимметрична; например, для гитары левая половина расширенной коробки увеличена, контрастируя с увеличением противоположной части розы и грифа (см. рис. 6А). Эти асимметрии размера и объема способствуют созданию искажений в представлении пространства и объекта и, таким образом, материализуют новое пространство, по словам самого Брака: « Что меня очень привлекало и что было основным направлением кубизма, так это материализация этого нового пространства. что я чувствовал.Так я стал делать в основном натюрморты, потому что в природе есть тактильное пространство, я бы сказал почти мануальное. Именно это пространство меня очень привлекало. Ибо это была первая кубистическая картина, искавшая пространство. « Г. Брак. (цит. по: Vallier, 1954).
Именно это пространство меня очень привлекало. Ибо это была первая кубистическая картина, искавшая пространство. « Г. Брак. (цит. по: Vallier, 1954).
РИСУНОК 6. Картины маслом Жоржа Брака. « Guitare et bouteille de marc sur une table» (1930) — Воспроизведено из Художественного музея Кливленда с разрешения (A) ; «Le duo» (1937) – Воспроизведено с фото Центра Помпиду, MNAM-CCI, Dist.RMN-Grand Palais/Philippe Migeat с разрешения (B) .
Г. Брак также применил эту новую материализацию пространства к телесному пространству. Картина маслом без названия «Le Duo», написанная в 1937 году, является иллюстрацией. Брак изобразил двух человек перед пианино. Тело женщины, сидящей перед роялем, бесформенно; телесное пространство разделено на две асимметричные половины: увеличенное левое полутело, если смотреть спереди и на свету, и сморщенное правое полутело, которое видно в профиль и в тени (см. рис. 6Б).Эта деконструкция-реконструкция телесного пространства и связанных с ним искажений позволила Жоржу Браку представить все возможные перспективы телесного пространства на одной плоскости со смещением средней оси тела. Это способствует созданию новой эстетической репрезентации телесного пространства, которую Брак будет углублять в своих последующих работах.
Это способствует созданию новой эстетической репрезентации телесного пространства, которую Брак будет углублять в своих последующих работах.
Интересно сравнить эти искажения с пространственными искажениями, производимыми пациентами с гиперсхематией.В этих двух априорно отдаленных ситуациях происходит потеря симметрии представления размера и объема и смещение представления средней оси. У Г. Брака эти искажения являются результатом творческого и сознательного процесса, а «гиперсхематические» — результатом бессознательного процесса, на который указывает неосведомленность больных о расстройстве. Тем не менее, в обоих случаях результат состоит в построении асимметричного представления пространства и средней линии тела.
Однако эти два типа искажений задают вопрос о нейронных процессах, лежащих в основе построения этих представлений о размере, объеме и телесном пространстве. Это результат баланса между процессами пространственного внимания двух полушарий. Здоровые участники, как правило, демонстрируют дискретное отклонение представительства срединной плоскости влево, отражая преобладание активности правого полушария головного мозга в контралатеральном пространстве. Это преобладание резко снижается после поражения правого полушария, вызывающего различные искажения внеличностного и телесного пространства (Irving-Bell et al., 1999; Валлар и Болоньини, 2014). Гиперсхематия представляет собой необычный пример искажения, влияющего на размер (и объем) и пространство. Нарушение чаще всего контралатерально поражению правого полушария, как левое пространственное игнорирование. Тем не менее, сообщалось о нескольких сообщениях об ипсилазионной правой гиперсхемации (Saj et al., 2011) и о ипсилозионной гиперэкстензии справа (Bisiach et al., 1998). В целом, эти искажения предполагают, что дисбаланс между пространственными процессами двух полушарий не ограничивается ипсильсиональной ориентацией пространственного внимания, которая может объяснять дефектные проявления пространственного пренебрежения, но также касается репрезентативного измерения (Bisiach et al., 1996; Савацци и др., 2007 г.; Манфредини и др., 2013; Валлар и Болоньини, 2014).
Это преобладание резко снижается после поражения правого полушария, вызывающего различные искажения внеличностного и телесного пространства (Irving-Bell et al., 1999; Валлар и Болоньини, 2014). Гиперсхематия представляет собой необычный пример искажения, влияющего на размер (и объем) и пространство. Нарушение чаще всего контралатерально поражению правого полушария, как левое пространственное игнорирование. Тем не менее, сообщалось о нескольких сообщениях об ипсилазионной правой гиперсхемации (Saj et al., 2011) и о ипсилозионной гиперэкстензии справа (Bisiach et al., 1998). В целом, эти искажения предполагают, что дисбаланс между пространственными процессами двух полушарий не ограничивается ипсильсиональной ориентацией пространственного внимания, которая может объяснять дефектные проявления пространственного пренебрежения, но также касается репрезентативного измерения (Bisiach et al., 1996; Савацци и др., 2007 г.; Манфредини и др., 2013; Валлар и Болоньини, 2014).
Подобные нейронные процессы могут работать во время художественного творчества, подтверждая идею о том, что одним интригующим аспектом «пространственного мозга» является его способность создавать неевклидовы представления внеличностных и телесных пространств. Это расширение левостороннего пространственного представления можно рассматривать как изменение внутренней функции измерения расстояний, также называемой в математике метрикой.Затем пациент представит непостоянную метрику справа налево, которая увеличит воспринимаемые расстояния в контрольной стороне. Бессознательно пациент равномерно распределяет свою картину в системе отсчета, расчет расстояний которой претерпевает градиент преобразования по правой/левой оси. По той же схеме художники-кубисты сделали бы добровольный выбор, основанный на более или менее сознательной оценке пространства, изменяя метрику своего рисунка локально на его элементах и, таким образом, производя множественные деформации в зависимости от положения на готовой работе аналогичным образом. как они делают, чтобы закодировать глубину в своих картинах.
Это расширение левостороннего пространственного представления можно рассматривать как изменение внутренней функции измерения расстояний, также называемой в математике метрикой.Затем пациент представит непостоянную метрику справа налево, которая увеличит воспринимаемые расстояния в контрольной стороне. Бессознательно пациент равномерно распределяет свою картину в системе отсчета, расчет расстояний которой претерпевает градиент преобразования по правой/левой оси. По той же схеме художники-кубисты сделали бы добровольный выбор, основанный на более или менее сознательной оценке пространства, изменяя метрику своего рисунка локально на его элементах и, таким образом, производя множественные деформации в зависимости от положения на готовой работе аналогичным образом. как они делают, чтобы закодировать глубину в своих картинах.
Раскрытие информации
Все авторы имеют полный доступ ко всем данным исследования и несут ответственность за целостность данных и точность анализа данных.
Вклад авторов
GR спроектировал полученную работу, проанализировал, сделал интерпретацию данных для работы и составил проект работы. Г.В. и Ю.Р. интерпретировали данные для работы и критически пересмотрели работу на предмет важного интеллектуального содержания. ЕК критически пересмотрел работу на предмет важного интеллектуального содержания.PR проанализировал данные для работы и критически пересмотрел работу на предмет важного интеллектуального содержания.
Заявление о конфликте интересов
Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Благодарности
Филипу Робинсону за помощь в написании.
Каталожные номера
Бисиах Э., Пиццемильо Л., Нико Д. и Антонуччи Г.(1996). Помимо одностороннего пренебрежения. Мозг 119, 851–857.
Академия Google
Бисиах Э. , Риччи Р. и Неппи Модона М. Н. (1998). Визуальное осознание и анизометрия представления пространства при одностороннем пренебрежении: панорамное исследование с помощью задачи на расширение линии. В сознании. Познан. 7, 327–355.
, Риччи Р. и Неппи Модона М. Н. (1998). Визуальное осознание и анизометрия представления пространства при одностороннем пренебрежении: панорамное исследование с помощью задачи на расширение линии. В сознании. Познан. 7, 327–355.
Реферат PubMed | Академия Google
Bisiach, E., Rusconi, M.L., Peretti, V.A., and Vallar, G. (1994). Оспаривание текущих счетов одностороннего пренебрежения. Нейропсихология 32, 1431–1434.
Реферат PubMed | Академия Google
Боннье, П. (1905). L’асхематика. Преподобный Нейрол. 13, 605–609.
Академия Google
Денес, Г. (1989). «Расстройства осознания тела и знания тела», в Справочнике по нейропсихологии , под редакцией Ф. Боллера и Дж. Графмана (Амстердам: Elsevier), 207–228.
Академия Google
Девинский, О. (2009). Бредовые ошибочные идентификации и дупликации: поражение правого полушария, бред левого полушария. Неврология 6, 80–87.
Реферат PubMed | Академия Google
Фредерикс, JAM (1969).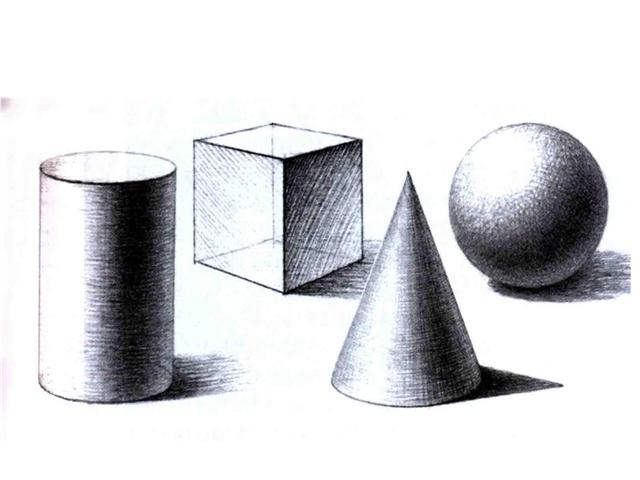 «Нарушения схемы тела», в Справочнике по клинической неврологии . Расстройства речи, восприятия и символического поведения , редакторы П. Дж. Винкен и Г. В. Брюйн (Амстердам: Северная Голландия), 207–240.
«Нарушения схемы тела», в Справочнике по клинической неврологии . Расстройства речи, восприятия и символического поведения , редакторы П. Дж. Винкен и Г. В. Брюйн (Амстердам: Северная Голландия), 207–240.
Академия Google
Гандевиа, С.К., и Феган, К.М. (1999). Перцептивные искажения образа человеческого тела, вызванные местной анестезией, болью и раздражением кожи. J. Physiol. 514, 609–616.
Реферат PubMed | Академия Google
Ирвинг-Белл, Л., Смолл, М., и Коуи, А. (1999). Искажение воспринимаемого пространства у пациентов с поражением правого полушария и зрительным полуигнорированием. Нейропсихология 37, 919–925.
Реферат PubMed | Академия Google
Кью, Дж., Райт, А., и Халлиган, П. В. (1998). Сомастетическая аура: опыт «Алисы в стране чудес». Ланцет 351:1934.
Академия Google
Кох, Г., Веньеро, Д., и Кальтаджироне, К. (2013). На другой стороне запущенного мозга: повышенная возбудимость левого интактного полушария. Невролог 19, 208–217. дои: 10.1177/1073858412447874
Невролог 19, 208–217. дои: 10.1177/1073858412447874
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Лермитт, Дж., и Черази, Э. (1937). L’image du moi corporel et ses патологические деформации. Энцефаль 32, 1–24.
Манфредини А., Манчини Ф., Постераро Л. и Савацци С.(2013). Две стороны пространственной репрезентации у пациентов с игнорированием: одно и то же пространственное искажение для разных моделей поведения. Нейропсихология 51, 1867–1877. doi: 10.1016/j.neuropsychologia.2013.06.013
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Милнер, А.Д., и Харви, М. (1995). Искажение восприятия размера при зрительно-пространственном игнорировании. Курс. биол. 5, 85–89.
Академия Google
Милнер, А. Д., Харви, М.и Притчард, К.Л. (1998). Обработка визуального размера в пространственном пренебрежении. Экспл. Мозг Res. 123, 192–200.
Академия Google
Пакерон, X. , Леген, М., Розенталь, Д., Кориат, П., Виллер, Дж. К., и Данзигер, Н. (2003). Феноменология искажений образа тела, вызванных регионарной анестезией. Мозг 126, 702–712.
, Леген, М., Розенталь, Д., Кориат, П., Виллер, Дж. К., и Данзигер, Н. (2003). Феноменология искажений образа тела, вызванных регионарной анестезией. Мозг 126, 702–712.
Реферат PubMed | Академия Google
Полхан, Дж. (1993). Брак или священная живопись . Париж: L’Echoppe, 1–19.
Подолл, К., и Робинсон, Д. (2002). Расщепление образа тела как симптом эстетической ауры при мигрени. Цефалгия 22, 62–65.
Реферат PubMed | Академия Google
Риччи, Р., Калхун, Дж., и Чаттерджи, А. (2000). Смещение ориентации при одностороннем пренебрежении: репрезентативный вклад. Кортекс 36, 671–677.
Реферат PubMed | Академия Google
Риччи, Р., Пиа, Л., и Джиндри, П. (2004). Эффекты иллюзорной пространственной анизометрии при одностороннем игнорировании. Экспл. Мозг Res. 154, 226–237.
Реферат PubMed | Академия Google
Роде Г., Мишель К., Россетти Ю., Буассон Д. и Валлар Г. (2006). Искажение левого размера (гиперсхематия) после повреждения правого полушария. Неврология 67, 1801–1808.
Искажение левого размера (гиперсхематия) после повреждения правого полушария. Неврология 67, 1801–1808.
Реферат PubMed | Академия Google
Роде Г., Пальяри К., Хучон Л., Россетти Ю. и Писелла Л. (2017). Семиология пренебрежения: обновление. Энн. физ. Реабилит. Мед. 60, 177–185.doi: 10.1016/j.rehab.2016.03.003
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Роде Г., Ронки Р., Револ П., Россетти Ю., Жакен-Куртуа С., Росси И. и др. (2014). Гиперсхема после повреждения правого полушария: значимая сущность? Перед. Гум. Неврологи. 8:8. doi: 10.3389/fnhum.2014.00008
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Роде Г., Валлар Г., Револ П., Тиликете К., Жакен-Куртуа С., Россетти Ю., и другие. (2012). Макросоматогнозия лица и боль при синдроме Валленберга: избирательное воздействие вестибулярной и чрескожной стимуляции. Нейропсихология 50, 245–253.
Академия Google
Ронки Р. , Болоньини Н., Галлуччи М., Чиапелла Л., Алджери Л., Спада М. С. и соавт. (2014). (Не)осознание одностороннего пространственного пренебрежения: количественная оценка выполнения зрительно-пространственных задач. Кортекс 61, 167–182. doi: 10.1016/j.cortex.2014.10.004
, Болоньини Н., Галлуччи М., Чиапелла Л., Алджери Л., Спада М. С. и соавт. (2014). (Не)осознание одностороннего пространственного пренебрежения: количественная оценка выполнения зрительно-пространственных задач. Кортекс 61, 167–182. doi: 10.1016/j.cortex.2014.10.004
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Ронки Р., Постераро Л., Фортис П., Бриколо Э. и Валлар Г. (2009). Сохранение левого пространственного пренебрежения; задания на рисование и отмену. Кортекс 45, 300–312. doi: 10.1016/j.cortex.2008.03.012
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Рускони М.Л., Маравита А., Боттини Г. и Валлар Г. (2002). Неповрежденная сторона действительно цела? Персеверативные реакции у больных с односторонним игнорированием: продуктивное проявление. Нейропсихология 40, 594–604.
Реферат PubMed | Академия Google
Садж, А., Каталано Чиуве, С., Брюггер, К., ван дер Меулен, М. , и Ассаль, Ф. (2011). Ипсилатеральная гиперсхема без пространственного игнорирования после поражения правой лобной доли. Дж. Нейрол. науч. 308, 142–143. doi: 10.1016/j.jns.2011.06.040
, и Ассаль, Ф. (2011). Ипсилатеральная гиперсхема без пространственного игнорирования после поражения правой лобной доли. Дж. Нейрол. науч. 308, 142–143. doi: 10.1016/j.jns.2011.06.040
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Савацци С., Постераро Л., Веронези Г. и Манчини Ф. (2007). Смещение пополам вправо и влево при пространственном пренебрежении.Две стороны одной медали? Мозг 130, 2070–2084.
Реферат PubMed | Академия Google
Струиксма, М.Е., Ноордзий, М.Л., и Постма, А. (2009). Какова связь между языком и пространственными образами? Поведенческие и нервные находки у слепых и зрячих людей. Спат. Работа. Мем. Снимок 132, 145–156. doi: 10.1016/j.actpsy.2009.04.002
Реферат PubMed | Полный текст перекрестной ссылки | Академия Google
Валлар, Г. (1998). Пространственное геминеглект у человека. Тенденции Cogn. науч. 2, 87–97.
Академия Google
Валлар, Г. , и Болоньини, Н. (2014). «Одностороннее пространственное пренебрежение», в Oxford Handbook of Attention , редакторы AC Nobre и S. Kastner (Oxford: Oxford University Press), 972–1027.
, и Болоньини, Н. (2014). «Одностороннее пространственное пренебрежение», в Oxford Handbook of Attention , редакторы AC Nobre и S. Kastner (Oxford: Oxford University Press), 972–1027.
Академия Google
Валлар, Г., и Папаньо, К. (2003). «Случаи телесной асхемации Пьера Боннье (1905)», в Classic Cases in Neuropsychology , Vol. 2, ред. C. Code, C.-W. Валлеш, Ю.Джоанетт и А. Р. Лекур (Hove: Psychology Press), 147–170.
Валлар Г. и Роде Г. (2009 г.). Комментарий к Bonnier P. L’aschematie. Преподобный Нейрол. 16, 397–400.
Валье, Д. (1954). Брак, la peinture et nous. Propos de l’artiste recueillis by Dora Vallier. Cahiers d’art N 2, 70–82.
Hélio Oiticica — Пространственный рельеф и рисунки, 1955–59 — Выставки
Galerie Lelong & Co. рада представить Hélio Oiticica: Пространственный рельеф и рисунки, 1955–59 , персональную выставку ранних рисунков художника гуашью и пример его подписи Relevo Espacial (Пространственный рельеф). На выставке будут представлены две серии Oiticica — Grupo Frente и Metaesquemas — из 1950-х годов, которые предвосхищают более позднюю серию Oiticica Relevo Espacial и исследования трехмерного пространства.
На выставке будут представлены две серии Oiticica — Grupo Frente и Metaesquemas — из 1950-х годов, которые предвосхищают более позднюю серию Oiticica Relevo Espacial и исследования трехмерного пространства.
Oiticica была частью базирующейся в Рио-де-Жанейро Grupo Frente, коллектива художников, возглавляемого Иваном Серпой с 1954 г. – 56. отказ от традиционных выразительных средств.За это время Оититика создал серию из работ Grupo Frente (1954 — 56), которые раскрывают раннее интуитивное понимание цвета и чувствительность к ритму. В таких работах, как Untitled (1955), поверхности словно вибрируют монохромными плоскостями, создающими пространственный мир.
После распада Grupo Frente Oiticica продолжала создавать инновации в цвете, линиях и формах. Он начал нарушать плотность и структуру своих ранних работ в серии гуашей на доске, Metaesquemas (1957 — 58), которую он иногда называл Sêco .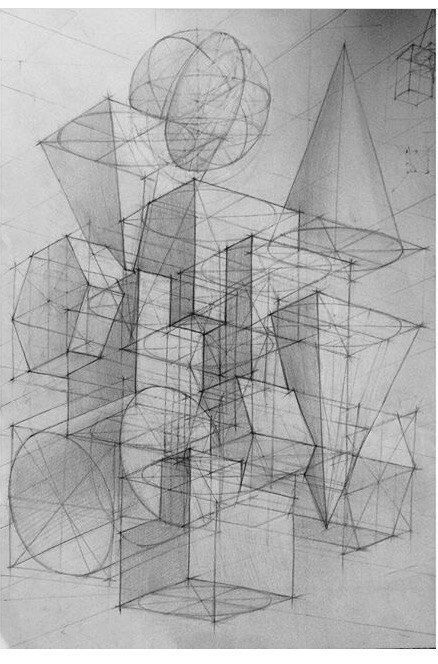 Изюминкой выставки являются два крупноформатных Metaesquemas 1958 года, которые никогда ранее не выставлялись в Соединенных Штатах; хотя Оититика был хорошо известен своими работами, мало что он создал в таком большем размере. В этих композициях, которые всегда были горизонтальны, толкающиеся формы, расположенные в виде сетки, как бы дрожат и искривляются.
Изюминкой выставки являются два крупноформатных Metaesquemas 1958 года, которые никогда ранее не выставлялись в Соединенных Штатах; хотя Оититика был хорошо известен своими работами, мало что он создал в таком большем размере. В этих композициях, которые всегда были горизонтальны, толкающиеся формы, расположенные в виде сетки, как бы дрожат и искривляются.
Наконец, желтый Relevo Espacial (Пространственный рельеф) (1959) демонстрирует, как Oiticica высвободила цвет в области участия.Его висячие деревянные конструкции перекликаются с его более ранними работами, где плоские плоскости ярких цветов меняются в зависимости от положения зрителя, чтобы стимулировать активный поисковый процесс. Oiticica стала фундаментом для формирования новаторского неоконкретного движения (1959–61), которое стремилось передать крайний рационализм конкретизма с эмоциями, чувственностью и субъективностью.
В 1960 году Оититика писал: «Опыт цвета, исключительный элемент живописи, стал для меня самой осью того, что я делаю, того, как я начинаю работу. Только теперь действительно начинается сложность отношений между цветом и структурой». Его последующие работы в 1960-х и 1970-х годах полностью активировали трехмерное пространство с иммерсивными инсталляциями, такими как Núcleos (Nuclei) (1960 — 66), и мультисенсорными средами, такими как Tropicália (1967) и Penetrável. Filtro (фильтр проникающий) (1972).
Только теперь действительно начинается сложность отношений между цветом и структурой». Его последующие работы в 1960-х и 1970-х годах полностью активировали трехмерное пространство с иммерсивными инсталляциями, такими как Núcleos (Nuclei) (1960 — 66), и мультисенсорными средами, такими как Tropicália (1967) и Penetrável. Filtro (фильтр проникающий) (1972).
Работа и влияние Оититики получили все большее признание после его смерти в 1980 году, совсем недавно благодаря знаменательной ретроспективе «Организовать бред » , которая дебютировала в Художественном музее Карнеги, штат Пенсильвания, в 2016 году и побывала в Художественном институте Чикаго. , Иллинойс, и Музей американского искусства Уитни, Нью-Йорк, до 2017 года.Его работы в настоящее время выставлены в Memories of Underdevelopment, Museum of Art of Lima, Peru; Southern Geometries, от Мексики до Патагонии, Fondation Cartier pour l’art contemporain, Франция; Комната 2 Инсталляция, Гленстонский музей, Мэриленд; и Исполнитель и участник , Тейт Модерн, Англия.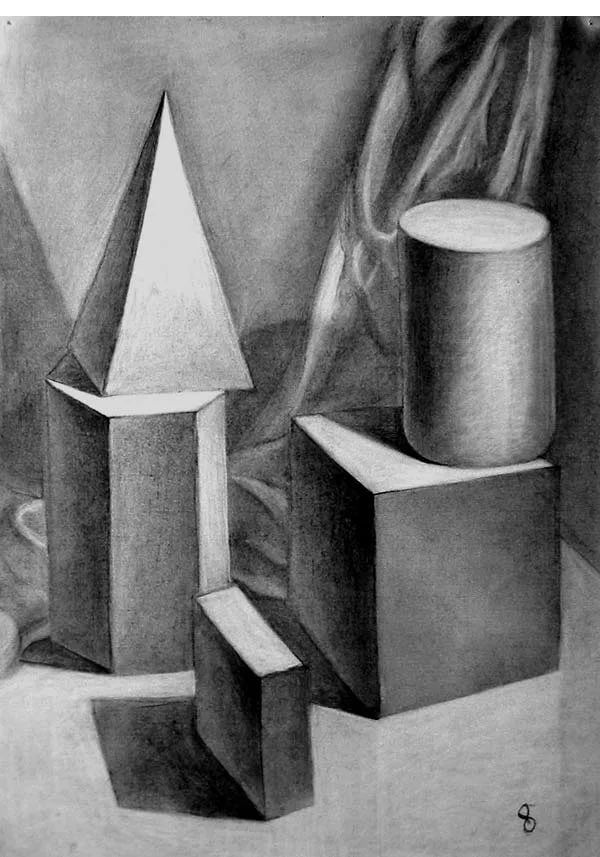 Oiticica представлена в учреждениях по всему миру, включая Художественный музей Карнеги в Пенсильвании; Музей современного искусства, Нью-Йорк; Фонд Гленстона, Мэриленд; Центр искусств Уокера, Миннесота; Museo de Arte Latinoamericano в Буэнос-Айресе, Аргентина; Inhotim Centro de Arte Contemporânea, Бразилия; Museu de Arte Moderna do Rio de Janeiro, Бразилия; Museu de Arte Moderna de São Paulo, Бразилия; Музей изящных искусств, Хьюстон; и Centro Nacional Museo de Arte Reina Sofía, Испания.Элио Оититика родился в Рио-де-Жанейро, Бразилия, в 1937 году и умер в 1980 году. Поместьем Элио Ойтисика управляет Projeto Hélio Oiticica в Рио-де-Жанейро.
Oiticica представлена в учреждениях по всему миру, включая Художественный музей Карнеги в Пенсильвании; Музей современного искусства, Нью-Йорк; Фонд Гленстона, Мэриленд; Центр искусств Уокера, Миннесота; Museo de Arte Latinoamericano в Буэнос-Айресе, Аргентина; Inhotim Centro de Arte Contemporânea, Бразилия; Museu de Arte Moderna do Rio de Janeiro, Бразилия; Museu de Arte Moderna de São Paulo, Бразилия; Музей изящных искусств, Хьюстон; и Centro Nacional Museo de Arte Reina Sofía, Испания.Элио Оититика родился в Рио-де-Жанейро, Бразилия, в 1937 году и умер в 1980 году. Поместьем Элио Ойтисика управляет Projeto Hélio Oiticica в Рио-де-Жанейро.
Чертеж — пространственное наложение
Чертеж — пространственное наложение
Пространственные наложения — это набор методов переноса данных между объектами на чертежах на основе их пространственных отношений друг к другу.
Например, предположим, что у нас есть рисунок, на котором штаты показаны в виде областей, а также набор точек, показывающих расположение городов. Предположим, что в каждой записи города есть поле с названием «Население», в котором указана численность населения в этом городе, но у нас нет значений для населения каждого штата. Мы могли бы использовать пространственные наложения, чтобы автоматически суммировать значения населения для всех городов в каждом штате и поместить это объединенное значение в поле «Население» для каждого штата.
Предположим, что в каждой записи города есть поле с названием «Население», в котором указана численность населения в этом городе, но у нас нет значений для населения каждого штата. Мы могли бы использовать пространственные наложения, чтобы автоматически суммировать значения населения для всех городов в каждом штате и поместить это объединенное значение в поле «Население» для каждого штата.
Пространственные наложения передают данные из полей исходного набора объектов в целевой набор объектов с использованием определенного метода. Конкретные правила, используемые для передачи данных, взяты из правил передачи, указанных для каждого столбца.
Элементы диалогового окна пространственного наложения
Источник | Выберите набор объектов в качестве источника данных. Варианты будут включать выборку, все сохраненные выборки и объекты в слоях чертежа при запуске с карты. |
Цель | Выберите набор объектов для получения передаваемых данных.Варианты будут включать выборку, все сохраненные выборки и объекты в слоях чертежа при запуске с карты. Целевой набор может содержать объекты только одного типа (то есть все области, все линии или все точки). |
Метод | Выберите способ передачи. Будут представлены только те операции, которые имеют смысл для объектов исходного и целевого наборов. Если исходный или целевой набор не содержит всех объектов одного типа, поле метода не будет активировано. |
Методы пространственного наложения
В поле «Методы» появятся следующие методы, соответствующие типам объектов, выбранным в исходном и целевом наборах.
Области в замкнутые области | Перенос полей из области А в области, полностью находящиеся внутри А. |
Области для содержащихся строк | Перенести поля из области A в строки, полностью находящиеся внутри A. |
Площади в содержащиеся точки | Перенос полей из области А в точки внутри А |
Области в содержащие области | Перенос полей из области A в области, полностью содержащие A. |
Площади в пересекающиеся области | Перенести поля из области A в области, которые хотя бы частично расположены внутри A (то есть не на границе). |
Площади пересекающихся линий | Перенести поля из области A в линии, которые хотя бы в каком-то месте находятся внутри области A (то есть не на границе). Исключает полностью содержащиеся строки. |
Районы к соседним районам | Перенести поля из области A в области, которые соприкасаются с A только на границе A (то есть не имеют общих местоположений, которые являются внутренними для A). |
Области до соседних линий | Перенести поля из области A в линии, которые касаются A только на границе A. |
Области до граничных точек | Перенос полей из области А в точки, лежащие на ее границе. |
Зоны касания | Перенос полей из области А в области, имеющие хотя бы одно общее местоположение с А. |
Области касания линий | Перенос полей из области A в строки, которые имеют хотя бы одно общее местоположение с A. |
строк в содержащиеся строки | Перенести поля из строки L в строки, полностью содержащиеся в L (то есть совпадающие с какой-то частью L). |
Линии к содержащимся точкам | Перенос полей из линии L в точки, лежащие на L. |
Линии к содержащим областям | Перенос полей из строки L в области, полностью содержащие L. |
строк, содержащих строки | Перенос полей из строки L в строки, полностью содержащие L (то есть совпадающие хотя бы на протяжении L). |
Линии к пересекающимся областям | Перенос полей из линии L в области, которые имеют хотя бы одно общее внутреннее местоположение с L. |
Линии на пересекающиеся линии | Перенос полей из строки L в строки, которые имеют хотя бы одно общее внутреннее местоположение (то есть местоположение, которое не является конечной координатой какой-либо ветви) с помощью L. |
Линии к соседним областям | Перенос полей из линии L в области, которые касаются L на их границе. |
Линии к соседним линиям | Перенести поля из строки L в строки, которые касаются (и касаются) L в конечных координатах любой ветви L. |
Линии к оконечным пунктам | Перенос полей из линии L в точки, лежащие на ее границе (т.е. конечные точки ответвлений). |
Линии к соприкасающимся областям | Перенос полей из линии L в области, которые имеют хотя бы одно общее местоположение с линией. |
Линии до соприкасающихся линий | Перенос полей из строки L в строки, которые имеют хотя бы одно общее местоположение с L. |
Указывает на содержащие области | Перенос полей из точки P в области, содержащие P. |
Указывает на содержащие строки | Перенос полей из точки P в строки, содержащие P. |
Указывает на соседние области | Перенести поля из точки P в области, которые содержат P на своей границе. |
Указывает на соседние строки | Перенести поля из точки P в строки, которые содержат P на своей границе. |
указывает на совпадающие точки | Перенос полей из точки P в точки, совпадающие с P. |
Пример
Давайте рассмотрим простой пример, чтобы увидеть, как работают пространственные наложения.
Мы создали чертеж с двумя площадями и девятью точками. Выберите точки и сохраните их как сохраненный выбор под названием «Точки» на панели «Выборки». Выберите две области и сохраните их как выделение под названием «Области» на панели выбора.
В таблице для этого чертежа показано, что имеется одно целочисленное поле «Население».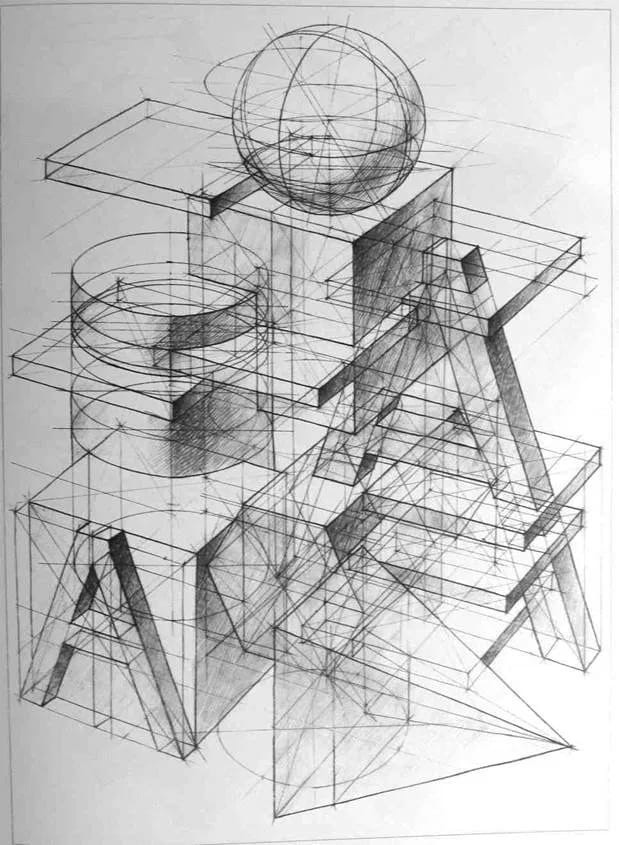 Каждая из точек имеет значение 1 для поля населения и отображается в таблице с красным цветом фона выделения.Эти две области имеют значения 0 для населения.
Каждая из точек имеет значение 1 для поля населения и отображается в таблице с красным цветом фона выделения.Эти две области имеют значения 0 для населения.
Откройте таблицу чертежа, щелкните правой кнопкой мыши столбец «Население» и выберите «Правила переноса».
В диалоговом окне «Правила передачи» выберите «Копировать» в качестве правила передачи для передач от 1 до N и выберите «Сумма» в качестве правила передачи для передач от N до 1.
Щелкните окно чертежа и выберите «Чертеж — Пространственное наложение».
В диалоговом окне «Пространственное наложение» выберите «Точки» в качестве источника и «Области» в качестве цели. Метод будет указывать на содержащие области. Нажмите ОК.
Результатом операции пространственных наложений является то, что одна область (треугольник) получает значение 2, а другая область (круг) получает значение 4.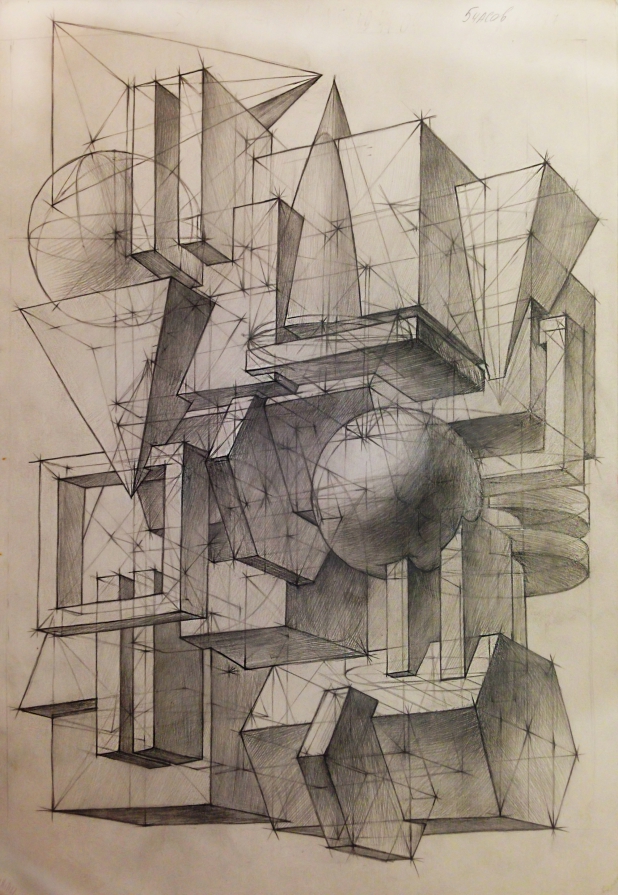 Эти новые значения представляют собой суммы значений точек внутри областей.
Эти новые значения представляют собой суммы значений точек внутри областей.
Географический пример
Применим описанную выше процедуру к географическим условиям. Мы просуммируем население городов, чтобы получить общее население каждого округа, содержащего города.
У нас есть рисунок под названием «Пример», на котором округа в районе залива Сан-Франциско показаны как районы вместе с точками, взятыми из файла Бюро переписи населения с названиями мест с населением.
Открыв таблицу примеров, мы видим, что есть десять областей, каждая со значением 0 в поле pop1990. Во многих городах есть население для каждого города.
Начнем с щелчка правой кнопкой мыши по заголовку столбца pop1990 в таблице и выбора правил передачи.
Мы устанавливаем правила передачи для этого поля на ber Sum for N to 1. Поскольку в каждом округе будет объединено много точек, это транзакция «многие к 1» или N к 1. Мы хотели бы, чтобы значения населения суммировались, чтобы получить значение для каждого округа.
Поскольку в каждом округе будет объединено много точек, это транзакция «многие к 1» или N к 1. Мы хотели бы, чтобы значения населения суммировались, чтобы получить значение для каждого округа.
Мы не хотим передавать какие-либо значения для полей округа или имени. Щелкните правой кнопкой мыши заголовок столбца округа, выберите «Правила переноса» и выберите «Нет» для правила переноса N к 1. Затем мы щелкаем правой кнопкой мыши заголовок столбца «Имя», выбираем «Правила передачи» и еще раз выбираем «Нет» для правила передачи «N к 1».
Если бы мы использовали пространственные наложения между разными слоями рисования на карте, мы могли бы пропустить этот шаг; однако, поскольку мы переносим значения между полями на одном и том же чертеже, мы будем использовать сохраненные выборки. Выберите все точки на чертеже и сохраните этот выбор как сохраненный выбор на панели «Выборы» под названием «Места». Выберите все точки на чертеже и сохраните этот выбор как сохраненный выбор под названием Counties.
Сфокусировавшись на окне рисования «Примеры», выберите «Рисование — Пространственное наложение».
В диалоговом окне «Пространственное наложение» выберите «Места» в качестве источника и «Округи» в качестве цели. Для Метода выберите Указывает на содержащие области и нажмите OK.
В таблице мы видим, что значения pop1990 заполнены суммой значений баллов для каждого округа. Это соответствует правилу передачи от N к 1, которое мы указали для этого поля. Обратите внимание, что нет никаких изменений в полях округа или имени для округов, поскольку мы указали None в качестве правил переноса для этих полей.
Пространственные наложения на картах
Пространственные наложения могут использоваться на картах, если карта содержит хотя бы один непустой рисунок. Чтобы использовать пространственные наложения между различными рисунками на карте, должно быть верно следующее:
Если для определенного поля не выполняются два вышеуказанных условия, оно вообще не будет передано.
См. также
Правила переноса. Правила переноса определяют, как объединяются или распределяются поля при создании новых объектов с помощью операторов панели инструментов преобразования.Пространственные наложения — это концепция, отличная от идеи использования правил переноса для агрегирования или распределения значений при создании объектов с преобразованиями. Однако это родственная концепция, поскольку агрегации или выделения используются для передачи значений полей между объектами.
Передача высоты контурной линии в точки — простой пример использования пространственного наложения.
Кратчайший путь над сушей — сложный пример, в котором используется пространственное наложение.
.


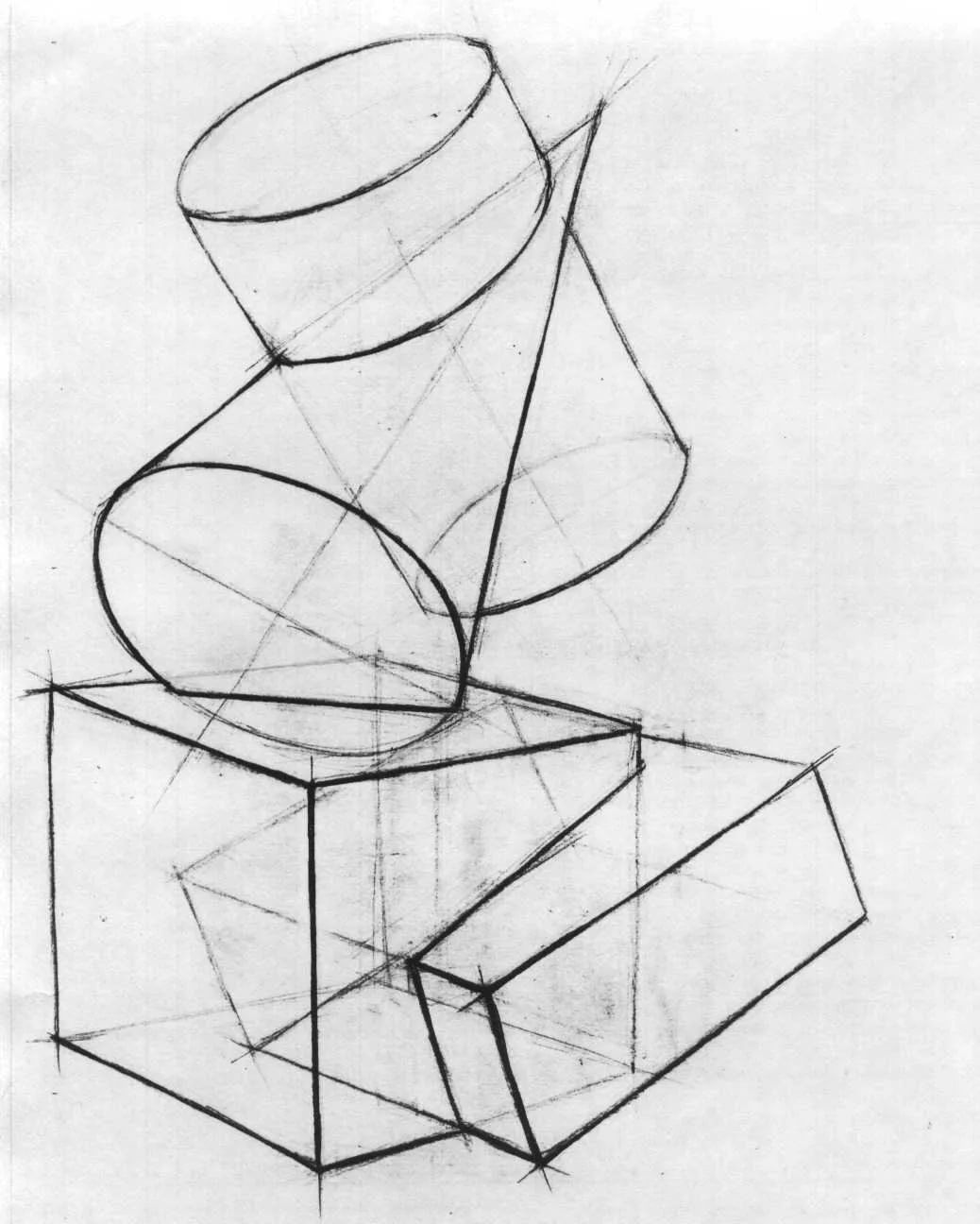 0 + (y1–y2)**2.0]
0 + (y1–y2)**2.0]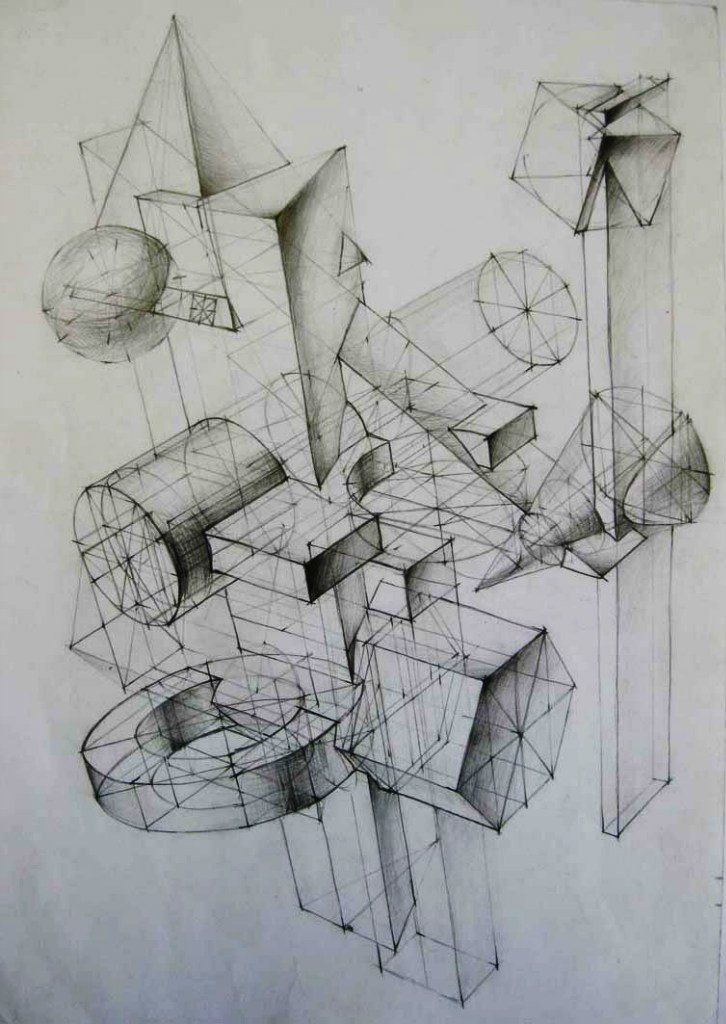 Возможно, вы не будете выполнять нормализацию ряда для пространственных весов.
Возможно, вы не будете выполнять нормализацию ряда для пространственных весов. В редких случаях эта структура будет хорошим отражением анализируемых данных и исследуемого явления. Например: хотя полигоны переписи (как и районы переписи) сформированы на основе численности населения, даже если ваш анализ связан с вопросами численности, вам все равно придется нормализовать веса, так как эти полигоны представляют всего один из множества способов представления данных. Для полигональных данных нормализация ряда пространственных весов выполняется практически всегда.
В редких случаях эта структура будет хорошим отражением анализируемых данных и исследуемого явления. Например: хотя полигоны переписи (как и районы переписи) сформированы на основе численности населения, даже если ваш анализ связан с вопросами численности, вам все равно придется нормализовать веса, так как эти полигоны представляют всего один из множества способов представления данных. Для полигональных данных нормализация ряда пространственных весов выполняется практически всегда.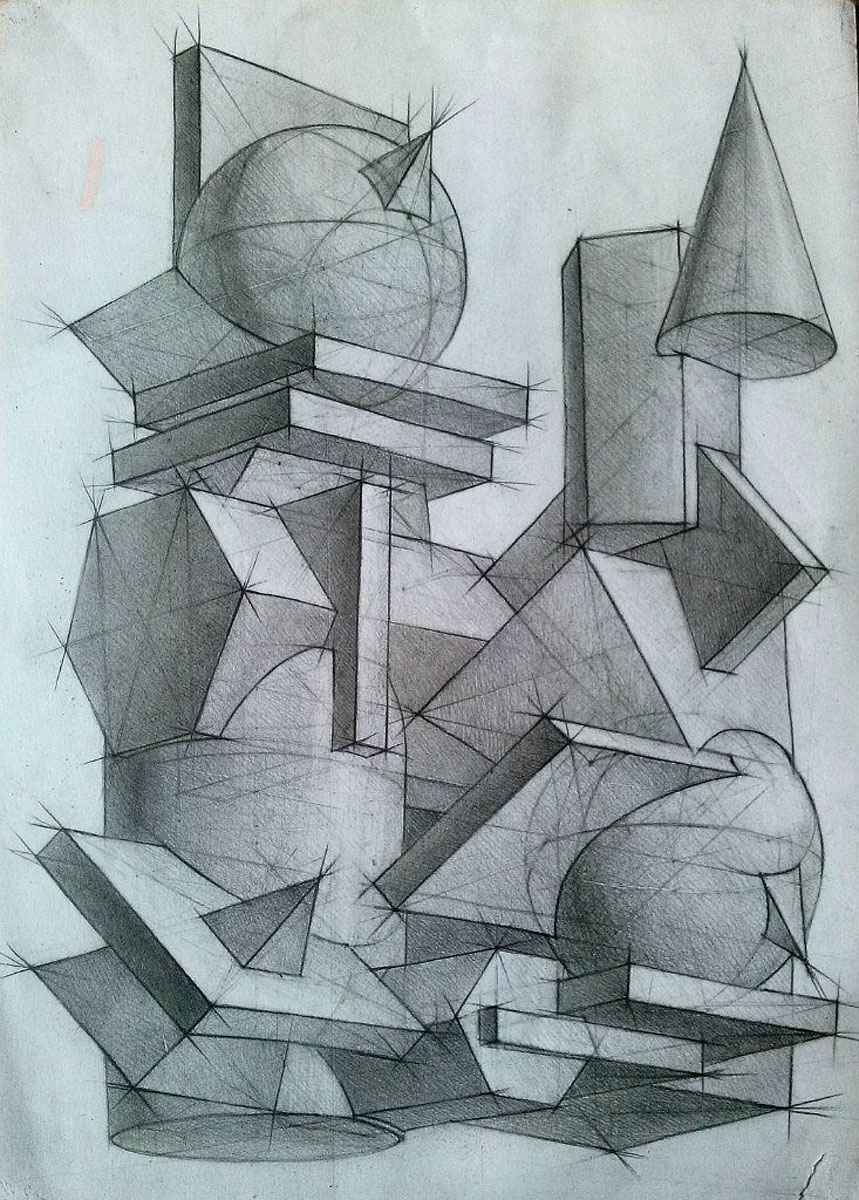

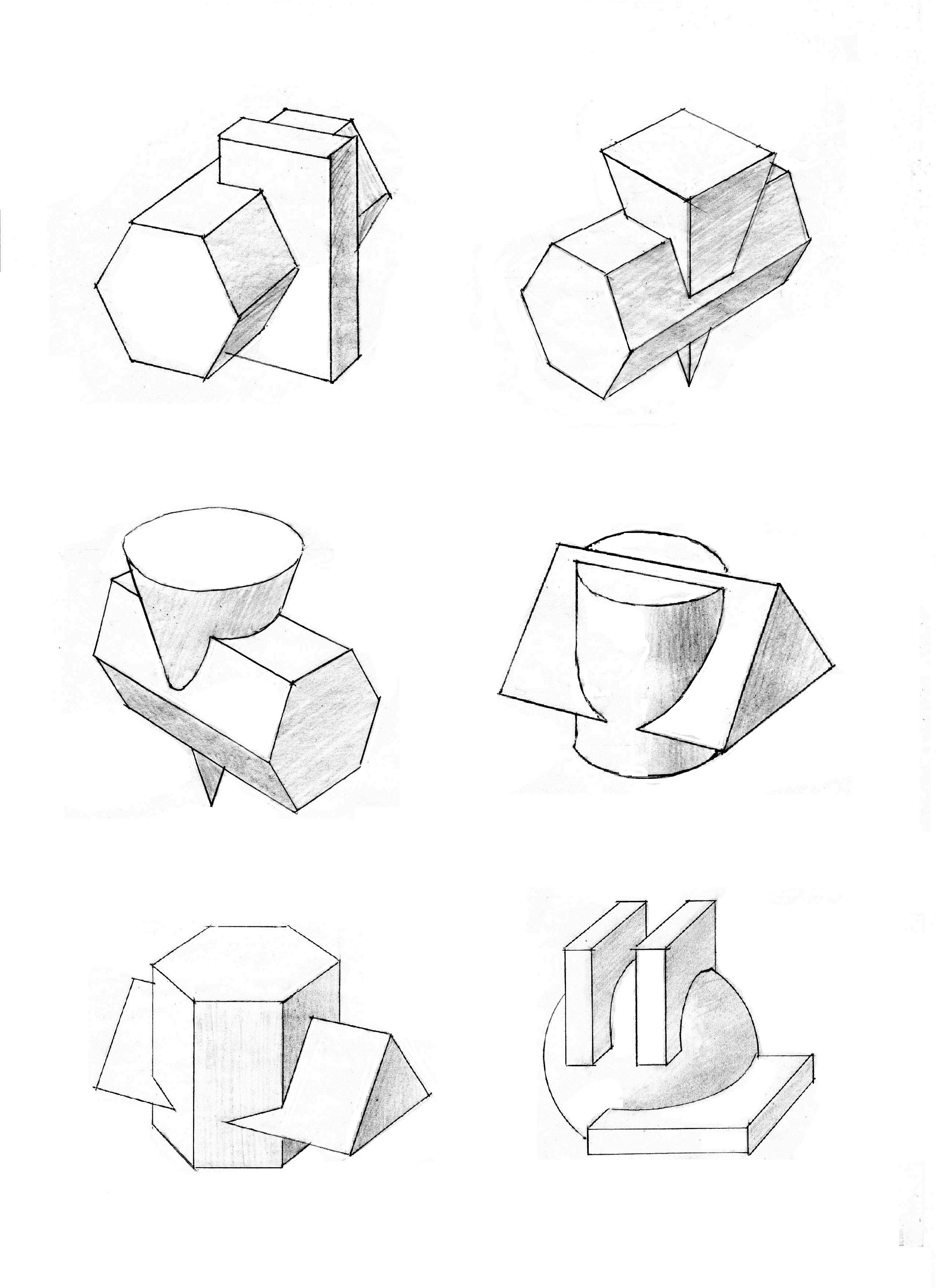
 Это от ID объекта.
Это от ID объекта.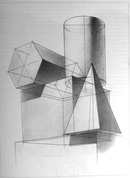
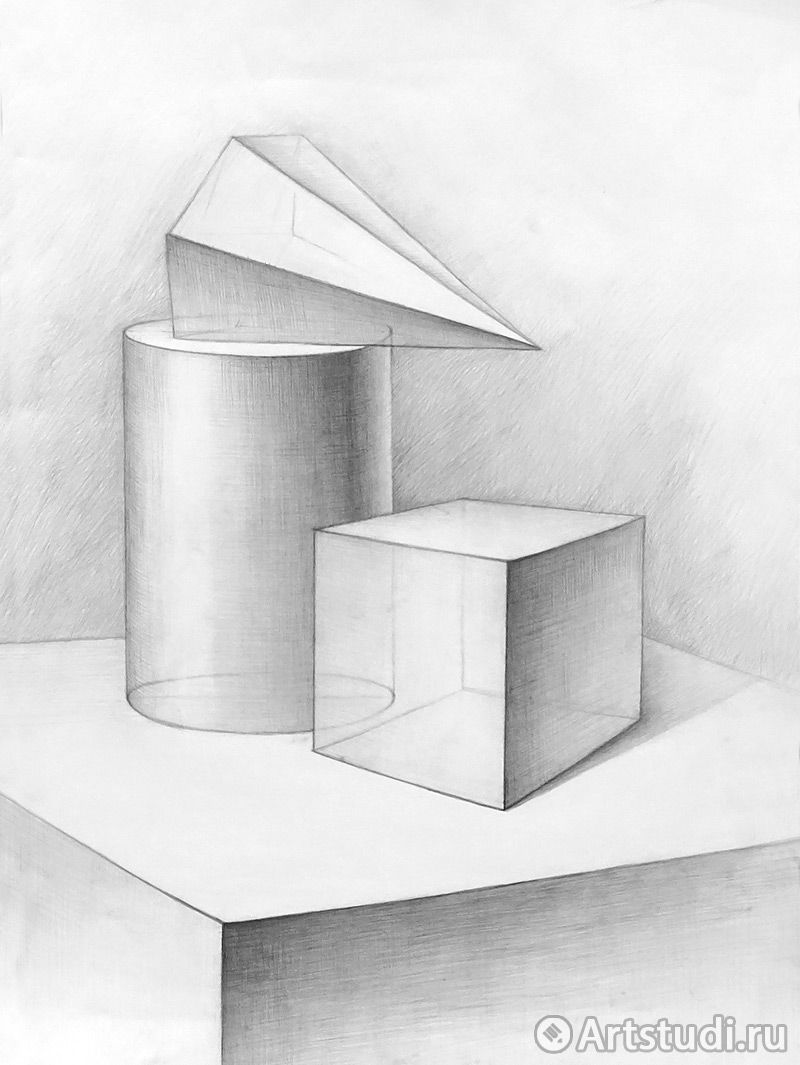
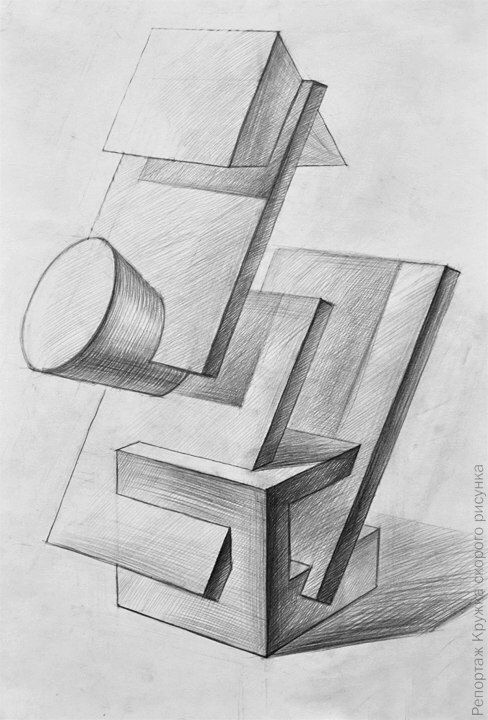 Нажмите кнопку Match symbols. Снимите флажок со строчки All other values. Окно свойств слоя должно принять вид, аналогичный представленному на рисунке. Нажмите ОК.
Нажмите кнопку Match symbols. Снимите флажок со строчки All other values. Окно свойств слоя должно принять вид, аналогичный представленному на рисунке. Нажмите ОК.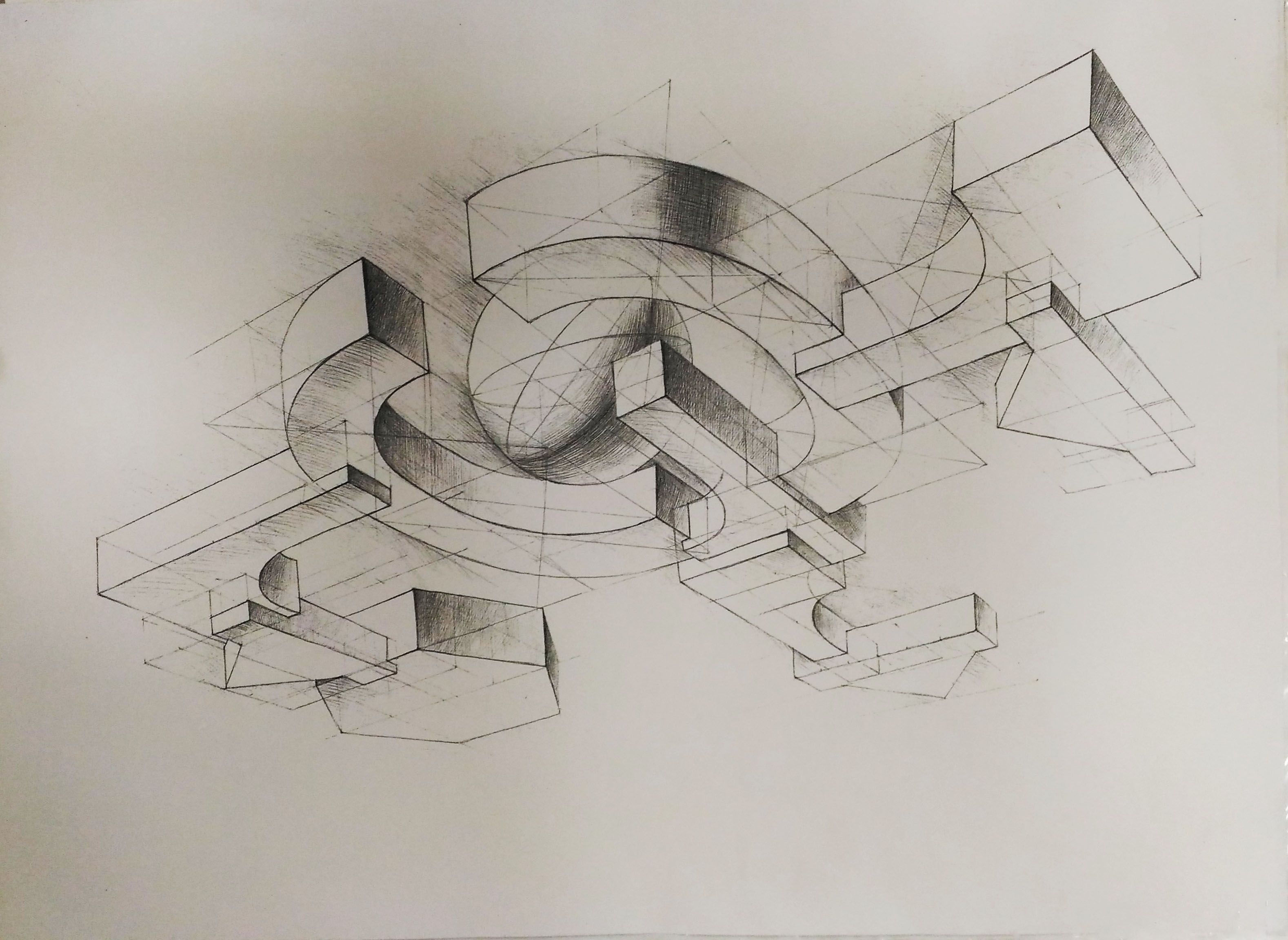
 . Раскройте его.
. Раскройте его. Доступ к инструментам геообработки осуществляется через окно ArcToolbox, где они сгруппированы по назначению. Некоторые наборы инструментов, такие как Spatial Analyst и 3D Analyst, являются дополнительными модулями ArcGIS, предназначенными для решения специализированного круга задач: растровый анализ, трехмерный анализ, сетевой анализ и т.д.
Доступ к инструментам геообработки осуществляется через окно ArcToolbox, где они сгруппированы по назначению. Некоторые наборы инструментов, такие как Spatial Analyst и 3D Analyst, являются дополнительными модулями ArcGIS, предназначенными для решения специализированного круга задач: растровый анализ, трехмерный анализ, сетевой анализ и т.д. gdb/SoilTypes/Intersect
gdb/SoilTypes/Intersect Там, где границы совпадают с контурами типов рельефа, они будут черного цвета, а там где они совпадают с контурами типов почв, будет красная линия с черной обводкой.
Там, где границы совпадают с контурами типов рельефа, они будут черного цвета, а там где они совпадают с контурами типов почв, будет красная линия с черной обводкой. Слияние — это один из методов генерализации.
Слияние — это один из методов генерализации.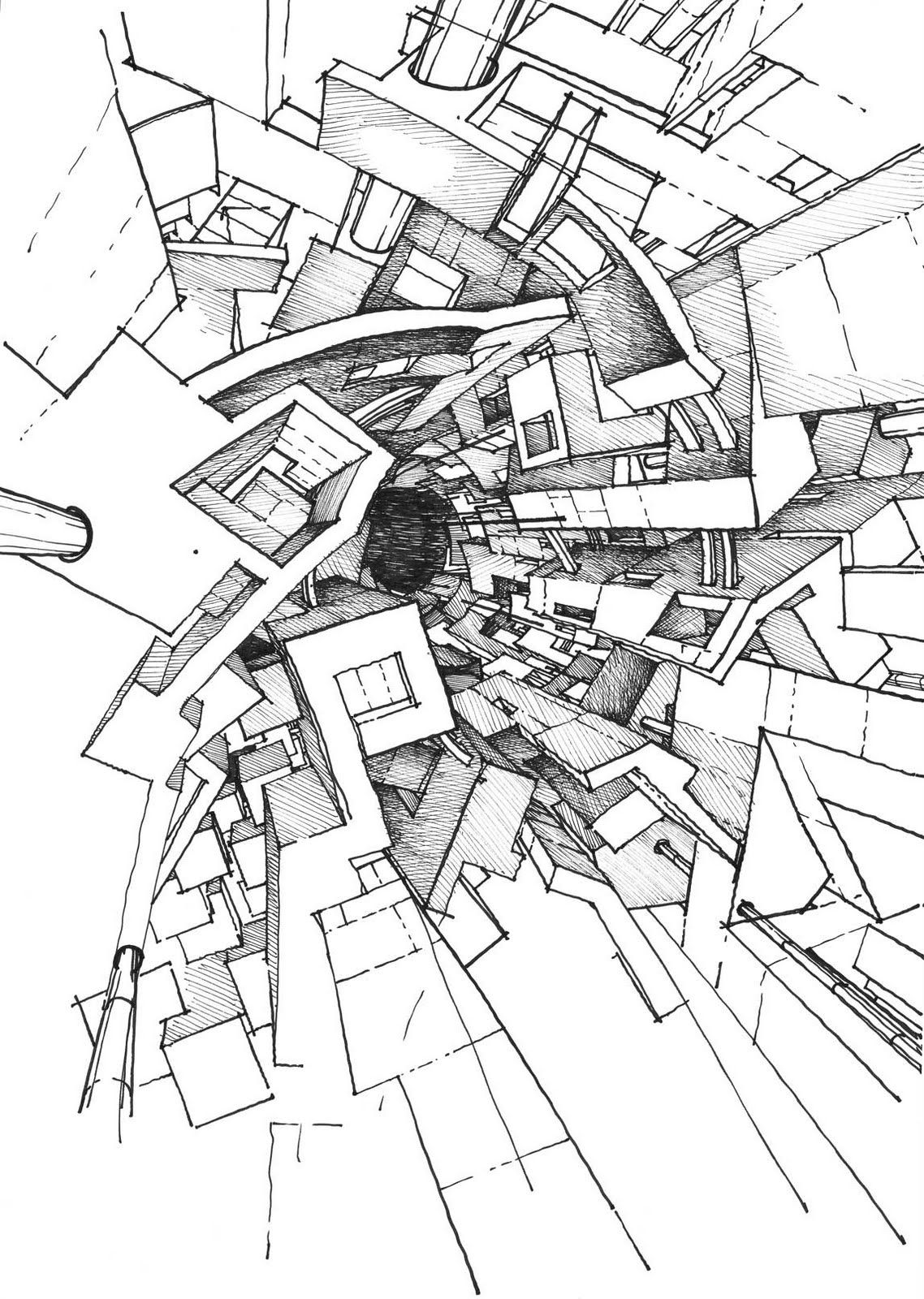 Диалог инструмента Dissolve примет вид, аналогичный представленному на рисунке ниже.
Диалог инструмента Dissolve примет вид, аналогичный представленному на рисунке ниже.

 Вы можете, например, умножить значение одного поля на 100 и записать в другое, соединить несколько текстовых полей в одно предложение или просто скопировать значение одного поля в другое.
Вы можете, например, умножить значение одного поля на 100 и записать в другое, соединить несколько текстовых полей в одно предложение или просто скопировать значение одного поля в другое.
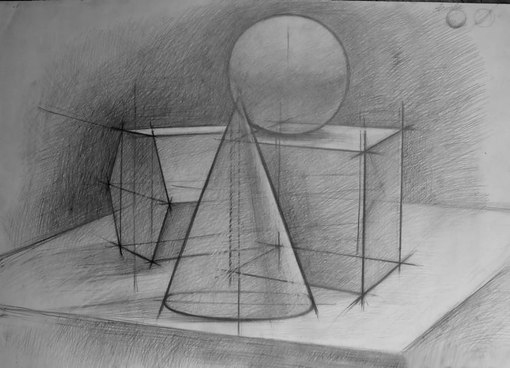 Исходный набор может содержать объекты только одного типа (то есть все площади, все линии или все точки).
Исходный набор может содержать объекты только одного типа (то есть все площади, все линии или все точки).