Как нарисовать геометрические фигуры куб конус шар: Урок «Шар, конус, цилиндр»
- Урок «Шар, конус, цилиндр»
- Геометрические фигуры из бумаги
- ЧЕРЧЕНИЕ. Школьный интернет-учебник — Чтение чертежей 3-4
- Нарисовать рисунок состоящий из геометрических фигур. Рисование геометрических тел
- Как нарисовать геометрические фигуры
- Как научиться ложить штрих по форме предмета. Штриховка
- Построение геометрических фигур.
- ПРИХОДИМ ФОРМУ(Ы) Сегодняшний урок…
- 10 заданий по описанию трехмерных фигур в детском саду — KindergartenWorks
- Просмотрите образовательные ресурсы по 3D-фигурам
- Обучение плоскостным фигурам и твердым телам
- 3D-формы и сети | SkillsYouNeed
- Трехмерные фигуры: вид спереди, сбоку и сверху — видео и стенограмма урока
- Что такое 3D-фигуры? | Определение и примеры
Урок «Шар, конус, цилиндр»
Шар, конус, цилиндр
Лукоянова Наталья Анатольевна,
учитель математики
МБОУ Гимназия
г. Новый Уренгой
У детей младшего подросткового возраста (6 класс) изменяется характер учебной деятельности. Содержание учебного материала представляет собой теперь систематическое изложение основ наук. Его усвоение приводит к формированию на протяжении всего подросткового возраста мышления в понятиях, это оказывает большое влияние на всё психическое развитие. Новые знания обогащают и расширяют представления младших подростков об окружающей действительности, открывают новые области явлений, а новый уровень мышления делает возможным сопоставлять и систематизировать свои представления и глубже проникать в причины и сущность явлений. Курс геометрии вносит свой вклад в формирование научного мировоззрения, а вместе с тем в нравственное воспитание учащихся.
Тема урока.
Шар, конус, цилиндр.
Цель изучения.
Познакомить учащихся с геометрическими телами — шаром, конусом, цилиндром и их элементами.
Научить различать в окружающем мире предметы, имеющие форму изучаемых фигур.
Прогнозируемый результат.
Уметь оперировать понятиями: шар, конус, цилиндр, многогранник, тело вращения, поверхность тела, сечение.
Уметь распознавать изученные геометрические фигуры.
Уметь приводить примеры предметов, имеющих форму изученных тел вращения.
Уметь рассказывать о шаре, конусе, цилиндре по плану.
План урока.
Организационный момент.
Актуализация знаний.
Изучение цилиндра.
Изучение конуса.
Изучение шара.
Многогранники и тела вращения.
Решение задач.
Подведение итога урока.
Домашнее задание.
Оборудование.
Чертежные инструменты.
Ребусы.
Рисунки к задачам.
Ход урока
Учитель. На сегодняшнем уроке вы познакомитесь с тремя новыми геометрическими фигурами. Чтобы лучше понять изучаемый материал будьте внимательными, активными и сообразительными. Тема урока состоит из трёх слов, которые зашифрованы с помощью ребусов. Разгадайте их и вы узнаете какие геометрические фигуры мы будем изучать сегодня.
Ученики. Шар. Ученики. Конус. Ученики. Цилиндр.
Учитель. Итак, тема урока «Шар. Конус. Цилиндр». Прежде чем начнем знакомиться с новыми геометрическими фигурами, ответьте на несколько вопросов.
— Какая фигура, по-вашему мнению, является лишней и почему? Возможны несколько вариантов ответов!
Варианты ответов:
лишняя, т. к. круглая;
к. круглая;
лишняя, т.к. красная;
лишняя, т.к. объемная.
Ученики. Выбирают правильный вариант ответа.
Учитель. Хочу заметить, что на уроках математики не имеет значения цвет предмета и материал, из которого он изготовлен. Важна форма и размеры изучаемой фигуры. По одной из предложенных вами классификаций лишним является прямоугольный параллелепипед, так как он является пространственной фигурой, а остальные фигуры плоские.
— Какие ещё пространственные фигуры вы знаете?
Ученики. Куб, параллелепипед, пирамида.
Учитель.
— Расскажите по представленным моделям о пирамиде.
Ученики. Рассказывают о пирамиде.
Учитель. Основные элементы пирамиды повторили, а теперь вспомним важные моменты, связанные с прямоугольным параллелепипедом и кубом. Для этого решим две задачи. Задача 1. Найдите объём аквариума, изображённого на рисунке.
Для этого решим две задачи. Задача 1. Найдите объём аквариума, изображённого на рисунке.
V = abc;
V = 5 м × 3м × 4м;
V = 60 м 3.
Ученики. Озвучивают еще раз ответ: V = 60 м3.
Учитель. Решаем следующую задачу. Задача 2. От куба отрезали угол. Сколько граней у получившейся фигуры?
Ученики. У получившейся фигуры 7 граней.
Учитель. Итак, все ранее изученные пространственные фигуры мы вспомнили, приступим к изучению новых фигур, которые будем изучать по плану, записанному на доске. Начнём с цилиндра. Оказывается, слово «цилиндр» произошло от греческого слова «кюлиндрос», означающего «валик», «каток». На рубеже XVIII – XIX веков мужчины многих стран носили твёрдые шляпы с небольшими полями, которые так и назывались цилиндрами из-за большого сходства с геометрической фигурой цилиндром.
— Какие ещё предметы имеют цилиндрическую форму?
Варианты ответов:
стакан, карандаш, многие баночки,
кастрюли, бидоны, часть скалки и т.д.
Ученики. Выбирают правильный вариант ответа.
Учитель. Внимательно посмотрите на цилиндр (демонстрируется модель). Цилиндр, как мы видим, пространственная или объёмная фигура. Поверхность цилиндра состоит из двух оснований и боковой поверхности.
— Что из себя представляют основания цилиндра?
Ученики. Основания цилиндра представляют из себя круги.
Учитель.
— Что вы можете сказать о размерах этих кругов?
Ученики. Одинаковые, т.е. радиусы этих кругов равны.
Учитель.— Что из себя представляет боковая поверхность?
Ученики. Затрудняются ответить.
Затрудняются ответить.
Учитель. Возьмём бумажный цилиндр, разрежем его следующим образом (показываю) и развернём.
— Так что же представляет собой боковая поверхность?
Ученики. Прямоугольник.
Учитель. Что ещё нужно знать о цилиндре? Высота цилиндра — это расстояние между основаниями, радиус цилиндра — радиус круга, являющегося основанием цилиндра.
Цилиндр
А сейчас представьте, что у каждого из вас в руках деревянный цилиндр и топорик, с помощью которого вы легко можете рассечь или расколоть цилиндр. «Аккуратно» топориком ударяем по верхнему основанию и раскалываем его
—Какой формы представляют основания цилиндра или сечение цилиндра?
Ученики. Имеет форму прямоугольника.
Учитель. А сейчас будем «пилить» цилиндр, положив его «на бок». Мысленно его распилим или рассечём.
— Какая геометрическая фигура получится на срезе или говорят в сечении цилиндра?
Ученики. Получается круг.
Учитель. Продолжаем трудиться дальше, опять положим цилиндр на боковую поверхность, но рассечём его уже «наискосок».
— Какая геометрическая фигура будет в сечении, т.е. на срезе?
Ученики. Овал.
Учитель. Овал, по-научному, эллипс (заранее записать на центральной доске под цилиндром).
— Итак, какие геометрические фигуры могут быть в сечении цилиндра?
Ученики. Прямоугольник, круг, эллипс.
Учитель. Все пункты плана разобраны, вы уже достаточно много знаете о цилиндре. Переходим к рассмотрению конуса. Слово «конус» произошло от греческого слова «конос», означающего сосновую шишку (показываю шишку). Действительно, есть некоторое сходство. Конус, как и цилиндр, является пространственной фигурой. Поверхность конуса состоит из круга, который называется основанием конуса и боковой поверхности.
Слово «конус» произошло от греческого слова «конос», означающего сосновую шишку (показываю шишку). Действительно, есть некоторое сходство. Конус, как и цилиндр, является пространственной фигурой. Поверхность конуса состоит из круга, который называется основанием конуса и боковой поверхности.
— Что же из себя представляет боковая поверхность?
Ученики. Затрудняются ответить.
Учитель. Трудно мысленно представить боковую поверхность конуса, поэтому, как и в случае с цилиндром, возьмём бумажный конус, разрежем его следующим образом
— Что является развёрткой боковой поверхности конуса? Что это такое? Частью какой геометрической фигуры является эта фигура?
Ученики. Часть круга.
Учитель. Конус, в отличие от цилиндра, имеет вершину (показываю вершину, высоту и радиус основания по рисунку на центральной доске).
Конус
Если вершину и верхнюю часть конуса отсечь (показываю на модели), то мы получим так называемый усечённый конус.
— Подумайте и скажите, какие предметы имеют форму конуса или усечённого конуса?
Ученики. Ведро, горшки для цветов, воронка, мороженое-рожок и др.
Учитель. А сейчас снова представим, что мы рассекаем деревянный конус.
— Формы каких геометрических фигур могут иметь сечения конуса?
Ученики. Треугольник, круг, эллипс.
Учитель. Оказывается, сечения конуса могут иметь формы других геометрических фигур, названия которых мы даже ещё не знаем, их будем изучать в старших классах, и поэтому о них пока говорить не будем. Снова все пункты плана нами рассмотрены. И, наконец, переходим к изучению шара.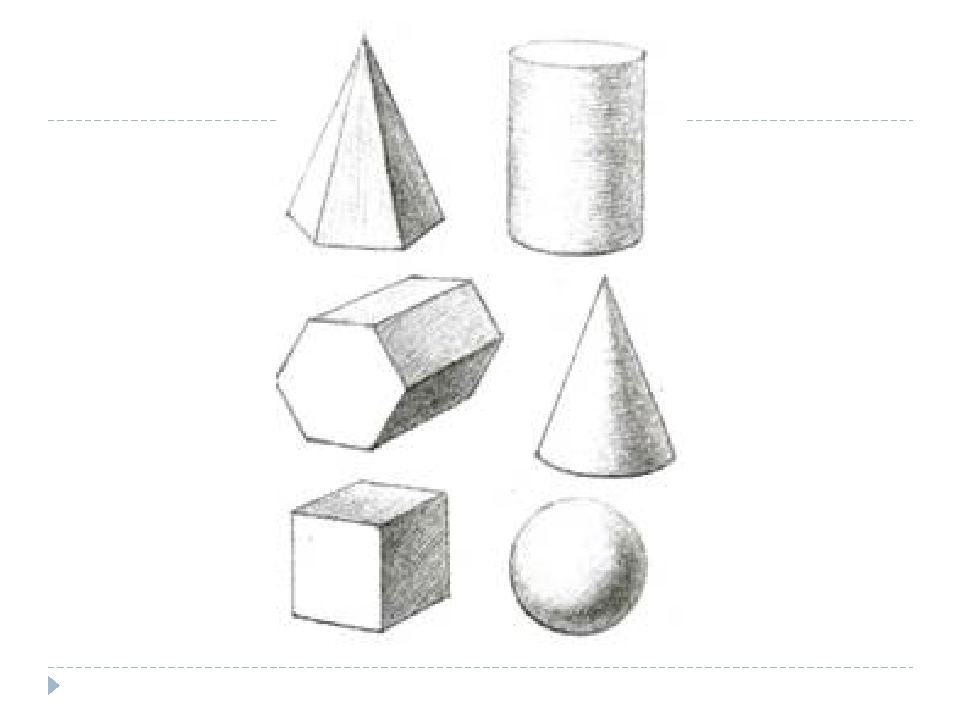 Шар — это наиболее знакомая вам геометрическая фигура. Мяч (показываю) — пример предмета шарообразной формы.
Шар — это наиболее знакомая вам геометрическая фигура. Мяч (показываю) — пример предмета шарообразной формы.
— Какие ещё предметы имеют форму шара? Ребята, кому я сейчас брошу этот мяч, нужно привести свой пример предмета, имеющего форму шара.
— Расскажите, что вы знаете о шаре? Сейчас о шаре нам расскажет …
Ученики. Он (она) заранее готовит сообщение «ШАР» и рассказывает его одноклассникам. Шар — это пространственная фигура. Поверхность шара называют сферой. Слово «сфера» произошло от греческого слова «сфайра», которое переводится на русский язык как «мяч». Не нужно путать понятия «шар» и «сфера». Сфера — это, можно сказать, оболочка или граница шара. Мяч, глобус — это сферы, а вот арбуз, апельсин, Солнце, Луна, Земля и остальные планеты имеют форму немного сплющенного шара (показывает рисунок).
Сфера обладает очень интересным свойством — все её точки одинаково удалены от центра шара. Отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара. На рисунке отрезки ОА, ОВ, ОD и ОС являются радиусами (показывает по рисунку).
Отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара. На рисунке отрезки ОА, ОВ, ОD и ОС являются радиусами (показывает по рисунку).
Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара. На рисунке отрезок СD является диаметром шара. Диаметр шара равен двум радиусам. Любое сечение шара имеет вид круга. Если рассекать шар ближе к центру, то круги будут больше, если дальше от центра, то радиусы кругов будут меньше.
Учитель. Итак, мы познакомились с тремя пространственными геометрическими фигурами — шаром, цилиндром и конусом. Вы должны знать, что пространственные геометрические фигуры ещё по-другому называют геометрическими телами. Оказывается, все геометрические тела математики раздели на две группы: так называемые многогранники и так называемые тела вращения. Внимательно посмотрите на геометрические тела (показываю модели) и попробуйте догадаться, какое геометрическое тело относится к какой группе.
— Как называется фигура, и к какой группе её отнесём?
Ученики. Действительно, шар, цилиндр, конус, усечённый конус — тела вращения. А куб, параллелепипед, пирамида — многогранники.
Учитель.
— Почему куб, параллелепипед, пирамиду вы отнесли к многогранникам?
Ученики. Потому что у них много граней.
Учитель. Логично! А вот почему шар, цилиндр, конус, усечённый конус назвали телами вращения, об этом я вам расскажу сама. Дело тут вот в чём! Если взять плоскую фигуру круг или даже достаточно половину круга (полукруг) и вращать его вокруг диаметра, то в воздухе он опишет шар. Значит, шар получился в результате вращения полукруга. Вот почему шар является телом вращения, а прямая, вокруг которой производили вращение, называется осью вращения шара или просто осью шара. Попробуйте догадаться:
— Какая плоская фигура при вращении опишет цилиндр?
Ученики. Прямоугольник.
Прямоугольник.
Учитель.
— Какая прямая будет его осью?
Ученики. Осью является неподвижная сторона прямоугольника.
Учитель.
— Какая плоская фигура при вращении опишет конус?
Ученики. Прямоугольный треугольник.
Учитель.
— Какая прямая будет его осью?
Ученики. Ось — неподвижная сторона.
Учитель. В дальнейшем на уроках математики будем более подробно изучать эти тела, и вы узнаете о существовании других многогранников, а также узнаете формулы, по которым находятся объёмы этих пространственных фигур. Решим несколько задач. Задача 1. Из предметов какой формы сложена башня? Называйте сверху вниз.
Ученики. Конус, куб, цилиндр.
Учитель. Решим следующую задачу. Задача 2. На рисунке изображены различные геометрические тела. Какие из них являются многогранниками?
Решим следующую задачу. Задача 2. На рисунке изображены различные геометрические тела. Какие из них являются многогранниками?
Ученики. Второе (пирамида), третье (наклонная призма).
Учитель. Решим третью задачу. Задача 3. На рисунке в первой строчке изображён вид фигуры спереди, а во второй строчке — вид фигуры сверху. Какая это фигура?
Варианты ответов:
1. Конус.
2. Цилиндр.
3. Четырёхугольная пирамида.
4. Прямоугольный параллелепипед.
5. Треугольная пирамида.
6. Шар.
Ученики. Выбирают правильный вариант ответа.
Учитель. Задача 4. На рисунке изображены некоторые геометрические тела. Возможно, точка зрения не очень привычна. Какие тела, если на них смотреть с соответствующей стороны, могут выглядеть, как на рисунке? Какие из рисунков могут соответствовать одному и тому же телу?
Ученики.
1. Куб или параллелепипед.
2. Пирамида или конус.
3. Конус, цилиндр или шар.
4. Параллелепипед.
2 и 3 рисунки могут соответствовать конусу,
а 1 и 4 — параллелепипеду.
Учитель. Итак, все задачи решены. Сейчас скажите:
— Чем мы сегодня занимались на уроке?
Ученики. Изучали тела вращения: конус, шар, цилиндр.
Учитель.
— На какие две группы делятся все геометрические тела?
Ученики. Многогранники, тела вращения.
Учитель.
— При вращении какой плоской фигуры образуется цилиндр?
Ученики. Прямоугольника.
Учитель.
— Приведите примеры тел конической формы.
Ученики. Воронка, ведро, горшок для цветов, мороженое-рожок и др.
Учитель.
— Какие фигуры могут быть в сечении конуса?
Ученики. Треугольник, круг, эллипс.
Учитель.
— Чем отличаются понятия «шар» и «сфера»?
Ученики. Сфера — это только поверхность шара, а шар — часть пространства, ограниченное сферой.
Домашнее задание: рассказ по плану: I ряду — о цилиндре, II ряду — о конусе, III ряду — о шаре; на альбомном листе нарисовать предметы, имеющие форму вновь изученных геометрических фигур.
Литература
Виленкин Н.Я. Математика: Учеб. для 6 кл. общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 6-е изд. – М.: Мнемозина, 2000. – 304 с.: ил.
Ерганжиева Л.
 Н. Наглядная геометрия. 5 – 6 кл.: Пособие для общеобразовательных учебных заведений / Ерганжиева Л.Н., Шарыгин И.Ф. – 3-е изд., стереотип. – М.: Дрофа, 2000. – 192 с.: ил.
Н. Наглядная геометрия. 5 – 6 кл.: Пособие для общеобразовательных учебных заведений / Ерганжиева Л.Н., Шарыгин И.Ф. – 3-е изд., стереотип. – М.: Дрофа, 2000. – 192 с.: ил.
Геометрические фигуры из бумаги
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.

- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры.
 Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. - Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание.
 С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы. - Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее.
 Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах. - Вырезаем и склеиваем фигуру.
- Пирамида готова!
Читайте также:
ЧЕРЧЕНИЕ. Школьный интернет-учебник — Чтение чертежей 3-4
Многообразие геометрических форм
На уроках математики вы уже познакомились с некоторыми геометрическими фигурами. Под фигурой понимают любую совокупность (множество) точек. Всякую сложную фигуру можно разделить на более простые.
Если все точки фигуры лежат в одной плоскости, фигуру называют плоской: треугольник, квадрат и др. Совокупность точек, расположенных в пространстве, образует пространственную фигуру: куб, цилиндр и др. Фигуры в пространстве называют геометрическими телами.
Предметы, которые нас окружают, детали машин имеют, как правило, сложную реальную геометрическую форму. Однако, присмотревшись к ним внимательно, можно заметить, что некоторые из них состоят из одного или нескольких простых геометрических тел или их видоизмененных частей. Такими геометрическими телами, образующими форму предметов, являются призмы, пирамиды, цилиндры, конусы, шары и др. (рис. 1)
Однако, присмотревшись к ним внимательно, можно заметить, что некоторые из них состоят из одного или нескольких простых геометрических тел или их видоизмененных частей. Такими геометрическими телами, образующими форму предметов, являются призмы, пирамиды, цилиндры, конусы, шары и др. (рис. 1)
Рис. 1. Геометрические тела
По форме простые геометрические тела делятся на многогранники и тела вращения. Плоскость является частным случаем поверхности.
Многогранники – геометрические тела, поверхность которых состоит из плоских многоугольников. Это куб, призма, параллелепипед, пирамида и др.
Тела вращения – геометрические тела, поверхность которых описывается какой-либо прямой или кривой (образующей) при её вращении вокруг неподвижной оси (например, конус, цилиндр, шар и т. п.).
Форма каждого геометрического тела имеет свои характерные признаки.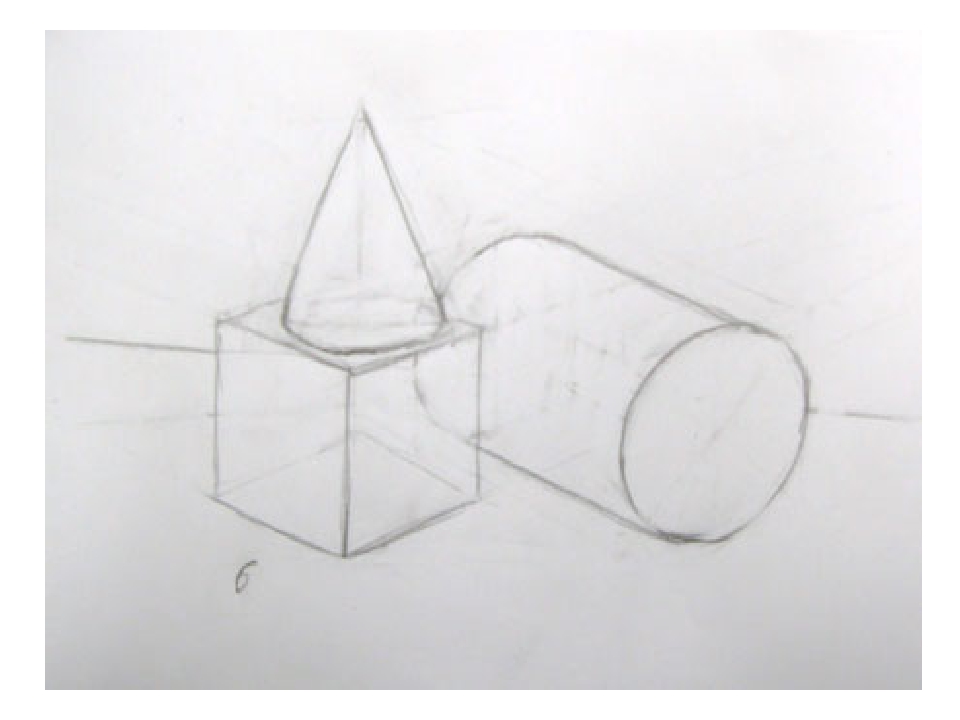 По ним мы отличаем призму от цилиндра, пирамиду от конуса и т. п. Эти признаки используются и при построении чертежей геометрических тел или состоящих из них предметов и деталей. Однако прежде чем выполнять такие чертежи, выясним, какие правила положены в основу способов их построения.
По ним мы отличаем призму от цилиндра, пирамиду от конуса и т. п. Эти признаки используются и при построении чертежей геометрических тел или состоящих из них предметов и деталей. Однако прежде чем выполнять такие чертежи, выясним, какие правила положены в основу способов их построения.
Поскольку форма большинства предметов представляет собой сочетание различных геометрических тел или их частей, для построения чертежей этих предметов необходимо знать, как изображается каждое геометрическое тело. Поэтому рассмотрим сначала построение чертежей и аксонометрических проекций простых тел. Это тем более необходимо, так как в сложной форме любого предмета всегда можно выделить простые геометрические тела, которые помогают представить форму предмета по его чертежу.
Изображение многогранников
Рассмотрим построение прямоугольных проекций призмы. Для примера возьмем треугольную призму (рис. 2) и шестиугольную призму (рис. 3). Их основания, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях — отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых — на тех, которым перпендикулярны. Грани, наклонные к плоскостям, изображаются на них искаженными.
3). Их основания, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях — отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых — на тех, которым перпендикулярны. Грани, наклонные к плоскостям, изображаются на них искаженными.
Рис. 2. Треугольная призма
Рис. 3. Шестиугольная призма.
Размеры призм определяются их высотами и размерами фигур основания. Штрихпунктирными линиями на чертеже изображаются оси симметрии.
Рассмотрим, как изображают на чертеже правильную четырехугольную пирамиду (рис. 4). Основание пирамиды проецируется на горизонтальную плоскость проекций в натуральную величину. На нём диагоналями изображаются проекции боковых ребер, идущих от вершин основания к вершине пирамиды.
Рис. 4. Четырехугольная пирамида
4. Четырехугольная пирамида
Фронтальная и профильная проекции пирамиды — равнобедренные треугольники. Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h.
Изображение тел вращения
Если круги, лежащие в основаниях цилиндра (рис. 5) и конуса 6), расположены параллельно горизонтальной плоскости проекций, их проекции на эту плоскость будут также кругами.
Рис. 5. Цилиндр
Рис. 6. Конус
Фронтальная и профильная проекции цилиндра в данном случае – прямоугольники, а конуса – равнобедренные треугольники.
На всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса.
Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря знаку диаметра Ø можно представить форму цилиндра и конуса даже по одной проекции (рис. 7, a и б). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях. Размеры цилиндра и конуса определяются их высотой h и диаметром основания d.
Кроме того, благодаря знаку диаметра Ø можно представить форму цилиндра и конуса даже по одной проекции (рис. 7, a и б). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях. Размеры цилиндра и конуса определяются их высотой h и диаметром основания d.
Рис. 7. Чертежи цилиндра, конуса и шара
Все проекции шара – круги, диаметр которых равен диаметру шара. На каждой проекции проводят центровые линии.
Благодаря знаку Ø, шар можно изображать в одной проекции (рис. 7, в). Но если по чертежу трудно отличить сферу от других поверхностей, то на чертеже добавляют слово «сфера», например: «Сфера Ø40».
Анализ геометрической формы
Вы знаете, что форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как они изображаются.
Форма каждого геометрического тела имеет свои характерные признаки. В основе формы деталей машин и механизмов также находятся геометрические тела. Чтобы понять по чертежу форму сложного предмета, его мысленно разделяют на части, представляющие собой геометрические тела, т. е. анализируют форму (рис. 8). Затем мысленно объединив эти части, воссоздают общую форму предмета.
В основе формы деталей машин и механизмов также находятся геометрические тела. Чтобы понять по чертежу форму сложного предмета, его мысленно разделяют на части, представляющие собой геометрические тела, т. е. анализируют форму (рис. 8). Затем мысленно объединив эти части, воссоздают общую форму предмета.
Рис. 8. Кофейник и его элементы
Геометрической формой называется внешний облик предмета, характеризующийся совокупностью его геометрических свойств. К геометрическим свойствам предметов относятся: размеры, пропорции, взаимное расположение составляющих элементов формы.
Предметы бывают простой и сложной формы. К предметам простой формы относятся те, которые представляют собой геометрические тела: цилиндр, конус, шар, призма, пирамида (рис. 9, а). К предметам сложной (составной) формы относятся такие, которые образованы сочетанием различных геометрических тел (рис. 9, б).
Рис. 9. Предметы простой (а) и сложной (б) формы
9. Предметы простой (а) и сложной (б) формы
Основные геометрические тела можно выявить в любой детали или предмете. Так, на рисунке 10, а в прямоугольной проекции изображена деталь, называемая валиком (от слова «вал»). В ней можно выделить такие геометрические тела, как усеченный конус 1, цилиндр 2, параллелепипед 3 и еще один цилиндр, большего диаметра – 4 (рис. 10, б).
Рис. 10. Анализ геометрической формы детали
Чтобы представить по чертежу общую форму любой детали, необходимо выявить форму всех ее элементов. Для этой цели сложную по форме деталь мысленно разделяют на отдельные конструктивные части, имеющие форму различных геометрических тел. Мысленное разделение предмета на основные геометрические тела называют анализом геометрической формы предмета. Используя изображение детали, размерные числа, условные знаки и надписи, можно воссоздать образ детали, т. е. представить по чертежу ее пространственную форму.
Ещё проанализируем форму детали (рис. 11), состоящей из трех геометрических тел: конусов (прямого кругового и усеченного) и цилиндра.
Рис. 11. Анализ геометрической формы детали «Конус» на основе расчленения ее на геометрические тела: 1 – конус; 2 – усеченный конус; 3 – цилиндр
Все части, составляющие форму рассматриваемого изделия, расположены на одной оси (т. е. соосны). К основанию конуса примыкает равновеликое основание усеченного конуса. Другое основание усеченного конуса совмещается с основанием цилиндра, диаметр которого меньше диаметра конуса.
Попробуйте выполнить чертеж детали, представленной на рисунке 12.
Рис. 12. Геометрическая разборка формы детали
Нарисовать рисунок состоящий из геометрических фигур. Рисование геометрических тел
/ Натюрморт
1 рис. Намечаем горизонт — линию стола. Компонуем натюрморт, посредством прямых линий. Получается форма домика, с небольшим наклоном в левый бок. Находим центр и проводим вертикальную ось, а затем и горизонтальную. Отлично мы закомпонавали композицию натюрморта.
Компонуем натюрморт, посредством прямых линий. Получается форма домика, с небольшим наклоном в левый бок. Находим центр и проводим вертикальную ось, а затем и горизонтальную. Отлично мы закомпонавали композицию натюрморта.
2 рис. Далее мы должны закомпоновать сами предметы в композицию. Будем использовать в компоновке форму круга и овала. Обратите внимание, как формы располагаются между линий, где заходят за линии, какой наклон имеют.
3 рис. Здесь наша задача — построить 3 объемных геометрических фигуры (куб, шар и цилиндр). Шар — найти центр и провести две оси, отмерить от центра равные стороны и сделать симметричную форму.
Куб
— найти точки лицевого квадрата, убедитесь, что линии параллельны, затем от точек «А», «Б» и «С» проведите параллельные друг другу диагонали, найдите на них точки при помощи линейки отмерьте одинаковую длину. Соедините точки. Цилиндр
— проведите по направлению длины (с наклоном) центральную ось, и найдите точки для перекрестных осей цилиндра. Отмеряем равные расстояния от центра осей при помощи линейки (как делали шар).
Отмеряем равные расстояния от центра осей при помощи линейки (как делали шар).
4 рис. Теперь нам нужно показать на предметах тень, свет и падающую тень от предметов. По направлению лучей света видно где на предметах будет тень и свет. Накладывая штрих по форме мы показываем основные градации. Смотрите внимательно на рисунок.
5 рис. Отлично! Теперь вам важно узнать, что такое рефлекс. Рефлекс — это отражение света. Как правило он изображается на теневой стороне (см.рис.). И есть такие понятия, как полутень и полусвет — это плавный переход из тени к свету. Здесь мы должны показать плотность штрихом. Нужно углубить тень, полутень, полусвет, рефлекс и падающую тень от предметов.
Как научиться ложить штрих по форме предмета- будем усовершенствовать свое мастерство владения карандашом и учиться создавать рисунок геометрических фигур, создавая их объем. В нашем арсенале есть куб, шар, конус и цилиндр.
Наша работа будет разделяться на две части. Первая часть- мы рисуем по- представлению. Возможно у вас есть макеты этих фигур, если нет, то
тогда можете заглянуть на страницу как сделать макет геометрических фигур и, собственно, сделать их,
но начнем мы с вами с другого. Мы начнем с понимания, анализа формы сначала без макетов. Вы можете сначала их создать и иногда посматривать
на них при рисовании, но главное сейчас- научиться анализировать, логически мыслить, вся ваша работа сейчас заключается в том, что- бы думая,
без натуры, научиться передавать форму этих основных фигур.
Изначально ведь работа проходит в голове, а не перед глазами. Верно?
Первая часть- мы рисуем по- представлению. Возможно у вас есть макеты этих фигур, если нет, то
тогда можете заглянуть на страницу как сделать макет геометрических фигур и, собственно, сделать их,
но начнем мы с вами с другого. Мы начнем с понимания, анализа формы сначала без макетов. Вы можете сначала их создать и иногда посматривать
на них при рисовании, но главное сейчас- научиться анализировать, логически мыслить, вся ваша работа сейчас заключается в том, что- бы думая,
без натуры, научиться передавать форму этих основных фигур.
Изначально ведь работа проходит в голове, а не перед глазами. Верно?
Вторая часть- будем рисовать с натуры, но так- же, как и в первом случае, не цепляемся к натуре сильно, а в первую очередь думаем и анализируем сами, и теперь уже проверяем себя с тем, что нам показывает натура.
Итак, первая часть. Можно рисовать на формате А3. Берем ватман, карандаш и рисуем фигуру, также не плохо
использовать знания перспективы при построении ее. А потом начинаете «ложить» штрих по форме, вылепливая объем фигуры при помощи своего ума и
карандаша.
Мы уже знаем, что светотень распределяется по форме предмета, создавая тональные градации, или зоны. Пока возьмем три основные- свет, полутень и тень. Ограничиваемся только фигурами, не используя все пространство.
Давайте нарисуем куб.
Избегаем ошибок. У меня на рисунке слева сильно передана перспектива , чересчур, так не делайте.
Здесь достаточно совсем немного передать ее, слегка исказив форму. Посмотрите на рисунок справа. Видите разницу между передней стенкой и задней?
Этого достаточно. Не такие у нас большие размеры используются, что- бы мы из малых форм превращали архитектуру.
Поговорим о светопередаче. Свет, тень и полутень показаны.
Но не забудьте о золотом правиле- свет удаляясь по форме предмета темнеет, тень- светлеет. Смотрите: свет, удаляясь в перспективу слегка теряет
свою яркость, добавьте туда немного штриховочки. А теперь полутень и тень, та- же картина, но в обратном порядке. Тень удаляясь слабеет, слегка
светлеет. Но все равно, общий тон тени никогда не будет светлее общего тона света, и полутень тоже не вырывается из своих тоновых границ. Все на своем месте.
Все на своем месте.
Смотрим еще: как мы проводили обучение с первого нашего урока, см. основы рисунка , о том не забываем и сейчас. Ближние к нам углы и грани выделяем, делаем на них акценты. Ближняя грань и углы у меня акцентированы, чем и берут основное внимание на себя, все остальное плавно уходит в пространство. Но сильно здесь это пространство не нужно передавать, так как расстояния у нас, в принципе, маленькие.
Замечание: как определить общий тон- прищурьте немного глаза. Резкость убавится и вы сможете увидеть все в общем. И еще не надо смотреть на работу «влоб», почаще отдаляйте ее от себя, рассеивайте зрение, не цепляйтесь за детали.
И дальше остальные фигуры. Эти фигуры, в общем, у нас достаточно обтекаемы, заокруглены, так- что замечаем следующее:
Допустим, первым в ряду стоит шар. Акцентом на нем здесь является тень и наиболее сильна она будет в том месте, где шар приближен к
нам более всего. По краям у меня акцентов нет, так как там форма ушла в пространство- учитывайте этот момент при рисовании обтекаемой формы.
Так- же дело обстоит и с цилиндром и конусом. Там, где форма начинает заворачиваться и уходит в пространство- акцент делать не стоит. Но где и нужно акцентировать форму, то там, где идет излом формы и там, где это будет ближе всего к нашим глазам.
Обратите внимание на конус- нижняя часть его к нам приближена больше, чем верхушка. Значит, нижняя часть его будет передана сильнее, а поднимаясь к верху слабее- смотрите на тень, внизу она сильнее, в то время как поднимаясь вверх она теряет свою активность. Не делайте ее одинаковой тональности по всей высоте. Величины эти здесь не огромны, но все равно существуют, иначе условное пространство правильно не передать.
Останавливаю ваше внимание на штриховке. Это что- ни- на- есть стопроцентный штрих, который ложится по форме.
Несмотря на то, что он несколько однообразен и скучноват, но очень полезен в плане обучения. Он учит дисциплинированности, концентрации
внимания, учит делать ровные линии и просто чистоте исполнения. Рекомендую выполнить эту работу с применением именно этого штриха,
просто старайтесь «вылепливать» форму геометрической фигуры, прочувствуйте руками и глазами весь ее объем и как ее форма
«живет» в пространстве. Написано странно, но стараюсь как можно сочнее передать вам всю прелесть этого упражнения. А о штрихах,
которые должны ложиться по форме предмета и какие ими не являются мы с вами дальше еще поговорим.
Написано странно, но стараюсь как можно сочнее передать вам всю прелесть этого упражнения. А о штрихах,
которые должны ложиться по форме предмета и какие ими не являются мы с вами дальше еще поговорим.
И непереживайте, если что- то не будет получаться. Никто не застрахован от ошибок, а их может быть много и идеального на свете не существует ничего. Но у каждого из нас есть возможность попробовать еще раз, дабы сделать еще лучше.
Как нарисовать геометрические фигуры
Как нарисовать геометрические фигуры- теперь попробуем нарисовать геометрические фигуры с окружением. Окутаем их воздухом, нарисуем в пространстве. Берем основные:
Первым у нас пусть пойдет цилиндр.
Ставим цилиндр на предметную плоскость- стол, освещение ставим так, что- бы тень от фигуры падала красиво на предметную плоскость,
не была ни сильно растянутой, ни маленькой- была гармоничной и подчеркивала объем фигуры.
Натяните бумагу на
планшет , чтобы создать чистый рисунок.
Берите планшет размером 30-40, для такой работы вполне достаточно.
Теперь нам нужно закомпоновать наш цилиндр в плоскости листа, найдите его гармоничное место в пространстве листа, учитывая и тени, обязательно. Используйте для поиска пропорций глазомер, подкрепляйте его ощущениями линейной перспективы.
Обязательно передайте предметную плоскость. Фигура у нас не «плавает» в пространстве, она находится на предметной плоскости!
При построении фигуры обязательно показывайте и невидимые грани, показывайте как строите- линии построения. Это нужно более вам, чем зрителю. Расставляйте акценты там, где это нужно, показывайте пересечение плоскостей. Не забывайте о перспективе. Если вы заметили, то нижняя плоскость цилиндра нам видна больше, чем верхняя, оно и правильно, так как линия горизонта (по крайней мере у меня, у вас может быть по- другому), дает такой обзор.
Посмотрите как строится тень- ее можно правильно передать, используя линии построений. Образно: от источника света идут лучи, которые
разделяются на два вида, одни- освещают фигуру, останавливаются на ней, потому за фигурой дальше света не будет.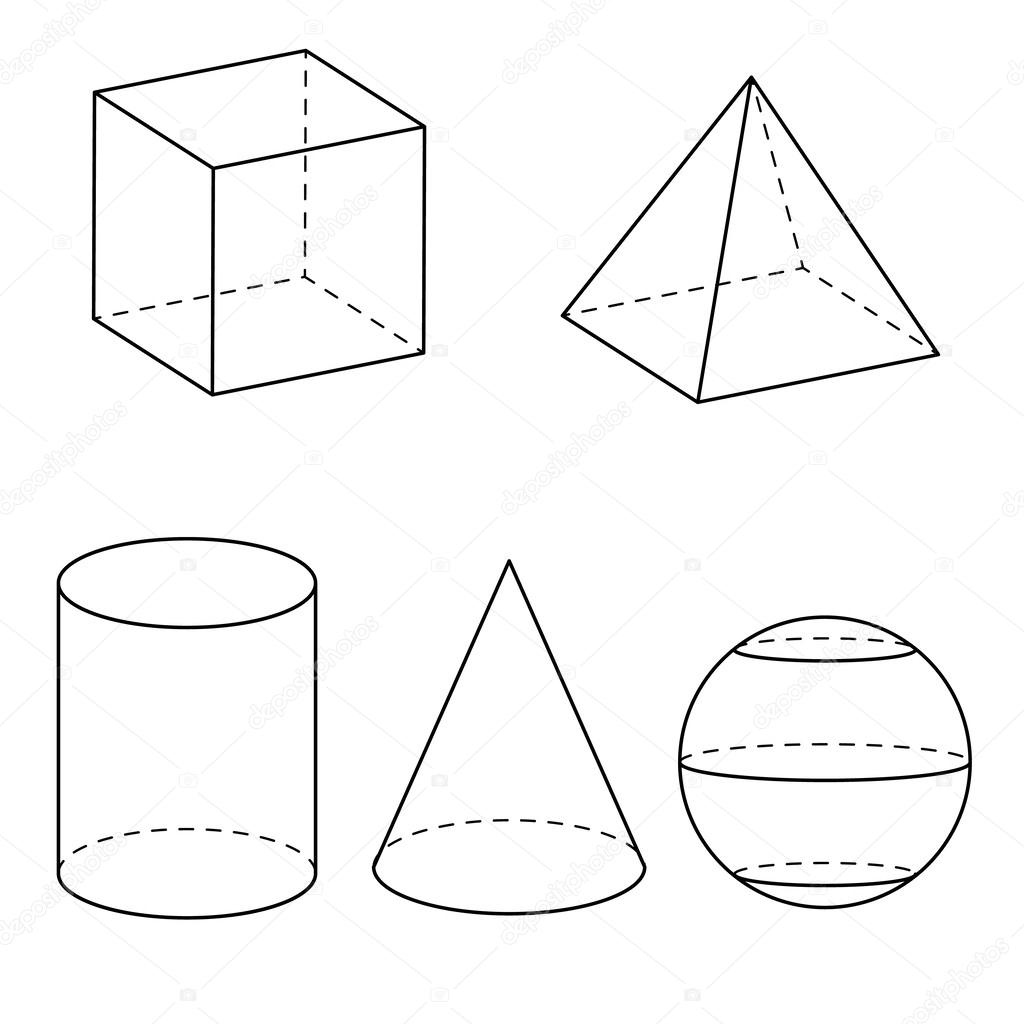 А лучи света, которые
не попадают на фигуру идут дальше, освещая все на своем пути.
И эту границу мы с вами можем показать. И еще: тень, удаляясь от фигуры, будет иметь тенденцию к некоторому увеличению, это напоминает
обратную перспективу. Понимаете почему? Если направить лучи наоборот, то линии построения тени сойдутся в одной точке- точке, из которой идет свет.
А лучи света, которые
не попадают на фигуру идут дальше, освещая все на своем пути.
И эту границу мы с вами можем показать. И еще: тень, удаляясь от фигуры, будет иметь тенденцию к некоторому увеличению, это напоминает
обратную перспективу. Понимаете почему? Если направить лучи наоборот, то линии построения тени сойдутся в одной точке- точке, из которой идет свет.
Вот примерно так у вас должно получиться.
Дальше в принципе натура нам уже и не нужна, так как все можно проанализировать самостоятельно. Включить аналитическое мышление и
логически рассуждать. Но, все- же, давайте разбирать дальше:
По фигуре видно, что свет падает со стороны и сверху. Значит, верхняя плоскость цилиндра у нас будет освещена более всего, и свет так- же
будет падать на предметную плоскость, так как она тоже как и плоскость цилиндра- горизонтальна. Вертикальные плоскости- стена и обрыв
предметной плоскости, а так- же, сам объем цилиндра будут получать меньше освещения, так как падающего основного света они не получают.
Дальше: предметную плоскость мы черной не делаем- угол предметной плоскости получает в данном случае достаточно света, что- бы тень не была здесь самой активной. Но выделить ее- предметную плоскость все- таки нужно. Это достигается за счет выделения угла предметной плоскости.
Дальше: наша предметная плоскость получает основной свет, но нам нужно показать, что она горизонтально расположена. И мы знаем, что удаляясь свет гаснет, слабеет. Вот чем дальше от нас предметная плоскость будет уходить, тем слабее ее свет будет- ложим штрих таким образом.
Теперь надо разобраться с той частью цилиндра, что будет находиться в тени. Цилиндр у нас расположен вертикально к предметной
плоскости, значит основной свет будет падать на горизонтальную его верхнюю плоскость. Все остальное- в тени, за исключением того участка,
где свет скользит по форме, так как свет падает не точно сверху, а немного со стороны- этот участок у меня выделен самым светлым на
вертикальной плоскости его. Общая- же тень цилиндра активнее стены, так как цилиндр имеет активную собственную тень и сам к нам ближе,
хоть стена также расположена вертикально.
Стена- же будет темнее предметной плоскости, потому как она вертикальна- значит света здесь будет меньше, и потому, что она будет находиться дальше всего, будет на заднем плане. Ложим штрих таким образом.
Падающая тень фигуры будет самой активной, но она так- же лежит на предметной плоскости, а потому- удаляясь на ней будет немного становиться слабее.
Ну и осталось расставить акценты там, где это необходимо- изломы форм, которые будут к нам располагаться ближе- будут акцентированы.
Если по началу рука не слушается, трудно держать
карандаш и трудно ложить штрих по форме, да и четко определить саму форму штрихом трудно, то есть возможность поработать так, как показано на рисунке слева.
Легонько намечаете изломы формы.
То- есть: допустим, вы в курсе, как распределяется свет по форме предмета. Вы знаете, что этих зон пять: блик, свет, полутень, тень и
рефлекс. Это все точно, но условно. Что- бы передать более качественно объем фигуры, вы можете намечать сколько угодно изломов, и
чем их будет больше, тем объем фигуры будет показан мягче. Зрительно разделяете фигуру на эти зоны и ложите обычный прямой штришок, но так,
что- бы вылепить объем- используете частоту стежка- штриха или силу нажима карандаша.
Зрительно разделяете фигуру на эти зоны и ложите обычный прямой штришок, но так,
что- бы вылепить объем- используете частоту стежка- штриха или силу нажима карандаша.
Здесь прошу вас не путать два понятия: как распределяется свет по форме предмета и как ложится штрих по форме предмета. В первом случае у нас- 5 зон, во втором- можем намечать столько зон, изломов формы, сколько вам будет нужно. Но не черните, все вспомагательные линии должны быть малозаметными.
Замечание: если вы могли заметить, посмотрев на этот рисунок, то увидели, что с более освещенной стороны
конуса стена на заднем плане темнее, а с другой, менее освещенной стороны конуса- стена светлее.
Дело в том, что стена одинакова и там и там, но так уж видит наш глаз.
Для остроты ощущения действительности, для наилучшего акцента света и тени, для гармоничного осязания нашим глазом рисунка, да и в
конце концов, давайте сделаем нашему глазу приятное! Пусть он видит в рисунке то, что видит в натуре. Это только легкий нюанс,
который только обогатит наш рисунок, можно ненавязчиво передать.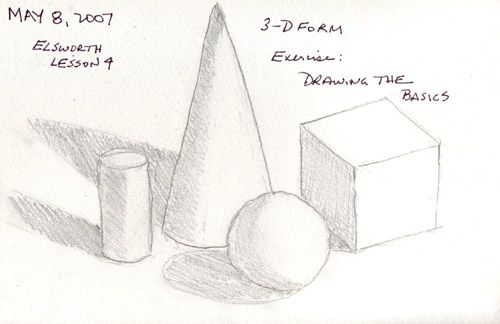
Дополнение: смотрите как строится тень у конуса.
Дальше давайте сделаем рисунок шара.
Построение вы можете увидеть слева.
Заметьте, как строится тень фигуры. С падающей мы уже разобрались, вроде: определяем с помощью глазомера и подкрепляем знаниями перспективы.
Не забывайте, что тень падает на предметную плоскость- это нужно передать и понимать.
А вот как дела обстоят с собственной тенью? Интересно, что если провести линии от точки освещения до центра шара, через который проходит диаметр, который образует круг тени, то этот диаметр будет перпендикулярен линии, проведенной до точки освещения. Если это понять, то и как ложить штрих по форме шара, дабы показать собственную тень- совсем не сложно.
Теперь мне что- то стало скучновато рисовать в одной манере и захотелось поэкспериментировать.
Посмотрите на работу справа. Как вы думаете, она выполнена штриховкой? Не похоже. Она выполнена тональным пятном с использованием
карандашей различой степени мягкости. Если вы возьмете карандаши с цельным грифелем, без деревянной оправы, и будете просто набирать
тон на бумаге, а не штриховать, то у вас тоже получится такой вот рисунок.
Если вы возьмете карандаши с цельным грифелем, без деревянной оправы, и будете просто набирать
тон на бумаге, а не штриховать, то у вас тоже получится такой вот рисунок.
А что еще, кроме техники исполнения у нас не так? Свет наместе, тени тоже, значит- все в порядке.
Но все- же рассмотрим детальнее. Самый яркий свет у нас будет на освещенной стороне шара, на плоскости он будет не таким активным и будет слабеть с удалением от нас. Самая темная тень будет падающая, на изломе предметной плоскости будет света немного больше, но тем не менее, акцентируем эту область.
Посмотрите на собственную тень шара- я ставлю акцент на той области его, которая будет ближе к нам, и заворачиваясь по форме, тень
будет терять активность. Помните: шар- форма обтекаемая.
Стена
в полутени, притом на заднем плане- вот пусть там ненавязчиво и остается. Единственное- она будет «играть» с объемом шара.
Со стороны света стена будет казаться несколько темнее, со стороны тени- светлее. Давайте и здесь сделаем нашему глазу приятное;)
Давайте и здесь сделаем нашему глазу приятное;)
Как научиться ложить штрих по форме предмета. Штриховка
Вот тут мы плавно подошли к тому, о чем уже говорили в самом начале этой страницы. Как ложится штрих по форме предмета и какой штрих таковым не является. Дело в том, что у каждого рисовальщика, в процессе работы или учебы вырабатывается свой определенный стиль штриха. Конечно, есть каноны, у различных исторических времен свои собственные каноны рисования и штриха, но совсем не обязательно им придерживаться. По желанию. Я считаю, если с помощью штриха можно передать объем фигуры и само пространство в листе, то абсолютно все равно, что с себя представляет этот штрих. Главное, что- бы было грамотно все сделано и красиво. По простому- не делайте соломы, учитесь рисовать красиво. К штриху это так- же относится. На этой странице мы учились делать штрих, продолжим еще немного.
Вот например вот так, как я рисую кубик, который у нас еще остался не нарисован.
1. Определяем место фигуры в листе
Определяем место фигуры в листе
2. Располагаем фигуру на предметной плоскости и находим его конструкцию и его тень, не забывая учитывать перспективу
3. Определяем место света и тени- ложим легкий штрих. Это дает нам возможность сразу определиться с распределением света и тени в нашем рисунке, разделить их
Если вы посмотрите на штрих, которым выполнена работа, то он достаточно необычен, верно? На уроках рисунка к такому штриху лучше не прибегать, не пугайте учителей, у них не такие современные прогрессивные взгляды, как у вас. Но в своих творческих работах такой штрих применять можно, почему бы и нет? Ведь рисунок сделан по всем законам. Передано пространство в листе, показана форма предмета, переданы основные тональные соотношения в нашем рисунке. Но к этому еще мы добавили штрих, который делает работу интересной и воздушной. Ну а дальше опять, разбираем рисунок, анализируем:
Давайте пройдемся по основным
тональным отношениям, для начала по теням:
самая темная тень- падающая, дальше идет собственная тень куба.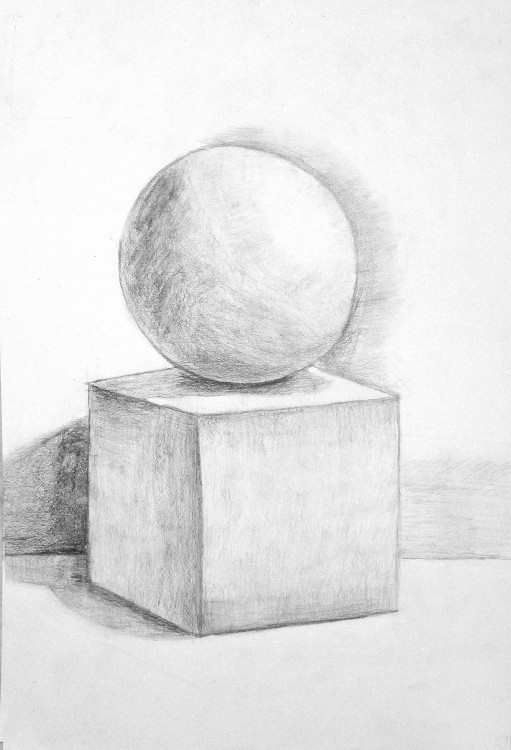 Излом предметной плоскости занимает третье место, ее мы выделяем,
но не черним, так как там достаточно света. И четвертая- стена, на которую тоже попадает свет, можно сказать, что стена находится
в полутени, но дальше всего. Смотрите как играет полутень стены с формой куба: со стороны освещенной части куба стена темнее, со
стороны тени- светлеет. Эти градации могут быть очень невелеки, но они присутствуют.
Излом предметной плоскости занимает третье место, ее мы выделяем,
но не черним, так как там достаточно света. И четвертая- стена, на которую тоже попадает свет, можно сказать, что стена находится
в полутени, но дальше всего. Смотрите как играет полутень стены с формой куба: со стороны освещенной части куба стена темнее, со
стороны тени- светлеет. Эти градации могут быть очень невелеки, но они присутствуют.
Дальше анализируем свет: самая светлая и освещенная часть будет верхняя плоскость куба, вторая по светлоте- предметная плоскость, которая находится перед нами горизонтально и уходя в пространство- теряет свет.
На изломах форм делаем акценты. Ближние грани куба и углы выделяем, это поможет вытащить его из пространства наперед.
И не забываем- свет удаляясь темнеет, гаснет, тень удаляясь теряет свою активность и несколько светлеет, но учитываем золотое правило: самый темный полутон на свету светлее самого светлого полутона в тени.
На последок: если вы решите поэкспериментировать со штриховкой. Так как и варьируется тональность свето- тени, которую мы передаем
в пространстве листа, так и штрих может изменять форму-
поиграйте с размером штриха. Стена выполнена штрихом среднего стежка, довольно статичная. Куб выполнен мелким и активным штришком,
придающим кубу динамику. А предметная плоскость выполнена длинными стежками, довольно тривиальными и малоинтересными. Так что,
даже штрих помогает выявить в картине главное действующее лицо- куб, который выполнен наиболее динамичным штрихом, притягивающим
внимание, на мой взгляд. А как вам кажется?
Так как и варьируется тональность свето- тени, которую мы передаем
в пространстве листа, так и штрих может изменять форму-
поиграйте с размером штриха. Стена выполнена штрихом среднего стежка, довольно статичная. Куб выполнен мелким и активным штришком,
придающим кубу динамику. А предметная плоскость выполнена длинными стежками, довольно тривиальными и малоинтересными. Так что,
даже штрих помогает выявить в картине главное действующее лицо- куб, который выполнен наиболее динамичным штрихом, притягивающим
внимание, на мой взгляд. А как вам кажется?
Попробуйде сделать что- то свое, поэкспериментируйте, тогда самая простая работа будет выполняться с удовольствием, большим
вниманием и огромным интересом. А когда вы сидите, выполняете работу, например- стараетесь ровно положить штрих по форме, да
еще у вас и получается, и при этом начинаете замечать, что от концентрации вашего внимания замирает дыхание, вот в эти самые
минуты и ощущаешь всю предесть рисунка и получаешь несказанное удовольствие.
С данного урока начинается наша программа обучения рисунку. В этом задании рассматривается тема рисования простых геометрических фигур .
Рисование геометрических фигур можно сравнить с изучением алфавита для того, кто осваивает иностранный язык. Геометрические формы – первая стадия построения объекта любой сложности. Это хорошо видно в компьютерном моделировании, где построение трехмерного космического корабля начинается с простого кубика. В рисунке все изображаемые предметы всегда состоят или делятся на простые геометрические формы. Для обучения рисунку это значит ровно одно: научившись правильно изображать геометрические фигуры, научитесь рисовать все остальное.
Построение геометрических фигур.
Начинать построение нужно с анализа модели, образно говоря, проникнуть вглубь конструкции на уровень вершин и линий. Это значит, представить геометрическую фигуру в виде каркаса, состоящего только из линий и вершин (место пересечения линий), путем воображаемого удаления плоскостей. Важным методологическим приемом является изображение невидимых, но существующих линий. Закрепление такого подхода с первых уроков станет полезным приемом для рисования более сложных моделей.
Важным методологическим приемом является изображение невидимых, но существующих линий. Закрепление такого подхода с первых уроков станет полезным приемом для рисования более сложных моделей.
Далее, под руководством педагога наметить на листе расположение линий и вершин, легкими, скользящими движениями, без нажима на карандаш.
Положению рисунка на листе стоит уделить отдельное внимание по нескольким причинам:
- Нахождение центральной оси листа поможет при дальнейшем построении как отправная точка для вертикальных линий конструкции.
- Определение линии горизонта, для правильного изображения перспективы.
- Учет светотеневой моделировки, собственные и падающие тени, чтобы они поместились в пространстве листа и уравновешивали друг друга.
После нанесения основных конструктивных линий следует детальная прорисовка видимых ребер предмета, в случае с объектами вращения (шар, конус) это внешние края формы.
За конструктивной частью следует штриховая моделировка. На мы подробно разбираем правила и технику нанесения штрихов на геометрические предметы.
На мы подробно разбираем правила и технику нанесения штрихов на геометрические предметы.
Профессиональное обучение рисунку легко сравнить с уроками музыки, где сухие правила и точные схемы в конечном итоге приводят будущего композитора к творческим произведениям. Так и в рисунке законы построения форм, правила перспективы, схемы расположения теней помогают художнику создавать уникальные шедевры.
Отчего опытные художники могут быстро наносить сложные рисунки, не тратя много времени на разметку, построение? Потому что вначале крепко заучили правила и каноны, и теперь достаточно ясно представляют строение любой формы. Схематичный рисунок освобождает внимание автора от конструкции и сосредотачивает фокус на композиции, идее, образе своего творения. Существует мнение, что заученные схемы не дадут художнику полностью раскрыться.
Стоит посмотреть, с чего начинали такие креативные мастера как Пикассо и Дали, чтобы понять ошибочность данного суждения. Но лучшей проверкой станет обучение в нашей студии, где вы на практике убедитесь в плюсах академического подхода.
Но лучшей проверкой станет обучение в нашей студии, где вы на практике убедитесь в плюсах академического подхода.
Ждем Вас в нашей художественной студии!
На простых объемных фигурах отрабатываются базовые навыки рисунка. Здесь важны и умение правильно измерить размеры и соотношения объектов, и грамотно построить перспективу, и скомпоновать изображение в листе, и точно передать светотени. Что же из себя представляют простые объемные фигуры?
Простые объёмные фигуры Под простыми объемными фигурами в рисовании подразумевают такие объемные фигуры, как: куб, параллелепипед, призма, конус, шар. В обучающих целях в рисовании используют фигуры, отлитые из гипса. Все они имеют правильные геометрические черты и гладкую белую поверхность.Геометрически правильные объемные тела помогают отрабатывать умение точно рисовать прямые и кривые линии. Например, в рисовании куба нужно точно определить перспективные сокращения и нарисовать от руки, без вспомогательных средств, ровные его грани. А, в рисовании шара, важно нарисовать правильный круг, опять же без дополнительных подручных средств. Только карандаш, бумага и стёрка.
А, в рисовании шара, важно нарисовать правильный круг, опять же без дополнительных подручных средств. Только карандаш, бумага и стёрка.
Особенности построения объемных фигур
для начинающих художников
В учебном рисунке начального уровня используется техника построения перспективы, при которой вертикальные линии изображаются строго вертикальными, а горизонтальные и диагональные отрисовываются с учетом перспективы.
Такие постулаты построения перспективы, с одной стороны, идут в разрез с современными трендами 3D графики, где машины уже обучены передавать практически не отличимые от реальных перспективные сокращения и мы привыкли к такому качеству отображения действительности. С другой стороны, в обучающих целях изображение вертикальных линий без учета перспективы упрощает начинающему художнику задачу построения пространства и предметов в нем. К тому же, на практике, строго вертикальные линии в работах новичков помогают правильно организовать пространство и смотрятся вполне гармонично.
Светотень в учебном рисунке объемных фигур
В общих чертах разберемся с концепцией учебного тонального рисунка объемных фигур. При нанесении тона в учебном рисунке объемных фигур важно сконцентрироваться на создании иллюзии объема и пространства. Первое достигается путем соблюдения общих основ теории теней. Здесь важно отметить, что при учебном рисовании объемных фигур желательно использовать штриховку по форме этих самых фигур и по направлению теней. Ощущение пространства в учебном рисунке достигается увеличением контрастности светотеневых градаций на переднем плане и смягчением теней на заднем плане.
Когда понадобится: для выявления типов личностей: руководитель, исполнитель, ученый, изобретатель и т. п.
ТЕСТ
«Конструктивный рисунок человека из геометрических фигур»
Инструкция
Нарисуйте, пожалуйста, фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Вы можете увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности.
Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10. Если при рисовании вы использовали большее количество фигур, то нужно зачеркнуть лишние, если же вами использовано фигур меньше чем 10, необходимо дорисовать недостающие.
Ключ к тесту «Конструктивный рисунок человека из геометрических фигур»
Описание
Тест «Конструктивный рисунок человека из геометрических фигур» предназначен для выявления индивидуально-типологических различий.
Сотруднику предлагают три листа бумаги размером 10 × 10 см. Каждый лист нумеруется и подписывается. На первом листе выполняется первый пробный рисунок, далее, соответственно, на листе втором – второй, на листе третьем – третий.
Сотруднику необходимо на каждом листе нарисовать фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Сотрудник может увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности. Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10.
Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10.
Если при рисовании сотрудник использовал большее количество фигур, то ему необходимо зачеркнуть лишние, если же использовал фигур меньше чем 10, ему необходимо дорисовать недостающие.
При нарушении инструкции данные не обрабатываются.
Пример рисунков, сделанных тремя оцениваемыми
Обработка результата
Подсчитайте количество затраченных в изображении человечка треугольников, кругов и квадратов (по каждому рисунку отдельно). Запишите результат в виде трехзначных чисел, где:
- сотни обозначают количество треугольников;
- десятки – количество кругов;
- единицы – количество квадратов.
Эти трехзначные цифры составляют так называемую формулу рисунка, по которой происходит отнесение рисующих к соответствующим типам и подтипам.
Интерпретация результата
Собственные эмпирические исследования, в которых получено и проанализировано более 2000 рисунков, показали, что соотношение различных элементов в конструктивных рисунках не случайно. Анализ позволяет выделить восемь основных типов, которым соответствуют определенные типологические характеристики.
Анализ позволяет выделить восемь основных типов, которым соответствуют определенные типологические характеристики.
Интерпретация теста основана на том, что геометрические фигуры, использованные в рисунках, различаются по семантике:
- треугольник обычно относят к острой, наступательной фигуре, связанной с мужским началом;
- круг – фигура обтекаемая, более созвучна с сочувствием, мягкостью, округлостью, женственностью;
- квадрат, прямоугольник интерпретируются как специфически техническая конструктивная фигура, технический модуль.
Типология, основанная на предпочтении геометрических фигур, позволяет сформировать своего рода систему индивидуально-типологических различий.
Типы
I тип – руководитель
Формулы рисунков: 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640. Наиболее жестко доминирование над другими выражено у подтипов 901, 910, 802, 811, 820; ситуативно – у 703, 712, 721, 730; при воздействии речью на людей – вербальный руководитель или преподавательский подтип – 604, 613, 622, 631, 640.
Обычно это люди, имеющие склонность к руководящей и организаторской деятельности, ориентированные на социально значимые нормы поведения, могут обладать даром хороших рассказчиков, основывающимся на высоком уровне речевого развития. Обладают хорошей адаптацией в социальной сфере, доминирование над другими удерживают в определенных границах.
Нужно помнить, что проявление данных качеств зависит от уровня психического развития. При высоком уровне развития индивидуальные черты развития реализуемы, достаточно хорошо осознаются.
При низком уровне они могут не выявляться в профессиональной деятельности, а присутствовать ситуативно, хуже, если неадекватно ситуациям. Это относится ко всем характеристикам.
II тип – ответственный исполнитель
Формулы рисунков: 505, 514, 523, 532, 541, 550.
Данный тип людей обладает многими чертами типа «руководитель», являясь расположенным к нему, однако в принятии ответственных решений часто присутствуют колебания. Такой человек ориентирован на умение делать дело, высокий профессионализм, обладает высоким чувством ответственности и требовательности к себе и другим, высоко ценит правоту, то есть характеризуется повышенной чувствительностью к правдивости. Часто он страдает соматическими заболеваниями нервного происхождения вследствие перенапряжения.
Часто он страдает соматическими заболеваниями нервного происхождения вследствие перенапряжения.
III тип – тревожно-мнительный
Формулы рисунков: 406, 415, 424, 433, 442, 451, 460.
Данный тип людей характеризуется разнообразием способностей и одаренности – от тонких ручных навыков до литературной одаренности. Обычно этим людям тесно в рамках одной профессии, они могут поменять ее на совершенно противоположную и неожиданную, иметь также хобби, которое по сути является второй профессией. Физически не переносят беспорядка и грязи. Обычно конфликтуют из-за этого с другими людьми. Отличаются повышенной ранимостью и часто сомневаются в себе. Нуждаются в подбадривании.
Кроме этого, 415 – «поэтический подтип» – обычно лица, имеющие такую формулу рисунка, обладают поэтической одаренностью; 424 – подтип людей, узнаваемых по фразе «Как это можно плохо работать? Я себе не представляю, как это можно плохо работать». Люди такого типа отличаются особой тщательностью в работе.
IV тип – ученый
Формулы рисунков: 307, 316, 325, 334, 343, 352, 361, 370.
Эти люди легко абстрагируются от реальности, обладают концептуальным умом, отличаются способностью разрабатывать все свои теории. Обычно обладают душевным равновесием и рационально продумывают свое поведение.
Подтип 316 характеризуется способностью создавать теории, по преимуществу глобальные, или осуществлять большую и сложную координационную работу.
325 – подтип, характеризующийся большой увлеченностью познания жизни, здоровья, биологическими дисциплинами, медициной. Представители этого типа часто встречаются среди лиц, занимающихся синтетическими видами искусства: кино, цирк, театрально-зрелищная режиссура, мультипликация и т. д.
V тип – интуитивный
Формулы рисунков: 208, 217, 226, 235, 244, 253, 262, 271, 280.
Люди этого типа обладают сильной чувствительностью нервной системы, ее высокой истощаемостью. Легче работают на переключаемости от одной деятельности к другой, обычно выступают адвокатами меньшинства. Обладают повышенной чувствительностью к новизне. Альтруистичны, часто проявляют заботу о других, обладают хорошими ручными навыками и образным воображением, что дает им возможность заниматься техническими видами творчества. Обычно вырабатывают свои нормы морали, обладают внутренним самоконтролем, то есть предпочитают самоконтроль, отрицательно реагируя на посягательства, касающиеся их свободы.
Обладают повышенной чувствительностью к новизне. Альтруистичны, часто проявляют заботу о других, обладают хорошими ручными навыками и образным воображением, что дает им возможность заниматься техническими видами творчества. Обычно вырабатывают свои нормы морали, обладают внутренним самоконтролем, то есть предпочитают самоконтроль, отрицательно реагируя на посягательства, касающиеся их свободы.
235 – часто встречается среди профессиональных психологов или лиц с повышенным интересом к психологии;
244 – обладает способностью к литературному творчеству;
217 – обладает способностью к изобретательской деятельности;
226 – имеет большую потребность в новизне, обычно ставит очень высокие критерии достижений для себя.
VI тип – изобретатель, конструктор, художник
Формулы рисунков: 109, 118, 127, 136, 145, 019, 028, 037, 046.
Часто встречается среди лиц с технической жилкой. Это люди, обладающие богатым воображением, пространственным видением, часто занимаются различными видами технического, художественного и интеллектуального творчества.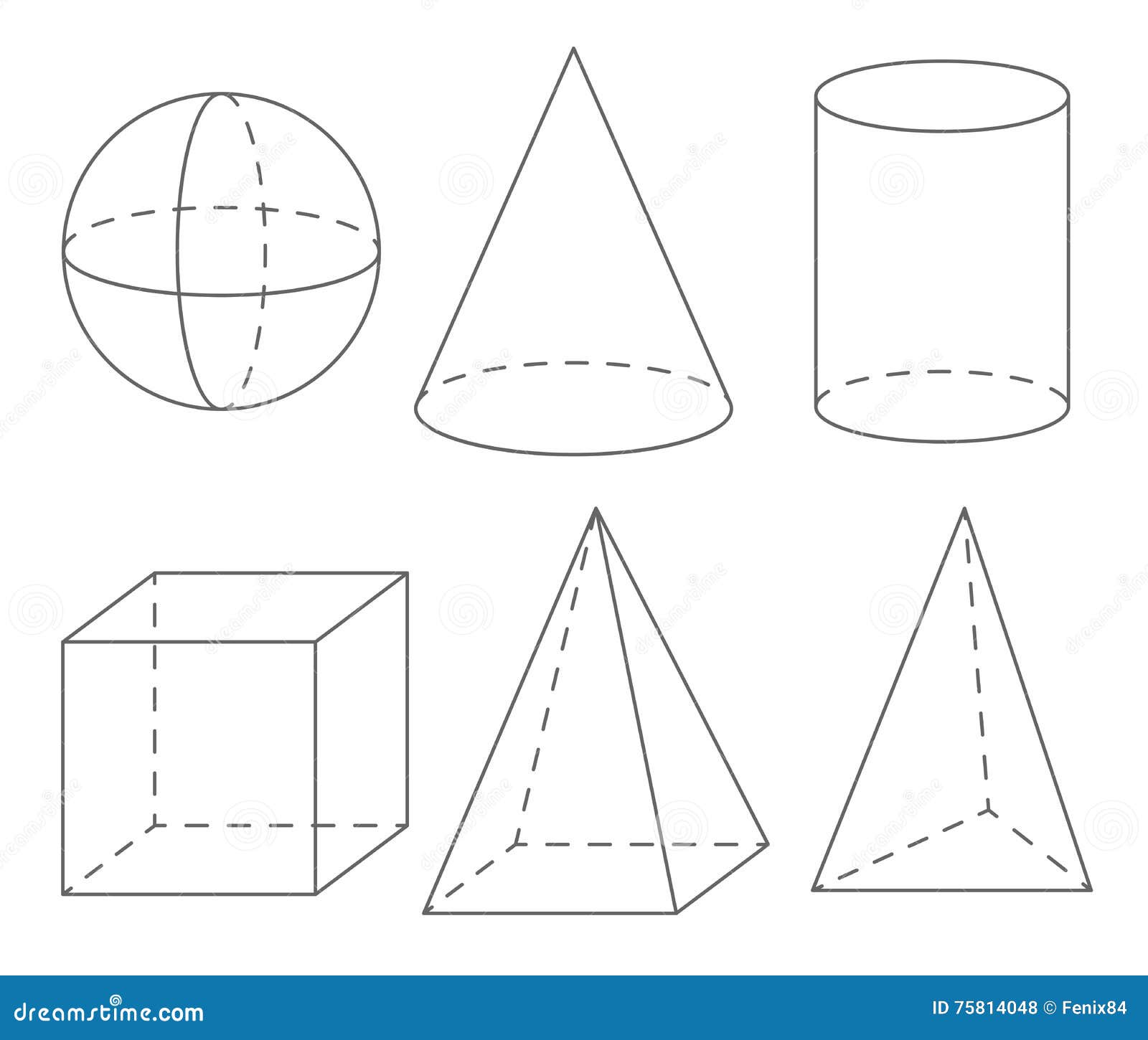 Чаще интровертированы, так же как интуитивный тип, живут собственными моральными нормами, не приемлют никаких воздействий со стороны, кроме самоконтроля. Эмоциональны, одержимы собственными оригинальными идеями.
Чаще интровертированы, так же как интуитивный тип, живут собственными моральными нормами, не приемлют никаких воздействий со стороны, кроме самоконтроля. Эмоциональны, одержимы собственными оригинальными идеями.
Также выделяют особенности следующих подтипов:
019 – встречается среди лиц, хорошо владеющих аудиторией;
118 – тип с наиболее сильно выраженными конструктивными возможностями и способностью к изобретениям.
VII тип – эмотивный
Формулы рисунков: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.
Обладают повышенным сопереживанием по отношению к другим, тяжело переживают жестокие кадры фильма, могут надолго быть выбитыми из колеи и быть потрясенными от жестоких событий. Боли и заботы других людей находят в них участие, сопереживание и сочувствие, на которое они тратят много собственной энергии, в результате становится затруднительной реализация их собственных способностей.
VIII тип – противоположность эмотивного
Формулы рисунков: 901, 802, 703, 604, 505, 406, 307, 208, 109.
Данный тип людей обладает противоположной тенденцией эмотивному типу. Обычно не чувствует переживаний других людей, или относится к ним с невниманием, или даже усиливает давление на людей. Если это хороший специалист, то он может заставить других делать то, что он считает нужным. Иногда для него характерна черствость, которая возникает ситуативно, когда в силу каких-либо причин человек замыкается в кругу собственных проблем.
ПРИХОДИМ ФОРМУ(Ы) Сегодняшний урок…
УРОК ТРЕТИЙ:
ПРИОБРЕТЕНИЕ ФОРМЫСегодняшний урок будет посвящен геометрическим фигурам и формам, а также тому, как передать их с помощью света и тени.
Теперь понятно, что очень мало того, что вы захотите нарисовать, будет состоять из идеальных сфер, кубов или конусов. Но почти каждая сложная, органическая форма? Можно свести к основным геометрическим компонентам. Нос может быть нестандартной геометрической формой, но вы можете построить его, скомбинировав сферы для кончика носа и ноздрей с прямоугольной призмой для переносицы — и если вы знаете, как визуализировать и затенить эти формы, затем затенить нос. становится намного легче.
становится намного легче.
Теперь сфера без тени, просто выглядит как круг. С более квадратными формами немного проще передать трехмерность только с помощью контуров, но иногда все же сложно передать глубину. Вы можете многое передать только контурами и линиями, но мы поговорим о технике, связанной с этим, на следующем уроке. Сегодня мы сосредоточимся на работе со светом и тенью, чтобы передать форму и глубину. Мы сосредоточимся в основном на простых геометрических формах, потому что это наши строительные блоки для построения более подробных, сложных изображений, когда мы чувствуем себя более комфортно с нашими навыками.
Для начала давайте удостоверимся, что мы определили некоторые термины:
- ФОРМА: Двумерная фигура. т. е. круг, квадрат, прямоугольник, треугольник и т. д.
- ФОРМА: Трехмерная фигура. т. е. сфера, куб, призма, конус и т. д.
Технически ничто из того, что мы рисуем, не является трехмерным, поскольку сама страница двумерна, но с помощью индикаторов затенения и глубины мы можем создать иллюзию трехмерное пространство в двухмерном чертеже.
Итак, вот наши термины по форме. Теперь, что касается света и тени, давайте рассмотрим еще несколько терминов:
- БЛЕСК: Область формы, обращенная к источнику света и отражающая больше всего света.
- ПОЛУТОНА: Что написано на банке.
- ОСНОВНАЯ ТЕНЬ: Область формы, наиболее удаленная от источника света, которая имеет самую глубокую область видимой тени.
- ОТРАЖАЮЩАЯ ПОДСВЕТКА: Область более тусклого света, где форма улавливает свет, отраженный другими поверхностями.
- ОТЛИЧАЕМАЯ ТЕНЬ: Тень, которую форма отбрасывает на поверхность, на которой она стоит, или на объекты вокруг нее.
На искривленной поверхности, такой, как мы видим в сфере выше, а также в конусах и цилиндрах, мы видим градиентное затенение. Вдоль одной и той же непрерывной поверхности происходит постепенный переход от области света к области тени.
На плоских поверхностях, таких как кубы, призмы или плоская вершина закрытого цилиндра, свет падает на все точки поверхности под более одинаковым углом, делая каждую видимую сторону сравнительно плоской областью света или тени.(Вы можете увидеть некоторую градацию в зависимости от близости источника света, отражений или небольших вариаций и несовершенств формы, но не до такой степени, как на сфере).
Теперь самый важный шаг в рисовании затененных объектов? ОПРЕДЕЛЯЕТ ВАШ ИСТОЧНИК СВЕТА.
На каждый из этих цилиндров свет падает с разных направлений. На втором цилиндре слева свет идет спереди; видна область самого яркого блика; область самой глубокой тени находится на дальней стороне цилиндра.На цилиндре сразу справа от него все наоборот — мы видим самую глубокую тень, а блик находится на дальней стороне.
В действительности часто бывает несколько источников света — две лампы в комнате, естественный свет из окна плюс внутренний свет, свет, отраженный от нескольких поверхностей и т. д. Но ради наших упражнений по рисованию мы действительно просто сконцентрируюсь на одном основном источнике света на данном рисунке, а также на небольшом количестве отраженного света.
д. Но ради наших упражнений по рисованию мы действительно просто сконцентрируюсь на одном основном источнике света на данном рисунке, а также на небольшом количестве отраженного света.
Если у вас есть несколько объектов на чертеже или сложный объект, состоящий из нескольких геометрических форм, важно отслеживать источник света! Это логически последовательно, и кажется, что все на вашем рисунке занимает одно и то же место. Я часто делаю маленькую стрелку, чтобы напомнить себе угол света, который я могу стереть позже.
Рекомендуемые материалы: Если у вас есть серая бумага и мелки/серая пастель, самое время их использовать.В противном случае отлично подойдет уголь или карандаш и бумага.
УПРАЖНЕНИЕ ПЕРВОЕ: ШКАЛА ЗНАЧЕНИЙ
Когда мы говорим о ценностях в рисовании, мы не говорим о наших моральных принципах (хотя есть фантастическая цитата Г. К. Честертона, что «искусство, как и мораль, состоит из где-то провести черту». ) Вместо этого мы говорим о свете и тьме в очень буквальном смысле.
) Вместо этого мы говорим о свете и тьме в очень буквальном смысле.
Прежде чем рисовать какие-либо фигуры, давайте на минутку изучим весь диапазон вашей шкалы значений.Нарисуйте не менее 9, скажем, 12 коробок одинакового размера, все в ряд соприкасающимися сторонами.
Теперь, начиная с одной стороны, заполните первое поле настолько темным и черным, насколько это возможно.
Используя свои материалы, на каком бы носителе вы ни находились, постарайтесь постепенно заполнить поля от одной стороны к другой, при этом противоположное поле должно быть белым (если вы рисуете на серой бумаге, вы будете хотите заполнить это поле белым мелом, конте или пастелью). Сделайте переход как можно более плавным и постепенным.В конце концов, это должно выглядеть примерно так:
Ценность этого упражнения (аааа, видите, что я там сделал?) заключается в том, чтобы заставить вас изучить ПОЛНЫЙ диапазон доступных вам значений, чтобы вы знали, насколько глубоко вы можете сделать свои тени по сравнению с вашими бликами. Многие люди мало внимания уделяют шейдингу вместо того, чтобы по-настоящему разобраться с полной шкалой значений. Прикрепите это как напоминание о том, что у вас есть в вашем распоряжении!
Многие люди мало внимания уделяют шейдингу вместо того, чтобы по-настоящему разобраться с полной шкалой значений. Прикрепите это как напоминание о том, что у вас есть в вашем распоряжении!
УПРАЖНЕНИЕ ВТОРОЕ: ФОРМЫ ДЛЯ РИСОВАНИЯ
На разных листах бумаги нарисуйте, а затем растушуйте:
реальная жизнь!)
Для каждой формы укажите направление источника света.Выясните свою область подсветки, область основной тени и отбрасываемую тень. Обратитесь к вашей шкале значений! Если вы настроены амбициозно, попробуйте нарисовать формы более одного раза, используя источник света под разными углами.
УПРАЖНЕНИЕ ТРЕТЬЕ: СТРОЙТЕСЬ
Теперь на новом листе попробуйте объединить и перекрыть формы , сохраняя постоянный источник света.
Если вы хотите сделать это со ссылками, вы можете посмотреть в Интернете, ИЛИ — посмотреть в вашей кладовой.Консервы и коробки — отличные простые геометрические ориентиры. Яйца, хотя и имеют яйцевидную форму, имеют оттенок, аналогичный сфере. Посветите настольной лампой на свою композицию, чтобы получить чистый источник света, а затем отойдите!
Посветите настольной лампой на свою композицию, чтобы получить чистый источник света, а затем отойдите!
Как всегда, мой ящик для вопросов открыт, добро пожаловать ко мне, и я буду рад предоставить обратную связь в сообщении, если спросят.
10 заданий по описанию трехмерных фигур в детском саду — KindergartenWorks
Описание трехмерных фигур в детском саду теперь является ожидаемым, поскольку это ключевой стандарт геометрии.Этот стандарт фокусируется на четырех основных трехмерных фигурах:
Учащиеся должны уметь описывать грани, вершины и ребра каждой фигуры.
Итак, какие 3D-фигуры для детского сада и ресурсы для отработки этого стандарта?
Давайте погрузимся!
Трехмерные фигуры в детском саду
Посмотрите на последовательность того, как мы учили фигуры до сих пор:
- В первой четверти мы должны были освоить название двухмерных фигур.
- Во второй четверти мы освоили описание этих фигур (круг, треугольник, прямоугольник, шестиугольник и квадрат).

- В этом третьем квартале мы идентифицируем трехмерные фигуры …
Угадайте, над чем мы работаем в следующем квартале?
Если вы проследили логику, то вы правы. Мы будем экспертами по описанию трехмерных форм .
Я обдумывал планы по внедрению этого стандарта в наши дни, чтобы я мог много раз повторять , не тратя много времени на отработку этих стандартов:
- К.Г.1.д. Определите и назовите следующие фигуры: кубы, конусы, цилиндры и сферы
- K.G.3.b. Определите фигуры как трехмерные и объемные.
- К.Г.4.б. Опишите трехмерные фигуры , чтобы определить их различные атрибуты, включая грани и ребра.
Упражнения и ресурсы
Вот некоторые из моих любимых ресурсов, которые могут сделать именно это — работать над этим стандартом небольшими порциями, чтобы студенты могли освоить его — , не тратя на это много времени.
1.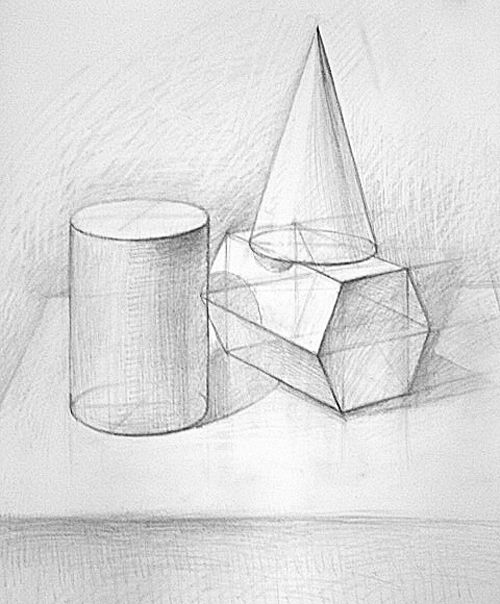 Форма Описание Песнопения. Эти песнопения представляют собой быстрые, знакомые обучающие песни. Мне нравится использовать песни, чтобы помочь учащимся вспомнить важную информацию и попрактиковаться.
Форма Описание Песнопения. Эти песнопения представляют собой быстрые, знакомые обучающие песни. Мне нравится использовать песни, чтобы помочь учащимся вспомнить важную информацию и попрактиковаться.
Они должны помочь ввести наиболее важные описания для каждой формы, включая грани и вершины (углы). Скачать здесь [условия использования]
Если мы говорим о обучении 3D фигурам в стиле детского сада , то использование музыки обязательно!
2. Идентификация или описание фигур. Бинго. Эта классическая игра включает в себя как примеры из реального мира, так и простые трехмерные фигуры для тренировки идентификации или описания фигур.
Фигуры также повернуты, так как предполагается, что учащиеся смогут идентифицировать их независимо от ориентации.
3. 3D Shapes That I Know Video — Вы оцените 3 минуты, которые вы потратите на просмотр всего несколько раз с вашими детьми.
3D Shapes That I Know Video — Вы оцените 3 минуты, которые вы потратите на просмотр всего несколько раз с вашими детьми.
Запоминающаяся мелодия запомнится им, чтобы помочь им вспомнить названия, а также сравнить их с примерами из реального мира.
Это 3D-фигуры детского сада видео является идеальным введением в сравнение того, почему предметы, имеющие форму конуса, имеют одинаковые качества (1 изогнутая грань… 1 плоская круглая грань).
4. Сокровища пиратов в прятки. Превратите эту игру-идентификацию в игру-описание, спрятав сокровище под трехмерной карточкой. Учащиеся называют описание формы, чтобы заглянуть под нее.
Игра продолжается до тех пор, пока не будет найден пиратский сундук с сокровищами. Включите это в свое календарное время и давайте 2 возможности в день, чтобы быстро и весело попрактиковаться.
5. Поэзия. Скопируйте это стихотворение на карманные полоски и поработайте над соединением объектов реального мира с названиями трехмерных фигур.
Это название основных трехмерных фигур для детского сада .
6. 3D Fluency Mat — этот коврик предназначен для работы с небольшими группами. Я использую метод управляемой математики для обучения своих детей, так что это разминка для нас.
Быстро вписывается и дает нужное количество повторений.
Превратите это в действие, описав фигуру, и тот, кто первым определит/закроет ее, сможет описать другую фигуру, и игра продолжится.
источник: детский сад.blogspot.com7. Реальная сортировка объектов. Эта бесплатная загрузка включает в себя карточки с изображениями объектов реального мира, которые учащиеся могут сортировать по группам фигур.
Он отлично подходит для категоризации и объяснения того, почему и какие черты объединяет все объекты.
Заламинируйте эти карточки и попросите учащихся обвести контур трехмерной фигуры с помощью вики-палочек, чтобы сделать его более интерактивным.
8. Буклет 3D Shape. Попросите учеников создать свой собственный буклет, находя в классе объекты (например, охоту), которые имеют ту же 3D-форму.
Вы всегда можете повысить уровень описания, используя цвета для обозначения типов граней, маркеры для обозначения краев фигуры и приклеивая горох, чтобы показать вершины (которые видны).
источник: mrsriccaskindergarten.blogspot.com9. 3D-карточки/плакаты для сортировки. Эти карточки и плакаты помогут вам создать собственное задание или дать учащимся предметы из реального мира для сортировки.
В этом уроке вместо картинок (например, № 7) представлены фотографии, поэтому он может быть более привлекательным для ваших учеников.
источник: mrsminersmonkeybusiness.com, plantpress.blogspot.com10. Поедание трехмерных фигур. Вот два способа употребления продуктов:
Найдите на Долларовом дереве любую еду, имеющую правильную трехмерную форму. Подумайте: жевательная резинка в форме цилиндра, бугели в форме конуса, сырные шарики в форме сферы и карамель в форме куба. Теперь совместите дегустацию с буклетом, упомянутым под номером 8 в этом списке, и попросите учащихся нарисовать или сфотографировать их для включения.
Предложите всем учащимся изучить, как будут двигаться их фигуры. Это, безусловно, упражнение, которое поможет вам объяснить, почему определенные фигуры будут двигаться одинаково … Например, будут ли катиться все формы с изогнутой поверхностью? Будут ли они все скользить? Почему? Создайте якорную диаграмму своих выводов, чтобы все закрепилось!
Заключение
Вот и все — десять упражнений, которые вы можете использовать для тренировки описания фигур в детском саду. Я надеюсь, эта коллекция поможет вам почувствовать себя подготовленным и поможет вам преподавать.
Если вы ищете способ объяснить, в чем разница между 2D- и 3D-фигурами, посмотрите, как объяснить 3D-фигуры в детском саду.
Если вам нравится то, что я делаю здесь, на KindergartenWorks, то обязательно подпишитесь сегодня. Я с нетерпением жду возможности делиться с вами идеями еженедельно.
Больше геометрии в детском саду
Просмотрите образовательные ресурсы по 3D-фигурам
Найдите образовательные ресурсы по 3D-фигурам
3D-фигуры — это твердотельные объекты, имеющие три измерения. Этими размерами являются длина, ширина и высота. В то время как 2D-формы плоские, 3D-объекты имеют глубину. Футбольный мяч представляет собой трехмерную форму, также известную как сфера, а круг на листе бумаги представляет собой двухмерную форму.Чтобы узнать больше о различных названиях и свойствах трехмерных фигур, см. наши ресурсы ниже.
Этими размерами являются длина, ширина и высота. В то время как 2D-формы плоские, 3D-объекты имеют глубину. Футбольный мяч представляет собой трехмерную форму, также известную как сфера, а круг на листе бумаги представляет собой двухмерную форму.Чтобы узнать больше о различных названиях и свойствах трехмерных фигур, см. наши ресурсы ниже.
Начало работы с 3D-фигурами
Поначалу с 3D-фигурами может быть сложно работать, потому что они имеют странные имена и свойства, отличные от привычных 2D-фигур. Мы составили список некоторых свойств распространенных 3D-фигур и общих уравнений, которые можно использовать при работе с 3D-фигурами.| 3D-форма | Свойства | Объем | Объем поверхности | Область площадью | |
|---|---|---|---|---|---|
| Сфера | У него NO кромки или вершины (угла) У него есть один поверхность Это идеально симметрично На поверхности находятся одинаковое расстояние «R» от центра | 4 / 3 × Π × R 3 | 4 × π × R 2 ×999 | ||
| цилиндр | У него есть квартира | π × r 2 × h | 2 × π × r × (r + h) | ||
| Конус | У него плоская база у него есть одна изогнутая сторона | 1 / 3 × π × R 2 × H | π × R × (R + S) | ||
| Cube | У него есть 6 Грани, каждая с 4 ребрами (и является квадратом) Имеет 12 ребер Имеет 8 вершин (угловых точек), в каждой из которых сходятся 3 ребра | (длина ребра) 3 | 6 × (длина ребра) 2 | ||
| Треугольная призма имеет одинаковые концы | |||||
| Площадь основания × длина | 2 × площадь основания + периметр основания × длина |
Теперь, когда у вас есть список некоторых распространенных 3D-фигур, погрузитесь в наши ресурсы, чтобы узнать, как применять эти и другие фигуры, или перейдите на нашу страницу объема, чтобы узнать, как рассчитать, сколько площади занимают эти 3D-фигуры.

Обучение плоскостным фигурам и твердым телам
Как и в случае с плоскими фигурами, дети учатся описывать твердые формы с точки зрения их атрибутов. Например:
- Округлость или плоскостность
- Способность катиться или скользить
- Количество сторон или углов
Они также увидят, как плоские формы образуют грани твердых тел. Это важная идея, так как реальный мир вокруг нас трехмерен и состоит из твердых форм! Место, где люди видят плоские плоские формы, обычно находится на гранях трехмерных объектов.Из-за этого принято сначала учить объемные формы, прежде чем переходить к плоским формам, что мы практикуем в HMH Into Math .
Обведение граней твердых тел поможет ребенку понять, что куб отличается от прямоугольной призмы тем, что все шесть его граней являются квадратами. Это обогатит способы, которыми они могут описывать и сравнивать твердые тела. Например, ребенок может увидеть, что хотя и цилиндр, и сфера могут катиться, сфера не имеет граней и не может скользить. С другой стороны, цилиндр имеет две круглые поверхности, поэтому он может как катиться, так и скользить.(Но некоторые цилиндры скользят легче, чем другие!)
С другой стороны, цилиндр имеет две круглые поверхности, поэтому он может как катиться, так и скользить.(Но некоторые цилиндры скользят легче, чем другие!)
Продлить урок
- Для тех, кто готов, вы можете показать, как грани кубов и прямоугольных призм должны встречаться под прямым углом, или все точки на поверхности сферы находятся на одинаковом расстоянии от центральной точки.
- Есть ли в вашей школе доступ к 3D-принтеру? Не просто описывайте такие формы, как кубы или сферы — на самом деле 90 165 создают 90 166 их! Представьте 3D-печатные объекты классу и попросите их поделиться тем, что они замечают и удивляются.
- Предложите учащимся идентифицировать твердые тела в реальном мире! Либо принесите предметы, такие как рожок мороженого, числовой кубик или футбольный мяч, чтобы учащиеся описали и классифицировали их, либо предложите учащимся найти предметы за пределами школы, чтобы поделиться ими. Подумайте, что интересует ваших учеников.
 Ищите здания рядом со школой и по всему миру с интересными формами или мячами из тех видов спорта, которыми любят заниматься ваши ученики.
Ищите здания рядом со школой и по всему миру с интересными формами или мячами из тех видов спорта, которыми любят заниматься ваши ученики. - Origami предлагает захватывающий способ превратить плоскую фигуру в твердое тело.Поищите в Интернете идеи для складывания, например, для создания куба. Вы также можете найти распечатки, которые позволяют учащимся создавать трехмерные фигуры или создавать кубы, пирамиды и другие объемные фигуры с помощью зубочисток и зефира.
Как только дети смогут распознавать и описывать признаки, отличающие плоские и объемные формы, например, отличающие треугольник от квадрата или цилиндр от конуса, они могут начать создавать и продолжать узоры. Когда дети создают или находят закономерности, они используют атрибуты не одной, а целой серии фигур, чтобы определить порядок или закономерность.
***
Повысьте уверенность учащихся в математике с помощью HMH Into Math , нашего основного решения по математике для классов K–8.
3D-формы и сети | SkillsYouNeed
На нашей странице, посвященной трехмерным фигурам, мы представили трехмерные фигуры, называемые многогранниками , которые имеют несколько плоских поверхностей ( граней ), состоящих из двумерных многоугольников , соединенных прямыми ребрами и острыми углами ( вершинами ). ).
Полезным свойством этих объемных форм является то, что они могут быть описаны визуально в двух измерениях формой сетью .
Сеть в данном контексте совсем не похожа на рыболовную сеть или баскетбольную сетку! Это просто двумерное изображение того, как выглядела бы трехмерная фигура, если бы все ее стороны были расправлены. Представьте, например, открытую картонную коробку.
2D-сетку можно сложить, чтобы получилась 3D-форма.
Сетки кубов и прямоугольных параллелепипедов
На приведенной ниже диаграмме вы можете увидеть знакомую маркировку игральных костей, но это не 3D-куб, как можно было бы ожидать, а плоское 2D-представление игральных костей. Вы можете вырезать это и склеить вместе, чтобы сделать куб:
Вы можете вырезать это и склеить вместе, чтобы сделать куб:
Шесть отдельных квадратов со знакомыми точками на игральных костях представляют собой сетку формы куба . Маленькие выступы по краям предназначены для склеивания кубиков.
Формовочная сетка для кубиков – однозначного ответа нет
Кубические сети — одни из самых простых для визуализации, и это забавная проверка ваших пространственных навыков, чтобы увидеть, сколько вы можете создать.На самом деле, существует сетей 11 форм, которые составляют куб .
На приведенной ниже диаграмме показано 16 различных расположений 6 квадратов, которые все выглядят так, как будто они могут быть кубическими сетями, но 6 из них таковыми не являются. Можете ли вы решить, какие сети куба являются действительными?
Ответ состоит в том, что 1, 4, 6, 7, 8, 9, 12, 13, 14 и 15 — все допустимые сети куба.
2, 3, 5, 10, 11 и 16 не могут составить куб, и они не являются сетями . Отсутствует одна действующая сеть…. Вы можете это решить?
Отсутствует одна действующая сеть…. Вы можете это решить?
Это довольно сложно…
Теперь, когда вы начали тренировать свои пространственные навыки с обычными кубами, вам будет легче понять сети фигур прямоугольного параллелепипеда.
Кубоид подобен кубу, но некоторые или все его стороны могут быть прямоугольными. Таким образом, сети имеют такие же характеристики, как и у куба, но выглядят совсем по-другому.
Вот сетка прямоугольного параллелепипеда со сторонами 10см, 20см и 40см.
В приведенной выше прямоугольной сети найдите вершину (угол), отмеченную красной точкой.Снова используя свои пространственные навыки, сможете ли вы определить, какие другие вершины, помеченные цифрами 1–6, соединятся с красной точкой, когда прямоугольный параллелепипед находится в своей трехмерной форме?
Сети могут рассказать нам больше….
Теперь, когда мы знаем размеры сети, мы можем узнать другие свойства этого тела, такие как его объем и площадь поверхности .
Объем прямоугольного параллелепипеда вычисляется как произведение его длины, ширины и высоты:
Длина × Ширина × Высота = 40 × 20 × 10 = 192
Таким образом, объем этого прямоугольного параллелепипеда составляет 8 000 см 3 или 8 литров.
Площадь поверхности — это общая площадь всех шести сторон, сложенная вместе.
У нас есть две стороны 20 × 40см, 10 × 20см и 10 × 40см.
2 × 20 × 40 = 1600
2 × 10 × 20 = 200
и 2 × 10 × 40 = 800
16 + 200 + 800 = 2800
Таким образом, прямоугольный параллелепипед имеет площадь поверхности 2800 см 2 или 0,28 м 2
Сетки призм, пирамид и других многоугольников
Как и в примере с кубом выше, любая трехмерная фигура может иметь несколько цепей, а не только одну, но вот некоторые трехмерные фигуры с примерами только одной из их цепей.Посмотрим, сможешь ли ты поработать еще.
Сетки криволинейных тел
Все приведенные выше примеры сосредоточены на многоугольниках с плоскими сторонами. Изогнутые формы тоже могут иметь сети. Их проще визуализировать и построить, если твердое тело имеет хотя бы одну плоскую поверхность. Вот несколько примеров.
Сфера или глобус
Сфера не имеет плоских поверхностей, это непрерывная кривая.
Создание плоской двухмерной сетки земного шара веками было проблемой для картографов (создателей карт).Когда мы смотрим на сетку сферы, мы можем понять, почему картографам было трудно ее использовать. Тем не менее, карты мира были произведены таким образом:
Представьте, что у вас есть апельсин, и вы разрезаете его на дольки. Когда вы съели мясо, у вас остались кусочки кожи. Если бы вы выстроили их в линию, то они были бы похожи на сетку сферы.
Однако у этого подхода есть недостаток. Независимо от того, сколько сегментов, каждый из них будет иметь плоскую поверхность.
Еще раз взглянув на ваши кусочки апельсиновой кожуры, вы увидите, что они не только изгибаются сверху вниз, но и изгибаются из стороны в сторону, в отличие от страницы, которая может изгибаться только в одном направлении. Это называется двойной кривизной . Поэтому невозможно создать полностью точную 2D-сеть 3D-формы с двойной кривизной. Даже если бы в приведенной выше сети было 100 сегментов, это все равно было бы приближением.
Картографы в конце концов преодолели эту проблему, создав карты на основе цилиндра, называемого проекцией .Это тоже приближение, но оно включает искаженное изображение поверхности земного шара, что позволяет точно измерять расстояния на плоской карте. Для получения дополнительной информации см. нашу страницу о полярных, цилиндрических и сферических системах координат .
Вывод: зачем вообще нужны сети?
Способность понять, как трехмерная форма состоит из двухмерных компонентов, является не только полезным навыком, если вам нужно построить коробку, но и жизненно важным навыком в любом аспекте трехмерного дизайна.
Инженеры и дизайнеры используют сложные и мощные пакеты автоматизированного проектирования (САПР) для проектирования всего, начиная от мебели в разобранном виде и заканчивая крупнейшими в мире круизными лайнерами.
Важные пространственные навыки, которые вы приобретете на основе базового понимания сетей формы, могут, таким образом, развиться в другие более сложные приложения проектирования.
Дополнительное чтение из навыков, которые вам нужны
Понимание геометрии
Часть руководства по необходимым навыкам счета
В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и тел.Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Трехмерные фигуры: вид спереди, сбоку и сверху — видео и стенограмма урока
Сферы и кубики
Начнем с нескольких простых. Давайте представим, что мы используем функцию, похожую на карту Google, где из космоса мы видим этот круглый объект на земле.Теперь давайте перетащим нашего маленького оранжевого человечка на уровень улицы. Что мы видим? Этот объект по-прежнему выглядит как круг со стороны. Хорошо, давайте кликнем по объекту. Что мы видим сейчас? Опять же, он всегда выглядит как круг, смотрим ли мы на него спереди, сбоку или сверху. Это сфера , геометрический объект круглой формы. Любая точка на поверхности сферы находится на одинаковом расстоянии от центра сферы. Наша собственная планета Земля является хорошим приближением к тому, как выглядит сфера.
Давайте представим, что мы используем функцию, похожую на карту Google, где из космоса мы видим этот круглый объект на земле.Теперь давайте перетащим нашего маленького оранжевого человечка на уровень улицы. Что мы видим? Этот объект по-прежнему выглядит как круг со стороны. Хорошо, давайте кликнем по объекту. Что мы видим сейчас? Опять же, он всегда выглядит как круг, смотрим ли мы на него спереди, сбоку или сверху. Это сфера , геометрический объект круглой формы. Любая точка на поверхности сферы находится на одинаковом расстоянии от центра сферы. Наша собственная планета Земля является хорошим приближением к тому, как выглядит сфера.
Хорошо, давайте снова уменьшим масштаб и будем искать вокруг нашей земли, пока не увидим квадрат сверху. Как этот объект выглядит на уровне улицы? Еще раз перетащите оранжевого человечка в сторону квадратной формы, и, оглядитесь, он тоже выглядит квадратом сбоку. Мы кружим вокруг него, и независимо от того, смотрим ли мы на него спереди, сбоку или сверху, он выглядит как квадрат.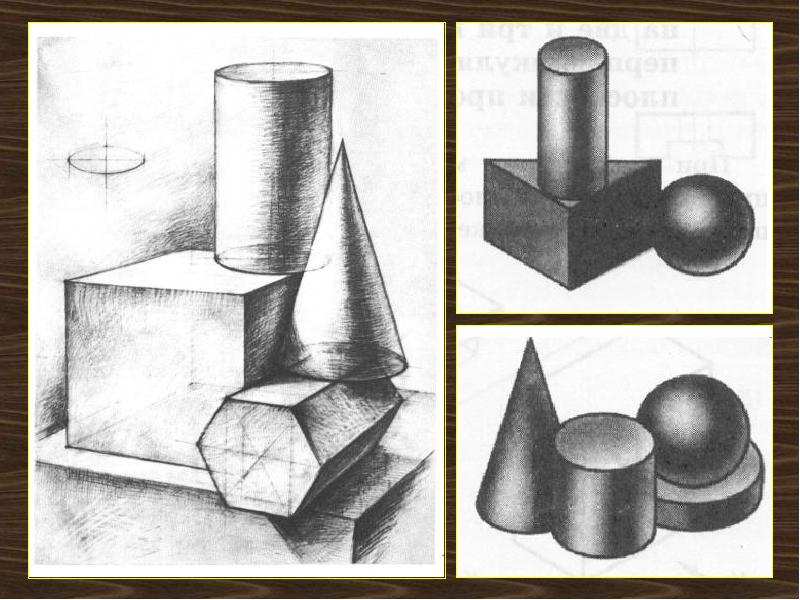 Что это за форма? Это куб , геометрический объект, стороны которого состоят из шести равных квадратов.Хорошим примером кубика является кубик сахара.
Что это за форма? Это куб , геометрический объект, стороны которого состоят из шести равных квадратов.Хорошим примером кубика является кубик сахара.
Цилиндр, конус и пирамида
Хорошо, давайте уменьшим масштаб. Рядом с той сферой, которую мы видели раньше, мы видим еще один круг сверху. Это другая сфера? Хм, давайте узнаем. Когда мы выходим на уровень улицы, мы видим, что это совсем не то. В то время как сфера выглядит как круг под любым углом, этот объект явно не такой. Спереди или сбоку он выглядит как прямоугольник, а сверху или снизу — как круг.Что это за форма? Это цилиндр , трехмерный объект с эллиптическим поперечным сечением, но прямым с параллельными сторонами. Отличным примером из реальной жизни является банка газировки.
При уменьшении масштаба мы видим еще один круг рядом со сферой и цилиндр сверху. Может быть, это другая сфера или цилиндр? Перетащив маленького оранжевого человечка в сторону этой фигуры, мы увидим, что у него нет ни круглой, ни прямоугольной формы сбоку.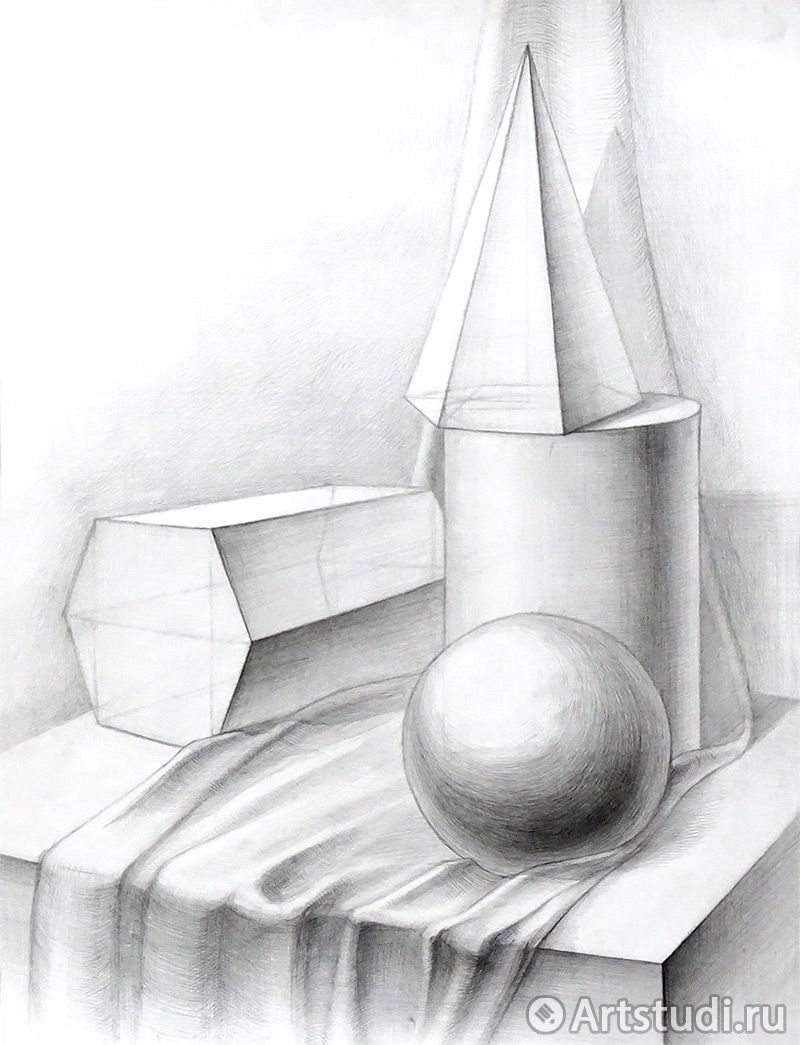 На самом деле передняя или боковая часть этого объекта выглядит как треугольник.Это конус , трехмерный объект с плоским, обычно круглым, основанием, сужающимся к острию. Если бы вы жили столетие или около того назад и вели себя плохо, вы бы носили на голове конусообразную шляпу в качестве наказания, известную как кепка дурака.
На самом деле передняя или боковая часть этого объекта выглядит как треугольник.Это конус , трехмерный объект с плоским, обычно круглым, основанием, сужающимся к острию. Если бы вы жили столетие или около того назад и вели себя плохо, вы бы носили на голове конусообразную шляпу в качестве наказания, известную как кепка дурака.
Ладно, последний урок. Давайте снова уменьшим масштаб. На этот раз мы видим квадрат сверху. Еще куб? Неа. Когда мы спускаемся на уровень улицы, то видим, что со стороны этот объект выглядит как треугольник, почти как конус. Это пирамида , геометрическая фигура с квадратным или треугольным основанием, треугольные стороны которого сходятся в вершине.Возможно, самым известным примером пирамиды является Великая пирамида Гизы.
Итоги урока
Надеюсь, сейчас у тебя на голове не конус. Если да, то, возможно, это потому, что вы не обращали внимания на этот урок! Итак, давайте рассмотрим, ради всех. Существует множество 3-D , или 3-мерных, объектов. Некоторые из них выглядят одинаково спереди, сбоку и сверху, а другие — нет. Сфера — это геометрический объект круглой формы, в котором любая точка на поверхности сферы находится на одинаковом расстоянии от центра сферы.Сфера будет выглядеть одинаково под любым углом. Куб — это геометрический объект, стороны которого состоят из шести равных квадратов. Спереди, сбоку или сверху он будет выглядеть как квадрат. Цилиндр — это трехмерный объект с эллиптическим поперечным сечением, но прямыми параллельными сторонами. Сверху он будет выглядеть как эллипс, например, как круг, а сбоку как прямоугольник или квадрат. Конус — это трехмерный объект с плоским, обычно круглым, основанием, сужающимся к острию.Сверху конус часто выглядит как круг, но сбоку он выглядит как треугольник. Другой объект, который со стороны выглядит как треугольник, — это пирамида , представляющая собой геометрическую фигуру с квадратным или треугольным основанием, треугольные стороны которой сходятся в вершине.
Некоторые из них выглядят одинаково спереди, сбоку и сверху, а другие — нет. Сфера — это геометрический объект круглой формы, в котором любая точка на поверхности сферы находится на одинаковом расстоянии от центра сферы.Сфера будет выглядеть одинаково под любым углом. Куб — это геометрический объект, стороны которого состоят из шести равных квадратов. Спереди, сбоку или сверху он будет выглядеть как квадрат. Цилиндр — это трехмерный объект с эллиптическим поперечным сечением, но прямыми параллельными сторонами. Сверху он будет выглядеть как эллипс, например, как круг, а сбоку как прямоугольник или квадрат. Конус — это трехмерный объект с плоским, обычно круглым, основанием, сужающимся к острию.Сверху конус часто выглядит как круг, но сбоку он выглядит как треугольник. Другой объект, который со стороны выглядит как треугольник, — это пирамида , представляющая собой геометрическую фигуру с квадратным или треугольным основанием, треугольные стороны которой сходятся в вершине. Сверху пирамида будет выглядеть как квадрат или треугольник, в зависимости от формы ее основания.
Сверху пирамида будет выглядеть как квадрат или треугольник, в зависимости от формы ее основания.
Что такое 3D-фигуры? | Определение и примеры
Мы живем в трехмерном мире. У каждого из нас есть высота, ширина и длина.Формы существуют и в нашем трехмерном мире: игральные кости, кубоиды, пончики, пирамиды, пляжные мячи, дорожные конусы. Все это трехмерных фигуры . Давайте посмотрим поближе.
Содержание
- Площадь и объем
- Математика трех измерений
- Примеры 3D-фигур
- Математические странности
Площадь и объем
Двумерные фигуры, такие как многоугольники и круги, занимают площадь, пространство на плоской поверхности (например, на плоскости).2D-фигуры имеют ширину и длину, но не высоту.
Трехмерные фигуры (3D) имеют объем ; они занимают место и имеют ширину, длину и высоту, толщину или глубину.
Вы занимаете все три измерения, как и большинство объектов вокруг вас.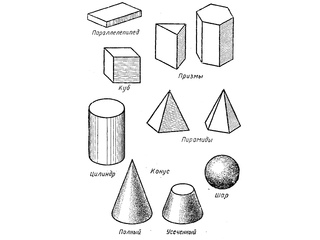 У вас должно быть место для всего, что имеет три измерения, чтобы вписаться в пространство, которое у вас есть. Два объекта не могут находиться в одном и том же пространстве одновременно.
У вас должно быть место для всего, что имеет три измерения, чтобы вписаться в пространство, которое у вас есть. Два объекта не могут находиться в одном и том же пространстве одновременно.
Предположим, вы сидите в кресле и изучаете. Ваша собака прыгает к вам на колени.Может ли ваша собака занимать то же место, что и вы? Нет, ваша собака может попытаться, но вы двое не можете быть в одном и том же месте в одно и то же время. Это один из способов узнать, что вы и ваша собака — трехмерные существа.
Математика трех измерений
Все фигуры, существующие в трех измерениях, имеют ширину и длину, как и их двумерные родственники, но имеют дополнительное измерение, высоту, которую также можно назвать глубиной или толщиной.
В математике бесконечное количество квадратов может занимать одну и ту же площадь на плоскости, потому что у них нет ни толщины, ни высоты.Добавляя третье измерение, это становится невозможным. Куб — трехмерная версия квадрата — будет иметь идентичные размеры по ширине, длине и высоте. Никакой другой куб не может занимать место, которое занимает он.
Никакой другой куб не может занимать место, которое занимает он.
[рассмотрите анимацию, показывающую бесконечную серию квадратов, покидающих математическую плоскость, как листы бумаги; рядом с ним один куб, который не может сдвинуться с места, если в него врежется другой куб]
В реальной жизни не может быть квадратов поверх квадратов, не занимающих места.Лист блокнотной бумаги может показаться очень тонким, но подумайте о упаковке из 200 листов — ее толщина поддается измерению. Один лист будет составлять 1/200 толщины всей стопки, поэтому даже лист бумаги является трехмерным объектом.
Примеры 3D-фигур
3D-тела — это выпуклые формы, имеющие ширину, длину и высоту (или глубину, или толщину). Они занимают пространство, то есть имеют объем. Вы знакомы со многими моделями этих трехмерных фигур:
- Кубики — кубики
- Коробка для обуви — кубовидная или прямоугольная призма
- Конус для мороженого — конус
- Глобус — шар
- сверхтяжелая или египетская гробница — пирамида
- Банка газировки — цилиндр
Также существует множество других трехмерных тел. Целая категория называется Платоновых тел :
Целая категория называется Платоновых тел :
- Тетраэдр — четыре треугольные грани
- Куб — шесть квадратных граней
- Октаэдр — восемь треугольных граней
- Додекаэдр — 12 пятиугольных граней
- Икосаэдр — 20 треугольных граней
[рассмотреть рисунки этих пяти фигур]
Математические странности
Необычные трехмерные фигуры в математике включают тор, который выглядит как пончик:
[вставить рисунок: тор; попробуйте здесь, например: http://mathworld.wolfram.com/Torus.html]
Еще одна странная форма — пентаграммная призма , которую можно найти в декабрьских украшениях и подарочных коробках:
[Чертеж-вставка: пентаграмматическая призма; http://mathworld.wolfram.com/PentagrammicPrism.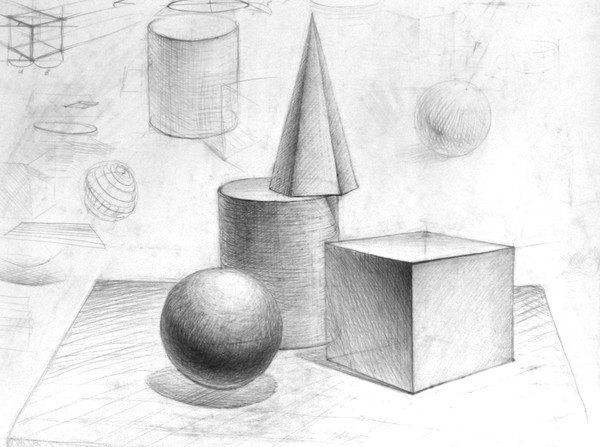 html]
html]
Даже наша собственная планета Земля имеет необычную трехмерную форму, поскольку она не является настоящей сферой. Это сплющенный сфероид :
.[Вставьте мультяшный рисунок земли, основанный на https://earthhow.com/форма-земли/]
Одной из самых необычных 3D-форм, обнаруженных совсем недавно, является скутоид . Как только математики и ученые «открыли» его, они обнаружили, что он уже используется в клетках кожи человека и насекомых!
[вставить рисунок двух соединенных скутоидов, доступен здесь: https://www.nature.com/articles/s41467-018-05376-1#rightslink]
Следующий урок:
ххх
. Post Categories: Разное
Post Categories: Разное
 Н. Наглядная геометрия. 5 – 6 кл.: Пособие для общеобразовательных учебных заведений / Ерганжиева Л.Н., Шарыгин И.Ф. – 3-е изд., стереотип. – М.: Дрофа, 2000. – 192 с.: ил.
Н. Наглядная геометрия. 5 – 6 кл.: Пособие для общеобразовательных учебных заведений / Ерганжиева Л.Н., Шарыгин И.Ф. – 3-е изд., стереотип. – М.: Дрофа, 2000. – 192 с.: ил.
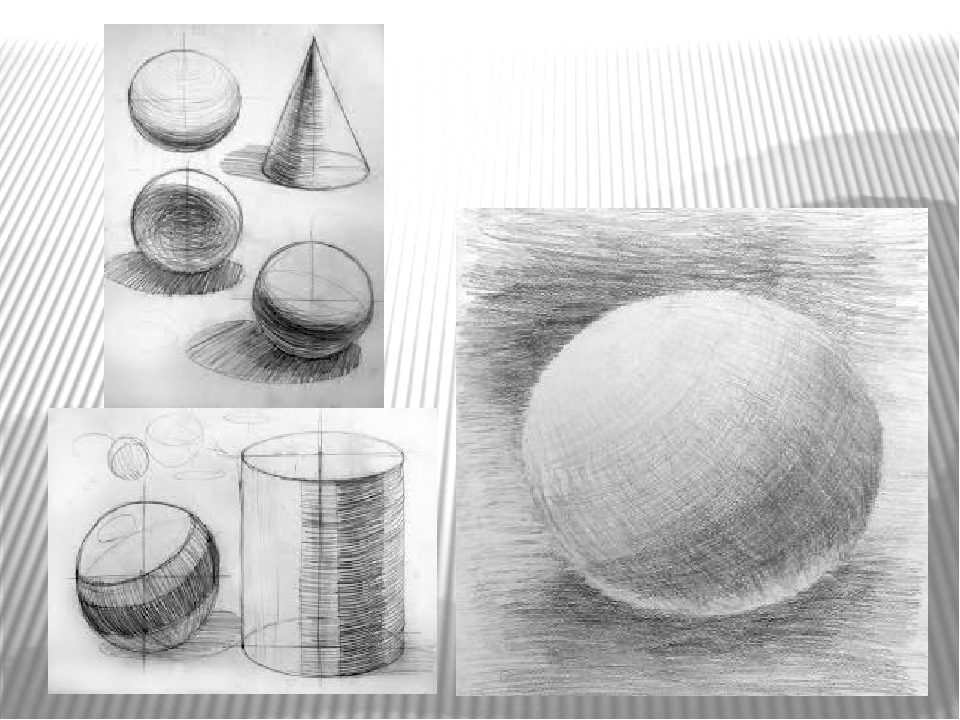 Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
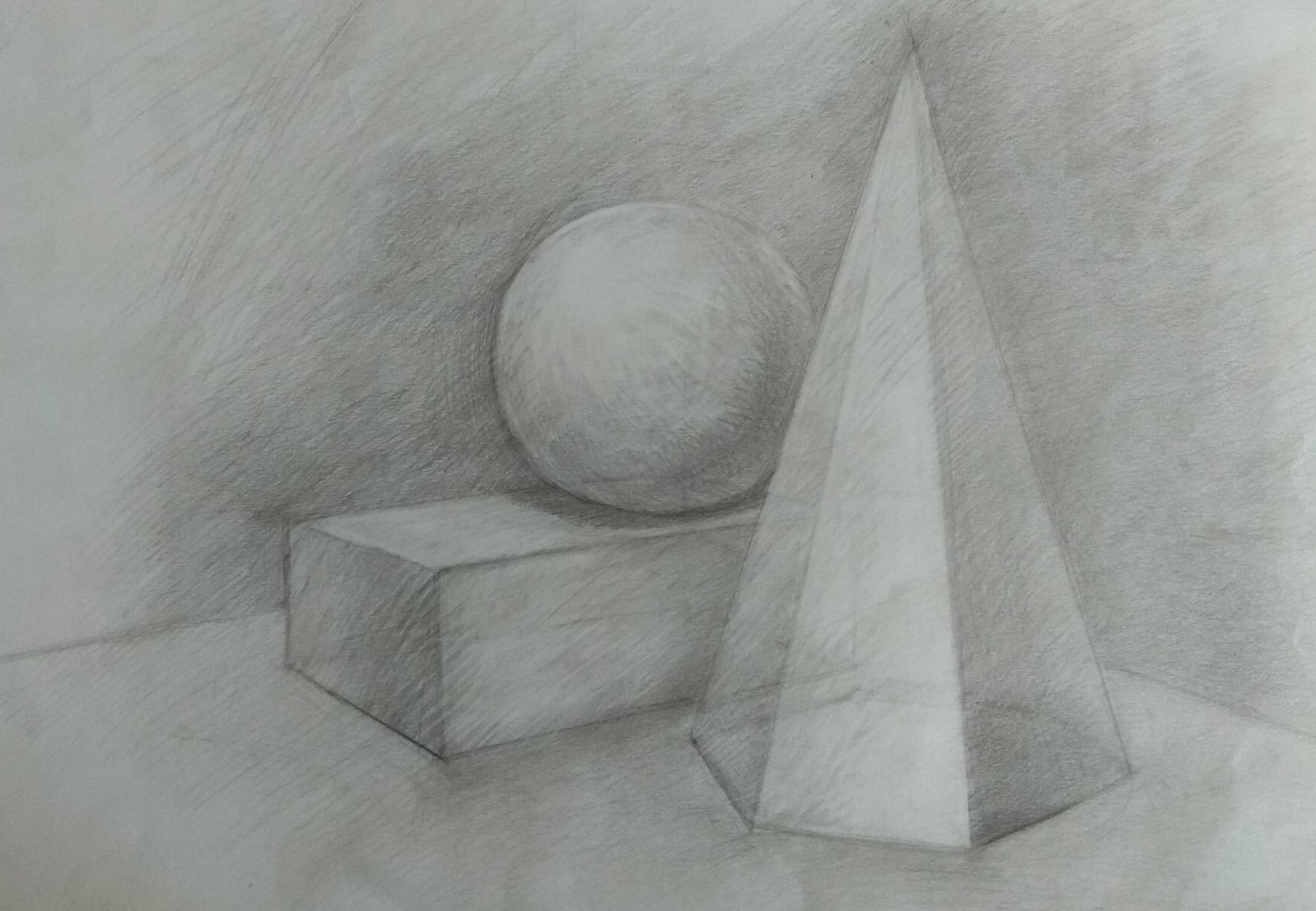 Ищите здания рядом со школой и по всему миру с интересными формами или мячами из тех видов спорта, которыми любят заниматься ваши ученики.
Ищите здания рядом со школой и по всему миру с интересными формами или мячами из тех видов спорта, которыми любят заниматься ваши ученики.