Ромб как рисуется: Как нарисовать ромб поэтапно, от руки и с линейкой?
- python — ‘нарисовать’ случайный ромб (ромб) на массиве numpy (тестирование определения угла Харриса)
- Техника создания ромбов малярной лентой
- Архив Галактики
- Фигура Ромб (бриллиант, алмаз) в техническом анализе
- Как начертить ромб с помощью линейки. Ромбы спицами ‒ простые узоры. Определение ромба, как геометрической фигуры
- Расшифруй свой «случайный рисунок» — Централизованная городская библиотечная система, г.Тюмень
- Inkscape tutorial: Фигуры | Inkscape
- — Как доказать, что можно сделать ромбы с любым количеством внутренних точек?
- открытых учебников | Сиявула
- Четырехугольники
- Ромбическая линия симметрии — значение, примеры и решаемые примеры
- Как найти угол в ромбе
- доказательств для ромбов — математический класс [видео 2021 года]
- Amazon.com: Настольный бегунок Ambesonne Rhombus, жирные полосы в стиле каракули, нарисованные кистью на простом фоне, прямоугольный бегунок для кухни в столовой, 16 «X 90», угольно-серый и белый: для дома и кухни
python — ‘нарисовать’ случайный ромб (ромб) на массиве numpy (тестирование определения угла Харриса)
Я пытаюсь создать случайный тест для реализации функции «harris_corner_detector» (ОЧЕНЬ ВООБЩЕ И НЕПРАВИЛЬНО: функция, которая находит углы на изображении) В тесте я хочу создать случайные простые формы в двоичной матрице numpy (это легко узнать координаты их углов) (например, прямоугольники, треугольники, ромб (ромб) и т. д.) и проверить, находит ли реализация Харриса правильные углы.
Я уже реализовал функцию, которая случайным образом «рисует» прямоугольник, параллельный оси, но я не могу найти эффективного способа сделать это, когда речь идет о формах, которые не параллельны осям.
Чтобы создать случайный прямоугольник, я случайным образом выбираю начальную и конечную точки на обеих осях и меняю значения всех ячеек в этих границах следующим образом:
Получение случайных координат:
def _get_random_coords(self, start, end):
x_start, y_start = np.
random.randint(start, end, 2)
x_end = np.random.randint(x_start + 7, end + 20)
y_end = np.random.randint(y_start + 7, end + 20)
return (x_start, x_end, y_start, y_end)
Рисование случайного прямоугольника (значения 255 для фона и 0 для формы):
mat = np.ones((1024, 1024)) * 255
mat[x_start: x_end, y_start: y_end] = np.zeros((x_end - x_start, y_end - y_start))
Но когда дело доходит до эффективного рисования ромбовидной формы, я не понимаю. Все, о чем я могу думать, — это запустить цикл, который создает такой алмаз:
def _get_rhombus(self, size):
rhombus = []
for i in range(size):
rhombus.append(np.zeros(i+1))
for i in range(size - 1, 0, -1):
rhombus.append(np.zeros(i))
return np.array(rhombus)
А затем еще один цикл, чтобы добавить его в большую матрицу. Но этот метод очень неэффективен, когда дело доходит до тестирования (поскольку я нарисую сотни из них, некоторые из них могут быть огромными).
Есть идеи получше? В качестве альтернативы — есть ли лучший способ проверить это?
Заранее спасибо.
2
user11712054 10 Дек 2020 в 23:56
Здесь возникает ряд вопросов, но главный из них — как создать массив из заполненных ромбов с учетом углов. Я отвечу на этот вопрос и оставлю другие вопросы, например, создание случайных ромбов и т. Д.
Чтобы заполнить выпуклый многоугольник, можно найти линию, заданную последующими углами, и заполнить выше или ниже этой линии, а затем and все заполненные области вместе.
import numpy as np
import matplotlib.pyplot as plt
# given two (non-vertical) points, A and B,
# fill above or below the line connecting them
def fill(A, B, fill_below=True, xs=10, ys=12):
# the equation for a line is y = m*x + b, so calculate
# m and b from the two points on the line
m = (B[1]-A[1])/(B[0]-A[0]) # m = (y2 - y1)/(x2 - x1) = slope
b = A[1] - m*A[0] # b = y1 - m*x1 = y intercept
# for each points of the grid, calculate whether it's above, below, or on
# the line.
Since y = m*x + b, calculating m*x + b - y will give
# 0 when on the line, <0 when above, and >0 when below
Y, X = np.mgrid[0:ys, 0:xs]
L = m*X + b - Y
# select whether, >=0 is True, or, <=0 is True, to determine whether to
# fill above or below the line
op = np.greater_equal if fill_below else np.less_equal
return op(L, 0.0)
Вот простой ромб с низким разрешением
r = fill((0, 3), (3, 8), True) & \
fill((3, 8), (7, 4), True) & \
fill((7,4), (5,0), False) & \
fill((5,0), (0,3), False)
plt.imshow(r, cmap='Greys', interpolation='nearest', origin='lower')
То есть приведенный выше рисунок является результатом объединения следующих заливок:
fig, ax = plt.subplots(1, 4, figsize=(10, 3))
fill_params = [((0, 3), (3, 8), True), ((3, 8), (7, 4), True), ((7, 4), (5, 0), False), ((5, 0), (0, 3), False)]
for p, ax in zip(fill_params, ax):
ax.imshow(fill(*p), cmap="Greys", interpolation='nearest', origin='lower')
Или можно сделать высокое разрешение, и у него может быть несколько сторон (хотя я думаю, что он должен быть выпуклым).
r = fill((0, 300), (300, 800), True, 1000, 1200) & \ fill((300, 800), (600,700), True, 1000, 1200) & \ fill((600, 700), (700, 400), True, 1000, 1200) & \ fill((700,400), (500,0), False, 1000, 1200) & \ fill((500,0), (100,100), False, 1000, 1200) & \ fill((100, 100), (0,300), False, 1000, 1200) plt.imshow(r, cmap='Greys', interpolation='nearest', origin='lower')
Очевидно, есть несколько вещей, которые нужно улучшить, например, не повторять вторую точку линии и первую точку новой линии, но я хотел, чтобы все это было чистым и простым (а также, чтобы заливка работала, точки просто нужны чтобы определить линию и не обязательно быть углом, поэтому в некоторых случаях этот более общий подход может быть предпочтительнее). Кроме того, в настоящее время необходимо указать, следует ли заливать выше или ниже линии, и это можно вычислить по-разному, но, вероятно, это проще всего при создании ромба.
1
tom10 11 Дек 2020 в 17:07
Хотя это немного менее надежно, чем уже опубликованный ответ, вот изящный трюк для формирования ромба с использованием концепции верхних и нижних треугольных матриц.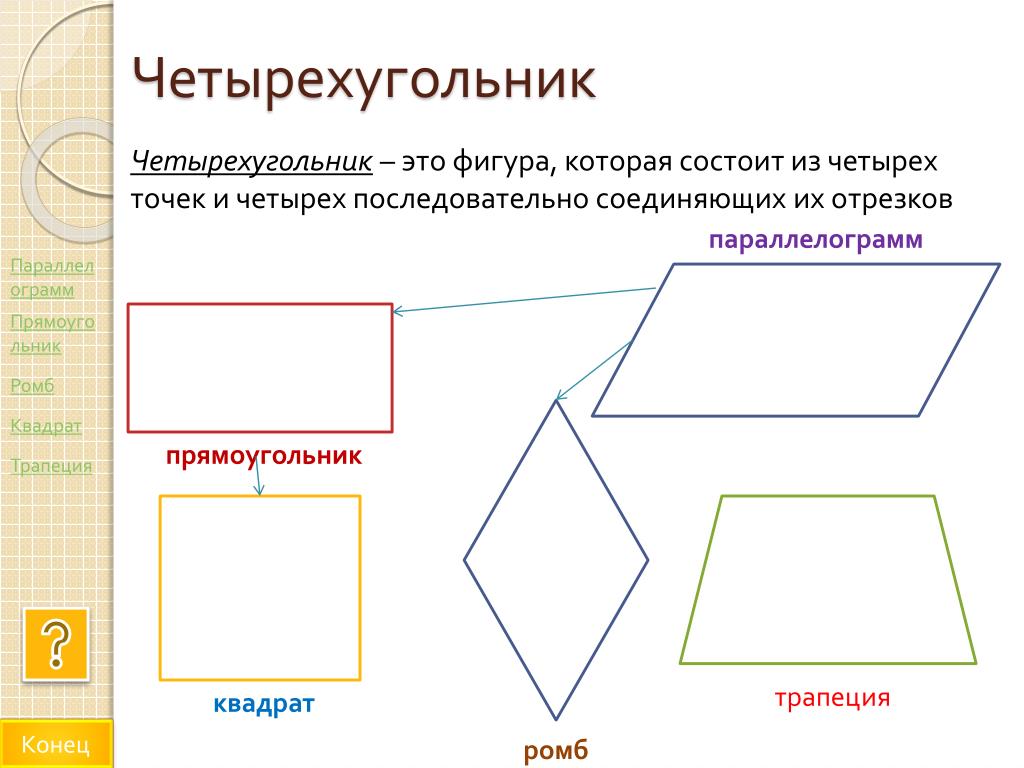
import numpy as np import matplotlib.pyplot as plt blank = np.zeros((10, 12)) anchorx, anchory = 2, 3 # better result for odd dimensions, because mid index exists # can handle h != w but the rhombus would still fit to a square of dimension min(h, w) x min(h, w) h, w = 7, 7 assert anchorx+h <= blank.shape[0], "Boundaries exceed, maintain 'anchorx+h <= blank.shape[0]' " assert anchory+w <= blank.shape[1], "Boundaries exceed, maintain 'anchory+w <= blank.shape[1]' " tri_rtc = np.fromfunction(lambda i, j: i >= j, (h // 2 + 1, w // 2 + 1), dtype=int) tri_ltc = np.flip(tri_rtc, axis=1) rhombus = np.vstack((np.hstack((tri_ltc, tri_rtc[:, 1:])), np.flip(np.hstack((tri_ltc, tri_rtc[:, 1:])), axis=0)[1:, :])) blank[anchorx:anchorx+h, anchory:anchory+w] = rhombus print(blank) plt.imshow(blank) plt.show()
[[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 1. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 1. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
1. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 1. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
1
sai 11 Дек 2020 в 09:40
Техника создания ромбов малярной лентой
Техника создания ромбов
Это классический элемент стиля является простым и экономически эффективным способом придать индивидуальность любой комнате. С помощью малярной ленты вы сможете оживить жилое пространство, придав ему определенной утонченности.
Необходимые инструменты:
- Малярная лента со слабым клеевым слоем
- Краска, кисть, валик и поддон
- Пласnиковая карта или жесткий шпатель
- Рулетка, карандаш, уровень
- Картон
- Т-образы или Г-образный угольник
Подготовка поверхности:
- Удаление гвоздей, масла и грязи
- Зашпаклюйте мелкие отверстия и затрите их шкуркой
- Убедитесь что с поверхности удалена пыль и поверхность сухая
Пошаговая инструкция:
- Нанесите малярную ленту вдоль выступа, плинтуса и потолочного молдинга.
 Используйте для этих целей малярную ленту со слабой клеевой основой.
Используйте для этих целей малярную ленту со слабой клеевой основой. - Окрасьте всю поверхность стены в базовый цвет и дайте ему высохнуть в течение 24 часов
- Вырежьте из картона шаблон в форме ромба.
- Найдите центр стены и поставьте на этом месте отметку. Приложите край шаблона к метке и слегка обрисуйте шаблон по периметру
- С помощью Т-образного угольника нарисуйте горизонталь, для создания метки первого ряда. Прочертив линию по всей стене, с помощью шаблона создайте рисунок на стене. Каждый последующий ряд отмеряйте угольником для обеспечения прямого угла между фигурами.
- Нанесите ленту вдоль контура. Подсказка: Контур должен быть внутри ограничиваемой области таким образом, чтобы закрасить в дальнейшем. Используйте пластиковую карту или жесткий шпатель для прижима ленты
- Выберите более темный цвет и закрасьте внутренний контур каждого ромба и дайте краске высохнуть 24 часа. Покраску нужно начинать от малярной ленты к центру ромба.
- Удалите ленту под углом 45 °.
 Если клей начинает переходить на поверхность, измените угол до 90 °. Если краска начинает подниматься вместе с лентой, острым ножом прорежьте аккуратно краску вдоль малярной ленты.
Если клей начинает переходить на поверхность, измените угол до 90 °. Если краска начинает подниматься вместе с лентой, острым ножом прорежьте аккуратно краску вдоль малярной ленты.
Шаг 1
Шаг 2
Шаг 3
Шаг 4
Шаг 5
Шаг 6
Шаг 7
Шаг 8
Полезные советы
Размеры ромбов должны соотноситься с размерами комнаты. Предварительно нужно нарисовать все в масштабе на бумаге. Это даст вам общее представление, как будут выглядеть ромбы и даст представление о конечном размере. Разметка малярной лентой даст вам дополнительное представление и возможность откорректировать размеры.
Выберите цвета, которые будут хорошо гармонировать с мебелью. Для того чтобы ромбы не выделялись сильно — возможно использовать краски одного цвета но с блеском и без него. Перед покупкой краски можно попробовать сочетание красок на любом материале.
Архив Галактики
Программирование для воссоздания картин: математика и искусство вместе
Блог тренера / 24.
 11.2016
11.2016
Ставлю проблему: почему так одиноки и разобщены друг с другом два школьных учебных предмета , которым бы, по хорошему, нужно дружить и всячески друг друга поддерживать? Математика и информатика, а конкретнее, отдельный раздел программы по информатике, где изучаются основы программирования.
Покажу, как это можно делать на примере отдельных заданий в среде карандашного программирования (pencilcode). Делать, при помощи третьего — ART- компонента. Среди произведений современной живописи встречаются удивительно удачные объекты, удачные с точки зрения их свойств — симметрии, наличия повторяющихся элементов, возможностей работать с цветом, как с параметром.
«Создаем картину» на основе картины художника-абстракциониста с помощью «пятен» и «квадратиков».
Уже после первого занятия по карандашному программированию, зная всего несколько команд: основные команды рисования (dot, box) и основные команды движения (fw, bk, rt, lt), можно воссоздать картины, состоящие из простых форм — кругов и квадратов.
Вот примеры работ учеников, созданные после 1-го занятия:
Работа1
Работа2
Работа3: Фрэнк Стелла
Работа4: Эльсуорт Келли
Работа5: Эльсуорт Келли (использованы абсолютные координаты)
Все — в Малевичи! Все — в Мондрианы! Геометрические фигуры в pencilcode
Кто бы что ни говорил, но дети, «кодирующие» Малевича после второго занятия карандашным программированием, начинают и про геометрические фигуры лучше понимать, и про координаты, и… про искусство. А как приятно-то работы cмотреть! Круче, чем в музее! Теперь подробнее…
Уже на втором уроке, когда мы познакомились с инструментом перо и заливка (pen и fill), можно поставить перед учениками задачу выбора какой-то из супрематических композиций Малевича и воссоздания ее средствами pencilcode.
На уроке ученики получают задание-упражнение: нарисовать с помощью черепашки следующие геометрические фигуры: круг, полукруг, квадрат, прямоугольник, ромб, треугольник. Сюда могут быть также добавлены параллелограмм и трапеция.
Проблема начинается с рисования ромба, собственно, она в этом и состоит, что ученики пытаются ромб именно нарисовать, а не построить. Ромб разъезжается — углы не те. Приходится вспомнить свойства углов и диагоналей ромба. Но результат — самостоятельно выбранная и воспроизведенная с помощью кода картина — очень радует!
Получается такой проект Геометрические фигуры
А вот готовые работы 9-классников
Малевич 1
Малевич 2
Малевич 3
Малевич 4
Мондриан
Для того, чтобы не ограничивать учеников в выборе инструментов, можно поставить задачу в более свободной формулировке. В PencilCode можно работать в двух системах координат — абсолютной (декартовой) и относительной — «черепашьей», когда все движения и перемещения совершаются относительно черепашки.
- 1 вариант: использовать черепашью графику, относительную система координат (рисование пером, команды движения, поворота и использование заливки): fw, bk, rt, lt, fill
- 2 вариант: используется абсолютная — декартова система координат, команды jumpto, moveto
Работы учителей-участников дистанционной мастерской:
Малевич Автор Васильева Евгения Владимировна (здесь использована черепашья система координат)
Малевич Автор Девятова Анастасия Юрьевна (здесь использована и черепашья система координат, и декартова)
Малевич/ Крестьянин Автор Горнбергер Ирина Ринатовна
Кандинский Автор Горнбергер Ирина Ринатовна (в этих работах использована, в основном, не черепашья, относительная система координат, а абсолютная — декартова.
Рисуем Вазарели
Еще один из таких объектов — картина Виктора Вазарели/
Задача состоит в том, чтобы воспроизвести ее с помощью тех инструментов — команд, которые есть у черепашки.
Изначально можно выбрать две разных стратегии ее рисования: первая — только с помощью черепашьих шагов и поворотов, вторая — с использованием координатной сетки и команды jumpto (x, y)
Примечание: для облегчения решения вначале не будем вообще думать о цвете (их подбором займемся потом, когда справимся с рисованием и повторением форм).
Вся картина представляет собой набор из 16 таких объектов, каждый из которых состоит из большого квадрата (возьмем его сторону равной 100) и либо повернутого на 45 градусов малого квадрата, либо малого круга. Объект квадрат черепашка рисует с помощью команды box, а объект круг — с помощью dot. Для продолжения рисования первого ряда, нам нужно определить координаты каждой пары объектов (в первом ряду это большой и малый квадрат внутри). Объекты в каждом новом столбце отличаются лишь по координате X (она увеличивается на 100 единиц для каждого столбца). Координата Y при этом остается неизменной.
Если внимательно рассматривать картину, то можно заметить, что формы фигур четвертого ряда копируют первый, а формы фигур третьего ряда копируют второй ряд. Это позволит скопировать код для рисования первого ряда, нужно будет лишь поменять координату по Y. Аналогично сделаем с кодом для четвертого (скопируем третий, не забыв уменьшить координату по y на 100 единиц.
Это позволит скопировать код для рисования первого ряда, нужно будет лишь поменять координату по Y. Аналогично сделаем с кодом для четвертого (скопируем третий, не забыв уменьшить координату по y на 100 единиц.
Когда с формой будет покончено, можно будет поменять цвета, подобрав их из этой таблицы цветов.
Результат получится такой:
Вазарели. Квадраты и круги. Автор Валерия Ланд. Первая стратегия.
Вазарели. Квадраты и круги 2. Автор Анна Осипенко. Первая стратегия.
Вазарели. Квадраты и круги 2 Автор Наталья Эрте. Вторая стратегия.
Рисуем Мондриана
Поскольку картин с квадратными формами и прямыми линиями у Пита Мондриана немало, среди них всегда найдется такая, которую было бы удобно воспроизводить, обладая даже малым набором инструментов.
Теперь, когда мы научились задавать случайные координаты на холсте, мы можем использовать инструмент box и задать для него три любимых цвета Мондриана: красный, желтый, синий. Ну и добавить черные полоски: вертикальные и горизонтальные.
Мондриан: квадраты и полосы
Посты по теме Доступны по мере публикации:
Карандашное программирование. Начало
Карандашное программирование: чужой код для решения своей задачи…
Карандашное программирование: циклы
Геометрия и карандашное программирование
Карандашное программирование: холст как координатная плоскость
Карандашное программирование: рисуем пейзажи масштабированием
Карандашное программирование: четыре черепашки и симметричный дизайн
Карандашное программирование: несколько черепашек и поворотная симметрия
Карандашное программирование: черепашка рисует паркеты и мозаики
Карандашное программирование: черепашка и оптические иллюзии
О творческих домашних заданиях, или Могут ли все ученики быть успешными?
Программирование для воссоздания картин: математика и искусство вместе
В начале была цифра?
Пляшущие черепашки
Искусство создания снежинки, или Как скоротать зиму…
Карандашное программирование: паркеты и жывёлы
Карандашное программирование: рекурсия
Ёлка в коде. МК
МК
Ёлка в коде. Этап 2. Шарики цветные
Связанные проекты
Какая математика бывает на картинах?
Математика и искусство — переплетение возможно!
Математика в стиле «мондриан» и «клее»
Математика и абстрактное искусство в STREAM-проекте
Идеи в духе STEAM: геометрический конструктор на основе рисунков Google
Идеи в духе STEAM: PicassoHead как конструктор
Постер как форма упаковки информации в STREAM-проекте: Колдер и Вазарели
STEAM-проект: генератор Кандинского и другие интерактивные апплеты в GeoGebra
STEAM-проект: черный квадрат Малевича в Desmos и GeoGebra
STEAM-проект: треугольник в GeoGebra, как получить картину?
STEAM-проект: мозаики Эшера в GeoGebra
STEAM-проект: задачи на картинах
МК «Другая математика с Desmos»: измени апплет и научись!
Цифровые артефакты для организации учебной деятельности
АРТ-математика: воплощаются ли идеи?
По следам мастер-класса АРТ-математика: идеи и воплощения
Богатая математика — бедная математика
Рисуем мандалы в GeoGebra, или Чудо поворотной симметрии
Урок виртуальной кройки: клетка, полоска, узор. ..
..
Геометрия лоскутного одеяла: новые идеи…
Спирали и спирографы: джазовые импровизации в GeoGebra
Кривые Безье и воспроизведение картин оп-арта в GeoGebra
Что общего между снежинкой и оп-артом?
«Случайная» красота в GeoGebra
С тегом Art в GeoGebra
Национальный узор и математика
Прекрасная геометрия на бумаге и не только…
Cмотри в зеркало, или Задачи на осевую симметрию в Geogebra
Конструкторы узоров для текстиля. Часть первая: рисунки Сони Делоне
«Угадать» ситчик! Ткани Варвары Степановой и Любови Поповой
Весенняя тема: создаем банданы и образцы ткани с «огурцами»
Бумага и цифра вместе…
Математика и искусство — переплетение возможно!
АРТ-математика: воплощаются ли идеи?
Ловим рыбку в море, или Игры, пазлы, мультики в GeoGebra
Суха теория, мой друг, а древо жизни вечно зеленеет…
Русский авангард и другие художники в Desmos
Как привести солнце в движение, или Послесловие к виртуальной выставке
«Полярные» витражи, или Крути калейдоскоп в Desmos!
STEAM
pencilcode
блочное программирование
искусство
математика
программирование
проект
Фигура Ромб (бриллиант, алмаз) в техническом анализе
Автор: Максим Михайлов
Многие трейдеры слышали про такой паттерн как Алмаз, его ещё иногда называют Бриллиантом или Ромбом. Эта модель встречается не так часто, особенно на Forex, но при этом она достаточно точная и очень хорошо работает на крупных тайм фреймах. Отличительной особенностью можно назвать высокую вероятность разворота, редкие нарушения пропорций и общей формы.
Эта модель встречается не так часто, особенно на Forex, но при этом она достаточно точная и очень хорошо работает на крупных тайм фреймах. Отличительной особенностью можно назвать высокую вероятность разворота, редкие нарушения пропорций и общей формы.
Записаться на курс «Снайпер для начинающих» можно здесь
Образование фигуры Бриллиант
Итак, паттерн ромб получается в ходе достаточно большого количества движений. Это гораздо более сложная модель по сравнению с Головой и плечами в том, что касается составляющих её элементов. Вместе с этим, простейшие графические построения позволяют быстро и точно определить, что перед именно фигура Алмаз, но до этого момента происходящее на графике выглядит довольно необычным. Можно выделить две основные фазы формирования паттерна:
- Левая половина модели. Она образует окончание тренда, но не так, как мы все привыкли это видеть – на графике появляется расширяющаяся формация. То есть цена идёт по тренду, допустим, вверх, затем разворачивается и корректируется.
 После этого тренд как бы возобновляется и перебивает предыдущий максимум. Затем снова происходит разворот вниз и обновляется минимум коррекции. И снова рост с обновлением максимума. Это достаточно сложная конструкция, в такие моменты трейдеры часто теряют деньги, ведь стоп по многим сделкам выносится за ближайший экстремум, после срабатывания сделки зачастую переворачивают и снова получают стоп. В общем, если видим начало расширения, то лучше просто ждать – это может быть, как началом формирования фигуры ромб, так и просто хаотичное поведение участников рынка, вызванное новостями или какими-либо ещё факторами.
После этого тренд как бы возобновляется и перебивает предыдущий максимум. Затем снова происходит разворот вниз и обновляется минимум коррекции. И снова рост с обновлением максимума. Это достаточно сложная конструкция, в такие моменты трейдеры часто теряют деньги, ведь стоп по многим сделкам выносится за ближайший экстремум, после срабатывания сделки зачастую переворачивают и снова получают стоп. В общем, если видим начало расширения, то лучше просто ждать – это может быть, как началом формирования фигуры ромб, так и просто хаотичное поведение участников рынка, вызванное новостями или какими-либо ещё факторами. - Правая половина модели. Она очень похожа на левую, это также множество движений, но каждое последующее колебание меньше по диапазону, чем предыдущее, то есть диапазон уменьшается. По сути это выходит обычный треугольник, которые мы часто видим на графике. Продолжительность сужения нередко бывает примерно равной продолжительности расширения, но это не обязательно – есть примеры короткого расширения и очень долгого треугольника. В целом, это никак не влияет на отработку паттерна Бриллиант.
Модели в разных направлениях движения цены
Для того, чтобы предположить образование модели, достаточно увидеть 3 последовательных обновления экстремума в левой половине. Это позволит провести образующие линии, которые и дадут нам отчётливую картину расширения и возможных границ колебаний. Стоить отметить, что хорошим подтверждающим сигналом к тому, что у нас формируется именно паттерн Алмаз, может послужить сильное движение прямо в середине фигуры, которое заканчивает формирование расширения и начинает формирование сужения. Оно есть не всегда, бывает и так, что вместо одного таких движений два, образующих V-образный разворот. На саму модель не влияет, для нас главной остаётся форма в виде ромба. Количество движений внутри фигуры может быть разным – обычно это 4-5 движений в каждом треугольнике, но бывает и больше, либо в одном 5, а в другом больше. Вариативность достаточно большая, но ключевой момент заключается в образующих линиях, а уж сколько там было колебаний, уже второстепенно.
Где образуется фигура Бриллиант
Бриллиант принято относить к разворотным паттернам, поэтому чаще всего мы его встретим в конце тренда. Это в большей степени относится к тайм фреймам от часового и выше. Поскольку сама фигура представляется сложной конструкцией, внешне напоминающей консолидацию, в качестве причин образования выделяют следующие:
- Крупный игрок фиксирует прибыль по своей позиции. Это не имеет никакого подтверждения, но обычно объёмы внутри паттерна Ромб сильно увеличиваются, а это всегда свидетельствует о крупных вливаниях в рынок. До тех пор, пока не будет сформирована первая половина модели и не начнёт формироваться вторая, у нас нет никакой уверенности в том, что это Алмаз, поэтому рассматриваем как простую консолидацию. А на старших периодах такие консолидации обычно предшествуют развороту тренда.
- Крупный игрок набирает позицию. В принципе, всё то же самое, сделки направлены в том же направлении, что и при фиксации прибыли. Впрочем, вполне возможно, что оба процесса протекают одновременно или последовательно, правды мы никогда не узнаем.
Быстрое и масштабное движение разделяет две половины паттерна
Также паттерн Бриллиант часто можно встретить после очень сильного и динамичного тренда. Обычно это какое-либо новостное движение, но только новость носит не локальное, а скорее глобальное значение, то есть не отыгрывается обратно буквально в течение пары часов. Происходит обычно так:
- Есть тренд, который относительно спокойно развивался.
- Выходит, экономическая статистика. Публикация, пресс-конференция или что-либо ещё, что оказывает сильное воздействие на цену, и она ускоряется, иногда практически вертикально.
- Затем происходит проторговка с образованием либо консолидации, либо паттерна Алмаз.
- После окончания формирования тренд разворачивается и теперь цена уже столь же динамично двигается в обратную сторону.
Замечено, что крупные периоды обычно дают хорошие и точные сигналы, в то время как на малых периодах от минутного до пятнадцатиминутного нередко можно увидеть прорыв ромба совершенно не в ту сторону, в которую ожидалось, часто встречается на форекс. В этом случае сама форма является просто совпадением, а остановка была не более чем простой консолидацией в рамках краткосрочного тренда. В общем, смотреть на малые периоды не стоит, на них данная сложная фигура отрабатывает плохо, это в большей степени уже гадание получается, а не торговля.
Такие ситуации не редкость, поэтому всегда следует дожидаться пробоя в нужную ст орону
Торговля по фигуре Бриллиант
Фигура Алмаз – одна из тех немногих моделей, которые торгуются по однозначному сценарию почти каждая свечная модель даёт нам вариативность входов, здесь же всё достаточно просто. Итак, входить в рынок можно двумя способами, которые мало отличаются друг от друга:
- Открываем сделку сразу после того, как цена пробивает образующую линию. Сам ордер следует располагать на небольшом удалении от неё, так как пробой может быть ложным, и цена ещё какое-то время будет ходить вверх-вниз в рамках модели. Некоторые используют не саму образующую, а ближайший экстремум, то есть точку, где цена до этого разворачивалась, пока ещё была внутри ромба. Это не самый лучший вариант, ведь увеличится размер стопа, а размер тейка сократится.
- Открываем сделку после того, как цена сделает ретест пробитой образующей линии. Это актуально только тогда, когда сама фигура Ромб формировалась достаточно медленно, а перед её появлением не было стремительного движения, о котором говорилось ранее. В этом случае ретест вероятен, но лучше всё же придерживаться первого варианта. Ретест хорошо торгуется тогда, когда у нас паттерн образовался на графике, допустим, дневного масштаба, а сам ретест смотрим на часовом или получасом. В этом случае можно действительно очень хорошо войти и быстро поставить безубыток.
Торговля по паттерну Бриллиант
Не стоит пытаться заходить в рынок до того момента, как будет пробита образующая линия. На этом множество трейдеров потеряли деньги. Дело в том, что движения внутри ромба обычно интенсивные, резко меняют направление. В начале дня цена может непрерывно падать, а уже к вечеру вернуться обратно, и ничто не поможет распознать этот разворот. Те, кто решит пренебречь этим советом, должны понимать, что торговать в таком случае следует только в направлении предполагаемой отработки. И не забываем, что паттерн часто выглядит практически законченным и вдруг ломается – цена уходит дальше по тренду, а эта ромбовидная формация остаётся в виде сложной коррекции.
Независимо от того, как осуществлялся вход в рынок, ограничение убытка у нас всегда стоит за границей самого паттерна Бриллиант. Дело в том, что при пробое образующей может быть резкой отскок и затем начинается мощное движение в противоположную сторону с пробоем противоположной образующей. Это не означает, что фигура сломалась, просто ещё некоторое время уйдёт на окончание формирования. А вот есть преодолевается экстремум, то есть цена уходит дальше границы ромба, то в этом случае можно сказать, что паттерн сломан и именно здесь разумно фиксировать убыток.
Пример ситуации, показывающий необходимость выносить стоп за экстремум
Прибыль фиксировать можно разными способами. Всё зависит от контекста образования фигуры Ромб. Какой из перечисленных далее способов выбирать – решать каждому самому, со временем появится достаточный опыт и можно будет правильно выбирать из следующего:
- Тейк профит равен по размеру диапазону Бриллианта. То есть мы измеряем расстояние от минимума до максимума и именно такое расстояние откладываем от уровня пробоя образующей линии. Здесь можно провести аналогию с Прайс Экшен, где многие модели торгуют именно так. Как правило, отработка паттерна идёт до этого уровня и дальше. То есть это как бы минимальная цель.
- Если паттерн сформировался после большого движения, то в этом случае потенциал отработки будет гораздо больше, чем в предыдущем варианте. Нужно сопоставить размер получившегося ромба с тем движением, которое ему предшествовало. Если оно значительно превышает саму модель, то разумно в качестве ориентира использовать 75-100% от это этого движения, то есть при самом благоприятном раскладе цена вернётся туда, откуда началось формирование последнего трендового движения перед этой консолидацией в виде ромба.
В принципе, ничего не мешает комбинировать эти методы и фиксировать прибыль постепенно, например, разделить весь участок предполагаемого движения на несколько частей и забирать часть прибыли на каждой отметке. Это уменьшит итоговый результат, но вместе с этим сохранить хотя бы часть профита, если вдруг произойдёт разворот. Также рекомендуется ставить безубыток после того, как цена сделала ретест образующей или же отошла уже достаточно далеко от неё.
Отклонения формы фигуры Алмаз
Полностью симметричную модель можно встретить совсем не часто. Обычно есть некоторые отклонения, изменения, которые не влияют на самое главное – последовательное расширение и сужение. К основным “дефектам” относятся следующие:
1. Разница в количестве составляющих треугольники элементов. Если в расширении было 7 волн, то вообще не факт, что в сужении их тоже будет 7. Запросто может оказаться 5 или 9, а то и вовсе 3. Именно поэтому нужно ориентироваться на пробой образующей, а не на что-либо ещё.
2. Продолжительность формирования первой половины отличается от продолжительности формирования второй половины. Это наиболее распространённое отклонение, правая часть обычно строится дольше. Если тренд перед фигурой развивался медленно, то возможны ложные пробои образующей линии.
Неравномерность в продолжительности формирования двух половин паттерна
3. Вылеты за образующие линии. Не очень критично, главное, чтобы по-прежнему угадывалась форма в виде ромба, это основное. А вот если после вылета цена продолжает рисовать уже плоскую коррекцию вместо треугольной, то в этом случае ориентироваться на паттерн не стоит, даже если и произойдёт разворот.
В целом, фигура считается сложной, но после того, как трейдер пару раз её проторгует, у него всё отложится в памяти и дальше глаз уже сам будет замечать такие последовательности движений. Главная же причина, по которой теряются деньги – это игнорирование рекомендаций по входу, слишком рано открытый ордер часто приводит к убыткам, что в контексте резких движений и смены направления может спровоцировать попытки быстро “отыграться”, а это приводит к ещё большим потерям.
Записаться на курс «Снайпер для начинающих» можно здесь
Прежде, чем вы приступите к торговле на финансовых рынках, вы должны учесть, что торговля валютой, акциями и
другими инвестиционными продуктами имеет рыночный характер и всегда сопряжена со значительной степенью риска.
В результате различных финансовых колебаний вы можете не только значительно приумножить свой капитал,
но и полностью потерять его.
Каждому клиенту необходимо всегда помнить про особые риски и факторы, оказывающие влияние на динамику
изменения валютных курсов и стоимость инвестиционных продуктов. В число таких рисков входят снижение
ликвидности, резкие изменения (скачки) цен, высокая волатильность и форс-мажорные обстоятельства.
Напоминаем вам, что мы не несём ответственности за ваши убытки при торговле по аналитическим материалам, мы
оказываем только информационные услуги.
Как начертить ромб с помощью линейки. Ромбы спицами ‒ простые узоры. Определение ромба, как геометрической фигуры
Классики вариант №2 и 3 Варианты игры «Классики» на улице:
1. Нарисовать длинную линию мелом. Можно играть и самым маленьким.
Ходить по линии. Не оступаться.
Прыгать на одной ноге.
Измерять количество ступней.
Прыгать то справа, то слева от линии. Можно на одной или на двух ногах.
2. Нарисовать длинную линию и треугольники прилегающие к ней. Прыгать как в варианте №1.
3. Классики вариант №3. Прыгать на двух или на одной ноге. Считать вслух прыжки. На линии не заступать.
Мультяшная сумка Cheese. Выглядит как нарисованная на бумаге, на самом деле является настоящей сумкой из канваса (парусина).
Мультяшная сумка Play Hooky. Выглядит как нарисованная на бумаге, на самом деле является настоящей сумкой из канваса (парусина).
Мультяшные сумки придумали две девушки дизайнеры из Тайвани. В 2012 году они выставлялись на неделях мод в Лондоне, Париже и Милане.
У сумки есть молния на дне, поэтому ее объем можно увеличить. Много в нее не влезет, но самое необходимое вполне вместится. Идеальное решение для планшетного компьютера.
(http://multyashniesumki.ru/)
Рисование пастелью — кошка породы Египетская Мау
1) В этом уроке я расскажу вам как нарисовать кота породы Египетская Мау. Это очень красивые кошки с крупными глазами цвета зеленой смородины или же желто-янтарного. У Египетской Мау замечательный и неповторимый окрас. Это и является их отличительной особенностью. Для этой картины нам понадобится пастельный лист темно-синего цвета формата А4. Белым, хорошо заточенным пастельным карандашом сделаем набросок.
2) Переходим к рисованию глаз и носа. Для глаз используйте зеленый, желтый, темно-оранжевый, черный пастельные карандаши. Заштрихуйте аккуратно глаз, зрачок сделайте черным, в конце добавьте белым пастельным карандашом блики. Для носа используйте белый, розовый, черный, красный пастельные карандаши. Вокруг глаз и носа заштрихуйте слегка белым карандашом и разотрите пальцем. При рисовании таких мелких деталей ваши карандаши должны быть хорошо заточены!
3) Ухо заштрихуйте сначала розовым пастельным карандашом, а поверх белым пастельным карандашом. Разотрите все пальцем. Добавьте черные оттенки и разотрите. Теперь заточите хорошо белый пастельный карандаш и нарисуйте белые волосинки быстрыми и легкими движениями.
4) Голову кошки заштрихуйте белым и серым пастельным карандашом. Где-то можете добавить несколько штрихов голубого цвета. После этого разотрите все пальцем.
5) Начинаем уточнять детали. Белым карандашом мелкими штрихами имитируем рост шерсти. Полоски нарисуйте мелкими штрихами черного цвета.
Нарисуй мне, пожалуйста, море,
Чтобы тихие волны мелькали,
Чтобы запахи счастья и воли
Мою грудь до краев наполняли.
Нарисуй мне песок под ногами,
Желтый-желтый, как солнечный лучик.
И укрась небо все облаками,
Не рисуй лишь, пожалуйста, тучи.
Нарисуй мне воздушного змея,
Чтобы ветер играл с ним мятежный.
Чтобы я, ничего не имея,
Продолжала быть доброй и нежной.
Нарисуешь мне море и небо?
И усеешь его облаками?
Нарисуешь мне вечное лето?
И песок под босыми ногами?
Нарисуй, но не ставь еще точку,
Я о главном тебе не сказала,
Нарисуй мне, пожалуйста, дочку,
И себя нарисуй у причала.
Как нарисовать картину красками
Подберите акварельные краски. С них легче всего начинать рисовать картину. Они могут передать все оттенки и придают яркости при просвечивании. Выберите, на какой поверхности будете рисовать – мокрой или сухой. При рисовании на мокрой поверхности размываются очертания предметов, что пригодится в пейзажных композициях или при фоновой заливке овощей и фруктов.
Возьмите чертежный ватман – от избытка воды он не набухает, и места, которые нужно исправить, можно легко смыть поролоном. Расположите бумагу под наклоном в 30-40 градусов для равномерного растекания краски.
Сделайте наброски карандашом основных предметов. Если это натюрморт, то определите расположение стола или другой поверхности и фруктово-овощной композиции. Если это портрет, то учтите пропорции человека, а если пейзаж, то здесь достаточно будет легких набросков – главную роль будут играть краски. В рисовании красками, особенно акварельными, учтите тот факт, что продумывать оттенок каждого мазка нужно заранее. Исправить ошибку можно лишь с помощью влажного поролона. Потом по уже хорошо высохшей поверхности нанесите нужные мазки.
Изобразите общий фон поролоном или широкой беличьей кистью. При окрашивании больших участков следите, чтобы на кисти было достаточно краски. Наносите фон от светлого места к темному. Учтите, что эффект белого при рисовании акварельными красками достигается лишь за счет неокрашенных или хорошо промытых водой мест. Следите за тем, чтобы не порвать бумагу и не скатать ее валиками.
Определите солнечную сторону и затененные места в картине. Отталкиваясь от этого, зарисуйте все предметы. Смешивайте краски на палитре – на рисунке наложение цветовых слоев может привести к простому искажению цвета темных оттенков. Каждый следующий мазок наносите рядом с предыдущим чуть смоченной кисточкой для плавного перехода.
Картины, нарисованные красками, обладают даром притягивать к себе взоры еще и еще. Неповторимая игра оттенков позволяет передать все до мелочей. Но вот как именно нарисовать картину красками?- чертежный ватман,
— карандаш,
— ластик,
— краски.
Нарисуйте детали нарцисса более точно. Из каждой вершины шестиугольника проведите прямые линии, сходящиеся к середине. Эти линии будут вертикальными осями для лепестков цветка. Обозначьте точки середины линий. Теперь с каждой вершины проведите штрихи, расширяющиеся до обозначенных точек. Далее штрихи доведите до середины цветка уже в виде прямых параллельных линий.
Для того чтобы нарисовать нарцисс, прорисуйте лепестки цветка плавными линиями – сгладьте основные контуры. Изобразите небольшое завертывание лепестков волнистыми линиями, располагающимися у их стенок. Прорисуйте середину нарцисса. Сначала границы овала сделайте зубчатыми с мелким шагом. С правой стороны овала дорисуйте небольшой купол, делающий середину более объемной.
Нарисуйте часть стебля нарцисса в виде трубчатой дуги, соединяющей непосредственно цветок и прямой тонкий стебель широкой стороной, направленной к лепесткам. Листок растения изобразите вытянутым нешироким с заостренной вершиной.
Зарисуйте цветок простым карандашом. Середину нарцисса плотно заштрихуйте прямыми тонкими линиями, расходящимися из середины к границам овала. На лепестках изобразите лучики, идущие по вертикальной серединной линии. Затените и левую сторону стебля, и верхнюю часть листка нарцисса.
Зарисуйте сам цветок желтым цветом. Середину сделайте на тон темнее. Листок и стебло зарисуйте ровным зеленым тоном.
Нарцисс – один из первых весенних цветов. Такой нежный и одновременно строгий, неприступный, замечающий только свою красоту. Такую красоту можно удержать надолго только на листике бумаги.- альбомный лист;
— карандаш;
— ластик.
Как нарисовать якорь
Нарисуйте современную конструкцию якоря с двумя острыми краями внизу. Посередине листа проведите вертикальную линию, чуть суженную в верхней части и расширенную в нижней части. Это будет веретено якоря. Вокруг верхней границы веретена изобразите круг, т.н. рым — место крепления троса или каната для поднятия или опускания якоря. В верхней части вертикали проведите горизонтальную линию – шток. Нижнюю часть веретена закрепите большой галочкой.
Прорисуйте отдельные части якоря более детально. Веретено изобразите в виде двух прямых линий, каждую из которых внизу нарисуйте отведенными в разные стороны, образуя якорь, его основную часть. Таким образом получите два рога якоря. Места стыка линий должны быть плавными. Сделайте каждый рог объемным, добавив еще одну линию, повторяющую очертания якоря. На кончиках рогов изобразите лопы — широкие пластины с острыми внешними вершинами. Обратите внимание, что пятка якоря должна быть достаточно острой.
Прорисуйте детально шток. От наклонной прямой линии на небольшом расстоянии проведите еще одну с таким же наклоном, но чуть выпуклую, разграничивая таким образом боковую и нижнюю части штока. Соедините обе линии несколькими вертикальными штрихами. Теперь прорисуйте еще одну повторяющую очертания наклонную линию и продолжите вертикальные штрихи под углом чуть большим 90 градусов. Над верхней границей штока изобразите шейку — нарисуйте небольшой прямоугольник и разделите его пополам вертикальной линией. Кольцо рым сделайте двойным.
Затемните отдельные участки якоря: нижнюю часть лопы и правый рог. Шток заштрихуйте короткими линиями и шейку, ее правую часть. Также затемните участок веретена, который идет вдоль правой границы вертикали, – нарисованный якорь готов.
Якорь – это специальная металлическая конструкция, которая предназначена для закрепления корабля на одном месте. Он имеет множество различных видов, но основа всегда одна – тяжелый низ, который закреплен на прямой металлической вертикали. Нарисованный якорь чаще всего используется в качестве морского символа.- альбомный лист;
— карандаш;
— ластик.
Иногда появляется необходимость сделать элементарное дело, при этом обнаруживается, что мы не знаем, как это сделать. Например — как нарисовать ромб. На самом деле все очень просто.
В данной статье вы узнаете, как правильно нарисовать ромб, и что это за геометрическая фигура.
Что такое ромб?
Ромб является разновидностью параллелограмма, особенностью которого является то, что противоположные стороны этой фигуры параллельны друг к другу, а у ромба они еще и равны между собой. Об определении ромба к общему виду параллелограмма говорит факт равенства противоположных углов.
Как нарисовать ромб
Нарисовать такую фигуру как ромб можно несколькими способами. В этой статье мы рассмотрим два простых способа.
Для первого способа нам понадобятся: ручка или карандаш, ластик, лист в клетку из школьной тетради, линейка или любой похожий на него прямой предмет, если размеры точные размеры ромба не важны.
- Итак, для начала нарисуем точку на одном из пересечений линий клеток. Лучше, конечно, разместить точку не слишком близко к краям. Определяемся с размерами фигуры.
- Далее от средней точки отсчитываем необходимое количество клеток влево (или вправо) и ставим еще одну точку. В противоположной стороне через такое же количество клеток рисуем третью точку. Теперь то же самое проделываем по направлению вверх и вниз. Последовательность не имеет значения, главное здесь — отсчитать одинаковое расстояние от средней точки влево и вправо и отдельно вверх и вниз. То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.
- Соединяем линейкой или любым другим подходящим предметом все точки между собой, кроме среднего. Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов.
Второй способ аналогичен первому, но рисовать мы будем на чистой бумаге без клеток. Нам нужно для этого: карандаш и/или ручка, ластик, чистый лист, линейка и угольник (или любой предмет с прямым углом).
08.08.2014
Рельефные узоры спицами ‒ это чередование при вязании лицевых и изнаночных петель, при этом полотно получается трёхмерным за счёт сочетания выпуклых и вогнутых участков, а также достаточно плотным (без просветов), поэтому такие узоры особенно выразительны. Рельефных узоров существует великое множество, различаются они маленьким или большим раппортом. Эти узоры идеально подходят для гладкой пряжи из хлопка, хлопка с вискозой, шёлка и смесовой льняной пряжи. Если пряжа толстая, то узор выглядит особенно рельефно, а если ‒ тонкая, то получится изысканная, благородная структура. Рельефные узоры достаточно просты в вязании, поэтому рекомендуются для начинающих, т.к. помогают им набраться сноровки и опыта. Уверенные вязальщицы тоже не обходят вниманием рельефные узоры, потому что они удобны для комбинирования с ажуром и придают ему особую нарядность. Чтобы очарование рельефных узоров не исчезло, не следует их утюжить и обрабатывать паром, достаточно увлажнить и дать высохнуть в расправленном виде.
Предлагаем вам большую коллекцию простых рельефных узоров с ромбами и ромбиками для вязания спицами с образцами, схемами, описанием и условными обозначениями.
Выбирайте и творите с удовольствием!
Внимание! Схемы узоров приведены так, как они выглядят с лицевой стороны.
Сокращения:
п. ‒ петля;
лиц. ‒ лицевая;
изн. ‒ изнаночная;
кром. ‒ кромочная;
скрещ. ‒ скрещенная.
Узор 81 «Гранат» (на 6 петель и 6 рядов)
Узор 80 «Простой рельеф» (на 14 петель и 12 рядов)
Узор 79 «Структурный орнамент» (на 11 петель и 30 рядов)
Узор 78 «Кофейные зёрна» (на 18 петель и 36 рядов)
Узор 77 «Ромбовые ячейки» (на 6 петель и 16 рядов)
Узор 76 «Выразительные ромбы» (на 16 петель и 18 рядов)
Узор 75 «Очарование» (на 18 петель и 24 ряда)
Узор 74 «Плато Гиза» (на 16 петель и 36 рядов)
Узор 73 «Ромбы со вставкой» (на 18 петель и 22 ряда)
Узор 72 «Фигурные ромбы» (на 22 петли и 32 ряда)
Узор 71 «Простые ромбы» (на 10 петель и 20 рядов)
Узор 70 «Пастила» (на 12 петель и 12 рядов)
Узор 69 «Паркет» (на 8 петель и 16 рядов)
Узор 68 «Вытянутые ромбы» (на 8 петель и 10 рядов)
Узор двусторонний, смотрится одинаково с лицевой и с изнаночной стороны.
Для образца набрать число петель кратное 8 + 2 кром.
1 ряд
2 ряд : 1 кром.; * 3 изн.; 4 лиц.; 1 изн.**; повторять от * до **; 1 кром.
3 ряд : 1 кром.; * 2 лиц.; 4 изн.; 2 лиц.**; повторять от * до **; 1 кром.
4 ряд : 1 кром.; * 1 изн.; 4 лиц.; 3 изн.**; повторять от * до **; 1 кром.
5 ряд
6 ряд : 1 кром.; * 4 изн.; 4 лиц.**; повторять от * до **; 1 кром.
7 ряд : 1 кром.; * 1 лиц.; 4 изн.; 3 лиц.**; повторять от * до **; 1 кром.
8 ряд : 1 кром.; * 2 изн.; 4 лиц.; 2 изн.**; повторять от * до **; 1 кром.
9 ряд : 1 кром.; * 3 лиц.; 4 изн.; 1 лиц.**; повторять от * до **; 1 кром.
10 ряд : 1 кром.; * 4 лиц.; 4 изн.**; повторять от * до **; 1 кром.
Повторять с 1-го по 10-й ряд.
Узор 67 «Графические ромбы» (на 28 петель и 16 рядов)
Узор 66 «Ромбы из треугольников» (на 14 петель и 14 рядов)
Узор 65 «Ромбики из треугольников» (на 8 петель и 16 рядов)
Узор 64 «Зачёркнутые ромбы» (на 14 петель и 32 ряда)
Узор 63 «Благородная структура» (на 14 петель и 30 рядов)
Узор 62 «Красивый рельеф» (на 12 петель и 32 ряда)
Узор 61 «Необычная структура» (на 10 петель и 20 рядов)
Узор 60 «Цепь из ромбов» (на 8 петель и 20 рядов)
Узор 59 «Изысканная структура» (на 16 петель и 32 ряда)
Узор 58 «Мотыльки» (на 12 п. и 24 ряда)
Узор 57 «Мотыльки» (на 10 п. и 20 рядов)
Узор 56 «Ромбита» (на 28 петель и 28 рядов)
Узор 55 «Нежность» (на 22 петли и 36 рядов)
Узор 54 «Отделочный ромб» (на 17 петель и 30 рядов)
Узор 53 «Шишки» обратная сторона узора «Свечи» (на 12 петель и 32 ряда)
Узор 52 «Свечи» обратная сторона узора «Шишки» (на 12 петель и 32 ряда)
Узор 51 «Гроздья» (на 8 петель и 28 рядов)
Узор 50 «Алмаз» (на 14 п. и 28 рядов)
Узор 49 «Алмаз» (на 10 п. и 24 ряда)
Узор 48 «Ромбы по зигзагу» (на 16 петель и 20 рядов)
Узор 47 «Бантики в ромбах» (на 20 петель и 18 рядов)
Узор 46 «Оригинальный рельеф» (на 26 петель и 34 ряда)
Узор 45 «Перекрёстки» (на 12 петель и 24 ряда)
Узор 44 «Парча» (на 20 петель и 14 рядов)
Узор 43 «Алмазная мозаика» (на 12 петель и 28 рядов)
Узор 42 «Шахматка из ромбов» (на 14 петель и 28 рядов)
Узор 41 «Комбинированная структура» (на 16 петель и 32 ряда)
Узор 40 «Бисерные ромбы» (на 12 петель и 32 ряда)
Узор 39 «Структурные ромбы» (на 12 петель и 18 рядов)
Узор 37 «Жемчужные ромбы по лицевой глади» (на 10 петель и 10 рядов)
Узор 36 «Виноградный рай» (на 10 петель и 24 ряда)
Узор 35 «Жемчужные ромбы» (на 10 петель и 20 рядов)
Узор 34 «Полосы из жемчужных ромбов» (на 10 петель и 16 рядов)
Узор 33 «Традиционные ромбы» (на 20 петель и 24 ряда)
Узор 32 «Треугольники» обратная сторона узора «Мираж» (на 16 петель и 32 ряда)
Узор 31 «Мираж» обратная сторона узора «Треугольники»(на 16 петель и 32 ряда)
Узор 30 «Ромбы в полоску» (на 18 петель и 36 рядов)
Узор 29 «Вертикаль из ромбов и бантиков» (на 22 петли и 18 рядов)
Узор 28 «Горизонталь из ромбов и бантиков» (на 22 петли и 20 рядов)
Узор 27 «Витраж» (на 14 петель и 14 рядов)
Узор 26 «Калейдоскоп» (на 12 петель и 12 рядов)
Узор 25 «Рельефные ромбы» (на 15 петель и 30 рядов)
Узор 24 «Репсовые ромбы» (на 6 петель и 12 рядов)
Узор 23 «Линейные ромбы» (на 12 петель и 12 рядов)
Узор 22 «Сетка рабица» (на 8 петель и 16 рядов)
Узор 21 «Сеточка» (на 8 петель и 14 рядов)
Узор 20 «Панцирная сетка» (на 14 петель и 28 рядов)
Ромб — это простая геометрическая фигура, имеющая четыре вершины и поэтому являющаяся одним из частных случаев параллелограмма. От других многоугольников этого рода ее отличает равенство длин всех сторон. Этой особенностью определяется и то, что углы в противоположных вершинах фигуры имеют одинаковую величину. Построить ромб можно несколькими способами — например, с использованием циркуля.
Вам понадобится
- Лист, карандаш, циркуль, линейка, транспортир.
Инструкция
- Поставьте на противоположных краях листа две произвольные точки, которые будут противоположными вершинами ромба, и обозначьте их буквами A и С.
- Поставьте вспомогательную точку приблизительно в том месте, где должна находиться третья вершина фигуры. Расстояние от нее до вершин A и C должно быть одинаковым, но соблюдать абсолютную точность на этом шаге не требуется.
- Отмерьте циркулем расстояние от точки A до вспомогательной точки и начертите полукруг с центром в точке A, обращенный в сторону точки C.
- Начертите такой же полукруг (не меняя отложенного на циркуле расстояния), имеющий центром точку C и направленный в сторону точки A.
- Поставьте точки B и D в местах верхнего и нижнего пересечения полукругов и проведите соединительные линии между точками A и B, B и C, C и D, D и A. На этом построение ромба с произвольной стороной и углами будет завершено.
- Если требуется построить ромб с заданной длиной сторон, то сначала отложите на циркуле это значение. Затем поставьте точку A, которая будет одной из вершин четырехугольника, и начертите полукруг в направлении предполагаемой противоположной вершины.
- Поставьте точку C в том месте, где вы хотели бы видеть противоположную вершину. Исходите из того, что расстояние от очерченного полукруга до этой вершины должно быть меньше отложенного на циркуле расстояния. Чем меньше будет это расстояние, тем шире получится ромб.
- Повторите действия, описанные в пятом и шестом шагах. После этого построение ромба со сторонами заданной длины будет завершено.
- Если требуется построить ромб с заданным углом, то сначала обозначьте произвольными точками A и B две соседние вершины ромба и соедините их отрезком.
- Отложите на циркуле длину отрезка AB и начертите полукруг с центром в точке A. Все последующие построения производите, не меняя отложенного на циркуле расстояния.
- Приложите транспортир к отрезку AB таким образом, чтобы нулевая отметка совпала с точкой A, отмерьте заданный угол и поставьте вспомогательную точку.
- Проведите отрезок прямой, начинающийся в точке A, проходящий через вспомогательную точку и заканчивающийся на начерченном ранее полукруге. Обозначьте точку окончания отрезка буквой D.
- Начертите два направленных друг к другу полукруга с центрами в точках B и D. Одной из точек пересечения полукружий будет уже существующая точка A, а другую обозначьте буквой C и соедините ее с точками B и D. На этом построение ромба с заданным углом будет завершено.
Цели урока
Продолжать знакомить учеников о такой геометрической фигуре, как ромб;
Закрепить знания о таких понятиях, как ромб и квадрат, а также научиться определять их разницу;
Освежить знания школьников о свойствах и признаках ромба;
Продолжать совершенствовать знания учащихся о геометрических фигурах в процессе решения задач.
Вызвать заинтересованность к урокам геометрии.
Задачи урока
Повторить, обобщить и закрепить полученные знания о такой геометрической фигуре, как ромб;
Продолжать формировать умения и навыки построения геометрических фигур;
Усовершенствовать навыки построения ромба с помощью чертежных инструментов;
Продолжать закреплять знания школьников с использованием практических заданий;
Продолжать развивать внимание, усидчивость и стремление к познавательному процессу.
План урока
1. Раскрытие главное темы урока, определение геометрической фигуры «Ромб».
2. Ознакомление со свойствами и признаками ромба.
3. Теоремы и их доказательство.
4. Как нарисовать ромб. Способы изображения ромба.
5. Как найти площадь ромба?
6. Повторение пройденного материала.
7. Интересные факты.
8. Домашнее задание.
Определение ромба, как геометрической фигуры
Ромб — это такой параллелограмм, у которого все стороны равны. Если же ромб имеет прямые углы, то он называется квадратом.
Сам термин «Ромб» в переводе с греческого языка, обозначает «бубен». Конечно же в нашем понимании бубен, как музыкальный инструмент, имеет круглую форму. Но это сейчас бубны делают круглыми, а в древние времена он как раз и имел квадратную форму или форму ромба.
Давайте остановимся на основных определениях ромба и попробуем понять, что же являет собой эта геометрическая фигура.
Ромб – это такой равносторонний параллелограмм, у которого равные стороны, но неравные углы.
В отличие от квадрата, ромб – это равносторонний косоугольник.
Как всегда мы получаем множество определений той или иной геометрической фигуры, но это не означает, что каждый ученик должен сесть и «зазубрить» именно эти определения. Отличие в определениях – это насколько широко они описывают нашу геометрическую фигуру. Самое главное, это понимание о чем говориться в определении и возможность представить фигуру. Если вы будете придерживаться этих двух правил, то и сами сможете написать или дополнить парочку определений.
Свойства ромба
2. Вторым его свойством является то, что все диагонали ромба пересекаются под прямым углом. В точке пересечения диагонали ромба делятся пополам.
3. Биссектрисами углов ромба являются его диагонали.
4. Чтобы найти сумму квадратов диагоналей ромба, необходимо квадрат его стороны умножить на четыре.
5. Противолежащие стороны ромба равны;
6. Сумма углов ромба, которые прилежат к одной его стороне, равна 180 градусов.
Признаки ромба
Параллелограмм является ромбом в том случае, если он соответствует следующим условиям:
1. Во-первых, у него все стороны равны между собой;
2. Во-вторых, диагонали ромба пересекаются под прямым углом.
3. В-третьих, если диагонали его углов являются биссектрисами.
4. В-четвертых, если его две смежные стороны равны между собой.
5. В-пятых, если хотя бы одна из диагоналей является биссектрисой параллелограмма.
Теоремы и их доказательство
Теперь давайте более подробно рассмотрим свойства и признаки ромба, доказав теоремы:
Теорема 1
Теорема 2
Из этого следует, что:
1. У ромба две оси симметрии – диагонали AC и BD.
2. Его диагонали взаимно перпендикулярны.
3. А также являются биссектрисами его углов.
Площадь ромба
Площадь ромба равна половине произведения его диагоналей. Но так как ромб, по сути, это параллелограмм, то его площадь можно узнать, умножив его стороны на высоту.
Формулы площади ромба:
Где:
a – является стороной ромба
D – обозначается его большая диагональ
d – имеет обозначение меньшая диагональ
α – это острый угол
β – является тупым углом
Площадь любой геометрической фигуры является частью поверхности, которая ограничивается замкнутым контуром данной фигуры. А величина площади ромба выражается числом заключающихся в него квадратных единиц.
Как нарисовать ромб
Чтобы нарисовать ромб воспользуемся свойствами диагоналей ромба. Нам уже известно, что диагонали нашей геометрической фигуры взаимно перпендикулярны и делятся пополам в точке пересечения. Поэтому построение ромба проще всего начать с построения его диагоналей.
Первый способ
И так, в первую очередь выбираем точку, от которой откладываем влево и право отрезки одной длины, в вверх и вниз одинаковые отрезки другой длины.
Теперь нам остается только соединить концы этих отрезков, и в результате мы получим ромб.
Второй способ
Ромб можно еще начертить без использования диагоналей. В этом случае нужно определить лишь концы диагоналей и потом соединить точки отрезками.
Третий способ
И наконец, третий способ, черчения ромба можно выполнить при помощи линейки. Так как мы с вами знаем, что ромб имеет равные стороны, то вначале нужно нарисовать его нижнюю часть. Затем необходимо отложить от нее равный отрезок. А так как третья сторона параллельна первой, то соединив концы первого и третьего отрезков, мы получим ромб.
Повторение
Вы уже познакомились с такой геометрической фигурой, как ромб и понимаете, что квадрат является его частным случаем.
1. Поэтому давайте вспомним определение, что такое квадрат? Дайте самостоятельно определение квадрата.
2. Какими свойствами обладает квадрат? Назовите их.
3. В чем все-таки разница между ромбом и квадратом, если квадрат является его частным случаем?
4. Какую фигуру называют четырехугольником, и относится ли ромб к этой геометрической фигуре?
5. Какие виды четырехугольников вы уже изучали? Назовите их.
6. Какие между ними существуют отличия?
Это интересно знать
Известно ли вам, что если взять прямоугольник и соединить отрезками середины его сторон, то в итоге мы получим ромб.
А если, наоборот, мы с вами возьмем ромб и попробуем соединить его середины сторон отрезками, то мы получим такую геометрическую фигуру, как прямоугольник.
Если вы возьмете параллелограмм с равными высотами, то такой параллелограмм является ромбом.
А знаете ли вы, что названием карточной масти бубны, имеющего ромбическую форму, появилось еще в те времена, когда бубен имел далеко не круглую форму, а вид ромба или квадрата.
Впервые слово «ромб» в своем лексиконе был использован Герроном и Паппой Александрийским.
Домашнее задание
1. Как вы думаете, является ли ромбом параллелограмм, который имеет хотя бы один прямой угол?
2. Верно ли утверждение, что каждый параллелограмм является ромбом?
3. Если диагонали параллелограмма равны 5 см и 7см, может ли быть ромбом этот параллелограмм?
4. Если диагонали параллелограмма равны, то может ли он быть ромбом?
5. Назовите особое свойство ромба, которым обладают его диагонали, помимо того, что они точкой пересечения делятся пополам?
6. Подумайте, где в повседневной жизни применяется такая геометрическая фигура, как ромб?
Расшифруй свой «случайный рисунок» — Централизованная городская библиотечная система, г.Тюмень
Дорогой друг !
Начался новый учебный год! Поздравляем! Ура!
Вспомни, как часто на уроках ты начинаешь рисовать на полях школьных (любимых) тетрадей. Проверь себя!
Возьми лист бумаги и сделай произвольный рисунок!
А потом расшифруй свой «случайный рисунок».
Если ты рисуешь случайные линии
Ты чувствуешь, что попал в неловкое положение. Каждая решительная жирная линия это атака, которую ты не решаешься предпринять. Если под конец ты обведёшь свой рисунок, это значит, что с проблемой покончено.
Если ты рисуешь квадратики, треугольники, ромбы и другие геометрические фигуры
У тебя чёткие цели и убеждения, ты почти никогда не скрываешь своего мнения. Обычно ты сосредоточен. Старайся смотреть на вещи проще.
Если ты рисуешь сердечки
Ты переполнен чувствами. Хочешь расцеловать весь мир.
Если ты рисуешь рожицы или человечков
Рожицы или человечки — это признак беспомощности или желание уклониться от какой-либо обязанности. Обычно рисуют человечков в тот момент, когда следовало бы сказать решительное «нет», но вы не можете себя заставить произнести это слово.
Если ты рисуешь спиральки, кружочки, волнистые линии
Чужие проблемы не слишком тебя заботят или вообще не интересуют. Если ты заметил, что начинаешь рисовать спирали, имей ввиду: сейчас тебе необходимо особо следить за собой, чтобы не вспылить и не нанести собеседнику оскорбление.
Если ты рисуешь цепочки или соединенные между собой колечки
Такой рисунок отражает желание участвовать в чем-либо. Ты чувствуешь, что находишься вне событий. Постарайся понять, почему ты «вне игры», и как-нибудь исправить положение.
Если ты рисуешь узоры
Узор говорит о том, что тебе скучно. Ты жаждешь перемен, мечтаешь о новых переживаниях и ощущениях.
Если ты рисуешь крестики
Кресты и крестики встречаются довольно часто. Они выражают чувство вины. Что-то тебя тяготит: или ты укоряешь себя сам, или тебя упрекает собеседник.
Если ты рисуешь цветочки, солнышко
На душе у тебя невесело. Ты больше всего мечтаешь о дружбе и нежности, а слова, которые вертятся на языке, невольно переносишь на бумагу: «Обратите на меня внимание!». Если твоя рука начинает выводить цветочки или солнышко, поспеши завести хороших друзей.
Если ты рисуешь шахматное поле
Шахматное поле говорит о том, что ты оказался в неприятном или, по
крайней мере, в затруднительном положении. Если такие рисунки появляются часто, ты, вероятней всего, страдаешь от скрытых комплексов.
Если ты рисуешь стрелы, молнии
Это обозначает гнев и агрессивную реакцию. Значит, в данный момент ты не можешь преодолеть какое-то препятствие.
Если ты рисуешь домики
Ты уверен в себе, с чем тебя и поздравляем!
Если ты рисуешь большие рисунки во всю страницу
Это признак откровенности и доверчивости. Маленькие рисунки, наоборот, говорят о застенчивости, сосредоточенности на себе.
Inkscape tutorial: Фигуры | Inkscape
К инструментам фигур относятся инструменты для рисования прямоугольников, эллипсов, звёзд и спиралей. Для начала давайте посмотрим на общие принципы работы с ними, а после ознакомимся с каждым более обстоятельно.
Use Ctrl+Arrows, mousewheel, or middle button drag to scroll the page down. For basics of object creation, selection, and transformation, see the Basic tutorial in .
У Inkscape есть четыре удобных инструмента для работы с фигурами, каждый из которых может создавать или редактировать только собственный тип фигур. Фигура — это объект, изменять который можно разными уникальными для него способами, используя узлы управления и числовые параметры, которые определяют внешний вид фигуры.
For example, with a star you can alter the number of tips, their length, angle, rounding, etc. — but a star remains a star. A shape is “less free” than a simple path, but it’s often more interesting and useful. You can always convert a shape to a path (Shift+Ctrl+C), but the reverse conversion is not possible.
К инструментам фигур относятся инструменты для рисования прямоугольников, эллипсов, звёзд и спиралей. Для начала давайте посмотрим на общие принципы работы с ними, а после ознакомимся с каждым более обстоятельно.
Основные приёмы
A new shape is created by dragging on canvas with the corresponding tool. Once the shape is created (and so long as it is selected), it displays its handles as white diamond, square or round marks (depending on the tools), so you can immediately edit what you created by dragging these handles.
All four kinds of shapes display their handles in all four shape tools as well as in the Node tool (F2). When you hover your mouse over a handle, it tells you in the statusbar what this handle will do when dragged or clicked with different modifiers.
Кроме того, каждая фигура отображает свои параметры в панели параметров инструмента (которая находится над холстом). Обычно панель настроек инструмента содержит несколько числовых полей для ввода и кнопку сброса значений в изначальное состояние. Когда фигура выбрана её «родным» инструментом, редактирование значений в панели настроек изменит выбранную фигуру.
Любые изменения в параметрах инструмента запоминаются и используются для следующей новой фигуры. Например, если вы измените количество лучей звезды, у всех последующих новых звёзд будет такое же количество лучей. Более того, новые параметры фигур запоминаются глобально для каждой новой сессии работы с Inkscape.
When in a shape tool, selecting an object can be done by clicking on it. Ctrl+click (select in group) and Alt+click (select under) also work as they do in Selector tool. Esc deselects.
Прямоугольники
Прямоугольник является простейшей, но, возможно, самой распространённой фигурой в дизайне и иллюстрировании. Inkscape пытается сделать создание и редактирование прямоугольников настолько простым и удобным, насколько это вообще возможно.
Переключитесь на инструмент редактирования прямоугольников F4 или щёлкните мышью по его значку (синий квадратик слева). Создайте новый прямоугольник рядом с приведённым ниже:
Теперь, не меняя инструмента, переключитесь с одного прямоугольника на другой, щёлкнув мышью по только что созданному.
Горячие клавиши для рисования прямоугольников:
With Ctrl, draw a square or an integer-ratio (2:1, 3:1, etc) rectangle.
With Shift, draw around the starting point as center.
Как видите, выбранный прямоугольник (только что созданный прямоугольник всегда выделен) показывает три управляющих ручки по углам. На самом деле их четыре, но две из них (вверху справа) накладываются друг на друга, если углы прямоугольника не закруглены. Эти две ручки называются ручками закругления; другие две (верхний левый и нижний правый) — ручки изменения размера.
Сперва обратим внимание на закругляющие ручки. Схватите один из них и потяните вниз — все четыре угла прямоугольника станут закруглёнными, и вы увидите вторую закругляющую ручку, которая стоит на месте в углу. Если вы хотите получить закруглённые углы, то это все, что вам нужно. Если же вы хотите получить закруглённые, но вытянутые в одну или другую сторону углы, вам нужно сдвинуть верхнюю ручку закругления влево.
Первые два прямоугольника, изображённые ниже, имеют круговые закруглённые углы, а другие два — эллиптические закруглённые углы:
По-прежнему используя инструмент для редактирования прямоугольников, щёлкните мышью по прямоугольникам и обратите внимание на расположение ручек закругления.
Зачастую, радиус закругления у фигуры должен быть постоянным в пределах всего документа, даже если размеры прямоугольников разные (подумайте о диаграмме с закруглёнными прямоугольниками разных размеров). Inkscape позволяет легко решить эту задачу. Переключитесь на инструмент выделения; в его панели настроек есть группа из четырёх кнопок, на второй слева изображены закруглённые углы. Это и есть способ контроля закруглённости углов при изменении размера прямоугольника.
For example, here the original red rectangle is duplicated and scaled several times, up and down, to different proportions, with the “Scale rounded corners” button off:
Обратите внимание: так как размер и форма закруглённых углов одинаковы у всех прямоугольников, угол закругления совпадает в общем для всех фигур в правом верхнем углу. Все голубоватые прямоугольники получены из красного простым изменением его размера посредством инструмента выделения без каких-либо ручных коррекций положения ручек закругления.
For a comparison, here is the same composition but now created with the “Scale rounded corners” button on:
Now the rounded corners are as different as the rectangles they belong to, and there isn’t a slightest agreement in the top right corner (zoom in to see). This is the same (visible) result as you would get by converting the original rectangle to a path (Ctrl+Shift+C) and scaling it as path.
Ниже приведены горячие клавиши для ручек закругления прямоугольника:
Drag with Ctrl to make the other radius the same (circular rounding).
Ctrl+click to make the other radius the same without dragging.
Shift+click to remove rounding.
You may have noticed that the Rectangle tool’s Controls bar shows the horizontal (Rx) and vertical (Ry) rounding radii for the selected rectangle and lets you set them precisely using any length units. The button does what is says — removes rounding from the selected rectangle(s).
An important advantage of these controls is that they can affect many rectangles at once. For example, if you want to change all rectangles in the layer, just do Ctrl+A () and set the parameters you need in the Controls bar. If any non-rectangles are selected, they will be ignored — only rectangles will be changed.
Теперь обратим внимание на узлы изменения размера прямоугольника. Вы можете спросить, зачем они нужны, если можно менять размер прямоугольника с помощью инструмента выделения.
Проблема использования инструмента выделения состоит в том, что понятие горизонтали и вертикали всегда такое же, как у документа. А вот у инструмента редактирования прямоугольников, напротив, изменение размера соответствующими ручками происходит всегда вдоль сторон прямоугольника. Для наглядности попробуйте изменить размер прямоугольника инструментом выделения, а после — при помощи его ручек, используя инструмент редактирования прямоугольников:
Так как ручек, меняющих размер, две, вы можете менять размер прямоугольника в любом направлении. Ручки управления всегда сохраняют угол закругления.
Ниже приведены горячие клавиши для управляющих ручек, меняющих размер:
Drag with Ctrl to snap to the sides or the diagonal of the rectangle. In other words, Ctrl preserves either width, or height, or the width/height ratio of the rectangle (again, in its own coordinate system which may be rotated or skewed).
Here is the same rectangle, with the gray dotted lines showing the directions to which the resize handles stick when dragged with Ctrl (try it):
Из скошенных, повёрнутых, с изменённым при помощи ручек прямоугольников размером, можно легко создать трёхмерную композицию:
Вот ещё несколько примеров композиций, созданных из прямоугольников, как с закруглением, так и с градиентной заливкой:
Эллипсы
Инструмент для редактирования эллипсов («Рисовать круги, эллипсы и дуги» F5) может создавать эллипсы и круги, которые вы можете превращать в сегменты или дуги. Горячие клавиши такие же, как и у инструмента редактирования прямоугольников:
With Ctrl, draw a circle or an integer-ratio (2:1, 3:1, etc.) ellipse.
With Shift, draw around the starting point as center.
Давайте исследуем ручки эллипса. Выберите красный эллипс:
Once again, you see three handles initially, but in fact they are four. The rightmost handle is two overlapping handles that let you “open” the ellipse. Drag that rightmost handle, then drag the other handle which becomes visible under it, to get a variety of pie-chart segments or arcs:
Чтобы получить сегмент, потяните ручку вне эллипса, а для получения дуги — внутри его. На верхнем примере 4 сегмента слева и 3 дуги справа. Дуги — это незакрытые фигуры, т.е. обводка идёт вдоль эллипса, но не соединена в концах дуги. Вы можете сделать это более наглядным, убрав заливку и оставив только обводку:
Note the fan-like group of narrow segments on the left. It was easy to create using angle snapping of the handle with Ctrl. Here are the arc/segment handle shortcuts:
With Ctrl, snap the handle every 15 degrees when dragging.
Shift+click to make the ellipse whole (not arc or segment).
The snap angle can be changed in Inkscape Preferences (in ).
Другие две ручки в эллипсе используются для изменения размера вокруг центра. Их горячие клавиши схожи с клавишами ручек, закругляющих прямоугольник:
Как и у прямоугольника, ручки управления, меняющие размер, регулируют ширину и высоту в собственных координатах эллипса. Это значит, что сплюснутый или повёрнутый эллипс может быть вытянут или сжат по линии собственных осей, оставаясь сплюснутым или повёрнутым. Попробуйте изменить размер этих эллипсов при помощи ручек, меняющих размер:
Звёзды
Звёзды — наиболее сложные и захватывающие фигуры в Inkscape. Если вы хотите поразить своих друзей, дайте им поиграться с инструментом, создающим звёзды. Это очень увлекательно, настолько, что может появиться зависимость!
Инструмент для создания и редактирования звёзд может создавать два типа объектов: звёзды и многоугольники. Звезда содержит два узла управления, которые определяют длину и форму лучей. Многоугольник содержит только одну ручку управления, которая просто поворачивает или меняет его тогда, когда за эту ручку тянут:
In the Controls bar of the Star tool, the first two buttons control how the shape is drawn (regular polygon or star). Next, a numeric field sets the number of vertices of a star or polygon. This parameter is only editable via the Controls bar. The allowed range is from 3 (obviously) to 1024, but you shouldn’t try large numbers (say, over 200) if your computer is slow.
Когда рисуете новую звезду или многоугольник:
Конечно, звезда — наиболее интересная фигура (хотя многоугольники зачастую более полезны на практике). Две управляющих ручки звезды немного отличаются по своим функциям. Первая ручка (изначально она на кончике острия) делает лучи звезды длиннее или короче, но когда вы поворачиваете её (относительно центра фигуры), другая ручка тоже поворачивается. Это значит, что вы не можете наклонить лучи звезды, используя эту ручку.
Другая ручка (изначально она находится во впадине угла между двумя остриями), напротив, свободна в лучевых и поверхностных движениях без воздействия на вторую ручку. На самом деле, эта ручка сама может стать вершиной, будучи смещённой дальше другой от центра звезды. Эта ручка может наклонять кончики звезды, результатом чего станут разновидности кристаллов, мандал, снежинок и дикообразов:
Если хотите получить обычную правильную звезду без лишних завихрений, вы можете заставить скашивающую ручку стать нескашивающей:
As a useful complement for the on-canvas handle dragging, the Controls bar has the field which defines the ratio of the two handles’ distances to the center.
В качестве полезного дополнения, в панели управления есть поле Отношение радиусов, которое определяет отношение расстояний от ручек до центра. У звёзд в Inkscape есть ещё две хитрости в запасе. В геометрии многоугольник — фигура с прямыми линиями и резкими углами. В реальности же разные виды криволинейности и закруглённости — нормальное явление, и Inkscape позволяет получить подобные эффекты. Закругление звезды или многоугольника получается немного иначе, чем закругление у прямоугольников. Вам не нужно использовать отдельную ручку для этого, но
«Касательно» — значит в направлении, перпендикулярном центру. Если вы «повернёте» ручку с нажатой клавишей Shift против часовой стрелки вокруг центра, то получите положительное закругление; поворот по часовой даст отрицательное закругление (смотрите далее примеры отрицательного закругления).
Ниже приведено сравнение закруглённого прямоугольника (с использованием инструмента создания и правки прямоугольников) с закруглённым четырёхконечным многоугольником (с использованием инструмента создания звёзд и многоугольников):
Как вы можете видеть, у закруглённого прямоугольника есть части из прямых линий и части c закруглением; закруглённый же многоугольник или звезда не имеют прямых линий вообще, кривизна мягко переходит от максимальной (в углах) к минимальной (в середине между углами). Inkscape делает это путём добавления коллинеарных касательных Безье к каждому узлу фигуры (вы можете увидеть их, если преобразуете фигуру в контур и проверите его инструментом редактирования узлов).
The parameter which you can adjust in the Controls bar is the ratio of the length of these tangents to the length of the polygon/star sides to which they are adjacent. This parameter can be negative, which reverses the direction of tangents. The values of about 0.2 to 0.4 give “normal” rounding of the kind you would expect; other values tend to produce beautiful, intricate, and totally unpredictable patterns. A star with a large roundedness value may reach far beyond the positions of its handles. Here are a few examples, each indicating its roundedness value:
If you want the tips of a star to be sharp but the concaves smooth or vice versa, this is easy to do by creating an offset (Ctrl+J) from the star:
Shift+dragging star handles in Inkscape is one of the finest pursuits known to man. But it can get better still.
Для более близкой имитации фигур из реального мира Inkscape может искажать случайным образом звёзды и многоугольники. Незначительное искажение такого рода делает звезду менее правильной и более «человечной», чаще забавной; сильное искажение случайным образом — это путь к получению разнообразных сумасшедших непредсказуемых фигур. Закруглённая звезда остаётся слегка закруглённой после искажения случайным образом. Вот горячие клавиши:
Когда будете смещать ручку звезды, подвергшейся эффекту «случайности», она будет дрожать, так как каждый шаг ручки соответствует собственному уникальному значению случайности. Смещение ручки звезды без нажатой клавиши Alt ещё раз применяет эффект случайности к фигуре с тем же уровнем случайности, в то время как Alt-смещение сохраняет искажение, но корректирует уровень. Ниже приведены звёзды с одинаковыми параметрами, но к каждой из них применён эффект случайности путём небольшого сдвига их ручек (уровень случайности везде равен 0,1):
А тут средняя звезда из предыдущего примера, но уже с переменным уровнем искажения от -0,2 до 0,2:
Alt+drag a handle of the middle star in this row and observe as it morphs into its neighbors on the right and left — and beyond.
Вероятно, вы найдёте собственное применение звёздам, искажённым случайным образом, но я использую их для закруглённых амёбовидных клякс и огромных грубых планет с фантастической поверхностью:
Спирали
Спираль в Inkscape —это многосторонняя форма, возможно, не такая полезная как звезда, но и она, при необходимости, может стать очень полезной. Спираль, как и звезда, рисуется от центра; и рисуется, и редактируется.
У нарисованной спирали есть две ручки: одна находится на конце внутри, другая — на конце снаружи. Обе ручки легко перемещаются, сворачивая и разворачивая спираль (как бы «продолжая» её, меняя количество витков). Горячие клавиши:
Внешняя ручка:
Внутренняя ручка:
Alt+drag vertically to converge/diverge.
Alt+click to reset divergence.
Shift+click to move the inner handle to the center.
The divergence of a spiral is the measure of nonlinearity of its winds. When it is equal to 1, the spiral is uniform; when it is less than 1 (Alt+drag upwards), the spiral is denser on the periphery; when it is greater than 1 (Alt+drag downwards), the spiral is denser towards the center:
Максимальное количество витков спирали равно 1024.
Как инструмент для создания эллипсов хорош для создания не только эллипсов, но и дуг (линий неизменной кривизны), так и инструмент для создания спиралей полезен для создания кривых со слабо меняющейся кривизной. Сравнивая обычные кривые Безье с дугами или спиралями, можно отметить, что последние более удобны, потому что вы можете укорачивать или удлинять их, смещая ручку по линии изгиба без искажения общей формы. А ещё вы можете получить интересный эффект, нарисовав обычную спираль, убрав обводку и добавив заливку.
Особенно интересны спирали с пунктирной обводкой — они объединяют гладкую крепость формы с правильно распределёнными метками (точками или чёрточками) для получения более красивых эффектов:
Заключение
Инструменты для работы с фигурами в Inkscape обладают огромный потенциалом. Изучите их особенности и применяйте их в своё удовольствие — это вам пригодится в творческой работе, потому что использование фигур вместо обычных контуров зачастую делает векторные работы быстро выполнимыми и более легко изменяемыми. Если у вас есть какие-либо идеи по дальнейшему улучшению инструментов фигур, не стесняйтесь сообщить о них разработчикам.
Authors:Bulia Byak; Jonathan Leighton; Colin Marquardt; Nicolas Dufour; Gellért Gyuris
Translators:Yura aka Xxaxx — 2005; Alexandre Prokoudine — 2006; Evgeniya Sinichenkova — 2012
Header / footer design: Esteban Capella — 2019
Геометрия— Как доказать, что можно сделать ромбы с любым количеством внутренних точек?
Если $ l $ — желаемое количество точек внутренней решетки, в качестве нечетного $ l $ возьмем ромб, определяемый точками
$ (0,0), ({l + 1 \ over 2}, {l-1 \ over 2}), ({l-1 \ over 2}, {l + 1 \ over 2}), (l , л) $
и даже для $ l $ ромб, определяемый точками
$ (0,0), ({l \ over 2} +1, — {l \ over 2}), (- {l \ over 2}, {l \ over 2} +1), (1, 1 ) $.
Пояснение: Ромб можно определить двумя векторами $ (a, b) $ и $ (c, d) $ равной длины, поместив вершины в $ (0,0), (a, b), (c, d), $ и $ (a + c, b + d) $.Согласно базовой линейной алгебре, любой параллелограмм, определенный таким образом, имеет площадь $ | ad-bc | $. Путем изменения метки мы можем предположить, что $ ad-bc> 0 $, поэтому область будет просто $ ad-bc $.
Теперь предположим, что $ a, b, c, d \ in \ mathbb {Z} $. Отрезок от $ (0,0) $ до $ (a, b) $ не будет иметь на нем точек решетки, кроме конечных точек, если и только если $ \ gcd (a, b) = 1 $, поскольку если $ (m, n) $ является другой точкой решетки на той же прямой, мы должны иметь $ m / n = b / a $ (наклон линии измеряется в двух направлениях). Но это означает, что $ b / a $ не в самых низких ценах.2 = 2i (l + 1) 9 000 долл. США 3
разделите на $ i $ и множите, чтобы получить
(d) $ [(a + c) + (b + d) i] [(- b + d) + (- a + c) i] = 2 (l + 1) $
Таким образом, $ a, b, c, d $ приводят к факторизации $ 2 (l + 1) $ в $ \ mathbb {Z} [i] $. Координаты вверху получены из решения (d) для $ a, b, c, d $ в факторизации
.$ 2 (l + 1) = [(l + 1) + (l + 1) i] [1-i]
долларов СШАНаконец, в обоих случаях быстро проверяется условие (b) на gcds, поскольку во всех случаях координаты $ (a, b) $ или $ (c, d) $ отличаются на 1 по абсолютной величине, и поэтому должны быть относительно простое.
открытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
Класс 7A
Марка 7Б
7 класс (A и B вместе)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 8A
Сорт 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
9 класс (A и B вместе)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Класс 4A
Класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (вместе A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 6А
Марка 6Б
6 класс (A и B вместе)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без марочного знака)
Эти небрендовые версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, изменять или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Четырехугольники
Инструменты четырехугольника содержат нормальный прямоугольник, прямоугольник под углом, параллелограмм, ромб, два способа рисования набора, трапецию, прямоугольники со скругленными углами и инструмент растрового изображения.
Щелчок правой кнопкой мыши на одной из сторон прямоугольника позволяет добавлять метки и текст к середине краев, включая возможность автоматически отмечать параллельные стороны или стороны равной длины. Вы также можете направить прямоугольник так, чтобы он делился на столбцы и строки.
Доступные параметры для прямоугольников
$ высота
$ ширина
$ периметр
$ площадь
Видео — Рисование квадратов
Инструмент «Прямоугольник под углом» очень похож на обычный прямоугольник, с той лишь разницей, что он определяется.Угловые прямоугольники определяются путем рисования одной из сторон (которая может быть под любым углом), и они перемещаются в третью точку, которая определяет высоту прямоугольника. Третья точка может быть не на прямоугольнике.
Щелчок правой кнопкой мыши на одной из сторон прямоугольника позволяет добавлять метки и текст к середине краев, включая возможность автоматически отмечать параллельные стороны или стороны равной длины.Вы также можете направить прямоугольник так, чтобы он делился на столбцы и строки.
Доступные параметры для прямоугольников
$ высота
$ ширина
$ периметр
$ площадь
Инструмент параллелограмма упрощает рисование параллелограммов. Первая линия может быть любой длины и направления.Третья точка определяет параллелограмм.
Щелчок правой кнопкой мыши на одной из сторон параллелограмма позволяет добавлять метки и текст к середине краев, включая возможность автоматически отмечать параллельные стороны или стороны равной длины.
Инструмент «Ромб» позволяет быстро и легко нарисовать ромб.
Два инструмента для рисования воздушных змеев обеспечивают два немного разных способа рисования воздушных змеев.
При использовании первого инструмента воздушного змея первая нарисованная линия является одной из сторон кайта. Третий пункт определяет кайт.
При использовании второго кайта первая линия определяет большую ось кайта.
Щелчок правой кнопкой мыши на одной из сторон воздушного змея позволит вам добавить отметки к середине линии.
Инструмент «трапеция» позволяет быстро нарисовать трапецию. Щелчок правой кнопкой мыши на одной из сторон трапеции позволяет добавлять метки и текст к середине краев, включая возможность автоматически отмечать параллельные стороны.
Инструмент «Прямоугольник со скругленными углами» рисует незатененные прямоугольники с закругленными углами. Закругленный прямоугольник с закругленными углами нарисует прямоугольник с закругленными углами, используя текущую заливку.
Если выбран прямоугольник с закругленными углами, вы увидите серый круглый ползунок, который управляет радиусом закругленных углов.
В качестве альтернативы вы можете щелкнуть правой кнопкой мыши по скругленному прямоугольнику и явно управлять радиусом.
Доступные параметры для прямоугольников со скругленными углами
$ высота
$ ширина
$ периметр
$ площадь
$ радиус
Ромбическая линия симметрии — значение, примеры и решаемые примеры
Ромб имеет две линии симметрии i.Горизонтальная линия симметрии и вертикальная линия симметрии. В ромбе линия симметрии делит его на две равные половины, и каждая половина ромба считается зеркальным отображением другой. Линии симметрии ромба проводятся из его диагоналей. В связи с этим говорят, что линии симметрии ромба являются его обеими диагоналями. У разных объектов разное количество линий симметрии. В этой статье мы обсудим, что такое симметрия, что такое линия симметрии, что означает линия симметрии в ромбе, вращательная симметрия ромба, Чем отличаются линии симметрии ромба от линии симметрии квадратов и т. Д.
Изображение будет скоро загружено
Что такое симметрия?
Определение симметрии гласит, что «симметрия — это зеркальное отображение». Любой объект или форма после поворота или переворота выглядят так же, как оригинал. Это называется симметрией. Симметрия в основном существует в узорах. Слово «симметрия» часто можно услышать в повседневной жизни, поскольку оно встречается повсюду вокруг нас, например, в природе, искусстве, архитектуре и т. Д. Это сбалансированное и пропорциональное сходство, которое можно увидеть в двух i.Одна половина фигуры является зеркальным отображением другой половины. Любая несимметричная форма имеет асимметричную форму.
Что называется линией симметрии?
Любая линия, разделяющая объект на две половины, так что две его части идентичны, называется линиями симметрии. Эти части также считаются симметричными друг другу.
Изображение будет загружено в ближайшее время
Например, изображения, приведенные выше, демонстрируют линию симметрии, которая разделяет очерченную красным фигуру на две абсолютно одинаковые половины.
Из приведенного выше примера мы можем увидеть следующие наблюдения:
Стороны изображения, разделенные линиями симметрии, должны выглядеть одинаково.
Если страница сложена (на которой формируется изображение) с соблюдением линии симметрии, каждая часть изображения будет полностью перекрывать другую часть.
Эти наблюдения помогают нам исследовать линию симметрии любой формы.
Примеры линий симметрии
Некоторые примеры линий симметрии приведены ниже:
Треугольник имеет 3, 1 или даже не имеет линий симметрии
Ромб имеет 2 линии симметрии
Равносторонний треугольник имеет три линии симметрии.
Правильный пятиугольник имеет 5 линий симметрии
Правильный семиугольник имеет 7 линий симметрии.
Линия симметрии в ромбе
Ромб имеет две линии симметрии, то есть горизонтальную линию симметрии и вертикальную линию симметрии. Обе линии симметрии ромба делят его на две равные половины. Линии симметрии ромба проводятся из его диагоналей. В связи с этим говорят, что линии симметрии ромба являются обеими диагоналями ромба.
Чем линии симметрии ромба отличаются от линий симметрии квадратов?
Квадрат и ромб — это двухмерные геометрические фигуры, все четыре стороны которых равны по длине, а противоположные стороны параллельны друг другу. Хотя ромб и квадрат имеют много общего, между ними есть некоторые различия. Это:
Все углы квадрата равны 90 градусам, то есть прямой угол образован в каждой вершине, тогда как противоположные стороны ромба имеют равные размеры.
Из-за разницы в измерении углов квадрата и ромба оба имеют разные линии симметрии.
Ромб имеет две линии симметрии, тогда как квадрат имеет 4 линии симметрии.
Изображение будет скоро загружено
Вращательная симметрия ромба.
Вращательная симметрия определяет, что когда объект вращается вокруг собственной оси, его форма выглядит такой же, как исходная.
Ромб — это двухмерная геометрическая фигура, все четыре стороны которой имеют одинаковую длину.В отличие от квадрата, измерение всех четырех углов ромба не равно 90 градусам. Ромб имеет 2 линии симметрии, то есть вертикальную линию симметрии и горизонтальную линию симметрии. Угол поворота ромба составляет 180 градусов, тогда как порядок симметрии вращения ромба равен 2.
Решенные примеры
Пунктирная линия на фигуре ниже представляет собой линию симметрии.
Изображение будет скоро загружено
Форму, приведенную выше, можно представить как бумагу, и если мы сложим бумагу через пунктирную линию, прозрачно формы обеих сторон линии не совпадают.
Итак, пунктирная линия на заданной фигуре не является линией симметрии.
Какая из следующих фигур не имеет линии симметрии?
Изображение будет загружено в ближайшее время
Решение:
Если мы сложим оба листа бумаги A и B сверху вниз, как показано на рисунках A1 и B1, мы получим линию симметрии на рисунке A, но не на рисунке B. Если мы сложим оба листа слева направо, как показано на рисунках A2 и B2 ниже, мы получим любую линию симметрии на обоих рисунках A и B.
Изображение будет загружено в ближайшее время
Время викторины
Ромб симметричен Около
Каждая из его диагоналей
Перпендикулярная биссектриса каждой из его сторон 9370 906 середина его противоположной стороны.
Ни одного из этих
2. Сколько линий симметрии имеет ромб?
1
2
3
4
Факты
Как найти угол в ромбе
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
доказательств для ромбов — математический класс [видео 2021 года]
Противоположные углы
Теорема о противоположных углах утверждает, что противоположные углы в ромбе равны.
Чтобы доказать это, давайте рассмотрим ромб ABCD , который имеет AB || CD и BC || CD .
Если мы проведем линию, соединяющую две точки B и D , будут созданы два треугольника: DAB и BCD .
Теперь в этих треугольниках AB = CD , AD = BC , а сторона DB является общей.Следовательно, согласно свойству треугольников сторона сторона сторона сторона, они конгруэнтны.
Следовательно, соответствующие углы будут равны.
То же самое можно доказать и для двух других углов. Следовательно, у ромба противоположные углы равны.
Диагонали ромба
Диагонали ромба пересекают друг друга пополам и перпендикулярны друг другу.
Рассмотрим тот же ромб ABCD , у которого AB || CD и BC || CD .
Нарисуем две диагонали, AC и BD , пересекающиеся друг с другом в точке O .
Рассмотрим два треугольника, образованных этим: AOD и COB .Линия DB является трансверсальной к параллельным линиям AD и BC . Таким образом, углы ADO и CBO будут равны при использовании теоремы об альтернативных внутренних углах параллельных прямых.
Аналогично, линия AC является трансверсальной к параллельным линиям CD и AB . Таким образом, углы DAO и BCO будут равны.
Также стороны AD и BC равны друг другу. Итак, используя свойство треугольников угол-сторона-угол, эти треугольники конгруэнтны.
Следовательно, соответствующие стороны этих треугольников будут равны.
Это доказывает, что O является средней точкой линий AC и BD .Таким образом, диагонали ромба делят друг друга пополам.
Теперь, чтобы доказать, что диагонали перпендикулярны в точке O , рассмотрим треугольники BOC и DOC .
В этих треугольниках мы уже доказали, что BO = OD . Мы знаем, что BC = DC и OC — это общая сторона. Следовательно, с использованием свойства сторона-сторона-сторона треугольники BOC и DOC совпадают.
Теперь соответствующие углы, BOC и DOC , равны.
Кроме того, сумма углов BOC и DOC составляет 180 градусов, потому что они находятся на прямой линии.
Поскольку эти углы равны, каждый из них будет составлять 90 градусов. Следовательно:
Таким образом, доказано, что диагонали перпендикулярны друг другу.
Диагонали и углы при вершинах
Диагонали ромба делят углы при вершинах пополам. Рассмотрим тот же ромб ABCD , у которого AB || CD и BC || CD .
Теперь нарисуем диагональ: DB .
DB действует как трансверсаль для пар параллельных линий, AD и BC , а также AB и CD .Следовательно, углы ADB и CBD равны, как и углы ABD и CDB , из-за свойства чередования внутренних углов параллельных линий.
Мы уже доказали, что противоположные углы ромба равны. Итак:
Это означает, что:
Следовательно:
То же самое можно сказать и о другом наборе углов.Таким образом, доказано, что диагонали делят углы при вершинах пополам.
Итоги урока
Хорошо, давайте рассмотрим. В этом уроке мы определили ромб как четырехугольник, у которого все стороны равны, а противоположные стороны параллельны друг другу. Затем мы рассмотрели некоторые важные теоремы, относящиеся к ромбам, а также увидели их доказательства.
- Противоположные углы в ромбе равны.
- Диагонали ромба пересекают друг друга и перпендикулярны друг другу.
- Диагонали ромба делят углы при вершинах пополам.
Amazon.com: Настольный бегунок Ambesonne Rhombus, жирные полосы в стиле каракули, нарисованные кистью на простом фоне, прямоугольный бегунок для кухни в столовой, 16 «X 90», угольно-серый и белый: для дома и кухни
Размер: 16 «X 90» | Цвет: Угольно-серый и белый
Украсьте обеденный стол стильно! Эти уникальные дизайны идеально подходят для развлекательных или повседневных ужинов.Они декоративные, удобные в использовании и стильные. Они добавят элегантности вашему столу и декору комнаты! Благодаря десяткам тысяч свежих и современных дизайнов вы можете найти подходящую дорожку для стола, подходящую к любой посуде, столовой посуде, салфеткам, салфеткам и другим украшениям. Отлично подходит для любого случая и любого мероприятия дома, в доме для вечеринок, в отеле, ресторане, кафе. Красочный дизайн украсит вашу столовую и гостиную, привнеся освежающие нотки. Экологически чистая, не содержит красителей, наносящих вред здоровью вашей семьи.Цвета не выцветают благодаря новым методам цифровой печати. Идеальная идея подарка для вашей мамы, папы, сестры, брата, бабушки, дедушки, жены, мужа, сына, дочери и всех других любимых людей с множеством удивительных дизайнов. В нашей коллекции Amazon вы можете найти дизайн и тему на любой вкус. Когда они откроют подарок, они будут шокированы превосходным качеством предмета. Индивидуальные, персонализированные продукты очень популярны. Как производители домашнего текстиля с цифровой печатью, мы следим за современными тенденциями и предлагаем вам новейшую домашнюю моду.Будь то подарок семье или лучшему другу, родственнику или парню, девушке или себе, этот предмет должен быть интересным и аутентичным. Мужчинам, женщинам, детям, подросткам, мальчикам, девочкам понравится этот товар! ИНСТРУКЦИИ ПО УХОДУ: Машинная стирка в холодном деликатном режиме с мягким моющим средством и водой; Не отбеливать.


 1. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 1. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
1. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 0. 0.]
[0. 0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 1. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
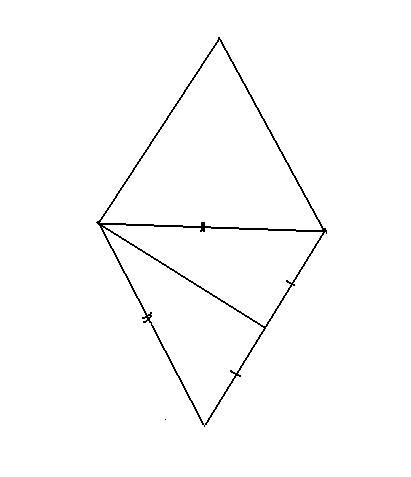 Используйте для этих целей малярную ленту со слабой клеевой основой.
Используйте для этих целей малярную ленту со слабой клеевой основой. Если клей начинает переходить на поверхность, измените угол до 90 °. Если краска начинает подниматься вместе с лентой, острым ножом прорежьте аккуратно краску вдоль малярной ленты.
Если клей начинает переходить на поверхность, измените угол до 90 °. Если краска начинает подниматься вместе с лентой, острым ножом прорежьте аккуратно краску вдоль малярной ленты. После этого тренд как бы возобновляется и перебивает предыдущий максимум. Затем снова происходит разворот вниз и обновляется минимум коррекции. И снова рост с обновлением максимума. Это достаточно сложная конструкция, в такие моменты трейдеры часто теряют деньги, ведь стоп по многим сделкам выносится за ближайший экстремум, после срабатывания сделки зачастую переворачивают и снова получают стоп. В общем, если видим начало расширения, то лучше просто ждать – это может быть, как началом формирования фигуры ромб, так и просто хаотичное поведение участников рынка, вызванное новостями или какими-либо ещё факторами.
После этого тренд как бы возобновляется и перебивает предыдущий максимум. Затем снова происходит разворот вниз и обновляется минимум коррекции. И снова рост с обновлением максимума. Это достаточно сложная конструкция, в такие моменты трейдеры часто теряют деньги, ведь стоп по многим сделкам выносится за ближайший экстремум, после срабатывания сделки зачастую переворачивают и снова получают стоп. В общем, если видим начало расширения, то лучше просто ждать – это может быть, как началом формирования фигуры ромб, так и просто хаотичное поведение участников рынка, вызванное новостями или какими-либо ещё факторами.