Нарисовать 5 плоских геометрических фигур: Изобрази 5 плоских геометрических фигур…
- Геометрические фигуры плоские и объёмные
- Рисование плоских фигур — Энциклопедия по машиностроению XXL
- Урок по математике для учащихся 1 класса «Модели плоских фигур».
- Раскраска узор из геометрических фигур. Карточки домана бесплатно, картинки геометрические фигуры, карточки геометрические фигуры, изучаем геометрические фигуры
- 1. Рисунки из геометрических фигур — Условия к выполнению заданий:
- Вы можете скачать и распечатать бесплатно все
- Как изготовить карточки Домана самостоятельно:
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
- Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
- Еще наши карточки Домана по методике «Вундеркинд с пеленок»:
- 1. Геометрические фигуры — Раскраска с умом — Условия заданий:
- сделать геометрические фигуры из бумаги — 25 рекомендаций на Babyblog.ru
- «Геометрические фигуры» Прозрачные. Контейнер 120 шт.
- Геометрические фигуры. Счет до 5. Плоские и объемные фигуры.
- Плоская геометрия
- трехмерных фигур — определение, свойства, типы трехмерных геометрических фигур, формулы
- Определение 3D-форм
- Типы 3D-фигур
- Свойства трехмерных фигур
- Формулы 3D-фигур
- 3D-фигуры, грани, края, вершины
- Часто задаваемые вопросы о 3D-фигурах
- Что такое трехмерная геометрическая форма?
- Что такое грань, ребро и вершина в 3D-фигуре?
- У трехмерной геометрической формы есть только плоская поверхность?
- Перечислите различия между 2D-формой и 3D-геометрической формой.
- Каковы площадь поверхности и объем трехмерной формы?
- В чем разница между площадью боковой поверхности и площадью криволинейной поверхности трехмерной формы?
- Какая 3D-форма не имеет граней, краев и вершин, а имеет только одну изогнутую поверхность?
- Каковы общие свойства трехмерных геометрических фигур?
- Что еще можно назвать трехмерной формой?
- Какие объекты имеют 3D-формы?
- Что такое объем 3D-формы?
- Что такое трехмерные формы?
- Информация об изучении 2D-форм
- Трехмерные формы | SkillsYouNeed
- различных имен форм (с полезным списком и типами) • 7ESL
- 2D и 3D фигур — объяснение, разница между 2D и 3D формами, решенные примеры
Геометрические фигуры плоские и объёмные
Цели урока:
- Познавательная: создать условия для ознакомления с понятиями плоские и объёмные геометрические фигуры, расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры.
- Коммуникативная: создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку.
- Регулятивная: создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
- Личностная: создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.

Планируемые результаты:
личностные:
- формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений; - формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.
метапредметные:
- овладение навыками самостоятельного приобретения новых знаний;
- организация учебной деятельности, планирования;
- развитие теоретического мышления на основе формирования умений устанавливать факты.
предметные:
- усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные:
- поиск и выделение необходимой информации;
- применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.

УУД личностные:
- оценивать свои и чужие поступки;
- проявление доверия, внимательности, доброжелательности;
- умение работать в паре;
- выражать положительное отношение к процессу познания.
Оборудование: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока: изучение нового материала.
Методы: словесные, исследовательские, наглядные, практические.
Формы работы: фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
— И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
— Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
— Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
— Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
— У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
Выполните это задание в парах.
— По какому признаку вы разделили эти фигуры?
- Плоские и объемные фигуры
- По основаниям объемных фигур
— С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
— Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)
— Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
— Чем они похожи?
— Можно ли сказать, что это одно и тоже?
— Чем же отличается куб от квадрата?
— Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
— Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой. )
)
— Можно ли куб полностью (весь) прижать к парте? Проверим.
— Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)
ПЛОСКИЕ
- Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
- занимают определённое пространство,
- возвышаются над плоской поверхностью.
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
— Какую форму имеют основания этих фигур?
— Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
— Предложите свои названия.
— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
+ Коробка – параллелепипед.
- Яблоко – шар.
- Пирамидка – пирамида.
- Банка – цилиндр.
- Горшок из-под цветка — конус.
- Колпачок – конус.
- Ваза – цилиндр.
- Мяч – шар.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар. )
)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа:
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку.)
Группа 1. (Для изучения параллелепипеда)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ .  |
Группа 2. (Для изучения пирамиды)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Группа 3. (Для изучения куба)
| Эта объемная фигура называется ______________ . Его стороны (грани) похожи на плоскую фигуру ______________ . Их ровно ______________ . Еще у этой фигуры есть углы – вершины, их ______________ . |
Далее каждая группа выступает, представляя свою объемную фигуру другим.
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
— Что нового вы для себя сегодня открыли?
+ Все геометрические фигуры можно разделить на объёмные и плоские.
+ А я узнал названия объёмных фигур
Рисование плоских фигур — Энциклопедия по машиностроению XXL
Овладев в достаточной мере приемами рисования плоских фигур, можно перейти к рисункам объемов. [c.143]Для приобретения достаточных навыков по выполнению технических рисунков, рекомендуется выполнить от руки на глаз следующие предварительные упражнения проведение горизонтальных, вертикальных и наклонных прямых, деление отрезков прямых на равные части, построение углов и их деление на равные части, рисование плоских фигур, очерченных прямыми линиями без сопряжений и с сопряжениями их дугами окружностей. Во всех этих упражнениях надо максимально сохранять заранее намеченные пропорции в размерах самих построений.
Рисование плоских фигур [c.163]
Для приобретения навыков в техническом рисовании рекомендуется начинать с изображения прямых линий, углов и деления их на равные части. Затем можно перейти к рисованию плоских фигур многоугольников, окружностей и эллипсов после этого следует приступить к рисованию геометрических тел и, наконец, освоить рисование производственных деталей.
[c.78]
Затем можно перейти к рисованию плоских фигур многоугольников, окружностей и эллипсов после этого следует приступить к рисованию геометрических тел и, наконец, освоить рисование производственных деталей.
[c.78]
| Фиг. 112. Рисование плоских фигур а — треугольника, б — восьмиугольника, в — шестиугольника |
Рисование плоских фигур и геометрических тел……. [c.374]
РИСОВАНИЕ ПЛОСКИХ ФИГУР, ГЕОМЕТРИЧЕСКИХ ТЕЛ И ТЕХНИЧЕСКИХ ДЕТАЛЕЙ [c.188]
Рассмотренные способы рисования углов 30 и 120° применяют при рисовании плоских фигур в изометрической проекции. [c.190]
Упражнения в рисовании плоских фигур являются хорошей подготовкой к рисованию геометрических тел, так как построение рисунков геометрических тел основывается на умении выполнять рисунки плоских фигур. [c.194]
[c.194]
При рисовании плоских фигур в аксонометрическом изображении используют метод координат, при котором вдоль аксонометрических осей откладывают соответствующие координаты точек, принадлежащих заданной плоской фигуре. Выполнение аксонометрического рисунка начинают с нанесения аксонометрических осей (рис. 228, б, в). Дальнейшие построения аналогичны вышеописанным. Всю разметку отрезков, нанесение единиц измерения производят по аксонометрическим осям или по линиям, им параллельным. Аксонометрические оси и вспомогательные линии рисунка не стирают. Основные линии контура плоской фигуры обводят линиями нормальной толщины. [c.207]
При помощи вспомогательных квадратов и прямоугольников можно нарисовать различные плоские фигуры — шестиугольники, восьмиугольники и др., поэтому этот прием широко используется в рисовании. [c.142]
В курсе черчения технический рисунок строится по правилам аксонометрических проекций (ГОСТ 2. 317—69) с соблюдением некоторых условностей, освещенных в учебнике. Технические рисунки начинают выполнять с простейших плоских фигур и изображения их в аксонометрических проекциях. Рисование окружностей в аксонометрии на начальном этапе обучения следует рисовать не изолированными, а вписанными в квадрат, как показано в учебнике. Оси эллипсов и стороны параллелограммов позволяют учащимся быстрее привык-
[c.313]
317—69) с соблюдением некоторых условностей, освещенных в учебнике. Технические рисунки начинают выполнять с простейших плоских фигур и изображения их в аксонометрических проекциях. Рисование окружностей в аксонометрии на начальном этапе обучения следует рисовать не изолированными, а вписанными в квадрат, как показано в учебнике. Оси эллипсов и стороны параллелограммов позволяют учащимся быстрее привык-
[c.313]
Проделав ряд упражнений по рисованию фигур, можно перейти к рисованию плоских геометрических тел. [c.132]
Фиг. из. Рисование плоских фигур а — окружности, б — эллипса о отношением осей 5 3. в — эллипса, вписаниого в ромб [c.82]
При рисовании ряда правильных плоских фигур — многоугольников и окружностей — используют приближенные способы их построения. Правильный треугольник приближенно строится способом построения угла в 60°, т. е. с использованием отношения 5 3 его высоты к половине стороны (рис. 169, а). Это отношение служит основой и для рисования треугальника. На рисунке среднюю точку основания совмещают с началом координат О,
[c.163]
е. с использованием отношения 5 3 его высоты к половине стороны (рис. 169, а). Это отношение служит основой и для рисования треугальника. На рисунке среднюю точку основания совмещают с началом координат О,
[c.163]
Урок по математике для учащихся 1 класса «Модели плоских фигур».
Краткосрочный план урока по математике № 1-1-27
*В контексте тем:«Все обо мне», «Моя школа»
Школа: ЗСШ №1
Дата: 19.10.17
ФИО учителя: Кудряшова К.В.
Класс: 1 «В» класс.
Количество присутствующих:
отсутствующих:
Тема урока:
Модели плоских фигур (1)
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):
1.3.1.2 различать плоские фигуры (треугольник, круг, квадрат, прямоугольник)/ пространственные фигуры (куб, шар, цилиндр, конус, пирамида) и соотносить их с предметами окружающего мира
Цели урока:
создать условия для организации творческой работы по созданию моделей плоских фигур из различных материалов; сформировать умение моделировать; организовать исследовательскую деятельность по поиску разнообразных способов создания моделей плоских фигур.
Критерии успеха
Учащиеся способны к выделению и формулированию познавательных целей и задач, выбору наиболее эффективных способов решения с помощью учителя; умеют осуществлять действия по образцу и заданному правилу, обозначая информацию моделью;
Привитие
ценностей
Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.
Межпредметные
связи
Взаимосвязь с предметами: обучение грамоте на родном языке, самопознание, познание мира, естествознание, музыка.
Навыки
использования
ИКТ
На данном уроке учащиеся используют ИКТ: презентация «Путешествие в страну геометрии»
Предваритель
ные
знания
Учащиеся могут назвать геометрические фигуры.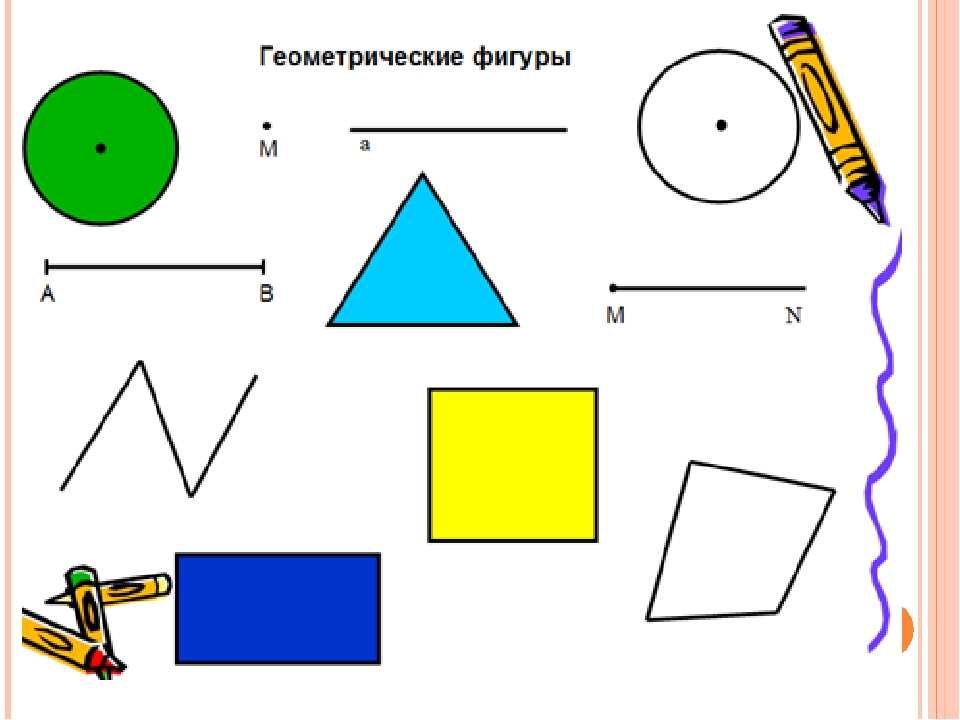
Предварительная работа
Перед началом работы предлагается первоклассникам обсудить, какие материалы и в каком количестве потребуются для создания треугольника. (Для создания треугольника потребуются три соломинки и три кусочка пластилина, так как у треугольника три стороны и три вершины)
Ход урока
Этапы урока
Запланированная деятельность на уроке
Ресурсы
Начало урока
А сейчас все дружно посчитали в обратном порядке.
Для того, чтобы отправиться в путешествие, что нужно составить путешественнику? (карту, или план), а геометрические фигуры нам в этом помогут.
2. Оптправляемся на известном нам паровозике «Чух-чух»
— Какие виды геометрических фигур вам известны
3. Город Чисел
Город Чисел
Презентация
Слайд 1
Слайд 2
Слайд 3 (видеосюжет)
Слайд 3
с муз.сопровождением
Слайд 4
Слайд 4 -5
Критерии успеха
Называют числа в порядке убывания и самостоятельно определяют тему урока.
Середина урока
Помогите необычным жителям цифрам заселиться в свой домик
-Отправляемся дальше
Работа в парах.
Мы проезжаем через озеро Фигур. И чтобы зайти в город нам нужно вспомнить признаки разбиения геометрических фигур.
-Сегодня мы научимся создавать модели плоских фигур. Какой способ получения плоских фигур им знаком?
(Можно обвести пространственную фигуру из набора,)- Плоские фигуры помогают обозначать окружающие нас предметы, имеющие объемные формы, например, на плане, карте или рисунке.
— А в жизни для чего нам нужны плоские фигуры?
(для создания карт, планов)
Сейчас вы самостоятельно сделаете на листе бумаги любую плоскую фигуру при помощи пространственной фигуры.( выбирают из набора любую пространственную фигуру и выполняют это задание самостоятельно, по своему выбору)
Паровозик.
Задание направлено на развитие умения определять вид плоской фигуры. Предложите учащимся рассмотреть изображение паровозика из плоских геометрических фигур — посчитать количество фигур каждого вида и внести результаты счета в таблицу.
— Я вам продемонстрирую модель плоской фигуры — треугольника, выполненную из магнитов.
Что это за фигура?
Эта фигура пространственная или плоская?
Каким способом она получена?
Работа с учебником. (стр 56)
(стр 56)
Как создать модель треугольника?
— Рассмотрите в учебнике этапы создания треугольника из трубочек для коктейля.
А сейчас вы самостоятельно создадите квадрат по алгоритму, данному в учебнике.
-Какие ресурсы потребуются нам для создания квадрата? (для создания квадрата потребуются четыре соломинки одинаковой длины и четыре кусочка пластилина, так как у квадрата четыре стороны и четыре вершины)
Сделай прямоугольник сам.
Реши.
— Какую фигуру можно получить из пяти соломинок и пяти кусочков пластилина. Если они не смогут выполнить задание, предложите поэкспериментировать на практике и найти ответ.
Ответ
Пятиугольник, так как у него 5 сторон и 5 вершин.
Слайд 6-9
Слайд 10 ( с муз.сопровождением)
Слайд 11-12
Слайд 14-15
Слайд 16
Слайд 17-19
Слайд 20
Слайд 21-23
Учебник:
Модели плоских фигур (1), с. 56—57. Рабочая тетрадь:
56—57. Рабочая тетрадь:
Рабочий лист 53 «Модели плоских фигур (1)», с. 55.
Рабочий лист 54 «Картина из фигур», с. 56. Ресурсы:
трубочки для коктейля или счетные палочки для каждого человека.
Критерии успеха
Учащиеся способны к выделению и формулированию познавательных целей и задач, выбору наиболее эффективных способов решения с помощью учителя; умеют осуществлять действия по образцу и заданному правилу, обозначая информацию моделью;
Конец урока
Создай проект «Детская площадка»
Первоклассники смогут создать картину из плоских фигур. Во время выполнения задания они дополнят изображение каждой фигуры таким образом, чтобы получились узнаваемые предметы. Также учащиеся смогут объединить все фигуры, чтобы создать из них единую картину.
Выставка работ. Создание проекта «Детская площадка» Учащиеся прикрепляют фигуры на ватман, тем самым дополняют проект.
Итог урока.
— Модели каких фигур мы создавали?
— Как можно получить плоские фигуры?
— Где могут пригодиться нам эти знания в будущем?
Музыкальноесопровождение
Mozart. HornConcertoNo3 — Allegro
Критерии успеха
учащиеся научатся:
создавать модели плоских фигур;
строить композиции из плоских фигур.
Самоанализ открытого урока математики
На тему: «Моделирование плоских фигур»
Цели обучения:.3.1.2 различать плоские фигуры (треугольник, круг, квадрат, прямоугольник)/ пространственные фигуры (куб, шар, цилиндр, конус, пирамида) и соотносить их с предметами окружающего мира
Цель урока:создать условия для организации творческой работы по созданию моделей плоских фигур из различных материалов; сформировать умение моделировать; организовать исследовательскую деятельность по поиску разнообразных способов создания моделей плоских фигур.
На уроке использованы интерактивные методики обучения: индивидуальная работа, работа в парах , в группах. При проведении работы в группе ставилась цель сплотить ребят, учить их работать вместе, сообща, выслушивая мнение других, предлагать свои идеи и делать общий вывод.
Урок проводился в занимательной форме — путешествия, что способствовало вовлечению всех учащихся класса в процесс обучения. Начало урока с музыкальным сопровождением позволило создать эмоциональный настрой на работу и обеспечить у учащихся необходимую мотивацию.
На уроке использовала различные виды деятельности: «Город Чисел» (повторение состава числа), логические упражнения: «Озеро Геометрических фигур» (разбить фигуры по форме, цвету и размеру), практическая работа ( совместно создать модели плоских геометрических фигур) . На всех этапах урока учащиеся были вовлечены в мыслительную и практическую деятельность. Им надо было не только использовать уже имеющие знания ( различие плоских и пространственных фигур), но и совместно найти способ получения плоской фигуры при помощи пространственной. Первоклассники на протяжении всего урока работали посильно, с удовольствием. В середине урока была включена физминутка. Для каждого ученика были созданы все условия успешной работы. Это способствовало повышению мотивации и познавательного интереса к предмету.
Первоклассники на протяжении всего урока работали посильно, с удовольствием. В середине урока была включена физминутка. Для каждого ученика были созданы все условия успешной работы. Это способствовало повышению мотивации и познавательного интереса к предмету.
Умственные действия опирались и подкреплялись практическими: (обводили объемную фигуру и получали плоскую, при помощи пластилина, трубочек, счетных палочек создавали модели различных плоских фигур) Учебный материал на протяжении всего урока работал на организацию посильного поиска и исследования первоклассников, соответствовал их жизненному опыту. Выбор формы проведения урока соответствует возрастным особенностям детей.Для урока я приготовила презентацию – путешествие. Где учащиеся, в ходе путешествия в страну «Моделирования» выполняли задания на закрепление уже имеющихся знаний, умений и навыков. В городе «Моделирования» учащиеся в группах создали модели плоских фигур. С помощью полученных моделей ребята создали проект детской площадки. На уроке соблюдалась организованность и дисциплина , создана атмосфера сотрудничества. Самостоятельное выполнение задания в рабочей тетради было самостоятельно оценено на «лестнице успеха»
На уроке соблюдалась организованность и дисциплина , создана атмосфера сотрудничества. Самостоятельное выполнение задания в рабочей тетради было самостоятельно оценено на «лестнице успеха»
Материал урока соответствовал принципу доступности и научности Учебное время на уроке использовалось эффективно.
Запланированный материал был выполнен. Не было перегрузки учащихся По окончанию урока было отведено время для обобщения новых знаний, умений и навыков. При затруднении учащимся была оказана индивидуальная помощь.
Урок своей цели был достигнут.
На будущее планирую:
1.Добиваться от учащихся полных ответов на поставленный вопрос.
2. Продолжать обучать учащихся работать в группах, в паре.
3. Продолжать учить умению слушать и слышать своих одноклассников
Раскраска узор из геометрических фигур. Карточки домана бесплатно, картинки геометрические фигуры, карточки геометрические фигуры, изучаем геометрические фигуры
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.
Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.
Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:
Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.
1. Рисунки из геометрических фигур — Условия к выполнению заданий:
Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления. Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.
- В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке.
 Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки. - Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки. Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.
Чтобы придать занятию больше энергии и энтузиазма — можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).
Скачать задание «Рисунки из геометрических фигур» вы можете во вложениях внизу страницы.
2. Геометрические фигуры в рисунках — 3 задания-раскраски:
Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).
Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).
В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.
Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.
Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.
Скачать задание «Геометрические фигуры в рисунках» вы можете во вложениях внизу страницы.
В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.
Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки «больше» «меньше» между картинками.
Скачать раскраску «Смешные рисунки из фигур» вы можете во вложениях внизу страницы.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Одновременно с изучением цветов, ребенку можно начать показывать карточки геометрические фигуры. На нашем сайте Вы сможете скачать их бесплатно.
Как изучить с ребенком фигуры по карточкам Домана.
1) Начинать нужно с простых фигур: круг, квадрат, треугольник, звезда, прямоугольник. По мере освоения материала, начинать изучать фигуры посложнее: овал, трапеция, параллелограмм и т.д.
2) Заниматься с ребенком по карточкам Домана нужно несколько раз в день. При демонстрации геометрической фигуры четко проговаривайте название фигуры. А если во время занятий вы будете еще пользоваться наглядными предметами, например, собирать вкладыши с фигурами или игрушку — сортер, то малыш очень быстро освоит материал.
3) Когда ребенок запомнит название фигур, можете переходить к более сложным заданиям: теперь показывая карточку говорите — это синий квадрат, у него 4 равные стороны. Задавайте ребенку вопросы, просите его самого описать, что он видит на карточке и т.д.
Такие занятия очень полезны для развития памяти и речи ребенка.
Здесь вы можете скачать карточки Домана из серии «Плоские геометрические фигуры» Всего 16 штук, в их числе карточки: плоские геометрические фигуры, восьмиугольник, звезда, квадрат, кольцо, круг, овал, параллелограмм, полукруг, прямоугольник, прямоугольный треугольник, пятиугольник, ромб, трапеция, треугольник, шестиугольник.
Занятия по карточкам Домана прекрасно развивают зрительную память, внимательность, речь ребенка. Это отличная зарядка для ума.
Вы можете скачать и распечатать бесплатно все
карточками Домана плоские геометрические фигурыКликните на карточку правой клавишей мышки, нажмите «Сохранить картинку как…» так вы сможете сохранить изображение на свой компьютер.
Как изготовить карточки Домана самостоятельно:
Распечатайте карточки на плотной бумаге или картоне по 2, 4 или 6 штук на 1 листе. Для проведения занятий по методике Домана карточки готовы, Вы их можете показывать малышу и называть название картинки.
Успехов и новых открытий Вашему малышу!
Развивающее видео для детей (малышей и дошкольников) выполненное по методике Домана «Вундеркинд с пеленок» — развивающие карточки, развивающие картинки на различные темы из части 1, части 2 методики Домана, которое можно смотреть бесплатно здесь или на нашем Канале Раннее развитие детей на youtube
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
Еще наши карточки Домана по методике «Вундеркинд с пеленок»:
- Карточки Домана Посуда
- Карточки Домана Национальные блюда
Здесь вы можете скачать и распечатать задания в картинках по математике «Геометрические фигуры — Раскраска для дошкольников». Что представляют собой эти задания? В первую очередь, это, конечно, ознакомление ребенка с основными фигурами науки геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска. В первой раскраске ребенок будет по команде взрослого раскрашивать фигуры и таким образом запоминать их. А во второй — отыскивать среди множества картинок именно геометрические формы и сразу же раскрашивать свои находки.
1. Геометрические фигуры — Раскраска с умом — Условия заданий:
Выполнять задание — Геометрические фигуры «Раскраска с умом» — необходимо под руководством взрослых (родителей или педагогов), так как задание предназначено для детей от 3-4 лет. Для начала, скачайте бланк с заданием во вложениях внизу данной страницы, распечатайте его на черно-белом принтере и подготовьте цветные карандаши или фломастеры. Прочитайте малышу задания в указанном порядке.
- В первом задании ребенок должен раскрасить в синий цвет все круги, а затем посчитать их количество.
- Во втором задании нужно раскрасить все треугольники в оранжевый цвет и также посчитать их.
- В третьем задании необходимо раскрашивать в красный цвет — квадраты, а в желтый — прямоугольники. После этого посчитать количество этих фигур и сравнить, чего больше, квадратов или прямоугольников.
- В четвертом задании ребенку нужно раскрасить зеленым цветом все овалы. Пересчитать их после раскрашивания.
Требование взрослого раскрасить фигуру в определенный цвет подразумевает под собой, что ребенок должен уже различать цвета. Если же малыш еще не выучил названия основных цветов, то представленные задания помогут ему потренироваться в этом деле.
Скачать геометрические фигуры «Раскраска с умом» вы можете во вложениях внизу страницы.
2. Развивающее задание «Раскрась геометрические фигуры»
Здесь вы найдете интересное развивающее задание по поиску и раскрашиванию геометрических фигур среди множества различных картинок. Детям очень нравятся игры, в которых нужно что-нибудь искать. Поэтому изучение геометрических фигур с помощью подобных игр проходит очень легко и эффективно, так как ребенок даже не подозревает, что он учится, а не играет. К тому же, все дети, без исключения, обожают раскраски!
Как проводить занятие. Скачайте во вложениях бланк с заданием, распечатайте его и дайте ребенку. На отдельном листе бумаги нарисуйте четыре фигуры — круг, квадрат, ромб и треугольник. Подпишите их названия. Раскрасьте фигуры в разные цвета: круги — в синий цвет , квадраты — в зеленый , ромбы — в желтый , треугольники — в красный цвет . Затем отдайте лист ребенку, пояснив, что именно такие фигуры ему нужно найти среди всех изображений бланка-задания и раскрасить их именно в такие цвета, как на листе. Оставьте ребенка одного справляться с заданием. Через несколько минут поинтересуйтесь у него — много ли он нашел на картинке геометрических фигур?
Это задание можно выполнять повторно. Для этого нужно распечатать бланк заново, а на отдельном листе указанные фигуры раскрасить в другие цвета.
Чтобы усложнить задачу для ребенка, можно не использовать отдельный лист с раскрашенными фигурами, а сказать устно, какие фигуры нужно найти и в какой цвет раскрасить. Так у ребенка будет более активно работать память и внимание. Ведь ему придется во время выполнения задания держать эту информацию в голове, без визуальной подсказки.
Скачать развивающее задание «Раскрась геометрические фигуры» вы можете во вложениях внизу страницы.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
сделать геометрические фигуры из бумаги — 25 рекомендаций на Babyblog.ru
В сегодняшней статье я хотела бы рассказать о том, как легко и увлекательно можно изучать геометрические фигуры с малышом, и зачем вообще в столь раннем возрасте грузить ребенка геометрией. Какие игры будут интересны малышу от 1 года, и какие материалы вам понадобятся для занятий — обо всем этом, читайте в статье. Кроме этого, вы найдете несколько полезных материалов для скачивания.
Зачем изучать геометрические фигуры с малышом?Геометрические формы встречаются нам повсюду, их можно разглядеть в большинстве окружающих нас предметов: мяч круглый, стол прямоугольный и т.д. Анализируя сходство окружающих предметов с геометрическими фигурами, ребенок замечательно тренирует ассоциативное и пространственное мышление.
- Изучение геометрических фигур полезно для общего развития малыша, расширения его знаний об окружающем мире. Если знакомить ребенка с формами в раннем возрасте, в школе ему придется гораздо проще.
На умении отличать геометрические фигуры основано множество интересных развивающих игр. Это конструирование, игры с сортером, мозаикой, математическим планшетом, блоками Дьенеша и т.п. Поэтому изучение форм в столь раннем возрасте будет способствовать дальнейшему успешному развитию ребенка.
Итак, игры для изучения и закрепления знаний о геометрических фигурах:
1. Называем геометрические фигуры всегда и вездеЕсли во время игр или чтения книг вам встречается какая-либо фигура, обязательно обращайте на нее внимание малыша и называйте ее («Посмотри, мячик похож на круг, а кубик — на квадрат»). Даже если вам кажется, что ребенок еще вряд ли запомнит названия фигур, все равно произносите их, и они обязательно отложатся у него в голове. Делать это можно уже до года. Поначалу указывайте только на основные фигуры (квадрат, круг, треугольник), затем, когда поймете, что малыш их усвоил, начинайте изучать и другие фигуры.
2. Играем в геометрическое лотоПри помощи лото можно изучать все, что угодно: цвета, геометрические фигуры, овощи, животных и т.д. А геометрическое лото к тому же довольно легко сделать самостоятельно: на листе бумаги или картона рисуем или распечатываем два одинаковых набора фигур, один из которых разрезаем на карточки. Все готово, можно играть. Наши шаблоны лото для изучения геометрических фигур можно СКАЧАТЬ ЗДЕСЬ.
Для первых занятий с малышом лучше использовать лото, где всего 3-4 фигуры. Когда малыш хорошо освоит такую игру, постепенно усложняйте поставленную задачу. Также полезно на первое время все фигуры на игровом поле сделать одного цвета и размера. В этом случае ребенок будет ориентироваться только на один признак — форму, другие же характеристики не будут ни отвлекать, ни подсказывать ему.
Накладывать на игровое поле можно как карточки с изображением фигур, так и объемные фигуры. Хорошо с этой целью подойдут блоки Дьенеша, фигурки от сортера, рамки-вкладыша.
Ну и самый нехлопотный вариант — это приобрести готовое лото с геометрическими фигурами.
3. Играем с сортеромПримерно в возрасте 1 года ребенок начинает замечать, что выбранную им фигурку сортера (Озон,Лабиринт, My-shop) можно протолкнуть далеко не в каждое отверстие. Поэтому во время игры необходимо акцентировать на этом внимание: «Так, вот у нас круг — сюда он не подходит, сюда не подходит, а куда же подходит?». Поначалу повернуть фигуру под правильным углом малышу может быть тяжеловато, но это не страшно, это вопрос практики. Главное, не забывайте вовремя увлекательного процесса «проталкивания» все время произносить названия фигур, и ребенок незаметно их все запомнит.
Важно! При выборе сортера обратите внимание на то, чтобы там были представлены все основные геометрические фигуры, а не только сердечки и полумесяцы.
4. Играем с рамкой-вкладышемПонадобится такая рамка-вкладыш, на которой представлены все основные фигуры. По своей сути игра аналогична сортеру.
5. Сортируем геометрические фигурыПроцесс сортировки предметов стал интересовать мою дочь в возрасте 1 года 4 месяцев. Мы сортировали предметы по цветам, по размеру и, конечно же, по форме. Думаю, эта игра очень нравилась Таисии, потому что мы часто привлекали в нее ее игрушечных друзей. Стоило, например, куклу Машу позвать в игру, она тут же сообщала, что любит играть только с треугольниками, а мишка говорил, что ему нравятся только прямоугольники. Вот и приходилось нам тщательно отбирать фигуры, чтобы никого не обидеть:)
6. РисуемВо время совместного рисования с ребенком также не забывайте произносить названия форм. «Так, нарисуем квадрат, теперь треугольник — получился домик», «Нарисуем круг, овал, палочку, палочку — получился человечек».
Примерно с 1,5 лет малышу уже можно предлагать обводить фигуры по трафаретам. Первые трафареты с геометрическими фигурами вы можете сделать самостоятельно из плотного картона, т.к. готовые трафареты, как правило, очень малы для самых первых опытов рисования. Первые трафареты для Таисии я сделала из не очень удачного набора карточек (картинки были не очень, а вот картон отличный), четырех основных фигур нам хватило за глаза (размер наших трафаретов 8×8 см).
Года в 2 Таисия полюбила рисовать по небольшим трафаретам Woody (аналог), а также в этом возрасте мы начали обводить с наружной стороны блоки Дьенеша, это было не менее интересно, хотя и потруднее.
7. КлеимИспользовать геометрические фигуры в занятиях по аппликации можно хоть с самого первого занятия. Когда малыш только знакомится с клеем (на мой взгляд, знакомство хорошо проходит в возрасте от 1 года 2-3 месяцев), ему больше интересен сам процесс приклеивания, нежели создание какой-то композиции. Поэтому не стоит в первых аппликациях с малышом создавать сложные картины, начните просто с хаотичного приклеивания бумажек на листочек, а еще лучше с хаотичного приклеивания геометрических фигур! Пока малыш увлечено мажет фигурку клеем (с вашей помощью) и прикладывает ее на листочек, вы говорите ему, как она называется. При такой игре все названия очень хорошо укладываются у малыша в голове, можно сказать, прочно «приклеиваются»
Когда у крохи уже будет получаться приклеивать элементы аппликации на заданные места (примерно с 1,5 лет), можно попробовать создать простую композицию.
Вы также можете в своих занятиях использовать различные готовые пособия, например:
- Школа семи гномов 1+. Форма, цвет (Ozon, My-shop)
- Развивающие наклейки для малышей. Форма (Ozon, My-shop)
- Чудесные наклейки. Веселая геометрия (Ozon, My-shop)
Для малышей чуть постарше (от 1 года 6-9 месяцев) очень полезно проводить аналогии между геометрическими фигурами и окружающими предметами. Во время чтения и игр, на прогулке обращайте внимание малыша на то, что тарелка — это круг, окно — прямоугольник, а песочница — квадрат и т.д. Таким образом, вы будете способствовать развитию пространственного и ассоциативного мышления ребенка.
Также можно выполнять задания на отыскание на картинке предметов, которые соответствуют заданной фигуре, например «Найди все круглые предметы». Несколько заданий можно СКАЧАТЬ ЗДЕСЬ.
Вот еще одна интересная игра на распознавание форм — «Найди похожую фигуру» (Лабиринт, My-shop). Несмотря на то, что возраст на ней указан 3-5 лет, она будет интересна ребенку 2-х лет и даже чуть раньше.
9. Учим формы по карточкам ДоманаНа самом деле, я считаю, что этот метод изучения форм самый эффективный. Если вы занимаетесь покарточкам Домана, ребенок очень быстро запомнит все фигуры, а вы потратите на это минимум усилий. Однако нужно заметить, что для того, чтобы знания, полученные по карточкам Домана, отложились у малыша в голове, их нужно закреплять посредством других игр (см. выше). Иначе ребенок быстро забудет все, что вы ему показывали. Поэтому я рекомендую начинать смотреть карточки Домана с геометрическими фигурами примерно в возрасте 1 года, так как в это время малышу становятся интересны сортеры, рамки-вкладыши, рисование, аппликация и т.п. И, изучив формы по картинкам, он сможет использовать полученные знания в этих играх.
10. Смотрим развивающие мультфильмыНу и, конечно, не помешает просмотр мультфильмов на тему «Геометрические фигуры», сейчас на просторах интернета их можно найти немало. Вот некоторые из них:
Вместо заключенияОчень часто процесс обучения ребенка геометрическим фигурам (да и не только фигурам) воспринимается родителями исключительно как постоянное экзаменирование ребенка, т.е. они пару раз показывают ребенку, например, квадрат, а в дальнейшем же обучение сводится к вопросу «Скажи, какая это фигура?». Такой подход крайне неправильный. Во-первых, потому что как и любой человек, ребенок не слишком любит, когда ему устраивают проверку знаний, и это только отбивает у него охоту заниматься. Во-вторых, прежде чем о чем-то спрашивать малыша, ему нужно очень много раз это объяснить и показать!
Поэтому постарайтесь сводить проверочные вопросы к минимуму. Просто повторяйте и повторяйте изучаемую информацию, будь то названия фигур или чего-то еще. Делайте это во время игр и бесед с малышом. А то, что ребенок все усвоил, вы вскоре и сами увидите без лишних проверок.
На этом у меня все, благодарю за внимание! Буду очень рада, если вы поделитесь с нами своими идеями игр для изучения фигур.
Искренне ваша, Яна Разначенко
«Геометрические фигуры» Прозрачные. Контейнер 120 шт.
ОписаниеИгровой набор «Геометрические фигуры» – это 120 плоских форм геометрических фигур из прозрачного цветного пластика: треугольник, трапеция, квадрат, 2 вида ромбов и шестигранник.
6 ярких и понятных ребенку цветов: красный, желтый, синий, зеленый, оранжевый, серый.
Все детали набора безопасны, выполнены из гипоаллергенного и ударопрочного пластика ABS и Celcon.
Набор прозрачных фигур идеально подходит для игр на световом столе, а также для отражения солнечных цветных отражений и лучиков на светлых поверхностях.
Все детали набора безопасны, выполнены из гипоаллергенного и ударопрочного пластика ABS и Celcon. Фигуры имеют приятную текстуру.
Поставляется в прозрачном контейнере с ручкой, для удобного хранения и переноски.
Игровой набор имеет огромный игровой потенциал как в игре дома с мамой, так и в кабинете специалиста.
Множество игровых и учебных задач можно решить с помощью набора геометрических фигур, например:
- изучение геометрических форм, количество граней/вершин,
- сравнение по размеру путем собирания фигур бОльшего размера,
- изучение цветов,
- деление и дроби,
- счет, как в пределах 10, как основа начала математических навыков, так и отработка примеров на сложение и вычитание с переходом через десяток.
Свободная игра с фигурками позволит развивать творческие способности. Дети с удовольствием создают разнообразные фигуры и целые сюжеты из разноцветных шестиугольников, ромбов, квадратов, трапеций, треугольников.
Пособие предназначено для развития математических навыков у детей.
Способствует изучению: чисел, паттернов, геометрии, дробей, а также развитию логического мышления.
Легко мыть. Можно работать в песке и воде. В воде не тонут.
Количество фигур – 120 шт.:
- Квадрат – 12 шт.
- Шестигранник – 12 шт.
- Трапеция – 24 шт.
- Ромб – 24 шт.
- Ромб узкий – 24 шт.
- Треугольник – 24 шт.
Размер элементов: от 2 до 5 см.
Возраст: 3-5 лет, 5-7 лет, 7-12 лет
Упаковка: пластиковый контейнер.
Материал: пластик.
Вес: 0.4
Страна: Тайвань
Геометрические фигуры. Счет до 5. Плоские и объемные фигуры.
11 марта 2020 г 9:50- 10:10
Познавательное развитие. ФЭМП
Тема: Геометрические фигуры. Счет до 5. Плоские и объемные фигуры.
Цель: Упражнять в нахождении геометрических фигур в предметах окружающих детей в группе, развивать внимание, сообразительность; закрепить учение считать до 5, умение удерживать в памяти нескольких действий. Рассказать детям о новых понятиях плоские и объемные фигуры.
Материалы и оборудования: цветные карандаши, карточки с цифрами от 1 до 5, картинки с изображенными на них 5 предметами; лист бумаги А5.
Ход.
I. Организационный момент. Сравнение геометрических фигур и предметов.
Воспитатель показывает картинки с предметами, дети определяют, на какую геометрическую фигуру похож тот или иной предмет.
Задание. Определите, из каких геометрических фигур состоит рисунок.
II. Объяснение выполнения задания. Счет до 5.
По указанию воспитателя дети выбирают и показывают нужную цифру.
К доске прикреплены картинки предметов. Воспитатель просит показать второй, четвертый, первый, пятый предметы.
Детям предлагаются полоски бумаги с изображением рядов геометрических фигур и цветов. Нужно закрасить второй овал в желтый цвет, четвертый треугольник – в красный, третий круг – в синий, раскрасить цветы, у которых 4 лепестка.
III. Физкультминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(дети «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
IV. Самостоятельная деятельность детей
— Посмотрите на доску. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
— У вас на столах лежат карточки с этими фигурами. Выполните это задание в парах.
— По какому признаку вы разделили эти фигуры?
Плоские и объемные фигуры
По основаниям объемных фигур
— С какими фигурами мы уже работали?
(Воспитатель показывает куб и квадрат.)
— Чем они похожи?
— Можно ли сказать, что это одно и тоже?
— Чем же отличается куб от квадрата?
— Давайте проведём опыт. (дети получают индивидуальные фигуры – куб и квадрат.)
— Попробуем приложить квадрат к плоской поверхности стола. Что видим? Он весь (целиком) лёг на поверхность стола? Вплотную?
! Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
— Можно ли куб полностью (весь) прижать к столу? Проверим.
— Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и столом?
! Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (воспитатель вывешивает на доске выводы.)
ПЛОСКИЕ
Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
занимают определённое пространство,
возвышаются над плоской поверхностью.
Объёмные фигуры: пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке. (куб, призма, цилиндр)
— Какую форму имеют основания этих фигур?
— Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
— Предложите свои названия.
— Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
— Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Соотнесение реальных объектов и объёмных тел.
— А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
+ Коробка – параллелепипед.
Яблоко – шар.
Пирамидка – пирамида.
Банка – цилиндр.
Горшок из-под цветка — конус.
Колпачок – конус.
Ваза – цилиндр.
Мяч – шар
V. Рефлексия.
Задание «Рисуем фигуры»
Детям раздаются листочки бумаги.
Воспитатель: — Нарисуйте на своих листочках 5 треугольников. Затем заштрихуем наши фигуры цветными карандашами, чтобы они стали красивее. Заштриховать фигуры постарайтесь, не выходя за пределы контура. Первый треугольник заштрихуйте красным карандашом. Второй треугольник заштрихуйте синим карандашом. Остальные треугольники заштрихуйте зеленым карандашом.
Давайте теперь посмотрим, сколько у нас красных треугольников, сколько синих, а сколько зеленых? Каких треугольников больше? Каких треугольников меньше?
Каких треугольников равное количество?
— Что нового узнали.
— Что больше всего понравилось.
На этом наше занятие закончилось. Наводим порядок на столе.
Плоская геометрия
Если вы любите рисовать, то геометрия для вас!
Плоская геометрия — это плоские формы, такие как линии, круги и треугольники … фигуры, которые можно нарисовать на листе бумаги
| Подсказка: попробуйте нарисовать некоторые формы и углы по мере изучения … это помогает. |
Точка, линия, плоскость и твердое тело
Точка не имеет размеров, только позиция
Линия одномерная
Плоскость двухмерная (2D)
Твердое тело трехмерное (3D)
Плоская геометрия — это все о формах на плоской поверхности (например, на бесконечном листе бумаги).
Полигоны
Многоугольник — это двумерная фигура, состоящая из прямых линий. Треугольники и прямоугольники — это многоугольники.
Вот еще несколько:
Круг
Теоремы о круге (расширенная тема)
Символы
В геометрии используется много специальных символов.Вот вам краткая справка:
Геометрические символы
Конгруэнтные и похожие
Уголки
Типы углов
Использование инструментов для рисования
Преобразования и симметрия
Преобразований:
Симметрия:
Координаты
Дополнительные разделы по геометрии плоскости
Пифагор
Конические секции
Теоремы о круге
Центры треугольника
Тригонометрия
Тригонометрия — отдельная тема, поэтому вы можете посетить:
трехмерных фигур — определение, свойства, типы трехмерных геометрических фигур, формулы
3D-фигуры — это твердые тела, состоящие из трех измерений, а именно длины, ширины и высоты.Слово «3D» означает «трехмерные геометрические фигуры». Каждая трехмерная геометрическая форма занимает определенное пространство в зависимости от ее размеров, и мы можем видеть так много трехмерных фигур вокруг нас в повседневной жизни. Некоторыми примерами трехмерных форм являются куб, кубоид, конус и цилиндр.
Определение 3D-форм
3D-фигуры — это твердые фигуры или объекты, имеющие три измерения (длина, ширина и высота), в отличие от двухмерных объектов, которые имеют только длину и ширину.Другие важные термины, связанные с трехмерными геометрическими фигурами, — это грани, ребра и вершины. У них есть глубина, поэтому они занимают некоторый объем. Некоторые 3D-формы имеют свою базовую и верхнюю части или поперечные сечения как 2D-формы. Например, у куба все грани имеют форму квадрата. Теперь мы подробно узнаем о каждой трехмерной фигуре. Трехмерные формы подразделяются на несколько категорий. Некоторые из них имеют криволинейные поверхности; некоторые имеют форму пирамид или призм.
Реальные примеры трехмерных геометрических фигур
В математике мы изучаем трехмерные объекты в концепции твердых тел и пытаемся применить их в реальной жизни.Ниже показаны некоторые реальные примеры трехмерных фигур: футбольный мяч, куб, ведро и книга.
Типы 3D-фигур
Существует множество трехмерных фигур, которые имеют разные основания, объемы и площади поверхности. Обсудим каждую из них.
Сфера
Сфера имеет круглую форму. Это трехмерная геометрическая фигура, у которой все точки на ее поверхности находятся на одинаковом расстоянии от ее центра. Наша планета Земля похожа на сферу, но это не так.Форма нашей планеты — сфероид. Сфероид похож на сферу, но радиус сфероида от центра до поверхности не одинаков во всех точках. Некоторые важные характеристики сферы следующие.
- Он имеет форму шара и идеально симметричен.
- Он имеет радиус, диаметр, окружность, объем и площадь поверхности.
- Каждая точка сферы находится на одинаковом расстоянии от центра.
- У него одна грань, без ребер и без вершин.
- Это не многогранник, так как у него нет плоских граней.
Куб и кубоид
Куб и кубоид — это трехмерные фигуры, которые имеют одинаковое количество граней, вершин и ребер. Основное различие между кубом и кубоидом заключается в том, что все шесть граней куба являются квадратом, а кубоид имеет все шесть граней прямоугольной формы. Куб и кубоид занимают разные объемы и имеют разные площади поверхности. Длина, ширина и высота куба одинаковы, тогда как для кубоида длина, высота и ширина различны.
Цилиндр
Цилиндр — это трехмерная форма, которая имеет две круглые грани, одну вверху, другую внизу, и одну изогнутую поверхность. Цилиндр имеет высоту и радиус. Высота цилиндра — это расстояние по перпендикуляру между верхней и нижней гранями. Некоторые важные характеристики цилиндра перечислены ниже.
- Имеет одну изогнутую грань.
- Форма остается неизменной от основания до верха.
- Это трехмерный объект с двумя одинаковыми концами круглой или овальной формы.
- Цилиндр, в котором оба круговых основания лежат на одной линии, называется правым цилиндром. Цилиндр, в котором одно основание размещено вдали от другого, называется наклонным цилиндром.
Конус
Конус — это еще одна трехмерная форма, имеющая плоское основание (имеющее круглую форму) и заостренный кончик наверху. Заостренный конец на вершине конуса называется «Вершиной». Конус также имеет изогнутую поверхность. Подобно цилиндру, конус можно также классифицировать как прямой круговой конус и наклонный конус.
- Конус имеет круглое или овальное основание с вершиной (вершиной).
- Конус — это повернутый треугольник.
- В зависимости от того, как вершина совмещена с центром основания, образуется прямой или наклонный конус.
- Конус, в котором вершина (или заостренный кончик) перпендикулярна основанию, называется правильным круговым конусом. Конус, вершина которого находится где-нибудь вдали от центра основания, называется косым конусом.
- Конус имеет высоту и радиус.Помимо высоты, у конуса есть наклонная высота, которая представляет собой расстояние между вершиной и любой точкой на окружности круглого основания конуса.
Тор
Тор — это трехмерная форма. Он образуется путем вращения меньшего круга радиуса (r) вокруг большего круга с большим радиусом (R) в трехмерном пространстве.
- Тор — это правильное кольцо, имеющее форму шины или бублика.
- У него нет ребер или вершин.
Пирамида
Пирамида — это многогранник с основанием многоугольника и вершиной с прямыми краями и плоскими гранями. Основываясь на совмещении их вершины с центром основания, их можно разделить на правильные и наклонные пирамиды. Пирамида с:
Призмы
Призмы — это твердые тела с одинаковыми концами многоугольника и плоскими сторонами параллелограмма. Некоторые характеристики призмы:
- Он имеет одинаковое поперечное сечение по всей длине.
- Различные типы призм: треугольные призмы, квадратные призмы, пятиугольные призмы, шестиугольные призмы и т. Д.
- Призмы также широко подразделяются на обычные и наклонные призмы.
Теперь давайте узнаем о трехмерных фигурах с правильными многогранниками (платоновых телах).
Многогранники
Многогранник — это трехмерная фигура, имеющая многоугольные грани (треугольник, квадрат, шестиугольник) с прямыми краями и вершинами.Его еще называют платоническим телом. Есть пять правильных многогранников. Правильный многогранник означает, что все грани выглядят одинаково. Например, у куба все грани имеют форму квадрата. Еще несколько примеров правильных многогранников приведены ниже:
- Тетраэдр с четырьмя равносторонне-треугольными гранями
- Октаэдр с восемью равносторонне-треугольными гранями
- Додекаэдр с двенадцатью правильными гранями пятиугольника
- Икосаэдр с двадцатью равносторонне-треугольными гранями
- Куб с шестью квадратными гранями (также известный как шестигранник)
Свойства трехмерных фигур
Каждая трехмерная форма имеет некоторые свойства, которые помогают нам легко их идентифицировать.Обсудим кратко каждую из них.
| 3D-фигуры | Недвижимость |
|---|---|
| Сфера (с радиусом (r)) |
|
| Цилиндр |
|
| Конус |
|
| Куб |
|
| Кубоид |
|
| Призма |
|
| Пирамида |
|
Формулы 3D-фигур
Как уже говорилось, все трехмерные геометрические формы имеют площадь поверхности и объем.Площадь поверхности — это область, покрытая трехмерной формой внизу, вверху и всеми гранями, включая изогнутые поверхности, если таковые имеются. Объем определяется как объем пространства, занимаемого трехмерной фигурой. Каждая трехмерная форма имеет разные площади поверхности и объемы.
| 3D форма | Формулы |
|---|---|
| Сфера | Диаметр = 2 × r (r — радиус) Площадь поверхности = 4πr 2 квадратных единиц Объем = (4/3) πr 3 кубических единиц |
| Цилиндр | Общая площадь поверхности = 2πr (h + r) квадратных единиц (r — радиус, а h — высота цилиндра) Объем = πr 2 ч куб |
| Конус | Площадь изогнутой поверхности = πrl квадратных единиц (где l — наклонная высота, а l = √h 2 + r 2 ) Общая площадь поверхности = πr (l + r) квадратных единиц Объем = (1/3) πr 2 ч куб |
| Куб | Площадь боковой поверхности = 4a 2 квадратных единиц (где ‘a’ — длина стороны куба) Общая площадь = 6a 2 квадратных единиц Объем = 3 кубических единиц |
| Кубоид | Площадь боковой поверхности = 2h (l + w) квадратных единиц (где h — высота, l — длина, а w — ширина) Общая площадь поверхности = 2 (lw + wh + lh) квадратных единиц Объем = (l × b × h) куб. Ед. |
| Призма | Площадь поверхности = [(2 × Площадь основания) + (Периметр × Высота)] квадратных единиц Объем = (площадь основания × высота) куб. Единиц |
| Пирамида | Площадь поверхности = [Базовая площадь + 1/2 × P × (наклонная высота)] квадратных единиц Объем = [(1/3) × Базовая площадь × высота] кубических единиц |
3D-фигуры, грани, края, вершины
Как упоминалось ранее, 3D-формы и объекты отличаются от 2D-форм и объектов из-за наличия трех измерений — длины, ширины и высоты.В результате этих трех измерений эти объекты имеют грани, ребра и вершины. Давайте разберемся с этими тремя подробнее.
Лица
- Под гранью понимается любая плоская или изогнутая поверхность твердого объекта.
- 3D-фигуры могут иметь несколько граней.
Кромки
- Ребро — это отрезок линии на границе, соединяющий одну вершину (угловую точку) с другой.
- Они служат стыком двух лиц.
вершины
- Точка пересечения двух или более прямых называется вершиной.
- Это угол.
- Точка пересечения ребер обозначает вершины.
| 3D-формы | Лица | Кромки | Вершины |
|---|---|---|---|
Сфера | 1 | 0 | 0 |
| Цилиндр | 3 | 2 | 0 |
| Конус | 2 | 1 | 1 |
| Куб | 6 | 12 | 8 |
| Прямоугольная призма | 6 | 12 | 8 |
Треугольная призма | 5 | 9 | 6 |
Пятиугольная призма | 7 | 15 | 10 |
Призма шестигранная | 8 | 18 | 12 |
Квадратная пирамида | 5 | 8 | 5 |
Треугольная пирамида | 4 | 6 | 4 |
Пятиугольная пирамида | 6 | 10 | 6 |
Пирамида шестиугольная | 7 | 12 | 7 |
Мы можем лучше понять трехмерные формы и их свойства , используя сети.Двухмерная форма, которую можно сложить в трехмерный объект, называется геометрической сеткой. У твердого тела могут быть разные сети. Проще говоря, сеть представляет собой развернутую форму трехмерной фигуры. Пожалуйста, обратите внимание на несколько двухмерных фигур, которые складываются в трехмерную.
Важные примечания
Вот несколько важных моментов, которые следует помнить о трехмерных фигурах.
- Трехмерные объекты имеют 3 измерения, а именно длину, ширину и высоту.
- 3D-фигуры имеют грани, кромки и вершины.
- Изучение трехмерных тел поможет нам в повседневной жизни, поскольку большая часть нашей деятельности вращается и зависит от них.
Темы, связанные с 3D-фигурами
Вот несколько интересных тем, связанных с трехмерными формами.
Часто задаваемые вопросы о 3D-фигурах
Что такое трехмерная геометрическая форма?
Фигура или твердое тело, имеющее три измерения, называется трехмерной фигурой.У них есть грань, ребро и вершина. Пространство, занятое этими формами, придает их объем. У 2D-форм есть площадь, а у 3D-фигур — площадь поверхности. Площадь поверхности означает площадь всех граней трехмерной формы. Некоторыми примерами трехмерных форм являются куб, кубоид, конус, цилиндр. Мы можем видеть вокруг себя множество реальных объектов, которые напоминают трехмерную фигуру. Например, книга, шапка на день рождения, банка из-под кокса — вот некоторые из реальных примеров трехмерных форм.
Что такое грань, ребро и вершина в 3D-фигуре?
Очень важной особенностью трехмерной формы является ее грань, вершина и край.Как правило, грань трехмерной формы представляет собой плоскую поверхность многоугольной формы. 3D-фигура имеет несколько граней, кроме сферы. Вершина — это острый угол. Край — это отрезок линии или расстояние между двумя соседними вершинами трехмерной формы. Различные 3D-формы имеют разное количество граней, вершин и ребер. Например, куб — это трехмерная фигура, имеющая 6 граней, 12 ребер и 8 вершин.
У трехмерной геометрической формы есть только плоская поверхность?
Нет, трехмерная фигура может иметь как плоские, так и изогнутые поверхности.Например, конус и цилиндр имеют плоские поверхности круга, а также изогнутые поверхности.
Перечислите различия между 2D-формой и 3D-геометрической формой.
Различия между 2D-формой и 3D-формой заключаются в следующем.
- Двумерные формы имеют длину и ширину, а трехмерные формы — длину, ширину и высоту.
- 2D-формы имеют площадь и не занимают никакого объема, тогда как 3D-фигуры имеют площадь поверхности и объем.
- Примерами 2D-форм являются треугольник, квадрат, прямоугольник, а примерами 3D-форм являются куб, кубоид, призма.
Каковы площадь поверхности и объем трехмерной формы?
Площадь поверхности означает площадь всех отдельных граней трехмерной формы. Все трехмерные формы имеют некоторую глубину. Пространство внутри трехмерной формы называется ее объемом.
В чем разница между площадью боковой поверхности и площадью криволинейной поверхности трехмерной формы?
Площадь боковой поверхности означает площадь всех поверхностей трехмерной формы, за исключением верхней и нижней поверхностей. Область криволинейной поверхности включает в себя область только криволинейной поверхности в трехмерной форме.Например, у куба 6 плоских граней. Площадь его боковой поверхности включает площадь всех 4 граней, исключая верхнюю и нижнюю грани. Цилиндр имеет две плоские грани и одну изогнутую поверхность. Таким образом, площадь изогнутой поверхности — это область изогнутой части между верхней и нижней гранями, имеющей круглую форму.
Какая 3D-форма не имеет граней, краев и вершин, а имеет только одну изогнутую поверхность?
Сфера — это трехмерная фигура, не имеющая граней, ребер и вершин. У него только одна изогнутая поверхность.Площадь поверхности сферы равна 4 πr 2 . Тор — это другая форма, у которой нет грани, ребра или вершины. Он имеет форму кольца. Он образован вращением меньшего круга вокруг большего круга в трехмерном пространстве.
Каковы общие свойства трехмерных геометрических фигур?
Общие свойства 3D-форм следующие.
- 3D-фигуры имеют длину, ширину и высоту. Сфера исключительна, поскольку у нее нет этих трех измерений, но она простирается в трех направлениях.
- 3D-формы могут иметь или не иметь грани, вершины, кромки и криволинейные поверхности.
- Грани большинства трехмерных фигур представляют собой многоугольники, такие как треугольник, квадрат, прямоугольник.
Что еще можно назвать трехмерной формой?
В геометрии трехмерную фигуру можно также назвать твердой формой.
Какие объекты имеют 3D-формы?
Объекты, которые являются трехмерными с определенными длиной, шириной и высотой, называются трехмерными фигурами.Несколько примеров трехмерных форм: игральные кости в форме куба, коробка для обуви в форме кубовидной или прямоугольной призмы, конус мороженого в форме конуса, глобус в форме сферы.
Что такое объем 3D-формы?
Объем 3D-фигур относится к количеству кубического пространства, заполненного внутри фигур. Чтобы найти объем, нам обычно требуется измерение трех измерений. Расчет объема трехмерных фигур становится проще, если мы знаем формулы каждой формы.
Что такое трехмерные формы?
3-мерные игры
Объем с использованием юнит-кубовЕдиничный куб — это куб, имеющий объем или емкость 1 юнит. Вы можете подсчитать количество единичных кубиков, которые могут поместиться в твердое тело, чтобы определить его объем.
охватывает Common Core Curriculum 5.MD.5.aИграть сейчасПосмотреть все игры по геометрии >>Учитесь с помощью полной программы обучения математике K-5
Что такое трехмерные формы? В геометрии трехмерную фигуру можно определить как твердую фигуру или объект или форму, имеющую три измерения — длину, ширину и высоту.В отличие от двухмерных форм, трехмерные формы имеют толщину или глубину.
Учитесь с помощью полной программы обучения математике K-5
Атрибуты трехмерной фигуры — это грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.
Куб, прямоугольная призма, сфера, конус и цилиндр — это основные трехмерные формы, которые мы видим вокруг себя.
Мы можем видеть кубик в кубике Рубика и игральную кость, прямоугольную призму в книге и коробке, сферу в глобусе и шаре, конус в моркови и рожок мороженого и цилиндр в ведре и бочка, вокруг нас.
Вот список трехмерных или трехмерных фигур с их названиями, изображениями и атрибутами.
| Название трехмерной формы : | Изображение 3D формы : | Атрибуты : |
| Куб | Лица — 6 Кромки — 12 вершин — 8 | |
| Прямоугольная призма или кубоид | Лица — 6 Кромки — 12 вершин — 8 | |
| Сфера | Изогнутая грань — 1 Кромки — 0 вершин — 0 | |
| Конус | Плоское лицо — 1 Изогнутая грань — 1 Кромки — 1 вершин — 1 | |
| Цилиндр | Плоское лицо — 2 Изогнутая грань — 1 Кромки — 2 вершин — 0 |
Интересные факты
|
Давайте споем!
3D-формы толстые, а не плоские.
Найди конус в шапке на день рождения!
Вы видите сферу в баскетбольном мяче,
И кубоид в таком высоком здании!
Вы видите куб в кости, которую вы бросаете,
И цилиндр в сияющем флагштоке!
Давайте сделаем это!
Вместо того, чтобы показывать видео о трехмерных фигурах вашим детям и воспитанникам детского сада, попросите их наблюдать и выделять предметы вокруг них, в которых они могут найти трехмерные формы.
Вы можете также попросить их определить и отсортировать трехмерную форму и ее атрибуты.
Сопутствующий математический словарь
Информация об изучении 2D-форм
2D-фигуры также называются двумерными фигурами, многоугольниками или плоскими фигурами. Это первые формы, которые учат дети. Дети в возрасте 2 лет могут начать распознавать простые двухмерные фигуры, такие как круги, и рисовать их.
1 Значение
Изучение 2D-форм — ключ к будущему обучению математике.Если учащиеся не распознают 2D-формы, они не смогут распознать 3D-формы и не смогут обрабатывать геометрию. Знание 2D-форм также важно для измерения, поскольку учащиеся, которые не могут распознать прямоугольник, не смогут правильно его измерить. Фигуры также помогают учащимся выучить такие словарные слова, как «сторона», «угол», «угол», «вершина», «прямая» и «линия».
2 Преимущества
Помимо того, что 2D-формы жизненно важны для обучения математике, они важны для искусства и жизненных навыков.Формы являются основой многих ранних уроков рисования и рисования, а также являются удобным способом для не-художников рисовать узнаваемые объекты, такие как люди-палки (круги и линии) и дома (треугольник на вершине квадрата). Студенты при заполнении форм и прохождении стандартных тестов должны «поставить галочку» или «заполнить кружок», чтобы ответить. Учащимся, которые не могут связать 2D-форму с ее письменным именем, будет сложно выполнить эти задания.
3 Функции
2D-формы — это те фигуры, которые можно измерить только по высоте и ширине; у них нет глубины.Обычно это картинки в книгах или фигуры, нарисованные на странице, хотя очень плоские объекты, такие как знаки, также можно описать именами 2D-форм. Формы физических объектов, таких как блоки или книги, являются трехмерными формами, потому что они имеют глубину, а также высоту и ширину.
4 Идентификация
Чтобы научиться определять формы, учащиеся должны видеть их примеры. Студентам необходимо показать простые изображения каждой двухмерной формы отдельно или с ее названием внизу, чтобы они действительно могли видеть свои контуры.Учителя или родители должны обсудить с учениками характеристики каждой формы, в том числе, сколько у нее сторон, сколько углов, все ли линии прямые или изогнутые, все ли стороны одинаковы. Студенты могут начать с изучения форм, которые легче всего различить: круга, треугольника и квадрата. Затем они могут перейти к прямоугольникам, овалам и пятиугольникам. Студенты также должны узнать о шестиугольниках, восьмиугольниках, параллелограммах и любых других двумерных многоугольниках, перечисленных в математических стандартах их штата.
5 Учебные задания
После того, как учащиеся познакомятся с 2D-фигурами, они должны выполнить задания, чтобы закрепить свои знания. Они должны искать 2D-формы в окружающем мире, рисовать с их помощью, сортировать их по разным категориям, создавать с ними узоры и сопоставлять 2D-формы с 2D-фигурами разных размеров, углов и цветов, например, маленький прямоугольный треугольник с большим один.
Трехмерные формы | SkillsYouNeed
На этой странице рассматриваются свойства трехмерных или «твердых» форм.
Двумерная фигура имеет длину и ширину. У трехмерной твердой формы тоже есть глубина. Трехмерные формы по своей природе имеют внутреннюю и внешнюю стороны, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.
На этой странице рассматриваются как твердые тела с прямыми сторонами, называемые многогранниками, которые основаны на многоугольниках, так и твердые тела с кривыми, такие как глобусы, цилиндры и конусы.
Многогранники
Многогранники (или многогранники) — это твердые тела с прямыми сторонами.Многогранники основаны на многоугольниках, двухмерных плоских формах с прямыми линиями.
См. Нашу страницу Свойства полигонов для получения дополнительной информации о работе с полигонами.
Многогранники определяются как имеющие:
- Прямые кромки .
- Плоские стороны называются гранями .
- углов, называемых вершинами .
Многогранники также часто определяются количеством ребер, граней и вершин, которые у них есть, а также тем, имеют ли их грани одинаковую форму и размер.Как и многоугольники, многогранники могут быть правильными (основанными на правильных многоугольниках) или неправильными (основанными на неправильных многоугольниках). Многогранники также могут быть вогнутыми или выпуклыми.
Один из самых простых и известных многогранников — это куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.
Правильные многогранники (Платоновы тела)
Пять правильных тел — это особый класс многогранников, все грани которых идентичны, причем каждая грань представляет собой правильный многоугольник.Платоновы тела:
- Тетраэдр с четырьмя равносторонними треугольными гранями.
- Куб с шестью квадратными гранями.
- Октаэдр с восемью равносторонними треугольными гранями.
- Додекаэдр с двенадцатью гранями пятиугольника.
- Икосаэдр с двадцатью равносторонними треугольными гранями.
На схеме выше показаны правильные многогранники.
Что такое призма?
Призма — это любой многогранник, у которого есть два совпадающих конца и плоские стороны .Если вы разрежете призму в любом месте по ее длине, параллельно концу, ее поперечное сечение будет одинаковым — вы получите две призмы. Стороны призмы составляют параллелограмма — четырехгранные формы с двумя парами сторон равной длины.
Антипризмы похожи на обычные призмы в том, что их концы совпадают. Однако стороны антипризм состоят из треугольников, а не параллелограммов. Антипризмы могут стать очень сложными.
Что такое пирамида?
Пирамида — это многогранник с основанием многоугольника , который соединяется с вершиной (верхняя точка) прямыми сторонами.
Хотя мы склонны думать о пирамидах с квадратным основанием, подобных тем, что строили древние египтяне, на самом деле они могут иметь любое основание многоугольника, правильное или неправильное. Кроме того, пирамида может иметь вершину в прямом центре ее основания, правую пирамиду , или может иметь вершину вне центра, когда это наклонная пирамида .
Более сложные многогранники
Есть еще много видов многогранников: симметричные и несимметричные, вогнутые и выпуклые.
Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.
Усеченный куб (как показано) представляет собой архимедово твердое тело с 14 гранями. Шесть граней — правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. У фигуры 36 ребер и 24 вершины (угла).
Трехмерные фигуры с кривыми
Твердые фигуры с закругленными или закругленными краями не являются многогранниками.Многогранники могут иметь только прямые стороны. Также см. Нашу страницу о двумерных изогнутых формах.
Многие из окружающих вас объектов будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными изогнутыми телами являются цилиндры, конусы, сферы и торы (множественное число для тора).
| Общие трехмерные формы с кривыми: | |
|---|---|
| Цилиндр | Конус |
| Цилиндр имеет одинаковое поперечное сечение от одного конца до другого.Цилиндры имеют два одинаковых конца в форме круга или овала. Несмотря на то, что цилиндры похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами. | Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание. |
| Сфера | Тор |
| Сфера, имеющая форму шара или земного шара, представляет собой полностью круглый объект.Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы. | Регулярный кольцевой тор в форме кольца, шины или бублика образуется путем вращения меньшего круга вокруг большего круга. Существуют также более сложные формы торов. |
Площадь
На нашей странице «Расчет площади» объясняется, как рассчитать площадь двумерных фигур, и вам необходимо понимать эти основы, чтобы рассчитать площадь поверхности трехмерных фигур.
Для трехмерных форм мы говорим о площади поверхности , чтобы избежать путаницы.
Вы можете использовать свои знания о площади двумерных фигур для вычисления площади поверхности трехмерной формы, поскольку каждая грань или сторона фактически является двумерной формой.
Таким образом, вы прорабатываете площадь каждой грани, а затем складываете их вместе.
Как и в случае плоских форм, площадь поверхности твердого тела выражается в квадратных единицах: см 2 , дюймы 2 , м 2 и т. Д.Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .
Примеры расчета площади поверхности
Куб
Площадь поверхности куба — это площадь одной грани (длина х ширина), умноженная на 6, потому что все шесть граней одинаковы.
Поскольку грань куба представляет собой квадрат, вам нужно выполнить только одно измерение — длина и ширина квадрата по определению одинаковы.
Следовательно, одна грань этого куба 10 × 10 см = 100 см 2 .Умножив на 6 количество граней куба, мы находим, что площадь поверхности этого куба составляет 600 см 2 .
Другие правильные многогранники
Точно так же площадь поверхности других правильных многогранников (платоновых тел) может быть вычислена, если найти площадь одной стороны и затем умножить ответ на общее количество сторон — см. Диаграмму основных многогранников выше.
Если площадь одного пятиугольника, составляющего додекаэдр, равна 22 см 2 , умножьте это на общее количество сторон (12), чтобы получить ответ 264 см 2 .
Пирамида
Для расчета площади поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:
Сначала определите площадь основания (квадрата) длина × ширина.
Затем проработайте площадь одной стороны (треугольник). Измерьте ширину по основанию, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.
Есть два способа вычислить площадь поверхности четырех треугольников:
Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь всех четырех сторон, или
Умножьте свой ответ на 2.
Наконец, сложите площадь основания и стороны вместе, чтобы найти общую площадь поверхности пирамиды.
Чтобы вычислить площадь поверхности для других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (боковая площадь). Возможно, вам придется измерить стороны индивидуально.
Диаграммы сети
Геометрическая сеть — это двухмерный «узор» трехмерного объекта. Сетки могут быть полезны при определении площади поверхности трехмерного объекта.На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды. Если пирамида «развернута», у вас остается сеть.
Для получения дополнительной информации о сетевых диаграммах см. Нашу страницу 3D-фигуры и сети .
Призма
Для расчета площади поверхности призмы :
Призмы имеют два конца одинаковые и плоские стороны параллелограмма.
Вычислите площадь одного конца и умножьте на 2.
Для обычной призмы (у которой все стороны одинаковые) вычислите площадь одной из сторон и умножьте на общее количество сторон.
Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.
Сложите два ответа (концы + стороны), чтобы найти общую площадь поверхности призмы.
Цилиндр
Пример:
Радиус = 5 см
Высота = 10 см
Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги.Если отрезать сторону по длине и приплюснуть, получится прямоугольник. Поэтому вам нужно найти площадь двух кругов и прямоугольника.
Сначала проработайте область одного из кругов.
Площадь круга равна π (пи) × радиус 2 .
Предполагая радиус 5 см, площадь одного из кругов составляет 3,14 × 5 2 = 78,5 см 2 .
Умножьте ответ на 2, так как есть два круга 157см 2
Площадь стороны цилиндра равна периметру окружности, умноженному на высоту цилиндра.
Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4
Измерьте высоту цилиндра — в этом примере высота составляет 10 см. Площадь поверхности стороны 31,4 × 10 = 314см 2 .
Общую площадь поверхности можно определить, сложив вместе площадь кругов и стороны:
157 + 314 = 471 см 2
Пример:
Радиус = 5 см
Длина наклона = 10 см
Конус
При расчете площади поверхности конуса необходимо использовать длину «склона», а также радиус основания.
Однако вычислить относительно просто:
Площадь круга у основания конуса равна π (пи) × радиус 2 .
В этом примере расчет: 3,14 × 5 2 = 3,14 × 25 = 78,5 см 2
Площадь боковой части, наклонного участка, может быть найдена по следующей формуле:
π (пи) × радиус × длина уклона.
В нашем примере расчет составляет 3,14 × 5 × 10 = 157 см 2 .
Наконец, добавьте площадь основания к боковой области, чтобы получить общую площадь поверхности конуса.
78,5 + 157 = 235,5 см 2
Теннисный мяч:
Диаметр = 2,6 дюйма
Сфера
Площадь поверхности сферы — это относительно простое разложение формулы для площади круга.
4 × π × радиус 2 .
Для сферы часто легче измерить диаметр — расстояние по сфере.Затем вы можете найти радиус, равный половине диаметра.
Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Следовательно, радиус составляет 1,3 дюйма. Для формулы нам понадобится радиус в квадрате. 1,3 × 1,3 = 1,69
Таким образом, площадь теннисного мяча составляет:
.4 × 3,14 × 1,69 = 21,2264 дюйма 2 .
Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см
Тор
Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.
Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.
Малый или малый радиус (r) измеряется от середины кольца до внешнего края.
На схеме показаны два вида примера тора и способы измерения его радиусов (или радиусов).
Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаковый для каждой детали.
Формула: площадь поверхности = (2πR) (2πr)
Для определения площади поверхности примера тора.
(2 × π × R) = (2 × 3,14 × 20) = 125,6
(2 × π × r) = (2 × 3,14 × 4) = 25,12
Умножьте два ответа вместе, чтобы найти общую площадь поверхности тора в примере.
125,6 × 25,12 = 3155,072 см 2 .
Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Хотите ли вы освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Заполнение твердого тела: объем
Для трехмерных фигур вам также может потребоваться знать, какой объем у них есть.
Другими словами, если вы наполните их водой или воздухом, сколько наполнения вам потребуется?
Это описано на нашей странице Расчет объема .
различных имен форм (с полезным списком и типами) • 7ESL
Вы ищете разные названия фигур на английском языке? Здесь вы найдете список фигур с разными типами и полезные примеры предложений. Если вы работаете в бизнесе, который требует использования математики, например, тогда очень важно знать английские названия фигур.
Однако это может быть не единственной причиной, по которой вам нужно узнать эту информацию. Принимая участие в повседневных беседах, вам нужно будет выучить названия форм, чтобы что-то описать или уметь понимать, о чем говорят, например, если человек говорит вам о «квадратной тарелке».’Здесь вы можете выучить названия форм и еще больше расширить свой словарный запас.
Фигуры
Что такое формы?
Фигуры — это геометрические фигуры или узор, в который попадает контур. Формы часто рисуются (тушью, карандашом или цифровым способом), но они встречаются и в жизни. Часто люди представляют 2D (двумерные или плоские) изображения, когда слышат слово «формы», поэтому большинство объектов, перечисленных в этом уроке, будут двухмерными, но некоторые будут также и трехмерными.
Различные типы фигур
Существует много-много разных типов фигур, и практически у всех есть названия.В следующем списке представлены более распространенные формы, с которыми вы, скорее всего, столкнетесь, или которые вам понадобятся или которые вы захотите узнать.
Названия форм с изображениями
Штифт
Двумерные (плоские) формы
- Круг: Круг имеет одинаковую круглую форму. Изобразите крышку банки, плоскую, сверху. Это круг. Колеса у машины тоже круглые. То же самое с отверстиями в большинстве линованных бумаг и блокнотов.
- Овал: Овал — это, по сути, слегка сплющенный круг.Чашечки накладных наушников обычно называют овальными. Таков профиль яйца. Некоторые проводят различие между кругами, сжатыми посередине, и кругами, сжатыми вверху, причем первый называется эллипсом, но при обычном использовании оба они рассматриваются как овалы.
- Прямоугольник: Прямоугольник — это фигура с четырьмя сторонами, состоящая из двух наборов параллельных линий с четырьмя прямыми углами (углы 90 градусов; изобразите заглавную L). Не имеет значения, имеют ли стороны одинаковые длины.Представьте себе простой лист бумаги для печати. Это прямоугольник, у которого один набор сторон (обычно верхняя и нижняя) короче другого набора сторон (обычно левая и правая).
- Квадрат: Квадрат — это очень специфический тип прямоугольника с четырьмя равными сторонами. Некоторые коробки имеют квадратную форму. Бумага для оригами квадратная.
- Треугольник: Треугольник — это фигура с тремя прямыми сторонами. Эти стороны могут быть любой длины, с любым углом наклона, если три стороны соединены своими концами.Многие предупреждающие знаки имеют треугольную форму. Кусочек круглой пиццы в основном имеет треугольную форму (корочка слишком округлая, чтобы быть идеальной).
- Пентагон: Пятиугольник — это фигура с пятью сторонами. Базовый чертеж дома с двумя линиями крыши, линией для каждой стороны и линией для дна, как правило, представляет собой пятиугольник.
Фигуры с большим количеством сторон обычно называют в зависимости от того, сколько у них сторон. Шестигранник имеет шесть сторон, семиугольник — семь, а восьмиугольник — восемь.
Трехмерные фигуры
Трехмерные формы — это фигуры, которые не просто лежат на бумаге, но также занимают место по вертикали. Лишь немногие из них действительно часто называются.
- Сфера: Сфера — это трехмерный круг, похожий на шар.
- Куб: Куб — это трехмерный квадрат, похожий на коробку.
- Пирамида: Пирамида — это трехмерный треугольник. Гигантские сооружения в Египте — пирамиды, как и Луксор в Лас-Вегасе.
Имена форм
Важно пополнить словарный запас на любом языке.Чем больше слов вы знаете и понимаете, тем лучше вы сможете общаться. Даже если вы нечасто используете эти слова, их понимание позволит вам продолжить разговор, даже если он выходит за пределы вашей зоны комфорта. Этот урок специально посвящен различным типам фигур.
Список фигур- Nonagon
- восьмиугольник
- семиугольник
- Шестиугольник
- Треугольник
- Чешуйчатый треугольник
- Правый треугольник
- Параллелограмм
- Ромб
- Квадрат
- Пентагон
- Круг
- овал
- Сердце
- Крест
- Стрелка
- Куб
- Цилиндр
- Звезда
- Полумесяц
Студент-математик измерил каждую сторону nonagon , пока не получил измерения для всех девяти ребер.
Штифт
ВосьмиугольникФорма сечения — четверть восьмиугольника .
Штифт
ШестигранникПагода имеет основание из семиугольника .
Штифт
ШестигранникШестигранник — шестигранная фигура.
Штифт
ТреугольникСумма всех углов треугольника равна 180 градусам.
Штифт
Чешуйчатый треугольникРазносторонний треугольник — это треугольник с тремя неравными сторонами.
Штифт
Правый треугольникГипотенуза — это самая длинная сторона прямоугольного треугольника .
Штифт
ПараллелограммЭто противоположные стороны параллелограмма .
Штифт
РомбРомб — это простой четырехугольник, все четыре стороны которого имеют одинаковую длину.
Штифт
КвадратВнутренние углы квадрата являются прямыми углами или углами в 90 градусов.
Штифт
ПентагонНарисуйте пятиугольник , правильную пятиугольную фигуру.
Штифт
КругУченики сидят в круге на полу.
Штифт
ОвальныйЗемля имеет форму овала .
Штифт
СердцеБассейн имел форму сердца .
Штифт
КрестКрест — символ христианства.
Штифт
СтрелкаПрям летела стрела .
Штифт
КубКоробка была куба -образной.
Штифт
ЦилиндрЦилиндр поворачивается на 180 градусов.
Штифт
ЗвездаОна разрезает эту бумагу на звездочки -образной формы.
Штифт
ПолумесяцУ него нож в форме полумесяца — .
Штифт
Фигуры | КартинкаУчите различные формы с изображениями, чтобы улучшить и расширить свой словарный запас, особенно форм и цветов словарных слова на английском языке.
PinShapes: разные имена фигур (с полезным списком, типами) Имена фигур ВидеоФигуры встречаются повсюду, поэтому ссылки на них часто встречаются.Надеюсь, после этого урока вы будете готовы работать с формами!
2D и 3D фигур — объяснение, разница между 2D и 3D формами, решенные примеры
Геометрия — это исследование форм. Его в целом подразделяют на два типа: плоская геометрия, называемая двухмерными формами, и твердотельная геометрия, называемая трехмерными формами. Нарисуем на листе бумаги изображение записной книжки. Мы наблюдаем простую картинку, нарисованную на бумаге. Он не занимает места, называемого 2-мерными фигурами, но если мы храним настоящий блокнот на этом листе бумаги, он занимает некоторое пространство, и такие фигуры называются 3d-фигурами или трехмерными фигурами.
Плоская геометрия или двухмерная геометрия имеют дело с плоскими фигурами, которые могут быть нарисованы на листе бумаги, такими как линии, кривые, многоугольники, четырехугольники и т. Д., В то время как сплошная геометрия или трехмерная геометрия имеет дело с твердыми формами или трехмерными формы. Примеры трехмерных форм: сфера, цилиндры, конусы и т. Д.
[Изображение будет загружено в ближайшее время]
Что такое 2D-формы?
В геометрии фигура или фигура, имеющая два измерения, а именно длину и ширину, называется 2D-формой.Другими словами, плоский объект, который имеет только длину и ширину, является двухмерной формой. Стороны этой фигуры составляют прямые или изогнутые линии. Также у этих фигурок может быть любое количество сторон.
Нет фиксированных свойств 2D-формы. Поскольку каждая форма имеет разное количество сторон и свойства каждой формы различаются. Но каждая 2D-форма плоская и закрытая.
Двумерная замкнутая фигура, ограниченная тремя или более чем тремя прямыми линиями, называется многоугольником.Треугольники, квадрат, прямоугольник, пятиугольник, шестиугольник — вот некоторые примеры многоугольников.
Например, треугольники и квадраты являются многоугольниками.
Примеры двумерных фигур:
[Изображение будет загружено в ближайшее время]
Что такое трехмерные формы?
Фигуры, занимающие пространство, называются трехмерными фигурами. Трехмерные формы также можно определить как твердые формы, имеющие три измерения длины, ширины и высоты. Футбольный мяч — это пример сферы, которая представляет собой трехмерную фигуру, а круг, нарисованный на листе бумаги, представляет собой двумерную фигуру.Точно так же нас окружает множество трехмерных фигур, таких как стол, стул, блокнот, ручка и т. Д. Вот некоторые из примеров трехмерных форм и свойств трехмерных фигур.
[Изображение будет загружено в ближайшее время]
Некоторые из атрибутов 3D-фигур:
Лица: 2D-фигуры 3D-фигур называются гранями 3D-фигур.
Кромки: сегмент линии, образованный двумя гранями, называется краями трехмерных фигур.
Вершины: угловая точка, в которой встречаются края трехмерных фигур, называются вершинами.
Давайте рассмотрим трехмерную фигуру, куб. На рисунке ниже представлены грани, ребра и вершины куба.
[Изображение будет загружено в ближайшее время]
Вот разница между двумерными и трехмерными фигурами, которые сделают концепцию более понятной.
Разница между 2D и 3D фигурами
Основа для сравнения | 2D-фигуры | 3D-фигуры |
Только базовые размеры 775 | это длина и ширина.Есть три измерения: длина, ширина и высота. | |
Формы | Квадрат, круг, треугольник, прямоугольник, шестиугольник и т. Д. | Куб, сфера, конус, кубоид и т. Д. |
Включает | Длина и ширина | Длина, ширина и высота |
Простота конструкции | Простота создания | Довольно сложная |
Края | Полностью видны на чертежах.Например, в квадрате видны все грани. | Не видно или скрыто из-за перекрытия. Однако, если мы возьмем пример куба, то невозможно отобразить все его грани под одним углом |
Решенные примеры:
Пример 1:
Найдите объем и площадь поверхности кубоида l = 10 см, b = 8 см и h = 6 см.
Решение: Объем куба = V = lxbxh
= 10 x 8 x 6
= 480 см2
Площадь поверхности = 2 (фунт + lh + bh)
= 2 (10×8 + 10×6 + 8×6)
= 2 (80 + 60 + 48)
= 376 см2
Пример 2:
Длина прямоугольного поля составляет 15 м, а ширина — 6 м.Найдите площадь и периметр поля
Решение:
Учитывая, что Длина = 15 м
Ширина = 6 м
У нас есть формула площади A = длина x ширина
= 15 x 6
= 90 м2
И Формула периметра P = 2 (длина + ширина)
= 2 x (15 + 6)
= 2 x 21
= 42 м.

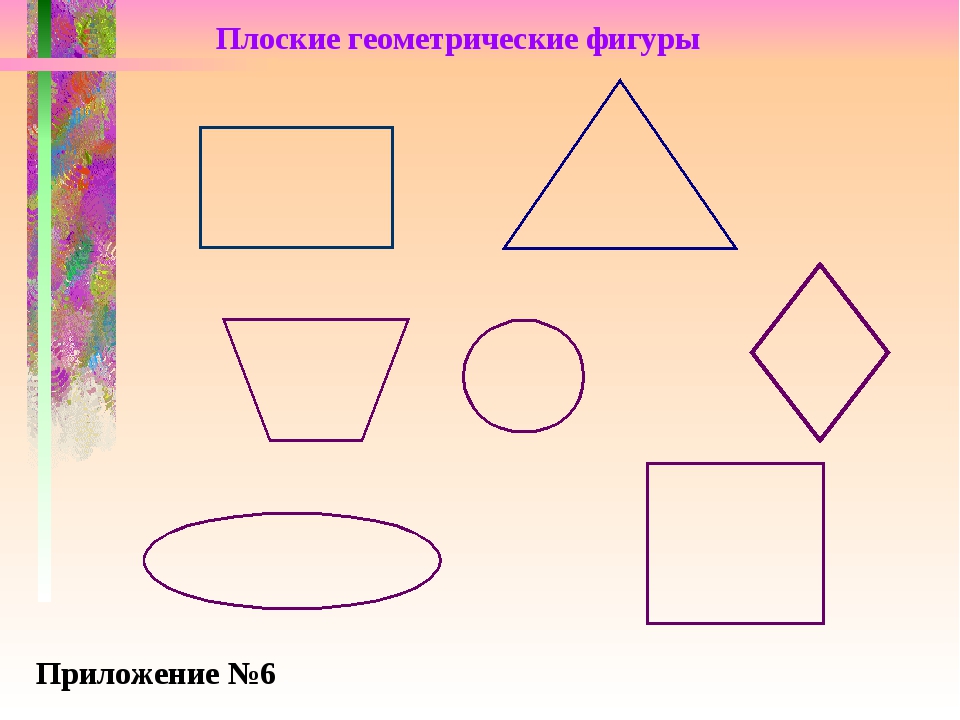


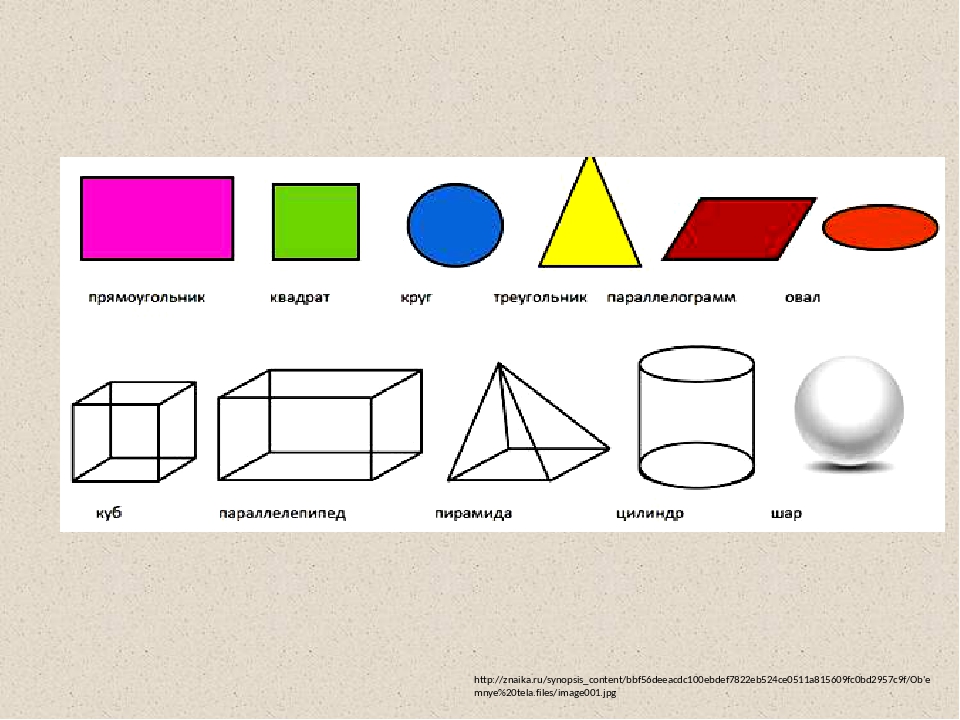 Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.