Как нарисовать в круге равносторонний треугольник: Как начертить равносторонний треугольник
- Как построить треугольник с помощью циркуля. Как построить треугольник с помощью циркуля Как построить треугольник помощью циркуля
- Построение треугольника по трем
- Задача 1
- Дано: отрезки
- Алгоритм построения
- Задача 2
- Дано: отрезок
- Алгоритм построения
- 10.
- 11.
- 12.
- 13.
- Построение равностороннего треугольника
- Построение равнобедренного треугольника
- Построение прямоугольного треугольника
- Построение тупоугольного треугольника по углу и двум прилегающим сторонам
- Построение остроугольного треугольника
- Вписанный треугольник
- Чертим описанный треугольник
- Как нарисовать остроугольный треугольник. Тупоугольный треугольник: длина сторон, сумма углов
- Разбираемся с понятиями
- Правильное начертание
- Основные линии
- Работа с окружностями
- Вписанные треугольники
- Описанные треугольники
- Построение равностороннего треугольника
- Построение равнобедренного треугольника
- Построение прямоугольного треугольника
- Построение тупоугольного треугольника по углу и двум прилегающим сторонам
- Построение остроугольного треугольника
- Вписанный треугольник
- Чертим описанный треугольник
- Черепашка в Python Часть 2 | SamAlex
- Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
- Как нарисовать шестиугольник в круге
- Построение правильных многоугольников. Построение правильных вписанных многоугольников
- Как вписать треугольник в окружность
- ДРУГОЕ
- Вам понадобится
- Инструкция
- Вам понадобится
- Инструкция
- Построение равностороннего треугольника
- Построение равнобедренного треугольника
- Построение прямоугольного треугольника
- Построение тупоугольного треугольника по углу и двум прилегающим сторонам
- Построение остроугольного треугольника
- Вписанный треугольник
- Чертим описанный треугольник
- Как построить равносторонний треугольник, вписанный в данный круг, с помощью циркуля и линейки или линейки
- Как построить (нарисовать) равносторонний треугольник
- Иллюстративная математика
- Равносторонний треугольник в круге —
- Могу ли я получить равносторонний треугольник внутри круга, сначала нарисовав случайный треугольник, сложив стороны треугольника и разделив на 3?
- Равносторонние треугольники, правильные шестиугольники, додекагоны и цветочные узоры
- Как нарисовать равносторонний треугольник в круге »OrigamiTree.com
Как построить треугольник с помощью циркуля. Как построить треугольник с помощью циркуля Как построить треугольник помощью циркуля
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №34 с углубленным изучением отдельных предметов
МАН, физико-математическая секция
«Геометрические построения с помощью циркуля и линейки»
Выполнила: ученица 7 «А» класса
Батищева Виктория
Руководитель: Колтовская В.В.
Воронеж, 2013
3. Построение угла равного данному.
Проведем произвольную окружность с центром в вершине А данного угла (рис.3). Пусть В и С — точки пересечения окружности со сторонами угла. Радиусом АВ проведем окружность с центром в точке О-начальной точке данной полупрямой. Точку пересечения этой окружности с данной полупрямой обозначим С 1 . Опишем окружность с центром С 1 и Рис.3
радиусом ВС.
Точка В
1
пересечения построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.
6. Построение перпендикулярных прямых.
Проводим окружность с произвольным радиусом r с центром в точке O рис.6. Окружность пересекает прямую в точках A и B. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей. Точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.
Искомая прямая проходит через точки С и О.
Рис.6
1. Задача Брахмагупты
Построить вписанный четырехугольник по четырем его сторонам. Одно из решений использует окружность Аполлония.
Решим задачу Аполлония, используя аналогию между трехокружником и треугольником. Как мы находим окружность, вписанную в треугольник: строим точку пересечения биссектрис, опускаем из нее перпендикуляры на стороны треугольника, основания перпендикуляров (точки пересечения перпендикуляра со стороной, на которую он опущен) и дают нам три точки, лежащие на искомой окружности. Проводим окружность через эти три точки – решение готово.
2. Задача Аполлония
Построить с помощью циркуля и линейки окружность, касающуюся трех данных окружностей. По легенде, задача сформулирована Аполлонием Пергским примерно в 220 г. до н. э. в книге «Касания», которая была потеряна, но была восстановлена в 1600 г. Франсуа Виетом, «галльским Аполлонием», как его называли современники.
Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
П
равильный (или равносторонний ) треугольник — это
правильный многоугольник
с тремя сторонами, первый из правильных многоугольников. Все
стороны
правильного
треугольника
равны между собой, а все
углы
равны 60°.
Чтобы построить равносторонний треугольник нужно разделить окружность на 3 равные части. Для этого необходимо провести дугу радиусом R этой окружности лишь из одного конца диаметра, получим первое и второе деление. Третье деление находится на противоположном конце диаметра. Соединив эти точки, получим равносторонний треугольник.
Соединив эти точки, получим равносторонний треугольник.
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения через деление окружности на 6 частей. Используем равенство сторон правильного шестиугольника радиусу описанной окружности. Из противоположных концов одного из диаметров окружности описываем дуги радиусом R. Точки пересечения этих дуг с заданной окружностью разделят её на 6 равных частей. Последовательно соединив найденные точки, получают правильный шестиугольник.
Построение правильного пятиугольника.
П
равильный пятиугольник может быть
построен с помощью циркуля и линейки, или вписыванием его в заданную
окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом
в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
Постройте окружность, в которую будет вписан пятиугольник и обозначьте её центр как O . (Это зелёная окружность на схеме справа).
(Это зелёная окружность на схеме справа).
Выберите на окружности точку A , которая будет одной из вершин пятиугольника. Постройте прямую через O и A .
Постройте прямую перпендикулярно прямой OA , проходящую через точку O . Обозначьте одно её пересечение с окружностью, как точку B .
Постройте точку C посередине между O и B .
C через точку A . Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D .
Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F .
Проведите окружность с центром в E через точку A G .
Проведите окружность с центром в F через точку A . Обозначьте её другое пересечение с первоначальной окружностью как точку H .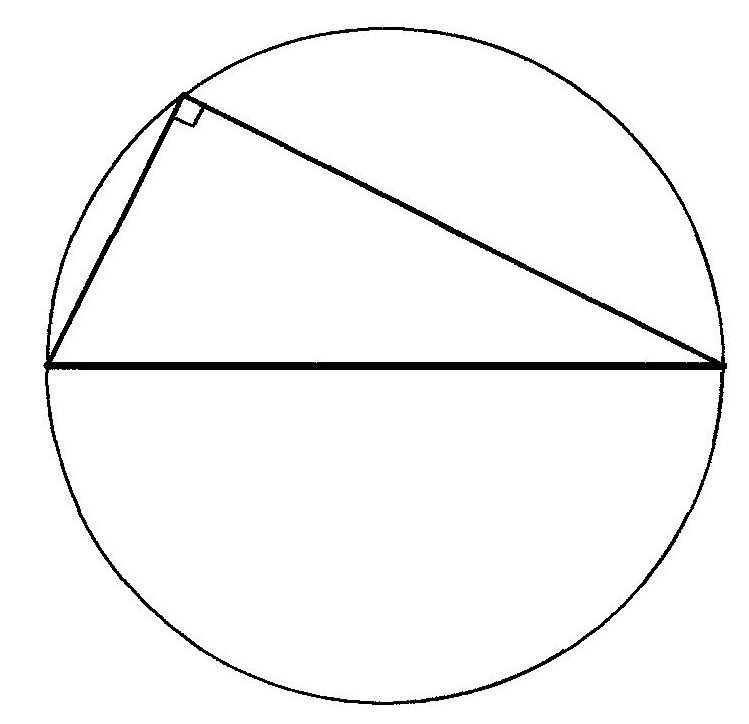
Постройте правильный пятиугольник AEGHF .
Следующие три задачи на построение были поставлены ещё в античности:
Трисекция угла — разбить произвольный угол на три равные части.
Иначе говоря, необходимо построить трисектрисы угла — лучи, делящие угол на три равные части. П. Л. Ванцель доказал в 1837 году, что задача разрешима только тогда, когда например, трисекция осуществима для углов α = 360°/n при условии, что целое число n не делится на 3. Тем не менее, в прессе время от времени публикуются (неверные) способы осуществления трисекции угла циркулем и линейкой.
Удвоение куба — классическая античная задача на построение циркулем и линейкой ребра куба, объём которого вдвое больше объёма заданного куба.
В современных обозначениях, задача сводится к решению уравнения
. Всё сводится к проблеме построения отрезка длиной
. П. Ванцель доказал в 1837 году, что эта задача не может быть решена с помощью циркуля и линейки.
Квадратура круга — задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого по площади данному кругу .
Как известно, с помощью циркуля и линейки можно выполнить все 4 арифметических действия и извлечение квадратного корня; отсюда следует, что квадратура круга возможна в том и только в том случае, если с помощью конечного числа таких действий можно построить отрезок длины π. Таким образом, неразрешимость этой задачи следует из неалгебраичности (трансцендентности) числа π, которая была доказана в 1882 году Линдеманом.
Другая известная неразрешимая с помощью циркуля и линейки задача — построение треугольника по трём заданным длинам биссектрис .
Причём эта задача остаётся неразрешимой даже при наличии трисектора.
Только в XIX веке было доказано, что все три задачи неразрешимы при использовании только циркуля и линейки. Вопрос возможности построения полностью решён алгебраическими методами, основанными на теории Галуа.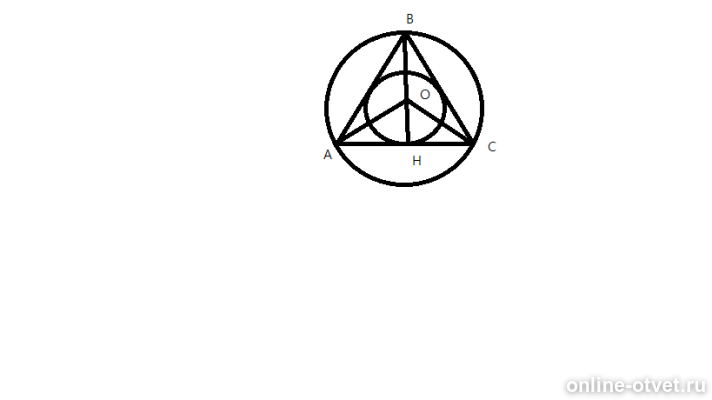
Когда-то в построение правильных многоугольников вкладывали мистический смысл.
Так, пифагорейцы, последователи религиозно-философского учения, основанного Пифагором, и жившие в древней Греции (V I-I V вв. до н. э.), приняли в качестве знака своего союза звездчатый многоугольник, образованный диагоналями правильного пятиугольника.
Правила строгого геометрического построения некоторых правильных многоугольников изложены в книге «Начала» древнегреческого математика Евклида, жившего в III в. до н.э. Для выполнения этих построений Евклид предлагал пользоваться только линейкой и циркулем, который в то время был без шарнирного устройства соединения ножек (такое ограничение в инструментах было непреложным требованием античной математики).
Правильные многоугольники нашли широкое применение и в античной астрономии. Если Евклида построение этих фигур интересовало с точки зрения математики, то для древнегреческого астронома Клавдия Птолемея (около 90 — 160 г. н. э.) оно оказалось необходимым как вспомогательное средство при решении астрономических задач. Так, в 1-й книге «Альмагесты» вся десятая глава посвящена построению правильных пяти- и десятиугольников.
н. э.) оно оказалось необходимым как вспомогательное средство при решении астрономических задач. Так, в 1-й книге «Альмагесты» вся десятая глава посвящена построению правильных пяти- и десятиугольников.
Однако помимо чисто научных трудов, построение правильных многоугольников было неотъемлемой частью книг для строителей, ремесленников, художников. Умение изображать эти фигуры издавна требовалось и в архитектуре, и в ювелирном деле, и в изобразительном искусстве.
В «Десяти книгах о зодчестве» римского архитектора Витрувия (жившего примерно в 63 -14 гг. до н. э.) говорится, что городские стены должны иметь в плане вид правильного многоугольника, а башни крепости «следует делать круглыми или многоугольными, ибо четырехугольник скорее разрушается осадными орудиями».
Планировка городов очень интересовала Витрувия, который считал, что нужно спланировать улицы так, чтобы вдоль них не дули основные ветры. Предполагалось, что таких ветров восемь и что они дуют в определенных направлениях.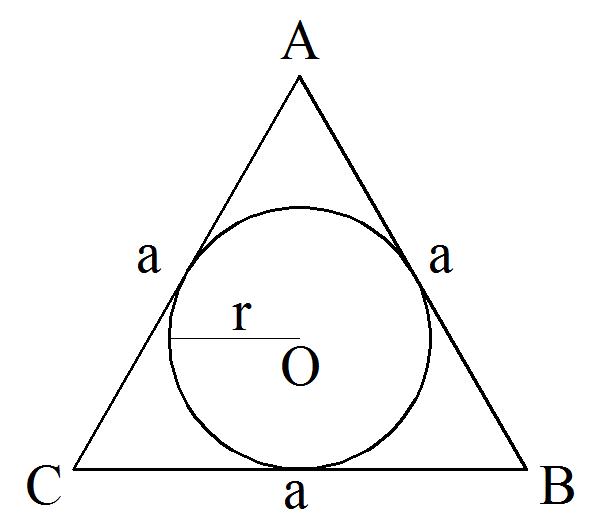
В эпоху Возрождения построение правильных многоугольников, и в частности пятиугольника, представляло не простую математическую игру, а являлось необходимой предпосылкой для построения крепостей.
Правильный шестиугольник явился предметом специального исследования великого немецкого астронома и математика Иоганна Кеплера (1571-1630), о котором он рассказывает в своей книге «Новогодний подарок, или о шестиугольных снежинках». Рассуждал о причинах того, почему снежинки имеют шестиугольную форму, он отмечает, в частности, следующее: «…плоскость можно покрыть без зазоров лишь следующими фигурами: равносторонними треугольниками, квадратами и правильными шестиугольниками. Среди этих фигур правильный шестиугольник покрывает наибольшую площадь»
0дним из наиболее известных ученых, занимавшихся геометрическими построениями, был великий немецкий художник и математик Альбрехт Дюрер (1471 -1528), который посвятил им значительную часть своей книги «Руководства…». Он предложил правила построения правильных многоугольников с 3. 4, 5… 16-ю сторонами. Методы деления окружности, предложенные Дюрером, не универсальны, в каждом конкретном случае используется индивидуальный прием.
4, 5… 16-ю сторонами. Методы деления окружности, предложенные Дюрером, не универсальны, в каждом конкретном случае используется индивидуальный прием.
Дюрер применял методы построения правильных многоугольников в художественной практике, например, при создании разного рода орнаментов и узоров для паркета. Наброски таких узоров были сделаны им во время поездки в Нидерланды, где паркетные полы встречались во многих домах.
Дюрер составлял орнаменты из правильных многоугольников, которые соединены в кольца (кольца из шести равносторонних треугольников, четырех четырехугольников, трех или шести шестиугольников, четырнадцати семиугольников, четырех восьмиугольников).
Итак, геометрические построения — это способ решения задачи, при котором ответ получают графическим путем. Построения выполняют чертежными инструментами при максимальной точности и аккуратности работы, так как от этого зависит правильность решения.
Благодаря этой работе я познакомилась с историей возникновения циркуля, подробнее познакомилась с правилами выполнения геометрических построений, получила новые знания и применила их на практике.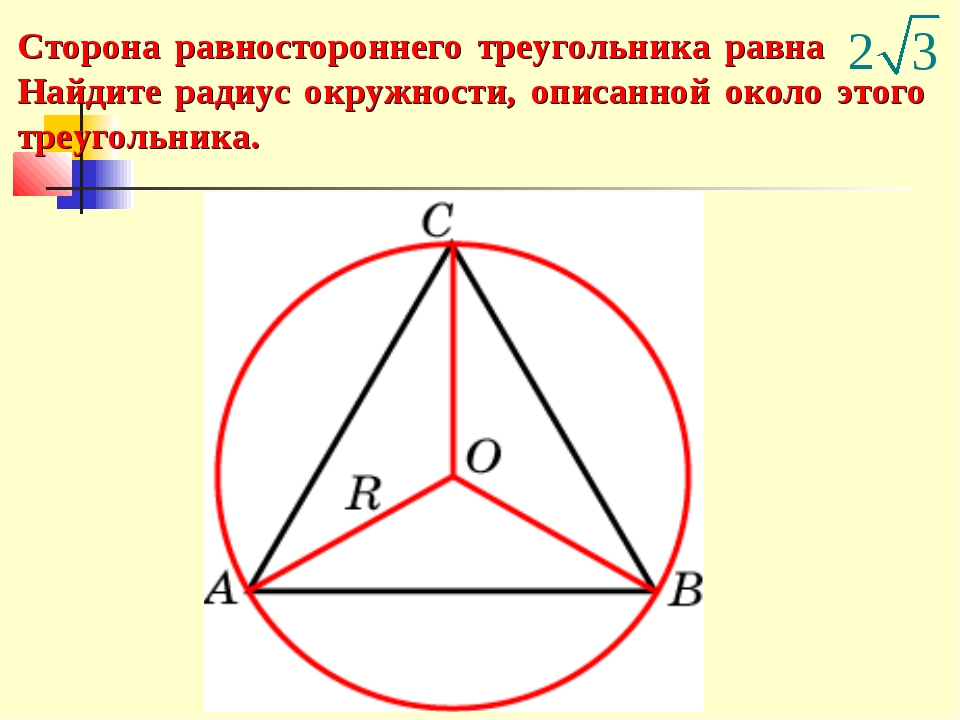
Решение задач на построение циркулем и линейкой – полезное времяпровождение, позволяющее по-новому посмотреть на известные свойства геометрических фигур и их элементов.
В данной работе рассмотрены наиболее актуальные задачи, связанные с геометрическими построениями с помощью циркуля и линейки. Рассмотрены основные задачи и даны их решения. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.
Таким образом, цель работы достигнута, поставленные задачи выполнены.
1. Какая фигура называется треугольником?
2. Какие виды треугольников вы знаете?
3. В чем заключается неравенство треугольника?
4. Известны стороны равнобедренного треугольника
6 см и 8 см. Чему равна третья сторона треугольника?
5. Существуют ли треугольники со сторонами
10 см; 15 см; 30 см?
6. Существуют ли треугольники со сторонами
11 см; 5 см; 6 см?
элементам сводится к решению трех
основных задач
1 задача — построение треугольника по двум
сторонам и углу между ними.

2 задача — построение треугольника по двум
углам и стороне между ними.
3 задача -построение треугольника по трем
сторонам.Задача 1
Построение треугольника по двум сторонам и углу
между нимиДано: отрезки
a
а
b
угол hp
b
h
p
Построить:
ABC по
двум сторонам и углу
между нимиАлгоритм построения
b
1. Проведем прямую d.
a
2. Отложим на ней с помощью
циркуля отрезок АВ, равный
M
отрезку a.
h
3. Построим угол ВАМ, равный
данному углу hp.
C
4. На луче АМ отложим отрезок
p
АС, равный отрезку b.
5. Проведём отрезок BC.
6. Построенный треугольник
АВС – искомый.
А
В
dЗадача 2
Построение треугольника по стороне и двум
прилежащим к ней угламДано: отрезок
a
h
p
m
n
а
угол hp
угол mn,
Построить:
ABC по
двум углам и сторонеАлгоритм построения
1.
 Проведем прямую d.
Проведем прямую d.2. Отложим на ней с помощью
циркуля отрезок АВ, равный
отрезку a.
3. Построим угол ВАМ, равный
данному углу hp.
4. Построим угол АВК, равный
данному углу mn.
5. Точку пересечения
лучей АМ и ВК обозначим С
6. Построенный треугольник
d
АВС – искомый.
m
n
p
М
K
С
А
a
В
10.
Задача 3Построение треугольника по трем сторонам
11.
Дано: отрезок аотрезок b
отрезок c
a
b
с
Построить:
ABC по
трем сторонам
12.
Алгоритм построения1. Проведем прямую а.
a
2. Отложим на ней с помощью
циркуля отрезок АВ, равный
отрезку а.
3. Построим окружность с
центром А и радиусом равным b.
4. Построим окружность с
центром В и радиусом равным c.
5. Одну из точек пересечения
этих окружностей обозначим
А
точкой С.
6. Проведём отрезки АС и ВС.
7. Построенный треугольник
АВС – искомый.

b
с
С
а
В
13.
Всегда ли, данная задачабудет иметь решение?
Задача 3 не всегда имеет
решение.
Если какой-нибудь из
отрезков больше или равен
сумме двух других отрезков,
то треугольник построить
будет не возможно.
b
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.

- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки.
 У нас получился искомый треугольник.
У нас получился искомый треугольник. - Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Помогите! Внучке задали. С помощью циркуля построить правильный треугольник. и получил лучший ответ
Ответ от КИНОголик[гуру]
Сначала постройте отрезок длиной равной длине будущего треугольника.
Затем растворите циркуль на длину этого отрезка и, поставив конец циркуля в начало отрезка, проведите окружность.
Поставьте циркуль в другой конец отрезка и проведите еще одну окружность.
Окружности пересекутся в двух точках — над и под отрезком. Соединив концы отрезка с одной из этих точек, вы получите правильный (равносторонний треугольник).
Ответ от Гриша Колосов [новичек]
спс
Ответ от Александр Жидайкин [новичек]
Окружность разделить на 4 равных части. В самую нижнюю точку поставить ножку циркуля и провести вторую окружность, этого же радиуса. Получили две точки пересечения-это две точки треугольника. Третья точка находится в самой верхней точки первой окружности. Соединяем, получаем)
Соединяем, получаем)
рисунок 61 в помощь
Ответ от Дед07 [гуру]
Начертите окружность. На окружности обозначьте точку (пусть А) . От этой точки по окружности в обе стороны отмерьте по 2 радиуса. Соедините полученные 3 точки
Ответ от *АпЕлЬсИнКа* [гуру]
ru.wikibooks.org/wiki/…/Построение_правильного_треугольника
Ответ от Елена яковлева [гуру]
Начертите окружность и тем же радиусом разделите её на 6 частей (поставьте 6 точек), затем соедините три точки (через одну) прямыми.
Ответ от Антип [гуру]
1) На прямой циркулем отметить отрезок произвольной длины
2) из одного конца отрезка циркулем, открытым на длину отмеченного отрезка, нарисовать дугу (достаточно длинную)
3) из другого конца отрезка сделать то же самое
4) дуги пересекутся
5) точку пересечения соединить с концами отрезка
6) вот и получился равносторонний треугольник — правильный
Ответ от Вега [гуру]
начертили окружность, потом ставите иглу на окружность и делаете две засечки на линиях, потом переставляете циркуль так, чтобы на засечке поставить карандаш, а иглу перенести дальше и сделать следующую засечку. {o }}\)
{o }}\)
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник.
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром!
В равностороннем треугольнике оказалось не \(12\) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3.
В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. \(R=2\cdot r\)
Уже должно быть очевидно, отчего так.
Посмотри на рисунок: точка\( O\) – центр треугольника.
Значит, \(OB\) – радиус описанной окружности (обозначили его \(R\)), а \(OK\) – радиус вписанной окружности (обозначим \(r\)).
Но ведь точка \(O\) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Поэтому \(OB=2\cdot OK\), то есть \(R=2\cdot r\).
Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.
Давай удостоверимся в этом.
Как нарисовать остроугольный треугольник. Тупоугольный треугольник: длина сторон, сумма углов
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
Разбираемся с понятиями
В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о. Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми. При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Правильное начертание
Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.
Основные линии
Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.
Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.
Так, биссектрисы делят угол пополам, а противоположную сторону — на отрезки, которые пропорциональны прилегающим сторонам.
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Серединный перпендикуляр — это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.
Работа с окружностями
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.
Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.
Вписанные треугольники
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.
Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.
Описанные треугольники
Также довольно часто приходится работать со вписанными окружностями. По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p — это полупериметр треугольника, c, v, b — его стороны.
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
- Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Черепашка в Python Часть 2 | SamAlex
Здравствуйте!!! Сегодня продолжим разбирать графический модуль черепашка.
В первой части мы рассмотрели пример как можно начертить квадрат, создали функцию которая чертит квадрат и при помощи цикла «for» создавать множество квадратов с различной стороной. Давайте добавим в нашу программу команду, которая позволяет менять скорость рисования. Эта команда так и называется скорость (speed( )), в скобках указывается скорость, если поставить 0, то скорость будет максимальная.
Черепашка в Python Часть 2Создадим функцию, которая будет рисовать равносторонний треугольник. Давайте разбираться: Сначала рисуем прямую, затем поворачиваем налево на 120 градусов (на 120 потому что нам внутри треугольника надо угол в 60 градусов, а развернутый угол 180 градусов, поэтому 180 – 60 = 120 градусов).
Черепашка в Python Часть 2Да, художник я еще тот…
Продолжим, и нам данные действия надо повторить еще 2 раза, поэтому будем использовать цикл «for». Запускаем и вот результат.
Черепашка в Python Часть 2Рассматривать, как нарисовать много треугольников не будем, это аналогично как мы рисовали квадраты в прошлой статье.
Следующая команда «circle( )» тут все просто, передаем ей радиус и она выводит нам круг.
Черепашка в Python Часть 2Можно поэкспериментировать с циклом, изменением радиуса и поворотом. Создадим переменную «a» она будет нам задавать начальный радиус, переменную «b» она нам будет давать смещение по оси с каждой итерацией цикла. В цикле «for» у нас будет рисоваться окружность, затем курсор будет проворачиваться по часовой стрелке на «b» градусов, далее радиус увеличивается на 5 пикселей. И цикл начинает новую итерацию. Вот как выглядит наш код.
Черепашка в Python Часть 2Запускаем и вот что он нам нарисовал.
Черепашка в Python Часть 2Красиво, вот только разноцветные узоры были бы еще красивей. В следующей статье обязательно разберем, как можно менять цвет, как линий, так и самих нарисованных объектов.
А на сегодня еще одна команда «shape (‘turtles’)» добавляем ее в код. Для примера начертим прямую линию.
Черепашка в Python Часть 2Запускаем…..
И вот она наша черепашка, про которую мы все время говорим, но не видим ее.
Черепашка в Python Часть 2А на сегодня все.
Спасибо за внимание.
До новых встреч!!!
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Напомним определение биссектрисы угла.
Определение 1. Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла). Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Рис. 1
Доказательство. Рассмотрим произвольную точку D, лежащую на биссектрисе угла BAC, и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE, а гипотенуза AD – общая. Следовательно,
DF = DE,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Рис. 2
Доказательство. Рассмотрим произвольную точку D, лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE, а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2. Окружность называют окружностью, вписанной в угол, если она касается касается сторон этого угла.
Теорема 3. Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство. Пусть точка D – центр окружности, вписанной в угол BAC, а точки E и F – точки касания окружности со сторонами угла (рис.3).
Рис.3
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности), а гипотенуза AD – общая. Следовательно
AF = AE,
что и требовалось доказать.
Замечание. Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных, проведенных к окружности из одной точки, равны.
Напомним определение биссектрисы треугольника.
Определение 3. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4. В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство. Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC, и обозначим точку их пересечения буквой O (рис. 4).
Рис. 4
Опустим из точки O перпендикуляры OD, OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC, то в силу теоремы 1 справедливо равенство:
OD = OE,
Поскольку точка O лежит на биссектрисе угла ACB, то в силу теоремы 1 справедливо равенство:
OD = OF,
Следовательно, справедливо равенство:
OE = OF,
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC. Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности.
Рис. 5
Следствие. В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения |
| Произвольный треугольник | Посмотреть вывод формулы | a, b, c – стороны треугольника, . | |
Посмотреть вывод формулы | |||
| Равнобедренный треугольник | Посмотреть вывод формулы | a – боковая сторона равнобедренного треугольника, | |
| Равносторонний треугольник | Посмотреть вывод формулы | a – сторона равностороннего треугольника, | |
| Прямоугольный треугольник | Посмотреть вывод формул | a, b – катеты прямоугольного треугольника, |
| Произвольный треугольник | |
где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Равнобедренный треугольник | |
где Посмотреть вывод формулы | |
| Равносторонний треугольник | |
где Посмотреть вывод формулы | |
| Прямоугольный треугольник | |
где Посмотреть вывод формул | |
| Произвольный треугольник |
где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Равнобедренный треугольник |
где Посмотреть вывод формулы |
| Равносторонний треугольник |
где Посмотреть вывод формулы |
| Прямоугольный треугольник |
где Посмотреть вывод формулы |
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).
Рис. 6
Доказательство. Из формулы
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
Рис. 7
Доказательство. Поскольку для произвольного треугольника справедлива формула
где
то, в случае равнобедренного треугольника, когда
получаем
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
Рис. 8
Доказательство. Поскольку для равнобедренного треугольника справедлива формула
то, в случае равностороннего треугольника, когда
b = a,
получаем
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
где a, b – катеты прямоугольного треугольника, c – гипотенуза, r – радиус вписанной окружности.
Доказательство. Рассмотрим рисунок 9.
Рис. 9
Поскольку четырёхугольник CDOF является прямоугольникомпрямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник – квадратквадрат. Следовательно,
СD = СF= r,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как нарисовать шестиугольник в круге
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
В широком смысле шестиугольник — это многоугольник с шестью углами. У правильного же шестиугольника углы и стороны равны. Нарисовать такой шестиугольник можно при помощи рулетки и транспортира, грубый шестиугольник — при помощи круглого предмета и линейки или еще более грубый шестиугольник — при помощи интуиции и карандаша. Если вы хотите знать, как нарисовать шестиугольник различными способами, просто читайте далее.
Построение шестигранника может производиться несколькими способами. Удобнее всего использовать стандартный набор чертежных инструментов: циркуль, линейку. Однако, в отсутствие циркуля, фигура этого типа может быть начерчена с помощью рейсшины, угольника заводского изготовления с углами 90/60/30°.
Шестигранники применяются для откручивания и закручивания болтов при ремонте и сборке мебели.
В обоих случаях особенностью построения является элементарное знание основ геометрии. В правильном шестиугольнике длина его стороны всегда равна радиусу окружности, описанной вокруг него, противоположные стороны параллельны, грани сопрягаются под углом 60°.
Способ вычерчивания шестиугольника циркулем, линейкой
Чтобы построить шестигранник при наличии циркуля, достаточно вычертить окружность, найти на ее дуге 6 точек, соединив их отрезками. Для этого достаточно настроить циркуль один раз, отложив на нем значение стороны многогранника. Линейка потребуется для строительства вспомогательных, основных линий.
Метод выглядит следующим образом:
Первый способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- циркулем вычерчивается окружность — радиус является размером стороны;
- по линейке проводится радиус — точки пересечения этого отрезка будут углами многоугольника;
- находятся два угла многоугольника — циркуль переставляется в одну из точек пересечения отрезка (проведенный на предыдущем этапе диаметр), на дуге делаются отметки;
- находятся оставшиеся два угла — циркуль перемещается в противоположную точку пересечения отрезка с дугой окружности, создаются отметки пересечения на второй стороне окружности.
Построение правильного шестигранника завершается соединением получившихся углов по линейке. Это самый точный способ, требующий минимального количества чертежного инструмента. При значительном размере сторон (например, крой листового металла, деревянных заготовок) можно использовать шнур с карандашом. Один край шнура крепится к карандашу/маркеру, второй неподвижно фиксируется в центре окружности, затем в точках пересечения диаметра с дугой окружности.
Построение занимает минимальное количество времени, точность целиком зависит от заточки карандаша, наличия фиксатора на циркуле.
Способ вычерчивания шестиугольника без циркуля
Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.
Способ построения выглядит следующим образом:
Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.
- к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
- на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
- операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
- разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
- уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
- строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
- контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком
Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.
Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.
Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.
В последнем случае удобнее несколько изменить технологию:
- после вычерчивания центрального отрезка по нему выравнивается рейсшина;
- инструмент откатывается вниз на произвольную величину;
- короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
- скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.
Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.
Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.
Построение правильных многоугольников. Построение правильных вписанных многоугольников
Для начала разберемся с том, какую окружность можно назвать вписанной в треугольник. Это вам не просто взять и нарисовать в треугольнике фигуру. Ту окружность можно назвать вписанной в треугольник, у которой есть три точки на дуге, соприкасающихся с тремя гранями треугольника.
Из этого определения следует, что в каждый треугольник можно вписать лишь одну единственную возможную окружность, центр которой находится на пересечении трех биссектрис внутренних углов данного треугольника.
Теперь подробнее о том, как вписать окружность в треугольник:
- Находим вершины треугольника, как помним, их три.
- Из каждой вершины необходимо с помощью циркуля провести окружности, можно произвольного радиуса.
- Теперь найдите точку пересечения двух окружностей (эта точка должна находиться на стороне треугольника, которая противоположна делимому углу) и соединяем с делимым углом.
- Такую операцию необходимо провести с каждым из трех углов. У вас получатся в результате три пересекающиеся биссектрисы.
- Центр окружности вписанной в треугольник будет находиться в точки пересечения его биссектрис.
- Далее при помощи циркуля рисуем окружность с центром в полученной точке.
Как вписать треугольник в окружность
Вписанным в окружность треугольником называют треугольник, у которого три вершины соприкасаются с окружностью. Тогда окружность называют описанной вокруг треугольника.
Из этого следует, что радиус этой окружности — это отрезок, соединяющий центр описанной окружности и вершину треугольника. Поэтому для того, чтобы вписать треугольник в окружность необходимо обозначить три точки на окружности и соединить их отрезками.
Внимание, только СЕГОДНЯ!
ДРУГОЕ
Часто в геометрии приходится сталкиваться с описанными окружностями и их радиусами. Это ведет к простому вопросу: как…
Как начертить треугольник?Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих…
Окружность считается вписанной в границы правильного многоугольника, в случае, если лежит внутри него, касаясь при этом…
Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин,…
Как разделить окружность на части?Для того чтобы разделить отрезок или угол на равные части, особых навыков не…
Чему равен радиус описанной окружности?Описанной окружностью многоугольника называется такая окружность, которая…
Делить окружность на равное количество частей — это не пустое занятие, нужное лишь для того, чтобы усложнить вам жизнь…
Кто-то из нас математику в школе просто прогуливал, кто-то проболел, а кто-то подзабыл за давностью школьных лет, но…
Диаметром окружности называют отрезок прямой, которая соединяет две наиболее удаленные друг от друга точки окружности,…
Каждый школьник в начальных классах пытался узнать, что такое треугольник и что такое периметр ттреугольника. Попробуем…
Задачи на геометрические построения весьма хорошо развивают пространственное и логическое мышление и потому являются одной из основных частей школьной программы обучения. Как и в любой предметной области, существуют типовые и нетиповые задачи. К типовым задачам можно отнести, например, построение равностороннего треугольника . В процессе построения треугольник оказывается вписанным в окружность . Но как быть, если нужно вписать равносторонний треугольник в окружность , которая уже построена?
Вам понадобится
- — линейка;
- — карандаш;
- — циркуль.
Инструкция
Постройте хорду заданной окружности. При помощи линейки начертите отрезок так, чтобы он пересекал окружность в двух точках. Пусть это будут точки A и B. Желательно, чтобы эти точки были расположены на достаточном удалении друг от друга.
Постройте перпендикуляр, пересекающий отрезок AB и делящий его точкой пересечения на две равные части. Установите между ножками циркуля расстояние, несколько меньшее длины отрезка AB, но заведомо большее длины половины этого отрезка. Установите иглу циркуля в точку A. Вычертите окружность . Установите иглу циркуля в точку B. Вычертите еще одну окружность . Проведите отрезок через точки пересечения вычерченных окружностей так, чтобы он пересек отрезок AB в одной точке (пусть это будет точка C) и первоначальную окружность в двух точках (пусть это будут точки D и E).
Постройте перпендикуляр, пересекающий отрезок DE и делящий его точкой пересечения на две равные части способом, аналогичным описанному во втором шаге. Пусть построенный отрезок пересекает окружность в точках F и G, а отрезок DE в точке O. Точка O будет являться центром окружности.
Установите расстояние между ножками циркуля равным радиусу окружности. Поместите иглу циркуля в точку D. Поместите конец другой ножки циркуля в точку O.
Найдите точки двух углов равностороннего треугольника , вписанного в окружность . Не изменяя положения ножки циркуля с иглой (в точке D) и расстояния между ножками циркуля, установленные на предыдущем шаге, начертите окружность . Эта окружность пересечет первоначальную окружность в двух точках. Пусть это будут точки H и I.
Впишите равносторонний треугольник в окружность . Попарно соедините отрезками точки E, H и I. Треугольник со сторонами EH, HI и EI будет равносторонним и вписанным в заданную изначально окружность .
Согласно определению, если все вершины многоугольника принадлежат окружности, он называется «вписанным». Построить на бумаге такую фигуру несложно, особенно если все составляющие ее стороны имеют одинаковую длину. Для правильного треугольника такое построение может быть выполнено несколькими способами, а выбор наиболее удобного зависит от имеющихся инструментов.
Вам понадобится
- Бумага, карандаш, циркуль, линейка, калькулятор, транспортир.
Инструкция
Если у вас есть возможность использовать при построении транспортир, начните с выбора произвольной точки на окружности, которая должна стать одной из вершин правильного треугольника . Обозначьте ее, например, буквой А.
Начертите вспомогательный отрезок, соединив точку А с центром окружности. К этому отрезку приложите транспортир таким образом, чтобы нулевое деление совпало с центром круга, и поставьте вспомогательную точку у отметки 120°. Через эту точку проведите еще один вспомогательный отрезок с началом в центре круга и окончанием на пересечении с окружностью . Точку пересечения обозначьте буквой В — это вторая вершина вписанного треугольника .
Повторите предыдущий шаг, но транспортир прикладывайте ко второму вспомогательному отрезку, а точку пересечения с окружностью обозначьте буквой С. Больше транспортир не понадобится.
Соедините точки А и В, В и С, С и А. На этом построение правильного треугольника вписанного в окружность будет завершено.
Если транспортира нет, но есть циркуль и калькулятор, то начните с вычисления длины стороны треугольника . Вы наверняка знаете, что ее можно выразить через радиус описанной окружности, умножив его на отношение тройки к квадратному корню из тройки, то есть примерно на 1,732050807568877. Округлите это число до нужной степени точности и умножьте на радиус круга.
Отметьте произвольную точку на окружности и обозначьте ее буквой А — это первая вершина правильного треугольника .
Отложите на циркуле найденную на пятом шаге длину стороны треугольника и начертите вспомогательный круг с центром в точке А. Точки пересечения двух окружностей обозначьте буквами В и С — это две другие вершины вписанного в круг правильного треугольника .
Соедините точки А и В, В и С, С и А и построение будет завершено.
Внимание, только СЕГОДНЯ!
Инструкция
Способ первый. Если вы хотите начертить в окружности правильный треугольник, из ее центра необходимо провести 3 отрезка ОВ, ОС и ОМ под углом 120о друг к другу. Точка О будет совпадать с центром окружности, а точки В, С и М будут находиться на самой окружности. Соедините эти точки между собой и получите равносторонний треугольник ВСМ.
Способ второй. Вам необходимо начертить в окружности треугольник, зная только две его стороны. Выберите на окружности точку О, которая будет являться вершиной треугольника АОС, а известные стороны будут АО и ОС. Из точки О отмерьте отрезок ОА так, чтобы точка А находилась на окружности. Таким же способом начертите отрезок ОС. Соединив точки А и С, получите необходимый треугольник.
Способ третий. Необходимо начертить в окружности треугольник, зная одну сторону и угол, прилегающий к этой стороне. Допустим, что в треугольнике АВС известна сторона АВ и угол ВАС. Начертите отрезок АВ так, чтобы точки А и В лежали на окружности, затем отмерьте угол ВАС и проведите отрезок АС так, чтобы точка С так же находилась на окружности. Соедините точки С и В для окончания построения треугольника.
Способ четвертый. Имеется некий треугольник ТМР. Необходимо нарисовать вокруг него окружность таким образом, чтобы он был вписан в окружность. Проведите перпендикуляры из середины каждой стороны треугольника. Точка их пересечения – точка О, будет являться центром окружности. Соедините точку О с любой вершиной треугольника ТМР, получившийся отрезок будет радиусом окружности.
Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.
Вам понадобится
- Линейка, циркуль.
Инструкция
Рассмотрим способ с линейкой и циркулем. Построим треугольник АВС. С помощью линейки начертите линию АВ, это будет одна из сторон треугольника , а точки А и В его вершинами.
С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С. Это будет третьей вершиной треугольника.
Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.
Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.
С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.
Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки.
Обратите внимание
Убедиться в том, что треугольник правильный можете с помощью транспортира, измерив углы.
Полезный совет
Равносторонний треугольник так же можно начертить на листе в клетку с помощью одной линейки. Вместо другой линейки используйте перпендикулярные линии.
Источники:
- Классификация треугольников. Равносторонние треугольники
- Что такое треугольник
- построение правильного треугольника
Если все вершины треугольник а лежат на одной окружности, то в этом случае он называется вписанным, а окружность, соответственно — описанной вокруг него. Построить треугольник на известной окружности очень просто, но как вписать треугольник в круг, если изначально существует именно он?
Вам понадобится
- — циркуль;
- — бумага;
- — карандаш;
- — линейка.
Инструкция
Для любого треугольника всегда возможно построить описанную окружность, поскольку эта кривая однозначно определяется тремя заданными точками.
Чтобы это обнаружить, достаточно предположить, что треугольник задан декартовыми координатами своих вершин. В этом случае радиус и координаты центра окружности, проходящей через все три точки, должны быть решениями системы из трех уравнений второй степени с тремя неизвестными.
Эта система будет иметь единственное решение в том случае, если заданные точки не лежат на одной прямой (в этом последнем случае она вовсе не имеет решений). Но три точки, лежащие на одной прямой, не могут быть вершинами треугольника, следовательно, этот случай можно даже не рассматривать. Итак, решение заведомо существует.
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.
- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки. У нас получился искомый треугольник.
- Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Ещё больше интересного
как начертить треугольник, как начертить треугольник в окружности, как начертить прямоугольный треугольник, как начертить циркулем треугольник, как начертить вписанный треугольник, как начертить описанный треугольник:Из нашей статьи вы узнаете, как начертить треугольник, а именно как изобразить следующие треугольники: разносторонний, равнобедренный, равносторонний, прямоугольный, тупоугольный, остроугольный, вписанный, описанный вокруг окружности, при помощи циркуля и линейки.
| ПРИМЕЧАНИЕ. Шаги с 1 по 7 такие же, как и для построения шестиугольника, вписанного в круг. В случае вписанного равностороннего треугольника мы используем все остальные точки на окружности. | ||
| 1 | A, B, C, D, E, F все лежат в центре окружности O | По конструкции. |
| 2 | AB = BC = CD = DE = EF | Все они были нарисованы с одинаковой шириной циркуля. |
| Из (2) мы видим, что пять сторон равны по длине, но последняя сторона FA не была нарисована циркулем. Это было «оставшееся» пространство, когда мы обошли круг и остановились у F. Итак, мы должны доказать, что это соответствует остальным пяти сторонам. | ||
| 3 | OAB — равносторонний треугольник | AB был нарисован с шириной компаса, установленной на OA, и OA = OB (оба радиуса круга). |
| 4 | м∠AOB = 60 ° | Все внутренние углы равностороннего треугольника равны 60 °. |
| 5 | м∠AOF = 60 ° | Как и в (4) m∠BOC, m∠COD, m∠DOE, m∠EOF все равны & 60deg; Так как все центральные углы складываются в 360 °, м∠AOF = 360 — 5 (60) |
| 6 | Треугольник BOA, AOF совпадают | SAS См. Тест на конгруэнтность, бок-угол-бок. |
| 7 | AF = AB | CPCTC — Соответствующие части конгруэнтных треугольников конгруэнтны |
| Итак, теперь мы можем доказать, что BDF — это равносторонний треугольник | ||
| 8 | Все шесть центральных углов (∠AOB, ∠BOC, ∠COD, ∠DOE, ∠EOF, ∠FOA) совпадают. | Из (4) и повторением для других 5 углов все шесть углов имеют меру 60 °. |
| 9 | Углы ∠BOD, ∠DOF, ∠BOF равны | Из (8) — Каждый из них представляет собой сумму двух углов по 60 ° |
| 10 | Треугольники BOD, DOF и BOF совпадают. | Стороны представляют собой равные радиусы окружности, а из (9) включенные углы совпадают. См. Тест на соответствие, сторона-угол-сторона |
| 11 | BDF — равносторонний треугольник. | Из (10) BD, DF, FB конгруэнтно. CPCTC — соответствующие части конгруэнтных треугольников конгруэнтны. Это, в свою очередь, удовлетворяет определению равносторонний треугольник. |
| 12 | BDF — равносторонний треугольник, вписанный в данную окружность | Из (11) и все три вершины B, D, F лежат на данной окружности. |
Как построить (нарисовать) равносторонний треугольник
Содержание
- Построение равностороннего треугольника
- Как нарисовать равносторонний треугольник с помощью циркуля
- Как построить равносторонний треугольник, вписанный в круг
- Постройте равносторонний треугольник, вписанный в круг Доказательство
- Как нарисовать равносторонний треугольник
- Нарисуйте доказательство равностороннего треугольника
Построение равностороннего треугольника
Равносторонние треугольники легко построить с помощью циркуля, линейки и карандаша, потому что внутренние углы 60 ° можно найти, используя только радиус круга вокруг треугольника (описанный круг).
Предположим, вам дана длина одной стороны требуемого равностороннего треугольника. Вы должны построить две одинаковые стороны, которые каким-то образом образуют три внутренних угла в 60 °.
Вот сегмент CE:
[вставить чертеж линейного сегмента CE]
- Поместите иглу циркуля для рисования в точку C, затем отрегулируйте рычаг карандаша так, чтобы он касался точки E.
- Поверните дугу вверх, образуя легкую строительную линию.
- Не регулируя компас, переместите стрелку в точку E.
- Поверните дугу вверх от точки C, образуя еще одну легкую строительную линию. [вставить чертеж, показывающий дуги поворота компаса для этих точек]
- В месте пересечения двух дуг находится точка третьей вершины равностороннего треугольника. Назовите это точкой A. Используйте линейку, чтобы соединить точки A и C, точки A и E. У вас есть равносторонний треугольник ACE!
Как нарисовать равносторонний треугольник с помощью компаса
Точки C и E — центры конгруэнтных окружностей с радиусами, равными CE.Длины AC и CE являются радиусами окружности C. Длины AE и CE также являются радиусами окружности E. По переходному свойству:
Три равные стороны означают, что треугольник должен быть равносторонним.
Как построить равносторонний треугольник, вписанный в круг
Предположим, вам дан круг, а не сторона. Предположим, вас попросили построить внутри этого круга равносторонний треугольник:
[вставить рисунок круга S]
Вы знаете только центральную точку, точку S, но из нее вы можете скопировать радиус (расстояние от центра, точки S, до самой окружности).
- Настройте циркуль для рисования и установите радиус.
- Сделайте отметку на круге в любом месте. Установите игольную консоль в эту точку.
- Не меняя циркуля, поверните две небольшие дуги выше и ниже точки окружности, чтобы дуги пересекали окружность.
- Переместите стрелку циркуля для рисования на одну из этих дуг.
- Снова поверните циркуль, чтобы образовать небольшую дугу на окружности.
- Повторите это еще два раза, чтобы создать шесть точек на окружности (исходная точка плюс шесть маленьких дуг, пересекающих ее).
- Используйте линейку, чтобы соединить все остальные точки на окружности. То есть нарисуйте линейные сегменты, скажем, от вашей первой точки на окружности до третьей точки, и еще один линейный сегмент от третьей точки до пятой точки. Еще одна линия, от пятой точки обратно к исходной точке, и вот она. Вы вписали в круг равносторонний треугольник!
[вставьте рисунок, показывающий это, или анимируйте конструкцию трех сторон]
Постройте равносторонний треугольник, вписанный в круг Доказательство
Представьте, что этот равносторонний треугольник состоит из трех меньших равнобедренных треугольников, имеющих точку S как общую вершину.Это означает, что каждый из трех треугольников имеет центральный угол (в точке S) 120 °, полученный путем деления полных 360 ° круга на 3 (количество центральных углов).
Каждый из этих меньших равнобедренных треугольников имеет две вершины на окружности, и каждый имеет одинаковые стороны с другими треугольниками. Таким образом, две из трех сторон треугольников совпадают.
Если две стороны равнобедренного треугольника совпадают, то третья сторона также определяется теоремой стороны-угла-стороны.
Как нарисовать равносторонний треугольник
Этот метод позволяет вам контролировать размер вашего равностороннего треугольника, потому что вы строите его с нуля.
- Настройте циркуль для рисования, чтобы нарисовать круг; назовем его Circle E.
- Используйте линейку, чтобы установить диаметр (отрезок прямой, проходящий через центральную точку E с конечными точками на самой окружности). Обозначьте конечные точки Точки B и R. [вставьте рисунок или анимацию, показывающую эти шаги]
- Не трогая циркуль, опустите иглу в точку R и сделайте еще один полный круг. Там, где новый круг пересекает старый в двух точках выше и ниже диаметра BR, обозначьте эти точки A и S.
- Соедините точку B с A, точку A с S и точку A с B. Он МЕДВЕДЬ замечает, что вы построили равносторонний треугольник!
Нарисуйте доказательство равностороннего треугольника
Вы можете доказать, что треугольник равносторонний, используя свои знания о том, что любой угол, вписанный в полукруг, является прямым углом, что дает вам прямые углы ∠BAR и ∠BSR, что создает два конгруэнтных прямоугольных треугольника △ BAR и △ BSR, имеющих общую гипотенузу, BR .
Таким образом, AB ≅ BS (соответствующие стороны равнобедренных треугольников), что означает, что △ BAS равнобедренный.Это делает ∠BAS и ∠BSA конгруэнтными (углы основания равнобедренного треугольника совпадают). Мы знаем, что ∠ABS составляет 60 °, оставляя два оставшихся угла в сумме до 120 °, так что каждый из них составляет 60 °. Все три внутренних угла △ BAS равны, что делает его равносторонним треугольником.
Следующий урок:
Как построить биссектрису угла
Иллюстративная математика
Задача
Предположим, нам дан круг радиуса $ r $. Цель этой задачи — построить равносторонний треугольник, три вершины которого лежат на окружности.Предположим, что $ \ overline {AB} $ — диаметр окружности. Нарисуйте круг с центром $ A $ и радиусом $ r $ и обозначьте две точки пересечения кругов $ P $ и $ Q $, как показано ниже:
- Докажите, что $ m (\ angle ABP) = 30 $ и $ m (\ angle ABQ) = 30 $.
- Покажи то $ \ треугольник PBQ $ — это равносторонний треугольник, вписанный в данную окружность.
IM Комментарий
Построение равностороннего треугольника, вписанного в круг, требует творческого подхода и хорошего знания геометрии и / или тригонометрии.Подход, принятый в данном решении, использует тот факт, что $ \ sin {30} = \ frac {1} {2} $. Следовательно, чтобы построить угол в 30 градусов, достаточно уметь построить прямоугольный треугольник, гипотенуза которого в два раза больше длины катета. Студентам необходимо знать, что $ \ angle APB $ правильный, поскольку он вписан в круг с одним лучом по диаметру круга. Отношение $ (2: 1) $ для гипотенузы к катету определяется с использованием диаметра окружности для гипотенузы и радиуса конгруэнтной окружности для катета.
В этой задаче реализованы многие важные идеи из геометрии, включая тригонометрические отношения, важные факты о треугольниках и отражения, если учащиеся предпочитают рассматривать $ \ треугольник ABQ $ как отражение $ \ треугольника ABP $ относительно $ \ overleftrightarrow {AB} $. В результате рекомендуется выполнять эту задачу относительно поздно в учебной программе по геометрии. Он также может быть дан в открытой форме, то есть с просьбой создать вписанный равносторонний треугольник внутри данного круга без предложения подхода или изображения.Альтернативный метод начинается с того, что если $ O $ — центр исходной окружности, то $ \ треугольник AOP $ равносторонний (все три стороны являются радиусами конгруэнтных окружностей). Мы можем продолжать рисовать круги с центрами $ P $ и $ Q $, и каждый раз мы получаем еще один равносторонний треугольник. Конечным результатом будет правильный шестиугольник, вписанный в круг: соединение всех остальных вершин этого шестиугольника дает равносторонний треугольник, вписанный в круг. Вариант этого аргумента, сфокусированный только на шестиугольнике, представлен в http: // www.illustrativemat Mathematics.org/illustrations/786.
Работа над этой задачей может развить навыки, связанные с MP1, понимать проблемы и настойчиво их решать, а также MP3, создавать жизнеспособные аргументы и критиковать рассуждения других. В первом случае аргумент сложен и требует объединения нескольких абстрактных аргументов, которые необходимо связать с построением желаемого равностороннего треугольника. Из-за своей сложности он идеально подходит для групповой работы, чтобы учащиеся могли объединить свои сильные стороны и навыки.
Равносторонний треугольник в круге —
Учебное пособиеОбъясните ученику разницу между рисованием и конструированием. Покажите ученику инструменты, традиционно используемые в геометрических конструкциях, и объясните назначение каждого из них. Убедитесь, что ученик понимает разницу между линейкой и линейкой.
Проведите ученика по этапам строительства. (Несколько различных методов описаны ниже.) Предложите студенту обосновать каждый шаг.Попросите учащегося удалить все ненужные или ошибочные отметки со своей работы. Попросите учащегося записать этапы строительства и сохранить их для использования в будущем.
Метод 1 : Используйте последовательные дуги 60 °, чтобы построить равносторонний треугольник, вписанный в окружность.
Шаг 1: Используйте заданный центр и линейку, чтобы построить радиус круга. Используйте циркуль, чтобы измерить радиус.
Шаг 2: Используя этот радиус, поместите точку циркуля в конечную точку радиуса на окружности и сделайте дугу, пересекающую окружность.
Шаг 3: Сохраняя тот же радиус, поместите точку циркуля в точку пересечения дуги (из шага 2) и сделайте еще одну дугу, которая пересекает круг.
Шаг 4: Продолжайте строить последовательные дуги вокруг окружности, как описано в шаге 3, пока окружность не будет разделена на шесть дуг 60º.
Шаг 5: Постройте стороны равностороннего треугольника, соединив концы трех последовательных дуг 120 °.
Метод 2 : Используйте конечные точки диаметра, чтобы построить равносторонний треугольник, вписанный в круг.
Шаг 1: Используйте центр и линейку, чтобы построить диаметр круга. Используйте циркуль, чтобы измерить радиус.
Шаг 2: Используя радиус окружности, поместите точку циркуля в конечную точку диаметра и сделайте две дуги, которые пересекают окружность в двух разных точках.
Шаг 3: Постройте стороны равностороннего треугольника, соединив эти две точки друг с другом и с другой конечной точкой диаметра.
Разрешите учащимся просматривать процесс строительства на веб-сайте, например.Учащийся может наблюдать за ходом строительства, но при необходимости может его приостановить. Чтобы просмотреть пошаговый процесс построения равностороннего треугольника с помощью циркуля и прямой кромки, перейдите по ссылке: и вместо того, чтобы соединять каждую точку пересечения для построения шестиугольника, соедините все остальные точки пересечения, чтобы построить равносторонний треугольник.
Попросите ученика построить равносторонний треугольник в круге, используя складывание бумаги:
Шаг 1: Получив круг на полупрозрачной бумаге, сложите бумагу так, чтобы две половины круга совпали.Изгиб складки равен диаметру круга. Обозначьте концы диаметра C и D .
Шаг 2: Согните так, чтобы конечная точка D совпала с центром круга, и сделайте твердую складку. Эта складка образует одну сторону равностороннего треугольника. Обозначьте концы этих боковых точек A и B .
Шаг 3: С помощью линейки и карандаша постройте, и. Треугольник ABC — равносторонний треугольник.
Попросите учащегося сравнить метод складывания бумаги с одним из методов построения, описанных выше.
Могу ли я получить равносторонний треугольник внутри круга, сначала нарисовав случайный треугольник, сложив стороны треугольника и разделив на 3?
Вы спрашиваете, одинаковы ли суммы сторон всех вписанных в круг треугольников, разделенные на 3. Это то же самое, что сказать, что суммы сторон всех таких треугольников одинаковы, БЕЗ деления на 3. Это должно быть так, если то, что вы предложили, было верным.
Но это не так.
Начнем с равностороннего треугольника. Я знаю, что длина каждой стороны «вписанного» равностороннего треугольника в √3 раз больше радиуса круга, поэтому сумма сторон равна 3√3 r.
Чтобы увидеть, что это не то же самое, что сумма сторон любого вписанного треугольника, нарисуйте треугольник, подобный этому: Начните с точки, близкой к вершине круга (с точки зрения бумаги, на которой вы ее нарисовали на.) Теперь нарисуйте одну сторону, которая ПОЧТИ диаметр круга.Он проходит чуть левее центра и пересекает точку почти точно напротив первой точки. Теперь нарисуйте другую сторону, которая также начинается от верхней точки, но проходит справа от центра и переходит в другую точку, почти точно противоположную первой точке. И, наконец, третья сторона треугольника соединяет две противоположные точки, которые вы создали, которые на самом деле очень близки друг к другу.
Теперь у вас есть треугольник с двумя длинными сторонами, почти равными диаметру круга, и одной короткой стороной, почти равной 0.Фактически, чем ближе вы сделаете две точки напротив исходной точки, тем ближе длинные стороны к диаметру (2r) и тем ближе короткая сторона к 0.
Итак, если вы сделаете две нижние точки ОЧЕНЬ близкими друг к другу, длины двух длинных сторон в сумме ОЧЕНЬ ОЧЕНЬ близки к d + d = 2r + 2r = 4r, а длина короткой стороны будет ОЧЕНЬ ОЧЕНЬ близкой к 0. Если вы сложите их, вы получите сумму сторон, которая ОЧЕНЬ ОЧЕНЬ близка к 4r. Это не может быть таким же, как 3√3 r.Таким образом, это показывает, что сумма сторон любого вписанного случайного треугольника не обязательно будет такой же, как сумма сторон вписанного равностороннего треугольника.
И есть другие способы показать это, используя другой пример «случайных» треугольников.
Значит, ваша процедура не сработает.
Равносторонние треугольники, правильные шестиугольники, додекагоны и цветочные узоры
Циркуль можно использовать для рисования круга.Но компас — это еще и инструмент для сравнения длин. Это один из способов увидеть рисование круга. Компас «находит» все точки на плоскости, которые находятся на одинаковом расстоянии от данной точки (точки, отмеченной острым концом компаса).
В каждом из следующих построений начните с постановки задачи и посмотрите, смогут ли некоторые ученики решить ее самостоятельно. Если вы работаете в группе, кто-нибудь обязательно это сделает, а затем они будут учить друг друга.
Как построить равносторонний треугольник? Начните с отрезка линии как одного из ребер треугольника.Поместите точку циркуля на один конец сегмента и поверните его по кругу. Вторая сторона равностороннего треугольника должна быть некоторым радиусом этого круга. Повторите то же самое для другого конца отрезка. Место пересечения двух кругов — это то же расстояние от каждой конечной точки сегмента, что и длина сегмента.
Равносторонний треугольник
Сколько градусов составляет каждый угол равностороннего треугольника? Три угла равны; углы складываются в 180 °; следовательно, каждый угол равен 60 °.
Цветок с шестиугольником
Попробуйте нарисовать круг, затем нарисовать такой же круг с центром в какой-то точке исходного круга, затем переместите циркуль в точки пересечения и повторите процесс. (Это всеми любимая конструкция!)
Интересно, что на исходной окружности умещается ровно шесть равных кругов. Это потому, что первые два круга воспроизводят конструкцию равностороннего треугольника; углы равностороннего треугольника составляют 60 ° каждый; и 6 х 60 ° = 360 °.Некоторым малышам этот «цветочный» узор станет уроком. Затем раскрасьте его или увеличьте узор, нарисовав круги в каждой из новых точек пересечения и т. Д.
Шестиугольник
Другие побочные эффекты: Найдите равносторонние треугольники. Найдите правильные шестиугольники. Разделите дуги, чтобы получилась 12-гранная фигура (двенадцатигранник).
Dodecagon
Как нарисовать равносторонний треугольник в круге »OrigamiTree.com
Поиск по ключевому слову
ДОБРО ПОЖАЛОВАТЬ!
Origami Tree предлагает БЕСПЛАТНЫЕ уроки ремесла на YouTube — дом для миллионов посетителей с ноября 2013 года.Копаться в архивах
Копаться в архивах Выберите месяц Апрель 2021 Сентябрь 2020 Октябрь 2019 Сентябрь 2019 Август 2019 Июль 2019 Июнь 2019 Май 2019 Апрель 2019 Март 2019 Февраль 2019 Январь 2019 Декабрь 2018 Ноябрь 2018 Октябрь 2018 Сентябрь 2018 Август 2018 Июль 2018 Июнь 2018 Май 2018 Апрель 2018 Март 2018 Февраль 2018 Январь 2018 Декабрь 2017 Ноябрь 2017 Октябрь 2017 Сентябрь 2017 Август 2017 Июль 2017 Июнь 2017 Май 2017 Апрель 2017 Март 2017 Февраль 2017 Январь 2017 Декабрь 2016 Ноябрь 2016 Октябрь 2016 Сентябрь 2016 Август 2016 Июль 2016 Июнь 2016 Май 2016 Апрель 2016 Март 2016 Февраль 2016 Январь 2016 Декабрь 2015 Ноябрь 2015 Октябрь 2015 Сентябрь 2015 Август 2015 Июль 2015 Июнь 2015 Май 2015 Апрель 2015 Март 2015 Февраль 2015 Январь 2015 Декабрь 2014 Ноябрь 2014 Октябрь 2014 Сентябрь 2014 Август 2014 Июль 2014 Июнь 2014 Май 2014 Апрель 2014 Март 2014 Февраль 2014 Январь 2014 Январь 2014 Декабрь 2013 Ноябрь 2013 Октябрь 201 3 июня 2013 г. март 2013 г. июнь 2011 г. декабрь 2010 г.Хотите помочь?
Поддержите продолжение бесплатных обучающих программ, сделав пожертвование сегодня!В этом уроке я покажу вам простой способ нарисовать треугольник внутри круга.С помощью этого метода вы можете построить равносторонний треугольник (все стороны треугольника равны) в данном круге. Вы можете изучить это для помощи в домашнем задании по геометрии / математике, или вы можете создать из них бумажный орнамент! Ага, верно! Вам понадобится циркуль, линейка, ручка или карандаш и лист бумаги.
Больше веселья!
Как сделать орнамент из бумаги (треугольник в единицах круга)
Нравится:
Нравится Загрузка…
Связанные 19 декабря 2016 г.

 У нас получился искомый треугольник.
У нас получился искомый треугольник. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. \(R=2\cdot r\)
В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной. \(R=2\cdot r\)