Как начертить объемный квадрат: Как научиться рисовать 3D куб карандашом поэтапно?
- Как рисовать объемный квадрат. Как построить правильный квадрат. Основные геометрические фигуры
- 3 способа как в фотошопе нарисовать квадрат и прямоугольник
- Тема урока «Как правильно нарисовать объемный шар в программе Paint»
- Красивые дома карандашом.
- ОТНОШЕНИЕ ПОВЕРХНОСТИ К ОБЪЕМУ
- Практическое обучение: область и объем
- Объем пирамиды
- Площадь, объем и время пребывания
- Как определить объем трехмерных объектов [Видео]
- Калькулятор объема коробки 📐
- Детерминанты и объемы
Как рисовать объемный квадрат. Как построить правильный квадрат. Основные геометрические фигуры
Хотите узнать Как нарисовать квадрат карандашом поэтапно, сделайте несколько простых шагов.
Шаг 1. Первое, что вы собираетесь нужно сделать, это схватить линейку. Правитель не должен иметь никаких вмятин вдоль края если вы хотите, чтобы ваш сквер встать на свои места. В реальности вы должны начать с построения горизонтальной линии. Это так вы можете нарисовать свои очки равномерно друг с другом. Так что начните с рисования светом линии с помощью линейки. Как только горизонтальный, как нарисовано, добавить две точки, по одной на каждой стороне линии. Эти очки позволят вам нарисовать перпендикулярные линии, которые должны оказаться под углом 90 градусов.
Шаг 2. Сделать то же самое вы сделали в шаге один, но когда вы делаете ваши очки, обязательно пользоваться линейкой, так что в итоге вы получите идеально прямые линии.
Шаг 3. Это просто быстрая схема, показывающая вам, как квадрат на 90 градусов на каждой стороне.
Шаг 4. Начните рисовать ваш горизонтальной линии из точки А в точку Б для верхней и нижней частей квадратной формы.
Шаг 6. Вот ваш идеальный квадрат. Теперь вы можете использовать его как стройматериал для чего-то, что вам нужно сделать, или вы можете использовать то, что вы только что узнали другим способом, а.
Все предметы и фигуры размещены в пространстве. Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.
Рисунок нужно воспринимать как пространство на бумаге, где существует плоскость и пропорции всех находящихся предметов, свет и тень, которая направляется по форме предмета.
Основные геометрические фигуры:
Двухмерные плоские фигуры
Трехмерные фигуры, у которых есть объем
Абсолютно все предметы в основе своего построения имеют эти фигуры.
Куб — фигура, основой которой является трехмерное изображение в пространственном соотношении листа. В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина . В самом кубе заложено понятие рисунка в целом.
Для начала понимания рисунка, мы поработаем именно с ним. При помощи образно-логических построений, мы с вами будем развивать мышление за счет аналитики формы . Для большего понимания и анализа рисунка есть несколько упражнений.
Упражнения
Садимся за мольберт, берем большой лист бумаги, можно недорогой, или вообще кусок обоев (в этом упражнении бумага особо значения не имеет) . Рисуем квадрат, естественно пытаемся сделать так, чтобы его стороны были ровными, а линии прямыми.
Итак, — мы видим обычный квадрат, совсем неинтересный и не впечатляющий, но это только в данный момент…
Делаем из квадрата куб карандашом: прорисовываем линии от граней примерно с углом 45 градусов . Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.
Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.
Чтобы нам чувствовать пространство, нужно придать рисунку плавности . То есть сделать так, чтобы нам было ясно, где передняя часть рисунка, а где задняя.
Сторону куба, находящуюся ближе к нам, нужно выделить, сделать четче и передать активнее. Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.
Вот таким способом мы передали пространство, чтобы добиться желаемого результата. Но это далеко не все. Сейчас важно правильно передать плавность, чтобы получить объемность в рисунке .
Представляем вашему вниманию небольшой видеоурок на тему оптических иллюзий.
Инструкция
Если есть возможность пользоваться измерительной линейкой и угольником, то задача до примитивности. Начните, например, с построения нижней стороны — поставьте точку А и начертите горизонтальный отрезок до точки В, отстоящей от А на расстояние заданной по условиям длины стороны. Затем по угольнику отмерьте то же расстояние вверх от точек А и В и поставьте точки D и С соответственно. После этого останется лишь соединить отрезками точки А и D, D и С, С и В.
Начните, например, с построения нижней стороны — поставьте точку А и начертите горизонтальный отрезок до точки В, отстоящей от А на расстояние заданной по условиям длины стороны. Затем по угольнику отмерьте то же расстояние вверх от точек А и В и поставьте точки D и С соответственно. После этого останется лишь соединить отрезками точки А и D, D и С, С и В.
Если в вашем распоряжении есть линейка и транспортир, то действовать можно так же, как и в предыдущем шаге. Постройте одну из сторон (АВ) квадрата, а затем приложите транспортир к проведенному отрезку так, чтобы его нулевая точка совпадала с точкой А. Поставьте вспомогательную отметку у транспортира, соответствующего 90°. На луче, исходящем из точки А через вспомогательную отметку, отложите длину отрезка АВ, поставьте точку D и соедините точки А и D. Затем проделайте такую-же операцию и точкой В, начертив сторону ВС. После этого соедините точки С и D и построение квадрата будет завершено.
Если в вашем распоряжении нет ни транспортира, ни , но есть циркуль, линейка и калькулятор, то и этого достаточно для построения квадрата с заданной длиной стороны. Если точные размеры квадрата не имеют значения, то можно обойтись и без калькулятора. Поставьте на листе точку в том месте, где хотите видеть одну из вершин квадрата (например, вершину А). Затем поставьте точку в противоположной ей вершине квадрата. Если длина стороны квадрата задана в условиях задачи, то расстояние между этими точками рассчитайте, исходя из теоремы Пифагора. Из нее вытекает, что нужная вам длина диагонали квадрата равна корню из удвоенного произведения длины стороны на саму себя. Посчитаете точное значение с помощью калькулятора или в уме и отложите полученное расстояние на циркуле. Проведите вспомогательный полукруг с центром в вершине А в направлении противоположной вершины С.
Если точные размеры квадрата не имеют значения, то можно обойтись и без калькулятора. Поставьте на листе точку в том месте, где хотите видеть одну из вершин квадрата (например, вершину А). Затем поставьте точку в противоположной ей вершине квадрата. Если длина стороны квадрата задана в условиях задачи, то расстояние между этими точками рассчитайте, исходя из теоремы Пифагора. Из нее вытекает, что нужная вам длина диагонали квадрата равна корню из удвоенного произведения длины стороны на саму себя. Посчитаете точное значение с помощью калькулятора или в уме и отложите полученное расстояние на циркуле. Проведите вспомогательный полукруг с центром в вершине А в направлении противоположной вершины С.
Отметьте на проведенной дуге точку С и проведите такой же вспомогательный полукруг с центром в этой вершине, направленный в сторону точки А. Проведите две вспомогательные линии — одна должна проходить через точки А и С, а другая — через точки пересечения двух полукружий. Эти линии будут пересекаться под прямым углом в центре будущего квадрата. На линии, перпендикулярной диагонали АС, отложите в обе стороны от точки пересечения по половине рассчитанной длины диагонали и поставьте точки В и D. И, наконец, по четырем полученным точкам вершин начертите квадрат.
На линии, перпендикулярной диагонали АС, отложите в обе стороны от точки пересечения по половине рассчитанной длины диагонали и поставьте точки В и D. И, наконец, по четырем полученным точкам вершин начертите квадрат.
Все предметы, которые нас окружают можно мысленно вписать в простые геометрические тела (куб, шар, конус, цилиндр, призма и др.). Изучая форму куба, мы узнаем, как нарисовать, к примеру, дом, потому что упрощенно дом рисуется с использованием тех же приемов что и куб. У него есть вершины, ребра и грани, как и у куба. Крыша дома – это многогранная призма.
Нарисуем куб с натуры, а затем будем использовать эти знания на наших для изображения более сложных предметов таких как дома и улицы.
Куб – геометрическое тело, образованное пересечением плоскостей. И, как всякий объемный предмет, при изображении на плоском листе он будет претерпевать изменения в соответствии с законами перспективы. На рисунке изображена линия горизонта это уровень плоскости зрения художника . На ней находятся точки схода параллельных линий. В нашем случае — это четыре горизонтальных линии, стремящихся в точку схода слева и четыре горизонтальных линии, стремящихся в точку схода справа.
На ней находятся точки схода параллельных линий. В нашем случае — это четыре горизонтальных линии, стремящихся в точку схода слева и четыре горизонтальных линии, стремящихся в точку схода справа.
Мы изображаем предметы в пространстве так, как их воспринимает наш глаз. (Чем дальше от зрителя, тем меньше выглядит предмет и т.д.)
Начало любой картины – это композиция. Легкими линиями намечаем наш предмет на листе. Сверху всегда должно быть чуть больше места от края, чем снизу. Интуитивно определите масштаб так, чтобы предмет не выглядел гигантским или слишком маленьким.
Расположите самое ближнее вертикальное ребро так, чтобы оно не совпадало с центром листа, проходящим через пересечение его диагоналей. Засечками отмечаем высоту, это самое высокое ребро в нашем изображении, так как оно ближе всех к зрителю. На глаз определяем угол наклона ребер лежащих на столе относительно горизонтали. Тренируйте зрительную память, запоминая угол. Взгляд переводите быстро то на куб, то на рисунок.
То же проделаем и с верхними ребрами. Как передавать пространство на листе нам объясняют основные законы линейной перспективы. Все параллельные линии сливаются к линии горизонта в одну точку. Поэтому, чтобы передать что ребро находится дальше от зрителя, мы изобразим его меньше и расположим выше . Таким образом, все ребра будут разной высоты.
При пересечении дальних горизонтальных ребер образовались вершины. Через них проходит самое дальнее, невидимое глазом, ребро. На начальном этапе изобразим куб прозрачным для понимания полной конструкции предмета.
Для того, чтобы узнать на сколько сократились боковые грани, воспользуемся методом визирования . При помощи этого метода происходит восприятие очертаний предмета, художник учится изображать предметы пропорциональными и в различных ракурсах.
Как он работает? Возьмите карандаш на вытянутой руке, прикройте один глаз, совместите карандаш и изображение ребра куба в пространстве. Верхний край карандаша должен совпадать с верхней вершиной ребра, а пальцем зажмите на карандаше точку, совпадающую с нижней вершиной.
После того, как закончены линейные построения, приступаем к воздушной перспективе , а значит к штриховке.
Основная задача художника передавать объемные формы предметов. У нашего кубика мы видим три грани, все они разные по тону. Левая грань самая темная — это собственная тень предмета. Благодаря отраженному свету от окружающих предметов или рефлексам, штриховку делаем немного светлее по мере удаления влево. Самое большое ребро делают контрастней, чем все остальные. Таким образом, показывают его приближенность на передний план.
Верхняя плоскость темнее , чем вертикальная справа. Свет по ней лишь скользит, образуя полутон. Обратите внимание, что чем ближе к источнику света, тем светлее будет тон. Штриховку можно наносить по диагонали. На ребре ластиком высветлим, чтобы передать блик.
Штриховку можно наносить по диагонали. На ребре ластиком высветлим, чтобы передать блик.
Для работы над самой светлой гранью возьмем твердый карандаш Н или 2Н . Он не даст сделать тон слишком темным. Штриховку нанесем вертикальную, по направлению плоскости.
Падающие тени всегда темнее, чем собственная тень предмета. Ближнее ребро – это линия перехода света и тени. Из нее начинается падающая тень. Чем ближе к предмету, тем насыщеннее тон. Отраженный свет от куба создает рефлекс внутри тени и она немного высветляется.
Рисование простых геометрических тел часто используется на и позволяет начинающему художнику научиться изображать предметы в пространстве, применяя законы перспективного построения и воздушной перспективы.
Доброго времени суток, начинающий художник и постоянный посетитель блога .
Надеюсь, было достаточно сфер? Так что давайте перейдем к важному, чрезвычайно разностороннему кубу . Куб настолько универсален, что вы будете использовать его для отрисовки рамок, домов, зданий, мостов, самолетов, автомобилей, цветов и рыб…рыб?? Да, куб поможет вам нарисовать даже маленьких рыб в 3D, а также лицо, цветы, ну и все, о чем вы можете подумать или увидеть вокруг. Так что приступим.
Так что приступим.
1. Начните с новой страницы вашего блокнота, напишите номер урока и заголовок, дату, время, местонахождение. Нарисуйте две точки напротив друг друга.
2. Поместите ваш палец между точками, используя другую руку. Затем нарисуйте точку над и под пальцем, как показано на рисунке.
Не стесняйтесь делать записи в блокноте, цитаты, и заметки. Чем больше вы вкладываете своих собственных мыслей и идей в свою записную книжку, тем большее она имеет значение для вас, тем больше вы будете ее использовать. В своем альбоме я делаю записи, напоминания, заметки, списки и все остальные вещи, которые нельзя нарисовать. Мой альбом – это первое место, куда я смотрю, когда мне нужно вспомнить что-то.
3. Взгляните на точки, которые вы нарисовали. Две новых точки должны располагаться близко друг от друга. Мы будем рисовать трапецию (квадрат в перспективе).
4. Проведите первую линию.
5. Проведите следующую линию.
6. Затем третью.
7. Закончите трапецию. Это очень важная форма для практики. Потренируйтесь, нарисовав такую трапецию еще несколько раз. ПРЕДУПРЕЖДЕНИЕ: рисуйте две средние точки очень близко друг к другу. Если они будут слишком далеко, у вас получится «полноразмерный» квадрат. А наша цель – «сплющенный».
В таком ракурсе объект искажается, и создает иллюзию, что одна часть находится ближе к зрителю. Для наглядного примера, вытащите монетку из кармана. Посмотрите на нее прямо. Она представляет собой плоский круг. 2D круг, который имеет длину и ширину (в двух измерениях), но не имеет высоты. Поверхность находится на одинаковом расстоянии от глаз. Теперь слегка наклоните монетку. Форма изменилась на эллипс, который теперь имеет высоту. Теперь у монеты есть все три измерения: длина, ширина и высота. Наклонив монетку, вы сместили край монеты подальше от ваших глаз, вы получили эллипс (круг в перспективе).
В основном, рисование трехмерных объектов сводится к тому, чтобы исказить изображения на плоском двумерном листе бумаги, чтобы создать иллюзию существования глубины. Рисунок 3D искажает формы, чтобы обмануть зрение и заставить объекты казаться ближе или дальше.
Рисунок 3D искажает формы, чтобы обмануть зрение и заставить объекты казаться ближе или дальше.
Теперь давайте вернемся к моему предупреждению о рисовании двух точек посередине. Если ваши точки будут слишком далеко друг от друга, ваш квадрат будет выглядеть вот так:
Если ваша фигура выглядит так, то перерисуйте ее несколько раз, размещая средние точки ближе друг к другу, пока ваша фигура не станет такой:
Ладно, достаточно об искажении пока. Держите эту мысль в голове, она очень важна и каждый урок будет начинаться с этого.
8. Нарисуйте стороны куба, с помощью двух вертикальных линий. Вертикальные, прямые линии сверху вниз без наклона. Вот подсказка: используйте сторону своего блокнота. Если вертикальные линии соответствуют сторонам страницы, ваш рисунок не наклонен.
9. Используя боковые опорные линии, нарисуйте среднюю линию немного длиннее и ниже. Использование нарисованных линий позволяет правильно определить позицию для вашей следующей линии, это очень важно при создании 3D изображений.
10. С помощью верхней крайней правой линии трапеции, нарисуйте нижнюю правую сторону куба. Просто повторите ее быстрым движением руки, смотря на верхнюю линию. Не переживайте, если вы вышли за пределы объекта, вы сможете подкорректировать это позже. Я предпочитаю рисунки с большим количеством дополнительных линий и черточек, которые выглядят трехмерно, а не которые имеют суперчистые и четкие линии.
11. Теперь нарисуйте нижнюю левую сторону куба, ссылаясь на верхнюю линию. Направляющие! Направляющие! Направляющие! Я настоятельно рекомендую вам потренироваться в использовании направляющих линий.
12. Теперь самое интересное — переходим к теням. Определите положение вашего воображаемого источника света. Свой я размещу справа сверху. Заметьте! Я использую направляющие линии, чтобы правильно выстроить угол тени. Путем продления нижнего правого ребра, нарисуйте падающую тень. Неплохо выглядит, правда? Похоже, что куб действительно «сидит» на земле? Это переломный момент, когда рисунок приобретает трехмерность.
13. Закончите ваш первый 3D куб, заштриховав грань противоположную от освещения. Заметьте, что я совсем ее не стал растушевывать. Я растушевываю тени только на округлых поверхностях.
УРОК 4: ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Давайте возьмем то, что мы узнали в основах рисования 3D куба, и добавим некоторые детали.
Мы собираемся нарисовать три кубика. Начните с первого с двух опорных точек. Говоря в следующих уроках «опорные точки», я буду иметь в виду эти точки.
1. Положите указательный палец посередине между опорными точками. Эта потрясающая привычка, которую вы сейчас приобретаете, к концу тридцатого урока станет для вас второй натурой.
2. Соедините точки в трапецию. Эта отличная фигура для практики в вашем альбоме, если у вас есть минута или около того. Например, когда находитесь в очереди или пробке. Поэтому всегда носите с собой свой альбом и карандаш, кто знает, когда у вас появится свободная минутка для рисования!
3. Нарисуйте вертикальные боковые линии и среднюю линию куба. Среднюю линию рисуйте всегда длиннее и ниже, чтобы она казалась ближе.
Среднюю линию рисуйте всегда длиннее и ниже, чтобы она казалась ближе.
4. Закончите рисовать куб, с помощью направляющих верхних линий.
6. Нарисуйте опорные точки в середине каждого ребра верхней грани куба.
7. Давайте начнем с первого. Давайте нарисуем на нем старомодный подарочный почтовый пакет, украшенный лентой, в котором мы получаем подарки от бабушки на Новый год. Проведите вертикальную линию вниз вблизи левой опорной точки, а затем по верхней грани к другой опорной точке.
8. Повторите это с другой стороны. Опорные точки помогают нарисовать линию внутри трапеции. Опорные точки являются чрезвычайно полезным инструментом в построении углов, как здесь. Мы часто будем пользоваться этими точками в последующих уроках (очень часто!).
9. Чтобы нарисовать такие линии в горизонтальном направлении, используйте опорные точки снова, только на середине вертикальных линий.
10. Проведите линии, соединяя опорные точки, используйте линии сверху как направляющие.
11. С помощью оберточной ленты вы можете закончить все три куба, представив их в виде посылки, игрального куба и подарка, завернутого в толстую ленту.
Еще одно хорошее задание для практики
Поместите любую коробку (обувную, из-под хлопьев или любую другую) на стол перед собой.
Присаживайтесь и разместитесь таким образом, чтобы вы могли увидеть верхнюю грань, похожую на трапецию, которую мы недавно рисовали.
Не паникуйте! Просто вспомните, что вы выучили в данном уроке, и пусть эти знания помогут вам нарисовать то, что видят ваши глаза. Взгляните, внимательно взгляните на тупые углы, затенения, падающую тень. Посмотрите, как надписи на коробке, также следуют за этими углами. Чем больше вы рисуете, тем больше вы буде те замечать множество увлекательных подробностей в реальном мире вокруг вас.
Делитесь вашими работами и получайте полезные советы в
3 способа как в фотошопе нарисовать квадрат и прямоугольник
Хоть квадрат и прямоугольник это простейшие геометрические фигуры, но, чтобы их нарисовать в фотошопе, нужно приложить некоторые усилия и обладать базовыми знаниями. Новичок без должной подготовки, скорее всего, не справится с этой задачей.
Новичок без должной подготовки, скорее всего, не справится с этой задачей.
В этой статье разберем 3 самых популярных способа как нарисовать прямоугольник или квадрат в фотошопе.
Но прежде, чем приступить к выбору способа рисования, нужно определиться с будущими параметрами. Прямоугольник/квадрат может быть:
- залит сплошным цветом или только с отрисовкой границ;
- произвольный или с точно заданными размерами;
- с возможностью в любое время менять его размеры без потери качества.
Способ 1. Инструмент произвольная фигура
В этом способе прямоугольник или квадрат будут нарисованы залитым сплошным цветом. Если вам нужна только граница, переходите к следующим двум способам.
На панели инструментов выберите инструмент Произвольная фигура. Дальше возможны два варианта развития событий:
Вариант 1. Квадрат или прямоугольник с дальнейшей возможностью изменять размеры без потери качества
Здесь, конечно, подразумевается использование векторной фигуры. Чтобы ее нарисовать нужно выбрать параметр Слой-фигура:
Чтобы ее нарисовать нужно выбрать параметр Слой-фигура:
В дальнейшем вы можете без потери качества изменять размеры этой фигуры. Для этого используйте инструмент Свободное трансформирование — Ctrl+T, и с помощью угловых маркеров изменяйте размер.
Для тех кто не знает: векторные фигуры состоят не из пикселей, а из специальные математических формул. Поэтому изменение размера — это не процесс растягивания/сжатия пикселей, а сложный математический пересчет, за счет чего не происходит никакой потери качества.
Вариант 2. Стандартный (растровый) квадрат/прямоугольник
Чтобы нарисовать сразу растровую фигуру используйте на панели параметров настройку Выполнить заливку пикселов. Но прежде чем начать ее рисовать — создайте новый слой!
Но на самом деле можно рисовать сразу и векторный, а потом просто растрировать его. Тут уже выбирайте сами.
Как сделать прямоугольник квадратным
Обыкновенное правило с зажатой клавишей Shift с произвольными фигурами не работает. Поэтому нужно воспользоваться панелью параметров инструмента и выбрать настройку, чтобы фотошоп рисовал именно квадрат.
Поэтому нужно воспользоваться панелью параметров инструмента и выбрать настройку, чтобы фотошоп рисовал именно квадрат.
В этой же панели, обратите внимание, вы можете указать точный размер необходимого прямоугольника/квадрата или рисовать его по заранее определенным пропорциям.
Совет
По умолчанию размеры определяются пикселями. Если вы хотите изменить единицу измерения, сначала введите в поле какое-либо значение, а затем кликните по нему правой кнопкой мыши. Появится окно выбора единиц измерения. Доступно: пиксели, дюймы, сантиметры, миллиметры, пункты и пики.
Прямоугольник или квадрат со скругленными углами
Чтобы получить фигуру со скругленными углами, делайте все то же самое, что описано выше, но в самом начале выберите инструмент Прямоугольник со скругленными краями. На панели параметров инструмента нужно будет указать только радиус закругления.
Способ 2. Обводка выделенной области
Этот способ простой, как 5 копеек. выберите инструмент Прямоугольная область и нарисуйте прямоугольник пунктирной линией. Чтобы нарисовать квадрат удерживайте нажатой клавишу Shift.
выберите инструмент Прямоугольная область и нарисуйте прямоугольник пунктирной линией. Чтобы нарисовать квадрат удерживайте нажатой клавишу Shift.
Теперь нужно сделать обводку границ этой выделенной области. Для этого перейдите в Редактирование — Выполнить обводку.
Затем в новом окне настройте вид обводки: укажите толщину рамки, желаемый цвет и отметьте как будет проходить обводка:
- Внутри — значит рамка ляжет по внутренней стороне выделенной области;
- По центру — значит рамка разделится поровну на часть проходящую внутри выделения и на часть со внешней стороны;
- Снаружи — значит рамка будет огибать пунктир выделения.
Вот как может получиться:
На скриншоте выше я специально не убрал пунктирную линию, поскольку у вас она также не исчезнет. Чтобы окончательно от нее избавиться нажмите Ctrl+D.
В этом способе, чтобы нарисовать фигуру точного размера, нужно сперва на панели параметров инструмента Прямоугольная область указать Стиль — Заданный размер или Заданные пропорции. После этого станут активными поля, куда введите значения ширины и высоты в пикселях. Кликом правой кнопкой мыши по одному из этих полей вызовет меню изменения единиц измерения.
После этого станут активными поля, куда введите значения ширины и высоты в пикселях. Кликом правой кнопкой мыши по одному из этих полей вызовет меню изменения единиц измерения.
Способ 2.1 Закрашивание выделения
Самый банальный способ рисования прямоугольника — нарисовать рамку выделения (как описано выше) и просто закрасить ее любым цветом. Вот вам и прямоугольник или квадрат.
Способ 3. Модификация выделения
На самом деле этот способ мне меньше всего нравится из-за очевидного минуса — углы прямоугольника будут подрезанными, а сама граница рамки в состоянии растушевки и повлиять на эти факты не представляется возможным.
Итак, нужно вновь выбрать инструмент Прямоугольная область, нарисовать рамку будущего прямоугольника или квадрата (с клавишей Shift), а затем отправляемся в меню Выделение и выбираем команду Модификация — Граница.
Появится новое окно, в котором, в нашем случае, мы указываем ширину границы прямоугольника. Допустим, укажу 7 пикселей. Получим такой результат:
Допустим, укажу 7 пикселей. Получим такой результат:
А теперь нужно просто закрасить получившуюся рамку. Для этого подойдет инструмент Кисть. Здесь, кстати, можно подойти к вопросу более творчески и закрасить, например, разными цветами. Результат:
Останется только снять выделение — Ctrl+D. Думаю этот способ подходит только для своих редких специфических задач, поскольку растушевка и подрезанные углы только все портят.
Заметили ошибку в тексте — выделите ее и нажмите Ctrl + Enter. Спасибо!
Тема урока «Как правильно нарисовать объемный шар в программе Paint»
Цель: приобретение необходимых навыков по использованию панели инструментов программы Paint.
Задачи:
- Дать учащимся представление о широких возможностях стандартной программы, научить передавать графическими средствами объёмные предметы.
- Использовать новые средства выразительности в работе над объёмным
предметом.

- Воспитывать умение смело и творчески подходить к обычным предметам.
- Укреплять межпредметные связи(информатика, изобразительное искусство).
Оборудование: персональные компьютеры с операционной системой Windows Professional, образец педагогического рисунка, схема работы над рисунком, презентация “Рисуем объёмный шар”.
Новые слова: светотень, рефлекс, тональность, блик.
Ход урока
Организационный момент. (Включение ПК, открывание программы Paint.) Проверка готовности к уроку, проверка присутствующих.
Повторение:
- панель инструментов, функция клавиши Shift, изменение палитры,
- что изображено на рисунке,
- за счёт каких средств передаётся объём шара,
- какую роль играет тень,
- нравится ли вам изображение.
Объяснение:
- Контур шара, с любой точки, виден в виде круга.

- Сложность выявления формы шара при помощи светотени.
- Определение соотношения тональности контура шара и фона.
- Блик на освещённой части шара и рефлекс в затенённой части.
- Падающая тень удаляясь кажется размытой.
Шар относится к телам вращения, поверхность которого образуется вращением
окружности вокруг оси (диаметра). Он имеет абсолютно симметричную форму, все
точки лежащие на поверхности шара находятся на равном удалении от центра.
Конструктивное построение шара в перспективе не представляет никакой сложности.
С какой бы точки мы не посмотрели на шар, мы видим его контур в виде круга.
Значительно сложнее выявить форму шара светотенью так, что бы он казался
объёмным. И сложность эта связана с множеством светотеневых колебаний (градаций
светотени) на его поверхности по сравнению с другими телами. Рисуя конус и
цилиндр мы наблюдали на их поверхностях плавный переход от света к тени, но
происходило это, в большей степени, только в направлении их образующих. В шаре
светотеневой переход наблюдается во всех направлениях и в этом основная
сложность. Вторая сложность при передаче формы шара светотенью возникает в
процессе определения соотношения тональности контура шара и фона. Контур шара на
фоне вокруг него должен быть нарисован мягко, убедительно и отличаться от фона
должен не контурной линией, а тональностью.
В шаре
светотеневой переход наблюдается во всех направлениях и в этом основная
сложность. Вторая сложность при передаче формы шара светотенью возникает в
процессе определения соотношения тональности контура шара и фона. Контур шара на
фоне вокруг него должен быть нарисован мягко, убедительно и отличаться от фона
должен не контурной линией, а тональностью.
Демонстрация учебной презентации “Рисуем объёмный шар”.
Рисунок шара необходимо начинать с размещения общего пятна рисунка на листе
бумаги с тем, что бы оно не казалось ни слишком большим, ни слишком маленьким.
Рисовать круг проще в квадрате, это мы уже усвоили. Вписав в квадрат окружность,
и удалив лишние линии, мы получаем плоское изображение круга, из которого нам
нужно сделать объёмное изображение шара. Определяем направление света, падающего
на шар. Если мысленно через центр шара провести плоскость перпендикулярную лучу
света, то плоскость разделит шар на условно освещённую и затенённую части. А
контур шара, лежащий в этой плоскости, мы будем видеть в виде овала. Здесь, на
линии овала и будет располагаться самая глубокая тень на поверхности шара.
А
контур шара, лежащий в этой плоскости, мы будем видеть в виде овала. Здесь, на
линии овала и будет располагаться самая глубокая тень на поверхности шара.
Практическая работа:
- Если прищурить глаза и посмотреть на освещённую часть шара, мы увидим самое светлое пятно, которое называют “блик”, это точки на поверхности шара расположенные перпендикулярно лучу света.
- Отражённые от горизонтальной поверхности лучи света создают “рефлекс” в затенённой части шара. Это мы уже наблюдали, когда рисовали цилиндр.
- Остаётся ещё определить падающую от шара тень и передать всё это в рисунке. Светотень должна очень мягко переходить от самого светлого пятна «блика» до самого тёмного пятна в собственной тени шара.
- Не забудьте про “рефлекс” и обратите внимание, что падающая тень не однородна, удаляясь, она кажется более размытой.
- А ещё нужно очень тонко отделить шар от фона и не контурной линией, а
светотенью.

Рис. 1
На предыдущих уроках мы научились пользоваться инструментами эллипс + Shift, карандаш, кисть. В ходе разбора учебной презентации вы уже осознали принцип работы над компьютерным рисунком. Сейчас вам предстоит своими руками при помощи виртуальных средств нарисовать объёмную геометрическую фигуру.
См. Приложение 1. (Презентация.)
В конце урока подписываем работы, сохраняем их в папке “9 класс”, присваиваем файлам атрибут Только чтение; вывешиваем работы для общего обсуждения.
Итог урока:
Посмотрите, какие разные получились работы. Наглядно виден стиль каждого автора. У одних учеников преобладает графичность, у других прослеживается тяга к живописи. Все работы достойны уважения, а перед вами лежат бескрайние просторы компьютерной графики. Довольны ли вы плодами своего труда? (Ученики отвечают на вопрос.)
Красивые дома карандашом.
 Учимся рисовать дома
Учимся рисовать домаСложность: (2 из 5).
Возраст: с трёх лет.
Материалы: лист плотной бумаги, восковые мелки, простой карандаш (на всякий случай), ластик, акварель, палитра с углублениями для воды, большая кисть.
Цель занятия: проходим и закрепляем знания о форме квадрат (дом, окно), треугольник (крыша), определение (линия горизонта).
Ход работы: ребенок рисует большой квадрат (будущий дом), затем маленький квадрат (окно), затем треугольник (крыша), разукрашиваем.
Располагаем лист вертикально, это значит короткой стороной к себе. Всегда обращайте на это внимание своего малыша, потому, что он должен знать такие понятия как вертикально и горизонтально. Чем чаще вы это будете упоминать на занятиях, тем быстрей ребенок это запомнит.
Теперь для стен дома выбирает любой цвет воскового мелка, который ему захочется и пробует нарисовать квадрат. Если малыш не уверен в себе, пусть рисует квадрат простым карандашом, пока у него не получится. Все наброски простым карандашом делаются легкими движениями без нажатия на него, что бы ластик легко удалил промахи.
Все наброски простым карандашом делаются легкими движениями без нажатия на него, что бы ластик легко удалил промахи.
Рисуем домику крышу в виде треугольника. И закрашиваем получившиеся части. Наш домик готов! Приступаем к раскрашиванию восковыми мелками.
Нарисуем линию горизонта. Еще одно определение, которое должен знать ваш ребенок. Повторяйте его чаще и малыш его запомнит. Линия горизонта – это линия соединения неба и земли. Нарисуйте ее простым карандашом.
Приступаем к одному из самых интересных этапов. Берем толстую кисть и разводим 2 цвета краски в палитре (синюю и зеленую), большим количеством воды. Макаем кисть в разведенную краску и наносим голубой цвет сверху (небо), с лева направо и двигаемся сверху вниз к линии горизонта. Но потом нам придется подождать, когда краска высохнет, иначе когда мы будем рисовать зеленым (землю) может получиться некрасиво. Проверяем небо на рисунки, если подсохло, то приступаем к заключительной части – рисуем землю. Рисуем ее также как и небо – слева на право и сверху вниз.
Рисуем ее также как и небо – слева на право и сверху вниз.
Каждому хочется иметь свое убежище, дабы прятаться там от мира сего. Расскажу Вам как рисовать дом с помощью карандаша. Возможно, в будущем Вы сможете построить свое собственное уютненькое убежище. Дом – перманентный обитель человеков и всего нажитого ими добра в виде телевизора, безлимитного интернета и кота. Тщательно бережется хозяином, утепляется на зиму и служит местом проведения культурно-массовых мероприятий. На территории Рашки чаще всего представляет собой коммуналку в хрущовке, реже – квартиру в центре Москвы или Бобруйска. В отдаленных от цивилизации местах это может быть двухэтажный сарай с протекающей крышей. Приносит убыток в виде постоянных евроремонтов и коммунальной дани, нуждается в дорогих бронированных дверях, чтобы защищать имущество и придавать красоты внешнему виду. Дарует защиту от кислотных дождей и ураганов мелкой потасовки, а так же от цыган, агентов Ейвон, и свидетелей Иеговы. Специфическая разновидность домов:
- Дурдом
(синонимы: психушка, психиатрическая больница, Кащенко) — Место обитания творческих и талантливых людей.
 Оборудован аппаратурой для проведения опытов над людьми
лечения и оздоровления души. Поселение по специальным приглашениям.
Оборудован аппаратурой для проведения опытов над людьми
лечения и оздоровления души. Поселение по специальным приглашениям. - Белый Дом . Прокачанная версия обычного дурдома для элиты мира сего. Во главе с Черным Властелином распространяет демократию во всем мире, абсолютно бесплатно, предпочтение отдается странам с нефтью и опасными террористами.
- Дом-2 – почти тоже самое, что и дурдом, только там пациентам еще и деньги платят.
А теперь давайте создадим проект вашего жилища.
Как нарисовать дом карандашом поэтапноШаг первый. Рисуем небольшой стандартный домик, как он выглядит в деревне, с треугольной крышей.
Шаг второй. Немного выровняем строение, добавим несколько формальных кустов вокруг и подправим края крыши.
Шаг третий. Добавим дизайна этой хате, красивое крыльцо и фасадный орнамент.
Шаг четвертый. Теперь нарисуем несколько окон спереди на обоих этажах, а так же со стороны несколько штук. Еще нужно немного деревьев на фоне и тропинка к входу.
Так будет выглядеть мой дом, а какой домик вы бы хотели построить? Нарисуйте и прикрепляйте свои работы внизу под этой статьей. Будет полезно для Вас еще узнать.
Наверное, не найти малыша, который не любил бы рисовать. Занятия творчеством позволяют ребенку отдохнуть и выразить свои мечты. Гораздо интереснее, если такой процесс происходит вместе с родителями. Довольно часто они спрашивают, как нарисовать дом, чтобы он стал для ребенка настоящим воплощением семейного очага и доброты.
Рисуем деревянное строение
Если семья живет в городе, то ей приходится видеть только каменные здания. Особой привлекательностью обладают сооружения из дерева, которые чаще всего встречаются в деревнях.
Как нарисовать дом поэтапно, чтобы он понравился ребенку и был реалистичным? Необходимо придерживаться такой последовательности:
- Требуется взять лист бумаги и провести простым карандашом линию в горизонтальном направлении. Затем нужно начертить вертикальную полоску.
 Это станет будущим углом дома.
Это станет будущим углом дома. - Далее следует переходить к изображению боковой стены. Ее части должны пересекаться в одной и той же точке.
- После этого нужно приступать к нанесению фасадов, где стены должны соединяться в одном месте.
- Теперь требуется начертить элементы крыши, изобразить фундамент, бревна и верх кровли.
- При желании разрешается добавить окна и дверь. Рисунок можно оставить черно-белым, растушевав простым карандашом.
Также можно добавить к домику деревья или другой пейзаж на выбор. Здесь ребенок сумеет подключить фантазию. В завершении творческого процесса нужно стереть лишние линии и разукрасить строение на свое усмотрение. В результате получится удивительный дом, изображение которого можно повесить в рамочку или на холодильник.
Рисунок дома из нескольких этажей
Как нарисовать домик, который состоит из нескольких этажей или другими словами, многоквартирное строение? Здесь тоже нет ничего сложного, если родители будут помогать своему малышу. Сначала необходимо изобразить вертикальную «гармошку», или перевернутые ступеньки. Затем требуется пририсовать окна, которые находятся в центре «гармошки». Таких проемов должно быть 3-4, в зависимости от высоты рисунка. На боковых изображениях требуется добавить изогнутые линии, которые будут служить как балконы. Внизу следует изобразить дверь. Она может быть разной, это зависит от личных предпочтений.
Сначала необходимо изобразить вертикальную «гармошку», или перевернутые ступеньки. Затем требуется пририсовать окна, которые находятся в центре «гармошки». Таких проемов должно быть 3-4, в зависимости от высоты рисунка. На боковых изображениях требуется добавить изогнутые линии, которые будут служить как балконы. Внизу следует изобразить дверь. Она может быть разной, это зависит от личных предпочтений.
На следующем этапе необходимо добавить дому объемности и удалить лишние линии. Но самый приятный процесс — раскрашивать полученный рисунок. Для этого понадобятся цветные карандаши. Стены нужно сделать желтого или коричневого цвета, окна можно сделать в голубом оттенке, а пейзажи добавляются разные.
Рисунки домика для самых маленьких
Очень важно научить самых маленьких детей, как рисовать дом. Таким деткам можно предложить следующий вариант:
- Сначала нужно нарисовать прямоугольник, с треугольником сверху. Эти фигуры будут служить фасадом и кровлей.
 Для этого процесса можно воспользоваться линейкой.
Для этого процесса можно воспользоваться линейкой. - Затем необходимо нарисовать еще один треугольник в большой фигуре. Слева на крыше требуется изобразить трубу.
- На следующем этапе рекомендуется расчертить горизонтальные линии на кровле. Этот процесс тоже можно сделать с помощью линейки и простого карандаша.
- Затем необходимо изобразить окна (обычно их рисуют два) и дверь, которая находится посередине основы-квадрата. Также внизу можно добавить ступеньку.
- Далее надо переходить к мелким деталям (подоконники, звонок и т.д.).
Когда все элементы будут прорисованы, то ребенку разрешается переходить к раскрашиванию домика. Здесь можно подключать фантазию и творческое мышление.
Если знать, как нарисовать дом карандашом поэтапно, то можно научить своего ребенка быстро и легко изображать любые строения. Это станет не только отличным развивающим занятием, но еще и сможет занять первое место в совместном досуге детей и родителей.
Сегодня наши детки осваивают творческие занятия, едва начинают уверенно ходить. Сначала мы покупаем им потом цветные карандашики, фломастеры и т.д. Но когда приходит время изучения букв и первых неловких попыток написать их, умение рисовать контур становится таким же важным, как знания и распознавание цветов.
Сначала мы покупаем им потом цветные карандашики, фломастеры и т.д. Но когда приходит время изучения букв и первых неловких попыток написать их, умение рисовать контур становится таким же важным, как знания и распознавание цветов.
Для того чтобы ребенок понял, что такое контуры, нужно учить его рисовать простым карандашом. К примеру, любимый сюжет детей — деревенский домик. Такое понятие, как перспектива, можно опустить, подрастут — разберутся. Раскрасить свое «творение» они смогут в любой момент, но сначала нужно вместе создать контурное изображение. В этой статье и будет рассказано о том, карандашом поэтапно.
Итак, как нарисовать деревянный дом? Понадобятся карандаши, бумага, ластик и ваше терпение.
Рисуем стены и крышу
Рисунок нужно начинать с контура элементарных геометрических фигур. Первым шагом будет рисование квадрата, к которому мы и будем «пристраивать» стены и крышу. К нему сверху дорисовываем треугольник. Какой он будет, равнобедренный или другой, это не столь важно. И уже на этом первом этапе ребенок узнает домик, тот самый, который он видел много раз.
И уже на этом первом этапе ребенок узнает домик, тот самый, который он видел много раз.
Перспектива
А теперь будем создавать нечто похожее на перспективу. Продолжаем учить ребенка тому, карандашом поэтапно. Делаем второй шаг — «пристраиваем» еще один квадрат рядом с первым. Но сверху рисуем уже не треугольник, как в предыдущем случае, а параллелограмм. Ребенок может не понять смысла этого художественного «эффекта». Вам необходимо будет доходчиво объяснить, как нужно проводить вертикальные линии и соединять их, чтобы получился вид «сбоку». Поверьте, дети очень быстро схватывают такие нюансы. Остается окошко, которое по форме является квадратом. Помимо того, что вы занимаетесь рисованием, у вас еще может состояться очень содержательная и познавательная беседа про квадраты, треугольники и прямоугольники, что очень хорошо запомнится.
Создаем объем
Карандашом поэтапно и удержать, хотя бы ненадолго, внимание ребенка? На третьем этапе начинаем наш домик облагораживать. Рисуем двери, которые имеют форму прямоугольника. На крыше у нас появится дымоход. Поскольку юный художник спрашивал о том, как нарисовать деревянный дом, одну стену с окном разрисуем полосками, имитирующими доски. Благодаря этому, мы получим иллюзию объема.
Рисуем двери, которые имеют форму прямоугольника. На крыше у нас появится дымоход. Поскольку юный художник спрашивал о том, как нарисовать деревянный дом, одну стену с окном разрисуем полосками, имитирующими доски. Благодаря этому, мы получим иллюзию объема.
Теперь, на четвертом этапе, отдаем инициативу в руки ребенка. Пусть нарисует черепицу сам. Как будет выглядеть крыша, в «рыбьей чешуе» или в «квадратиках», это уже не имеет значения. Главное — аккуратно «вписать» узор, не выходя за границы контура. Слуховое окошко над входной дверью тоже важный элемент, он — овальный.
Рисуем забор и кустики
О том, как нарисовать дом карандашом поэтапно, вы должны подумать заранее, уделив внимание развитию фантазии ребенка. Для этого вам придется применить все собственные творческие способности. Ваш домик почти готов! Теперь, на пятом этапе, осталось только облагородить участок вокруг него. Рисуем заборчик и кустики за домиком.
Как же нарисовать домик карандашом поэтапно? В этой статье мы и будем учиться это делать. Может показаться, что нарисовать домик очень сложно, но это совсем не так.
Может показаться, что нарисовать домик очень сложно, но это совсем не так.
Мы рисуем домик, а не дом:) Поэтому рисовать будем с видом сбоку без прорисовки объемных фигур. Это значительно упростит процесс рисования, разумеется, если вы чувствуете в себе силы, то можете дорисовать объемные элементы домика, то есть вторую стену и прорисовать крышу.
На бумаге мы будем изображать самый обычный деревенский домик, который можно встретить почти в каждом городе мира. Итак, приступим!
Поэтапный пример рисования
Рисовать мы будем карандашами, поэтому запаситесь обычным карандашом, цветными, ластиком и точилкой. Ну и, разумеется, бумагой.
1 этап
Домик будет состоять из двух частей (можете посмотреть готовый рисунок), рисуем прямоугольник и делим его на две части. Обратите внимание, что прямоугольник нужно поделить не по середине, а немного со смещением в левую часть.
2 этап
На втором шаге намечаем крышу и дверной проход. Дверной проход мы намечаем таким широким не просто так. Дверной проход такой широкий, потому что в нем будет не одна дверь, а целых две.
Дверной проход такой широкий, потому что в нем будет не одна дверь, а целых две.
3 этап
Теперь карандашом детализируем крышу и вставляем окна в наш домик. Окна не обязательно должны быть квадратными, очень часто в зданиях установлены прямоугольные окна.
Тем не менее, окна обязательно должны находиться на одной высоте, иначе ваше здание получится очень нереалистичным. Для точной разметки можете даже воспользоваться линейкой. А если у вас глаз-алмаз, то линейкой пользоваться не обязательно:)
Также, по всему низу здания нужно нарисовать декоративную полоску.
4 этап
Обводим окна и дверь еще одной линией, это немного придаст эффекту объемности, не смотря на то, что нашей целью не является нарисовать объемный дом.
На крыше обязательно нужно изобразить дымовую трубу, иначе куда же Санта будет приносить подарки к Рождеству?
5 этап
Пятый — очень важный шаг, потому что пришло время детализировать всё здание. Вставляем двери, под ними подрисовываем лестницу. В окна вставляем стекла, также детализируем крышу и нижнюю, декоративную полоску здания.
Вставляем двери, под ними подрисовываем лестницу. В окна вставляем стекла, также детализируем крышу и нижнюю, декоративную полоску здания.
ОТНОШЕНИЕ ПОВЕРХНОСТИ К ОБЪЕМУ
ОТНОШЕНИЕ ПОВЕРХНОСТИ К ОБЪЕМУ РАЗМЕРЫ ОРГАНИЗМОВ: ПОВЕРХНОСТЬ: ОБЪЕМНОЕ ОТНОШЕНИЕВведение: Двух- и трехмерные параметры организмов (т.е. площадь поверхности и объем) не обязательно увеличиваются или уменьшаются пропорционально увеличению или уменьшению в одномерном или линейном, параметры (например, длина). Например, чем больше диаметр одноклеточного Чем меньше площадь поверхности у него относительно его объема.В Отношение площади поверхности к объему — это способ выражения отношения между эти параметры по мере изменения размеров организма.
Важность: Изменения отношения площади поверхности к объему
важные последствия для пределов или ограничений размера организма, и
помогите объяснить некоторые изменения, наблюдаемые у более крупных организмов.
Вопрос: Как рассчитывается отношение площади поверхности к объему, и как именно он меняется при изменении размера? Какие модификации делают более крупные организмы выставляются, чтобы обойти эту проблему?
Переменные:
| S | Площадь поверхности (единицы в квадрате) |
| В | объем (ед. В кубе) |
| л | длина (шт.) |
| r | радиус (шт.) |
Методы: Для одноклеточного организма (или
клетка в теле многоклеточного организма), поверхность
является важным связующим звеном между организмом / клеткой и окружающей средой.Обмен материалами часто происходит в процессе диффузии, в
растворенные молекулы или другие частицы перемещаются из областей более высоких
концентрации в области с более низкой концентрацией (хотя некоторый обмен
опосредовано клеточными механизмами). Этот тип обмена — пассивный процесс,
и, как следствие, накладывает ограничения на размер одноклеточного организма.
или сотовый. Материалы должны иметь возможность быстро достигать всех частей ячейки, и
когда объем слишком велик по отношению к площади поверхности, диффузия не может происходить
при достаточно высоких скоростях, чтобы обеспечить это.
Этот тип обмена — пассивный процесс,
и, как следствие, накладывает ограничения на размер одноклеточного организма.
или сотовый. Материалы должны иметь возможность быстро достигать всех частей ячейки, и
когда объем слишком велик по отношению к площади поверхности, диффузия не может происходить
при достаточно высоких скоростях, чтобы обеспечить это.
Начнем с напоминания об основных геометрических формулы. Площадь поверхности и объем куба можно найти с помощью следующих уравнения:
и
, где S = площадь поверхности (в квадратах), В = объем (в кубах), и л = длина одной стороны
куб.
Уравнения для площади поверхности и объема сфера бывают:
и
, где r — радиус сферы.
 Например, при удвоении длины (т. Е. х = 2) площадь поверхности в четыре раза (2 2 = 4) не в два раза,
и объем составляет в восемь раз (2 3 = 8), а не в три раза.сходным образом
при увеличении длины втрое ( x = 3) площадь поверхности увеличивается в девять раз
(3 2 = 9), а объем увеличивается в двадцать семь раз (3 3 = 27). Увеличение объема всегда больше, чем увеличение поверхности.
площадь. Это верно для кубов, сфер или любого другого объекта размером
увеличился без изменения формы.
Например, при удвоении длины (т. Е. х = 2) площадь поверхности в четыре раза (2 2 = 4) не в два раза,
и объем составляет в восемь раз (2 3 = 8), а не в три раза.сходным образом
при увеличении длины втрое ( x = 3) площадь поверхности увеличивается в девять раз
(3 2 = 9), а объем увеличивается в двадцать семь раз (3 3 = 27). Увеличение объема всегда больше, чем увеличение поверхности.
площадь. Это верно для кубов, сфер или любого другого объекта размером
увеличился без изменения формы. Интерпретация: Каждая точка на графике ниже
представляет площадь поверхности и объем кубиков, которые увеличиваются на
одна единица длины, начиная с куба л = 1.Чем больше
оранжевая точка — размер куба ( l = 6), площадь поверхности которого
и объем имеют равные значения (хотя единицы разные
ед. 2 и одна ед. 3 ). Для кубиков меньше, чем
при этом площадь поверхности больше по отношению к объему, чем в больших кубах
(где объем больше по сравнению с площадью поверхности).
Иногда график, показывающий, как отношения изменения между двумя переменными более поучительны.Например, график отношения площади поверхности к объему,
,
ясно показывает, что размер объекта
увеличивается (без изменения формы), это соотношение уменьшается. Математически,
это говорит нам о том, что знаменатель (объем) увеличивается быстрее по сравнению с
числитель (площадь поверхности) по мере увеличения размера объекта. Звезда на
линия (при l = 6) представляет ту же точку, упомянутую выше: это
— размер куба, где S и V имеют равные значения,
и поэтому отношение площади поверхности к объему равно единице.
Выводы: Организмы проявляют разнообразие
модификации, как физиологические, так и анатомические, для компенсации изменений
в отношении площади поверхности к объему, связанной с различиями в размерах. Один
Примером этого является более высокий уровень метаболизма у небольших (гомеотермных)
животные. Из-за большой площади поверхности по отношению к объему малые
животные теряют тепло гораздо быстрее, чем крупные животные, и поэтому
должен выделять больше тепла, чтобы компенсировать влияние теплопроводности.Другой
Примером может служить множество внутренних транспортных систем, которые
в растениях и животных для активного перемещения материалов по организму,
тем самым позволяя им обойти ограничения, налагаемые пассивной диффузией.
Многие организмы развили структуры, которые фактически увеличивают их поверхность.
область: листья на деревьях, микроворсинки на слизистой оболочке тонкой кишки,
корневые волоски и капилляры, а также извитые стенки артерий, чтобы назвать
но несколько.
Из-за большой площади поверхности по отношению к объему малые
животные теряют тепло гораздо быстрее, чем крупные животные, и поэтому
должен выделять больше тепла, чтобы компенсировать влияние теплопроводности.Другой
Примером может служить множество внутренних транспортных систем, которые
в растениях и животных для активного перемещения материалов по организму,
тем самым позволяя им обойти ограничения, налагаемые пассивной диффузией.
Многие организмы развили структуры, которые фактически увеличивают их поверхность.
область: листья на деревьях, микроворсинки на слизистой оболочке тонкой кишки,
корневые волоски и капилляры, а также извитые стенки артерий, чтобы назвать
но несколько.
Дополнительные вопросы: Расчет и построение графика отношение площади поверхности к объему сфер, увеличивающееся с шагом в одну единицу (начиная с r = 1).Сравните соотношение сфер S : V и кубики сопоставимых размеров (2 r или диаметр = l ).
Дополнительный кредит: нанесите на график площади поверхности (ось x) и
объемы (ось Y) этих сфер на стандартном графике и графике логарифма. Что происходит с линией? Почему?
Что происходит с линией? Почему?
Источники: Schmidt-Nielson, K. 1984. Масштабирование: Почему так важен размер животного? Cambridge University Press, Нью-Йорк, NY.
Фогель, С. 1988. Устройства Жизни: Физический мир животных и растений . Princeton University Press, Принстон, Нью-Джерси.
авторское право 2000, М. Билс, Л. Гросс, С. Харрелл
Практическое обучение: область и объем
Объем вторичного использования
Просмотрите понятие объема, попросив учащихся принести из дома чистые, пустые контейнеры для еды, такие как банки, кувшины и картонные коробки. Объясните, что эти контейнеры помечены разными способами измерения объема (например,г., галлоны, унции, литры, чашки). Начните текстовую стену, на которой отображаются как термины, так и предметы, используя кнопки и клей, чтобы удерживать контейнеры. Дети могут снимать этикетки с банок и вырезать предметы из каталога и журнальную рекламу. Скоро они будут свободно говорить на языке объема.
Скоро они будут свободно говорить на языке объема.
Прямоугольник Art
Раздайте линейки и попросите учащихся использовать их, чтобы рисовать квадраты и прямоугольники разных размеров на миллиметровой бумаге, цветной бумаге или журналах. После того, как они вырежут фигуры, предложите детям создать картинки или рисунки, приклеивая фигуры на картон, следя за тем, чтобы они не пересекались.Попросите их найти площадь каждой формы, а затем общую площадь дизайна. Попросите учащихся показать свои работы, повесив их на доске объявлений или полке в порядке от наименьшего к наибольшему. Сделайте классную фреску, попросив учащихся расположить свои рисунки на одном листе мясной бумаги, а затем вычислить общую площадь всех фигур.
Раствор для обуви
Спросите студентов, могут ли они определить объем коробки из-под обуви с помощью кубов Unifix. Нужно ли им заполнять поле, чтобы найти ответ? Выровняйте дно коробки кубиками.Сколько прикрыть дно? Какова площадь основания коробки? Теперь спросите, сколько слоев им понадобится, чтобы заполнить коробку. Предложите учащимся поэкспериментировать в небольших группах. Некоторые захотят полностью заполнить коробку кубиками, чтобы найти объем, в то время как другие могут понять, что им нужно только найти высоту коробки в кубах и умножить ее на площадь основания. Обдумывая стратегии, которые они использовали для поиска объема, учащиеся должны обнаружить, что «кратчайший путь» к поиску объема — это умножение длины, ширины и высоты.
Предложите учащимся поэкспериментировать в небольших группах. Некоторые захотят полностью заполнить коробку кубиками, чтобы найти объем, в то время как другие могут понять, что им нужно только найти высоту коробки в кубах и умножить ее на площадь основания. Обдумывая стратегии, которые они использовали для поиска объема, учащиеся должны обнаружить, что «кратчайший путь» к поиску объема — это умножение длины, ширины и высоты.
Высокие и короткие контейнеры
Из двух одинаковых кусков плотной бумаги сделайте цилиндры: один высокий и тонкий, другой короткий и толстый. Скрепите каждый цилиндр скотчем, совместив швы так, чтобы они не перекрывали друг друга. Спросите студентов, какой цилиндр вмещает больше. Поместите высокий тонкий цилиндр в короткий толстый цилиндр. Заполните высокий цилиндр доверху сухими ингредиентами, такими как рис, попкорн или арахис из пенополистирола. Поднимите высокий цилиндр, позволяя сухим ингредиентам заполнить короткий цилиндр.Дети увидят, что в коротком цилиндре все еще есть место для большего, и, следовательно, он имеет большую вместимость.
Музей математики
Раздайте каждому учащемуся по 20 квадратных единиц и попросите их сделать из квадратов любую форму или рисунок, который они захотят. Проведите с учениками экскурсию, чтобы увидеть формы, созданные другими в классе. Когда они вернутся на свои места, спросите, что общего у всех рисунков (все они квадратные и имеют площадь 20 квадратных единиц). Затем попросите учащихся найти периметр своих фигур, посчитав единицы по внешним краям.У чьей формы самый маленький периметр? Самый большой? Они обнаружат, что периметр не зависит от площади.
Загадочные фигурки
Предложите учащимся работать в парах с перегородкой между ними. Раздайте каждому по стопке квадратных плиток и предложите им составить фигуру с заданной площадью квадратных единиц. Когда они построят свои фигуры, позвольте им приподнять перегородку и сравнить. Имеют ли две фигуры с одинаковой площадью одинаковый периметр или форму?
Танграм Тизер
Раздайте учащимся наборы частей головоломки танграм и попросите их найти область каждой части. (Что касается ромба, им нужно будет разделить его на два треугольника и один квадрат, определить площадь каждого из них, а затем найти общую сумму.) Попросите учащихся записать площадь на каждом кусочке головоломки. Теперь попросите их сложить части вместе, чтобы получился один большой квадрат, и найдите площадь квадрата. Если они складывают площади семи меньших частей, их ответ должен быть равен (или близок) к общей площади большого квадрата.
(Что касается ромба, им нужно будет разделить его на два треугольника и один квадрат, определить площадь каждого из них, а затем найти общую сумму.) Попросите учащихся записать площадь на каждом кусочке головоломки. Теперь попросите их сложить части вместе, чтобы получился один большой квадрат, и найдите площадь квадрата. Если они складывают площади семи меньших частей, их ответ должен быть равен (или близок) к общей площади большого квадрата.
Вызов емкости
Выстройте в ряд пять или шесть контейнеров разного размера и формы и попросите учащихся выяснить, как они сравниваются по объему.Это можно делать с водой в теплый день или с сухими ингредиентами в помещении. Предложите группам учащихся поделиться своими стратегиями.
Губка математика
Твердые контейнеры — не единственные вместительные. Контейнеры, которые меняют форму, такие как воздушные шары, губки и даже наши легкие, тоже обладают вместимостью. Принесите губки разного размера, формы и плотности. Предложите учащимся угадать, какие губки будут удерживать больше всего воды, расположив губки в порядке от наименьшей к наибольшей вместимости в соответствии с их прогнозами.Поместите губки в ванну с водой на 10 минут, затем позвольте ученикам выжать воду в отдельные градуированные цилиндры, чтобы оценить, сколько воды вмещает каждая губка. Старшие ученики могут измерить объем каждой губки (длина, умноженная на ширину, умноженную на высоту для прямоугольных и квадратных призм) до и после того, как она окажется в воде, как если бы это был пустой контейнер. Как рассчитанный объем соотносится с количеством воды, которое может вместить губка?
Предложите учащимся угадать, какие губки будут удерживать больше всего воды, расположив губки в порядке от наименьшей к наибольшей вместимости в соответствии с их прогнозами.Поместите губки в ванну с водой на 10 минут, затем позвольте ученикам выжать воду в отдельные градуированные цилиндры, чтобы оценить, сколько воды вмещает каждая губка. Старшие ученики могут измерить объем каждой губки (длина, умноженная на ширину, умноженную на высоту для прямоугольных и квадратных призм) до и после того, как она окажется в воде, как если бы это был пустой контейнер. Как рассчитанный объем соотносится с количеством воды, которое может вместить губка?
Geometry Online
Наконец, что касается цифровых технологий, представьте «Настройка сцены с геометрией», новую математическую программу, призванную помочь учащимся развить базовые навыки измерения 2D- и 3D-форм.Он включает в себя дополнительные мероприятия и рабочие листы.
Объем пирамиды
А
пирамида
является многогранником с одним основанием, которое является произвольным
многоугольник
.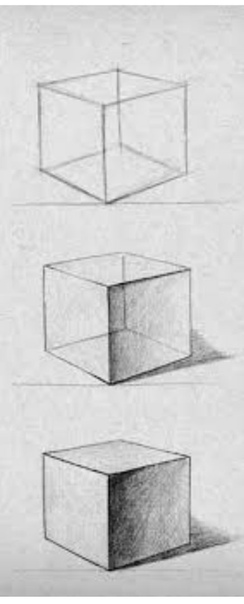 Остальные его грани — треугольники.
Остальные его грани — треугольники.
В объем из 3 -размерное твердое тело — это объем занимаемого пространства. Объем измеряется в кубических единицах ( в 3 , футов 3 , см 3 , м 3 и так далее).Перед вычислением объема убедитесь, что все измерения относятся к одной и той же единице.
Громкость V пирамиды составляет одну треть площади основания B раз больше высоты час .
V знак равно 1 3 B час
Пример:
Найдите объем правильной квадратной пирамиды со сторонами основания 10 см и высота 18 см.
Решение
Нарисуйте фигуру.
Формула объема пирамиды:
V знак равно 1 3 B час
Поскольку основание пирамиды представляет собой квадрат, площадь основания равна 10 2 или 100 см 2 .
Итак, заменим 100 для B а также 18 для час в формуле.
V знак равно 1 3 ( 100 ) ( 18 ) знак равно 600
Следовательно, объем квадратной пирамиды равен
600
см
3
.
Площадь, объем и время пребывания
Невозможно переоценить важность получения точной оценки площади вашего пруда. Большинство владельцев прудов оценивают площадь своего пруда визуально, что обычно приводит к завышению истинной площади пруда. Площадь пруда и объем воды следует рассчитывать на основе простых измерений. Усилия, необходимые для оценки площади поверхности пруда, напрямую связаны с формой и однородностью вашего пруда.Самый простой метод — использование основных уравнений для общих форм — можно применить, если ваш пруд очень похож по форме на круг, квадрат, прямоугольник или трапецию.
Формы пруда
Круглый
Форма пруда может быть оценена путем измерения расстояния вокруг береговой линии пруда в футах. Возведите расстояние от береговой линии в квадрат и разделите на 547 390, чтобы получить площадь пруда в акрах. Например, пруд, окружающий береговую линию на 450 футов, будет иметь площадь = (450 футов) 2/547 390 или 0,37 акра.
Площадь прямоугольной или квадратной формы
оценивается путем простого измерения длины и ширины сторон пруда в футах. Умножьте длину на ширину, чтобы получить площадь поверхности в квадратных футах. Это значение можно преобразовать в акры, разделив на 43 560 фут2 / акр. Таким образом, пруд размером 150 футов в длину и 100 футов в ширину будет иметь площадь = 150 футов X 100 футов = 15 000 кв. Футов или 0,34 акра.
Трапеция
Многие пруды могут иметь примерно прямоугольную форму, но одна сторона может быть значительно короче другой.Площадь этой формы лучше всего оценить по формуле трапеции, умножив среднюю длину двух неравных сторон на ширину пруда. Например, пруд длиной 200 футов с одной стороны, 300 футов с противоположной стороны и шириной 100 футов будет иметь площадь = 250 футов X 100 футов = 25 000 футов 2 или 0,57 акра.
Неправильная форма
Многие пруды имеют неправильную форму, площадь поверхности которой не может быть адекватно оценена с использованием формул для обычных геометрических форм. В этом случае можно использовать три метода в зависимости от желаемой степени точности. Имейте в виду, что точность оценки площади вашего пруда может быть очень важной, особенно для безопасного использования водных гербицидов. Три метода описаны в порядке от наименее точного до наиболее точного. Вы должны стремиться использовать наиболее точный метод, который вы можете разумно выполнить.
В этом случае можно использовать три метода в зависимости от желаемой степени точности. Имейте в виду, что точность оценки площади вашего пруда может быть очень важной, особенно для безопасного использования водных гербицидов. Три метода описаны в порядке от наименее точного до наиболее точного. Вы должны стремиться использовать наиболее точный метод, который вы можете разумно выполнить.
- Метод средней длины и ширины: Выполните многочисленные измерения, чтобы определить среднюю длину и среднюю ширину.Убедитесь, что вы получаете как самые длинные и самые короткие расстояния при вычислении средней длины, так и самые широкие и самые узкие расстояния для определения средней ширины. Чем больше измерений вы сделаете, тем точнее будет ваш результат. Затем площадь рассчитывается путем умножения средней ширины на среднюю длину. Если вы будете измерять в футах, результат будет в квадратных футах. Вы можете преобразовать квадратные футы в акры, разделив их на 43 560 кв.
 Футов на акр. В зависимости от количества выполненных измерений ширины и длины конечная площадь, вероятно, будет в пределах примерно ± 20 процентов от фактической площади поверхности пруда.
Футов на акр. В зависимости от количества выполненных измерений ширины и длины конечная площадь, вероятно, будет в пределах примерно ± 20 процентов от фактической площади поверхности пруда. - Метод нескольких трапеций: Более точный метод определения площади пруда необычной формы — разделение пруда на несколько трапеций. Новая трапеция определяется везде, где береговая линия быстро меняет направление. Обратите внимание, что вместо горизонтальных разрезов этот метод требует измерения расстояния между каждым вертикальным разрезом. Проще всего это сделать зимой, когда пруд замерзнет, а разрезы легко разметить и измерить.Этот метод требует дополнительных измерений и усилий, но окончательная оценка площади, вероятно, будет в пределах от ± 5 до 10 процентов от фактической площади пруда.
- Портативные системы глобального позиционирования (GPS): Портативные системы GPS стали довольно распространенными за последние пять лет, поскольку они стали более доступными.
 Сейчас они обычно используются для отдыха на природе (охота, походы, кемпинг и т. Д.) И навигации. Устройства GPS позволяют определять ваше точное местоположение на Земле с помощью нескольких спутников в космосе.Различные местоположения или «путевые точки» могут быть сохранены в устройстве GPS для использования с картографическим программным обеспечением, которое либо прилагается к устройству, либо может быть приобретено отдельно. Программа может соединять путевые точки и вычислять площадь внутри получившейся формы.
Сейчас они обычно используются для отдыха на природе (охота, походы, кемпинг и т. Д.) И навигации. Устройства GPS позволяют определять ваше точное местоположение на Земле с помощью нескольких спутников в космосе.Различные местоположения или «путевые точки» могут быть сохранены в устройстве GPS для использования с картографическим программным обеспечением, которое либо прилагается к устройству, либо может быть приобретено отдельно. Программа может соединять путевые точки и вычислять площадь внутри получившейся формы. - Сайты географической информации: В Интернете также есть программы географической информации, такие как Google Earth или Bing Maps, которые используют спутниковые изображения для отображения карты вашего пруда или озера. Эти инструменты веб-сайта могут упростить определение площади вашего водного ресурса.
Площадь поверхности пруда можно оценить, пройдя по периметру пруда и остановившись в различных путевых точках вдоль береговой линии пруда. Если путевые точки хранятся в каждом месте, где изменяется форма пруда, полученная площадь будет очень точной, вероятно, в пределах 1 процента от фактической площади пруда. Даже если у вас нет системы GPS, друзья или члены семьи, которые любят отдыхать на природе, могут владеть устройством, которое можно использовать для оценки площади вашего пруда.
Если путевые точки хранятся в каждом месте, где изменяется форма пруда, полученная площадь будет очень точной, вероятно, в пределах 1 процента от фактической площади пруда. Даже если у вас нет системы GPS, друзья или члены семьи, которые любят отдыхать на природе, могут владеть устройством, которое можно использовать для оценки площади вашего пруда.
Измерение глубины и объема пруда
Объем воды в прудах часто выражается в единицах, называемых «акро-футы».«Акро-фут представляет собой один акр поверхности, глубиной в один фут. Чтобы рассчитать акро-фут воды в пруду, вам понадобится площадь поверхности в акрах, как рассчитано выше, и средняя глубина воды в пруду. для типичного пруда в форме чаши средняя глубина может быть оценена как 0,4 максимальной глубины. Таким образом, пруд с максимальной глубиной 12 футов будет иметь среднюю глубину около 4,8 фута.
Более точный метод расчета средней глубины состоит в том, чтобы сделать много измерений и вычислить среднее значение. Чаще всего это делается путем измерения глубины водоема по двум трансектам — одной по ширине и одной по длине. Обязательно выбирайте трансекты, которые представляют мелкую и глубокую части пруда. Глубину можно легко измерить с каноэ или лодки с помощью груза и веревки с метками в футах. Чем больше измерений глубины вы сделаете, тем точнее будет ваше окончательное среднее значение. В примере, показанном на следующей странице, глубины пруда были взяты в шести точках по длине пруда и в пяти точках по ширине пруда.Среднюю глубину пруда можно рассчитать как среднее значение всех этих измерений.
Чаще всего это делается путем измерения глубины водоема по двум трансектам — одной по ширине и одной по длине. Обязательно выбирайте трансекты, которые представляют мелкую и глубокую части пруда. Глубину можно легко измерить с каноэ или лодки с помощью груза и веревки с метками в футах. Чем больше измерений глубины вы сделаете, тем точнее будет ваше окончательное среднее значение. В примере, показанном на следующей странице, глубины пруда были взяты в шести точках по длине пруда и в пяти точках по ширине пруда.Среднюю глубину пруда можно рассчитать как среднее значение всех этих измерений.
Объем воды в пруду (в акро-футах) рассчитывается простым умножением площади пруда (в акрах) на среднюю глубину пруда в футах. Имейте в виду, что один акро-фут воды равен 325 851 галлону.
Еще лучший способ рассчитать среднюю глубину пруда — разделить пруд на множество (по крайней мере, четыре) подобласти (так же, как мы это делали в методе трапеций). Возьмите хотя бы одну глубину в каждой подобласти и используйте ее для расчета общей средней глубины пруда. Этот способ особенно хорош, если дно пруда имеет неправильную форму, а не чашу.
Этот способ особенно хорош, если дно пруда имеет неправильную форму, а не чашу.
Время пребывания
Еще одним важным параметром, который должен знать управляющий прудом или озером, является «время пребывания» вашего водного ресурса. Время пребывания — это время, в течение которого вода находится в пруду, с момента ее попадания в пруд до момента, когда она уходит через водослив или переливную трубу. Этот расчет важен для внесения гербицидов или известкования в пруд. Если вода течет через ваш пруд слишком быстро, это может оказаться неэффективным.
Мы рассчитываем время пребывания по формуле: 226 умноженный на объем пруда в акро-футах, разделенный на скорость перелива в галлонах в минуту. Например, если у нас есть пруд площадью акров со средней глубиной 5 футов и скоростью перелива 10 галлонов в минуту, наше время пребывания будет: 226 (5) / (10) = 113 дней. В среднем вода, поступающая в этот пруд, остается в пруду 113 дней, прежде чем достигнет уровня перелива. В некоторых прудах может быть слишком сложно получить скорость перелива, чтобы произвести такой расчет.
A Final Word
Использование методов, описанных в этом информационном бюллетене, позволит вам рассчитать площадь поверхности и объем воды в вашем пруду с разумной точностью. Эти цифры имеют решающее значение для безопасного и правильного использования различных мероприятий по управлению водоемами, таких как использование водных гербицидов, известкование, зарыбление и использование устройств для аэрации.
Дополнительные ресурсы
Для получения дополнительной информации и публикаций по управлению водоемами в Пенсильвании посетите веб-сайт Penn State Extension или свяжитесь с вашим местным офисом Penn State Extension.
Подготовлено Брайаном Р. Суистоком, младшим специалистом, и Томом Маккарти, преподавателем дополнительного образования в округе Камберленд.
Как определить объем трехмерных объектов [Видео]
Привет, ребята! Добро пожаловать в этот видеоролик об объемах трехмерных объектов.
Начнем с определения объема. Объем — это измерение того, сколько места занимает жидкость или газ, или сколько места жидкость или газ занимают в данном объекте.
Возможно, вы этого не знаете, но люди используют объем каждый день.Объем используется для расчета количества питья. Количество воды, которое вы можете удерживать в чашке, зависит от ее объема. Есть несколько других способов использования громкости.
Теперь давайте посмотрим, как рассчитать объем треугольной призмы, прямоугольной призмы, сферы и конуса.
Объем треугольной призмы
Площадь треугольника равна \ (A = \ frac {1} {2} bh \). По сути, чтобы найти объем треугольной призмы, вы умножаете площадь треугольника на длину или глубину.{3} \). Важно знать, что при работе с объемом у нас всегда будут кубические единицы, потому что мы умножаем единицы сами на себя 3 раза.
Объем куба или прямоугольной призмы
Чтобы найти такой же объем куба или прямоугольной призмы, воспользуйтесь той же формулой. Как и в случае с треугольной призмой, вам нужно найти площадь одной стороны, а затем умножить ее на длину. Однако важно знать, что формула, которую вы используете для определения площади треугольника, отличается от формулы, которую вы используете для определения площади квадрата или прямоугольника.Формула для определения площади как квадрата, так и прямоугольника: \ (A = b h \). Итак, чтобы найти объем куба или прямоугольной призмы, вы должны найти площадь квадрата или прямоугольника, а затем умножить ее на длину. Таким образом получается формула \ (V = bhl \).
Однако важно знать, что формула, которую вы используете для определения площади треугольника, отличается от формулы, которую вы используете для определения площади квадрата или прямоугольника.Формула для определения площади как квадрата, так и прямоугольника: \ (A = b h \). Итак, чтобы найти объем куба или прямоугольной призмы, вы должны найти площадь квадрата или прямоугольника, а затем умножить ее на длину. Таким образом получается формула \ (V = bhl \).
Вот пример:
Здесь у нас есть куб, который представляет собой прямоугольную призму, но все стороны представляют собой полных квадратов . Поскольку это куб, мы знаем, что все стороны находятся на одинаковом расстоянии. Итак, все, что нам нужно сделать, это умножить себя 10 раз на 3 раза.{3} \). Когда вы делаете то, что называется доказательством, чтобы доказать, что это формула, а пока мы просто подставим числа в данную формулу.
Сфера имеет диаметр 20 метров. Это вся информация, которая нам нужна для решения нашего уравнения. Мы ищем радиус, и мы знаем, что радиус равен половине диаметра, что означает, что наш радиус равен 10 метрам. Когда мы подставляем 10 в нашу формулу и решаем, мы получаем 4 188,9 метра в кубе.
Мы ищем радиус, и мы знаем, что радиус равен половине диаметра, что означает, что наш радиус равен 10 метрам. Когда мы подставляем 10 в нашу формулу и решаем, мы получаем 4 188,9 метра в кубе.
Объем конуса
Формула для объема конуса очень похожа на формулу для площади круга.{3} \).
Отличная работа, ребята. Изучение новых формул может быть трудным. Важно продолжать практиковаться, чтобы вы могли распознать, какую формулу вам нужно использовать, и запомнить формулы. Я надеюсь, что это было полезно. Увидимся в следующий раз!
Калькулятор объема коробки 📐
Быстрая навигация:
- Формула объема ящика
- Как рассчитать объем ящика?
- Пример: найти объем прямоугольного ящика
- Расчет груза в кубических метрах / кубических футах
- Другие приложения
Объем прямоугольного ящика можно рассчитать, зная его три размера: ширину, длину и высоту. Формула объем коробка = ширина x длина x высота . На рисунке ниже:
Формула объем коробка = ширина x длина x высота . На рисунке ниже:
Измерение сторон прямоугольного ящика или резервуара очень просто. Результат вычисления с использованием нашего калькулятора объема прямоугольного ящика или иным образом всегда будет в используемой единице длины, кубе. Убедитесь, что все измерения указаны в одной и той же единице, если вы делаете математику вручную, а если используете наш калькулятор — обязательно выберите соответствующую метрику.Если вы измерили длину в дюймах, результат будет в кубических дюймах. Если длина была в футах, результат будет в кубических футах, и так далее для ярдов 3 , миль 3 , мм 3 , см 3 , метров 3 .
Как рассчитать объем ящика? Чтобы рассчитать объем прямоугольного ящика или резервуара, вам нужно сделать три измерения, а затем умножить их. В практических ситуациях у вас может быть план или инженерная схема, в которой даны все измерения, что значительно облегчит вашу задачу. Это довольно легко сделать в уме, если числа маленькие, но быстро становится неудобно, если числа становятся большими, когда объем ящичного калькулятора, подобного приведенному выше, становится действительно полезным.
Это довольно легко сделать в уме, если числа маленькие, но быстро становится неудобно, если числа становятся большими, когда объем ящичного калькулятора, подобного приведенному выше, становится действительно полезным.
Следует отметить, что «объем коробки» не может быть точным термином, поскольку, если мы примем коробку за абстрактное математическое понятие, ее стенки имеют нулевую толщину, а сама коробка имеет нулевой объем. Однако на практике мы обычно говорим об объеме с точки зрения пространства, заключенного в коробке или резервуаре, и это то, что вычисляет калькулятор выше.Если это то, что вы рассчитываете и хотите знать, что он может вместить, обязательно измерьте его внутренние, а не внешние размеры, иначе вам нужно будет затем вычесть объем стен.
Пример: найти объем прямоугольной коробки
Для вычисления объема любого ящика прямоугольной формы необходимо знать три измерения: длины двух сторон его основания, а также высоту. Например, если две стороны основания имеют длину 3 дюйма и 6 дюймов соответственно, а высота коробки составляет 2 дюйма, то использование уравнения объема коробки дает 3 x 6 x 2 = 18 x 2 = 36 дюймов. 3 (кубические дюймы).
3 (кубические дюймы).
В качестве альтернативы можно указать площадь одной стороны коробки и высоту относительно этой стороны. В этом случае просто умножьте площадь на высоту. Например, если основание коробки составляет 25 квадратных футов, а длина стороны коробки, перпендикулярной ему, составляет 4 фута, то объем коробки составляет 25 x 4 = 100 кубических футов.
Расчет грузов в кубических метрах / кубических футахЧасто необходимо рассчитать объем транспортных контейнеров, ящиков, ящиков, цистерн и других транспортных средств.Обычно производитель предоставляет техническую спецификацию или, по крайней мере, вы знаете стандарт, на основе которого был изготовлен контейнер, с указанием минимально допустимых размеров.
Если вам нужен более специализированный калькулятор, который подскажет, сколько предметов при заданных размерах вы можете уместить, попробуйте наш калькулятор контейнеров и наш калькулятор поддонов.
Другие приложения Прямоугольная коробка — одна из наиболее широко используемых форм корпуса в науке, технике и архитектуре благодаря своим хорошим структурным свойствам и устойчивости к силе с разных сторон. Большинство домов и комнат в них представляют собой прямоугольные коробки, большинство транспортных контейнеров представляют собой коробки или имеют коробчатую форму. Другими распространенными способами использования являются расчет объема аквариума, объема бассейна или объема почвы, мульчи или питательных веществ для растений, необходимых для данного участка сада. Ящики и резервуары из дерева, стали, кирпича, бетона, стекла и других материалов также легко производить по сравнению с более сложными формами.
Большинство домов и комнат в них представляют собой прямоугольные коробки, большинство транспортных контейнеров представляют собой коробки или имеют коробчатую форму. Другими распространенными способами использования являются расчет объема аквариума, объема бассейна или объема почвы, мульчи или питательных веществ для растений, необходимых для данного участка сада. Ящики и резервуары из дерева, стали, кирпича, бетона, стекла и других материалов также легко производить по сравнению с более сложными формами.
Еще одним преимуществом прямоугольной формы является то, насколько легко меньшие формы могут вписываться в более крупные без необходимости сложных вычислений, поворотов и общего расположения.Итак, у этого калькулятора объема коробки есть много возможных применений.
Детерминанты и объемы
Пусть A — матрица размера n × n со столбцами v1, v2, …, vn, и пусть T: Rn → Rn — соответствующее преобразование матрицы T (x) = Ax. Тогда T (e1) = v1 и T (e2) = v2, поэтому T переводит единичный куб C в параллелепипед P, определяемый v1, v2, . .., vn:
.., vn:
Поскольку единичный куб имеет объем 1 и его изображение имеет объем | det (A) |, преобразование T масштабировало объем куба в | det (A) |.Перефразируя:
Обозначение T (S) означает изображение области S при преобразовании T. В обозначении построителя множеств это подмножество
T (S) = CT (x) | xinSD.
Фактически, T масштабирует объем любой области в Rn с тем же коэффициентом, даже для округлых областей.
Проба
Пусть C — единичный куб, пусть v1, v2, …, vn — столбцы A, и пусть P — паралелепипед, определяемый этими векторами, так что T (C) = P и vol (P) = | det (А) |. Для A> 0 обозначим AC кубом со сторонами A, i.е., паралелепипед, определяемый векторами Ae1, Ae2, …, Aen, и AP мы определяем аналогично. По второму определяющему свойству T переводит AC в AP. Объем AC равен An (мы масштабировали каждый из n стандартных векторов с коэффициентом A), а объем AP равен An | det (A) | (по той же причине), поэтому мы показали, что T масштабирует объем AC на | det (A) |.
По первому определяющему свойству образ транслитера AC является транслятом AP:
Т (х + АС) = Т (х) + АТ (С) = Т (х) + AP.
Поскольку перевод не изменяет объемы, это доказывает, что T масштабирует объем перевода AC на | det (A) |.
На этом этапе нам нужно использовать методы многомерного исчисления, поэтому мы дадим только представление об остальной части доказательства. Любую область S можно аппроксимировать набором очень маленьких кубиков вида x + AC. Затем изображение T (S) аппроксимируется изображением этого набора кубов, который представляет собой набор очень маленьких паралелепипедов вида T (x) + AP.
Объем S приблизительно равен сумме объемов кубов; фактически, когда A стремится к нулю, предел этой суммы в точности равен vol (S). Точно так же объем T (S) равен сумме объемов паралеллепипедов, считая в пределе A → 0. Ключевым моментом является то, что объем каждого куба масштабируется на | det (A) |.




 Это станет будущим углом дома.
Это станет будущим углом дома.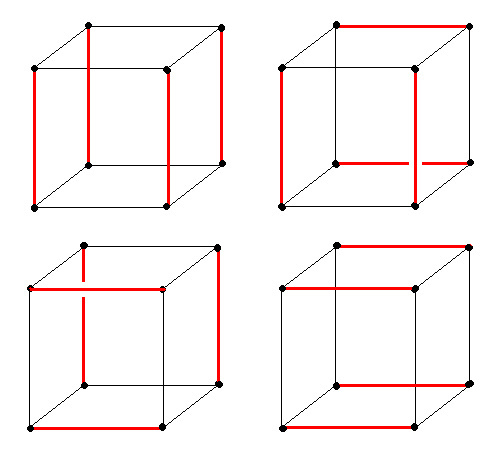 Для этого процесса можно воспользоваться линейкой.
Для этого процесса можно воспользоваться линейкой. Футов на акр. В зависимости от количества выполненных измерений ширины и длины конечная площадь, вероятно, будет в пределах примерно ± 20 процентов от фактической площади поверхности пруда.
Футов на акр. В зависимости от количества выполненных измерений ширины и длины конечная площадь, вероятно, будет в пределах примерно ± 20 процентов от фактической площади поверхности пруда. Сейчас они обычно используются для отдыха на природе (охота, походы, кемпинг и т. Д.) И навигации. Устройства GPS позволяют определять ваше точное местоположение на Земле с помощью нескольких спутников в космосе.Различные местоположения или «путевые точки» могут быть сохранены в устройстве GPS для использования с картографическим программным обеспечением, которое либо прилагается к устройству, либо может быть приобретено отдельно. Программа может соединять путевые точки и вычислять площадь внутри получившейся формы.
Сейчас они обычно используются для отдыха на природе (охота, походы, кемпинг и т. Д.) И навигации. Устройства GPS позволяют определять ваше точное местоположение на Земле с помощью нескольких спутников в космосе.Различные местоположения или «путевые точки» могут быть сохранены в устройстве GPS для использования с картографическим программным обеспечением, которое либо прилагается к устройству, либо может быть приобретено отдельно. Программа может соединять путевые точки и вычислять площадь внутри получившейся формы.