Что нарисовать из треугольника детям: геометрические фигуры для детей
- Изображения из геометрических фигур для детей. Картинки животных из геометрических фигур
- Как понять Геометрию? Основы с нуля
- Методика «Учебная деятельность» Л.И. Цеханской
- Виды треугольников. 2-й класс
- Рисуем мелками!
- Урок 28. треугольники — Математика — 5 класс
- Конспект НОД для старшей группы «Веселые геометрические фигуры» (Нетрадиционная техника рисования)
- Тема треугольника
- Домашнее обучение искусству: оптическая иллюзия для детей: нарисуй треугольник | Алисия Робинсон
- Что такое треугольник? — [Определение, факты и примеры]
- С какого возраста ребенок может нарисовать треугольник?
- Что должен уметь рисовать двухлетний ребенок?
- Когда малыши могут рисовать фигуры?
- Что должен знать трехлетний ребенок в учебном процессе?
- Должен ли двухлетний ребенок знать азбуку?
- Может ли двухлетний ребенок нарисовать человека?
- Какие 5 этапов рисования?
- Должен ли двухлетний ребенок знать цвета?
- Что должен знать 2,5-летний ребенок?
- Что должен знать 2-3-летний ребенок в академическом плане?
- Математика + рисование с палочками Kwik
- Праздник математики для детей
- Использование искусственного интеллекта для оживления детских рисунков
- Почему автоматические инструменты анимации ИИ не работают с детскими рисунками
- Идентификация человекоподобных фигур с помощью обнаружения объектов
- Поднятие человекоподобной фигуры из сцены с помощью маскирования символов
- Подготовка к анимации с помощью оснастки
- Анимация 2D-фигур с помощью 3D-захвата движения
- Использование ИИ для создания более сложных анимаций
Изображения из геометрических фигур для детей. Картинки животных из геометрических фигур
Когда понадобится: для выявления типов личностей: руководитель, исполнитель, ученый, изобретатель и т. п.
ТЕСТ
«Конструктивный рисунок человека из геометрических фигур»
Инструкция
Нарисуйте, пожалуйста, фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Вы можете увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности.
Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10. Если при рисовании вы использовали большее количество фигур, то нужно зачеркнуть лишние, если же вами использовано фигур меньше чем 10, необходимо дорисовать недостающие.
Ключ к тесту «Конструктивный рисунок человека из геометрических фигур»
Описание
Тест «Конструктивный рисунок человека из геометрических фигур» предназначен для выявления индивидуально-типологических различий.
Сотруднику предлагают три листа бумаги размером 10 × 10 см. Каждый лист нумеруется и подписывается. На первом листе выполняется первый пробный рисунок, далее, соответственно, на листе втором – второй, на листе третьем – третий.
Сотруднику необходимо на каждом листе нарисовать фигуру человека, составленную из 10 элементов, среди которых могут быть треугольники, круги, квадраты. Сотрудник может увеличивать или уменьшать эти элементы (геометрические фигуры) в размерах, накладывать друг на друга по мере надобности. Важно, чтобы все эти три элемента в изображении человека присутствовали, а сумма общего количества использованных фигур была равна 10.
Если при рисовании сотрудник использовал большее количество фигур, то ему необходимо зачеркнуть лишние, если же использовал фигур меньше чем 10, ему необходимо дорисовать недостающие.
При нарушении инструкции данные не обрабатываются.
Пример рисунков, сделанных тремя оцениваемыми
Обработка результата
Подсчитайте количество затраченных в изображении человечка треугольников, кругов и квадратов (по каждому рисунку отдельно). Запишите результат в виде трехзначных чисел, где:
Запишите результат в виде трехзначных чисел, где:
- сотни обозначают количество треугольников;
- десятки – количество кругов;
- единицы – количество квадратов.
Эти трехзначные цифры составляют так называемую формулу рисунка, по которой происходит отнесение рисующих к соответствующим типам и подтипам.
Интерпретация результата
Собственные эмпирические исследования, в которых получено и проанализировано более 2000 рисунков, показали, что соотношение различных элементов в конструктивных рисунках не случайно. Анализ позволяет выделить восемь основных типов, которым соответствуют определенные типологические характеристики.
Интерпретация теста основана на том, что геометрические фигуры, использованные в рисунках, различаются по семантике:
- треугольник обычно относят к острой, наступательной фигуре, связанной с мужским началом;
- круг – фигура обтекаемая, более созвучна с сочувствием, мягкостью, округлостью, женственностью;
- квадрат, прямоугольник интерпретируются как специфически техническая конструктивная фигура, технический модуль.

Типология, основанная на предпочтении геометрических фигур, позволяет сформировать своего рода систему индивидуально-типологических различий.
Типы
I тип – руководитель
Формулы рисунков: 901, 910, 802, 811, 820, 703, 712, 721, 730, 604, 613, 622, 631, 640. Наиболее жестко доминирование над другими выражено у подтипов 901, 910, 802, 811, 820; ситуативно – у 703, 712, 721, 730; при воздействии речью на людей – вербальный руководитель или преподавательский подтип – 604, 613, 622, 631, 640.
Обычно это люди, имеющие склонность к руководящей и организаторской деятельности, ориентированные на социально значимые нормы поведения, могут обладать даром хороших рассказчиков, основывающимся на высоком уровне речевого развития. Обладают хорошей адаптацией в социальной сфере, доминирование над другими удерживают в определенных границах.
Нужно помнить, что проявление данных качеств зависит от уровня психического развития. При высоком уровне развития индивидуальные черты развития реализуемы, достаточно хорошо осознаются.
При низком уровне они могут не выявляться в профессиональной деятельности, а присутствовать ситуативно, хуже, если неадекватно ситуациям. Это относится ко всем характеристикам.
II тип – ответственный исполнитель
Формулы рисунков: 505, 514, 523, 532, 541, 550.
Данный тип людей обладает многими чертами типа «руководитель», являясь расположенным к нему, однако в принятии ответственных решений часто присутствуют колебания. Такой человек ориентирован на умение делать дело, высокий профессионализм, обладает высоким чувством ответственности и требовательности к себе и другим, высоко ценит правоту, то есть характеризуется повышенной чувствительностью к правдивости. Часто он страдает соматическими заболеваниями нервного происхождения вследствие перенапряжения.
III тип – тревожно-мнительный
Формулы рисунков: 406, 415, 424, 433, 442, 451, 460.
Данный тип людей характеризуется разнообразием способностей и одаренности – от тонких ручных навыков до литературной одаренности. Обычно этим людям тесно в рамках одной профессии, они могут поменять ее на совершенно противоположную и неожиданную, иметь также хобби, которое по сути является второй профессией. Физически не переносят беспорядка и грязи. Обычно конфликтуют из-за этого с другими людьми. Отличаются повышенной ранимостью и часто сомневаются в себе. Нуждаются в подбадривании.
Обычно этим людям тесно в рамках одной профессии, они могут поменять ее на совершенно противоположную и неожиданную, иметь также хобби, которое по сути является второй профессией. Физически не переносят беспорядка и грязи. Обычно конфликтуют из-за этого с другими людьми. Отличаются повышенной ранимостью и часто сомневаются в себе. Нуждаются в подбадривании.
Кроме этого, 415 – «поэтический подтип» – обычно лица, имеющие такую формулу рисунка, обладают поэтической одаренностью; 424 – подтип людей, узнаваемых по фразе «Как это можно плохо работать? Я себе не представляю, как это можно плохо работать». Люди такого типа отличаются особой тщательностью в работе.
IV тип – ученый
Формулы рисунков: 307, 316, 325, 334, 343, 352, 361, 370.
Эти люди легко абстрагируются от реальности, обладают концептуальным умом, отличаются способностью разрабатывать все свои теории. Обычно обладают душевным равновесием и рационально продумывают свое поведение.
Подтип 316 характеризуется способностью создавать теории, по преимуществу глобальные, или осуществлять большую и сложную координационную работу.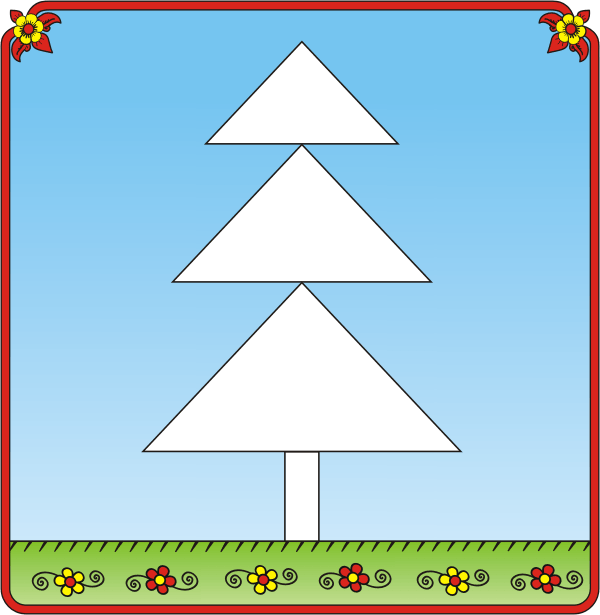
325 – подтип, характеризующийся большой увлеченностью познания жизни, здоровья, биологическими дисциплинами, медициной. Представители этого типа часто встречаются среди лиц, занимающихся синтетическими видами искусства: кино, цирк, театрально-зрелищная режиссура, мультипликация и т. д.
V тип – интуитивный
Формулы рисунков: 208, 217, 226, 235, 244, 253, 262, 271, 280.
Люди этого типа обладают сильной чувствительностью нервной системы, ее высокой истощаемостью. Легче работают на переключаемости от одной деятельности к другой, обычно выступают адвокатами меньшинства. Обладают повышенной чувствительностью к новизне. Альтруистичны, часто проявляют заботу о других, обладают хорошими ручными навыками и образным воображением, что дает им возможность заниматься техническими видами творчества. Обычно вырабатывают свои нормы морали, обладают внутренним самоконтролем, то есть предпочитают самоконтроль, отрицательно реагируя на посягательства, касающиеся их свободы.
235 – часто встречается среди профессиональных психологов или лиц с повышенным интересом к психологии;
244 – обладает способностью к литературному творчеству;
217 – обладает способностью к изобретательской деятельности;
226 – имеет большую потребность в новизне, обычно ставит очень высокие критерии достижений для себя.
VI тип – изобретатель, конструктор, художник
Формулы рисунков: 109, 118, 127, 136, 145, 019, 028, 037, 046.
Часто встречается среди лиц с технической жилкой. Это люди, обладающие богатым воображением, пространственным видением, часто занимаются различными видами технического, художественного и интеллектуального творчества. Чаще интровертированы, так же как интуитивный тип, живут собственными моральными нормами, не приемлют никаких воздействий со стороны, кроме самоконтроля. Эмоциональны, одержимы собственными оригинальными идеями.
Также выделяют особенности следующих подтипов:
019 – встречается среди лиц, хорошо владеющих аудиторией;
118 – тип с наиболее сильно выраженными конструктивными возможностями и способностью к изобретениям.
VII тип – эмотивный
Формулы рисунков: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280, 154, 163, 172, 181, 190, 055, 064, 073, 082, 091.
Обладают повышенным сопереживанием по отношению к другим, тяжело переживают жестокие кадры фильма, могут надолго быть выбитыми из колеи и быть потрясенными от жестоких событий. Боли и заботы других людей находят в них участие, сопереживание и сочувствие, на которое они тратят много собственной энергии, в результате становится затруднительной реализация их собственных способностей.
Боли и заботы других людей находят в них участие, сопереживание и сочувствие, на которое они тратят много собственной энергии, в результате становится затруднительной реализация их собственных способностей.
VIII тип – противоположность эмотивного
Формулы рисунков: 901, 802, 703, 604, 505, 406, 307, 208, 109.
Данный тип людей обладает противоположной тенденцией эмотивному типу. Обычно не чувствует переживаний других людей, или относится к ним с невниманием, или даже усиливает давление на людей. Если это хороший специалист, то он может заставить других делать то, что он считает нужным. Иногда для него характерна черствость, которая возникает ситуативно, когда в силу каких-либо причин человек замыкается в кругу собственных проблем.
Способ рисования человечков из геометрических фигур использовался в психологии давно.Некоторые считают, что он был предложен графологом из Сан-Франциско Э. Махони. Но данных подтверждающих это, к сожалению, не было найдено. Систематическое изучение результатов, получаемых по данному тесту, начато сравнительно недавно. Большую коллекцию такого рода рисунков собрал А. В. Либин.
Большую коллекцию такого рода рисунков собрал А. В. Либин.
Целью теста является определение индивидуальных типологических характеристик человека на основе соотношения геометрических фигур в рисунке, а также графических особенностей его выполнения.
Инструкция: нарисуйте человечка из десяти геометрических фигур — треугольника, круга и квадрата. Фигуры можно увеличивать или уменьшать в размере, накладывать друг на друга. Важно, чтобы они все использовались в рисунке, то есть нельзя нарисовать человечка из 10 квадратов, 10 треугольников или 10 кругов.
Обработка данных : подсчитайте сколько у вас получилось треугольников, кругов и квадратов в рисунке человечка, и запишите это количество трёхзначным числом, например: треугольников — 3, кругов – 2, квадратов — 5. Получается число: 325 . Таким образом, мы получаем трехзначное число, которое обозначает «формулу рисунка».
На основании различий в предпочтениях геометрических фигур при выполнении рисунков человечков образуется восемь основных типов(или групп) и 63 подтипа.
Если у вас получилось число из этого ряда: 901, 910, 802, 811, 820, 703, 712, 721, 604, 613, 622, 631, 640 — вы относитесь к Типу 1 «Руководитель».
Числа: 505, 514, 523, 532, 541, 550 — Тип 2 «Ответственный исполнитель».
Числа: 406, 415, 424, 433, 442, 451, 460 — Тип 3 «Тревожно-мнительный».
Числа: 307, 316, 325, 334, 343, 352, 361, 370 — Тип 4 «Ученый».
Числа: 208, 217, 226, 235, 244, 253, 262, 271, 280 — Тип 5 «Интуитивный».
Числа: 109, 118, 127, 136, 145, 019, 028, 037, 046 — Тип 6 «Изобретатель, конструктор».
Числа: 550, 451, 460, 352, 361, 370, 253, 262, 271, 280,154, 163, 172, 181, 190, 055, 064, 073, 082, 091 — Тип 7 «эмотивный».
Числа: 901, 802, 703, 604, 505, 406, 307, 208, 109 — Тип 8 «противоположный эмотивному».
Некоторые комментарии к психологическому портрету можно сделать и по особенности изображения человечков:
Маленький размер рисунков может быть связан с утомленностью, скованностью, дискомфортом;
Усиленная штриховка — с внутренним напряжением, подозрительностью, иногда с состоянием
предзаболевания;
Прорисовка лица связана чаще с повышенной общительностью, а отсутствие ее — со сложностями в общении, которое целесообразно выяснить;
Наличие «шеи» у человечка свидетельствует часто о высокой ранимости человека, которая затрудняет общение и от которой целесообразно избавиться;
Наличие квадратных карманов на теле человека может свидетельствовать о повышенной заботе по отношению к детям;
Наличие круглых «пуговок» — о сочувственной заботе к старшим близким;
Наличие «треугольников» — о необходимости сделать какое-либо распоряжение, указания.
Ключ к тесту «Рисунок человечка из геометрических фигур»:
Тип 1 – «Руководитель» (901, 910, 802, 811, 820, 703, 712, 721, 604, 613, 622, 631, 640). Для «руководителя» характерны наличие организаторских и ораторских способностей, ориентация на общественные нормы поведения, высокий уровень социальной адаптации. Лица данного типа обладают ярко выраженным целенаправленным поведением, что и характеризует их как лидеров. В достижении цели могут не считаться со своим здоровьем, стрессоустойчивы. Ораторские навыки, способности хорошего рассказчика позволяют им заниматься преподавательской работой и педагогической деятельностью. Их воля и энергия заметны всем, поскольку представляют собой их наиболее яркие качества. Способность к интенсивному волевому усилию, длительному и устойчивому, отражается на их внутренней жизни и внешнем поведении. Их твердость, настойчивость, выдержка и самообладание ставит их в центр внимания окружающих. Им всегда присуще ясное осознание того, что они хотят, к чему стремятся и какими путями могут достичь желаемое. Это люди, в которых сама природа вложила способность влиять на других людей, направляя их согласно своим планам и намерениям. Способность к энергичному и длительному напряжению, способность к борьбе за свои интересы, самообладанию и сопротивлению способствуют тому, что эти люди обычно становятся талантливыми администраторами, представителями исполнительной власти, руководителями предприятий. Людям этого типа приходится по многу раз пересматривать свои выводы и переделывать свои проекты прежде, чем окончательно убедиться в их правильности. Отсюда их известный консерватизм, неодобрительное отношение к «потрясению основ», к критике установленных принципов. Когда речь идет о выполнении того, что они считают своей обязанностью, то ни соблазны личного характера, ни просьбы близких людей, не в состоянии свернуть их с избранного пути, который им представляется единственно правильным.У них особо развито чувство собственного достоинства, иногда переходящее в сильное самолюбие и самомнение от того, что человек, стремящийся к власти и вынужденный вступать из-за этого в борьбу с окружающими не может не охранять своего «Я» от посягательств.
Это люди, в которых сама природа вложила способность влиять на других людей, направляя их согласно своим планам и намерениям. Способность к энергичному и длительному напряжению, способность к борьбе за свои интересы, самообладанию и сопротивлению способствуют тому, что эти люди обычно становятся талантливыми администраторами, представителями исполнительной власти, руководителями предприятий. Людям этого типа приходится по многу раз пересматривать свои выводы и переделывать свои проекты прежде, чем окончательно убедиться в их правильности. Отсюда их известный консерватизм, неодобрительное отношение к «потрясению основ», к критике установленных принципов. Когда речь идет о выполнении того, что они считают своей обязанностью, то ни соблазны личного характера, ни просьбы близких людей, не в состоянии свернуть их с избранного пути, который им представляется единственно правильным.У них особо развито чувство собственного достоинства, иногда переходящее в сильное самолюбие и самомнение от того, что человек, стремящийся к власти и вынужденный вступать из-за этого в борьбу с окружающими не может не охранять своего «Я» от посягательств.
Тип 2- «Ответственный исполнитель» (505, 514, 523, 532, 541, 550). Обладает многими чертами, сходными с типом «руководитель», но часто колеблется в принятии важных решений. Люди данного типа обычно обладают высоким уровнем профессионализма. Они отличаются повышенной требовательностью к себе и другим. Преобладание обдуманных и рассудочных действий над всеми душевными движениями, накладывает своеобразный отпечаток на все качества личности. Людей этого типа часто можно встретить среди владельцев и управляющих торговых и промышленных предприятий, банков, т. е. среди людей, которые имеют дело с организацией, составленной из большого числа материально-технических объектов и документации, что требует для ведения и поддержания дел в порядке не только упорного труда, но и интеллекта.
Осторожность и расчетливость помогает им быть экономными и бережливыми, а их устойчивость и постоянство способствуют прочности дела, которое они развивают медленно, но верно. Они не рискуют, несмотря на открывающиеся блестящие перспективы, а предпочитают действовать наверняка.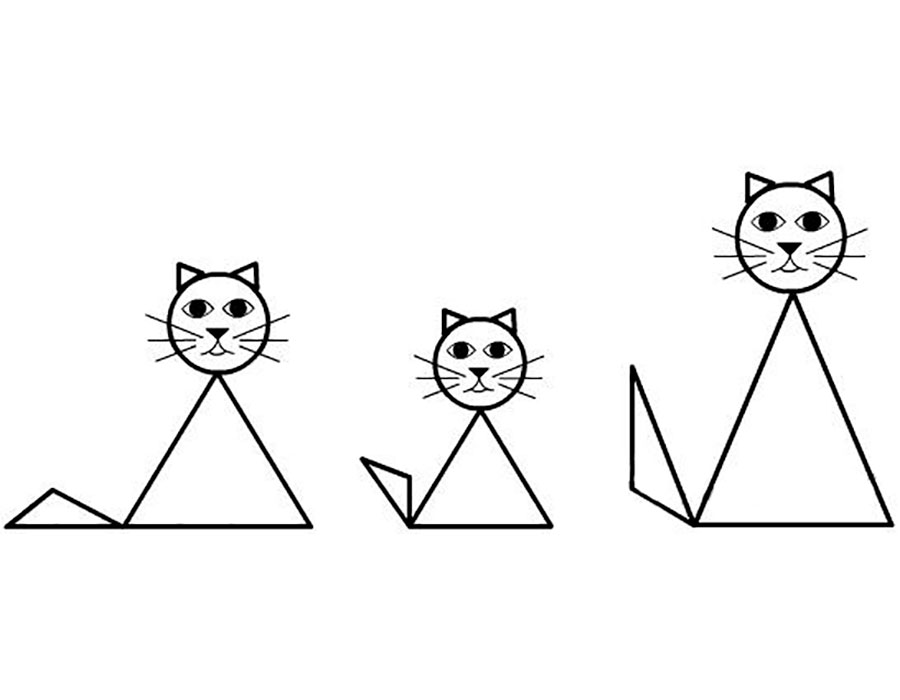 Они консервативны в политике или умеренно-либеральны, никогда не следуя крайним воззрениям. Благоразумная сдержанность и расчетливость свойственным им и в вопросах любви и брака. Они способны подчинить свои любовные увлечения требованиям рассудка. Обладая достаточно развитым интеллектом и волей, они хорошо разбираются в жизненных реалиях и своих делах, которые исполняют с большой аккуратностью. Нередко являются правдолюбцами. Из-за повышенных требований к себе могут работать, не замечая усталости, подрывая здоровье. Болезни нервного происхождения — их частые спутники. Поэтому «ответственным исполнителям» необходимо тщательно следить за соблюдением режима труда и отдыха.
Они консервативны в политике или умеренно-либеральны, никогда не следуя крайним воззрениям. Благоразумная сдержанность и расчетливость свойственным им и в вопросах любви и брака. Они способны подчинить свои любовные увлечения требованиям рассудка. Обладая достаточно развитым интеллектом и волей, они хорошо разбираются в жизненных реалиях и своих делах, которые исполняют с большой аккуратностью. Нередко являются правдолюбцами. Из-за повышенных требований к себе могут работать, не замечая усталости, подрывая здоровье. Болезни нервного происхождения — их частые спутники. Поэтому «ответственным исполнителям» необходимо тщательно следить за соблюдением режима труда и отдыха.
Тип 3 — «Тревожно-мнительный» (406, 415, 424, 433, 442, 451, 460).
Этот тип характеризуется разнообразием способностей — от литературных до способностей к точным ручным навыкам. Несмотря на обилие талантов, нуждается в мягком подбадривании, так как часто необоснованно не верит в свои силы, сомневается в себе.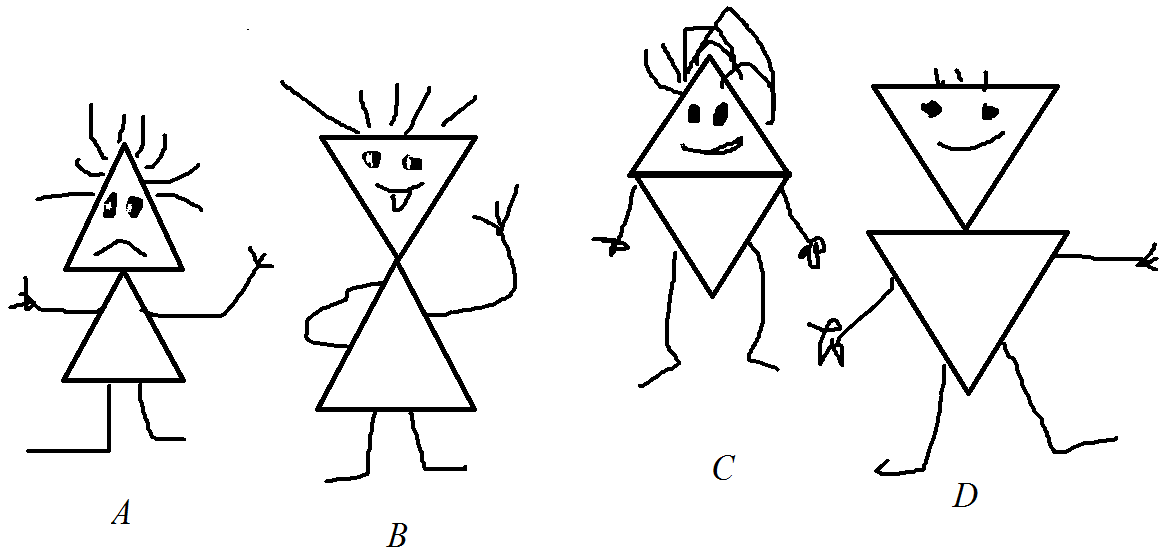 «Тревожно-мнительный» тип обладает повышенным вниманием к порядку и чистоте, физически не приемля грязь и беспорядок. Люди данного типа могут неожиданно для других изменить свою профессию. Обычно им тесно в рамках одной специальности, они имеют хобби, в котором весьма преуспевают. Часто этой новой профессией для них становится искусство. Поэтому мы можем наблюдать, как врач становится певцом или артистом эстрады, бывший строитель выходит на сцену и читает пародии, а редактор журнала начинает создавать изделия декоративно-прикладного искусства. Часто встречаются случаи, когда люди этого типа проявляют свои незаурядные способности в других видах искусства, например, музыкант имеет склонность к живописи или скульптуре, поэт увлекается музыкой,
«Тревожно-мнительный» тип обладает повышенным вниманием к порядку и чистоте, физически не приемля грязь и беспорядок. Люди данного типа могут неожиданно для других изменить свою профессию. Обычно им тесно в рамках одной специальности, они имеют хобби, в котором весьма преуспевают. Часто этой новой профессией для них становится искусство. Поэтому мы можем наблюдать, как врач становится певцом или артистом эстрады, бывший строитель выходит на сцену и читает пародии, а редактор журнала начинает создавать изделия декоративно-прикладного искусства. Часто встречаются случаи, когда люди этого типа проявляют свои незаурядные способности в других видах искусства, например, музыкант имеет склонность к живописи или скульптуре, поэт увлекается музыкой,
актер совершенствуется в вокальном мастерстве и т. д.
Для людей этого типа занятия искусством имеет существенное значение, составляет эпицентр их жизни, который поглощает их. Искусству они отдают большую часть своего времени. Это связано и с особенностью их эмоциональной сферы, на которую сильно влияют их фантазии. Обладая способностями к тонким эстетическим переживаниям, эстетические наслаждения они предпочитают всему остальному. Они отличаются наблюдательностью, живой восприимчивостью, развитым воображением, а их обостренная наблюдательность позволяет многое подмечать, из того, что ускользает от глаз окружающих.
Обладая способностями к тонким эстетическим переживаниям, эстетические наслаждения они предпочитают всему остальному. Они отличаются наблюдательностью, живой восприимчивостью, развитым воображением, а их обостренная наблюдательность позволяет многое подмечать, из того, что ускользает от глаз окружающих.
415 — поэтический подтип, характерен для людей, способных к стихосложению, поэтической одаренности.
424 — данный подтип отличается тем, что все, за что берется, делает с чрезвычайной тщательностью.
Тип 4 — «Ученый» (307, 316, 325, 334, 343, 352, 361, 370). Люди данного типа в своих суждениях могут легко абстрагироваться от реальности, делать интересные теоретические обобщения, «на все иметь свою теорию». Как правило, они имеют склонность к ясному, последовательному мышлению, результатом которой является способность к установлению закономерностей, связей и отношений между происходящим. Этих людей часто можно застать в состоянии вдумчивой и напряженной работы мысли. Анализируя факты, они могут, в случае настойчивости и методичности, делать обобщения, превращая беспорядочную груду материала в стройное, разработанное здание науки, если наука является их увлечением или профессией. Такого рода способности помогают людям занять достойное место в различных областях деятельности. Так политический деятель с научным складом ума будет ценен тем, что хорошо ориентируется в сложном взаимодействии факторов, влияющих на общественную жизнь. Педагог может разобраться в сложных процессах усвоения знаний учащимися, а бизнесмен учитывать наиболее рискованные обстоятельства в своих сделках.
Анализируя факты, они могут, в случае настойчивости и методичности, делать обобщения, превращая беспорядочную груду материала в стройное, разработанное здание науки, если наука является их увлечением или профессией. Такого рода способности помогают людям занять достойное место в различных областях деятельности. Так политический деятель с научным складом ума будет ценен тем, что хорошо ориентируется в сложном взаимодействии факторов, влияющих на общественную жизнь. Педагог может разобраться в сложных процессах усвоения знаний учащимися, а бизнесмен учитывать наиболее рискованные обстоятельства в своих сделках.
Люди этого типа, обладая идейными интересами, над которыми работают сознательно и настойчиво, часто стремятся в своей карьере к научной деятельности, обобщая свой профессиональный опыт диссертационной работой или книгой. Они рациональны, тщательно продумывают свое поведение. Однако при всей рациональности обладают весьма значительными артистическими способностями, не теряются на сцене, знают, что нужно сделать, когда просят «сыграть что-либо». Тяготеют к «синтетическим» видам искусства: театру, кино, цирку, эстраде.
Тяготеют к «синтетическим» видам искусства: театру, кино, цирку, эстраде.
316 — в области науки это, как правило, «глобальные теоретики», занимающиеся междисциплинарными, методологическими или науковедческими проблемами; на практике из таких людей обычно получаются отличные координаторы различных служб.
325 — подтип с такой комбинацией часто тяготеет к биологии, медицине, ботанике. Любит выращивать растения, ухаживать за животными.
235 — подтип, часто встречающийся среди психологов;
217 — подтип, для которого характерны способности к техническому изобретательству.
244 — подтип, распространенный среди людей, пишущих сценарии, инструкции.
226 — подтип, характеризующийся установлением высочайшей планки в своих достижениях, а также высокими критериями оценки других людей.
Тип 6- «Изобретатель, конструктор» (109, 118, 127, 136, 145, 019,028, 037, 046). Люди данного типа обладают «технической жилкой», богатым воображением, пространственным видением, часто занимаются какими-либо техническими видами творчества, заняты в технических профессиях, склонны к конструированию, изобретательству. Придерживаются тех социальных норм, которые сами создают себе. Более ориентированы на предметную деятельность. Эмоциональны, одержимы собственными оригинальными идеями. Иногда их творчество проявляется не только в технической, материализованной, но и в интеллектуальной сфере, сфере идей. Люди этого типа обладают хорошей памятью, наблюдательностью. Внешний материальный мир их обычно интересует больше, чем субъективные переживания. Факты в их глазах имеют гораздо большую ценность, чем рассуждения и теории. Их воля и энергия устремляются на материализацию идей, изобретения, рационализацию, переустройство технических объектов. Обладая большой трудоспособностью, они часто добиваются значительных результатов в избранной ими деятельности. В их доме обычно много инструментов, поскольку их склонность мастерить, исправлять, ремонтировать, часто является не только их профессией, но и хобби.
Придерживаются тех социальных норм, которые сами создают себе. Более ориентированы на предметную деятельность. Эмоциональны, одержимы собственными оригинальными идеями. Иногда их творчество проявляется не только в технической, материализованной, но и в интеллектуальной сфере, сфере идей. Люди этого типа обладают хорошей памятью, наблюдательностью. Внешний материальный мир их обычно интересует больше, чем субъективные переживания. Факты в их глазах имеют гораздо большую ценность, чем рассуждения и теории. Их воля и энергия устремляются на материализацию идей, изобретения, рационализацию, переустройство технических объектов. Обладая большой трудоспособностью, они часто добиваются значительных результатов в избранной ими деятельности. В их доме обычно много инструментов, поскольку их склонность мастерить, исправлять, ремонтировать, часто является не только их профессией, но и хобби.
019 — подтип, обладающий способностями интересных форм взаимодействия с аудиторией, например, неподражаемый конферансье.
145 — подтип, увлекающийся композиторской деятельностью, или любящий петь, часто имеет музыкальное образование.
Тип 7 – «эмотивный» (550, 451, 460, 352, 361, 370, 253, 262, 271, 280,154, 163, 172, 181, 190, 055, 064, 073,082, 091). Люди данного типа обладают повышенным сопереживанием по отношению к другим людям. Они мягки и добросердечны. Тяжело переносят жестокие кадры фильма или выдержки из уголовной хроники, особенно чувствительны к несчастьям других, настолько, что какие-либо неприятные известия или события могут надолго выбить их из колеи. Боль, страдание других людей отзываются в них с особой силой, на это уходит много энергии, что часто мешает им реализовать свои возможности. Люди этого типа обладают сильной эмоциональной памятью, глубиной и устойчивостью чувств. Они обладают теплотой, сердечностью и отзывчивостью, видя своим назначением помогать людям в горе и нуждах.
Особенности их душевного склада позволяют назвать этих людей альтруистами, способными к самопожертвованию. Они отличаются скромностью, пытаясь умалить и скрыть свои заслуги, свое значение, не рассчитывая на похвалы со стороны окружающих. Кроткие, чуткие и деликатные, они не в состоянии ни сами обижаться, ни обидеть других. Зато в том, что касается их личных душевных убеждений, они могут быть непреклонны, не поддаются угрозам и не отступают ни на шаг от того, что считают справедливым. Они обладают способностями интуитивного проникновения в душевную жизнь и душевный склад другого человека. Они верят в возможность просвещения и идейно-нравственного перерождения человечества и обладают горячей и самоотверженной любовью к людям, терпящим нужду и лишения. Они деятельны и энергичны при осуществлении идей, которые их глубоко захватывают. Их милосердие часто не знает границ.
Они отличаются скромностью, пытаясь умалить и скрыть свои заслуги, свое значение, не рассчитывая на похвалы со стороны окружающих. Кроткие, чуткие и деликатные, они не в состоянии ни сами обижаться, ни обидеть других. Зато в том, что касается их личных душевных убеждений, они могут быть непреклонны, не поддаются угрозам и не отступают ни на шаг от того, что считают справедливым. Они обладают способностями интуитивного проникновения в душевную жизнь и душевный склад другого человека. Они верят в возможность просвещения и идейно-нравственного перерождения человечества и обладают горячей и самоотверженной любовью к людям, терпящим нужду и лишения. Они деятельны и энергичны при осуществлении идей, которые их глубоко захватывают. Их милосердие часто не знает границ.
Тип 8 — обладающий противоположными эмотивному типу свойствами (901, 802, 703, 604, 505, 406, 307, 208, 109). Это люди, испытывающие сочувствие к другим, однако придерживающиеся достаточно жестких требований. Таким образом внешне наблюдается сочувствие к другим, но в конкретных случаях они проявляют жесткую требовательность, порой чрезмерную. Из таких выходят чрезвычайно требовательные педагоги, которые «заставят» делать то, что нужно, невзирая на сопротивление, недуги и прочие причины, на которые ссылаются их ученики. Их можно встретить среди режиссеров, про которых говорят, что они «деспоты», среди руководителей, которые сверхтребовательно относятся к своим подчиненным. Людей этого типа можно часто встретить за прилавком магазина. Они, как правило, проявляют свою властность, даже грубость. Это их способы самоутверждения. Они хорошо чувствуют людей, на которых «можно давить» и не стесняются это делать. Стремление во что бы то ни стало возвыситься в жизни, сделать карьеру заставляет людей этого типа сосредоточить всю свою энергию и интеллектуальные возможности для достижения своих целей, пользуясь часто хитростью, лицемерием и изворотливостью. Обладая уязвленным самолюбием, иногда в самых простых и невинных шутках они видят обиду, насмешку или издевательство.
Таким образом внешне наблюдается сочувствие к другим, но в конкретных случаях они проявляют жесткую требовательность, порой чрезмерную. Из таких выходят чрезвычайно требовательные педагоги, которые «заставят» делать то, что нужно, невзирая на сопротивление, недуги и прочие причины, на которые ссылаются их ученики. Их можно встретить среди режиссеров, про которых говорят, что они «деспоты», среди руководителей, которые сверхтребовательно относятся к своим подчиненным. Людей этого типа можно часто встретить за прилавком магазина. Они, как правило, проявляют свою властность, даже грубость. Это их способы самоутверждения. Они хорошо чувствуют людей, на которых «можно давить» и не стесняются это делать. Стремление во что бы то ни стало возвыситься в жизни, сделать карьеру заставляет людей этого типа сосредоточить всю свою энергию и интеллектуальные возможности для достижения своих целей, пользуясь часто хитростью, лицемерием и изворотливостью. Обладая уязвленным самолюбием, иногда в самых простых и невинных шутках они видят обиду, насмешку или издевательство.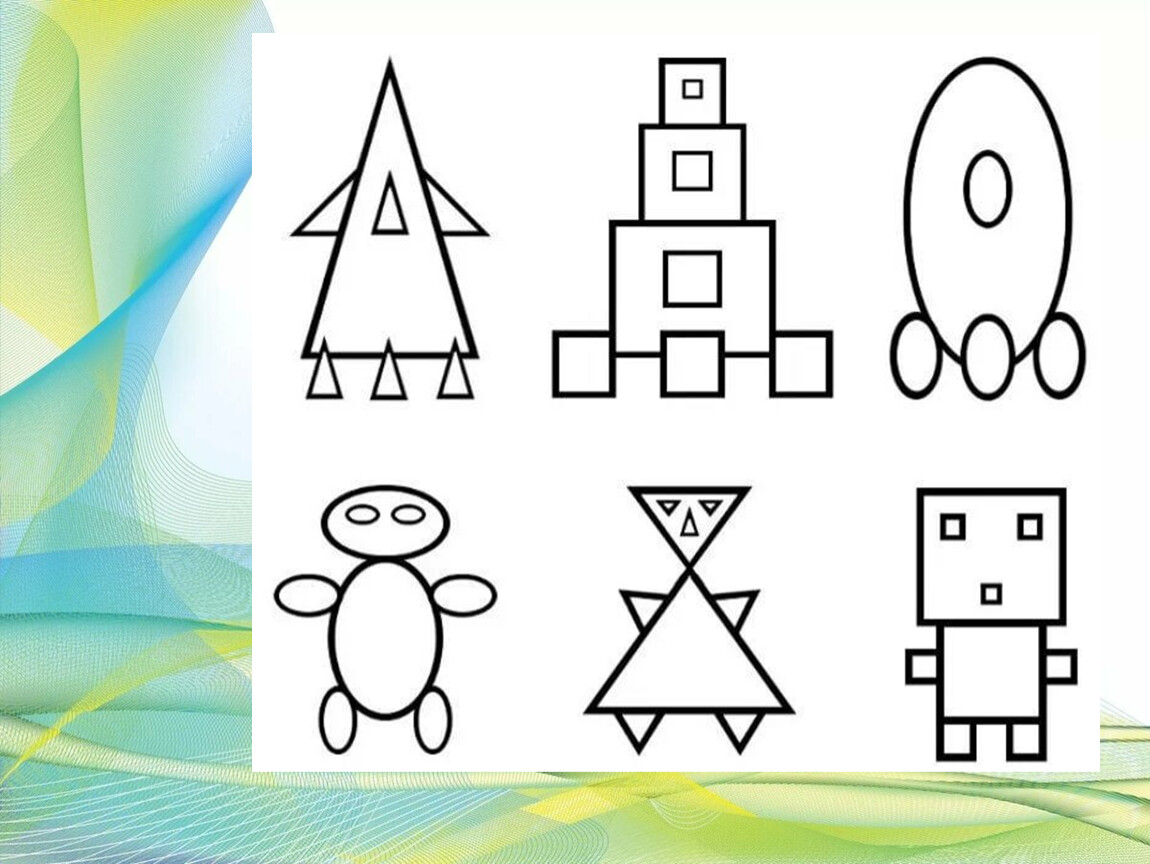 Они могут быть мстительными и стремятся отомстить обидчику.
Они могут быть мстительными и стремятся отомстить обидчику.
Этот проективный психогеометрический онлайн тест создан на основе модификации психоаналитиком А.Ф. Ермошиным идеографического теста Либиных. Тест базируется на комбинации трех принципов психографического анализа личности:
- предпочтения семантики основных геометрических форм
- конструктивные рисунки
- психографическое изображение фигуры человека
Пройдя тест, Вы узнаете тип Вашей личности и его описание, а также экспертную оценку, отношения с противоположным полом, свой общепсихологический статус и самоописание людей с таким же типом психики как у Вас (возможно, и Вы говорите что-то подобное).
Инструкция к тесту
Из геометрических фигур — треугольника, квадрата, круга — требуется составить рисунок человека. При этом, во-первых, нужно использовать ровно десять фигур, а, во-вторых, каждая геометрическая фигура (треугольник, квадрат, круг) должна использоваться хотя бы один раз. Фигуры можно масштабировать, вращать, накладывать друг на друга. Особой аккуратности и художественной достоверности не требуется. Рисуйте так, как Вам подсказывает Ваша фантазия. Когда все десять фигур будут использованы, появится кнопка «Результат теста».
Фигуры можно масштабировать, вращать, накладывать друг на друга. Особой аккуратности и художественной достоверности не требуется. Рисуйте так, как Вам подсказывает Ваша фантазия. Когда все десять фигур будут использованы, появится кнопка «Результат теста».
Управление фигурами
перетаскивание: клик на элементе + перемещение мыши
масштаб: указатель мыши над фигурой + колесико мыши
масштаб по ширине: клавиша «W» + колесико мыши
масштаб по высоте: клавиша «H» + колесико мыши
вращение: клавиша «R» + колесико мыши
добавить фигуру: перетащите фигуру в рабочую область (прямоугольник бледно-желтого цвета)
удалить фигуру: перетащите фигуру за пределы рабочей области
14.11.2016 119092 +928
Пройти бесплатные психологические тесты——
Умеете ли вы составлять животных из геометрических фигур?
Никогда не пробовали?
Тогда стоит посмотреть картинки на сайте, где из геометрических фигур сложены разнообразные животные. Предложите эти рисунки своим детям: наверняка они оценят их оригинальность.
Предложите эти рисунки своим детям: наверняка они оценят их оригинальность.
Как использовать картинки в работе с детьми
Вполне понятно, что встает вопрос: одно дело художники, но зачем детям такое видение мира?
Конечно, картинки с животными из геометрических фигур не ставят целью навязать малышу неординарное видение мира. Однако почему бы ни показать, что и такая трактовка всего, что нас окружает, возможна.
По картинкам можно интересно и увлекательно изучать названия геометрических фигур. От простого показа и повторения ребенок быстро устает и начинает отказываться от занятий, даже если их проводит мама в домашних условиях. Другое дело, если фигуры необходимо отыскать в животных. Тут просыпается неподдельное любопытство.
Когда вы полностью изучите с ребенком названия фигур и их внешний вид, попросите ребенка проявить свое видение мира. Пусть для примера будет взято животное или любой предмет.
Спросите: на какую геометрическую фигуру он похож.
Такие упражнения:
- — развивают наблюдательность;
- — совершенствуют логическое и пространственное мышление;
- — способствуют видению скрытого за внешней оболочкой предмета.
Малыш учится видеть и наблюдать то, что не могут или не умеют видеть другие . Это ли не воспитание художника и творческой личности?
А можно поиграть в обратную игру. Представьте, что вы художники-абстракционисты. Пусть один из вас нарисует что-нибудь, состоящее из геометрических фигур, а другой попытается отгадать, что нарисовано. Живописцы постмодернизма часто зашифровывали свои рисунки на полотне, заполненной квадратами, прямоугольниками, трапециями… такие же головоломки предлагали ранее детские журналы.
Вы и сами можете создать такую головоломку: нужно лишь немного фантазии и взгляд на мир сквозь призму геометрии.
Примеры страниц тетради с аппликациями для детей от 1 года до 3 лет.
Как понять Геометрию? Основы с нуля
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
- симметрия
- равенство или подобие составных частей.
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
- Точки лежат на данной прямой. Или еще говорят, что прямая проходит через эти точки — на рисунке выше такими точками являются А и В. При решении задач для краткости используют запись A ∈ a (читается так: точка А принадлежит прямой a или точка А лежит на прямой a), аналогично будет и для точки В (B ∈ b).
- Точки не лежат на данной прямой. Говорят так: прямая не проходит через эти точки — на рисунке такими точками являются С и D. При решении задач для краткости используют запись C ∉ a (читается так: точка С не принадлежит прямой a или точка С не лежит на прямой a), аналогично будет и для точки D (D ∉ a).
Важно знать
Через любые две точки можно провести прямую и притом только одну.
Если рассмотреть две прямые, то возможны два варианта их расположения:
- Прямые пересекаются, то есть имеют одну общую точку.

Для записи пересекающихся прямых используют специальный знак — ∩ , то есть a ∩ b (читают: прямая a пересекает прямую b).
- Прямые не пересекаются, то есть не имеют общих точек.
Для записи не пересекающихся прямых используют специальный знак — ,
то есть m n (читают: прямая m не пересекает прямую n).
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
- Луч ОА, точка О — начало луча ОА; конца у луча ОА нет.
- Луч ОВ, точка О — начало луча ОВ; конца у луча ОВ нет.
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
Есть разные виды углов, выделим самые часто встречающиеся:
- Если градусная мера угла меньше 90° — угол острый.

- Если градусная мера угла равна 90° — угол прямой.
- Если градусная мера угла больше 90°, но меньше 180° — угол тупой.
- Если градусная мера угла равна 180° — угол развернутый.
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает..jpg)
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
- две стороны и угол между ними;
- два угла и сторону;
- три стороны.
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Неравенство треугольника Сумма любых двух сторон треугольника больше его третьей стороны. |
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
Первый признак равенства треугольников звучит так:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
ΔABC = ΔA1B1C1, так как AC = A1C1, AB = A1B1 и ∠A = ∠A1 (∠A лежит между сторонами AC и AB, а ∠A1 между A1C1 и A1B1).
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
ΔABC = ΔA1B1C1, так как AB = A1B1, ∠A = ∠A1, ∠B = ∠B1.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
ΔABC = ΔA1B1C1, так как AC = A1C1, AB = A1B1 и BC = B1C1.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
∠ А = A1, ∠ В = B1, ∠ С = C1,
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾.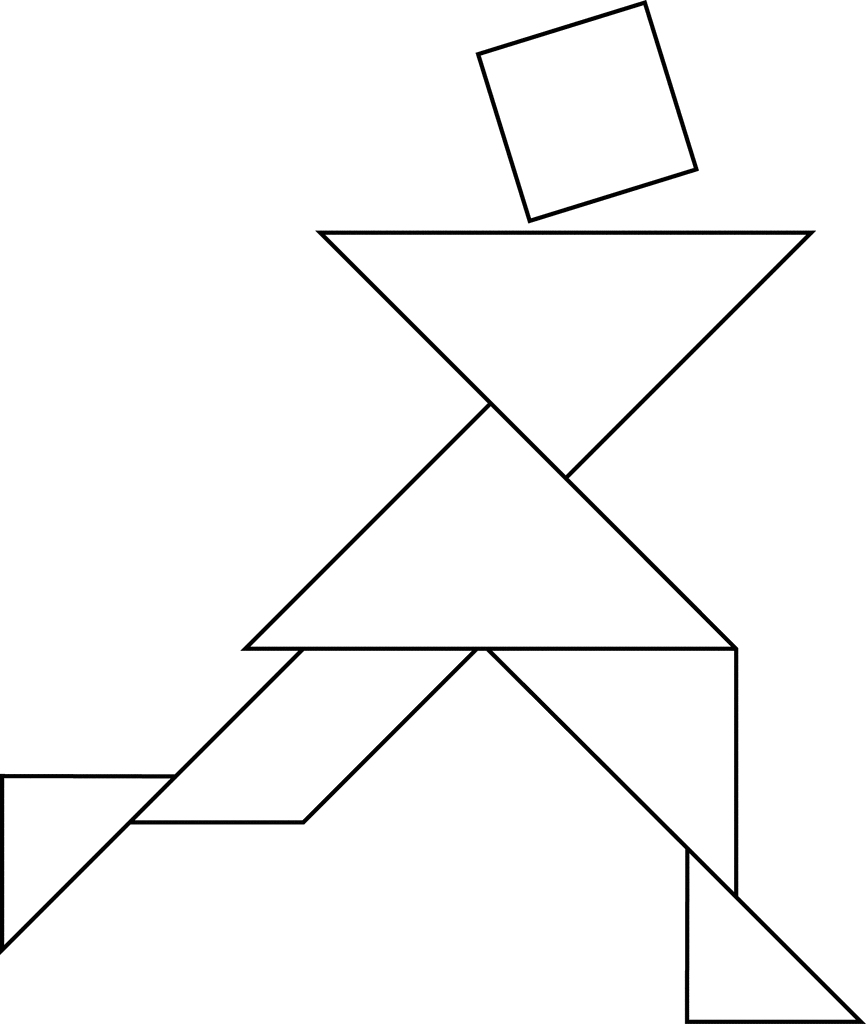 На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Теорема о средней линии звучит так:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
Свойства прямоугольного треугольника
- Теорема Пифагора: сумма длин квадратов катетов равна квадрату гипотенузы
- Свойство медианы: медиана, проведенная из вершины с прямым углом, равняется половине гипотенузы.
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
Вот эти случаи:
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d < r), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности (d = r), то прямая и окружность имеют только одну общую точку. В этом случае прямая называется касательной по отношению к окружности.
- Если расстояние от центра окружности до прямой больше радиуса окружности (d > r), то прямая и окружность не имеют общих точек.
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Методика «Учебная деятельность» Л.И. Цеханской
Методика «Учебная деятельность» Л. И. Цеханской
И. ЦеханскойЦель: определение уровня овладения элементами учения, доступными дошкольникам: умение подчинять свои действия правилу, слушать и последовательно выполнять указания взрослого.
Ребенку дается задание – составить узор под диктовку взрослого путем соединения расположенных рядами фигурок с соблюдением заранее заданных правил.
Рис. 1. Материал для заданий методики «Учебная деятельность»
(а – образец узора для первой страницы, б – материал для выполнения заданий)
Материал. Тетрадь, состоящая из четырех страниц. На каждой странице изображены 3 ряда мелких геометрических фигур размером 2×2 мм. Верхний ряд состоит из треугольников, средний – из кружков, нижний – из квадратов. Фигурки верхнего и нижнего рядов расположены друг под другом, среднего – в промежутках между ними (см. рис. 1, б). В верхней части первой страницы расположена кроме того короткая полоска из этих фигур, на которой дан образец узора (рис.1, а).
Детям предлагается нарисовать несколько узоров под диктовку, соединяя геометрические фигуры по трем определенным правилам. Первая страница предназначена для того, чтобы дети познакомились с правилами и научились рисовать под диктовку взрослого.
Первая страница предназначена для того, чтобы дети познакомились с правилами и научились рисовать под диктовку взрослого.
Инструкция. Детям говорится: «Мы будем учиться рисовать узор. У вас на листочке нарисованы ряды треугольников, квадратов и кружков. Вы будете соединять треугольники и квадраты, чтобы получился узор. Надо внимательно слушать и делать то, что я буду говорить. У нас будут такие три правила:
- два треугольника, два квадрата или квадрат с треугольником можно соединять только через кружок;
- линия узора должна идти только вперед;
- каждое новое соединение надо начинать с той фигурки, на которой остановилась линия, тогда линия будет непрерывной и в узоре не получится промежутков.

В процессе обучения дети производят 4 соединения, а взрослый проверяет выполнение задания и в случае необходимости исправляет ошибки и объясняет ребенку, в чем тот ошибся. После этого детям говорится: «Теперь вы будете рисовать на другом листочке. Вы должны внимательно слушать и соединять те фигуры, которые я буду называть, но не забывайте о правилах. (Правила соединения повторяются.) Если ошибетесь, то не исправляйте ошибку, а начинайте со следующей фигурки». Взрослый диктует детям последовательность соединения фигурок медленно, но не повторяя одно и то же дважды. После первой серии следуют вторая и третья, которые отличаются только характером узора (см. рис.2).
Рис. 2. Образцы правильного выполнения заданий методики «Учебная деятельность»
(а – вводная серия, б – первая серия, в – вторая серия, г – третья серия)
Ошибки могут быть двух типов. Первый тип связан с неточным выполнением предписаний диктанта: неправильно выбраны элементы соединения, некоторые соединения повторяются, наблюдается пропуск отдельных элементов.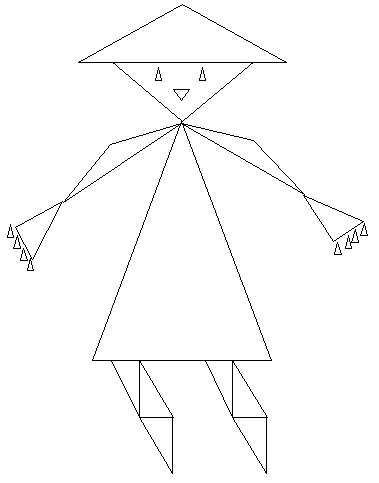
Ошибки второго типа допускаются за счет нарушения правил: соединение фигур минуя кружок, «разрывы» между соединениями, соединение фигур, находящихся одна под другой.
Данная методика выявляет продвижение ребенка в овладении предпосылками учебной деятельности, которое выражается в постепенном совершенствовании необходимых для выполнения задания умений. Для более дифференцированной характеристики таких умений необходимо обратиться к анализу допущенных ребенком ошибок.
Каждое правильное соединение оценивается в два балла. Правильным считается соединение, соответствующее диктанту. Штрафные очки (по одному) начисляются за лишние соединения, не предусмотренные диктантом (кроме находящихся в начале и в конце узора, т.е. предваряющих диктант и следующих за ним), а также за «разрывы» между правильными соединениями (пропуски «зон» соединения).
Все остальные виды ошибок не учитываются вовсе, так как их наличие автоматически снижает количество начисляемых баллов.
Реальное количество баллов в каждой серии будет равно разнице между набранными и штрафными баллами. Максимальное количество баллов в каждой серии – 24, а за выполнение всего задания – 72.
| Методика «Учебная деятельность» | Уровень | |
| сырые | стандартные | |
| 72 | 13 | Высокий |
| 71-68 | 11 | |
| 67-64 | 10 | |
| 63-59 | 9 | Средний |
| 58-52 | 8 | |
| 51-43 | 7 | |
| 42-35 | 6 | |
| 34-18 | 5 | Низкий |
| 17-4 | 4 | |
| 3-1 | 3 | |
| 0 | 2 | |
Примечание. По результатам стандартизации 1995 года обнаружилось, что методика «Учебная деятельность» недостаточно дифференцирует сильных детей. Это объясняется тем, что в последнее время изменилось содержание образовательно-воспитательной работы в детских садах, возникла устойчивая тенденция к усилению учебной работы с детьми старших дошкольных возрастов. Это приводит к более раннему развитию предпосылок учебной деятельности, в частности, умения действовать по правилу.
Это объясняется тем, что в последнее время изменилось содержание образовательно-воспитательной работы в детских садах, возникла устойчивая тенденция к усилению учебной работы с детьми старших дошкольных возрастов. Это приводит к более раннему развитию предпосылок учебной деятельности, в частности, умения действовать по правилу.
Источник:
|
Виды треугольников. 2-й класс
Задачи:
- Образовательная: Повторить изученные геометрические фигуры, закрепить умения строить различные виды треугольников, находить периметр треугольника
- Развивающая: развивать внимание, память, воображение, логическое мышление.
- Воспитательная : Привитие интереса к предмету “геометрия”, воспитание любви к домашним животным.

Оборудование: рабочая тетрадь, чертежные инструменты, геометрические фигуры, компьютер, проектор, экран.
Ход урока
I. Организационный момент:
Учитель: Сегодня на уроке мы вспомним, какие геометрические фигуры вы знаете, подробно остановимся на треугольниках, будем моделировать на их основе разные предметы. Презентация. (Слайд 1).
– А готовность ребят к уроку я проверю, загадав загадки. Их подготовил для вас ученый Ластик, который весь год учился с вами строить различные геометрические фигуры, выполнять логические задания.
- То я в клетку, то в линейку
Написать на мне сумей-ка,
Можешь и нарисовать
Что такое Я? (Тетрадь.)
- Палочка волшебная есть у меня, друзья,
Палочкой этой
Могу построить я
Башню, дом, и самолет,
И большущий пароход. (Карандаш.)
(Карандаш.)
- В тетради я бываю
Косая и прямая,
В другом своем значении –
Я – планка для черчения.
И, наконец, порою,
В шеренгу вас построю. (Линейка.)
II. Задание на внимание:
Учитель: Чтобы узнать, какие вы внимательные, ученый Ластик предлагает вам нарисовать в тетради следующий рисунок по памяти.
(3–5 сек для запоминания, рисуют дети в тетрадях.)
III. Повторение знаний о геометрических фигурах:
Учитель: Какие геометрические фигуры вы нарисовали в задании на внимание?
Дети: Круг, квадрат, треугольник, прямоугольник…..
Учитель: Почему их так назвали?
– Давайте вспомним стихи об этих фигурах,
- Три вершинки, три угла, (Слайд 2).
Три сторонки – вот и я.
- Познакомьтесь и со мной, (Слайд 3).

Каждый угол мой прямой.
Все четыре стороны-
Одинаковой длины.
- Нет углов у меня (Слайд 4).
и похож на блюдце я,
На тарелку, и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья?
- Четыре палочки сложил, (Слайд 5).
Прямоугольник получил,
Прямоугольник квадрата длиннее,
Фигура попроще, рисуем смелее.
IV. Повторение и обобщение изученного материала по теме:“ треугольники”.
Учитель: Вспомните, пожалуйста, какие виды треугольников вы знаете?
– По какому признаку мы их так называли?
Дети: По углу: – остроугольные
– прямоугольные,
– тупоугольные.
Практическая работа:
– Начертите такие треугольники по одному в своих тетрадях.
(2-е ребят работают у доски).
– А теперь покажите и назовите номера треугольников по этому признаку:
(Слайд 6).
1.2 – прямоугольные треугольники.
3.5.6. – остроугольные треугольники.
4.7. – тупоугольные треугольники.
Учитель: Что характерно для каждого вида?
Дети: У тупоугольных и прямоугольных 1 угол прямой или тупой, а остальные острые; У остроугольных – все углы острые.
в) По сторонам:
разносторонние треугольники,
равносторонние треугольники,
равнобедренные треугольники.
Учитель: Назовите номера этих треугольников и почему их так называют:
Дети:
3.6. равносторонние – все стороны равны.
1.2. разносторонние – все стороны разные.
4.5.7. равнобедренные – по 2 одинаковых стороны.
Учитель: Найдите периметр любого треугольника, построенного в вашей тетради. Какая формула вам в этом поможет?
V. Физкультминутка. (Слайд 7).
Рыбки плавают в воде,
Рыбки роются в песке,
То нырнут, то вынырнут,
Рыбки плавают в воде.
Воспитательный момент.
Учитель: У кого есть дома рыбки в аквариуме? Чем вы кормите, как ухаживаете за ними?
VI. Задание на развитие воображения.
– Выложите из треугольников, которые у вас на парте рыбку.
– Какие предметы вы можете еще выложить из данных треугольников?
(Елка, лодочка, бантик, песочные часы.)
VII. Задания на логическое мышление.
– Раздели фигуры на группы.
VIII. Задание на внимание: (Слайд 8).
У пушистой кошки Мурки треугольные фигурки.
Призадумалась она – сосчитать их все должна.
Вы ребята, помогайте, треугольники считайте. (10 штук).
IХ. Итог урока.
– Ученый Ластик с удовольствием выполнял с вами задания. Какое задание вам
больше всего понравилось выполнять?
– Что показалось трудным для выполнения?
– Какая геометрическая фигура встречалась на уроке чаще других?
Х. Домашнее задание.
Домашнее задание.
Дорисовать предметы из треугольника.
Рисуем мелками!
Вот и настало долгожданное тепло! А значит можно брать яркие мелки и вместе с детворой идти рисовать на асфальте! Интерес к мелкам у детей просыпается лет с трех, до этого больше интересно жевать, а не рисовать, все тянут в рот.
Начинаем рисовать с простых деталей, легких фигур — треугольник, круг. Дайте детям самим рисовать, да каляки-маляки, но это тоже игра, тоже развитие.
Когда дети вдоволь «нарисуются» можно уже и обучение включать в вашу игру.
1. Изучаем круг. Нарисуйте круг. Из него можно сделать массу интересных вещей – часы, мячик, мордашки эмоций. Обратите внимание малыша на то, что у круга нет углов (поэтому мячик легко катится). «Нанижите» бусинки-кружочки на нарисованную ниточку. Начните рисовать бусы для бабушки, предложите малышу продолжить. Можно сочетать с изучением цветов. Рисуйте разноцветные бусинки, поиграйте в игру продолжи ряд – взрослый рисует красную, синюю, белую бусинку, а малыш продолжает рисовать цветную цепочку в том же порядке. Рисуйте пуговицы с разным количеством дырочек, сравнивайте их, находите одинаковые. Дальше можно нарисовать кофточку и предложить малышу «пришить» пуговицы. Еще нарисуйте плодовое дерево, а малыш дорисует яблоки. Считайте ваши яблочки, говорите о том, какие находятся выше, какие ниже, справа, слева и т.д.
Рисуйте пуговицы с разным количеством дырочек, сравнивайте их, находите одинаковые. Дальше можно нарисовать кофточку и предложить малышу «пришить» пуговицы. Еще нарисуйте плодовое дерево, а малыш дорисует яблоки. Считайте ваши яблочки, говорите о том, какие находятся выше, какие ниже, справа, слева и т.д.
2. Изучаем овал. Нарисуйте овал, скажите ребенку, что это дупло, а он белочка. Пусть попрыгает из одного дупла в другой. Прыгать можно в дупло, из дупла. Заодно проговаривайте, что малыш внутри или снаружи. Можно разукрасить овалы. Предложите ребенку прыгнуть в красное дупло, в синее, позже не в красное и не в желтое (малыш должен сообразить в какое). Овалы сделайте разного размера. Теперь можно усложнить задачу: «Прыгни не в синее и не в маленькое дупло. Прыгни в дупло, которое слева от желтого» и т.д.
3. Изучаем треугольник. Скажите крохе, что треугольник – это платочек. Но он у нас некрасивый. Предложите его разукрасить. И рисуйте на нем все, что хотите. Если рисуете различные геометрические фигуры, то расскажите малышу, что они находятся внутри треугольника. Из нескольких треугольников нарисуйте елку. Их можно сделать много и разного размера – это будет лес (понятия большой, средний, маленький). Еще пусть треугольник превратится у вас в гору. Изучаем понятия вершина и подножье горы. Предложите малышу пальчиками дойти до самой верхушки – чем вам не пальчиковая гимнастика?
Если рисуете различные геометрические фигуры, то расскажите малышу, что они находятся внутри треугольника. Из нескольких треугольников нарисуйте елку. Их можно сделать много и разного размера – это будет лес (понятия большой, средний, маленький). Еще пусть треугольник превратится у вас в гору. Изучаем понятия вершина и подножье горы. Предложите малышу пальчиками дойти до самой верхушки – чем вам не пальчиковая гимнастика?
4. Изучаем квадрат. Теперь квадраты – это клетки для животных в зоопарке. Расселите туда животных. Можно нарисовать их, а можно и посадить выдуманных (палочки, веточки, листики, камешки). Еще поиграйте в игру «Робот». Нарисуйте ряд квадратиков. Предложите малышу быть роботом – он будет выполнять ваши команды: « Вперед на один квадратик, назад на два квадратика, влево на один». Потом поменяйтесь местами.
5. Изучаем прямоугольник. Нарисуйте многоэтажный дом. Обязательно проговаривайте название фигуры. Скажите, что дом прямоугольный, а крыша треугольная. Можно нарисовать в этом доме окошки разной формы. Поселите в квартиры жильцов (палочки, листики, все, что угодно). Посчитайте, сколько этажей в вашем доме. Пусть ребенок найдет того, кто живет под прямоугольником, выше квадрата, между двумя овалами, слева от трапеции, справа то круга и т.д. Можно нарисовать несколько домов – это будет город, нарисуйте дороги, светофор. Смотрите, какой формы различные предметы. Пусть по вашим дорогам ездят игрушечные машины, ходят куклы-пешеходы. Еще один вариант игры с прямоугольником – представить, что это ковер-самолет. Скажите ребенку, что он волшебный. А для того, чтобы он мог лететь, его нужно разукрасить. Еще можно предложить другим геометрическим фигурам покататься на ковре-самолете. Пусть малыш «посадит» их.
Можно нарисовать в этом доме окошки разной формы. Поселите в квартиры жильцов (палочки, листики, все, что угодно). Посчитайте, сколько этажей в вашем доме. Пусть ребенок найдет того, кто живет под прямоугольником, выше квадрата, между двумя овалами, слева от трапеции, справа то круга и т.д. Можно нарисовать несколько домов – это будет город, нарисуйте дороги, светофор. Смотрите, какой формы различные предметы. Пусть по вашим дорогам ездят игрушечные машины, ходят куклы-пешеходы. Еще один вариант игры с прямоугольником – представить, что это ковер-самолет. Скажите ребенку, что он волшебный. А для того, чтобы он мог лететь, его нужно разукрасить. Еще можно предложить другим геометрическим фигурам покататься на ковре-самолете. Пусть малыш «посадит» их.
6. Изучаем трапецию. Расскажите малышу, что трапеция – это мостик через реку. Нарисуйте трапеции разного размера и реки разные (широкие, средние, узкие). Предложите малышу подобрать к каждой реке свой мостик. А когда задание успешно выполнено, покатайте по мостам машины. Еще можно одеть куклу, причем одежда должна быть из геометрических фигур. Например, кофта – прямоугольник, юбка – трапеция. Третий вариант: трапеция – это снежная горка. Покатайтесь на санках (листике) с горы, а пассажиры – пальчики малыша.
Еще можно одеть куклу, причем одежда должна быть из геометрических фигур. Например, кофта – прямоугольник, юбка – трапеция. Третий вариант: трапеция – это снежная горка. Покатайтесь на санках (листике) с горы, а пассажиры – пальчики малыша.
7. Изучаем линии. Проведите прямую линию, пусть малыш продолжит ее рисовать. Нарисуйте прямоугольник (это будет забор), пусть кроха проводит вертикальные линии – рисует дощечки забора. Верхушки – небольшие треугольники. Волнистая линия – волны на море. Отличный способ поговорить о морских жителях и растительности.
В данные игры можно играть не только на улице, но и дома с карандашами, фломастерами, красками. Приятных вам игр и интересного изучения геометрических фигур!
Урок 28. треугольники — Математика — 5 класс
Математика
5 класс
Урок №28
Треугольники
Перечень рассматриваемых вопросов:
— треугольники;
— элементы треугольника;
— виды треугольников.
Тезаурус
Треугольник – это геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых между собой.
Периметр треугольника – сумма длин всех сторон треугольника.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Среди всех многоугольников наименьшее число сторон и углов имеет треугольник. Он является простейшей фигурой, и казалось бы, его изучение не может быть интересным. Однако существует множество видов треугольников. О них мы и поговорим.
О них мы и поговорим.
Отметим какие-нибудь три точки, не лежащие на одной прямой – например, А, В, С. Соединим их с помощью линейки. Получим геометрическую фигуру, которая называется треугольником. Отмеченные три точки А, В, С называются вершинами, отрезки АВ, ВС, АС – сторонами треугольника, а углы А, В, С – углами треугольника.
Все треугольники можно разделить на группы по сторонам:
— если равных сторон нет – это разносторонний треугольник;
— если две стороны равны – это равнобедренный треугольник;
— если все стороны равны – это равносторонний треугольник.
Треугольники можно разделить на группы в зависимости от углов:
— если есть тупой угол – это тупоугольный треугольник;
— если все углы острые – это остроугольный треугольник;
— если есть прямой угол – это прямоугольный треугольник.
Треугольники, соединяясь друг с другом, могут образовывать другие фигуры.
Попробуем нарисовать прямоугольный треугольник на листе в клетку.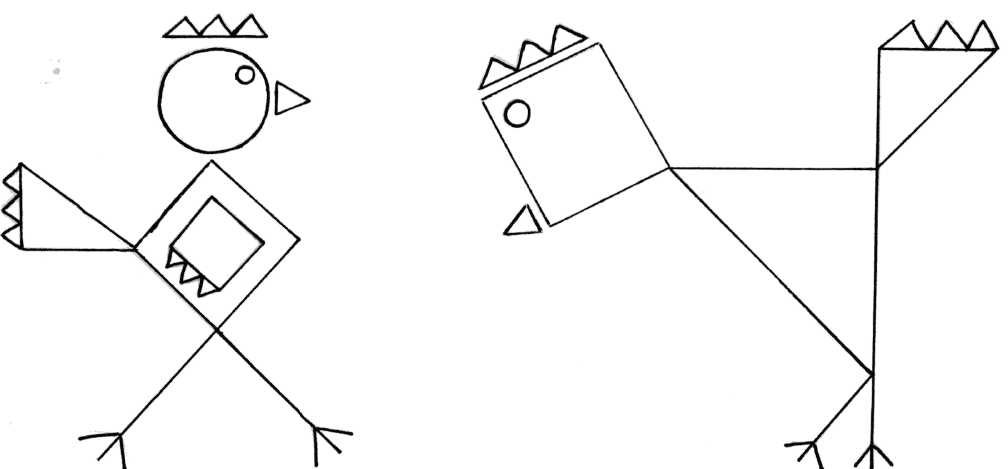 Мы знаем, что сторона стандартной клетки – пять миллиметров, следовательно, две клетки – это один сантиметр.
Мы знаем, что сторона стандартной клетки – пять миллиметров, следовательно, две клетки – это один сантиметр.
По сторонам клетки проведём отрезки заданной длины из одной точки. В нашем случае из точки А проведём отрезки длиной четыре и три сантиметра, что соответствует восьми и шести клеткам. На концах отрезков поставим точки В и С и соединим их между собой. Таким образом, мы построили прямоугольный треугольник АВС.
А теперь рассмотрим свойства треугольников. Одно из них – жёсткость. Это свойство заключается в том, что, если взять три рейки и соединить их попарно, то получится треугольник, изменить форму которого можно лишь сломав рейку.
Рассмотрим ещё одно свойство треугольников. Оно заключается в том, что длина каждой стороны треугольника всегда меньше суммы двух других сторон.
Это свойство можно использовать для проверки возможности построения треугольника по определённым сторонам. То есть, если свойство не выполняется, то такого треугольника не может быть.
Если мы знаем стороны треугольника, то можем найти его периметр как сумму длин всех его сторон. Например, периметр треугольника АВС – это сумма сторон АВ, АС и ВС.
Р = АВ + ВС + АС
Измерим с помощью линейки стороны треугольника и рассчитаем его периметр.
По результатам измерения стороны, соответственно, равны пяти, шести и семи сантиметрам.
Значит, периметр равен восемнадцати сантиметрам, то есть сумме всех сторон.
Говоря о треугольниках, стоит упомянуть, что они бывают как одинаковыми, так и разными. Определить, равные или разные треугольники, можно способом наложения. Если треугольник полностью накладывается на другой треугольник, такие треугольники равны. В противном случае треугольники не будут равными.
Рисунки из треугольников
Многие люди, как маленькие, так и взрослые, очень любят рисовать. Но иногда одного желания рисовать недостаточно. Для того чтобы облегчить процесс создания простейших картинок, инженер Эриф Мд. Вейлиула Байан, разработчик инновационного контента для детей, создал схемы, по которым, имея базовые навыки работы с чертёжными инструментами, можно создать милые и забавные картинки с животными и птицами.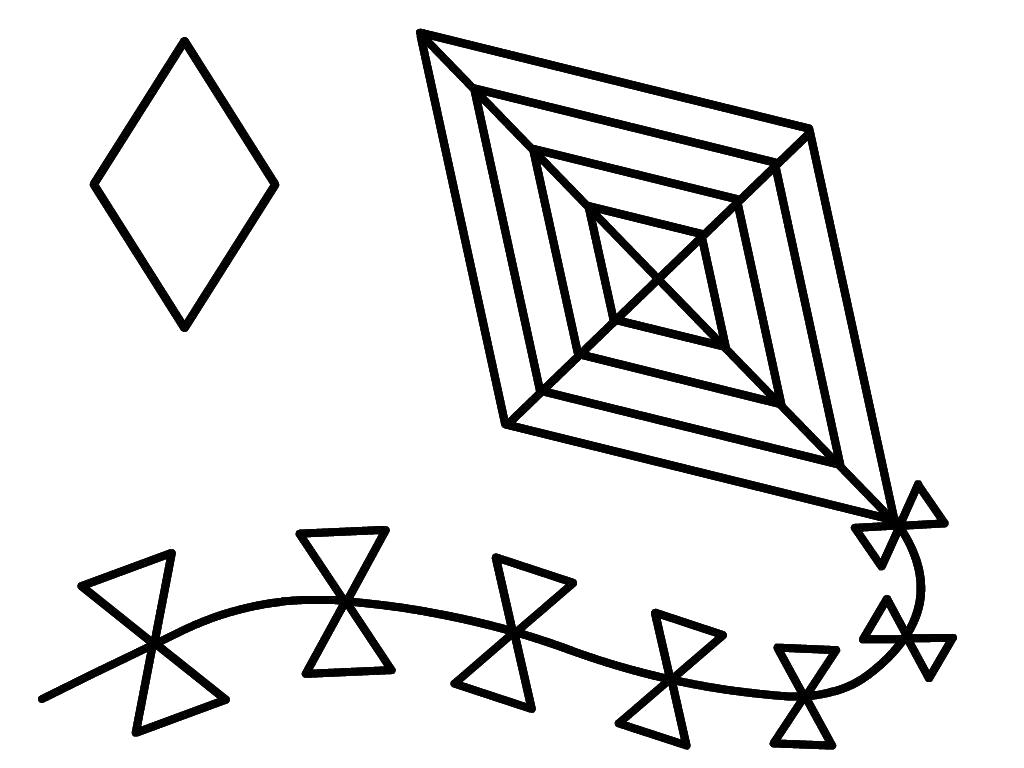
Похожие схемы частично есть в открытом доступе, поэтому каждый желающий может приобщиться к миру изобразительного искусства через поэтапное прорисовывание простых картинок.
Тренировочные задания
№ 1. В треугольнике все стороны равны 15 см. Чему равен периметр треугольника?
Решение: для нахождения периметра используем формулу Р = АВ + АС + ВС.
Так как у этого треугольника стороны равны, то Р = 15 см + 15 см + 15 см = 45 см
№ 2. Сопоставьте треугольники с их видами (по углам).
Решение: в задаче требуется сопоставить треугольники со следующими видами по углам: остроугольный, прямоугольный, тупоугольный. Согласно определению, прямоугольный треугольник имеет один угол 90 градусов: этому треугольнику соответствует второй треугольник. А тупоугольный треугольник имеет один угол больше 90 градусов: он отображён третьим по счёту. Как мы знаем, остроугольный треугольник имеет три угла меньше 90 градусов, так что в этом случае подходит треугольник, изображённый первым слева.
Конспект НОД для старшей группы «Веселые геометрические фигуры» (Нетрадиционная техника рисования)
Конспект НОД
по ОО «Художественно – эстетическое развитие»
Рисуем по шаблону «Веселые геометрические фигуры»
Старшая группа
Цель занятия: познакомить детей с новой техникой рисования — шаблонография.
Задачи:
— учить детей рисовать, используя шаблоны геометрических фигур;
— расширять представление детей о строении сложных предметов;
— Развивать воображение, координацию движений, мелкую моторику.
Материалы для занятий: альбомный лист, шаблоны геометрических фигур разного размера (деревянные кубики: треугольник, квадрат, круг, прямоугольник), простой карандаш, цветные карандаши.
Предварительная работа: создание из геометрических фигур объектов на фланелеграфе, из цветного картона, из счетных палочек.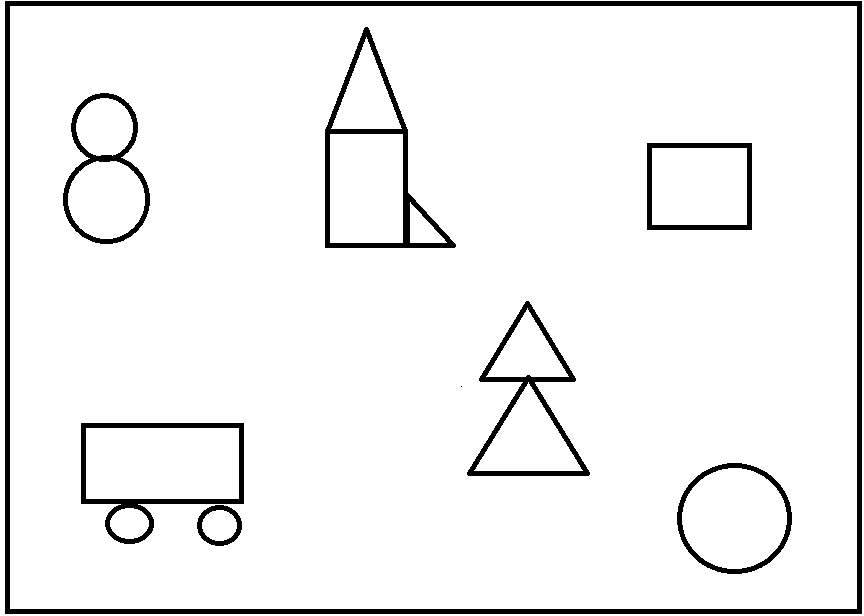
Ход занятия.
Воспитатель: наш мир состоит из множества предметов, вещей, и если внимательно на них посмотреть, можно увидеть, что все они имеют определенную форму. Какие вы знаете геометрические формы?
Дети: круг, квадрат, треугольник, прямоугольник, овал.
Воспитатель предлагает детям отгадать загадки: назвать отгадку и определить форму предмета, о котором идет речь.
Квадрат.
В нашей комнате есть волшебное окно, в том окошечке – кино.
(Телевизор)
Набита пухом, лежит под ухом…
(Подушка)
В доме есть оно, называется …
(Окно)
Круг.
На небе круглая она, ночью в окно к нам светит…
(Луна)
Круглый бок, румяный бок, покатился …
(Колобок)
Любит он на солнце греться, в полосатое одеться, и, как сахар, он на вкус, а зовут его …
(Арбуз)
Треугольник.
Уступая ветру в споре, увлекает судно в море.
(Парус)
Крыльев нет у этой птицы, но нельзя не подивиться: лишь распустит птица хвост – и поднимется до звезд.
(Ракета)
Подними глаза повыше, антенну увидишь ты на нашей…
(Крыша)
Прямоугольник.
Она ни в город, ни во двор не просится гулять, на миг заглянет в коридор и в комнату опять.
(Дверь)
Много, много окон в нем, это большой и красивый наш…
(Дом)
Не куст, а с листочками, не рубашка, а сшита, не человек, а рассказывает.
(Книга)
Разгадывание загадок подкрепляется рисунками – разгадками, где хорошо просматривается геометрическая форма.
Воспитатель. А вот некоторые предметы имеют сложное строение, они могут состоять сразу из нескольких и разных геометрических фигур.
Приводится пример: домик, снеговик, машина, светофор, шкаф и др. Предлагается детям привести свои примеры.
Физкультминутка.
Покажу вам треугольник, будем весело шагать,
Вы увидели квадрат, будем дружно приседать,
А вот это вот кружок, прыгай веселей дружок.
Воспитатель показывает фигуры, а дети выполняют движения. Далее показывает фигуры без слов, в другом порядке, дети выполняют движения соответствующие каждой фигуре.
Далее показывает фигуры без слов, в другом порядке, дети выполняют движения соответствующие каждой фигуре.
Воспитатель. Мы с вами убедились, что все предметы вокруг нас в своем строении имеют одну или несколько разных геометрических форм. Сегодня мы с вами будем составлять изображение объектов из готовых геометрических фигур – шаблонов. А послужат нам шаблонами ваши кубики. Отберите 4 формы – треугольник, квадрат, прямоугольник, круг, но только мы не будем с ними играть, а будем их обводить, и в результате у вас должно получиться изображение целой фигуры.
Практическая часть.
Воспитатель. Давайте пофантазируем над вашими будущими рисунками, какие они у вас будут, из каких объектов будут состоять, а эти объекты из каких геометрических форм будут состоять.
Дети продумывают содержание рисунка, если дети затрудняются, педагог помогает определиться с сюжетом.
Воспитатель показывает и объясняет последовательность выполнения работы.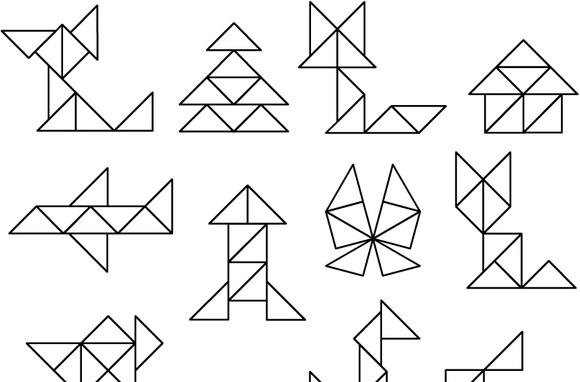
- Начинать создание объекта в следующей последовательности: вначале нужно обрисовать основную форму, самую крупную, и только потом переходить к деталям.
- Простым карандашом обрисовать геометрические формы — составляющие персонажа или предмета – таким образом, чтобы готовое изображение представляло единое целое.
- Каждый шаблон необходимо как можно ближе прикладывать к нарисованному контуру предыдущей формы, не оставляя между ними промежутков. Одной рукой плотно придерживать кубик на поверхности листа, а другой рукой карандашом обводить его вокруг.
- Готовую композицию выполнить в цвете цветными карандашами.
Заключительная часть.
Педагог вместе с детьми рассматривает рисунки, отмечает наиболее интересные по содержанию, по сложности строения и расположению объектов в композиции и еще раз подводит детей к тому, что, если внимательно приглядеться, можно увидеть, что все предметы , окружающие нас, по форме на что – то похожи.
Используемая литература
Давыдова Г.Н. 22 занятия по рисованию для дошкольников. Нетрадиционные техники. – М.: Издательство СКРИПТОРИЙ 2003, 2018 – 112с.
ФОТООТЧЕТ
Автор: Е.В. Куницкая
Тема треугольника
Тема дошкольного треугольника
См. также мои страницы для всех форм, круга, квадрата, ромба, прямоугольника, овала, звезды и сердца.
Список книг
Как партнер Amazon я зарабатываю на соответствующих покупках
Песни и фингерплеи
Треугольная песня
Вот треугольник.
(расставить указательный и средний пальцы; правый указательный палец образует основание)
Вот треугольник.
(нарисуйте в воздухе маленький треугольник)
Теперь нарисуйте еще один со мной.
(рисовать в воздухе)
Вы можете их сосчитать?
Вы готовы? Один!
(повторить первое действие)
Два!
(повторить второе действие)
Три!
(повторить третье действие)
~ Представлено Шерил
Песня о треугольнике — поется на «POP! Goes the Weasel»
Я маленький треугольник
У меня есть три стороны, вы видите.
У меня тоже три угла.
Они как раз для меня.
~ Представлено Шерил
Треугольники — поется в «Jingle Bells»
Треугольники, треугольники,
Иметь три стороны.
Треугольники, треугольники,
Иметь три стороны.
Вы можете рисовать большие треугольники
В воздухе,
(Двумя руками нарисуйте в воздухе треугольник.)
Приятно использовать свои руки
И сделать их где угодно.
~ Барбара Конахан
This Is a Triangle — поется на «Frere Jacques»
Это треугольник, это треугольник.
Как вы можете сказать? Как вы можете сказать?
Имеет три стороны
Эти соединения образуют три точки.
Это треугольник, это треугольник.
~ Жанна Петти
One-Two-Three — поется на «Лондонский мост»
Все треугольники имеют три стороны,
Иметь три стороны, иметь три стороны.
Все треугольники имеют три стороны,
Считай их раз-два-три
~ Кэти МакКаллоу
Найден треугольник — поется на «Клементину»
Найден треугольник,
Найден треугольник,
Нашел треугольник с тремя сторонами.
Он не может катиться,
Он не может шарить,
Он просто сидит там, где он лежит.
~ Джин Уоррен
Искусство и Ремесло
Треугольная ведьма
3 черных треугольника среднего размера для рук и шляпы; 1 большой черный треугольник для платья; 1 маленький желтый треугольник для метлы; 1 круг для головы.
Предложите детям наклеить фигуры на цветную бумагу, чтобы получилась ведьма. Волосы, черты лица, поля шляпы и ручку метлы можно добавить мелками.
~ Представлено Синди
Некоторые идеи треугольника
* Делайте треугольные отпечатки, используя треугольные предметы (блоки, игрушки). Падение треугольник в краску и прижать к бумаге.
* Пусть дети вырежут треугольники, разрезав сплошную черную линию и приклеив их к большому треугольнику.
* сделать треугольный коллаж, склеивая разные материалы, похожие на треугольник.
* сделать изображение или дизайн, используя треугольные формы.
~ Представлено Сьюзен Н.
Идеи темы
Изготовление треугольников
Для каждого из ваших детей наполните небольшой пластиковый пакет пряжей разной длины, от 10 дюймов и короче.Украсьте маленький чемодан большим треугольником и положите внутрь мешочки с пряжей.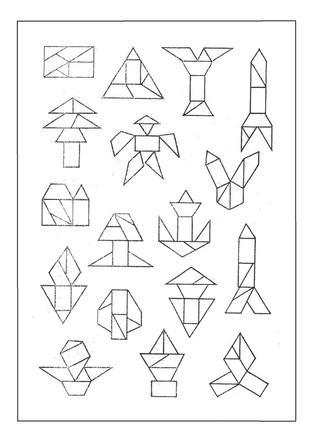 Скажите детям, что этот треугольный чемодан полон треугольников. Откройте чемодан и достаньте полиэтиленовый пакет. Выразите удивление, что он полон пряжи. Спросите детей, что они могут сделать из пряжи, чтобы сделать треугольники. После краткого обсуждения дайте каждому ребенку мешочек с пряжей и позвольте им построить из кусочков пряжи треугольники на полу. Поощряйте их делать много разных видов и размеров треугольников. Сравните результаты.
Скажите детям, что этот треугольный чемодан полон треугольников. Откройте чемодан и достаньте полиэтиленовый пакет. Выразите удивление, что он полон пряжи. Спросите детей, что они могут сделать из пряжи, чтобы сделать треугольники. После краткого обсуждения дайте каждому ребенку мешочек с пряжей и позвольте им построить из кусочков пряжи треугольники на полу. Поощряйте их делать много разных видов и размеров треугольников. Сравните результаты.
Расширение: предложите детям работать вместе, соединяя их пряжу, чтобы сделать гигантский треугольник.
Все виды треугольников
Из бумаги или фетра вырежьте разнообразные треугольники. Отрежьте некоторые с тремя равными сторонами, некоторые с двумя равными сторонами, а третьи с тремя сторонами разной длины. Также вырежьте круг, квадрат, сердце, овал и ромб. Покажите детям треугольники и объясните, что все треугольники имеют три стороны и три угла.Сосчитайте стороны и углы всех представленных треугольников. Помогите детям увидеть, что, хотя стороны могут быть разной длины, если фигура имеет три стороны и три угла, это треугольник. Смешайте все формы вместе. Возьмите по одному и пусть группа скажет вам, является ли фигура треугольником или нет. Положите все треугольники вместе на большую бумагу в форме треугольника на полу. Поместите другие формы в продуктовый пакет. Когда все фигуры рассортированы, убедитесь, что все предметы на полу имеют три стороны и три угла.
Помогите детям увидеть, что, хотя стороны могут быть разной длины, если фигура имеет три стороны и три угла, это треугольник. Смешайте все формы вместе. Возьмите по одному и пусть группа скажет вам, является ли фигура треугольником или нет. Положите все треугольники вместе на большую бумагу в форме треугольника на полу. Поместите другие формы в продуктовый пакет. Когда все фигуры рассортированы, убедитесь, что все предметы на полу имеют три стороны и три угла.
Найдите треугольник
Положите прямоугольный блок, квадратный блок и треугольный блок в темную наволочку. Предложите добровольцу залезть в сумку, не глядя, и пощупать разные формы. Попросите его выбрать треугольник и вынуть его из пакета. Если фигура не треугольник, попросите ребенка положить ее обратно в сумку и повторить попытку.Верните блок в сумку и повторите упражнение с новым добровольцем.
Большой треугольник
Обозначьте троих детей, сидящих далеко друг от друга в круге, цифрами 1, 2 и 3. Первому ребенку дайте клубок пряжи. Пусть ребенок 1 держится за конец пряжи и катит мяч ребенку 2. Пусть этот ребенок ловит мяч, держится за нить там, где он находится, а затем катит его ребенку 3. Теперь пусть ребенок 3 держит мяч.
на пряжу и прикатайте шарик к ребенку 1.В этот момент в кругу должен быть большой треугольник пряжи. Пусть дети отпустят пряжу. Перемотайте клубок пряжи и начните снова с еще трех детей. Продолжайте до тех пор, пока каждый ребенок не повернется.
Первому ребенку дайте клубок пряжи. Пусть ребенок 1 держится за конец пряжи и катит мяч ребенку 2. Пусть этот ребенок ловит мяч, держится за нить там, где он находится, а затем катит его ребенку 3. Теперь пусть ребенок 3 держит мяч.
на пряжу и прикатайте шарик к ребенку 1.В этот момент в кругу должен быть большой треугольник пряжи. Пусть дети отпустят пряжу. Перемотайте клубок пряжи и начните снова с еще трех детей. Продолжайте до тех пор, пока каждый ребенок не повернется.
С помощью пряжи свяжите треугольник.
~ Представлено Сьюзен Н.
Ссылки
Треугольная рыба — DLTK’s Crafts For Kids
Tommy Triange Shapes Buddy — DLTK
Треугольники — Preschool Express
Треугольники с заданиями — SchoolExpress.com
Рабочие листы с треугольниками — Teach-nology.com
Определение треугольника для детей дошкольного возраста — Bright Hub Education
Напишите мне!
Куда бы вы хотели пойти сейчас?
Графика на этой странице сделана.
 …
… сайт закрыт
Copyright 2004 — 2019 * Jana’s Web Design * Все права защищены
Домашнее обучение искусству: оптическая иллюзия для детей: нарисуй треугольник | Алисия Робинсон
Стенограммы 1.Введение: Привет и легко делитесь и добро пожаловать в оптические иллюзии и рисование треугольника. Я знаю, что это название звучит скучно, но это действительно классный проект, в котором вы узнаете, как сделать один из этих действительно классных треугольников. Вы не только сделаете один из этих треугольников, но и поиграете с цветами и узорами. Мне нравится рука с оптическими иллюзиями, потому что так весело смотреть на что-то и думать, а что это? На что я смотрю? Почему я смотрю на это? И научиться его делать очень весело.Поэтому я очень надеюсь, что вам понравится этот класс, и спасибо, что присоединились ко мне. 2. Расходные материалы. Материалы, которые вам понадобятся для этого проекта, включают пару листов картона или карточек, или большой лист картона для плакатов. Вы просто хотите, чтобы бумага была толще, когда вы используете фломастеры и маркеры. Более плотная бумага лучше удерживает цвет и в целом выглядит лучше. Также вам понадобится циркуль для рисования. Вы хотите. И прочный компас для рисования, открывающийся не менее чем на пять дюймов.Вам также понадобится линейка, карандаш и ластик, а также пакет или коробка цветных фломастеров. Вам также понадобится маркер. Я начинаю с ультратонкого маркера Sharpie. Но вы также можете использовать обычный тонкий наконечник Sharpie и пройтись им по концам, чтобы сделать свои черные линии темнее, если хотите. Итак, я, это все, что вам нужно для этого проекта. Я надеюсь, что у вас есть много прекрасного творчества. 3. Проект: В этом проекте мы будем создавать треугольник оптической иллюзии. Треугольник будет равносторонним, а это значит, что у него три равные стороны.Поэтому вам нужно будет знать, как измерять и как отмечать измерения. После того, как мы завершили общий треугольник, мы поговорим о добавлении цветов и узоров к треугольнику и создании нескольких треугольников, чтобы вы могли вырезать их и создавать разные цветовые узоры.
Вы просто хотите, чтобы бумага была толще, когда вы используете фломастеры и маркеры. Более плотная бумага лучше удерживает цвет и в целом выглядит лучше. Также вам понадобится циркуль для рисования. Вы хотите. И прочный компас для рисования, открывающийся не менее чем на пять дюймов.Вам также понадобится линейка, карандаш и ластик, а также пакет или коробка цветных фломастеров. Вам также понадобится маркер. Я начинаю с ультратонкого маркера Sharpie. Но вы также можете использовать обычный тонкий наконечник Sharpie и пройтись им по концам, чтобы сделать свои черные линии темнее, если хотите. Итак, я, это все, что вам нужно для этого проекта. Я надеюсь, что у вас есть много прекрасного творчества. 3. Проект: В этом проекте мы будем создавать треугольник оптической иллюзии. Треугольник будет равносторонним, а это значит, что у него три равные стороны.Поэтому вам нужно будет знать, как измерять и как отмечать измерения. После того, как мы завершили общий треугольник, мы поговорим о добавлении цветов и узоров к треугольнику и создании нескольких треугольников, чтобы вы могли вырезать их и создавать разные цветовые узоры.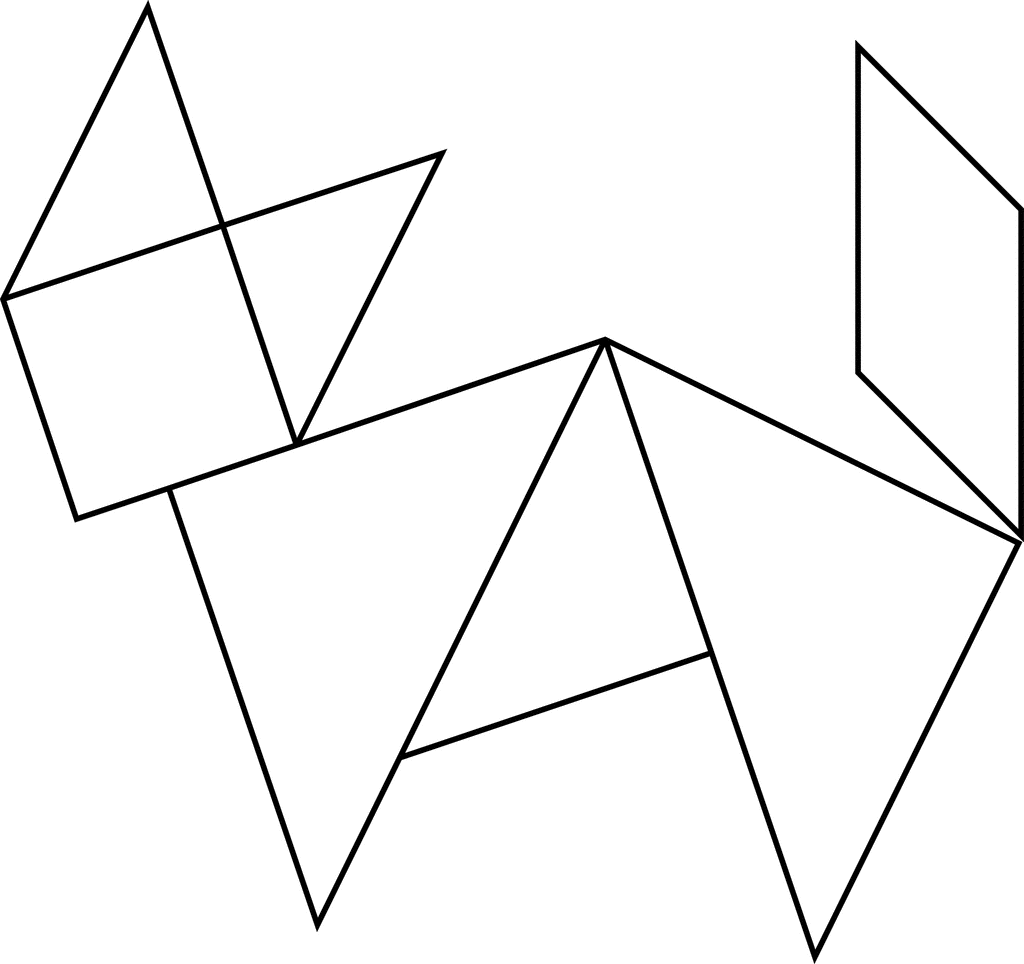 Таким образом, вы можете складывать их вместе и располагать их по-разному, чтобы создавать новые и забавные оптические иллюзии. Я привожу несколько примеров того, как вы можете соединить эти треугольники, чтобы создать собственную забавную оптическую иллюзию.Так что для этого проекта проявите творческий подход. Вы можете создать столько треугольников, сколько захотите. Вы можете добавить столько цветов и узоров, сколько захотите. Идея состоит в том, чтобы просто поиграть с этим треугольником и посмотреть, какие забавные вещи вы можете создать с его помощью. И я хотел бы увидеть эти проекты, когда вы закончите. Поэтому, если вы сфотографируете их и добавите в раздел проектов класса, они будут серыми, и я смогу их увидеть. Другие одноклассники могут их видеть и комментировать. 4. Создание 7-дюймового квадрата: Чтобы начать наш проект, мы собираемся сделать семидюймовый квадрат, на котором мы собираемся нарисовать наш треугольник.Итак, у меня есть артборд. У меня есть линейка, карандаш и ножницы.
Таким образом, вы можете складывать их вместе и располагать их по-разному, чтобы создавать новые и забавные оптические иллюзии. Я привожу несколько примеров того, как вы можете соединить эти треугольники, чтобы создать собственную забавную оптическую иллюзию.Так что для этого проекта проявите творческий подход. Вы можете создать столько треугольников, сколько захотите. Вы можете добавить столько цветов и узоров, сколько захотите. Идея состоит в том, чтобы просто поиграть с этим треугольником и посмотреть, какие забавные вещи вы можете создать с его помощью. И я хотел бы увидеть эти проекты, когда вы закончите. Поэтому, если вы сфотографируете их и добавите в раздел проектов класса, они будут серыми, и я смогу их увидеть. Другие одноклассники могут их видеть и комментировать. 4. Создание 7-дюймового квадрата: Чтобы начать наш проект, мы собираемся сделать семидюймовый квадрат, на котором мы собираемся нарисовать наш треугольник.Итак, у меня есть артборд. У меня есть линейка, карандаш и ножницы. Итак, чтобы сделать семидюймовый квадрат, я собираюсь выровнять мой 0 на линейке с верхним углом моей бумаги. И я собираюсь сделать отметку в семь. Затем я собираюсь опустить часть света на мою бумажную линию, мой 0 вверх по краю моей бумаги. И я собираюсь подойти к 7 и сделать отметку. Итак, из этих двух линий я собираюсь соединить их с моей линейкой. Затем я буду измерять от этого угла Y минус Z.И я собираюсь отмерить семь дюймов вниз, так что я не зашел достаточно далеко, так что я просто уменьшу эту линию до семи дюймов. Так что это моя семидюймовая отметка. И я собираюсь сделать то же самое на этой стороне моего листа. Лима 0 вверх с вершиной и спуститесь туда, где находится семерка, и сделайте отметку. Теперь я собираюсь выровнять этот угол и эту разметку, чтобы получилась нижняя часть моего квадрата. Итак, теперь у меня должен быть квадрат размером 7 дюймов и 57 дюймов. Теперь я собираюсь вырезать это. 5. Равносторонний треугольник без компаса. Теперь у меня есть семидюймовый квадрат.
Итак, чтобы сделать семидюймовый квадрат, я собираюсь выровнять мой 0 на линейке с верхним углом моей бумаги. И я собираюсь сделать отметку в семь. Затем я собираюсь опустить часть света на мою бумажную линию, мой 0 вверх по краю моей бумаги. И я собираюсь подойти к 7 и сделать отметку. Итак, из этих двух линий я собираюсь соединить их с моей линейкой. Затем я буду измерять от этого угла Y минус Z.И я собираюсь отмерить семь дюймов вниз, так что я не зашел достаточно далеко, так что я просто уменьшу эту линию до семи дюймов. Так что это моя семидюймовая отметка. И я собираюсь сделать то же самое на этой стороне моего листа. Лима 0 вверх с вершиной и спуститесь туда, где находится семерка, и сделайте отметку. Теперь я собираюсь выровнять этот угол и эту разметку, чтобы получилась нижняя часть моего квадрата. Итак, теперь у меня должен быть квадрат размером 7 дюймов и 57 дюймов. Теперь я собираюсь вырезать это. 5. Равносторонний треугольник без компаса. Теперь у меня есть семидюймовый квадрат. Итак, этот треугольник, я покажу вам, как это сделать без компаса. Итак, мы будем составлять либо равносторонний треугольник с помощью линейки и карандаша. Итак, теперь у меня есть семидюймовый квадратный корень. Извините меня. Я собираюсь выровнять линейку по 0, по краю бумаги. И я собираюсь поставить отметку на полпути. Таким образом, половина седьмого будет 3,5 месяца на отметке прямо там. А теперь я собираюсь измерить свою пятидюймовую линию. Так что, если я хочу, чтобы это была центральная точка моей пятидюймовой линии, я поставлю ее на 2.5. Теперь моя линейка находится на этой отметке в 2,5 дюйма. И затем я собираюсь нарисовать на этой стороне пятерку, а на этой стороне ноль. Теперь у меня есть пятидюймовая линия в центре моего листа. Я собираюсь перейти к началу моей статьи. И я собираюсь сделать отметку на полпути. Итак, семь. Собираюсь перейти на 3.5. Маленькая светлая отметка Фила на 3,5. Затем я перейду от этой центральной линии к этой центральной линии и проведу очень тонкую линию.
Итак, этот треугольник, я покажу вам, как это сделать без компаса. Итак, мы будем составлять либо равносторонний треугольник с помощью линейки и карандаша. Итак, теперь у меня есть семидюймовый квадратный корень. Извините меня. Я собираюсь выровнять линейку по 0, по краю бумаги. И я собираюсь поставить отметку на полпути. Таким образом, половина седьмого будет 3,5 месяца на отметке прямо там. А теперь я собираюсь измерить свою пятидюймовую линию. Так что, если я хочу, чтобы это была центральная точка моей пятидюймовой линии, я поставлю ее на 2.5. Теперь моя линейка находится на этой отметке в 2,5 дюйма. И затем я собираюсь нарисовать на этой стороне пятерку, а на этой стороне ноль. Теперь у меня есть пятидюймовая линия в центре моего листа. Я собираюсь перейти к началу моей статьи. И я собираюсь сделать отметку на полпути. Итак, семь. Собираюсь перейти на 3.5. Маленькая светлая отметка Фила на 3,5. Затем я перейду от этой центральной линии к этой центральной линии и проведу очень тонкую линию. Хорошо? Итак, теперь я буду рисовать из этой точки, положу линейку, вот это, пять дюймов в этой точке.Я собираюсь поднести линейку к тому месту, где 0 касается линии, которую я нарисовал в центре. Теперь у меня есть пятидюймовая линия. Итак, есть сторона 5 дюймов, сторона 15 дюймов, а затем принесите сюда мой маршрут, мой карандаш. Если я положу свою линейку на 5, где мой карандаш, и соединим мой 0 с той, что там, должно совпасть. А потом у меня есть еще одна пятидюймовая сторона. Итак, есть пятидюймовый равносторонний треугольник. Теперь вы можете стереть эту центральную линию. И есть равносторонний треугольник без использования компаса. 6. Равносторонний треугольник с циркулем. Чтобы сделать равносторонний треугольник с помощью циркуля, вам понадобится семидюймовый квадрат, который мы вырезали, линейка и карандаш.Итак, для начала мы собираемся измерить пятидюймовую линию на нашей бумаге. Мы постараемся попасть в центр. Итак, я собираюсь выровнять мой 0 с краем моей бумаги, приблизить его к низу, чтобы у нас было достаточно места для треугольника здесь вверху.
Хорошо? Итак, теперь я буду рисовать из этой точки, положу линейку, вот это, пять дюймов в этой точке.Я собираюсь поднести линейку к тому месту, где 0 касается линии, которую я нарисовал в центре. Теперь у меня есть пятидюймовая линия. Итак, есть сторона 5 дюймов, сторона 15 дюймов, а затем принесите сюда мой маршрут, мой карандаш. Если я положу свою линейку на 5, где мой карандаш, и соединим мой 0 с той, что там, должно совпасть. А потом у меня есть еще одна пятидюймовая сторона. Итак, есть пятидюймовый равносторонний треугольник. Теперь вы можете стереть эту центральную линию. И есть равносторонний треугольник без использования компаса. 6. Равносторонний треугольник с циркулем. Чтобы сделать равносторонний треугольник с помощью циркуля, вам понадобится семидюймовый квадрат, который мы вырезали, линейка и карандаш.Итак, для начала мы собираемся измерить пятидюймовую линию на нашей бумаге. Мы постараемся попасть в центр. Итак, я собираюсь выровнять мой 0 с краем моей бумаги, приблизить его к низу, чтобы у нас было достаточно места для треугольника здесь вверху. А то я свой файлик найду, ну так семь. И я собираюсь найти свою точку на полпути. Это то, что я нахожу. Итак, половина от 7,53, так что я собираюсь поставить небольшую отметку на линии 3,5 дюйма. Я собираюсь довести свою линейку до отметки 2,5 дюйма, потому что половина пяти равна 2.5 дюймов. Так что это моя 2,5-дюймовая линия на отметке, которую я только что сделал. Я собираюсь провести линию к 5 и я собираюсь провести линию к 0. Теперь у меня есть пятидюймовая линия внизу листа. Итак, чтобы сделать это с помощью компаса, чтобы сделать другие стороны с помощью компаса, я собираюсь открыть свой компас. Вы поместите остроконечную точку, но не поводок, а точку, которая группируется на левом краю вашего треугольника. Вы откроете свой компас до пятерки, до конца строки. Так что смотрите, моя линия помещается между моей, точкой моего компаса и стержнем карандаша.Собираюсь положить это вниз. Точка в конце этой строки. Поместите мой карандаш на другой край, и я собираюсь сделать линию. Теперь у меня есть эта большая арка.
А то я свой файлик найду, ну так семь. И я собираюсь найти свою точку на полпути. Это то, что я нахожу. Итак, половина от 7,53, так что я собираюсь поставить небольшую отметку на линии 3,5 дюйма. Я собираюсь довести свою линейку до отметки 2,5 дюйма, потому что половина пяти равна 2.5 дюймов. Так что это моя 2,5-дюймовая линия на отметке, которую я только что сделал. Я собираюсь провести линию к 5 и я собираюсь провести линию к 0. Теперь у меня есть пятидюймовая линия внизу листа. Итак, чтобы сделать это с помощью компаса, чтобы сделать другие стороны с помощью компаса, я собираюсь открыть свой компас. Вы поместите остроконечную точку, но не поводок, а точку, которая группируется на левом краю вашего треугольника. Вы откроете свой компас до пятерки, до конца строки. Так что смотрите, моя линия помещается между моей, точкой моего компаса и стержнем карандаша.Собираюсь положить это вниз. Точка в конце этой строки. Поместите мой карандаш на другой край, и я собираюсь сделать линию. Теперь у меня есть эта большая арка. Тогда я собираюсь сделать то же самое. На этот раз мы поместим наконечник на этот конец линии. И мое лидерство на том конце моей линии. И я собираюсь сделать то же самое. Так что это с моими двумя арками, крест является точкой моего пятидюймового треугольника. Теперь вы можете отложить компас в сторону. Возьмите линейку вместо карандаша в той точке, где пересекаются эти две арки, соедините ее с краем, с левым краем вашей линии или с левой точкой ваших линий и нарисуйте линию.Теперь, если вы опустите свой валик на 0 и поместите его туда, позвольте мне повернуть вставку на дюймы. А вы выстраиваете. Эта линия, этот край вашего треугольника будет составлять пять дюймов. Затем вы просто делаете то же самое с другой стороны. И эта линия должна быть пять дюймов. И вот как вы делаете равносторонний треугольник с компасом. Теперь вы можете вернуться и стереть эту дугообразную линию. 7. Маркировка измерений: теперь, когда у нас нарисован равносторонний треугольник, использовали ли мы только линейку и карандаш или нашу компанию, наш чертежный циркуль.
Тогда я собираюсь сделать то же самое. На этот раз мы поместим наконечник на этот конец линии. И мое лидерство на том конце моей линии. И я собираюсь сделать то же самое. Так что это с моими двумя арками, крест является точкой моего пятидюймового треугольника. Теперь вы можете отложить компас в сторону. Возьмите линейку вместо карандаша в той точке, где пересекаются эти две арки, соедините ее с краем, с левым краем вашей линии или с левой точкой ваших линий и нарисуйте линию.Теперь, если вы опустите свой валик на 0 и поместите его туда, позвольте мне повернуть вставку на дюймы. А вы выстраиваете. Эта линия, этот край вашего треугольника будет составлять пять дюймов. Затем вы просто делаете то же самое с другой стороны. И эта линия должна быть пять дюймов. И вот как вы делаете равносторонний треугольник с компасом. Теперь вы можете вернуться и стереть эту дугообразную линию. 7. Маркировка измерений: теперь, когда у нас нарисован равносторонний треугольник, использовали ли мы только линейку и карандаш или нашу компанию, наш чертежный циркуль.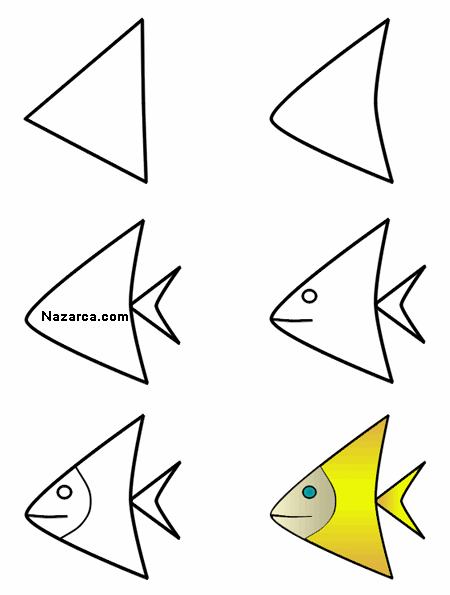 Мы начнем подготавливать его к линиям внутри нашего треугольника, которые будут создавать иллюзию. Итак, первое, что мы собираемся сделать, мы собираемся измерить нижнюю часть нашего треугольника, чтобы выбрать одну сторону вашего треугольника и поставить отметку на середине. Так вот, и один из них, вероятно, уже на полпути. Теперь я хочу, чтобы вы хотели свой свет, вы хотите, чтобы ваши следы были светлыми. Так что не делайте тяжелых светлых меток, потому что в конце мы их сотрем. Я собираюсь сделать свои темными, чтобы вам было легче их разглядеть в камере.Вы держите свой слайд. Так что у меня есть моя половина пути там. Я собираюсь поставить свою отметку на полпути на этой стороне моего треугольника. Итак, я соединяю в верхнем углу верхний угол с боковым углом и ставлю маркет 2,5 дюйма. И затем я собираюсь сделать то же самое на последней стороне. Выравнивание моего ряда C вверху по верхнему углу. У меня пятерка на нижнем угле, и собираюсь дойти до 2,5. Теперь я собираюсь провести линию от этой средней отметки на одном краю или одной стороне моего треугольника до верхней точки.
Мы начнем подготавливать его к линиям внутри нашего треугольника, которые будут создавать иллюзию. Итак, первое, что мы собираемся сделать, мы собираемся измерить нижнюю часть нашего треугольника, чтобы выбрать одну сторону вашего треугольника и поставить отметку на середине. Так вот, и один из них, вероятно, уже на полпути. Теперь я хочу, чтобы вы хотели свой свет, вы хотите, чтобы ваши следы были светлыми. Так что не делайте тяжелых светлых меток, потому что в конце мы их сотрем. Я собираюсь сделать свои темными, чтобы вам было легче их разглядеть в камере.Вы держите свой слайд. Так что у меня есть моя половина пути там. Я собираюсь поставить свою отметку на полпути на этой стороне моего треугольника. Итак, я соединяю в верхнем углу верхний угол с боковым углом и ставлю маркет 2,5 дюйма. И затем я собираюсь сделать то же самое на последней стороне. Выравнивание моего ряда C вверху по верхнему углу. У меня пятерка на нижнем угле, и собираюсь дойти до 2,5. Теперь я собираюсь провести линию от этой средней отметки на одном краю или одной стороне моего треугольника до верхней точки. И это будет светлая линия.Вы же не хотите, чтобы было очень темно. Моя линия будет темнее, чтобы вы могли ее видеть. Итак, вы хотите, чтобы ваша линия была светлой, а не такой темной. И я сделаю то же самое для обеих сторон, соединив свою сторону с точкой, с моим углом. Теперь у вас будет треугольник, который выглядит примерно так, за исключением того, что ваши линии светлее внутри. Теперь мы начнем делать четверть дюйма вдоль внешних сторон, сторон нашего треугольника. Итак, выровняйте линейку по верхней точке, по верхнему углу, 0 в точке, где вам пять, будет внизу в этой нижней точке.Я собираюсь начать очень легко. Вы собираетесь сделать очень легко. Я сделаю темнее, поставив счет через каждую четверть дюйма. И если вы заметили, что моя линейка находится внутри моего треугольника, значит, мои подсчеты находятся снаружи. А у вас легкие. Мы просто маркируем каждую четверть дюйма. У нас уже есть отметка на полпути. Вот и готова одна сторона. Затем делаю следующую сторону. То же вино выстраивает мой 0 до одного угла до 1 и мою пятерку до другого угла.
И это будет светлая линия.Вы же не хотите, чтобы было очень темно. Моя линия будет темнее, чтобы вы могли ее видеть. Итак, вы хотите, чтобы ваша линия была светлой, а не такой темной. И я сделаю то же самое для обеих сторон, соединив свою сторону с точкой, с моим углом. Теперь у вас будет треугольник, который выглядит примерно так, за исключением того, что ваши линии светлее внутри. Теперь мы начнем делать четверть дюйма вдоль внешних сторон, сторон нашего треугольника. Итак, выровняйте линейку по верхней точке, по верхнему углу, 0 в точке, где вам пять, будет внизу в этой нижней точке.Я собираюсь начать очень легко. Вы собираетесь сделать очень легко. Я сделаю темнее, поставив счет через каждую четверть дюйма. И если вы заметили, что моя линейка находится внутри моего треугольника, значит, мои подсчеты находятся снаружи. А у вас легкие. Мы просто маркируем каждую четверть дюйма. У нас уже есть отметка на полпути. Вот и готова одна сторона. Затем делаю следующую сторону. То же вино выстраивает мой 0 до одного угла до 1 и мою пятерку до другого угла. А потом каждую четверть ребра делаешь отметку и держишь слайд.И тогда я собираюсь сделать последнюю сторону. Теперь ваш треугольник должен выглядеть так. 8. Рисование внутренних линий. С нашим предварительным треугольником мы начнем рисовать внутренние линии, которые дадут нам решение. Итак, мы начнем с правой стороны нашего треугольника и начнем соединяться. Наши линии — это совпадения, но мы не собираемся соединяться с внешними краями нашего треугольника. Мы соединяем внутренние линии, которые мы нарисовали на полпути. Но я собираюсь выровнять линейку по этим отметкам снаружи.Так что я положу туда свой карандаш снаружи, чтобы мне было легче управлять линейкой своими точками. Я не собираюсь отслеживать весь путь. Я собираюсь начать трассировку на этой линии. И я собираюсь проследить эту линию. Таким образом, ваша первая строка будет выглядеть так. Затем вы собираетесь переместить линейку вниз. Вы должны быть очень осторожны, когда делаете эти линии, чтобы убедиться, что вы соединяете правильные отметки в четверть дюйма с обеих сторон вашего треугольника.
А потом каждую четверть ребра делаешь отметку и держишь слайд.И тогда я собираюсь сделать последнюю сторону. Теперь ваш треугольник должен выглядеть так. 8. Рисование внутренних линий. С нашим предварительным треугольником мы начнем рисовать внутренние линии, которые дадут нам решение. Итак, мы начнем с правой стороны нашего треугольника и начнем соединяться. Наши линии — это совпадения, но мы не собираемся соединяться с внешними краями нашего треугольника. Мы соединяем внутренние линии, которые мы нарисовали на полпути. Но я собираюсь выровнять линейку по этим отметкам снаружи.Так что я положу туда свой карандаш снаружи, чтобы мне было легче управлять линейкой своими точками. Я не собираюсь отслеживать весь путь. Я собираюсь начать трассировку на этой линии. И я собираюсь проследить эту линию. Таким образом, ваша первая строка будет выглядеть так. Затем вы собираетесь переместить линейку вниз. Вы должны быть очень осторожны, когда делаете эти линии, чтобы убедиться, что вы соединяете правильные отметки в четверть дюйма с обеих сторон вашего треугольника. Иногда я немного отвлекаюсь. Видишь, как я пропустил это.Так что не торопитесь, обратите внимание на то, что вы делаете. Это становится немного запутанным, чем больше строк мы получаем здесь. Так что просто не торопитесь. Итак, я собираюсь подключиться от этой точки к этой точке. Теперь у меня две линии. Так что я собираюсь сделать еще три. Итак, я хочу, чтобы вы сделали еще три линии на правой стороне вашего треугольника. Соединяем снаружи отметки в четверть дюйма, которые мы только что сделали несколько минут назад. И снова вам нужно обратить внимание на то, чтобы убедиться, что вы выровнены с правильными отметками в четверть дюйма.Итак, 1234. Мне нужен еще один. Теперь у вас есть треугольник, который выглядит так, где у вас есть пять линий на этой стороне. Теперь мы собираемся соединить их с другой стороной. Итак, теперь переходим к левой стороне моего треугольника. И снова мы собираемся соединить все наши четвертьдюймовые линии с внешними. Но мы собираемся начать наши линии на этой диагонали.
Иногда я немного отвлекаюсь. Видишь, как я пропустил это.Так что не торопитесь, обратите внимание на то, что вы делаете. Это становится немного запутанным, чем больше строк мы получаем здесь. Так что просто не торопитесь. Итак, я собираюсь подключиться от этой точки к этой точке. Теперь у меня две линии. Так что я собираюсь сделать еще три. Итак, я хочу, чтобы вы сделали еще три линии на правой стороне вашего треугольника. Соединяем снаружи отметки в четверть дюйма, которые мы только что сделали несколько минут назад. И снова вам нужно обратить внимание на то, чтобы убедиться, что вы выровнены с правильными отметками в четверть дюйма.Итак, 1234. Мне нужен еще один. Теперь у вас есть треугольник, который выглядит так, где у вас есть пять линий на этой стороне. Теперь мы собираемся соединить их с другой стороной. Итак, теперь переходим к левой стороне моего треугольника. И снова мы собираемся соединить все наши четвертьдюймовые линии с внешними. Но мы собираемся начать наши линии на этой диагонали. Так что я собираюсь положить свой карандаш здесь. Итак, я удостоверяюсь, что моя линейка выдерживает ток должным образом, правильно и подключается, но я только, я подключаю ее к этой точке здесь.Так что это моя первая линия на той стороне. И я собираюсь двигаться дальше. Это может немного сбить с толку. Здесь я немного запутался и должен убедиться, что я нахожусь на правильных отметках в четверть дюйма. Некоторые соединяют эту отметку с этой диагональю. И я собираюсь делать это до той линии, где я остановился. Большинство пропустили это. Упс. Я испортил. Итак, видите, я думал, что я напортачил, и это может случиться, вы просто сотрите это и исправите. Итак, теперь у меня пять линий на этой стороне и пять жизней на этой стороне.Что ж, нам нужно продолжать движение по центру. Так что будем продолжать. И мы собираемся подключить его к этой линии сейчас. И как только я нарисую это, я покажу вам, что один идет к тому, этот идет к этому, начиная мою линию здесь и соединяясь с там. Итак, теперь моя линия соединяет эту линию с этой линией.
Так что я собираюсь положить свой карандаш здесь. Итак, я удостоверяюсь, что моя линейка выдерживает ток должным образом, правильно и подключается, но я только, я подключаю ее к этой точке здесь.Так что это моя первая линия на той стороне. И я собираюсь двигаться дальше. Это может немного сбить с толку. Здесь я немного запутался и должен убедиться, что я нахожусь на правильных отметках в четверть дюйма. Некоторые соединяют эту отметку с этой диагональю. И я собираюсь делать это до той линии, где я остановился. Большинство пропустили это. Упс. Я испортил. Итак, видите, я думал, что я напортачил, и это может случиться, вы просто сотрите это и исправите. Итак, теперь у меня пять линий на этой стороне и пять жизней на этой стороне.Что ж, нам нужно продолжать движение по центру. Так что будем продолжать. И мы собираемся подключить его к этой линии сейчас. И как только я нарисую это, я покажу вам, что один идет к тому, этот идет к этому, начиная мою линию здесь и соединяясь с там. Итак, теперь моя линия соединяет эту линию с этой линией.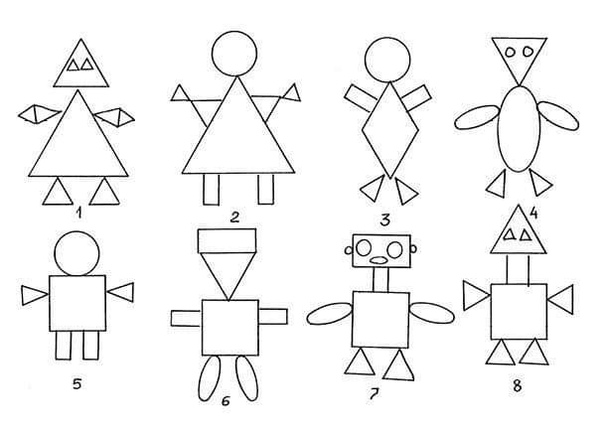 И я буду делать это до тех пор, пока не закончу эту очередь прямо здесь. Это слайд. Я не думаю, что смогу добавить еще один. Нет. Хорошо. Так что внутри всего две строчки. Теперь мы собираемся повернуть наш треугольник таким образом, и мы собираемся заполнить линии, идущие таким образом.Так что теперь я просто собираюсь соединить эту линию и эту линию, и эту линию и эту точку, и так до того места, где мы закончим треугольник. Так что теперь у нас есть этот. Ну, куда это идет? Ну, мы должны убедиться, что мы подключаем его к правильной линии снаружи. Так что один идет с этим. И этот идет со следующим. Итак, теперь ваш треугольник выглядит так. 9. Обведение линий. Теперь у нас нарисованы все линии карандашом. Теперь мы собираемся войти с нашим тонким наконечником Sharpie и обвести наши линии.Итак, мы собираемся проследить все линии, кроме этих внутренних диагональных линий. Мы собираемся стереть все это через минуту. Итак, проследите внешнюю сторону и все линии, кроме диагоналей, которые идут от точки до средней отметки на наших сторонах.
И я буду делать это до тех пор, пока не закончу эту очередь прямо здесь. Это слайд. Я не думаю, что смогу добавить еще один. Нет. Хорошо. Так что внутри всего две строчки. Теперь мы собираемся повернуть наш треугольник таким образом, и мы собираемся заполнить линии, идущие таким образом.Так что теперь я просто собираюсь соединить эту линию и эту линию, и эту линию и эту точку, и так до того места, где мы закончим треугольник. Так что теперь у нас есть этот. Ну, куда это идет? Ну, мы должны убедиться, что мы подключаем его к правильной линии снаружи. Так что один идет с этим. И этот идет со следующим. Итак, теперь ваш треугольник выглядит так. 9. Обведение линий. Теперь у нас нарисованы все линии карандашом. Теперь мы собираемся войти с нашим тонким наконечником Sharpie и обвести наши линии.Итак, мы собираемся проследить все линии, кроме этих внутренних диагональных линий. Мы собираемся стереть все это через минуту. Итак, проследите внешнюю сторону и все линии, кроме диагоналей, которые идут от точки до средней отметки на наших сторонах. Вот и готова моя первая сторона. А потом закончу остальные. Как только вы начертите все эти линии черным маркером, вы закончите оптическую иллюзию треугольника. Теперь вы можете вернуться в любую гонку. И если вы заметили, из-за того, что я сделал свои метки темными, мои метки не вырастут до конца.Вы все равно сможете увидеть мою. Вот почему я хотел, чтобы вы использовали очень легкие линии и метки. И у них завершенная прогулка по треугольнику создает оптическую иллюзию законченности. 10. Для развлечения: добавление цветов и узоров. Итак, теперь, когда вы закончили черно-белую оптическую иллюзию своего треугольника, что еще вы можете сделать с этим проектом? Ну, мы можем добавить цвет, потому что во многих искусствах оптических иллюзий художники используют цвет, а также узоры и линии для создания других иллюзий и эффектов.Для некоторых треугольников я добавил синий и оранжевый. И я сделал это узором AB или синим, оранжевым, сине-оранжевым, сине-оранжевым узором. И если вы заметите, когда будете склеивать их вместе, это как бы продолжит шаблон.
Вот и готова моя первая сторона. А потом закончу остальные. Как только вы начертите все эти линии черным маркером, вы закончите оптическую иллюзию треугольника. Теперь вы можете вернуться в любую гонку. И если вы заметили, из-за того, что я сделал свои метки темными, мои метки не вырастут до конца.Вы все равно сможете увидеть мою. Вот почему я хотел, чтобы вы использовали очень легкие линии и метки. И у них завершенная прогулка по треугольнику создает оптическую иллюзию законченности. 10. Для развлечения: добавление цветов и узоров. Итак, теперь, когда вы закончили черно-белую оптическую иллюзию своего треугольника, что еще вы можете сделать с этим проектом? Ну, мы можем добавить цвет, потому что во многих искусствах оптических иллюзий художники используют цвет, а также узоры и линии для создания других иллюзий и эффектов.Для некоторых треугольников я добавил синий и оранжевый. И я сделал это узором AB или синим, оранжевым, сине-оранжевым, сине-оранжевым узором. И если вы заметите, когда будете склеивать их вместе, это как бы продолжит шаблон. Это выглядит круто, и вы можете вращать части. Таким образом, вы можете использовать для этого два цвета, а можете использовать три или четыре цвета и создать свой собственный узор. Я собираюсь показать вам, как я сделал свой узор на этих двух треугольниках. У меня есть несколько треугольников, которые я создал.И я собираюсь сделать этот с фиолетовым и желтым, потому что они дополняют друг друга. А этот с красным и зеленым, потому что они дополняют друг друга. И если вам интересно, что такое дополнительные цвета, они противоположны цвету, противоположны цветам на цветовом круге. Итак, если вы найдете цвет, цветовой круг, вы увидите, что они находятся прямо напротив друг друга. Так что это синий и оранжевый бесплатно. Это будут желтый и фиолетовый. И мне просто нравится начинать с одного из моих цветов.И то, что я обычно делаю, поскольку я сначала отметил свой шаблон. Итак, я начну с того, что просто отмечу, что это будет фиолетовый цвет. Тогда я собираюсь пропустить фиолетовый, фиолетовый, фиолетовый.
Это выглядит круто, и вы можете вращать части. Таким образом, вы можете использовать для этого два цвета, а можете использовать три или четыре цвета и создать свой собственный узор. Я собираюсь показать вам, как я сделал свой узор на этих двух треугольниках. У меня есть несколько треугольников, которые я создал.И я собираюсь сделать этот с фиолетовым и желтым, потому что они дополняют друг друга. А этот с красным и зеленым, потому что они дополняют друг друга. И если вам интересно, что такое дополнительные цвета, они противоположны цвету, противоположны цветам на цветовом круге. Итак, если вы найдете цвет, цветовой круг, вы увидите, что они находятся прямо напротив друг друга. Так что это синий и оранжевый бесплатно. Это будут желтый и фиолетовый. И мне просто нравится начинать с одного из моих цветов.И то, что я обычно делаю, поскольку я сначала отметил свой шаблон. Итак, я начну с того, что просто отмечу, что это будет фиолетовый цвет. Тогда я собираюсь пропустить фиолетовый, фиолетовый, фиолетовый. А в этом я хочу, чтобы внутри была желтая. Итак, я собираюсь сделать фиолетовый, фиолетовый, фиолетовый, фиолетовый. И я обычно сначала размечаю свою выкройку, чтобы, если случайно напортачу и начну раскрашивать не ту, или пометлю не той. Это всего лишь маленькое пятнышко, которое мне нужно прикрыть, а не целая полоса или секция. Таким образом, вы, ребята, можете определить любые цвета, которые вы хотите.Если вы хотите добавить цвета, вы можете даже сделать трехцветный узор: фиолетовый, желто-зеленый, фиолетовый, желтый, зеленый, фиолетовый, желтый. Это зависит от вас. Вы можете сделать столько треугольников, сколько захотите. И мужчину сколько угодно цветов. Я делаю шесть, и я покажу вам, почему в следующем видео. Я собираюсь сделать шестиугольник из этих забавных форм. Так что вперед, выбирайте цвета и создавайте узоры. 11. Для большего удовольствия: перестановка треугольников: как только вы закончите создавать все треугольники, которые хотите сделать, и создадите шаблоны, которые хотите сделать.
А в этом я хочу, чтобы внутри была желтая. Итак, я собираюсь сделать фиолетовый, фиолетовый, фиолетовый, фиолетовый. И я обычно сначала размечаю свою выкройку, чтобы, если случайно напортачу и начну раскрашивать не ту, или пометлю не той. Это всего лишь маленькое пятнышко, которое мне нужно прикрыть, а не целая полоса или секция. Таким образом, вы, ребята, можете определить любые цвета, которые вы хотите.Если вы хотите добавить цвета, вы можете даже сделать трехцветный узор: фиолетовый, желто-зеленый, фиолетовый, желтый, зеленый, фиолетовый, желтый. Это зависит от вас. Вы можете сделать столько треугольников, сколько захотите. И мужчину сколько угодно цветов. Я делаю шесть, и я покажу вам, почему в следующем видео. Я собираюсь сделать шестиугольник из этих забавных форм. Так что вперед, выбирайте цвета и создавайте узоры. 11. Для большего удовольствия: перестановка треугольников: как только вы закончите создавать все треугольники, которые хотите сделать, и создадите шаблоны, которые хотите сделать.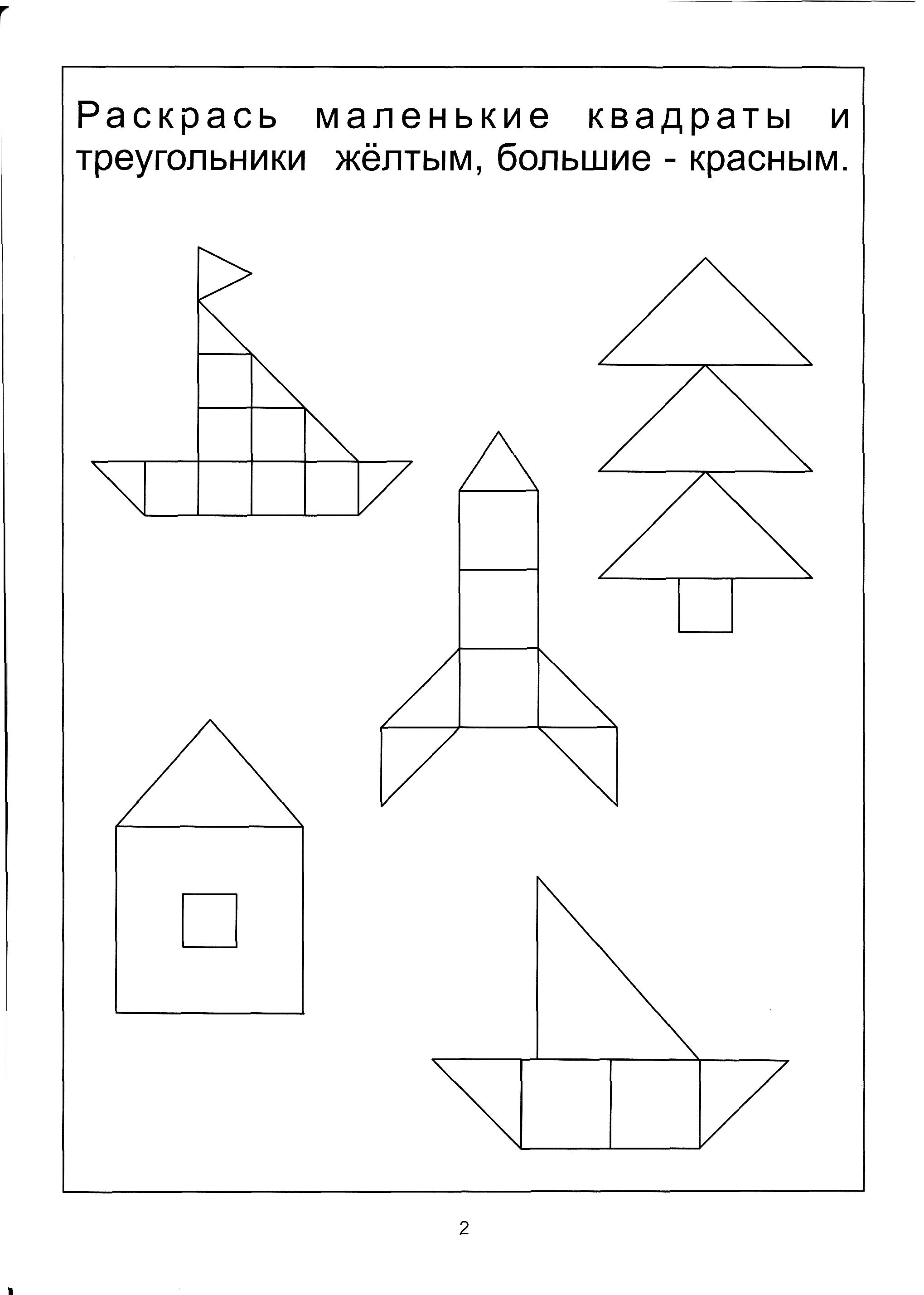 Вы можете начать играть с размещением и посмотреть, что вы можете создать с помощью треугольников, которые у вас есть. Один из вариантов — создать шестиугольник. И вы можете чередовать свой узор. У меня все точки поворачиваются к середине. Или вы можете повернуться в другом направлении и посмотреть, что происходит и как это выглядит, когда все указывает в разных направлениях. Вы можете изменить внешний вид своей оптической иллюзии, просто повернув ее. Если вы не хотите делать шестиугольник, вы всегда можете просто сделать прямую линию.Различные узоры. Вы можете положить их так и перевернуть одну таким образом. Так что поиграйте со своими треугольниками. Что вы хотите создать? Как вы хотите, чтобы это выглядело? Возможности этих входов — это то, что вы можете сделать больше и изменить цвета и узоры. Так что получайте удовольствие, создавая и придумывая любые узоры и цвета оптических иллюзий, которые вам нравятся.
Вы можете начать играть с размещением и посмотреть, что вы можете создать с помощью треугольников, которые у вас есть. Один из вариантов — создать шестиугольник. И вы можете чередовать свой узор. У меня все точки поворачиваются к середине. Или вы можете повернуться в другом направлении и посмотреть, что происходит и как это выглядит, когда все указывает в разных направлениях. Вы можете изменить внешний вид своей оптической иллюзии, просто повернув ее. Если вы не хотите делать шестиугольник, вы всегда можете просто сделать прямую линию.Различные узоры. Вы можете положить их так и перевернуть одну таким образом. Так что поиграйте со своими треугольниками. Что вы хотите создать? Как вы хотите, чтобы это выглядело? Возможности этих входов — это то, что вы можете сделать больше и изменить цвета и узоры. Так что получайте удовольствие, создавая и придумывая любые узоры и цвета оптических иллюзий, которые вам нравятся.
Что такое треугольник? — [Определение, факты и примеры]
Что такое треугольник?
В геометрии треугольник — это замкнутая двумерная фигура с тремя прямыми сторонами. Треугольник также является многоугольником.
Треугольник также является многоугольником.
Мы можем найти форму треугольника на флаге, треугольнике музыкального инструмента и придорожной вывеске.
Свойства треугольника- Треугольник имеет три стороны, три вершины и три угла.
- Сумма трех внутренних углов треугольника всегда равна 180°.
- Сумма длин двух сторон треугольника всегда больше длины третьей стороны.
- Треугольник с вершинами P, Q и R обозначается как △PQR.
- Площадь треугольника равна половине произведения его основания на высоту.
Различные типы треугольников
Чтобы классифицировать треугольники по их углам, мы измеряем каждый из его внутренних углов. Треугольники можно классифицировать по углам, как:
В остроугольном треугольнике все внутренние углы острые (меньше 90°), в прямоугольном треугольнике один угол прямой (равный 90°), а в тупоугольном треугольнике один угол тупой (больше 90°).
Чтобы классифицировать треугольники по их сторонам, мы измеряем длину каждой из его сторон. Треугольники можно классифицировать по их сторонам, как:
Чтобы классифицировать треугольники по углам и сторонам, мы измеряем внутренние углы и длину сторон треугольника. Вот несколько примеров треугольников, классифицированных по углам и сторонам:
|
Интересные факты
|
Давайте петь!
Дженна любит треугольники!
Крошечные треугольники на ее блузке,
Красная крыша ее кукольного домика,
Кусочек сыра для мышки.
Давай сделаем это!
Вместо того, чтобы раздавать детям листы с заданиями по математике, попросите ребенка наблюдать/отмечать предметы треугольной формы.
Вы также можете дать им зубочистки или соломинки и попросить составить из них всевозможные треугольники.
Связанный математический словарь-
С какого возраста ребенок может нарисовать треугольник?
6 лет. К 6-7 годам у ребенка появляется свой стиль рисования, который обычно узнают взрослые. К тому времени, когда ей исполнится 7 лет, она сможет правильно рисовать круги, квадраты, прямоугольники, треугольники и ромбы на своих рисунках.
Что должен уметь рисовать двухлетний ребенок?
В возрасте около 2 лет у вашего малыша улучшатся навыки рисования, и он начнет экспериментировать, рисуя линии. После того, как им покажут, как это сделать, они также смогут скопировать круг и несколько вертикальных линий .
Когда малыши могут рисовать фигуры?
В возрасте от двух до пяти лет большинство детей начинают учиться рисовать основные формы и линии. По словам трудотерапевта и матери Кристи Кили, большинство детей сначала рисуют эти фигуры путем подражания (то есть они смотрят, как вы рисуете, а затем сразу же повторяют шаги).
По словам трудотерапевта и матери Кристи Кили, большинство детей сначала рисуют эти фигуры путем подражания (то есть они смотрят, как вы рисуете, а затем сразу же повторяют шаги).
Что должен знать трехлетний ребенок в учебном процессе?
В возрасте от 3 до 4 лет ваш ребенок должен уметь:
- Произносить свое имя и возраст.
- Говорить от 250 до 500 слов.
- Отвечайте на простые вопросы.
- Говорить предложениями из пяти-шести слов и говорить целыми предложениями к 4 годам.
- Говорить четко, хотя до 4 лет они могут быть непонятны полностью.
- Рассказывать истории.
Должен ли двухлетний ребенок знать азбуку?
К 2 годам: Дети начинают узнавать некоторые буквы и могут петь или произносить вслух песенку «Азбука» . К 3 годам: дети могут узнавать около половины букв алфавита и начинать связывать буквы с их звуками. … К 4 годам: Дети часто знают все буквы алфавита и их правильный порядок.
К 3 годам: дети могут узнавать около половины букв алфавита и начинать связывать буквы с их звуками. … К 4 годам: Дети часто знают все буквы алфавита и их правильный порядок.
Может ли двухлетний ребенок нарисовать человека?
В то время как типичные дети начинают рисовать узнаваемые формы, представляющие окружающие предметы, примерно в возрасте 3 или 4 лет (Golomb, 1992; Kellogg, 1969; Matthews, 1984), некоторые дети производят свои первые репрезентативные рисунки в возрасте лет. 2.
Какие 5 этапов рисования?
ЭТАПЫ ХУДОЖЕСТВЕННОГО РАЗВИТИЯ
- КРИБЛ. (от 2 до 4 лет) Этап Scribble состоит из четырех подэтапов. …
- ПРЕСХЕМАТИЧЕСКАЯ. (от 4 до 6 лет) …
- СХЕМА. (от 7 до 9 лет) …
- РАССВЕТНЫЙ РЕАЛИЗМ. (от 9 до 11 лет) …
- ПСЕВДОРЕАЛИСТИЧЕСКАЯ ЭТАП. (от ll до 13 лет)
Должен ли двухлетний ребенок знать цвета?
2-летние дети могут понять концепцию цвета и могут распознавать цвета и узнавать о них уже в 18 месяцев . Изучение цветов может стать увлекательным занятием для вас и вашего ребенка, когда вы будете практиковаться вместе. Начните с одного цвета за раз, используйте карточки, чтобы показать ребенку цвет, и попросите его произнести название вместе с вами.
Изучение цветов может стать увлекательным занятием для вас и вашего ребенка, когда вы будете практиковаться вместе. Начните с одного цвета за раз, используйте карточки, чтобы показать ребенку цвет, и попросите его произнести название вместе с вами.
Что должен знать 2,5-летний ребенок?
В этом возрасте ваш ребенок должен уметь:
- Стоять на цыпочках.
- Удар по мячу.
- Начать работу.
- Залезать на мебель и спускаться с нее без посторонней помощи.
- Ходите вверх и вниз по лестнице, держась за руки.
- Бросок мяча сверху.
- Во время прогулки носите с собой большую игрушку или несколько игрушек.
Что должен знать 2-3-летний ребенок в академическом плане?
Около двух лет малыши могут использовать предложения из 2–3 слов и говорить «я», «ты» и «я». Ваш малыш выучит и будет использовать много слов, и его будет легче понимать во время разговора. В три года малыши обычно могут использовать предложения из 3-5 слов, а то и больше .
Ваш малыш выучит и будет использовать много слов, и его будет легче понимать во время разговора. В три года малыши обычно могут использовать предложения из 3-5 слов, а то и больше .
Математика + рисование с палочками Kwik
Научите моего ребенка треугольникам.Давайте поговорим о ТРЕУГОЛЬНИКАХ и расширим словарный запас наших детей по математике, предоставив им возможность проявить творческий подход!
Научите моего ребенка треугольникам — это задание FAST Prep. Вы можете подготовить это занятие менее чем за 3 минуты. Это веселое, обучающее занятие после школы. Отлично подходит для художников и классных учителей тоже!
Bonus – это открытая образовательная деятельность, подходящая для разных возрастов. Я положила 4 листа бумаги и коробку Kwik Stix на кухонный стол после того, как дети вернулись домой.(подробнее об этом ДЕЙСТВИТЕЛЬНО КРУТОМ продукте позже).
Лучшее для детей от 3 до 9 лет
Продолжительность: 15 минут – 1 час в зависимости от интереса ребенка.
Большое спасибо компании The Pencil Grip, Inc. за организацию этой беседы и за то, что вдохновили детей на творчество! Все мнения на 100% мои собственные. Партнерские ссылки.
Научите моего ребенка треугольникам: развитие математического словаря с помощью треугольников
Наши младшие детишки только начинают обозначать различные фигуры в нашем мире. Умение замечать, а затем идентифицировать треугольник — один из первых шагов.
- Укажите на треугольники, когда вы видите их дома или в своем районе.
- Сосчитай стороны.
- Подсчет вершин (точек).
Основное понимание состоит в том, что если у него 3 стороны и 3 вершины, то это треугольник.
Но есть еще кое-что о треугольниках, которыми вы можете поделиться со своими детьми! По мере того, как дети проходят обучение в раннем детстве, они знакомятся с большим количеством математической лексики.Если вы являетесь родителем или опекуном, возможно, ваш ребенок уже слышал некоторые из этих слов. Попросите их рассказать вам больше о треугольниках. Будьте тем, кто начнет разговор!
Попросите их рассказать вам больше о треугольниках. Будьте тем, кто начнет разговор!
Посмотрите, что ваш ребенок уже знает, и дополните эту информацию.
Существует множество различных треугольников. Их названия основаны на длине сторон и измерении угла. Углы измеряются транспортиром. Хотя транспортир обычно не знакомят с ним до старшей или средней школы, учащиеся знакомятся с различными типами треугольников гораздо раньше.
Научите моего ребенка треугольникам: определения
Равносторонний треугольник имеет 3 равные стороны и 3 равных угла.
Равнобедренные треугольники имеют 2 равные стороны и 2 равных треугольника.
Разносторонние треугольники НЕ имеют равных сторон и равных углов.
Прямоугольные треугольники имеют один угол, равный ровно 90 градусам.
Научите моего ребенка треугольникам: задание Kwik Stix Triangle Challenge
В этом задании ребенок должен нарисовать картинку, используя треугольник одного из выбранных типов.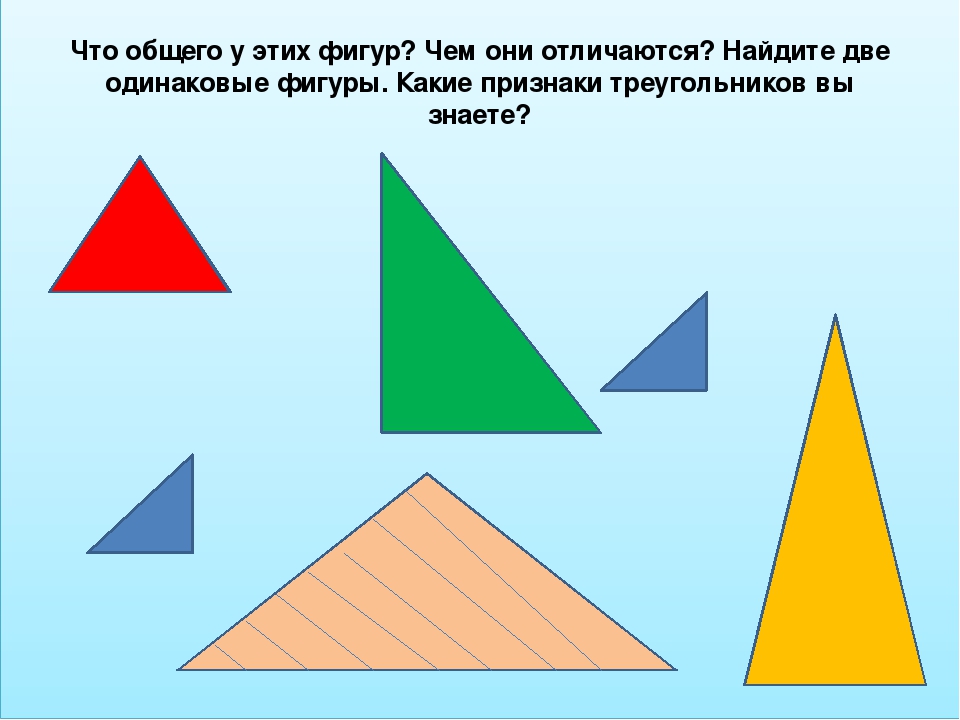 (Пролистайте статью, чтобы увидеть треугольные творения моих детей!)
(Пролистайте статью, чтобы увидеть треугольные творения моих детей!)
Необходимые материалы
Как пройти Triangle Challenge
1. Расскажите о различных видах треугольников. Отправляйтесь на прогулку по треугольнику вокруг своего дома или района, чтобы найти треугольники.
2. Раздайте детям бумагу и Kwik Stix. Попросите их выбрать один тип треугольника и создать картинку, используя этот треугольник.
3. Когда они закончат, попросите их рассказать вам о своей картине и объяснить тип треугольника, который они нарисовали.
*Совет учителю: убедитесь, что у ваших детей достаточно времени для изучения этих красок перед выполнением этого задания. Я обнаружил, что им НУЖНО время на бесплатное исследование искусства, чтобы узнать, как использовать материалы и познакомиться с тем, как они движутся и окрашиваются.
О Kwik Stix
Если вам нравится гладкость краски, когда она скользит по бумаге…
Если вам нравится держать пластиковый тюбик так, чтобы краска не стекала вам в руку…
Если вам нравятся яркие цвета маркеров…
Если вам нравится низкое беспорядок, волнительный проект…
Тогда Kwik Stix должен быть добавлен к вашим ремесленным принадлежностям!
Kwik Stix устраняет любой беспорядок, созданный рисованием, сохраняя при этом все удовольствие.
Вы видели белый стол, на котором мы рисовали, на картинках выше? Должен признаться, я немного беспокоился о том, чтобы позволить им рисовать прямо на нем. (обычно мы используем газеты). Я должен был волноваться, потому что мой 3-летний ребенок закрасил его ВЕСЬ.
К счастью, краска стерлась со стола и очень легко смылась с рук и лица. Я БЫЛ ВПЕЧАТЛЕН, и это случается нечасто, так как я очень критично отношусь к моющимся художественным принадлежностям.
Мало того, они высыхают за 90 секунд! ДА – нет фотографий, разбросанных по комнате и сохнущих.Я мог бы просто сложить их прямо вверх.
Это так просто:
Снимите крышку, поверните и покрасьте
Вызовы:
Hard to Color Mix: Сохнет так быстро, что затрудняет смешивание цветов. Дети могли смешивать, используя два одновременно. Однако эффект был очень тонким.
Дополнительно пробовали эти краски на
- картон
- плотная бумага
- картон
- холст бумага для принтера
- .

На бумаге для принтера края загнулись на следующий день. Подкладываем бумаги под тяжелую книгу, чтобы они распрямились. Если вы рисовали что-то, чтобы повесить на стену, вы можете использовать более прочную бумагу.
Kwik Stix можно заказать в упаковках по 6, 12 и 96 штук вместе с в моем любимом магазине на AMAZON! (Каждый год на день рождения прошу Прайм!!!)
Праздник математики для детей
Добро пожаловать в самый удивительный проект праздника математического искусства, который вы только можете себе представить! Сделайте елку из фрактального треугольника Серпинского.
Этот рождественский проект по математике — отличное занятие в STEAM для детей, которое они могут выполнять дома, а также в классе, где дети, работая вместе, могут построить огромное фрактальное дерево.
Для непосвященных… Треугольник Серпинского — это математически сгенерированный узор, в котором самоподобные формы повторяются в разных масштабах в бесконечной петле обратной связи. С точки зрения непрофессионала, одна и та же форма повторяется в разных размерах до бесконечности.
С точки зрения непрофессионала, одна и та же форма повторяется в разных размерах до бесконечности.
Фрактал назван в честь Вацлава Серпинского, польского математика, внесшего вклад в теорию множеств и теорию чисел.Вы можете прочитать больше о математике, связанной с треугольником Серпинского, здесь.
Вы можете увидеть мой проект по рисованию треугольника Серпинского в моей книге STEAM Kids Christmas , а теперь я предлагаю вам взять этот рисунок и превратить его в трехмерный фрактальный треугольник !
Взгляните на двухмерную рождественскую елку Серпинского:
Узнайте, как нарисовать фрактальное дерево в наборе STEAM Kids Christmas .
Хорошо, а теперь поговорим о трехмерном фрактальном математическом искусстве.
Сначала посмотрите видео, чтобы ощутить волшебство, или прокрутите вниз, чтобы найти письменные инструкции и фотографии с практическими рекомендациями.
Примечание: хотя мы сделали этот проект в виде рождественской елки, вы можете сделать его в любое время года без праздничной тематики.
Как сделать трехмерное дерево Серпинского
Что вам нужно:
- Шаблон тетраэдра. Получите печатную версию здесь. Вам понадобится 4 тетраэдра, чтобы сделать маленькое базовое дерево, и 16 тетраэдров, чтобы сделать большое фрактальное дерево.
- Плотная бумага любого цвета.
- Ножницы
- Лента
Инструкции:
Распечатайте шаблон.
Вырежьте тетраэдр, согните по сплошным линиям, сложите в объемную форму.
Подверните клапаны и закрепите края скотчем.
Сделайте базовое дерево, соединив вместе 4 тетраэдра, чтобы получился один большой тетраэдр. Три тетраэдра являются основанием, а один тетраэдр находится сверху, как показано на фотографии ниже.
Сделайте четыре таких основных дерева.
Соедините 4 основных дерева в большой тетраэдр. Опять же, три основных дерева образуют основу, а одно базовое дерево располагается сверху. Этот большой тетраэдр будет состоять из 16 исходных тетраэдров.
Поздравляю. Вы только что сделали свой первый фрактал Серпинского!
Сделайте столько больших тетраэдров, сколько пожелаете, чтобы продолжать масштабировать свой фрактальный дизайн. Следуйте правилу, согласно которому вам потребуется четыре устройства каждого размера для увеличения масштаба.
Если вы делаете это как праздничный проект, вы можете увенчать фрактальное дерево звездой. СОВЕТ: в STEAM Kids Christmas Я включил инструкции по изготовлению фрактальной звезды, также известной как «снежинка Коха»! См. ниже краткий обзор математической снежинки!
Не забывайте в течение года делать еще больше потрясающих STEAM-проектов, в том числе красивых математических художественных проектов и рисунков. У моей команды есть удивительный ресурс, который, я уверен, вам понравится.
У моей команды есть удивительный ресурс, который, я уверен, вам понравится.
Хотите, чтобы ваши дети любили быть отключенными от сети?
Подпишитесь на нашу рассылку и в качестве благодарности получите 10 игр-ожиданий, в которые дети могут играть в любое время и в любом месте.
Ваша электронная почта *никогда* не будет передана или продана третьим лицам. Нажмите здесь, чтобы посмотреть нашу политику конфиденциальности.Использование искусственного интеллекта для оживления детских рисунков
Дети рисуют удивительно уникальных и изобретательных персонажей, которые развивают наше воображение и требуют от нас немного другого мышления, чтобы узнавать людей и предметы на их рисунках. Хотя родителю или учителю может быть довольно просто увидеть, что должен показать рисунок ребенка, ИИ борется с этой задачей. Детские рисунки часто строятся абстрактно, причудливо, поэтому, если ноги фигуры расположены ненадежно или если обе руки находятся на одной стороне ее тела, это сбивает с толку даже самые современные системы искусственного интеллекта, которые превосходно обнаруживают объекты.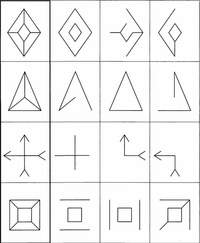 в фотореалистичных изображениях и рисунках.
в фотореалистичных изображениях и рисунках.
Исследователи мета-ИИ работают над решением этой проблемы, чтобы системы ИИ могли лучше распознавать рисунки человеческих фигур самыми разнообразными способами, которыми их создают дети.
Мы рады объявить о первом в своем роде методе автоматической анимации нарисованных детьми фигурок людей и человекоподобных персонажей (например, персонажа с двумя руками, двумя ногами, головой и т. д.), который приносит эти рисунки оживают за считанные минуты с помощью ИИ. Загружая их в нашу систему прототипов, родители и дети могут испытывать волнение, наблюдая, как их рисунки превращаются в движущихся персонажей, которые танцуют, прыгают и прыгают.И они даже могут загрузить свои анимированные рисунки, чтобы поделиться ими с друзьями и семьей. Если родители захотят, они также могут отправить эти рисунки, чтобы помочь улучшить модель ИИ.
Что-то пошло не так
У нас возникли проблемы с воспроизведением этого видео. Чтобы посмотреть видео, обновите веб-браузер.
Обучая ИИ эффективно работать с этой типичной для человека формой творчества, мы надеемся, что этот проект приблизит нас к созданию ИИ, способного понимать мир с человеческой точки зрения.Мы также надеемся, что эта работа подтолкнет к дальнейшим исследованиям в области использования ИИ для повышения креативности людей и вдохновит на творческие новые способы использования этой технологии.
Почему автоматические инструменты анимации ИИ не работают с детскими рисунками
Наша цель состояла в том, чтобы создать систему ИИ, которая может идентифицировать и автоматически анимировать человекоподобные фигуры на детских рисунках с высокой вероятностью успеха и без какого-либо вмешательства со стороны человека. В то время как многие инструменты и методы искусственного интеллекта предназначены для обработки реалистичных изображений людей, детские рисунки добавляют уровень разнообразия и непредсказуемости, что значительно усложняет определение того, что изображено.«Люди» на детских рисунках бывают самых разных форм, цветов, размеров и масштабов, с небольшим сходством, когда речь идет о симметрии тела, морфологии и точке зрения.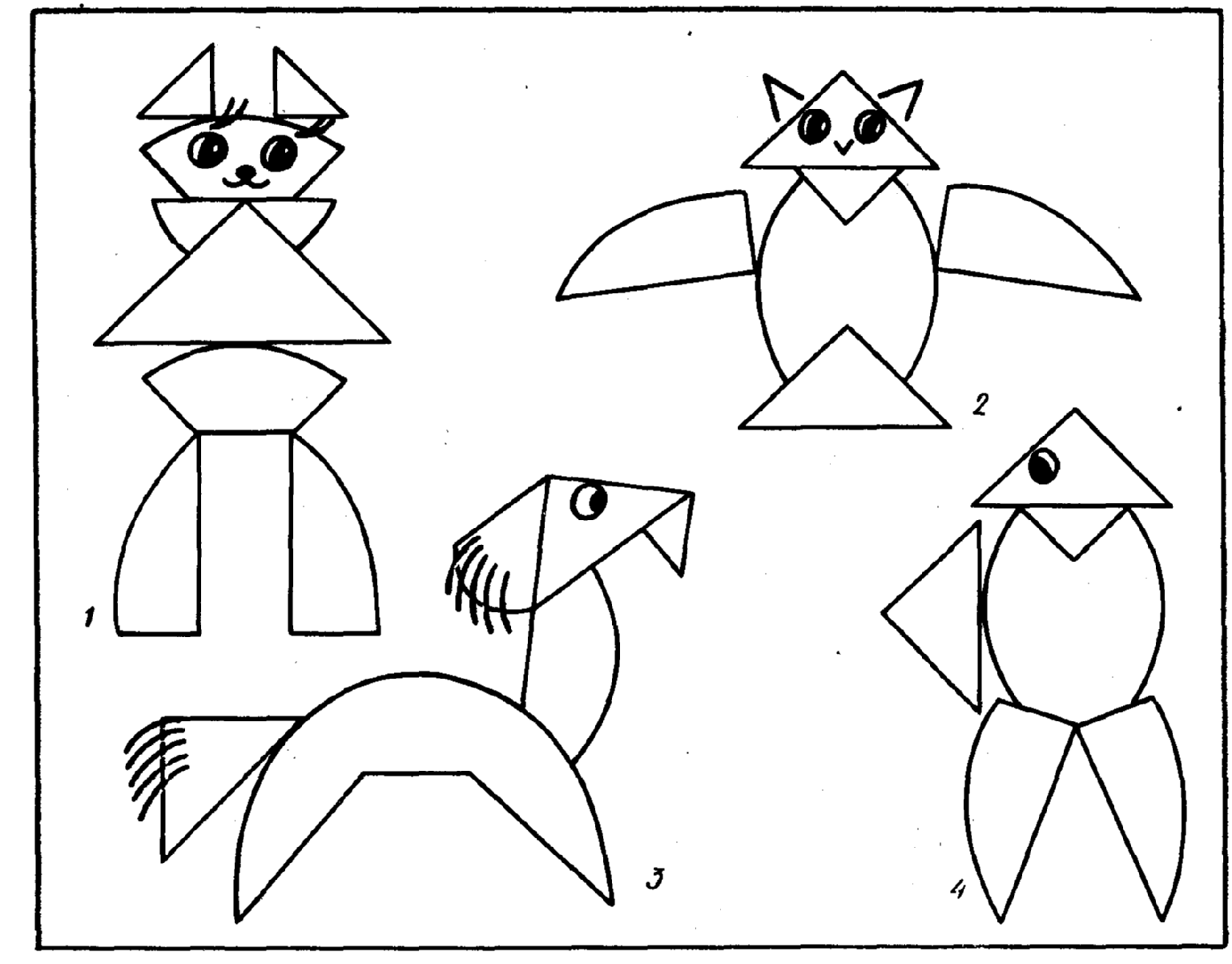 Мы подошли к этой задаче искусственного интеллекта с помощью четырехэтапного процесса, точно настраивая наш подход на каждом этапе, чтобы адаптироваться к огромному разнообразию детских рисунков.
Мы подошли к этой задаче искусственного интеллекта с помощью четырехэтапного процесса, точно настраивая наш подход на каждом этапе, чтобы адаптироваться к огромному разнообразию детских рисунков.
Что-то пошло не так
У нас возникли проблемы с воспроизведением этого видео. Чтобы посмотреть видео, обновите веб-браузер.
Идентификация человекоподобных фигур с помощью обнаружения объектов
Первым шагом в оживлении детских рисунков людей является выделение человеческих фигур на фоне и других типов персонажей на картинке.Обнаружение объектов с помощью существующих методов работает достаточно хорошо на детских рисунках, но маски сегментации недостаточно точны, чтобы их можно было использовать для анимации. Чтобы решить эту проблему, мы вместо этого используем ограничивающие рамки, полученные от детектора объектов, и применяем ряд морфологических операций и шагов обработки изображения для получения масок.
При извлечении человекоподобных персонажей из детского рисунка для обработки мы используем модель обнаружения объектов на основе сверточной нейронной сети Meta AI, Mask R-CNN, реализованную в Detectron2. Mask R-CNN предварительно обучен на одном из крупнейших общедоступных наборов данных сегментации, но он состоит из фотографий реальных объектов, а не рисунков. Для работы с чертежами модель необходимо было отрегулировать, что мы и сделали с ResNet-50+FPN, чтобы предсказать один класс — «человеческая фигура». Мы предложили нашим коллегам из Meta поделиться и анимировать рисунки своих детей с помощью нашей системы, и мы получили около 1000 рисунков, которые помогли нам обучить ИИ.
Mask R-CNN предварительно обучен на одном из крупнейших общедоступных наборов данных сегментации, но он состоит из фотографий реальных объектов, а не рисунков. Для работы с чертежами модель необходимо было отрегулировать, что мы и сделали с ResNet-50+FPN, чтобы предсказать один класс — «человеческая фигура». Мы предложили нашим коллегам из Meta поделиться и анимировать рисунки своих детей с помощью нашей системы, и мы получили около 1000 рисунков, которые помогли нам обучить ИИ.
После тонкой настройки сеть хорошо распознала человеческие фигуры в наборе тестовых данных.Случаи сбоев, которые мы наблюдали, относились к четырем различным категориям: не включая всю фигуру, не отделяя фигуру от фона, не разделяя несколько близко расположенных фигур и неправильно идентифицируя нечеловеческие фигуры (например, деревья). Мы считаем, что эти типы сбоев связаны с большим разнообразием человеческих фигур в тренировочном наборе, и модель будет продолжать улучшаться по мере того, как она будет получать больше рисунков для обучения.
Что-то пошло не так
У нас проблемы с воспроизведением этого видео.Для просмотра видео обновите веб-браузер.
Поднятие человекоподобной фигуры из сцены с помощью маскирования символов
После идентификации и извлечения человеческой фигуры из рисунка следующим шагом подготовки к анимации является отделение ее от других частей сцены и фона в процессе, называемом маскированием . Маска должна точно отражать контуры фигуры, потому что она будет использоваться для создания сетки, которая затем будет деформирована для создания анимации. Если все сделано правильно, маска будет включать в себя все части персонажа и ничего из фона.
Несмотря на то, что Mask R-CNN может выводить маски, мы обнаружили, что они не подходят для анимации. Предсказанные маски часто не могли захватить всю фигуру, когда части тела сильно различались по внешнему виду, как, например, на рисунке ниже, на котором показан большой желтый треугольник для тела и один карандашный штрих для руки. Предсказанные маски также часто терпели неудачу из-за пропуска середины «полых» символов или символов, нарисованных в виде контуров и не окрашенных.
Предсказанные маски также часто терпели неудачу из-за пропуска середины «полых» символов или символов, нарисованных в виде контуров и не окрашенных.
Вместо этого мы разработали классический подход, основанный на обработке изображений, который более устойчив к этим вариациям.С помощью этого метода мы обрезаем изображение, используя его предсказанную ограничивающую рамку для каждого обнаруженного символа. Затем мы применяем адаптивную пороговую обработку и морфологические операции закрытия/диапазона, заливку заливкой от краев блока и предполагаем, что маска представляет собой самый большой полигон, не затронутый заливкой заливки. Хотя этот метод прост и эффективен для извлечения точных масок, подходящих для анимации, он может дать сбой, если фон загроможден, символы нарисованы близко друг к другу или на бумаге есть морщины, разрывы или тени на странице.
Маски сегментации от Mask R-CNN иногда не соответствовали форме персонажа (середина, верх) или не включали все части персонажа, например, руки-палки (середина, низ).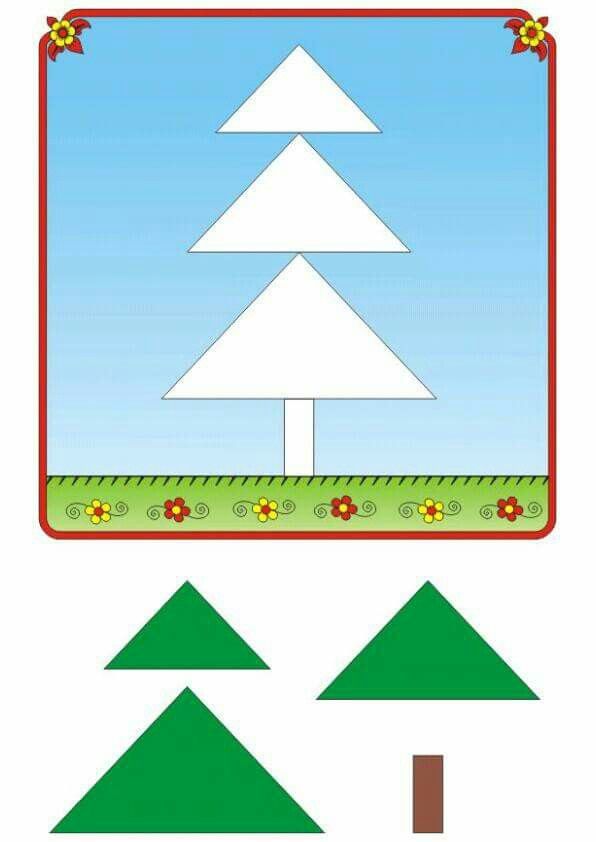 Во многих ситуациях использование конвейера обработки изображений в предсказанной ограничивающей рамке Mask R-CNN приводит к маскам, более подходящим для анимации (справа).
Во многих ситуациях использование конвейера обработки изображений в предсказанной ограничивающей рамке Mask R-CNN приводит к маскам, более подходящим для анимации (справа).
Подготовка к анимации с помощью оснастки
Дети рисуют фигуры с самыми разнообразными формами тела, намного превосходящими обычную человеческую форму с головой, руками, ногами и туловищем.Многие дети начинают изображать людей как так называемых «головастиков», без туловища, с руками и ногами, прикрепленными непосредственно к голове. Некоторые дети переходят к «переходным» фигурам, у которых ноги отходят от головы, а руки отходят от верхних конечностей. Нам нужен был метод оснастки, который мог бы справиться с этим типом морфологических вариаций.
Мы используем AlphaPose, модель, обученную распознаванию поз человека, для определения ключевых точек на человеческих фигурах, которые могут служить бедрами, плечами, локтями, коленями, запястьями и лодыжками.AlphaPose был обучен на изображениях реальных людей, поэтому, прежде чем мы смогли адаптировать его для обнаружения поз на детских рисунках, нам пришлось переобучить его для обработки типов вариаций, присутствующих в детских рисунках. Мы сделали это, внутренне собрав и аннотировав небольшой набор данных детских рисунков человеческих фигур. Затем с помощью детектора позы, обученного на этом исходном наборе данных, мы создали внутренний инструмент, который позволяет родителям загружать и анимировать рисунки своих детей, а нам позволяет использовать загруженные рисунки для дополнительного обучения.По мере поступления новых данных мы итеративно переобучали модель, пока не достигли высокого уровня точности.
Мы сделали это, внутренне собрав и аннотировав небольшой набор данных детских рисунков человеческих фигур. Затем с помощью детектора позы, обученного на этом исходном наборе данных, мы создали внутренний инструмент, который позволяет родителям загружать и анимировать рисунки своих детей, а нам позволяет использовать загруженные рисунки для дополнительного обучения.По мере поступления новых данных мы итеративно переобучали модель, пока не достигли высокого уровня точности.
Анимация 2D-фигур с помощью 3D-захвата движения
Когда у нас есть маска и совместные прогнозы, у нас есть все необходимое для создания анимации. Мы начинаем с использования извлеченной маски для создания сетки, текстурируя ее с помощью исходного рисунка. Используя предсказанные места соединений, мы создаем скелет персонажа. Вращая кости и используя новые места соединений для деформации сетки, мы можем перемещать персонажа в различные позы.Перемещая персонажа в серию последовательных поз, мы можем создать анимацию. Мы можем выбирать различные движения для применения в зависимости от того, насколько точны предсказания суставов: в случаях, когда обе руки и ноги были предсказаны правильно, анимация может происходить плавно. Но если на чертеже нет конечности, то значения ее совместной достоверности будут низкими, и нам придется отказаться от анимаций, требующих этой конечности, попросить пользователя исправить прогноз или объявить анимацию неудачной.
Мы можем выбирать различные движения для применения в зависимости от того, насколько точны предсказания суставов: в случаях, когда обе руки и ноги были предсказаны правильно, анимация может происходить плавно. Но если на чертеже нет конечности, то значения ее совместной достоверности будут низкими, и нам придется отказаться от анимаций, требующих этой конечности, попросить пользователя исправить прогноз или объявить анимацию неудачной.
Чтобы анимировать 2D-фигуры с помощью 3D-захвата движения, мы используем тот факт, что многие дети рисуют, используя то, что мы называем искривленной перспективой. Многие дети обычно сначала рисуют части тела с их наиболее узнаваемой точки зрения, которая может отличаться от того, как они выглядят на реальных людях. Например, они склонны рисовать ноги и ступни сбоку, а головы и туловища — спереди.
Мы воспользуемся этой перспективой на этапе перенацеливания движения.Независимо для нижней и верхней части тела мы автоматически определяем, является ли движение более узнаваемым при виде спереди или сбоку.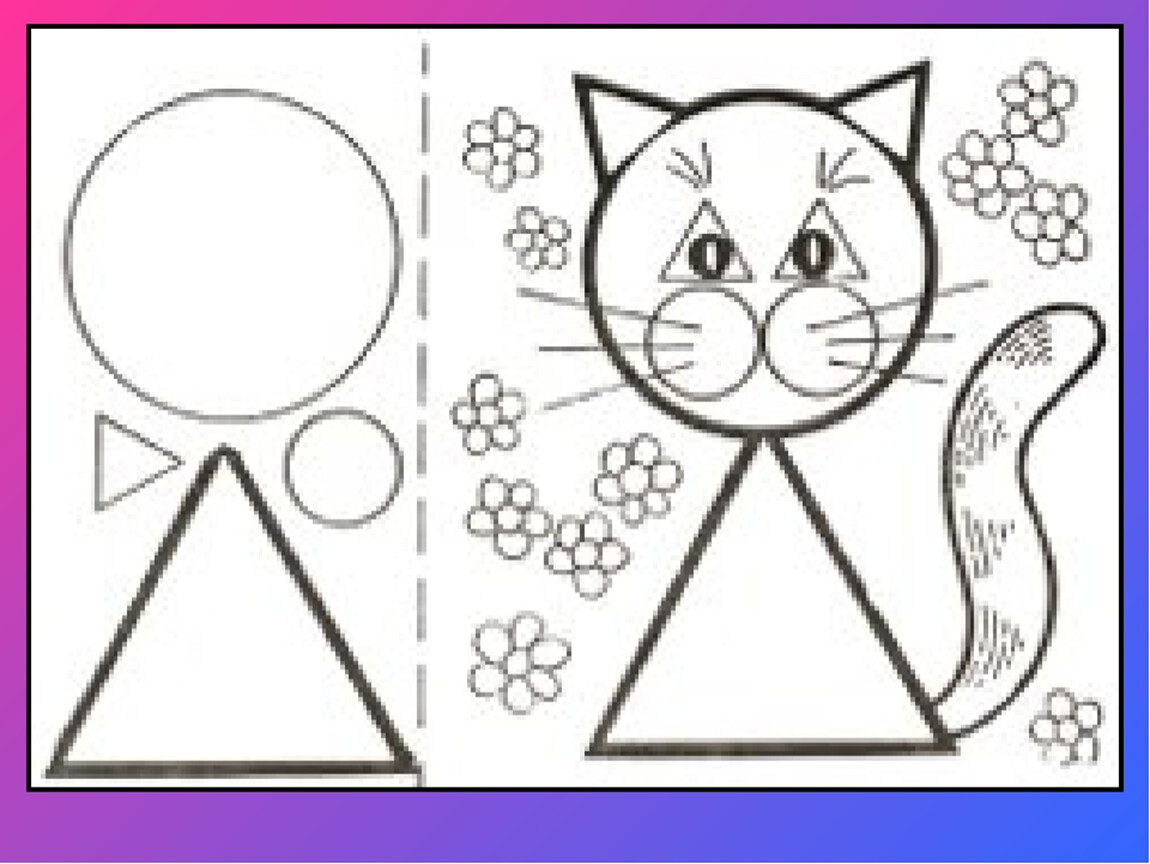 Используя выбранные виды, мы проецируем движение на одну 2D-плоскость и используем ее для управления персонажем. Мы проверяем результаты такого подхода к перенацеливанию движения, используя исследования восприятия пользователей, проводимые через Mechanical Turk.
Используя выбранные виды, мы проецируем движение на одну 2D-плоскость и используем ее для управления персонажем. Мы проверяем результаты такого подхода к перенацеливанию движения, используя исследования восприятия пользователей, проводимые через Mechanical Turk.
Слева: Перед анимацией мы создаем персонажа из рисунка. Справа: мы успокаиваем персонажа, проецируя кадр данных захвата движения на 2D-плоскость и поворачивая конечности персонажа, чтобы они соответствовали конечностям проекта.Мы можем проецировать данные захвата движения спереди (верхний ряд), сбоку (средний ряд) и с искривленной точки зрения (снизу).
Принятие во внимание искривленной перспективы полезно, потому что многие типы движения не попадают точно в одну плоскость проекции. Например, при прыжках со скакалкой руки и запястья стремятся двигаться преимущественно во фронтальной плоскости, а сгибаемые ноги стремятся двигаться в сагиттальной плоскости. Из-за этого мы не определяем единую плоскость движения для позы захвата движения, а определяем плоскости проекции для верхней и нижней частей тела отдельно.
Использование ИИ для создания более сложных анимаций
ИИ стал мощным инструментом для творчества, расширяющим возможности художников; вдохновляющие новые формы самовыражения, такие как эффекты дополненной реальности; предоставление модных советов; и даже создавать новые танцевальные номера. Мы надеемся, что наш инструмент для анимации вдохновит людей экспериментировать со своими рисунками и направить их в неизведанные направления.
Делясь своими работами, мы также надеемся стимулировать работу компьютерного зрения в области любительских рисунков. Будущие исследования для этого проекта могут быть сосредоточены на выявлении и применении более адаптированных движений к подкатегориям фигур, таким как супергерои, принцессы, монстры и ниндзя.Более детальный анализ частей персонажа также был бы полезен для определения антенн, хвостов и плащей, например, и применения вторичных элементов движения для повышения привлекательности анимации. Возможно, когда-нибудь система искусственного интеллекта сможет взять сложный рисунок, а затем мгновенно создать подробный анимационный мультфильм, используя несколько фантастических персонажей, взаимодействующих друг с другом и элементами фона.


 (Карандаш.)
(Карандаш.)

