Урок по геометрии и ИЗО на тему «Геометрические фигуры»
Муниципальное бюджетное общеобразовательное учреждение «Колодезянская школа»
КРАСНОГВАРДЕЙСКИЙ РАЙОН
РЕСПУБЛИКА КРЫМ
Геометрия
7 класс
Интегрированный урок
математики и изобразительного искусства
по теме
«Геометрические фигуры в орнаменте»
Подготовила и провела
учитель математики
Трандах А. Н.
с. Колодезное
Геометрические фигуры в орнаменте.
Интегрированный урок математики и изобразительного искусства.
Тип урока: Интегрированный урок (математика и изобразительное искусство)
Цели урока:
Образовательная: ознакомление учащихся с комбинациями изученных геометрических фигур, используемых в орнаменте. Приобщение к народно-прикладному искусству. Применение геометрических фигур в практике составления орнамента.
Приобщение к народно-прикладному искусству. Применение геометрических фигур в практике составления орнамента.
Развивающая: развитие интереса к прикладному искусству, формирование умений и навыков по применению геометрических фигур в практике составления орнамента, выработка смекалки, ловкости, глазомера, пространственного воображения, интуиции.
Воспитательная: привитие интереса к народной культуре, любви к родному краю, воспитания у детей стремления к реализации своих учебных возможностей.
Методическое обеспечение урока:
выставка методических пособий
на классной доске — геометрические фигуры
раздаточные листы с фрагментами узоров
Ход урока
1. Организация класса.
2. Вступительная беседа.
Из уроков истории вы знаете, что во все времена человек стремился к прекрасному. Люди с давних времен украшали свою одежду, жилище, орудия труда и предметы быта различными орнаментами, узорами.
Изначально в глубокой древности изображения на орнаментах должны были защищать дом от злых сил, то есть это были не просто рисунки, а магические символы, которые должны были защищать их обладателей от нечистой силы.
Каждый элемент орнамента имел смысл. То есть зная, что обозначает в орнаменте тот или иной символ, можно было «прочитать», что хотел выразить автор орнамента. Эти символы мы встречаем в национальной одежде, рушниках, полотенцах. Позже орнамент превратился просто в элементы украшения дома.
(приложение)
Слово «орнамент» в переводе с латинского (ornamentum) означает «украшение». Орнаментом называют узор, построенный на повторе и чередовании составляющих его элементов. Орнамент — это украшение, которое состоит из рисунков и они повторяются через определенные расстояния или интервалы. Что такое интервал? (промежуток во времени, в расстоянии) Вот например, салют… Салют, потом маленький перерыв. А мы ждем. Когда появятся новые огоньки в небе. Потом снова салют, потом ждем, и так повторяется много раз. Вот также интервал есть и в орнаменте.
А мы ждем. Когда появятся новые огоньки в небе. Потом снова салют, потом ждем, и так повторяется много раз. Вот также интервал есть и в орнаменте.
Орнамент встречается в нашей жизни везде. Он украшает наши дома, например, каменный орнамент. Очень красивы деревенские дома: ставни окон могут быть украшены орнаментом, который вырезали резчики. Он может быть очень красивым, различные узоры украшают посуду, мебель.
(приложение)
Учитель: Приведите примеры, где дома мы можем увидеть орнамент?
б) Орнамент можно встретить и у себя дома — на обоях, на дорожке, на посуде. Орнаментом и раньше украшалась не только одежда и полотенца, узор покрывал прялки, шкатулки, лавки и сундуки. Его даже можно его увидеть на печенье, которое все мы любим. Он может состоять из ромбиков, кружочков, квадратиков. То есть орнамент украшает нашу жизнь.
Учитель: С чем можно сравнить орнамент?
Учитель: Вывод: орнамент придает предметам нарядный и праздничный вид.
Источником создания оригинальных композиций для орнамента современного человека стала природа. Любуясь природой, человек заметил в ней множество необычных форм и интересных цветовых оттенков: плоды и листочки разных растений, узоры на крыльях бабочек и птиц.
Не осталась в стороне и математика: художники, дизайнеры, стеклодувы и т.д. используют геометрические фигуры для создания орнаментов.
Для выполнения узора используются контрастные цвета:
Красный — зеленый
Оранжевый — синий
Фиолетовый – желтый
Цвет в узоре имел особое значение. Красный цвет выражал восторг, радость. Это цвет солнца, огня, жизни. Красный цвет олицетворял мужское начало. Белый цвет связывался со светом, чистотой и олицетворял женское начало. Черный цвет придает выразительность узору.
Математик: Сегодня мы будем выполнять геометрический орнамент. А раз орнамент геометрический, то нам нужно вспомнить геометрические фигуры, которые вам известны. А вспоминать мы будем, отгадывая загадки.
А вспоминать мы будем, отгадывая загадки.
2. Геометрические фигуры.
Загадки:
Узнает очень просто Меня любой дошкольник: Три стороны и три угла –
Зовусь я — треугольник!
Он давно знакомый мой. Каждый угол в нем прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
А зовут его? Квадрат!
Я — известный всем овал. У меня есть верный друг. Без него я никуда.
А зовут его все — круг!
Это всем известно в мире Что у нас всего четыре. Четыре стороны
И столько же вершин. Четырежды важные дела
Мы четырежды совершим! Прямоугольник.
3) Беседа.
Итак, мы с вами повторили наш материал. Теперь интересная часть нашего сегодняшнего урока. Посмотрите, пожалуйста, следующий рисунок. Какие на ваш взгляд здесь использованы геометрические фигуры? Квадраты — «сундучки»
На следующем рисунке использованы такие геометрические фигуры, как окружность, треугольник означает «солнце, свет, добро».
Следующий орнамент с использованием овала, ромба может означать «лодку, озеро, глаза»
4) Творческая работа учащихся.
1. Букет из «треугольников»
2. «Геометрический» гусь, собачка ….
а) демонстрация орнаментов: («проба пера»)
Теперь каждому из вас дается индивидуальная работа, то есть в течение 10 минут, вы должны используя геометрические фигуры придумать и создать свой орнамент (Если останется время, желающие могут рассказать о своей работе, какие геометрические фигуры они использовали.)
б) Раскраска закладок.
5) Подведение итогов. Выставление оценок.
Спасибо за работы, итак, к какому главному итогу нашего урока мы можем прийти? Геометрические фигуры широко используются у всех народов. И каждое значение той или иной фигуры различно. Оказывается, не так уж просто взять и нарисовать определенную геометрическую фигуру. Чтобы правильно и красиво нарисовать узор нужно иметь хорошее трудолюбие, усердие и правильный глазомер.
И каждое значение той или иной фигуры различно. Оказывается, не так уж просто взять и нарисовать определенную геометрическую фигуру. Чтобы правильно и красиво нарисовать узор нужно иметь хорошее трудолюбие, усердие и правильный глазомер.
Спасибо за урок, до свидания!
Индивидуальный проект по математике «Необычные геометрические фигуры» (7 класс)
Министерство образования и науки Челябинской области
Муниципальное автономное общеобразовательное учреждение
“Миасская средняя общеобразовательная школа № 16”
Индивидуальный проект
«Необычные геометрические фигуры»
Тип проекта: информационно-познавательный
Автор проекта: Ходова Виктория,
обучающаяся 7-а класса МАОУ «МСОШ № 16»,
Наставник проекта: Доронина Елена Александровна,
учитель математики
Миасс
2019
Содержание:
Введение……………………………………………………………………………………. …3
…3
1. Теоретическая часть…………………………………………………………………….….4
1.1. Виды геометрических фигур……………………………………………………………..4
1.2. Необычные геометрические фигуры……………………………………………………..…5
2. Практическая часть…………………………………………………………………….….12
2.1. Построение необычных геометрических фигур………………………………………12
2.2. Коллекция головоломок………………………………………………………………..12
Заключение…………………………………………………………………………………….13
Список литературы………………………………………………………………………….14
Приложение……………………………………………………………………………………..15
Аннотация
В данной работе рассказывается о тех геометрических фигурах, которые мы не изучаем на уроках геометрии в школе, но именно они окружают нас в действительности, в архитектуре, в компьютерных играх и головоломках. Автор дает определение необычной и удивительной геометрическим фигурам, рассмотрев их виды.
В программе GNU Dr. Geo создала необычную геометрическую фигуру, и собрала коллекцию головоломок, состоящую из геометрических фигур, разгадывая которые можно составить необычную геометрическую фигуру.
Geo создала необычную геометрическую фигуру, и собрала коллекцию головоломок, состоящую из геометрических фигур, разгадывая которые можно составить необычную геометрическую фигуру.
Введение
Существуют различные виды геометрических фигур. На уроках математике я изучала плоские и объёмные геометрические фигуры. Но в реальном мире существуют и другие фигуры, которые называются необычные. Я уверена, что необходимо знать не только простые виды геометрических фигур, изучаемые по школьной программе, но и другие необычные геометрические фигуры.
Я не нашла определения необычных геометрических фигур и обратилась к словарь русского языка [4].
Необычный — не такой, как все, не похожий на обычное или привычное.
Фигура- это часть плоскости, ограниченная замкнутой линией.
Необычная геометрическая фигура с моей точки зрения – эта фигура, состоящая из обычных геометрических фигур, но не обычно сформированных. Можно в любой сложной фигур рассмотреть простые геометрические фигуры, которые мы изучаем в школе.
Можно в любой сложной фигур рассмотреть простые геометрические фигуры, которые мы изучаем в школе.
Основанием для работы над темой проекта послужило, желание познакомиться с многообразием геометрических фигур, узнать их применение и стремление заинтересовать в это своих одноклассников.
Цель проекта: выяснить определение и применение необычных геометрических фигур.
Задачи проекта:
Проанализировать литературу по теме проекта и подобрать необходимую информацию.
Изучить виды необычных геометрических фигур и их применение.
Собрать коллекцию головоломок, состоящих из необычных геометрических фигур.
1. Теоретическая часть
1.1. Виды геометрических фигур
Геометрия, как и всякая наука, возникла под влиянием жизненных потребностей. Слово «геометрия» означает «землемерие» и ясно указывает на источник его происхождения.
Слово «геометрия» означает «землемерие» и ясно указывает на источник его происхождения.
Занимались измерениями особые специалисты, их называли «натягивателями веревки» – гарпетонаптами. Фигуры используются повсюду: в строительстве (строят зданий в виде геометрических фигур), технике (изобретают новые приборы), науке (изучают их строение) и одежду (рисуют и моделируют).
Основатель и ведущий исследователь в области фрактальной геометрии, лауреат премии Вольфа по физике, Бенуа Мандельброт говорил: «Геометрию часто называют «холодной» и «сухой». Одна из причин этого состоит в ее неспособности описать форму облака, горы, береговой линии или дерева. Облака — не сферы, горы — не конусы, береговые линии — не окружности, древесная кора не гладкая, молния распространяется не по прямой. Многие природные объекты настолько иррегулярны и фрагментированы, что по сравнению со стандартной геометрией Евклида природа обладает не просто большей сложностью, а сложностью совершенно иного уровня» [2].
Что же такое геометрическая фигура?
Геометрическая фигура— это множество точек на поверхности, которые образуют конечное количество линий.
Геометрических фигур много. Те фигуры, которые известны людям с древних времён, носят греческие (или латинские имена), потому что именно греки создали геометрию и дали фигурам имена. Названия геометрических фигур первоначально были названиями предметов, имеющих форму близкую к форме фигур. Это показывает, что геометрия возникла для решения практических задач и тесно связана с человеческим трудом. Названия некоторых геометрических фигур отражают их свойства. Конус «conos» (греч.) — сосновая шишка. Это показывает, что геометрия возникла для решения практических задач и тесно связана с человеческим трудом.
Я поняла, что названия геометрических фигур совсем не странные, а очень даже разумные и понятные. Просто почти все они пришли к нам из греческого или латинского языков.
С самого начала мы на уроках геометрии изучаем простые фигуры, которые являются плоскими, то есть располагаются на одной плоскости.
Плоские фигуры – это фигуры, связные замкнутые линии, ограниченное конечным числом попарно не пересекающихся кривых [5].
В случае, если все входящие в состав границы плоской фигуры кривые являются ломаными, то фигура называется многоугольной фигурой. Односвязная многоугольная фигура является многоугольником.
Виды плоских фигур:
Квадрат — правильный четырёхугольник или ромб, у которого все углы прямые, или параллелограмм, у которого все стороны и углы равны.
Прямоугольник — это параллелограмм, у которого все углы прямые (равны 90 градусам)
Ромб — это четырёхугольник, у которого все стороны равны. Ромб является параллелограммом. Ромб с прямыми углами называется квадратом.
Трапеция — четырёхугольник, у которого только одна пара противолежащих сторон параллельна.
Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника (смотри рисунок 1).
Далее, перед нами открывается мир объёмных фигур, которые необходимо представлять и понимать, как они расположены и как грамотно их нарисовать, чтобы было понятно не только вам, но и окружающим.
Итак, перечень основных фигур можно изучить ниже.
Рис.1. Виды плоских фигур
Объёмные геометрические фигуры — это фигуры занимающиеся определённое пространство, возвышается над плоской поверхностью.
Виды объёмных геометрических фигур вы можете увидеть в таблице 1 (приложение 2).
1.2. Виды сложных (необычных) геометрических фигур
На протяжении долгого времени психологи использовали геометрические фигуры разного рода при изучении человеческой личности. С начала века было разработано более 200 фигур и иллюзий для анализа психологических аспектов зрительного процесса и умственной деятельности пациентов. Они рассматривали эти объекты и пытались понять их. При помощи таких экспериментов, когда глазу предлагалась противоречивая информация, было получено множество новых сведений о типах личности. Некоторые из этих фигур даже включают в себя невозможные объекты.
Очень интересно наблюдать за человеком, рассматривающим невозможный объект, и так же интересно наблюдать за тем, как он пытается понять его. Невозможные объекты важны для психологов, выясняющих, что же привлекает внимание людей.
Удивительные фигуры:
Трибар
Эта фигура – возможно, первый опубликованный в печати невозможный объект показан на рисунке 2 (смотри приложение 1), С первого взгляда трибар кажется просто изображением равностороннего треугольника. Однако стороны, сходящиеся вверху рисунка, кажутся перпендикулярными. В то же время левая и правая грани внизу тоже кажутся перпендикулярными. Вы смотрите на каждый угол треугольника под разным углом зрения. Если рассматривать отдельные части этого треугольника, как бы он ни назывался, то их еще можно считать реальными, но в общем, эта фигура не может существовать в действительности.
Тройной деформированный трибар
Эта простая фигура изображена на рисунке 3 (смотри приложение 1) , но более глубокая разработка треугольника Пенроуза. На примере первого трибара можно было увидеть лишь одно невозможное соединение, а в этой фигуре – несколько. Предмет кажется довольно убедительным, но если вы попробуете построить что-то подобное в реальности, то у вас ничего не выйдет. Вот в чем суть всех невозможных объектов!
Предмет кажется довольно убедительным, но если вы попробуете построить что-то подобное в реальности, то у вас ничего не выйдет. Вот в чем суть всех невозможных объектов!
Крылатый трибар
Еще одна разработка концепции трибара показана на рисунке 4 (смотри приложение 1). Она показывает, как легко можно создать уникальные и интересные вариации на одну и ту же тему. Из трибара можно получить множество интересных фигур!
Тройное домино
Чтобы построить эту фигуру, состоящую из трех элементов, в реальности потребуется четыре элемента изображена на рисунке 5 (смотри приложение 1). Попытайтесь-ка сами смастерить ее, играя в домино! При ближайшем рассмотрении становится ясно, что данная фигура основана на неправильном повороте в перспективе. В действительности эта фигура – не что иное как трибар, в котором три основных элемента были заменены известными элементами из игры в домино.
Кубик со штифтами
Эта более замысловатая версия трибара была придумана благодаря детским кубикам. Объект показан на рисунке 6 (смотри приложение 1), и содержит два дополнительных компонента, похожих на штифты, которые пронизывают кубик и соединяются снаружи невероятным образом. Но только само по себе соединение делает невозможную фигуру возможной, по крайней мере на бумаге.
Объект показан на рисунке 6 (смотри приложение 1), и содержит два дополнительных компонента, похожих на штифты, которые пронизывают кубик и соединяются снаружи невероятным образом. Но только само по себе соединение делает невозможную фигуру возможной, по крайней мере на бумаге.
Усеченный трибар
Это трибар, один угол которого отрезали, «отсекли» изображён на рисунке 7 (смотри приложение 1). В результате у фигуры получилось четыре стороны. Так же, как и в случае с невозможным трибаром, поначалу глаз воспринимает эту фигуру как стереометрический объект, но потом – как нечто похожее на оконную раму. Эта фигура не может существовать в реальности, но опять же – на нее нельзя не обратить внимание Эффект «усеченного трибара» достигается как при помощи смещенной перспективы, так и благодаря неправильному соединению.
Перекрещенный ромб
Эта фигура показана на рисунке 8 (смотри приложение 1), представляет собой не что иное, как два трибара, соединенных вместе в форме ромба. Вы можете расширить эту конструкцию, присоединяя дополнительные трибары. Как уже говорилось ранее, Эшер в своей знаменитой композиции соединил вместе три трибара. Здесь нет никаких ограничений. Теоретически можно соединить много таких трибаров по образцу лоскутного одеяла или другого дизайна.
Вы можете расширить эту конструкцию, присоединяя дополнительные трибары. Как уже говорилось ранее, Эшер в своей знаменитой композиции соединил вместе три трибара. Здесь нет никаких ограничений. Теоретически можно соединить много таких трибаров по образцу лоскутного одеяла или другого дизайна.
Головоломка из кубиков
Эта фигура – еще одна версия известного трибара изображена на рисунке 9 (смотри приложение1). На сей раз объект как бы поставлен соответствующим (хотя и невозможным) образом на дыбы на всеобщее обозрение. Из-за странной взаимосвязи между реальностью и фантазией кажется, что эта фигура слегка пикирует и парит в воздухе! Дополнительная иллюзия «полета» создается смещением акцентов на заднем и переднем плане.
Усеченный деформированный трибар
Это выразительное произведение мини-искусства изображён на рисунке 10 (смотри приложение 1), может опять же дать толчок для развития массы новых идей по созданию всего, что угодно, начиная со стульев; для сада и заканчивая скульптурами для городской площади!
Визуальные виды искусства удовлетворяют огромное количество человеческих потребностей. Невозможные фигуры, похожие на эту, представляют собой увлекательное сочетание занимательности и развлечения. Их можно назвать «искусством для отдыха»
Невозможные фигуры, похожие на эту, представляют собой увлекательное сочетание занимательности и развлечения. Их можно назвать «искусством для отдыха»
Летучий шестиугольник
Эта новая интересная вариация трибара показана на рисунке 11 (смотри приложение 1), основанная на симметрии и повторении, напоминает изображение, которое можно увидеть в калейдоскопе. Вы можете заметить, что основной лежащий в основе трибара принцип присутствует и в этой уникальной конструкции.
Прямоугольный триэдр (трехгранник)
Эта фигура имеет такие же правила построения, как и остальные виды трибара изображена на рисунке 12 (смотри приложение 1). В основном это трехмерный равносторонний треугольник, составленный из прямоугольных тел. Пытаясь понять эту фигуру, вы неизбежно будете перескакивать взглядом с одного края на другой.
Необычные геометрические фигуры:
Полимино
Полимино, или полиомино (англ. «polyomino») — плоские геометрические фигуры, образованные путём соединения нескольких равных квадратов по их сторонам (смотри рисунок 13). Это полиформы, сегменты которых являются квадратами.
«polyomino») — плоские геометрические фигуры, образованные путём соединения нескольких равных квадратов по их сторонам (смотри рисунок 13). Это полиформы, сегменты которых являются квадратами.
Рис. 13. Полимино
Иначе говоря, клетки каждого полимино можно обойти за конечное число ходов шахматной ладьи. Название «полимино», или «полиомино» было придумано Соломоном Голомбом в 1953 году, и затем популяризировано Мартином Гарднером. По аналогии с полимино строятся полиамонды, сформированные из равносторонних треугольников; полигексы, сформированные из правильных шестиугольников, а также другие плоские полиформы. Полимино также обобщаются на случай более высоких размерностей (сформированные из кубов — поликубы, или из гиперкубов — полигиперкубы).
Применение полимино
Полимино использовались в занимательной математике по крайней мере с 1907 года, а известны были ещё в древности. Многие результаты с фигурами, содержащими от 1 до 6 квадратов, были впервые опубликованы в журнале «FairyChessReview» в период с 1937 по 1957 г., под названием «Проблемы рассечения». Кроме того, полимино широко используются в различных головоломках и логических задачах. Одна из популярнейших игр в истории была создана малоизвестным российским программистом Алексеем Пажитновым. Он работал в Вычислительном Центре при Академии Наук СССР и занимался изучением проблем искусственного интеллекта, компьютерной графикой и вопросами компьютерного распознавания голоса. В основу идеи «Тетриса» была положена американская головоломка «PentominoPuzzle», придуманная математиком Соломоном Голомбом. Она состояла из пяти квадратов (пентомино – от греч. «пента» – пять) и ставила задачей правильно расположить в коробке геометрические фигуры. Планируя создать компьютерный вариант «Пентомино», Пажитнов успешно дополнил идею: собирать фигурки предстояло в реальном времени, и по задумке во время падения они должны были переворачиваться.
Многие результаты с фигурами, содержащими от 1 до 6 квадратов, были впервые опубликованы в журнале «FairyChessReview» в период с 1937 по 1957 г., под названием «Проблемы рассечения». Кроме того, полимино широко используются в различных головоломках и логических задачах. Одна из популярнейших игр в истории была создана малоизвестным российским программистом Алексеем Пажитновым. Он работал в Вычислительном Центре при Академии Наук СССР и занимался изучением проблем искусственного интеллекта, компьютерной графикой и вопросами компьютерного распознавания голоса. В основу идеи «Тетриса» была положена американская головоломка «PentominoPuzzle», придуманная математиком Соломоном Голомбом. Она состояла из пяти квадратов (пентомино – от греч. «пента» – пять) и ставила задачей правильно расположить в коробке геометрические фигуры. Планируя создать компьютерный вариант «Пентомино», Пажитнов успешно дополнил идею: собирать фигурки предстояло в реальном времени, и по задумке во время падения они должны были переворачиваться.
Полиамонд
Полиамонд— геометрическая фигура в виде многоугольника, составленного из нескольких одинаковых равносторонних треугольников (смотри рисунок 14). Наряду с полимино, широко распространена в занимательной математике, в основном в задачах на составление фигур. Одним из основных вопросов о полиамондах
Рис. 14. Полиамонд
является вопрос о количестве полиамондов, которые можно составить из данного числа треугольников. Как и в случае полимино, различают «свободные» полиамонды, для которых повороты и отражения не считаются различными формами; «односторонние», когда фигуры при зеркальных отражениях считаются различными, и «фиксированные», различаемые также и при поворотах.
Применение
полиамондов аналогично с использованием полимино в практической жизни. Эти геометрические фигуры широко применяются в различных логических задачах и головоломках.
История
Название «полиамонды» придумано математиком Т.О’Бейрном по аналогии с «полимино» и одним из английских названий ромба — диамонд. Поскольку диамонд можно составить из двух равносторонних треугольников, то фигуру из трёх равносторонних треугольников О’Бейрн назвал триамондом, из четырёх — тетриамондом и т. д. О’Бейрн также придумал большинство названий гексиамондов.
Фрактал
Фракта́л (лат. «fractus» — дроблёный, сломанный, разбитый) — сложная геометрическая фигура (смотри рисунок 15), обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает следующим свойством: фигура является самоподобной или приближённо самоподобной.
Рис. 15. Фрактал
История
Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы». Природные объекты часто имеют фрактальную форму.
Применение
Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, снежинки, кровеносная система и система альвеол человека или животных и т. д.). Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера. Так, например, в физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т.п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).
Применение необычных геометрических фигур:
В архитектуре – они окружают нас, формируют эстетическую городскую среду, богатую на многочисленные художественные образы (смотри рисунок 16).
Рис. 16. Необычные геометрические фигуры в архитектуре
В живописи – художники рисуют картины с использованием необычных геометрических фигур (смотри рисунок 17).
Рис. 17. Необычные геометрические фигуры в живописи
В дизайне — геометрические фигуры способны создавать эффект динамики и движения в интерьере, задавать вектор для конкретного стиля. На это не влияет ни размер, ни форма комнаты, ведь даже в самом скромном по объёмам помещении можно расставить акцентные пятна (смотри рисунок 18). Даже цветочные горшки и террариумы с их угловатостью могут стать великолепным настольным или настенным украшением [8]
Даже цветочные горшки и террариумы с их угловатостью могут стать великолепным настольным или настенным украшением [8]
Рис. 18. Необычные геометрические фигуры в дизайне
Таким образом спектр применения геометрических фигур разнообразен.
2. Практическая часть
2.1. Построение необычных геометрических фигур
Я создала необычную геометрическую фигуру, используя программу GNU Dr. Geo — это интерактивное программное обеспечение для геометрии (смотри рисунок 19), которое позволяе создавать и управлять интерактивными геометрическими набросками. Это бесплатное программное обеспечение, созданное Hilaire Fernandes, оно является частью проекта GNU. Он работает над морфической графической системой [6].
Тогда я решила самостоятельно в данной программе создать макет необычной геометрической фигуры (смотри приложение 3).
Рис. 19. Программа для построения
необычных геометрических фигур
2. 2. Коллекция головоломок
2. Коллекция головоломок
Изучая, многообразие необычных геометрических фигур и определив их применение, я решила создать свою коллекцию головоломок [3] и [7], состоящую их этих фигур. Подробное описание головоломок вы можете увидеть (смотри приложение 4).
В коллекцию вошли следующие головоломки:
1. Головоломка «Листик»;
2. Т-образная головоломка;
3. Головоломка «Летчик»;
4. Головоломка «Танграм»
5. Кубик — Рубика
6. Тетрис
7. Шестигранная колючка
8. Змейка
Заключение
Освещение информации о геометрических фигурах, изучение которых не входит в разделы, познаваемые в рамках школьной программы, позволяет приобрести новые знания и иными глазами посмотреть на знакомые предметы. Доказано, что математика развивает уровень общего развития, скорость мышления и сообразительность человека.
Доказано, что математика развивает уровень общего развития, скорость мышления и сообразительность человека.
Таким образом, можно сказать, что мир необычных геометрических фигур чрезвычайно интересен и многообразен. Изучение фигур имеет довольно важное значение не только с точки зрения геометрии, но и с точки зрения искусства, архитектуры и дизайна.
Увлечение головоломками улучшает пространственное воображение, развивает глазомер и умение мысленно оперировать объёмными предметами, знакомит на практике с основными геометрическими понятиями, учит аккуратности, последовательности, формирует терпение, смекалку.
Список литературы:
Федер Е. Фракталы. — М: «Мир», 1991;
Голомб С. В. Полимино. — Пер. с англ. В.Фирсова. — М.: Мир, 1975. — с.143—147;
Гарднер М. Математические головоломки и развлечения. — Пер. с англ.
 Ю.А.Данилова. — М.: Мир, 1971. — 511 с.
Ю.А.Данилова. — М.: Мир, 1971. — 511 с.
Электронные источники:
GUFO.ME. Толковый словарь Ожегова [Электронный ресурс]. – Режим доступа: еhttps://gufo.me/dict/dal/. Заглавие с экрана. – (Дата обращения 03.03.2019).
Плоские фигуры [Электронный ресурс]. – Режим доступа: https://www.sites.google.com/site/klassifikacii/ploskie-figury. Заглавие с экрана. – (Дата обращения 23.02.2019)
Программа для построения необычных геометрических фигур GNU Dr. Geo [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/. 5. Заглавие с экрана. – (Дата обращения 01.03.2019).
Каталог головоломок [Электронный ресурс]. – Режим доступа: https://inteltoys.ru/catalog/266/prod3367.html Заглавие с экрана. – (Дата обращения 27.02.2019).
Необычные геометрические фигуры в дизайне [Электронный ресурс].
 – Режим доступа: https://museum-design.ru/the-appeal-of-the-charm-of-geometric-shapes/ Заглавие с экрана. – (Дата обращения 03.03.2019).
– Режим доступа: https://museum-design.ru/the-appeal-of-the-charm-of-geometric-shapes/ Заглавие с экрана. – (Дата обращения 03.03.2019).Необычные геометрические фигуры в архитектуре [Электронный ресурс]. – Режим доступа: https://sibac.info/studconf/science/xxxiv/88784 Заглавие с экрана. – (Дата обращения 03.03.2019).
Приложение
Приложение 1.
Таблица 1. Виды удивительных фигур
Рис. 2. Трибар
Рис. 3. Тройной деформированный трибар
Рис. 4. Крылатый трибар
Рис. 5. Тройное домино
Рис. 6. Кубик со штифтами
Рис. 7.
Усеченный трибар
Рис.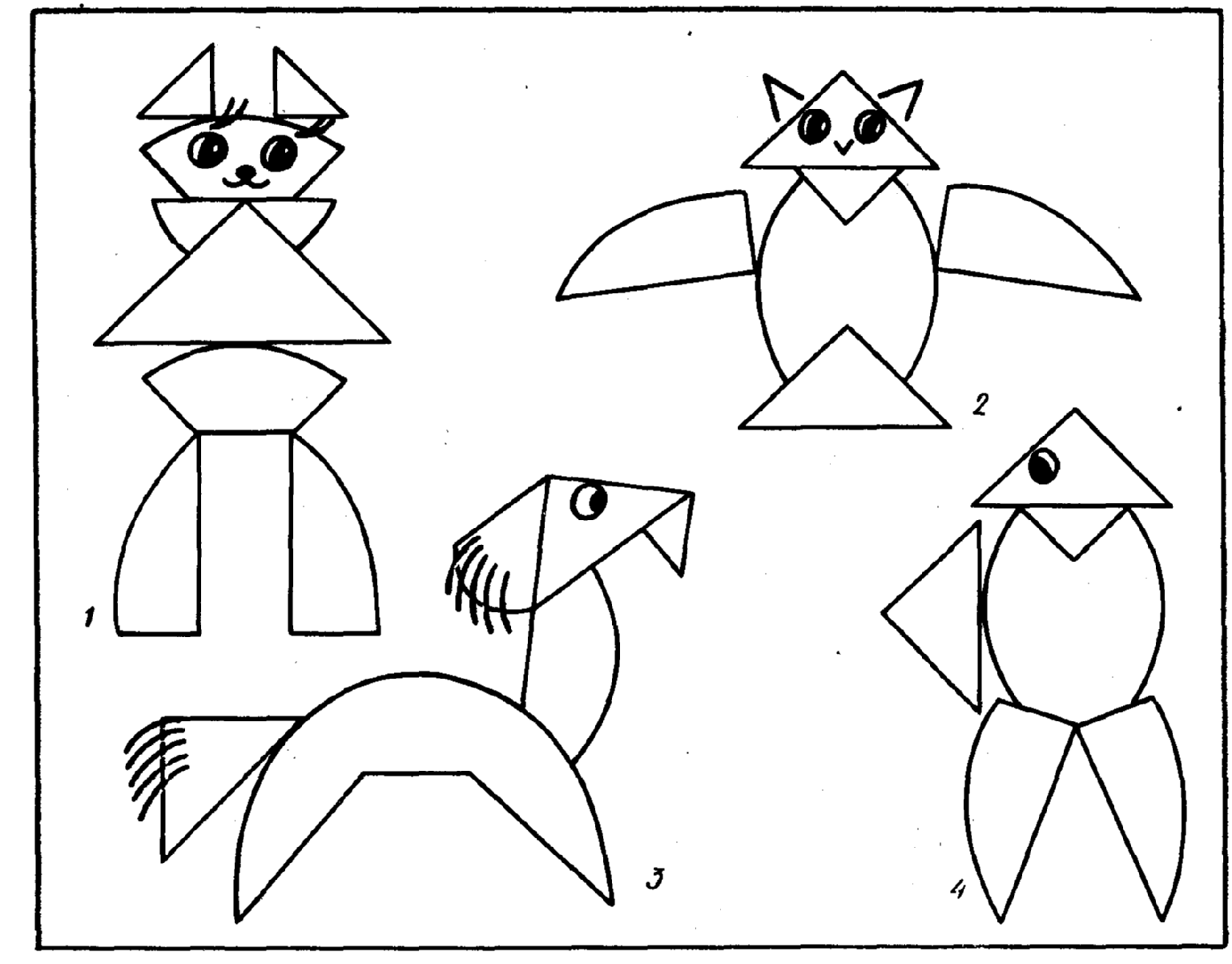 8. Перекрещенный ромб
8. Перекрещенный ромб
Рис. 9. Головоломка из кубиков
Рис. 10. Усеченный деформированный трибар
Рис. 11. Летучий шестиугольник
Рис. 12. Прямоугольный триэдр (трехгранник)
Приложение 2
Таблица 2. Виды объемных геометрических фигур
п/п
Объёмная геометрических фигура
Изображение
Описание
Конус
Тело, состоящее из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих вершину с точками основания.
Треугольная призма
Это многогранник имеет в качестве граней треугольное основание, его копию, полученную в результате параллельного переноса и 3 грани, соединяющие соответствующие стороны.
Цилиндр
Тело, состоящее из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом и всех отрезков, соединяющих соответствующие точки этих кругов.
Сфера
это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки.
Треугольная пирамида
Это пирамида, основанием которой является правильный треугольник, а вершина проецируется в центр основания. Важно: если длина ребра правильной треугольной пирамиды равна длине стороны основания, то такая пирамида называется тетраэдром.
Прямоугольный параллелепипед
Многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником. Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине взаимно перпендикулярны.
Рёбра параллелепипеда, сходящиеся в одной вершине взаимно перпендикулярны.
Куб
Прямоугольный параллелепипед, у которого все грани — квадраты.
Шестиугольная призма
Шестиугольник с основанием. У этого многогранника 8 граней, 18 рёбер и 12 вершин.
Тор
Поверхность вращения, которая получается методом вращения образующей окружности вокруг оси, которая лежит в плоскости этой окружности, но при этом не проходит через её центр. Причем ось вращения может пересекать окружность, касаться ее и располагаться вне окружности.
Приложение 3
Рис. 20 Макет необычной геометрической фигуры
Рис. 21 Макет необычной геометрической фигуры 2
Приложение 4
Таблица 3. Виды головоломок
Виды головоломок
п/п
Название
Изображение
Описание
1.
Головоломка «Листик»
Головоломка мира, или геометрические конструкторы, относятся к наиболее эффективным игровым пособиям для развития умственных и творческих способностей детей старшего дошкольного и младшего школьного возраста.
2.
Т-образная головоломка
Головоломка представляет собой букву «Т», разделенную параллельными линиями на 5 частей (треугольник, две трапеции, ромб и еще одна часть неправильной формы). Из них на плоскости составляются силуэты человека, животных, видов транспорта и т.д., которые потом можно перенести на бумагу, дорисовать и раскрасить.
3.
Головоломка «Летчик»
Головоломка представляет собой квадрат, разрезанный на 13 неравных частей – геометрических фигур: 2 больших, 4 средних и 4 маленьких треугольника, 2 больших и 1 маленький прямоугольник.
4.
Развивающая головоломка «Танграм»
Древняя китайская игра, которая представляет собой квадрат, разрезанный на прямоугольники и треугольники разных размеров.
Геометрические иллюзии
Содержание
Вступление
Оптические иллюзии
- Что такое оптические иллюзии?
- Как возникают оптические иллюзии?
- Виды оптических иллюзий
Геометрические иллюзии
- Иллюзии размера
- Иллюзии параллельности
- Иллюзии формы
Мои иллюзии
Заключение
Источники информации
Приложение 1: виды оптических иллюзий
Приложение 2: примеры геометрических иллюзий
Приложение 3: применение геометрических иллюзий
- Вступление
В окружающим нас мире мы можем наблюдать такое явление, как иллюзии. Так, например, в одном из павильонов на ВВЦ есть музей иллюзий, иллюзии можно наблюдать в рекламе, они часто встречаются в интернете. В этом году я начала изучение геометрии. А можно ли встретить иллюзии в геометрии? Я думаю, если на уроках геометрии для изучения геометрических понятий использовать иллюзии, то это повысит интерес школьников к изучаемому предмету.
Так, например, в одном из павильонов на ВВЦ есть музей иллюзий, иллюзии можно наблюдать в рекламе, они часто встречаются в интернете. В этом году я начала изучение геометрии. А можно ли встретить иллюзии в геометрии? Я думаю, если на уроках геометрии для изучения геометрических понятий использовать иллюзии, то это повысит интерес школьников к изучаемому предмету.
Таким образом, целью моей работы является выявление особых геометрических иллюзий и создание собственных образцов таких иллюзий:
Задачи:
— изучить литературных и интернет-источники по вопросам , связанным с иллюзиями, видами иллюзий , причинами их возникновения;
— отдельно выделить группу геометрических иллюзии;
— выявить принципы построения геометрических иллюзий;
— на основе выявленных принципов создать собственные образцы геометрических иллюзий;
— проверить успешность созданных образцов геометрических иллюзий.
Считаю, что из общей массы различных иллюзий можно выделить особую группу геометрических иллюзий и создать свои образцы таких геометрических иллюзий – это составляет гипотезу моего исследования.
В своем исследовании я использовала следующие методы:
— изучение и обработка различных источников информации;
— сравнение, анализ, аналогия;
— практическая работа;
— социологический опрос.
- Оптические иллюзии
Что такое оптические иллюзии?
Изучая различные источники информации, я узнала, что человеческий организм – сложнейшая саморегулирующая система. Наши органы чувств передают информацию об окружающем мире и изменениях вокруг, позволяя организму запоминать и по-своему интерпретировать результаты. Но иногда даже совершенная система может давать сбой и ошибаться. Иногда это происходит со зрительным анализатором, и тогда возникают оптические иллюзии, которые с давних времен заставляли человечество удивляться.
На иллюстрации выше показана схема зрительного восприятия. На пути к сетчатке лучи света проходят через несколько прозрачных сред: роговицу, хрусталик и стекловидное тело. На сетчатке получается изображение, резко уменьшенное и перевернутое вверх ногами и справа налево. Дальше информация идёт в мозг, который интерпретирует её, и мы видим данный субъект.
На пути к сетчатке лучи света проходят через несколько прозрачных сред: роговицу, хрусталик и стекловидное тело. На сетчатке получается изображение, резко уменьшенное и перевернутое вверх ногами и справа налево. Дальше информация идёт в мозг, который интерпретирует её, и мы видим данный субъект.
Оптические или зрительные иллюзии – это явление, при котором мы видим совершенно иное, чем оно есть на самом деле. Одни из существующих иллюзий давно научно объяснены и подтверждены практическим путем, другие также непонятны.
2. Как возникают оптические иллюзии?
Основные причины возникновения оптических иллюзий:
1) В мозг приходит неправильная информация, из-за ошибочного восприятия глазами света от предмета.
2) Нарушения работы нервов во время передачи информации.
3) Мозг неправильно анализирует информацию.
Т.е. иллюзии это следствие неверной, специфической работы нашего организма.
- Виды оптических иллюзий:
Все оптические иллюзии в зависимости от их происхождения можно разделить на 3 вида:
1) Естественные (созданные природой). Например, мираж.
Например, мираж.
2) Искусственные (придуманные человеком). Этот вид часто используют фокусники-иллюзионисты. Такие иллюзии имеют конструктивный секрет и объясненный механизм возникновения и действия.
3) Смешанные (естественные иллюзии, которые воссоздал человек) – это и модель миража, и иллюзионные картинки.
В зависимости от восприятия можно выделить следующие виды:
- Иллюзии движения. Изображенные на картинках фигуры при просмотре начинают двигаться или пульсировать, хотя на самом деле недвижимы.
- Зрительные искажения. Буквы, фигуры или линии в изображениях на самом деле расположены по-другому относительно друг друга.
- Иллюзия искажения размера. Одинаковые по размеру фигуры или предметы кажутся различными.
- Иллюзии цвета и контраста. Количество используемых для изображения цветов и оттенков кажется большим, чем есть на самом деле; нарушается цветовое восприятие объекта.

- Невозможные фигуры. Изображение нереальных фигур, которые не могут быть воспроизведены в трехмерном пространстве. Невозможные фигуры сначала кажутся обыкновенными фигурами, но при детальном рассмотрении становится понятно, что в них скрыто множество противоречивых элементов.
Примеры различных видов оптических иллюзий смотрите в приложении 1.
Геометрические иллюзии
Геометрия — это наука, занимающаяся изучением формы предметов, определяющая их размеры и взаимное расположение. Поэтому из всех оптических иллюзий я выделила геометрические, то есть те, которые связаны с изображением геометрических фигур на плоскости – это иллюзии размера, формы и параллельности.
- Иллюзия размера
Какой из внутренних квадратов больше? Черный или белый?
На самом деле они одинаковые.
Эта иллюзия основана на явлении иррадиации. Явление иррадиации состоит в том, что светлые предметы на темном фоне кажутся больше, чем на самом деле, они как бы захватывают часть темного фона. Когда мы рассматриваем светлую поверхность на темном фоне, вследствие несовершенства хрусталика, как бы раздвигаются границы этой поверхности, и эта поверхность кажется нам больше своих истинных геометрических размеров. На рисунке за счет яркости цветов белый квадрат кажется значительно большим относительно черного квадрата на белом фоне.
Явление иррадиации состоит в том, что светлые предметы на темном фоне кажутся больше, чем на самом деле, они как бы захватывают часть темного фона. Когда мы рассматриваем светлую поверхность на темном фоне, вследствие несовершенства хрусталика, как бы раздвигаются границы этой поверхности, и эта поверхность кажется нам больше своих истинных геометрических размеров. На рисунке за счет яркости цветов белый квадрат кажется значительно большим относительно черного квадрата на белом фоне.
Любопытно отметить, что зная о данном свойстве черного цвета скрадывать размеры, дуэлянты в XIX веке предпочитали стреляться именно в черных костюмах в надежде на то, что противник промахнется при стрельбе.
Вот несколько примеров иллюзии размера.
а) Иллюзия Болдуина
Какая линия больше А или Б?
Они абсолютно равны, хотя линия Б кажется гораздо длиннее.
б) Иллюзия Мюллера-Лайера (Franz Muller-Lyer, 1889)
(перенесение свойств целой фигуры на ее отдельные части)
Какой из горизонтальных отрезков длиннее?
Они все равны.
Другие примеры иллюзии размеров смотрите в приложении 2.
Вывод:
Рассмотрев разные варианты геометрических иллюзий размера, я выделила несколько принципов их построения:
- Влияние фона или окружения объекта.
Если вокруг объекта разместить объекты большего размера, то первый объект будет казаться меньше. Если добавляемые объекты будут меньше по размеру от исходного, то он станет визуально больше.
- Применение опыта из повседневной жизни.
В обычной жизни мы привыкли к определённым свойствам различных объектов. Так например, при удалении предмета, он кажется все меньше и меньше. Поэтому художники, создавая свои картины используют перспективу для более реалистичного изображения предметов. А вот иллюзии, воспроизводящие перспективу, искажают реальные размеры фигур.
- Использование явления иррадиации.

О нём мы уже знаем. Просто помещаем светлые фигуры на тёмный фон, а тёмные на светлый. Иллюзия готова.
- Перенесение свойств целой фигуры на ее отдельные части.
Если объекты, которые нужно преобразовать в иллюзию, сделать частью другой фигуры, то они могут перенять её свойства.
Параллелограмм Зандера (1926): Какой отрезок длиннее AB или BC?
На самом деле, отрезки AB и BC равны.
- Расположение предметов.
Узкие фигуры в вертикальном положении кажутся больше, чем в горизонтальном.
- Иллюзии параллельности.
Параллельные прямые — это две непересекающиеся прямые, лежащие в одной плоскости.
Иллюзии данного вида искажают параллельность. Прямые кажутся нам не параллельными, а вогнутыми или выпуклыми кривыми.
а) Иллюзия Геринга (иллюзия веера)
Прямые, на самом деле, параллельны.
б) Иллюзия Вундта (1896)
Линии в центре, в действительности, параллельны.
г) Иллюзия Цолльнера (Zolliner, 1860).
Параллельные прямые кажутся изогнутыми.
Другие примеры иллюзии параллельности смотрите в приложении 2.
Вывод:
Рассмотрев разные варианты геометрических иллюзий параллельности, я выделила несколько принципов их построения:
- Влияние фона или окружения.

а) Острые углы, помещённые между двумя параллельными прямыми, визуально делают их выпуклыми; тупые углы — вогнутыми.
б) Перечёркнутые наклонными штрихами, часто и в разные стороны, параллельные линии перерастают нами восприниматься, как параллельные, кажется, что они могут пересечься.
в) Перенос свойств целой фигуры на ее отдельные части.
В данной иллюзии центральные части ломаных линий параллельны. Однако из-за их расположения, визуально они кажутся пересекающимися, если их продлить.
- 3. Иллюзии формы
Под этими иллюзиями я понимаю невозможные фигуры или импоссибилизм. Этот термин был введен в обращение Тедди Бруниусом, профессором искусствоведения Копенгагенского университета. Импоссибилизм, это изображение предметов, которые кажутся реальными, но не могут существовать в физической реальности.
Импоссибилизм, это изображение предметов, которые кажутся реальными, но не могут существовать в физической реальности.
Основоположником «невозможных фигур» по праву считается швед Оскар Рутервард. Родился он в 1915 году в Стокгольме. В 1934 году создал первую невозможную фигуру — невозможный треугольник, составленный из набора кубиков. За годы своего творчества он создал более 2500 невозможных фигур. Все они выполнены в японской (параллельной) перспективе.
Его первая невозможная фигура появилась случайно, когда он в 1934 г. в последнем классе гимназии на уроке «чиркал» в учебнике латинской грамматики, рисуя в нем геометрические фигуры. Это был псевдотреугольник, который получил у математиков называние треугольника Рутерсварда.
а) Треугольник Рутерсварда.
б) Независимо от Рутерсвэрда английский математик и физик Роджер Пенроуз повторно открывает невозможный треугольник и публикует его изображение в британском журнале по психологии в 1958 г. В иллюзии использована «ложная перспектива».
Треугольник Пенроуза
в) А вот еще невероятная невозможная лестница Пенроуза
Если вы пойдете по ней по часовой стрелке, то будете все время спускаться, а если против часовой стрелки, то будете всегда подниматься…
Другие примеры иллюзий формы смотрите в приложении 2.
Вывод:
Рассмотрев разные варианты невозможных фигур, я выделила несколько принципов их построения:
- Составление крупной фигуры из фигур меньшего размера.
При соединении маленьких фигур в большую легко допустить «ошибку» и создать невозможную фигуру.
- Невозможные соединения.
Вся фигура может стать невозможной из-за одного неверного соединения её частей.
- Переход из части фигуры в пространство.
Часть невозможной фигуры может очень плавно перейти в пространство.
- Мои иллюзии
На основе выделенных принципов построения иллюзий, я создала свои.
- Иллюзия размера прямоугольников.
Эта иллюзия создана по принципу «влияние фона или окружения объекта». Прямоугольник, окружённый маленькими чёрточками кажется меньше, чем тот, который окружают чёрточки большего размера. На самом деле они равны.
- Иллюзия размера шаров.
Благодаря перспективе, игре света и тени, расположению шаров создаётся впечатление что один из них больше, а другой меньше, но на самом деле они равны.
- Иллюзия параллельности.
Эта иллюзия создана по принципу «перенос свойств всей фигуры на её отдельные части». Листья сужающиеся к верху, создают ощущение, что прямые тоже сужаются, но они параллельны.
- Невозможная призма.
Данная призма является невозможной фигурой. Её нельзя воспроизвести в трёхмерном пространстве, т.к. видимые её линии плавно переходят в невидимые.
Чтобы понять, удачно ли составлены мои иллюзии, я провела опрос учеников 5-7 классов своей гимназии и получила, что:
- Иллюзия размера прямоугольников.
Прямоугольники разного размера для 16 человек и одинакового для 10. Считаю, что иллюзия получилась. Достаточно большое количество голосов, поданных за одинаковый размер, говорит о том, что опрашиваемые понимают, что имеют дело с иллюзиями, и на самом деле прямоугольники одинакового размера.
- Иллюзия размера шаров.
Шары разного размера для 24 человек и одинакового для 17 человек. Считаю, что иллюзия получилась.
- Иллюзия параллельности.
Прямые параллельны для 5 человек и не параллельны для 18 человек. Считаю, что эта лучшая из получившихся иллюзий.
- Невозможная призма.
Призма возможна для 11 человек и не возможна для 12 человек.
Считаю, что эта иллюзия не ориентирована на данную аудиторию. У учеников 5-7классов возникали вопросы по поводу пунктирных линий.
- Заключение
Моя гипотеза подтвердилась. Я выделила отдельную группу геометрических иллюзий, которая разделилась ещё на иллюзии размера, параллельности и формы. Из каждой подгруппы я выделила принципы построения иллюзий, и теперь могу сделать вывод, что в основном причинами образования геометрических иллюзий являются: объекты, расположенные рядом; положение самого объекта рядом с другими; состав объекта. С помощь выше перечисленных способов образования иллюзия я создала свои, успешность которых была проверена опросом школьников.
С помощь выше перечисленных способов образования иллюзия я создала свои, успешность которых была проверена опросом школьников.
- VI. Источники информации
- Джанни А. Сарконе, Мари-Джо Ваэбер «Рисуем оптические иллюзии», М., АРТ-РОДНИК, 2013, с. 128
- С. Толанский «Оптические иллюзи», М., Мир, 1967, с. 128
- http://www.optical-illusions.ru
- http://www.pressmaket.ru/illuzii.html
- http://www.psy.msu.ru/illusion/size.html
- http://www.diagram.com.ua/illusions/2.shtml
- http://obychnogo.net/opticheskie-illyuzii-zritelnye-iskazheniya
- http://im-possible.info/russian/articles/reut_imp/
- http://art-science-world.diary.ru/p174185185.htm?oam
- http://ppt4web.ru/geometrija/mir-nevozmozhnykh-figur.html
ПРИЛОЖЕНИЕ 1.
Виды оптических иллюзий:
- Иллюзии движения.

- Изображенные на картинках фигуры при просмотре начинают двигаться или пульсировать, хотя на самом деле недвижимы.
- Эти красные круги на малиновом фоне интенсивно пульсируют, напоминая минивзрывы.
- Смотрите в центр изображенной фигуры и замечайте пульсирование и движение. Иллюзия усилиться, если двигать головой влево-вправо.
- Зрительные искажения.
- Буквы в изобрааженном слове на самом деле параллельны друг другу.
- И горизонтальные линии на следующем рисунке также параллельны между собой.
- В центре рисунка изображены квадраты, а не фигуры с неровными сторонами.
 А еще мы можем увидеть несуществующие пульсирующие квадраты по всему полю рисунка.
А еще мы можем увидеть несуществующие пульсирующие квадраты по всему полю рисунка.
- Иллюзия искажения размера.
- Кто выше карлик на переднем плане или человек на заднем? Человек на заднем плане и карлик на переднем — одного роста.
- Какая линия длиннее AC или AB? AC и AB равны.
- Посмотрите на цифры «3» и»8″. Верхняя половина каждой цифры равна нижней, не правда ли?
А теперь перевернем эти цифры.
Разница в размере верхних и нижних половин становится очевидной.
- Иллюзии цвета и контраста.

- Посчитайте, сколько оттенков, кроме белого, присутствует на картинке? А их оказывается только два – красный и зеленый!
- А здесь спирали какого цвета вы видите? А голубых-то и нет на самом деле. Только зеленые!
- Невозможные фигуры
Невозможные фигуры сначала кажутся обыкновенными фигурами, но при детальном рассмотрении становится понятно, что в них скрыто множество противоречивых элементов. Эти фигуры не могут быть воспроизведении в трёхмерном пространстве.
ПРИЛОЖЕНИЕ 2: Геометрические иллюзии
- Иллюзии размера.
а) Иллюзия Ястрова (Jastrow, 1891).
Какая из фигур больше?
Они абсолютно одинаковые.
б) Иллюзия железнодорожных пулей (Mario Ponzo, 1913).
Верхняя горизонтальная линия кажется длиннее.
Эта линия продолжает восприниматься как более длинная, в каком бы положении мы ни рассматривали рисунок. Попробуйте повернуть голову на 90 градусов.
в) Иллюзия кинескопа.
Какая из красных линий длиннее?
Красные линии на рисунке одной длины.
г) Квадратура круга.
Левая окружность кажется больше правой.
д) Иллюзия перспективы.
Какой из параллелепипедов больше?
Они равны.
2.Иллюзии параллельности.
а) Иллюзия Поггендорфа (Poggendorf, 1860)
На одной прямой лежат линии BC, а не AC, как кажется.
б) Иллюзия с витыми веревками (James Frazer, 1908).
Это прямые или нет?
Это параллельные прямые.
в) Иллюзия Липпса
Центральные части линий параллельны друг другу.
г) Иллюзия У. Эренштейна (W. Ehrenstein, 1921)
Эренштейна (W. Ehrenstein, 1921)
Квадрат кажется искаженным.
д) Синие квадраты кажутся нарисованными неровно
е) Все квадраты не самом деле не искажены.
ж) Узор как бы выступает вперед?
На рисунке все квадраты не искажены.
з) На данном рисунке все прямые параллельны.
- Иллюзии формы.
а) Впервые эта иллюзия была опубликована в журнале «Mad» в 1965 году (художник Норман Минго).
б) Невозможный куб Эшера.
ПРИЛОЖЕНИЕ 3
Применение геометрических иллюзий
Каждый день мы сталкиваемся с геометрическими иллюзиями в обычной жизни, но как правило их не замечаем. Я выделила основные направления использования этих иллюзий в быту:
- Дизайн одежды
Благодаря иллюзиям женщины имеют уникальную возможность подкорректировать своё тело без каких-либо лишних воздействий. Достаточно правильно выбрать орнамент на платье. Например, иллюзия Геринга поможет сконцентрировать внимание на одной части, а другую сделать незаметнее.
- Дизайн интерьера
Часто в дизайне интерьера используется техника анаморфоз. Она создаёт объёмные и реалистичные изображения в пространстве, которые принимают чёткие очертания лишь с определённой точки. Наиболее распространены иллюзии с геометрическими фигурами. Самым известным мастером современности, творящем в этом направлении, является Феличе Варини.
Самым известным мастером современности, творящем в этом направлении, является Феличе Варини.
- Архитектура и украшение улиц.
- Скульптура невозможного треугольника, в центре бельгийской деревни Опховен (Ophoven), где живет в настоящее время художник и математик Матье Хэмакерзом (Mathieu Heamekers).
А это фотография скульптуры с другой точки обзора.
Вот на такие ухищрения пришлось пойти, чтобы скульптура смотрелась в анфас…
- Анаморфоз применяется не только в интерьерах, но и в украшении целых зданий.
- Иллюзии параллельности в архитектуре.
- Иллюзии в рекламе и логотипах.
Основная задача реклам и логотипов — привлекать к себе внимание и быть запоминающимися. Иллюзии справляются с этой задачей блестяще, поэтому стали неотъемлемой частью маркетинга.
Иллюзии справляются с этой задачей блестяще, поэтому стали неотъемлемой частью маркетинга.
- Иллюзии в психологии.
На приёме у психолога Вам могут показать иллюзии и спросить, что Вы видите. Это особый метод изучения внутреннего состояния человека.
Тема проекта: «Город из геометрических фигур»
КОНСПЕКТ. «Сложение»
МУНИЦИПАЛЬНОЕ ДОШКОЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ДЕТСКИЙ САД 79 КОМБИНИРОВАНОГО ВИДА» КОНСПЕКТ занятия по математическому и сенсорному развитию в старшей группе на тему: «Сложение» Подготовила: воспитатель
ПодробнееПУТЕШЕСТВИЕ В СТРАНУ ФИГУРИЮ
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ДОШКОЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ДЕТСКИЙ САД КОМБИНИРОВАННОГО ВИДА 21 «НЕЗАБУДКА» ЗЕЛЕНОДОЛЬСКОГО МУНИЦИПАЛЬНОГО РАЙОНА РЕСПУБЛИКИ ТАТАРСТАН ПУТЕШЕСТВИЕ В СТРАНУ ФИГУРИЮ КОНСПЕКТ
ПодробнееКонспект урока математики.
 3 класс
3 классКонспект урока математики 3 класс УМК: «Планета знаний» Тема: «Строим фигуры из кубиков» Тип урока: открытие нового знания. Цель: сформировать представление о том, что объем фигуры измеряют единичными
ПодробнееУМК по математике для 1-4 классов
УМК по математике для 1-4 классов drofa-ventana.ru muravins.ru Покупка учебников в печатной и электронной форме Содержание линии «Геометрические фигуры» Раздел «Пространственные отношения. Геометрические
ПодробнееЗАНЯТИЕ 1. Тема: ЗДРАВСТВУЙ, ШКОЛА!
Тема: ЗДРАВСТВУЙ, ШКОЛА! ЗАНЯТИЕ 1 Цели: 1. знакомство с детьми; 2. знакомство детей друг с другом; 3. знакомство с правилами поведения в школе; 4. обучение штриховке; 5. знакомство с полем тетрадного
ПодробнееПланируемые результаты изучения
1 научиться использовать геометрический язык и геометрическую символику для описания предметов окружающего мира; проводить несложные рассуждения и обоснования в процессе решения задач, предусмотренных
ПодробнееТема урока: «Длина окружности».

Муниципальное общеобразовательное учреждение «Заречная средняя общеобразовательная школа» Открытый урок по математике в 6 классе Тема урока: «Длина окружности». Урок подготовила и провела учитель математики
Подробнеепо теме: «Занимательная математика»
Муниципальное бюджетное образовательное учреждение Центр развития ребенка- детский сад 5 «Теремок» города Новоалтайска Алтайского края Конспект непосредственно — образовательной деятельности по теме: «Занимательная
ПодробнееЗАНЯТИЕ ПО ТЕМЕ «ТАИНСТВЕННЫЙ НЕЗНАКОМЕЦ»
Шевашкевич Людмила Алексеевна воспитатель высшей категории логопедической группы Муниципальное автономное дошкольное образовательное учреждение г.мурманска детский сад комбинированного вида 93 г.мурманск
ПодробнееПояснительная записка
Пояснительная записка Рабочая программа курса «Наглядная геометрия» обязательной предметной области » Математика и информатика» для начального общего образования разработана на основе авторской программы
ПодробнееГеометрия 7 класс.
 Содержание курса.
Содержание курса.Геометрия 7 класс. Содержание курса. Геометрические фигуры Фигуры в геометрии и в окружающем мире Геометрическая фигура. Формирование представлений о метапредметном понятии «фигура». Точка, линия, отрезок,
ПодробнееКакое слово получилось? (квадрат)
Тема: Удивительный квадрат. Цель: Обучающие -познакомить учащихся с понятием «квадрат», научить чертить квадрат, учить отличать квадрат от других геометрических фигур, изготавливать из квадрата пароход;
ПодробнееКОНСПЕКТ ОТКРЫТОГО ПРОСМОТРА ПО
Муниципальное бюджетное дошкольное образовательное учреждение Детский сад 23 КОНСПЕКТ ОТКРЫТОГО ПРОСМОТРА ПО ПОЗНАВАТЕЛЬНОМУ РАЗВИТИЮ (ФОРМИРОВАНИЕ ЭЛЕМЕНТАРНЫХ МАТЕМАТИЧЕСКИХ ПРЕДСТАВЛЕНИЙ) Подготовила
ПодробнееПодготовил: воспитатель 1кв.
 к. Лисицинская Н.В.
к. Лисицинская Н.В.Конспект занятия Подготовил: воспитатель 1кв.к. Лисицинская Н.В. Интеграция областей: «Познавательное развитие», «Речевое развитие», «Художественно-эстетическое развитие», «Физическое развитие», «Социально-коммуникативное
ПодробнееЛичностные результаты
Технологическая карта урока математики Класс 6б Дата 30.11.2018 Учитель математики Масленникова Мария Васильевна Тема Виды треугольников. Построение равностороннего треугольника. Тип урока Урок получения
ПодробнееI.Самоопределение к деятельности. Задачи: Организовать эффективное самоопределение учащихся к учебной деятельности; Включить учащихся в деятельность по выявлению готовности. | Регулятивные: — волевая саморегуляция Коммуникативные: — планирование учебного сотрудничества с учителем и со сверстниками. Личностные: — положительное отношение к процессу познания. | 1: Здравствуйте, ребята и уважаемые гости нашего урока! Сегодня мы проводим необычный урок – интегрированный. Занятие охватывает две дисциплины, математику и ИКТ, мы разработали для вас специальный рабочий лист. Все задания вы будете выполнять именно в нем и получите оценку за каждый предмет. Для этого вам придется плодотворно поработать. 2: Во время занятия вам придется организовывать собственную деятельность и оценивать ее, анализировать рабочую ситуацию, нести ответственность за результаты своей работы, использовать информационно-коммуникационные технологии, работать в команде. И пусть сегодняшний урок принесёт нам всем радость общения. Приступаем к работе! | Эмоциональный настрой на урок. Проверяют готовность к уроку. Оформляют свои рабочие листы. | Полная готовность класса к работе; быстрое включение учащихся в деловой ритм, организация внимания всех учащихся. | II. Целеполагание. | Личностные: развитие логического мышления, познавательной активности. Регулятивные: развитие умения формулировать тему урока в соответствии с задачами и нормами предметов. | 2: Чтобы определить тему нашего урока, посмотрите на экран. 1: Ребята, какие элементы были использованы в анимации? (треугольник, квадрат…) 1: Как в математике называются эти элементы? (геометрические фигуры) 2: С помощью какой программы была создана данная композиция? (с помощью графического редактора Paint) 1,2: Как вы думаете, чем мы будем заниматься на уроке? Сформулируйте тему нашего урока. ( Геометрические фигуры. Создание рисунков в графическом редакторе Paint посредством геометрических фигур). | Слушают учителя, смотрят слайд, отвечают на вопросы. Высказывают предположения на основе эвристической беседы. Формулируют тему урока и цель своей деятельности. | Определены тема и цель урока. | III. Актуализация знаний. Задачи: Актуализировать необходимые знания, умения и способы деятельности. | Регулятивные: — уметь планировать своё действие в соответствии с поставленной задачей Личностные: развитие логического мышления, познавательной активности. Познавательные: — формировать умения обобщать знания и делать выводы; — самостоятельно выполнять действия по задуманному плану; — формировать вычислительные навыки | 1: Прежде чем приступить к дальнейшей работе, мы предлагаем вам вспомнить то, что вы знаете по данным темам. 2: 1 вариант выполняет тест на компьютере по информатике, 2 вариант выполняет тест по математике в рабочих листах, затем наоборот. Интерактивный тест по информатике. Вопросы теста: 1. Графическим редактором называется программа, предназначенная для … 2. Укажите элементы окна программы Paint: а) палитра; б) рабочая область; в) панель форматирования; г)полосы прокрутки. 3. Укажите инструменты графического редактора: а) Ластик; б) Карандаш; в) Ножницы; г) Ручка; д) Заливка 4. Инструмент «Масштаб»: а) Изменяет размер области рисунка; б) Изменяет размер рисунка на печать; в) Изменяет размер рисунка на экране; г) Изменяет размер рисунка в файле. 5. Какую клавишу необходимо удерживать в нажатом состоянии при рисовании в графическом редакторе, чтобы получить окружность, а не эллипс? а) Alt б) Ctrl в) Shift г) CapsLock 6. а) Программы / Стандартные / Paint б) Пуск / Стандартные / Программы / Paint в) Пуск / Программы / Стандартные / Paint Тест по математике. Вопросы: 1. Выберите формулу площади прямоугольника. А) S=4a, Б) S=2(a+b), В) S=ab, Г) S=a2 2. Выберите формулу периметра квадрата А) P=ab, Б) P=4a, В) P=2(a+b), Г) P=a2 3. Вычислите периметр квадрата со стороной 6 см А) 24 см, Б) 36 см, В) 18 см, Г) 24 см2 4. Чему равна сторона квадрата, площадь которого 64 см2 А) 16 см, Б) 8 см, В) 4 см, Г) 8 см2 5. Стороны прямоугольника равны 6см и 8 см. Чему равна его площадь? А) 48 см, Б) 28 см, В) 28 см2, Г) 48 см2 1: Жители нашего дома – «геометрические фигуры» решили покрасить стену дома. 2: Необходимые все данные для решения этой задачи вы найдете в рабочем листе. Приступаем к работе. Задача. Выполни необходимые измерения и вычисли площадь закрашенной фигуры. Схема поэлементного анализа выполнения задания (представлена на слайде с расчетами)
| Выполняют тесты. -выполняют интерактивный тест по информатике, полученные баллы переносят в оценочный лист. — выполняют тест по математике, сравнивают с эталоном (слайд 3 взаимоконтроль), переносят баллы в оценочный лист. Работа в парах Ученики выполняют необходимые измерения (стороны геометрических фигур) и вычислительную часть. | Безошибочное написание теста; по математике -взаимоконтроль по критериям: за каждый правильный ответ – 1 балл; по информатике-интерактивный контроль Правильное и быстрое выполнение задания. Сравнивают с эталоном, делают самооценку в баллах. Выставляют баллы в оценочный лист. | IV. Творческая практическая работа в группах. Задачи: Развитие навыков проектной деятельности. | Регулятивные: — уметь планировать своё действие в соответствии с поставленной задачей. —проявлять познавательную инициативу, — контролировать свои действия. Познавательные: — формировать умения обобщать знания и делать выводы; — устанавливать аналогии; — самостоятельно выполнять действия по задуманному плану. Коммуникативные: — развивать умение вступать в диалог и участвовать в групповом обсуждении проблем. | Работы в группах. 1: А сейчас поработаем в группах. Мы предлагаем вам немного пофантазировать и выполнить небольшую творческую работу — составить рисунок, используя графический шаблон из нашей задачи не менее двух раз, дополнив его моделями других геометрических фигур по — своему усмотрению. 2: Просим занять свои места. Распределите обязанности в группе (во время выполнения критерии оценивания проекта высвечиваются на экране). По окончании работы рисунки, созданные учениками, вывешиваются на доску, и оцениваются в соответствии с критериями по 1 баллу: 1 использован графический шаблон исходной фигуры 2.использованы другие геометрические фигуры 3. целостность композиции 4. цветовое решение 5. аккуратность выполнения | Самостоятельно выполняют работу в группах: составляют свой рисунок из геометрических фигур. | Оценивают свою работу в оценочных листах. | V. Компьютерный практикум. Задачи: По составленному алгоритму проекта выполнить рисунок | Познавательные: — формировать умения обобщать знания и делать выводы, анализируя и сравнивая предлагаемые задания; — формировать умение создавать алгоритм; — формировать умение использовать графический редактор Paint для создания изображений по подготовленному проекту. Регулятивные: — уметь планировать своё действие в соответствии с поставленной задачей Личностные: — развивать внимание, зрительную и слуховую память, логическое мышление, информационной культуры. Коммуникативные: — развивать умение вступать в диалог и участвовать в групповом обсуждении проблем; — выражать свои мысли с достаточной полнотой и точностью. | 2: Можете ли вы поменять цвета элементов ваших готовых рисунков? (нет) 1: С помощью чего вы смогли бы многократно менять цвет, размер, положение фигур при составлении рисунка? (с помощью красок, карандашей, бумаги, ножниц…) 2: А если у вас нет под рукой данных инструментов, как выйти из положения? (можно использовать графический редактор). 2: Давайте ребята, выполним один наш проект в графическом редакторе (выбор готового проекта). 1: Во время работы за компьютером надо быть предельно внимательным, поэтому повторим правила техники безопасности.
2: Работаем в парах, для начала ваша задача продумать алгоритм создания рисунка. После этого, мы обсудим его и подготовим один общий план работы. По истечении времени обсудить алгоритм одной пары, выслушать другие предложения и прийти к одному общему плану работы. План должен получиться примерно такой: 1. Установить необходимый основной цвет и нарисовать прямоугольник — стену. 2. Установить цвет и нарисовать окно -квадрат. 3. Установить цвет и нарисовать треугольник — крышу. 4. Выделить и скопировать «дом». 5. Вставить 2 раза скопированный фрагмент. 6. Закрасить дома по своему дизайну. 7. Вставить текст, указав в нем Ф. И., выполнивших данный рисунок. 8. Добавить дополнительные элементы по своему усмотрению. 2: Приступаем к компьютерной практике. (во время выполнения критерии оценивания высвечиваются на экране, учитель следит за работой учащихся; консультирует, координирует действия). По окончании работы рисунки, созданные учениками (1-2 варианта), выводятся на экран и оцениваются в соответствии с критериями (по 1 баллу за): 1. полнота выполненного задания (количество обязательных элементов). 2. использование операции — копирование выделенного фрагмента. 3. использование инструмента- заливка. 4. наличие вставки текста в изображение (Ф. И., выполнивших работу). 5. целостность композиции. 6. гармоничное цветовое сочетание (дизайн). 7. аккуратность выполнения. | Отвечают на вопросы. Вырабатывают алгоритм создания рисунка. Самостоятельно выполняют практическую работу за компьютером (работа в парах). Каждая пара учеников обменивается работой со своими соседями и оценивают работы друг друга согласно критериям. | Нарисованный в графическом редакторе Paint по составленному проекту рисунок. Оценивают свою работу в оценочных листах. | VI. Этап информирования обучающихся о домашнем задании, инструктаж по его выполнению. | Регулятивные: Соотносить то, что известно и то, что предстоит выполнить самостоятельно. Личностные: — формировать навыки самоорганизации; — формировать навыки исследовательской работы; — формировать умение использовать графический редактор Paint для создания изображений по составленному проекту. | Слайд с домашним заданием (по уровням сложности: базовый, повышенный, высокий). Учитель предлагает на выбор: математика 1. № 805, 2. Практическое задание «Геометрия в быту». Вычислить периметр, площадь самой большой комнаты в квартире (доме). 3. Выполнить презентацию «Геометрия в быту» информатика 1. Используя только данные геометрические фигуры составить рисунок на бумаге. 2. Используя только данные геометрические фигуры составить рисунок в графическом редакторе Paint. 3. Используя только данные геометрические фигуры составить рисунок и алгоритм по его созданию в графическом редакторе Paint. | Выбирают задания в соответствии с желанием. | Дифференцированное домашнее задание. | VII. Подведение итогов урока. Рефлексия учебной деятельности на уроке. Задачи: Организовать работу по самооценке учащимися результатов своей учебной деятельности. | Регулятивные: -уметь соотносить цель и результат. -волевая саморегуляция, самооценка -выделение и осознание учащимися того, что уже усвоено и что ещё подлежит усвоению. Коммуникативные: — уметь выражать свои мысли. Личностные: — развивать способность к самооценке на основе критерия успешной учебной деятельности. | Подведем итог нашего урока: скажем «пять слов». — Как сказал древнегреческий философ Саади: «Ученик, который учится без желания — это птица без крыльев». И мне бы хотелось, чтобы у вас было желание учиться, узнавать что-то новое, неопознанное не только на сегодняшнем уроке, а всегда и только в этом случае вы будете «взлетать» все выше и выше. | Составляют синквейн: графический редактор | Оценивают свою работу в оценочных листах. Определяют индивидуальный уровень (базовый, повышенный, высокий) овладения темой, выставляют отметки по математике и отдельно по информатике. |
АВ | ВС | АС | Р | Вид треугольника | |
1 | 2 см | 3 см | 7 см | ||
2 | 3 см | 3 см | 3 см | ||
3 | 6 см | 6 см | 4 см | ||
4 | 9 см | равносторонний | |||
5 | 3 см | 11 см | равнобедренный | ||
6 | 3 см | 4 см | 10 см | ||
7 | 3 см | 2 см | 10 см |
Построение геометрических фигур в текстовом редакторе / Открытый урок
Цели и задачи:
1. Научить строить геометрические фигуры в текстовом редакторе Word.
2. Развивать аккуратность в строениях и воспитывать некоторые правила поведения.
Требования к знаниям и умениям:
Учащиеся должны знать:
— что такое прикладные программы, текстовый редактор, назначение, возможности текстового редактора Word.
— понятие редактирования и форматирования текста.
— геометрические фигуры на плоскости.
— фигуры в пространстве.
Учащиеся должны уметь:
— вычислять объёмы фигур на плоскости;
— вычислять объёмы фигур в пространстве.
Программно-дидактическое обеспечение: ПК,презентация к уроку в программе Power Point.
Ход урока
Слайд 1
Тема урока
Слайд 2
Цели и задачи урока
Слайд 3
Геометрические фигуры на плоскости
Слайд 4
Рисование фигур средствами компьютерной графики
Понятие растровой и векторной графики доклад ученицы 11 А класса Капустник Елены
Слайд 5
Построение геометрических фигур в текстовом редакторе Word
Для вставки новой фигуры, или графического объекта,
в документ необходимо:
1. Выбрать на панели Рисование фигуру (например, овал, прямоугольник).
Выбрать на панели Рисование фигуру (например, овал, прямоугольник).
2. Щёлкнуть на одной из выбранных фигур.
3. Выбрать из базовых форм, нажав Автофигуры.
После щелчка на выбранной фигуре курсор принимает форму перекрестья +
Слайд 6
4. Появляется зона для создания рисунка.
Устанавливаем курсор в нужном месте в документе и, нажав Левую кнопку мыши рисуем фигуру, определив тем самым её размеры, местоположение и пропорции.
5. Для того, чтобы закрасить фигуру
необходимо её выбрать.
6. На панели Рисование выбираем значок Цвет заливки
Слайд 7
Вопрос к ученикам: Какие фигуры в пространстве вы знаете?
Слайд 8
Пирамиды вокруг нас
Слайд 9
Рисование объёмных фигур
Для того, чтобы придать фигуре объём, необходимо
1. Выбрать фигуру
Выбрать фигуру
2. На панели Рисование
выбрать значок меню Объёма
3. Фигура обрела выбранный объём
Слайд 10
Для того, чтобы в фигуру вписать текст необходимо:
1. Выбрать фигуру
2. Щёлкнуть Правой кнопкой мыши внутри фигуры, чтобы открыть контекстное меню и выбрать строку Добавить текст
3. Внутри фигуры появляется курсор, добавляем текст
Учащиеся решают задачи:
- На вычисление объёма воздуха в автобусе с пассажирами.
- Вычисление объёма жидкости в бутылке.
Слайд 11
Показ драгоценных камней с гранями, пример из песни «Лучшие друзья девушек – это бриллианты».
Слайд 12
Выполнение практической работы на построение фигур в текстовом редакторе Word. (15 мин).
(15 мин).
Закрепление изученного
Ответы на вопросы, поставленные в начале урока.
Слайд 13
Слайд 14
Проверь себя!
Тест по пройденной теме.
1. Текстовый редактор Word — это
2. Чтобы нарисовать геометрическую фигуру необходимо:
3. Чтобы закрасить геометрический объект необходимо:
4. Чтобы придать объём геометрической фигуре необходимо:
Итоги урока
Оцениваем работу класса и называем учащихся, отличившихся на уроке.
Домашнее задание
Придумать рисунок, используя геометрические фигуры текстового редактора.
Вычислить объём построенных фигур.
Ревизия углов | Построение геометрических фигур
w3.org/1999/xhtml»> В этой главе вы научитесь точно рисовать геометрические фигуры. Вы также узнаете, какими свойствами обладают разные фигуры.Ревизия углов
Когда две линии указывают в разных направлениях, мы говорим, что они составляют под углом друг к другу. Если направления почти одинаковы, мы говорим, что угол между ними мал. Если направления сильно различаются, мы говорим, что угол между ними большой.
слов, которые мы используем для описания углов:- Плечи угла: две линии, угол друг к другу
- Вершина: точка, где встречаются две руки
- Вершины: во множественном числе ‘вершина’
Стрелки на линиях означают, что линии продолжаются. Длина плеч уголка не влияет на размер угла.Независимо от того, длинные или короткие руки, размер угла остается неизменным.
Длина плеч уголка не влияет на размер угла.Независимо от того, длинные или короткие руки, размер угла остается неизменным.
Есть двух углов на vertex , поэтому важно показать, о каком из них идет речь.
Обозначение углов:Существует много разных способов обозначения углов. Посмотрите на примеры ниже:
Угол справа можно назвать по-разному. способы: вы можете сказать \ (A \ hat {B} C \) или \ (C \ hat {B} A \) или просто \ (\ hat {B} \). Шляпа на письме показывает, где находится угол.
Редакция: углы обзора и описание углов
Посмотрите на рисунок справа.
А эти линии под углом друг к другу?
Должны ли линии встречаться под углом?
Нарисуйте линии карандашом и линейкой.
 немного дольше, чтобы они встретились.Вы меняли угол между линиями, когда
продлил их?
немного дольше, чтобы они встретились.Вы меняли угол между линиями, когда
продлил их?
Расположите углы от наибольшего до самый маленький. Просто напишите буквы от (a) до (f) в правильном порядке.
Как можно вы проверяете, что угол является прямым, без использования специальной математики оборудование? ( Подсказка : подумайте, где можно найти прямые углы вокруг тебя.)
У этих двух углов одинаковый размер? Опишите, как вы нашли свой ответ. ( Подсказка : макулатура может помогите!)
Две линии нарисованы, удерживая линейка и рисование линий с двух сторон.
 Что вы можете сказать о двух
линии?
Что вы можете сказать о двух
линии?Посмотрите на аналоговый циферблат на верно.Минутная и часовая стрелки образуют угол. Сосредоточьтесь на меньшем угол пока.
Объясните, почему угол между стрелками на 8 часах такой же, как угол на 4 часы.
Сравните угол на отметке 2 часа с углом в 4 часа. Что ты заметил? Почему это так?
Угол на отметке 3 часа такой же, как угол? в четверть десятого? Объяснять.
При открытии обложки в твердом переплете Книгу можно сделать под разными углами. Вы можете вспомнить хотя бы пять других ситуации в повседневной жизни, когда предметы поворачиваются под углом? Чего-чего руки и вершины есть в каждом из ваших примеров.

Градус: единица измерения углов
Представьте, если бы у нас не было единиц измерения длины.
Как портные делают одежду нужного размера без рулетки? Как мог архитектор спроектировать безопасный и красивый дом без линейки? Как можно было выложить профессионал футбольное поле без возможности точного измерения в метрах?
Единицы и измерительные приборы нужны нам во многих ситуациях. Вы знаете, что для измерения длины мы используем метры, сантиметры, километры, миллиметры и т. Д.
Мы также должны
есть единицы измерения углов.Единицы, которые мы используем для измерения углов, очень
древний. Сегодня никто не знает, почему, но наши предки решили, что многие
тысячи лет назад революцию нужно было разделить на 360 равных частей. Мы называем эти части степенями. Обозначается градус °.
Мы называем эти части степенями. Обозначается градус °.
Некоторые знакомые углы в градусах
Завершено таблицу, заполнив размер каждого описанного угла.
прямой угол
90 °
прямой угол
революция
360 °
половина прямого угла
треть прямого угла
четверть прямого угла
22,5 °
половина прямого угла
три четверти оборота
треть оборота
Посмотрите на показанные часы.
 Сколько степеней:
Сколько степеней:минутная стрелка движется внутрь час?
часовая стрелка перемещается за час?
В 6 классе вы узнали, что углы классифицированы по типам. Заполнить таблицу. Первый был сделан как пример для вас.
Острый угол
Между 0 ° и 90 °
Прямой угол
Тупой угол
Прямой угол
Угол отражения
Revolution
Вам нужен лист бумаги формата А4.По углам у вас четыре прямых угла. Пронумеруйте их и оторвите уголки, как показано на схеме. Не делайте их слишком маленькими.
Теперь используйте прямые углы для исследования следующих ситуаций:
Покажите, что прямой угол — это два прямых угла.
Вы можете сделать набросок того, что вы сделали
Показать что оборот равен четырем прямым углам.
Вы можете сделать набросок того, что вы сделали
Создать под прямым углом, используя три ваших угла.
Вы можете сделать набросок того, что вы сделали
Опишите как вы можете использовать один из ваших углов, чтобы проверить, острый ли угол, прямой или тупой.

Загните угол 1, чтобы по нему можно было измерить 45 °.
Загните угол 2 так, чтобы вы можете использовать его для измерения 30 °.
Загните угол 3 так, чтобы вы можете измерить 22,5 °.
Что больше: право угол или половина прямого угла + треть прямого угла + четверть прямой угол? Можете ли вы сделать расчет, чтобы это показать?
Важно: Сохраните сложенные листы бумаги для следующего урока!
Использование транспортира
У нас есть специальный прибор для измерения углов. Он называется транспортиром . Посмотрите на изображение типичного транспортира с обозначенными его важными частями.
Он называется транспортиром . Посмотрите на изображение типичного транспортира с обозначенными его важными частями.
Транспортиры могут быть большими или маленькими, но все они точно так же измеряйте углы. В размер транспортира не имеет значения размер угла.
Измерение знакомых углов
Вам понадобятся четыре загнутых уголка из предыдущего упражнения. Если вы этого не делали, вернитесь сейчас и следуйте инструкциям в вопросе 5.
В группе из трех или четырех человек с помощью транспортира измерьте углы, которые вы сделано: 90 °; 45 °; 30 ° и 22,5 °.
Вы измеряли угол правильного размера? Если нет, то спроси себе следующие вопросы:
Как использовать транспортир для измерения угла
Шаг 1. Достаточно ли длинные угловые рычаги?
Угловые рычаги должны быть немного длиннее, чем расстояние от начала транспортира до его края.Если они слишком короткие, используйте острый карандаш и линейку, чтобы сделать их длиннее. Будьте осторожны, чтобы выровнять линейку с рукой.
Теперь вы готовы приступить к измерению угла.
Шаг 2: Выровняйте угол и транспортир
Поместите транспортир поверх уголка. Убедитесь в следующем:
Убедитесь в следующем:
- начало координат точно на вершине угла, а
- базовая линия находится точно на вершине одного из плеч угла.
Продолжайте регулировать положение транспортира, пока исходная точка и базовая линия не будут точно выровнены.
Когда транспортир окажется в правильное место держите палец на транспортире, чтобы он не двигался. Если оно движется ¢  € ¦ начать заново! Теперь вы готовы сделать измерение.
Шаг 3: Измерьте угол
Транспортир показывает по часовой стрелке
шкала градусов и шкала градусов против часовой стрелки.Вы выбираете правильный масштаб
найти ту, которая начинается с 0 ° на угловом рычаге. Посмотри где
другое угловое плечо проходит под градусной шкалой. Вот где твой
измерение есть.
Вот где твой
измерение есть.
Вы также можете установить транспортир на угол, используя другую руку. Тогда правильная позиция будет выглядеть так:
Угол на фотографиях выше 37 °. Ты согласен? Вы видите, что есть два способа измерить угол?
Практика измерения с помощью транспортира
Измерьте углы и заполните таблицу на следующей странице.Вы можете продлить оружие, если нужно; не имеет значения, проходят ли они по тексту или другому Рисунок.
Измерьте все пронумерованные углы в следующий рисунок.
 Некоторые углы можно измерить напрямую, другие — нет. Ваш
Транспортир не может измерять углы рефлекса, такие как углы 7 и 8. Поэтому вам придется
Составьте план!
Некоторые углы можно измерить напрямую, другие — нет. Ваш
Транспортир не может измерять углы рефлекса, такие как углы 7 и 8. Поэтому вам придется
Составьте план!1
2
3
4
5
6
7
8
9
10
11
12
Напишите себе небольшую заметку об измерении углы рефлекса здесь:
Посмотрите свои ответы на вопрос 2.
Как сделать углы 3 и 4 сравнивать?
А как насчет углов 6 и 7?
А как насчет углов 4 и 5?
Есть несколько интересных идей здесь. Попробуйте провести дальнейшее расследование и показать учителю, что вы обнаружить.
Использование транспортира для построения углов
Построение углов к заданной прямой
Работайте вместе с партнером над этим мероприятием. Вам понадобится транспортир, острый карандаш и прямая линейка.
Ваша первая задача — построить линию под прямым углом к ниже. Начните с выбора точки на линии. Вы должны четко и аккуратно отметить эту точку маленькой точкой.потом Используйте свое понимание транспортира, чтобы нарисовать угол 90 °.
Теперь заполните пропущенных слов в шагах:
Шаг 1: Выберите точку в любом месте линии. Сделайте небольшую отметку на линии. (Здесь не всегда есть выбор. Иногда нужно использовать определенную точку на линии.)
Шаг 2: Поместите транспортир так, чтобы ______ на линию, а его начало точно на ______
Шаг 3: Сделайте небольшую четкую отметку на ______
Шаг 4: С помощью линейки выровняйте два ______ и проведите прямую линию, которая проходит точно через них.
Постройте углы, используя приведенную ниже линию. В
линия ниже будет одной из сторон углов, которые вы собираетесь построить. Вершина
для каждого из ваших углов — это точка с надписью O, где крошечная вертикальная линия
разрезает длинный горизонтальный. Ваши углы должны быть измерены против часовой стрелки от линии.
В
линия ниже будет одной из сторон углов, которые вы собираетесь построить. Вершина
для каждого из ваших углов — это точка с надписью O, где крошечная вертикальная линия
разрезает длинный горизонтальный. Ваши углы должны быть измерены против часовой стрелки от линии.
23 °
45 °
65 °
79 °
90 °
121 °
154 °
180 °
200 °
270 °
300 °
Угол направление
Линия у вас
приведенный ниже, называется контрольной линией .
Обычно математики Измерьте углы против часовой стрелки от базовой линии.
Используйте строка ниже. На каждом конце нужно провести линии под углом 60 ° к образуют треугольник. Что это за треугольник?
Завершить четырехугольник внизу. Угол при P должен составлять 52 °, а угол при Q, 23 °.
Параллельные и перпендикулярные линии
Перпендикулярные линии пересекаются друг с другом на угол 90 °.
На эскизе показаны две перпендикулярные линии.
Мы говорим: AB перпендикулярно DC.
Пишем: AB \ (\ perp \) DC
Параллельные линии никогда не пересекаются. Они находятся на равном расстоянии друг от друга. У них то же направление.
У них то же направление.
На эскизе показаны две параллельные линии.
Мы говорим: PQ параллельно RS.
Пишем: PQ \ (\ parallel \) RS
Стрелки в середине линий показывают, что линии параллельны друг другу.
Построение перпендикулярных и параллельных прямых
При построении параллельных линий помните, что линии всегда находятся на одинаковом расстоянии друг от друга. Выполните следующие действия, чтобы нарисовать перпендикулярные и параллельные линии с помощью транспортира и линейки.
Мы хотим чтобы провести линию, параллельную XY и проходящую через точку A.
Шаг 1. Проведите перпендикулярную линию между A и XY.
Использование транспортиром, чтобы провести линию, проходящую через точку A под углом 90 ° к XY.
 Label
точка C, где ваша новая линия касается XY. Посмотрите на эскиз ниже, если вы
застрять.
Label
точка C, где ваша новая линия касается XY. Посмотрите на эскиз ниже, если вы
застрять.Шаг 2: Измерьте перпендикулярное расстояние между точкой и линией.
Запишите длину AC:
Шаг 3: начертите точку это такое же расстояние от линии.
Ничья другая линия, перпендикулярная линии XY. Отметьте ту же длину, что и AC на Эскиз показывает, что вы должны делать.
Шаг 4: Проведите параллельную линию.
Присоединиться к A с новой точкой, которая находится на равном расстоянии от XY.Теперь у вас есть параллельная линия.
Попрактикуйтесь в конструировании в своей тетради. перпендикулярные и параллельные линии с помощью транспортира и линейки.

Круги — особенные фигуры
А теперь немного о другом. . . давайте посмотрим на кругов .
Круг со шнурком
Здесь вам может понадобиться поработать с партнером.Вам понадобятся два острых карандаша и короткая веревка, лист бумаги формата А4 и линейка.
Завяжите веревку к обоим карандашам двойными узлами. Узлы должны быть прочными, но не в обтяжку. Нить должна легко вращаться вокруг карандашей, не падая. Один раз вы связали веревку, расстояние между карандашами, когда веревка плотно не должно быть больше 8 см.
Ваш партнер должен держать один карандаш вертикально острием в центре лист бумаги.

Теперь внимательно перемещайте кончик другого карандаша вокруг среднего, рисуя по ходу движения. Пытаться чтобы веревка была натянутой , а карандаш вертикально , когда вы рисовать. Если вы были осторожно, у вас есть круг (ну, надеюсь, что-то довольно близкое к кругу). Теперь вы можете поменяться местами, чтобы у вашего партнера тоже была розыгрыш хода, пока вы держите центральный карандаш.
Марк три точки на окружности. Измерьте расстояние между точкой и центром круга для каждого. Если у вас есть круг, вы должны обнаружить, что расстояния одинаковые.
Подумайте об этом
Можете ли вы придумать любую другую фигуру, где расстояние между центром и краем постоянно во всех направлениях?
- Квадрат?
- Шестиугольник?
- А как насчет овальной формы (эллипса)?
Проведите небольшое расследование, чтобы увидеть, что вы можете найти.
Круги особенные по многим причинам. Наиболее важная причина следующая:
Расстояние от центра круга до края одинаково в любом направлении.
Это расстояние называется радиусом . Мы произнесите это «ра-ди-нас».
Множественное число радиус составляет радиусов . Мы произнесите это: «луч-ди-глаз».
Вы согласны с тем, что два карандаша и веревка — не лучший способ рисовать круги? Струна эластичная.Радиус поменять сложно. Кроме того, карандаш для рисования может отклоняться от курса и образовывать спираль или шаткую кривую. Нам нужно что-то получше.
Использование компаса
Нам понадобится специальный инструмент для рисования кругов. У него должен быть заостренный кончик, как у центрального карандаша. У него также должен быть кончик для рисования, как у карандаша, который вы перемещали. Если вы можете установить расстояние между этими двумя наконечниками, вы можете рисовать круги любого радиуса. Этот инструмент называется компасом , или часто просто компасом .
Если вы можете установить расстояние между этими двумя наконечниками, вы можете рисовать круги любого радиуса. Этот инструмент называется компасом , или часто просто компасом .
Построение кругов с помощью циркуля
Вверху следующей страницы вы увидите точку с меткой A. Следуйте инструкциям ниже и на следующей странице нарисовать круг радиусом 2 см. Центр должен быть в A.
Шаг 1: Поместите заостренный кончик на нулевую линию линейки. Осторожно расширьте угол между руками. Переместите кончик карандаша, пока он не окажется ровно на 2 см.Убедитесь, что заостренный наконечник все еще находится на нуле. Будьте осторожны, чтобы не изменить зазор, если он установлен на 2 см.
Шаг 2: Осторожно вставьте острие в точку A.
 Вдавите бумагу достаточно глубоко, чтобы она оставалась на месте. Это будет центр вашего круга.
Вдавите бумагу достаточно глубоко, чтобы она оставалась на месте. Это будет центр вашего круга.Шаг 3: Удерживайте ручку между указательным и большим пальцами пишущей руки. Держите вторую руку в стороне. Рисуя круг циркулем, используйте только одну руку.
Шаг 4: Поверните ручку между большим и указательным пальцами. Если вы правша, проще всего повернуть компас по часовой стрелке. Если вы левша, поверните против часовой стрелки. Пусть кончик карандаша проведет по бумаге. Не давите на карандаш слишком сильно. Лучше слегка надавить на заостренную руку во время рисования. Кончик карандаша должен двигаться плавно и легко.
Нарисуйте концентрические окружности в центре A выше с помощью радиусом 3 см, 4 см, 5 см и 6 см.Каждый раз тщательно устанавливайте зазор. Написать радиус на краю каждого круга.
Концентрические окружности имеют одинаковую середину.
Научиться пользоваться компасом — все равно что научиться ездить на велосипеде. Это требует координации и практики. Не смущайтесь, если что-то пойдет не так. Со временем вы очень хорошо в этом научитесь. Если ваши круги превращаются в шаткие линии, просто начните снова!
Вот несколько советов по рисованию кругов:- Если ваши круги превращаются в спирали, это потому, что стрелки вашего компаса переехали.Снова проверьте их ширину по линейке.
- Если стрелки вашего компаса не остаются в том положении, в котором вы их установили, это потому, что гайка на шарнире под ручкой ослабла. Попросите учителя помочь вам, если вы не можете затянуть его самостоятельно.
- Если вы не можете сделать скручивание, представьте, что у вас есть небольшой кусок мягкой глины между большим и указательным пальцами, и вы пытаетесь свернуть его в небольшую полоску. Для поворота компаса используется тот же тип скользящего движения.
 Позвольте компасу висеть у вас в руке в воздухе и поверните ручку. Затем попробуйте несколько раз использовать макулатуру, пока не сможете легко повернуть компас.
Позвольте компасу висеть у вас в руке в воздухе и поверните ручку. Затем попробуйте несколько раз использовать макулатуру, пока не сможете легко повернуть компас.
Кружки на окружностях
Пришло время немного повеселиться с компасом и научиться им пользоваться. Следуйте этим инструкциям, чтобы нарисовать красивый узор, показанный справа в тетради.
Марка убедитесь, что ваш карандаш острый; затем поместите его в компас.
Установить радиус до 4 см. Нарисуйте круг в центре страницы. Важно: ваш радиус должен оставаться неизменным на протяжении всей деятельности.
Положите компас точка в любом месте на краю круга. Нарисуйте еще один круг. Этот круг должен пройти через центр вашего первого круга (у них одинаковые радиус).

Ваш второй circle разрезает первый круг в двух точках.Выберите одну из этих точек. Место ваш компас укажет в этой точке. Нарисуйте еще один круг радиуса 4 см.
Повторить шаг 3 с вашим третьим кругом, четвертым кругом и т.д. У вас должно получиться шесть кругов на ваш первый круг. То есть всего семь кругов.
Оформить как Вы, пожалуйста. (Вы можете дополнительно украсить свой узор, добавив больше кругов или соединение точек прямыми линиями и т. д.Посмотрите, какие узоры и формы вы можно найти среди всех кругов.)
Использование кругов для рисования других фигур
Геометрические фигуры прячутся в кругах
w3.org/1999/xhtml»> Ниже представлен набор из семи кругов, подобных тому, который вы нарисовали. Сядьте с партнером и попытайтесь найти скрытые многоугольники.Вы найдете эти многоугольники, соединив точки, в которых круги пересекают друг друга. Точки будут вершинами многоугольников.Смотри внимательно. Есть треугольники, четырехугольники, пятиугольники и шестиугольники. Когда вы увидите их, аккуратно и аккуратно обработайте их карандашом по бокам. Если на приведенном ниже наборе кругов недостаточно места, перерисуйте круги на отдельном листе бумаги и покажите там фигуры. При желании вы можете измерить углы в каждой вершине и длину сторон.
Дуги окружностей
Для построения фигур нам необязательно рисовать целые круги.Нас действительно интересуют только точки пересечения кругов, поэтому мы можем просто нарисовать дуги там, где они пересекаются. В следующем году вы будете использовать дуги в своих геометрических конструкциях.
В следующем году вы будете использовать дуги в своих геометрических конструкциях.
Дуга — это небольшая часть окружности. Мы используем термин , окружность , когда говорим о расстоянии вокруг круга или вокруг любой другой изогнутой формы.
Сделайте в своей тетради следующее:
Нарисуйте дугу с помощью радиус 3 см.
Нарисуйте дугу больше четверть круга, используя радиус 5 см.
Нарисуйте дугу меньше четверть круга, используя радиус 5 см.
Расширение
Закончив работу в разделе 4.8, поэкспериментируйте с рисованием только тех дуг, которые вам нужны в различных конструкциях. Вот пример, показывающий, как построить правильный шестиугольник только из дуг:
Знакомые фигуры в шаблоне из семи кругов
Для этого упражнения вам понадобятся пять наборов из семи кругов, подобных тем, которые были нарисованы в предыдущих двух упражнениях. Начните с рисования их на чистых листах бумаги. Не делайте радиус больше 4 см. Пронумеруйте свои наборы цифр от 2 до 6. Пометьте каждую цифру, как показано справа.
Начните с рисования их на чистых листах бумаги. Не делайте радиус больше 4 см. Пронумеруйте свои наборы цифр от 2 до 6. Пометьте каждую цифру, как показано справа.
Следуйте инструкции ниже.
- Рисунок 1: Используйте рисунок рядом. Проведите линии, соединяющие AB, BC, CD ,. . . до FA.
- Рисунок 2: Проведите линии, соединяющие A, O и B.
- Рисунок 3: Проведите линии, соединяющие B, F и D.
- Рисунок 4: Проведите линии, соединяющие BC, CE, EF и FB.
- Рисунок 5: Проведите линии, соединяющие CD, DE, EF и FC.
- Рисунок 6: Проведите линии, соединяющие AB, BC, CE и EA.
Заполните таблицу ниже.
Показывает название каждой фигуры и ее свойства.
Рисунок 1 (на справа) сделано в качестве примера.

1
Шестигранник правильный
6-гранная фигура.Все стороны равны. Все внутренние углы равны.
2
3
4
5
6
Постройте еще несколько фигур
Внимательно прочтите инструкции и точно следуйте им.
Проведите линию в ваша тетрадь. Линия должна быть длиной от 3 до 6 см. Нарисуйте это в середина вашей страницы.
Обозначьте концы A и B.
Поместите точку вашего компас в точке А. Тщательно установите радиус компаса на расстояние между А и Б.
Нарисуйте круг с точка компаса в точке A.
Нарисуйте еще один круг с компас укажет на точку B без изменения ширины радиуса.
Круги пересекаются в два точки. Выберите одну из этих точек. Обозначьте его C. Убедитесь, что вы находитесь на верный путь, сравнив свой эскиз с тем, что справа.

Тщательно выровняйте линии AC и BC.
Что за фигура ABC? Проверьте это, измерив углы. Как вы думаете, почему это произошло?
Нарисуйте в упражнении две линии PQ и QR. книга.
- Линии пересекаются и образуют угол в точке Q.
- Уголок можно сделать любого размера.
- Измените длину лески.
- Не делайте линии длиннее 6 см каждая.
Место ваш компас укажет на точку Q. Установите радиус компаса на расстояние QP.Поместите точку циркуля в R. Нарисуйте круг.

Поместите точку компаса обратно в Q. Установите радиус равным длине QR. Поместите точку компаса на P. Нарисуйте круг.
Два круга пересекаются в два очка. Решите, какая точка будет вершиной параллелограмма. Вызов этот пункт S.
Присоединяйтесь к линиям SP и SR. PQRS — это параллелограмм?
Кое-что задуматься
Почему этот метод формирует параллелограмм?
Параллельные и перпендикулярные прямые с окружностями
Параллельные и перпендикулярные
Ревизия: Дополните эти определения.
Когда одна строка параллельно другой линии, линии
Когда одна линия перпендикулярна другой линии, линии
Семь кругов рисунок был нарисован ниже.
 Точки пересечения отмечены. Линия
сегмент втянут.Используйте линейку и карандаш, чтобы соединить пары точек, чтобы
что строки:
Точки пересечения отмечены. Линия
сегмент втянут.Используйте линейку и карандаш, чтобы соединить пары точек, чтобы
что строки:параллельно линии сегмент
перпендикулярно отрезок.
Когда две строки (или дуги) пересекают друг друга, мы говорим, что они пересекают .
точка пересечения — это место их встречи.
У вас должно быть нарисовано 7 линий (2 параллельных и 5 перпендикулярных отрезку). Сравните ваши строки со строками друга. Ты согласен?
В вашем тетрадь, нарисуйте несколько кругов одинакового радиуса вдоль линии. Начать с рисование линии. Затем с помощью циркуля нарисуйте круг со средней точкой на линия.

Сохраните ширину циркуля и нарисуйте еще один круг с центром. где первый круг пересек линию.Повторяйте столько раз, сколько хотите. В пример внизу предыдущей страницы только три круга были нарисовано.
Можете ли вы найти это пример в семикруге? Смотрите внимательно, пока не увидите это.
Вы видите, где вы можно построить линии, перпендикулярные данной линии? Нарисуй их осторожно карандашом и линейкой.
Вы видите два линии, которые параллельны данной линии? Нарисуй их тоже.
Используйте круги для построения линия, перпендикулярная линии ниже.
Используйте круги, чтобы постройте линию, параллельную линии ниже.

Добавочный номер
Установите компас на определенном расстоянии, чтобы пример 3 см, и исследуйте точки, которые находятся на одинаковом расстоянии от фиксированного точка, P.
Используйте компас и исследуйте все точки которые находятся на одинаковом расстоянии, например, 3 см, от двух фиксированных точек, A и Б.
В этой главе вы узнает о различных видах 2D-форм. Вы узнаете имена, данные разные формы. Вы также узнаете о различных свойствах, которые разные типы форм имеют в зависимости от их сторон и углов.
Треугольники, четырехугольники, окружности и др.
Решите, что есть что, и нарисуйте несколько фигур.
Треугольник — это замкнутая фигура с тремя прямыми сторонами и тремя углами.
Четырехугольник имеет четыре прямые стороны и четыре угла.
Окружность круглая, а край всегда находится на одинаковом расстоянии от центра.
Какие фигуры на противоположной странице круги?
Какие фигуры на противоположной странице треугольники?
Какие фигуры на противоположной странице четырехугольники?
Используйте линейку для следующих действий:
Сделать рисование одного треугольника с тремя острыми углами, а другого треугольника с одним тупой угол.
Нарисуйте четырехугольник с двумя тупыми углами.
Можете ли вы нарисовать треугольник с двумя тупыми углами?
Нарисуйте треугольник с одним прямым углом и треугольник без прямых углов.

Можете ли вы нарисовать треугольник? с двумя прямыми углами?
Можете ли вы нарисовать четырехугольник с четырьмя прямыми углами?
Эти четыре строки образуют четырехугольник ABCD.
Две красные стороны, BC и AD, называются противоположными сторонами четырехугольника ABCD.
Какие две другие стороны ABCD также являются противоположными сторонами?
Линии DA и AB на рисунке в вопрос 7 называются соседними сторонами . Они встречаются в точке, которая является одной из вершины (угловые точки) четырехугольника.
Назовите еще два смежные стороны в ABCD.

AB примыкает к DA в четырехугольнике ABCD.Какая другая сторона ABCD также примыкает к DA?
Уильям говорит:
«Каждая сторона четырехугольника имеет две смежные стороны.
Каждая сторона четырехугольника также имеет две противоположные стороны ».
Уильям прав? Обоснуйте свой ответ.
Уильям также говорит:
«В треугольнике каждая сторона примыкает ко всем остальным сторонам.»
Это правда? Обоснуйте свой ответ.
В каждом случае укажите, две стороны являются противоположными сторонами или смежными сторонами четырехугольника PQRS.
QP и PS
QP и SR
PQ и RQ
PS и QR
SR и QR
Различные типы треугольников
Равносторонние, равнобедренные, разносторонние и прямоугольные треугольники
Треугольник с двумя равными сторонами называется равнобедренным треугольником .
Треугольник с тремя равными сторонами называется равносторонним треугольником .
Треугольник с прямым углом называется прямоугольным треугольником .
Треугольник с тремя сторонами разной длины и без прямого угла называется разносторонним треугольником .
Измерьте каждый угол в каждом из равнобедренных треугольников , указанных выше. Делать вы заметили что-нибудь особенное? Если не уверены, нарисуйте больше равнобедренных треугольников. в тетради.
Измерьте углы и стороны следующие треугольники. Что особенного в этих треугольниках? Другими словами, что чем эти треугольники отличаются от других?
Эти треугольники называются равносторонними треугольниками .
Измерьте каждый угол в каждом из следующих треугольников.
 Вы замечаете что-нибудь особенное в этих углах?
Вы замечаете что-нибудь особенное в этих углах?Определите самый длинный стороны в каждом из треугольников. Если вы не уверены, какой из них самый длинный сторона, измерьте стороны. Что вы заметили в самой длинной стороне каждого из эти треугольники?
Эти треугольники называются прямоугольными треугольниками .
Сравнение и описание треугольников
Когда две или более сторон фигуры равны по длине, мы показываем это с помощью коротких линий на равных сторонах.
Используйте следующие треугольники, чтобы ответить на следующие вопросы:
Какой треугольник имеет только две стороны, которые равны?
Как называется этот тип треугольника?
В каком треугольнике есть все три стороны равны?
Как называется этот тип треугольника?
Какой треугольник имеет угол равно 90 °?
Как называется этот тип треугольника?
Запишите тип каждого из следующих треугольников в поле предоставлено:
Нахождение неизвестных сторон в треугольниках
Назовите каждый тип треугольника ниже.
Используйте данную информацию, чтобы определить длину сторон:
AB:
г. до н. Э .:
EF:
Можете ли вы определить длину GH и HI? Поясните свой ответ.
Площадь в углу ул. \ (\ треугольник \) JKL показывает, что это прямой угол. Назовите причину для каждого из ваших ответы ниже.
Это треугольник разносторонний, равнобедренный или равносторонний?
Назовите две стороны треугольника, которые равный.
Какая длина JK?
Назовите два равных угла в этом треугольнике.
Какой размер \ (\ hat {J} \) и \ (\ hat {L} \)?
Различные типы четырехугольников
Исследование четырехугольников
Два на следующих страницах показаны различные группы четырехугольников.
В котором группы обе пары противоположных сторон параллельны?
В каких группах всего несколько соседние стороны равны?
В каких группах все четыре углы равны?
В каких группах находятся все стороны в каждом четырехугольнике равны?
В каких группах все четыре стороны равны?
В каких группах находится каждая сторона перпендикулярно прилегающим к нему сторонам?
В каких группах противоположные стороны равны?
В каких группах есть хотя бы одна пара соседних сторон равны?
В каких группах есть хотя бы одна пара противоположных сторон параллельна?
В каких группах находятся все углы прямые углы?
Фигуры группы 1 называются параллелограммов .
Что вы наблюдаете про противоположные стороны параллелограммов?
Что вы заметили об углах параллелограммы?
Фигуры группы 2 называются воздушных змеев .
Что вы наблюдаете о сторонах воздушных змеев?
Что еще вы заметили в воздушных змеях?
Группа 1
Группа 2
Группа 3
Группа 4
Группа 5
Группа 6
Цифры в группа 3 называется ромбов .
Что вы наблюдаете о сторонах ромбов?
Что еще вы заметили в ромбах?
Примечание: один ромб ; два или более ромбов .
Фигуры группы 4 называются прямоугольников .
Что вы наблюдаете про противоположные стороны прямоугольников?
Что вы заметили об углах прямоугольники?
Что вы заметили на соседних сторонах прямоугольники?
Фигуры группы 5 называются трапеции .Что вы наблюдаете по поводу противоположных сторон трапеции?
Стрелками показаны стороны, параллельные друг другу.
Фигуры группы 6 называются квадратов .
Что вы наблюдаете о сторонах квадратов?
Что вы заметили об углах квадраты?
Сравнение и описание форм
Имя каждую фигуру в каждой группе.
Группа A
Группа B
Каким образом одинаковы ли цифры в каждой группе?
Группа A:
Группа B:
Как выглядит одна из фигур в каждой группе отличаются от двух других фигур в группе?
Группа A:
Группа B:
Поиск неизвестных сторон четырехугольника
Используйте свои знания о сторонах и углах четырехугольника, чтобы ответить на следующие вопросы. Обоснуйте свои ответы.
Какой четырехугольник у ABCD?
Назовите сторону, равную AB.
Какова длина BC?
Какой четырехугольник у EFGH?
Какова длина следующих сторон?
EF:
GH:
Какой четырехугольник у JKLM?
Какая длина JK?
Рисунок PQRS — воздушный змей с PQ = 4 см и QR = 10 см.Завершите следующий рисунок:
маркировка вершин кайта
показывает на чертеже равные стороны
маркировка длины каждой стороны.
Круги
Сделайте точку в середине круга справа.Напишите букву M рядом с точкой. Если ваша точка находится в середине круга, она называется средней точкой или центром .
Проведите линии MA, MB и MC от M до красных точек A, B и C.
три красные точки находятся на окружности со средней точкой M.
Прямая линия, такая как AC, проведенная через окружность, проходящая через ее середину, называется диаметром круг.
Измерьте MA, MB и MC.
Если MA, MB и MC равны по длине, вы хорошо выбрали среднюю точку. Если они не равны, вы можете улучшить свой набросок круга и его частей.
Прямая линия от середины круга до точка на окружности называется радиусом окружности.
Синяя линия MA — это радиус .Любая прямая линия от центра до круга радиус.
Черная линия AB соединяет две точки на окружности. Мы называем это аккордом круг.
В На следующих двух диаграммах цветные секции представляют собой сегментов круг. Сегмент — это область между хордой и дугой.
В круге справа красный участок называется сектором круга.Как видите, сектор — это область между двумя радиусами и дугой.
Подобные и совпадающие формы
На этой и следующей страницах показаны три группы четырехугольников.
Чем каждая группа отличается от других, кроме цвета?
Группа А:
Группа B:
Группа C:
Группа A
Группа B
Группа C
Фигуры одинаковой формы, такие как синие фигуры на предыдущей странице, считаются на похожими друг на друга.Подобные формы могут отличаться по размеру, но всегда будут иметь одинаковую форму.
Пример аналогичной формы
Пример конгруэнтных форм
Фигуры одинаковой формы и размера, такие как красные фигуры на предыдущей странице, называются конгруэнтными друг другу. Эти формы всегда имеют одинаковый размер и форму.
Красные фигуры на предыдущей странице похожи друг на друга?
Посмотрите на группы D, E, F и G на этом страницу и следующую.В каждом случае скажите, похожи ли формы и конгруэнтный, подобный, но не конгруэнтный, или ни подобный, ни конгруэнтный.
Группа D:
Группа E:
Группа F:
Группа G:
Группа D
Группа E
Группа F
Группа G
Редакция
Не следует использовать калькулятор по любому из вопросов в этом разделе.Покажи свои шаги работающий.
Работа с целыми числами
Сделайте приведенные ниже числовые предложения истинными. В первый блок каждого вопроса, напишите знак умножения или деления. Во второй блок напишите либо 10, либо 100 или 1 000.
8 ☐ ☐ = 800
740 000 ☐ ☐ = 740
Обведите все цифры приведенное ниже число округляется до 60 000.
62 495; 54 498; 65 000; 56 002; 67 024
Рассчитать следующий:
\ (274 561 + 367 238 \)
\ (4 672 — 3 937 \)
\ (3 458 \ раз 43 \)
\ (6 624 \ div 18 \)
Запишите недостающее числа в блоках.
8; 15; 22; 29; ☐
Туми выполняет последовательность числа, используя следующее правило: «Возьмите половину предыдущее число, а затем прибавьте 12. «Напишите следующие три числа в последовательности:
56; 40; 32;
Сложены два трехзначных числа вместе, как показано, и дают трехзначный ответ, но некоторые цифры отсутствующий.Введите недостающие цифры, чтобы расчет был правильным.
59 ☐ + 3 ☐9 = ☐53
Исмаил имеет следующие номера:
71; 72; 73; 74; 75; 76; 77; 78; 79; 80
Он хочет их отсортировать поместив их на диаграмму сортировки ниже. Помогите Исмаилу, разместив числа в правильных блоках.
Запишите, используя только номеров из облака:
Все простые числа
Вся площадь числа
Все числа куба
Все кратно 8
Все факторы 8
Учитель Рамушвана утверждает:
«Даже каждые число (больше или равно 6) можно записать как сумму
пара нечетных простых чисел числа , например \ (10 = 3 + 7 \).«
Запишите два пары нечетных простых чисел, сумма каждой из которых равна 20.
Выберите любое четное число больше 30 и напишите это как сумма двух нечетных простых чисел.
Запишите следующее как произведение простых чисел. факторы:
576
600
Найдите (i) HCF и (ii) LCM 576 и 600.
HCF
LCM (оставьте свой ответ как произведение простые множители)
Сколько часов займет Семья Адамс доберется до места отдыха, если оно находится на расстоянии 495 км, и они ехать со средней скоростью 110 км / ч?
Грэм, Тули и Андил вместе работали над праздниками, косили газоны их соседи.Они собрали в общей сложности 1 200 рандов, и теперь им нужно поделиться. Они согласны с тем, что, поскольку не все они работали одинаково, деньги должны быть делится между Грэмом, Тули и Андилом в соотношении 4: 6: 5. Сколько денег получит Тули?
Г-н Хумало решает попробовать заработать немного денег на покупке и продаже подержанной мебели. У него в банке 6 000 рандов. счета, и использует часть денег, чтобы купить старую кровать и матрас для R800, комод на R2 500, два шкафчика по R300 каждый, стиральная машина для R900.
Сколько осталось в его банковский счет после этих покупок?
Предположим, он продает основание кровати и матрас для R980, комод для R2 950 и оба шкафчика на общую сумму R750. Хотя, похоже, никому не нужна его стиральная машина. На этом этапе у него есть сделал убыток. Какова стоимость проигрыша?
Сколько ему нужно продать белье машина для получения общей прибыли в 1 000 рэндов?
Миссис Стейн берет ссуду в 55 000 рандов от Fidelity Bank.Банк взимает простые проценты в размере 500 рандов за месяц. Сколько денег должна будет миссис Стейн после \ (1 \ frac {1} {2} \) годы?
Джон зарабатывает 480 рандов в субботу. Он работает с 08:00 до 14:00. Рассчитайте его почасовую ставку.
Экспоненты
Рассчитайте.
\ (12 \ раз 12 \)
\ (8 \ раз 8 \)
\ (7 \ раз 7 \ раз 7 \)
\ (3 \ раза 3 \ умножить на 3 \)
\ (6 \ раз 6 \ раз 6 \)
\ (13 \ раз 13 \)
Объясните разницу между \ (4 \ times 3 \) и \ (4 ^ 3 \).5 \) в развернутом виде.
Запишите следующее в экспоненциальной форма:
\ (2 \ раза 2 \ раз 2 \)
\ (3 \ раза 3 \ раза 3 \ раза 3 \ раза 3 \ раза 3 \ раза 3 \ раза 3 \)
Запишите числа в экспоненциальной форме.Проверять ваши ответы.
81
10 000
Завершено:
- 5 в квадрате
5 в кубе
- 5 в квадрате
Вычислить:
\ ( 7 ^ 2 \)
\ (15 ^ 2 \)
\ (3 ^ 2 \ раз 4 ^ 2 \)
\ (\ sqrt {16} \)
следующие утверждения верны или ложны? Объясни свои ответы. 3 = 175 616 \), запишите значение \ (\ sqrt [3] {175 616} \).
Геометрия прямых
Учитывайте показанную сетку рядом.
PS это линия, луч или отрезок?
Нарисуйте на сетке отрезок прямой через R это будет перпендикулярно PS. Обозначьте это ТУ.
Нарисуйте линию на сетке что параллельно с PS.Обозначьте это WX.
Обеспечьте правильное имя для каждого из геометрических элементов AB и CD, показанных на диаграмма:
AB:
CD:
Имеется геометрическая связь между отрезками PR и QS, показанными на схеме.Опишите отношения добавив правильное слово в пунктирную линию:
PR — это ____________ QS.
Нарисуйте луч и линию это никогда не встретится.
Построение геометрических фигур
Используйте транспортир для точного измерения следующих углов, как показано на диаграмму ниже, и запишите ответы в предоставленную таблицу:
\ (\ hat {B} \)
\ (A \ hat {D} B \)
\ (D \ hat {A} B \)
\ (C \ hat {D} B \)
рефлекс \ (C \ hat {A} B \)
\ (\ hat {B} \)
\ (A \ hat {D} B \)
\ (D \ hat {A} B \)
\ (C \ hat {D} B \)
Рефлекс \ (C \ hat {A} B \)
Рефлекс
Постройте полукруг с радиусом 3 см.{\ circ} \)
Используйте круги, чтобы постройте две прямые CD и EF, параллельные прямой AB ниже. Линия CD должен быть выше линии AB, а линия EF ниже линии AB. Обозначьте обе строки.
Рассмотреть диаграмму рядом. Запишите названия пары перпендикулярных линий.
Геометрия фигур
Дайте полное название формы, которая подходит под данные описания:
Трехсторонняя форма, имеет ровно две стороны равной длины
Четырехсторонняя форма с обеими парами противоположных стороны параллельны и равны по длине, без прямых углов
Четырехсторонняя форма только с одной парой противоположные стороны параллельны
Каков правильный термин для каждого из следующие части круга с центром B, как показано рядом?
Линия AB
Заштрихованная область
На пл. рядом с сеткой нарисованы две стороны воздушного змея.Используйте линейку и завершите воздушный змей на сетке.
Даррел говорит: «Четырехсторонние формы, о которых я думаю имеют хотя бы одну пару равных смежных сторон. Какие они? »Запишите имена всех форм, подходящие под его описание.
DEFG — воздушный змей, DE = 4 см и EF = 5,2 см. Запишите длины DG и GF.
STUV — прямоугольник. Запишите значение \ (\ hat {T} + \ hat {V} \). Дать причина вашего ответа.
Рассмотрите диаграмму рядом.
Запишите буквы всех форм, которые соответствуют форме B.
Запишите буквы всех форм которые на похожи на на форму B.
Равнобедренный треугольник LMN имеет LM = 4. см и периметром 16 см. Изучите и запишите все возможных длины MN и LN.
В каждом случае говорят, что обе стороны являются противоположными сторонами или соседними сторонами четырехугольника DEFG.
GD и DE
DE и GF
Оценка
В этом разделе числа, указанные в скобках в конце вопроса, указывают количество баллов, которые стоит поставить за этот вопрос.Используйте эту информацию, чтобы определить, сколько работы вам потребуется.
Общее количество оценок, присвоенных оценка 60.
Не пользуйтесь калькулятором!
Вот пять однозначных карт:
Двузначные числа могут быть составлены размещая две карты рядом друг с другом — так, например, взяв 1 и 2 и поместив их рядом, получится число 12 (двенадцать).
Выберите по две карты каждую пора составить следующие двузначные числа:
Нечетное число
Кратное 9
Коэффициент 126
Квадратный номер
Аянда имеет колоду карт, пронумерованных от С 1 по 16.Он случайным образом выбирает четыре карты из колоды:
- Один фактор 39.
- Два эт. кратно 4.
- Три сотки четное.
- Всего четыре числа больше 45, но меньше 50.
Запишите значения четырех чисел.
Все 769 учеников из Сибанье Начальная школа собирается на спортивную встречу.Школа арендует автобусы от местная компания. Каждый автобус вмещает всего 52 пассажира, и каждый автобус должен иметь два учителя на борту. Сколько автобусов придется нанять школе, чтобы добраться всех на встречу?
Рассчитать общее количество тестов калитки, взятые четырьмя лучшими игроками в истории крикета Proteas (данные верны по состоянию на июнь 2013 г.):
- Шон Поллок: 421
- Махая Нтини: 390
- Дейл Стейн: 332
- Аллан Дональд: 330
Используйте простые множители, чтобы найти НОК 42 и 18.
Семье Динтла нужно добраться до Полокване, в 330 км, к 11.00. Если они выезжают в 7. {\ circ} \).
Используйте свой линейка и транспортир, чтобы нарисовать линию, параллельную нарисованному отрезку FG ниже, и проходит через точку H.
Четыре круги нарисованы так, чтобы они аккуратно умещались в квадрат со стороной 6 см, как показано (, а не в масштабе). Запишите радиус каждого круг.
Каково геометрическое имя фигуры, изображенной на точечной сетке ниже?
Нарисуйте две фигуры, которые похожи на на показанную форму, в любом месте сетки. Каждая фигура, которую вы рисуете, должна иметь разный размер.
г. На следующей диаграмме показан квадрат, нарисованный на точечной сетке.Площадь разделена на четыре треугольника, а именно A, B, C и D.
Запишите буквы всех прямоугольных треугольников.
Запишите буквы всех равнобедренные треугольники.
Запишите буквы двух конгруэнтные треугольники.
Я четырехугольник с двумя пары противоположных сторон равны, смежные стороны не равны, и нет прямых углов. Какая я форма?
Какое особое название мы даем по периметру круга?
Нарисуйте ромб любого размера на точечная сетка ниже.Добавьте соответствующие символы на диаграмму, чтобы показать, что противоположные стороны ромба параллельны.
В трапеции JKLM, JK параллельна противоположной стороне.
Завершить выписка:
JK ||
Изучите следующую схему:
Зачеркнуть неверное слово или символ в каждой скобке:
AD — это (параллельно / перпендикулярно) BC.Это можно обозначить следующими символами:
(н.э. \ (\ perp \) до н.э. / AB || ДО Н.Э).
Нарисуйте (от руки, линейкой и транспортиром, а также техникой) геометрические фигуры в заданных условиях. Сосредоточьтесь на построении треугольников из трех углов или сторон, обращая внимание на то, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
Стороны треугольников:Учащимся предлагается определить, определяет ли треугольник заданная длина.
Тип: Формирующая оценка
Рисование треугольников SSS:Учащимся предлагается нарисовать треугольник с заданной длиной сторон и объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующая оценка
Рисование треугольников SSA:Учащимся предлагается нарисовать треугольник с учетом длины двух сторон и величины невключенного угла и решить, определяют ли эти условия уникальный треугольник.
Тип: Формирующая оценка
Рисование треугольников SAS:Учащимся предлагается нарисовать треугольник с учетом размеров двух сторон и их угла, а также объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующая оценка
Рисование треугольников ASA:Учащимся предлагается нарисовать треугольник с учетом размеров двух углов и их стороны и объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующая оценка
Рисование треугольников AAS:Учащимся предлагается нарисовать треугольник с двумя углами и стороной без учета и объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующая оценка
Рисование треугольников AAA:Учащимся предлагается нарисовать треугольник с заданными углами и объяснить, определяют ли эти условия уникальный треугольник.
Тип: Формирующая оценка
Задачи кодирования геометрии # 1-7, 14 и 15:Этот набор задач по геометрии фокусируется на создании множества многоугольников по мере того, как учащиеся решают задачи и думают, когда они учатся кодировать с помощью программного обеспечения для блочного кодирования.Студент должен будет использовать свои знания об атрибутах многоугольников и математических принципах геометрии для выполнения заданных задач. Задачи начинаются с довольно простых и переходят к более сложным ситуациям, в которых учащиеся могут исследовать в своем собственном темпе или работать в команде. Стандарты компьютерных наук неразрывно связаны со стандартами математики, в то же время предлагая «Шаг вперед!» и «Прыгай!» возможности для повышения строгости.
Тип: План урока
Задача кодирования геометрии №16, 18 и 19:Этот набор задач по геометрии фокусируется на создании множества многоугольников с использованием координатной плоскости, когда учащиеся решают задачи и думают, когда они учатся кодировать с помощью программного обеспечения блочного кодирования.Студент должен будет использовать свои знания об атрибутах многоугольников и математических принципах геометрии для выполнения заданных задач. Задачи начинаются с довольно простых и переходят к более сложным ситуациям, в которых учащиеся могут исследовать в своем собственном темпе или работать в команде. Стандарты компьютерных наук неразрывно связаны со стандартами математики, в то же время предлагая «Шаг вперед!» и «Прыгай!» возможности для повышения строгости.
Тип: План урока
Исследование неравенства треугольника:Студенты используют практические материалы, чтобы понять, что только определенные комбинации длин позволят создать замкнутые треугольники.
Тип: План урока
Designing Geo-World: тематический парк на основе геометрии:На этом уроке учащиеся исследуют контекстную задачу, в которой им нужно будет построить двухмерный многоугольник, вычислить фактическую длину и площадь, а затем воспроизвести масштабный чертеж фигуры в другом масштабе.Студенты также будут использовать бесплатное приложение GeoGebra (см. Ссылку для скачивания в разделе «Предлагаемые технологии»), чтобы помочь им спроектировать свои парки.
Тип: План урока
Математика для 7-го класса — Блок 6: Геометрия
Краткое описание агрегата
В Разделе 6 ученики седьмого класса изучают широкий круг тем, от отношений углов до кругов и многоугольников до твердых фигур.Стандарты геометрии для седьмого класса относятся к категории дополнительных стандартов, однако в подразделении есть несколько возможностей, позволяющих учащимся выполнять основную работу класса. В начале урока учащиеся используют и решают уравнения, чтобы представить отношения между углами и найти недостающие меры углов. Исследуя круги, ученики обнаруживают пропорциональную зависимость между длиной окружности круга и его диаметром и понимают π как отношение этих двух величин.Студенты также будут использовать свои навыки выражения для написания числовых выражений, которые можно использовать для определения площади поверхности и объема трехмерных фигур.
На протяжении всего модуля учащиеся сталкиваются с несколькими словарными словами, такими как дополнительные углы, вертикальные углы, радиус и окружность. Многие из этих слов позволяют учащимся быть более точными в общении друг с другом (МР.6). Студенты также столкнутся со сложными диаграммами углов и трехмерными фигурами, где им нужно будет понять, какую информацию они могут почерпнуть из диаграммы, и спланировать путь решения, прежде чем переходить к ней (МП.1). Учащиеся должны иметь доступ к нескольким инструментам, которые они могут использовать на уроке, включая линейки, транспортиры, компасы и справочные листы (МР.5).
Базовые навыки для стандартов в этом блоке относятся к четвертому – шестому классам. В четвертом классе ученики изучали принципы измерения углов и считали, что измерение угла является аддитивным. В пятом классе ученики развили понимание трехмерного объема, которое они в дальнейшем развили в шестом классе.Шестиклассники также начали различать трехмерное пространство, которое занимает объект, и площадь поверхности, которая его покрывает.
В восьмом классе учащиеся будут увеличивать масштаб прямоугольных треугольников и применять теорему Пифагора для определения длин сторон прямоугольных треугольников. Они также продолжат решать реальные приложения площади и объема с добавлением конусов, сфер и цилиндров.
Темп: 23 учебных дня (21 урок, 1 гибкий день, 1 контрольный день)
Инструкции по корректировке темпа на 2020-2021 учебный год из-за закрытия школ см. В нашем разделе «Рекомендуемые корректировки для 7-го класса и последовательности».
10 исследований геометрического искусства для изучения математики
В следующих упражнениях учащиеся используют словарный запас геометрии и изучают математические понятия, включая: измерение, площадь и периметр, дроби и шаблоны!
1. Спиральные треугольникиСоздайте спиральный дизайн из равносторонних треугольников! Чтобы создать дизайн, начните с большого треугольника.Затем вырежьте треугольник, длина стороны которого равна высоте большого треугольника. Вставьте сторону треугольника по центру большего треугольника, чтобы она покрывала половину большого треугольника. Продолжайте создавать меньшие треугольники со сторонами, соответствующими высоте предыдущего треугольника, чтобы получилась спираль!
2. Квадратная стопка Это художественное задание принадлежит Lucky To Be In First.Студенты отмерили , вырезали и вставили квадраты в порядке убывания. Каждый квадрат на 1/2 дюйма меньше предыдущего.
Примечание. Вы также можете попросить детей вычислить площадь и периметр каждого квадрата на отдельном листе бумаги.
Пример
1. Площадь = 25, периметр = 20
2. Площадь = 20,25, периметр = 18
3. Площадь = 16, периметр = 16
4. Площадь = 12,25, периметр = 14
5. Площадь = 9, периметр = 12
6. площадь = 6,25, периметр = 10
7.площадь = 4, периметр = 8
8. площадь = 2,25, периметр = 6
9. площадь = 1, периметр = 4
Объедините математику и искусство, создав линейный рисунок. Дети используют линейку и рисуют на бумаге случайные линии. Затем они становятся исследователями полигонов! Они рассматривают свои изображения и цвета в многоугольниках с одинаковым количеством сторон.
4. МногоугольникиИсследуйте вершины и диагонали, ища узоры в многоугольниках! Попросите детей угадать количество диагоналей треугольника, квадрата, пятиугольника, шестиугольника, семиугольника и восьмиугольника. Разделите детей на команды. Затем попросите их решить проблему, нарисовав диагонали на контурах фигуры. Убедитесь, что дети используют маркеры разного цвета для каждой диагонали (чтобы они могли их сосчитать).Также попросите товарища по команде подсчитать каждую нарисованную диагональ. Могут ли они найти выкройку ?! Сколько диагоналей у шестиугольника ?!
5. Квадратный взрывПодарите детям ножницы и бумажный квадрат и посмотрите, что они могут создать!
6.Frac-Geo-BotFrac-Geo-Bot — это увлекательная математическая игра, позволяющая детям проявить творческий подход. Они конструируют робота из различных полигонов. Затем они вычисляют дробь для каждой формы и цвета. Дети постарше могут создавать более сложных ботов, подобных приведенному выше. Дети младшего возраста могут создавать более простых ботов, используя простые формы.
7.Передайте статью: сотрудничествоЭтот совместный проект в области математического искусства создан Incredible Art! Дети показывают свои знания геометрических терминов , создавая искусство! Каждому ребенку дается листок бумаги. Им дается инструкция (например, сделать 3 точки). Затем они передают свой лист бумаги. Дается еще одна инструкция (например, используйте циркуль, чтобы создать 3 круга из 3 точек). Студенты рисуют на бумаге своих сверстников. Затем они передают бумагу. Бумаги распространяются, пока не достигнут своего «хозяина».”Владелец украшает линейный рисунок, чтобы создать уникальное произведение искусства!
8. Торговые карточки формы Дети рисуют форму и заполняют обратную сторону открыток. Щелкните здесь, чтобы распечатать.Примечание. Не обрезайте по центральной линии.Карта складывается пополам, так что есть лицевая и оборотная стороны.
9. Асимметричный звездообразование Студенты изучают геометрию и искусство, создавая асимметричные рисунки со вспышками звезд!
1. Нарисуйте отрезок линии длиной от 3 до 5 дюймов в центре листа.
2. Нарисуйте точки вокруг отрезка линии. (Без точек на горизонтальной линии)
10 точек (5 вверху, 5 внизу для младших школьников / 15-20 точек для старших учеников)
3.Соедините точки! — но, в узор. (Соедините один конец линейного сегмента с точкой, обратно к другому концу линейного сегмента) — повторите (конец линейного сегмента-точка-другой конец линейного сегмента) — используйте линейку
Примечание: Чтобы упростить это попросите детей сделать их горизонтальную линию другим цветом или добавить яркие цветные точки в конец отрезка линии. Затем они смогут увидеть, куда они проводят свои линии.
Math Connection: Посетите I Love That Teaching Idea, чтобы задать вопросы детям, пока они конструируют!
10.Математическое оп-арт
Студенты используют свои математические навыки для создания оп-арта! Во-первых, попросите учащихся измерить расстояние между параллельными линиями. В примере между каждой линией имеется зазор в 1/2 дюйма. После того, как учащиеся проведут свои параллельные линии с помощью линейки, они выбирают пять многоугольников для включения в свою композицию. Они рисуют свои формы с помощью линейки. После того, как их формы нарисованы, они создают узор AB, используя два маркера разного цвета, раскрашивая их формы.Затем они возвращаются и раскрашивают свои формы, чтобы создать оптическую иллюзию! (см. пример).
Common Core Math: класс 7: геометрия
Геометрические фигуры
Просмотр и анализ геометрических фигур.
Если возможно, нарисуйте треугольник с заданной длиной сторон (CCSS.Math.Content.7.G.A.2):
Рисование фигур с заданными условиями (CCSS.Math.Content.7.G.A.2):
Другие примеры
Геометрические измерения
Вычислить измерения двух- и трехмерных фигур.
Решите для измерения кругов (CCSS.Math.Content.7.G.B.4):
Решение для измерений трехмерных тел (CCSS.Math.Content.7.G.B.6):
Другие примеры
Математика 7 класс, Блок 1 — Семейные материалы
Масштабированные копии
На этой неделе ваш ученик узнает о масштабировании фигур.Изображение представляет собой копию оригинала в масштабе , если форма растянута таким образом, чтобы не искажать ее. Например, вот оригинальная картинка и пять копий. Изображения C и D являются копиями оригинала в масштабе, а изображения A, B и E — нет.
В каждой масштабированной копии стороны в определенное количество раз превышают длину соответствующих сторон оригинала. Мы называем это число масштабным коэффициентом . Размер масштабного коэффициента влияет на размер копии. Коэффициент масштабирования больше 1 делает копию больше оригинала.Коэффициент масштабирования меньше 1 делает копию меньше.
Вот задание, которое можно попробовать со своим учеником:
- Для каждой копии укажите, является ли она масштабированной копией исходного треугольника. Если да, то каков масштабный коэффициент?
- Нарисуйте еще одну масштабированную копию исходного треугольника с другим масштабным коэффициентом.
Решение:
- Копия 1 — это уменьшенная копия исходного треугольника. Коэффициент масштабирования равен 2, поскольку каждая сторона копии 1 вдвое длиннее соответствующей стороны исходного треугольника.5 \ boldcdot 2 = 10, 4 \ boldcdot 2 = 8, (6.4) \ boldcdot 2 = 12.8
- Копия 2 — это уменьшенная копия исходного треугольника. Коэффициент масштабирования равен \ frac12 или 0,5, потому что каждая сторона копии 2 вдвое короче соответствующей стороны исходного треугольника. 5 \ boldcdot (0,5) = 2,5, 4 \ boldcdot (0,5) = 2, (6,4) \ boldcdot (0,5) = 3,2
- Копия 3 не является масштабированной копией исходного треугольника. Форма была искажена. Углы бывают разных размеров, и нет одного числа, которое мы могли бы умножить на длину каждой стороны исходного треугольника, чтобы получить соответствующую длину стороны в Копии 3.
- Ответы различаются. Пример ответа: прямоугольный треугольник с длиной стороны 12, 15 и 19,2 единиц будет масштабированной копией исходного треугольника с масштабным коэффициентом 3.
Чертежи в масштабе
На этой неделе ваш ученик будет изучать масштабные чертежи. Чертеж в масштабе — это двухмерное изображение реального объекта или места. Карты и планы этажей являются примерами масштабных чертежей.
Масштаб говорит нам, какую длину на чертеже в масштабе представляет в действительной длине.Например, масштаб «от 1 дюйма до 5 миль» означает, что 1 дюйм на чертеже представляет 5 фактических миль. Если на рисунке показана дорога длиной 2 дюйма, мы знаем, что на самом деле она имеет длину 2 \ boldcdot 5 или 10 миль.
Масштаб может быть записан с единицами измерения (например, от 1 дюйма до 5 миль) или без единиц (например, от 1 до 50 или от 1 до 400). Если на шкале нет единиц измерения, для расстояний на чертеже шкалы и фактических расстояний используются одни и те же единицы. Например, масштаб от «1 до 50» означает, что 1 сантиметр на чертеже соответствует 50 фактическим сантиметрам, 1 дюйм представляет 50 дюймов и т. Д.
Вот задание, которое можно попробовать со своим учеником:
Киран нарисовал план этажа своего класса, используя масштаб от 1 дюйма до 6 футов.
- Рисунок Кирана имеет ширину 4 дюйма и длину 5 \ frac12 дюймов. Каковы размеры фактического класса?
- Стол в классе имеет ширину 3 фута и длину 6 футов. Какого размера она должна быть на чертеже в масштабе?
- Киран хочет сделать увеличенный чертеж того же класса. Какие из этих весов он мог использовать?
- 1 до 50
- 1 до 72
- от 1 до 100
Решение:
- 24 фута в ширину и 33 фута в длину.Поскольку каждый дюйм на чертеже представляет собой 6 футов, мы можем умножить на 6, чтобы найти фактические размеры. Фактическая ширина классной комнаты составляет 24 фута, потому что 4 \ boldcdot 6 = 24. Классная комната имеет длину 33 фута, потому что 5 \ frac12 \ boldcdot 6 = 5 \ boldcdot 6 + \ frac12 \ boldcdot 6 = 30 + 3 = 33.
- \ frac12 дюймов в ширину и 1 дюйм в длину. Мы можем разделить на 6, чтобы найти размеры на чертеже. 6 \ div 6 = 1 и 3 \ div 6 = \ frac12.
- A, от 1 до 50. Шкала «от 1 дюйма до 6 футов» эквивалентна шкале «от 1 до 72», потому что в 6 футах 72 дюйма.Масштаб «от 1 до 100» сделает чертеж в масштабе меньше, чем масштаб «от 1 до 72», потому что каждый дюйм на новом чертеже будет представлять более фактическую длину. Масштаб «от 1 до 50» сделает чертеж в масштабе больше, чем масштаб «от 1 до 72», потому что Kiran потребуется больше дюймов на чертеже для представления той же фактической длины.
Пойдите по математике для 7-го класса. Ключ к ответам Глава 8 Моделирование геометрических фигур — Пойдите по математике.
Идите по математике для 7-го класса. Ключ ответов к главе 8. Моделирование геометрических фигур: . Присоединяйтесь к списку лучших учащихся, используя ключ-ответ для 7-го класса по математике.Получите доступ к бесплатной загрузке Go Math Grade 7 Answer Key Chapter 8 Modeling Geometric Figures. Мы должны подготовить решения таким образом, чтобы все студенты могли легко понять концепцию. Быстрое и легкое обучение возможно только с помощью нашего ключа ответов HMH Go Math.
Go Math Grade 7 Answer Key Глава 8 Моделирование геометрических фигур
Мы предлагаем студентам обратиться к главе 8 «Моделирование геометрических фигур» по математике для 7 класса, чтобы получить наивысший балл на экзаменах.Это вызывает у студентов интерес к изучению математики. Изучите понятия геометрических фигур таким образом, чтобы самостоятельно подготовить вопросы. Нажмите на прикрепленные ниже ссылки и получите пошаговое объяснение.
Глава 8 — Моделирование геометрических фигур — Урок: 1
Глава 8 — Моделирование геометрических фигур — Урок: 2
Глава 8 — Моделирование геометрических фигур — Урок: 3
Глава 8 — Моделирование геометрических фигур — Урок: 4
Глава 8. Моделирование геометрических фигур
Практическое руководство — стр.240
Вопрос 1.
Размер комнаты на чертеже составляет 3 дюйма: 5 футов. Стена на том же чертеже — 18 дюймов. Заполните таблицу.
а. Какова длина самой стены?
______ футов
Ответ: 30 футов
Пояснение:
Мы заполняем таблицу, используя прямую пропорциональность.
3 дюйма: 5 футов.
Стена на том же чертеже имеет размер 18 дюймов на 30 футов.
Вопрос 1.
b. Окно в комнате имеет фактическую ширину 2,5 фута. Найдите ширину окна на чертеже.
______ дюймов
Ответ: 1,5 дюйма
Пояснение:
Мы определяем количество дюймов, соответствующее 1 футам на реальном окне
3 дюйма / 5 дюймов
Умножаем и делим на 5
(3 дюйма ÷ 5) / (5 футов ÷ 5) = 0,6 / 1 фут
Таким образом, 1 фут соответствует 0,6 дюйма, поэтому ширина окна в таблице составляет
2,5 × 0,6 = 1,5 дюйма
Вопрос 2.
Масштаб чертежа составляет 2 дюйма: 4 фута. Каковы длина и ширина фактического помещения? Найдите площадь реальной комнаты.
Ширина: _________ футов
Длина: _________ футов
Площадь: _________ квадратных футов
Ответ:
Ширина: 28 футов
Длина: 14 футов
Площадь: 392 кв. Футов
Пояснение:
Мы определяем количество футов, соответствующее 1 дюйму на чертеже
2 дюйма / 4 дюйма = (2 дюйма ÷ 2) / (4 дюйма ÷ 2) = 1/2
Таким образом, 1 дюйм соответствует 2 футам от реальных габаритов помещения.
Определяем реальную длину комнаты, обозначенную на чертеже 14 дюймами.
14 × 2 = 28 футов
Определяем реальную ширину комнаты, обозначенную на чертеже как 7 дюймов.
7 × = 14 футов
Мы вычисляем площадь реальной комнаты:
28 × 14 = 392 квадратных фута.
Вопрос 3.
Масштаб на чертеже 2 см: 5 м. Какова фактическая длина и ширина комнаты? Найдите площадь реальной комнаты.
Ширина: _________ м
Длина: _________ м
Площадь: _________ кв.м
Ответ:
Ширина: 25 м
Длина: 15 м
Площадь: 375 кв.м
Пояснение:
Определяем количество метров, соответствующее 1 сантиметру на чертеже:
2 см / 5 см = (2 см ÷ 2) / (5 см ÷ 2) = 1 см / 2.5 м
Определяем реальную длину помещения, обозначенную на чертеже 10 см:
10 × 2,5 = 25 м
Определяем реальную ширину помещения, обозначенную на чертеже 6 см:
6 × 2,5 = 15 м
Вычисляем площадь комнаты:
25 × 15 = 375 квадратных футов.
Вопрос 4.
Чертеж столовой в масштабе нарисован на бумаге с сантиметровой сеткой, как показано. Масштаб 1 см: 4 м.
а. Нарисуйте прямоугольник на бумаге с сантиметровой сеткой в масштабе 1 см: 6 м.
Введите ниже:
_____________
Ответ:
Вопрос 4.
г. Какова фактическая длина и ширина кафетерия при исходных масштабах? Каковы реальные размеры кафетерия при использовании новых весов?
Длина: _________ м
Ширина: _________ м
Ответ:
В исходном масштабе размеры на чертеже равны
l1 = 9 см
w1 = 6 см
Реальную длину определяем по исходному масштабу:
9 × 4 = 36
Определяем фактическую ширину с помощью исходный масштаб:
6 × 4 = 24
Во втором масштабе размеры на чертеже равны
l2 = 6 см
w1 = 4 см
Реальную длину определяем с использованием исходного масштаба:
6 × 6 = 36
We Определите фактическую ширину, используя исходный масштаб:
4 × 6 = 24
Таким образом, длина равна 36 м
Ширина равна 24 м
Регистрация основных вопросов
Вопрос 5.
Если у вас есть точный, полный чертеж в масштабе и масштаб, какие размеры объекта чертежа вы можете найти?
Введите ниже:
_____________
Ответ:
Если у нас есть точный, полный чертеж в масштабе и масштабе, мы можем определить все измерения объекта, потому что все они пропорциональны размерам на чертеже, а соотношение является масштабом.
Независимая практика — стр. № 241
Вопрос 6.
Art
У Мари есть уменьшенная копия знаменитой картины Рене Магритта «Школьный учитель».Ее копия имеет размеры 2 на 1,5 дюйма. Масштаб копии — 1 дюйм: 40 см.
а. Найдите размеры оригинальной картины.
Длина: _________ см
Ширина: _________ см
Ответ:
Длина: 80 см
Ширина: 60 см
Пояснение:
Нам даны данные
Масштаб: 1 дюйм: 40 см
Копия l1 = 2 дюйма
w1 = 1,5 дюйма
Определяем длину l оригинальной картины
l = 2 × 40 = 80см
Определяем ширина w оригинальной картины
w = 1.5 × 40 = 60 см
Вопрос 6.
b. Найдите область оригинальной картины.
_____________ кв см
Ответ: 4800 кв. См
Пояснение:
Определяем ширину w исходной картины
A = l.w
A = 80 × 60 = 4800 кв. См
Вопрос 6.
c. Так как 1 дюйм равен 2,54 см, найдите размеры оригинальной картины в дюймах.
Длина: _________ дюймов
Ширина: _________ дюймов
Ответ:
Определяем длину l оригинальной картины в дюймах:
1 дюйм.= 2,54 см
l = 80 / 2,54 см ≈ 31,5 дюйма
Определяем ширину w исходной картины в дюймах:
w = 60 / 2,54 ≈ 23,6 дюйма
Вопрос 6.
d. Найдите площадь оригинальной картины в квадратных дюймах
_____________ квадратных дюймов
Ответ: 743,4 кв. Дюйма
Пояснение:
Мы находим площадь оригинальной картины в квадратных дюймах:
l × w = 31,5 × 23,6 = 743,4 квадратных дюйма
Таким образом, площадь оригинальной картины равна 743.4 квадратных дюйма.
Вопрос 7.
Игровая комната имеет пол 120 на 75 футов. В масштабном чертеже пола на сетке используется масштаб 1 единица: 5 футов. Каковы размеры чертежа в масштабе?
Длина: _________ шт.
Ширина: _________ шт.
Ответ:
Длина: 24 шт.
Ширина: 15 шт.
Пояснение:
Нам даны данные:
Масштаб: 1 единица: 5 футов
Фактические размеры: l = 120 футов, w = 75 футов
Мы определяем количество единиц на чертеже, соответствующее 1 футу, исходя из фактических размеров.
1 единица / 5 футов
(1 единица ÷ 5) / (5 футов ÷ 5) = 0,2 единицы / 1 фут
Определяем длину чертежа в масштабе:
120 × 0,2 = 24 единицы
Определяем ширину чертеж в масштабе:
75 × 0,2 = 15 шт.
Вопрос 8.
Множественные представления
Длина стола 6 футов. На чертеже в масштабе длина составляет 2 дюйма. Напишите три возможных масштаба рисунка.
Введите ниже:
_____________
Ответ:
l = 6 футов
l1 = 2 дюйма
l = фактическая длина
l1 = длина на чертеже в масштабе
2 дюйма: 6 футов
1 дюйм: 3 фута
2/6 × 12 = 2/72 = 1/36
1 см: 36 см
Вопрос 9.
Анализировать взаимосвязи
Масштаб чертежа составляет 10 см: 1 мм. Что больше, реальный объект или масштабный рисунок? Объяснять.
_____________
Ответ:
Нам дан масштаб
10 см: 1 мм
100 мм: 1 м
Это означает, что соответствующий фактический размер для 100 мм чертежа равен 1 мм, поэтому большему на чертеже соответствует меньший фактический размер. расстояние, поэтому масштаб чертежа больше.
Вопрос 10.
Архитектура
Масштабная модель здания 5.4 фута высотой.
а. Если первоначальное здание было 810 метров в высоту, в каком масштабе была сделана модель?
______ футов: ______ м
Ответ: 1 фут: 150 м
Пояснение:
Отметим:
h2 = высота на масштабе модели
h = фактическая высота
Нам даны данные
h2 = 5,4 фута
h = 810 метров
Определяем масштаб модели
h2 / h = 5,4 фута / 810 м = (5,4 фута ÷ 5,4) / (810 ÷ 5,4)
1 фут / 150 м
1 фут: 150 м
Вопрос 10.
г. Если модель сделана из крошечных кирпичей, каждый размером 0,4 дюйма, сколько кирпичей в высоту эта модель?
___________ кирпич
Ответ: 14 кирпичей
Пояснение:
Определяем масштаб для модели:
х2 / 0,4 = 5,4 / 0,4 = 13,5
Количество кирпичей: 14
Стр. № 242
Вопрос 11.
Вас попросили построить масштабную модель вашей школы из зубочисток. Представьте, что ваша школа имеет высоту 30 футов. Ваш масштаб — 1 фут: 1.26 см.
а. Если высота зубочистки 6,3 см, сколько зубочисток будет у вашей модели?
______ зубочистки
Ответ: 6
Пояснение:
Учитывая, что
h = 30 футов
1 фут: 1,26 см
h2 = высота на масштабной модели
h = фактическая высота
Мы определяем высоту h2 модели:
h2 = 30 × 1,26 = 37,8 см
h2 / 6,3 = 37,8 / 6,3 = 6
Таким образом, количество зубочисток = 6
Вопрос 11.
b. У вашей матери закончились зубочистки, и она предлагает вам использовать вместо них ватные палочки.Вы измеряете их, а они высотой 7,6 см. Сколько ватных тампонов высотой будет у вашей модели?
______ ватные палочки
Ответ: 5
Пояснение:
Находим количество хлопковых салфеток
h2 / 7,6 = 37,8 / 7,6 ≈ 5
Таким образом, количество хлопковых мазков = 5
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 12.
Выводы по розыгрышу
Площадь квадратного пола на чертеже в масштабе составляет 100 квадратных сантиметров, а масштаб чертежа составляет 1 см: 2 фута.Какова реальная площадь пола? Каково соотношение площади рисунка к фактической площади?
Площадь = ______ кв. Футов
Ответ: 400 кв. Футов
Пояснение:
A1 = площадь чертежа
A = площадь фактического пола
Нам даны данные:
A1 = 100 см²
1 см: 2 фута
1 см соответствует 2 футам
1 см × 1 см соответствует 2 футам × 2 футам
1 см² соответствует 4 футам 2
A = 100. 4 = 400 фут²
Мы определяем отношение площади на чертеже к фактической площади:
1 фут = 0.3048 м = 30,48 см
A1 / A = 100/400 × 30,48² ≈ 0,0003
Вопрос 13.
Несколько представлений
Опишите, как перерисовать масштабный чертеж с новым масштабом.
Введите ниже:
_____________
Ответ:
Чтобы перерисовать масштабный чертеж с новым масштабом, мы выполняем 2 шага:
1. Находим, во сколько раз новый масштаб оказался больше или меньше старого.
2. Мы умножаем этот масштабный коэффициент на размеры старого масштабного чертежа, чтобы получить новый чертеж.
Вопрос 14.
Представление реальных проблем
Опишите, как несколько рабочих мест или профессий могут использовать масштабные чертежи на работе.
Введите ниже:
_____________
Ответ:
Масштабные чертежи чрезвычайно полезны в работах, которые должны представлять большие площади на небольших устройствах, таких как
1. Архитектура / конструкции
2. Медицина
3. Сельское хозяйство
4. Туризм
5. Транспорт
Практическое руководство — Стр. № 245
Укажите, создает ли каждая фигура условия для образования уникального треугольника, более одного треугольника или отсутствия треугольника.
Вопрос 1.
Введите ниже:
_____________
Ответ: Уникальный треугольник
Пояснение:
Нам даны два угла и включенная сторона, таким образом, получается уникальный треугольник, поскольку стороны, выходящие из B и A, пересекаются в единственной точке.
Вопрос 2.
Введите ниже:
_____________
Ответ: Нет треугольника
Пояснение:
Нам даны три стороны треугольника. Мы проверяем, больше ли сумма любых двух сторон другой.
4 + 11 = 15> 3
11 + 3 = 14> 4
3 + 4 = 7 не больше 11.
Поскольку одно неравенство не проверено, треугольник не существует.
Вопрос 3.
Введите ниже:
_____________
Ответ: Уникальный треугольник
Пояснение:
Нам даны два угла и включенная сторона, таким образом, получается уникальный треугольник, поскольку стороны, выходящие из B и A, пересекаются в единственной точке.
Вопрос 4.
Введите ниже:
_____________
Ответ: Уникальный треугольник
Пояснение:
Нам даны три стороны треугольника.Мы проверяем, больше ли сумма любых двух сторон другой.
6 + 12 = 18> 7
12 + 7 = 19> 6
6 + 7 = 13> 12
Так как все неравенства проверены, существует единственный треугольник.
Регистрация основных вопросов
Вопрос 5.
Опишите длины трех сегментов, которые нельзя использовать для образования треугольника.
Введите ниже:
_____________
Ответ:
Найдите длины трех отрезков, которые не должны быть сторонами треугольника, хотя бы одна сумма двух сторон должна быть меньше другой стороны.
Пусть a, b, c — длины трех сегментов.
a + b не> a + b + k = c
Независимая практика
Вопрос 6.
На отдельном листе бумаги попробуйте нарисовать треугольник с длиной стороны 3 и 6 сантиметров и включенным углом 120 °. Определите, образуют ли данные сегменты и угол уникальный треугольник, более одного треугольника или нет треугольника.
Введите ниже:
_____________
Ответ: Уникальный треугольник
Пояснение:
∠A = 120 °
AB = 6
AC = 3
Рисуем отрезок AB, угол A и отрезок AC, затем соединяем B и C.В результате получился уникальный треугольник.
Вопрос 7.
Ландшафтный архитектор представил заказчику проект цветочного сада в форме треугольника с длиной сторон 21 фут, 37 футов и 15 футов. Объясните, почему не наняли архитектора для создания цветника.
Введите ниже:
_____________
Ответ:
Нам даны стороны треугольника
21 + 37 = 58> 15
37 + 15 = 52> 21
15 + 21 = 36 not> 37
Мы проверили три неравенства треугольника
Таким образом, треугольник не существуют, поэтому архитектора не наняли для создания цветника.
Стр. № 246
Вопрос 8.
Сделайте предположение
Углы на реальном дорожном знаке в форме треугольника имеют размер 60 °. Углы на чертеже знака в масштабе имеют размер 60 °. Объясните, как вы можете использовать эту информацию, чтобы решить, можно ли использовать три заданные угловые меры для образования уникального треугольника или нескольких треугольников.
Введите ниже:
_____________
Ответ: Три заданные угловые меры, сумма которых равна 180 °, могут быть использованы для образования бесконечного количества треугольников, имеющих свойство пропорциональности их соответствующих сторон.
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 9.
Сообщайте математические идеи
На рисунке слева показан отрезок линии длиной 2 дюйма, образующий угол 45 °, с пунктирной линией, длина которой не указана. На рисунке справа показан компас, установленный на ширину 1 \ (\ frac {1} {2} \) дюймов с точкой на верхнем конце 2-дюймового сегмента. Строится дуга, дважды пересекающая пунктирную линию.
Объясните, как можно использовать этот рисунок, чтобы решить, можно ли использовать две стороны и угол, не входящий между ними, для образования уникального треугольника, более одного треугольника или без треугольника.
Введите ниже:
_____________
Ответ:
Треугольник не существует, потому что одна сторона короче двух других. Круг пересекает пунктирную линию только один раз, так что один угол составляет 45 °, поэтому есть только одно решение. Круг с центром в точке B дважды пересекает пунктирную линию, таким образом образуя два треугольника.
Вопрос 10.
Критическое мышление
Две стороны равнобедренного треугольника имеют длину 6 дюймов и 15 дюймов соответственно.Найдите длину третьей стороны. Объясните свои рассуждения.
_______ дюймов
Ответ: 15 дюймов
Пояснение:
Даны две стороны равнобедренного треугольника
a = 6
b = 15
Есть две возможности, третья сторона равна a или b. Давайте изучим их оба.
Случай 1: a = c = 6, b = 15
a + c = 6 + 6 = 12, не более 15 = b
Мы проверим три неравенства треугольника
a + b = 6 + 15 = 21> 15 = c
a + c = 6 + 15 = 21> 15 = b
b + c = 15 + 15 = 30> 6 = a
Случай 2: a = 6, b = c = 15
Таким образом, третий сторона треугольника равна 15.
Практическое руководство — Страница № 249
Опишите каждое поперечное сечение.
Вопрос 1.
Введите ниже:
_____________
Ответ: Треугольник / Четырехугольный треугольник
Данное поперечное сечение в кубе представляет собой треугольник / равносторонний треугольник.
Вопрос 2.
Введите ниже:
_____________
Ответ: Прямоугольник
Заданное поперечное сечение цилиндра — прямоугольник.
Вопрос 3.
Введите ниже:
_____________
Ответ: Треугольник
Пояснение:
Поперечное сечение призмы — треугольник.
Вопрос 4.
Введите ниже:
_____________
Ответ: Кривая в форме радуги
Данное сечение конуса представляет собой кривую в форме радуги.
Регистрация основных вопросов
Вопрос 5.
Каков первый шаг в описании того, что получается, когда данная плоскость пересекает данную трехмерную фигуру?
Введите ниже:
_____________
Ответ:
Первый шаг в описании того, какая фигура получается, когда данная плоскость пересекает данную трехмерную фигуру, — это установить количество сторон, которые имеет поперечное сечение.
Независимая практика
Вопрос 6.
Опишите различные способы, которыми плоскость может пересекать цилиндр, и полученное поперечное сечение.
Введите ниже:
_____________
Ответ:
Поперечное сечение может быть:
1. круг
2. эллипс
3. прямоугольник
Стр. № 250
Вопрос 7.
Сделайте гипотезу
Какие поперечные сечения вы можете увидеть, когда плоскость пересекает конус, чего вы не увидите, когда плоскость пересекает пирамиду или призму?
Введите ниже:
_____________
Ответ:
Сечение может быть:
1.окружность
2. эллипс
3. парабола
4. гипербола
5. треугольник
H.O.T.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 8.
Критическое мышление
Две фигуры слева внизу показывают, что вы можете сформировать поперечное сечение куба, представляющего собой пятиугольник. Представьте себе плоскость, разрезающую куб под углом таким образом, чтобы разрезать пять из шести граней куба. Нарисуйте пунктирные линии на третьем кубе, чтобы показать, как образовать поперечное сечение шестиугольника.
Введите ниже:
_____________
Ответ:
Рисуем плоскость, разрезающую куб так, чтобы сечение было шестиугольником: для этого берем середину из 6 смежных сторон:
Вопрос 9.
Анализ взаимосвязей
Сфера имеет радиус 12 дюймов. Горизонтальная плоскость проходит через центр сферы.
а. Опишите поперечное сечение, образованное плоскостью и сферой
Тип ниже:
_____________
Ответ: Круг
Пояснение:
Нам дана сфера и поперечное сечение, проходящее через центр сферы:
Поперечное сечение, проходящее через центр сферы, представляет собой окружность, радиус которой равен радиусу сферы.
Вопрос 9.
b. Опишите поперечные сечения, образовавшиеся, когда плоскость пересекает внутреннюю часть сферы, но удаляется от центра.
Введите ниже:
_____________
Ответ: Поперечные сечения, образованные плоскостью, пересекающей внутреннюю часть сферы за пределами центра, представляют собой окружности.
Вопрос 10.
Сообщайте математические идеи
Правая прямоугольная призма пересекается горизонтальной плоскостью и вертикальной плоскостью. Поперечное сечение, образованное горизонтальной плоскостью и призмой, представляет собой прямоугольник размером 8 дюймов.и 12 дюймов. Поперечное сечение, образованное вертикальной плоскостью и призмой, представляет собой прямоугольник с размерами 5 дюймов и 8 дюймов. Опишите грани призмы, включая их размеры. Затем найдите его объем.
Введите ниже:
_____________
Ответ: 480 куб. Дюймов
Пояснение:
Горизонтальное сечение имеет размеры 8 × 12, а вертикальное — 5 × 8.
Призма имеет размеры:
5 дюймов, 8 дюймов, 12 дюймов
Находим объем призмы:
5 × 8 × 12 = 480 кубических дюймов
Вопрос 11.
Представляют проблемы реального мира
Опишите ситуацию реального мира, которая может быть представлена плоскостями, разрезающими трехмерную фигуру для формирования поперечных сечений.
Введите ниже:
_____________
Ответ:
Примеры реальных ситуаций, которые могут быть представлены плоскостями, разрезающими трехмерные фигуры для образования поперечных сечений:
— электрические провода
— водопроводные / газовые трубы
— проект дома
— геология
— сейсмология
Практическое руководство — стр.256
Для 1–2 используйте рисунок.
Вопрос 1.
Словарь
Сумма измерений ∠UWV и ∠UWZ равна 90 °, поэтому UWV и ∠UWZ равны _____ углам.
Введите ниже:
_____________
Ответ: Дополнительные углы
Пояснение:
Сумма ∠UWV и ∠UWZ равна 90 °, поэтому UWV и ∠UWZ являются дополнительными углами.
Вопрос 2.
Словарь
∠UWV и ∠VWX имеют общую вершину и одну сторону. Они не перекрываются, поэтому ∠UWV и ∠VWX — это _____ углы.
Введите ниже:
_____________
Ответ: Смежные углы
Пояснение:
∠UWV и ∠VWX имеют общую вершину и одну сторону. Они не перекрываются, поэтому ∠UWV и ∠VWX — смежные углы.
Для 3–4 используйте рисунок.
Вопрос 3.
∠AGB и ∠DGE — _____ углы, поэтому m∠DGE = _____.
Введите ниже:
_____________
Ответ: ∠AGB и ∠DGE — вертикальные углы, поэтому m∠DGE = m∠AGB = 30 °
Вопрос 4.
Найдите меру ∠EGF.
_______ °
Ответ: 100 °
Пояснение:
m∠CGD + m∠DGE + m∠EGF = 180 °
50 ° + m∠AGB + m∠EGF = 180 °
50 ° + 30 ° + 2x = 180 °
2x = 180 ° — 80 °
2x = 100 °
мм EGF = 2x = 100 °
Вопрос 5.
Найдите значение x и меру ∠MNQ.
x = _______ °
мMNQ = _______ °
Ответ:
∠MNQ + ∠QNP = 90 °
3x — 13 ° + 58 ° = 90 °
3x = 90 ° + 13 ° — 58 °
3x = 45 °
x = 15 °
м∠MNQ = 3x — 13 °
= 3 × 15 ° — 13 °
= 45 ° — 13 °
= 32 °
Регистрация основных вопросов
Вопрос 6.
Предположим, что вы знаете, что ∠T и ∠S являются дополнительными и что m∠T = 3 (m∠S). Как найти m∠T?
Введите ниже:
_____________
Ответ:
m∠T + m∠S = 180 °
m∠T = 3 (m∠S)
m∠S = m∠T / 3
Сформируем второе уравнение, запишем m∠S через m∠ Т
м∠Т + м∠Т / 3 = 3 × 180 °
3 м∠Т + м∠Т = 3 × 180 °
4 м∠Т = 540 °
м∠Т = 540 ° / 4
м∠Т = 135 °
Независимая практика — стр. № 257
Для 7–11 используйте цифру.
Вопрос 7.
Назовите пару смежных углов. Объясните, почему они рядом.
Введите ниже:
_____________
Ответ:
Пара смежных углов:
∠SUR и ∠RUN (общая вершина U и одна общая сторона — UR — без перекрытия)
∠NUQ и ∠QUP (общая вершина U и одна общая сторона — UQ — без перекрытия )
∠PUT и ∠TUS (общая вершина U и одна общая сторона — UT — без перекрытия)
Вопрос 8.
Назовите пару острых вертикальных углов.
Введите ниже:
_____________
Ответ:
Глядя на рисунок выше, мы можем сказать, что ∠SUR и ∠PUQ — это вертикальные углы.
Вопрос 9.
Назовите пару дополнительных углов.
Введите ниже:
_____________
Ответ:
На рисунке выше показано, что ∠SUR и ∠RUQ являются дополнительными углами.
Вопрос 10.
Обоснуйте рассуждение
Найдите m∠QUR. Обосновать ответ.
_______ °
Ответ:
Мы должны найти m∠QUR.
∠SUR и ∠QUR — дополнительные уголки.
м∠SUR + m∠QUR = 180 °
м∠QUR + 41 ° = 180 °
м∠QUR = 180 ° — 41 °
м∠QUR = 139 °
Вопрос 11.
Выводы по розыгрышу
Что больше, m∠TUR или m∠RUQ? Объяснять.
Введите ниже:
_____________
Ответ:
m∠QUR = 139 °
m∠TUR = m∠TUS + m∠SUR
90 ° + 41 ° = 131 °
Находим m∠TUR
139 °> 131 °
m∠QUR> m∠
Для 12–13 используйте цифру. Велосипедная дорожка пересекает дорогу, как показано. Решите для каждой указанной угловой меры или переменной.
Вопрос 12.
x =?
_______ °
Ответ: x = 21 °
Пояснение:
KMI и ∠HMG расположены вертикально, поэтому совпадают.
Определяем x:
84 ° = 4x
4x = 84 °
x = 84 ° / 4
x = 21 °
Вопрос 13.
м∠KMH =?
_______ °
Ответ: 96 °
Пояснение:
KMI и ∠KMH являются дополнительными.
Определяем m∠KMH:
м∠KMH + m∠KMI = 180 °
м∠KMH + 84 ° = 180 °
м∠KMH = 180 ° — 84 °
м∠KMH = 96 °
Для 14–16 используйте цифру. Решите для каждой указанной угловой меры.
Вопрос 14.
м∠CBE =?
_______ °
Ответ: 118 °
Пояснение:
Определяем m∠CBE:
м∠CBE + m∠EBF = 180 °
м∠CBE + 62 ° = 180 °
м∠CBE = 180 ° — 62 °
м∠CBE = 118 °
Вопрос 15.
m∠ABF =?
_______ °
Ответ: 28 °
Пояснение:
Определяем m∠ABF
m∠ABF + m∠EBF = 90 °
м∠ABF + 62 ° = 90 °
м∠ABF = 90 ° — 62 °
м∠ABF = 28 °
Вопрос 16.
м∠CBA =?
_______ °
Ответ: 152 °
Пояснение:
Определяем m∠CBA
m∠CBA = m∠DBF = m∠DBE + m∠EBF
90 ° + 62 ° = 152 °
м∠CBA = 152 °
Вопрос 17.
Измерение A на 4 ° больше меры measureB.Эти два угла дополняют друг друга. Найдите размер каждого угла.
мА = __________ °
мБ = __________ °
Ответ:
мА = 47 °
мБ = 43 °
Пояснение:
Нам даны данные:
m∠A = m∠B + 4 °
m∠A + m∠B = 90 °
m∠B + 4 ° + m∠B = 90 °
2m∠B = 90 ° — 4 °
2m∠B = 86 °
m∠B = 86 ° / 2
m∠B = 43 °
m∠A = m∠B + 4 °
m∠A = 43 ° + 4 °
м∠A = 47 °
Вопрос 18.
Измерение ∠D в 5 раз больше меры ∠E.Два угла являются дополнительными. Найдите размер каждого угла.
мД = __________ °
мЭ = __________ °
Ответ:
mD = 150 °
mE = 30 °
Пояснение:
Нам даны данные
м∠D = 5 (м∠E)
м∠D + m∠E = 180 °
5 (м∠E) + m∠E = 180 °
6 м∠E = 180 °
м∠E = 180 ° / 6
м∠E = 30 °
м∠D = 5 (м∠E)
м∠D = 5 × 30 °
м∠D = 150 °
Стр. № 258
Вопрос 19.
Астрономия
Иногда астрономы используют угловые меры, разделенные на градусы, минуты и секунды.Один градус равен 60 минутам, а одна минута равна 60 секундам. Предположим, что ∠J и ∠K дополняют друг друга, а величина ∠J составляет 48 градусов, 26 минут, 8 секунд. Какова мера ∠K?
_______ ° _______ ‘_______”
Ответ: 41 ° 33 ‘52 ″
Пояснение:
Нам даны данные
м∠Дж + м∠К = 90 °
м∠Дж = 48 ° 26 ‘8 ″
90 ° — 48 ° 26′ 8 ″
89 ° 60 ‘- 48 ° 26 ‘8 ″
89 ° 59’60 ”- 48 ° 26′ 8 ″ = 41 ° 33 ’52 ″
Таким образом, размер ∠K составляет 41 ° 33′ 52 ″
H.О.
Сосредоточьтесь на мышлении высшего порядка
Вопрос 20.
Представляют проблемы реального мира
Железнодорожные пути пересекаются с дорогой, как показано. Город разрешит парковку под углом K, если угол K больше 38 °. Можно ли построить парковку под углом К? Почему или почему нет?
_______
Ответ:
m∠K = 180 ° — 50 ° — 90 ° = 40 °
Поскольку m∠K = 40 °> 38 °, парковка может быть построена.
Вопрос 21.
Обоснование рассуждений
Кендра говорит, что она может нарисовать ∠A и ∠B так, что m∠A равно 119 °, а A и ∠B являются дополнительными углами.Ты согласен или несогласен? Объясните свои рассуждения.
_______
Ответ:
Нам даны данные
m∠A = 119 °
m∠A + m∠B = 90 °
m∠B = 90 ° — m∠A
= 90 ° — 119 ° = -29 °
Поскольку m∠B <0, Кендра ошибается, она не может рисовать углы.
Вопрос 22.
Вывод заключения
Если два угла дополняют друг друга, каждый угол называется дополнением другого. Если два угла являются дополнительными, каждый угол называется добавлением другого.
а. Предположим, что m∠A = 77 °.Какова мера дополнения к A? Объяснять.
_______ °
Ответ: 77 °
Пояснение:
90 ° — (90 ° — m∠A) = 90 ° — (90 ° — 77 °)
90 ° — 77 ° = 13 °
77 °
Вопрос 22.
b. Какой вывод можно сделать о дополнении угла? Объяснять.
Введите ниже:
_____________
Ответ:
Дополнением к углу является сам угол:
90 ° — (90 ° — m∠A)
90 ° — 90 ° + m∠A
8.1 Подобные формы и чертежи в масштабе — Стр. № 259
Вопрос 1.
План дома имеет масштаб 1 дюйм: 4 фута. Длина и ширина каждой комнаты в реальном доме показаны в таблице. Заполните таблицу, найдя длину и ширину каждой комнаты на чертеже.
Введите ниже:
_____________
Ответ:
Таким образом, на каждые 4 фута в фактическом измерении на чертеже приходится 1 дюйм.
8.2 Геометрические чертежи
Вопрос 2.
Можно ли сформировать треугольник со сторонами 8 см, 4 см и 12 см?
______
Ответ:
Нам даны длины сторон
8 + 12 = 20> 4
4 + 12 = 16> 8
8 + 4 not> 12
Поскольку одно из неравенств не проверено, три заданные длины сторон не могут образовать треугольник.
Вопрос 3.
Треугольник имеет длину стороны 11 см и 9 см. Каким может быть значение третьей стороны, 20 см или 15 см?
______
Ответ: 15 см
Пояснение:
Нам даны длины сторон
11, 9
11 + 9 = 20 not> 20
Мы проверяем неравенства треугольника, если добавляем третью сторону 20 см.
Поскольку одно из неравенств не проверено, три заданная длина сторон не может образовывать треугольник.
11, 9, 15
11 + 9 = 20> 15
11 + 15 = 26> 9
15 + 9 = 24> 11
Проверяем, что неравенства треугольника проверены, 15 может быть значением третьей стороны.
8.3 Поперечные сечения
Вопрос 4.
Назовите одно возможное поперечное сечение сферы.
Введите ниже:
_____________
Ответ: Окружность
Одно из возможных поперечных сечений сферы — это круг.
Вопрос 5.
Назовите хотя бы две формы, которые являются поперечными сечениями цилиндра.
Введите ниже:
_____________
Ответ: Три возможных поперечных сечения цилиндра — это круг, эллипс и прямоугольник.
Регистрация основных вопросов
Вопрос 5.
Как можно моделировать геометрические фигуры для решения реальных задач?
Введите ниже:
_____________
Ответ: Можно моделировать геометрию для постройки зданий и небоскребов, а также магазинов.
8.4 Угловые отношения
Вопрос 6.
∠BGC и ∠FGE — _____ углы, поэтому m∠FGE = _____
_____ °
Ответ: ∠BGC и ∠FGE — вертикальные углы, поэтому m∠FGE = m∠BGC = 90 ° — 40 ° = 50 °
Вопрос 7.
Предположим, вы знаете, что ∠S и ∠Y дополняют друг друга и что m∠S = 2 (m∠Y) — 30 °. Найдите MY.
м? Y = _____ °
Ответ: 40 °
Пояснение:
m∠S + m∠Y = 90 °
m∠S = 2 (m∠Y) — 30 °
Заменим выражение m∠S из второго уравнения на первое, мы можем найти m∠Y
2 (m∠Y) — 30 ° + m∠Y = 90 °
3m∠Y = 90 ° + 30 °
3m∠Y = 120 °
m∠Y = 120 ° / 3
m∠Y = 40 °
Выбранный ответ — № страницы260
Вопрос 1.
Какое число можно прибавить к 15, чтобы получить сумму 0?
Опции:
а. -10
б. -15
с. 0
г. 15
Ответ: -15
Пояснение:
Число, которое мы добавляем к числу, чтобы получить нулевую сумму, является его противоположностью. В любом случае мы должны добавить -15 к 15.
15 + (-15) = 0
Таким образом, правильный ответ — вариант B.
Вопрос 2.
Ученики рисуют задник для школьного спектакля. Фон имеет ширину 15 футов и высоту 10 футов.Каждые 16 дюймов на масштабном чертеже представляют 5 футов на заднем плане. Какова площадь масштабного чертежа?
Опции:
а. 150 в 2
б. 6 в 2
c. 3096
г. 1536 в 2
Ответ: 1536 в 2
Пояснение:
Нам даны размеры l и w фона и масштаб чертежа:
l = 15 футов
w = 10 футов
16 дюймов: 5 футов
16 дюймов / 5 футов = (16 дюймов ÷ 5 ) / (5 футов ÷ 5) = 3,2 дюйма / 1 фут
l1 = 15 × 3.2 = 48 дюймов
w1 = 10 × 32 = 320 дюймов
l1 × w1 = 48 × 32 = 1536 квадратных дюймов
Таким образом, правильный ответ — вариант D.
Вопрос 3.
Две стороны треугольника имеют размер 8 см и 12 см. Что из перечисленного НЕ МОЖЕТ быть мерой третьей стороны?
Опции:
а. 4
г. 12
г. 8
г. 16
Ответ: 4 см
Пояснение:
Даны две стороны треугольника
a. 4
4 + 8 не> 12
б. 12
12 + 8> 12
12 + 12> 8
c.8
8 + 8> 12
8 + 12> 12
д. 16
8 + 12> 16
8 + 16> 12
12 + 16> 8
Таким образом, единственное измерение, которое не может быть мерой третьей стороны треугольника, составляет 4 см.
Таким образом, правильный ответ — вариант А.
Вопрос 4.
Поперечное сечение — это пересечение трехмерной фигуры и _____.
Опции:
а. пункт
б. самолет
c. линия
д. набор
Ответ: Самолет
Пояснение:
Поперечное сечение — это взаимодействие трехмерной фигуры и плоскости.
Таким образом, правильный ответ — вариант Б.
Для 5–6 используйте диаграмму.
Вопрос 5.
Каков показатель ∠BFC?
Опции:
а. 18
г. 108
г. 72
г. 144
Ответ: 108 °
Пояснение:
∠BFC + ∠BFA = 180 °
∠BFC + 72 ° = 180 °
∠BFC = 180 ° — 72 °
∠BFC = 108 °
Углы ∠BFC и ∠BFA являются дополнительными. Определяем ∠BFC.
Таким образом, правильный ответ — вариант Б.
Вопрос 6.
Что описывает отношения между ∠BFA и ∠CFD?
Опции:
а. смежные уголки
б. дополнительные углы
c. дополнительные уголки
d. вертикальные углы
Ответ: вертикальные углы
Пояснение:
Углы ∠BFA и ∠CFD являются вертикальными углами, потому что они представляют собой противоположные углы, образованные на пересечении двух прямых.
Таким образом, правильный ответ — вариант D.
Вопрос 7.
Вся одежда уценена на 15%. Какое выражение представляет новую розничную цену?
Опции:
а.0,85x
б. 1.15x
c. 1.85x
г. 0,15 х
Ответ: 0,85x
Объяснение:
x = начальная цена
Поскольку цена снизилась на 15%, новая цена будет уменьшена на 15/100 x
x — 0,15x = 0,85x
Таким образом, правильный ответ — вариант A.
Мини-задачи
Вопрос 8.
Ира построила модель Великой пирамиды в Египте для школьного проекта. Великая пирамида имеет квадратное основание со сторонами длиной 756 футов. Высота Великой пирамиды 481 фут.Ира построил свою модель пирамиды в масштабе 1 дюйм: 20 футов.
а. Какова длина каждой стороны основания пирамиды Иры?
_____ в
Ответ: 37,8 дюйма
Мы вычисляем количество дюймов, соответствующее 1 футу, исходя из фактических размеров:
1 дюйм / 20 фут = (1 дюйм ÷ 20) / (20 футов ÷ 20) = 0,05 дюйма / 1 фут.
На 1 фут 0,05 дюйма.
Определяем длину основания пирамиды Иры:
756 × 0,05 = 37,8 дюйма
Вопрос 8.
b. Какова площадь основания пирамиды Иры?
_____ квадратных дюймов
Ответ: 1428.84 квадратных дюйма
Пояснение:
Определяем площадь основания пирамиды Иры:
37,8 × 37,8 = 1428,84 квадратных дюйма.
Вопрос 8.
c. Какова высота пирамиды Иры?
_____ в
Ответ:
Определяем высоту пирамиды Иры:
481 × 0,05 = 24,05 дюйма
Вопрос 8.
d. Ира построила свою модель, используя поперечные сечения, вырезанные параллельно основанию.

 Ю.А.Данилова. — М.: Мир, 1971. — 511 с.
Ю.А.Данилова. — М.: Мир, 1971. — 511 с. – Режим доступа: https://museum-design.ru/the-appeal-of-the-charm-of-geometric-shapes/ Заглавие с экрана. – (Дата обращения 03.03.2019).
– Режим доступа: https://museum-design.ru/the-appeal-of-the-charm-of-geometric-shapes/ Заглавие с экрана. – (Дата обращения 03.03.2019).



 А еще мы можем увидеть несуществующие пульсирующие квадраты по всему полю рисунка.
А еще мы можем увидеть несуществующие пульсирующие квадраты по всему полю рисунка.

 Приступаем к работе.
Приступаем к работе. Какой командой можно запустить программу MS Paint?
Какой командой можно запустить программу MS Paint? Давайте поможем им вычислить площадь этой стены.
Давайте поможем им вычислить площадь этой стены.






 .
. Мотивация урока.
Мотивация урока. Используя рисунок, назовите эти фигуры.
Используя рисунок, назовите эти фигуры.


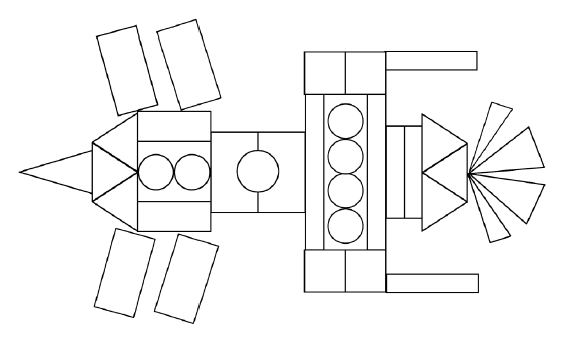 Итоги урока. Рефлексия.
Итоги урока. Рефлексия. немного дольше, чтобы они встретились.Вы меняли угол между линиями, когда
продлил их?
немного дольше, чтобы они встретились.Вы меняли угол между линиями, когда
продлил их? Что вы можете сказать о двух
линии?
Что вы можете сказать о двух
линии?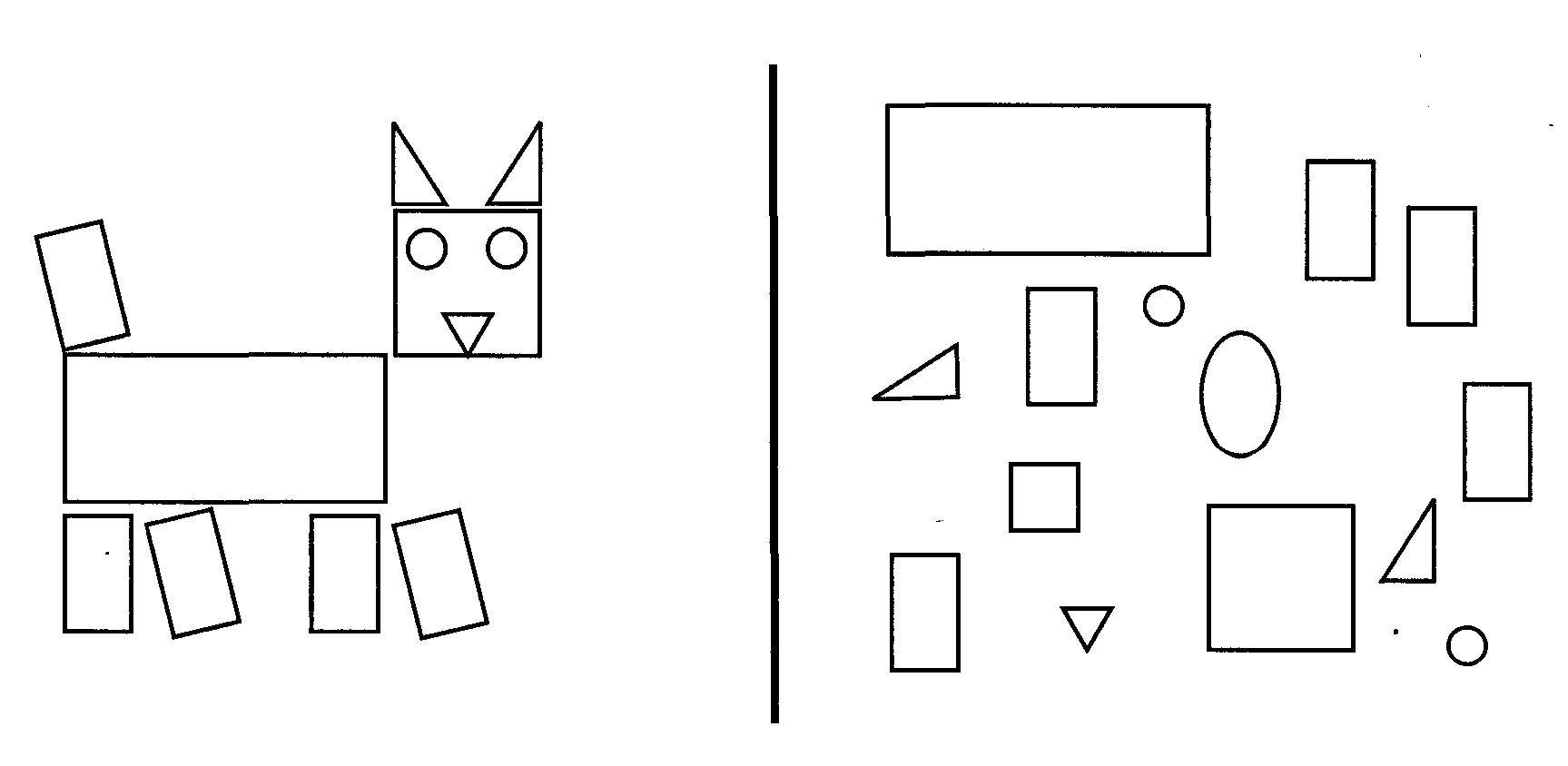
 Сколько степеней:
Сколько степеней:
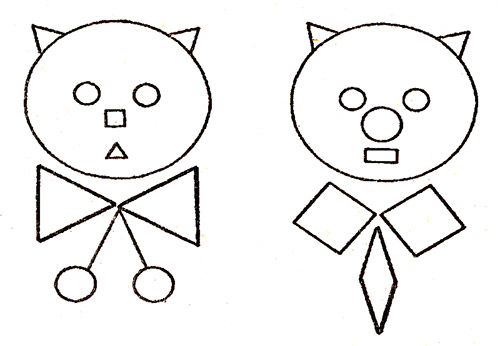 Некоторые углы можно измерить напрямую, другие — нет. Ваш
Транспортир не может измерять углы рефлекса, такие как углы 7 и 8. Поэтому вам придется
Составьте план!
Некоторые углы можно измерить напрямую, другие — нет. Ваш
Транспортир не может измерять углы рефлекса, такие как углы 7 и 8. Поэтому вам придется
Составьте план!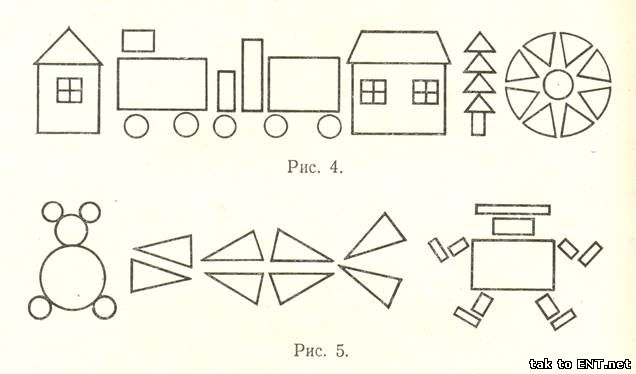 Label
точка C, где ваша новая линия касается XY. Посмотрите на эскиз ниже, если вы
застрять.
Label
точка C, где ваша новая линия касается XY. Посмотрите на эскиз ниже, если вы
застрять.

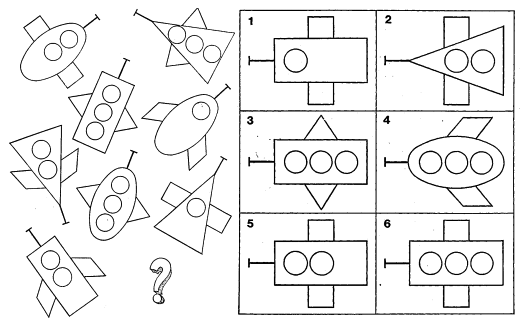 Вдавите бумагу достаточно глубоко, чтобы она оставалась на месте. Это будет центр вашего круга.
Вдавите бумагу достаточно глубоко, чтобы она оставалась на месте. Это будет центр вашего круга. Позвольте компасу висеть у вас в руке в воздухе и поверните ручку. Затем попробуйте несколько раз использовать макулатуру, пока не сможете легко повернуть компас.
Позвольте компасу висеть у вас в руке в воздухе и поверните ручку. Затем попробуйте несколько раз использовать макулатуру, пока не сможете легко повернуть компас.



 Точки пересечения отмечены. Линия
сегмент втянут.Используйте линейку и карандаш, чтобы соединить пары точек, чтобы
что строки:
Точки пересечения отмечены. Линия
сегмент втянут.Используйте линейку и карандаш, чтобы соединить пары точек, чтобы
что строки:


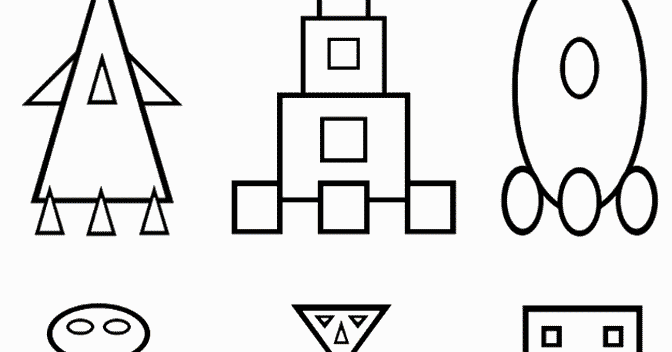
 Вы замечаете что-нибудь особенное в этих углах?
Вы замечаете что-нибудь особенное в этих углах?