Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположениеТочка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
ABCточка 1, точка 2, точка 3
123Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? AAAЛиния — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
abcЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру.Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороныДаже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
BAПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторонуУ луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
BAЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
CBAОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину. Длина отрезка — это расстояние между его начальной и конечной точками
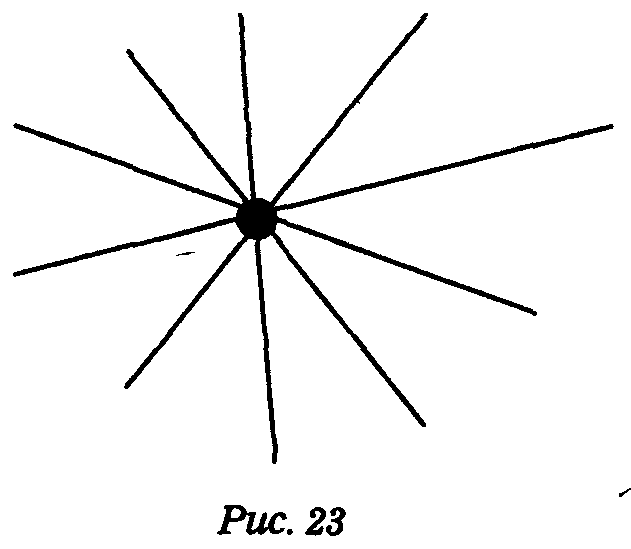
Длина отрезка — это расстояние между его начальной и конечной точкамиЧерез одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
BAпрямая линия AB
BAОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ BA✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
BAЗадача: где прямая, луч, отрезок, кривая?Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная.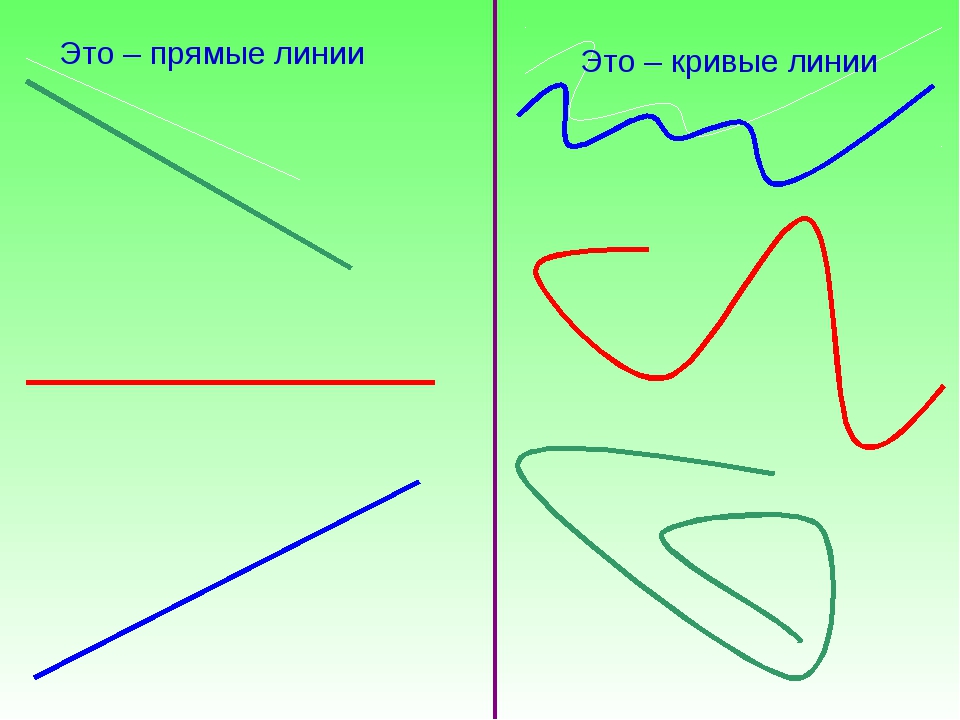 Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
ABCDE646212752Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см.Многоугольник — это замкнутая ломанная линияУ второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
ABCDEF120605812298141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
Точка, отрезок, луч, прямая — числовая прямая
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
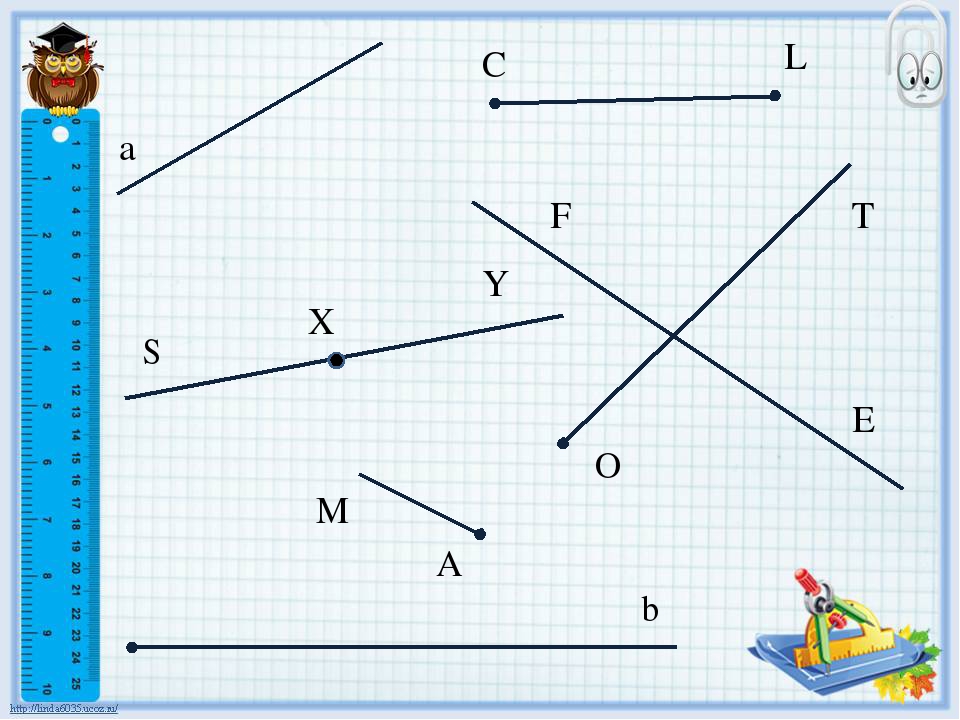
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки [A;C],[C;D],[D;M],[M;F],[F;E] и [E;T], а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.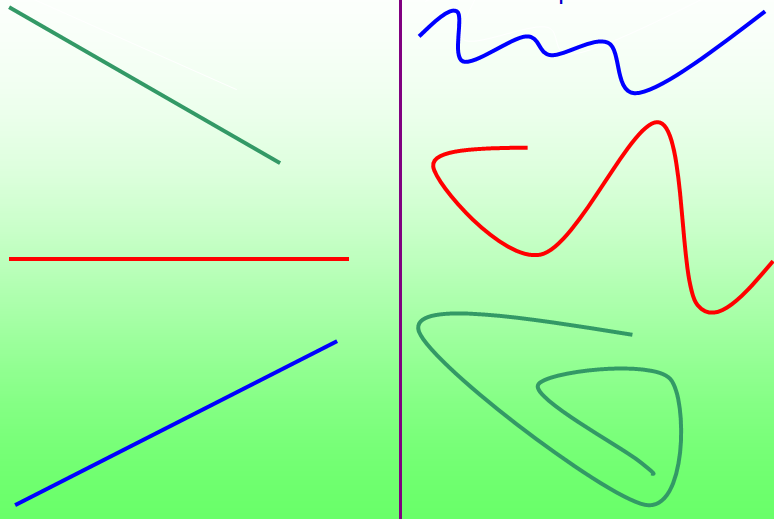 Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Нужна помощь в учебе?
Предыдущая тема: Сложение и вычитание дробей с одинаковыми знаменателями: ПРИМЕРЫ
Следующая тема:   Чтение и запись больших натуральных чисел: разряды, классы + ПРИМЕР
Математика 2 класс.
 Урок: «Прямая. Луч. Отрезок». | План-конспект урока по математике (2 класс):
Урок: «Прямая. Луч. Отрезок». | План-конспект урока по математике (2 класс):П 2. 3. 2.
Что означает ТОЧКА? Что это? Из какой науки?
Как и где найти ответ на вопрос?
Словарь, учебник. Интернет
Давайте попробуем разобраться сами, с чем можно связать точку, где встретить.
Есть наука геометрия. Там точка — это основная и самая простая геометрическая фигура.
— В геометрии точка обозначается заглавной латинской буквой или цифрой. Какие ещё фигуры вы знаете? Какая тема урока у нас ?
В огромном космическом пространстве корабль. Как точка. Для него нужно начертить маршрут. Космос – это фантастика, неразгаданные тайны. Ведь наше путешествие необычное, фантастическое. С чем мы встретимся? Еще неизвестно. Главное в космосе дисциплина и правильная посадка. В иллюминаторе нашего корабля видна планета. Это новая планета. Это планета Туманности.
Это могут быть разные линии ТЕМА-«Прямая. Отрезок. Луч».
Итак цель нашего урока- выявить признаки прямой, луча и отрезка, научиться их распознавать.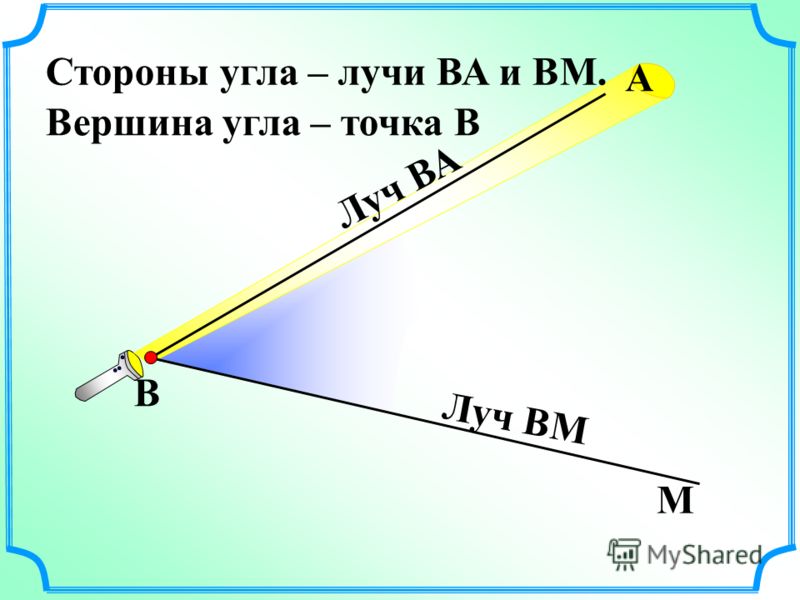
В огромном космическом пространстве корабль. Как точка. Для него нужно начертить маршрут. Космос – это фантастика, неразгаданные тайны. Ведь наше путешествие необычное, фантастическое. С чем мы встретимся? Еще неизвестно. Главное в космосе дисциплина и правильная посадка. В иллюминаторе нашего корабля видна планета. Это новая планета. Это планета Туманности.
-Построим красивую дорожку. Растянем нить двух катушек в разные стороны (два ребенка растягивают нить). Какая получилась линия?(прямая).
(учитель ослабляет нить).
— А вот такая линия будет прямой? (нет).
— А дальше продолжить прямую линию можно? До каких пор?
Без конца и края, линия прямая.
Хоть сто лет по ней иди, не найдешь конца пути.
-У людей есть имена, у животных клички. А прямую линию можно обозначить одной или двумя буквами.
ВЫВОД. У прямой линии нет ни начала, ни конца. Ее можно продолжить.
— Какие прямые линии вы знаете? (горизонтальные, вертикальные, параллельные, наклонные).
-Наша веселая точка поможет нам еще поработать с прямой линией. Поставьте точку, проведите через нее прямую линию.
(дети работают в тетрадях).
— Можно ли еще провести линию через эту точку? Сколько прямых линий можно провести через одну точку? Множество.
-Поставьте 2 точки.Через эти точки проведите прямую линию. Можно ли еще провести?
Стр.7 №2. Отметь цветным карандашом начало каждого луча и обозначь их. Пилот рассчитывает
Стр. 72 №3. Соедини фигуры с их названиями. (Самооценка в табличке)
ВЫВОД. Через одну точку можно провести сколько угодно точек, а через две точки только одну линию.
-Теперь на прямую я помещаю солнышко точку. На сколько частей разбилась наша прямая?. (на две).
-Что они напоминают? Значит как их назовем?(лучами).
(учитель разрезает нить в обозначенной точке, к месту разреза прикрепляются точки).
— Сколько получилось лучей?(2)
О новой фигуре разносится весть.
Конца в ней пусть нет,
Начало то есть!
И солнце тихонько,
Взойдя из -за туч.
Сказало:»Друзья, назовем его луч!»
-Можно ли продолжить луч со стороны разреза? (нет, мешает точка).
-А с другой стороны? (можно, до бесконечности).
-Луч обозначается двумя буквами, причем на первом месте всегда указывается начало луча.
— Чем похожи и чем отличаются луч и прямая?(луч это часть прямой линии, ограниченная с одной стороны).
Вывод: Луч – прямая линия ограниченная с одной стороны. Из одной точки можно провести бесконечное множество лучей.
-Молодцы, вы нашли признак луча. А теперь сделаем на одном из лучей еще один разрез. Что получилось? (отрезок). Я прикрепляю еще одну точку.
-Сравните луч и отрезок.
Дети: У луча есть только начало, а отрезок имеет и начало и конец.
Точки две поставь в тетради,
Чтоб потом нарисовать между ними.
Под линеечку прямую.
И окажется мой друг,
Что отрезок вышел вдруг.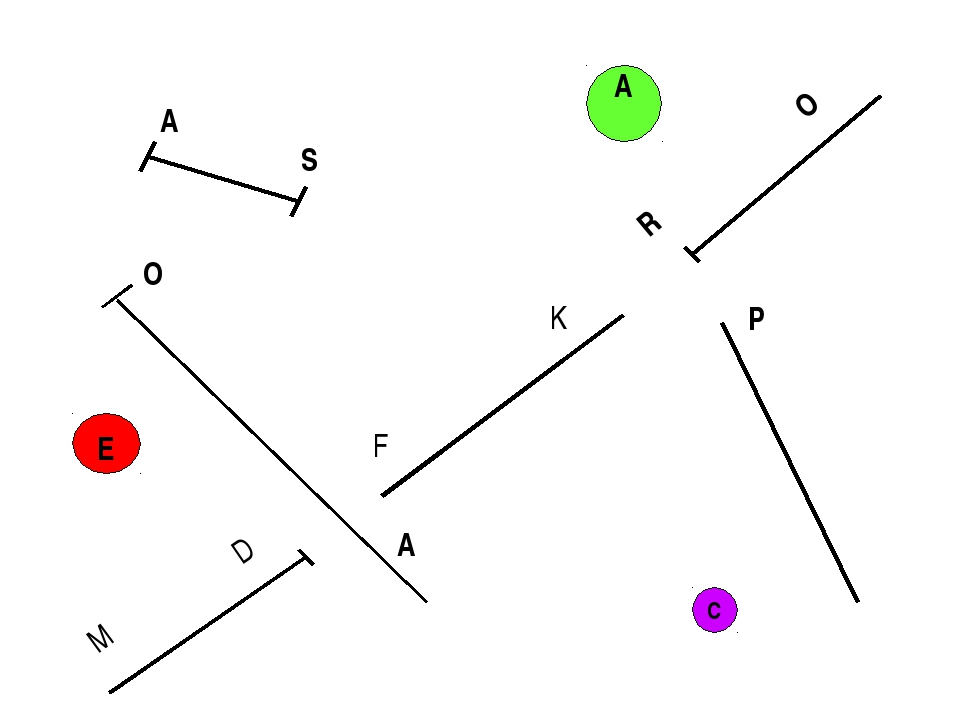
Только точкам имена.
Дать ты не забудь!
-Отрезок обозначается двумя буквами.
— А можно из одной прямой сделать несколько отрезков?
ВЫВОД. Отрезок это прямая, ограниченная с двух сторон. На прямой линии может быть несколько отрезков.
Отрезок, угол, луч — геометрия и искусство
Из истории. Единицы измерения углов.
Градусное измерение углов возникло в Древнем Вавилоне задолго до новой эры. Жрецы считали, что свой дневной путь Солнце совершает за 180 «шагов», и, значит, один «шаг» равен 1/180 развернутого угла.
В Вавилоне была принята шестидесятиричная система счисления, т. е. фактически числа записывались в виде суммы степеней числа 60, а не 10, как это принято в нашей десятеричной системе. Естественно поэтому, что для введения более мелких единиц измерения углов один «шаг» последовательно делился на 60 частей.
Вавилонская система измерения углов оказалась достаточно удобной, и ее сохранили математики Греции и Рима.
Термины, которыми мы пользуемся для названия угловых величин, имеют латинские корни. Слово «градус» происходит от латинского gradus (шаг, ступень). В переводе с латинского minutus означает «уменьшенный». Наконец, secunda переводится как «вторая». Имеется в виду следующее: деление градуса на 60 частей, т. е. минуты,— это первое деление; деление минуты на 60 секунд — второе деление градуса. Малоупотребительное название 1/60 секунды — терцина, латинское tercina означает «третье» (деление градуса).
Принятая сейчас система обозначения величин углов получила широкое распространение на рубеже XVI и XVII вв.; ею уже пользовались такие известные астрономы, как Н. Коперник и Т. Браге. Но еще К. Птолемей (II в. н. э.) количество градусов обозначал кружком, число минут — штрихом, а секунд — двумя штрихами.
Другая единица измерения углов — радиан — введена совсем недавно. Первое издание (это были экзаменационные билеты), содержащее термин «радиан», появилось в 1873 г. в Англии. Сначала в обозначениях указывалось, что имеется в виду радианная мера , но вскоре инадекс R (или г) стали опускать. Сам термин «радиан» происходит от латинского radius (спица, луч).
в Англии. Сначала в обозначениях указывалось, что имеется в виду радианная мера , но вскоре инадекс R (или г) стали опускать. Сам термин «радиан» происходит от латинского radius (спица, луч).
Если вспомнить определение угла в один радиан (центральный угол, длина дуги которого равна радиусу окружности), то выбор корня «рад» для названия такого угла представляется совершенно естественным.
Нарисовать координатный луч. Как построить координатный луч. Работа в тетрадях
Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.
Yandex.RTB R-A-339285-1
Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.
Определение 1
Луч — это геометрическая фигура, которая имеет начало отсчета координатного луча и направление движения. Прямую обычно изображают горизонтально, указывая направление направо.
Прямую обычно изображают горизонтально, указывая направление направо.
На примере мы видим, что O является началом луча.
Пример 1
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Пример 2
Определение 2
Единичный отрезок — это расстояние от 0 до точки, выбранной для измерения.
Пример 3
От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.
Благодаря манипуляциям, которые мы проделали с лучом, он стал координатным. Подпишите штрихи натуральными числами в последовательности от 1 — например, 2 , 3 , 4 , 5 …
Пример 4
Определение 3
– это шкала, которая может длиться до бесконечности.
Зачастую его изображают лучом с началом в точке O , и откладывают единственный единичный отрезок. Пример указан на рисунке.
Пример 5
Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.
Вы можете записывать числа как удобно – под лучом или над ним.
Пример 6
Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.
Принцип изображения координатной прямой практически не отличается от изображения луча. Все просто — прочертите луч и дополните до прямой, придав положительное направление, которое указывается стрелочкой.
Пример 7
Проведите луч в противоположную сторону, дополнив его до прямой
Пример 8
Отложите единичные отрезки по примеру, указанному выше
С левой стороны запишите натуральные числа 1 , 2 , 3 , 4 , 5 … с противоположным знаком. Обратите внимание на пример.
Пример 9
Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.
Пример 10
Определение 4
– это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0 , единичным отрезком и заданным направлением движения.
Соответствие между точками координатной прямой и действительными числами
Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.
Определение 5
Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.
Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.
Пример 11
Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка.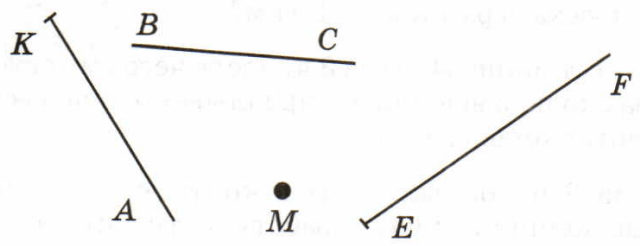 На примере можно подробно рассмотреть данное правило.
На примере можно подробно рассмотреть данное правило.
Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.
Отмеченные отрезки помогут нам отыскать на координатной прямой необходимую точку. Это могут быть как целые, так и дробные числа. Однако на прямой существуют точки, которые очень сложно найти с помощью единичных отрезков. Этим точкам соответствуют десятичные дроби. Для того, чтобы искать подобную точку, придётся откладывать единичный отрезок, десятую, сотую, тысячную, десятитысячную и другие его доли. Одной точке координатной прямой отвечает иррациональное число π (= 3 , 141592 . . .) .
Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.
Определение 6
Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.
Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
§ 1 Координатный луч
В этом уроке Вы научитесь строить координатный луч, а также определять координаты точек, расположенных на нем.
Чтобы построить координатный луч, нам сначала потребуется, конечно же, сам луч.
Обозначим его OX, точка O — начало луча.
Забегая вперед, скажем, что точку O называют началом отсчета координатного луча.
Луч можно изображать в любом направлении, однако во многих случаях луч проводят горизонтально и вправо от его начала.
Итак, начертим луч ОХ горизонтально слева направо и обозначим его направление стрелкой. Отметим на луче точку Е.
Над началом луча (точкой О) напишем 0, над точкой Е — цифру 1.
Отрезок ОЕ называют единичным.
Так, шаг за шагом, откладывая единичные отрезки, получим бесконечную шкалу.
Числа 0, 1, 2 называют координатами точек О, Е и А. Пишут точка О и в скобках указывают ее координату ноль — О(о), точка Е и в скобках ее координата один — Е(1), точка А и в скобках ее координата два — А(2).
Таким образом, для построения координатного луча необходимо:
1. начертить луч ОХ горизонтально слева направо и обозначить его направление стрелкой, над точкой O написать число 0;
2. нужно задать так называемый единичный отрезок. Для этого на луче нужно отметить какую-нибудь точку, отличную от точки O (на этом месте принято ставить не точку, а штрих), и над штрихом записать число 1;
3. на луче от конца единичного отрезка нужно отложить еще один отрезок, равный единичному и тоже поставить штрих, далее от конца уже этого отрезка нужно отложить еще один единичный отрезок, также отметить штрихом и так далее;
4. чтобы координатный луч принял законченный вид, осталось записать над штрихами слева направо числа из натурального ряда чисел: 2, 3, 4, и так далее.
чтобы координатный луч принял законченный вид, осталось записать над штрихами слева направо числа из натурального ряда чисел: 2, 3, 4, и так далее.
§ 2 Определение координат точки
Давайте выполним задание:
На координатном луче нужно отметить следующие точки: точку М с координатой 1, точку Р с координатой 3 и точку А с координатой 7.
Построим координатный луч с началом в точке О. Единичный отрезок этого луча выберем 1 см, то есть 2 клетки (через 2 клетки от нуля поставим штрих и число 1, дальше еще через две клетки — штрих и число 2; затем 3; 4; 5; 6; 7 и так далее).
Точка М будет расположена правее нуля на две клетки, точка Р будет расположена правее нуля на 6 клеток, так как 3 умножить на 2, будет 6, и точка А — правее нуля на 14 клеток, так как 7 умножить на 2, получится 14.
Следующее задание:
Найдите и запишите координаты точек А; В; и С отмеченных на данном координатном луче
Данный координатный луч имеет единичный отрезок, равный одной клетке, значит координата точки А равна 4, координата точки В равна 8, координата точки С равна 12.
Подведем итог, луч ОХ с началом отсчета в точке О, на котором указаны единичный отрезок и направление, называют координатным лучом. Координатный луч представляет собой не что иное, как бесконечную шкалу.
Число, которое соответствует точке координатного луча, называется координатой этой точки.
Например: А и в скобках 3.
Читают: точка А с координатой 3.
Следует заметить, что очень часто координатный луч изображают лучом с началом в точке O, и откладывают от его начала единственный единичный отрезок, над концами которого записывают числа 0 и 1. В этом случае подразумевается, что мы при необходимости можем легко продолжить построение шкалы, последовательно откладывая единичные отрезки на луче.
Таким образом, в этом уроке Вы научились строить координатный луч, а также определять координаты точек, расположенных на координатном луче.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер.
 — М: 2013.
— М: 2013. - Дидактические материалы по математике 5 класс. Автор — Попов М.А. – 2013.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. – 2014.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012.
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.
Математика
Тема: Восстановление начала координатного луча и единичного отрезка по координатам
Цель:
1. Показать учащимся рациональный способ восстановления начала координатного луча и единичного отрезка;
2. Повторить арифметические действия с многозначными числами;
3. Развивать логическое мышление.
Оборудование: карточки с заданиями, фотографии, учебники.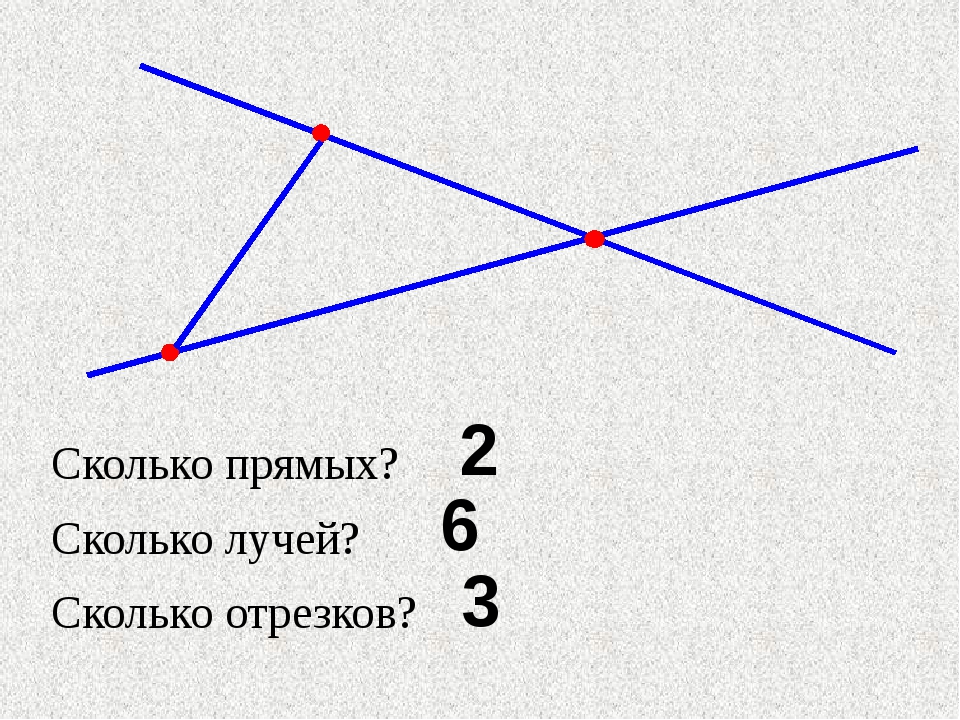
Оформление доски:
Классная работа
Сыскное агентство
«Логика + Интуиция»
Фотографии сыщиковhttps://pandia.ru/text/78/605/images/image001_53.gif»> : 1: 8 * 8: 50 * 1
https://pandia.ru/text/78/605/images/image002_13.gif»>.gif»>
I. Организационный момент
1. Сегодня наш класс – это не класс.
Мы открываем агентство у нас.
Будем исследовать, будем искать
Задачи, поставленные, будем решать.
Что такое «сыскное агентство»?
Кто такие сыщики? (синонимы: детективы, исследователи)
Каких литературных героев вы знаете?
3. Исследование фотографии
Из какого произведения?
Может ли сыщик работать один без помощников?
Мы сегодня создали свое сыскное агентство, только оно у нас с математическим уклоном. И назвали мы его «Логика + Интуиция».
Что такое логика?
Что такое интуиция?
«Логика» – наука о законах мышления, ход рассуждений, закономерность чего – нибудь.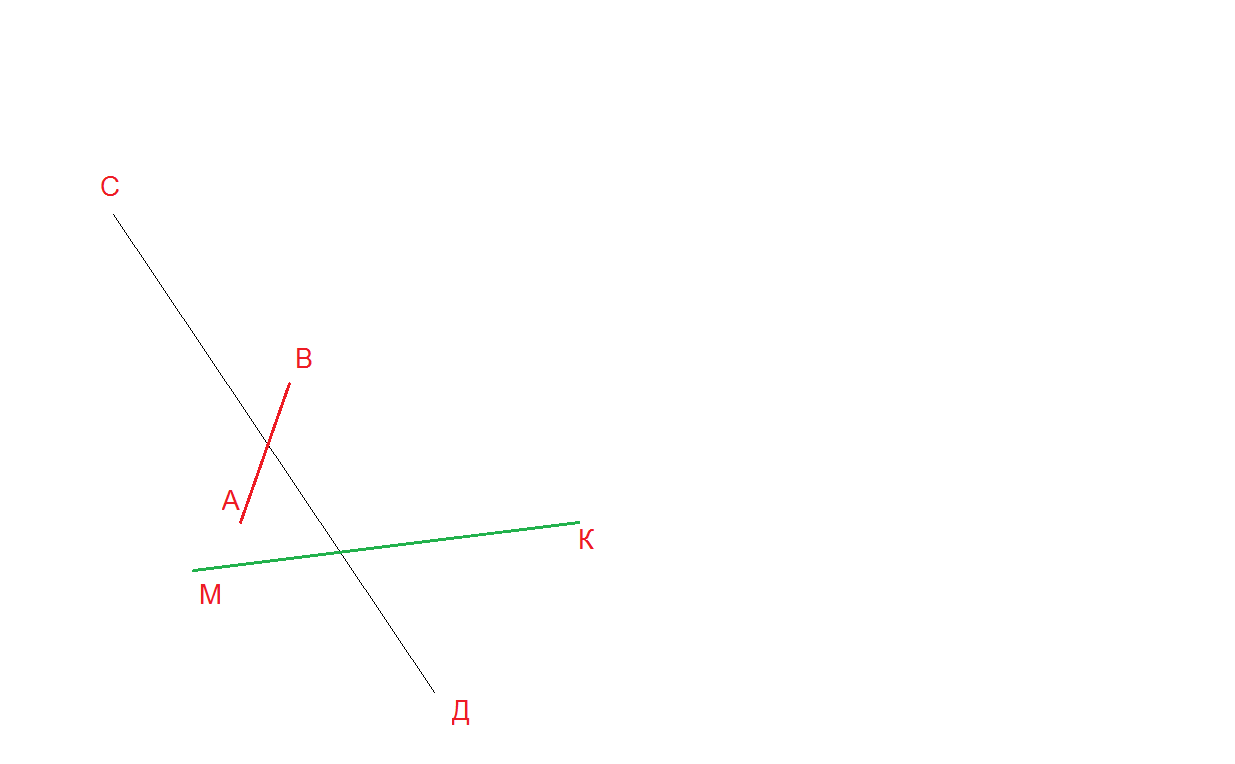
«Интуиция» — в переводе с латинского тонкое понимание чего – нибудь, чутье.
В нашем агентстве будет работать 3 группы, во главе со знаменитым сыщиком. Не забывайте, что главное – это взаимопомощь и поддержка. Давайте пригласим наших героев.
4. Представление сыщиков
Я, Шерлок Холмс, господа!
(Кто написал это произведение?)
Я, сыщик Колобок!
Я, сыщик Пинчер старший, лучший сыщик с дипломом!
II. Закрепление пройденного материала.
1. Работа по карточкам для сыщиков.
Вам дается право выбрать себе рабочую группу, но для этого вам необходимо решить первую задачу;
Что вы можете сказать об этой цепочке?
(она состоит из геометрических фигур)
Кто первый справился и выдал больше информации, тот может выбрать рабочую группу.
2. Работа в группах
Ну а сейчас настроимся и попробуем решить первую проблему.
Найти значение выражения.
Повторить название компонентов.
(действия какой ступени выполняются первыми?)
III. Работа над новым материалом.
Работа над новым материалом.
Давайте продолжим наше исследование, откроем свои записные книжки и впишем число, чтобы не забыть эту дату.
1. Постановка проблемы
А вот и первая проблема, с которой мы постараемся справиться.
а) рассмотрите чертеж
б) что на нем изображено?
Что здесь лишнее? (коорд. луч)
Почему? (отрезок, луч, прямая, ломаная — это геометрические понятия, а координатный луч — алгебраическое)
Что не отмечено на координатном луче? (начало, единичный отрезок)
Что такое отрезок, луч?
2. Работа в тетрадях
Построить корд. луч, отметить начало, ед. отрезок.
3. Работа с учебником
А сейчас давайте откроим учебники, именно он будет подбрасывать нам задачи, с которыми ми должны справиться, а вы – сыщики являетесь координаторами, которые должны помочь каждому в своей группе.
Что изображено в учебнике?
Какие координаты отмечены на координатном луче?
Восстановите начало и единичный отрезок
Какой способ верный?
4. Закрепление.
Закрепление.
Построить координатный луч
Выбрать единичный отрезок равный 1см
Отметить точки равные координатам 2, 4 ,6 ,8
5. Физкультминутка
Ну что устали?
Даже таким известным сыщикам нужен отдых
Я буду называть числа, если они четные — встают девочки, если нечетные — мальчики.
42,19, 8, 64, 1160, 500, 913. 0(не натуральное число)
6. Решение задачи
Ой, ребята, кто — то стучится. Нам — письмо. Это от ребят третьего класса. Они отправились в соседнюю деревню, поможем им вернуться.
Решение задачи на движение
Мальчики до деревни прошли пешком 20 км, двигаясь со скоростью 5км в час. А обратно они ехали на велосипеде в 2 раза быстрее. За сколько часов они проедут это расстояние?
Молодцы.
7. Решение системы неравенств
Наше агентство помогает всем, только во всем нужна система. Включите свою логику, пусть поможет вам ваша интуиция, и помогите Шалтаю – Болтаю (откуда взялся этот герой?)
Решение системы неравенств у доски
X > 97 X > 98, 99, 100, 101, 102, 103, 104
X
8. Решение задачи на смекалку
Решение задачи на смекалку
Сыщики – это люди, которые даже отдыхают с пользой для дела, попробуем и мы.
Ты живешь в первом подъезде? (да – остаются квартиры с 1 по 32)
Номер твоей квартиры больше 16? (нет — остаются квартиры с 1 по 16)
Номер твоей квартиры больше 8? (да – остаются квартиры с 8 по 16)
Номер твоей квартиры больше 12? (да – остаются квартиры с 13по 16)
Номер твоей квартиры больше 14? (да – номер Гришиной квартиры 15)
Каково наибольшее количество таких вопросов? (6 вопросов)
9. Дополнительный материал: Решение уравнений
(x — 3)*7 =14 (x + 2)*7 =49
X – 3=14:7 x +2 = 49:7
X – 3 = 2 x + 2 =7
X = 3+2 x = 7 — 2
IV. Итог
Рефлексия деятельности
Что узнали нового?
Подведение итогов
ОАОУ СПО «Астраханский социально-педагогический колледж»
ПРОБНЫЙ УРОК ПО МАТЕМАТИКЕ
Класс 4 «В» МБОУ «Гимназия № 1» г. Астрахани
Учитель: Беккер Ю. А.
А.
Тема: «Восстановление начала координатного луча и единичного отрезка по координатам»
Выполнила студентка 3 «Б» группы Галимарданова Алина Фаилевна
Отметка за урок:
Учитель: Беккер Ю.А.__________
Методист: Власенкова А.Ш. __________
Астрахань 2015
Школа: МБОУ г. Астрахань «Гимназия № 1»
Программа: система Занкова
Учебник: Математика 4 класс. Часть 1. Авторы: И.И.Аргинская, Е.И.Ивановская
Тема: «Восстановление начала координатного луча и единичного отрезка по координатам»
Класс: 4 «В»
Тип урока: Повторение и закрепление изученного материала (3 класс)
Цель урока:
Образовательная: Обобщить и создать условия для систематизации понятий о числовом луче и единичном отрезке.
Развивающая: Способствовать формированию учебно-интеллектуальных умений и навыков: анализа, синтеза, сравнения, конкретизации, учебно-коммуникативных: умение работать в группе, вести учебный диалог.
Воспитательная : Воспитывать уважение участникам своей команды и команды соперников к на основе дружбы, внимания, заботы
Задачи урока:
Находить определенное значение на координатном луче
Выполнять умножение многозначных чисел на круглые числа
Решать задачи на движение
Оборудование: ПК, ИКТ проектор, экран, презентация урока, учебник, тетрадь, карандаш, линейка.
Ход урока
-А сейчас откройте свои тетради, запишите число, месяц, классная работа, пропускаем 2 клетки вниз, и записываем ответы.Посмотрите на доску:
Записаны примеры.
1)59*2=118
2)59*10=590
3)59*100=5900
4)59*20=59*(2*10)=(59*2)*10=1.180
5)59*200=59*(2*100)=(59*2)*100=11.800
(проверка на слайде устно)
Скажите ребята значение каких выражений вы умеете находить? А кто решил последние два выражения? Как?
Какой закон применяется в этих выражениях?
С помощью 2 и 3 найдите значения оставшихся произведений (иррационально)
Пользуясь найденным способом найди значения произведений:
164*3=492
164*30=164*(3*10)=(164*3)*10=4. 920
920
164*300=164*(3*100)=(164*3)*100=49.200
164*3000=164*(3*1.000)=(164*3)*1.000=492.000
(проверка у доски)
Учащиеся внимательно слушают, думают логически и записывают ответы в тетрадь
1)59*2=118
2)59*10=590 3)59*100=5900
(умножение на круглое число, при умножении числа на разрядную единицу к нему достаточно приписать справа столько нулей, сколько их содержится в записи этой разрядной единицы)
Как 2 и 3 выражение
Переместительный закон умножения
Выходят к доске 3 человека
3Актуализация знаний.
Ребята посмотрите мультик 38 попугаев (Как измерять удава)
О чем мы сегодня с вами будем говорить?
Какая тема нашего урока?
Смотрят
О координатном луче
Восстановление начала координатного луча и единичного отрезка по координатам
Подведение к теме урока.
Ребята посмотрите у вас на парте листочки с заданием, что необходимо выполнить?
Давайте вспомним что такое луч?
Что является началом луча?
(дети выполняют на листочках)
Можем ли мы сразу задать начало координатному лучу?
Почему?
А как найти начало луча?
Как вы нашли начало координатного луча?
Восстановить начало координатного луча.
Луч-это отрезок, имеет начало, но не имеет конца.
Точка
Необходимо найти начало луча
Для этого нужно найти единичный отрезок.
Нашли единичный отрезок измерив расстояние между 12 и 13=7мм.Затем отложили 6 единичных отрезка от точки 6
4. Работа с учебником
Ребята, а теперь откройте стр учебника 42, посмотрите какими способами ученики (Аня и Юра) выполнили задания?
Твой способ совпадает с одним из предложенных?
Какой способ ты считаешь более удобным?
Почему?
А теперь посмотрите на 2 задание на листочках. Похожее задание вы найдете на стр 42 Читай:
Начертите координатный луч с единичным отрезком 5 мм и отметьте на нем точки А(4), В(9), С(7), D(10).
Решают у доски, остальные в тетради и проверяют
А теперь выполним самопроверку. Нарисуйте на полях линейку оценивания. Поднимите руку, те кто отметил на самой нижней шкале?…
Да, Юрин
Анин
Потому что она не находила единичный отрезок.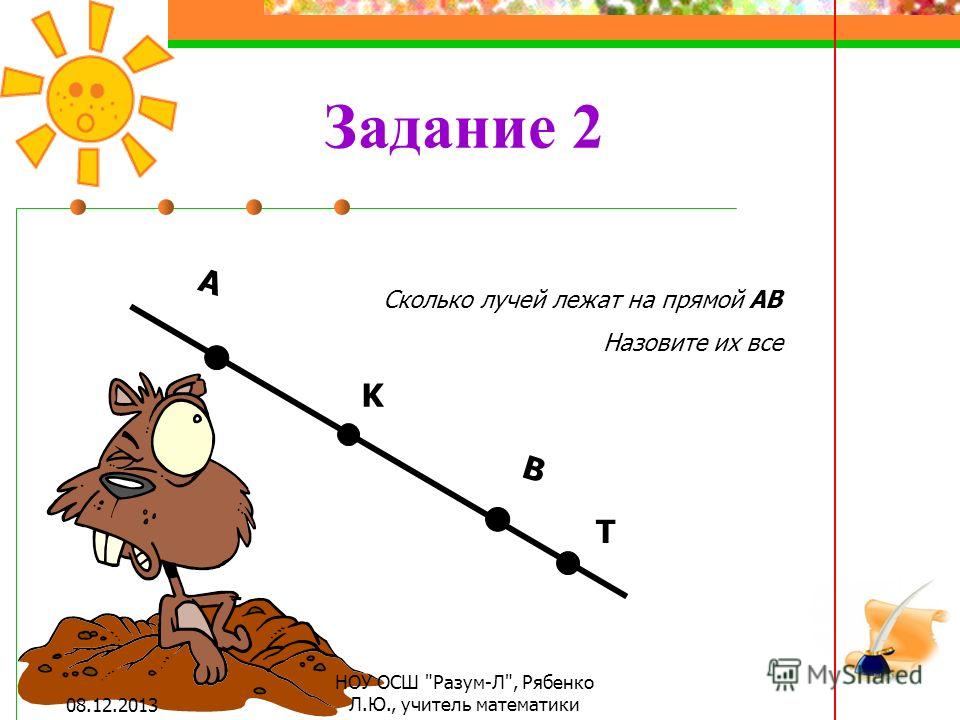 Она отмерила расстояние между 6 и 12(6 единичных отрезков по 7 мм=42мм=4см и 2мм) , а затем приложила его от точки 6 тем самым получила начало координатного луча.
Она отмерила расстояние между 6 и 12(6 единичных отрезков по 7 мм=42мм=4см и 2мм) , а затем приложила его от точки 6 тем самым получила начало координатного луча.
Выходят к доске.
5.Физкультминутка
Дружно с вами мы считали
И про числа рассуждали.
А теперь мы дружно встали
Свои косточки размяли.
На счет «раз» кулак сожмем.
На счет «два» в локтях сожмем.
На счет «три» – прижмем к плечам.
На четыре – к небесам.
Хорошо прогнулись
И друг другу улыбнулись
6.Продолжение работы
А теперь давайте откроем наши пособия задач на стр 190 и решим задачу №2.Прочитайте ее про себя. (схема задачи на слайде)
Из двух сел, расстояние между которыми 81 км, одновременно навстречу друг друга выехали 2 велосипедиста. Скорость одного велосипедиста 12 км/ч. С какой скоростью ехал другой велосипедист, если они встретились через 3 ч?
Какая это задача?
Кто хочет решить задачу?
Теперь отроем стр 208 и решим задачу № 4. Прочитайте. (схема задачи на слайде)
Прочитайте. (схема задачи на слайде)
Жуки-плавунцы поплыли одновременно в противоположных направлениях. Через 9 с расстояние между жуками-плавунцами было 81 дм. Одина жук-плавунец плыл со скоростью 5 дм/с. С какой скоростью плыл другой жук-плавунец?
Какая это задача?
На движение. (встречное)
Решение:
1)81:3=27(км/ч)-Скорость сближения
2)27-12=15 (км/ч)-Скорость 2-ого велосипедиста.
Решают у доски
(проверка у доски)
На противоположное движение
Решают в тетрадях
Решение:
1)81:9=9(дм/с)-общая скорость удаления
2)9-5=4(дм/с)-Скорость 2-ого жука-плавунца
(проверка на слайде)
7.Домашнее задание
Пособие. Стр 189 № 1
Записывают
8.Итог урока. Рефлексия
Ребята какую тему мы сегодня с вами изучали?
Что такое координатный луч? Как задать начало координатного луча, если оно не задано?
Какие трудности у вас возникли?
Что вам понравилось?
На какой ступени лесенки успеха вы себе поставили бы плюс?
Спасибо за урок, мне было приятно с вами работать.
Отвечают
Так единичный отрезок и его десятая, сотая и так далее доли позволяют нам попасть в точки координатной прямой, которым будут соответствовать конечные десятичные дроби (как в предыдущем примере). Однако на координатной прямой существуют точки, в которые мы не можем попасть, но к которым мы можем подойти сколь угодно близко, использую все меньшие и меньшие до бесконечно малой доли единичного отрезка. Этим точкам соответствуют бесконечные периодические и непериодические десятичные дроби. Приведем несколько примеров. Одной из таких точек на координатной прямой соответствует число 3,711711711…=3,(711) . Чтобы подойти к этой точке нужно отложить 3 единичных отрезка, 7 его десятых долей, 1 сотую долю, 1 тысячную, 7 десятитысячных долей, 1 стотысячную, 1 миллионную долю единичного отрезка и так далее. А еще одной точке координатной прямой отвечает пи (π=3,141592… ).
Так как элементами множества действительных чисел являются все числа, которые можно записать в виде конечных и бесконечных десятичных дробей, то вся вышеизложенная в этом пункте информация позволяет утверждать, что каждой точке координатной прямой мы поставили в соответствие конкретное действительное число, при этом понятно, что разным точкам соответствуют разные действительные числа.
Также достаточно очевидно, что это соответствие является взаимно однозначным. То есть, мы можем указанной точке на координатной прямой поставить в соответствие действительное число, но мы также можем по данному действительному числу указать конкретную точку на координатной прямой, которой отвечает данное действительное число. Для этого нам придется отложить от начала отсчета в нужном направлении определенное количество единичных отрезков, а также десятых, сотых и так далее долей единичного отрезка. Например, числу 703,405 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 703 единичных отрезка, 4 отрезка, составляющих десятую долю единичного, и 5 отрезков, составляющих тысячную долю единичного.
Итак, каждой точке на координатной прямой отвечает действительное число, и каждое действительное число имеет свое место в виде точки на координатной прямой. Вот почему координатную прямую очень часто называют числовой прямой .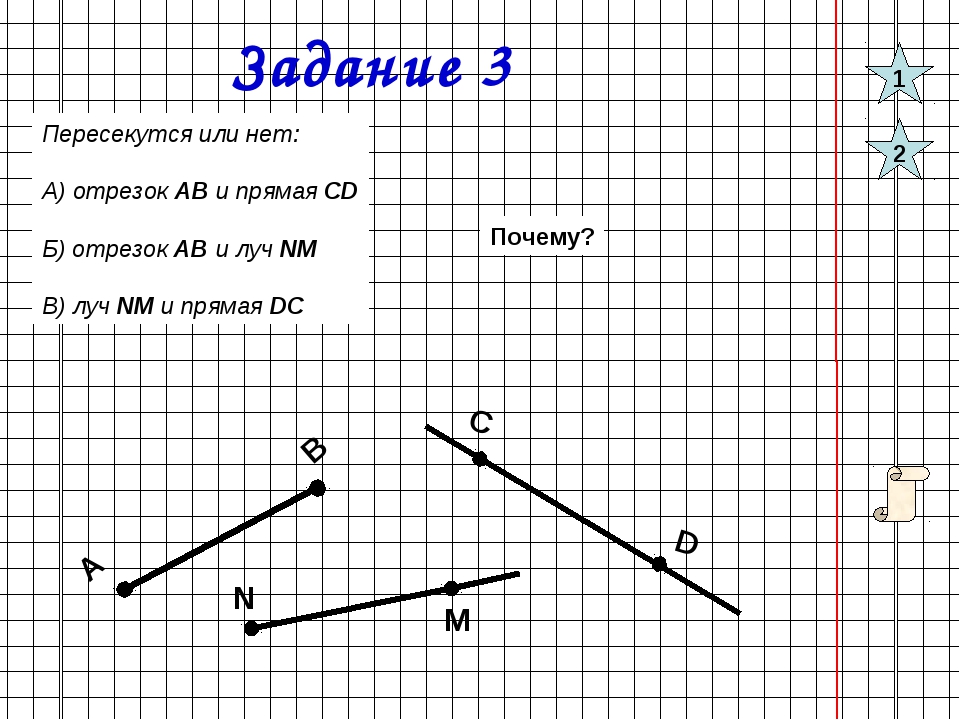
Координаты точек на координатной прямой
Число, соответствующее точке на координатной прямой, называется координатой этой точки .
В предыдущем пункте мы сказали, что каждому действительному числу соответствует единственная точка на координатной прямой, поэтому, координата точки однозначно определяет положение этой точки на координатной прямой. Иными словами, координата точки однозначно задает эту точку на координатной прямой. С другой стороны каждой точке на координатной прямой соответствует единственное действительное число – координата этой точки.
Осталось сказать лишь о принятых обозначениях. Координату точки записывают в круглых скобках справа от буквы, которой обозначена точка. Например, если точка М имеет координату -6 , то можно записать М(-6) , а запись вида означает, что точка М на координатной прямой имеет координату .
Список литературы.
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика: учебник для 5 кл.
 общеобразовательных учреждений.
общеобразовательных учреждений. - Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Как нарисовать лучи солнца
Если вы любите рисовать плотными красками, например, гуашью или акрилом, рано или поздно вы задумываетесь о рисовании света. Высветление водой, как с акварелью, тут не подходит.
Из этой статьи вы узнаете общие принципы изображения солнечного света густыми красками.
Как изобразить солнечный свет.
Вам понадобятся: кисть плоская №6, белая, желтая и оранжевая краски.
Смешайте небольшое количество белой и жёлтой краски. Оттенок подбирайте по гамме своей картины. Но жёлтой краски требуется совсем чуть-чуть.
Наберите краску, затем слегка промокните кисть об ткань или салфетку, и на уже готовый рисунок добавьте лучи. Для этого проводите кистью прямые линии по направлению от солнца к освещённым объектам.
Основные советы:
* Солнечные лучи изобразите, как спицы на колесе
* Движения руки должны быть лёгкие и быстрые
* Наносите краску, пока не добьётесь нужной яркости
* Лучи должны оставаться очень размытыми и едва видимыми, тогда рисунок будет реалистичнее.
* Предметы можно сделать ярче, добавив по их краям смесь белой и жёлтой или белой и оранжевой красок. Тут главное не переборщить. Во всём нужна мера.
* Заранее определите, где будут источник света и самые светлые места.
И помните, что все великие художники рисовали с натуры или хотя бы с фотографии. Так творил и Иван Иванович Шишкин. Поэтому чаще рассматривайте природу и её изображения, чтобы ваши рисунки получались живописными и солнечными.
Теперь вы знаете, как нарисовать свет гуашью или другими плотными красками. Создавайте свои прекрасные картины и загружайте в галерею на сайте Рисовашки.тв
Маленькие дети очень любят рисовать солнце. Начинают они с того, что берут жёлтый фломастер или карандаш и начинают рисовать часть круга в уголке листа. Есть даже строчка из детской песенки – «Солнечный круг, небо вокруг…». Как же рисовать солнце, чтобы оно украшало рисунок и делало его живым и поистине солнечным?
Начинают они с того, что берут жёлтый фломастер или карандаш и начинают рисовать часть круга в уголке листа. Есть даже строчка из детской песенки – «Солнечный круг, небо вокруг…». Как же рисовать солнце, чтобы оно украшало рисунок и делало его живым и поистине солнечным?
Материалы, используемые для рисования солнышка
Чтобы нарисовать солнце, дети могут использовать самые разные материала жёлтого, красного и оранжевого цветов. Для основы лучше использовать яркий жёлтый, а для украшения лучей – оранжевого и красного.
Материалы:
- акварельные краски;
- гуашь;
- цветные карандаши;
- фломастеры;
- мелки;
- акварельные карандаши;
- медовые краски;
- масляные краски.
Художникам-экспериментаторам понравится работать с аквагримом, пищевыми красителями и совершенно неожиданными для рисования материалами. Солнышко можно рисовать на листе бумаги, на лице, кафельной или стеклянной поверхности. Важно лишь подобрать правильный материал и выбрать качественные кисти.
Важно лишь подобрать правильный материал и выбрать качественные кисти.
Как нарисовать солнышко с милым лицом
Солнышко с милым лицом – украшение любого детского рисунка. Чтобы нарисовать такое солнышко, можно воспользоваться циркулем или начертить круг от руки. Можно также обвести круглый предмет, например, дно кружки. Этому способу нужно научить ребёнка как можно раньше, ведь он значительно облегчает жизнь.
Материалы:
- лист бумаги;
- ластик;
- простой карандаш или циркуль;
- чёрный фломастер;
- жёлтый фломастер;
- розовый фломастер.
Можно также использовать чёрный линер или тонкий маркер, чтобы обводить линии, сделанные простым карандашом.
Следуя простой инструкции, можно нарисовать солнышко с очень милым личиком:
- Расположить лист бумаги перед собой. Циркулем или простым карандашом начертить круг желаемого диаметра.
- От руки набросать линии, исходящие от солнца.
 Это лучи. Желательно придерживаться одинакового расстояния между лучами, для этого можно воспользоваться линейкой, но этот инструмент нежелателен в рисовании.
Это лучи. Желательно придерживаться одинакового расстояния между лучами, для этого можно воспользоваться линейкой, но этот инструмент нежелателен в рисовании. - Простым карандашом нарисовать глаза солнышку. Это должны быть слегка удлинённые круги. С правой стороны глазок нарисовать блики – два небольших овала.
- Нарисовать ротик – небольшой полукруг. Чем ближе рот расположен к глазкам, тем милее получится личико солнца. Можно добавить розовые щёчки прямо под глазками. Блики на щёчках можно сделать корректором, а можно оставить их естественными.
- Аккуратно закрасить круг и лучи жёлтым цветом.
- Обвести все детали чёрным фломастером.
- Чёрным фломастером закрасить глазки солнышку, оставив блики белыми. Если случайно закрасили блики, то их можно сделать заново с помощью корректора (замазки). Можно добавить реснички.
- Ротик солнышка раскрасить розовым цветом.
- По желанию украсить солнышко элементами декора – бантиком, стразами или бусинами.

Такое милое солнышко с личиком может стать чармом для браслета, основой для кулона или серёжек из полимерной глины.
Как нарисовать солнце с необычными лучами
Лучи в виде звуковых волн у солнца всегда смотрятся оригинально и необычно. Для того чтобы нарисовать солнышко с такими лучами, потребуются следующие материалы:
- лист бумаги формата А4;
- жёлтый, оранжевый и чёрный фломастеры;
- простой карандаш;
- ластик;
- шерстяные нитки оранжевого цвета;
- клей.
Для того чтобы нарисовать оригинальное солнышко, нужно:
- Расположить перед собой лист бумаги и начертить круг.
- Раскрасить круг жёлтым фломастером, по желанию нарисовать мордочку у солнца.
- Обвести круг чёрным фломастером.
- Оранжевым фломастером нарисовать лучи в виде звуковых волн. Волна, которая находится ближе к солнышку, должна быть больше. Волны рисовать по убыванию. Цвета волн можно чередовать – оранжевый с жёлтым или оранжевый с красным.

- По желанию можно наклеить оранжевые шерстяные нити по рисунку волн. Так рисунок получится объёмным и будет смотреться ещё красивее.
Как нарисовать солнышко с острыми лучами
Один из самых аккуратных и точных вариантов рисования солнышка для детей – это рисунок солнца с острыми лучами. Такие лучи представляют собой равнобедренные треугольники с высокими боковыми сторонами и небольшим основанием. Чтобы нарисовать такое солнышко, можно воспользоваться любыми материалами, но для него обязательно понадобятся простой карандаш и линейка.
Следуя простейшей инструкции, можно нарисовать замечательное солнышко с острыми лучами:
- Расположить перед собой лист бумаги, сделать набросок простым карандашом.
- После того как круг-основа начерчен, необходимо поставить четыре равноудалённых друг от друга точки на начерченной линии круга.
- Провести от точки лучи с помощью линейки. К лучу с двух сторон провести по два отрезка – они образуют треугольник.
 Когда Вы проделаете то же самое со всех четырёх сторон, солнышко станет похоже на компас. Такой расчёт позволит сделать фигурку идеально ровной, она будет смотреться максимально аккуратно.
Когда Вы проделаете то же самое со всех четырёх сторон, солнышко станет похоже на компас. Такой расчёт позволит сделать фигурку идеально ровной, она будет смотреться максимально аккуратно. - Между двумя треугольниками нарисовать ещё один луч, по бокам от него – ещё два. Заполнить все пустое пространство треугольными лучами.
- Закрасить солнышко по желанию.
Рисовать солнце – увлекательно и интересно. Можно использовать разные техники для рисования лучей, а также пользоваться различными материалами, чтобы получить интересный результат. Ребёнка очень просто научить рисовать солнце, это один из любимых объектов рисования многих детишек. Чтобы солнце получилось ярким и красочным, следует использовать чистые, яркие оттенки жёлтого цвета – краски без примесей, чистую гуашь или толстый фломастер, который не оставит разводов.
«Солнечный круг»
– Здравствуйте, ребята. А вы любите отгадывать загадки?
А вы любите отгадывать загадки?
-ну, тогда попробуйте отгадать мои загадки:
Без него плачемся,
От него прячемся! (солнце)
Доброе, хорошее, на всех глядит,-
А на себя – не велит! (солнце)
По небу ходит маляр без кистей,
Краской коричневой красит людей. (солнце)
Жёлтая тарелка на небе висит.
Жёлтая тарелка всем тепло дарит. (солнце)
– молодцы! Как вы быстро все загадки отгадали.
2.введение в тему.
– и мы сегодня с вами будем рисовать…… Солнце!
– что такое солнце? – солнце, это самая близкая к нашей планете звезда! Это огромный огненный шар!
– Солнце – это источник жизни, тепла и света.
3. объяснение нового материала.Теория.
– какая геометрическаяфигура лежит в основе изображения солнца?- правильно, круг.
– вот круг (показываю бумажный круг) , он похож на солнце? – пожалуй, не совсем. Ведь круглую форму имеют и другие предметы: тарелка, колесо, апельсин… (ДЕТИ НАЗЫВАЮТ ПРЕДМЕТЫ КРУГЛОЙ ФОРМЫ)
– чего же не хватает, чтоб этот круг превратился в солнышко?
– ну конечно же ему не хватает солнечных лучей!
Нарисую жёлтый круг,
После – лучики вокруг,
Пусть на белом свете
Ярче солнце светит!
– вот теперь всем сразу ясно, что это не колесо, не тарелка, не луна, а это солнышко лучистое-золотистое!
– скажите,ребята, а может быть солнышко в виде половинки круга?
– да, может! Когда солнце выходит (утро) или заходит (вечер) за горизонт, вот в это время мы и наблюдаем только часть солнечного круга (картинка).
– а можно увидеть на небе четвертинку солнца? Пожалуй нет. Только дети в своих рисунках изображают солнце в углу листа – вот и получается четверть солнечного диска. (картинка)
– Ребята, а на какой цветок похоже солнце?
– правильно, на подсолнух! – растёт под солнцем. (картинка)
– а этот цветок похож на солнце? (картинка)
– да. Одуванчики тоже похожи на маленькие солнышки. Когда появляется солнышко, они просыпаются, а когда оно прячется, то и одуванчики закрываются и не показывают свои жёлтые цветочки. Так и мы с вами: ночью спим, а как только солнышко проснулось, стало светло и тепло – мы просыпаемся.
Сегодня мы с вами нарисуем два солнышка – одно реалистическое, т.е. такое, каким мы его реально видим на небе каждый день, а второе солнышко изобразим сказочное, мультяшное,- такое, каким его изображают художники в мультфильмах, на страницах сказочных книг.
Давайте посмотрим, как художники изображают солнце на своих картинах. (просмотр, краткий анализ).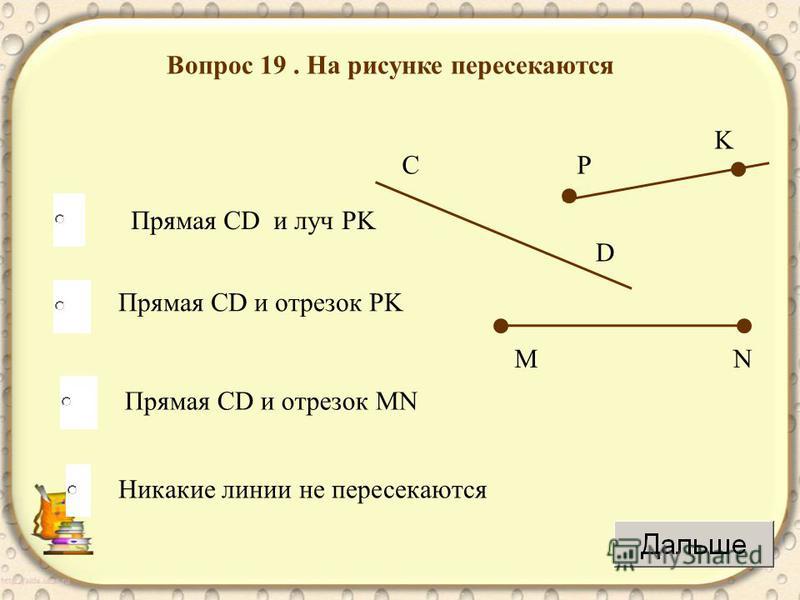
– вот как в своих работах художники рисуют солнце.
4. Практика. Поэтапное рисование.
(Педагог показывает, объясняет – дети рисуют по образцу)
А сейчас давайте и мы с вами попробуем нарисовать настоящее солнце!
Но, прежде чем приступить к работе, давайте немного разомнёмся.
Надоело долго ждать,будем солнце рисовать! (рисуют в воздухе пальцами солнце)
Нарисуем солнце, приклеим на оконце, (смотрим в окно на небо)
Станет в комнате светлей, сразу станет веселей! (дети улыбаются друг другу)
Я скажу вам не тая, жить без солнышка нельзя! (садятся на свои места)
Итак, приступаем к работе.
Сначала нужно что нарисовать?- круг.
– нарисовать круг от руки очень сложно. С помощью чего можно нарисовать красивый ровный круг? (ответы детей: циркуль, стакан, тарелка, лекало…)
– а мы сегодня научимся рисовать круг с помощью линейки!смотрите, как я показываю, так вы и делайте:
– в центре листа ставим точку;
– прикладываем к точке уголок линейки;
– выбираем радиус солнечного круга, соответственно размеру листа бумаги;
– постепенно, вращая линейку по кругу, не отрывая уголка линейки от срединной точки, ставим метки (точки) карандашом до тех пор, пока линейкани вернётся в своё исходное, первоначальное положение;
– убираем линейку, соединяем от руки все наши метки (точки) – и у нас получился красивый, ровный круг – солнечный диск.
– теперь осталось только пририсовать лучи, чтоб наш круг превратился в сияющее солнце!
– для этого возьмём жёлтый и голубой карандаши. Чтоб солнце получилось настоящим, сверкающим – середину солнечного диска каким цветом будем делать? – белым! А бумага у нас и так белая, значит, просто оставляем не закрашенную середину круга.
– затем, слегка нажимая на жёлтый карандаш, заштриховываем края диска – штрихи кладём по кругу;
– затем сами лучи рисуем более сильным нажимом, штрихуя от центра;
– далее жёлтый цвет карандаша плавно переходит в голубой цвет неба.
– вот и засияли наши солнышки, ну совсем как настоящие.
5.Итог. (анализ, просмотр)
Дети встают в круг со своими рисунками, звучит песня «Солнечный круг».
Педагог вместе с детьми просматривают рисунки, отмечая наиболее удавшиеся работы.
Вопросы педагога: – как сегодня мы рисовали круг?
– как изобразить сияющее солнце? (какими цветами?)
– а лучи от солнце в каком направлении рисуются?
Молодцы! Сейчас положите свои работы и немного отдохните.
Продолжаем наше занятие.
– Итак, на первом занятии мы успели нарисовать настоящее, реалистическое солнце.
– а сейчас вы, ребята, попробуйте нарисовать солнце в мультяшном стиле. Оно будет совсем не похоже на предыдущее! Это будет солнышко из сказки: с глазками, с улыбкою, с веснушками, а может быть с косичками?! И даже может с ручками…. А может даже с ножками….
2.объяснение темы, задания.
– посмотрите, ребята, на вот этот круг с глазками – на что он похож?
– ответы детей: на смайлик.. на колобка…
– вот ваша сегодняшняя задача превратить этот смайлик (колобок) в солнышко, да в непростое, а в сказочное. Ведь только в сказках и мультфильмах солнце оживает, оно может смотреть, говорить, смеяться – ну совсем как человек!
– давайте сейчас посмотрим, как художники-иллюстраторы детских книг и журналов изображают сказочное солнышко.(просмотр картинок с изображениями разных вариантов солнышка).
– Видите, сколько сказочных солнышек ?- и все они разные, нет двух одинаковых.
– каждый из вас сейчас должен проявить максимум фантазии, придумать и нарисовать своё, неповторимое солнышко!
– давайте вспомним, с чего будете начинать рисовать?
– ответы детей: ставим точку в центре, с помощью линейки по кругу расставляем метки-точки, потом соединяем все точки от руки – получается солнечный круг (диск).
– а к этому кругу, солнечному диску, уже каждый самостоятельно пририсует детали: глазки, ротик, волосы, лучики и т.д.
– всем понятно задание?- приступайте.
3.Практическая часть. Самостоятельная работа.
– простым карандашом рисуют лицо, чтоб получился смайлик,
– фантазируют с лучами: волосы, косички, чёлка, ручки, ножки…
– уточняют рисунок с помощью чёрного контура (обводка).
Во время работы читаю стихотворение:
«Что такое солнышко?»
Нам от солнышка тепло,
Нам от солнышка светло.
Всё под добрыми лучами
Улыбнулось, расцвело.
Что такое солнышко?
Золотое зёрнышко.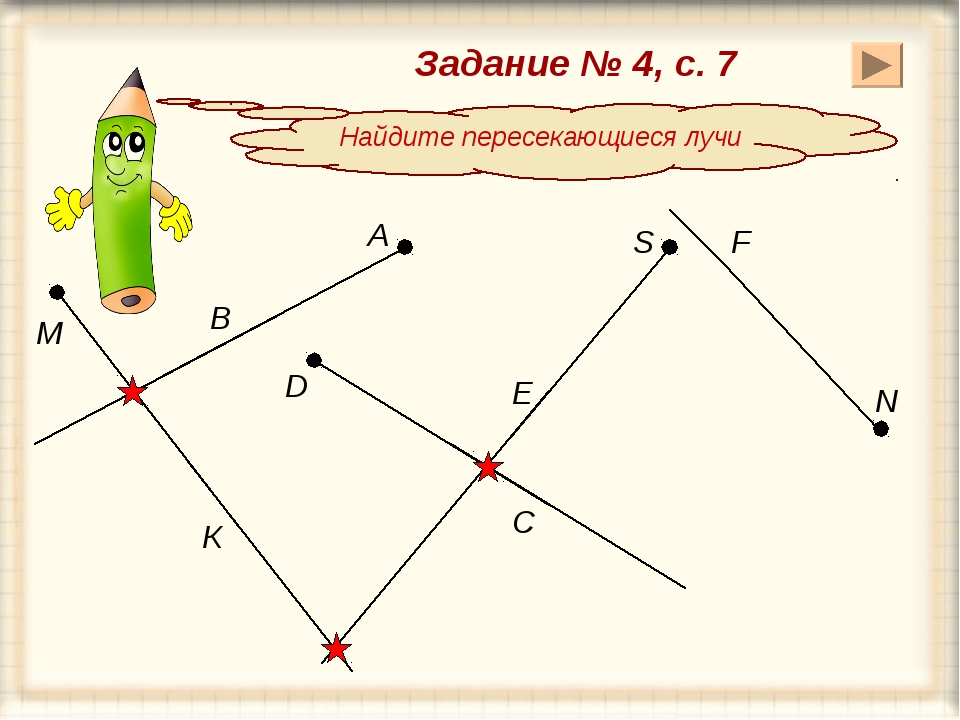
В небе огненной Жар-птицы
Потерялось пёрышко?
Поднимая к небу пальчик,
Нам двухлетний кроха мальчик
(Мама, папа – вот оно!)
Сразу скажет: «Солнце – мячик!»
В небе солнышко давно.
Вдруг соскучится одно?
Тайну шепотом открою:
Небо звёздами полно.
Вот и солнышко – звезда.
В середине занятия проводим физминутку:
Нарисуем жёлтый круг- (рисуем солнце с лучами пальчиками в воздухе)
После – лучики вокруг.
Пусть на белом свете
Ярче солнце светит!
На детей и на цветы, (приседаем и встаём: «цветы» -сели, «дети» -встали…)
смотрит солнце с высоты! (смотрим в окно… вдаль….)
Чтоб росли скорее
Их теплом согреет. (присели и медленно встаём – растём)
– выросли под солнышком и дальше продолжаем работу.
Звучат детские песни про солнце, про солнечный день.
Дети встают в круг (под песню «Солнечный круг»), имитируя солнечный диск, демонстрируя друг другу свои чудесные рисунки сказочных солнышек.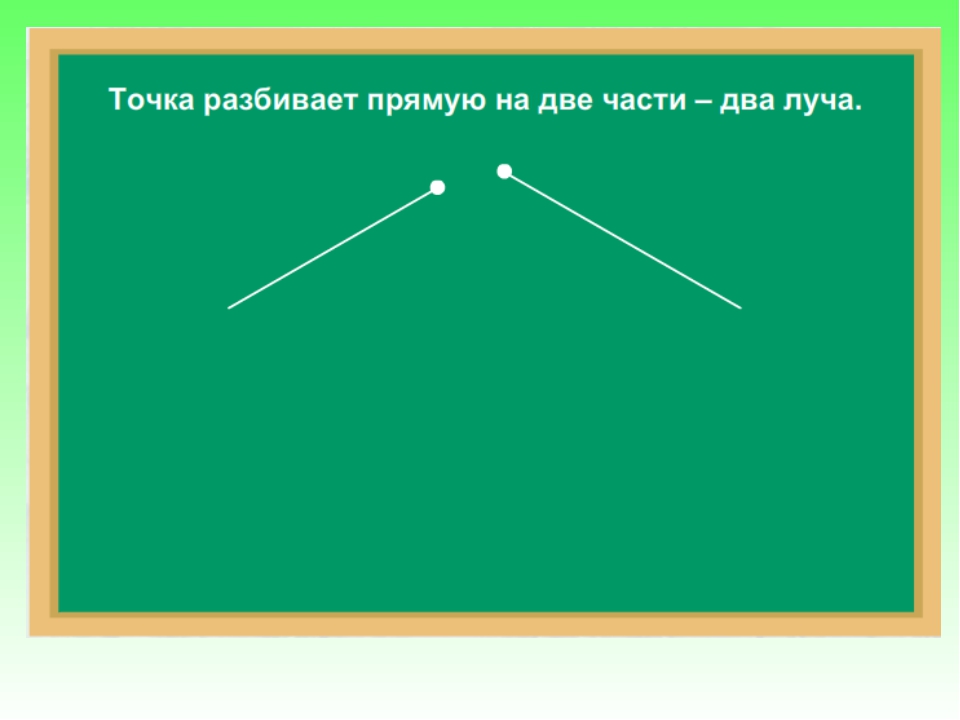 Вместе смотрим, анализируем. Вопросы педагога:
Вместе смотрим, анализируем. Вопросы педагога:
– понравилось рисовать солнце?
– а какое солнышко вам понравилось больше рисовать?- реалистическое, или мультяшное, сказочное? Почему? (ответы детей)
Все ребята молодцы, постарались от души!
Занятие закончилось, складываем работы в свои папки.
По теме: методические разработки, презентации и конспекты
Конспект занятия «Кто снами рядом живёт» во второй младшей группеКонспект занятия по ознакомлению с окружающим » Степашка в гостях у ребят» в первой младшей группе.
Дополнительное образование по факультативному курсу «Театр», ориентировано на развитие творческих способностей ребёнка через приобщение его к миру театра.
Занятия в сенсорной комнате с младшими школьниками как новые возможности школы по здоровьесбережению детей.
Учитель: Лапина Виктория ФранцевнаКласс: 2-в (VIII вид, 2 вариант)Предмет: Развитие речи и окружающий мирТип урока: интегрированныйФорма урока: урок-занятие «Пусть всегда будет солнце!»Цел.
Закрепить знания детей об объекте неживой природы-Солнце. Для детей с умеренной умственной отсталостью.
Формировать представления о звёздах, Солнце и созвездиях.
Конспект урока в 1 классе по ОКМ, УМК «Школа России». Тема «Почему солнце светит днем, а звезды ночью?".
необычные возможности и принцип работы. Оптимизация под SSE
Вступление
В данной статье рассматривается оригинальный графический движок для компьютерных игр, основанный на методе трассировки лучей — совершенно отличном от используемых в современных популярных трёхмерных играх. Соответственно, движком не используются(!) 3D-акселераторы, без которых, казалось бы, немыслима игровая графика.
Соответственно, движком не используются(!) 3D-акселераторы, без которых, казалось бы, немыслима игровая графика.
Речь пойдет о необычных возможностях, предоставляемых движком, и принципах его работы. Кроме того, будут рассмотрены аспекты оптимизации приложений под SIMD расширения. В первую очередь, под SSE — дополнительный набор процессорных команд, впервые реализованный в процессорах Pentium III, Celeron II. Наконец, будут приведены показатели производительности программы на новейших процессорах.
Автор выражает надежду, что чтение данной статьи не вызовет затруднений у любого читателя iXBT.com, для которого эта статья будет не первой.
Зачем?
Действительно, зачем нужно изобретать ещё один движок, когда их и так огромное количество? Что ещё нужно, когда есть потрясающие по качеству движки Quake III и Unreal?
Возьмите в руки самую мощную базуку, развернитесь к какой-нибудь стене и стреляйте бесконечно долго. Ничего не случится: уровень современной трёхмерной игры выточен из абсолютно твёрдого тела. Это не сильно обедняет gameplay, игровой процесс, если вы спустились в эти катакомбы пострелять пару часов. А если вам тут жить? Что-то хочется достроить, что-то — расширить. Может, вам самому захочется построить себе дворец. Может, другим игровым персонажам захочется его разрушить.
Это не сильно обедняет gameplay, игровой процесс, если вы спустились в эти катакомбы пострелять пару часов. А если вам тут жить? Что-то хочется достроить, что-то — расширить. Может, вам самому захочется построить себе дворец. Может, другим игровым персонажам захочется его разрушить.
Все подобные возможности должны поддерживаться графическим движком игры. Играющему дано делать только то, что позволяет движок и ничего более. А если играющий захочет всё взорвать? А если захочет выключить один светильник и включить другой в другом месте? В ответ подобным поползновениям движок лишь промолчит.
Соответственно, и игр таких в полном 3D нет. Почему так? Всё просто: чтобы быстро рисовать большие уровни, их заранее долго просчитывают и при отрисовке кадра используют записанную информацию. Например, есть комната, заранее определяется, какие другие комнаты видны из неё и, когда играющий находится внутри этой комнаты, рисуются только эта комната и видимые из неё. Это позволяет многократно уменьшить количество рисуемых за кадр треугольников. Зато, выломать стену комнаты нельзя: алгоритм даст сбой, не будет рисовать то, что открылось. Так как это не просчитано заранее.
Зато, выломать стену комнаты нельзя: алгоритм даст сбой, не будет рисовать то, что открылось. Так как это не просчитано заранее.
Ладно бы были проблемы только с видимостью: рисовали бы уровни поменьше, пока ускорители недостаточно мощные. Проблема гораздо глубже. Дело в том, что нужно ещё рассчитывать тени от объектов, стен, лестниц и т.д. Чтобы сцена выглядела реалистично, она должна быть реалистично освещена. Под лестницей темновато, около окна светловато. Сломайте лестницу, закройте окно — освещение никто не изменит, поскольку его очень долго вычислять на базе современных алгоритмов рисования треугольников с помощью z-буфера. Доказывать тут нечего: если бы было легко, это давно бысделали, благо акселераторы уже весьма мощные. Источник света даже подвигать нельзя — как в таком доме жить?
Подойдём к проблеме с другой стороны. Уровень, вместе со всей предварительно просчитанной информацией, занимает весьма нехило — мегабайты. А если уровни нужно очень часто подгружать в многопользовательской игре по интернет?
Что?
Я решил создать графический движок, удовлетворяющий следующим требованиям: нет никакой предварительной обработки сцены, положение и количество источников света и объектов может меняться произвольным образом в любое время. То есть, каждый кадр рисуется как бы новая сцена. Это должно позволить создавать новые оригинальные игры и расширить известные жанры.
То есть, каждый кадр рисуется как бы новая сцена. Это должно позволить создавать новые оригинальные игры и расширить известные жанры.
Ничто не даётся задаром, всегда приходится чем-то жертвовать. Я пожертвовал представлением объектов посредством треугольников. В качестве базовых примитивов были выбраны сферы. То есть, объекты будут представляться не совокупностью треугольников, а совокупностью сфер.
Ясное дело, что как из треугольников, так и из сфер можно составить любой объект. Вопрос стоит лишь в количестве необходимых примитивов. Надо стараться обойтись как можно меньшим, иначе производительность упадёт ниже нижнего.
Почему в качестве примитивных элементов выбраны именно сферы, а в качестве метода — метод трассировки лучей? Дело в том, что при полигональном представлении объектов, треугольниками, например, очень много труда уходит на рассчет тени от объекта. Существуют разные методы — см. статью «Обзор алгоритмов построения теней в реальном времени». Они либо неявно требуют предварительную информацию об объекте, как метод теневых объёмов — иначе этот метод будет страшно долго работать на сложных объектах, либо требуют многократной отрисовки объекта (в текстуру) и нещадно эксплуатируют видео-ускоритель, как методы наложения теней с помощью проективных текстур. Отмечу ещё один их существенный недостаток, который не очень заметен в различных демонстрационных программах: если объект отбрасывает тень на удалённый предмет, то тень от него будет очень угловатой. Чтобы этого не случилось, объект необходимо отрисовывать в теневую текстуру с гигантским разрешением.
Отмечу ещё один их существенный недостаток, который не очень заметен в различных демонстрационных программах: если объект отбрасывает тень на удалённый предмет, то тень от него будет очень угловатой. Чтобы этого не случилось, объект необходимо отрисовывать в теневую текстуру с гигантским разрешением.
Shadowcast — демонстрационная программа от NVidia. Не самая новая, GF3 не требует.
Видимо, не случайно затеняемая площадка мала. Но всё равно заметно, как с увеличением расстояния от объекта до тени, тень огрубляется.
Далее, возникают проблемы с самозатенением объекта: когда объект отбрасывает тень сам на себя, а не на отделённый от него предмет. Эти проблемы носят на самом деле фундаментальный характер, в том смысле, что они органически присущи методу визуализации посредством отрисовки треугольников и применения z-буфера.
Рассчитывать тень от сферических объектов легко, рисовать сферы методом трассировки лучей тоже относительно легко — это и определило мой выбор.
Скорость трассировки лучей
Одним из свойств алгоритмов трассировки лучей заключается в большой зависимости скорости работы от разрешения экрана. Типичная формула времени работы выглядит таким образом: c1*n*ln(n)+c2*n*n+c3*ScreenWidth*ScreenHeight. c1, c2, с3 — некоторые константы, n-количество объектов на сцене. В первую очередь, рассмотрим главный член — c2*n*n, имеющий второй порядок по количеству объектов на сцене. Его происхождение просто: это время расчёта теней. Как ни крути, в этом вопросе от квадратичной зависимости далеко не уйти. Различные методы оптимизации, кластеризация объектов и т.п., в общем случае позволяют лишь уменьшить константу c2, не более. Этот член жестко лимитирует количество объектов на сцене. Начиная с некоторого момента, незначительное увеличение числа объектов вызывает очень большое падение производительности.
Влияние первого члена на общее время работы не очень существенно. Таким образом, когда сцена заполнена объектами в наибольшем возможном количестве, на первое место выходит последний член, зависящий от разрешения экрана. Эта величина отражает скорость собственно трассировки лучей, соответствующих точкам экрана. Это константа, но гигантская! Гигантская благодаря большой величине площади экрана в пикселях. Например, 800*600=480000, 1024*768=786432. Для современных процессоров получается всего около 100 тактов на обработку луча при частоте кадров около 25.
Эта величина отражает скорость собственно трассировки лучей, соответствующих точкам экрана. Это константа, но гигантская! Гигантская благодаря большой величине площади экрана в пикселях. Например, 800*600=480000, 1024*768=786432. Для современных процессоров получается всего около 100 тактов на обработку луча при частоте кадров около 25.
Некоторое недоумение вызывает независимость c3 от количества объектов. Дело в том, что анализ сцены перед запуском цикла трассировки позволяет существенно оптимизировать расчёты в самом цикле. За счёт этого, сколько бы ни было объектов на сцене, будет искаться пересечение луча с фиксированным количеством объектов. В принципе, с3 зависит от n, но этой зависимостью можно пренебречь.
Одним из главных последствий существования этой константы стала невозможность осуществления трассировки лучей в реальном времени на старых персональных компьютерах, оснащённых процессорами PentiumII и ниже. Эта константа даже на маленьких разрешениях — 400х300 — полностью съедала всю мощность процессора. Но сейчас этот барьер пройден! Производительности новейших процессоров для персональных компьютеров хватает для осуществления трассировки лучей в высоких разрешениях.
Но сейчас этот барьер пройден! Производительности новейших процессоров для персональных компьютеров хватает для осуществления трассировки лучей в высоких разрешениях.
Далее я приступаю к описанию созданного мною графического движка VirtualRay, умеющего рисовать только объекты из сфер, зато позволяющего радикально изменять сцену в реальном времени.
Движок VirtualRay
Рабочими разрешениями движка VirtualRay на процессорах Pentium III с SSE являются разрешения 640×480 и 800×600 с глубиной цвета 32бит, то есть, движок работает в true color.
Естественно, очень много произвольно расположенных сфер отрисовывать не получилось. С приемлемой скоростью рисуются сцены, состоящие из нескольких тысяч сфер. Соответственно, движок хорошо рисует те объекты, для которых представление сферами легко возможно. Например, космос: планеты, звёзды, космические корабли и космические станции. Чудовищ, инопланетян, иномирян и их жилища. Технические объекты. Символы, абстрактные создания и сюрреалистические миры.
Поддерживается наложение и билинейная фильтрация текстур, что обеспечивает качественное изображение.
В угоду быстродействию выбрана простейшая модель освещённости, все источники света считаются точечными.
Возможна прозрачность сфер, причём коэффициенты прозрачности могут динамически меняться, и могут быть различными для каждого цветового канала.
Источника света также могут быть цветными.
Движок может работать в произвольном разрешении, как 320×240 и ниже, так и 1600×1200 и выше. Весь вопрос в скорости работы.
Более описывать нет смысла, как говорится, лучше один раз увидеть, чем сто раз услышать. На сайте www.virtualray.ru, находится текущая демо-версия движка и скриншоты. Ввиду моих низких художественных и моделлерских способностей создать высокоэстетичную демо-версию со стильными текстурами не очень получилось, получилось — технологическую демо-программу. Однако, её можно использовать в качестве игрушечного строительного конструктора из шаров.
Для ознакомления с демкой требуется компьютер с процессором PentiumMMX и выше и видео-карточка, поддерживающая true color в 32-битном формате. (совместимости с Intel 740 нет, так как там true color только в формате 24 бита. Но практически все современные карточки поддерживают необходимый формат). Одно замечание: иногда формат представления цвета в видеокарте определяется неправильно и, например, небо получается желтым вместо голубого. В этом случае рекомендуется угадать и выбрать в меню более подходящий формат. Так как на больших мониторах низкие разрешения выглядят слишком зернисто, для повышения быстродействия вместо уменьшения разрешения лучше слегка уменьшить площадь экрана.
Ниже я приведу несколько скриншотов из демо-версии. Они весьма неполно передают возможности движка, так как одним из его достоинств является динамическая игра света и тени, непередаваемая статическим изображением.
Производительность
Частота кадров — показатель, на который обращают внимание в первую очередь. Мы ещё коснёмся производительности движка на различных системах, сейчас же рассмотрим показатели на системе на базе PentiumIII800EB. Отмечу, так как движок не использует видео-ускорители, его производительность практически полностью определяется мощностью процессора.
Мы ещё коснёмся производительности движка на различных системах, сейчас же рассмотрим показатели на системе на базе PentiumIII800EB. Отмечу, так как движок не использует видео-ускорители, его производительность практически полностью определяется мощностью процессора.
Типичная частота кадров — 20 в разрешении 800x600x32 (800x450x32). Вроде бы совсем не впечатляет на сегодняшний день. Однако, FPS движка обладает двумя очень полезными свойствами, которые отчасти компенсируют её относительно небольшую величину. Первое свойство заключается в близости минимального и среднего FPS. Среднее FPS может быть 25, а минимальное — 22. А минимальное FPS, это даже более важный параметр, чем среднее. Во многих играх когда ходишь — частота кадров около 50, а только начнётся стрельба, враги появятся, FPS сразу упадёт вдвоё и больше.
Второе важное свойство — стабильность частоты кадров. Что это такое? Допустим, есть 50 кадров в секунду. Вроде бы, много. По идее, каждый кадр отрисовывается за 20 миллисекунд. Но в реальности некоторые кадры могут рендерится значительно дольше 20 миллисекунд, а другие — соответственно быстрее. В частности, такое может быть из-за необходимости периодически кэшировать данные, например, при повороте камеры. В результате, при формально высоком среднем FPS движение может не быть плавным. Движок VirtualRay рисует кадры независимо и демонстрируемый FPS реалистичен.
Но в реальности некоторые кадры могут рендерится значительно дольше 20 миллисекунд, а другие — соответственно быстрее. В частности, такое может быть из-за необходимости периодически кэшировать данные, например, при повороте камеры. В результате, при формально высоком среднем FPS движение может не быть плавным. Движок VirtualRay рисует кадры независимо и демонстрируемый FPS реалистичен.
В общем, для чемпионата профессиональных квакеров не подойдёт, но играть вполне возможно. Особенно в игры, жанр которых не требует исключительно стрельбы.
Хочу также отметить, что не все оптимизирующие алгоритмы проверены, не все оптимизирующие алгоритмы придуманы. Я надеюсь, что ещё удастся увеличить скорость работы движка.
Устройство Сферического движка
Сферический движок почти полностью основан на алгоритмах, хорошо известных в компьютерной графике и многократно и детально описанных в книжках, посвящённых методу трассировки лучей. Мне практически не пришлось придумывать оригинальные алгоритмы, только адаптировать известные к сферам и real-time. Я отсылаю заинтересованного читателя, например, к книжке Е.В. Шикина, А.В. Борескова «Компьютерная графика. Динамика, реалистические изображения» Москва.: «Диалог-МИФИ». В интернете можно найти достаточно примеров из этой книжки. Видимо, где-то есть и текст. Если же у вас нет трудностей при чтении английских текстов, то просто море информации о трассировке лучей к вашим услугам в англоязычном интернете. Правда, я в большей степени основывался на знаниях из учебника по аналитической геометрии.
Я отсылаю заинтересованного читателя, например, к книжке Е.В. Шикина, А.В. Борескова «Компьютерная графика. Динамика, реалистические изображения» Москва.: «Диалог-МИФИ». В интернете можно найти достаточно примеров из этой книжки. Видимо, где-то есть и текст. Если же у вас нет трудностей при чтении английских текстов, то просто море информации о трассировке лучей к вашим услугам в англоязычном интернете. Правда, я в большей степени основывался на знаниях из учебника по аналитической геометрии.
Рассмотрим принципиальную схему работы движка. Engine разбит на две существенно различающиеся части: в первой части осуществляется предварительный анализ сцены, вторая часть — двойной цикл трассировки лучей, отвечающих точкам экрана.
На входе движок получает описание сцены: положение и свойства сфер, расположение и параметры источников света. Эти данные попадают в блок первичного анализа — первую часть блока предварительного анализа сцены. В нём происходит отсечение не попавших в кадр сфер и источников света, зоны действия которых не видны.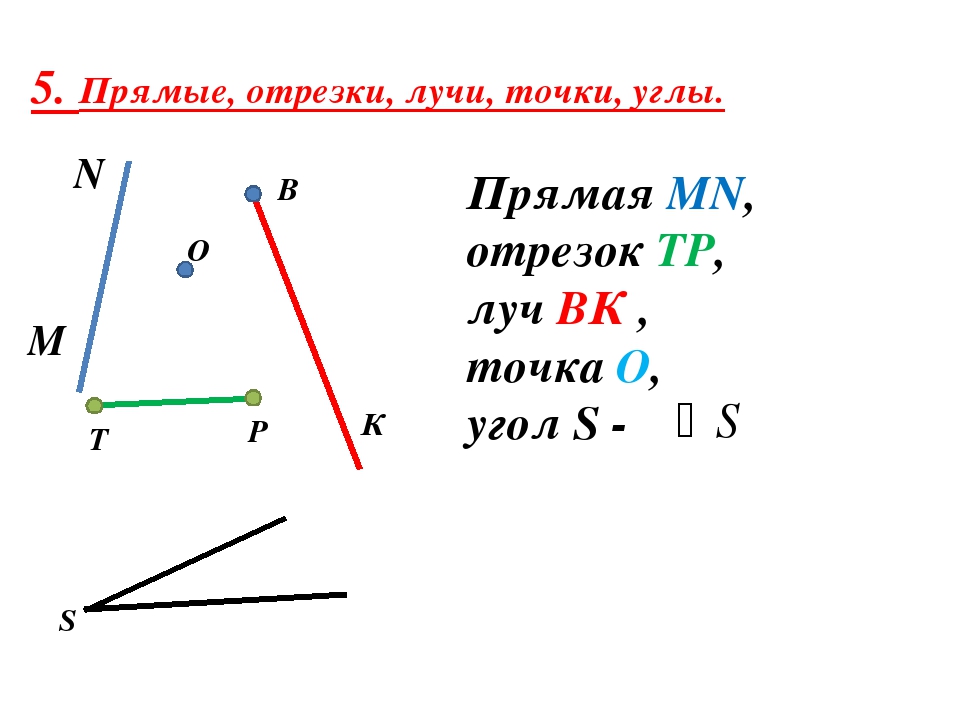 Происходит приведение координат объектов относительно положения наблюдателя, рассчитываются часто используемые далее величины, вроде расстояний до сфер.
Происходит приведение координат объектов относительно положения наблюдателя, рассчитываются часто используемые далее величины, вроде расстояний до сфер.
Далее начинает работу блок распределения сфер по областям экрана. Экран разбивается на много прямоугольных областей, для каждой из которых вычисляется массив потенциально видимых сфер. То есть тех сфер, с которыми могут пересечься лучи, отвечающие точкам экрана, составляющим данную область.
Путём измельчения областей можно добиться, что бы почти на любую область приходилось всего несколько сфер, что сильно снижает затраты в гигантском цикле трассировки лучей.
Затем осуществляется расчёт отношения затенённости. Для каждой сферы определяется, сколько источников света её освещают. Если их много, то выбираются несколько, вносящие основной вклад в освещённость.
Для каждой сферы находятся все сферы, затеняющие её. Это несложно сделать благодаря простоте геометрической формы сферы. Теперь, когда затенители определены, точка сферы в цикле трассировки проверяется на затенение лишь ограниченным кругом сфер. Информация о затеняющих сферах, как то относительное положение и расстояние, упаковывается в оптимальный для вычислений при помощи SSE. Подробно об оптимизации под SSE — позднее.
Информация о затеняющих сферах, как то относительное положение и расстояние, упаковывается в оптимальный для вычислений при помощи SSE. Подробно об оптимизации под SSE — позднее.
Всё, можно запускать цикл трассировки.
Замечание к реализации. Первая часть, реализующая сложные и разнообразные алгоритмы, целиком написана на языке C++. Вторая часть, исходный код которой значительно меньше в размере, полностью написана на ассемблере и имеет три варианта, написанные для различных процессоров. Варианты различаются набором используемых команд. Оптимально использование SSE, но возможна работа и на компьютерах без SSE, необходима только поддержка технологии MMX. Конечно, на стареньком Pentium166MMX программа будет работать в режиме слайд-шоу, но в маленьком окошке можно посмотреть.
| Набор команд | Процессоры |
|---|---|
| SSE + Enhanced MMX | Pentium III, Pentium4, Celeron II, AthlonXP |
| FPU + Enhanced MMX | Athlon, Duron, (K6-III, K6-2+) |
| FPU + MMX | Pentium MMX, Pentium II, Celeron, K6-2 |
Отмечу, что для работы с вещественными числами используется SSE/FPU, для работы с целыми числами и числами с фиксированной точкой используется MMX.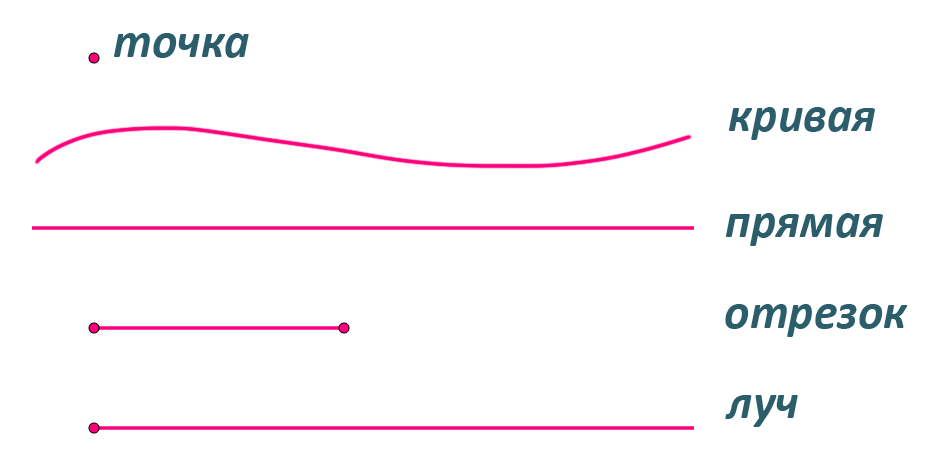 Обычные регистры (eax, ebx, ecx, edx, esi, edi) используются для хранения и вычисления адресов и флагов.
Обычные регистры (eax, ebx, ecx, edx, esi, edi) используются для хранения и вычисления адресов и флагов.
Программа откомпилирована при помощи IntelC++Compiler4.5, встроенного в Microsoft Visual C++ 6.0.
Области применения Сферического движка
Где можно использовать столь необычный движок, очень хорошо делающий одно и крайне плохо другое? Область применения сферического движка можно разделить на две части: использование в компьютерных играх и применение в иных целях. Начнём с не совсем игровых приложений.
Очевидно узкоспециальное приложение к визуализации моделей молекул и атомов. Правда, тени там выглядят неуместными: атом ведь не шарик. Описание шара занимает даже меньше места, чем описание треугольника, а шар всё-таки более богатая фигура. Это наталкивает на мысль о применении движка в интернете. Можно рисовать и легко пересылать эмблемы, логотипы, символические анимированные сценки. Для этих целей производительности движка вполне хватит — это же не на полный экран выводить сцену с большой частотой кадров. Плюс — практически полная независимость от видео-карточки: не нужно возится с драйверами, не нужно тестировать на миллионе конфигураций, не нужно обращать внимание на поддержку операционной системой графических библиотек. Есть ли DirectX, какая версия OpenGL — все эти вопросы особой роли не играют. Обеспечивается идентичность изображения у всех пользователей, с точностью до монитора, конечно. Это не так, как у видео-ускорителей: один поддерживает одно, другой — другое. На одном тени видны, на другом — нет, на третьем видны, но жутко тормозят.
Плюс — практически полная независимость от видео-карточки: не нужно возится с драйверами, не нужно тестировать на миллионе конфигураций, не нужно обращать внимание на поддержку операционной системой графических библиотек. Есть ли DirectX, какая версия OpenGL — все эти вопросы особой роли не играют. Обеспечивается идентичность изображения у всех пользователей, с точностью до монитора, конечно. Это не так, как у видео-ускорителей: один поддерживает одно, другой — другое. На одном тени видны, на другом — нет, на третьем видны, но жутко тормозят.
Плавно перейдём в другую область применения движка. Онлайновые игры через интернет — вот где замечательно проявляются достоинства сферического движка. Как хорошо в многопользовательских играх дать возможность участникам в полном 3D в режиме реального времени строить и разрушать игровой уровень по своему усмотрению! И относительная низость FPS не так важна — всё равно связь мешает точному прицеливанию. Да и суть многопользовательской игры не всегда полностью состоит из одной стрельбы.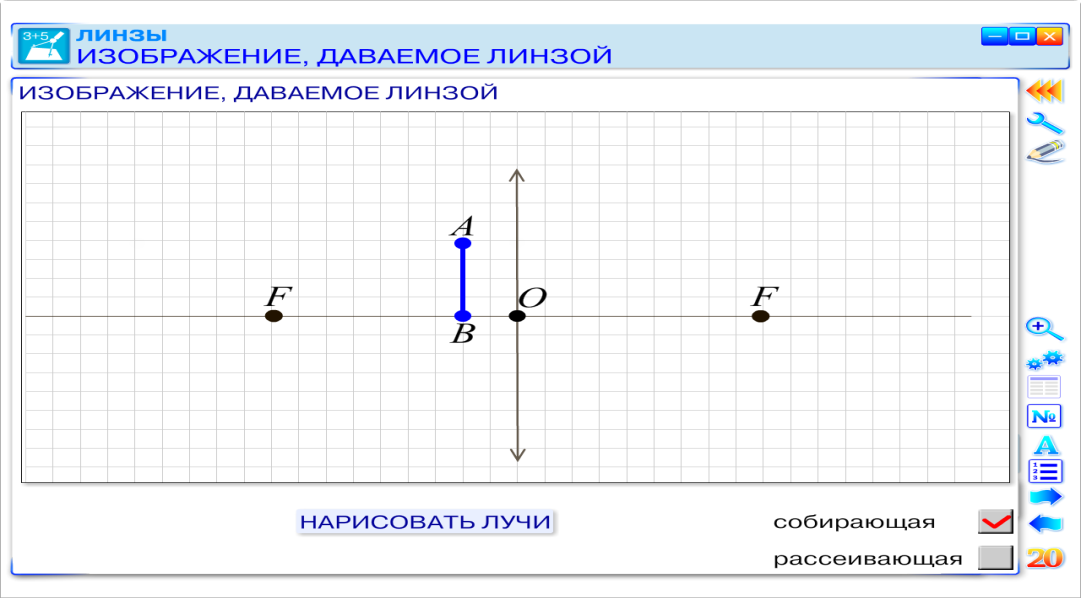
Игровую вселенную можно разбить на анклавы, представленные автономными сценам, между ними организовать какие-нибудь гиперпереходы. При перемещении новая сцена будет грузиться мгновенно.
Космические симуляторы любых видов — ещё одно поле приложения движка VirtualRay. Планетные системы, астероидные поля, космические аппараты — всё это прекрасно изображается при помощи сфер. Можно составить этакую «Звезду Смерти» и взорвать её при необходимости.
Игры аркадного толка также вполне могут базироваться на Сферическом движке.
Возможны приложения в играх экзотических жанров. Например, в играх, основанных на конструировании механизмов или создании живых существ.
CPU MultiMedia 3D Test!
Есть ещё одно, самое очевидное, приложение Сферического движка. Производительность — это палка о двух концах: можно измерять скорость работы программы на данной системе, а можно — тестировать производительность системы при помощи измерения скорости работы данной программы. В демо-версию встроен CPUMultiMedia3DTest! — графический тест производительности подсистемы процессор + память. Сейчас я расскажу о специфике и преимуществах данного теста, и мы также коснёмся вопроса быстродействия программы на процессорах PentiumIII и AthlonMP. Читатели, не интересующиеся тестированием процессоров, могут пропустить этот раздел.
В демо-версию встроен CPUMultiMedia3DTest! — графический тест производительности подсистемы процессор + память. Сейчас я расскажу о специфике и преимуществах данного теста, и мы также коснёмся вопроса быстродействия программы на процессорах PentiumIII и AthlonMP. Читатели, не интересующиеся тестированием процессоров, могут пропустить этот раздел.
CPU MultiMedia 3D Test! — это тест процессора с точки зрения геометрических расчётов.
Графическое приложение, будь то студия трёхмерной графики или графический движок трёхмерного шутера, принципиально есть реализация на компьютере решения некоторой геометрической задачи. А решение любой геометрической задачи в конечном итоге разбивается на простые операции — в первую очередь, скалярное произведение векторов, вычисление нормы вектора, операции сложения-умножения векторов и матриц.
Ещё раз, эти операции постоянно повторяются в любом графическом приложении, более того, основная вычислительная нагрузка приходится именно на их выполнение.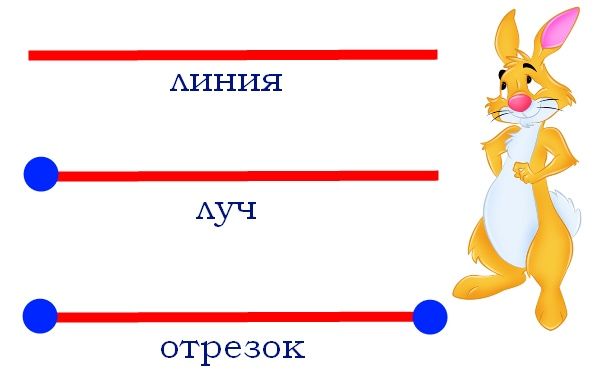
Данный тест как раз и предназначен для определения производительности процессора в такого рода задачах.
Тест основан на измерении скорости отрисовки сцены графическим движком «VirtualRay». Как уже упоминалось, этот движок построен на методе обратной трассировки луча и не использует видеоускорители. В процессе его работы выполняется огромное количество сложных геометрических расчётов.
Полная «софтовость» движка позволяет практически полностью нивелировать влияние видеосистемы, скорости прокачки текстур через AGP и т.п. на результаты тестирования. Таким образом, получается чистая производительность системы процессор + память.
Особенности различных вариантов блока трассировки лучей (второй составляющей движка)
Как уже отмечалось выше, написанный на ассемблере цикл трассировки лучей имеет три варианта, отличающиеся набором используемых команд. SSE+EMMX вариант, FPU+EMMX вариант, FPU+MMX вариант.
Движок изначально проектировался с ориентацией на технологию SSE (Streaming SIMD Extension), так что SSE+MMX вариант полностью использует возможности SSE, там данные организованы специальным образом, мало переходов, используется инструкция предварительного кэширования данных, хранения часто используемых операндов в регистрах SSE. В этой части вообще нет команд FPU, поэтому использование MMX не вызывает обычных затруднений из-за несовместимости с FPU.
В этой части вообще нет команд FPU, поэтому использование MMX не вызывает обычных затруднений из-за несовместимости с FPU.
В FPU вариантах вместо SSE используется FPU, происходит постоянный swap регистров FPU в память, поскольку вместимость регистров FPU в четыре раза меньше, чем регистров SSE, и доступ к ним затруднён из-за стековой организации. Совершаются также лишние операции сохранения/восстановления регистров MMX и переключения из режима MMX в режим FPU и обратно.
В FPU+MMX режиме дополнительно к режиму FPU+EMMX происходит эмуляция недостающих в MMX команд EMMX, что вызывает дополнительную нагрузку на блок MMX и дополнительный swap MMX регистров.
Ввиду специальной оптимизации под SSE и отсутствия команд FPU, первый вариант является хорошим тестом качества реализации SSE.
Использование MMX
С помощью MMX происходит работа с цветом, в первую очередь, текстурирование, билинейная фильтрация и т.п. В связи с этим, если сцену выводить без текстур, то влияние MMX части будет крайне незначительно на общую производительность.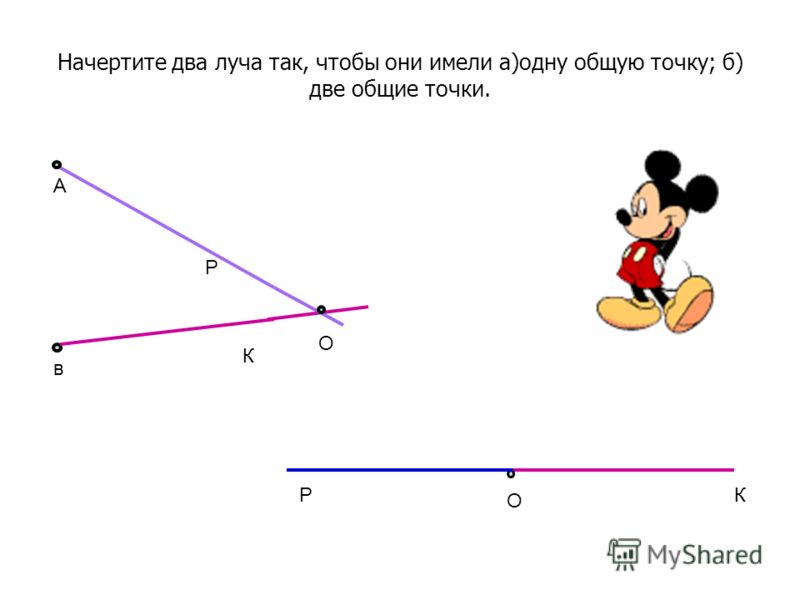 Будет также уменьшено влияние памяти, так как выборка элемента текстуры может приводить к задержкам.
Будет также уменьшено влияние памяти, так как выборка элемента текстуры может приводить к задержкам.
Таким образом, можно получить индекс производительности MMX — выводить сцену одинаковой геометрии, текстурированной и без текстур, и сравнивать результаты. И это несмотря на слитность MMX кода и других частей программы.
Метод измерения
Для получения результатов измеряется среднее время работы различных блоков движка на некотором периоде времени при отрисовке динамической сцены. Движение сцены синхронизировано с течением реального времени и не зависит от fps. Таким образом, в разное время несколько изменяется характер вычислительной нагрузки.
Конечный индекс производительности есть обратная величина среднего времени работы соответствующего блока при отрисовке одного кадра.
- FPUС++ Index — первая часть движка, которая написана на C++
- SSE+EMMX Index — соответствующий вариант второй части движка.
- FPU+EMMX Index — соответствующий вариант второй части движка.

- FPU+MMX Index — соответствующий вариант второй части движка.
- Overall Index — совместное время работы двух блоков.
Этот результат можно интерпретировать как fps, который был бы, если бы работала только данная часть. Поскольку основная вычислительная нагрузка, как правило, приходится на цикл трассировки лучей (вторая составляющая), то её индекс близок к реальному fps. Однако, можно создать такую сцену, где бы большая часть нагрузки приходилась на первый блок анализа сцены.
Отметим, что реальный fps зависит от дополнительных факторов, как то синхронизация переключения страниц с частотой обновления монитора, времени работы процедуры изменения сцены и т.д.
Интерпретация
FPUС++ Index отражает производительность системы при выполнении сложных, вычислительно тяжёлых алгоритмов, насыщенных ветвлениями. Алгоритмов, написанных на языках высокого уровня без всякой SIMD оптимизации.
SSE+MMX Index отражает производительность SSE (+EMMX) в задачах 3D-графики на специально оптимизированном под SSE коде, с минимальным количеством переходов, при использовании оптимальной для SSE организации данных.
FPU+EMMX, FPU+MMX Index есть индекс производительности FPU (+MMX) в геометрических — графических приложениях, интенсивно работающих с векторами, матрицами и рисующих изображения.
Overall Index — комплексный показатель производительности системы.
Результаты тестов Pentium III, Athlon MP, Pentium 4, Athlon XP, etc
Мне пока не удалось провести обширного тестирования различных процессоров. Но это тестирование идет и во второй части этой статьи я представлю массу цифр и графиков, а также дам комментарии.
Замечание об акселераторах
Мне могут возразить и возразят, что нынешние самые современные видео-ускорители всё равно круче. Скоро, мол, цена на gf3 упадёт до 50$, никакой сферический движок не будет нужен. В ответ я хотел бы ответить следующее: с научно-исследовательской точки зрения некорректно сравнивать производительность программно реализованных алгоритмов, и ,так сказать, hardware accelerated алгоритмов. Может быть, если бы рейтрейсинг ускоряли с помощью железа, то такая производительность была бы — закачаешься.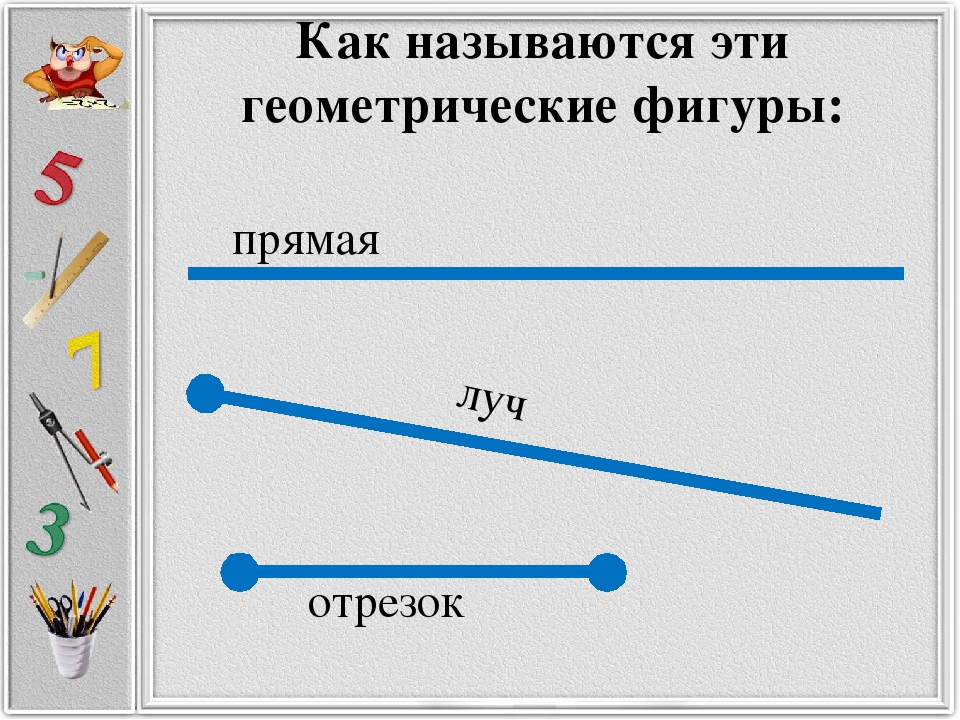
Давайте сравнивать с программными движками, базирующимися на отрисовке треугольников при мощи z-буфера. C QuakeI и Unreal. Unreal, кстати, разрабатывался как софтовый движок, там, между прочим, применили продвинутый метод программного сглаживания текстур. В нём до сих пор остались следы этой первоначальной ориентации.
Quake неплохо работает, в отличии от Сферического движка, на старых компьютерах, и на новых PentiumIII показывает более высокий FPS. Но динамического освещения, теней, сглаженных текстур и true color там и близко нет. Как его возможности расширить до возможностей движка VirtualRay, совершенно не видно. Отмечу, что Сферический движок тоже не очень-то расширишь до QI. То есть, они не сравнимы.
Unreal, вроде бы, более развитый движок, чем QI, но скорость его работы гораздо ниже. В высоких разрешениях (640x480x16, 800x600x16) средний FPS около 20, минимальный вообще бывает около 15. Ничего принципиально нового там не появилось. И качество изображения всё равно оставляет желать лучшего.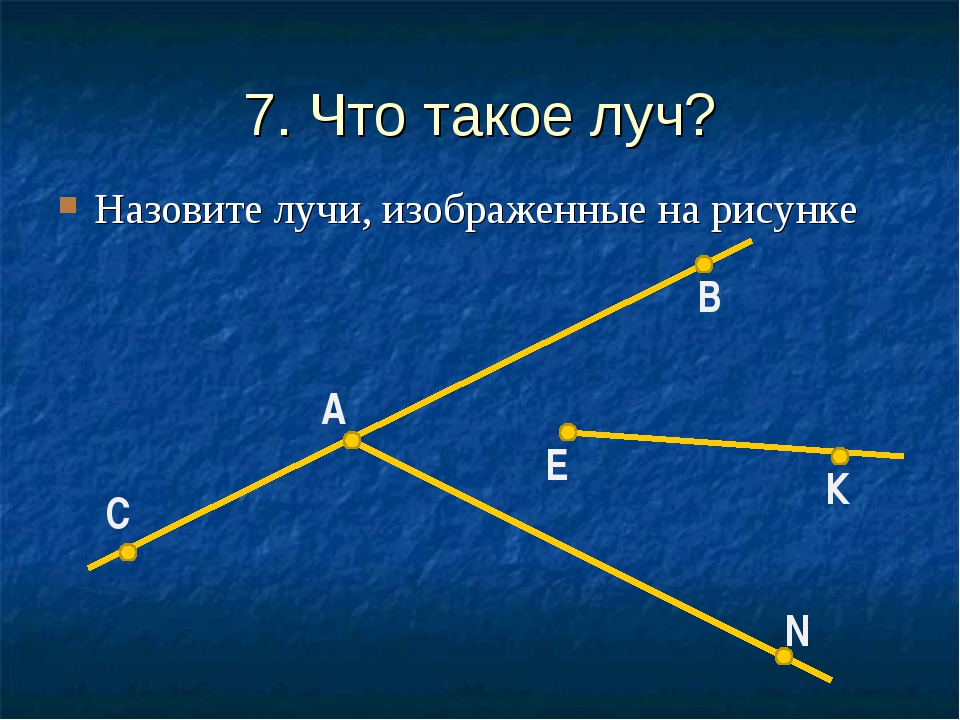
Возможно, как раз тогда индустрия зашла в алгоритмический тупик, но появление видео-ускорителей разрешило экстенсивное развитие, развитие не в глубь, а вширь. В течение довольно долгого периода времени почти все усовершенствования сводились к увеличению числа полигонов в кадре. Ничего принципиального не добавлялось.
Гораздо интереснее рассмотреть аспекты совместной работы Сферического движка и 3D-акселераторов. Принципиально можно часть изображения и специальные эффекты нарисовать с помощью ускорителя и обогатить изображение. Конечно, частично теряется независимость движка, но, в некоторых случаях это, может быть оправдано. Однако, как всегда и бывает, искусственные препоны мешают делу. Отсутствие интерфейса чтения/записи в z-буфер ускорителя сильно затрудняет совмещение изображений. Объекты, нарисованные различными методами, не будут правильно заслонять друг друга. Тем не менее, готовится версия движка, умеющая рисовать при помощи акселератора разнообразные эффекты, сияния вокруг источников света, частицы и т.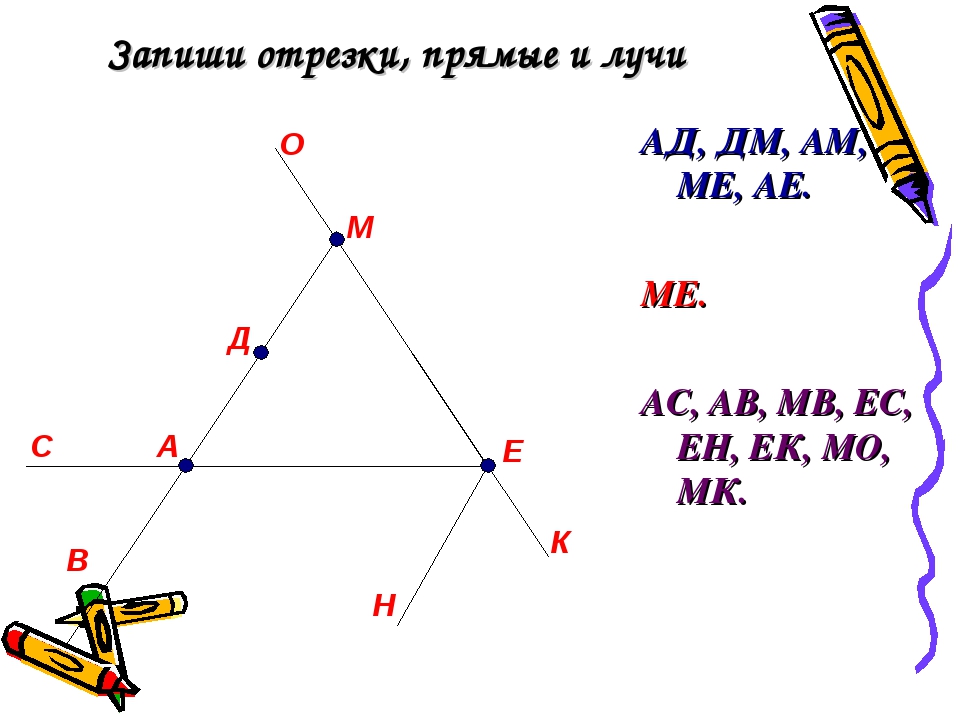 п.
п.
Оптимизация под SSE
Достижение приемлемой производительности в высоких разрешениях стало возможно в первую очередь благодаря оптимизации под набор команд SSE. На процессорах без SSE программа выглядит бледно.
SSE — Streaming SIMD Extension. Потоковое SIMD расширение, если дословно переводить. SIMD — Single Instruction Multiple Data. Одна инструкция выполняет действия сразу с несколькими операндами.
Специфика движка состоит в том, что сотни тысяч раз выполняется процедура трассировки луча, и этот цикл занимает больше всего времени. Эту относительно небольшую процедуру и необходимо оптимизировать в первую очередь, поскольку самый небольшой выигрыш скорости умножается многократно.
В движке использовано два основных приёма оптимизации: специальная организация данных для SIMD технологии и хранение данных непосредственно в регистрах SSE.
Рассказ о SSE
Чтобы было более понятно, я приведу небольшой рассказ про SSE. Подробная спецификация команд SSE доступна на сайте корпорации Intel, в книжных магазинах уже давно появились книги, описывающие предмет. Я же расскажу в общем.
Я же расскажу в общем.
Итак, к стандартной архитектуре добавились 8 новых регистров. Это регистры прямого доступа, в отличие от регистров FPU, которые организованы в стек, что существенно усложняет программирование на ассемблере для FPU. В терминах языка C регистры имеют тип float[4] float=single — число одинарной точности, занимающее 4 байта. Таким образом, общий размер SSE регистров целых 128 байт, 32 числа с плавающей точкой, в 4 раза больше, чем FPU. FPU, правда, умеет работать с числами с повышенной точностью, но в движке они не используются.
С этими регистрами возможны следующие действия: загрузить/ выгрузить в память, перетасовать элементы одного или двух регистров. Например, первые два элемента одного регистра заменят последние два другого. Арифметические действия (сложение, вычитание, умножение, деление) с парой регистров как с векторами, то есть, операции производятся поэлементно. Извлечение квадратного корня из каждого элемента регистра и нахождение приближённого значения обратной величины и обратной к квадратному корню величины.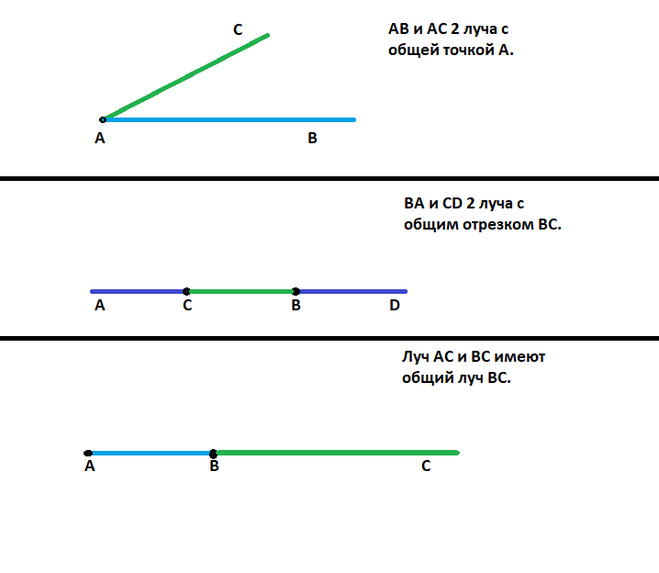
Покомпонентное сравнение двух регистров и покомпонентное нахождение максимума и минимума.
Конвертация в целое число, причём можно сразу записать значение в MMX регистр.
Побитовые логические операции с регистрами, как с последовательностью бит. Регистры как бы имеют тип bool[128].
Инструкции загрузки в кэш данных, которые будут востребованы позже. Эти инструкции призваны предотвращать простой процессора в ожидании данных из памяти.
Почти все вышеупомянутые операции можно так же проводить с одними (одним) первыми элементами регистров. Это сделано, в первую очередь, для удобства.
Обобщая, можно сказать, что добавлены команды для выполнения арифметических операций с четырёхмерными векторами и вспомогательные инструкции.
Основа оптимизации программы под SSE — такая организация кода, чтобы было естественно выполнение одной арифметической операции над четырьмя независимыми парами операндов.
Какие к этому могут быть препятствия? Вообще-то, далеко не всегда подряд выполняются четыре однотипные операции, четыре сложения или четыре умножения. Но это ещё полбеды, операции можно переставить. Очень часто проведение последующей операции зависит от результата предыдущих. Например, между двумя сложениями стоит сравнение и ветвление.
Но это ещё полбеды, операции можно переставить. Очень часто проведение последующей операции зависит от результата предыдущих. Например, между двумя сложениями стоит сравнение и ветвление.
Наиболее естественная область приложения SSE — оптимизация как раз линейной алгебры. Умножение-сложение матриц от 4×1 до 4×4 — «любимые» операции SSE. Там нет ветвлений и действия однотипны.
Для поддержки разработчиков Intel выпустил специальную библиотеку — Small Matrix Library. В ней реализованы класс матрица, класс вектор. Операторы, отвечающие арифметическим действиям, реализованы как inline функции, написанные в кодах SSE. Есть и FPU вариант, и при компиляции можно указывать целевую платформу. Очень удобно, можно сразу получить два варианта: для процессоров с SSE и без. И при разработке вообще не думать ни о каком SSE, просто использовать классы, отвечающие матрицам и векторам. Благо, IntelC++Compiler для всех операторов искусно вставит SSE-оптимизированный код.
В дистрибутив Small Matrix Library (SML) входит интересная программа, демонстрирующая преимущества SML. Она считает время выполнения операции при оптимизации под SSE и FPU.
Она считает время выполнения операции при оптимизации под SSE и FPU.
Ниже я привожу её лог.
| Операция | SSE/FPU | Время выполнения* |
|---|---|---|
| 3×3 * 3×1 | FPU | 31 |
| 3×3 * 3×1 | SSE | 29 |
| Transpose(3×3) * 3×1 | SSE | 23 |
| 4×4 * 4×1 | FPU | 53 |
| 4×4 * 4×1 | SSE | 31 |
| Transpose(4×4) * 4×1 | SSE | 27 |
| 3×3 * 3×3 | FPU | 79 |
| 3×3 * 3×3 | SSE | 59 |
| 4×4 * 4×4 | FPU | 172 |
| 4×4 * 4×4 | SSE | 90 |
| 6×6 * 6×1 | FPU | 113 |
| 6×6 * 6×1 | SSE | 60 |
| 6×6 * 6×6 | FPU | 652 |
| 6×6 * 6×6 | SSE | 307 |
| 4×4 * 4×4 (general case) | SSE | 529 |
| Inverse 4×4 | FPU | 392 |
| Inverse 4×4 | SSE | 209 |
| Inverse 6×6 | FPU | 1118 |
| Inverse 6×6 | SSE | 600 |
*Время выполнения указано в тактах процессора. Замеры производились на PIII 800EB.
Замеры производились на PIII 800EB.
Отмечу, что при замерах все данные находились в кэше.
Необходимые пояснения. 4×4 * 4×4 (general case) — 4×4 матрицы перемножаются как mxn матрицы, с использованием циклов. В остальных случаях размер матриц известен заранее, что позволяет избавиться от циклов и добиться таким образом серьёзной оптимизации.
Проанализируем результаты. Первое, что бросается в глаза, это маленькое различие в скорости между SSE и FPU вариантами 3×3 * 3×1 и неожиданная прибавка производительности в случае транспонирования матрицы. Это объясняется необходимостью в одном из вариантов дополнительно тасовать содержимое регистров, что бы строки матрицы правильно «легли» для умножения на вектор.
Естественен разрыв относительного выигрыша в производительности между умножениями трёхмерных и чётырёхмерных матриц. Напомню, что регистры SSE четырёх элементные.
Тем не менее, в части движка, написанной на C++, SML почти не используется. Дело в том, что в блоке предварительного анализа сцены мало умножений и обращений матриц и много ветвлений. В основном, только умножение трёхмерной матрицы на вектор. И вектора, в основном, трёхмерные. Ввиду этого, я решил сконцентрироваться на оптимизации под SSE процедуры трассировки луча.
В основном, только умножение трёхмерной матрицы на вектор. И вектора, в основном, трёхмерные. Ввиду этого, я решил сконцентрироваться на оптимизации под SSE процедуры трассировки луча.
Выше было написано, что в SSE есть, теперь надо сказать, чего в SSE нет. Там нет простой реализации главной для локальной геометрии пространства, в котором мы живём, операции — скалярного произведения трёхмерных векторов.
Чтобы эффективно выполнять эту операцию при помощи SSE, надо восемь векторов поставить на попа и загнать в таком виде в регистры SSE. Тогда можно тремя умножениями и двумя сложениями получить значения четырёх скалярных произведений.
| 4 элемент | 3 элемент | 2 элемент | 1 элемент | Регистр SSE |
|---|---|---|---|---|
| XMM7 | ||||
| XMM6 | ||||
| VectorB4.x | VectorB3.x | VectorB2.x | VectorB1.x | XMM5 |
VectorB4. y y | VectorB3.y | VectorB2.y | VectorB1.y | XMM4 |
| VectorB4.z | VectorB3.z | VectorB2.z | VectorB1.z | XMM3 |
| VectorA4.x | VectorA3.x | VectorA2.x | VectorA1.x | XMM2 |
| VectorA4.y | VectorA3.y | VectorA2.y | VectorA1.y | XMM1 |
| VectorA4.z | VectorA3.z | VectorA2.z | VectorA1.z | XMM0 |
Ввиду этого, при помощи SSE оптимизирована только процедура обработки луча, зато она целиком написана на ассемблере, вообще без применения FPU, и скалярные произведения вычисляются оптимальным образом. Соответственно, данные, например, информация о затенителях сфер, записаны в оптимальном для загрузки в SSE-регистры виде, что обеспечивает наилучшую производительность.
Сравнение SSE, SSE2, 3DNow!, 3DNow!Pro
Проведём теперь сравнительный анализ различных SIMD-расширений процессорных команд. 3DNow! — SIMD-расширение от AMD, впервые появившееся в процессорах k6-2. С появлением новых процессоров AMD 3DNow! пополнялось новыми командами, но принципиальных изменений не происходило. Главных отличий от SSE два: регистры 3DNow! двухэлементные, а не четырёхэлементные, как регистры SSE. Можно сказать, имеют тип float[2]. И набор команд аналогичен SSE, только они работают с двумя парами операндов. И второе отличие: 3DNow! и FPU не могут работать параллельно, приходится вызывать специальную довольно медленную команду переключения в режим FPU с потерей всего содержимого регистров 3DNow!, так как они физически совпадают с регистрами FPU. И MMX тоже особенно не попользуешься, поскольку MMX приходится делить с 3DNow! все те же 8 регистров.
С появлением новых процессоров AMD 3DNow! пополнялось новыми командами, но принципиальных изменений не происходило. Главных отличий от SSE два: регистры 3DNow! двухэлементные, а не четырёхэлементные, как регистры SSE. Можно сказать, имеют тип float[2]. И набор команд аналогичен SSE, только они работают с двумя парами операндов. И второе отличие: 3DNow! и FPU не могут работать параллельно, приходится вызывать специальную довольно медленную команду переключения в режим FPU с потерей всего содержимого регистров 3DNow!, так как они физически совпадают с регистрами FPU. И MMX тоже особенно не попользуешься, поскольку MMX приходится делить с 3DNow! все те же 8 регистров.
Сразу отмечу, размер регистров — 2 у 3DNow! и 4 у SSE — довольно косвенно связан с быстродействием. Он, скорее, влияет на программирование под эти расширения. Рассмотрим это влияние. Двухэлементные регистры легче полностью использовать, чем четырёхэлементные. Нужно тратить меньше усилий на организацию данных. В 3DNow! есть полезная возможность складывать между собой два элемента одного регистра, чего нет в SSE. Видимо, это следствие меньшего размера регистров. В SSE нельзя легко сложить между собой все четыре элемента, что очень сильно затрудняет программирование. Зато если уж организовали данные нужным образом, то больший объём регистров SSE позволяет обойтись меньшим числом команд. Далее, больший объём позволяет хранить часто используемые операнды в регистрах SSE, что затруднительно при использовании 3DNow!
Видимо, это следствие меньшего размера регистров. В SSE нельзя легко сложить между собой все четыре элемента, что очень сильно затрудняет программирование. Зато если уж организовали данные нужным образом, то больший объём регистров SSE позволяет обойтись меньшим числом команд. Далее, больший объём позволяет хранить часто используемые операнды в регистрах SSE, что затруднительно при использовании 3DNow!
AMD выпустила специальную библиотеку для работы с векторами, в которой векторные и матричные операции реализованы inline функциями, написанными на 3DNow! Выше было рассказано об аналогичной библиотеке SML от Intel. Так вот, библиотека AMD гораздо лучше оптимизирована для работы с трёхмерными векторами и матрицами, и скалярное произведение векторов тоже существенно лучше реализовано. В библиотеке SML, по всей видимости, скалярное произведение векторов вообще реализовано с помощью FPU.
SSE2-развитие SSE в процессорах Pentium4. SSE2 использует те же регистры, что и SSE, но теперь они имеют тип double[2].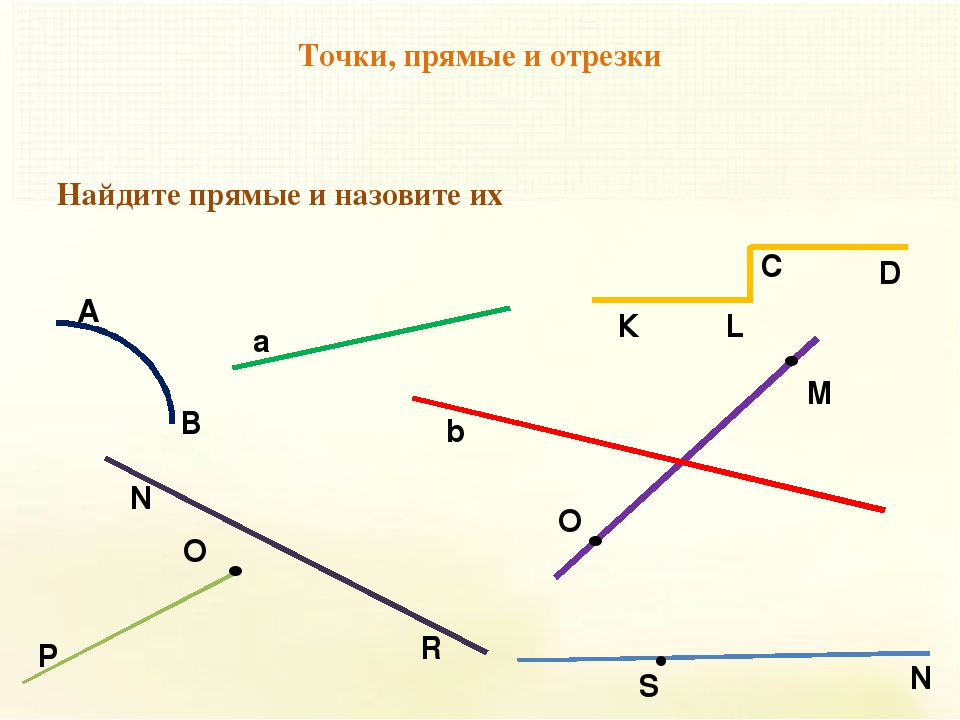 Набор команд, соответственно, аналогичен SSE. В SSE2 появились также команды для работы с целыми числами, регистры интерпретируются как имеющие тип int с различной разрядностью. Этакий Double MMX (регистры SSE2 имеют размер 128 бит, в два раза больше, чем 64 — размер регистров MMX).
Набор команд, соответственно, аналогичен SSE. В SSE2 появились также команды для работы с целыми числами, регистры интерпретируются как имеющие тип int с различной разрядностью. Этакий Double MMX (регистры SSE2 имеют размер 128 бит, в два раза больше, чем 64 — размер регистров MMX).
SSE2 получился аналогичен 3DNow! только работает не с float, а с double.
Рассмотрим, наконец, 3DNowProfessional — продолжение 3DNow! в самых последних процессорах AMD — AthlonXP, AthlonMP. Самое важное, что в 3DNowPro включили SSE, так что теперь SSE поддерживают новейшие процессоры всех основных производителей. Вместе с введением поддержки SSE, AMD в который раз расширило 3DNow!, добавив туда команды, облегчающие работу с регистрами 3DNow! в случае их интерпретации как комплексных чисел. Действительно, двухэлементный регистр 3DNow!, естественно, представлять содержащим действительную и мнимую части комплексного числа. Комплексные числа используются в преобразованиях Фурье, а преобразования Фурье — в кодировании звука и изображения.
Теперь можно провести анализ ситуации с различными расширениями. Перефразируя известную фразу, скажу: «Если появляются SIMD-расширения, значит это зачем-то кому-то нужно».
3DNow! — само название говорит об одной из целей производителя: привлечь, строго говоря, обмануть, покупателя. Выигрыш от использования 3DNow! не больше полутора, максимум, SQRT(3) разов, что никак не тянет на «3DNow!». Это, кстати, почти всегда завышенная оценка. В реальности относительная выгода не так велика (на Athlon’ах с хорошим сопроцессором). К тому же, даже 3D программа далеко не вся может быть оптимизирована под 3DNow!, так что общая добавка производительности ещё меньше.
Хочется сделать ещё одно замечание: многие программы, показывающие фантастический прирост производительности при оптимизации под SIMD — это касается и 3DNow! и SSE — просто не были до этого хорошо оптимизированы. Их взялись оптимизировать и сразу под SIMD. Поделюсь своим личным опытом в этой области. Я решил переписать на ассемблер относительно небольшую часто вызываемую функцию. Мой ассемблерный код имел в полтора раза меньший размер, по сравнению со сгенерированным IntelC++Compiler4.5, но работал практически также. Переписал с использованием SSE. Правда, задействовались только первые два элемента регистров SSE, поскольку нужно было вычислять скалярные произведения двух, а не четырёх пар векторов. И этот вариант работал с прежней скоростью. Дело в том, что изначально код на C++ был хорошо написан, и компилятор его не испортил при компиляции.
Мой ассемблерный код имел в полтора раза меньший размер, по сравнению со сгенерированным IntelC++Compiler4.5, но работал практически также. Переписал с использованием SSE. Правда, задействовались только первые два элемента регистров SSE, поскольку нужно было вычислять скалярные произведения двух, а не четырёх пар векторов. И этот вариант работал с прежней скоростью. Дело в том, что изначально код на C++ был хорошо написан, и компилятор его не испортил при компиляции.
Вспомним, что в те времена, когда появилась 3DNow!, процессоры AMD были хуже Intel’овских в операциях с плавающей точкой из-за плохого конвейера для сопроцессора, а скорость SIMD меньше зависит от качества реализации конвейера, так что 3DNow! была призвана исправить ситуацию в вычислениях с вещественными числами.
Рассмотрим SSE. С ним ситуация, как ни странно, вполне аналогична. Как известно, SSE имеет титул: The Internet Streaming SIMD Extension. В определённые дни на компьютерные рынки приходят маркетологи корпорации Intel и демонстрируют покупателям, как SSE помогает при работе с Internet.
Известно, что, в угоду возможности наращивания частоты, конвейер процессора Pentium4 сделан не оптимальным образом. И опять SIMD-расширение призвано выправить положение. Без использования SIMD, Pentium4 значительно проигрывает в некоторых тестах многим процессорам меньшей частоты, иногда даже PentiumIII. Есть все основания предполагать, что с увеличением частоты процессора Pentium4 разрыв между производительностью SIMD и неSIMD кода будет только увеличиваться.
Выводы
На основании проведённого анализа можно сделать более-менее достоверные выводы о перспективах использования SIMD. Так как SSE поддерживают и последние процессоры AMD, с оптимизацией под 3DNow! почти никто больше возиться не будет. Зачем это надо, если SSE есть и у PentiumIII и у CeleronII, не говоря уже про Pentium4. А 3DNow! актуально только для старых Athlon, которые скоро заменят новые AthlonXР. Зато оптимизация под SSE станет обязательной, поскольку иначе на Pentium 4 будет плохо работать. Какой-нибудь Pentium 4 3GHz будет работать, как PentiumIII 1. 5GHz.
5GHz.
Конечно, этот прогноз верен в том случае, если Intel останется лидером продаж. Если же рынок неожиданно заполонят непонятно от куда взявшиеся какие-нибудь AthlonXP3000+, которые отлично работают безо всякого SSE, то лень разработчиков помешает выпуску оптимизированных под SSE программ, что окончательно погубит этот самый Pentium4. Однако, якобы AthlonXP3000+ неоткуда взяться, поскольку оптимальный конвейер не совместим с высокой частотой.
Введение поддержки SSE в последние процессоры AMD может говорить о том, что AMD тоже собирается пойти по стопам Intel в деле повышения частоты, и будущие процессоры AMD тоже будут плохо работать на программах без SIMD оптимизации.
Печалит, однако, тенденция перекладывания производителями процессоров своих проблем на разработчиков. Необходимость оптимизировать программу под процессор не есть хорошо. К тому же, компиляторы, которые бы эту проблему решали автоматически, без участия программиста, очень тяжело сделать. Главные достижения в этой области — автоматическая подставка SSE-оптимизированной процедуры умножения четырёх мерных матриц и векторная библиотека от AMD.
Нет бы сделать что-то действительно хорошее, ту же геометрию оптимизировать по-человечески. Например, увеличили бы стек сопроцессора, чтобы в него помещалось несколько матриц, и добавили бы несколько настоящих 3D команд, вроде таких:
- fLoadVector mem
- fLoadMatrix mem
- fStoreVector mem
- fStoreMatrix mem
- fMulVectorScalar r1,r2
- fMulVectorVector r1,r2
- fMulVectorMatrix r1,r2
- fMulMatrixScalar r1,r2
- fMulMatrixMatrix r1,r2
- fAddVectorVector r1,r2
- fAddMatrixMatrix r1,r2
- fDotProduct r1,r2
- fNormalizeVector r1,r2
- fInverseMatrix r1,r2
Тогда было бы не стыдно назвать расширение Super Enhanced 3D Extension.
Правда, объективно установить баланс между оптимизацией железа под софт и софта под железа невозможно.
Оптимизация трассировки лучей под SSE
Рассмотрим идеи оптимизации трассировки лучей под SIMD-расширения процессорных команд. Как правило, перед запуском цикла трассировки в ходе предварительной обработки сцены для каждого луча находится множество объектов, с которыми он может пересечься. Делается это путём, например, группировки лучей, отвечающих некоторым областям экрана, и нахождения всех объектов, которые могут пересекаться с каким-нибудь лучом группы. После этого связанную с лучом информацию можно скомпоновать, что бы её можно было легко загружать в регистры SSE и проверять пересечение параллельно с четырьмя объектами. Это хорошо получается, когда объекты однотипны: например, поверхности первого порядка, поверхности второго порядка. Тут есть элемент спекулятивного выполнения: вдруг не все четыре пересечения нужно будет считать, например, из-за того, что уже первое пересечение дало положительный результат. Однако, когда объектов много, это вполне оправдывается.
Делается это путём, например, группировки лучей, отвечающих некоторым областям экрана, и нахождения всех объектов, которые могут пересекаться с каким-нибудь лучом группы. После этого связанную с лучом информацию можно скомпоновать, что бы её можно было легко загружать в регистры SSE и проверять пересечение параллельно с четырьмя объектами. Это хорошо получается, когда объекты однотипны: например, поверхности первого порядка, поверхности второго порядка. Тут есть элемент спекулятивного выполнения: вдруг не все четыре пересечения нужно будет считать, например, из-за того, что уже первое пересечение дало положительный результат. Однако, когда объектов много, это вполне оправдывается.
Аналогичная идея может применяться для оптимизации трассировки отражённого луча или лучей, направленных на источники света. Для каждого объекта формируется массив объектов, с которыми может пересечься отражённый луч. И, с помощью SSE, считается пересечение сразу с четырьмя объектами.
Интересно, что в случае увеличения размера SIMD-регистров до 8, 16, 32, 64, 128 и т. д. эта идея также проходит.
д. эта идея также проходит.
В состав SSE входят команды быстрого приближённого вычисления обратной величины и обратного квадратного корня. Для выполнения геометрических расчётов их использование проблематично из-за больших погрешностей. Их лучше использовать для вычисления таких величин, как освещённость, цвет, которые всё равно будут отображаться с округлением до 1/256.
Заключение
Пути развития неисповедимы. Трудно заранее определённо сказать о перспективах той или иной технологии. Несомненна некоторая научная ценность движка VirtualRay. Однако, найдётся ли ему практическое применение в какой-либо области, покажет время. Быть может, некоторые идеи, заложенные в движок, продолжат своё развитие и найдут своё воплощение в совершенно иной форме.
Учебное пособие по физике: лучевые диаграммы — вогнутые зеркала
Тема этого раздела заключалась в том, что мы видим объект, потому что свет от объекта попадает в наши глаза, когда мы видим линию на объект.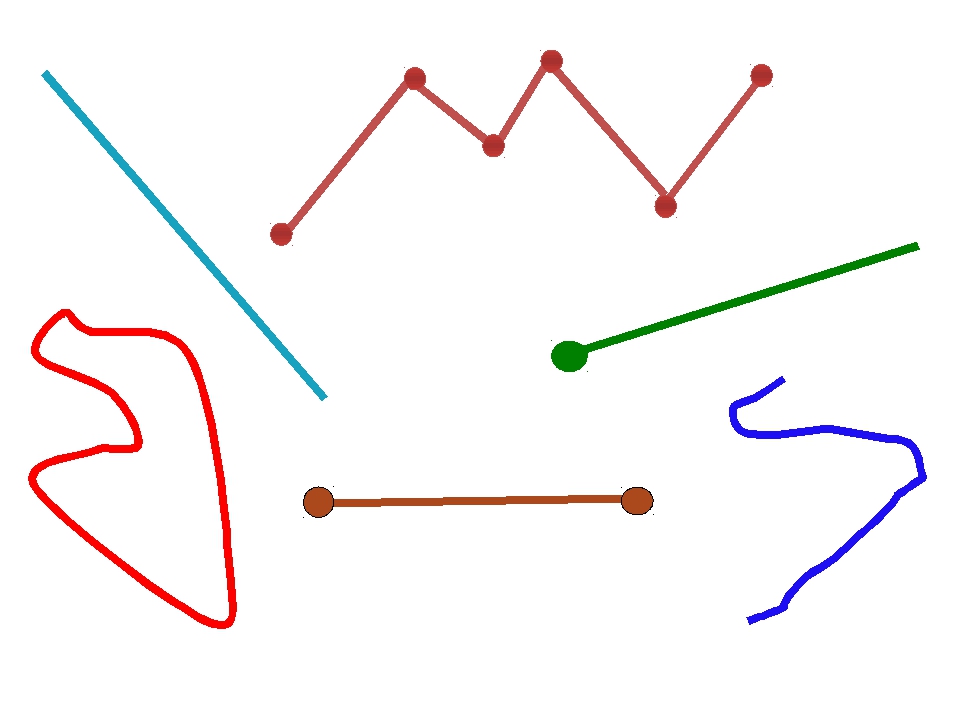 Точно так же мы видим изображение объекта, потому что свет от объекта отражается от зеркала и направляется к нашим глазам, когда мы смотрим на место изображения объекта. Исходя из этих двух основных предпосылок, мы определили местоположение изображения как место в пространстве, из которого кажется, что свет расходится.Диаграммы лучей были ценным инструментом для определения пути света от объекта до зеркала и наших глаз. В этом разделе Урока 3 мы исследуем метод построения лучевых диаграмм для объектов, размещенных в различных местах перед вогнутым зеркалом.
Точно так же мы видим изображение объекта, потому что свет от объекта отражается от зеркала и направляется к нашим глазам, когда мы смотрим на место изображения объекта. Исходя из этих двух основных предпосылок, мы определили местоположение изображения как место в пространстве, из которого кажется, что свет расходится.Диаграммы лучей были ценным инструментом для определения пути света от объекта до зеркала и наших глаз. В этом разделе Урока 3 мы исследуем метод построения лучевых диаграмм для объектов, размещенных в различных местах перед вогнутым зеркалом.
Чтобы нарисовать эти диаграммы, мы должны вспомнить два правила отражения для вогнутых зеркал:
Ранее в этом уроке была показана следующая диаграмма, показывающая путь света от объекта до зеркала к глазу.
На этой диаграмме изображены пять падающих лучей и соответствующие им отраженные лучи. Каждый луч пересекается в месте нахождения изображения, а затем расходится к глазу наблюдателя. Каждый наблюдатель будет наблюдать одно и то же место изображения, и каждый световой луч подчиняется закону отражения. Однако для определения местоположения изображения потребуются только два из этих лучей, поскольку для нахождения точки пересечения требуется только два луча. Из пяти нарисованных падающих лучей два соответствуют падающим лучам, описанным нашими двумя правилами отражения для вогнутых зеркал.Поскольку это самая легкая и предсказуемая пара лучей для рисования, они будут использоваться в оставшейся части урока.
Однако для определения местоположения изображения потребуются только два из этих лучей, поскольку для нахождения точки пересечения требуется только два луча. Из пяти нарисованных падающих лучей два соответствуют падающим лучам, описанным нашими двумя правилами отражения для вогнутых зеркал.Поскольку это самая легкая и предсказуемая пара лучей для рисования, они будут использоваться в оставшейся части урока.
Метод построения лучевых диаграмм для вогнутого зеркала описан ниже. Метод применяется к задаче построения диаграммы лучей для объекта, расположенного на за пределами центра кривизны (C) вогнутого зеркала.Тем не менее, тот же метод работает для рисования диаграммы лучей для любого местоположения объекта.
1. Укажите точку на вершине объекта и нарисуйте два падающих луча, идущих к зеркалу.
Используя линейку, аккуратно нарисуйте один луч так, чтобы он проходил точно через точку фокусировки на пути к зеркалу.Нарисуйте второй луч так, чтобы он двигался точно параллельно главной оси. Поместите стрелки на лучи, чтобы указать направление их движения.
2.Как только эти падающие лучи попадают в зеркало, отразите их в соответствии с двумя правилами отражения для вогнутых зеркал.
Луч, который проходит через точку фокусировки на пути к зеркалу, будет отражаться и проходить параллельно главной оси. Используйте прямую кромку, чтобы точно нарисовать путь. Луч, который прошел параллельно главной оси на пути к зеркалу, будет отражаться и проходить через точку фокусировки. Поместите стрелки на лучи, чтобы указать направление их движения.Вытяните лучи за точку их пересечения.
3. Отметьте изображение верхней части объекта.
Точка изображения верхней части объекта — это точка пересечения двух отраженных лучей. Если бы вы нарисовали третью пару падающих и отраженных лучей, то третий отраженный луч также прошел бы через эту точку.Это просто точка, где весь свет от верхней части объекта пересекается при отражении от зеркала.Конечно, остальная часть объекта также имеет изображение, и его можно найти, применив те же три шага к другой выбранной точке. (См. Примечание ниже.)
4. Повторите процесс для нижней части объекта.
Цель лучевой диаграммы — определить расположение, размер, ориентацию и тип изображения, которое формируется вогнутым зеркалом. Как правило, для этого требуется определить, где находится изображение верхнего и нижнего крайних точек объекта, а затем проследить все изображение.После выполнения первых трех шагов было найдено только положение изображения верхнего края объекта. Таким образом, процесс необходимо повторить для точки в нижней части объекта. Если нижняя часть объекта лежит на главной оси (как в этом примере), то изображение этой точки также будет лежать на главной оси и находиться на том же расстоянии от зеркала, что и изображение верха объекта.. На этом этапе можно заполнить все изображение.
Некоторым ученикам трудно понять, как можно вывести все изображение объекта после определения одной точки на изображении.Если объект является выровненным по вертикали объектом (например, объект стрелки, используемый в приведенном ниже примере), тогда процесс прост. Изображение представляет собой просто вертикальную линию. Теоретически необходимо выбрать каждую точку объекта и нарисовать отдельную диаграмму лучей, чтобы определить местоположение изображения этой точки. Для этого потребуется множество лучевых диаграмм, как показано ниже.
К счастью, ярлык существует. Если объект представляет собой вертикальную линию, то изображение также является вертикальной линией.Для наших целей мы будем иметь дело только с более простыми ситуациями, когда объект представляет собой вертикальную линию, нижняя часть которой расположена на главной оси. Для таких упрощенных ситуаций изображение представляет собой вертикальную линию с нижней конечностью, расположенной на главной оси.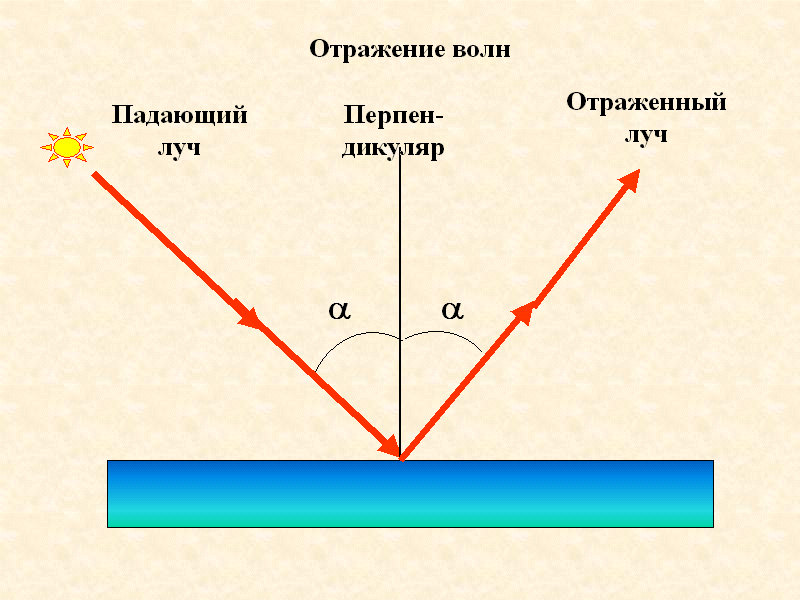
Лучевая диаграмма выше показывает, что, когда объект расположен в позиции за пределами центра кривизны, изображение располагается в положении между центром кривизны и точкой фокусировки.Кроме того, изображение инвертируется, уменьшается в размере (меньше объекта) и становится реальным. Это тип информации, которую мы хотим получить из лучевой диаграммы. Эти характеристики изображения будут рассмотрены более подробно в следующем разделе Урока 3.
После того, как метод рисования лучевых диаграмм будет отработан пару раз, он станет таким же естественным, как дыхание. Каждая диаграмма дает конкретную информацию об изображении. На двух диаграммах ниже показано, как определить местоположение, размер, ориентацию и тип изображения для ситуаций, когда объект расположен в центре кривизны и когда объект расположен между центром кривизны и точкой фокусировки.
Следует отметить, что процесс построения лучевой диаграммы одинаков вне зависимости от того, где находится объект. Хотя результат лучевой диаграммы (расположение, размер, ориентация и тип изображения) отличается, одни и те же два луча — это всегда нарисовано . Два правила отражения применяются, чтобы определить место, где все отраженные лучи, по-видимому, расходятся (что для реальных изображений также является местом пересечения отраженных лучей).
Хотя результат лучевой диаграммы (расположение, размер, ориентация и тип изображения) отличается, одни и те же два луча — это всегда нарисовано . Два правила отражения применяются, чтобы определить место, где все отраженные лучи, по-видимому, расходятся (что для реальных изображений также является местом пересечения отраженных лучей).
В трех описанных выше случаях — в случае, когда объект расположен за пределами C, в случае, когда объект расположен в C и в случае, когда объект находится между C и F, — световые лучи сходятся к точке после отражения с зеркала. В таких случаях формируется реальное изображение . Как обсуждалось ранее, реальное изображение формируется всякий раз, когда отраженный свет проходит через местоположение изображения. В то время как плоские зеркала всегда создают виртуальные изображения, вогнутые зеркала способны создавать как реальные, так и виртуальные изображения.Как показано выше, реальные изображения создаются, когда объект находится на расстоянии более одного фокусного расстояния от зеркала. Виртуальное изображение формируется, если объект расположен на расстоянии менее одного фокусного расстояния от вогнутого зеркала. Чтобы понять, почему это так, можно использовать диаграмму лучей.
Виртуальное изображение формируется, если объект расположен на расстоянии менее одного фокусного расстояния от вогнутого зеркала. Чтобы понять, почему это так, можно использовать диаграмму лучей.
Лучевая диаграмма для формирования виртуального изображения
Лучевая диаграмма для случая, когда объект расположен на расстоянии от , точка фокусировки показана на схеме справа.Обратите внимание, что в этом случае световые лучи расходятся после отражения от зеркала. Когда световые лучи расходятся после отражения, формируется виртуальное изображение. Как и в случае с плоскими зеркалами, местоположение изображения можно найти, проследив все отраженные лучи назад, пока они не пересекутся.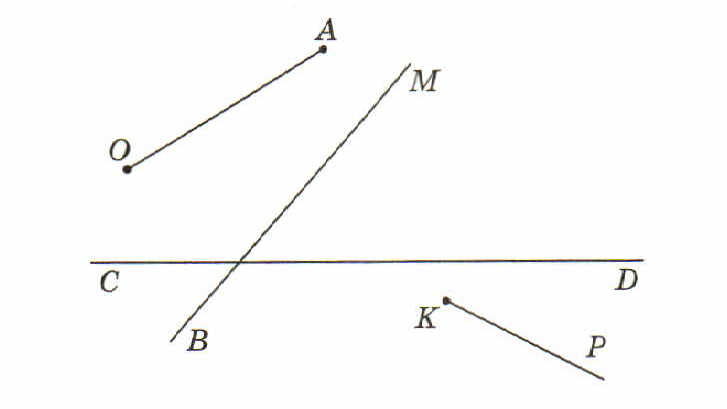 Каждому наблюдателю казалось бы, что отраженные лучи расходятся от этой точки. Таким образом, точка пересечения протяженных отраженных лучей и есть точка изображения. Поскольку свет на самом деле не проходит через эту точку (свет никогда не проходит за зеркалом), изображение называется виртуальным изображением.Заметьте, что когда объект расположен на перед фокусной точкой на , его изображение представляет собой вертикальное увеличенное изображение, расположенное с другой стороны зеркала. Фактически, одно обобщение, которое можно сделать в отношении всех виртуальных изображений, создаваемых зеркалами (как плоскими, так и изогнутыми), заключается в том, что они всегда находятся в вертикальном положении и всегда расположены с другой стороны зеркала.
Каждому наблюдателю казалось бы, что отраженные лучи расходятся от этой точки. Таким образом, точка пересечения протяженных отраженных лучей и есть точка изображения. Поскольку свет на самом деле не проходит через эту точку (свет никогда не проходит за зеркалом), изображение называется виртуальным изображением.Заметьте, что когда объект расположен на перед фокусной точкой на , его изображение представляет собой вертикальное увеличенное изображение, расположенное с другой стороны зеркала. Фактически, одно обобщение, которое можно сделать в отношении всех виртуальных изображений, создаваемых зеркалами (как плоскими, так и изогнутыми), заключается в том, что они всегда находятся в вертикальном положении и всегда расположены с другой стороны зеркала.
До сих пор мы видели с помощью лучевых диаграмм, что реальное изображение создается, когда объект находится на расстоянии более одного фокусного расстояния от вогнутого зеркала; и виртуальное изображение формируется, когда объект находится на расстоянии менее одного фокусного расстояния от вогнутого зеркала (т.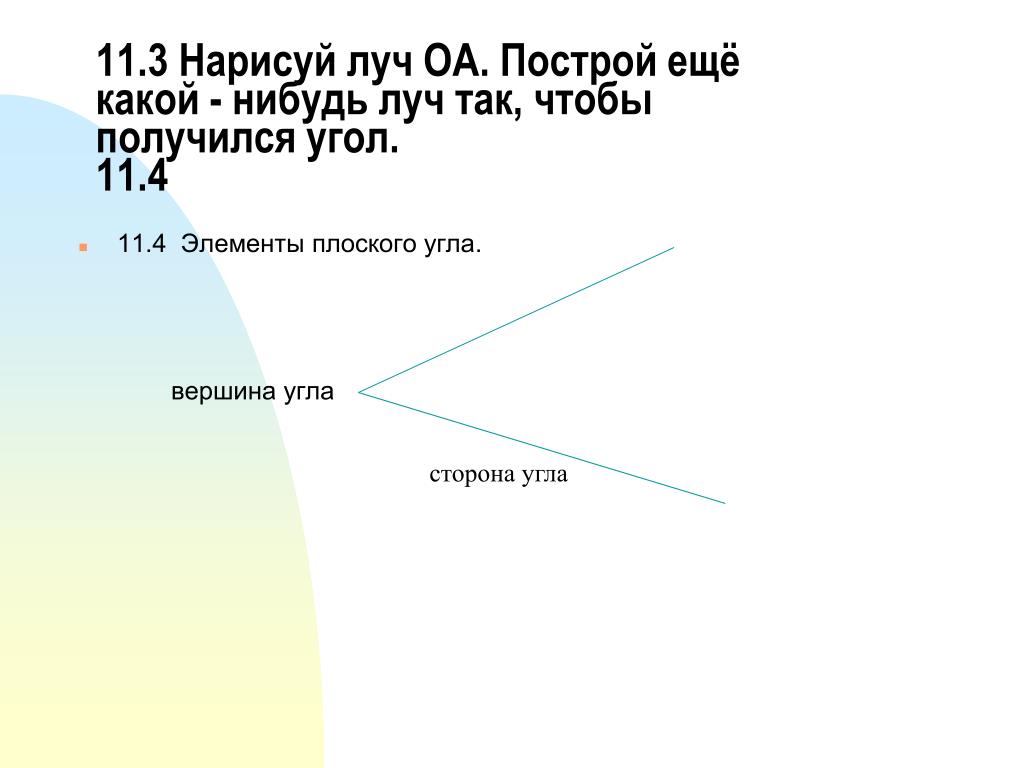 е.е., перед F ). Но что происходит, когда объект находится в точке F? То есть какой тип изображения формируется, когда объект находится ровно на одном фокусном расстоянии от вогнутого зеркала? Конечно, лучевая диаграмма всегда помогает найти ответ на такой вопрос. Однако, когда в этом случае используется диаграмма лучей, возникает непосредственная трудность. Падающий луч, который начинается с верхнего края объекта и проходит через точку фокусировки, не попадает в зеркало.Таким образом, необходимо использовать другой падающий луч, чтобы определить точку пересечения всех отраженных лучей. Любой падающий световой луч будет работать до тех пор, пока он встречается с зеркалом. Напомним, что единственная причина, по которой мы использовали те два, что у нас есть, заключается в том, что их можно удобно и легко нарисовать. На приведенной ниже диаграмме показаны два падающих луча и соответствующие им отраженные лучи.
е.е., перед F ). Но что происходит, когда объект находится в точке F? То есть какой тип изображения формируется, когда объект находится ровно на одном фокусном расстоянии от вогнутого зеркала? Конечно, лучевая диаграмма всегда помогает найти ответ на такой вопрос. Однако, когда в этом случае используется диаграмма лучей, возникает непосредственная трудность. Падающий луч, который начинается с верхнего края объекта и проходит через точку фокусировки, не попадает в зеркало.Таким образом, необходимо использовать другой падающий луч, чтобы определить точку пересечения всех отраженных лучей. Любой падающий световой луч будет работать до тех пор, пока он встречается с зеркалом. Напомним, что единственная причина, по которой мы использовали те два, что у нас есть, заключается в том, что их можно удобно и легко нарисовать. На приведенной ниже диаграмме показаны два падающих луча и соответствующие им отраженные лучи.
В случае объекта, расположенного в фокусной точке (F), световые лучи не сходятся и не расходятся после отражения от зеркала. Как показано на диаграмме выше, отраженные лучи движутся параллельно друг другу. Следовательно, световые лучи не будут сходиться на стороне объекта зеркала, чтобы сформировать реальное изображение; они также не могут быть вытянуты назад на противоположной стороне зеркала, чтобы пересекаться и образовывать виртуальное изображение. Итак, как следует интерпретировать результаты лучевой диаграммы? Ответ: изображения нет !! Удивительно, но когда объект расположен в фокусной точке, нет места в пространстве, в котором наблюдатель может видеть, от которого все отраженные лучи кажутся расходящимися.Изображение не формируется, когда объект находится в фокусе вогнутого зеркала.
Как показано на диаграмме выше, отраженные лучи движутся параллельно друг другу. Следовательно, световые лучи не будут сходиться на стороне объекта зеркала, чтобы сформировать реальное изображение; они также не могут быть вытянуты назад на противоположной стороне зеркала, чтобы пересекаться и образовывать виртуальное изображение. Итак, как следует интерпретировать результаты лучевой диаграммы? Ответ: изображения нет !! Удивительно, но когда объект расположен в фокусной точке, нет места в пространстве, в котором наблюдатель может видеть, от которого все отраженные лучи кажутся расходящимися.Изображение не формируется, когда объект находится в фокусе вогнутого зеркала.
Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие — это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom.
 Мы хотели бы предложить вам совместить чтение этой страницы с использованием наших интерактивных приложений Optics Bench Interactive или Name That Image Interactive.Вы можете найти это в разделе Physics Interactives на нашем сайте. Optics Bench Interactive предоставляет учащимся интерактивную среду для изучения формирования изображений с помощью линз и зеркал. Интерактивное приложение Name That Image Interactive предлагает учащимся интенсивную умственную тренировку для распознавания характеристик изображения для любого заданного местоположения объекта перед изогнутым зеркалом.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием наших интерактивных приложений Optics Bench Interactive или Name That Image Interactive.Вы можете найти это в разделе Physics Interactives на нашем сайте. Optics Bench Interactive предоставляет учащимся интерактивную среду для изучения формирования изображений с помощью линз и зеркал. Интерактивное приложение Name That Image Interactive предлагает учащимся интенсивную умственную тренировку для распознавания характеристик изображения для любого заданного местоположения объекта перед изогнутым зеркалом.
На схеме ниже показаны два световых луча, исходящих из верхней части объекта и падающих в сторону зеркала.Опишите, как можно нарисовать отраженные лучи для этих световых лучей без использования транспортира и закона отражения.
Веб-сайт класса физики
Диаграммы лучей для вогнутых зеркал — Дело A
Объект, расположенный за центром кривизны
Диаграммы лучей — полезный инструмент для определения положения изображения, созданного вогнутым зеркалом.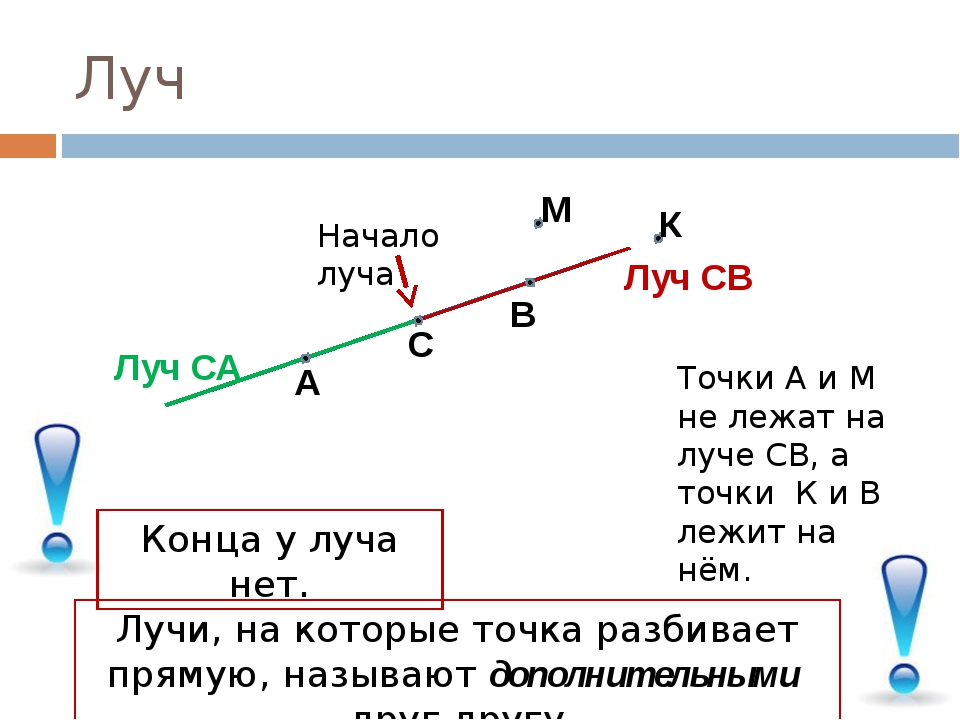 Чтобы определить местоположение изображения с помощью диаграммы лучей, необходимо построить по крайней мере два набора падающих и отраженных лучей для стратегических положений на объекте. Изображение объекта — это место, где световые лучи от этого объекта пересекаются при отражении от зеркала. Построив по крайней мере два набора падающих и отраженных лучей, можно легко найти это местоположение изображения.
Чтобы определить местоположение изображения с помощью диаграммы лучей, необходимо построить по крайней мере два набора падающих и отраженных лучей для стратегических положений на объекте. Изображение объекта — это место, где световые лучи от этого объекта пересекаются при отражении от зеркала. Построив по крайней мере два набора падающих и отраженных лучей, можно легко найти это местоположение изображения.
Если объект представлен стрелкой, то обычно в качестве отправных точек для падающих и отраженных лучей выбирают два крайних положения (верхнее и нижнее положение стрелки).Построение луча приведет к определению местоположения изображения для этих двух крайних положений на объекте. Полное изображение — это просто стрелка, соединяющая эти два местоположения изображения. Эта задача дополнительно упрощается, если объект расположен в виде стрелки , стоящей на главной оси зеркала. Если это так, то изображение будет , стоящим на на главной оси зеркала (и либо перевернутым, либо вертикальным).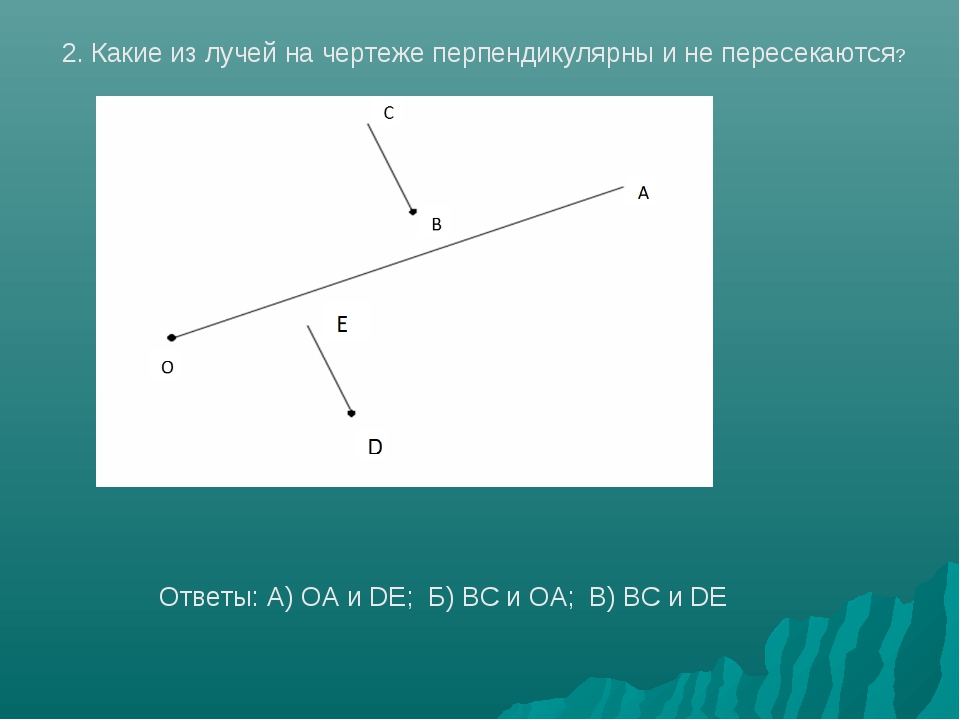
Из всех лучей, которые исходят из вершины стрелки объекта и падают на зеркало, есть два луча, поведение которых на поверхности зеркала можно легко предсказать.Это два падающих луча, которые используются при построении луча. Один из лучей движется параллельно главной оси и отражается через точку фокусировки. Второй луч проходит через точку фокусировки на пути к зеркалу и отражается параллельно главной оси. Все диаграммы лучей вогнутого и выпуклого зеркала могут быть построены на основе знания поведения этих двух лучей.
В приведенной выше анимации объект, расположенный правой стороной вверх, расположен над главной осью в позиции за центром кривизны ( C ).Лучевая диаграмма показывает, что изображение этого объекта расположено в виде перевернутого изображения, расположенного между центром кривизны ( C ) и точкой фокусировки ( F ). Фактически, можно обобщить, что каждый раз, когда объект находится за пределами центра кривизны, изображение будет располагаться где-то между центром кривизны и точкой фокусировки. В таких случаях изображение будет инвертировано и уменьшено в размере (то есть меньше объекта). Такие изображения называются реальными изображениями , потому что они сформированы фактическим схождением отраженных световых лучей в месте расположения изображения.Реальные изображения всегда формируются на той же стороне зеркала, что и объект.
В таких случаях изображение будет инвертировано и уменьшено в размере (то есть меньше объекта). Такие изображения называются реальными изображениями , потому что они сформированы фактическим схождением отраженных световых лучей в месте расположения изображения.Реальные изображения всегда формируются на той же стороне зеркала, что и объект.
Для получения дополнительной информации о лучевой природе света посетите The Physics Classroom Tutorial. Подробная информация доступна по следующим темам:
Почему формируется изображение?Анатомия изогнутого зеркала
Отражение света и формирование изображения
Два правила отражения для вогнутых зеркал
Лучевые диаграммы — вогнутые зеркала
Характеристики изображения для вогнутых зеркал
Уравнение зеркала — вогнутые зеркала
Веб-сайт класса физики
Диаграммы лучей для вогнутых зеркал — Случай B
Объект, расположенный в центре кривизны
Диаграммы лучей — полезный инструмент для определения положения изображения, созданного вогнутым зеркалом. Чтобы определить местоположение изображения с помощью диаграммы лучей, необходимо построить по крайней мере два набора падающих и отраженных лучей для стратегических положений на объекте. Изображение объекта — это место, где световые лучи от этого объекта пересекаются при отражении от зеркала. Построив по крайней мере два набора падающих и отраженных лучей, можно легко найти это местоположение изображения.
Чтобы определить местоположение изображения с помощью диаграммы лучей, необходимо построить по крайней мере два набора падающих и отраженных лучей для стратегических положений на объекте. Изображение объекта — это место, где световые лучи от этого объекта пересекаются при отражении от зеркала. Построив по крайней мере два набора падающих и отраженных лучей, можно легко найти это местоположение изображения.
Если объект представлен стрелкой, то обычно в качестве отправных точек для падающих и отраженных лучей выбирают два крайних положения (верхнее и нижнее положение стрелки).Построение луча приведет к определению местоположения изображения для этих двух крайних положений на объекте. Полное изображение — это просто стрелка, соединяющая эти два местоположения изображения. Эта задача дополнительно упрощается, если объект расположен в виде стрелки , стоящей на главной оси зеркала. Если это так, то изображение будет , стоящим на на главной оси зеркала (и либо перевернутым, либо вертикальным).
Из всех лучей, которые исходят из вершины стрелки объекта и падают на зеркало, есть два луча, поведение которых на поверхности зеркала можно легко предсказать.Это два падающих луча, которые используются при построении луча. Один из лучей движется параллельно главной оси и отражается через точку фокусировки. Второй луч проходит через точку фокусировки на пути к зеркалу и отражается параллельно главной оси. Все диаграммы лучей вогнутого и выпуклого зеркала могут быть построены на основе знания поведения этих двух лучей.
На приведенной выше анимации объект, расположенный правой стороной вверх, расположен над главной осью в центре кривизны ( C ).Лучевая диаграмма показывает, что изображение этого объекта расположено в виде перевернутого изображения, расположенного в центре кривизны ( C ). Фактически, можно обобщить, что каждый раз, когда объект находится в центре кривизны, изображение также будет располагаться в центре кривизны. В таких случаях изображение будет перевернуто и будет такого же размера, как и объект. Такие изображения называются реальными изображениями , потому что они сформированы фактическим схождением отраженных световых лучей в месте расположения изображения.Реальные изображения всегда формируются на той же стороне зеркала, что и объект.
В таких случаях изображение будет перевернуто и будет такого же размера, как и объект. Такие изображения называются реальными изображениями , потому что они сформированы фактическим схождением отраженных световых лучей в месте расположения изображения.Реальные изображения всегда формируются на той же стороне зеркала, что и объект.
Для получения дополнительной информации о лучевой природе света посетите The Physics Classroom Tutorial. Подробная информация доступна по следующим темам:
Почему формируется изображение?Анатомия изогнутого зеркала
Отражение света и формирование изображения
Два правила отражения для вогнутых зеркал
Лучевые диаграммы — вогнутые зеркала
Характеристики изображения для вогнутых зеркал
Уравнение зеркала — вогнутые зеркала
Преломление и лучевая модель света
Одной из тем разделов «Отражение» и «Преломление» учебного пособия по физике было то, что мы видим объект, потому что свет от объекта проходит к нашим глазам, когда мы видим объект вдоль линии.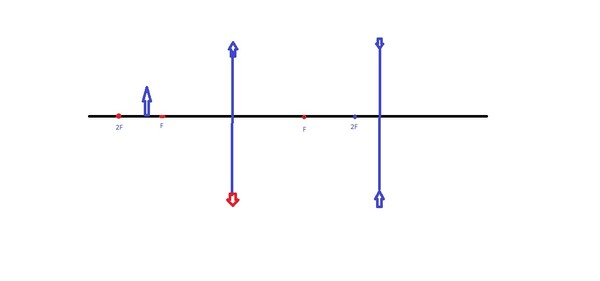 Точно так же мы видим изображение объекта, потому что свет от объекта отражается от зеркала или преломляется через прозрачный материал и попадает в наши глаза, когда мы смотрим на место изображения объекта. Исходя из этих двух основных предпосылок, мы определили местоположение изображения как место в пространстве, из которого кажется, что свет расходится. Поскольку свет, исходящий от объекта, сходится или кажется отклоняющимся от этого места, в этом месте создается копия или подобие объекта. Как для сценариев отражения, так и для сценариев преломления лучевые диаграммы были ценным инструментом для определения пути света от объекта к нашим глазам.
Точно так же мы видим изображение объекта, потому что свет от объекта отражается от зеркала или преломляется через прозрачный материал и попадает в наши глаза, когда мы смотрим на место изображения объекта. Исходя из этих двух основных предпосылок, мы определили местоположение изображения как место в пространстве, из которого кажется, что свет расходится. Поскольку свет, исходящий от объекта, сходится или кажется отклоняющимся от этого места, в этом месте создается копия или подобие объекта. Как для сценариев отражения, так и для сценариев преломления лучевые диаграммы были ценным инструментом для определения пути света от объекта к нашим глазам.
В этом разделе Урока 5 мы исследуем метод построения лучевых диаграмм для объектов, размещенных в различных местах перед двойной выпуклой линзой. Чтобы нарисовать эти лучевые диаграммы, нам нужно вспомнить три правила преломления для двойной выпуклой линзы:
- Любой падающий луч, идущий параллельно главной оси собирающей линзы, преломляется через линзу и проходит через точку фокусировки на противоположной стороне линзы.

- Любой падающий луч, проходящий через точку фокусировки на пути к линзе, преломляется через линзу и проходит параллельно главной оси.
- Падающий луч, проходящий через центр линзы, по сути, будет продолжать движение в том же направлении, что и при входе в линзу.
Ранее в этом уроке была показана следующая диаграмма, иллюстрирующая путь света от объекта через линзу к глазу, размещенному в различных местах.
На этой диаграмме показаны пять падающих лучей и соответствующие им преломленные лучи. Каждый луч пересекается в месте нахождения изображения, а затем попадает в глаз наблюдателя. Каждый наблюдатель будет наблюдать одно и то же место изображения, и каждый световой луч будет следовать закону преломления Снеллиуса. Однако для определения местоположения изображения потребуются только два из этих лучей, поскольку для нахождения точки пересечения требуется только два луча. Из пяти нарисованных падающих лучей три соответствуют падающим лучам, описанным нашими тремя правилами рефракции для собирающихся линз. Мы будем использовать эти три луча в оставшейся части этого урока просто потому, что их легче всего рисовать. Конечно, два луча — это все, что нужно; все же третий луч обеспечит проверку точности нашего процесса.
Мы будем использовать эти три луча в оставшейся части этого урока просто потому, что их легче всего рисовать. Конечно, два луча — это все, что нужно; все же третий луч обеспечит проверку точности нашего процесса.
Метод построения лучевых диаграмм для двояковыпуклой линзы описан ниже. Описание применяется к задаче построения лучевой диаграммы для объекта, расположенного на за пределами точки 2F двойной выпуклой линзы.
1. Укажите точку на вершине объекта и нарисуйте три падающих луча, идущих к линзе.
Используя линейку, аккуратно нарисуйте один луч так, чтобы он проходил точно через точку фокусировки на пути к линзе. Нарисуйте второй луч так, чтобы он двигался точно параллельно главной оси. Нарисуйте третий падающий луч так, чтобы он проходил точно в центр линзы. Поместите стрелки на лучи, чтобы указать направление их движения.
2.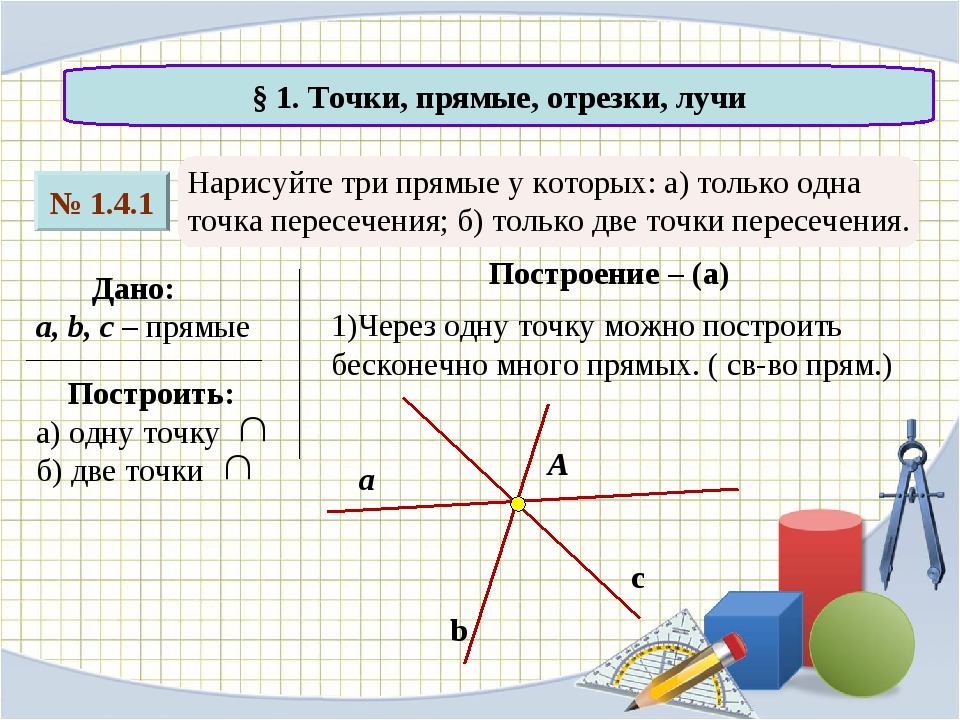 Как только эти падающие лучи падают на линзу, преломляйте их в соответствии с тремя правилами рефракции для собирающих линз.
Как только эти падающие лучи падают на линзу, преломляйте их в соответствии с тремя правилами рефракции для собирающих линз.
Луч, который проходит через точку фокусировки на пути к линзе, преломляется и перемещается параллельно главной оси. Используйте прямую кромку, чтобы точно нарисовать путь. Луч, который прошел параллельно главной оси на пути к линзе, преломляется и проходит через точку фокусировки.И луч, который прошел точно в центр линзы, продолжит движение в том же направлении. Поместите стрелки на лучи, чтобы указать направление их движения. Вытяните лучи за точку их пересечения.
3. Отметьте изображение верхней части объекта.
Точка изображения верхней части объекта — это точка пересечения трех преломленных лучей. Все три луча должны пересекаться в одной и той же точке.Эта точка — просто точка, где весь свет от верхней части объекта пересекается при преломлении через линзу. Конечно, остальная часть объекта также имеет изображение, и его можно найти, применив те же три шага к другой выбранной точке.(См. Примечание ниже.)
4. Повторите процесс для нижней части объекта.
Одна из целей лучевой диаграммы — определить местоположение, размер, ориентацию и тип изображения, формируемого двойной выпуклой линзой.Как правило, для этого необходимо определить, где находится изображение верхнего и нижнего крайних точек объекта, а затем проследить все изображение. После выполнения первых трех шагов было найдено только положение изображения верхнего края объекта. Таким образом, процесс необходимо повторить для точки в нижней части объекта. Если нижняя часть объекта лежит на главной оси (как в этом примере), то изображение этой точки также будет лежать на главной оси и находиться на том же расстоянии от зеркала, что и изображение верха объекта. .На этом этапе можно заполнить все изображение.
Некоторым ученикам трудно понять, как можно вывести все изображение объекта после определения одной точки на изображении. Если объект представляет собой просто вертикальный объект (такой как объект стрелки, используемый в примере ниже), то процесс прост. Изображение представляет собой просто вертикальную линию. Теоретически необходимо выбрать каждую точку объекта и нарисовать отдельную диаграмму лучей, чтобы определить местоположение изображения этой точки.Для этого потребуется много диаграмм лучей, как показано на диаграмме ниже.
Если объект представляет собой просто вертикальный объект (такой как объект стрелки, используемый в примере ниже), то процесс прост. Изображение представляет собой просто вертикальную линию. Теоретически необходимо выбрать каждую точку объекта и нарисовать отдельную диаграмму лучей, чтобы определить местоположение изображения этой точки.Для этого потребуется много диаграмм лучей, как показано на диаграмме ниже.
К счастью, ярлык существует. Если объект представляет собой вертикальную линию, то изображение также является вертикальной линией. Для наших целей мы будем иметь дело только с более простыми ситуациями, когда объект представляет собой вертикальную линию, нижняя часть которой расположена на главной оси. Для таких упрощенных ситуаций изображение представляет собой вертикальную линию с нижней конечностью, расположенной на главной оси.
Лучевая диаграмма выше показывает, что, когда объект расположен в позиции за пределами точки 2F, изображение будет расположено в позиции между точкой 2F и точкой фокусировки на противоположной стороне линзы.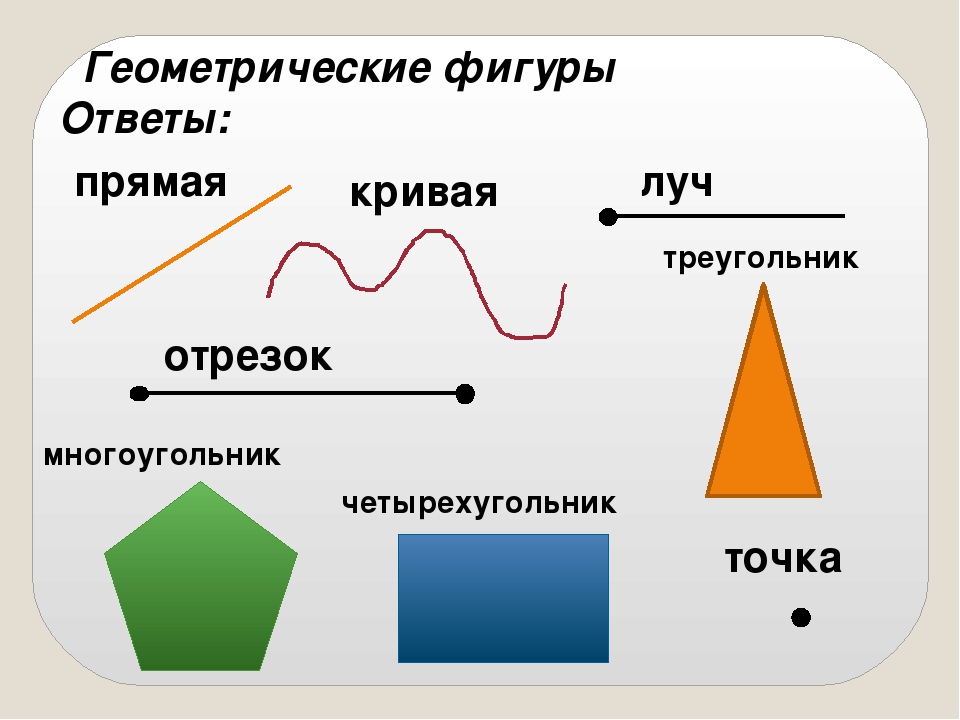 Кроме того, изображение будет инвертировано, уменьшено в размере (меньше размера объекта) и будет реальным. Это тип информации, которую мы хотим получить из лучевой диаграммы. Эти характеристики изображения будут рассмотрены более подробно в следующем разделе Урока 5.
Кроме того, изображение будет инвертировано, уменьшено в размере (меньше размера объекта) и будет реальным. Это тип информации, которую мы хотим получить из лучевой диаграммы. Эти характеристики изображения будут рассмотрены более подробно в следующем разделе Урока 5.
После того, как метод рисования лучевых диаграмм будет отработан пару раз, он станет таким же естественным, как дыхание. Каждая диаграмма дает конкретную информацию об изображении. На двух диаграммах ниже показано, как определить местоположение, размер, ориентацию и тип изображения для ситуаций, когда объект расположен в точке 2F и когда объект расположен между точкой 2F и точкой фокусировки.
Следует отметить, что процесс построения лучевой диаграммы одинаков вне зависимости от того, где находится объект. Хотя результат лучевой диаграммы (расположение, размер, ориентация и тип изображения) отличается, одни и те же три луча — это всегда , нарисованное . Три правила преломления применяются для определения места, в котором все преломленные лучи, по-видимому, расходятся (что для реальных изображений также является местом пересечения преломленных лучей).
В трех описанных выше случаях — в случае, когда объект расположен за пределами 2F, в случае, когда объект расположен в 2F, и в случае, когда объект находится между 2F и F, — световые лучи сходятся к точке после преломления. сквозь линзы. В таких случаях формируется реальное изображение . Как обсуждалось ранее, реальное изображение формируется всякий раз, когда преломленный свет проходит через местоположение изображения.В то время как расходящиеся линзы всегда создают виртуальные изображения, собирающие линзы способны создавать как реальные, так и виртуальные изображения. Как показано выше, реальные изображения создаются, когда объект находится на расстоянии более одного фокусного расстояния от объектива. Виртуальное изображение формируется, если объект расположен на расстоянии менее одного фокусного расстояния от собирающей линзы. Чтобы понять, почему это так, можно использовать диаграмму лучей.
Чтобы понять, почему это так, можно использовать диаграмму лучей.
Лучевая диаграмма для случая, когда объект расположен на расстоянии от , точка фокусировки показана на схеме справа.Обратите внимание, что в этом случае световые лучи расходятся после преломления через линзу. Когда преломленные лучи расходятся, формируется виртуальное изображение. Местоположение изображения можно найти, проследив все световые лучи назад, пока они не пересекутся. Каждому наблюдателю казалось бы, что преломленные лучи расходятся от этой точки; таким образом, точка пересечения протяженных преломленных лучей является точкой изображения. Поскольку свет на самом деле не проходит через эту точку, изображение называется виртуальным изображением. Заметьте, что когда объект расположен на перед фокусной точкой собирающей линзы, его изображение представляет собой вертикальное увеличенное изображение, расположенное на стороне объекта линзы.Фактически, одно обобщение, которое можно сделать в отношении всех виртуальных изображений, создаваемых линзами (как сходящихся, так и расходящихся), заключается в том, что они всегда находятся в вертикальном положении и всегда располагаются на стороне линзы объекта.
До сих пор мы видели с помощью лучевых диаграмм, что реальное изображение создается, когда объект находится на расстоянии более одного фокусного расстояния от собирающей линзы; и виртуальное изображение формируется, когда объект находится на расстоянии менее одного фокусного расстояния от собирающей линзы (т.е.е., перед F ). Но что происходит, когда объект находится в точке F? То есть, какой тип изображения формируется, когда объект находится ровно на одном фокусном расстоянии от собирающей линзы? Конечно, лучевая диаграмма всегда помогает найти ответ на такой вопрос. Однако, когда в этом случае используется диаграмма лучей, возникает непосредственная трудность. На схеме ниже показаны два падающих луча и соответствующие им преломленные лучи.
В случае объекта, расположенного в фокусной точке (F), световые лучи не сходятся и не расходятся после преломления через линзу. Как показано на диаграмме выше, преломленные лучи движутся параллельно друг другу. Впоследствии световые лучи не будут сходиться, чтобы сформировать реальное изображение; они также не могут быть вытянуты назад на противоположной стороне линзы, чтобы пересекаться для формирования виртуального изображения. Итак, как следует интерпретировать результаты лучевой диаграммы? Ответ: изображения нет !! Удивительно, но когда объект расположен в фокусной точке, в пространстве нет места, в котором наблюдатель мог бы видеть, откуда, кажется, исходят все преломленные лучи.Изображение не может быть найдено, если объект находится в фокусе собирающей линзы.
Как показано на диаграмме выше, преломленные лучи движутся параллельно друг другу. Впоследствии световые лучи не будут сходиться, чтобы сформировать реальное изображение; они также не могут быть вытянуты назад на противоположной стороне линзы, чтобы пересекаться для формирования виртуального изображения. Итак, как следует интерпретировать результаты лучевой диаграммы? Ответ: изображения нет !! Удивительно, но когда объект расположен в фокусной точке, в пространстве нет места, в котором наблюдатель мог бы видеть, откуда, кажется, исходят все преломленные лучи.Изображение не может быть найдено, если объект находится в фокусе собирающей линзы.
 Вы можете найти это в разделе Physics Interactives на нашем сайте.Optics Bench Interactive предоставляет учащимся интерактивную среду для изучения формирования изображений с помощью линз и зеркал. Это похоже на полный набор инструментов для оптики на вашем экране.
Вы можете найти это в разделе Physics Interactives на нашем сайте.Optics Bench Interactive предоставляет учащимся интерактивную среду для изучения формирования изображений с помощью линз и зеркал. Это похоже на полный набор инструментов для оптики на вашем экране.Работа с линзами и зеркалами
Диаграммы лучей могут выглядеть устрашающе, но это не обязательно! В этом сообщении блога мы рассмотрим пять примеров диаграмм лучей.
В следующих задачах мы хотим выяснить, какая диаграмма лучей представляет объект и его изображение. Для этого нам нужно отследить несколько лучей от объекта и определить, как они отражаются или преломляются.
Задача 1: выбрать правильную диаграмму лучей
В этой задаче мы имеем дело с выпуклой линзой. Нарисуем три луча, исходящие из верхней части объекта.
Сначала мы проводим луч через точку фокусировки на той же стороне, что и объект.Этот луч преломляется параллельно земле.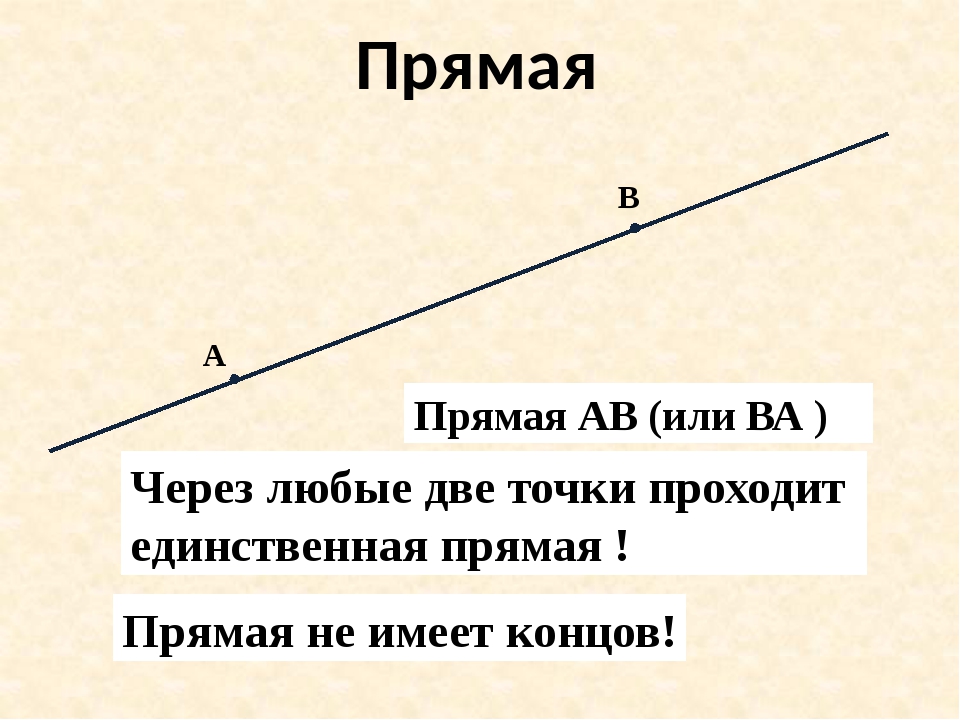 Далее мы рисуем луч, параллельный объекту. Этот луч будет преломляться через точку фокусировки на противоположной стороне линзы. Наконец, мы проводим луч через центр линзы. Этот луч не преломляется. Другими словами, он продолжит движение по своей первоначальной траектории.
Далее мы рисуем луч, параллельный объекту. Этот луч будет преломляться через точку фокусировки на противоположной стороне линзы. Наконец, мы проводим луч через центр линзы. Этот луч не преломляется. Другими словами, он продолжит движение по своей первоначальной траектории.
Теперь давайте объединим эти три луча и проследим их пути до точки пересечения. Точка пересечения ограничивает верхнюю часть изображения. Правильный ответ — А.
Как вы помните, объект в пределах фокусного расстояния собирающей линзы формирует вертикальное виртуальное изображение на той же стороне линзы, что и объект. Теперь вы можете нарисовать лучевые диаграммы, чтобы проиллюстрировать этот момент самому себе!
Задача 2
: выбрать правильную диаграмму лучей Здесь у нас есть еще одна выпуклая линза, но на этот раз наш объект находится на за пределами фокальной точки линзы. Опять же, давайте нарисуем три луча, каждый исходящий из верхней части объекта.
Сначала мы проводим луч через точку фокусировки на той же стороне, что и объект. Этот луч преломляется параллельно земле. Далее мы рисуем луч, параллельный земле. Этот луч будет преломляться через точку фокусировки на противоположной стороне линзы. Наконец, мы проводим луч через центр линзы. Как и в случае с предыдущей задачей, этот луч продолжит двигаться по своей первоначальной траектории.
Теперь давайте объединим эти три луча и проследим их пути до точки пересечения и обнаружим, что правильный ответ — D.Вывод здесь заключается в том, что объект за пределами фокусного расстояния линзы будет формировать перевернутое реальное изображение на противоположной стороне линзы.
Задача 3
: выбрать правильную диаграмму лучейТеперь у нас есть вогнутая линза, которая рассеивает свет, создавая виртуальное изображение на объектной стороне линзы.
Сначала мы рисуем пунктирную линию от кончика объекта до фокальной точки на противоположной стороне. Затем мы рисуем луч, движущийся в направлении пунктирной линии.Этот луч преломляется параллельно земле. Далее рисуем луч, параллельный земле. Затем мы проводим пунктирную линию от левого фокуса до линзы. Луч будет преломляться вдоль этой линии. Наконец, мы проводим луч через центр линзы. Как и в случае с предыдущей задачей, этот луч продолжит двигаться по своей первоначальной траектории.
Затем мы рисуем луч, движущийся в направлении пунктирной линии.Этот луч преломляется параллельно земле. Далее рисуем луч, параллельный земле. Затем мы проводим пунктирную линию от левого фокуса до линзы. Луч будет преломляться вдоль этой линии. Наконец, мы проводим луч через центр линзы. Как и в случае с предыдущей задачей, этот луч продолжит двигаться по своей первоначальной траектории.
Теперь давайте объединим эти три луча и проследим их траектории до точки пересечения и обнаружим, что правильный ответ — D. Вывод состоит в том, что вогнутая линза создает вертикальное виртуальное изображение на стороне линзы, являющейся объектом.
Задача 4
: выбрать правильную диаграмму лучей Теперь у нас есть вогнутое зеркало, которое может создавать виртуальное прямое изображение или реальное перевернутое изображение в зависимости от расположения объекта. В этой задаче объект находится в пределах фокусного расстояния, поэтому зеркало будет создавать вертикальное виртуальное изображение на противоположной стороне зеркала.
Напомним, что для линз нам нужно нарисовать три луча. Однако для зеркал нам нужно нарисовать только два.
Сначала мы проводим пунктирную линию от левого фокуса до зеркала.По этой траектории проводим луч от предмета к зеркалу. Этот луч будет отражаться параллельно земле. Далее рисуем луч, параллельный земле. Этот луч будет отражаться через левую точку фокусировки. Наконец, мы прослеживаем лучи до точки пересечения и видим, что ответ — B, виртуальное вертикальное изображение на противоположной стороне зеркала.
Вывод здесь заключается в том, что вогнутое зеркало создает виртуальное вертикальное изображение, когда объект находится в пределах фокусного расстояния зеркала.
Задача 5
: выбрать правильную диаграмму лучейНаша последняя задача связана с выпуклым зеркалом. Выпуклые зеркала рассеивают свет и создают виртуальные вертикальные изображения на противоположной стороне зеркала.
Как и в предыдущей задаче о зеркале, здесь нам нужно нарисовать только два луча. Сначала мы рисуем пунктирную линию от кончика объекта до фокальной точки на противоположной стороне зеркала. По этой траектории проводим луч от кончика предмета до зеркала.Этот луч будет отражаться параллельно земле.
Сначала мы рисуем пунктирную линию от кончика объекта до фокальной точки на противоположной стороне зеркала. По этой траектории проводим луч от кончика предмета до зеркала.Этот луч будет отражаться параллельно земле.
Далее мы рисуем луч, параллельный земле. От точки, где луч попадает в зеркало, мы проводим пунктирную линию до фокальной точки на другой стороне зеркала. Луч будет отражаться по траектории этой пунктирной линии.
Наконец, мы прослеживаем лучи до точки пересечения и видим, что ответ — B, виртуальное вертикальное изображение с другой стороны зеркала.
Вывод здесь заключается в том, что выпуклое зеркало всегда создает виртуальное вертикальное изображение на противоположной стороне зеркала.
Наши преподаватели физики — докторанты и кандидаты наук. В нашу команду также входят кандидаты на степень доктора медицины, доктора медицины и доктора наук. Наши преподаватели физики находятся на передовых позициях в своей области и имеют обширный опыт преподавания двух AP, SAT II и GRE Subject Test, а также раздела MCAT по физике. Многие студенты работают с репетитором в течение всего учебного года, используя еженедельные занятия, чтобы закрепить сложные концепции, проанализировать наборы задач и подготовиться к экзаменам. Все наши репетиторы по физике могут помочь студентам с расчетами, необходимыми для более продвинутых курсов по физике.
Многие студенты работают с репетитором в течение всего учебного года, используя еженедельные занятия, чтобы закрепить сложные концепции, проанализировать наборы задач и подготовиться к экзаменам. Все наши репетиторы по физике могут помочь студентам с расчетами, необходимыми для более продвинутых курсов по физике.
Хотите узнать больше об услугах репетиторства по физике? Ознакомьтесь с некоторыми другими полезными сообщениями в блоге ниже !:
Советы по сдаче экзаменов по предмету SAT Тест по физике
Проверка ответов по физике
Что таблицы с уравнениями физики могут сделать для вас и чего они на самом деле не могут
Что такое луч в геометрии? | Определение и примеры (видео)
Найдите светодиодный фонарик.Войдите в темную комнату и включите фонарик. Вы только что смоделировали луч, плоскую фигуру в геометрии, которая имеет одну конечную точку, но вечно продолжается в другом направлении.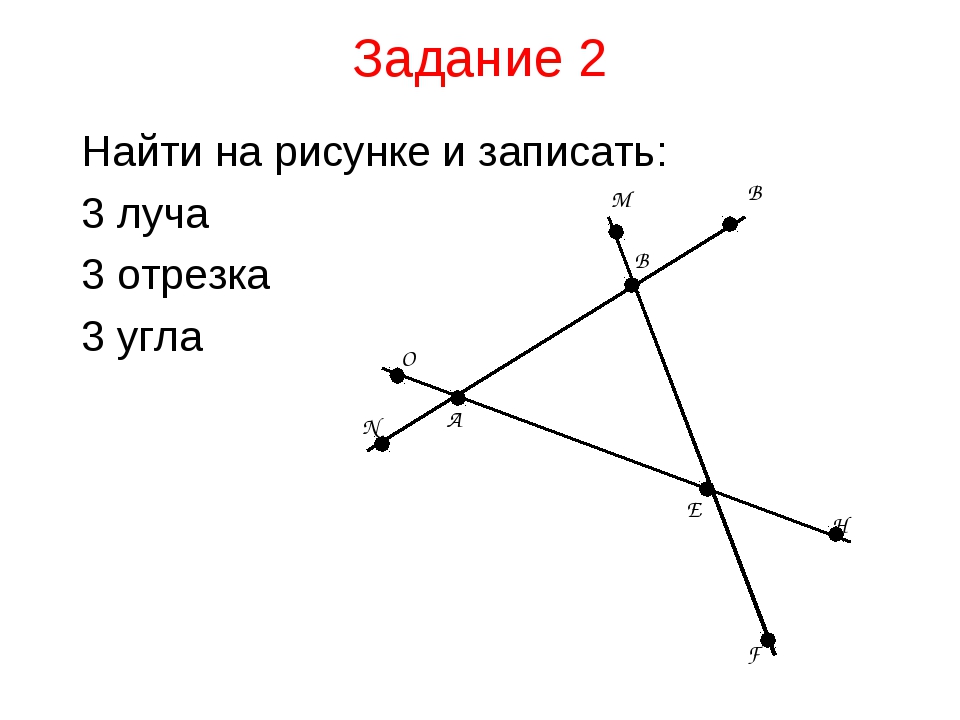 Лучи и реальные примеры лучей есть повсюду.
Лучи и реальные примеры лучей есть повсюду.
Содержание
- Видео
- Определение луча в геометрии
- Как нарисовать луч по математике
- Символ и этикетка Ray
- Луч в примерах геометрии
Определение лучей в геометрии
Луч можно рассматривать как фрагмент или сегмент линии.В плоской геометрии луч легко построить по двум точкам. Один будет конечной точкой, началом луча. Другой момент — это просто указатель, способ дать лучу имя. Линия, соединяющая две точки, тянется бесконечно только в одном направлении:
Вместо того, чтобы позволять обоим концам линии длиться вечно, мы обрезаем одну сторону в заданной точке. Теперь у нас есть луч.
Как нарисовать луч по математике
Чтобы нарисовать луч, поместите две точки на листе бумаги.Обозначьте обе точки заглавными буквами. Выберите одну точку в качестве конечной. Используйте линейку, чтобы нарисовать линию, начиная с конечной точки и продолжая через вторую точку. Нарисуйте одну стрелку на открытом конце вашей линии (тот, который находится напротив конечной точки). Там! У вас есть луч:
Нарисуйте одну стрелку на открытом конце вашей линии (тот, который находится напротив конечной точки). Там! У вас есть луч:
Символ и этикетка Ray
Чтобы обозначить и обозначить луч, нам нужно идентифицировать эту конечную точку. Нам также понадобится еще одна точка на односторонней линии. Затем мы записываем конечную точку и другую точку вместе заглавными буквами, ограниченными крошечной односторонней стрелкой (указывающей вправо):
Это символ Рэя Р.Н. →, названного в честь квотербека НФЛ, который может бросать футбольный мяч, который движется почти как луч.Гравитация тянет мяч вниз, но скорость и сила рук квотербэков могут сделать короткие передачи похожими на прямые лучи. Он конечная точка; Путешествующий футбол — это линия с односторонним движением.
Луч в примерах геометрии
Луч солнечного света есть луч. Он берет начало у нашей звезды, Солнца, и движется в одном направлении, ударяясь о Землю примерно через восемь минут после того, как покинул свою «конечную точку», Солнце.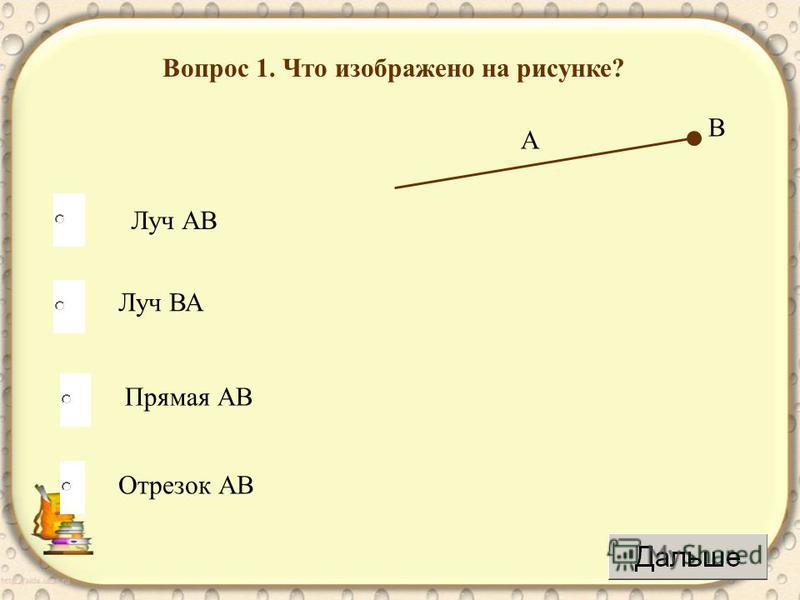
Профессиональный теннисист Рафаэль Надаль, как известно, подает теннисные мячи со скоростью около 217 км / ч (135 миль / ч), которая так хорошо сопротивляется силе гравитации, что кажется, будто летит по прямой, как луч.
Луч света от классного ЖК-проектора — луч; так же свет от кинопроектора в вашем местном кинотеатре.
Путь, по которому стрела идет из лука, представляет собой луч и имеет дополнительное преимущество в том, что он имеет форму стрелы.
Лазеры являются прекрасным примером лучей, потому что в отличие от спортивных мячей на них не сильно влияет земная гравитация, поэтому они светят ровными прямыми односторонними линиями от своего источника.
Предупреждение
Поскольку англоговорящие люди, читатели и писатели двигают глазами слева направо, почти все лучи, которые вы видите в математических символах, будут иметь левые конечные точки и правые стрелки.Однако имейте в виду, что геометрия — это чистая наука .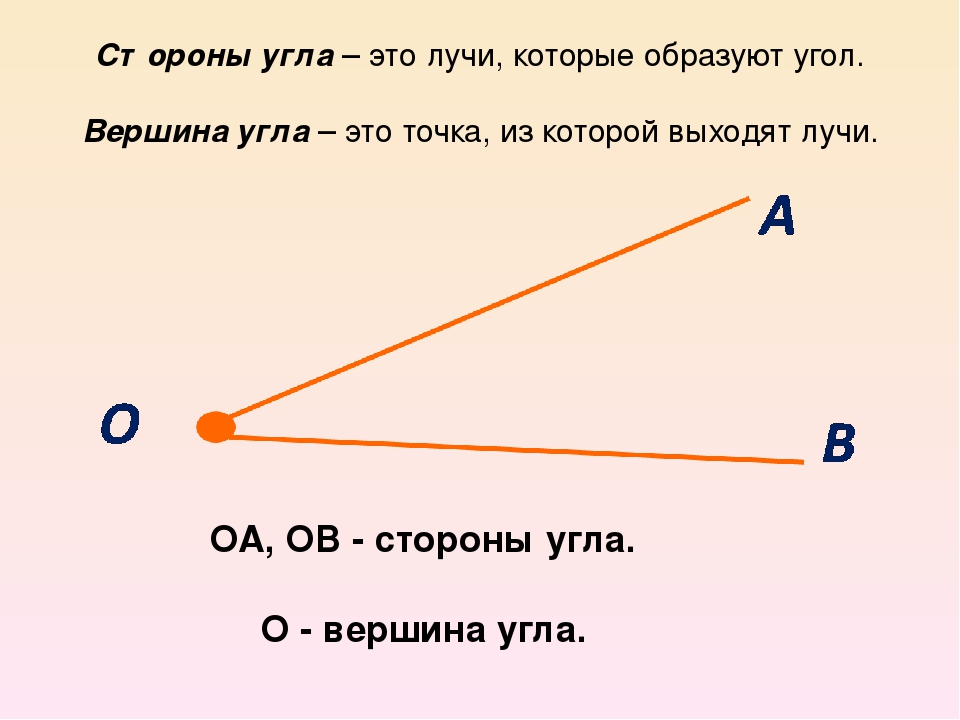 Лучи могут идти в любом направлении, например, вверх, вниз, влево, вправо и по диагонали.
Лучи могут идти в любом направлении, например, вверх, вниз, влево, вправо и по диагонали.
Следующий урок:
Что такое прямая линия?
9.3.2: Линзы и трассировка лучей
В этом разделе мы узнаем, как использовать точки фокусировки, чтобы определить, как линзы изгибают световые лучи. Для каждой из наших линз есть три луча, которые легко найти, если мы знаем только точку фокусировки и положение объекта — мы называем эти специальные лучи основными лучами .Мы покажем, как найти главные лучи как для собирающей, так и для расходящейся линзы.
Начнем с некоторых общих замечаний, касающихся как собирающих, так и расходящихся линз. В задаче линзы мы начинаем с объекта , реального предмета, отражающего реальный свет. Обычно мы представляем этот объект в виде стрелки, чтобы по окончательному изображению можно было определить, перевернут ли объект линзой.
Мы обсудили, что является фокусом для объектива; для симметричной линзы у нас есть две точки фокусировки с каждой стороны. Для собирающей линзы лучи, параллельные оптической оси, падающие на правую сторону линзы, фокусируются слева, параллельные лучи слева фокусируются справа.
Для собирающей линзы лучи, параллельные оптической оси, падающие на правую сторону линзы, фокусируются слева, параллельные лучи слева фокусируются справа.
Фокусное расстояние объектива \ (f \) говорит нам, как далеко от объектива находятся точки фокусировки. Величина , фокусного расстояния — это расстояние от линзы до каждой точки фокусировки, а знак сообщает нам, сходится ли линза или расходится. Для собирающей линзы возьмем \ (f> 0 \), а для расходящейся линзы — \ (f <0 \).Типичная диаграмма объектива и его характеристики (т. Е. Точки фокусировки и оптическая ось) показаны ниже.
Как видно из рисунка выше, на визуальных схемах линз обычно не отображается вся линза. Мы делаем приближение, что линза тонкая и что преломление (изгиб) происходит только один раз в центре линзы. Чтобы сделать это приближение ясным, мы изображаем линзу вертикальной линией и стрелками, направленными наружу и внутрь, чтобы указать нам, сходится ли линза или расходится соответственно.
Как найти изображение по сформированному ниже объекту? На данный момент позвольте нам просто спросить о кончике стрелки. Мы знаем, что чтобы найти изображение точки, мы должны смотреть на несколько лучей из этой точки и видеть, куда они идут. Начнем с рисования множества разных лучей, исходящих от объекта. Каждый из этих лучей преломляется. Из нарисованных падающих лучей есть три луча (обозначенные ниже 1, 2 и 3), для которых мы можем нарисовать преломленный луч, не выполняя никаких вычислений.
Луч 1 параллелен оптической оси; мы знаем, что лучи, параллельные оптической оси, падающие на линзу, преломляются через точку фокусировки на другой стороне линзы.Мы также обсудили, насколько тонкая линза, поэтому мы можем приблизительно представить луч 2, проходящий через центр, как проходящий через тонкий лист стекла; она не преломляется заметно.
Сделанные выше выводы можно отобразить визуально:
Луч, помеченный цифрой 3, требует большего внимания.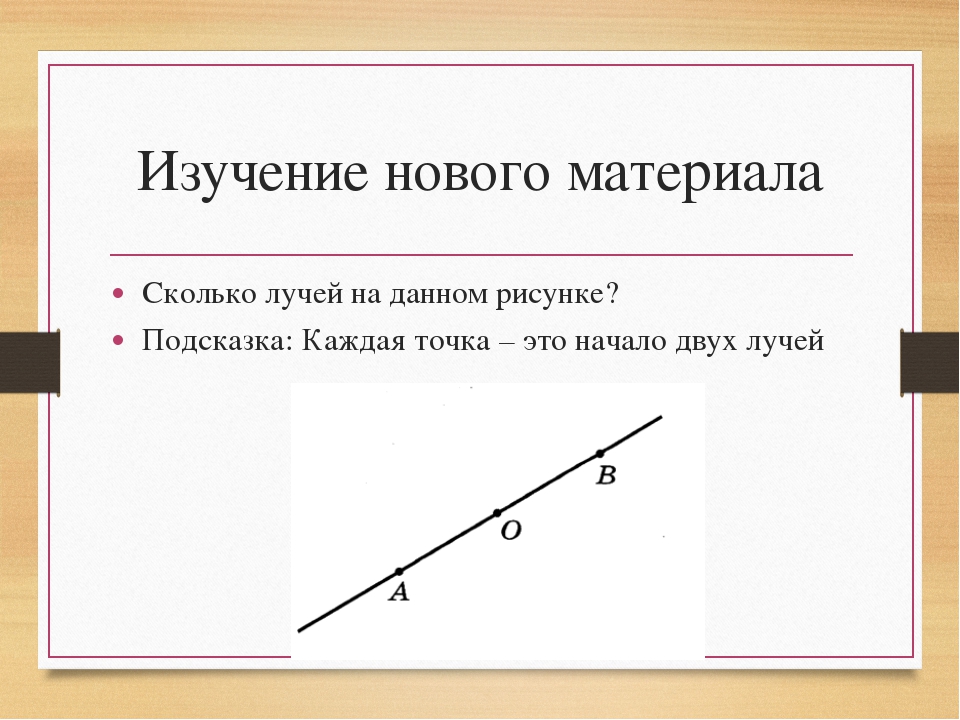 Во-первых, вспомните из закона Снеллиуса, что преломление происходит симметрично в любом направлении (не имеет значения, какая среда имеет метку «1» или «2»; они обратимы).Как следствие, мы видим, что свет, который попадает в линзу с через точку фокусировки , преломляется в направлении , параллельном оптической оси .
Во-первых, вспомните из закона Снеллиуса, что преломление происходит симметрично в любом направлении (не имеет значения, какая среда имеет метку «1» или «2»; они обратимы).Как следствие, мы видим, что свет, который попадает в линзу с через точку фокусировки , преломляется в направлении , параллельном оптической оси .
На диаграмме ниже этот вывод явно показан на луче 3:
Обратите внимание, что все эти лучи пересекаются в определенном месте. Это то место, где острие стрелки будет казаться любому наблюдателю справа от линзы. Световые лучи, проходящие мимо этой точки, выглядят так, как если бы здесь был помещен настоящий наконечник стрелы.Поскольку разработчик линзы (мы предполагаем) сделал линзу точно, все остальные световые лучи должны быть сфокусированы так же, как первые три, которые мы нарисовали. Рисуя все световые лучи, мы получаем картинку:
. Обратите внимание, что из этого анализа мы видим только то, где будет изображение наконечника стрелки. Поскольку мы не знаем, где будет изображение основания, мы просто нарисовали вопросительные знаки внизу стрелки. Точки на оптической оси немного сложнее отследить лучи, потому что все основные лучи, представленные там, проходят через центр линзы.Мы вернемся к вопросу об оптической оси после обсуждения расходящихся линз. Поскольку в этом примере световые лучи фактически пересекаются, мы назвали бы это реальным изображением .
Поскольку мы не знаем, где будет изображение основания, мы просто нарисовали вопросительные знаки внизу стрелки. Точки на оптической оси немного сложнее отследить лучи, потому что все основные лучи, представленные там, проходят через центр линзы.Мы вернемся к вопросу об оптической оси после обсуждения расходящихся линз. Поскольку в этом примере световые лучи фактически пересекаются, мы назвали бы это реальным изображением .
Если нас интересует только расположение изображения, то нам нужно только узнать, где пересекаются три главных луча. Три главных луча:
- Луч, попадающий в линзу параллельно оптической оси; этот луч изгибается, чтобы пройти через точку фокусировки.
- Луч, проходящий через центр; этот луч не гнет.
- Луч, проходящий через точку фокусировки в линзу; этот луч преломляется, чтобы быть параллельным оптической оси.
В типичных оптических задачах мы будем рисовать только главные лучи, хотя важно понимать, что — все световые лучи, которые проходят через линзу и отвечают за формирование изображения.
Наша процедура получения расходящихся линз аналогична описанной выше для собирающих линз.Сначала мы должны нарисовать три основных луча. Первый главный луч, луч 1, выходит из объекта параллельно оптической оси и изгибается так, что кажется, что луч исходит из точки фокусировки, как показано ниже. Пунктирный луч показывает, откуда, по-видимому, исходит световой луч. Мы также включаем луч 2, который проходит через центр без преломления.
Третий главный луч снова получается с учетом обратимости рефракции (и симметрии линзы).Мы знаем, что любой свет, идущий параллельно оптической оси, изгибается так, что кажется, что он исходит на из фокальной точки. Думая о свете, движущемся в другую сторону, мы можем видеть, что свет от стрелки, направленной в сторону фокуса с правой стороны, преломляется линзой, чтобы быть параллельным оптической оси. Мы показываем это ниже, где мы отмечаем, что пунктирная линия справа указывает, куда бы прошел световой луч , если бы там не было линзы.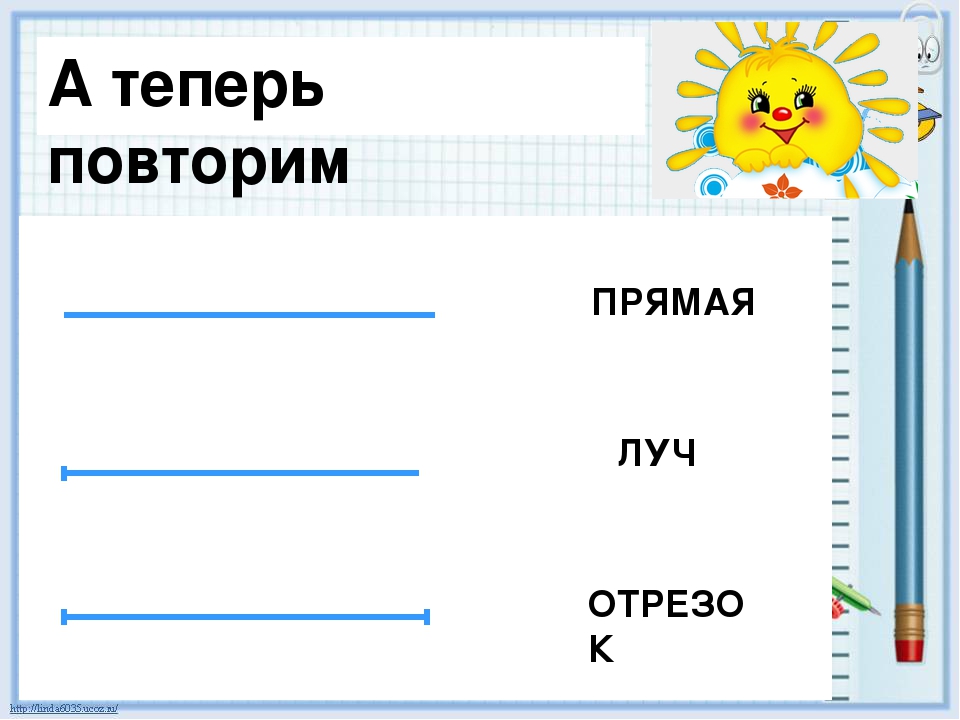
Обычно мы не рисуем там, где бы прошел световой луч ; это полезно только для того, чтобы показать вам, где провести черту.Пунктирная линия слева, показывающая, откуда, по-видимому, исходит свет, невероятно важна; Человек, наблюдающий за светом справа от линзы, может подумать, что этот луч движется параллельно оптической оси.
Сложим все три луча вместе:
Отметим, что в отличие от нашего предыдущего примера световые лучи (сплошные линии) на самом деле никуда не пересекаются. Однако наблюдатель справа от нашей линзы может подумать, что свет исходит из точки пересечения пунктирных линий.Поскольку изображение расположено на пересечении воображаемых лучей, а не реальных световых лучей, мы называем это виртуальным изображением .
Чтобы было немного понятнее, почему изображение, которое видит человек справа, совпадает с маленькой стрелкой на пересечении пунктирных линий, полезно вспомнить, что такое изображение. Мы могли бы спросить: «Если бы не было линзы, объект какого размера нам понадобился бы и где нам нужно было бы его разместить, чтобы свет, который доходит до нас, выглядел точно так же?» В приведенных выше примерах мы покажем, как найти эту информацию.
Мы могли бы спросить: «Если бы не было линзы, объект какого размера нам понадобился бы и где нам нужно было бы его разместить, чтобы свет, который доходит до нас, выглядел точно так же?» В приведенных выше примерах мы покажем, как найти эту информацию.
В обоих примерах вы можете заменить линзу и исходную стрелку стрелкой в точке пересечения лучей. Мы видим, что эти конфигурации кажутся абсолютно одинаковыми любому наблюдателю справа. Если вы стоите справа, единственная информация, которую имеют ваши глаза, — это световые лучи, которые попадают в них, и вы не можете различить эти две ситуации. Мы можем видеть, что световые лучи перед попаданием в линзу выглядят совершенно иначе, но это не влияет на наблюдателя справа от линзы.
Мы завершаем этот раздел, резюмируя, как найти три основных луча для расходящейся линзы:
- Луч, идущий параллельно оптической оси, преломляется так, что кажется, что он исходит из фокальной точки на стороне линзы объектива.
- Луч, проходящий через центр, не отклоняется.

- Луч, который прошел бы через точку фокусировки на дальней стороне линзы, преломляется и становится параллельным оптической оси.
Пока что мы нашли расположение изображения только для кончиков представленных стрелок.Попытка найти местоположение изображения для основания стрелки приводит к проблеме для рассмотренных до сих пор примеров, потому что основание стрелки находилось на оптической оси. Как для собирающих, так и для расходящихся линз проблема связана с оптической осью. Причина в том, что луч, который проходит через центр линзы , также проходит через обе точки фокусировки. Наш метод построения трех главных лучей не работает ни в одной точке на оптической оси, поскольку все три главных луча одинаковы.
Однако мы знаем, что точки на оптической оси имеют изображения на оптической оси. Мы знаем это, потому что один главный луч, который мы можем нарисовать для точки на оптической оси, всегда находится на оптической оси, и мы знаем, что на изображении лучи, проходящие через ось, встречаются (или кажутся исходящими).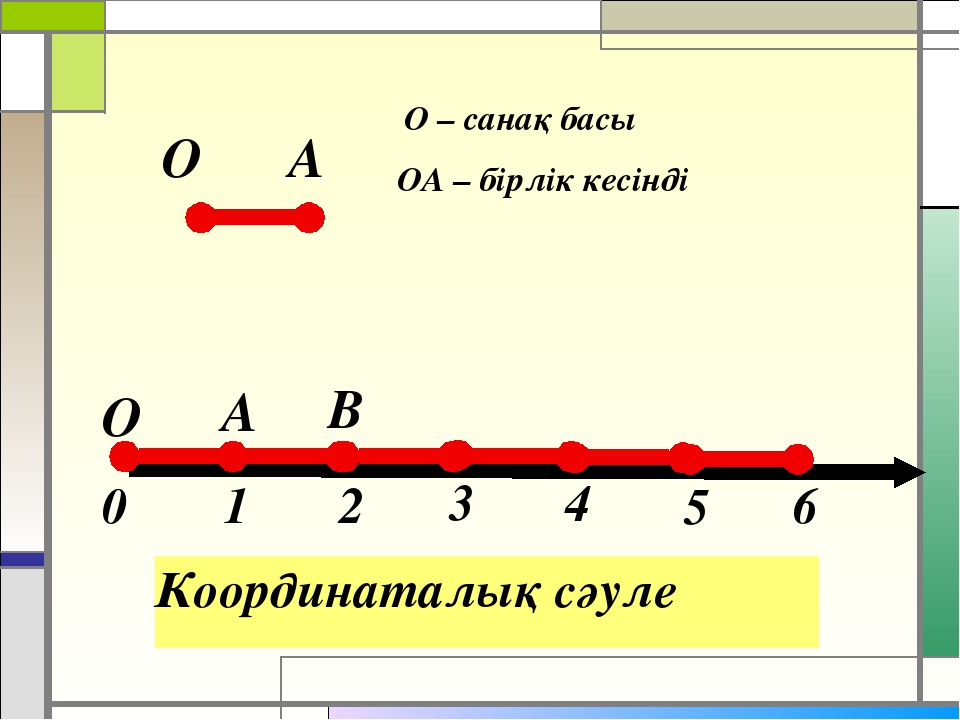 Поскольку у нас есть один луч, который всегда находится на оптической оси, изображение также должно быть на оптической оси.
Поскольку у нас есть один луч, который всегда находится на оптической оси, изображение также должно быть на оптической оси.
Так как же нам найти там, где вдоль оптической оси формируется изображение? Один из способов найти это — нарисовать точку, которая очень близко к оптической оси, но не совсем на ней, и вместо этого выполнить трассировку лучей для этой точки.Другой способ использует информацию, которую мы представим позже, — уравнение для тонкой линзы . Какой бы способ вы ни выбрали, в результате расстояние изображения для основания стрелки будет таким же, как расстояние до изображения для кончика стрелки (при условии, что кончик исходной стрелки находится непосредственно над основанием). Отсюда мы будем рисовать наши изображения стрелок вниз (или вверх) от кончика к оптической оси. Если основание вашего объекта не находится на оптической оси, отдельная трассировка лучей для основы необходима для завершения всего изображения.
.

 Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
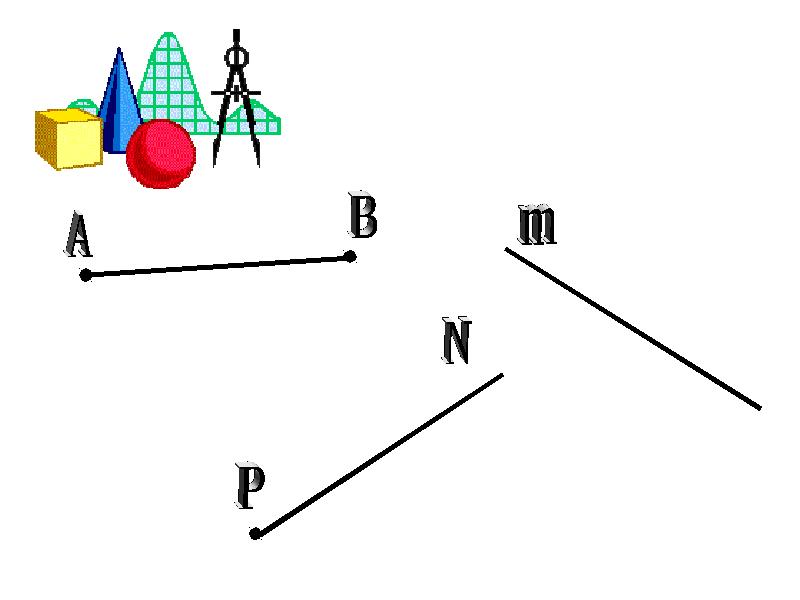 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.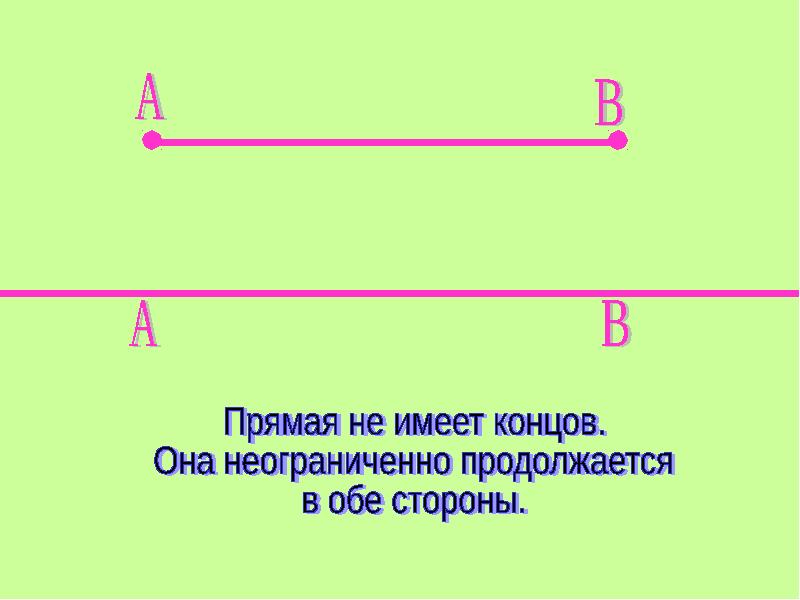 У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
 — М: 2013.
— М: 2013. общеобразовательных учреждений.
общеобразовательных учреждений. Это лучи. Желательно придерживаться одинакового расстояния между лучами, для этого можно воспользоваться линейкой, но этот инструмент нежелателен в рисовании.
Это лучи. Желательно придерживаться одинакового расстояния между лучами, для этого можно воспользоваться линейкой, но этот инструмент нежелателен в рисовании.

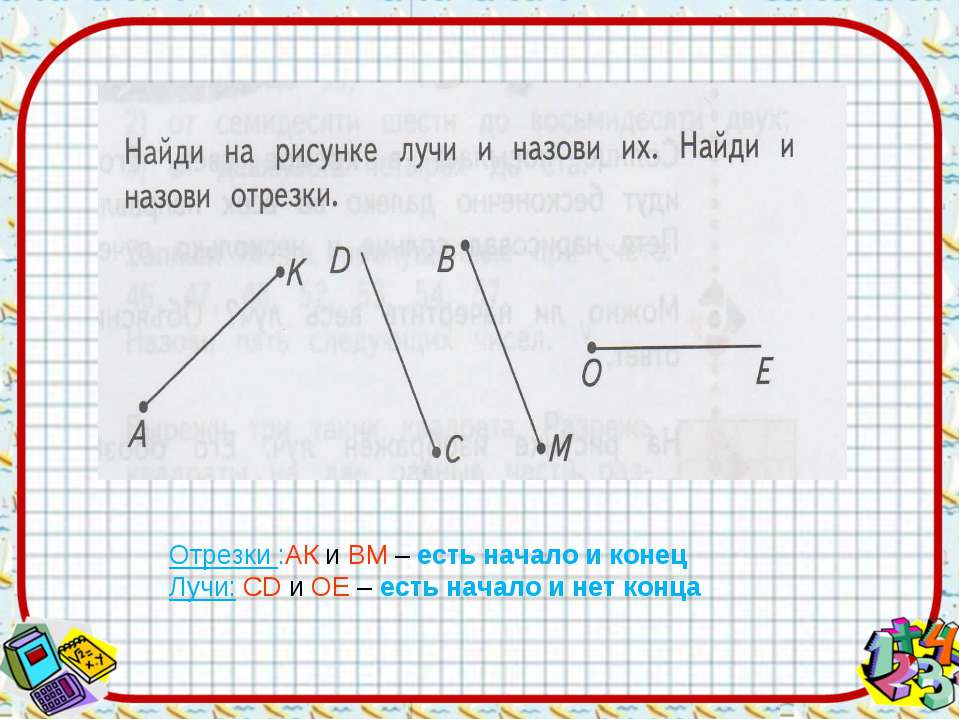 Когда Вы проделаете то же самое со всех четырёх сторон, солнышко станет похоже на компас. Такой расчёт позволит сделать фигурку идеально ровной, она будет смотреться максимально аккуратно.
Когда Вы проделаете то же самое со всех четырёх сторон, солнышко станет похоже на компас. Такой расчёт позволит сделать фигурку идеально ровной, она будет смотреться максимально аккуратно.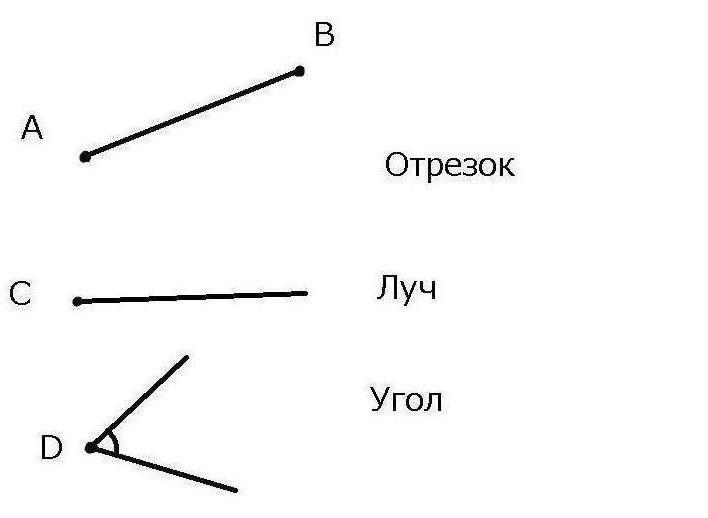
 Нарисуйте второй луч так, чтобы он двигался точно параллельно главной оси. Поместите стрелки на лучи, чтобы указать направление их движения.
Нарисуйте второй луч так, чтобы он двигался точно параллельно главной оси. Поместите стрелки на лучи, чтобы указать направление их движения. Это просто точка, где весь свет от верхней части объекта пересекается при отражении от зеркала.Конечно, остальная часть объекта также имеет изображение, и его можно найти, применив те же три шага к другой выбранной точке. (См. Примечание ниже.)
Это просто точка, где весь свет от верхней части объекта пересекается при отражении от зеркала.Конечно, остальная часть объекта также имеет изображение, и его можно найти, применив те же три шага к другой выбранной точке. (См. Примечание ниже.) . На этом этапе можно заполнить все изображение.
. На этом этапе можно заполнить все изображение.
 (См. Примечание ниже.)
(См. Примечание ниже.)