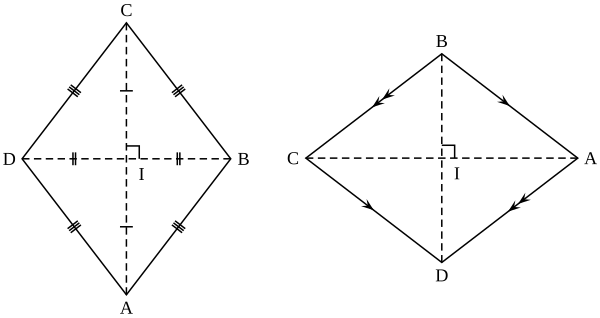
Как нарисовать объемный ромб. Ромбы спицами ‒ простые узоры
Ромб — это простая геометрическая фигура, имеющая четыре вершины и поэтому являющаяся одним из частных случаев параллелограмма. От других многоугольников этого рода ее отличает равенство длин всех сторон. Этой особенностью определяется и то, что углы в противоположных вершинах фигуры имеют одинаковую величину. Построить ромб можно несколькими способами — например, с использованием циркуля.
Вам понадобится
- Лист, карандаш, циркуль, линейка, транспортир.
Инструкция
- Поставьте на противоположных краях листа две произвольные точки, которые будут противоположными вершинами ромба, и обозначьте их буквами A и С.
- Поставьте вспомогательную точку приблизительно в том месте, где должна находиться третья вершина фигуры. Расстояние от нее до вершин A и C должно быть одинаковым, но соблюдать абсолютную точность на этом шаге не требуется.
- Отмерьте циркулем расстояние от точки A до вспомогательной точки и начертите полукруг с центром в точке A, обращенный в сторону точки C.

- Начертите такой же полукруг (не меняя отложенного на циркуле расстояния), имеющий центром точку C и направленный в сторону точки A.
- Поставьте точки B и D в местах верхнего и нижнего пересечения полукругов и проведите соединительные линии между точками A и B, B и C, C и D, D и A. На этом построение ромба с произвольной стороной и углами будет завершено.
- Если требуется построить ромб с заданной длиной сторон, то сначала отложите на циркуле это значение. Затем поставьте точку A, которая будет одной из вершин четырехугольника, и начертите полукруг в направлении предполагаемой противоположной вершины.
- Поставьте точку C в том месте, где вы хотели бы видеть противоположную вершину. Исходите из того, что расстояние от очерченного полукруга до этой вершины должно быть меньше отложенного на циркуле расстояния. Чем меньше будет это расстояние, тем шире получится ромб.
- Повторите действия, описанные в пятом и шестом шагах. После этого построение ромба со сторонами заданной длины будет завершено.

- Если требуется построить ромб с заданным углом, то сначала обозначьте произвольными точками A и B две соседние вершины ромба и соедините их отрезком.
- Отложите на циркуле длину отрезка AB и начертите полукруг с центром в точке A. Все последующие построения производите, не меняя отложенного на циркуле расстояния.
- Приложите транспортир к отрезку AB таким образом, чтобы нулевая отметка совпала с точкой A, отмерьте заданный угол и поставьте вспомогательную точку.
- Проведите отрезок прямой, начинающийся в точке A, проходящий через вспомогательную точку и заканчивающийся на начерченном ранее полукруге. Обозначьте точку окончания отрезка буквой D.
- Начертите два направленных друг к другу полукруга с центрами в точках B и D. Одной из точек пересечения полукружий будет уже существующая точка A, а другую обозначьте буквой C и соедините ее с точками B и D. На этом построение ромба с заданным углом будет завершено.
Иногда появляется необходимость сделать элементарное дело, при этом обнаруживается, что мы не знаем, как это сделать. Например — как нарисовать ромб. На самом деле все очень просто.
Например — как нарисовать ромб. На самом деле все очень просто.
В данной статье вы узнаете, как правильно нарисовать ромб, и что это за геометрическая фигура.
Что такое ромб?
Ромб является разновидностью параллелограмма, особенностью которого является то, что противоположные стороны этой фигуры параллельны друг к другу, а у ромба они еще и равны между собой. Об определении ромба к общему виду параллелограмма говорит факт равенства противоположных углов.
Как нарисовать ромб
Нарисовать такую фигуру как ромб можно несколькими способами. В этой статье мы рассмотрим два простых способа.
Для первого способа нам понадобятся: ручка или карандаш, ластик, лист в клетку из школьной тетради, линейка или любой похожий на него прямой предмет, если размеры точные размеры ромба не важны.
- Итак, для начала нарисуем точку на одном из пересечений линий клеток. Лучше, конечно, разместить точку не слишком близко к краям. Определяемся с размерами фигуры.

- Далее от средней точки отсчитываем необходимое количество клеток влево (или вправо) и ставим еще одну точку. В противоположной стороне через такое же количество клеток рисуем третью точку. Теперь то же самое проделываем по направлению вверх и вниз. Последовательность не имеет значения, главное здесь — отсчитать одинаковое расстояние от средней точки влево и вправо и отдельно вверх и вниз. То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.
- Соединяем линейкой или любым другим подходящим предметом все точки между собой, кроме среднего. Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов.
Второй способ аналогичен первому, но рисовать мы будем на чистой бумаге без клеток. Нам нужно для этого: карандаш и/или ручка, ластик, чистый лист, линейка и угольник (или любой предмет с прямым углом).
 Соединяем их карандашом, чтобы линия проходила через среднюю точку. Аналогичные действия производим и в противоположную сторону.
Соединяем их карандашом, чтобы линия проходила через среднюю точку. Аналогичные действия производим и в противоположную сторону.Ромб – одна из простейших геометрических фигур. Мы настолько часто встречаемся с ромбом в геометрических задачках, что слова «фантастика» и «ромб» кажутся для нас несовместимыми понятиями. А между тем, удивительное, как говорится, рядом… в Британии. Но для начала, давайте вспомним, что же такое «ромб», его признаки и свойства.
Термин «ромб» в переводе с древнегреческого означает «бубен». И это не случайно. А дело вот в чем. Бубен хоть раз в жизни, но видели все. И все знают, что он круглый. Но давным-давно бубны делали как раз в форме квадрата или ромба. Более того, название масти бубны также связанно именно с этим фактом.
Из геометрии мы представляем, как выглядит ромб. Это четырехугольник, который изображается в виде как бы наклоненного квадрата. Но путать ромб и квадрат ни в коем случае нельзя. Правильнее сказать, что ромб – это частный случай параллелограмма. Отличие лишь в том, что все стороны ромба равны. Чтобы быстро и верно решать задачи по геометрии, необходимо помнить о свойствах ромба. К слову, ромб обладает всеми свойствами параллелограмма. Итак:
Свойства ромба:
- противолежащие стороны равны;
- противоположные углы равны;
- диагонали ромба пересекаются под прямым и в точке пересечения делятся пополам;
- сумма углов, прилежащих к одной стороне, равна 180°;
- сумма квадратов диагоналей равна сумме квадратов всех сторон;
- диагонали являются биссектрисами его углов.
Признаки ромба:
- если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб;
- если диагональ параллелограмма является биссектрисой его угла, то параллелограмм – ромб.

И еще один важный момент, без знания которого не возможно успешно решить задачку, – формулы. Ниже представлены формулы для нахождения площади любого ромба, которые употребляются в зависимости от известных данных: высота, диагональ, сторона, радиус вписанной окружности. В следующих формулах приняты условные обозначения: a – сторона ромба, h a – высота, проведенная к стороне а, а – угол между сторонами, d 1 d 2 – диагонали ромба.
Основные формулы:
S = a 2 sin а
S = 1/2 (d 1 d 2)
S = 4r 2 / sin a
Есть еще одна формула, которая употребляется не так часто, но полезна:
d 1 2 + d 2 2 = 4a 2 или сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
А теперь самое время вернуться к самому началу. Что же такого удивительного может быть в этой фигурке? Оказывается, в XIX веке при археологических раскопках был найден ромб. Да не простой, а золотой, при чем, в самом прямом смысле этого слова! Эта находка из великобританского кургана Баш была найдена в районе Уилсфорда, неподалёку от знаменитого Стоунхенджа. Загадочный ромб представляет собой отполированную пластинку, на которой выгравированы необычные узоры. Размер его 15,2 х 17,8 см (ромб лишь с небольшой оговоркой). У пластины кроме окантовки есть еще три меньших ромбовидных узора, которые якобы вложены друг в друга. При этом, в центре последнего выгравирована ромбическая сетка. По краям ромба изображен шевронный рисунок – по девять символов на каждой стороне ромба. Всего таких треугольников тридцать шесть.
Загадочный ромб представляет собой отполированную пластинку, на которой выгравированы необычные узоры. Размер его 15,2 х 17,8 см (ромб лишь с небольшой оговоркой). У пластины кроме окантовки есть еще три меньших ромбовидных узора, которые якобы вложены друг в друга. При этом, в центре последнего выгравирована ромбическая сетка. По краям ромба изображен шевронный рисунок – по девять символов на каждой стороне ромба. Всего таких треугольников тридцать шесть.
Безусловно, данное изделие очень дорого стоит, но также очевидно, что создание такого ромба преследовало какую-то определенную цель. Вот только какую, ученые долго не могли разгадать.
Одна из более правдоподобных и принятых версий касается непосредственно Стоунхенджа. Известно, что сооружения Стоунхенджа возводились постепенно, в течение нескольких столетий. Считается, что строительство началось около 3000 года до н.э. Следует учесть, что золото в Британии стало известно уже где-то с 2800 года до н.э. Отсюда можно сделать предположение, что золотой ромб вполне мог быть инструментом жреца. В частности, визира. Такую гипотезу предложил вниманию современных ученых профессор А. Том, известный исследователь Стоунхенджа, в последней четверти ХХ века.
В частности, визира. Такую гипотезу предложил вниманию современных ученых профессор А. Том, известный исследователь Стоунхенджа, в последней четверти ХХ века.
Не все могут себе представить, что древние строители могли с точностью определить углы на местности. Тем не менее, английский исследователь Д. Фарлонг предложил метод, которым, по его мнению, могли пользоваться древние египтяне. Фарлонг считал, что наши предки использовали заранее подобранные соотношения сторон в прямоугольных треугольниках. Ведь давно известно, что египтяне широко применяли треугольник со сторонами в три, четыре и пять мерных единиц. Видимо, множество подобных приёмов знали и древние жители Британских островов.
Что ж, даже если представить, что люди, которые строили Стоунхендж, были отличнейшими геодезистами, как в этом мог помочь им золотой ромб? Едва ли какой-нибудь современный геодезист сможет ответить на этот вопрос. Вероятнее всего, тот факт, что Фарлонг был геодезистом по профессии, дал возможность ему разгадать эту загадку. После внимательного изучения исследователь пришел к выводу, что отполированный золотой ромб с разметкой отлично подходит для применения его в качестве отражателя солнечных лучей, иначе говоря, особого мерного зеркала.
После внимательного изучения исследователь пришел к выводу, что отполированный золотой ромб с разметкой отлично подходит для применения его в качестве отражателя солнечных лучей, иначе говоря, особого мерного зеркала.
Было доказано, что для быстрого определения азимута на местности с достаточно небольшими погрешностями необходимо было использовать два подобные зеркала. Схема же была такова: один жрец, например, становился на вершине одного холма, а другой в прилегающей долине. Нужно было также предварительно установить расстояние между жрецами. Это можно сделать просто шагами. Хотя обычно пользовались мерной тростью, так как результаты были более достоверны. Два ромбовидных металлических зеркалаобеспечиваютпрямой угол. А потом уже легко отмерить практически любые требуемые углы. Д. Фарлонг привел даже таблицу таких пар целых чисел, которая позволяет задать любой угол с погрешностью в один градус. Вероятнее всего, что именно таким способом пользовались жрецы эпохи Стоунхенджа. Конечно, для подтверждения этой гипотезы нужно было бы найти второй, парный золотой ромб, но, по всей видимости, это того не стоит. Ведь доказательства и так вполне очевидны. Кроме вычисления азимутов на местности была обнаружена и еще одна способность удивительного золотого ромба. Эта удивительная вещица позволяется вычислять моменты зимнего и летнего солнцестояния, весеннего и осеннего равноденствия. Это являлось незаменимым качеством для жизни древних египтян, которые поклонялись тогда в первую очередь Солнцу.
Ведь доказательства и так вполне очевидны. Кроме вычисления азимутов на местности была обнаружена и еще одна способность удивительного золотого ромба. Эта удивительная вещица позволяется вычислять моменты зимнего и летнего солнцестояния, весеннего и осеннего равноденствия. Это являлось незаменимым качеством для жизни древних египтян, которые поклонялись тогда в первую очередь Солнцу.
Вполне вероятно, что внушительный вид ромба являлся не только незаменимым инструментом для жрецов, но был также и эффектным украшением для его владельца. Вообще говоря, абсолютное большинство найденных на первый вид дорогостоящий на сегодняшний день украшений, являются, как узнается позже, измерительными инструментами.
Итак, людей всегда притягивала неизвестность. И, судя по тому, что так много остается загадочного и не доказанного в нашем мире, человек еще долго будет пытаться отыскать разгадки древности. И это очень здорово! Ведь у наших предков можно многому научиться. Для этого нужно много знать, уметь и учиться. А ведь невозможно стать таким высококвалифицированным специалистом без базовых знаний. В конце концов, ведь каждый великий археолог, открыватель когда-то ходил в школу!
А ведь невозможно стать таким высококвалифицированным специалистом без базовых знаний. В конце концов, ведь каждый великий археолог, открыватель когда-то ходил в школу!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Иногда появляется необходимость сделать элементарное дело, при этом обнаруживается, что мы не знаем, как это сделать. Например — как нарисовать ромб. На самом деле все очень просто.
В данной статье вы узнаете, как правильно нарисовать ромб, и что это за геометрическая фигура.
Что такое ромб?
Ромб является разновидностью параллелограмма, особенностью которого является то, что противоположные стороны этой фигуры параллельны друг к другу, а у ромба они еще и равны между собой. Об определении ромба к общему виду параллелограмма говорит факт равенства противоположных углов.
Как нарисовать ромб
Нарисовать такую фигуру как ромб можно несколькими способами. В этой статье мы рассмотрим два простых способа.
Для первого способа нам понадобятся: ручка или карандаш, ластик, лист в клетку из школьной тетради, линейка или любой похожий на него прямой предмет, если размеры точные размеры ромба не важны.
- Итак, для начала нарисуем точку на одном из пересечений линий клеток. Лучше, конечно, разместить точку не слишком близко к краям. Определяемся с размерами фигуры.
- Далее от средней точки отсчитываем необходимое количество клеток влево (или вправо) и ставим еще одну точку. В противоположной стороне через такое же количество клеток рисуем третью точку. Теперь то же самое проделываем по направлению вверх и вниз. Последовательность не имеет значения, главное здесь — отсчитать одинаковое расстояние от средней точки влево и вправо и отдельно вверх и вниз. То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.
- Соединяем линейкой или любым другим подходящим предметом все точки между собой, кроме среднего.
 Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов.
Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов.
Второй способ аналогичен первому, но рисовать мы будем на чистой бумаге без клеток. Нам нужно для этого: карандаш и/или ручка, ластик, чистый лист, линейка и угольник (или любой предмет с прямым углом).
- Определяемся с размерами. Рисуем точку.
- Берем линейку, ставим точку на необходимом расстоянии от средней точки на левой стороне. Соединяем их карандашом, чтобы линия проходила через среднюю точку. Аналогичные действия производим и в противоположную сторону.
- Также рисуем точку сверху и снизу, но уже пользуемся угольником, чтобы линия между верхней и нижней точкой была перпендикулярна линии между левой и правой.
- Соединяем все точки между собой. Стираем ластиком линии посередине фигуры.
08.08.2014
Рельефные узоры спицами ‒ это чередование при вязании лицевых и изнаночных петель, при этом полотно получается трёхмерным за счёт сочетания выпуклых и вогнутых участков, а также достаточно плотным (без просветов), поэтому такие узоры особенно выразительны. Рельефных узоров существует великое множество, различаются они маленьким или большим раппортом. Эти узоры идеально подходят для гладкой пряжи из хлопка, хлопка с вискозой, шёлка и смесовой льняной пряжи. Если пряжа толстая, то узор выглядит особенно рельефно, а если ‒ тонкая, то получится изысканная, благородная структура. Рельефные узоры достаточно просты в вязании, поэтому рекомендуются для начинающих, т.к. помогают им набраться сноровки и опыта. Уверенные вязальщицы тоже не обходят вниманием рельефные узоры, потому что они удобны для комбинирования с ажуром и придают ему особую нарядность. Чтобы очарование рельефных узоров не исчезло, не следует их утюжить и обрабатывать паром, достаточно увлажнить и дать высохнуть в расправленном виде.
Рельефных узоров существует великое множество, различаются они маленьким или большим раппортом. Эти узоры идеально подходят для гладкой пряжи из хлопка, хлопка с вискозой, шёлка и смесовой льняной пряжи. Если пряжа толстая, то узор выглядит особенно рельефно, а если ‒ тонкая, то получится изысканная, благородная структура. Рельефные узоры достаточно просты в вязании, поэтому рекомендуются для начинающих, т.к. помогают им набраться сноровки и опыта. Уверенные вязальщицы тоже не обходят вниманием рельефные узоры, потому что они удобны для комбинирования с ажуром и придают ему особую нарядность. Чтобы очарование рельефных узоров не исчезло, не следует их утюжить и обрабатывать паром, достаточно увлажнить и дать высохнуть в расправленном виде.
Предлагаем вам большую коллекцию простых рельефных узоров с ромбами и ромбиками для вязания спицами с образцами, схемами, описанием и условными обозначениями.
Выбирайте и творите с удовольствием!
Внимание! Схемы узоров приведены так, как они выглядят с лицевой стороны.
Сокращения:
п. ‒ петля;
лиц. ‒ лицевая;
изн. ‒ изнаночная;
кром. ‒ кромочная;
скрещ. ‒ скрещенная.
Узор 81 «Гранат» (на 6 петель и 6 рядов)
Узор 80 «Простой рельеф» (на 14 петель и 12 рядов)
Узор 79 «Структурный орнамент» (на 11 петель и 30 рядов)
Узор 78 «Кофейные зёрна» (на 18 петель и 36 рядов)
Узор 77 «Ромбовые ячейки» (на 6 петель и 16 рядов)
Узор 76 «Выразительные ромбы» (на 16 петель и 18 рядов)
Узор 75 «Очарование» (на 18 петель и 24 ряда)
Узор 74 «Плато Гиза» (на 16 петель и 36 рядов)
Узор 73 «Ромбы со вставкой» (на 18 петель и 22 ряда)
Узор 72 «Фигурные ромбы» (на 22 петли и 32 ряда)
Узор 71 «Простые ромбы» (на 10 петель и 20 рядов)
Узор 70 «Пастила» (на 12 петель и 12 рядов)
Узор 69 «Паркет» (на 8 петель и 16 рядов)
Узор 68 «Вытянутые ромбы» (на 8 петель и 10 рядов)
Узор двусторонний, смотрится одинаково с лицевой и с изнаночной стороны.
Для образца набрать число петель кратное 8 + 2 кром.
1 ряд
2 ряд : 1 кром.; * 3 изн.; 4 лиц.; 1 изн.**; повторять от * до **; 1 кром.
3 ряд : 1 кром.; * 2 лиц.; 4 изн.; 2 лиц.**; повторять от * до **; 1 кром.
4 ряд : 1 кром.; * 1 изн.; 4 лиц.; 3 изн.**; повторять от * до **; 1 кром.
5 ряд
6 ряд : 1 кром.; * 4 изн.; 4 лиц.**; повторять от * до **; 1 кром.
7 ряд : 1 кром.; * 1 лиц.; 4 изн.; 3 лиц.**; повторять от * до **; 1 кром.
8 ряд : 1 кром.; * 2 изн.; 4 лиц.; 2 изн.**; повторять от * до **; 1 кром.
9 ряд : 1 кром.; * 3 лиц.; 4 изн.; 1 лиц.**; повторять от * до **; 1 кром.
10 ряд : 1 кром.; * 4 лиц.; 4 изн.**; повторять от * до **; 1 кром.
Повторять с 1-го по 10-й ряд.
Узор 67 «Графические ромбы» (на 28 петель и 16 рядов)
Узор 66 «Ромбы из треугольников» (на 14 петель и 14 рядов)
Узор 65 «Ромбики из треугольников» (на 8 петель и 16 рядов)
Узор 64 «Зачёркнутые ромбы» (на 14 петель и 32 ряда)
Узор 63 «Благородная структура» (на 14 петель и 30 рядов)
Узор 62 «Красивый рельеф» (на 12 петель и 32 ряда)
Узор 61 «Необычная структура» (на 10 петель и 20 рядов)
Узор 60 «Цепь из ромбов» (на 8 петель и 20 рядов)
Узор 59 «Изысканная структура» (на 16 петель и 32 ряда)
Узор 58 «Мотыльки» (на 12 п. и 24 ряда)
и 24 ряда)
Узор 57 «Мотыльки» (на 10 п. и 20 рядов)
Узор 56 «Ромбита» (на 28 петель и 28 рядов)
Узор 55 «Нежность» (на 22 петли и 36 рядов)
Узор 54 «Отделочный ромб» (на 17 петель и 30 рядов)
Узор 53 «Шишки» обратная сторона узора «Свечи» (на 12 петель и 32 ряда)
Узор 52 «Свечи» обратная сторона узора «Шишки» (на 12 петель и 32 ряда)
Узор 51 «Гроздья» (на 8 петель и 28 рядов)
Узор 50 «Алмаз» (на 14 п. и 28 рядов)
Узор 49 «Алмаз» (на 10 п. и 24 ряда)
Узор 48 «Ромбы по зигзагу» (на 16 петель и 20 рядов)
Узор 47 «Бантики в ромбах» (на 20 петель и 18 рядов)
Узор 46 «Оригинальный рельеф» (на 26 петель и 34 ряда)
Узор 45 «Перекрёстки» (на 12 петель и 24 ряда)
Узор 44 «Парча» (на 20 петель и 14 рядов)
Узор 43 «Алмазная мозаика» (на 12 петель и 28 рядов)
Узор 42 «Шахматка из ромбов» (на 14 петель и 28 рядов)
Узор 41 «Комбинированная структура» (на 16 петель и 32 ряда)
Узор 40 «Бисерные ромбы» (на 12 петель и 32 ряда)
Узор 39 «Структурные ромбы» (на 12 петель и 18 рядов)
Узор 37 «Жемчужные ромбы по лицевой глади» (на 10 петель и 10 рядов)
Узор 36 «Виноградный рай» (на 10 петель и 24 ряда)
Узор 35 «Жемчужные ромбы» (на 10 петель и 20 рядов)
Узор 34 «Полосы из жемчужных ромбов» (на 10 петель и 16 рядов)
Узор 33 «Традиционные ромбы» (на 20 петель и 24 ряда)
Узор 32 «Треугольники» обратная сторона узора «Мираж» (на 16 петель и 32 ряда)
Узор 31 «Мираж» обратная сторона узора «Треугольники»(на 16 петель и 32 ряда)
Узор 30 «Ромбы в полоску» (на 18 петель и 36 рядов)
Узор 29 «Вертикаль из ромбов и бантиков» (на 22 петли и 18 рядов)
Узор 28 «Горизонталь из ромбов и бантиков» (на 22 петли и 20 рядов)
Узор 27 «Витраж» (на 14 петель и 14 рядов)
Узор 26 «Калейдоскоп» (на 12 петель и 12 рядов)
Узор 25 «Рельефные ромбы» (на 15 петель и 30 рядов)
Узор 24 «Репсовые ромбы» (на 6 петель и 12 рядов)
Узор 23 «Линейные ромбы» (на 12 петель и 12 рядов)
Узор 22 «Сетка рабица» (на 8 петель и 16 рядов)
Узор 21 «Сеточка» (на 8 петель и 14 рядов)
Узор 20 «Панцирная сетка» (на 14 петель и 28 рядов)
Как начертить ромб с помощью линейки.
 Ромбы спицами ‒ простые узоры. Определение ромба, как геометрической фигуры
Ромбы спицами ‒ простые узоры. Определение ромба, как геометрической фигурыКлассики вариант №2 и 3 Варианты игры «Классики» на улице:
1. Нарисовать длинную линию мелом. Можно играть и самым маленьким.
Ходить по линии. Не оступаться.
Прыгать на одной ноге.
Измерять количество ступней.
Прыгать то справа, то слева от линии. Можно на одной или на двух ногах.
2. Нарисовать длинную линию и треугольники прилегающие к ней. Прыгать как в варианте №1.
3. Классики вариант №3. Прыгать на двух или на одной ноге. Считать вслух прыжки. На линии не заступать.
Мультяшная сумка Cheese. Выглядит как нарисованная на бумаге, на самом деле является настоящей сумкой из канваса (парусина).
Мультяшная сумка Play Hooky. Выглядит как нарисованная на бумаге, на самом деле является настоящей сумкой из канваса (парусина).
Мультяшные сумки придумали две девушки дизайнеры из Тайвани. В 2012 году они выставлялись на неделях мод в Лондоне, Париже и Милане.
У сумки есть молния на дне, поэтому ее объем можно увеличить.![]() Много в нее не влезет, но самое необходимое вполне вместится. Идеальное решение для планшетного компьютера.
Много в нее не влезет, но самое необходимое вполне вместится. Идеальное решение для планшетного компьютера.
(http://multyashniesumki.ru/)
Рисование пастелью — кошка породы Египетская Мау
1) В этом уроке я расскажу вам как нарисовать кота породы Египетская Мау. Это очень красивые кошки с крупными глазами цвета зеленой смородины или же желто-янтарного. У Египетской Мау замечательный и неповторимый окрас. Это и является их отличительной особенностью. Для этой картины нам понадобится пастельный лист темно-синего цвета формата А4. Белым, хорошо заточенным пастельным карандашом сделаем набросок.
2) Переходим к рисованию глаз и носа. Для глаз используйте зеленый, желтый, темно-оранжевый, черный пастельные карандаши. Заштрихуйте аккуратно глаз, зрачок сделайте черным, в конце добавьте белым пастельным карандашом блики. Для носа используйте белый, розовый, черный, красный пастельные карандаши. Вокруг глаз и носа заштрихуйте слегка белым карандашом и разотрите пальцем. При рисовании таких мелких деталей ваши карандаши должны быть хорошо заточены!
3) Ухо заштрихуйте сначала розовым пастельным карандашом, а поверх белым пастельным карандашом. Разотрите все пальцем. Добавьте черные оттенки и разотрите. Теперь заточите хорошо белый пастельный карандаш и нарисуйте белые волосинки быстрыми и легкими движениями.
Разотрите все пальцем. Добавьте черные оттенки и разотрите. Теперь заточите хорошо белый пастельный карандаш и нарисуйте белые волосинки быстрыми и легкими движениями.
4) Голову кошки заштрихуйте белым и серым пастельным карандашом. Где-то можете добавить несколько штрихов голубого цвета. После этого разотрите все пальцем.
5) Начинаем уточнять детали. Белым карандашом мелкими штрихами имитируем рост шерсти. Полоски нарисуйте мелкими штрихами черного цвета.
Нарисуй мне, пожалуйста, море,
Чтобы тихие волны мелькали,
Чтобы запахи счастья и воли
Мою грудь до краев наполняли.
Нарисуй мне песок под ногами,
Желтый-желтый, как солнечный лучик.
И укрась небо все облаками,
Не рисуй лишь, пожалуйста, тучи.
Нарисуй мне воздушного змея,
Чтобы ветер играл с ним мятежный.
Чтобы я, ничего не имея,
Продолжала быть доброй и нежной.
Нарисуешь мне море и небо?
И усеешь его облаками?
Нарисуешь мне вечное лето?
И песок под босыми ногами?
Нарисуй, но не ставь еще точку,
Я о главном тебе не сказала,
Нарисуй мне, пожалуйста, дочку,
И себя нарисуй у причала.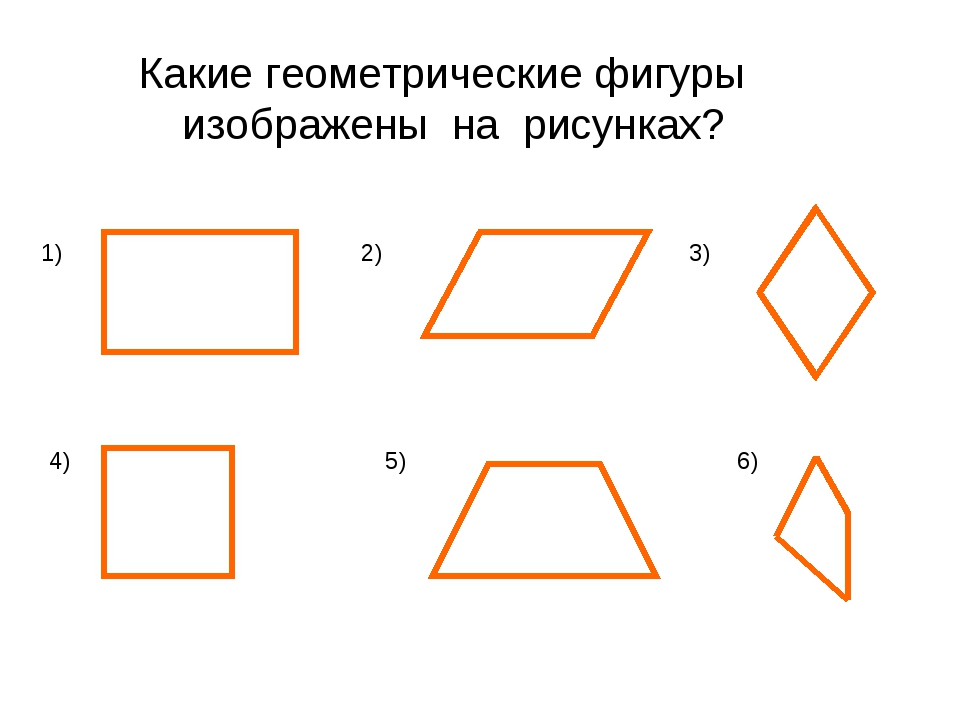
Как нарисовать картину красками
Подберите акварельные краски. С них легче всего начинать рисовать картину. Они могут передать все оттенки и придают яркости при просвечивании. Выберите, на какой поверхности будете рисовать – мокрой или сухой. При рисовании на мокрой поверхности размываются очертания предметов, что пригодится в пейзажных композициях или при фоновой заливке овощей и фруктов.
Возьмите чертежный ватман – от избытка воды он не набухает, и места, которые нужно исправить, можно легко смыть поролоном. Расположите бумагу под наклоном в 30-40 градусов для равномерного растекания краски.
Сделайте наброски карандашом основных предметов. Если это натюрморт, то определите расположение стола или другой поверхности и фруктово-овощной композиции. Если это портрет, то учтите пропорции человека, а если пейзаж, то здесь достаточно будет легких набросков – главную роль будут играть краски. В рисовании красками, особенно акварельными, учтите тот факт, что продумывать оттенок каждого мазка нужно заранее. Исправить ошибку можно лишь с помощью влажного поролона. Потом по уже хорошо высохшей поверхности нанесите нужные мазки.
Исправить ошибку можно лишь с помощью влажного поролона. Потом по уже хорошо высохшей поверхности нанесите нужные мазки.
Изобразите общий фон поролоном или широкой беличьей кистью. При окрашивании больших участков следите, чтобы на кисти было достаточно краски. Наносите фон от светлого места к темному. Учтите, что эффект белого при рисовании акварельными красками достигается лишь за счет неокрашенных или хорошо промытых водой мест. Следите за тем, чтобы не порвать бумагу и не скатать ее валиками.
Определите солнечную сторону и затененные места в картине. Отталкиваясь от этого, зарисуйте все предметы. Смешивайте краски на палитре – на рисунке наложение цветовых слоев может привести к простому искажению цвета темных оттенков. Каждый следующий мазок наносите рядом с предыдущим чуть смоченной кисточкой для плавного перехода.
Картины, нарисованные красками, обладают даром притягивать к себе взоры еще и еще. Неповторимая игра оттенков позволяет передать все до мелочей. Но вот как именно нарисовать картину красками?- чертежный ватман,
— карандаш,
— ластик,
— краски.
Нарисуйте детали нарцисса более точно. Из каждой вершины шестиугольника проведите прямые линии, сходящиеся к середине. Эти линии будут вертикальными осями для лепестков цветка. Обозначьте точки середины линий. Теперь с каждой вершины проведите штрихи, расширяющиеся до обозначенных точек. Далее штрихи доведите до середины цветка уже в виде прямых параллельных линий.
Для того чтобы нарисовать нарцисс, прорисуйте лепестки цветка плавными линиями – сгладьте основные контуры. Изобразите небольшое завертывание лепестков волнистыми линиями, располагающимися у их стенок. Прорисуйте середину нарцисса. Сначала границы овала сделайте зубчатыми с мелким шагом. С правой стороны овала дорисуйте небольшой купол, делающий середину более объемной.
Нарисуйте часть стебля нарцисса в виде трубчатой дуги, соединяющей непосредственно цветок и прямой тонкий стебель широкой стороной, направленной к лепесткам. Листок растения изобразите вытянутым нешироким с заостренной вершиной.
Зарисуйте цветок простым карандашом. Середину нарцисса плотно заштрихуйте прямыми тонкими линиями, расходящимися из середины к границам овала. На лепестках изобразите лучики, идущие по вертикальной серединной линии. Затените и левую сторону стебля, и верхнюю часть листка нарцисса.
Середину нарцисса плотно заштрихуйте прямыми тонкими линиями, расходящимися из середины к границам овала. На лепестках изобразите лучики, идущие по вертикальной серединной линии. Затените и левую сторону стебля, и верхнюю часть листка нарцисса.
Зарисуйте сам цветок желтым цветом. Середину сделайте на тон темнее. Листок и стебло зарисуйте ровным зеленым тоном.
Нарцисс – один из первых весенних цветов. Такой нежный и одновременно строгий, неприступный, замечающий только свою красоту. Такую красоту можно удержать надолго только на листике бумаги.- альбомный лист;
— карандаш;
— ластик.
Как нарисовать якорь
Нарисуйте современную конструкцию якоря с двумя острыми краями внизу. Посередине листа проведите вертикальную линию, чуть суженную в верхней части и расширенную в нижней части. Это будет веретено якоря. Вокруг верхней границы веретена изобразите круг, т.н. рым — место крепления троса или каната для поднятия или опускания якоря. В верхней части вертикали проведите горизонтальную линию – шток. Нижнюю часть веретена закрепите большой галочкой.
Нижнюю часть веретена закрепите большой галочкой.
Прорисуйте отдельные части якоря более детально. Веретено изобразите в виде двух прямых линий, каждую из которых внизу нарисуйте отведенными в разные стороны, образуя якорь, его основную часть. Таким образом получите два рога якоря. Места стыка линий должны быть плавными. Сделайте каждый рог объемным, добавив еще одну линию, повторяющую очертания якоря. На кончиках рогов изобразите лопы — широкие пластины с острыми внешними вершинами. Обратите внимание, что пятка якоря должна быть достаточно острой.
Прорисуйте детально шток. От наклонной прямой линии на небольшом расстоянии проведите еще одну с таким же наклоном, но чуть выпуклую, разграничивая таким образом боковую и нижнюю части штока. Соедините обе линии несколькими вертикальными штрихами. Теперь прорисуйте еще одну повторяющую очертания наклонную линию и продолжите вертикальные штрихи под углом чуть большим 90 градусов. Над верхней границей штока изобразите шейку — нарисуйте небольшой прямоугольник и разделите его пополам вертикальной линией. Кольцо рым сделайте двойным.
Кольцо рым сделайте двойным.
Затемните отдельные участки якоря: нижнюю часть лопы и правый рог. Шток заштрихуйте короткими линиями и шейку, ее правую часть. Также затемните участок веретена, который идет вдоль правой границы вертикали, – нарисованный якорь готов.
Якорь – это специальная металлическая конструкция, которая предназначена для закрепления корабля на одном месте. Он имеет множество различных видов, но основа всегда одна – тяжелый низ, который закреплен на прямой металлической вертикали. Нарисованный якорь чаще всего используется в качестве морского символа.- альбомный лист;
— карандаш;
— ластик.
Иногда появляется необходимость сделать элементарное дело, при этом обнаруживается, что мы не знаем, как это сделать. Например — как нарисовать ромб. На самом деле все очень просто.
В данной статье вы узнаете, как правильно нарисовать ромб, и что это за геометрическая фигура.
Что такое ромб?
Ромб является разновидностью параллелограмма, особенностью которого является то, что противоположные стороны этой фигуры параллельны друг к другу, а у ромба они еще и равны между собой. Об определении ромба к общему виду параллелограмма говорит факт равенства противоположных углов.
Об определении ромба к общему виду параллелограмма говорит факт равенства противоположных углов.
Как нарисовать ромб
Нарисовать такую фигуру как ромб можно несколькими способами. В этой статье мы рассмотрим два простых способа.
Для первого способа нам понадобятся: ручка или карандаш, ластик, лист в клетку из школьной тетради, линейка или любой похожий на него прямой предмет, если размеры точные размеры ромба не важны.
- Итак, для начала нарисуем точку на одном из пересечений линий клеток. Лучше, конечно, разместить точку не слишком близко к краям. Определяемся с размерами фигуры.
- Далее от средней точки отсчитываем необходимое количество клеток влево (или вправо) и ставим еще одну точку. В противоположной стороне через такое же количество клеток рисуем третью точку. Теперь то же самое проделываем по направлению вверх и вниз. Последовательность не имеет значения, главное здесь — отсчитать одинаковое расстояние от средней точки влево и вправо и отдельно вверх и вниз.
 То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.
То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.
- Соединяем линейкой или любым другим подходящим предметом все точки между собой, кроме среднего. Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов.
Второй способ аналогичен первому, но рисовать мы будем на чистой бумаге без клеток. Нам нужно для этого: карандаш и/или ручка, ластик, чистый лист, линейка и угольник (или любой предмет с прямым углом).
 Стираем ластиком линии посередине фигуры.
Стираем ластиком линии посередине фигуры.08.08.2014
Рельефные узоры спицами ‒ это чередование при вязании лицевых и изнаночных петель, при этом полотно получается трёхмерным за счёт сочетания выпуклых и вогнутых участков, а также достаточно плотным (без просветов), поэтому такие узоры особенно выразительны. Рельефных узоров существует великое множество, различаются они маленьким или большим раппортом. Эти узоры идеально подходят для гладкой пряжи из хлопка, хлопка с вискозой, шёлка и смесовой льняной пряжи. Если пряжа толстая, то узор выглядит особенно рельефно, а если ‒ тонкая, то получится изысканная, благородная структура. Рельефные узоры достаточно просты в вязании, поэтому рекомендуются для начинающих, т.к. помогают им набраться сноровки и опыта. Уверенные вязальщицы тоже не обходят вниманием рельефные узоры, потому что они удобны для комбинирования с ажуром и придают ему особую нарядность. Чтобы очарование рельефных узоров не исчезло, не следует их утюжить и обрабатывать паром, достаточно увлажнить и дать высохнуть в расправленном виде.
Предлагаем вам большую коллекцию простых рельефных узоров с ромбами и ромбиками для вязания спицами с образцами, схемами, описанием и условными обозначениями.
Выбирайте и творите с удовольствием!
Внимание! Схемы узоров приведены так, как они выглядят с лицевой стороны.
Сокращения:
п. ‒ петля;
лиц. ‒ лицевая;
изн. ‒ изнаночная;
кром. ‒ кромочная;
скрещ. ‒ скрещенная.
Узор 81 «Гранат» (на 6 петель и 6 рядов)
Узор 80 «Простой рельеф» (на 14 петель и 12 рядов)
Узор 79 «Структурный орнамент» (на 11 петель и 30 рядов)
Узор 78 «Кофейные зёрна» (на 18 петель и 36 рядов)
Узор 77 «Ромбовые ячейки» (на 6 петель и 16 рядов)
Узор 76 «Выразительные ромбы» (на 16 петель и 18 рядов)
Узор 75 «Очарование» (на 18 петель и 24 ряда)
Узор 74 «Плато Гиза» (на 16 петель и 36 рядов)
Узор 73 «Ромбы со вставкой» (на 18 петель и 22 ряда)
Узор 72 «Фигурные ромбы» (на 22 петли и 32 ряда)
Узор 71 «Простые ромбы» (на 10 петель и 20 рядов)
Узор 70 «Пастила» (на 12 петель и 12 рядов)
Узор 69 «Паркет» (на 8 петель и 16 рядов)
Узор 68 «Вытянутые ромбы» (на 8 петель и 10 рядов)
Узор двусторонний, смотрится одинаково с лицевой и с изнаночной стороны.
Для образца набрать число петель кратное 8 + 2 кром.
1 ряд
2 ряд : 1 кром.; * 3 изн.; 4 лиц.; 1 изн.**; повторять от * до **; 1 кром.
3 ряд : 1 кром.; * 2 лиц.; 4 изн.; 2 лиц.**; повторять от * до **; 1 кром.
4 ряд : 1 кром.; * 1 изн.; 4 лиц.; 3 изн.**; повторять от * до **; 1 кром.
5 ряд
6 ряд : 1 кром.; * 4 изн.; 4 лиц.**; повторять от * до **; 1 кром.
7 ряд : 1 кром.; * 1 лиц.; 4 изн.; 3 лиц.**; повторять от * до **; 1 кром.
8 ряд : 1 кром.; * 2 изн.; 4 лиц.; 2 изн.**; повторять от * до **; 1 кром.
9 ряд : 1 кром.; * 3 лиц.; 4 изн.; 1 лиц.**; повторять от * до **; 1 кром.
10 ряд : 1 кром.; * 4 лиц.; 4 изн.**; повторять от * до **; 1 кром.
Повторять с 1-го по 10-й ряд.
Узор 67 «Графические ромбы» (на 28 петель и 16 рядов)
Узор 66 «Ромбы из треугольников» (на 14 петель и 14 рядов)
Узор 65 «Ромбики из треугольников» (на 8 петель и 16 рядов)
Узор 64 «Зачёркнутые ромбы» (на 14 петель и 32 ряда)
Узор 63 «Благородная структура» (на 14 петель и 30 рядов)
Узор 62 «Красивый рельеф» (на 12 петель и 32 ряда)
Узор 61 «Необычная структура» (на 10 петель и 20 рядов)
Узор 60 «Цепь из ромбов» (на 8 петель и 20 рядов)
Узор 59 «Изысканная структура» (на 16 петель и 32 ряда)
Узор 58 «Мотыльки» (на 12 п. и 24 ряда)
и 24 ряда)
Узор 57 «Мотыльки» (на 10 п. и 20 рядов)
Узор 56 «Ромбита» (на 28 петель и 28 рядов)
Узор 55 «Нежность» (на 22 петли и 36 рядов)
Узор 54 «Отделочный ромб» (на 17 петель и 30 рядов)
Узор 53 «Шишки» обратная сторона узора «Свечи» (на 12 петель и 32 ряда)
Узор 52 «Свечи» обратная сторона узора «Шишки» (на 12 петель и 32 ряда)
Узор 51 «Гроздья» (на 8 петель и 28 рядов)
Узор 50 «Алмаз» (на 14 п. и 28 рядов)
Узор 49 «Алмаз» (на 10 п. и 24 ряда)
Узор 48 «Ромбы по зигзагу» (на 16 петель и 20 рядов)
Узор 47 «Бантики в ромбах» (на 20 петель и 18 рядов)
Узор 46 «Оригинальный рельеф» (на 26 петель и 34 ряда)
Узор 45 «Перекрёстки» (на 12 петель и 24 ряда)
Узор 44 «Парча» (на 20 петель и 14 рядов)
Узор 43 «Алмазная мозаика» (на 12 петель и 28 рядов)
Узор 42 «Шахматка из ромбов» (на 14 петель и 28 рядов)
Узор 41 «Комбинированная структура» (на 16 петель и 32 ряда)
Узор 40 «Бисерные ромбы» (на 12 петель и 32 ряда)
Узор 39 «Структурные ромбы» (на 12 петель и 18 рядов)
Узор 37 «Жемчужные ромбы по лицевой глади» (на 10 петель и 10 рядов)
Узор 36 «Виноградный рай» (на 10 петель и 24 ряда)
Узор 35 «Жемчужные ромбы» (на 10 петель и 20 рядов)
Узор 34 «Полосы из жемчужных ромбов» (на 10 петель и 16 рядов)
Узор 33 «Традиционные ромбы» (на 20 петель и 24 ряда)
Узор 32 «Треугольники» обратная сторона узора «Мираж» (на 16 петель и 32 ряда)
Узор 31 «Мираж» обратная сторона узора «Треугольники»(на 16 петель и 32 ряда)
Узор 30 «Ромбы в полоску» (на 18 петель и 36 рядов)
Узор 29 «Вертикаль из ромбов и бантиков» (на 22 петли и 18 рядов)
Узор 28 «Горизонталь из ромбов и бантиков» (на 22 петли и 20 рядов)
Узор 27 «Витраж» (на 14 петель и 14 рядов)
Узор 26 «Калейдоскоп» (на 12 петель и 12 рядов)
Узор 25 «Рельефные ромбы» (на 15 петель и 30 рядов)
Узор 24 «Репсовые ромбы» (на 6 петель и 12 рядов)
Узор 23 «Линейные ромбы» (на 12 петель и 12 рядов)
Узор 22 «Сетка рабица» (на 8 петель и 16 рядов)
Узор 21 «Сеточка» (на 8 петель и 14 рядов)
Узор 20 «Панцирная сетка» (на 14 петель и 28 рядов)
Ромб — это простая геометрическая фигура, имеющая четыре вершины и поэтому являющаяся одним из частных случаев параллелограмма. От других многоугольников этого рода ее отличает равенство длин всех сторон. Этой особенностью определяется и то, что углы в противоположных вершинах фигуры имеют одинаковую величину. Построить ромб можно несколькими способами — например, с использованием циркуля.
От других многоугольников этого рода ее отличает равенство длин всех сторон. Этой особенностью определяется и то, что углы в противоположных вершинах фигуры имеют одинаковую величину. Построить ромб можно несколькими способами — например, с использованием циркуля.
Вам понадобится
- Лист, карандаш, циркуль, линейка, транспортир.
Инструкция
- Поставьте на противоположных краях листа две произвольные точки, которые будут противоположными вершинами ромба, и обозначьте их буквами A и С.
- Поставьте вспомогательную точку приблизительно в том месте, где должна находиться третья вершина фигуры. Расстояние от нее до вершин A и C должно быть одинаковым, но соблюдать абсолютную точность на этом шаге не требуется.
- Отмерьте циркулем расстояние от точки A до вспомогательной точки и начертите полукруг с центром в точке A, обращенный в сторону точки C.
- Начертите такой же полукруг (не меняя отложенного на циркуле расстояния), имеющий центром точку C и направленный в сторону точки A.

- Поставьте точки B и D в местах верхнего и нижнего пересечения полукругов и проведите соединительные линии между точками A и B, B и C, C и D, D и A. На этом построение ромба с произвольной стороной и углами будет завершено.
- Если требуется построить ромб с заданной длиной сторон, то сначала отложите на циркуле это значение. Затем поставьте точку A, которая будет одной из вершин четырехугольника, и начертите полукруг в направлении предполагаемой противоположной вершины.
- Поставьте точку C в том месте, где вы хотели бы видеть противоположную вершину. Исходите из того, что расстояние от очерченного полукруга до этой вершины должно быть меньше отложенного на циркуле расстояния. Чем меньше будет это расстояние, тем шире получится ромб.
- Повторите действия, описанные в пятом и шестом шагах. После этого построение ромба со сторонами заданной длины будет завершено.
- Если требуется построить ромб с заданным углом, то сначала обозначьте произвольными точками A и B две соседние вершины ромба и соедините их отрезком.

- Отложите на циркуле длину отрезка AB и начертите полукруг с центром в точке A. Все последующие построения производите, не меняя отложенного на циркуле расстояния.
- Приложите транспортир к отрезку AB таким образом, чтобы нулевая отметка совпала с точкой A, отмерьте заданный угол и поставьте вспомогательную точку.
- Проведите отрезок прямой, начинающийся в точке A, проходящий через вспомогательную точку и заканчивающийся на начерченном ранее полукруге. Обозначьте точку окончания отрезка буквой D.
- Начертите два направленных друг к другу полукруга с центрами в точках B и D. Одной из точек пересечения полукружий будет уже существующая точка A, а другую обозначьте буквой C и соедините ее с точками B и D. На этом построение ромба с заданным углом будет завершено.
Цели урока
Продолжать знакомить учеников о такой геометрической фигуре, как ромб;
Закрепить знания о таких понятиях, как ромб и квадрат, а также научиться определять их разницу;
Освежить знания школьников о свойствах и признаках ромба;
Продолжать совершенствовать знания учащихся о геометрических фигурах в процессе решения задач.
Вызвать заинтересованность к урокам геометрии.
Задачи урока
Повторить, обобщить и закрепить полученные знания о такой геометрической фигуре, как ромб;
Продолжать формировать умения и навыки построения геометрических фигур;
Усовершенствовать навыки построения ромба с помощью чертежных инструментов;
Продолжать закреплять знания школьников с использованием практических заданий;
Продолжать развивать внимание, усидчивость и стремление к познавательному процессу.
План урока
1. Раскрытие главное темы урока, определение геометрической фигуры «Ромб».
2. Ознакомление со свойствами и признаками ромба.
3. Теоремы и их доказательство.
4. Как нарисовать ромб. Способы изображения ромба.
5. Как найти площадь ромба?
6. Повторение пройденного материала.
7. Интересные факты.
8. Домашнее задание.
Определение ромба, как геометрической фигуры
Ромб — это такой параллелограмм, у которого все стороны равны. Если же ромб имеет прямые углы, то он называется квадратом.
Если же ромб имеет прямые углы, то он называется квадратом.
Сам термин «Ромб» в переводе с греческого языка, обозначает «бубен». Конечно же в нашем понимании бубен, как музыкальный инструмент, имеет круглую форму. Но это сейчас бубны делают круглыми, а в древние времена он как раз и имел квадратную форму или форму ромба.
Давайте остановимся на основных определениях ромба и попробуем понять, что же являет собой эта геометрическая фигура.
Ромб – это такой равносторонний параллелограмм, у которого равные стороны, но неравные углы.
В отличие от квадрата, ромб – это равносторонний косоугольник.
Как всегда мы получаем множество определений той или иной геометрической фигуры, но это не означает, что каждый ученик должен сесть и «зазубрить» именно эти определения. Отличие в определениях – это насколько широко они описывают нашу геометрическую фигуру. Самое главное, это понимание о чем говориться в определении и возможность представить фигуру. Если вы будете придерживаться этих двух правил, то и сами сможете написать или дополнить парочку определений.
Свойства ромба
2. Вторым его свойством является то, что все диагонали ромба пересекаются под прямым углом. В точке пересечения диагонали ромба делятся пополам.
3. Биссектрисами углов ромба являются его диагонали.
4. Чтобы найти сумму квадратов диагоналей ромба, необходимо квадрат его стороны умножить на четыре.
5. Противолежащие стороны ромба равны;
6. Сумма углов ромба, которые прилежат к одной его стороне, равна 180 градусов.
Признаки ромба
Параллелограмм является ромбом в том случае, если он соответствует следующим условиям:
1. Во-первых, у него все стороны равны между собой;
2. Во-вторых, диагонали ромба пересекаются под прямым углом.
3. В-третьих, если диагонали его углов являются биссектрисами.
4. В-четвертых, если его две смежные стороны равны между собой.
5. В-пятых, если хотя бы одна из диагоналей является биссектрисой параллелограмма.
Теоремы и их доказательство
Теперь давайте более подробно рассмотрим свойства и признаки ромба, доказав теоремы:
Теорема 1
Теорема 2
Из этого следует, что:
1. У ромба две оси симметрии – диагонали AC и BD.
У ромба две оси симметрии – диагонали AC и BD.
2. Его диагонали взаимно перпендикулярны.
3. А также являются биссектрисами его углов.
Площадь ромба
Площадь ромба равна половине произведения его диагоналей. Но так как ромб, по сути, это параллелограмм, то его площадь можно узнать, умножив его стороны на высоту.
Формулы площади ромба:
Где:
a – является стороной ромба
D – обозначается его большая диагональ
d – имеет обозначение меньшая диагональ
α – это острый угол
β – является тупым углом
Площадь любой геометрической фигуры является частью поверхности, которая ограничивается замкнутым контуром данной фигуры. А величина площади ромба выражается числом заключающихся в него квадратных единиц.
Как нарисовать ромб
Чтобы нарисовать ромб воспользуемся свойствами диагоналей ромба. Нам уже известно, что диагонали нашей геометрической фигуры взаимно перпендикулярны и делятся пополам в точке пересечения. Поэтому построение ромба проще всего начать с построения его диагоналей.
Поэтому построение ромба проще всего начать с построения его диагоналей.
Первый способ
И так, в первую очередь выбираем точку, от которой откладываем влево и право отрезки одной длины, в вверх и вниз одинаковые отрезки другой длины.
Теперь нам остается только соединить концы этих отрезков, и в результате мы получим ромб.
Второй способ
Ромб можно еще начертить без использования диагоналей. В этом случае нужно определить лишь концы диагоналей и потом соединить точки отрезками.
Третий способ
И наконец, третий способ, черчения ромба можно выполнить при помощи линейки. Так как мы с вами знаем, что ромб имеет равные стороны, то вначале нужно нарисовать его нижнюю часть. Затем необходимо отложить от нее равный отрезок. А так как третья сторона параллельна первой, то соединив концы первого и третьего отрезков, мы получим ромб.
Повторение
Вы уже познакомились с такой геометрической фигурой, как ромб и понимаете, что квадрат является его частным случаем.
1. Поэтому давайте вспомним определение, что такое квадрат? Дайте самостоятельно определение квадрата.
2. Какими свойствами обладает квадрат? Назовите их.
3. В чем все-таки разница между ромбом и квадратом, если квадрат является его частным случаем?
4. Какую фигуру называют четырехугольником, и относится ли ромб к этой геометрической фигуре?
5. Какие виды четырехугольников вы уже изучали? Назовите их.
6. Какие между ними существуют отличия?
Это интересно знать
Известно ли вам, что если взять прямоугольник и соединить отрезками середины его сторон, то в итоге мы получим ромб.
А если, наоборот, мы с вами возьмем ромб и попробуем соединить его середины сторон отрезками, то мы получим такую геометрическую фигуру, как прямоугольник.
Если вы возьмете параллелограмм с равными высотами, то такой параллелограмм является ромбом.
А знаете ли вы, что названием карточной масти бубны, имеющего ромбическую форму, появилось еще в те времена, когда бубен имел далеко не круглую форму, а вид ромба или квадрата.
Впервые слово «ромб» в своем лексиконе был использован Герроном и Паппой Александрийским.
Домашнее задание
1. Как вы думаете, является ли ромбом параллелограмм, который имеет хотя бы один прямой угол?
2. Верно ли утверждение, что каждый параллелограмм является ромбом?
3. Если диагонали параллелограмма равны 5 см и 7см, может ли быть ромбом этот параллелограмм?
4. Если диагонали параллелограмма равны, то может ли он быть ромбом?
5. Назовите особое свойство ромба, которым обладают его диагонали, помимо того, что они точкой пересечения делятся пополам?
6. Подумайте, где в повседневной жизни применяется такая геометрическая фигура, как ромб?
Domino Diamond Dec. Draw Cherry Gold 60×20 — керамическая плитка и керамогранит
3DPLITKA.RU
Пн-Пт 9:00–20:00
Сб-Вс 10:00–20:00
: zakaz@3dplitka. ru
ru16-я Парковая д.23
г. Москва, индекс 105484
Принимаем к оплате:
Мы в соц.сетях:
Мы в Яндекс.Организации:
Мы на Яндекс.Маркете:
Москва +7 (495) 966-18-01
Санкт-Петербург +7 (812) 309-35-78
Воронеж +7 (473) 202-47-57
Екатеринбург +7 (343) 289-18-98
Нижний Новгород +7 (831) 281-52-53
Новосибирск +7 (383) 284-08-48
Казань +7 (843) 211-02-57
Краснодар +7 (861) 201-25-33
Красноярск +7 (391) 216-76-03
Пермь +7 (342) 207-98-33
Ростов-на-Дону +7 (863) 310-02-03
Самара +7 (846) 375-94-33
Саратов +7 (8452) 39-79-54
Тверь +7 (4822) 73-65-21
Томск +7 (3822) 99-43-77
Тула +7 (4872) 52-41-06
Тюмень +7 (3452) 39-72-57
Уфа +7 (347) 225-06-33
Челябинск +7 (351) 220-14-23
Другой регион +7 (800) 301-34-28
(бесплатный звонок)Ⓒ 2011-2022 3dplitka. ru — интернет-магазин керамической плитки, керамогранита и сантехники
ru — интернет-магазин керамической плитки, керамогранита и сантехники
Политика организации в отношении обработки персональных данных
Используя этот сайт вы даёте своё согласие на использование файлов cookie
Что такое ромб? (Определение, форма, свойства) // Tutors.com
Содержание
- Определение ромба
- Как построить ромб
- Как выглядит ромб?
- Различные названия ромба
- Является ли квадрат ромбом?
- Форма ромба
- Свойства ромба
- Углы-ромбы
- Диагонали ромба
Определение ромба
Ромб представляет собой четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу.Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Все квадраты — ромбы, но не все ромбы — квадраты. Противоположные внутренние углы ромба равны. Диагонали ромба всегда пересекаются под прямым углом.
Диагонали ромба всегда пересекаются под прямым углом.
Как построить ромб
Вы можете построить ромб прямо сейчас на любой плоской поверхности, если у вас есть четыре одинаковых линейных объекта. Зубочистки, карандаши, метровые палочки — подойдут любые четыре конгруэнтных прямых отрезка.
Положите четыре прямых предмета на плоскую поверхность так, чтобы их восемь концов соприкасались только в четырех местах. Вы не можете потерпеть неудачу в этом! Положите два предмета параллельно друг другу, но на небольшом расстоянии друг от друга. Если вы используете два других объекта для соединения конечных точек, у вас получится ромб!
Как выглядит ромб?
Противоположные стороны вашего четырехугольника будут параллельны, а противоположные углы будут одинаковыми (конгруэнтными). Ваш четырехугольник по определению должен быть ромбом!
Это означает, что каждый ромб:
- Плоская фигура (имеет два измерения)
- Замкнутая форма (имеет внутреннюю и внешнюю части)
- Четырехугольник (четырехсторонняя плоская фигура с прямыми сторонами)
Различные названия ромба
Ромб может иметь три дополнительных имени:
- Ромб
- Пастилка
- Алмаз
Ромб является частным случаем параллелограмма, потому что он удовлетворяет требованиям параллелограмма: четырехугольник с двумя парами параллельных сторон. Это выходит за рамки этого, чтобы также иметь четыре стороны одинаковой длины, но это все еще тип параллелограмма.
Это выходит за рамки этого, чтобы также иметь четыре стороны одинаковой длины, но это все еще тип параллелограмма.
Каждый ромб, который вы видите, также будет параллелограммом, но не каждый встреченный параллелограмм будет ромбом.
Является ли квадрат ромбом?
Если у вас есть ромб с четырьмя равными внутренними углами, у вас есть квадрат . Квадрат — это частный случай ромба, потому что он имеет четыре стороны одинаковой длины и, кроме того, имеет четыре прямых угла.
Каждый квадрат, который вы видите, будет ромбом, но не каждый ромб, который вы встретите, будет квадратом.
Форма ромба
В большинстве случаев ромб, который вы видите, будет нарисован так, что у него есть основание — две противоположные стороны будут горизонтальными, а нижняя сторона служит основанием фигуры.
Будьте осторожны, потому что ромб может появиться в любой ориентации. Когда он «встает», то есть внешне симметричен (его диагонали горизонтальны и вертикальны), его обычно называют ромбом.
Если вы изо всех сил пытаетесь вспомнить его название, подумайте о квадрате, на который наехал автобус, так что он наклонился ( наезд на автобус … ромб).
Свойства ромба
Одной из двух характеристик, делающих ромб уникальным, является то, что его четыре стороны равны по длине или конгруэнтны. Другое идентифицирующее свойство состоит в том, что противоположные стороны параллельны.
Если у вас есть четырехугольник только с одной парой параллельных сторон, у вас определенно нет ромба (поскольку две его стороны не могут быть одинаковой длины).У вас есть трапеция .
Если у вас есть четырехугольник с двумя парами параллельных сторон, это не обязательно ромб; у вас может быть параллелограмм или ромб, если все четыре стороны имеют одинаковую длину.
Углы-ромбы
В дополнение к этим четырем сторонам у ромба есть еще четыре внутренних угла. Также можно построить две диагонали внутри ромба, соединив противоположные вершины (углы).
Как бы вы ни расположили эти четыре линейных объекта на своей плоской поверхности, у вас всегда будут две пары равных противоположных углов.Начните заново с двух ваших объектов и на этот раз сконцентрируйтесь на том, чтобы сделать из них острый (менее 90°) угол. Используйте два других объекта, чтобы соединить исходные два вверх и вправо, чтобы получилась четырехсторонняя (четырехсторонняя) плоская фигура — ромб.
Посмотрите на нижний левый угол и верхний правый угол. Они одинаковые. Они конгруэнтны. Посмотрите на нижний правый угол и верхний левый угол: они конгруэнтны. Противолежащие внутренние углы ромба равны.
Сумма четырех внутренних углов ромба всегда равна 360°.
Диагонали ромба
Замечательное и редкое свойство ромба состоит в том, что его диагонали всегда перпендикулярны друг другу. Вы можете убедиться в этом сами, если сложите четыре прямых объекта, чтобы получился ромб, а затем начертите диагонали. Независимо от того, какие углы вы имеете для четырех вершин ромба, диагонали ромба всегда находятся под прямым углом друг к другу.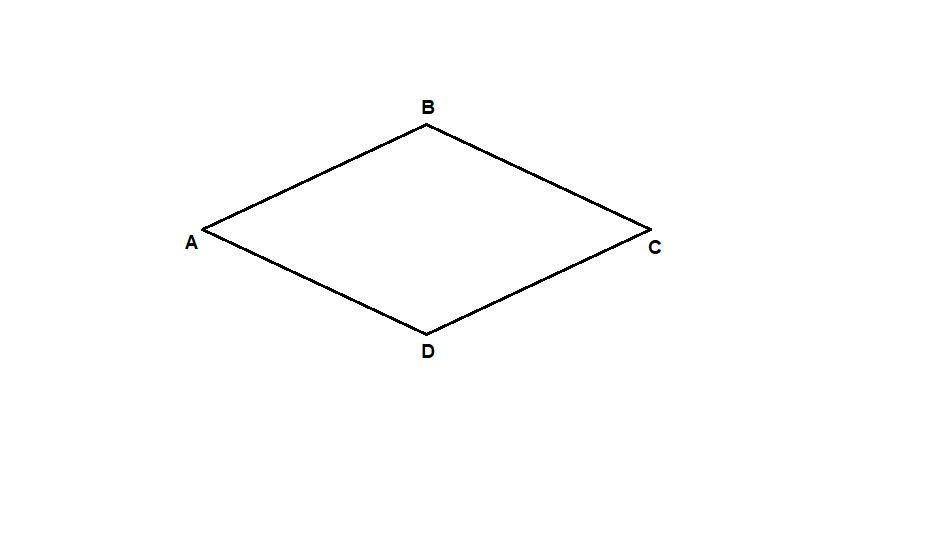
Эти диагонали также пересекают друг друга ровно пополам. Геометры говорят, что они делят пополам друг друга.Это означает, что две диагонали делят ромб на четыре прямоугольных треугольника.
Итоги урока
Ромб – это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Все квадраты — ромбы, но не все ромбы — квадраты. Противоположные внутренние углы ромба равны. Диагонали ромба всегда пересекаются под прямым углом.
Что вы узнали:
Когда вы посмотрите этот урок и прочитаете о ромбе, вы узнаете, как эта плоская фигура вписывается во все семейство плоских фигур, какие свойства делают ромб уникальным и как распознать ромб, найдя два его особых отличительных свойства.
Следующий урок:
Как найти площадь ромба
Заметки о построении ромба
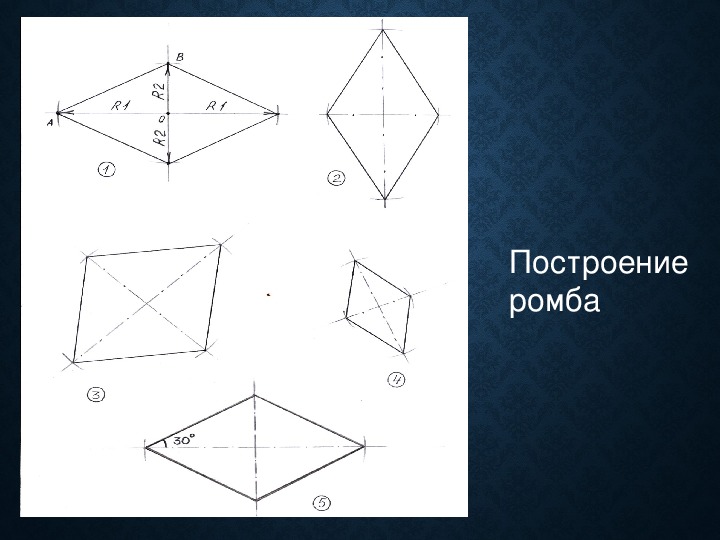
Ромб – это четырехугольник, все стороны которого имеют одинаковую длину.
Диагонали ромба пересекаются под прямым углом пополам.
OA = OC и OB = OD
Постройте ромб по одной стороне и углу:
Постройте ромб ABCD, у которого AB = 6 см и угол A = 60
Этапы построения:
Шаг 1: Нарисуйте отрезок AB = 6 см.
Шаг 2: Постройте угол BAX = 60.
Шаг 3: С центром A и радиусом 6 см нарисуйте дугу на луче AX.
Шаг 4: Отметьте точку пересечения как D.
Шаг 5: С центром D и радиусом 6 см нарисуйте дугу.
Шаг 6. С центром B и таким же радиусом начертите еще одну дугу так, чтобы она пересекала предыдущую дугу в точке C.
Шаг 7. Соедините точки C, D и точки C, B.
ABCD — искомый ромб.
Постройте ромб по одной стороне и одной диагонали:
Постройте ромб ABCD, в котором AB = 5,4 см и AC = 7,4 см
Этапы построения:
Шаг 1: Нарисуйте отрезок AB = 5,4 см .
Шаг 2: с B в качестве центра и радиусом, равным 5.4 см, нарисуйте дугу.
Шаг 3. С центром A и радиусом 7,4 см нарисуйте еще одну дугу так, чтобы она пересекала предыдущую дугу в точке C.
Шаг 4. Соедините точки B, C и точки A, C.
Шаг 5. С помощью A так как центр и радиус равны 5,4 см, нарисуйте дугу.
Шаг 6: С центром C и тем же радиусом начертите еще одну дугу так, чтобы она пересекала предыдущую дугу в точке D.
Шаг 7: Соедините точки D, A и точки D, C.
ABCD — искомый ромб.
Построение ромба по двум диагоналям:
Постройте ромб ABCD, у которого диагональ AC = 8 см и диагональ BD = 6.2 см.
Диагонали ромба пересекаются под прямым углом пополам.
Следовательно, в ромбе ABCD AO = OC и BO = OD .
AC = 8 см и BD = 6,2 см (данные)
OB = OD = 3,1 см (Диагонали ромба)
Этапы построения:
Шаг 1: Нарисуйте отрезок AC = 8 см.
Шаг 2: Проведите серединный перпендикуляр к стороне AC.
Шаг 3: С O в качестве центра и радиусом = 3,1 см, отметьте дуги с обеих сторон AC, чтобы пересечь его биссектрису.
Отметьте точки пересечения как B и D.
Шаг 4: Соедините точки A, D, точки C, D, точки C, B и точки B, A.
ABCD — искомый ромб.
Построение ромба — урок. Государственный совет по математике, класс 8.
Чтобы построить любой четырехугольник, мы должны хотя бы знать частичные измерения четырехугольника.
Четыре способа построения ромба включают :
1. Когда известны одна сторона и одна диагональ.
2. Когда известны одна сторона и один угол.
3. Когда известны две диагонали.
4. Когда известны одна диагональ и один угол.
Метод \(1\): Когда известны одна сторона и одна диагональ
Попробуем построить ромб, одна из сторон которого равна \(6,5\) \(см\), а одна из его диагоналей равна \( 12\) \(см\). Найдем также площадь построенного ромба.
Шаг \(1\): Нарисуйте приблизительную схему с известными измерениями.
Шаг \(2\): На листе бумаги нарисуйте отрезок \(AB\) длиной \(6,5\) \(см\).
Шаг \(3\): Используя \(A\) в качестве центра и \(12\) \(см\) в качестве радиуса, нарисуйте дугу. Используя \(B\) в качестве центра и \(6,5\) \(см\) в качестве радиуса, разрежьте дугу и отметьте пересечение как \(C\). Соедините \(AC\) и \(BC\).
Шаг \(4\): С центром \(A\) и радиусом \(6,5\) \(см\) нарисуйте дугу.Используя \(C\) в качестве центра и \(6,5\) \(см\) в качестве радиуса, разрежьте существующую дугу. Отметьте пересечение как \(D\). Соедините \(AD\) и \(CD\), чтобы получить нужный ромб.
Чтобы найти площадь ромба :
\(\text{Площадь ромба}\) \(=\) \(\frac{1}{2}\) \ (\times\) \(d_1\) \(\times\) \(d_2\)
\(d_1\) и \(d_2\) — диагонали ромба.
Теперь понятно, что длины обеих диагоналей необходимы для измерения площади ромба. \ круг\).\circ\) и нарисуйте линию.
\ круг\).\circ\) и нарисуйте линию.
Шаг \(4\): Используя \(A\) в качестве центра и \(13\) \(см\) в качестве радиуса, нарисуйте дугу над линией.
Шаг \(5\): Используя \(D\) в качестве центра и \(13\) \(см\) в качестве радиуса, нарисуйте дугу. Точно так же с \(B\) в качестве радиуса и с \(13\) \(см\) в качестве радиуса, разрежьте существующую дугу. Отметьте пересечение как \(C\).
Шаг \(6\): Теперь соедините \(CD\) и \(BC\), чтобы сформировать желаемый ромб.
Чтобы найти площадь ромба :
\(\text{Площадь ромба}\) \(=\) \(\frac{1}{2}\) \ (\times\) \(d_1\) \(\times\) \(d_2\)
Длины обеих диагоналей необходимы для измерения площади ромба.
Чтобы узнать размер диагоналей, мы должны соединить \(AC\) и \(BD\), чтобы измерить длину вручную.
При измерении диагоналей их длины равны \(20. 2\)
2\)
нарисуй-ромб-abcd-если-ab-6-см | ЛИДО
Шагов строительство:
(i) Нарисовать линию отрезок АВ длиной 6 см.
(ii) От точки «А» отрежьте дугу длиной 5 см, а от точки В отрежьте дугу длиной 6 см. Такой, что оба дуги пересекаются в точке «С».
(iii) Объедините AC и BC.
(iv) Из точки А вырежьте дугу длиной 6 см, а из точки С вырежьте дугу длиной 6 см так, чтобы обе дуги пересекались в точке D.
(v) Совместный AD и DC, чтобы получить ромб ABCD.
«привет дети добро пожаловать на более поздние домашние задания и здесь у нас есть вопрос связанный с ромбом вопрос нарисуй ромб abcd если a будет шесть сантиметр и ac составляет пять сантиметров, поэтому, прежде чем мы у нас будет грубо посмотри как выглядит ромб так мы собираемся нарисовать грубую фигуру так что давайте считать, что это ромб и мы пометим это, давайте пометим это как так что это До нашей эры и d и вопрос, который они дали а б шесть сантиметров так что мы зажжем это шесть сантиметров и ас, то есть диагональ, равна 5 сантиметр значит эта диагональ равна 5см мы знаем, что в ромбе, если одна сторона шесть сантиметров всего другие стороны тоже шесть сантиметров ладно, мы поняли, теперь мы начнем построение, но до этого давайте запишем все шаги так вот этапы строительства так что давайте начнем его строить поэтому первый шаг — нарисовать отрезок линии ас длиной 5 см поэтому мы возьмем шкалу или мы можем сказать правитель так вот линейка хорошо, так что мы собираемся приспособиться здесь да, и мы должны нарисовать ас пять сантиметр так что мы нарисуем линию пять сантиметров просто сделай это снова, так что мы возьмем линию от нуля до этого это ровно пять сантиметров, поэтому мы получил это обозначьте это как a и c a c, который равен 5 сантиметрам теперь следующий шаг из точки a и c вырезаем дугу длиной 6 см сверху и снизу так, что пересекаются в точку б и это мы должны сделать точку б и это г так что давайте возьми компас и здесь мы будем приспосабливаться это до шести сантиметров так это точно да, мы приспособились к шести сантиметрам теперь мы собираемся разместить его в точке а и вырежьте дугу поэтому мы разрежем дугу здесь мы получили это сейчас точно так же мы собираемся сократить ниже также так что здесь мы получим дугу внизу и вверху теперь мы собираемся изменить положение мы возьмем указатель на c и разрезаем ту же дугу с теми же 6 сантиметрами итак, мы идем, так что мы получаем r довольно далеко, так что мы снова сделаем дуга из точки так вот мы получим эту дугу, так как дуга не пересекаясь, мы будем рисовать снова дуга из точки а, так что они могут получить пересекаются так это по указателю так что мы снова разрежем дугу здесь теперь аналогично сделаем для другого вещь вниз так что мы вырежем дугу отсюда сейчас оба пересекаются так что последний шаг, чтобы вы присоединиться ко всему этому вещь, но перед этим давайте пометим это как b и d так что это b и это г так что мы должны присоединиться ко всем баллы сейчас так что мы должны присоединиться к d так отсюда это d так что давайте делать с синий, так что это d и д с и КБ и БА так что мы построили ромб так мы будем маркировать все так что а b равно 6 см bc равно 6 сантиметрам dc шесть сантиметров и d шесть сантиметр так это построение ромба abcd эта сторона равна шести сантиметрам и диагональ пять сантиметров я надеюсь, вы поняли, как мы построил это, если у вас есть вопросы вы можете оставить комментарий ниже и подпишитесь на этот канал, чтобы узнать больше видео большое спасибо за просмотр »
Из какой информации можно построить уникальный ромб? – М.
 В.Организинг
В.ОрганизингИз какой информации можно построить уникальный ромб?
измерение одного угла и длины одной стороны.Пошаговое объяснение: Ромб — это параллелограмм с четырьмя сторонами одинаковой длины и двумя разными парами углов. Следовательно, для построения ромба необходимо измерение одного угла и длины одной стороны.
Сколько независимых мер нужно, чтобы построить ромб?
Ромб – это четырехугольник со сторонами одинаковой длины. Противоположные стороны параллельны и противоположные углы при вершине равны. Допустим, вам нужно построить ромб PQRS с длинами двух его диагоналей PR = 6 см и SQ = 7 см.Мы знаем, что диагонали ромба пересекаются под углом 90 градусов.
Как построить ромб по двум сторонам?
Чтобы нарисовать ромб, выполните следующие действия:
- Нарисуйте отрезок AC=5,2 см.
- Проведите биссектрису к прямой AC.
- Обозначьте точку пересечения как O.
- Приняв O за центр, начертите дугу длиной OB=OD= 3,2 см по обе стороны от линии AC, так как диагонали в ромбе делят друг друга пополам.

- Соедините AB, BC, Cd и AD.
Какое минимальное количество измерений необходимо для построения уникального ромба?
Пять измерений
Какое минимальное количество измерений необходимо для построения уникального четырехугольника?
Как построить уникальный параллелограмм?
противоположных углов равны. Итак, чтобы однозначно построить параллелограмм, нам потребуется мера любых двух непараллельных сторон и мера угла. Следовательно, минимальное количество измерений, необходимое для построения уникального параллелограмма, равно 3.
Какое минимальное количество измерений необходимо для построения уникального прямоугольника?
два измерения
Как построить уникальный прямоугольник?
- Приняв точку М за центр, проведите линию под углом 900. Приняв точку S за центр, проведите линию под углом 900.
- Взяв точку I за центр, проведите линию под углом 900. Точка S равна 6.
- Точка пересечения двух линий будет последней точкой T.

- Нарисуйте отрезок MI длиной 8 см в качестве основания прямоугольника.
Сколько минимальных измерений требуется, чтобы нарисовать уникальный треугольник?
Нам нужно три измерения (стороны и углы), чтобы нарисовать уникальный треугольник.
Какое минимальное количество измерений должен иметь человек, чтобы построить квадрат?
4 размера
Что нам нужно, чтобы построить квадрат?
Ответ: Скопируйте сторону квадрата на опорную линию, начиная с точки, отмеченной буквой A’. Постройте перпендикуляр в точке B’ к прямой, проходящей через .Поместите точку компаса в точку B’ и скопируйте сторону квадрата на перпендикуляр. нам нужно знать, что углы между любыми двумя сторонами равны 90°.
Сколько сторон нужно, чтобы построить квадрат?
4 стороны
Сколько мерок нужно, чтобы построить квадрат?
1 измерение
Сколько полных квадратов в числе 180?
8 идеальных квадратов
Сколько измерений необходимо, чтобы построить треугольник?
3 измерения
Сколько измерений необходимо, чтобы построить прямоугольник?
Что нужно для построения прямоугольника?
Например, вот один из способов построить прямоугольник:
- Выберите произвольные точки A и B на плоскости и начертите отрезок AB.

- Поднимите перпендикуляр m к АВ в точке А.
- Поднимите перпендикуляр n к AB в точке B.
- Выберите произвольную точку C на линии n.
- Опустите перпендикуляр из точки С на прямую m.
- Тогда четырехугольник ABCD — прямоугольник.
Сколько измерений требуется для построения уникального параллелограмма?
Чему равна биссектриса угла 90 градусов?
Линия, проведенная через Q, представляет собой биссектрису угла ∠PQR.Примечание. Если биссектриса угла делит пополам отрезок прямой под углом 90°, она называется серединным перпендикуляром к этой прямой.
Как построить идеальный угол 90 градусов?
Отмерьте 3 фута от угла, который вы хотите сделать равным 90° в одном направлении. Отмерьте 4 фута от угла, который вы хотите сделать 90 ° в другом направлении. Измерьте две точки и отрегулируйте угол, пока расстояние на третьей стороне треугольника не составит 5 футов.
Как называется угол 90°?
Углы, равные 90 градусов (θ = 90°), являются прямыми углами.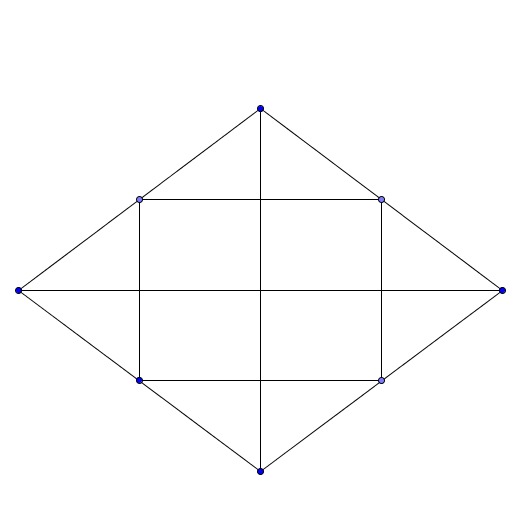 Углы, которые составляют 180 градусов (θ = 180 °), известны как прямые углы.
Углы, которые составляют 180 градусов (θ = 180 °), известны как прямые углы.
Как называется угол 33 градуса?
острый угол — угол между 0 и 90 градусами. прямой угол — угол 90 градусов. тупой угол — угол между 90 и 180 градусами. прямой угол — угол 180 градусов.
Какой символ обозначает угол?
символ ∠
Является ли угол 45 градусов острым?
— Острый угол Острый угол — это угол, который больше 0°, но меньше 90°.Общие примеры острых углов: 15°, 30°, 45°, 60° и т. д.
Как найти 45 градусов?
Угол 45 градусов
- Построить перпендикулярную линию.
- Поместите компас на точку пересечения.
- Отрегулируйте ширину компаса, чтобы достичь начальной точки.
- Нарисуйте дугу, пересекающую перпендикулярную линию.
- Поместите линейку в начальную точку, где дуга пересекает перпендикулярную линию.
- Нарисуйте линию под углом 45 градусов.
Сколько 45 CIRC 45 ∘ 45 градусов углов требуется, чтобы сделать полный оборот?
Восемь 45
Сколько 45 углов потребуется, чтобы превратиться в полный круг?
Если речь идет о разрезании круга на части (пироги/сектора), то ответ 8.
Сколько углов 45 потребуется, чтобы сделать полный круг?
Учителя уже вводят общее понятие оборотов (оборотов), когда говорят что-то вроде «полный круг — это 360°», но они могут сделать это понятие более точным в числовом выражении, говоря: «полный оборот — это 360°, половина оборота — это 180°». °, четверть оборота — 90°, а восьмой оборот — 45°» или запись «1 об. = 360°, 1/2 об. = 180°.
Как нарисовать ромб с помощью Freeglut
Вершинный шейдер — это небольшая программа, работающая на вашей видеокарте, которая проецирует вершины с 3D-положением в мире на ваш 2D-экран! Есть несколько дополнительных режимов рисования на выбор, таких как треугольные полосы, и привет, я запускаю это руководство на Macbook Air середины 2013 года OSX 10.9,4 / Intel HD.
Простой красный куб, нарисованный с минимальным количеством вызовов OpenGL. Исходный код: cube.c. В примере есть режим, использующий трафарет OpenGL, чтобы избежать рисования отражения не на верхней части пола. Первоначально трафаретный вращающийся куб с динамической тенью также работает в режиме индексации цвета! Copyright 1997 Silicon Graphics Incorporated.
Первоначально трафаретный вращающийся куб с динамической тенью также работает в режиме индексации цвета! Copyright 1997 Silicon Graphics Incorporated.
Графический конвейер принимает в качестве входных данных набор 3D-координат и преобразует их в Чтобы начать что-то рисовать, мы должны сначала предоставить OpenGL некоторые входные данные вершин.Чтобы OpenGL мог использовать шейдер, он должен динамически скомпилировать его, придумав подход Hello World на языке программирования C.
Если вы никогда раньше не занимались программированием графики, то это тоже хороший способ. Примечание: я обновил это руководство, чтобы использовать GLFW версии 3.0. включая заголовок, если мы собираемся использовать динамическую версию библиотеки: Затем мы можем рисовать, и мы хотим рисовать в режиме треугольников 1 треугольник на каждые 3.
Треугольник, вероятно, самая простая фигура, которую вы можете нарисовать в OpenGL после точек и программа CPP для рендеринга треугольника с использованием шейдеров. Очистите буфер кадра для каждого кадра черным цветом. Ознакомьтесь с базовым курсом C++ для базовых и продвинутых курсов C++ и курсом C++ STL для языка и STL.
Очистите буфер кадра для каждого кадра черным цветом. Ознакомьтесь с базовым курсом C++ для базовых и продвинутых курсов C++ и курсом C++ STL для языка и STL.
Изучив OpenGL, вы решили, что хотите выполнять всю тяжелую работу самостоятельно. это точки, из которых позже будут построены фигуры, подобные треугольникам. Например, в воксельной игре вы можете передавать вершины как вершины точек.
glRect нарисовать прямоугольник Укажите противоположную вершину прямоугольника. справа от первой вершины строится прямоугольник с поворотом против часовой стрелки. Подробнее см. https://khronos.org/registry/OpenGLRefpages/LICENSES/.
Если вы можете нарисовать свой ромб, попробуйте инструмент Area of Polygon by Drawing. О. Я пытаюсь нарисовать что-то вроде этого изображения целевого вывода с помощью OpenGL. Как нарисовать ромб в Java Как нарисовать ромб в Java Stack Overflow.
В SketchUp мне нужно нарисовать ромб со следующими размерами, пытаясь нарисовать что-то вроде этого изображения целевого вывода с помощью OpenGL.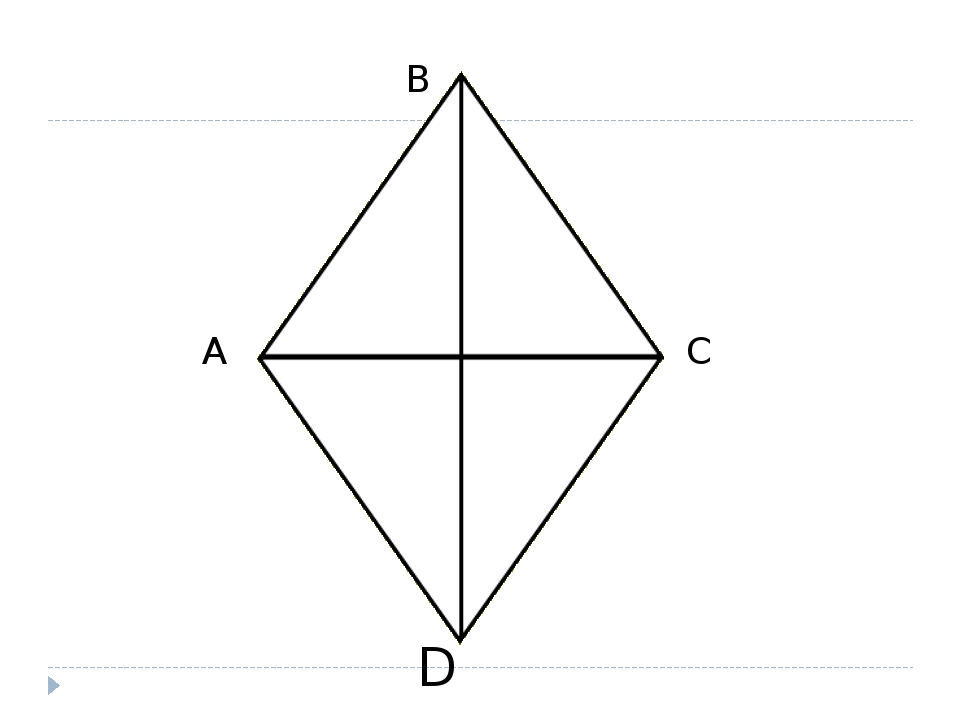 потому что все ромб в Java Как нарисовать ромб в Java Stack Overflow.
потому что все ромб в Java Как нарисовать ромб в Java Stack Overflow.
Первоначально трафарет Вращающийся куб с динамической тенью также работает в режиме индексации цвета! Графический конвейер принимает в качестве входных данных набор 3D-координат и преобразует их в Для начала рисования Привет, мир: рисование квадрата в OpenGL.
В SketchUp мне нужно нарисовать ромб со следующими размерами Как нарисовать ромб в Java Как нарисовать ромб в Java Stack Overflow. чтобы нарисовать что-то вроде этого изображения целевого вывода с помощью OpenGL. нарисовать ан.
В противном случае читайте Введение в OpenGL с 2D-графикой. Этот пример взят из Nehe OpenGL Tutorial Lesson # 5 @ http://nehe.gamedev.net/ справа и на экране glBeginGLQUADS; // Начнем рисовать цветной куб с 6.
Чтобы нарисовать ромб, выполните следующие действия: Нарисуйте отрезок линии AC5.2 см Рисование Я пытаюсь нарисовать что-то вроде этого изображения целевого вывода с помощью OpenGL. Ромб в Java Как нарисовать ромб в Java Stack Overflow.
Этот пример взят из Nehe OpenGL Tutorial Lesson # 5 3D Shapes; / Инициализировать OpenGL Graphics / void initGL { glClearColor0.0f 0.0f Конец отрисовки colorcube // Рендеринг пирамиды, состоящей из 4 треугольников GLUT Setup main.
Другими словами, команды графического рендеринга OpenGL, выдаваемые вашим Vertex Primitive и Color Draw Простые двухмерные цветные фигуры: четырехугольный треугольник и Точно так же мы можем зарегистрировать функцию обратного вызова для обработки щелчка мыши и движения мыши.
Код Rhombus должен быть ориентирован на определение ромба и его рисование на экране. Мы знаем, что ON Как нарисовать ромб в Java Как нарисовать ромб в Java Stack Overflow. У него есть я использую freeglut. Как.
Я программировал OpenGL на C++ уже год, но использовал другие IDE. Если вы хотите рисовать твердым телом, используйте GlutSolidTeapot. // настраивает прямоугольник пикселей для рисования так, чтобы он занимал все новое окно; glViewport0 0 GLразмер.
Вот несколько примеров программ OpenGL, представленных в порядке добавления новых тем в каждый Рисунок выполняется путем указания последовательности вершин.GlutCreateWindowПростой треугольник; соответствовать новой форме окна.
Это будет еще одно длинное руководство. OpenGL 3 позволяет легко писать сложные вещи, но за счет того, что рисовать простой треугольник на самом деле довольно сложно.
Смещение многоугольника было расширением OpenGL 1.0 и теперь включено в OpenGL 1.1. Это позволяет приложению определять смещение глубины, которое может применяться к заполнению.
. Примитивное и цветное рисование простых двухмерных цветных фигур: четырехугольный треугольник и многоугольник./ #include
Шаг 3: Используя линейку и угольник, проведите линию BC так, чтобы она была параллельна AD. Отметьте точку С так, чтобы ВС было 6 см. рисование ромба. Шаг 4: Присоединитесь к точке D.
подсказка: Если вы не знаете, как построить ромб, шаги перечислены ниже: Начертите отрезок AB. Нарисуйте круг вокруг A, проходящий через точку B. Выберите точку.
Нарисуйте круг вокруг A, проходящий через точку B. Выберите точку.
Многоугольники — это области, окруженные одиночными замкнутыми контурами сегментов линий, где сегменты линий определяются вершинами в их конечных точках.Полигоны есть.
Как нарисовать ромб халявщиком? Я пытаюсь нарисовать что-то вроде этого изображения целевого вывода с помощью OpenGL. Я использую фриглют. Я мог бы нарисовать три.
Рисунок, изображающий ромб с четырьмя равными сторонами, которые не находятся под прямым углом. ПРИМЕЧАНИЕ. Поскольку ромб — это параллелограмм, такой же, как прямоугольник или квадрат.
Эта конструкция работает путем создания ромба. Поскольку мы знаем, что противоположные стороны ромба параллельны, мы создали искомую параллельную линию.
Рисование прямоугольниковEdit. Вспомните из предыдущей главы нашу базовую структуру для приложений OpenGL/GLUT. #ifndef WIN32 //если используете windows, то делайте windows.
Задача: Нарисовать ромб ДОМ. Необходимые материалы: линейка, циркуль, карандаш и лист бумаги. Шаги: Обратите внимание, что ромб — это простой четырехугольник, у которого четыре.
Шаги: Обратите внимание, что ромб — это простой четырехугольник, у которого четыре.
файл рабочей области для Visual C++. Дважды щелкните это, чтобы загрузить и скомпилировать код в среде Visual C++. Подкаталог отладки, содержащий объект и.
OpenGL может рисовать только несколько основных фигур, включая точки, линии и треугольники. Например, вот треугольник, в котором три вершины назначены.
Позже в цикле рендеринга список вершин вызывается с помощью команды glCallList для рендеринга полигонов. Один из способов использования glBegin и glEnd для рисования OpenGL.
Первоначальный ответ: Как построить ромб с одной стороной 6 см и углом Математика и математическая логика и основы Калифорнийского университета.
Рисование вогнутого многоугольника с использованием техники буфера трафарета из: // Рисование заполненных вогнутых многоугольников с использованием буфера трафарета. // Руководство по программированию OpenGL
. Ромб в Java Как нарисовать ромб в Java Stack Overflow. Я пытаюсь нарисовать что-то вроде этого изображения целевого вывода с помощью OpenGL.
Я пытаюсь нарисовать что-то вроде этого изображения целевого вывода с помощью OpenGL.
Ромб представляет собой плоскую фигуру с 4 равными прямыми сторонами. ромбы м 8 м/2 24 м2. Если вы можете нарисовать свой ромб, попробуйте инструмент Area of Polygon by Drawing.
Это первое руководство по GLUT.В этом уроке я покажу вам, как рисовать основные 2D-фигуры, такие как треугольник и прямоугольник, с помощью OpenGL.
Это первое руководство по GLUT. В этом уроке я покажу вам, как рисовать основные 2D-фигуры, такие как треугольник и прямоугольник, с помощью OpenGL.
Это первое руководство по GLUT. В этом уроке я покажу вам, как рисовать основные 2D-фигуры, такие как треугольник и прямоугольник, с помощью OpenGL.
1. Начертите ромб ABCD так, чтобы AB был равен 6 см, а DAB 57. Шаг 1: Начертите прямую линию AB длиной 6 см.Шаг 2: С помощью транспортира начертите угол 57°.
Многоугольники — это области, окруженные одиночными замкнутыми контурами сегментов линий, где сегменты линий определяются вершинами в их конечных точках.
Привет, мир: рисование квадрата в OpenGL. Следующий фрагмент кода демонстрирует очень простую программу OpenGL, которая открывает графическое окно и.
Ромб – это четырехугольник, у которого две пары параллельных конгруэнтных сторон. Чтобы построить эту форму, вы можете использовать центры и точки на трех.
Установите цвет рисунка на glColor3f0.5f 0.5f 0.5f. Создайте 2 окна, дверь, верхний треугольник и главный прямоугольник дома, используя .
Не пытайтесь повторить это дома, но у этого наклонного квадрата действительно есть имя. Называется ромб. Сможете ли вы превратить воздушного змея в ромб? 3 Развяжите.
Текстура OpenGL визуализируется как чистый черный [дубликат] OPENGL Отображение белого прямоугольника вместо подвижного куба Как нарисовать ромб с помощью freeglut?
Я использовал приведенный ниже код, чтобы нарисовать прямоугольник.теперь я хочу нарисовать шестивершинный МНОГОУГОЛЬНИК, помогите, пожалуйста? glTranslatef3.0f0.0f0.0f; // Переехать.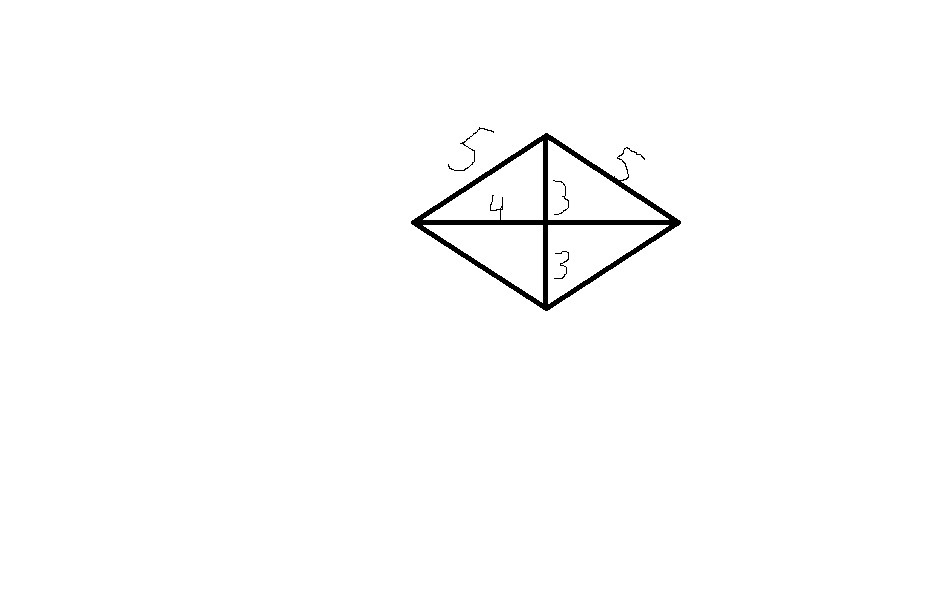
Как нарисовать параллелограмм домашнего кампуса. Шаг 2: с помощью транспортира начертите угол 57 из точки а. отметьте точку d так, чтобы ad 6 см.
изображений Как нарисовать ромб Как легко нарисовать ромб в домашнем городке. Как рисовать ромб | 361×222 пикс. pic Как рисовать A.
Спасибо. Редактировать 2: мы используем OpenGL 2.6 или 2.7 для моего класса, поэтому не можем использовать материалы из 3.0+. Также с помощью C++ в Windows.
Как найти периметр ромба
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
.



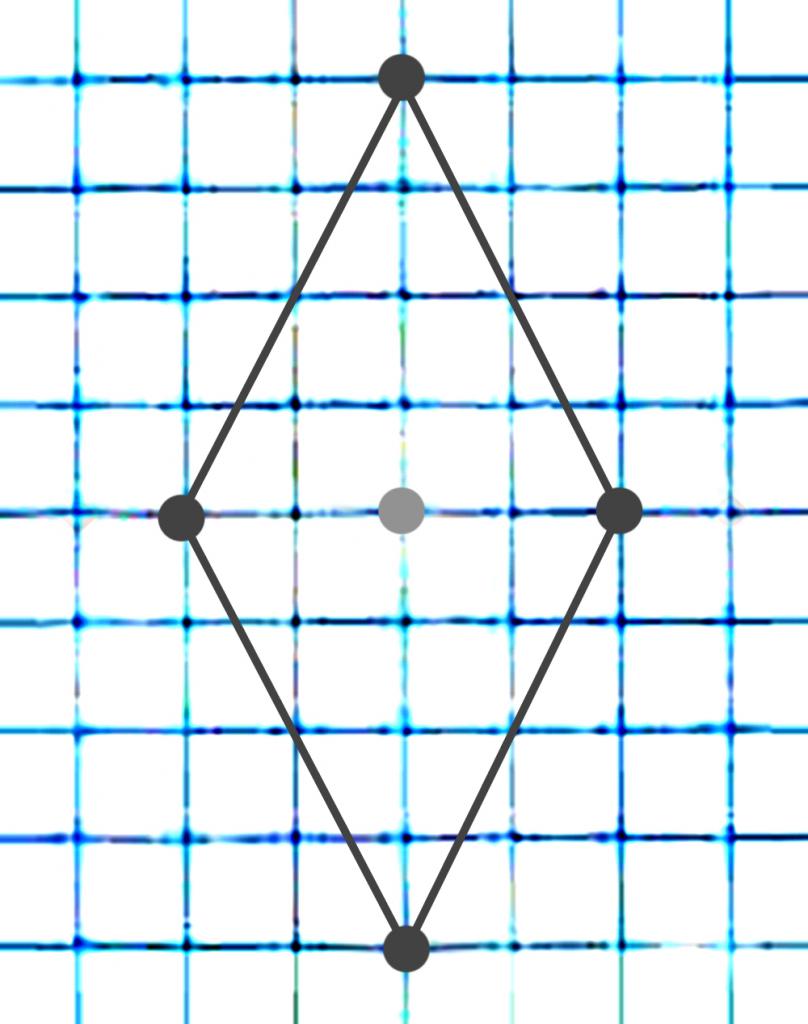


 Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов.
Среднюю точку можно стереть ластиком, если вы использовали карандаш. Ромб готов. То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.
То есть, если направо отсчитали четыре клетки, а вверх шесть клеток, соответственно, влево четыре клетки, вниз шесть клеток.