Объемный квадрат рисунок карандашом. Как рисовать объемные фигуры и тела карандашом
Попробуем понять принцип взаимодействия квадрата и окружности на перспективном рисунке. Научиться проверять правильность квадрата, вписывая в него окружность.
Изобразите в перспективе горизонтальный и вертикальный квадраты. Проверьте правильность их изображения при помощи вписанных окружностей.
Прежде, чем приступать к выполнению этого задания, внимательно рассмотрите схему на рис. 2.8. Точки касания сторон квадрата к окружности (точки 1, 2, 3, 4) делят стороны квадрата пополам. Средние линии квадрата и его диагонали пересекаются в центре окружности. Противолежащие стороны квадрата и соответствующие им средние линии параллельны и расположены на равном расстоянии друг от друга. Рассмотрите также рис. 2.9. На примере окружности и квадрата во фронтальной перспективе хорошо видно, что центр эллипса и центр окружности — две разные точки. Диаметр окружности, являющийся малой осью эллипса, делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю — больше, дальний — меньше (по закону перспективного сокращения), а точка центра эллипса делит этот же диаметр — малую ось эллипса — ровно пополам.
Нарисовать квадрат в перспективе можно в разной последовательности, например, сначала изобразить одну прямую — сторону квадрата, а затем другую, ей перпендикулярную, отложить на этих прямых от точки их пересечения отрезки, равные стороне квадрата, а затем от полученных вершин достроить остальные стороны, сводя параллельные прямые в точки схода. Или иначе — сначала провести две параллельные прямые, а затем еще две, перпендикулярные двум первым. В любом случае эта задача кажется простой только на первый взгляд. На самом деле слишком много позиций (степень схождения параллельных сторон квадрата, их направления и размеры) рисовальщику приходится определять на основании своего личного опыта, а его, как известно, иногда бывает недостаточно. Именно поэтому правильность квадрата необходимо проверить, например, вписав в него окружность. При любом положении квадрата для того, чтобы вписать в него окружность (в перспективном рисунке — эллипс), необходимо найти точки касания сторон квадрата к вписанной окружности (точки 1 — 4) и определить положение осей эллипса. Если вписанный эллипс касается сторон квадрата в заданных точках и симметричен относительно осей, то квадрат нарисован верно.
Если вписанный эллипс касается сторон квадрата в заданных точках и симметричен относительно осей, то квадрат нарисован верно.
Горизонтальный квадрат. Нарисуйте горизонтальный квадрат по представлению (рис. 2.10). Найдите точки касания, для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода (рис. 2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис.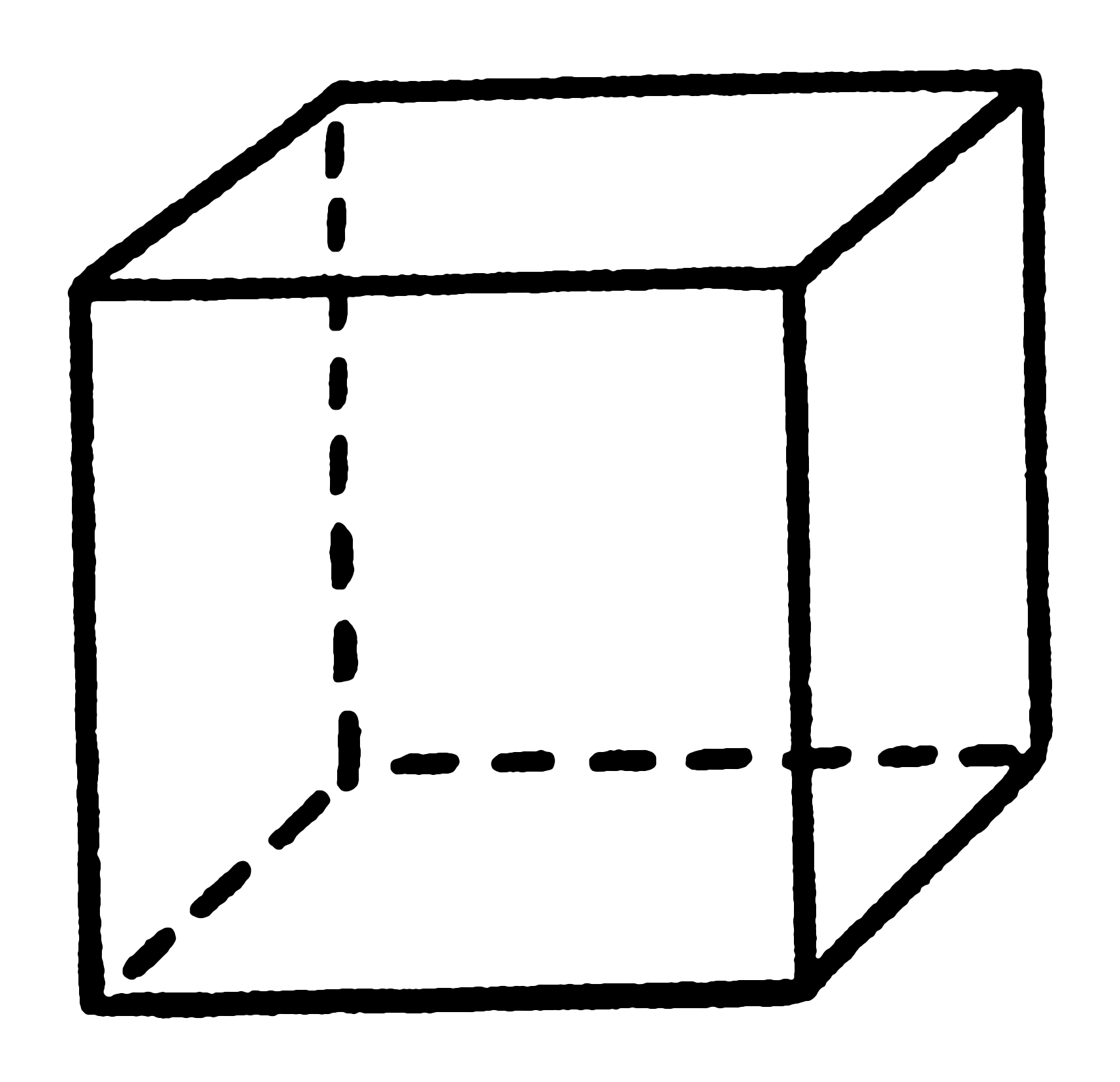 2.13). Проверьте симметричность полученного эллипса относительно его осей.
2.13). Проверьте симметричность полученного эллипса относительно его осей.
Вертикальный квадрат. При вертикальном положении квадрата точки 1, 2, 3, 4 найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис. 2.14).
Несколько сложнее определить направление осей эллипса. Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры. Задача значительно упрощается в том случае, если вертикальный квадрат, в который вы вписываете окружность, является гранью куба. Тогда ось цилиндра (она же малая ось эллипса) параллельна горизонтальным ребрам куба и на рисунке идет с ними в одну точку схода. Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).
Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).
На рисунках, иллюстрирующих последовательность вписывания окружности в горизонтальный и вертикальный квадраты, представлены идеальные ситуации. В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.
Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе. Именно поэтому современная методика предлагает не проверять и исправлять подобным образом уже нарисованные квадраты, а строить их, описывая вокруг окружности.
Хоть квадрат и прямоугольник это простейшие геометрические фигуры, но, чтобы их нарисовать в фотошопе, нужно приложить некоторые усилия и обладать базовыми знаниями. Новичок без должной подготовки, скорее всего, не справится с этой задачей.
В этой статье разберем 3 самых популярных способа как нарисовать прямоугольник или квадрат в фотошопе.
Но прежде, чем приступить к выбору способа рисования, нужно определиться с будущими параметрами. Прямоугольник/квадрат может быть:
- залит сплошным цветом или только с отрисовкой границ;
- произвольный или с точно заданными размерами;
- с возможностью в любое время менять его размеры без потери качества.
Способ 1. Инструмент произвольная фигура
В этом способе прямоугольник или квадрат будут нарисованы залитым сплошным цветом. Если вам нужна только граница, переходите к следующим двум способам.
На панели инструментов выберите инструмент . Дальше возможны два варианта развития событий:
Вариант 1.
 Квадрат или прямоугольник с дальнейшей возможностью изменять размеры без потери качества
Квадрат или прямоугольник с дальнейшей возможностью изменять размеры без потери качестваЗдесь, конечно, подразумевается использование векторной фигуры. Чтобы ее нарисовать нужно выбрать параметр Слой-фигура :
В дальнейшем вы можете без потери качества изменять размеры этой фигуры. Для этого используйте инструмент — Ctrl+T , и с помощью угловых маркеров изменяйте размер.
Для тех кто не знает : векторные фигуры состоят не из пикселей, а из специальные математических формул. Поэтому изменение размера — это не процесс растягивания/сжатия пикселей, а сложный математический пересчет, за счет чего не происходит никакой потери качества.
Вариант 2. Стандартный (растровый) квадрат/прямоугольник
Чтобы нарисовать сразу растровую фигуру используйте на панели параметров настройку Выполнить заливку пикселов . Но прежде чем начать ее рисовать — !
Но на самом деле можно рисовать сразу и векторный, а потом просто его. Тут уже выбирайте сами.
Как сделать прямоугольник квадратным
Обыкновенное правило с зажатой клавишей Shift с произвольными фигурами не работает. Поэтому нужно воспользоваться панелью параметров инструмента и выбрать настройку, чтобы фотошоп рисовал именно квадрат.
В этой же панели, обратите внимание, вы можете указать точный размер необходимого прямоугольника/квадрата или рисовать его по заранее определенным пропорциям.
По умолчанию размеры определяются пикселями. Если вы хотите изменить единицу измерения, сначала введите в поле какое-либо значение, а затем кликните по нему правой кнопкой мыши. Появится окно выбора единиц измерения. Доступно: пиксели, дюймы, сантиметры, миллиметры, пункты и пики.
Прямоугольник или квадрат со скругленными углами
Чтобы получить фигуру со скругленными углами, делайте все то же самое, что описано выше, но в самом начале выберите инструмент Прямоугольник со скругленными краями . На панели параметров инструмента нужно будет указать только радиус закругления.
Способ 2. Обводка выделенной области
Этот способ простой, как 5 копеек. выберите инструмент и нарисуйте прямоугольник пунктирной линией. Чтобы нарисовать квадрат удерживайте нажатой клавишу Shift .
Теперь нужно сделать обводку границ этой выделенной области. Для этого перейдите в Редактирование — Выполнить обводку .
Затем в новом окне настройте вид обводки: укажите толщину рамки, желаемый цвет и отметьте как будет проходить обводка:
- Внутри — значит рамка ляжет по внутренней стороне выделенной области;
- По центру — значит рамка разделится поровну на часть проходящую внутри выделения и на часть со внешней стороны;
- Снаружи — значит рамка будет огибать пунктир выделения.
Вот как может получиться:
На скриншоте выше я специально не убрал пунктирную линию, поскольку у вас она также не исчезнет. Чтобы окончательно от нее избавиться нажмите Ctrl+D .
В этом способе, чтобы нарисовать фигуру точного размера, нужно сперва на панели параметров инструмента указать Стиль — Заданный размер или Заданные пропорции. После этого станут активными поля, куда введите значения ширины и высоты в пикселях. Кликом правой кнопкой мыши по одному из этих полей вызовет меню изменения единиц измерения.
После этого станут активными поля, куда введите значения ширины и высоты в пикселях. Кликом правой кнопкой мыши по одному из этих полей вызовет меню изменения единиц измерения.
Способ 2.1 Закрашивание выделения
Самый банальный способ рисования прямоугольника — нарисовать рамку выделения (как описано выше) и просто закрасить ее любым цветом. Вот вам и прямоугольник или квадрат.
Способ 3. Модификация выделения
На самом деле этот способ мне меньше всего нравится из-за очевидного минуса — углы прямоугольника будут подрезанными, а сама граница рамки в состоянии и повлиять на эти факты не представляется возможным.
Итак, нужно вновь выбрать инструмент , нарисовать рамку будущего прямоугольника или квадрата (с клавишей Shift ), а затем отправляемся в меню Выделение и выбираем команду Модификация — Граница .
Появится новое окно, в котором, в нашем случае, мы указываем ширину границы прямоугольника. Допустим, укажу 7 пикселей. Получим такой результат:
Получим такой результат:
А теперь нужно просто закрасить получившуюся рамку. Для этого подойдет . Здесь, кстати, можно подойти к вопросу более творчески и закрасить, например, разными цветами. Результат:
Останется только снять выделение — Ctrl+D . Думаю этот способ подходит только для своих редких специфических задач, поскольку растушевка и подрезанные углы только все портят.
Заметили ошибку в тексте — выделите ее и нажмите Ctrl + Enter . Спасибо!
Все предметы, которые нас окружают можно мысленно вписать в простые геометрические тела (куб, шар, конус, цилиндр, призма и др.). Изучая форму куба, мы узнаем, как нарисовать, к примеру, дом, потому что упрощенно дом рисуется с использованием тех же приемов что и куб. У него есть вершины, ребра и грани, как и у куба. Крыша дома – это многогранная призма.
Нарисуем куб с натуры, а затем будем использовать эти знания на наших для изображения более сложных предметов таких как дома и улицы.
Куб – геометрическое тело, образованное пересечением плоскостей. И, как всякий объемный предмет, при изображении на плоском листе он будет претерпевать изменения в соответствии с законами перспективы. На рисунке изображена линия горизонта это уровень плоскости зрения художника . На ней находятся точки схода параллельных линий. В нашем случае — это четыре горизонтальных линии, стремящихся в точку схода слева и четыре горизонтальных линии, стремящихся в точку схода справа.
Мы изображаем предметы в пространстве так, как их воспринимает наш глаз. (Чем дальше от зрителя, тем меньше выглядит предмет и т.д.)
Начало любой картины – это композиция. Легкими линиями намечаем наш предмет на листе. Сверху всегда должно быть чуть больше места от края, чем снизу. Интуитивно определите масштаб так, чтобы предмет не выглядел гигантским или слишком маленьким.
Расположите самое ближнее вертикальное ребро так, чтобы оно не совпадало с центром листа, проходящим через пересечение его диагоналей. Засечками отмечаем высоту, это самое высокое ребро в нашем изображении, так как оно ближе всех к зрителю. На глаз определяем угол наклона ребер лежащих на столе относительно горизонтали. Тренируйте зрительную память, запоминая угол. Взгляд переводите быстро то на куб, то на рисунок.
Засечками отмечаем высоту, это самое высокое ребро в нашем изображении, так как оно ближе всех к зрителю. На глаз определяем угол наклона ребер лежащих на столе относительно горизонтали. Тренируйте зрительную память, запоминая угол. Взгляд переводите быстро то на куб, то на рисунок.
То же проделаем и с верхними ребрами. Как передавать пространство на листе нам объясняют основные законы линейной перспективы. Все параллельные линии сливаются к линии горизонта в одну точку. Поэтому, чтобы передать что ребро находится дальше от зрителя, мы изобразим его меньше и расположим выше . Таким образом, все ребра будут разной высоты.
При пересечении дальних горизонтальных ребер образовались вершины. Через них проходит самое дальнее, невидимое глазом, ребро. На начальном этапе изобразим куб прозрачным для понимания полной конструкции предмета.
Для того, чтобы узнать на сколько сократились боковые грани, воспользуемся методом визирования . При помощи этого метода происходит восприятие очертаний предмета, художник учится изображать предметы пропорциональными и в различных ракурсах.
Как он работает? Возьмите карандаш на вытянутой руке, прикройте один глаз, совместите карандаш и изображение ребра куба в пространстве. Верхний край карандаша должен совпадать с верхней вершиной ребра, а пальцем зажмите на карандаше точку, совпадающую с нижней вершиной. Не убирая палец с карандаша, разверните под прямым углом и измеряйте расстояние между двумя ребрами. Таким образом, мы увидим соотношение высоты и ширины одной грани. Запомните это соотношение и передайте его на рисунке. Этим методом можно измерять и изображать так же соотношение ребер.
После того, как закончены линейные построения, приступаем к воздушной перспективе , а значит к штриховке.
Основная задача художника передавать объемные формы предметов. У нашего кубика мы видим три грани, все они разные по тону. Левая грань самая темная — это собственная тень предмета. Благодаря отраженному свету от окружающих предметов или рефлексам, штриховку делаем немного светлее по мере удаления влево. Самое большое ребро делают контрастней, чем все остальные. Таким образом, показывают его приближенность на передний план.
Таким образом, показывают его приближенность на передний план.
Верхняя плоскость темнее , чем вертикальная справа. Свет по ней лишь скользит, образуя полутон. Обратите внимание, что чем ближе к источнику света, тем светлее будет тон. Штриховку можно наносить по диагонали. На ребре ластиком высветлим, чтобы передать блик.
Для работы над самой светлой гранью возьмем твердый карандаш Н или 2Н . Он не даст сделать тон слишком темным. Штриховку нанесем вертикальную, по направлению плоскости.
Падающие тени всегда темнее, чем собственная тень предмета. Ближнее ребро – это линия перехода света и тени. Из нее начинается падающая тень. Чем ближе к предмету, тем насыщеннее тон. Отраженный свет от куба создает рефлекс внутри тени и она немного высветляется.
Рисование простых геометрических тел часто используется на и позволяет начинающему художнику научиться изображать предметы в пространстве, применяя законы перспективного построения и воздушной перспективы.
Доброго времени суток, начинающий художник и постоянный посетитель блога .
Надеюсь, было достаточно сфер? Так что давайте перейдем к важному, чрезвычайно разностороннему кубу . Куб настолько универсален, что вы будете использовать его для отрисовки рамок, домов, зданий, мостов, самолетов, автомобилей, цветов и рыб…рыб?? Да, куб поможет вам нарисовать даже маленьких рыб в 3D, а также лицо, цветы, ну и все, о чем вы можете подумать или увидеть вокруг. Так что приступим.
1. Начните с новой страницы вашего блокнота, напишите номер урока и заголовок, дату, время, местонахождение. Нарисуйте две точки напротив друг друга.
2. Поместите ваш палец между точками, используя другую руку. Затем нарисуйте точку над и под пальцем, как показано на рисунке.
Не стесняйтесь делать записи в блокноте, цитаты, и заметки. Чем больше вы вкладываете своих собственных мыслей и идей в свою записную книжку, тем большее она имеет значение для вас, тем больше вы будете ее использовать.
В своем альбоме я делаю записи, напоминания, заметки, списки и все остальные вещи, которые нельзя нарисовать. Мой альбом – это первое место, куда я смотрю, когда мне нужно вспомнить что-то.
3. Взгляните на точки, которые вы нарисовали. Две новых точки должны располагаться близко друг от друга. Мы будем рисовать трапецию (квадрат в перспективе).
4. Проведите первую линию.
5. Проведите следующую линию.
6. Затем третью.
7. Закончите трапецию. Это очень важная форма для практики. Потренируйтесь, нарисовав такую трапецию еще несколько раз. ПРЕДУПРЕЖДЕНИЕ: рисуйте две средние точки очень близко друг к другу. Если они будут слишком далеко, у вас получится «полноразмерный» квадрат. А наша цель – «сплющенный».
В таком ракурсе объект искажается, и создает иллюзию, что одна часть находится ближе к зрителю. Для наглядного примера, вытащите монетку из кармана. Посмотрите на нее прямо. Она представляет собой плоский круг. 2D круг, который имеет длину и ширину (в двух измерениях), но не имеет высоты. Поверхность находится на одинаковом расстоянии от глаз. Теперь слегка наклоните монетку. Форма изменилась на эллипс, который теперь имеет высоту. Теперь у монеты есть все три измерения: длина, ширина и высота. Наклонив монетку, вы сместили край монеты подальше от ваших глаз, вы получили эллипс (круг в перспективе).
Поверхность находится на одинаковом расстоянии от глаз. Теперь слегка наклоните монетку. Форма изменилась на эллипс, который теперь имеет высоту. Теперь у монеты есть все три измерения: длина, ширина и высота. Наклонив монетку, вы сместили край монеты подальше от ваших глаз, вы получили эллипс (круг в перспективе).
В основном, рисование трехмерных объектов сводится к тому, чтобы исказить изображения на плоском двумерном листе бумаги, чтобы создать иллюзию существования глубины. Рисунок 3D искажает формы, чтобы обмануть зрение и заставить объекты казаться ближе или дальше.
Теперь давайте вернемся к моему предупреждению о рисовании двух точек посередине. Если ваши точки будут слишком далеко друг от друга, ваш квадрат будет выглядеть вот так:
Если ваша фигура выглядит так, то перерисуйте ее несколько раз, размещая средние точки ближе друг к другу, пока ваша фигура не станет такой:
Ладно, достаточно об искажении пока. Держите эту мысль в голове, она очень важна и каждый урок будет начинаться с этого.
8. Нарисуйте стороны куба, с помощью двух вертикальных линий. Вертикальные, прямые линии сверху вниз без наклона. Вот подсказка: используйте сторону своего блокнота. Если вертикальные линии соответствуют сторонам страницы, ваш рисунок не наклонен.
9. Используя боковые опорные линии, нарисуйте среднюю линию немного длиннее и ниже. Использование нарисованных линий позволяет правильно определить позицию для вашей следующей линии, это очень важно при создании 3D изображений.
10. С помощью верхней крайней правой линии трапеции, нарисуйте нижнюю правую сторону куба. Просто повторите ее быстрым движением руки, смотря на верхнюю линию. Не переживайте, если вы вышли за пределы объекта, вы сможете подкорректировать это позже. Я предпочитаю рисунки с большим количеством дополнительных линий и черточек, которые выглядят трехмерно, а не которые имеют суперчистые и четкие линии.
11. Теперь нарисуйте нижнюю левую сторону куба, ссылаясь на верхнюю линию. Направляющие! Направляющие! Направляющие! Я настоятельно рекомендую вам потренироваться в использовании направляющих линий.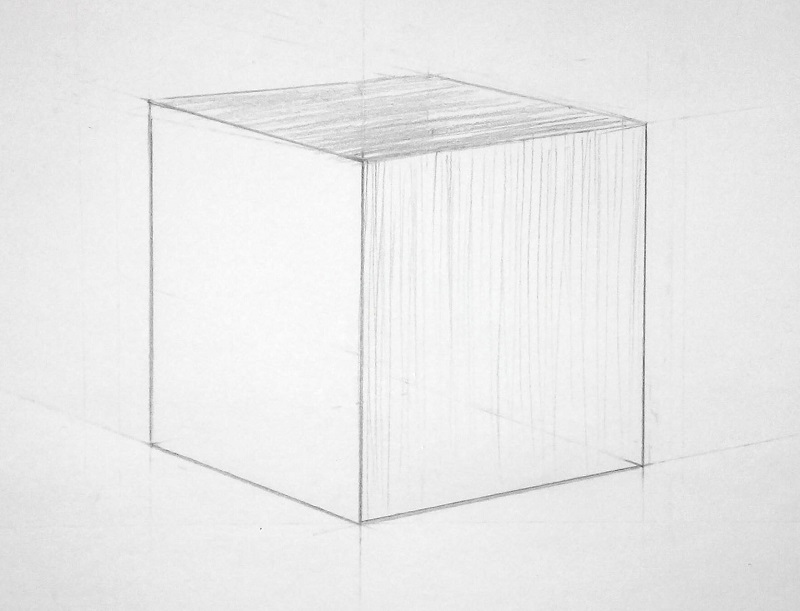
12. Теперь самое интересное — переходим к теням. Определите положение вашего воображаемого источника света. Свой я размещу справа сверху. Заметьте! Я использую направляющие линии, чтобы правильно выстроить угол тени. Путем продления нижнего правого ребра, нарисуйте падающую тень. Неплохо выглядит, правда? Похоже, что куб действительно «сидит» на земле? Это переломный момент, когда рисунок приобретает трехмерность.
13. Закончите ваш первый 3D куб, заштриховав грань противоположную от освещения. Заметьте, что я совсем ее не стал растушевывать. Я растушевываю тени только на округлых поверхностях.
УРОК 4: ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Давайте возьмем то, что мы узнали в основах рисования 3D куба, и добавим некоторые детали.
Мы собираемся нарисовать три кубика. Начните с первого с двух опорных точек. Говоря в следующих уроках «опорные точки», я буду иметь в виду эти точки.
1. Положите указательный палец посередине между опорными точками. Эта потрясающая привычка, которую вы сейчас приобретаете, к концу тридцатого урока станет для вас второй натурой.
2. Соедините точки в трапецию. Эта отличная фигура для практики в вашем альбоме, если у вас есть минута или около того. Например, когда находитесь в очереди или пробке. Поэтому всегда носите с собой свой альбом и карандаш, кто знает, когда у вас появится свободная минутка для рисования!
3. Нарисуйте вертикальные боковые линии и среднюю линию куба. Среднюю линию рисуйте всегда длиннее и ниже, чтобы она казалась ближе.
4. Закончите рисовать куб, с помощью направляющих верхних линий.
6. Нарисуйте опорные точки в середине каждого ребра верхней грани куба.
7. Давайте начнем с первого. Давайте нарисуем на нем старомодный подарочный почтовый пакет, украшенный лентой, в котором мы получаем подарки от бабушки на Новый год. Проведите вертикальную линию вниз вблизи левой опорной точки, а затем по верхней грани к другой опорной точке.
8. Повторите это с другой стороны. Опорные точки помогают нарисовать линию внутри трапеции. Опорные точки являются чрезвычайно полезным инструментом в построении углов, как здесь.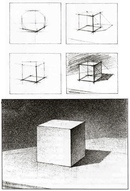 Мы часто будем пользоваться этими точками в последующих уроках (очень часто!).
Мы часто будем пользоваться этими точками в последующих уроках (очень часто!).
9. Чтобы нарисовать такие линии в горизонтальном направлении, используйте опорные точки снова, только на середине вертикальных линий.
10. Проведите линии, соединяя опорные точки, используйте линии сверху как направляющие.
11. С помощью оберточной ленты вы можете закончить все три куба, представив их в виде посылки, игрального куба и подарка, завернутого в толстую ленту.
Еще одно хорошее задание для практики
Поместите любую коробку (обувную, из-под хлопьев или любую другую) на стол перед собой.
Присаживайтесь и разместитесь таким образом, чтобы вы могли увидеть верхнюю грань, похожую на трапецию, которую мы недавно рисовали.
Не паникуйте! Просто вспомните, что вы выучили в данном уроке, и пусть эти знания помогут вам нарисовать то, что видят ваши глаза. Взгляните, внимательно взгляните на тупые углы, затенения, падающую тень. Посмотрите, как надписи на коробке, также следуют за этими углами. Чем больше вы рисуете, тем больше вы буде
те замечать множество увлекательных подробностей в реальном мире вокруг вас.
Чем больше вы рисуете, тем больше вы буде
те замечать множество увлекательных подробностей в реальном мире вокруг вас.
Делитесь вашими работами и получайте полезные советы в
Как нарисовать квадратные рисунки. Как рисовать объемные фигуры и тела карандашом
Все предметы и фигуры размещены в пространстве. Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.
Рисунок нужно воспринимать как пространство на бумаге, где существует плоскость и пропорции всех находящихся предметов, свет и тень, которая направляется по форме предмета.
Основные геометрические фигуры:
Двухмерные плоские фигуры
Трехмерные фигуры, у которых есть объем
Абсолютно все предметы в основе своего построения имеют эти фигуры.
Куб — фигура, основой которой является трехмерное изображение в пространственном соотношении листа. В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина . В самом кубе заложено понятие рисунка в целом.
В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина . В самом кубе заложено понятие рисунка в целом.
Для начала понимания рисунка, мы поработаем именно с ним. При помощи образно-логических построений, мы с вами будем развивать мышление за счет аналитики формы . Для большего понимания и анализа рисунка есть несколько упражнений.
Упражнения
Садимся за мольберт, берем большой лист бумаги, можно недорогой, или вообще кусок обоев (в этом упражнении бумага особо значения не имеет) . Рисуем квадрат, естественно пытаемся сделать так, чтобы его стороны были ровными, а линии прямыми.
Итак, — мы видим обычный квадрат, совсем неинтересный и не впечатляющий, но это только в данный момент…
Делаем из квадрата куб карандашом: прорисовываем линии от граней примерно с углом 45 градусов . Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.
Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.
Чтобы нам чувствовать пространство, нужно придать рисунку плавности . То есть сделать так, чтобы нам было ясно, где передняя часть рисунка, а где задняя.
Сторону куба, находящуюся ближе к нам, нужно выделить, сделать четче и передать активнее. Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.
Вот таким способом мы передали пространство, чтобы добиться желаемого результата. Но это далеко не все. Сейчас важно правильно передать плавность, чтобы получить объемность в рисунке .
Представляем вашему вниманию небольшой видеоурок на тему оптических иллюзий.
Доброго времени суток, начинающий художник и постоянный посетитель блога .
Надеюсь, было достаточно сфер? Так что давайте перейдем к важному, чрезвычайно разностороннему кубу . Куб настолько универсален, что вы будете использовать его для отрисовки рамок, домов, зданий, мостов, самолетов, автомобилей, цветов и рыб…рыб?? Да, куб поможет вам нарисовать даже маленьких рыб в 3D, а также лицо, цветы, ну и все, о чем вы можете подумать или увидеть вокруг. Так что приступим.
Так что приступим.
1. Начните с новой страницы вашего блокнота, напишите номер урока и заголовок, дату, время, местонахождение. Нарисуйте две точки напротив друг друга.
2. Поместите ваш палец между точками, используя другую руку. Затем нарисуйте точку над и под пальцем, как показано на рисунке.
Не стесняйтесь делать записи в блокноте, цитаты, и заметки. Чем больше вы вкладываете своих собственных мыслей и идей в свою записную книжку, тем большее она имеет значение для вас, тем больше вы будете ее использовать. В своем альбоме я делаю записи, напоминания, заметки, списки и все остальные вещи, которые нельзя нарисовать. Мой альбом – это первое место, куда я смотрю, когда мне нужно вспомнить что-то.
3. Взгляните на точки, которые вы нарисовали. Две новых точки должны располагаться близко друг от друга. Мы будем рисовать трапецию (квадрат в перспективе).
4. Проведите первую линию.
5. Проведите следующую линию.
6. Затем третью.
7. Закончите трапецию. Это очень важная форма для практики. Потренируйтесь, нарисовав такую трапецию еще несколько раз. ПРЕДУПРЕЖДЕНИЕ: рисуйте две средние точки очень близко друг к другу. Если они будут слишком далеко, у вас получится «полноразмерный» квадрат. А наша цель – «сплющенный».
В таком ракурсе объект искажается, и создает иллюзию, что одна часть находится ближе к зрителю. Для наглядного примера, вытащите монетку из кармана. Посмотрите на нее прямо. Она представляет собой плоский круг. 2D круг, который имеет длину и ширину (в двух измерениях), но не имеет высоты. Поверхность находится на одинаковом расстоянии от глаз. Теперь слегка наклоните монетку. Форма изменилась на эллипс, который теперь имеет высоту. Теперь у монеты есть все три измерения: длина, ширина и высота. Наклонив монетку, вы сместили край монеты подальше от ваших глаз, вы получили эллипс (круг в перспективе).
В основном, рисование трехмерных объектов сводится к тому, чтобы исказить изображения на плоском двумерном листе бумаги, чтобы создать иллюзию существования глубины. Рисунок 3D искажает формы, чтобы обмануть зрение и заставить объекты казаться ближе или дальше.
Рисунок 3D искажает формы, чтобы обмануть зрение и заставить объекты казаться ближе или дальше.
Теперь давайте вернемся к моему предупреждению о рисовании двух точек посередине. Если ваши точки будут слишком далеко друг от друга, ваш квадрат будет выглядеть вот так:
Если ваша фигура выглядит так, то перерисуйте ее несколько раз, размещая средние точки ближе друг к другу, пока ваша фигура не станет такой:
Ладно, достаточно об искажении пока. Держите эту мысль в голове, она очень важна и каждый урок будет начинаться с этого.
8. Нарисуйте стороны куба, с помощью двух вертикальных линий. Вертикальные, прямые линии сверху вниз без наклона. Вот подсказка: используйте сторону своего блокнота. Если вертикальные линии соответствуют сторонам страницы, ваш рисунок не наклонен.
9. Используя боковые опорные линии, нарисуйте среднюю линию немного длиннее и ниже. Использование нарисованных линий позволяет правильно определить позицию для вашей следующей линии, это очень важно при создании 3D изображений.
10. С помощью верхней крайней правой линии трапеции, нарисуйте нижнюю правую сторону куба. Просто повторите ее быстрым движением руки, смотря на верхнюю линию. Не переживайте, если вы вышли за пределы объекта, вы сможете подкорректировать это позже. Я предпочитаю рисунки с большим количеством дополнительных линий и черточек, которые выглядят трехмерно, а не которые имеют суперчистые и четкие линии.
11. Теперь нарисуйте нижнюю левую сторону куба, ссылаясь на верхнюю линию. Направляющие! Направляющие! Направляющие! Я настоятельно рекомендую вам потренироваться в использовании направляющих линий.
12. Теперь самое интересное — переходим к теням. Определите положение вашего воображаемого источника света. Свой я размещу справа сверху. Заметьте! Я использую направляющие линии, чтобы правильно выстроить угол тени. Путем продления нижнего правого ребра, нарисуйте падающую тень. Неплохо выглядит, правда? Похоже, что куб действительно «сидит» на земле? Это переломный момент, когда рисунок приобретает трехмерность.
13. Закончите ваш первый 3D куб, заштриховав грань противоположную от освещения. Заметьте, что я совсем ее не стал растушевывать. Я растушевываю тени только на округлых поверхностях.
УРОК 4: ПРАКТИЧЕСКОЕ ЗАДАНИЕ
Давайте возьмем то, что мы узнали в основах рисования 3D куба, и добавим некоторые детали.
Мы собираемся нарисовать три кубика. Начните с первого с двух опорных точек. Говоря в следующих уроках «опорные точки», я буду иметь в виду эти точки.
1. Положите указательный палец посередине между опорными точками. Эта потрясающая привычка, которую вы сейчас приобретаете, к концу тридцатого урока станет для вас второй натурой.
2. Соедините точки в трапецию. Эта отличная фигура для практики в вашем альбоме, если у вас есть минута или около того. Например, когда находитесь в очереди или пробке. Поэтому всегда носите с собой свой альбом и карандаш, кто знает, когда у вас появится свободная минутка для рисования!
3. Нарисуйте вертикальные боковые линии и среднюю линию куба. Среднюю линию рисуйте всегда длиннее и ниже, чтобы она казалась ближе.
Среднюю линию рисуйте всегда длиннее и ниже, чтобы она казалась ближе.
4. Закончите рисовать куб, с помощью направляющих верхних линий.
6. Нарисуйте опорные точки в середине каждого ребра верхней грани куба.
7. Давайте начнем с первого. Давайте нарисуем на нем старомодный подарочный почтовый пакет, украшенный лентой, в котором мы получаем подарки от бабушки на Новый год. Проведите вертикальную линию вниз вблизи левой опорной точки, а затем по верхней грани к другой опорной точке.
8. Повторите это с другой стороны. Опорные точки помогают нарисовать линию внутри трапеции. Опорные точки являются чрезвычайно полезным инструментом в построении углов, как здесь. Мы часто будем пользоваться этими точками в последующих уроках (очень часто!).
9. Чтобы нарисовать такие линии в горизонтальном направлении, используйте опорные точки снова, только на середине вертикальных линий.
10. Проведите линии, соединяя опорные точки, используйте линии сверху как направляющие.
11. С помощью оберточной ленты вы можете закончить все три куба, представив их в виде посылки, игрального куба и подарка, завернутого в толстую ленту.
Еще одно хорошее задание для практики
Поместите любую коробку (обувную, из-под хлопьев или любую другую) на стол перед собой.
Присаживайтесь и разместитесь таким образом, чтобы вы могли увидеть верхнюю грань, похожую на трапецию, которую мы недавно рисовали.
Не паникуйте! Просто вспомните, что вы выучили в данном уроке, и пусть эти знания помогут вам нарисовать то, что видят ваши глаза. Взгляните, внимательно взгляните на тупые углы, затенения, падающую тень. Посмотрите, как надписи на коробке, также следуют за этими углами. Чем больше вы рисуете, тем больше вы буде те замечать множество увлекательных подробностей в реальном мире вокруг вас.
Делитесь вашими работами и получайте полезные советы в
Попробуем понять принцип взаимодействия квадрата и окружности на перспективном рисунке. Научиться проверять правильность квадрата, вписывая в него окружность.
Изобразите в перспективе горизонтальный и вертикальный квадраты. Проверьте правильность их изображения при помощи вписанных окружностей.
Прежде, чем приступать к выполнению этого задания, внимательно рассмотрите схему на рис. 2.8. Точки касания сторон квадрата к окружности (точки 1, 2, 3, 4) делят стороны квадрата пополам. Средние линии квадрата и его диагонали пересекаются в центре окружности. Противолежащие стороны квадрата и соответствующие им средние линии параллельны и расположены на равном расстоянии друг от друга. Рассмотрите также рис. 2.9. На примере окружности и квадрата во фронтальной перспективе хорошо видно, что центр эллипса и центр окружности — две разные точки. Диаметр окружности, являющийся малой осью эллипса, делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю — больше, дальний — меньше (по закону перспективного сокращения), а точка центра эллипса делит этот же диаметр — малую ось эллипса — ровно пополам.
Нарисовать квадрат в перспективе можно в разной последовательности, например, сначала изобразить одну прямую — сторону квадрата, а затем другую, ей перпендикулярную, отложить на этих прямых от точки их пересечения отрезки, равные стороне квадрата, а затем от полученных вершин достроить остальные стороны, сводя параллельные прямые в точки схода. Или иначе — сначала провести две параллельные прямые, а затем еще две, перпендикулярные двум первым. В любом случае эта задача кажется простой только на первый взгляд. На самом деле слишком много позиций (степень схождения параллельных сторон квадрата, их направления и размеры) рисовальщику приходится определять на основании своего личного опыта, а его, как известно, иногда бывает недостаточно. Именно поэтому правильность квадрата необходимо проверить, например, вписав в него окружность. При любом положении квадрата для того, чтобы вписать в него окружность (в перспективном рисунке — эллипс), необходимо найти точки касания сторон квадрата к вписанной окружности (точки 1 — 4) и определить положение осей эллипса. Если вписанный эллипс касается сторон квадрата в заданных точках и симметричен относительно осей, то квадрат нарисован верно.
Или иначе — сначала провести две параллельные прямые, а затем еще две, перпендикулярные двум первым. В любом случае эта задача кажется простой только на первый взгляд. На самом деле слишком много позиций (степень схождения параллельных сторон квадрата, их направления и размеры) рисовальщику приходится определять на основании своего личного опыта, а его, как известно, иногда бывает недостаточно. Именно поэтому правильность квадрата необходимо проверить, например, вписав в него окружность. При любом положении квадрата для того, чтобы вписать в него окружность (в перспективном рисунке — эллипс), необходимо найти точки касания сторон квадрата к вписанной окружности (точки 1 — 4) и определить положение осей эллипса. Если вписанный эллипс касается сторон квадрата в заданных точках и симметричен относительно осей, то квадрат нарисован верно.
Горизонтальный квадрат. Нарисуйте горизонтальный квадрат по представлению (рис. 2.10). Найдите точки касания, для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода (рис. 2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис. 2.13). Проверьте симметричность полученного эллипса относительно его осей.
2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис. 2.13). Проверьте симметричность полученного эллипса относительно его осей.
Вертикальный квадрат. При вертикальном положении квадрата точки 1, 2, 3, 4 найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис. 2.14).
Несколько сложнее определить направление осей эллипса. Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры. Задача значительно упрощается в том случае, если вертикальный квадрат, в который вы вписываете окружность, является гранью куба. Тогда ось цилиндра (она же малая ось эллипса) параллельна горизонтальным ребрам куба и на рисунке идет с ними в одну точку схода. Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).
Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры. Задача значительно упрощается в том случае, если вертикальный квадрат, в который вы вписываете окружность, является гранью куба. Тогда ось цилиндра (она же малая ось эллипса) параллельна горизонтальным ребрам куба и на рисунке идет с ними в одну точку схода. Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).
На рисунках, иллюстрирующих последовательность вписывания окружности в горизонтальный и вертикальный квадраты, представлены идеальные ситуации. В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.
В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.
Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе. Именно поэтому современная методика предлагает не проверять и исправлять подобным образом уже нарисованные квадраты, а строить их, описывая вокруг окружности.
Хоть квадрат и прямоугольник это простейшие геометрические фигуры, но, чтобы их нарисовать в фотошопе, нужно приложить некоторые усилия и обладать базовыми знаниями. Новичок без должной подготовки, скорее всего, не справится с этой задачей.
В этой статье разберем 3 самых популярных способа как нарисовать прямоугольник или квадрат в фотошопе.
Но прежде, чем приступить к выбору способа рисования, нужно определиться с будущими параметрами. Прямоугольник/квадрат может быть:
- залит сплошным цветом или только с отрисовкой границ;
- произвольный или с точно заданными размерами;
- с возможностью в любое время менять его размеры без потери качества.
Способ 1. Инструмент произвольная фигура
В этом способе прямоугольник или квадрат будут нарисованы залитым сплошным цветом. Если вам нужна только граница, переходите к следующим двум способам.
На панели инструментов выберите инструмент . Дальше возможны два варианта развития событий:
Вариант 1. Квадрат или прямоугольник с дальнейшей возможностью изменять размеры без потери качества
Здесь, конечно, подразумевается использование векторной фигуры. Чтобы ее нарисовать нужно выбрать параметр Слой-фигура :
В дальнейшем вы можете без потери качества изменять размеры этой фигуры. Для этого используйте инструмент — Ctrl+T
, и с помощью угловых маркеров изменяйте размер.
Для тех кто не знает : векторные фигуры состоят не из пикселей, а из специальные математических формул. Поэтому изменение размера — это не процесс растягивания/сжатия пикселей, а сложный математический пересчет, за счет чего не происходит никакой потери качества.
Вариант 2. Стандартный (растровый) квадрат/прямоугольник
Чтобы нарисовать сразу растровую фигуру используйте на панели параметров настройку Выполнить заливку пикселов . Но прежде чем начать ее рисовать — !
Но на самом деле можно рисовать сразу и векторный, а потом просто его. Тут уже выбирайте сами.
Как сделать прямоугольник квадратным
Обыкновенное правило с зажатой клавишей Shift с произвольными фигурами не работает. Поэтому нужно воспользоваться панелью параметров инструмента и выбрать настройку, чтобы фотошоп рисовал именно квадрат.
В этой же панели, обратите внимание, вы можете указать точный размер необходимого прямоугольника/квадрата или рисовать его по заранее определенным пропорциям.
По умолчанию размеры определяются пикселями. Если вы хотите изменить единицу измерения, сначала введите в поле какое-либо значение, а затем кликните по нему правой кнопкой мыши. Появится окно выбора единиц измерения. Доступно: пиксели, дюймы, сантиметры, миллиметры, пункты и пики.
Прямоугольник или квадрат со скругленными углами
Чтобы получить фигуру со скругленными углами, делайте все то же самое, что описано выше, но в самом начале выберите инструмент Прямоугольник со скругленными краями . На панели параметров инструмента нужно будет указать только радиус закругления.
Способ 2. Обводка выделенной области
Этот способ простой, как 5 копеек. выберите инструмент и нарисуйте прямоугольник пунктирной линией. Чтобы нарисовать квадрат удерживайте нажатой клавишу Shift .
Теперь нужно сделать обводку границ этой выделенной области. Для этого перейдите в Редактирование — Выполнить обводку .
Затем в новом окне настройте вид обводки: укажите толщину рамки, желаемый цвет и отметьте как будет проходить обводка:
- Внутри — значит рамка ляжет по внутренней стороне выделенной области;
- По центру — значит рамка разделится поровну на часть проходящую внутри выделения и на часть со внешней стороны;
- Снаружи — значит рамка будет огибать пунктир выделения.

Вот как может получиться:
На скриншоте выше я специально не убрал пунктирную линию, поскольку у вас она также не исчезнет. Чтобы окончательно от нее избавиться нажмите Ctrl+D .
В этом способе, чтобы нарисовать фигуру точного размера, нужно сперва на панели параметров инструмента указать Стиль — Заданный размер или Заданные пропорции. После этого станут активными поля, куда введите значения ширины и высоты в пикселях. Кликом правой кнопкой мыши по одному из этих полей вызовет меню изменения единиц измерения.
Способ 2.1 Закрашивание выделения
Самый банальный способ рисования прямоугольника — нарисовать рамку выделения (как описано выше) и просто закрасить ее любым цветом. Вот вам и прямоугольник или квадрат.
Способ 3. Модификация выделения
На самом деле этот способ мне меньше всего нравится из-за очевидного минуса — углы прямоугольника будут подрезанными, а сама граница рамки в состоянии и повлиять на эти факты не представляется возможным.
Итак, нужно вновь выбрать инструмент , нарисовать рамку будущего прямоугольника или квадрата (с клавишей Shift ), а затем отправляемся в меню Выделение и выбираем команду Модификация — Граница .
Появится новое окно, в котором, в нашем случае, мы указываем ширину границы прямоугольника. Допустим, укажу 7 пикселей. Получим такой результат:
А теперь нужно просто закрасить получившуюся рамку. Для этого подойдет . Здесь, кстати, можно подойти к вопросу более творчески и закрасить, например, разными цветами. Результат:
Останется только снять выделение — Ctrl+D . Думаю этот способ подходит только для своих редких специфических задач, поскольку растушевка и подрезанные углы только все портят.
Заметили ошибку в тексте — выделите ее и нажмите Ctrl + Enter . Спасибо!
Продолжаю рассказывать об упражнениях, улучшающих навык рисования, в данном случае геометрических фигур. Будем тренироваться рисовать их двухмерное отображение, трехмерное отображение и затенение фигур.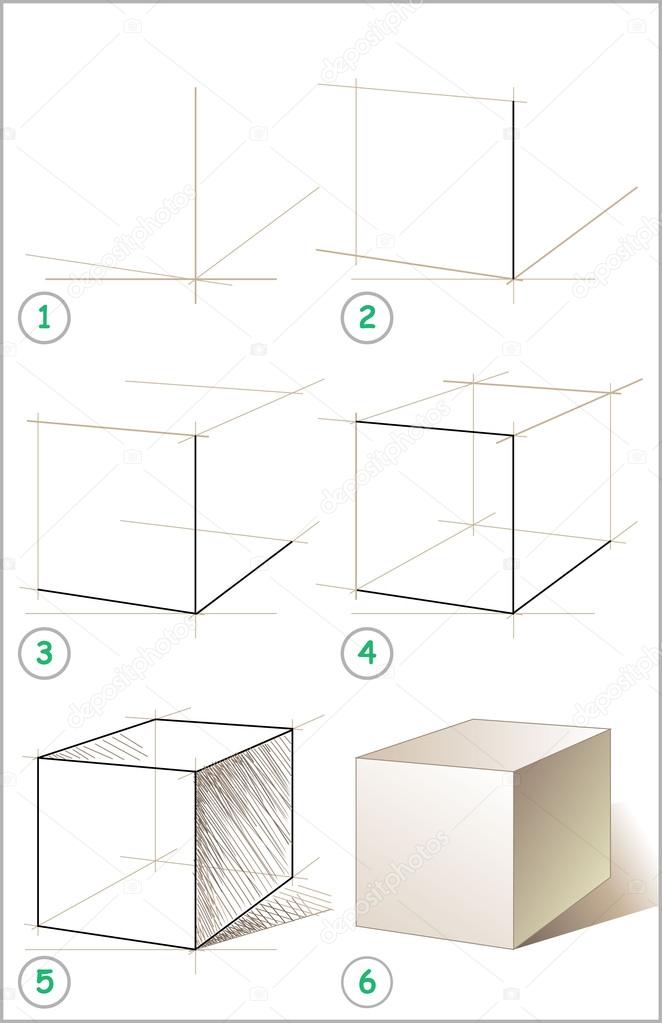 Итак, Упражнения для рисования. Часть 2. Приступим.
Итак, Упражнения для рисования. Часть 2. Приступим.
Но прежде, чем приступить к упражнениям, напоминаю, что есть .
Двумерные фигуры
Круг. Сначала будет сложно нарисовать ровный красивый круг, поэтому поможем себе с помощью циркуля. Легкой линией нарисуем окружность и обведем ее. Один раз, потом еще, запоминаем характер движения и пытаемся воспроизвести. Можно помогать себе проставив несколько точек для начала. Со временем, если выполнять это упражнение, круги будут получаться все лучше и краше. 🙂
Треугольник. Пробуем нарисовать равносторонний треугольник. Опять же, чтобы себе помочь для начала можем нарисовать окружность с помощью циркуля и уже в нее вписать нашу фигуру. Но потом обязательно пробуем нарисовать самостоятельно.
Квадрат. Да, сложно с первого раза нарисовать все стороны одинаковыми и все углы 90 градусов. Поэтому, чтобы запомнить правильную форму используем линейку. Потом рисуем по точкам, а потом самостоятельно, без вспомогательных инструментов.
После квадрата рисуем ромб, то есть тот же квадрат, но повернутый на 45 градусов.
Рисуем 5-конечную звезду, рисуем не отрывая карандаш от бумаги. Для первого раза можно воспользоваться циркулем и вписать звезду в окружность, чтобы добиться симметрии.
Шестиконечная звезда. Рисуется как 2 равносторонних треугольника.
Восьмиконечная звезда. Рисуется как 2 квадрата.
Яйцо. Это овал, который на одном конце уже, чем на другом.
Полумесяц. Эту фигуру нарисовать не так просто, как может показаться на первый взгляд. Сначала попробуйте нарисовать его самостоятельно, а потом уже при помощи циркуля, помня, что месяц это фактически часть двух пересекающихся окружностей.
Трехмерные фигуры
Переходим к трехмерным фигурам. Начнем с куба. Рисуем квадрат, потом еще один квадрат чуть выше и правее, соединяем углы ровными линиями. Получаем прозрачный куб. Теперь попробуем нарисовать тот же куб, но уже без видимых линий внутри.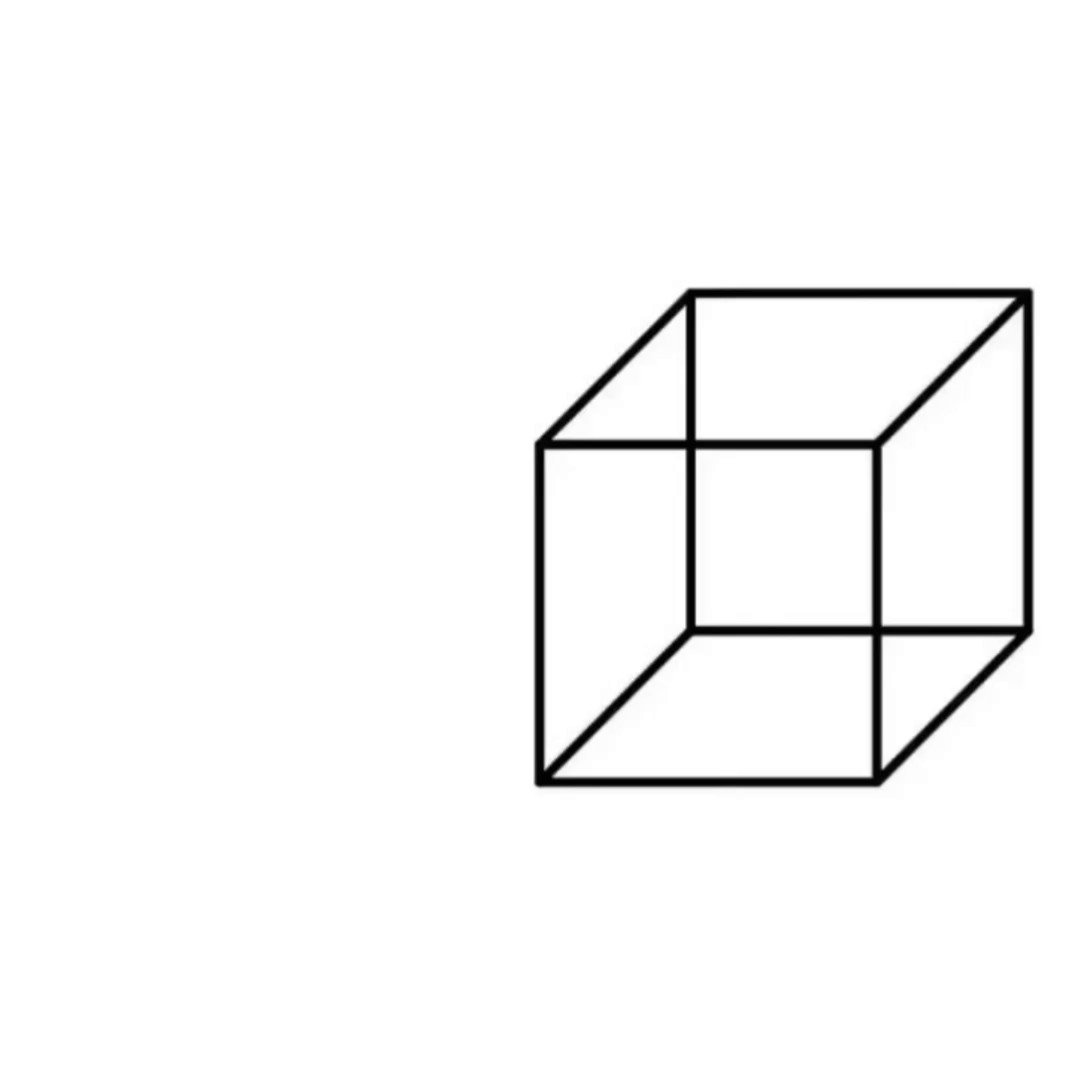
Теперь рисуем куб в другом ракурсе. Для этого сначала рисуем плоский параллелограмм в форме ромба, опускаем них перпендикуляры и рисуем такую же фигуру в основании. И такой же куб, но без видимых линий.
Теперь попробуем нарисовать цилиндр в разных ракурсах. Первый цилиндр будет прозрачный, рисуем овал, опускаем вертикали вниз и рисуем овал-основание. Затем рисуем цилиндр с невидимой нижней внутренней гранью и цилиндр с невидимой верхней внутренней гранью.
И завершаем этот цикл фигур рисованием конуса в разных ракурсах.
Рисуем круг. Намечаем легкой штриховкой тень в левом нижнем углу. Тень должна быть в форме полумесяца. Далее добавляем тона в тень при помощи большего нажима на карандаш, затеняем от центра к краю по принципу от светлого к темному, при этом у границы круга оставляем небольшой участок более светлой тени, это рефлекс. Дальше затеняем падающую тень, чем дальше от основания шара, тем светлее. Тень находится с противоположной от источника света стороны.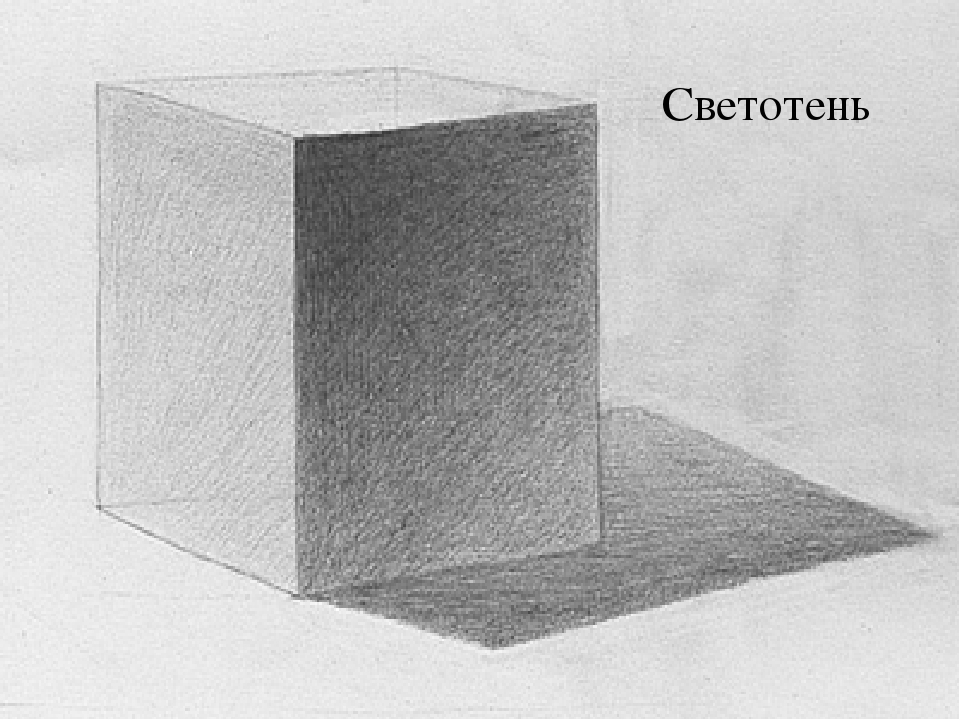 То есть в нашем случае источник света находится в верхнем правом углу.
То есть в нашем случае источник света находится в верхнем правом углу.
Теперь затеняем куб. В данном случае свет также находится в верхнем правом углу, а значит самая темная тень будет с противоположной стороны, сверху тени не будет, а правая видимая грань будет иметь более светлый тон. Соответственно с этим и наносим штриховку.
По такому же принципу затеняем стороны на кубе и конусе, важно следить за формой объекта и тем, как на него ложится свет. И падающая тень также должна соответствовать форме объекта.
И еще, в упражнениях для затенения используется диагональная штриховка, но я бы советовала пробовать в дальнейшем штриховать по форме объекта, тогда объект будет более объемный. Но штриховка по форме, да и вообще штриховка — тема довольно обширная, я уже начала ее изучать и скажу, что без тренировки рук и ровного быстрого штриха тут никуда, так что даже если делать только то, что я уже выложила, делать регулярно, то рисунки неизбежно будут становиться все лучше.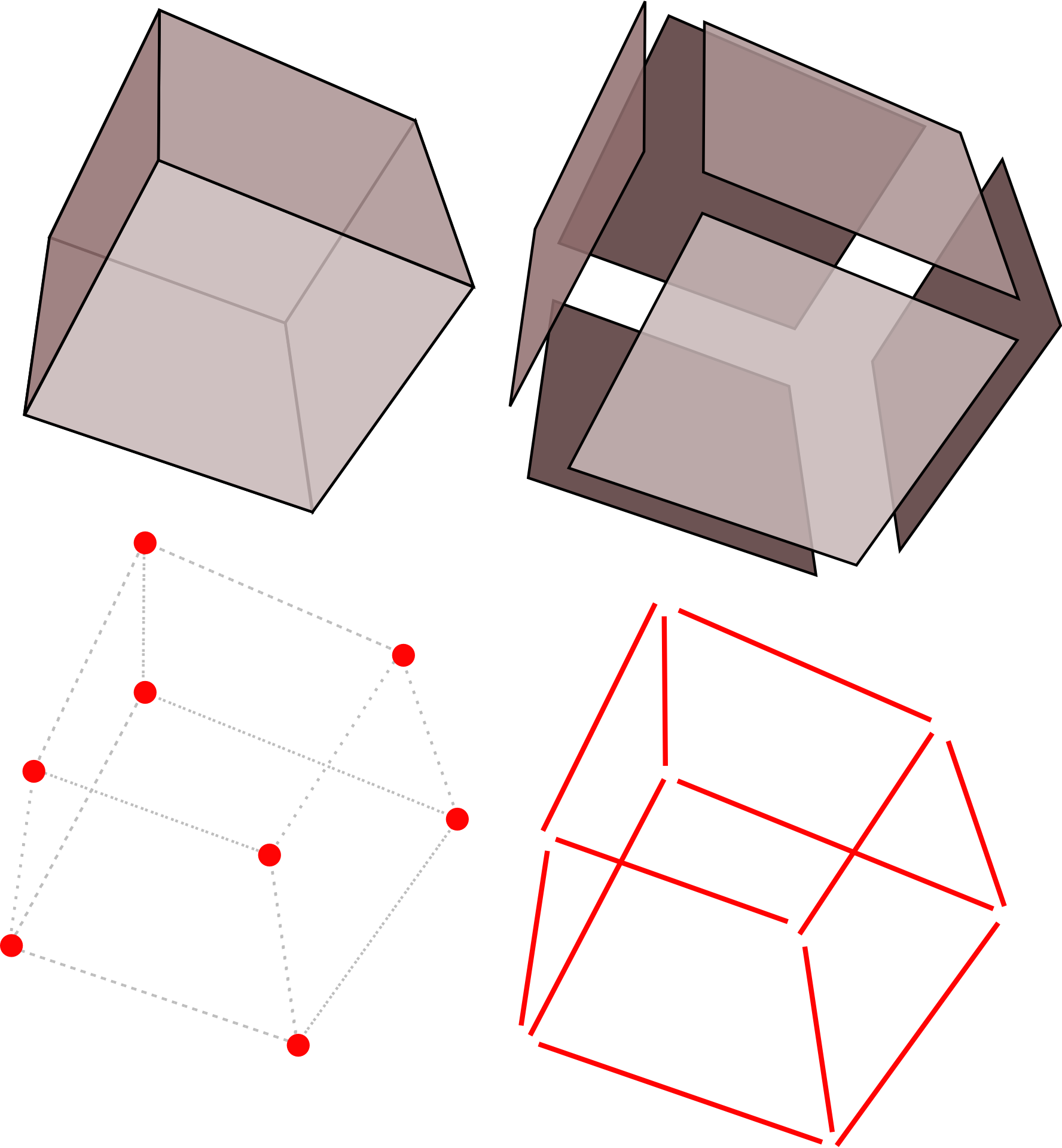
Дорисовываем и продолжаем 🙂
Графический редактор Paint. Создание объемной модели кубика Рубика
Практическая работа. Растровые графические изображения. Форматы растровых графических файлов. (2 урока)
Планируемые образовательные результаты
- предметные — систематизированные представления об инструментах создания графических изображений; развитие основных навыков и умений использования графических редакторов;
- метапредметные — умения подбирать и использовать инструментарий для решения поставленной задачи;
- личностные — интерес к изучению вопросов, связанных с компьютерной графикой.
Решаемые учебные задачи:
- обобщение представлений учащихся об интерфейсе графических редакторов;
- повторение основных приемов работы в растровом графическом редакторе;
- повторение основных приемов работы в векторном графическом редакторе.

Основные понятия, рассматриваемые на уроке:
- графический редактор;
- растровый графический редактор;
- векторный графический редактор;
- интерфейс графических редакторов;
- палитра графического редактора;
- инструменты графического редактора;
- графические примитивы.
Средства ИКТ , используемые на уроке:
- персональный компьютер (ПК) учителя,
- мультимедийный проектор,
- экран;
- ПК учащихся.
Единая коллекция цифровых образовательных ресурсов:
Цветовая модель RGB
Цветовая модель CMYK
http://school-collection.edu.ru/catalog/search/?text=
%F6%E2%E5%F2%EE%E2%E0%FF%20%EC%EE%E4%E5%EB%FC&tg=
Электронное приложение к учебнику:
презентация «Создание графических изображений». http://metodist.lbz.ru/authors/informatika/3/flash/7kl/gl3/3.php
На ленте: Вид —> Линии сетки Вкл. Вид – Масштаб – 400% и выше отображается сетка: одна клетка сетки – один пиксель. | |
Рисование правильных фигур (круг, квадрат, линия) – с нажатой клавишей Shift Нарисовать квадрат размером 50Í50 пикселей: (Shift) | |
Копировать рисунок – удерживая нажатой клавишу CTRL: выделить рисунок, удерживая клавишу ctrl, лев.кн.мыши перетащить рисунок в нужное место. Вкл. Главная – Выделить – Прозрачное выделение. | |
Изменение размеров и наклона Главная – изменить размер; Главная — Повернуть | |
Для каждого из цветов возможны 256 уровней интенсивности цвета Уровни интенсивности цвета задаются кодами от 0 до 255 Графический редактор Paint: Вкладка Главная – Изменение цветов |
|
Практическая работа.
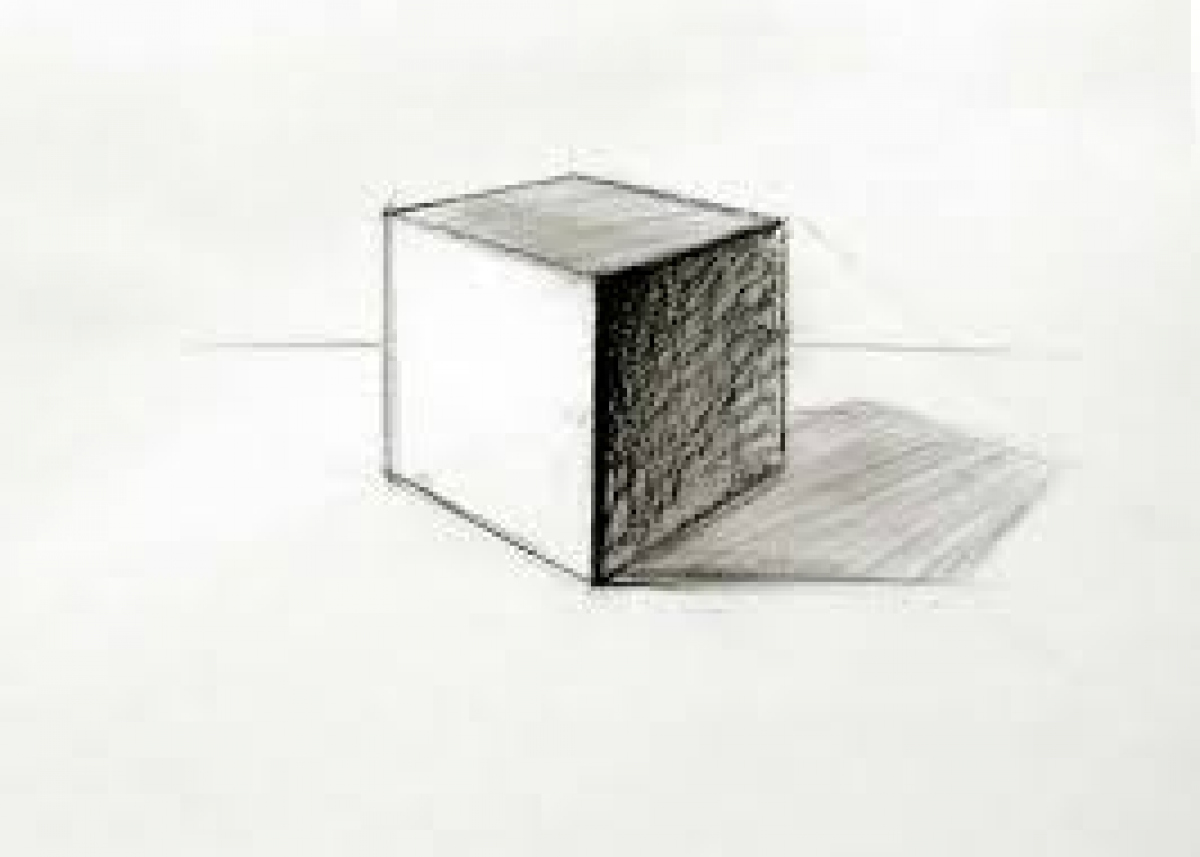
Рисование и редактирование объектов в растровом графическом редакторе Paint. Кубик Рубика
1. Нарисовать вид кубика спереди.
- Нарисовать скругленный квадрат размером 50 x 50 пикселей с толщиной контура 3 пикселя. (для этого – увеличить масштаб, отобразить сетку, выбрать толщину линий)
- Скопировать полученный квадрат. Совместить копию с первым квадратом. Получится первый ряд кубика.
- Перемещением копий постройте вид спереди кубика из 9 квадратов.
2. Создать вид кубика сбоку.
- Скопировать вид кубика спереди и перетащить его в сторону – это заготовка вида сбоку. Не снимая выделения, выбрать команду:
Изменить размер. В окне Изменение размеров и наклона снять флажок – сохранить пропорции. В поле изменить размер – по горизонтали – ввести сжатие 35% . В поле Наклон – по вертикали – ввести угол наклона 45 градусов. Образуется вид сбоку. Не снимая выделения, перетащите копию вида сбоку вверх как заготовку вида сверху.
3. Создать вид сверху.
- Выбрать команду Повернуть – Повернуть на 90° вправо.
- Выбрать команду Повернуть – Отразить по горизонтали.
4. Из трех видов сложить кубик.
4. Раскрасить кубик используя цвета следующих интенсивностей:
(цветов больше, чем сторон у кубика, для того, чтобы видеть изменения цвета при сохранении в различных форматах)
цвет | R | G | B |
| 255 | 128 | 0 |
| 0 | 166 | 0 |
| 5 | 201 | 250 |
| 255 | 128 | 255 |
| 188 | 105 | 220 |
| 255 | 255 | 70 |
| 223 | 223 | 0 |
Форматы растровых графических редакторов
Формат | Особенности формата |
BMP | Имеет большой информационный объем т. |
GIF | Сжатие без потерь информации. Уменьшает объем файла в несколько раз, ограниченная палитра (до 256 цветов). Используется для хранения диаграмм, графиков, рисунков с ограниченным кол-вом цветов. Используется для Web. Не используется для полиграфии. |
PNG | Усовершенствованный GIF. Сжатие без потерь. До 16 млн. цветов. Для публикации высококачественной графики в Интернете. |
jpeg | Уменьшает объем файла в десятки раз. Отбрасывает избыточные для человеческого восприятия цвета. Сжатие приводит к необратимой потере информации. (В Интернете – для публикации полноцветных фотографий), для хранения фото. |
Tiff | Изображение наилучшего качества. |
1. В своей папке создать 2 копии файла с кубиком
№ | Тип файла | Качество | Информационный объем |
1 | Монохромный рисунок | 134 Кбайт | |
2 | 16-цветный .bmp |
|
|
4 | 256-цветный .bmp |
|
|
5 | 24-разрядный рисунок |
|
|
6 | JPEG |
|
|
7 | GIF |
|
|
8 | TIFF |
|
|
9 | PNG |
|
|
2. В MS Word создать таблицу:
В MS Word создать таблицу:
3. Сохранить кубики в различных форматах.
4. Сохраненное изображение копировать в графу «Качество изображения»
? Во сколько раз размер рисунка, сохраненного в формате bmp превышает размер рисунка, сохраненного в формате jpeg.
Том
Можно вычислить
масса
любого объекта путем умножения
плотность
материала по объему объекта.
Объем объекта – это трехмерное пространство,
заняты объектом, и нас учат
формулы для вычисления объема некоторых простых трехмерных
предметы в средней школе. На этом слайде мы перечисляем некоторые уравнения для
вычисление объема объектов, которые часто встречаются в
аэрокосмический.Есть аналогичные уравнения
для вычисления
площадь
объектов.
Величина
аэродинамические силы
зависит от площади поверхности объекта, а
сила гравитации
и определенные
термодинамические эффекты
зависит от объема предмета.
Уравнения для вычисления площади и объема используются каждый день
инженеры-конструкторы.
Простая проверка любой формулы площади или объема это размерная проверка .Площадь — это двумерное пространство, которое занимает объект. Площадь измеряется вдоль поверхности объекта и имеет размеры длина в квадрате; например, квадратные футы материала или квадратные сантиметры. Объем — это трехмерное пространство, которое занимает объект. Объем имеет размеры длина в кубе; например, кубические футы материала или кубические сантиметры (см).
Для сферы расстояние от одной точки поверхности до другой точка на поверхности, измеренная через центр сферы, называется диаметр .3
Вот некоторые специальные уравнения объема, которые используются для носовых обтекателей ракет:
Для конуса расстояние от вершины до основания называется высота . Основание представляет собой круг диаметром d . Объем V конуса равен pi (3,14159), умноженному на диаметр d квадрат умножить на высоту ч разделить на двенадцать;
V = пи * д ^ 2 * ч / 12
Параболический конус имеет гладкую криволинейную поверхность и острый заостренный носик. 2)
2)
Примечание. Для всех фигур с изогнутыми (круглыми) поверхностями мы используем диаметр круг при выводе объема.Мы не используем радиус, который часто используется в математике. текстовые книги. Причина такого выбора в том, что большинство стандартных инженерных измерений основаны на диаметре, а не на радиусе. Легче точно измерить диаметр круглого объекта, чем для измерения радиуса. Чтобы использовать радиус, вам нужно определить, где лежит центр окружности. Для трубы в центре круга нет материала. Для сферы, до центра нельзя добраться, так как он находится внутри тела.Вы можете преобразовать диаметр в радиус (радиус = диаметр / 2).
Деятельность:
Экскурсии с гидом
Навигация ..
- Домашняя страница руководства для начинающих
Весна 2002 г.
Эскизное задание SK1: сдать в понедельник 30.06 в начале класс
Аналитический эскиз
Цели: Практика аналитического черчения
Научиться видеть
базовая структура объектов
Развитие навыков
нужен для быстрого скетчинга
В своем классе Демонстрация и упражнение
Рисование объекта в вашем
владение: что-то в вашем наборе для рисования, сумочке или рюкзаке.
Назначение
Используйте лист любой бумаги для рисования формата Letter,
твердый карандаш для рисования, чтобы наметить и установить прозрачный объемный
каркас для форм и более мягкий карандаш для придания плотности/веса
контурные линии и создают ощущение трехмерной формы за счет затенения.
Заполните всю страницу. НЕ СТИРАТЬ СВЕТИЛЬНУЮ РАМКУ
РЕГУЛИРОВОЧНЫЕ ЛИНИИ.
- Использование аналитического процессе рисования, попрактикуйтесь в рисовании кубов с разных точек зрения. Создайте не менее 12 кубов в разных позиций, по одной на лист.
- Собрать
три-четыре пустые картонные коробки разного размера. Сложите их на
этаж, причем некоторые вписываются в объемы других.
 Смотрите коробки как
геометрические формы, имеющие гладкие прямоугольные плоскости со всех четырех сторон,
пересекающиеся по прямым линиям. Используя аналитический процесс
чертеж, описать геометрические формы ящиков. Создайте три разных
композиции, перемещая коробки или меняя точку зрения.
Смотрите коробки как
геометрические формы, имеющие гладкие прямоугольные плоскости со всех четырех сторон,
пересекающиеся по прямым линиям. Используя аналитический процесс
чертеж, описать геометрические формы ящиков. Создайте три разных
композиции, перемещая коробки или меняя точку зрения. - Собрать
две стеклянные бутылки, одна с высоким цилиндрическим корпусом, а другая с
квадратное или прямолинейное сечение. Создание ортогональных видов
из двух бутылок , чтобы найти регулирующие линии, определяющие
пропорции и форма. Расставьте бутылки так, чтобы одна стояла на конце и
другой лежит на боку. Используя аналитический процесс рисования,
описать геометрические формы бутылок. Обратите особое внимание на
важные осевые и пропорциональные соотношения. Создайте 2 композиции из
тот же вид, включая на каждом листе орфографические наброски, определяющие
регулирующие линии объектов.

- Найти предмет мебели, состоящий из деревянных или металлических компонентов. Это может быть мягкой, но она должна иметь открытую деревянную или металлическую конструкцию или орнамент. Найдите деревянную или металлическую часть предмета, которая демонстрирует некоторые геометрическая СЛОЖНОСТЬ и создать серию аналитических исследований, чтобы нарисовать этот компонент. Найдите что-нибудь с достаточным разнообразием форм, и это вы можете разместить его на странице альбома для рисования, показывая объект в деталях.Делать столько набросков, сколько необходимо для получения достаточно точного и узнаваемое изображение этого компонента. Попробуйте просмотреть компонент из под разными углами, чтобы получить динамичную и интересную композицию. Не забудьте заняться орфографией, первый.
Примеры: оборудование, ножка стола/стула, суставы, скульптурное украшение и т.д.
Все чертежи должны выглядеть
что-то вроде примеров на следующих страницах.![]()
|
|
|
|
|
|
Коды для рисования — Digital Craft Lab @ CCA
Эндрю Ковач
Описание проекта
1.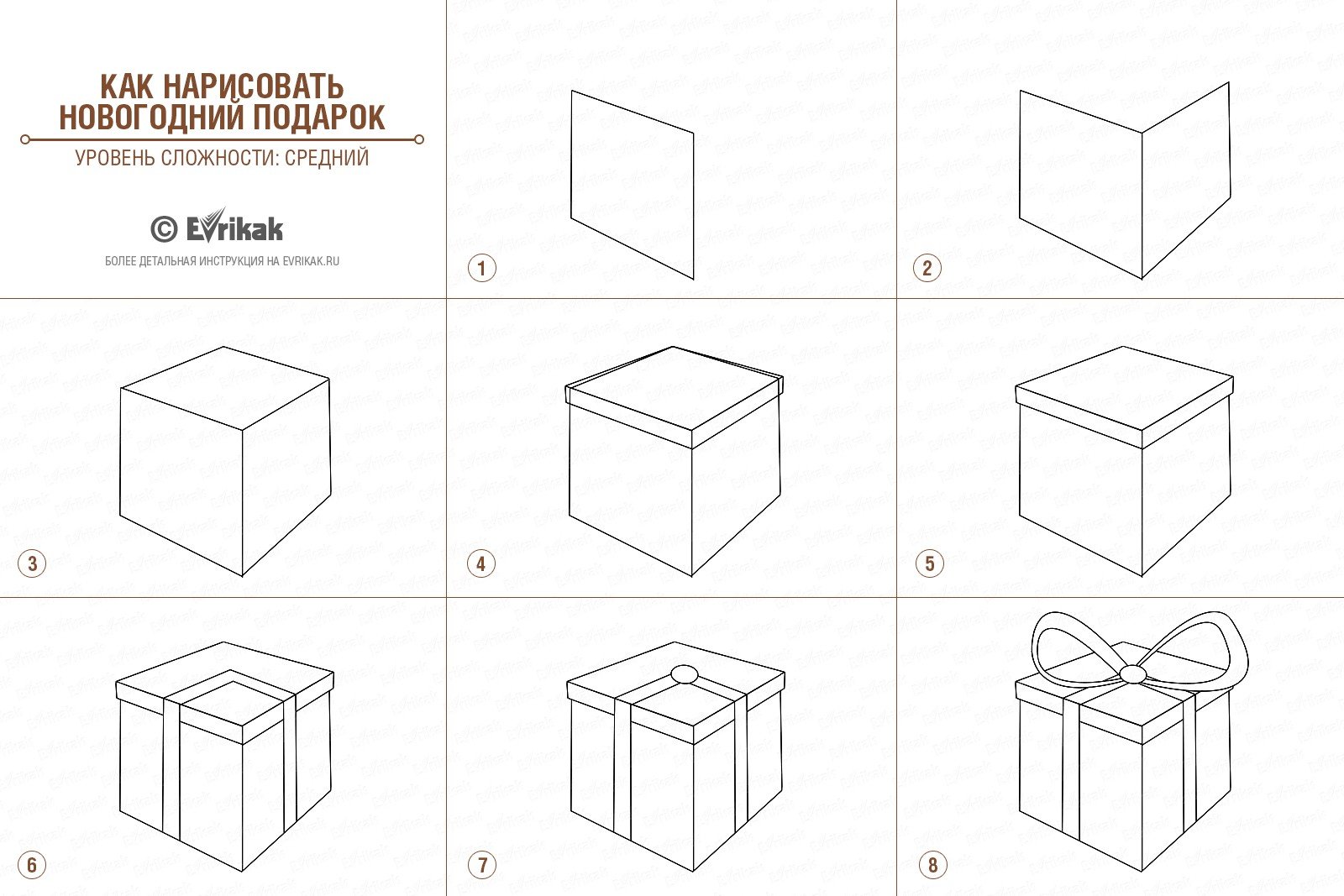 Откройте план этажа в Photoshop.
Откройте план этажа в Photoshop.
а. Для удобства выбора план этажа должен иметь в основном прямые стены.
2. Выберите инструмент «Прямоугольное выделение» (M).
3.Перетащите мышь на выделение стены, которую вы хотите вырезать.
а. Обязательно выбирайте архитектурно привлекательные стены.
4. Выберите инструмент «Перемещение» (V).
5. Щелкните правой кнопкой мыши и удалите стену с общего плана этажа.
6. Перетащите часть стены в отдельный файл Photoshop. Это станет вашим стандартным файлом новых стен, сделанных из старых стен.
7. С помощью Rectangular Marquee Tool (M) очистите старую стену. Края должны быть прямыми.
а. Удалите все пустое пространство со старой стены.
б. Стены должны быть открытыми и не полностью загораживать пространство.
1. Никаких закрытых квадратов, кругов, треугольников и т. д.
8. Созерцайте все новые стены, которые были сделаны из старых стен и собраны в отдельный файл Photoshop, стандартный файл новых стен.
а. Убедитесь, что новые стены не перекрывают друг друга.
б. Новые стены должны быть организованы по размеру и толщине линии.
9. Создайте новый файл в Photoshop, это будет ваш шейп-файл.
а. Размеры шейп-файла произвольны и могут быть скорректированы для любого конкретного использования.
б. Последователи этих шагов могут выбрать размер своего документа.
10. Выберите инструмент «Форма» (U).
11. Выберите форму.
а. Пользователи могут выбрать любую из фигур, предлагаемых Photoshop, образцы фигур из других источников или создать свою собственную фигуру.
б. Фигуры могут быть многоуровневыми, сложенными или перекрывающимися.
12. Перетащите фигуру до нужного размера и положения в документе.
а. Небольшой запас белого пространства должен быть оставлен со всех сторон формы.
13. Залейте форму цветом #ff0000.
14. Используя фигуру в качестве ориентира, начните перетаскивать стены с помощью инструмента «Перемещение» (V) из исходного файла, содержащего новые стены, сделанные из старых стен, в файл формы.
а. Все стены должны быть разными.
б. Все стены должны быть тесно связаны с другими стенами по своей толщине.
c. Все стены должны вращаться вокруг одной оси и не быть параллельными друг другу.
д. Все стены должны иметь расстояние между собой и не соприкасаться.
эл. Некоторые стены должны пространственно смыкаться с соседними стенами.
ф. Все стены должны плотно заполнять форму.
г. Все толщины стенок должны оставаться одинаковыми для каждой отдельной стены.
з. Все края стены должны быть прямыми, где бы стена не заканчивалась.
1. Об этом следует позаботиться на шагах 7 и 7a.
и. Все стены должны быть уникальными и красивыми.
15.Не используйте одну и ту же стену дважды из стандартного файла в любом файле формы.
16. Обязательно выровняйте края фигуры со стенками, чтобы показать контур любой выбранной вами фигуры.
а. Время от времени выключайте слой формы, чтобы увидеть, как развивается ваш проект.
1. Выбранная форма должна быть разборчивой для зрителя.
17. Общая организация стен должна быть лабиринтной, без полного замыкания пространства. Вы должны представить себе людей, блуждающих в форме новых стен.
а. Если форма новой стенки не выглядит лабиринтной, повторите шаги 14а – 14и.
18. Если у вас закончились стены, вы можете зайти на archiveofaffinities.tumblr.com.
19. Сделайте новые стены из планов старых стен, которые были собраны там.
20. Вернитесь к шагу 1.
Биография
Эндрю Ковач — приглашенный доцент Калифорнийского университета в Лос-Анджелесе по архитектуре и городскому дизайну. Ковач изучал архитектуру в Сиракузском университете, Архитектурной ассоциации в Лондоне и Принстонском университете.С 2012 по 2013 год Ковач был первым научным сотрудником Калифорнийского университета в Лос-Анджелесе, для которого он подготовил ИСПОЛЬЗУЕМЫЕ ТОВАРЫ: ПРОДАЖА АРХИТЕКТУРНОГО ДВОРА в Jai and Jai Gallery в Лос-Анджелесе. Работы Ковача по архитектуре и градостроительству широко публиковались, включая Pidgin, Project, Perspecta, Manifest, Metropolis, Clog, Domus и Fulcrum. Ковач является создателем и куратором Archive of Affinities, веб-сайта, посвященного сбору и показу архитектурных би-сайдов. Его недавняя дизайнерская работа включает в себя предложение по созданию парка для собак в центре Лос-Анджелеса и переоборудование трейлера Airstream в магазин мобильной розничной торговли, который путешествует по шоссе Тихоокеанского побережья.
Работы Ковача по архитектуре и градостроительству широко публиковались, включая Pidgin, Project, Perspecta, Manifest, Metropolis, Clog, Domus и Fulcrum. Ковач является создателем и куратором Archive of Affinities, веб-сайта, посвященного сбору и показу архитектурных би-сайдов. Его недавняя дизайнерская работа включает в себя предложение по созданию парка для собак в центре Лос-Анджелеса и переоборудование трейлера Airstream в магазин мобильной розничной торговли, который путешествует по шоссе Тихоокеанского побережья.
Калькулятор длины, ширины и высоты в объеме
Нажмите «Сохранить настройки», чтобы перезагрузить страницу с уникальным адресом веб-страницы для добавления в закладки и обмена текущими настройками инструмента
✕ очистить настройки
Инструмент «Отразить» с текущими настройками и рассчитать длину, ширину или высоту
К сожалению, здесь нельзя отобразить графику, так как ваш браузер не поддерживает HTML5 Canvas.Родственные инструменты
Руководство пользователя
Этот онлайн-инструмент вычисляет объем прямоугольной коробки, твердого тела или пространства по размерам длины, ширины и высоты. Нет необходимости вводить значения в одних и тех же единицах измерения, просто выберите предпочтительные единицы для каждого измерения и расчетного объема.
Нет необходимости вводить значения в одних и тех же единицах измерения, просто выберите предпочтительные единицы для каждого измерения и расчетного объема.
После того, как будут введены размеры длины, ширины и высоты, расчетный объем будет показан в поле ответа. Также будет показана графика масштабированного 3D-чертежа с правильными пропорциями и помечена каждым размером и рассчитанным объемом.
Формула
Формула, используемая этим калькулятором для расчета объема объекта прямоугольной формы:
В = Д · Ш · В
Символы
- В = Объем
- Д = Длина
- Ш = Ширина
- Н = высота
Размеры тома – длина, ширина и высота
Введите размеры длины, ширины и высоты прямоугольной формы.
Следующие коэффициенты преобразования единиц СИ в метры (м) используются для преобразования единиц измерения, указанных для длины, ширины и высоты:
Единицы длины метрического префикса СИ
- йоктометр (мкм) – 1 x 10 -24 м
- зептометр (zm) – 1 x 10 -21 м
- аттометр (ам) – 1 x 10 -18 м
- фемтометр (fm) – 1 x 10 -15 м
- пикометр (пм) – 1 x 10 -12 м
- нанометр (нм) – 1 x 10 -9 м
- мкм (мкм) – 0.
 000001 м
000001 м - миллиметр (мм) – 0,001 м
- сантиметр (см) – 0,01 м
- дециметр (дм) – 0,1 м
- метр (м) – 1 м
- декаметр (дамба) – 10 м
- гектометр (хм) – 100 м
- км (км) – 1000 м
- мегаметр (Мм) – 1 000 000 м
- гигаметр (Gm) – 1 x 10 +9 м
- тераметр (Тм) – 1 x 10 +12 м
- петаметр (Pm) – 1 x 10 +15 м
- экзамен (Em) – 1 x 10 +18 м
- зеттаметр (Zm) – 1 x 10 +21 м
- йоттаметр (Ym) – 1 x 10 +24 м
Имперские и американские единицы длины
- тысячная часть дюйма (тысяч) – 0.0000254 м
- дюйм (дюйм) – 0,0254 м
- футов (футов) – 0,3048 м
- ярдов (ярдов) – 0,9144 м
- миль (ми) – 1609,344 м
- морских миль (нми) – 1852 м
Астрономические единицы
- астрономическая единица (а.е.) – 149 597 870 700 м
- световых лет (лет) – 9 460 730 472 580 800 м
- парсек (пк) – 30 856 775 814 913 672,789… м
- килопарсек (кпк) – 3,0856775814
2789… x 10 +19 м - мегапарсек (Мпк) – 3.
 0856775814
08567758142789… x 10 +22 м - гигапарсек (Гпк) – 3,0856775814
2789… x 10 +25 м Расчет объема
Это объем прямоугольной формы, который соответствует введенным размерам длины, ширины и высоты. Объем рассчитывается путем перемножения каждого измерения и последующего преобразования его в выбранные объемные единицы.
Следующие коэффициенты пересчета в кубических метрах (м³) используются для преобразования расчетного объема в другие объемные единицы:
Метрические объемные единицы
- кубический нанометр (куб. нм) – 1 x 10 -27 м³
- кубический микрометр (куб.мкм) – 1 x 10 -18 м³
- кубический миллиметр (куб. мм) – 1 x 10 -9 м³
- кубический сантиметр (см3) – 1 x 10 -6 м³
- миллилитр (мл) – 1 x 10 -6 м³
- чайная ложка (т. л., метрическая) – 5 x 10 -6 м³
- столовая ложка (Tbsp, метрическая) – 1.
 5 x 10 -5 м³
5 x 10 -5 м³ - чашка (метрическая) – 2,5 x 10 -4 м³
- литр (л) – 1 x 10 -3 м³
- кубический метр (куб. м) – 1 м³
- килолитр (кл) – 1 м³
- мегалитр (ML) – 1000 м³
- кубических километров (куб.км) – 1 x 10 +9 м³
Английские имперские единицы объема
- тыс. куб. (тыс. куб.) – 1,6387064 x 10 -14 м³
- куб. дюйм (куб. дюйм) – 1,6387064 x 10 -5 м³
- жидкая унция (жидкая унция, империал) – 2.84130625 x 10 -5 м³
- пинта (pt, британская) – 5,6826125 x 10 -4 м³
- галлонов (галлонов, имперских) – 4,54609 x 10 -3 м³
- кубических футов (куб. футов) – 0,028316846592 м³
- кубических ярдов (куб. ярдов) – 0,764554857984 м³
- кубических миль (куб. миль) – 4168181825,440579584 м³
- кубических морских миль (куб. миль) – 6352182208 м³
Объемные единицы США
- тыс.
 куб. (тыс. куб.) – 1,6387064 x 10 -14 м³
куб. (тыс. куб.) – 1,6387064 x 10 -14 м³ - чайных ложек (tsp, USA) – 4.92892159375 x 10 -6 м³
- столовая ложка (Tbsp, США) – 1,478676478125 x 10 -5 м³
- куб. дюйм (куб. дюйм) – 1,6387064 x 10 -5 м³
- жидкая унция (жидкие унции, США) – 2,95735295625 x 10 -5 м³
- чашка (США) – 2.365882365 x 10 -4 м³
- пинта (пт, США, жидкость) – 4,73176473 x 10 -4 м³
- галлон (галлон, США, жидкость) – 3,785411784 x 10 -3 м³
- кубических футов (куб. футов) – 0.028316846592 м³
- баррель (баррель, нефть) – 0,158987294928 м³
- кубических ярдов (куб. ярдов) – 0,764554857984 м³
- кубических миль (куб. миль) – 4168181825,440579584 м³
- кубических морских миль (куб. миль) – 6352182208 м³
Литры Метрическая префикс Объемные единицы
- йоктолитров (л) – 1 x 10 -27 м³
- зептолитров (zL) – 1 x 10 -24 м³
- аттолитров (aL) – 1 x 10 -21 м³
- фемтолитр (fL) – 1 x 10 -18 м³
- пиколитр (пл) – 1 x 10 -15 м³
- нанолитр (кв.
 л) – 1 x 10 -12 м³
л) – 1 x 10 -12 м³ - микролитр (кв.мкл) – 1 x 10 -9 м³
- миллилитров (кв.мл) – 0.000001 м³
- сантилитр (кв. л) – 0,00001 м³
- децилитр (дл) – 0,0001 м³
- литр (кв. л) – 0,001 м²
- декалитров (дал) – 0,01 м³
- гектолитры (гл) – 0,1 м³
- килолитр (кв. л) – 1 м³
- мегалитр (ML) – 1000 м³
- гигалитров (GL) – 1 000 000 м³
- тералитров (TL) – 1 x 10 +9 м³
- петалитр (PL) – 1 x 10 +12 м³
- exalitre (EL) – 1 x 10 +15 м³
- зетталитр (ZL) – 1 x 10 +18 м³
- йотталитр (YL) – 1 x 10 +21 м³
Кубические метры Префикс метрической системы СИ Объемные единицы
- кубический йоктометр (куб.м) – 1 x 10 -72 м³
- кубический зептометр (куб. м) – 1 x 10 -63 м³
- куб. аттометр (куб. ам) – 1 x 10 -54 м³
- кубический фемтометр (куб.
 фм) – 1 x 10 -45 м³
фм) – 1 x 10 -45 м³ - кубический пикометр (куб.м) – 1 x 10 -36 м³
- кубический нанометр (куб.нм) – 1 x 10 -27 м³
- кубический микрометр (куб.мкм) – 1 x 10 -18 м³
- кубический миллиметр (куб.мм) – 1 x 10 -9 м³
- кубических сантиметров (см3) – 0.000001 м³
- кубический дециметр (ку дм) – 0,001 м³
- кубический метр (куб. м) – 1 м³
- кубических декаметров (куб. дм) – 1000 м³
- гектометр кубический (куб.м) – 1 000 000 м³
- кубических километров (куб.км) – 1 x 10 +9 м³
- кубический мегаметр (куб. Мм) – 1 x 10 +18 м³
- кубический гигаметр (ку Гм) – 1 x 10 +27 м³
- куб. тераметр (куб.м) – 1 x 10 +36 м³
- кубических петаметров (куб.м) – 1 x 10 +45 м³
- куб. экз. (cu Em) – 1 x 10 +54 м³
- кубический зеттаметр (куб.
 Зм) – 1 x 10 +63 м³
Зм) – 1 x 10 +63 м³ - кубических йоттаметров (cu Ym) – 1 x 10 +72 м³
Кубические астрономические единицы
- кубическая астрономическая единица (у.е. а.е.) – 3.347928975810748964239359243 x 10 +33 м³
- кубических световых лет (cu ly) – 8,4678666462371516595551248694562 x 10 +47 м³
- кубических парсеков (куб. пк) – 2,937998946096347255544756436543… x 10 +49 м³
- кубических килопарсек (куб. кпк) – 2,937998946096347255544756436543… x 10 +58 м³
- кубических мегапарсек (куб. Мпк) – 2,937998946096347255544756436543… x 10 +67 м³
- кубических гигапарсек (куб. гпк) – 2,937998946096347255544756436543… x 10 +76 м³
Применение
Используйте этот калькулятор длины x ширины x высоты для определения объема в следующих приложениях:
- Объем отправляемой упаковки для добавления к отгрузочным документам
- Объем гравия , необходимый для заполнения дорожки, автостоянки или подъездной дороги.

- Емкость прямоугольного накопительного бака.
- Объем грузового отсека автомобиля, грузовика или фургона.
- Грузовой объем автомобиля для перемещения склада.
- Максимальный объем емкости для воды.
- Сколько топлива требуется для заполнения бака.
- Размер насыпи, необходимой для удержания утечек и разливов из контейнеров IBC.
- Количество мешков, необходимое для каждого материала для строительного проекта.
- Количество почвы, необходимое для заполнения ящика для рассады.
- Количество воды, необходимое для заполнения аквариума.
- Емкость для заполнения пруда.
- Вместимость складского помещения от габаритов.
- Вместимость IBC.
- Объем заполнения бассейна.
- Возможно место для багажа внутри чемодана.
- Цементная смесь, необходимая для заливки фундаментов/фундаментов.
- Вместимость кузова пикапа.
- Объем корпуса аудиодинамика.

- Емкость кормушки для кормления животных.
- Объем цементной подушки для садового сарая, солярия или теплицы.
Справка
Бак размером 25 x 10 x 12 дюймов в галлонах США
Сколько галлонов США вмещает бак шириной 10 дюймов, высотой 12 дюймов и длиной 25 дюймов?
При внутренних размерах или отсутствии толщины стенок объем резервуара составляет 12,987013 галлонов США.
Объем твердого тела с известным поперечным сечением
В этом разделе мы узнаем, как найти объем твердого тела, имеющего известное поперечное сечение.
Мы рассматриваем твердые тела, поперечное сечение которых представляет собой обычные формы, такие как треугольники, квадраты, прямоугольники, трапеции и полукруги.
Определение: объем твердого тела с использованием интегрирования
Пусть \(S\) — твердое тело, и предположим, что площадь поперечного сечения в плоскости, перпендикулярной оси \(x-\), равна \(A\left( x \right)\) для \(a \ ле х \ле б.
 2}}}\] и плоскость \(z = 1.2}\] и ось \(x-\). Найдите объем твердого тела, если его сечения представляют собой равносторонние треугольники, перпендикулярные оси \(х-\).
2}}}\] и плоскость \(z = 1.2}\] и ось \(x-\). Найдите объем твердого тела, если его сечения представляют собой равносторонние треугольники, перпендикулярные оси \(х-\).Пример 4
Найдите объем правильной квадратной пирамиды со стороной основания \(a\) и высотой \(H.\)
Пример 1.
Твердое тело имеет основание, лежащее в первом квадранте плоскости \(xy-\) и ограниченное линиями \(y = x,\) \(x = 1,\) \(y = 0.\) Каждая плоское сечение, перпендикулярное оси \(x-\), представляет собой полуокружность.1 = \frac{{\sqrt 3}}{4}\left[ {\left( {1 — \frac{2}{3} + \frac{1}{5}} \right) — \left({ — 1 + \frac{2}{3} — \frac{1}{5}} \right)} \right] = \frac{{\sqrt 3 }}{2}\left( {1 — \frac{ 2}{3} + \frac{1}{5}} \right) = \frac{{4\sqrt 3 }}{{15}}.\]
Пример 4.
Найдите объем правильной квадратной пирамиды со стороной основания \(a\) и высотой \(H.\)
Раствор.
Рис. 5.Площадь квадратного сечения в точке \(х\) записывается в виде
\[A\left( x \right) = {\left( {a \cdot \frac{x}{H}} \right)^2} = \frac{{{a^2}{x^2} }}{{{Н^2}}}.
 2}H}}{3}.\]
2}H}}{3}.\]Дополнительные проблемы см. на стр. 2.
ЧТО ТАКОЕ ПРОЗРАЧНЫЙ РИСУНОК
ПРЕДСТАВИТЕЛЬСТВО МЕРТВО. ПРОЗРАЧНОСТЬ МЕРТВА. ПРОЗРАЧНОСТЬ ЭТО ЗАМЕНА.
Прозрачный рисунок — это знание формы. Отказываясь от непрозрачности, вы можете познать в одном аналоговом рисунке целостный объект. TD используется для познания существующих форм и для познания ранее невообразимых форм. Он продвигает различные режимы рисования и сборки чертежей, чтобы помочь вам получить эти целостные знания.
С «Прозрачным рисованием» вы на пути к знаниям.
РИСОВАНИЕ С ХУДОЖЕСТВЕННЫМ НАСТРОЙКОМ УМЕРЛО. РИСУНОК С ПРОЗРАЧНОСТЬЮ ЗАМЕНА.
Не рисуй как художник. Вы создатель форм. Линии, которые вы рисуете, напрямую формируют то, что существует в физическом мире.
ПРОЗРАЧНЫЙ РИСОВАНИЕ О ЗНАНИЯХ.
Когда вы рисуете прозрачно, вы лучше понимаете свой объект. Когда вы рисуете прозрачно, вы одновременно понимаете внешнюю форму и внутреннее пространство.

КАК ТЫ МОЖЕШЬ ЗНАТЬ ФОРМУ, ЕСЛИ НЕ РИСУЕШЬ ТО, ЧЕГО НЕ ВИДИШЬ?
Обладая художественным складом ума, мы не рисуем того, чего не видим. И поскольку мы этого не рисуем, мы не можем этого понять. Прозрачное рисование позволяет нам сразу увидеть и понять весь объект или корпус. Прозрачный рисунок способствует целостному пониманию объема.
Аналог. Карандаш и бумага. Один рисунок. Ничего скрытого. Все раскрылось.
СМОТРИТЕ ПРОЗРАЧНЫЙ МАНИФЕСТ РИСУНКОВ ЗДЕСЬ!
ПРОЗРАЧНЫЙ РИСУНОК КАК ТЕОРЕТИЧЕСКАЯ ПОЗИЦИЯ
TD считает, что наше классическое понимание линейной перспективы и двухмерного рисунка имеет ограниченную пропускную способность.
Теория предполагает, что мы используем прозрачные рисунки, чтобы оживить наше человеческое понимание того, как устроен мир. Простой акт создания рисунков, в которых разрешены все стороны объекта, лежит в основе теории.
Теория работает на пересечении визуальных и литературных компонентов нашей культуры.
 TD утверждает, что в нашей культуре визуальное должно быть выше или равноценно буквальному.
TD утверждает, что в нашей культуре визуальное должно быть выше или равноценно буквальному.Обращается внимание на ранее не изученные аспекты акта проектирования.Некоторые из них включают:
— психология интерфейса клиент/дизайнер
— визуальные факты
— прозрачные методы рисования путешествий
— новые проекции рисования; Choisey One Point
— методы получения свежей формыПРОЗРАЧНЫЙ ЧЕРТЕЖ ОТКЛОНЯЕТ ВСЕ ЦИФРОВЫЕ ИЗОБРАЖЕНИЯ; ЭТО НЕ РИСУНКИ.
«Прозрачное рисование» ищет повторное участие и интеграцию наших телесных наблюдений. Использование этой теории приведет только к тому, что дизайнеры станут лучше в том, что они делают.
КОРОТКО
Чтобы рисовать прозрачно, вы просто показываете все стороны объекта на листе бумаги. Так что вместо рисования
это вы рисуете это
Обратите внимание, как вы можете видеть все стороны простой формы фронтона.
 Как дизайнер, изображение справа должно быть нашим значением по умолчанию. Тем не менее, изображение слева — это то, что нас учат рисовать, и это наш культурный стандарт.
Как дизайнер, изображение справа должно быть нашим значением по умолчанию. Тем не менее, изображение слева — это то, что нас учат рисовать, и это наш культурный стандарт.Все изображения на этом сайте принадлежат Курту Оферу.
www.altonview.com
Никаких прав на воспроизведение или каких-либо прав на картины, изображения и текст, если только разрешение не предоставлено художником.
Четыре измерения
Четыре измеренияHPS 0410 Эйнштейн для всех Вернуться на главную страницу
Джон Д. Нортон
Факультет истории и философии науки
Университет ПиттсбургаМы уже видели, что нет ничего страшного таинственно о добавлении одного измерения к пространству, чтобы сформировать пространство-время.Тем не менее трудно устоять перед затянувшимся беспокойство по поводу идеи четырехмерного пространства-времени.
 Проблема время не является частью четырехмерного пространства-времени; это четыре . Легко представить себе три оси трехмерного
пространство: вверх-вниз, поперек и задом наперед. Но куда нам девать четвертую
оси, чтобы сделать четырехмерное пространство?
Проблема время не является частью четырехмерного пространства-времени; это четыре . Легко представить себе три оси трехмерного
пространство: вверх-вниз, поперек и задом наперед. Но куда нам девать четвертую
оси, чтобы сделать четырехмерное пространство? Моя нынешняя цель — показать вам, что на самом деле ничего нет. все таинственное в четырех измерениях пространства-времени.Для этого я буду полностью отбросить временную часть. я просто рассмотреть четырехмерное пространство; то есть пространство такое же, как наша тройка многомерное пространство, но с одним дополнительным измерением. Каково это?
Без каких бы то ни было усилий я могу визуализировать трехмерное -мерное пространство — и вы можете слишком. Каково было бы жить в трехмерном кубе? Чтобы спросить визуализировать это все равно, что просить дышать или моргать. Это легко. Мы сидим в кубе с шестью квадратными стенками и восемью углами.Наш мысленный взор позволяет нам парить внутри.

Могу ли я представить, каково это жить в четырех мерный аналог куба, четырехмерный куб или «тессеракт»? я не может визуализировать это с такой же легкой непосредственностью. я сомневаюсь, что ты может также. Но это почти единственное, что мы не можем сделать. В противном случае мы может определить все свойства тессеракта и каково было бы жить в одном из них. Существует множество методик для делая это. Я покажу вам один ниже.Он включает в себя продвижение через последовательность измерений, экстраполирующая естественные выводы на каждом шагу вверх к четвертому измерению. Как только вы увидели, как это делается для спец. случае тессеракта, у вас не возникнет проблем с применением его к другим случаям. Дверь в четвертое измерение открывается.
Одномерный интервал
Одномерный аналог куба — интервал. это формируется путем взятия безразмерной точки и ее перетаскивания на определенное расстояние.Это расстояние может быть 2 дюйма или 3 фута или что-то еще.
 Давайте позвоним
расстояние «Л».
Давайте позвоним
расстояние «Л». Интервал имеет длину L. Он ограничен 2 точками, так как его лица — две точки на каждом конце интервала.
Двумерный квадрат
Двумерным аналогом куба является квадрат. это образованный перетаскиванием одномерного интервала на расстояние L в второе измерение.
Квадрат имеет площадь L 2 .Он ограничен гранями на 4 стороны. Грани — это интервалы длины L. Мы знаем, что их четыре. их, поскольку его двумерные оси должны быть закрыты с обоих концов гранями.
Итак, у нас есть 2 измерения x 2 грани в каждой = 4 грани. лица вместе образуют периметр длиной 4xL.
Трехмерный куб
Чтобы сформировать куб, мы берем квадрат и перетаскиваем его на расстояние L в третьем измерении.
Объем куба L 3 .Он ограничен гранями на 6 сторон. Грани представляют собой квадраты площадью L 2 . Мы знаем, что их 6 из них, поскольку его трехмерные оси должны быть закрыты с обоих концов лица.

Итак, у нас есть 3 измерения x 2 грани в каждой = 6 граней. лица вместе образуют поверхность площадью 6xL 2 . Нанесение изображения трехмерный куб на двумерной поверхности одинаково легко. Мы принимаем две его грани — два квадрата — и соедините углы.
Есть несколько способов сделать рисунок, который соответствует взгляду на куб под разными углами.На рисунке показано два способа сделать это. Первый дает косой обзор; второй смотрит вдоль одна из осей.
Четырехмерный куб: тессеракт
Пока я надеюсь, что вы нашли наши конструкции полностью безупречный. Следующий шаг в четыре измерения можно сделать одинаково механически. Мы просто систематически повторяем каждый шаг выше. Единственный разница в том, что на этот раз мы не можем легко сформировать ментальную картину того, что мы строим. Но мы можем знать все его свойства!
Чтобы сформировать тессеракт, мы берем куб и перетаскиваем его расстояние L в четвертом измерении .
. Мы не можем точно представить, как это выглядит, но примерно так:
Мы не можем точно представить, как это выглядит, но примерно так: Тессеракт имеет объем L 4 . Он ограничен лица с 8 сторон. Грани представляют собой кубы объема L 3 . Мы знаем там их 8, так как его четыре оси должны быть закрыты с обоих концов грани — две кубические грани на ось. Опять же, мы не можем визуализировать все четыре из этих ограниченных измерений. В лучшем случае мы можем визуализировать три направления, перпендикулярные друг другу.Потом как-то добавляем в четвертый (красный):
Итак, у нас есть 4 измерения по 2 грани в каждой = 8 граней. лица вместе образуют «поверхность» (на самом деле трехмерный объем) 8xL 3 по объему. Рисование изображения четырехмерного тессеракта в трехмерном пространстве просто. Берем два его грани — два куба — и соединить углы.
Есть несколько способов сделать рисунок, который соответствует взгляду на тессеракт под разными углами.
 Фигура
показывает два способа сделать это. Первый дает косой обзор; второй смотрит
по одной из осей.
Фигура
показывает два способа сделать это. Первый дает косой обзор; второй смотрит
по одной из осей. Итак, теперь мы, кажется, знаем все, что нужно знать о тессеракт! Мы знаем его объем в четырехмерном пространстве, как он выражается вместе из восьми кубов как поверхностей и даже каков объем его поверхность (8xL 3 ).
Стереовидение
«Чертежи» тессеракта плохо видны. Это потому, что они действительно должны быть трехмерными моделями в трехмерное пространство.Итак, что у нас есть выше, это два габаритные чертежи трехмерных моделей четырехмерного тессеракт. Неудивительно, что он становится грязным!
Изображения ниже представляют собой стереопары. Если вы знакомы с как просмотреть их, вы увидите, что они дают вам хороший стереофонический вид трехмерная модель. Если они новые для вас, они требуют практики, чтобы увидеть. Вам нужно расслабить свой взгляд, пока ваш левый глаз не увидит левое изображение и правый глаз смотрит на правильное изображение.

Но как научиться этому? мне проще всего начать, если я сижу далеко от экрана и смотрю вдаль над верхней части экрана.Я вижу два несколько размытых изображения на краю мое поле зрения. Пока я не сосредотачиваюсь на них, они начинают дрейфовать вместе. Это то движение, которое вам нужно. Чем больше они дрейфуют вместе, тем лучше. Я стараюсь максимально усилить дрейф, осторожно перемещая смотреть на изображения. Цель состоит в том, чтобы объединить два изображения. Когда они делаю, я продолжаю смотреть на объединенные изображения, фокус улучшается и резко появляется трехмерный стереоэффект. Эффект поразительный и стоит немного усилий.
Эту пару легче сплавить:
и этот немного сложнее:
Сводная таблица
Мы можем подытожить развитие свойств tesseract следующим образом:
Размер Рисунок Лицо Том Количество граней Объем
поверхности/периметра1 интервал точка л 1×2=2 два очки 2 квадрат интервал л 2 2×2=4 4 л 3 куб квадрат л 3 3×2=6 6 л 2 4 тессеракт куб л 4 4×2=8 8 л 3 Вместительный вызов
Если бы вы жили в тессеракте, вы могли бы выбрать жить на его трехмерной поверхности, подобно двумерному человеку.
 выберите жить в 6 квадратных комнатах, которые образуют двухмерную поверхность
куб.Таким образом, вашим домом будут восемь кубов, образующих поверхность тессеракта. Представьте, что есть двери
где когда-либо два из этих кубов встречаются. Если вы находитесь в одной из этих комнат, как
много дверей вы бы видели? Как бы выглядела следующая комната, если бы вы прошли
через одну из дверей? Через сколько дверей нужно пройти, чтобы попасть в
самая дальняя комната? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо
окна снаружи тессеракта? Как насчет окон внутрь?
тессеракт?
выберите жить в 6 квадратных комнатах, которые образуют двухмерную поверхность
куб.Таким образом, вашим домом будут восемь кубов, образующих поверхность тессеракта. Представьте, что есть двери
где когда-либо два из этих кубов встречаются. Если вы находитесь в одной из этих комнат, как
много дверей вы бы видели? Как бы выглядела следующая комната, если бы вы прошли
через одну из дверей? Через сколько дверей нужно пройти, чтобы попасть в
самая дальняя комната? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо
окна снаружи тессеракта? Как насчет окон внутрь?
тессеракт? Некоторые из этих вопросов непростые.Чтобы ответить на них, перейдите вернемся к простому случаю трехмерного куба с гранями, состоящими из квадраты. Задайте аналогичные вопросы там и просто экстраполируйте ответы к тессеракту.
Запутанный вызов
Доступ к четвертому измерению делает возможным многое иначе это было бы совершенно невозможно. Чтобы увидеть, как это работает, мы будем использовать стратегия обдумывания процесса в трехмерном пространстве.
 Тогда мы
воспроизвел его в четырехмерном пространстве.
Тогда мы
воспроизвел его в четырехмерном пространстве.Рассмотрим монету, лежащую в рамке на столе.
Монета не может быть извлечена из рамка в пределах двухмерной поверхности Таблица. Теперь вспомните, что у нас есть доступ к третьему измерению. Монета легко снимается простым поднятием в третье измерение, высота над столом.
После этого мы можем свободно перемещать монету по своему усмотрению на верхнем уровне. а затем опуститься обратно на столешницу вне рамы.
При подъеме следует обратить внимание на то, что движение вообще не двигает монету в двух горизонтальных направлениях двух объемное пространство. Таким образом, движение никогда не приближает его к кадру, и отсутствие опасности столкновения с рамой.
Теперь повторите этот анализ для своего аналога в одном Высшее измерение, мрамор, запертый внутри трехмерная коробка. 
Мрамор можно снять точно таким же образом, «подняв» его, на этот раз в четвертый измерение. Как и в случае с монетой в рамке, ключ к Обратите внимание, что при этом подъемном движении положение шарика в три пространственных направления ящика неизменны. То мрамор никогда не приближается к стенам и нет опасности столкнуться с ними. Как только он поднимается в новое трехмерное пространство, он можно свободно перемещать в этом пространстве и опускать обратно в исходное трехмерное пространство, но теперь за пределы коробка.
Теперь, наконец, рассмотрим два зацепленных колец в некотором трехмерном пространстве.  Можем ли мы разделить
они используют доступ к четвертому измерению?
Можем ли мы разделить
они используют доступ к четвертому измерению?Это можно сделать с помощью точно такого же процесса поднять одно из колец в четвертое измерение. Как и прежде, обратите внимание что поднятие не двигает кольцо ни в одном из трех направления трехмерного пространства, удерживающие изначально связанные кольца. Так что движения рисков нет столкновения перемещаемого кольца с другим. Подъем просто поднимает перемещенное кольцо на новый трехмерный слой из четырех размерное пространство, в котором нет ни одной части другого кольца.То перемещенное кольцо может быть свободно перемещено в этот новый слой, и если мы с удовольствием опустился обратно в исходное трехмерное пространство в совсем другое место. А теперь самое сложное. Мы знакомы в нашем трехмерное пространство с завязыванием узлов на веревке.
 Некоторые узлы просто
кажущиеся клубки, которые могут довольно легко разойтись. Другие реальны и могут
расстегнуть только продев конец веревки в петлю.Так возьми это
быть настоящим узлом: таким, который нельзя развязать
любые манипуляции с веревкой, если мы не можем ухватиться за концы. (Представьте, если
вам нравится, что каждый из них прикреплен к стене и не может быть удален.)
Некоторые узлы просто
кажущиеся клубки, которые могут довольно легко разойтись. Другие реальны и могут
расстегнуть только продев конец веревки в петлю.Так возьми это
быть настоящим узлом: таким, который нельзя развязать
любые манипуляции с веревкой, если мы не можем ухватиться за концы. (Представьте, если
вам нравится, что каждый из них прикреплен к стене и не может быть удален.)Задача состоит в том, чтобы убедить себе, что на веревках в четырехмерном пространстве нет настоящих узлов. Основная помощь, которая вам понадобится, — это манипуляция выше связанного кольца. Для начала представьте, как бы вы использовали четвертое измерение. чтобы развязать какой-нибудь простой узел, который вы легко можете себе представить.
Использование цветов для визуализации дополнительных размер
Общая идея «поднятия» объекта в четвертое измерение все еще кажется неуловимым? Если да, то вот техника для визуализация этого может просто помочь. Хитрость заключается в том, чтобы представить, что различия в положении в дополнительном измерении пространства могут быть представлены различиями цветов.

Вот как это работает, когда мы начинаем с двойки пространственных измерений и подняться в третье измерение.Объекты в исходное двумерное пространство черное. Когда мы поднимаемся через В третьем измерении они последовательно окрашиваются в синий, зеленый и красный цвета.
Теперь давайте применим этот трюк с цветным слоем к более ранний пример подъема монеты из рамки. Монета начинается через то же двухмерное пространство, что и кадр. Мы поднимаем его в третье измерение в более высокое пространственное слой, который у нас окрашен в красный цвет.В этом более высоком слое монета может свободно двигаться влево/вправо и вперед/назад, не пересекаясь рамка. Мы перемещаем его вправо, пока он не пройдет над кадром. Затем опускаем обратно вниз снаружи. Теперь представьте, что мы не можем воспринимать непосредственно третье измерение.  Вот как мы изобразим монету
побег. Он начинается внутри кадра в пространстве кадра.Это
затем поднимается из кадра в третье измерение. При этом
момент, это обозначено призрачным
красная монета. Его пространственное положение слева/справа и
направление вперед/назад не изменилось. Все, что изменилось, это его
высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево
или справа, или спереди и сзади, в этом красном слое уже не
пересекает рамку и может двигаться прямо над ней. Мы не увидим, как он движется
однако через рамку.Насколько нам известно, он будет просто двигаться
через это.
Вот как мы изобразим монету
побег. Он начинается внутри кадра в пространстве кадра.Это
затем поднимается из кадра в третье измерение. При этом
момент, это обозначено призрачным
красная монета. Его пространственное положение слева/справа и
направление вперед/назад не изменилось. Все, что изменилось, это его
высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево
или справа, или спереди и сзади, в этом красном слое уже не
пересекает рамку и может двигаться прямо над ней. Мы не увидим, как он движется
однако через рамку.Насколько нам известно, он будет просто двигаться
через это.Движение монеты в этом трехмерном спасательном проходе проиллюстрировано призрачным красным монета.
Этот последний анализ монеты в кадре является шаблон для работы с реальным случаем шарика, заключенного в трехмерную коробку.  Если мрамор
перемещается в любом из трех известных измерений (вверх/вниз, влево/вправо).
и спереди/сзади), его движение пересекает стенки ящика и
не может убежать.Итак, мы поднимаем мрамор в четвертое измерение,
не меняя своего положения в трех знакомых измерениях. В
На рисунке это показано тем, что мрамор становится призрачно красным. В красном пространстве,
мрамор может свободно двигаться вверх/вниз, влево/вправо и вперед/назад, без
пересекающие стенки коробки. Затем мрамор перемещается так, что проходит
над одной из стен. Затем его опускают из красного пространства обратно
в исходное трехмерное пространство коробки, но теперь за пределы
стены.
Если мрамор
перемещается в любом из трех известных измерений (вверх/вниз, влево/вправо).
и спереди/сзади), его движение пересекает стенки ящика и
не может убежать.Итак, мы поднимаем мрамор в четвертое измерение,
не меняя своего положения в трех знакомых измерениях. В
На рисунке это показано тем, что мрамор становится призрачно красным. В красном пространстве,
мрамор может свободно двигаться вверх/вниз, влево/вправо и вперед/назад, без
пересекающие стенки коробки. Затем мрамор перемещается так, что проходит
над одной из стен. Затем его опускают из красного пространства обратно
в исходное трехмерное пространство коробки, но теперь за пределы
стены.Тот же анализ относится к связанным кольцам. Одно кольцо поднимается из трех размерное пространство исходной установки. В этом красном пространстве кольцо может свободно двигаться, не пересекая другое кольцо.  Мы хорошо двигаемся
от другого кольца, а затем верните его обратно в исходное
трехмерное пространство. Теперь он не связан с другим кольцом.
Мы хорошо двигаемся
от другого кольца, а затем верните его обратно в исходное
трехмерное пространство. Теперь он не связан с другим кольцом.Что следует знать
- Свойства квадратов, кубов и тессерактов.
- Как получить свойства тессеракта и других четырехмерные фигуры путем экстраполяции методов, используемых для получения свойства куба.
Авторское право Джон Д. Нортон. февраль 2001 г.; июль 2006 г., 2 февраля 2008 г.; 6 февраля 2012 г.; 30 апреля 2014 г.
.
- мегапарсек (Мпк) – 3.

 В своем альбоме я делаю записи, напоминания, заметки, списки и все остальные вещи, которые нельзя нарисовать. Мой альбом – это первое место, куда я смотрю, когда мне нужно вспомнить что-то.
В своем альбоме я делаю записи, напоминания, заметки, списки и все остальные вещи, которые нельзя нарисовать. Мой альбом – это первое место, куда я смотрю, когда мне нужно вспомнить что-то.
 Главная —> Фигуры —> Выбрать прямоугольник, толщину линии.
Главная —> Фигуры —> Выбрать прямоугольник, толщину линии.
 к. хранятся все коды точек изображения. Поддерживается многими графическими редакторами (универсальный), но используется только для средств Windows. Не используют для Web, для печати, для переноса и хранения.
к. хранятся все коды точек изображения. Поддерживается многими графическими редакторами (универсальный), но используется только для средств Windows. Не используют для Web, для печати, для переноса и хранения. Используется в издательских системах.
Используется в издательских системах. Смотрите коробки как
геометрические формы, имеющие гладкие прямоугольные плоскости со всех четырех сторон,
пересекающиеся по прямым линиям. Используя аналитический процесс
чертеж, описать геометрические формы ящиков. Создайте три разных
композиции, перемещая коробки или меняя точку зрения.
Смотрите коробки как
геометрические формы, имеющие гладкие прямоугольные плоскости со всех четырех сторон,
пересекающиеся по прямым линиям. Используя аналитический процесс
чертеж, описать геометрические формы ящиков. Создайте три разных
композиции, перемещая коробки или меняя точку зрения. 

 000001 м
000001 м 0856775814
0856775814 5 x 10 -5 м³
5 x 10 -5 м³ куб. (тыс. куб.) – 1,6387064 x 10 -14 м³
куб. (тыс. куб.) – 1,6387064 x 10 -14 м³ л) – 1 x 10 -12 м³
л) – 1 x 10 -12 м³ фм) – 1 x 10 -45 м³
фм) – 1 x 10 -45 м³

 2}}}\] и плоскость \(z = 1.2}\] и ось \(x-\). Найдите объем твердого тела, если его сечения представляют собой равносторонние треугольники, перпендикулярные оси \(х-\).
2}}}\] и плоскость \(z = 1.2}\] и ось \(x-\). Найдите объем твердого тела, если его сечения представляют собой равносторонние треугольники, перпендикулярные оси \(х-\).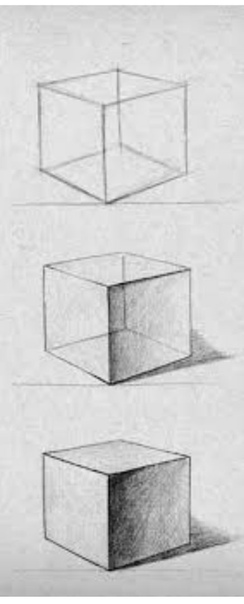 2}H}}{3}.\]
2}H}}{3}.\]
 TD утверждает, что в нашей культуре визуальное должно быть выше или равноценно буквальному.
TD утверждает, что в нашей культуре визуальное должно быть выше или равноценно буквальному. Проблема время не является частью четырехмерного пространства-времени; это четыре . Легко представить себе три оси трехмерного
пространство: вверх-вниз, поперек и задом наперед. Но куда нам девать четвертую
оси, чтобы сделать четырехмерное пространство?
Проблема время не является частью четырехмерного пространства-времени; это четыре . Легко представить себе три оси трехмерного
пространство: вверх-вниз, поперек и задом наперед. Но куда нам девать четвертую
оси, чтобы сделать четырехмерное пространство? 
 Давайте позвоним
расстояние «Л».
Давайте позвоним
расстояние «Л». 
 Мы не можем точно представить, как это выглядит, но примерно так:
Мы не можем точно представить, как это выглядит, но примерно так:  Фигура
показывает два способа сделать это. Первый дает косой обзор; второй смотрит
по одной из осей.
Фигура
показывает два способа сделать это. Первый дает косой обзор; второй смотрит
по одной из осей. 
 выберите жить в 6 квадратных комнатах, которые образуют двухмерную поверхность
куб.Таким образом, вашим домом будут восемь кубов, образующих поверхность тессеракта. Представьте, что есть двери
где когда-либо два из этих кубов встречаются. Если вы находитесь в одной из этих комнат, как
много дверей вы бы видели? Как бы выглядела следующая комната, если бы вы прошли
через одну из дверей? Через сколько дверей нужно пройти, чтобы попасть в
самая дальняя комната? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо
окна снаружи тессеракта? Как насчет окон внутрь?
тессеракт?
выберите жить в 6 квадратных комнатах, которые образуют двухмерную поверхность
куб.Таким образом, вашим домом будут восемь кубов, образующих поверхность тессеракта. Представьте, что есть двери
где когда-либо два из этих кубов встречаются. Если вы находитесь в одной из этих комнат, как
много дверей вы бы видели? Как бы выглядела следующая комната, если бы вы прошли
через одну из дверей? Через сколько дверей нужно пройти, чтобы попасть в
самая дальняя комната? Сколько путей ведут в эту самую дальнюю комнату? Можете ли вы иметь какие-либо
окна снаружи тессеракта? Как насчет окон внутрь?
тессеракт?  Тогда мы
воспроизвел его в четырехмерном пространстве.
Тогда мы
воспроизвел его в четырехмерном пространстве.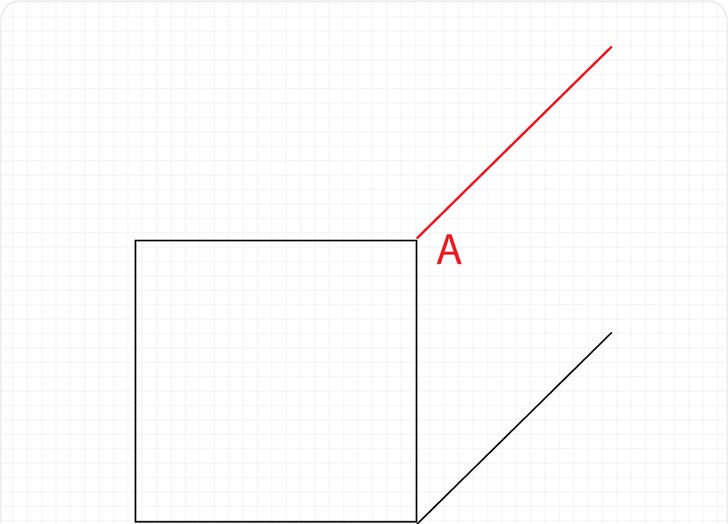
 Можем ли мы разделить
они используют доступ к четвертому измерению?
Можем ли мы разделить
они используют доступ к четвертому измерению?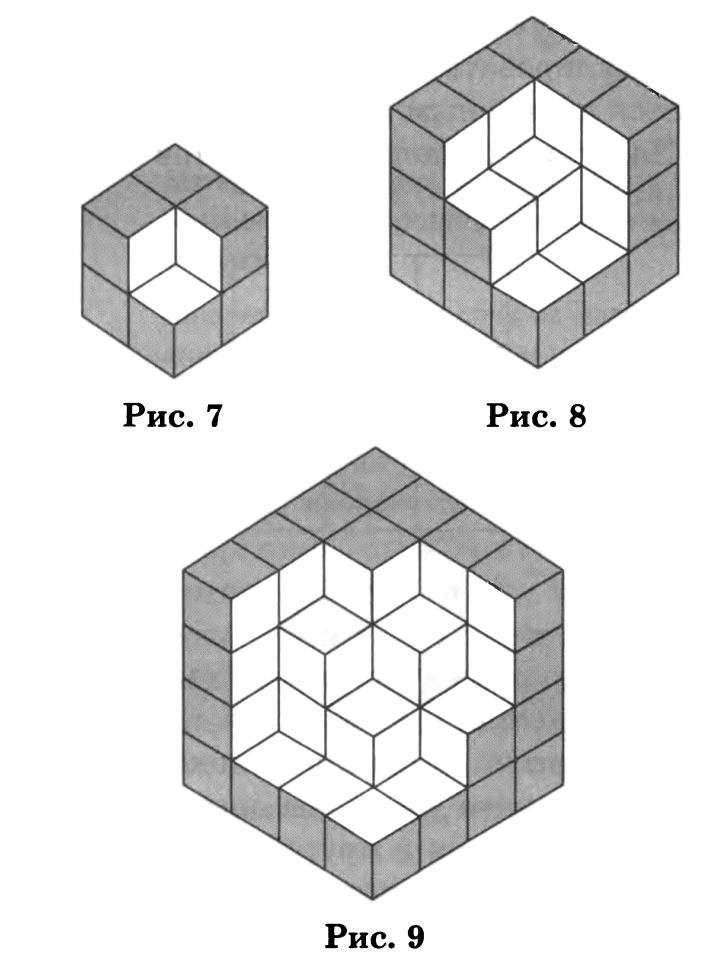 Некоторые узлы просто
кажущиеся клубки, которые могут довольно легко разойтись. Другие реальны и могут
расстегнуть только продев конец веревки в петлю.Так возьми это
быть настоящим узлом: таким, который нельзя развязать
любые манипуляции с веревкой, если мы не можем ухватиться за концы. (Представьте, если
вам нравится, что каждый из них прикреплен к стене и не может быть удален.)
Некоторые узлы просто
кажущиеся клубки, которые могут довольно легко разойтись. Другие реальны и могут
расстегнуть только продев конец веревки в петлю.Так возьми это
быть настоящим узлом: таким, который нельзя развязать
любые манипуляции с веревкой, если мы не можем ухватиться за концы. (Представьте, если
вам нравится, что каждый из них прикреплен к стене и не может быть удален.)
 Вот как мы изобразим монету
побег. Он начинается внутри кадра в пространстве кадра.Это
затем поднимается из кадра в третье измерение. При этом
момент, это обозначено призрачным
красная монета. Его пространственное положение слева/справа и
направление вперед/назад не изменилось. Все, что изменилось, это его
высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево
или справа, или спереди и сзади, в этом красном слое уже не
пересекает рамку и может двигаться прямо над ней. Мы не увидим, как он движется
однако через рамку.Насколько нам известно, он будет просто двигаться
через это.
Вот как мы изобразим монету
побег. Он начинается внутри кадра в пространстве кадра.Это
затем поднимается из кадра в третье измерение. При этом
момент, это обозначено призрачным
красная монета. Его пространственное положение слева/справа и
направление вперед/назад не изменилось. Все, что изменилось, это его
высота. Теперь он находится на красном слое высоты. Если мы переместим монету влево
или справа, или спереди и сзади, в этом красном слое уже не
пересекает рамку и может двигаться прямо над ней. Мы не увидим, как он движется
однако через рамку.Насколько нам известно, он будет просто двигаться
через это.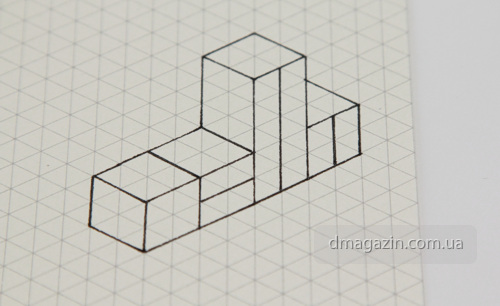 Если мрамор
перемещается в любом из трех известных измерений (вверх/вниз, влево/вправо).
и спереди/сзади), его движение пересекает стенки ящика и
не может убежать.Итак, мы поднимаем мрамор в четвертое измерение,
не меняя своего положения в трех знакомых измерениях. В
На рисунке это показано тем, что мрамор становится призрачно красным. В красном пространстве,
мрамор может свободно двигаться вверх/вниз, влево/вправо и вперед/назад, без
пересекающие стенки коробки. Затем мрамор перемещается так, что проходит
над одной из стен. Затем его опускают из красного пространства обратно
в исходное трехмерное пространство коробки, но теперь за пределы
стены.
Если мрамор
перемещается в любом из трех известных измерений (вверх/вниз, влево/вправо).
и спереди/сзади), его движение пересекает стенки ящика и
не может убежать.Итак, мы поднимаем мрамор в четвертое измерение,
не меняя своего положения в трех знакомых измерениях. В
На рисунке это показано тем, что мрамор становится призрачно красным. В красном пространстве,
мрамор может свободно двигаться вверх/вниз, влево/вправо и вперед/назад, без
пересекающие стенки коробки. Затем мрамор перемещается так, что проходит
над одной из стен. Затем его опускают из красного пространства обратно
в исходное трехмерное пространство коробки, но теперь за пределы
стены. Мы хорошо двигаемся
от другого кольца, а затем верните его обратно в исходное
трехмерное пространство. Теперь он не связан с другим кольцом.
Мы хорошо двигаемся
от другого кольца, а затем верните его обратно в исходное
трехмерное пространство. Теперь он не связан с другим кольцом.