Рисование композиции из геометрических фигур. Основы композиции
Фотография — это то, чем становятся живопись, композиция, пластический ритм, геометрия, размещенные в считанных долях секунды (Анри Картье-Брессон).
Когда мы думаем о композиции в фотографии , первое, что приходит в голову — это , правило третей, …
Но есть еще один важный элемент в композиции — геометрия . Геометрия в фотографии — это простые формы, такие как квадрат, треугольник, круг, прямые и кривые линии.
Геометрические объекты обычно вспомогательные, они усиливают восприятие и могут объединять отдельные элементы фотографии в единое целое. Выбирая ту или иную геометрическую форму в фотографии, автор может заранее акцентировать внимание будущего зрителя на его определенных зонах. Установлено, например, что углы квадрата оказываются очень активными зонами, а для круга или овала — это центр. Не случайно, с давних времен сложилась традиция портретов в овале. Углы не отвлекали внимание от главного — изображения лица.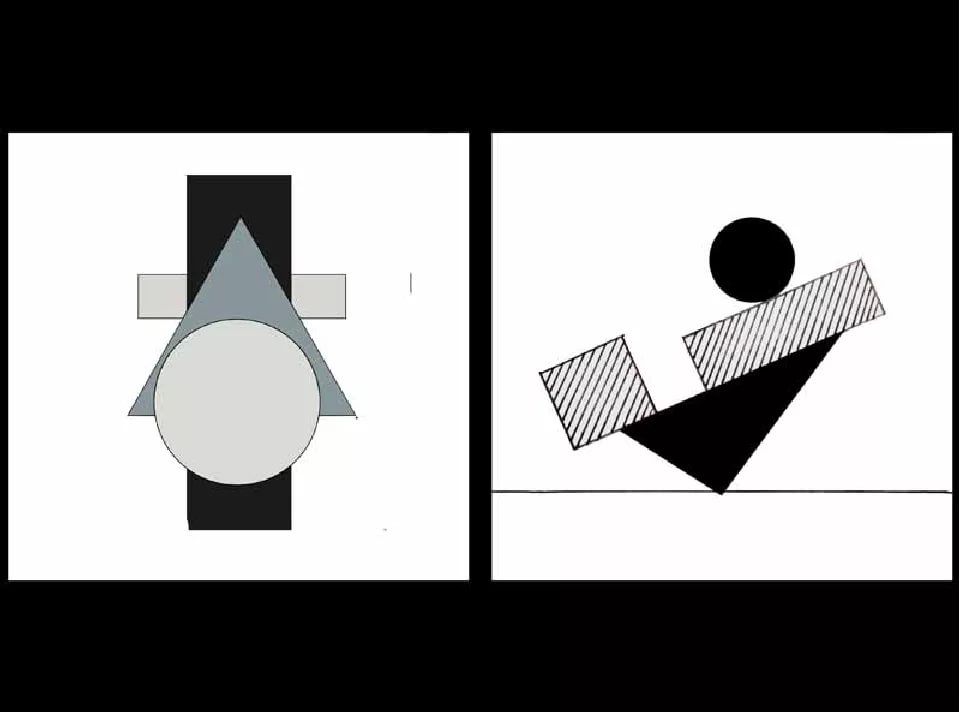 Наиболее распространенный и наиболее разносторонний геометрический инструмент — это линии . Более подробно о них читайте в нашей отдельной .
Наиболее распространенный и наиболее разносторонний геометрический инструмент — это линии . Более подробно о них читайте в нашей отдельной .
Фактически, любой объект окружающей среды можно сравнить с какой-либо геометрической фигурой, но все они пробуждают у зрителя разные эмоции и чувства. Простые геометрические формы, такие как круг и квадрат, намного быстрее фиксируются нашим глазом и воспринимаются мозгом, а следовательно и лучше запоминаются, нежели сложные и неправильные. Вообще выделяют три базовых фигуры. Это прямоугольник, треугольник и круг . Всё остальное — овал, квадрат, трапеция, эллипс, ромб всего лишь их вариации. Все они отличаются как графически, так и (не удивляйтесь) эмоционально.
КВАДРАТ В КОМПОЗИЦИИ
Квадрат — это самая устойчивая, законченная форма, готовая вызывать утверждающие образы. Он ассоциируется с такими понятиями, как порядок, стабильность, надежность, прочность. В то же время, квадрат воспринимается несколько приземленно и тяжеловесно.
Фото: Robertino Nikolic. “Свет играет с геометрией или геометрия со светом?”. Победитель конкурса Black & White Spider Awards, 2007.
Фото: Alma (источник — 1510.deviantart.com)
ПРЯМОУГОЛЬНИК В КОМПОЗИЦИИ
Прямоугольник, расположенный̆ большей̆ стороной̆ по горизонтали вызывает ощущение стабильности, покоя, основательности.
Особенно гармонично смотрится, если он выполнен в пропорциях «золотого сечения». Прямоугольник, расположенный̆ большей̆ стороной̆ вдоль вертикали, создаёт ощущение лёгкости, воздушности.
ТРЕУГОЛЬНИК В КОМПОЗИЦИИ
Треугольник — наиболее часто встречающаяся в природе форма. Треугольник — самая динамичная, неустойчивая форма, которая ассоциируется с движением, развитием, скоростью. В положении «вершиной вверх» вызывает образы устойчивости, стабильности (пирамида). Несколько треугольников — позитивное динамическое движение. В положении «вершиной вниз» — шаткое равновесие, балансировка. В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.
В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.
КРУГ В КОМПОЗИЦИИ
В форме круга более чем, в какой̆ — либо, выражена идея природы, земли, мироздания. Круги изобилуют как в природе, так и в мире рукотворных предметов. Поэтому такие понятия как «добро», «жизнь», «счастье», «процветание» ассоциируются у человека именно с этой̆ формой̆. Данная форма направляет взгляд внутрь кадра. Круг ассоциируется с чем-то легким, воздушным и при этом — уравновешенным. Но, в отличие от квадрата, это равновесие ближе к физическому понятию «неустойчивое равновесие». Круги — самые приятные глазу фигуры, которые можно смело использовать в кадре. Они сразу приковывают внимание зрителя и, благодаря своей идеальной симметричности, привносят в изображение гармонию. Поскольку у круга нет углов, он прекрасно контрастирует с прямоугольным обрезом кадра.
Как и треугольник, круг — очень эффектная геометрическая фигура, которую можно с пользой применить в композиции кадра, хотя и с другим смыслом. В отличие от диагоналей, заряжающих кадр динамикой и напряжением, кривые линии создают гармонию. Таким образом, можно создавать выразительные и информативные композиции, основанные на простых геометрических фигурах.
Геометрические объекты можно условно разделить на три группы по их функциям: направляющие линии, разделители пространства и обрамление . Разделители пространства делят снимок на отдельные зоны, несущие свою смысловую нагрузку, но работающие вместе для создания единой композиции. Примером, простейшего разделителя пространства может послужить линия горизонта, отделяющая небо от поверхности моря. Очень хорошо смотрятся в качестве разделителя пространства треугольники, но и такие элементы, как диагонали и незамкнутые линии, тоже уверенно можно использовать.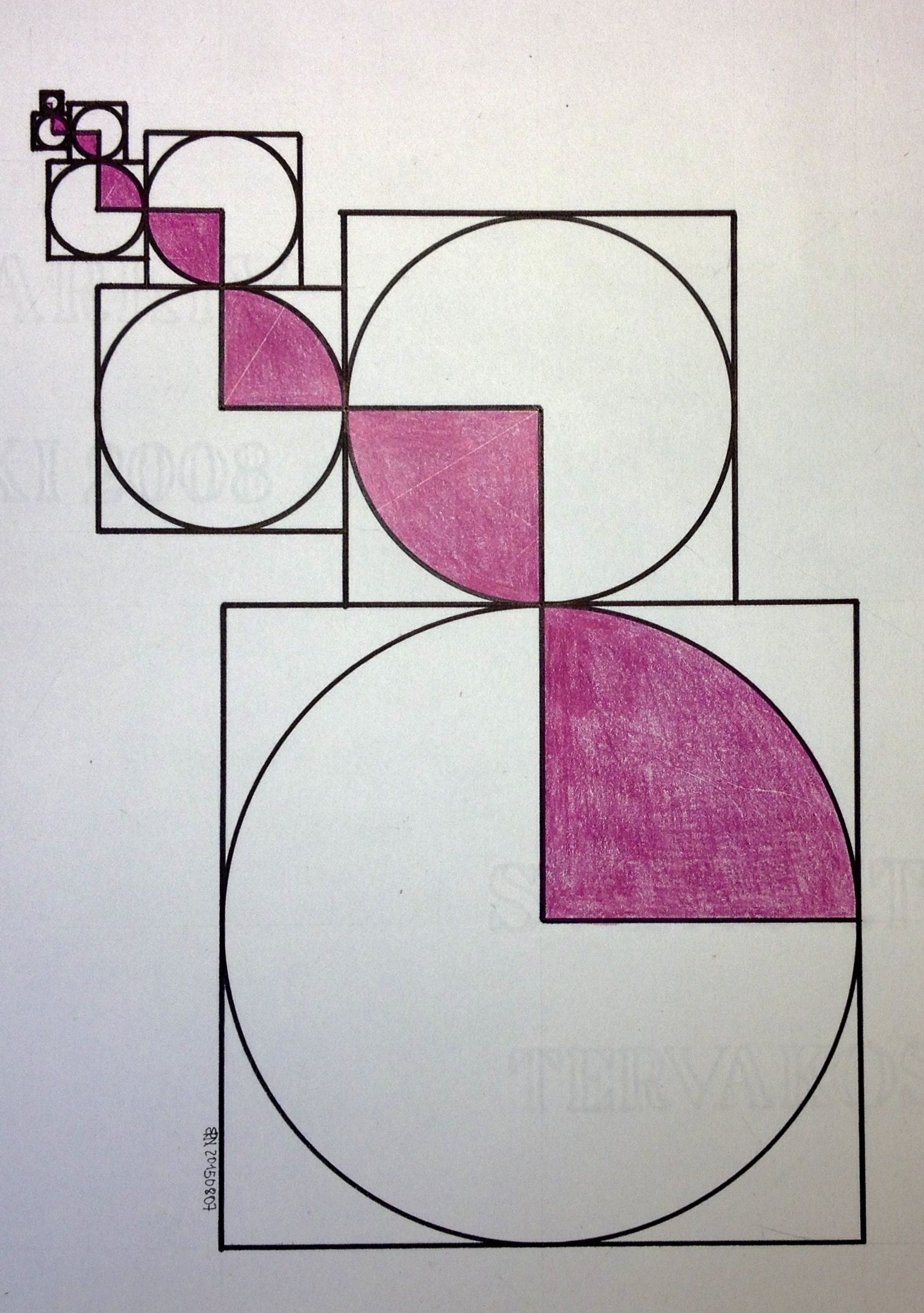
Обрамления носят функцию притяжения взгляда зрителя и его фокусировку на основном объекте. В качестве обрамляющих элементов отлично работают дверные проемы, арки, окна. Кроме того, великолепно с этой функцией справляются и естественные элементы, например, ветви деревьев. Важно чтобы обрамление присутствовало, как минимум, с двух сторон снимка и было выполнено в спокойной тональности, желательно более темной, чем главный объект, чтобы не отвлекать зрителя. Обрамляющий элемент должен иметь интересный цвет, форму, текстуру или иные примечательные характеристики, но стоит помнить, что обрамляющие элементы должны направлять, а не отвлекать. Особенно хорошо в этом плане работают треугольники или арки. Арка способна создать интересную динамичную композицию.
Пробуйте, экспериментируйте и не забывайте, что в одном снимке вы можете использовать сразу несколько геометричских фигур для построения композиции.
Перспектива
композиции выполняется по индивидуальному
заданию. Номер индивидуального задания
соответствует порядковому номеру по
списку в журнале группы. Индивидуальные
задания в таблице №3
Номер индивидуального задания
соответствует порядковому номеру по
списку в журнале группы. Индивидуальные
задания в таблице №3
Таблица№
№Варианта | Параллелепипед | Пирамида | Конус | Цилиндр | |
Т=10, =60, АВ=80, АЕ=40, | |||||
T=20, =55, | |||||
T=10, =60, | |||||
T=10, =50, | |||||
T=10, =50, | |||||
T=20, =60, | |||||
T=40, =50, | |||||
T=20, =50, | |||||
T=30, =50, | |||||
T=10, =60, | |||||
T=25, =55, | |||||
T=15, =60, | |||||
T=20, =50, | |||||
T=10, =50, | |||||
T=10, =55, | |||||
T=10, =50, | |||||
T=30, =55, | |||||
T=15, =60, | |||||
T=40, =50, | |||||
Указания к выполнению ЛИСТА 1
Перед выполнением
перспективного изображения композиции
геометрических тел следует сначала
составить саму композицию, т.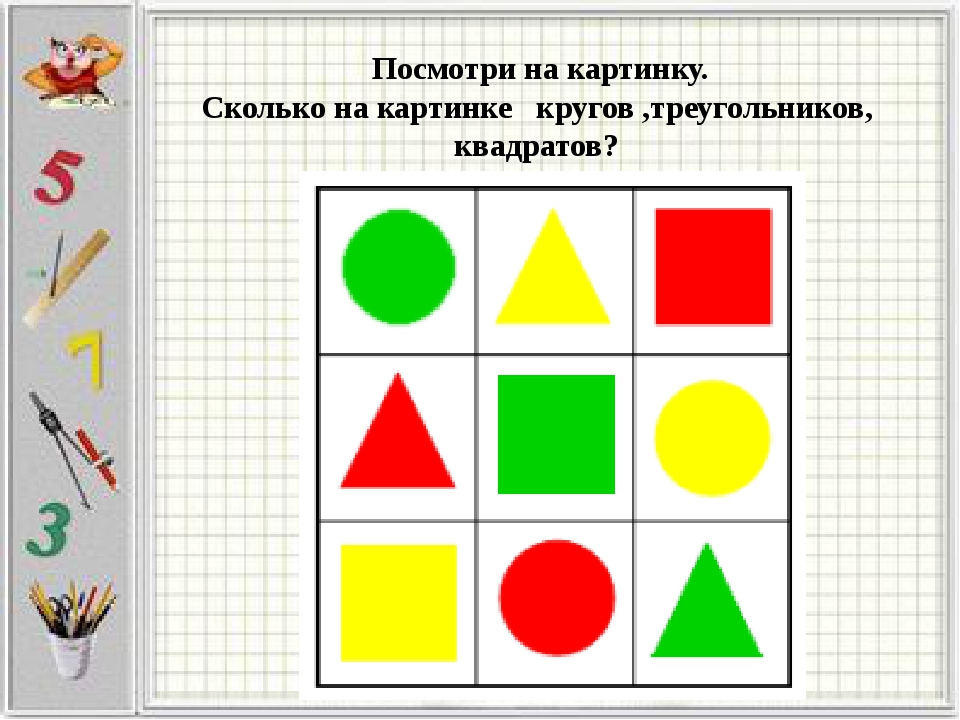 е. определить
взаимное расположение объектов, их
положение относительно главной линии
картины, расстояния от плоскости картины.
В зависимости от составленной композиции
можно выбирать положение точки зрения
(высоту точки зрения и дистанцию).
Дальность точки зрения выбирается
равной одному габариту композиции.
Высота точки зрения выбирается или
несколько меньшей или несколько большей
высоты самого высокого объекта.
е. определить
взаимное расположение объектов, их
положение относительно главной линии
картины, расстояния от плоскости картины.
В зависимости от составленной композиции
можно выбирать положение точки зрения
(высоту точки зрения и дистанцию).
Дальность точки зрения выбирается
равной одному габариту композиции.
Высота точки зрения выбирается или
несколько меньшей или несколько большей
высоты самого высокого объекта.
В индивидуальном задании определена форма объектов, их размер, угол поворота к картинной плоскости, расстояние от плоскости картины. Требуется построить перспективу композиции дух гранных тел, одно из которых расположено фронтально по отношению к картинной плоскости, другое – с заданным углом поворота к картине и одного тела вращения.
При выполнении
перспективного изображения композиции
геометрических тел имеет смысл провести
подготовительную работу – построить
план будущей композиции. Этот план можно
просто нарисовать или, вырезав из бумаги
контуры планов геометрических тел и
двигая их по плоскости, выбрать наилучшее
композиционное решение, а также определить
положение объектов на предметной
плоскости и расстоянии между ними. При
этом выяснится общий габаритный размер
композиции, что определит положение
высоты точки зрения, и дистанцию
(расстояние от наблюдателя до картины).
При
этом выяснится общий габаритный размер
композиции, что определит положение
высоты точки зрения, и дистанцию
(расстояние от наблюдателя до картины).
Пример ЛИСТА 1 — перспективного изображения композиции геометрических тел приведен на(рис. 91 )
Перспектива интерьера
Интерьером
называется внутренний вид помещения в
целом или отдельных его частей. В практике
построения интерьеров известны различные
способы изображения интерьеров, в
зависимости от задачи, которую ставит
перед собой художник. В данном пособии
рассматривается один из способов
построения интерьера с помощью
перспективных масштабов. В зависимости
от расположения стен помещения
относительно картины изображение
интерьера может быть фронтальным или
угловым. Если одна из стен помещения
расположена параллельно картине, то
такое изображение называется фронтальной
перспективой интерьера. Если стены
помещения находятся под углом к картинной
плоскости, то такое изображение называется
угловой перспективой интерьера.
Тема: Закономерности контраста, нюанса как средство организации элементов в единую устойчивую систему (п. 1.2.8).
Последовательность выполнения задания:
Лист условно разделить на две части. В первой части листа:
1. Выполнить композицию в черно-белой графике путем наложения простых элементов (геометрических фигур) друг на друга с использованием контраста по размеру и форме.
Рис. 29. Организация плоскости с помощью подобных элементов
Рис. 30. Организация плоскости с помощью подобных элементов
Рис. 31. Закономерности метра и ритма как средство организации элементов в единую устойчивую систему
Рис. 32. Закономерности метра и ритма как средство организации элементов в единую устойчивую систему
Рис. 33. Закономерности метра и ритма как средство организации элементов в единую устойчивую систему
2. Выполнить композицию в черно-белой графике путем наложения
элементов друг на друга с использованием нюансных отношений по размеру и форме.
На второй части листа: создать методом аппликации образную композицию с применением контраста или нюанса. Композиция должна иметь четко выраженный характер. Примеры выполнения данной работы показаны на (рис 34, 35, 36, 37).
Типичные ошибки:
контраст или нюанс выражен недостаточно последовательно. Композиция носит пограничный характер;
нет равновесия форм.
Материалы: Формат листа А-3, цветная бумага, клей ПВА, тушь, рапидограф, ножницы.
Рис. 34. Организация плоскости с помощью контрастных и нюансных отношений
Рис. 35. Организация плоскости с помощью контрастных и нюансных отношений
Рис. 36. Организация плоскости с помощью контрастных и нюансных отношений
Рис. 37. Организация плоскости с помощью контрастных и нюансных отношений
Какие мысли, какие понятия приходят к вам в голову в первую очередь, когда вы вспоминаете о фотографической композиции? Многие скажут: равновесие в кадре, правило третей, ритмика, направляющие линии… Да, всё это так. Всё это влияет на композицию кадра. Всё это работает и работает прекрасно. Но не только это! Еще есть ракурс, перспектива, взаимоотношение тонов, цветов, контрастов… Всё это фотографу нужно знать и обязательно изучать композицию, законы построения изображения на плоскости. Те, кто недавно решил серьезно заняться фототоворчеством, кто только-только пришел в фотографию и пока еще открывает ее для себя, знакомится с правилами и законами композиции, порой даже и предположить не может, как много интересного включает в себя это интереснейшее искусство. Законы композиции намного глубже, чем это может показаться на первый взгляд. Но приступая к изучению композиции, волноваться ни в коем не стоит. Это не так уж и сложно. Просто постепенно знакомясь с ее законами, осваивая их, нужно тренироваться. Как? Как говаривал известный киногерой, «Элементарно. Ватсон!». Больше фотографировать! Благо, нынешняя техника позволяет фотографировать много. В фотопленке и дорогих расходных материалах сегодня нужды практически нет.
Всё это влияет на композицию кадра. Всё это работает и работает прекрасно. Но не только это! Еще есть ракурс, перспектива, взаимоотношение тонов, цветов, контрастов… Всё это фотографу нужно знать и обязательно изучать композицию, законы построения изображения на плоскости. Те, кто недавно решил серьезно заняться фототоворчеством, кто только-только пришел в фотографию и пока еще открывает ее для себя, знакомится с правилами и законами композиции, порой даже и предположить не может, как много интересного включает в себя это интереснейшее искусство. Законы композиции намного глубже, чем это может показаться на первый взгляд. Но приступая к изучению композиции, волноваться ни в коем не стоит. Это не так уж и сложно. Просто постепенно знакомясь с ее законами, осваивая их, нужно тренироваться. Как? Как говаривал известный киногерой, «Элементарно. Ватсон!». Больше фотографировать! Благо, нынешняя техника позволяет фотографировать много. В фотопленке и дорогих расходных материалах сегодня нужды практически нет.
Сегодня же мы решили поговорить с вами о геометрии в композиции. Да-да! Не удивляйтесь! Именно геометрия является одним из самых важных аспектов композиции. И в этой статье мы попробуем вам это доказать.
Основная масса имеющих фотоаппарат, сами о том не думая, при фотографировании неосознанно используют свои познания в геометрии, вводя в тот или иной кадр различные геометрические формы. Не верите? Читайте статью дальше — и вы убедитесь в нашей правоте. Хочется думать, что изложенная чуть ниже информация даст вам толчок к дальнейшему развитию владения композицией, к дальнейшему совершенствованию вашего мастерства в фотоискусстве.
Прямоугольники
Использование в композиции фотографии этих, пожалуй, самых популярных в геометрии фигур сродни использованию правила третей. Но, в отличие от этого известного правила, кадр делится не на три воображаемые равные части, а на воображаемые прямоугольники самых разных размеров. Посмотрите хотя бы вот на этот снимок. Нижняя часть фотографии, берег и трава, образуют горизонтальный прямоугольник. А левая сторона снимка, там где большое голубое пятно водной глади — прямоугольник вертикальный. Эти два прямоугольника в композиции снимка очень хорошо выделяют стоящий на берегу фонарь. Он выглядит как изолированный, самостоятельный объект.
Нижняя часть фотографии, берег и трава, образуют горизонтальный прямоугольник. А левая сторона снимка, там где большое голубое пятно водной глади — прямоугольник вертикальный. Эти два прямоугольника в композиции снимка очень хорошо выделяют стоящий на берегу фонарь. Он выглядит как изолированный, самостоятельный объект.
Круги
У кругов своя энергетика. Они как бы концентрируют в себе некую энергию, и тем самым направляют взгляд зрителя в глубину кадра. Для того чтобы создавать эффектную композицию, опытные фотографы и хорошие художники часто используют не только круги, но и полукруги. Вот на этой фотографии, которую мы привели для примера, это очень хорошо видно. Круги в ее композиции концентрируют внимание рассматривающего снимок и постепенно подводят его к главному в кадре — к рассматриванию находящихся вдалеке красивых горных вершин.
Треугольники
Треугольник — самый, пожалуй, часто встречающийся в композиции любого изображения на плоскости геометрический элемент. Посмотрите внимательно хотя бы на свои собственные фотографии. Обратите внимание: треугольники повсюду! Они буквально рассыпаны по вашим снимкам! Вот вам для примера — самый обыкновенный горный пейзаж. Треугольники на этой фотографии создают воображаемый, но вполне естественный путь, который ведет взгляд зрителя, рассматривающего снимок, от изгороди на переднем плане по направлению к собственно горам. Да и сами горы, приглядитесь, тоже имеют форму треугольника!
Посмотрите внимательно хотя бы на свои собственные фотографии. Обратите внимание: треугольники повсюду! Они буквально рассыпаны по вашим снимкам! Вот вам для примера — самый обыкновенный горный пейзаж. Треугольники на этой фотографии создают воображаемый, но вполне естественный путь, который ведет взгляд зрителя, рассматривающего снимок, от изгороди на переднем плане по направлению к собственно горам. Да и сами горы, приглядитесь, тоже имеют форму треугольника!
Многоугольники
Смотря в видоискатель фотокамеры, большинство фотографов, особенно начинающих, вряд ли думают о том, что вот сейчас, мысленно работая над композицией будущего кадра, они будут представлять себе какие-то многоугольники. Но потом, когда свои снимки они увидят уже на экране монитора, будут очень и очень удивлены: многоугольников на них будет огромное количество! Именно они и придают фотографиям визуальный смысл. Обратите внимание вот на эти снимки. На них хорошо видно, что геометрические многоугольники появляются в плоскости кадра не только за счет формы самих объектов съемки. Они хорошо просматриваются также и за счет контраста отдельных участков, за счет световых пятен и теней.
Они хорошо просматриваются также и за счет контраста отдельных участков, за счет световых пятен и теней.
Квадраты
Квадрат считается идеальной фигурой не только в геометрии, но и вообще в изобразительном искусстве в целом. Вспомните, хотя бы, знаменитый «Черный квадрат» Казимира Малевича. И для фотографии квадрат — идеальная форма. Посмотрите на эту иллюстрацию. Главный объект фотографии легко и непринужденно вписывается в квадрат. И этот квадрат, в свою очередь, прекрасно гармонирует с другими квадратами — квадратами, образующимися из книг и книжных полок на втором плане.
Арки
Арки в своем проявлении в композиции построения изображения на плоскости в чем-то повторяют «работу» окружностей. Но, в отличие от окружностей, арки — это, скорее, фоновый элемент, нежели чем самостоятельная геометрическая форма. Вот на этой фотографии, например, женские руки, держащие розу и сложенные в форме сердца, образуют собой целых три арки! И эти воображаемые арки образуют как бы рамку, обрамляющую красивый и нежный цветок.
Сходящиеся и параллельные линии
Любой опытный фотограф или художник вам скажет о том, что правильно использовать в композиции различного рода линии бывает очень тяжело. Тем не менее, это вполне возможно. И сходящиеся линии, и параллельные, могут, и даже, больше того, должны быть эффектно использованы в композиции кадра! Особенно эффектно работают такие линии при компоновке фона. Вот посмотрите на этот снимок. На нем легко увидеть и сходящиеся, и параллельные линии. Они очень хорошо направляют взгляд зрителя к главному объекту фотографии — к сидящему на траве человеку. Плюс ко всему, эти линии визуально как бы отражаются друг от друга.
Отношение и баланс пространства
Если вы хотите добавить в свои фотоработы побольше смысла, в некотором роде увеличить их эмоциональное воздействие на зрителя, то постарайтесь разобраться с пониманием пространства. В некоторых случаях, композиционно фотографии могут быть на первый взгляд достаточно просты. Вот как эти, например. Что тут важнее всего? Правильно. Близость зрителя к показанной автором скамейке и наличием пространства, а точнее даже, пустоты непосредственно за ней. Подобного рода композиционное построение кадра позволяет зрителю мысленно, на уровне подсознания воссоздать в своем представлении историю этого сюжета, основываясь на своих переживаниях, на своем личном опыте, на своих эмоциях.
Вот как эти, например. Что тут важнее всего? Правильно. Близость зрителя к показанной автором скамейке и наличием пространства, а точнее даже, пустоты непосредственно за ней. Подобного рода композиционное построение кадра позволяет зрителю мысленно, на уровне подсознания воссоздать в своем представлении историю этого сюжета, основываясь на своих переживаниях, на своем личном опыте, на своих эмоциях.
Не пожалейте своего времени для того, чтобы разобраться со всем тем, о чем мы вам сегодня рассказали. Постарайтесь понять, как влияют геометрические элементы на композицию изображения на плоскости. Возможно, это понимание придет к вам не сразу. Но это совсем не страшно. Главное, нам кажется, что мы, так сказать, посеяли свое семечко. Вам же осталось дожидаться сначала всходов, а через некоторое время и плодов.
Выберите один-два лучших наброска и заключите их в рамки, пропорции которых соответствуют пропорциям будущего рисунка. Так, лист формата А-3 размером 30 на 40 сантиметров имеет пропори 3 к 4 (рис 172) В поисках наиболее удачной композиции листа, вам возможно, придется корректировать точку зрения, а в некоторых случаях даже вносить изменения в саму постановку.
Компонуя лист, следует также учитывать расположение освещенных и теневых поверхностей, а также границы падающих теней. Помните, что светотень может нарушить композиционную гармонию линейного рисунка.
Стадия 1.
Рисунок 173 Начиная рисунок на большом листе, постарайтесь достаточно точно перенести на него расположение предметов, зафиксированное в лучшем эскизе. Наметьте место каждого геометрического тела легкими линиями. Еще раз проверьте размер всей композиции, а также ее соответствие размеру листа. Внесите необходимые изменения в рисунок и продолжайте работу, уточняя размер каждого геометрического тела по отношению к другим телам и ко всей композиции в целом.
Стадия 2.
Рисунок 174. Изобразите линейно все геометрические тела. В ходе работы уделяйте особое внимание соответствию раскрытия квадратов и эллипсов, лежащих в горизонтальных и вертикальных плоскостях.
Стадия 3.
Рисунок 175. На этой стадии необходимо усилить те линии, которые находятся ближе к зрителю, таким образом, вы создадите эффект глубины пространства уже в линейно-конструктивном рисунке. Наметьте линии собственных и падающих теней и прокройте все тени легким штрихом.
Наметьте линии собственных и падающих теней и прокройте все тени легким штрихом.
Стадия 4.
Рисунок 176. Продолжайте работу в тенях, делая их интенсивнее по направлению к зрителю и к источнику света, а падающие тени еще и к предмету, отбрасывающему тень. Постепенно переходите к работе в свету. Тщательно моделируйте форму, используя знания о распределении светотени на геометрических телах. На круглых поверхностях создавайте плавные светотеневые переходы; на телах, образованных плоскостями, — резкие и четкие.
Сравнивая светлые и темные тона гипса в натуре, нужно стремиться верно передать их отношения на рисунке, однако необходимо знать и об особых приемах, помогающих рисовальщику создать ощущение трехмерного пространства на плоском листе:
1. Разделение тональной шкалы на световую и теневую части: на рисунке самое светлое место в тени должно быть темнее самого темного места в свету, иными словами, тень всегда должна быть темнее, чем свет. В натуре это не всегда так. Например, когда рядом с постановкой находится достаточно хорошо освещенная поверхность, рефлексы от нее на натуре могут быть такими же яркими, как свет. Их необходимо «притушить», сделав темнее, иначе на вашем рисунке они будут разрушать форму изображаемых предметов.
Например, когда рядом с постановкой находится достаточно хорошо освещенная поверхность, рефлексы от нее на натуре могут быть такими же яркими, как свет. Их необходимо «притушить», сделав темнее, иначе на вашем рисунке они будут разрушать форму изображаемых предметов.
2. «Воздушная перспектива». Это явление, о котором мы уже упоминали, в натуре можно наблюдать на больших расстояниях, когда значительно удаленные от зрителя предметы выглядят менее контрастными за счет толщи воздушной среды, ослабляющей тени и утемняющей свет. При незначительных размерах изображаемой постановки нельзя наблюдать этот эффект. Он создается в рисунке искусственно: геометрические тела, находящиеся на первом плане, имеют больший контраст между светом и тенью, чем тела, находящиеся на дальнем плане, в то время, как на натуре разница в освещенности ближних и дальних планов может быть почти незаметна.
Главная задача архитектурного рисунка — не передача состояния объекта, а по возможности вер
ное изображение формы, создание объема. Именно поэтому, рисуя, мы не копируем натуру, а стараем
Именно поэтому, рисуя, мы не копируем натуру, а стараем
ся увидеть, отобрать и перенести в свою работу лишь определенные черты, которые помогают нам ре-
шить эту задачу.
Стадия 5.
Рисунок 177. Обобщите рисунок. Еще раз внимательно проследите за тональным решением освещенных и теневых поверхностей. На финальной стадии рисующий работает не с отдельным предметом, деталью, частью изображения, но со всем листом одновременно, добиваясь цельности работы, гармоничной соподчиненное™ ее частей. Для этого, при необходимости, усильте тон освещенных поверхностей на дальних планах и теневых поверхностей на первом плане.
70 глава III
72 глава III
светотеневой рисунок простых геометрических тел 73
74 глава III
Линейно-конструктивный рисунок композиции из геометрических тел по представлению.
Сделайте эскиз композиции, соблюдая заданные пропорции геометрических тел (рис.178). Определите общий характер будущей композиции, положение линии горизонта, направления горизонтальных ребер, основные врезки. Сразу предупредим вас о характерной ошибке, которую часто совершает тот, кто работает над своей первой композицией по представлению. Размещая на листе геометрические тела, начинающий рисовальщик достаточно вольно ставит рядом круглые тела (например, шар и конус) или круглые тела и тела, имеющие наклонные плоскости (например, шар и шестигранную призму). Врезки таких тел друг в друга очень сложны. Учитывая ограниченное время выполнения экзаменационного задания, было бы правильнее использовать в композиции простые врезки, когда круглые тела и тела с наклонными поверхностями пересекаются горизонтальными и вертикальными плоскостями.
Сразу предупредим вас о характерной ошибке, которую часто совершает тот, кто работает над своей первой композицией по представлению. Размещая на листе геометрические тела, начинающий рисовальщик достаточно вольно ставит рядом круглые тела (например, шар и конус) или круглые тела и тела, имеющие наклонные плоскости (например, шар и шестигранную призму). Врезки таких тел друг в друга очень сложны. Учитывая ограниченное время выполнения экзаменационного задания, было бы правильнее использовать в композиции простые врезки, когда круглые тела и тела с наклонными поверхностями пересекаются горизонтальными и вертикальными плоскостями.
Не стоит излишне тщательно прорисовывать эскиз — в мелком масштабе вы все равно не сможете решить все композиционные вопросы. Даже очень подробно проработанный эскиз невозможно точно перенести на большой лист. Второстепенные и незначительные по размеру элементы неизбежно подвергнутся довольно серьезным изменениям, а потому не стоит уделять им излишнее внимание на стадии эскизирования. Заключите эскиз в рамку соответствующих пропорций (3×4), внесите необходимые коррективы в композицию и приступайте к работе над листом большого формата, стараясь сохранить определенные в эскизе главную идею, основные закономерности и движения крупных масс.
Продолжая работу над композицией, уточните размеры и пропорции геометрических тел. Проследите за соответствием раскрытия квадратов и окружностей, лежащих в горизонтальных и вертикальных плоскостях, а также за равномерным схождением параллельных линий в перспективе. Внимательно простройте врезки геометрических тел, изображая линии пересечения не только видимых, но и невидимых зрителю поверхностей. Работая над отдельными элементами, старайтесь подчинить их общей композиционной идее, добивайтесь цельности и гармоничности в работе.
Рисунок должен быть выполнен четкими, выразительными линиями и легко проработан условным тоном: определите положение источника света и прокройте несколькими слоями штриха поверхности, оказавшиеся в тени. Рассмотрите рисунки 179,180,181,182,183, изображающие примеры таких композиций.
светотеневой рисунок простых геометрических тел
светотеневой рисунок простых геометрических тел 77
светотеневой рисунок простых геометрических тел 70
80 глава IV
Глава IV. Рисунок архитектурных деталей
К архитектурным деталям относятся архитектурные профили (гусек, каблучок, вал, четвертной вал, выкружка, скоция), геометрические и растительные орнаменты, капители, розетки, вазы, ионики, кронштейны, опорные и замковые камни арок, антаблементы. Из всего этого многообразия для выполнения учебных рисунков на вечерних подготовительных курсах МАРХИ выбраны ваза, капитель и ионик.
Приступая к рисунку архитектурной детали, сначала определите ее геометрическую основу, представьте сложную форму в виде сочетания простых геометрических тел. Изобразив на листе упрощенную схему в перспективе, постепенно усложняйте ее, насыщая деталями и внимательно изучая в линейно-конструктивном рисунке отдельные элементы. Парные симметричные объемы намечайте одновременно, при этом условии легче проследить за перспективными сокращениями. Если изображение какой-либо части архитектурной детали вызывает у вас некоторые затруднения, сделайте ее небольшие зарисовки на полях вашего рисунка — перспективные наброски с разных точек и ортогональные проекции. Завершая линейную стадию, введите в рисунок легкий тон, предварительно наметив линии собственных и падающих теней: это позволит вам уточнить основные массы и выявить возможные ошибки перед началом тональной работы.
Светотень на архитектурных деталях также распределяется по законам рисования простых геометрических тел. На кривых поверхностях переходы от света к тени мягкие, постепенные, на граненых — резкие, чёткие. Чем ближе свет и тень на предмете к рисующему и источнику света, тем сильнее светотеневой контраст, и, наоборот, удаленные части предметов имеют более тусклый свет и блёклую тень. Падающие тени сильнее насыщены тоном, собственные — высветлены рефлексами, а поэтому более воздушны и прозрачны. И в линейно-конструктивном и в светотеневом рисунке старайтесь вести работу равномерно по всему листу, постоянно сравнивая отдельные части изображения с целым. На заключительной стадии уточните тональное решение и обобщите работу, стремясь к ощущению завершенности и гармонии.
Рисунок вазы.
В качестве объекта для рисования вам предлагается гипсовый слепок с греческой вазы (амфоры), датируемой IV веком до н.э. Мастеров того времени отличало удивительное чувство пропорций и конструктивной логики.
Начните рисунок вазы, как и рисунок любой сложной архитектурной детали, с анализа её формы. Внимательно рассмотрите вазу (рис.184). Мысленно расчлените её на отдельные объемы и сравните их с простыми геометрическими телами. Тело вазы имеет сложную каплеобразную форму, которую можно условно представить как сочетание двух шаров и конуса, таким образом, контур тела вазы по высоте может быть разбит на три части, каждая из которых имеет свою кривизну. Шейка вазы сходна с цилиндром, имеющим заметное утонение в середине, и ограничена сверху и снизу узкими полочками. Венчает вазу массивная горловина в форме четвертного вала. Опорная часть (основание) вазы состоит из двух цилиндров разного диаметра, соединённых профилем в виде гуська. Ручки вазы имеют сложную трехчастную структуру и утолщаются в местах их присоединения к шейке и телу вазы.
Продолжая изучение натуры, сделайте рисунок фронтальной проекции вазы. Для этого вам придётся воспользоваться не только методом визирования, но и длинной полоской бумаги и даже линейкой. Проекция должна быть достаточно крупной, только тогда вы сможете отразить в ней всю полученную вами информацию: пропорциональное соотношение основных масс, размеры отдельных частей по высоте и ши-
рисунок архитектурных деталей 81
рине, их взаимосвязь, соподчинённость и функциональную обоснованность. Постарайтесь достаточно точно передать пропорции вазы, отметьте, сколько раз её ширина укладывается в высоте, сколько раз шейка укладывается в теле вазы по горизонтали и вертикали, и т.д. (рис.185).
Изобразив фасад вазы, вы заметите, что на этой проекции шейка вазы выглядит слишком толстой, тело — более массивным, основание — легче и изящнее, чем в натуре. Из всех способов изображения перспектива является наиболее близким к реальному восприятию человеческим глазом. Ортогональная проекция объекта всегда отличается от его восприятия в натуре. Но именно ортогональные проекции, в силу их точности и информативности, помогут вам сейчас наилучшим образом изучить сложную архитектурную форму, а в будущем станут удобным и естественным средством вашего профессионального общения.
Вернёмся к натуре. Как вы уже заметили, основной объем вазы — симметричная форма. Все её горизонтальные сечения представляют собой окружности разного диаметра с центром, лежащим на одной вертикали (ось вазы). В перспективном рисунке эти окружности изображаются в виде эллипсов разного размера и раскрытия. Малые оси этих эллипсов совпадают с осью вазы, а большие ей перпендикулярны.
Меняя своё положение относительно натуры по вертикали (а, следовательно, уровень линии горизонта), проследите за сокращением вертикальных размеров отдельных элементов и всей вазы, а также за тем, как одни части вазы перекрывают другие.
Выберите точку, при взгляде с которой перспективные вертикальные сокращения будут незначительными (например, когда линия горизонта проходит несколько выше горловины вазы или ниже её основания). Положение, когда линия горизонта проходит через тело вазы не рекомендуется по причине некоторых сложностей, которые могут возникнуть у начинающего рисовальщика с определением раскрытия эллипсов. К тому же, такое положение является наименее удачным для создания выразительного рисунка.
| |
82 глава IV
Стадия 1.
Рисунок 186. Определите габариты вазы на листе, посередине листа наметьте её ось. Разбейте общий вертикальный размер на отрезки, соответствующие крупным частям вазы: горловине, шейке, телу, основанию. Наметьте ширину этих элементов.
Стадия 2.
Рисунок 187. Обозначьте на рисунке положение и размеры мелких деталей вазы.
Стадия 3.
Рисунок 188. Наметьте контур вазы в ортогональной проекции. Такой контур не учитывает перспективных изменений, но является четкой конструктивной основой для дальнейшей работы.
Стадия 4.
Рисунок 189. На горизонтальных осях, в местах характерных сечений, изобразите эллипсы. Помните, что раскрытие эллипса тем больше, чем дальше он находится от линии горизонта. Соедините эллипсы касательными дугами в местах сопряжения одной формы с другой. Наметьте ручки вазы, обобщив их до простой прямоугольной формы, и только убедившись в правильности основных отношений, проработайте их детали.
Стадия 5.
Рисунок 190. Последний этап — тональная проработка. Начните, как обычно, с определения линий собственной и падающей тени. Для этого воспользуйтесь натурой и уже полученными знаниями о характере светотени на простых геометрических телах. Собственные тени на шейке вазы, поясках, полочках основания, а также ручках — аналогичны теням на цилиндре; тень на горловине подобна тени на шаре; тень на теле вазы можно представить как сложное сочетание тени на двух шарах и конусе. Внимательно рассмотрите падающие тени на вазе. Проанализируйте, от каких форм падают тени на шейку вазы, её тело, основание, ручки. Иногда это удобно сделать при помощи карандаша. Если медленно передвигать острие карандаша по линии собственной тени на вазе, тень от острия карандаша будет также передвигаться по линии падающей тени, фиксируя в каждый момент этого движения некую пару: точку и тень от неё.
После определения положения линий собственных и падающих теней, продолжайте тональный рисунок в обычной последовательности. Сначала наберите достаточную силу тона в тенях, отделив их от света. Затем необходимо усилить собственные тени по направлению к зрителю и источнику света, а падающие тени — еще и по направлению к источнику падающей тени. Продолжая работу в тенях, постепенно выходите в сеет, создавая плавные светотеневые переходы на шарообразных и цилиндрических поверхностях. Завершая рисунок, обобщите светотеневые отношения, стараясь гармонично подчинить все элементы изображения общему тональному замыслу.
Предлагаемая вам стадийность ведения работы не случайна: в ней заключено важное правило, обязательное для всех, а особенно для начинающих рисовальщиков: ведение рисунка от общего к частному и от частного к общему. Всегда начинайте рисунок с общей массы и лишь потом приступайте к деталям. Но не прорабатывайте сразу одну из деталей до конца. Ведите рисунок по всему листу, переходя от одной его части к другой, сверяя части с общим, постоянно охватывая взглядом целое. Это правило верно как для линейно-конструктивного, так и для светотеневого рисунка.
Естественно ваше желание как можно быстрее увидеть окончательный результат, перескочить на следующий этап, не закончив предыдущего. Если хотите — попробуйте сделать это — и увидите, как логичная и спокойная работа превратится в хаотичное метание от одной детали к другой в стремлении собрать воедино «рассыпающийся» у вас на глазах рисунок.
Помните также о том, что конструкция лежит в основе любой формы. Ошибки в построении невозможно скрыть самой виртуозной тональной проработкой. Поэтому обнаруженные в ходе работы ошибк в построении и пропорциях необходимо незамедлительно исправлять.
рисунок архитектурных деталей 83
86 глава IV
рисунок архитектурных деталей 87
88 глава IV
Рисунок дорической капители.
Капителью называется верхняя часть колонны, которая, в свою очередь, является частью архитектур, ного ордера. Ордер — строго выверенная художественная система, выражающая суть работы стоечно-балоч-ной конструкции. Название ордер происходит от латинского «ordo» — строй, порядок. Классические ордера — дорический и ионический — сформировались в античной Греции. Несколько позднее, в архитектуре Рима они получили свое дальнейшее развитие. Ордер состоит из несущих и несомых элементов, нагрузка передается от вышележащих элементам к расположенным ниже. От антаблемента (несомой части) к колонне (несущей) нагрузка передается через капитель, которая становится одной из важнейших составляющих всей ордерной композиции.
В качестве объекта для рисования вам предлагается капитель римского дорического ордера. Римские ордера несколько суше по своим формам, чем греческие, однако, как и все ордерные системы, они отличаются строгой логикой формообразования, выверенностью пропорций и простотой. Дорический ордер — самый лаконичный, строгий и мужественный из всех. Начинающему архитектору необходимо учиться понимать и чувствовать логику работы конструкции, выраженную в художественной форме, что в архитектуре называется тектоникой. Постарайтесь почувствовать в рисунке капители, как форма изменяется от верхних, квадратных в плане частей, к нижним, круглым, как каждый из профилей рассчитан на поддержку расположенных выше элементов и на передачу давления сверху вниз.
Начните рисунок с анализа формы капители (рис.191). Верхняя часть капители — квадратная в плане абака (абак) — плита с каблучком и полочкой. Эхин представляет собой четверть вала и сопрягается с шейкой колонны через три последовательно уменьшающихся пояска. Астрагал, состоящий из валика и полочки, переходит в ствол колонны через выкружку. Ствол колонны декорирован двадцатью длинными полукруглыми в плане бороздками — каннелюрами, имеющими полукруглые же завершения.
Сделайте рисунок фронтальной проекции капители. Рисунок должен быть достаточно крупным, чтобы детали были хорошо видны. Подпишите на рисунке названия всех частей капители. Так вам будет проще их запомнить. Проанализируйте основные пропорции капители, выберите в качестве единицы измерений общую высоту эхина и поясков. Сравните свой рисунок с рисунком 192.
Продолжая изучать форму, обойдите капитель вокруг и рассмотрите её с разных точек. Вы заметите, что основной объём, представляющий собой круглую симметричную форму, остаётся без изменений. Меняется лишь положение квадратной абаки. Выберите такую точку зрения для рисунка, чтобы одна сторона абаки была раскрыта для вас больше, а другая — меньше. Оптимальное соотношение 1/2-1/3. Линия горизонта должна проходить чуть ниже капители, тогда её пропорции будут близки к ортогональным. При необходимости сделайте эскиз, чтобы точнее определить композицию листа.
рисунок архитектурных деталей
Стадия 1.
Рисунок 193. Разместите на листе будущее изображение, определив его габариты по вертикали и горизонтали. Наметьте углы абаки, главную ось, а также определите размеры, соответствующие основным частям капители. Очень важно на этой стадии линейного рисунка найти верное соотношение раскрытия верхнего эллипса эхина и квадрата абаки. Традиционно, рисовальщики изображают сначала абаку, а затем испытывают значительные трудности при вписывании в неё эллипса. Поступите иначе: определившись с размером и раскрытием эллипса, нарисуйте его. Затем опишите вокруг эллипса квадрат, сверяя направления его сторон с натурой. Стадия 2.
Рисунок 194. Разметьте все части капители по вертикали и определите их горизонтальные размеры. Прорисуйте основные массы с учётом перспективных сокращений. Изображая эллипсы поясков, шейки, астрагала и нижнего среза колонны, соотнесите их раскрытия друг с другом и с уже нарисованным верхним эллипсом эхина. Стадия 3.
Рисунок 195. Прорисуйте каннелюры. Грамотно их изобразить вам поможет план ствола колонны. Если у вас нет возможности поместить план на самом рисунке, то подколите к вашей работе дополнительный лист бумаги. Перенесённые с плана на перспективное изображение точки сделают рисунок точным и убедительным. На этой стадии рисунок в основном носит линейный характер, но при уточнении основных элементов возможно применение тона, который помогает графически выявить «движение» основных поверхностей. При этом тон должен быть очень лёгким, предполагающим дальнейшую конструктивную проработку формы. Стадия 4.
Рисунок 196. Выявите форму капители средствами светотени. Ясное представление о взаимном Расположении в пространстве источника света, объекта и рисующего, даёт возможность разобраться в геометрии собственных и падающих теней, а также выявить основные тональные отношения. Определяя линии собственных и падающих теней, воспользуйтесь знаниями о характере светотени на простых Формах: мысленно расчлените капитель на отдельные объемы и сравните их с уже известными вам гео-метрическими телами.
Стадия 5.
Рисунок 197 Детально проработайте формы в тенях и на свету, обобщите светотеневые отношения
изображения, гармонично соподчините их между собой с учётом воздушной перспективы.
92 глава IV
рисунок архитектурных деталей 93
94 глава IV
рисунок архитектурных деталей 95
Рисунок ионика.
Ионик — архитектурный орнаментальный элемент, состоящий из срезанной сверху яйцеобразной формы, обрамленной «скорлупкой», профилированным валиком, а также обращенными острием вниз стрельчатыми листьями. В архитектуре ионики широко применяются на капителях и карнизах ионического и коринфского ордеров. Ионик имеет две оси симметрии, одна из них проходит по яйцеобразной форме, другая — по середине стрельчатого листа. Изучая форму, сделайте план, фасад и боковой фасад (рис.198). Это поможет вам лучше понять структуру ионика, а также значительно облегчит дальнейшую работу над рисунком.
Стадия 1.
Рисунок 199. Наметьте габариты будущего изображения на листе. Изобразите в перспективе прямоугольную плиту, являющуюся основой для ионика.
Стадия 2.
Рисунок 200. Проведите диагонали плиты основания ионика и простройте вертикальную среднюю линию — главную ось симметрии. Обобщенную форму ионика представьте в виде сплошного четвертного вала со скошенным верхом, к которому снизу примыкает маленький валик. Прорисуйте на верхней поверхности ионика его план, отделите центральный яйцеобразный объем от боковых объемов, наметьте оси симметрии, проходящие по центру стрельчатых листьев, и уточните главную ось. На этой стадии особое внимание обращайте на перспективное сокращение равных по длине горизонтальных отрезков.
Стадия 3.
Рисунок 201. Прорисуйте детали — яйцо, скорлупки, профилированный валик, листья. Изображая листья, сделайте на полях их крупный вид спереди (рис.202). Это поможет вам правильно нарисовать листья в перспективе.
Стадия 4.
Рисунок 203. Нанесите линии собственных и падающих теней. Начните, как обычно, с теневых мест и проштрихуйте их несколько раз, отделяя от света. Затем необходимо усилить падающие тени по направлению к предмету, отбрасывающему тень, зрителю и источнику света. Одновременно усильте линии собственных теней, формируя зоны рефлексов. На этой стадии не увлекайтесь деталями, «лепите» общую форму в соответствии с законом воздушной перспективы и основными принципами распределения светотени на простых геометрических телах.
Стадия 5.
Рисунок 204. Продолжая работу, переходите клепке крупной формы в свету и затем к деталям. Завершите рисунок обобщением формы, гармоничным соподчинением всех ее частей.
| |
| |
98 глава IV
рисунок гипсовой головы 99
Рисунок гипсовой головы
Голова человека — сложнейшая природная структура. Это обусловлено ее сложной функцией в организме человека. Приступать к рисунку головы можно, только имея достаточно развитое пространственное представление, основательное знание общих положений рисунка и хорошую практику в изображении более простых форм.
Практический раздел «Рисование гипсовой головы» начинают с исследования ее внешней формы в «ознакомительном рисунке». Этот первый опыт станет основой дальнейшего, более подробного анализа. В рисунке черепа анализируют структуру костной основы головы. В рисунке экорше Гудона изучают расположение и принцип работы основных мышц, а также хрящевидные ткани. Для подробного рассмотрения черепа и мышц будет целесообразно обратиться к анатомическим атласам и пособиям. В следующих рисунках особое внимание уделяют основным деталям головы: носу, губам, глазам и уху. И, наконец, возвращаясь к рисунку гипсовой головы на новом уровне понимания ее архитектоники (т.е. взаимосвязи внутренней структуры и внешней формы), вы сможете закрепить и постепенно совершенствовать свои навыки в рисунках гипсовых слепков с античных скульптур: Цезаря, Афродиты, Дорифора, Диадумена, Сократа, Антиноя и Апоксиомена, традиционно предлагаемых для рисунка на вступительных экзаменах в Московском Архитектурном институте.
Рисование «антиков» — продолжение старых академических традиций. Пластическое совершенство классической скульптуры, ее статичность и необыкновенная выразительность позволит вам быстрее понять общую объемно-пространственную структуру головы, разобраться в ее деталях и основных соразмерностях.
24. Ознакомительный рисунок. Голова Дорифора.
Скульптура Дорифора создана в V веке до нашей эры греческим скульптором Поликлетом, представителем пелопонесской школы. Поликлет был не только скульптором, но и теоретиком искусства. Им был создан трактат «Канон», где очень подробно разрабатывались идеальные пропорции человеческого тела. Фигура Дорифора — юноши воина-гоплита (копьеносца) — явилась воплощением этого канона. Одновременно она должна была стать олицетворением идеального гражданина греческого полиса: человека, подобного бессмертным богам, равно прекрасного телом и духом, мужественного защитника родного города. Лицо Дорифора схематично, оно лишено индивидуальных черт и выражения, именно поэтому голова Дорифора предлагается для первой «ознакомительной» работы, в результате которой вы получите начальное, во многом упрощенное представление о форме головы.
Голова имеет мозговую и лицевую части. Ее внешняя пластика познается с помощью целого ряда анатомических точек — узлов (опорных точек или маяков) и линий. Так, на голове хорошо видны: подбородочные бугры, линия нижней челюсти, углы рта, линии, ограничивающие область рта, линия разреза губ, фильтр, основание, кончик и крылья носа, переносье, скулы, скуловые дуги, глазничные края, слезники, бровные дуги, линии, ограничивающие бровные дуги, лобные бугры, височные линии, макушка, ушные раковины, слуховые отверстия, сосцевидные отростки височных костей, теменные и затылочные бугры, выйная линия, граница шеи и подбородка, яремная ямка и выступ седьмого шейного позвонка. Найдите все эти точки и линии на рисунках 205 и 206, а затем и на гипсовой голове.
Зная анатомические пункты — маяки и характерные линии, вы никогда не запутаетесь в деталях и всегда сможете отличить главное от случайного. Для лучшего понимания внешних пространственных связей точек головы часто пользуются упрощенной схемой, представляющей ее структуру в виде неправильного многогранника. Нельзя, однако, злоупотреблять подобными схемами в рисунке. Они необходимы лишь в качестве наглядных пособий для грамотного и убедительного изображения головы человека.
100 глава V
рисунок архитектурных деталей 101
Прорись с рисунка П.И.Чурилина
из учебного пособия «Строение головы человека»
102 глава v
Прорись с рисунка ПИЧурилина
из учебного пособия «Строение головы человека»
Голову человека также принято изучать, анализируя ее разрезы в трех взаимно-перпендикулярнь плоскостях: сагиттальной, горизонтальной и фронтальной (рис.207).
Сагиттальная плоскость является плоскостью симметрии тела. Ее название происходит от латинского «sagttta» — стрела. Разрез в этой плоскости дает нам среднюю линию, которая является основой проф» ш ной линии лица и очень важна для рисунка головы.
Горизонтальная плоскость проходит через основание затылка и основание носа.
Фронтальная плоскость перпендикулярна двум первым и «рассекает» голову в самом широком месте. Она проходит через макушку, теменные бугры и точки опоры черепа на позвоночник. Изучение этих разрезов, а также ортогональных проекций головы: вида спереди, сзади, сбоку и сверху поможет вам лучше понять внешнюю пластику головы и точнее передать ее в вашем рисунке.
рисунок гипсовой головы 103
Задача «ознакомительного» рисунка — хорошая композиция на листе, верно переданный общий объем, а также точно найденное место и размер каждой детали головы.
Стадия 1.
Рисунок 208. Начиная работу, определите положение линии горизонта и ракурс. Для этого мысленно заключите голову в куб. Найдите общие габариты и разместите будущее изображение на листе при помощи коротких засечек. Помните, что если вы рисуете голову в фас — пространства слева и справа должны быть равными, чтобы изображение не «заваливалось», если же вы рисуете голову в профиль, в 3\4 или в 7\8 — пространство листа перед головой (со стороны лица) должно быть больше, чем со стороны затылочной части. Легкими линиями наметьте контур головы (абрис).
Стадия 2.
Рисунок 209. Прорисуйте основные крупные части: отделите массу головы от шеи, наметьте лицевую часть, ее переднюю плоскость и легко нанесите осевую профильную линию. Уточняя профильную линию, найдите лежащие на ней характерные точки: точку верха лба (на линии роста волос), точку между бровями, точку основания крыльев носа и точку перелома подбородка. Этими точкам определяются основные канонические пропорциональные отношения частей головы. Согласно греческому классическому канону, расстояния между этими точками должны быть равными. Проведите через эти точки горизонтальные линии (на рисунке уходящие в точку схода на горизонте) и отметьте на них соответственно ширину лба, основания носа и подбородка. Для правильного выбора направлений этих линий, воспользуйтесь методом визирования.
В соответствии с античным каноном, по линии глаз античная голова делится на две равные части -от макушки до линии глаз и от линии глаз до основания подбородка. Отрезок от надбровных дуг (точки между бровями) до основания крыльев носа делится на три равные части — по верхней линии деления проходит линия глаз, по нижней — отделяются основание и крылья носа. Отрезок между точкой основания крыльев носа и переломом подбородка также делится на три равные части. По верхней линии деления проходит средняя линия рта, которую еще называют линией разреза губ, нижняя линия делит подбородок пополам. Расстояние между глазами равно длине глаза, т.е. линия глаз также делится на три равные части. Высота уха равна длине носа.
©2015-2019 сайт
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-02-13
Раздел долгосрочного плана: 1В: Геометрические фигуры.
| Школа: | |||||||||||||||||||
Дата: | ФИО учителя: | |||||||||||||||||||
Класс: 1 | Количество присутствующих: | Отсутствующих: | ||||||||||||||||||
Тема урока: Построение плоских геометрических фигур(2). | ||||||||||||||||||||
Цели обучения | 1.3.1.различать плоские фигуры (треугольник, круг, квадрат, прямоугольник) / пространственные фигуры (куб, шар, цилиндр, конус, пирамида) и соотносить их с предметами окружающего мира. | |||||||||||||||||||
Цели урока | · Различать плоские и пространственные фигуры · Создавать композицию из плоских фигур. | |||||||||||||||||||
Критерии оценивания | · Различает плоские фигуры (треугольник, круг, квадрат, прямоугольник) и пространственные фигуры (куб, шар, цилиндр, конус, пирамида) · Создает композицию из плоских фигур. | |||||||||||||||||||
Языковые цели
| Предметная лексика и терминология: плоские геометрические фигуры, треугольник, круг, квадрат, прямоугольник,пространственные фигуры, куб, шар, цилиндр, конус, пирамида, композиции из моделей плоских фигур и их частей. | |||||||||||||||||||
Привитие ценностей
| Воспитание уважения к мнению других, умение слушать и сотрудничать. Воспитание интереса к изучению математики. | |||||||||||||||||||
Межпредметные связи | Искусство: учащиеся должны уметь рисовать, использовать геометрические фигуры и шаблоны. Познание мира: наблюдение за объектами окружающего мира. | |||||||||||||||||||
Навыки использования ИКТ | Просмотр презентации. | |||||||||||||||||||
Предварительные знания
| Знает геометрические фигуры, тела. Определяет их сходство и различия. | |||||||||||||||||||
Ход урока | ||||||||||||||||||||
Запланированные этапы урока | Запланированная деятельность на уроке
| Ресурсы | ||||||||||||||||||
Начало урока 0-13 минут
| 1.Утренний круг. Математика сложна, Но говорим с почтением, Что математика
нужна 2. (К)Актуализация. Устный счет. Игра «Молчанка» (ответы показываются на веере цифр) — назови число, которое следует за числом 5, 15.25. — назови число, которое стоит перед числом 7,17,27 — назови соседей числа 10,30,50.
«Продолжи по закономерности» 1,3, 5, 7,….(9,11,13) 2,12,22,32,42,…(52,62,72) 3,5,6,10,9,15(12,20,15,25) — Обоснуй ответ.
Повторить состав чисел 12-14. 14=__+__ 13=__+__ 12=___+___
3. Повторение. Просмотр видеоролика «Учим геометрические фигуры и тела с паровозиком Чух-Чухом»
4. (Г) Игра «Таинственный чертёж» Определить по чертежу что за фигура загадана. — Из каких плоских геометрических фигур состоит эта фигура? (круг и треугольник.) -Какое объемное тело спряталось на чертеже? (конус) -По каким особенностям ты догадался? (если в воображении соединить круг, как основание, а треугольник, как верхушка фигуры, то получится конус) -О чем пойдёт речь на уроке? (О геометрических фигурах)
Физминутка. | Презентация. Веер с числами.
Видеоролик.
Чертежи для игры «Таинственный чертёж» (с плоскими геометрическими фигурами).
| ||||||||||||||||||
Середина урока 13-35 минут
| -Сегодня на уроке мы будем делать плоские фигуры, посредством объёмных, и создавать композицию из них. (Д)Подготовительная работа. · Рассмотрите аппликацию «Зайчик» -Кто это? -Как вы догадались? -Из каких фигур состоит аппликация? -Посчитайте, сколько фигур? -Какие это фигуры?
· Повторить способ создания плоских фигур, посредством объемных: 1) выбрать фигуру. 2) обвести основание на цветной бумаге. 3) вырезать по контуру.
· Расширить представление учащихся о способах создания фигур путёмперекроя. 1) Из квадрата четыре треугольника ичетыре квадрата, два прямоугольника и т.д. 2) Из прямоугольника два квадрата, четыре треугольника 3) Из треугольника треугольник и трапецию и т.д. 4) Из квадрата круг, из прямоугольника овал (срезая уголки). · Рассмотреть аппликации животных, выполненных из плоских фигур. · Повторение ТБ при работе с ножницами.
(П)Практическая работа в парах. План работы: 1) Рассмотреть аппликацию или задумать свою. 2) Определить из каких фигур она состоит. 3) Вырезать необходимые геометрические фигуры. 4) Выложить композицию. 5) Наклеить. 6) Украсить узорами из геом. фигур.
Критерии оценивания работы:
Презентация своей работы в группах по 2-3пары. Взаимопроверка. Выставление баллов.
Выставка работ учащихся.
Физминутка.
(С, П) Работа в тетради с.55-56. Выполнение заданий на закрепление темы урока. Само оценивание в тетради по «Лесенке успеха»
|
Готовые аппликации животных из геом. фигур.
Картон, ножницы, линейки карандаши, клей, альбом.
Карточка- подсказка.
Учебник, рабочая тетрадь | ||||||||||||||||||
Конец урока 36-40 минут
| (К)Подведение итога урока: -Грань какой объемной фигуры надо обвести, чтобы получился квадрат? (куб) -Какая плоская фигура получится, если обвести грань параллелепипеда? (прямоугольник) Модели каких геометрических фигур можно сделать из квадрата, прямоугольника, треугольника, круга?
Рефлексия. Лесенка успеха (на доске).
| Магниты. | ||||||||||||||||||
Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности | ||||||||||||||||||
Используется метод дифференциации «Ускорение». Учащимся испытывающим трудности будет оказана поддержка одноклассниками, со стороны учителя инструктаж, и карточки –помощники. | ФО На каждом этапе урока будет обратная связь от учителя и учащихся.
| Физминутка, смена видов деятельности. Соблюдение гигиенических норм и правил пользования ИКТ, безопасности на уроке.
| ||||||||||||||||||
Конспект на тему Модели плоских фигур.1 класс
(К) Работа с учебником математики.
-Откройте учебник на стр.56-57.
-Обратите внимание на картинки в книге.
-Порассуждайте, из чего изготовлены геометрические фигуры?
-А из чего еще можно изготовить модели фигур?
(Г) Задание:Изготовить модель геометрической фигуры.
На ваших рабочих местах лежат геометрические фигуры (квадрат, круг, треугольник, прямоугольник.)
1гр.- изготавливает модель треугольника.
2 гр.- изготавливает модель прямоугольника.
3 гр.- изготавливает модель круга
4 гр.- изготавливает модель квадрата.
5 гр.- изготавливает любые три фигуры.
— Обсудите и расскажите в группе, как можно изготовить эти фигуры из трубочек или из счётных палочек.
-Выполните все шаги и объясните, как вы получили треугольник, квадрат, прямоугольник. При демонстрации своих моделей, используйте словосочетания: «модель треугольника», «модель квадрата», «модель прямоугольника».
Давайте повторим правила работы в группе.
Правила при работе в группе.
В группе есть спикер.
Каждый работает на групповой результат.
Спикер говорит, класс слушает.
Если есть вопросы, высказывай корректно.
-Что такое модель геометрической фигуры?
-Каждая группа презентует свою модель.
— Как же называются фигуры, которые мы уже знаем и которые помещаются на листе? (Плоские.) Назовите их.
— А как называются фигуры, которые вы лепили? (Объемные.)
-Молодцы. Вы хорошо потрудились.
А сейчас мы отдохнем.
(К) Физминутка .
(К) работа в тетради по математике. стр.55.
Модели плоских фигур (1)
Паровозик
-Посчитай фигуры, из которых состоит паровозик. Напиши количество фигур цифрами в таблице.
Формативное оценивание.
Цель: 1.3.2.3. составлять композиции из моделей плоских фигур и их частей.
Уровни мыслительных навыковКруг, треугольник и квадрат . Стоунхендж и пирамиды Египта
Легче других геометрических форм изобразить круг. Для этого достаточно циркуля или шнурка, колышка и маркера. Два взаимосвязанных круга можно получить, передвинув кончик циркуля на окружность первого круга и нарисовав второй равного размера. В образовавшейся весике могут быть получены три самых важных «корня»(√2, √3 и √5) (рис. 31).
Если принять радиус кругов за 1, тогда корень квадратный из двух (√2) может быть получен из диагонали квадрата, образованного линией между двумя центрами и двумя перпендикулярными к ней радиусами. Корень квадратный из трех (√3) образуется линией, соединяющей две точки пересечения кругов весики. Корень квадратный из пяти (√5) дает диагональ прямоугольника со сторонами 2 и 1. Этот прямоугольник можно использовать для обнаружения золотой пропорции (см. рис 35, на рис. 36, 37 и 38 показаны другие способы получения золотой пропорции). Позже мы увидим, что весика и пря моугольник со сторонами 2 и 1 служили ключом к получению древних единиц измерения.
Треугольник рассматривался как переходная форма между квадратом и кругом. Со временем он стал изображать триаду богов и богинь, обычно — как в Египте — отца, мать и сына. Эта концепция служит центральным стержнем многих религиозных систем и проявляет себя в христианстве в виде Бога Отца, Сына и Святого духа.
Идеальным считался равносторонний треугольник, в котором равны все стороны и углы. Широко использовался и другой треугольник, обычно приписываемый Пифагору, но явно существовавший задолго до него. Этот треугольник имеет стороны, выраженные целыми числами 3: 4: 5. Он является простейшим вариантом прямоугольного треугольника (90°) со сторонами, выражаемыми целыми числами. Благодаря простым отношениям чисел его использовали в топографии, а также в искусстве и скульптуре. На нем основана пирамида Хафры.
Круг, треугольник, квадрат и прямоугольник образуют основу культовой архитектуры. Они традиционно были связаны друг с другом особыми пропорциями. Последние призваны были отобразить собственную гармонию космоса.
Одна такая пропорция — «гномон» была определена Аристотелем следующим образом: «Любая фигура, которая, будучи добавленной к исконной фигуре, дает в результате фигуру, подобную исконной». Иными словами, сохраняются соотношения между всеми дополнительными шагами. Примером этого служит золотое сечение, которое может быть выражено числами 1, 1, 2, 3, 5, 8, 13, 23 и т д., где отношения между любыми двумя соседними числами быстро сходятся в одной точке по мере движения по ряду. Ряд Фибоначчи является самым известным примером гномонического отношения, но есть и другие.
Рис. 39. Гномоничесжие спирали, построенные из отношения квадрата 2:1
В своей книге «Священная геометрия» Роберт Лолор приводит примеры «гномонических» спиралей, подобных основанной на ряде Фибоначчи, полученной из отношения 1:2. Эти расширяющиеся схемы иногда называют «завихренными квадратами», поскольку они дают спирали, которые часто встречаются в природе (рис. 39).
Изучая «гномоны» с разными отношениями, я сделал важное открытие «Гномон», основанный на отношении 1:3, имеет непосредственное отношение к пирамидам Гизы. Получается, что из этого отношения могут быть получены основные пропорции пирамид Хуфу, Хафры и Менкаура (рис. 40). Все начинается с трех квадратов, соединенных в линию и образующих прямоугольник со сторонами 3 и 1. Затем чертится квадрат на длинной стороне на каждом этапе увеличения.
Первый квадрат образует прямоугольник с отношением сторон 3:4. При его удвоении получается отношение пирамиды Хафры — 6:4. При добавлении еще двух последовательных квадратов к прямоугольнику 3:4 получаем отношение пирамиды Хуфу — 7:11. Еще один добавленный квадрат дает пропорции пирамиды Менкаура — 11:18. Этот прием добавления квадратов к прямоугольнику 3:1 драматическим образом обнаруживает, что пирамиды отражают естественную математическую прогрессию в отношениях их высоты к основанию. Так или иначе, но они связаны гармоничным геометрическим рядом.
Что примечательного могло быть в отношении 3:1? Может быть, оно отражало символизм египетской троицы — Осириса, Исиды и Гора. Возможно, мы никогда этого не узнаем наверняка, но этот рисунок позволяет нам лучше понять методы египтян.
Это открытие согласуется с тем, что нам известно о египетских методах проектирования, которые, похоже, всегда основывались на схемах квадратной сетки. В египетском искусстве имеются многочисленные примеры, показывающие, что художники и скульпторы сначала рисовали сетку на стене, которую предстояло расписать или вырезать, для того чтобы сохранить установленные пропорции. Простые числовые отношения этих сеток служат сердцевиной всех великих художественных произведений египтян.
Тот же метод использовался многими художниками Возрождения, в том числе и Леонардо да Винчи. В Древнем Египте это нашло своевоплощение в Великой пирамиде, что и подкрепляется ее тесной связью с узором на Марлборо-Даунс.
Есть ли песни в которых упоминаются геометрические фигуры?
Чаще всего в песнях упоминаются такие геометрические фигуры, как круг и треугольник.
Круг.
Самая, наверно, известная песня — «Пусть всегда будет солнце!», которая часто публикуется под названием «Солнечный круг», сл. А. Островского, муз. Л Ошанина.
Круг символизирует связь единомышленников, дружеское братство:
«Орлятский круг» — вечерняя песня «орлят».
«У меня всё окей» — авторская песня рэпера из Белоруссии ЛСП (Савченко Олег Вадимович).
«Добрый жук» («Встаньте, дети, встаньте в круг.») из кинофильма «Золушка», сл. Е. Шварца, муз. А. Спадавеккиа.
«Ходит песенка по кругу» — сл. М. Танича, муз. И. Шаферана.
Песня Криса Кельми и Маргариты Пушиной о жизни «Замыкая круг».
О любви песня Ирины Салтыковой «Заколдованный круг».
Про треугольники обычно речь идёт в контексте любовных отношений, поэтому с названием «Любовный треугольник» песен найдётся больше десятка. Наболее известнаяиз них из к/ф «Приморский бульвар», муз. В Добрынина, сл. Л. Рубальской.
А ещё есть у Трофима (Сергей Трофимов), Антона Бизеева, «Фабрики звёзд».
Есть и «Любовный квадрат» у рэпера Колюни, и «Любовный многоугольник» — у «Фабрики звёзд».
Есть орлятская песня «Треугольник», сл. М. Пляцковского, муз. С. Туликова — о дружбе.
Со названием «Пирамида» или «Пирамиды» тоже есть несколько песен: у группы «Сплин», Анжелики Варум.
Со словом призма — «Призма нашей любви» исполняет Сергей Версаль, у рэпера h2Gh (Михаил Ключка) — «Призма времени».
Наверно, и с названием других геометрических фигур есть песни, если хорошо поискать.
Как развить в себе взгляд фотографа. Часть девятая
Девятой частью заканчиваются упражнения среднего уровня и начиная с десятой мы перейдём к развитию взгляда фотохудожника и вырабатывания собственного фотографического почерка. Поэтому тем, кто просто хочет иметь красивые картинки для домашнего фотоальбома, сайта, странички в «одноклассниках» уже достигнутого вполне хватит с лихвой. Тем же, у кого есть желание развиваться дальше и выйти на иной фотографический уровень, предстоит не лёгкий, но интересный путь. Упражнения девятой части, это ещё цветочки. Ягодки с десятой начнутся. Но, как и любые ягодки (образно говоря) они растут в разных местах. И за ними ещё походить надо будет.
В упражнении №24 мы работали с естественными рамками и осваивали фотосъёмку с использованием различных препятствий (съёмка сквозь что-то). Данный приём активно используется при фотосъёмке диких животных, позволяя создать эффект «присутствия».
Продолжим изучение способов выделения главного объекта (акцентирования). Теперь опираясь на отработанный материал и освоенные приёмы изучим другие варианты. Помимо техники создания акцента начнём осваивать законы композиции с помощью выполняемых упражнений.
Без неё никуда. Что главное в фотоснимке для простого зрителя? Красота, необычность, яркость? Тоже не последние параметры, но на первом месте стоит комфортность восприятия. Увидев какую-либо картинку, не обязательно фотографию, рекламный плакат или иллюстрацию, сначала мы оцениваем её на уровне подсознания. То есть, нравится – не нравится. А уж затем, если понравилось, начинаем разглядывать в деталях. Поэтому снимок должен быть удобен для восприятия (разумеется если автор не преследует иные цели). Это и достигается с помощью соблюдения законов композиции.
Упражнение №25 Базовые фигурыВообще выделяют три базовых фигуры. Это прямоугольник, треугольник и круг. Всё остальное – овал, квадрат, трапеция, эллипс, ромб всего лишь их вариации. Они отличаются друг от друга не только графически, но и (не удивляйтесь) эмоционально. Не понятно? Рассматривание этих фигур вызывает у человека различные чувства. Круг одни, треугольник другие, прямоугольник третьи.
Прямоугольник. Вариации прямоугольника – ромб, квадрат, трапеция. Наиболее устойчивая форма, квадрат. Он выражает утверждающие, весомые образы. Фигура тяжёлая, при некоторых условиях даже монументальная, ей чуждо движение и динамика.
Треугольник. Наиболее часто встречающаяся в природе форма. Посмотрите внимательно на сделанные вами фотографии, и вы увидите на них множество треугольных форм. Форма эта активная, развивающаяся, динамичная. При определённой постановке может подчеркнуть агрессивность образа. При любом положении треугольника, у него будут присутствовать как минимум две диагонали.
В положении вершиной вверх вызывает образы устойчивости, стабильности (пирамиды). В положении вершиной вниз – шаткое равновесие, балансировка. В отличие от прямоугольника, стороны не противостоят друг другу, а меняют направление развития. Это может быть использовано для создания конкретных образов. Треугольник естественным образом вносит в композицию ощущение глубины пространства.
Круг. Символ гармонии, спокойствия, помимо этого ассоциируется с мирозданием. Округлые формы, в плане восприятия несут в себе особую энергетику, сильно отличающуюся от энергетики предыдущих фигур. Данная форма направляет взгляд внутрь кадра.
Задание первое. Отправляемся на улицу и поочерёдно делаем снимки в последовательности – прямоугольник, треугольник, круг. Просто ищем и фотографируем фигуры.
Я выбрал достаточно обыденный объект, который можно повсеместно встретить на улицах города. Урны для мусора.
Хотя и среди них встречаются интересные вариации.
Когда достаточно поднаторели на фотосъёмке простых геометрических фигур переходим к поиску архитектурных форм, использующих геометрические орнаменты.
Ограды, решётки, элементы декора, необычно оформленные предметы уличного антуража.
Вот пример.
Задание второе. В первом задании мы искали и фотографировали геометрические фигуры, созданные людьми. Теперь займёмся творениями природы. Задача такая же, найти образы, созданные деревьями, камнями, облаками, водой. Одним словом, природные аналоги, составляющие пару снимкам, сделанным при выполнении первого задания.
Как видите человек не первооткрыватель. В этом плане природа его давно опередила.
Задание третье. Наиболее сложное. Необходимо выполнить фотопортреты людей, которые ассоциируются у вас с геометрическими фигурами. Нет, не внешностью, это было бы слишком просто. Характером. А чтобы было легче выполнить, приведу краткую психологическую характеристику каждой фигуры.
Квадрат – постоянный труженик. Трудолюбивый, усердный, внимательный к деталям и мелочам. Выносливый и терпеливый, методичный. Постоянно находится в поиске новой информации. Любит порядок и не любит перемен. Предпочитает предсказуемость, не приемлет «сюрпризов судьбы» и изменений привычного хода событий. Действует по плану и старается людей вокруг себя организовать таким же образом.
Треугольник – прирождённый лидер. Главная черта – способность концентрации на главной цели. Энергичен, неудержим, сильная личность. В отличие от квадрата, может игнорировать детали сосредотачиваясь на главном. Отсекая второстепенное он ориентирует мыслительный анализ на поиск наиболее эффективного решения. Очень уверен в себе, старается принимать решения не только за себя, но и за других. Часто идёт на риск, бывает нетерпим к тем, кто медлит в принятии решений.
Круг – самый лучший коммуникатор. Умеет выслушать. Обладает высокой чувствительностью, способностью сопереживать, сочувствовать. Он очень заботится о стабильности коллектива, в котором находится. Тяжело переносит межличностные конфликты. Всегда пытается сохранить мир и спокойствие. Он счастлив, когда все ладят друг с другом. Но если дело касается вопросов морали и справедливости, проявляет завидную твёрдость.
Более направлен на людей, чем на дело. Поэтому в коллективе зачастую выполняет роль связующего звена.
Вот вам характеристики трёх психотипов, хотя разумеется их гораздо больше. Просто я выбрал те, которые имеют наиболее яркую проявленость.
Упражнение №26 ЛинииС фигурами поработали, теперь займёмся линиями. Рассмотрим те, которые интересуют нас с точки зрения фотографии. Разновидностей линий три – прямая, ломаная и дуга. Остальное, зигзаг, S-образная кривая, парабола, угол, арка и т.д. всего лишь их вариации. Но в композиции, линии играют не меньшую роль, чем фигуры.
Какие основные задачи могут выполнять линии в кадре? Линии могут направлять, разделять, соединять, обрамлять, подчёркивать и акцентировать.
Направляющие линии. Всё понятно из названия, то есть направляет взгляд зрителя. К какому – либо объекту к которому хотели бы привлечь внимание или от переднего плана к фону.
Она может добавить движения в статичную фотографию или связать между собой различные элементы в ней.
Разделяющие линии. Наиболее яркий пример – это линия горизонта. С одной стороны, она разделяет кадр на землю и небо, озеро и лес, горы и равнину. Либо может делить кадр по диагонали или вертикали. Как понимаете, наиболее часто используется горизонтальное деление.
Обрамление, различные арки, дуги, ломаные кривые, все они могут создавать обрамление или выполнять акцентирующую роль.
Помимо этого, диагонали и дуги, а также другие незамкнутые кривые служат хорошими направляющими линиями.
Задание первое. Фотографируем различные линии. Прямые, кривые, ломаные. Нарабатываем навык.
Задание второе. Используем линии как элемент композиции. Попробуйте разные варианты – пейзаж, городская фотосъёмка, концептуальная фотография.
Задание третье. По традиции наиболее сложное. Линия как один из основных объектов в кадре. Не просто как вспомогательный элемент, а как неотъемлемая часть сюжета. То есть фотография должна быть выполнена так, что удаление из неё линии приведёт к полному изменению снимка.
Возьмём эту фотографию. Если убрать снежную дорожку из кадра, то дома, стоящие вдали просто потеряются на общем фоне.
Упражнение №27 Упорядочивание формУ каждого объекта форма своя. И сколько бы похожими они не казались, двух одинаковых не бывает. Однако с точки зрения фотографии нас интересуют менее явно выраженные формы. То есть те, которые подразумеваются, вызывая соответствующие ассоциации у зрителя. Или оставляют поле для размышления. Они хороши тем, что легко придают изображению узнаваемость. И хотя на первый взгляд кажется, что фигур бесконечное множество, как я уже и говорил ранее, базовых всего три – прямоугольник, треугольник, круг. Каждая из этих фигур тесно связана и графически, и эмоционально с линиями их образующими.
Прямоугольник – горизонтальные и вертикальные линии.
Треугольник – диагонали.
Круг – кривые.
С учётом того, что одна из основных задач линии, направить взгляд, то формы упорядочивают элементы изображения. А упорядоченное построение – суть любой композиции.
Задание первое. В двадцать пятом упражнении мы работали с базовыми фигурами. Вернёмся к ним, поищем и сфотографируем объекты, содержащие все три базовые фигуры. Самое простое, найти их в собственном населённом пункте. Там, где вы проживаете.
Думаете тяжело найти? Отнюдь. Вот вам наглядный пример. Данное сооружение содержит квадратные, прямоугольные, круглые, дугообразные, треугольные и прочие геометрические формы. Культовое сооружение.
А вот чисто городская постройка. Как видите тоже не отстаёт в плане многообразия.
Задание второе. Роль направляющих, разделяющих, обрамляющих и акцентирующих линий могут выполнять не только конкретные линии, но и складки одежды, предметы в руках, различные аксессуары.
Вот пример необычной линии – радуга.
Выходим на свежий воздух. Занимаем позицию где-нибудь в сторонке и фотографируем модели, соответствующие выше изложенным требованиям.
Пример ниже. В этом случае полозья санок и отскочившая ручка образовавшие ломаную линию акцентируют внимание на выпавшем из санок ребёнке.
Или другой пример. Граница растущей травы и дорожки образуют направляющую линию приводящую взгляд к девочке на санках.
Задание третье. Необходимо выполнить портрет одного из ваших знакомых использовав для раскрытия образа (или придания определённого образа) геометрические формы и направляющие линии.
Это могут быть украшения, детали одежды, предметы окружающие человека или те, которые он держит в руках. Поэкспериментируйте. Посмотрите, как за счёт изменения антуража, меняется восприятие.
Отработали? Порядок. Теперь вы достаточно поднаторели в области фотосъёмки и начиная с десятой части будем формировать собственный узнаваемый фотопочерк.
Треугольник, круг, квадрат… | Блогер hrobachik на сайте SPLETNIK.RU 23 июля 2011
Опубликовано пользователем сайта
Мода hrobachikКак часто мы задумываемся о том, что в большинстве своем современные модные тенденции берут начало из уже существующих направлений? Но в другом виде искусства? Кажется, наибольшее влияние на моду оказала живопись. К примеру, откуда в современной моде взялись простейшие геометрические фигуры и сочетание разнообразных и контрастных ярких красок, оттенков и комбинаций? В 1915 году на «Последней футуристической выставке картин 0,10» известный всему миру Казимир Малевич выставил 49 «супрематических» картин, оформив ими целый выставочный зал. Позже он выпустил небольшую программную брошюру под названием «От кубизма к супрематизму. Новый живописный реализм», поясняющую художественную концепцию супрематизма. Именно этому художнику мы обязаны появлением термина “супрематизм” в авангардистском искусстве первой половины ХХв. КАЗИМИР МАЛЕВИЧ Супрематическая композиция (синий прямоугольник поверх красного луча). 1916. Холст, масло. 88 x 70,5. Собрание наследников Малевича Супрематизм стал разновидностью абстракционизма, который выражается в комбинациях разноцветных плоскостей геометрических очертаний ( прямая линия, квадрат, круг, прямоугольник, овал, треугольник). Основа супрематизма — уравновешенное сочетание в композиции разноцветных и разновеликих геометрических фигур. На начальном етапе термин означал доминирование цвета над всеми остальными свойствами живописи. Впервые краска стала была освобождена от подсобной роли. КАЗИМИР МАЛЕВИЧ Мистический супрематизм (черный крест на красном овале). 1920–1922. Холст, масло. 100,5 x 60. Собрание наследников Малевича Супрематизм в отличие от других авангардных направлений не получил широкого распространения среди художников и поэтов. Но в Витебске, куда Малевич переехал вместе с семьей в 1919 супрематизм нашел своих преданных последователей. Здесь образовалась и супрематическая группировка под названием УНОВИС (Утвердители нового искусства). К стати, именно в честь этой группы была названа дочь Малевича, Уна. Но супрематизм быстро вырвался из рамок академического искусства и нашел себя в повседневной жизни Витебска того времени: фасады зданий украшались спрематическими пано, жители покупали супрематические ткани, посуду с супрематическим декором и мебель. вывеска «Столовая» Помимо живописи, наиболее широкое применение супрематизм получил в оформлении советского фарфора 1920–30-х годов Сохранились и редкие проекты создания супрематической мебели (1920-е) (автор Николай Суетин) Даже гроб, в котором в 1935 году похоронили самого Малевича, был изготовлен по эскизам Суетина и имел форму супрематического архитектона: Таким образом, такой красоте в моде мы обязаны супрематизму и, конечно же Казимиру Малевичу. Весенне-летняя коллекция Gucci полна ярких взрывных красок Камилла Белль Ким Кардашьян Ирман КАЗИМИР МАЛЕВИЧ «Атлеты» КАЗИМИР МАЛЕВИЧ «Девушки в поле» КАЗИМИР МАЛЕВИЧ «Три женщины» КАЗИМИР МАЛЕВИЧ Женщина с граблями, 1928-1932. // Диор. Черно-белое пальто из шелкового фая и черно-белая юбка из плотного льна. Коллекция haute couture весна-лето 2002. Весенне-летняя коллекция Versus:
Оставьте свой голос:основных и дополнительных предметов; Треугольники
Теперь, когда вы определились с тем, что включить в кадр и убедились, что ваше изображение ровное по горизонтали и вертикали, следующее, что вы хотите выбрать, — это ваш объект: на чем вы хотите, чтобы внимание зрителей было сосредоточено? В этой статье мы рассмотрим основные и второстепенные предметы. В конце вы также изучите другую технику создания стабильных изображений. (Сообщил: Тацуя Танака)
Основные и второстепенные предметы: ваши ведущие и второстепенные актеры
Главный (основной) и второстепенный объекты на фотографии подобны главным и второстепенным персонажам фильма соответственно.Если вы не сбалансируете их как следует, вы не сможете передать зрителю свое фотографическое намерение.
Основная тема
В качестве главного героя главный объект должен привлекать большую часть внимания зрителя. Вы должны выделить его, внимательно изучив такие факторы, как:
— Где разместить
— С какого ракурса снимать с
— Сколько места занимает в составе
Второстепенный предмет
В качестве второстепенного персонажа второстепенный субъект обеспечивает визуальную поддержку основного объекта.Часто это достигается за счет уравновешивания композиции, добавления визуального интереса или привлечения большего внимания к основному объекту. Он не должен конкурировать за внимание с основным предметом.
Дополнительные примеры снимков с основными и второстепенными предметами с описанием того, как они были созданы, см .:
Захват более привлекательных снимков блюд на столе
Использование второстепенного предмета для выделения основного предмета
Часто задаваемые вопросы о камере # 20: Как мне более эффектно сфотографировать цветы?
Типичные ошибки
1.Второстепенный предмет привлекает больше внимания, чем основной предмет
Красный: Основной предмет
Синий: Дополнительный предмет
Когда и главный, и второстепенный субъекты кажутся одинаковыми по размеру, они будут привлекать равное внимание, все остальные предметы остаются неизменными. Такие факторы, как цвет, могут повлиять на внимание зрителя. Некоторым зрителям светло-зеленый цвет второстепенного объекта сделает его более заметным, чем основной объект.
2.Не могу сказать, какой предмет является основным, а какой второстепенным.
Красный: Основной предмет
Синий: Дополнительный предмет
Объекты теперь расположены рядом, но трактор по-прежнему привлекает меньше внимания, чем идеально, из-за его более темного цвета, из-за чего он выглядит меньше.
Решение: поместите основной объект в центр и убедитесь, что он выглядит большим по сравнению с
Красный: Основной предмет
Синий: Дополнительный предмет
Здесь я подошел ближе к трактору, чтобы он занимал большую часть рамы.Это заставляет его выглядеть больше, и его легче идентифицировать как главный объект. (На гифке ниже первый неудачный снимок сравнивается с текущим снимком).
Важно то, что вы ставите в центр внимания
Также очень важно, чтобы главный объект находился в фокусе. Независимо от размера объекта на изображении, он не будет привлекать столько внимания, если не в фокусе.
Это было снято в дождливый день. Поскольку фокус был сделан на деревьях, мы почти не могли видеть дождь.Дерево становится главным предметом.
Та же сцена, но в фокусе — дождь. Деревья сливаются с фоном, а дождь становится главным объектом.
Совет: где разместить главный объект на глубоко сфокусированных снимках
Если вам нужно, чтобы все элементы изображения были в фокусе, например, в глубоко сфокусированном снимке, поместите главный объект на наиболее видное место. Второстепенный (е) предмет (ы) должен быть поблизости.
Треугольная композиция: способ создания визуальной устойчивости
Треугольная композиция предполагает формирование или использование треугольника в изображении. Треугольники, расположенные правой стороной вверх, хороши для создания устойчивости из-за широкого основания.
Примеры треугольной композиции
1. Гроздь цветов треугольной формы
Равносторонний треугольник, образованный крошечной гроздью цветов, помогает создать сбалансированную композицию.
2. Архитектурные сооружения с конической крышей
Форма архитектурного сооружения широкая у основания и сужается к крыше в центре. Вы можете использовать эти контуры, чтобы создать в композиции большой треугольник.
3. Подразумеваемые треугольные композиции
Дерево, стоящее на снежном поле, вместе со своей тенью образуют две стороны прямоугольного треугольника.Дерево само по себе образует треугольник, но ключевой момент в композиции имеет предполагаемый треугольник большего размера.
4. Обратные треугольники
EOS RP / RF24-105mm f / 4L IS USM / FL: 63 мм / AE с приоритетом диафрагмы (f / 5,6, 1/1034 с, EV-1) / ISO 100 / WB: ручной
Перевернутые треугольники или треугольники под интересными углами могут добавить графически интересный элемент к обычному снимку, как на этом снимке озера в кратере, сделанном с помощью EOS RP.
Совет: треугольники могут привлечь внимание к элементам на их вершине
Каждый край треугольника действует как ведущая линия, привлекающая внимание зрителей к тому, что находится на его вершине или даже на каждом из его углов. Вы можете использовать это качество, чтобы подчеркнуть свой основной предмет. Однако будьте осторожны с другими несущественными элементами, которые вы размещаете рядом с этим местом.
~~~
Теперь, когда вы изучили эти концепции, вам нужно поиграть с ними! Ищите очевидные и подразумеваемые треугольники в том, что вы видите.Поэкспериментируйте с различными способами размещения основных и второстепенных предметов или с тем, как можно использовать треугольники, чтобы привлечь внимание к разным объектам изображения. Вы даже можете комбинировать техники и использовать треугольную композицию, чтобы сбалансировать основные и второстепенные предметы.
Далее: Профессиональные техники композиции (2): «Паттерн и ритм» и «S-образная кривая»
Получайте последние новости, советы и рекомендации в области фотографии.
Станьте частью сообщества SNAPSHOT.
Зарегистрироваться сейчас!ПРИНЦИПЫ ГРАФИЧЕСКОГО ДИЗАЙНА — bbagraphicdesign2
Принципы дизайна (вкусные фастфуды)
Просмотрите эту ссылку, прежде чем перейти к разделу 3:
Что такое графика Дизайн PDF
Следуйте инструкциям для каждого «Принципа».
Разместите все свои выводы в чистой организованной форме в своем портфолио.
Все сообщения должны быть в блоке 3.
У каждого свой заголовок.
Вы должны быть в состоянии выполнить как минимум два из них за один урок. Это означает, что вам следует заполнить этот блок в четырех академических периодах.
Если у вас не хватает времени во время обычного урока, используйте Flex или даже время дома, чтобы завершить Работа.
СТОП !!!
Из-за гибридного обучения я изменил ожидания для этой страницы и набора проекты!
Я хочу, чтобы вы прочитали текст по каждому принципу, посмотрели примеры и посмотрели короткое видео для каждый.
Как только вы это сделаете, вам нужно будет найти по одному «жизненному» примеру для каждого принципа и сфотографировать его. с вашим iPad.
Затем вы разместите пример в своем портфолио с письменным объяснением того, как конкретный элемент реализовано в найденном вами примере.
1) Контраст — Принцип конструкции
Контраст возникает, когда 2 или более визуальных элемента в композиции используются для создания эффекта, выделения важности, создания захватывающей графики и визуального интереса.
Контекст является неотъемлемой частью контраста.
Нам может казаться, что выбранный визуальный объект в композиции что-то говорит о себе. Но чаще всего его значение придает визуальный элемент.
Контраст возникает, когда два или более элемента в композиции различны.
Принцип дизайна — Контраст
В альбоме для рисования;
Создайте квадрат размером 4 на 4 дюйма, в котором нарисуйте пример контраста, используя только базовые формы.Квадрат, треугольник, круг и т. Д. Вы также можете использовать цвет в этом дизайне, чтобы подчеркнуть контраст.
Также найдите один пример контраста из реальной жизни. Просмотрите журналы, плакаты, вывески, упаковку, чтобы найти свой образец. Не снимайте это с интернета.
Сфотографируйте нарисованный дизайн и найденный вами образец и загрузите их в свое портфолио в галерею.
2) Иерархия — Принцип проектирования
Иерархия обычно создается за счет контраста между визуальными элементами в композиции, обычно визуальные элементы с наибольшим контрастом замечаются первыми.
Создание четкой визуальной иерархии важно, потому что она скрепляет дизайн. Эффективное использование иерархии может упростить сложное сообщение.
Примеры базовой иерархии:
Общие практические примеры иерархии:
Принцип дизайна — иерархия
В альбоме для рисования;
Создайте квадрат размером 4 x 4 дюйма, в котором нарисуйте пример иерархии, используя только базовые формы.Квадрат, треугольник, круг и т. Д. Вы также можете использовать цвет в этом дизайне, чтобы подчеркнуть Иерархию.
Также найдите один пример иерархии из реальной жизни. Просмотрите журналы, плакаты, вывески, упаковку, чтобы найти свой образец. Не снимайте это с интернета.
Сфотографируйте нарисованный дизайн и найденный вами образец и загрузите их в свое портфолио в галерею.
3) Центровка — Принцип конструкции
Выравнивание можно использовать для достижения определенного внешнего вида.
Один раз всегда нужно осознавать при работе с выравниванием для достижения намеченного результата.
В дизайне следует избегать появления произвольных решений, когда визуальные элементы не выровнены, это заметно и может обесценить часть работы, если выполнено непреднамеренно.
Но если сделать это намеренно, он может быть радикальным, динамичным или свободным.
Использование сетки может быть полезно для достижения правильного выравнивания.
Принцип дизайна — выравнивание
В альбоме для рисования;
Создайте квадрат размером 4 на 4 дюйма, в котором нарисуйте пример выравнивания, используя только базовые формы. Квадрат, треугольник, круг и т. Д. Вы также можете использовать цвет в этом дизайне, чтобы подчеркнуть выравнивание.
Также найдите один пример из реальной жизни. Просмотрите журналы, плакаты, вывески, упаковку, чтобы найти свой образец. Не снимайте это с интернета.
Сфотографируйте нарисованный дизайн и найденный вами образец и загрузите их в свое портфолио в галерею.
4) Весы — Принцип конструкции
Баланс — это визуальный вес композиции.
Баланс используется для создания стабильности, структуры, акцента и динамики.
В дизайне пытаются разместить визуальные элементы в эстетически приятном расположении или конкретном расположении для выполнения цели или достижения определенного внешнего вида.
Есть три основных типа баланса;
Симметричный баланс (формальный)
Асимметричный баланс (неформальный)
Радиальный баланс
Три основных типа баланса:
Принцип дизайна — баланс
В альбоме для рисования;
Создайте квадрат размером 4 x 4 дюйма, в котором нарисуйте пример баланса, используя только базовые формы.Квадрат, треугольник, круг и т. Д. Вы также можете использовать цвет в этом дизайне, чтобы подчеркнуть Баланс.
Также найдите один реальный пример Balance. Просмотрите журналы, плакаты, вывески, упаковку, чтобы найти свой образец. Не снимайте это с интернета.
Сфотографируйте нарисованный дизайн и найденный вами образец и загрузите их в свое портфолио в галерею.
5) Proximity / Unity — Принцип проектирования
Близость — это группировка и формирование объектов в композиции.
Близость используется для создания отношений между элементами. Создание релевантности, иерархии, организации и добавления структуры.
Его также можно использовать для рассеивания связей, предполагая отсутствие связей между элементами. Нарушение организации и структуры.
Перемещение элементов ближе или дальше друг от друга помогает показать связь или ее отсутствие.
В дизайне элементы должны быть сгруппированы вместе, чтобы их можно было рассматривать как группу.
Несвязанные элементы не должны находиться в непосредственной близости друг от друга.
Аудитория будет считать, что элементы, которые не находятся рядом друг с другом в дизайне, не связаны.
Следует стараться избегать видимости принятия произвольных решений.
Когда визуальные элементы появляются случайным образом или неправильно расположены, это заметно и может обесценить работу, если выполнено непреднамеренно.
Близость может стать решающим фактором между хорошим и потрясающим дизайном.
Практические примеры макетов Proximity:
Хорошее против плохого
Принцип дизайна — близость
Нарисуйте горизонтальный прямоугольник размером 4 на 6 дюймов. В этом прямоугольнике вы собираетесь использовать концепцию близости, чтобы создать себе визитную карточку.
Ваша «Дизайнерская Компания».
Вам нужно будет указать название вашей компании, адрес, адрес электронной почты, номер телефона (может быть вымышленным).
Этот дизайн должен содержать хотя бы одну форму. Эту форму можно придать любым способом, но она должна быть включена.
Помните, как эти элементы расположены в непосредственной близости друг от друга.
Сначала это будет сделано на бумаге, а позже будет воссоздано цифровыми средствами.Думайте об этом как о прототипе вашего готового дизайна позже.
Вы можете использовать только 3 цвета.
После завершения сфотографируйте его и загрузите в свое портфолио.
6) Повторение / движение — Принцип конструкции
Хорошая практика проектирования направлена на повторение некоторых аспектов дизайна на протяжении всей работы, будь то простая или сложная работа.
Повторение в графическом дизайне не означает узор.
Повторение используется для обозначения единства и последовательности во всем дизайне.
Повторение создает особый стиль и творческую сплоченность, создает акцент, высокую иерархию, структуру и силу в дизайне.
Конечная цель любого графического дизайна — произвести впечатление, надеюсь, неизгладимое впечатление. Если дизайн достигает этой цели, он будет выполнять свою задачу, общаться и настаивайте на особом сообщении, которое задерживается и становится знакомым.
Чем больше мы что-то видим, тем больше мы с этим знакомимся и, в свою очередь, запоминаем. Подумайте о кока-коле.
«Повторение незабываемо»
Сохранение визуальной структуры во всем дизайне способствует сосредоточенности и согласованности.
На телефоне или iPad вы найдете 4 примера повторения дизайна.
Помните, что дизайн вокруг вас каждый день.Подумайте о вещах, с которыми вы контактируете или наблюдаете в течение дня.
В своем портфолио разместите эти изображения в галерее.
Напишите описание того, почему каждое изображение повторяется в графическом дизайне.
КОНТРОЛЬНЫЙ ОПРОС
Прочтите эту ссылку и сделайте заметки. Вы можете использовать свои альбомы для рисования, iPad или онлайн-портфолио, чтобы взять Примечания.
Будет проведен тест, основанный на терминах на этих страницах.
50 терминов графического дизайна
Достаточно знать 1 — 46
ПРИВЫЧКИ ОБУЧЕНИЯ КОНТРОЛЬНЫЙ СПИСОК РУБРИК
Комбинации элементов и принципов дизайна.
Комбинации элементов и принципов дизайна
Что такое форма и форма в элементах дизайна? — Мворганизация.org
Что такое форма и форма в элементах дизайна?
Форма — это двух- или трехмерный объект, который выделяется из пространства рядом с ним из-за определенной или подразумеваемой границы. Фигура может находиться в разных областях пространства и иметь другие элементы, такие как линия, цвет, текстура или движение. Как и формы, формы бывают двух разных типов: геометрические и органические.
В чем разница между формой и формой?
В изобразительном искусстве форма — это плоская замкнутая область произведения искусства, созданная линиями, текстурами, цветами или областью, заключенной другими формами, такими как треугольники, круги и квадраты.Точно так же форма может относиться к трехмерной композиции или объекту в трехмерной композиции.
Какие две категории формы?
Форма — это свойство двухмерной формы, обычно определяемое линией вокруг нее или изменением цвета. Есть два основных типа форм: геометрические и органические.
Что такое органические формы?
Органические формы неправильные и несовершенные. Естественно, все эти формы будут немного отличаться друг от друга.Они часто бывают изогнутыми и плавными и могут казаться непредсказуемыми. Использование органических форм может сделать произведение искусства или дизайн более естественным и реалистичным.
Как еще называют органические формы?
Органические формы неправильны, криволинейны и обычно встречаются в природе. формы произвольной формы. Другое слово используется как синоним органических форм.
Какие бывают примеры органических форм?
ОРГАНИЧЕСКИЕ: формы, часто криволинейные по внешнему виду, похожие на те, что встречаются в природе, например растения, животные и камни.ГЕОМЕТРИЧЕСКИЕ: любые формы и основанные на математических принципах, такие как квадрат, круг и треугольник.
Каковы четыре основные формы в природе?
- Овальный.
- Круг.
- кв.
- Прямоугольник.
- Треугольник.
- Бриллиант.
Какие 5 основных форм в искусстве?
И это действительно все, что мы здесь собираемся сделать, за исключением того, что мы используем карандаш и упрощаем сложную фигуру до пяти основных геометрических фигур — треугольника, овала, продолговатого, круга и квадрата.
Является ли человек органической формой?
Органическая форма Это органическая форма, потому что это человеческая рука. Органические формы — это реальные формы, а не круги, квадраты или прямоугольники.
Какая форма у человека?
Форма человеческого тела — сложное явление со сложными деталями и функциями. Общая форма или фигура человека определяется главным образом формированием скелетных структур, а также распределением мускулов и жира.
Что такое позитивная форма?
Положительные формы представляют твердые объекты, а отрицательные формы показывают окружающее пространство.Геометрические формы идеальны и правильны. Органические формы неправильные и естественные.
Сердце имеет органическую форму?
Органические формы также называются криволинейными, состоящими из кривых, углов или и того, и другого. Эта структура имеет форму сердца. Это геометрическая форма, поскольку у нее есть прямые и изогнутые линии. Что такое геометрическая форма в искусстве?
Сердце — это форма или форма?
Другие формы В математическом мире вы найдете другие типы фигур. Кардиоиды похожи на круги с ямочкой на одной стороне.Хорошим примером кардиоиды является форма сердца.
В чем разница между органическими формами и геометрическими формами в искусстве?
Геометрические формы, такие как круги, треугольники или квадраты, имеют идеальные, однородные размеры и не часто встречаются в природе. Органические формы ассоциируются с вещами из природного мира, такими как растения и животные.
Что подразумевается под геометрическими формами?
Геометрическая форма — это геометрическая информация, которая остается, когда местоположение, масштаб, ориентация и отражение удаляются из описания геометрического объекта.Такие формы называются многоугольниками и включают треугольники, квадраты и пятиугольники. Другие формы могут быть ограничены кривыми, такими как круг или эллипс.
Сколько существует типов геометрических форм?
В зависимости от размеров существует множество геометрических фигур. Круг, Треугольник, Квадрат, Прямоугольник, Воздушный змей, Трапеция, Параллелограмм, Ромб и различные типы многоугольников — это двумерные формы. Куб, Кубоид, Сфера, Конус и Цилиндр — это основные трехмерные формы.
Какая самая основная форма?
Квадрат, круг и треугольник — самые простые формы на Земле, поддерживающие как синтетические, так и натуральные конструкции.
Каковы 16 основных форм?
Термины в наборе (16)
- равносторонний треугольник. Треугольник со всеми сторонами равной длины.
- равнобедренный треугольник. Треугольник с двумя сторонами равной длины.
- разносторонний треугольник. Треугольник, стороны которого не равны по длине.
- разносторонний прямоугольный треугольник.
- равнобедренный прямоугольный треугольник.
- кв.
- прямоугольник.
- параллелограмм.
Как вы называете 9-стороннюю форму?
В геометрии нонагон (/ ˈnɒnəɡɒn /) или эннеагон (/ ˈɛniəɡɒn /) — это многоугольник с девятью сторонами или 9-угольник.
Каковы 9 основных форм?
Квадраты, прямоугольники, треугольники, конусы, цилиндры, круги, овалы… это основные формы, которые помогут вам более точно рисовать объекты.
Как называется 7-сторонняя форма?
семиугольник
Как называется 1000000000000000 двусторонняя форма?
чилигон
Как называется форма с 666 сторонами?
гекса
Как называется 12-сторонняя форма?
Додекагон
Как вы называете 20-гранную форму?
В геометрии икосугольник или 20-угольник — это двадцатигранный многоугольник.Сумма внутренних углов любого икосагона составляет 3240 градусов.
Как называется 50-сторонняя форма?
пятиугольник
Как называется форма с 1 миллиардом сторон?
Обычный мегагон
Как вы называете 10000-стороннюю форму?
В геометрии мириугольник или 10000-угольник — это многоугольник с 10000 сторонами. Некоторые философы использовали обычный мириагон, чтобы проиллюстрировать проблемы, связанные с мышлением.
Как называется 11-сторонняя форма?
hendecagon
Как называется 13-сторонняя форма?
трехугольник
Squid game: что означают круг, треугольник и квадрат?
Южнокорейский сериал The Squid Game — самая популярная игра Netflix , которая продолжает вызывать у поклонников шум из-за смертоносных игр, в которых персонажи подвергаются испытанию.Однако есть еще одна загадочная деталь, которая привела к появлению теорий о его значении.
В соцсетях подписчики программы подчеркнули, что охранники носят розовые костюмы, чтобы сохранить свою личность в секрете. Они также носят шлемы с разными символами (круг, треугольник и квадрат), и каждый из них служит для обозначения их ранга.
Как мы могли видеть, круг — для рабочих, треугольник — для солдат, а квадрат — для начальников. Что касается слухов о X как четвертом символе, нет ничего подтвержденного ни внутри, ни за пределами вымысла.
ВЫ МОЖЕТЕ УВИДЕТЬ: Среда, разочарование года для любителей ужасов: без боли и славы
Следует отметить, что в программе важна иерархия власти. В одной из первых глав одна из них ругает рабочего, напоминая ему, что он не может говорить, пока его начальство не даст на это разрешения.
Squid Game возглавляет десятку лучших на Netflix в Перу. Фото: Netflix
Игра «Кальмар: что случилось в конце»?
Ги-Хун сумел выиграть игру после серии смертельных испытаний и получить награду миллионера.Однако он не может наслаждаться своими деньгами из-за внезапной смерти матери и возвращается к своей прежней жизни.
В последние минуты сериала главный герой воссоединяется с таинственным человеком, который его завербовал. Хотя он не может связаться с ним, он получает карточку с его номером и угрозой: он должен сесть в самолет и продолжить свою жизнь.
ВЫ МОЖЕТЕ УВИДЕТЬ: Cry Macho, обзор: фильм разрушает миф о мачо и переопределяет наследие Иствуда
Игра «Кальмар 2»: будет ли у нее второй сезон?
На данный момент потоковая платформа Netflix не делала официального заявления о новых сериях, но открытый финал не закрывает возможности для проведения второго сезона популярного шоу.Несмотря на это, создатель признался, что у него нет планов по поводу новой партии.
«У меня нет хороших планов относительно игры Squid 2. Сейчас довольно утомительно думать об этом. Но если бы мне пришлось, я бы точно не справился один. Я бы подумал об использовании комнаты для сценаристов и хотел бы, чтобы несколько опытных режиссеров продолжили сюжет », — сказал Хван в прошлом интервью для Variety.
Что символизирует кукла в игре «Кальмар»?
В главе 1, после набора участников, они сталкиваются с первой проблемой, которая помещает их на игровую площадку для детей. Люди в красном с оружием в руках, группа удивлена гигантской куклой. Через мегафоны объясняются правила игры, а кукла поет песню под названием «Зеленый свет, красный свет» .
Эта цифра представляет того, кто станет палачом, поскольку игроки, которые до этого момента не знали, что с ними произойдет, должны сражаться за свои жизни. Если они не пройдут установленную черту, они умрут.
Игра Squid — новый хит корейского сериала стримингового сервиса.Фото: композиция / Netflix
Теория бесконечных категорий предлагает взгляд на математику с высоты птичьего полета
Осенним осенним днем в Новой Англии, когда я учился на первом курсе колледжа, я проходил мимо входа в метро, когда мое внимание привлекла математическая задача. Человек стоял возле нескольких головоломок, которые он нацарапал на стене, одна из которых требовала построения с помощью воображаемой линейки и циркуля куба, объем которого вдвое больше, чем у другого данного куба.
Это остановило меня.Я видел эту проблему раньше. Фактически, этому вызову более двух тысячелетий, и он был приписан Платону через Плутарха. С помощью линейки можно удлинить линейный сегмент в любом направлении, а с помощью циркуля можно нарисовать круг с любым радиусом от выбранного центра. Уловка этой конкретной головоломки состоит в том, что любые точки или длины, появляющиеся на окончательном чертеже, должны быть либо присутствовать в начале, либо их можно построить на основе ранее предоставленной информации.
Чтобы удвоить объем куба, вы начинаете с его стороны.Здесь это значение может быть равно 1, потому что это единственная указанная единица измерения. Чтобы построить куб большего размера, вам нужно найти способ нарисовать одну из его сторон с новой необходимой длиной, равной 2 (кубический корень из двух), используя в качестве инструментов только линейку и циркуль.
Это сложная проблема. Более 2000 лет никому не удавалось ее разгадать. Наконец, в 1837 году Пьер Лоран Ванцель объяснил, почему никому не удалось добиться успеха, доказав, что это невозможно. В его доказательстве использовалась передовая математика того времени, основы которой заложил его французский современник Эварист Галуа, погибший в 20 лет на дуэли, которая, возможно, была связана с несчастным любовным романом.В зрелом возрасте 20 лет я достиг значительно менее впечатляющих математических достижений, но я, по крайней мере, понял доказательство Вантцеля.
Вот идея: учитывая точку в качестве начала координат и длину расстояния 1, относительно просто использовать линейку и циркуль для построения всех точек на числовой прямой, координаты которых являются рациональными числами (игнорируя, как математики склонны делать , невозможность построить бесконечно много точек за конечный промежуток времени).
Ванцель показал, что если использовать только эти инструменты, каждая вновь построенная точка должна быть решением квадратного полиномиального уравнения ax 2 + bx + c = 0, коэффициенты которого a , b и c относятся к числу ранее построенных точек. Напротив, точка ∛2 является решением кубического многочлена x 3 — 2 = 0, а теория «расширений поля» Галуа убедительно доказывает, что вы никогда не сможете получить решение неприводимого кубического многочлена, решая квадратичные уравнения, по сути потому, что никакая степень двойки не делит число 3 равномерно.
Кредит: Маттео ФаринеллаВооруженный этими фактами, я не мог удержаться от общения с этим человеком на улице. Как и ожидалось, моя попытка объяснить, откуда я знал, что его проблема не может быть решена, на самом деле ни к чему не привела. Вместо этого он утверждал, что мое образование сделало меня ограниченным и неспособным «мыслить нестандартно». В конце концов моей девушке удалось вывести меня из спора, и мы продолжили свой путь.
Но остается интересный вопрос: как я, все еще мокрый за ушами студент третьего года обучения в университете, смог научиться удобно манипулировать абстрактными системами счисления, такими как поля Галуа, всего за несколько коротких недель? Этот материал пришел в конце курса, наполненного группами симметрии, кольцами многочленов и связанными с ними сокровищами, которые взорвали бы умы математических гигантов, таких как Исаак Ньютон, Готфрид Лейбниц, Леонард Эйлер и Карл Фридрих Гаусс.Как получается, что математики могут быстро научить каждое новое поколение студентов открытиям, которые удивили экспертов предыдущего поколения?
Предоставлено: Маттео Фаринелла. Частично ответ на этот вопрос связан с последними достижениями в математике, которые обеспечивают «взгляд с высоты птичьего полета» на эту область за счет постоянно растущих уровней абстракции. Теория категорий — это раздел математики, который объясняет, как различные математические объекты могут считаться «одинаковыми». Его фундаментальная теорема говорит нам, что любой математический объект, каким бы сложным он ни был, полностью определяется его отношениями к подобным объектам.С помощью теории категорий мы обучаем молодых математиков новейшим идеям, используя общие правила, которые широко применяются к категориям всей математики, вместо того, чтобы углубляться в отдельные законы, применимые только в одной области.
По мере того, как математика продолжает развиваться, у математиков расширилось представление о том, когда две вещи являются «одинаковыми». В последние несколько десятилетий я и многие другие исследователи работали над расширением теории категорий, чтобы разобраться в этом новом расширенном понятии уникальности.Эти новые категории, называемые категориями бесконечности (∞-категориями), расширяют теорию категорий до бесконечных измерений. Язык ∞-категорий дает математикам мощные инструменты для изучения проблем, в которых отношения между объектами слишком тонкие, чтобы их можно было определить в традиционных категориях. Перспектива «уменьшения масштаба до бесконечности» предлагает новый способ осмыслить старые концепции и путь к открытию новых.
Категории
Как и многие другие математики, которых я знаю, я увлекся этой темой отчасти из-за моей плохой памяти.Это сбивает с толку многих людей, которые помнят школьную математику как изобилующую формулами для запоминания — на ум приходят тригонометрические тождества. Но меня успокаивал тот факт, что наиболее часто используемые формулы могут быть выведены из sin 2 θ + cos 2 θ = 1, что само по себе имеет элегантное геометрическое объяснение: это применение теоремы Пифагора вправо. треугольник с гипотенузой длины 1 и острым углом θ градусов.
Это утопическое видение математики, где все просто «имеет смысл» и ничего не нужно запоминать, в некоторой степени распадается на университетском уровне.На этом этапе студенты знакомятся с зоопарком математических объектов, которые возникли в течение последних нескольких столетий. «Группы», «кольца» и «поля» относятся к области математики, известной как алгебра, это слово взято из книги IX века персидского математика и астронома Мухаммада ибн Мусы аль-Хорезми, название которой иногда переводится как Наука восстановления и баланса. В течение следующего тысячелетия алгебра эволюционировала от изучения природы решений полиномиальных уравнений к изучению абстрактных систем счисления.Поскольку никакое действительное число x не удовлетворяет уравнению x 2 + 1 = 0, математики построили новую систему счисления — теперь известную как комплексные числа — добавив мнимое число i и наложив условие, что i 2 + 1 = 0.
Алгебра — лишь один из предметов в программе бакалавриата по математике. Другие краеугольные камни включают топологию — абстрактное исследование пространства — и анализ, который начинается со строгой обработки исчисления вещественных функций перед переходом к более экзотическим областям вероятностных пространств и случайных величин, а также комплексных многообразий и голоморфных функций.Как ученику все это понять?
Предоставлено: Маттео ФаринеллаПарадоксальная идея математики заключается в упрощении посредством абстракции. Как пишет Юджиния Ченг в книге «Искусство логики в нелогичном мире», « мощным аспектом абстракции является то, что многие различные ситуации становятся одинаковыми, когда вы забываете некоторые детали». Современная алгебра была создана в начале 20-го века, когда математики решили объединить свои исследования многих примеров алгебраической структуры, которые возникли при рассмотрении решений полиномиальных уравнений или конфигураций фигур на плоскости.Чтобы связать исследования этих структур, исследователи выделили «аксиомы», описывающие их общие свойства. Группы, кольца и поля были введены в математическую вселенную вместе с идеей о том, что математический объект может быть описан в терминах свойств, которые он имеет, и исследован «абстрактно», независимо от конкретных примеров или конструкций.
Джон Хортон Конвей, как известно, размышлял над любопытной онтологией математических вещей: «Нет сомнений в том, что они действительно существуют, но вы не можете толкать и подталкивать их, кроме как думая о них.Это довольно удивительно, и я до сих пор этого не понимаю, несмотря на то, что всю свою жизнь был математиком. Как что-то может быть там, не будучи на самом деле? »
Но этот мир математических объектов, которые могут существовать, не будучи на самом деле там, создал проблему: такой мир слишком велик для понимания любого человека. Даже в алгебре есть слишком много математических вещей, которые нужно изучать, чтобы было время, чтобы их все осмыслить. Примерно на рубеже 20-го века математики начали исследовать так называемую универсальную алгебру, относящуюся к «множеству», которое могло быть набором симметрий, чисел в какой-то системе или что-то совсем другое вместе с различными операциями, например , сложение и умножение — удовлетворяющие списку соответствующих аксиом, таких как ассоциативность, коммутативность или дистрибутивность.Делая разные выборы — частично или полностью определена операция? Обратимо ли оно? — приходим к стандартным алгебраическим структурам: группам, кольцам и полям. Но субъект не ограничен этими выборами, которые представляют собой исчезающе малую часть бесконечного множества возможностей.
Предоставлено: Маттео Фаринелла. Распространение новых абстрактных математических объектов вносит свою сложность. Один из способов упростить — ввести дополнительный уровень абстракции, на котором, что удивительно, мы можем доказывать теоремы о большом количестве математических объектов одновременно, не уточняя, о каких именно объектах идет речь.
Теория категорий, созданная в 1940-х годах Сэмюэлем Эйленбергом и Сондерсом Мак Лейном, делает именно это. Хотя изначально он был введен, чтобы дать строгое определение разговорного термина «естественная эквивалентность», он также предлагает способ универсального мышления об универсальной алгебре и других областях математики. С помощью языка Эйленберга и Мак Лейна мы теперь можем понять, что каждое разнообразие математических объектов относится к своей собственной категории , , которая представляет собой определенный набор объектов вместе с набором преобразований, изображенных в виде стрелок между объектами.Например, в линейной алгебре изучаются абстрактные векторные пространства, такие как трехмерное евклидово пространство. Соответствующие преобразования в этом случае называются линейными преобразованиями, и каждое из них должно иметь заданное исходное и целевое векторное пространство, указывающее, какие типы векторов возникают в качестве входных и выходных. Подобно функциям, преобразования в категории могут быть «составными», то есть вы можете применять одно преобразование к результатам другого преобразования. Для любой пары преобразований f: A → B (читается как « f — это преобразование из A в B ») и g: B → C, категория определяет уникальный составное преобразование, записанное как g ∘ f: A → C (читается как « g составлено f — это преобразование из A в C »).Наконец, этот закон состава ассоциативен, то есть h ∘ ( g ∘ f ) = ( h ∘ g ) ∘ f . Он также является унитальным: каждый объект B имеет «преобразование идентичности», обычно обозначаемое 1 B со свойством, что г ∘ 1 B = г и 1 B ∘ f = f для любых преобразований g и f , источник и цель которых, соответственно, равны B.
Как категории помогают незадачливому студенту, столкнувшемуся со слишком большим количеством математических объектов и недостатком времени, чтобы изучить их все? Любой класс структур, который вы можете определить в универсальной алгебре, может отличаться от всех других, но категории, в которых находятся эти объекты, очень похожи в способах, которые могут быть точно выражены через категориальный язык.
Обладая достаточным опытом, математики могут знать, чего ожидать, когда они сталкиваются с новым типом алгебраической структуры.Эта идея отражена в современных учебниках по этому предмету, в которых теории групп, колец и векторных пространств развиваются последовательно, главным образом потому, что теории параллельны. Есть и другие, более свободные аналогии между этими категориями и теми, с которыми студенты сталкиваются на курсах топологии или анализа, и эти сходства позволяют им быстрее усваивать новый материал. Такие шаблоны позволяют студентам тратить больше времени на изучение специальных тем, которые различают отдельные математические дисциплины, хотя исследования в области математики часто вдохновляются новыми и удивительными аналогиями между ранее не связанными областями.
Симметрии
Каскадные уровни абстракции, от конкретных математических структур до аксиоматических систем и далее до общих объектов, принадлежащих к категориям, представляют собой новую проблему: уже не очень ясно, что значит сказать, что одна вещь «то же самое» как другое дело. Рассмотрим, например, группу, которая в математике представляет собой абстрактную совокупность симметрий, элементы которой Эми Уилкинсон из Чикагского университета любит описывать как «движения», которые переворачивают или вращают объект перед установкой его в нечто вроде исходной позиции.
Например, мы могли бы изучить симметрию футболки. Одну симметрию можно рассматривать как «ход идентичности», когда человек просто носит футболку, как обычно. Другая симметрия соответствует движению, когда владелец вынимает руки из отверстий для рук и, не снимая футболки с шеи, поворачивает рубашку на 180 градусов, чтобы вставить руки в противоположные отверстия: футболка остается правой. стороной наружу, но теперь изнашивается задом наперед. Другая симметрия соответствует движению, при котором футболку полностью снимают, переворачивают наизнанку и снова надевают таким образом, чтобы каждая рука проходила через отверстие, в котором она была изначально.Футболка теперь вывернута наизнанку и перевернута. Окончательная симметрия объединяет эти два хода: нетипично для групп, эти движения могут выполняться в любом порядке без изменения конечного результата. Каждый из этих четырех ходов считается «симметрией», потому что они приводят к тому, что рубашка надета практически так же, как и в начале игры.
Кредит: Маттео ФаринеллаДругая группа — это «группа переворачивания матрасов», которая описывает симметрию матраса. В дополнение к движению идентичности, которое применяется, когда матрас остается в исходном положении, человек может перемещать матрас, вращая его сверху вниз, переворачивая назад вперед или выполняя оба движения последовательно.(Матрасы, как правило, не квадратные, но если бы они были квадратными, симметрии было бы больше, чем описано здесь). Хотя футболка не имеет ничего общего с матрасом, в некотором смысле две группы симметрии имеют одинаковое значение. «форма.» Во-первых, обе группы симметрий имеют одинаковое количество ходов (в данном случае четыре), и, что особенно важно, вы можете соединить каждое движение в группе футболки с движением в группе переворачивания матраса так, чтобы композиции соответствующих ходы тоже соответствуют. Другими словами, вы можете сопоставить ходы из двух групп (сопоставить идентичность с идентичностью, флип с флипом, вращение с вращением и т. Д.).Во-вторых, если вы возьмете два хода из одной группы и выполните их последовательно, конечная позиция будет соответствовать конечному результату последовательного выполнения соответствующих ходов из другой группы. С технической точки зрения эти группы связаны «изоморфизмом» — термином, этимология которого — от греческого isos, , означающего «равный», и morphe, , означающего «форма», — указывает на его значение.
Мы можем определить понятие изоморфизма в любой категории, что позволяет нам переносить это понятие между математическими контекстами.Изоморфизм между двумя объектами A, и B в категории задается парой преобразований: f: A → B и g: B → A, со свойством, что композиты g ∘ f и f ∘ g — это тождества 1 A и 1 B соответственно. В категории топологических пространств категоричное понятие изоморфизма представлено обратной парой непрерывных функций.Например, существует непрерывная деформация, которая позволит вам преобразовать невыпеченный пончик в форму, похожую на кофейную кружку: отверстие для пончика становится ручкой, а чашка формируется за счет углубления, которое вы делаете большим пальцем. (Чтобы деформация была непрерывной, вы должны сделать это, не разрывая тесто, поэтому не следует выпекать пончик до попытки эксперимента.)
Этот пример вдохновил на шутку о том, что тополог не может отличить кофейную кружку от пончика: как абстрактные пространства, эти объекты одинаковы.На практике многие топологи, вероятно, гораздо менее наблюдательны, чем это, потому что принято более гибкое соглашение относительно ситуаций, когда два пространства «одинаковы», идентифицируя любые два пространства, которые просто «гомотопически эквивалентны». Этот термин относится к понятию изоморфизма в более экзотической гомотопической категории пространств. Гомотопическая эквивалентность — это еще один тип непрерывной деформации, но в этом случае вы можете идентифицировать отдельные точки. Например, представьте, что вы начинаете с пары брюк, а затем сокращаете длину ног до тех пор, пока не останетесь с стрингами, еще одним «пространством» с той же фундаментальной топологической структурой — все еще есть два отверстия для ног — даже несмотря на то, что Первоначальная двухмерная одежда была сжата до одномерного бита.
Предоставлено: Маттео Фаринелла. Еще одна гомотопическая эквивалентность сворачивает бесконечное пространство трехмерного евклидова пространства до единой точки посредством «обратного большого взрыва», при котором каждая точка возвращается в исходное положение, причем скорость этого движения увеличивается с расстоянием. от места первого большого взрыва.
Интуиция о том, что мы можем заменять изоморфные вещи друг друга без фундаментального изменения природы конструкции или аргумента, настолько сильна, что фактически теоретики категорий переопределили слово «the» так, чтобы оно означало нечто близкое к «a» в разговорном английском.Например, существует концепция, известная как несвязанное объединение двух наборов A, и B. Как и обычное объединение, несвязанное объединение A, ⨆ B имеет копию каждого элемента A, и копия каждого элемента B. Однако, в отличие от обычного объединения, если A и B имеют общий элемент, то непересекающееся объединение A ⨆ B имеет две копии этого элемента, одна из которых каким-то образом помнит, что это произошло из A, , а другой почему-то помнит, что он пришел из B.
Есть много разных способов построить дизъюнктное объединение, используя аксиомы теории множеств, которые не дадут точно такое же множество, но обязательно будут производить изоморфные. Вместо того, чтобы тратить время на споры о том, какая конструкция является наиболее канонической, удобнее просто скрыть эту двусмысленность и сослаться на «непересекающееся объединение», когда речь идет о любом конкретном множестве, удовлетворяющем желаемому универсальному свойству. В другом примере математики называют группу симметрии футболки и группу переворачивания матраса «группой четырех Клейна».”
Бесконечные категории
Часто рассказываемая история о происхождении фундаментальной теоремы теории категорий состоит в том, что молодой математик по имени Нобуо Йонеда описал Мак Лейну «лемму» или вспомогательную теорему на вокзале Гар-дю-Нор в Париже в 1954 году. начал объяснение леммы на платформе и продолжил ее в поезде перед отъездом со станции. Следствием этой леммы является то, что любой объект в любой категории полностью определяется его отношением к другим объектам в категории, как закодировано преобразованиями в этот объект или из него.Таким образом, мы можем охарактеризовать топологическое пространство X , исследуя его с помощью непрерывных функций f: T → X , отображая другие пространства T. Например, точки пространства X соответствуют непрерывным функциям x : * → X, , домен которого представляет собой пространство с единственной точкой. Мы можем ответить на вопрос о том, подключено или отключено пространство X , рассмотрев отображения p: I → X, , домен которых представляет собой интервал I = [0,1].Каждое такое отображение определяет параметризованный «путь» в пространстве X от точки p (0) до точки p (1), которую можно рассматривать как возможную траекторию, по которой муравей может идти, когда пространство X
Мы можем использовать точки и пути пространства для перевода проблем топологии в задачи алгебры: каждое топологическое пространство X имеет связанную категорию π 1 X , называемую «фундаментальным группоидом» X. Объекты этой категории — это точки пространства, а преобразования — это пути. Если один путь может быть преобразован в другой в пространстве, в то время как его конечные точки остаются фиксированными, эти два пути определяют одно и то же преобразование. Эти деформации, которые технически называются гомотопиями , , необходимы для композиции путей для определения ассоциативной операции, как того требует категория.
Предоставлено: Маттео ФаринеллаКлючевое преимущество фундаментальной конструкции группоида состоит в том, что она является «функториальной», то есть непрерывная функция f: X → Y между топологическими пространствами порождает соответствующее преобразование π 1 f : π 1 X → π 1 Y между фундаментальными группоидами.Это присвоение учитывает состав и идентичность, то есть π 1 ( g ∘ f ) = π 1 g ∘ π 1 f и π 1 (1 X ) = 1 π1 X соответственно. Эти два свойства, которые в совокупности называются «функториальностью», предполагают, что фундаментальная группа захватывает некоторую важную информацию о топологических пространствах. В частности, если два пространства не гомотопически эквивалентны, то их фундаментальные группоиды обязательно неэквивалентны.
Однако фундаментальный группоид не является полным инвариантом. Он может легко отличить круг от твердого диска, который ограничивает круг. В фундаментальном группоиде круга различные извивающиеся версии пути между двумя точками могут быть помечены целыми числами, которые записывают, сколько раз траектория наматывается вокруг круга, и знаком + или -, указывающим, соответственно, направление по часовой стрелке или против часовой стрелки. транзита. Напротив, в фундаментальном группоиде диска существует только один путь до гомотопии между любой парой точек.Фундаментальный группоид пространства, образованного надувной внешней частью пляжного мяча, сферой в топологических терминах, также имеет такое описание: существует единственный путь вплоть до гомотопии между любыми двумя точками.
Предоставлено: Маттео Фаринелла. Большая проблема фундаментального группоида состоит в том, что точки и пути не обнаруживают многомерную структуру пространства, потому что точка и интервал сами являются нуль- и одномерными соответственно. Решением является также рассмотрение непрерывных функций из двумерного диска, называемых гомотопиями, и «высших гомотопий», определяемых непрерывными функциями из твердого трехмерного шара, и аналогично для других шаров в 4, 5, 6 или более измерениях.
Естественно спросить, какую алгебраическую структуру образуют точки, пути, гомотопии и высшие гомотопии в пространстве X: эта структура π ∞ X («pi бесконечность X »), называемая фундаментальной ∞-группоид X, определяет пример ∞-категории, бесконечномерный аналог категорий, впервые введенных Эйленбергом и Мак Лейном. Как и обычная категория, ∞-категория имеет объекты и преобразования, визуализированные в виде одномерных стрелок, но она также содержит «высшие преобразования», изображенные двумерными стрелками, трехмерными стрелками и так далее.Например, в π ∞ X объекты и стрелки являются точками и путями, которые больше не рассматриваются вплоть до покачивания, в то время как преобразования более высоких измерений кодируют гомотопии высших измерений. Как и в обычной категории, стрелки в любом фиксированном размере могут быть составлены: если у вас есть две стрелки f: X → Y и g: Y → Z, также должна быть стрелка g ∘ f: X → Z. Но есть одна загвоздка: при попытках запечатлеть естественные примеры, такие как фундаментальный ∞-группоид пространства, закон композиции должен быть ослаблен.Для любой составной пары стрелок должна существовать составная стрелка, но больше не существует уникальной указанной составной стрелки.
Предоставлено: Маттео Фаринелла. Этот недостаток уникальности усложняет определение ∞-категорий в классических основах математики, основанных на множествах, потому что мы больше не можем думать о композиции как об операции, напоминающей операции в универсальной алгебре. Хотя ∞-категории становятся все более центральными в современных исследованиях во многих областях математики, от квантовой теории поля до алгебраической геометрии и алгебраической топологии, они часто считаются «слишком сложными» для всех, кроме специалистов, и не регулярно включаются в учебные программы, даже в учебных заведениях. выпускной уровень.Тем не менее, многие другие и я рассматриваем ∞-категории как революционно новое направление, которое может позволить математикам мечтать о новых связях, которые в противном случае было бы невозможно строго сформулировать и доказать.
Краткое руководство по современной математической терминологии
Категория: указанный набор объектов и преобразований между ними с правилом композиции
Состав: для применения одного преобразования к результатам другого
Идентичность: преобразование объекта в себя, которое никоим образом не меняет его
Симметрия: обратимое преобразование объекта в себя
Изоморфизм: структурное понятие «сходства», которое может существовать между парой объектов в категории
Фундаментальный группоид: категория, объекты которой являются точками в пространстве и чьи преобразования являются путями между ними, вплоть до гомотопии
Гомотопия: «путь между путями», определяемый непрерывной деформацией от одного пути к другому
Бесконечная категория: бесконечномерный аналог категории, который добавляет трансформации более высоких измерений и ослабляет правило композиции.
Фундаментальный группоид бесконечности: бесконечная категория точек, путей, гомотопий и высших гомотопий в пространстве
Горизонт будущего
Исторический опыт показывает, однако, что самая экзотическая математика сегодня будет считаться достаточно простой, чтобы преподавать математику студентам бакалавриата в будущем.Как исследователь теории ∞-категорий интересно размышлять о том, как можно упростить этот предмет. В данном случае есть лингвистический трюк — усиленная версия категориального «the» — который может сделать ∞-категории столь же легкими для понимания студентами конца 21-го века, как обычные категории сегодня. Ключевой аксиомой в обычной категории является наличие уникального составного преобразования g ∘ f: X → Z для каждой составной пары преобразований f: X → Y и g: Y → Z, выбран из всех элементов набора преобразований от X до Z. Напротив, в ∞-категории есть пространство стрелок, ведущих от X к Z, , которое в фундаментальном ∞-группоиде можно понимать как своего рода «пространство путей». Правильным аналогом уникальности композитов в обычной категории является утверждение, что в ∞-категории пространство композитов является «сжимаемым», что означает, что каждая из его точек может быть непрерывно свернута посредством обратного Большого взрыва в одну точку. происхождения.
Обратите внимание, что сжимаемость не означает, что существует уникальная композиция: действительно, как мы видели в фундаментальном ∞-группоиде, может быть большое количество составных путей.Но сжимаемость гарантирует, что любые два составных пути гомотопны, любые две гомотопии, связывающие два составных пути, связаны более высокой гомотопией и так далее.
Предоставлено: Маттео ФаринеллаЭта идея уникальности как типа условия сжимаемости является центральной в новой системе основ математики, предложенной Владимиром Воеводским и другими. Математики всего мира совместно разрабатывают новые компьютерные «помощники по доказательству», которые могут построчно проверять формальное доказательство математического результата.У этих помощников доказательства есть механизм, который имитирует обычную математическую практику передачи информации об одном предмете другому, который понимается как одно и то же посредством явного изоморфизма или гомотопической эквивалентности. В этом случае механизм позволяет пользователю транспортировать доказательство, включающее одну точку в пространстве, по пути, который соединяет ее с любой другой точкой, давая строгую формулировку топологического понятия тождества.
В эссе 1974 года математик Майкл Атия писал: «На самом деле цель теории в значительной степени состоит в систематической организации прошлого опыта таким образом, чтобы следующее поколение, наши ученики, их ученики и так далее могли максимально безболезненно усвоить существенные аспекты, и это единственный способ, с помощью которого вы можете кумулятивно наращивать любой вид научной деятельности, не заходя в конечном итоге в тупик.Теория категорий, вероятно, играет эту роль в современной математике: если математика — это наука аналогий, изучение закономерностей, то теория категорий — это изучение закономерностей математического мышления — «математика математики», как сказала Евгения Ченг из Школы математики. Институт искусств Чикаго поставил это.
Причина того, что сегодня мы можем охватить так много вопросов в бакалавриате, заключается в том, что наше понимание различных математических концепций было упрощено за счет абстракции, которую можно рассматривать как процесс отступления от конкретной рассматриваемой проблемы и принятия более широкого решения. взгляд на математику.Многие мелкие детали невидимы с этого уровня — числовые приближения, например, или вообще что-нибудь, имеющее отношение к числам, — но примечательно то, что теоремы в алгебре, теории множеств, топологии и алгебраической геометрии иногда верны для та же основная причина, и когда это так, эти доказательства выражаются на языке теории категорий.
