как нарисовать куб с любого ракурса — Gamedev на DTF
Советуем приготовить планшет или лист бумаги и ручку, чтобы все сразу попробовать. Читать эту статью просто так не имеет смысла — тут все про практику.
12 415 просмотров
Зачем художнику уметь рисовать куб с любого ракурса?
Освоив кубы, вы сможете рисовать любые объекты: машин, людей, архитектуру. Тоже с любого ракурса, быстро и понятно. Например, вот так можно свести к кубам фигуру человека:
Например, вот так можно свести к кубам фигуру человека:
Известный художник Скотт Робертсон рисует технику, отталкиваясь от геометрических примитивов.
Этому методу следует и Moderndayjames:
Дальше будет много примеров. Советуем попробовать нарисовать основные моменты, чтобы лучше понять, о чем речь. Получится своеобразный конспект.
Статья написана по материалам ресурса How to sketch.
Что такое перспектива?
Рисовать куб с любого ракурса — это рисовать его в перспективе. Представьте камеру — она заменит нам наблюдателя. На расстоянии от камеры стоит куб. Между камерой и кубом находится стекло.
Представьте камеру — она заменит нам наблюдателя. На расстоянии от камеры стоит куб. Между камерой и кубом находится стекло.
Расположение объектов.
Стекло здесь — так называемая картинная плоскость. Проведем от камеры сквозь стекло линию — получится то, что называется лучом зрения (ЛЗ). Луч зрения всегда перпендикулярен картинной плоскости. Эти обозначения понадобятся нам дальше.
Нам нужно знать, как линии нашего объекта расположены в пространстве относительно чего-либо. Положение камеры — наша путеводная звезда. Рисовать в перспективе — значит представлять изображение с определенной точки зрения. Не бывает изображения без зрителя.
Не бывает изображения без зрителя.
Дальше мы будем рассматривать сцену с двух точек зрения: то, как ее видит камера, и то, как она расположена относительно объекта. Это нужно, чтобы проще ориентироваться в пространстве.
Куб начинается с квадрата
Куб состоит из шести квадратных плоскостей, соединенных вместе. Чтобы нарисовать куб, нам нужно знать, как правильно расположить в пространстве квадрат во всех без исключения случаях и с любого возможного ракурса.
Шесть квадратных плоскостей в пространстве.
Здесь мы добавим в наш словарь новое слово — нормальная линия или просто нормаль. Нормаль — это линия, перпендикулярная какой-либо поверхности. Если вы поставите карандаш вертикально на стол, он будет совпадать с направлением нормальной линии. Вы можете встретить этот термин в 3D, но в 2D его тоже используют.
У каждой плоскости есть бесконечное количество этих нормальных линий. Для простоты мы нарисуем только одну по центру.
Возьмем квадрат и расположим его перед камерой. Если нормаль перпендикулярна картинной плоскости и тем самым совпадает с лучом зрения, значит, мы видим поверхность без каких-либо искажений. В данном случае — обычный квадрат.
В данном случае — обычный квадрат.
Слева — расположение объектов, справа — что видит камера.
Если мы наклоним нашу фигуру в каком-либо направлении, то нормаль больше не будет смотреть прямо на картинную плоскость. Поверхность прямоугольника сожмётся в том направлении, куда смотрит нормаль. Этот принцип называется сжатие по нормали. Каждая плоскость всегда сжимается только по своей нормальной линии.
Слева — расположение объектов, по центру — что видит камера, справа — реальный размер плоскости.
На приведенном примере боковые стороны прямоугольника сужаются кверху (с точки зрения камеры). Так получается потому, что это параллельные линии, которые уходят вдаль (относительно картинной плоскости). А вот линии, параллельные картинной плоскости, никогда не сходятся.
Так получается потому, что это параллельные линии, которые уходят вдаль (относительно картинной плоскости). А вот линии, параллельные картинной плоскости, никогда не сходятся.
Слева — расположение объектов, справа — что видит камера.
Что такое линия горизонта?
Параллельные линии, которые уходят вдаль, сходятся на линии горизонта. Эта истина так широко известна и непреложна, что авторы никогда не пересматривают ее обоснование. А мы пересмотрим — чтобы лучше понять, о чем речь.
Наша камера стоит строго вертикально, то есть ее нижняя плоскость параллельна плоскости земли. Представим себе не один, а несколько горизонтальных прямоугольников перед камерой. По мере того, как эти плоскости всё выше поднимаются над землёй, они всё сильнее сжимаются. В какой-то момент плоскость визуально сожмется в плоскую линию — это будет линия горизонта.
Представим себе не один, а несколько горизонтальных прямоугольников перед камерой. По мере того, как эти плоскости всё выше поднимаются над землёй, они всё сильнее сжимаются. В какой-то момент плоскость визуально сожмется в плоскую линию — это будет линия горизонта.
Слева — расположение объектов, справа — что видит камера.
Находим линию горизонта.
Слева — расположение объектов, справа — что видит камера.
Параллельные линии, расположенные на горизонтальных плоскостях (на любой из них) сходятся на линии горизонта. Точки, в которых они сходятся, называются точками схода (ТС).
Точки, в которых они сходятся, называются точками схода (ТС).
Слева — расположение объектов, справа — что видит камера.
Как видите, у каждого набора параллельных линий есть своя собственная точка схода. Для перспективы типично наличие центральной (ЦТС), левой (ЛТС) и правой (ПТС) точек схода.
Ориентируемся в пространстве
Теперь попробуем разобраться в том, как прямоугольники изменяются по мере увеличения расстояния от зрителя.
Возьмем несколько прямоугольников и выстроим их в ряд. Все они имеют одинаковый размер и расположены впритык друг к другу. И хотя в действительности все они имеют одинаковый физический размер, каждый последующий прямоугольник в перспективе становится меньше. Благодаря этому явлению параллельные линии «сходятся на линии горизонта».
Прямоугольники в пространстве.
Благодаря изменению размера наш мозг воспринимает глубину. Но оно происходит не линейно: каждый прямоугольник сжимается по своей нормали, когда его наклоняют относительно зрителя. Плоскость сжимается тем сильнее, чем она ближе к линии горизонта.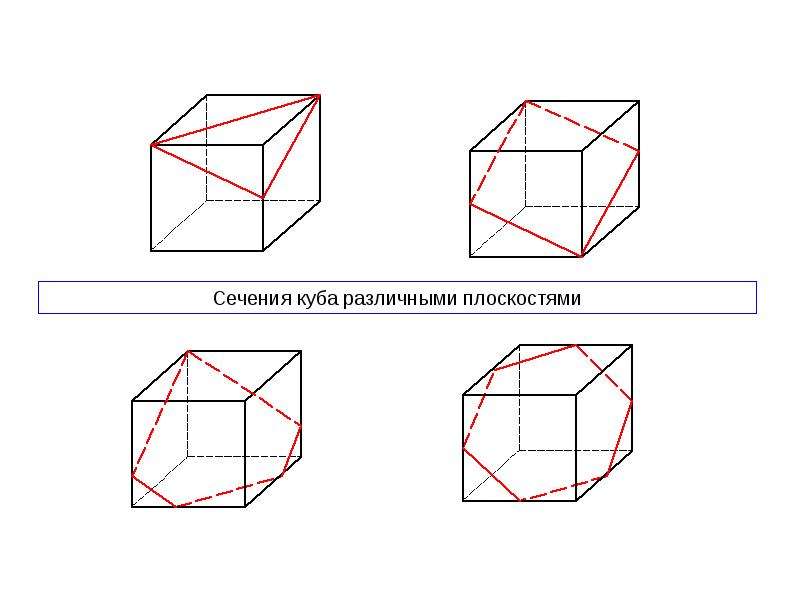
Разница в размере между парами прямоугольников, лежащих ближе к зрителю, ярче выражена, чем между теми, которые ближе к горизонту.
Измеряем глубину
Проведём три горизонтальные линии в перспективе аналогично прямоугольникам выше. Изменяем только одно требование: интервалы между ними должны быть одинаковыми. Что мы увидим? Отрезок B в два раза короче, чем A, но C в шесть раз короче, чем B.
Каждый следующий сантиметр на бумаге вмещает в себя все больше и больше пространства по мере приближения к горизонту.
Это важно понимать при рисовании не только механизмов, но и природных форм. Даже фигуры человека. Как и любой другой объект, тело существует в пространстве. Важно точно знать, где именно расположены ключевые точки тела. А для этого нужно освоить измерения в перспективе. Набравшись опыта, вы сможете делать обоснованные догадки, уже не рисуя вспомогательные конструкции.
Для правильного куба придется узнать кое-что об эллипсах
Теперь нам нужно нарисовать эллипсы. Тут нам пригодятся те же знания, что мы получили, изучая квадратные плоскости: потому, что плоскость может быть любой формы, в том числе овальной или круглой. У плоского круга или овала тоже есть нормальная линия, и она точно так же перпендикулярна поверхности плоскости.
У плоского круга или овала тоже есть нормальная линия, и она точно так же перпендикулярна поверхности плоскости.
Нормальная линия плоского эллипса всегда совпадает по направлению с его малой осью.
Принцип тот же, что и в случае с прямоугольниками. Слева — вид сверху, справа — что видит камера.
Важно помнить, что у круга всегда одинаковый диаметр, в каком бы направлении мы его не провели. После сжатия круг превращается в овал, и у него появляется самый длинный (большая ось эллипса) и самый короткий (малая ось эллипса) диаметры.
Большая ось не меняет свою длину, как бы сильно мы ни наклоняли плоскость.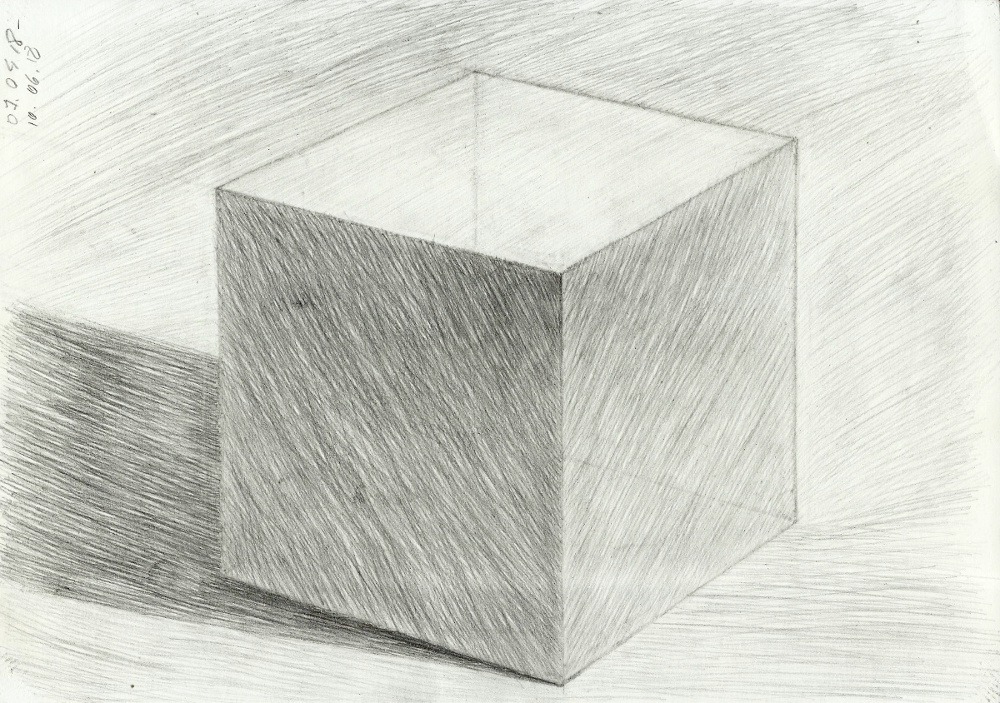 Малая ось перпендикулярна большой, а ее направление совпадает с нормальной линией. Длина малой оси меняется сильнее всего, когда мы наклоняем плоскость по отношению к камере.
Малая ось перпендикулярна большой, а ее направление совпадает с нормальной линией. Длина малой оси меняется сильнее всего, когда мы наклоняем плоскость по отношению к камере.
Большая ось сейчас расположена горизонтально, а малая — вертикально. По ней и происходит сжатие. Размеры большой оси не меняются.
Зачем в тексте про кубы информация про эллипсы?
Эллипсы помогают определить направление нормальной линии поверхности, поэтому их удобно использовать, даже если на рисунке нет видимых круглых плоскостей. Они подсказывают, в каком направлении сжимать плоскость, когда она наклонена по отношению к зрителю.
Слева плоскость расположена прямо относительно камеры, справа — наклонена относительно камеры.
Еще эллипс может пригодится, чтобы определить угол наклона плоскости относительно зрителя. Сильнее наклон, сильнее сжатие.
Нет наклона = нет сжатия. В центре и справа плоскости наклонены относительно зрителя.
И, последний, самый важный пункт. Эллипс помогает найти пропорции идеального квадрата: круг, вписанный в квадрат, касается каждой из четырех сторон точно посередине.
Круг всегда касается сторон квадрата посередине.
Первый угол — 90 градусов
Помимо пропорций квадрата, нам нужно убедиться, что у нашей фигуры есть четыре прямых угла (по 90 градусов). Для этого необходимо правильно построить хотя бы один угол — три остальных встанут на свои места.
Эллипс поможет найти правильный угол между двумя линиями на одной плоскости.
Исходное расположение объектов. Смотрите ниже, как мы превращаем круг в квадрат.
Смотрите ниже, как мы превращаем круг в квадрат.
Определяем пропорции квадрата с заданного ракурса, используя эллипс.
Слева — что видит камера, справа — расположение камеры относительно фигуры, вид сверху.
Проведем нормальную линию (она здесь вертикальная, потому что плоскость горизонтальная). Её можно проводить в разных местах — в зависимости от того, как мы хотим развернуть к себе угол будущего квадрата.
Как далеко нормаль должна выходить за пределы эллипса до той точки, где она пересекается с касательными? Это зависит от угла наклона эллипса.
Вид из камеры. Нормаль выходит из центра эллипса. Чем меньше его наклон по отношению к камере, тем длиннее линия.
Чем ближе линия горизонта к эллипсу (с учётом его размера), тем сильнее перспективное искажение, и тем быстрее сходятся линии. Это также значит, что объект или находится близко к зрителю, или он большой. Изображение выглядит так, как будто снято через широкоугольный объектив.
Если линия горизонта находится далеко от эллипса, перспективное искажение будет слабым. Линии будут сходиться медленно, объект покажется маленьким или будет расположен далеко от зрителя.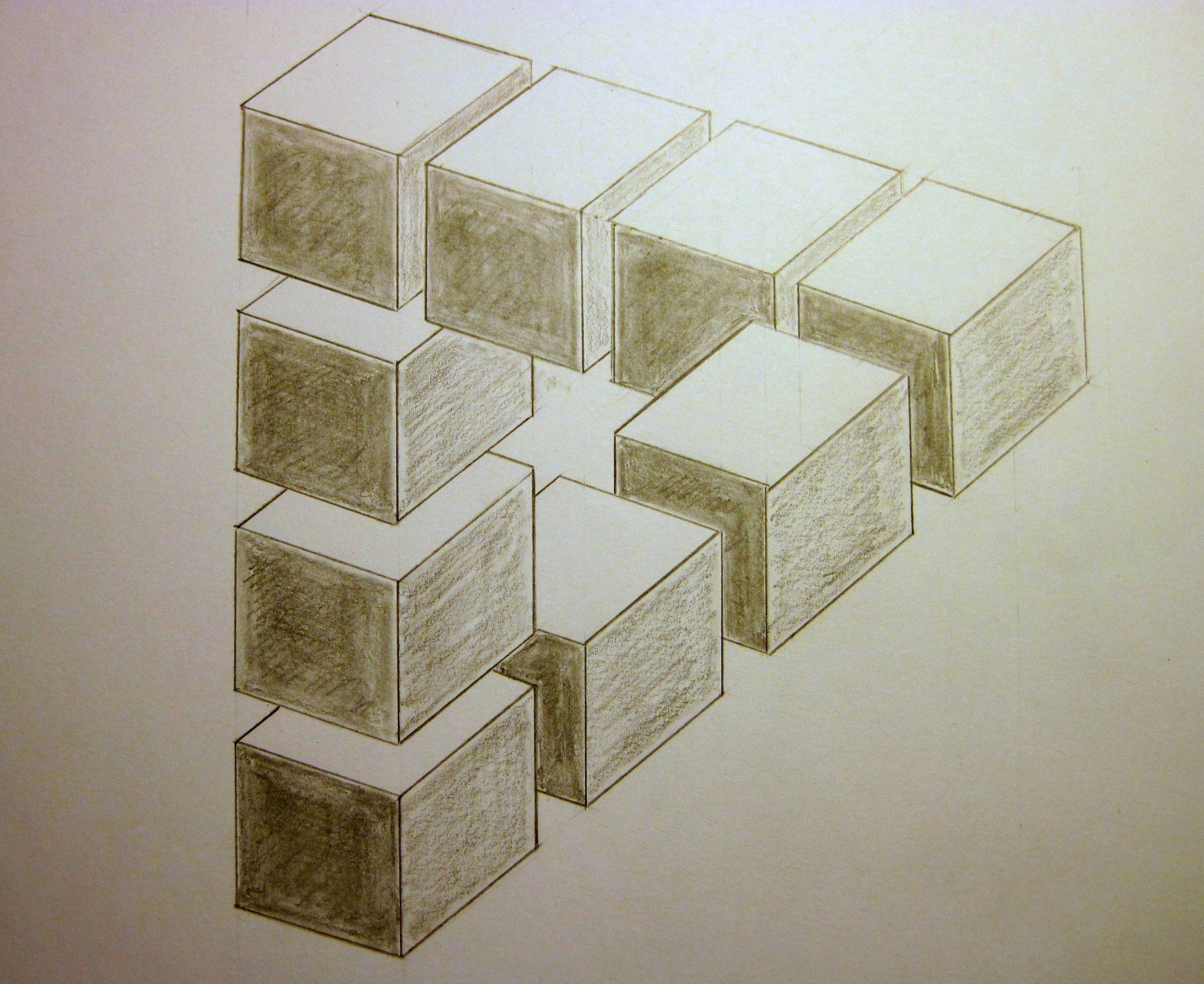 Это эффект длиннофокусного объектива.
Это эффект длиннофокусного объектива.
Слева горизонт очень близко и линии сходятся быстрее, справа горизонт далеко и линии сходятся медленнее.
Здесь видно, что вертикальная линия в обоих случаях выходит за пределы эллипса на одно и то же расстояние. Нижний угол квадрата одинаковый. Разница только в силе перспективы. И ещё раз напоминаем: линия горизонта перпендикулярна нормали эллипса (малой оси).
Горизонт — это по сути ещё одна плоскость, параллельная нашему эллипсу. Просто она полностью наклонена по отношению к зрителю.
Итак, наш эллипс готов.
Превращаем эллипс в куб
У куба шесть граней, но одновременно мы можем увидеть лишь три из них. Так что, простоты ради, мы сосредоточимся только на видимых сторонах (пока). Начнем с верхней грани. Вы уже знаете, как изобразить горизонтальный квадрат в любом возможном положении, так что сделайте это — нарисуйте квадрат вокруг эллипса.
Теперь нужно дорисовать две боковые грани. Чтобы найти их, используйте вертикально расположенные рёбра куба — нормали к верхней плоскости.
Осталось еще узнать длину вертикального ребра. Оно параллельно картинной плоскости и становится длиннее, когда перемещается ближе к нам в пространстве (как и любой другой объект), в соответствии с конвергенцией (сближением) линий.
Мы предполагаем, что ребро немного длиннее, чем большая ось нашего верхнего эллипса, на которую тоже не действует перспективное сокращение.
Есть одна хитрость, которая помогает проверить, правильно ли мы построили боковые грани. Это можно сделать с помощью эллипса. Нарисуйте эллипс, малая ось которого направлена в правую точку схода. Эллипс должен касаться рёбер куба посередине. Затем просто закройте снизу левую грань с помощью линии, идущей к левой точке схода. А потом правую грань — линией, идущей к правой точке схода:
Наш куб готов:
Как клонировать наши кубы
Для этого вернемся к рисованию прямоугольников. У каждого прямоугольника есть диагонали, они пересекаются в его центре. Диагонали помогают нам рисовать одинаковые прямоугольники.
Диагонали прямоугольника пересекаются в его центре.
Давайте потренируемся. Найдите центр прямоугольника, используя диагонали.
Нарисуйте среднюю линию прямоугольника и продолжите ее в том направлении, куда собираетесь клонировать прямоугольник. Средняя линия пересечёт сторону прямоугольника в точке А.
Продолжите стороны прямоугольника в том же направлении.
Найдите центр прямоугольника. Продлите линии в ту сторону, куда будете его клонировать.
Проведите через точку A линию из дальнего угла прямоугольника. Она пересечет его продлённую сторону в точке B. Точка B отмеряет ширину нового, точно такого же прямоугольника.
Теперь проведите вертикальную линию. Она станет дальней стороной нового прямоугольника.
Удвоение прямоугольника
Вы можете удваивать прямоугольники с помощью диагонали не только на плоскости, но и в перспективе. Сначала найдите центр прямоугольника, затем размножьте его во всех направлениях. Заполните всю страницу такими конструкциями.
Клонирование прямоугольника во всех направлениях.
Следует помнить, что в перспективе центр прямоугольника смещается по отношению к зрителю. Это происходит из-за схождения линий. Когда перспективное искажение небольшое (горизонт далеко по сравнению с размерами объектов), линии сходятся медленно, и центр прямоугольника смещается незначительно. И наоборот, смещение центра очень ярко выражено в случае сильного перспективного искажения.
Смещение центра.
Время активной практики. Клонируем кубы.
Постройте куб. Нижняя грань параллельна земле, никаких причудливых наклонов. Затем клонируйте любую грань куба с помощью метода диагоналей. Наметьте линии, которые будут направлены в точки схода.
Нарисуйте куб в перспективе.
Помните, квадраты сжимаются сильнее по мере удаления от зрителя. Если сравнивать первый и второй квадраты, этот эффект выражен ярко. Для каждого последующего квадрата он менее очевиден, но присутствует всегда.
Постройте новые кубы, клонируя квадратные плоскости.
Нарисуйте кубы один за другим. Заполните ими всю страницу.
Рисуйте «насквозь»
Сквозное построение означает, что вы рисуете твердые тела так, будто они прозрачные. Так вы всегда будете знать, где именно в пространстве находятся те участки поверхности тела, которые недоступны глазу. Это поможет правильно располагать тела по отношению друг к другу.
Переходим к практике:
Рисуем куб «насквозь», со всеми с невидимыми гранями.
Клонируем куб в сторону ПТС. Не забываем оставить между ними пространство величиной с такой же куб.
Теперь клонируйте куб в сторону левой точки схода. И снова оставьте между ними расстояние, куда мог бы поместиться третий куб.
Повторяем упражнение к ЛТС.
Интересная деталь. Как вы могли заметить, уходя вдаль, некоторые плоскости сильнее сжимаются (мы уже знаем почему), а другие — наоборот, больше открываются зрителю.
Это происходит потому, что угол между лучом зрения и поверхностью этих плоскостей приближается к прямому (90 градусов).
Как нарисовать куб с любого ракурса за пять шагов?
Теперь переходим к самому интересному!
Шаг 1. Нарисуйте эллипс. Он может располагаться на любой грани куба. Здесь вас должны волновать только сжатие и направление нормали.
Шаг 2. Проведите нормальную линию исходя из того, как вы хотите развернуть ближайшее к зрителю ребро куба. Линия горизонта для этого куба фактически не будет горизонтальной. Да, получился немного каламбур.
Какой она тогда должна быть? Просто перпендикулярной нормали нашей плоскости. Это единственное требование.
Шаг 3. Определитесь с силой перспективного искажения. В нашем случае линия горизонта находится за пределами холста, поэтому оно выражено слабо.
Шаг 4. Определите правильную длину «вертикального» ребра куба, используя эллипс или просто на глаз. Проведите линию к правой точке схода, чтобы закрыть грань снизу.
Шаг 5. Последняя грань сама станет на место. Просто постройте правильные параллельные линии к тем, которые уже есть.
Еще один способ: построение с помощью масс
Масса — это простое сферическое или колбасоподобное тело, используемое в качестве основы для построения сложных форм. Думайте о ней как о комке глины, существующем в трехмерном пространстве.
Это не плоская фигура на бумаге, у нее есть реальный физический объем.
Используя массы, легче воссоздать чувство размера в рисунке. Они же помогут решить проблемы перспективного искажения и наложения объектов друг на друга. Как видите, метод масс работает со всеми тремя ключевыми компонентами глубины в вашем рисунке.
Давайте теперь создадим куб из сферической массы. Независимо от того, как он развернут, куб идеально вписывается в сферу.
Куб, вписанный в сферу.
- Нарисуйте круг.
Постройте куб, используя знания, усвоенные из предыдущих блоков. Разворачивайте его как хотите, просто попробуйте соотнесите друг с другом его рёбра внутри массы.
Прямо сейчас нарисуйте целую страницу кубов, вписанных в сферы. Меняйте размер и ракурс.
Основная идея: каждая масса имеет центр. Центр сферической (или яйцеобразной) массы всегда совпадает с ее геометрическим центром. Давайте построим несколько одинаковых по размеру масс с равными промежутками между ними.
Постройте квадраты в перспективе.
- Нарисуйте сферу вокруг каждой точки. Контур каждой сферы должен касаться линий, которые направлены в центральную точку схода, — если вы хотите, чтобы сферы были одинакового размера.
Нарисуйте сферическую массу вокруг обозначенной точки.
Встройте кубы внутрь сферических масс. Разворачивайте их, как хотите, они всё равно будут одного размера, и расстояния между их центрами будут одинаковыми.
Нарисуйте куб внутри каждой сферы.
Поднимем кубы над землей
- Нарисуйте на земле квадрат, затем проведите внутри него прямую линию. Эта линия представляет собой расстояние между двумя кубами. Обозначьте точку схода, в которую направлена линия.
Проведите прямую линию внутри квадрата.
Постройте вертикальную плоскость.
Нарисуйте первую сферу и линию к точке схода так, чтобы она касалась контура сферы. Эта же линия должна касаться и контура второй сферы.
Нарисуйте массы одинакового размера с центрами в верхних углах плоскости.
Впишите куб в каждую массу.
Рисуем кубы в пространстве по произвольной траектории
Для начала вспомним про диагонали и построим с помощью них кривую в перспективе. Вот, как это сделать.
Нарисуйте квадрат.
Проведите произвольную кривую внутри него.
Нарисуйте диагонали и средние линии квадрата. Это прямоугольное построение поможет вам перенести кривую в перспективу.
Шаг 1. Кривая в ортогональном виде, то есть без перспективных искажений, прямо перед зрителем.
На новом слое с помощью эллипса определите, как будет выглядеть квадрат в перспективе. Проведите линию горизонта.
Шаг 2 выглядит так. Помните, чем ближе линия горизонта к эллипсу, тем сильнее перспективное искажение.
Нарисуйте квадрат в одноточечной перспективе, где линии параллельны либо картинной плоскости (тогда они вообще не сходятся), либо лучу зрения. Те, которые параллельны лучу зрения, сходятся в центре линии горизонта. Эта точка называется центральной точкой схода, как вы, возможно, помните. Это самый простой способ нарисовать прямоугольник.
Шаг 3. Постройте квадрат вокруг вашего круга.
Затем проведите диагонали и средние линии. Они будут служить вашим ориентиром.
Перенесите точки пересечения кривой с этими линиями из вашего ортографического рисунка. Например, если кривая касается верхней стороны квадрата по центру, она будет делать то же самое и в перспективе.
Шаг 4. Перенесите кривую из вида сверху в перспективный вид, опираясь на опорные точки.
Объединяем два упражнения
Наша цель — построить кубы одинакового размера с одинаковым расстоянием между ними, но расположенные на неправильной траектории.
Шаг 1. Постройте кривую в перспективе.
Отметьте на кривой точки, соблюдая равные интервалы между ними. Каждая точка соответствует центру массы. Определите размеры масс, которые находятся далеко от зрителя. Тогда вам будет легче определить на глаз размеры масс, расположенных в промежутках.
- Вот как это можно сделать: проведите прямую, проходящую через две точки, и продолжайте её, пока она не пересечётся с горизонтом в точке схода. Линии, по которым мы будем выравнивать размер масс (они касаются контуров обеих сфер), тоже должны быть направлены в эту точку схода.
Шаг 2. Отметьте на теле кривой точки с равными интервалами.
Шаг 3. Нарисуйте массы одинакового размера. Точки на кривой — это их центры.
Заполните всю длину кривой такими сферами.
Теперь можно начинать рисовать внутри масс кубы. Поворачивайте их как хотите.
Впишите куб в каждую массу.
А теперь пора нарисовать пару десятков кубов!
С разных ракурсов, в разных местах, с перекрытиями. Попробуйте разную силу перспективного искажения. Обязательно нарисуйте, даже если считаете, что все поняли. Это ОЧЕНЬ поможет рисовать потом любые другие предметы. Верьте в практику!
Что можно сделать:
Пример домашнего задания.
Дополнительные материалы
Здесь можно посмотреть еще видео по теме.
Когда разберетесь с этими упражнениями, можно попробовать порисовать технику, как в этом плейлисте ModernDayJames. Стартовать можно отсюда:
А тут рассказывают, как понимание геометрических примитивов поможет в рисовании динамичных поз:
Текст переведен авторами Smirnov School. Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.
Кубические композиции | Artisthall — Художественная мастерская
Следующим интересным заданием из нашей программы по рисунку являются кубические композиции.
Это авторское задание, разработанное нашими преподавателями, представляет завершающий этап изучения геометрических фигур, закрепления навыков построения и анализа конструкции.
На листе необходимо изобразить куб в различных ракурсах и проекциях. Предварительно можно сделать поисковые эскизы, чтобы правильно разместить фигуры в пространстве листа.
Для усложнения задания на плоскостях куба можно изобразить вписанную окружность, это позволит лучше понять формообразование эллипса в различных наклонах и ракурсах.
Также можно добавить к кубам усложненную пластическую моделировку и разбить плоскости на небольшие кубические сегменты. Это также совершенствует умение строить геометрических формы в разных ракурсах.
В этом задании есть интересная особенность: оно объединяет в себе программы по рисунку и композиции, такие, как геометрические врезки и цветовые аппликации. Оно требует от ученика изобразить на листе предметы, расположенные в пространстве, составив их сначала в своей голове, а затем перенеся мысли на лист бумаги. Под руководством педагога на бумаге должны появиться объемные фигуры, построенные в определенной последовательности и объединенные общим композиционным решением.
Благодаря таким заданиям развивается способность создавать на листе абстрактные композиции без натуры, основываясь на знаниях конструкции и принципах ее построения.
Это задание полезно выполнять в качестве тренировки навыков построения объемных геометрических фигур в пространстве. Также это задание хорошо выполнять тем, кто занимается композицией.
Существуют несколько вариантов таких композиций, подробнее о которых вы сможете узнать в процессе обучения, так как для определенного направления занятий (о которых Вы можете почитать на странице занятия рисунком) подбираются необходимые задания и их последовательности.
Работы, представленные в статье, выполнены нашими учениками.
По всем вопросам о занятиях рисунком вы можете узнать по телефону 8 903 669-80-89, 8 903 669-49-59 или пишите на почту: [email protected]
Смотрите также:
Световой бокс куб GRIFON LED 770 II
X
Перед приездом необходимо сделать заказ на сайте!
пл. Горького, 4
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Ванеева, 25/88, 1
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Бекетова, 35
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
пр-т. Ленина, 8
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
Проспект Ленина, 77
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
пр. Кораблестроителей, 1
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Плотникова, 4
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Академика Сахарова, 115 корп. 1
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Белинского, 110
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Янки Купалы, 2
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Передовая/ ш. Московское, 146Б
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
пр-т Ленина, 41
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Красных зорь, 27
Время работы: Пн-Пт 09:00-20:00, Сб-Вс 10:00-18:00
БЕЛИНСКОГО УЛ, 32, цокольный этаж, офис 7
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Усольская, 49
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
Мещерский б-р, 7
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Родионова, 195к2
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Пятигорская, 1
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
пр-т Гагарина, 101, корп.3
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Дьяконова, 6
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Ларина, 26к1
Время работы: Пн-Пт 08:00-20:00, Сб-Вс 09:00-20:00
ГЕРОЯ СМИРНОВА УЛ, 17
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Ефремова, 2
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Ошарская, 14
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
пр-т Ленина, 67/1
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. В.Печерская, 14Б
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
Московское ш., 300
Время работы: Пн-Пт 08:00-20:00, Сб-Вс 09:00-20:00
ул. Родионова, 18
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул.Медицинская, 12, пом.3
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
Казанское шоссе, 29
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Бурнаковская, 51а, вход №5, цокольный этаж
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Никиты Рыбакова, 19
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
ул. Гордеевская, 7, 102
Время работы: Пн-Пт 10:00-20:00, Сб-Вс 10:00-18:00
Как построить правильный квадрат. Как нарисовать куб карандашом Квадрат с рамкой
Хоть квадрат и прямоугольник это простейшие геометрические фигуры, но, чтобы их нарисовать в фотошопе, нужно приложить некоторые усилия и обладать базовыми знаниями. Новичок без должной подготовки, скорее всего, не справится с этой задачей.
В этой статье разберем 3 самых популярных способа как нарисовать прямоугольник или квадрат в фотошопе.
Но прежде, чем приступить к выбору способа рисования, нужно определиться с будущими параметрами. Прямоугольник/квадрат может быть:
- залит сплошным цветом или только с отрисовкой границ;
- произвольный или с точно заданными размерами;
- с возможностью в любое время менять его размеры без потери качества.
Способ 1. Инструмент произвольная фигура
В этом способе прямоугольник или квадрат будут нарисованы залитым сплошным цветом. Если вам нужна только граница, переходите к следующим двум способам.
На панели инструментов выберите инструмент . Дальше возможны два варианта развития событий:
Вариант 1. Квадрат или прямоугольник с дальнейшей возможностью изменять размеры без потери качества
Здесь, конечно, подразумевается использование векторной фигуры. Чтобы ее нарисовать нужно выбрать параметр Слой-фигура :
В дальнейшем вы можете без потери качества изменять размеры этой фигуры. Для этого используйте инструмент — Ctrl+T , и с помощью угловых маркеров изменяйте размер.
Для тех кто не знает : векторные фигуры состоят не из пикселей, а из специальные математических формул. Поэтому изменение размера — это не процесс растягивания/сжатия пикселей, а сложный математический пересчет, за счет чего не происходит никакой потери качества.
Вариант 2. Стандартный (растровый) квадрат/прямоугольник
Чтобы нарисовать сразу растровую фигуру используйте на панели параметров настройку Выполнить заливку пикселов . Но прежде чем начать ее рисовать — !
Но на самом деле можно рисовать сразу и векторный, а потом просто его. Тут уже выбирайте сами.
Как сделать прямоугольник квадратным
Обыкновенное правило с зажатой клавишей Shift с произвольными фигурами не работает. Поэтому нужно воспользоваться панелью параметров инструмента и выбрать настройку, чтобы фотошоп рисовал именно квадрат.
В этой же панели, обратите внимание, вы можете указать точный размер необходимого прямоугольника/квадрата или рисовать его по заранее определенным пропорциям.
По умолчанию размеры определяются пикселями. Если вы хотите изменить единицу измерения, сначала введите в поле какое-либо значение, а затем кликните по нему правой кнопкой мыши. Появится окно выбора единиц измерения. Доступно: пиксели, дюймы, сантиметры, миллиметры, пункты и пики.
Прямоугольник или квадрат со скругленными углами
Чтобы получить фигуру со скругленными углами, делайте все то же самое, что описано выше, но в самом начале выберите инструмент Прямоугольник со скругленными краями . На панели параметров инструмента нужно будет указать только радиус закругления.
Способ 2. Обводка выделенной области
Этот способ простой, как 5 копеек. выберите инструмент и нарисуйте прямоугольник пунктирной линией. Чтобы нарисовать квадрат удерживайте нажатой клавишу Shift .
Теперь нужно сделать обводку границ этой выделенной области. Для этого перейдите в Редактирование — Выполнить обводку .
Затем в новом окне настройте вид обводки: укажите толщину рамки, желаемый цвет и отметьте как будет проходить обводка:
- Внутри — значит рамка ляжет по внутренней стороне выделенной области;
- По центру — значит рамка разделится поровну на часть проходящую внутри выделения и на часть со внешней стороны;
- Снаружи — значит рамка будет огибать пунктир выделения.
Вот как может получиться:
На скриншоте выше я специально не убрал пунктирную линию, поскольку у вас она также не исчезнет. Чтобы окончательно от нее избавиться нажмите Ctrl+D .
В этом способе, чтобы нарисовать фигуру точного размера, нужно сперва на панели параметров инструмента указать Стиль — Заданный размер или Заданные пропорции. После этого станут активными поля, куда введите значения ширины и высоты в пикселях. Кликом правой кнопкой мыши по одному из этих полей вызовет меню изменения единиц измерения.
Способ 2.1 Закрашивание выделения
Самый банальный способ рисования прямоугольника — нарисовать рамку выделения (как описано выше) и просто закрасить ее любым цветом. Вот вам и прямоугольник или квадрат.
Способ 3. Модификация выделения
На самом деле этот способ мне меньше всего нравится из-за очевидного минуса — углы прямоугольника будут подрезанными, а сама граница рамки в состоянии и повлиять на эти факты не представляется возможным.
Итак, нужно вновь выбрать инструмент , нарисовать рамку будущего прямоугольника или квадрата (с клавишей Shift ), а затем отправляемся в меню Выделение и выбираем команду Модификация — Граница .
Появится новое окно, в котором, в нашем случае, мы указываем ширину границы прямоугольника. Допустим, укажу 7 пикселей. Получим такой результат:
А теперь нужно просто закрасить получившуюся рамку. Для этого подойдет . Здесь, кстати, можно подойти к вопросу более творчески и закрасить, например, разными цветами. Результат:
Останется только снять выделение — Ctrl+D . Думаю этот способ подходит только для своих редких специфических задач, поскольку растушевка и подрезанные углы только все портят.
Заметили ошибку в тексте — выделите ее и нажмите Ctrl + Enter . Спасибо!
Продолжаю рассказывать об упражнениях, улучшающих навык рисования, в данном случае геометрических фигур. Будем тренироваться рисовать их двухмерное отображение, трехмерное отображение и затенение фигур. Итак, Упражнения для рисования. Часть 2. Приступим.
Но прежде, чем приступить к упражнениям, напоминаю, что есть .
Двумерные фигуры
Круг. Сначала будет сложно нарисовать ровный красивый круг, поэтому поможем себе с помощью циркуля. Легкой линией нарисуем окружность и обведем ее. Один раз, потом еще, запоминаем характер движения и пытаемся воспроизвести. Можно помогать себе проставив несколько точек для начала. Со временем, если выполнять это упражнение, круги будут получаться все лучше и краше. 🙂
Треугольник. Пробуем нарисовать равносторонний треугольник. Опять же, чтобы себе помочь для начала можем нарисовать окружность с помощью циркуля и уже в нее вписать нашу фигуру. Но потом обязательно пробуем нарисовать самостоятельно.
Квадрат. Да, сложно с первого раза нарисовать все стороны одинаковыми и все углы 90 градусов. Поэтому, чтобы запомнить правильную форму используем линейку. Потом рисуем по точкам, а потом самостоятельно, без вспомогательных инструментов.
После квадрата рисуем ромб, то есть тот же квадрат, но повернутый на 45 градусов.
Рисуем 5-конечную звезду, рисуем не отрывая карандаш от бумаги. Для первого раза можно воспользоваться циркулем и вписать звезду в окружность, чтобы добиться симметрии.
Шестиконечная звезда. Рисуется как 2 равносторонних треугольника.
Восьмиконечная звезда. Рисуется как 2 квадрата.
Яйцо. Это овал, который на одном конце уже, чем на другом.
Полумесяц. Эту фигуру нарисовать не так просто, как может показаться на первый взгляд. Сначала попробуйте нарисовать его самостоятельно, а потом уже при помощи циркуля, помня, что месяц это фактически часть двух пересекающихся окружностей.
Трехмерные фигуры
Переходим к трехмерным фигурам. Начнем с куба. Рисуем квадрат, потом еще один квадрат чуть выше и правее, соединяем углы ровными линиями. Получаем прозрачный куб. Теперь попробуем нарисовать тот же куб, но уже без видимых линий внутри.
Теперь рисуем куб в другом ракурсе. Для этого сначала рисуем плоский параллелограмм в форме ромба, опускаем них перпендикуляры и рисуем такую же фигуру в основании. И такой же куб, но без видимых линий.
Теперь попробуем нарисовать цилиндр в разных ракурсах. Первый цилиндр будет прозрачный, рисуем овал, опускаем вертикали вниз и рисуем овал-основание. Затем рисуем цилиндр с невидимой нижней внутренней гранью и цилиндр с невидимой верхней внутренней гранью.
И завершаем этот цикл фигур рисованием конуса в разных ракурсах.
Рисуем круг. Намечаем легкой штриховкой тень в левом нижнем углу. Тень должна быть в форме полумесяца. Далее добавляем тона в тень при помощи большего нажима на карандаш, затеняем от центра к краю по принципу от светлого к темному, при этом у границы круга оставляем небольшой участок более светлой тени, это рефлекс. Дальше затеняем падающую тень, чем дальше от основания шара, тем светлее. Тень находится с противоположной от источника света стороны. То есть в нашем случае источник света находится в верхнем правом углу.
Теперь затеняем куб. В данном случае свет также находится в верхнем правом углу, а значит самая темная тень будет с противоположной стороны, сверху тени не будет, а правая видимая грань будет иметь более светлый тон. Соответственно с этим и наносим штриховку.
По такому же принципу затеняем стороны на кубе и конусе, важно следить за формой объекта и тем, как на него ложится свет. И падающая тень также должна соответствовать форме объекта.
И еще, в упражнениях для затенения используется диагональная штриховка, но я бы советовала пробовать в дальнейшем штриховать по форме объекта, тогда объект будет более объемный. Но штриховка по форме, да и вообще штриховка — тема довольно обширная, я уже начала ее изучать и скажу, что без тренировки рук и ровного быстрого штриха тут никуда, так что даже если делать только то, что я уже выложила, делать регулярно, то рисунки неизбежно будут становиться все лучше.
Дорисовываем и продолжаем 🙂
Все предметы, которые нас окружают можно мысленно вписать в простые геометрические тела (куб, шар, конус, цилиндр, призма и др.). Изучая форму куба, мы узнаем, как нарисовать, к примеру, дом, потому что упрощенно дом рисуется с использованием тех же приемов что и куб. У него есть вершины, ребра и грани, как и у куба. Крыша дома – это многогранная призма.
Нарисуем куб с натуры, а затем будем использовать эти знания на наших для изображения более сложных предметов таких как дома и улицы.
Куб – геометрическое тело, образованное пересечением плоскостей. И, как всякий объемный предмет, при изображении на плоском листе он будет претерпевать изменения в соответствии с законами перспективы. На рисунке изображена линия горизонта это уровень плоскости зрения художника . На ней находятся точки схода параллельных линий. В нашем случае — это четыре горизонтальных линии, стремящихся в точку схода слева и четыре горизонтальных линии, стремящихся в точку схода справа.
Мы изображаем предметы в пространстве так, как их воспринимает наш глаз. (Чем дальше от зрителя, тем меньше выглядит предмет и т.д.)
Начало любой картины – это композиция. Легкими линиями намечаем наш предмет на листе. Сверху всегда должно быть чуть больше места от края, чем снизу. Интуитивно определите масштаб так, чтобы предмет не выглядел гигантским или слишком маленьким.
Расположите самое ближнее вертикальное ребро так, чтобы оно не совпадало с центром листа, проходящим через пересечение его диагоналей. Засечками отмечаем высоту, это самое высокое ребро в нашем изображении, так как оно ближе всех к зрителю. На глаз определяем угол наклона ребер лежащих на столе относительно горизонтали. Тренируйте зрительную память, запоминая угол. Взгляд переводите быстро то на куб, то на рисунок.
То же проделаем и с верхними ребрами. Как передавать пространство на листе нам объясняют основные законы линейной перспективы. Все параллельные линии сливаются к линии горизонта в одну точку. Поэтому, чтобы передать что ребро находится дальше от зрителя, мы изобразим его меньше и расположим выше . Таким образом, все ребра будут разной высоты.
При пересечении дальних горизонтальных ребер образовались вершины. Через них проходит самое дальнее, невидимое глазом, ребро. На начальном этапе изобразим куб прозрачным для понимания полной конструкции предмета.
Для того, чтобы узнать на сколько сократились боковые грани, воспользуемся методом визирования . При помощи этого метода происходит восприятие очертаний предмета, художник учится изображать предметы пропорциональными и в различных ракурсах.
Как он работает? Возьмите карандаш на вытянутой руке, прикройте один глаз, совместите карандаш и изображение ребра куба в пространстве. Верхний край карандаша должен совпадать с верхней вершиной ребра, а пальцем зажмите на карандаше точку, совпадающую с нижней вершиной. Не убирая палец с карандаша, разверните под прямым углом и измеряйте расстояние между двумя ребрами. Таким образом, мы увидим соотношение высоты и ширины одной грани. Запомните это соотношение и передайте его на рисунке. Этим методом можно измерять и изображать так же соотношение ребер.
После того, как закончены линейные построения, приступаем к воздушной перспективе , а значит к штриховке.
Основная задача художника передавать объемные формы предметов. У нашего кубика мы видим три грани, все они разные по тону. Левая грань самая темная — это собственная тень предмета. Благодаря отраженному свету от окружающих предметов или рефлексам, штриховку делаем немного светлее по мере удаления влево. Самое большое ребро делают контрастней, чем все остальные. Таким образом, показывают его приближенность на передний план.
Верхняя плоскость темнее , чем вертикальная справа. Свет по ней лишь скользит, образуя полутон. Обратите внимание, что чем ближе к источнику света, тем светлее будет тон. Штриховку можно наносить по диагонали. На ребре ластиком высветлим, чтобы передать блик.
Для работы над самой светлой гранью возьмем твердый карандаш Н или 2Н . Он не даст сделать тон слишком темным. Штриховку нанесем вертикальную, по направлению плоскости.
Падающие тени всегда темнее, чем собственная тень предмета. Ближнее ребро – это линия перехода света и тени. Из нее начинается падающая тень. Чем ближе к предмету, тем насыщеннее тон. Отраженный свет от куба создает рефлекс внутри тени и она немного высветляется.
Рисование простых геометрических тел часто используется на и позволяет начинающему художнику научиться изображать предметы в пространстве, применяя законы перспективного построения и воздушной перспективы.
Все предметы и фигуры размещены в пространстве. Даже в простом рисунке стоит понимать совсем неразные предметы, а все, что находится на нем, и все, что мы хотим изобразить. Стоит рассматривать это как один поток форм и линий, белого и черного цвета, света и тени.
Рисунок нужно воспринимать как пространство на бумаге, где существует плоскость и пропорции всех находящихся предметов, свет и тень, которая направляется по форме предмета.
Основные геометрические фигуры:
Двухмерные плоские фигуры
Трехмерные фигуры, у которых есть объем
Абсолютно все предметы в основе своего построения имеют эти фигуры.
Куб — фигура, основой которой является трехмерное изображение в пространственном соотношении листа. В кубе есть все геометрические параметры, такие как: вертикальность, горизонтальность и глубина . В самом кубе заложено понятие рисунка в целом.
Для начала понимания рисунка, мы поработаем именно с ним. При помощи образно-логических построений, мы с вами будем развивать мышление за счет аналитики формы . Для большего понимания и анализа рисунка есть несколько упражнений.
Упражнения
Садимся за мольберт, берем большой лист бумаги, можно недорогой, или вообще кусок обоев (в этом упражнении бумага особо значения не имеет) . Рисуем квадрат, естественно пытаемся сделать так, чтобы его стороны были ровными, а линии прямыми.
Итак, — мы видим обычный квадрат, совсем неинтересный и не впечатляющий, но это только в данный момент…
Делаем из квадрата куб карандашом: прорисовываем линии от граней примерно с углом 45 градусов . Дорисовываем заднюю часть и… у нас получается кубик. Но снова никакого пространства у нас в листе мы не видим. Свободно можно попутать ближайшие и дальние грани. Сейчас это просто несколько линий на бумаге.
Чтобы нам чувствовать пространство, нужно придать рисунку плавности . То есть сделать так, чтобы нам было ясно, где передняя часть рисунка, а где задняя.
Сторону куба, находящуюся ближе к нам, нужно выделить, сделать четче и передать активнее. Берем свой карандаш и наведем жирным тоном передние грани. Сейчас мы уже можем увидеть, где ближняя сторона, а где сторона находится дальше от нас.
Вот таким способом мы передали пространство, чтобы добиться желаемого результата. Но это далеко не все. Сейчас важно правильно передать плавность, чтобы получить объемность в рисунке .
Представляем вашему вниманию небольшой видеоурок на тему оптических иллюзий.
Попробуем понять принцип взаимодействия квадрата и окружности на перспективном рисунке. Научиться проверять правильность квадрата, вписывая в него окружность.
Изобразите в перспективе горизонтальный и вертикальный квадраты. Проверьте правильность их изображения при помощи вписанных окружностей.
Прежде, чем приступать к выполнению этого задания, внимательно рассмотрите схему на рис. 2.8. Точки касания сторон квадрата к окружности (точки 1, 2, 3, 4) делят стороны квадрата пополам. Средние линии квадрата и его диагонали пересекаются в центре окружности. Противолежащие стороны квадрата и соответствующие им средние линии параллельны и расположены на равном расстоянии друг от друга. Рассмотрите также рис. 2.9. На примере окружности и квадрата во фронтальной перспективе хорошо видно, что центр эллипса и центр окружности — две разные точки. Диаметр окружности, являющийся малой осью эллипса, делится точкой центра окружности на два разных по величине отрезка: ближний к зрителю — больше, дальний — меньше (по закону перспективного сокращения), а точка центра эллипса делит этот же диаметр — малую ось эллипса — ровно пополам.
Нарисовать квадрат в перспективе можно в разной последовательности, например, сначала изобразить одну прямую — сторону квадрата, а затем другую, ей перпендикулярную, отложить на этих прямых от точки их пересечения отрезки, равные стороне квадрата, а затем от полученных вершин достроить остальные стороны, сводя параллельные прямые в точки схода. Или иначе — сначала провести две параллельные прямые, а затем еще две, перпендикулярные двум первым. В любом случае эта задача кажется простой только на первый взгляд. На самом деле слишком много позиций (степень схождения параллельных сторон квадрата, их направления и размеры) рисовальщику приходится определять на основании своего личного опыта, а его, как известно, иногда бывает недостаточно. Именно поэтому правильность квадрата необходимо проверить, например, вписав в него окружность. При любом положении квадрата для того, чтобы вписать в него окружность (в перспективном рисунке — эллипс), необходимо найти точки касания сторон квадрата к вписанной окружности (точки 1 — 4) и определить положение осей эллипса. Если вписанный эллипс касается сторон квадрата в заданных точках и симметричен относительно осей, то квадрат нарисован верно.
Горизонтальный квадрат. Нарисуйте горизонтальный квадрат по представлению (рис. 2.10). Найдите точки касания, для этого через точку пересечения диагоналей проведите прямые, параллельные сторонам квадрата и уходящие с ними в одну точку схода (рис. 2.11). Окружность, лежащая в горизонтальной плоскости, изображается на перспективном рисунке в виде эллипса с вертикальной и горизонтальной осями. Проведите через точку пересечения диагоналей вертикальную линию — малую ось эллипса. Большая ось эллипса перпендикулярна малой оси и проходит через точку, смещенную от пересечения диагоналей квадрата (центра окружности) ближе к зрителю (рис. 2.12). Таким образом, мы получили две оси эллипса и четыре точки, определяющие его габариты. Продолжите рисунок: сначала легкими движениями карандаша наметьте эллипс, затем уточните линию, добиваясь того, чтобы она действительно касалась сторон квадрата в точках 1, 2, 3, 4 (рис. 2.13). Проверьте симметричность полученного эллипса относительно его осей.
Вертикальный квадрат. При вертикальном положении квадрата точки 1, 2, 3, 4 найдите, как и в предыдущем примере: проведите через точку пересечения диагоналей квадрата прямые, параллельные его сторонам (рис. 2.14).
Несколько сложнее определить направление осей эллипса. Чтобы это сделать, представьте, что изображаемый эллипс является основанием цилиндра, лежащего на горизонтальной плоскости (рис. 2.15). Ось цилиндра на перспективном рисунке всегда перпендикулярна большой оси эллипса основания и совпадает с его малой осью. Проведите ось цилиндра через точку пересечения диагоналей квадрата. Направление этой оси можно определить, опираясь на опыт рисунка с натуры. Задача значительно упрощается в том случае, если вертикальный квадрат, в который вы вписываете окружность, является гранью куба. Тогда ось цилиндра (она же малая ось эллипса) параллельна горизонтальным ребрам куба и на рисунке идет с ними в одну точку схода. Таким образом, мы определили положение малой оси эллипса. Большая ось будет ей перпендикулярна и пройдет через центр эллипса, смещенный от пересечения диагоналей (центра окружности) ближе к зрителю (рис. 2.16). На двух осях и по четырем точкам касания изобразите эллипс (рис. 2.17).
На рисунках, иллюстрирующих последовательность вписывания окружности в горизонтальный и вертикальный квадраты, представлены идеальные ситуации. В действительности эллипс, вписанный в квадрат, часто получается несимметричным относительно осей, а потому его приходится уточнять и, как следствие, изменять очертания квадрата. В этом случае работа идет как бы методом последовательных приближений и уточнений, что трудно и долго. Часто на рисунках остаются не вполне правильные квадраты и не вполне правильные эллипсы, а лишь фигуры, близкие к ним.
Правильный эллипс нарисовать легче, чем построить правильный квадрат в перспективе. Именно поэтому современная методика предлагает не проверять и исправлять подобным образом уже нарисованные квадраты, а строить их, описывая вокруг окружности.
Как правильно рисовать объемные фигуры карандашом. Рисование геометрических фигур. Ждем Вас в нашей художественной студии
Продолжаю рассказывать об упражнениях, улучшающих навык рисования, в данном случае геометрических фигур. Будем тренироваться рисовать их двухмерное отображение, трехмерное отображение и затенение фигур. Итак, Упражнения для рисования. Часть 2. Приступим.
Но прежде, чем приступить к упражнениям, напоминаю, что есть .
Двумерные фигуры
Круг. Сначала будет сложно нарисовать ровный красивый круг, поэтому поможем себе с помощью циркуля. Легкой линией нарисуем окружность и обведем ее. Один раз, потом еще, запоминаем характер движения и пытаемся воспроизвести. Можно помогать себе проставив несколько точек для начала. Со временем, если выполнять это упражнение, круги будут получаться все лучше и краше. 🙂
Треугольник. Пробуем нарисовать равносторонний треугольник. Опять же, чтобы себе помочь для начала можем нарисовать окружность с помощью циркуля и уже в нее вписать нашу фигуру. Но потом обязательно пробуем нарисовать самостоятельно.
Квадрат. Да, сложно с первого раза нарисовать все стороны одинаковыми и все углы 90 градусов. Поэтому, чтобы запомнить правильную форму используем линейку. Потом рисуем по точкам, а потом самостоятельно, без вспомогательных инструментов.
После квадрата рисуем ромб, то есть тот же квадрат, но повернутый на 45 градусов.
Рисуем 5-конечную звезду, рисуем не отрывая карандаш от бумаги. Для первого раза можно воспользоваться циркулем и вписать звезду в окружность, чтобы добиться симметрии.
Шестиконечная звезда. Рисуется как 2 равносторонних треугольника.
Восьмиконечная звезда. Рисуется как 2 квадрата.
Яйцо. Это овал, который на одном конце уже, чем на другом.
Полумесяц. Эту фигуру нарисовать не так просто, как может показаться на первый взгляд. Сначала попробуйте нарисовать его самостоятельно, а потом уже при помощи циркуля, помня, что месяц это фактически часть двух пересекающихся окружностей.
Трехмерные фигуры
Переходим к трехмерным фигурам. Начнем с куба. Рисуем квадрат, потом еще один квадрат чуть выше и правее, соединяем углы ровными линиями. Получаем прозрачный куб. Теперь попробуем нарисовать тот же куб, но уже без видимых линий внутри.
Теперь рисуем куб в другом ракурсе. Для этого сначала рисуем плоский параллелограмм в форме ромба, опускаем них перпендикуляры и рисуем такую же фигуру в основании. И такой же куб, но без видимых линий.
Теперь попробуем нарисовать цилиндр в разных ракурсах. Первый цилиндр будет прозрачный, рисуем овал, опускаем вертикали вниз и рисуем овал-основание. Затем рисуем цилиндр с невидимой нижней внутренней гранью и цилиндр с невидимой верхней внутренней гранью.
И завершаем этот цикл фигур рисованием конуса в разных ракурсах.
Рисуем круг. Намечаем легкой штриховкой тень в левом нижнем углу. Тень должна быть в форме полумесяца. Далее добавляем тона в тень при помощи большего нажима на карандаш, затеняем от центра к краю по принципу от светлого к темному, при этом у границы круга оставляем небольшой участок более светлой тени, это рефлекс. Дальше затеняем падающую тень, чем дальше от основания шара, тем светлее. Тень находится с противоположной от источника света стороны. То есть в нашем случае источник света находится в верхнем правом углу.
Теперь затеняем куб. В данном случае свет также находится в верхнем правом углу, а значит самая темная тень будет с противоположной стороны, сверху тени не будет, а правая видимая грань будет иметь более светлый тон. Соответственно с этим и наносим штриховку.
По такому же принципу затеняем стороны на кубе и конусе, важно следить за формой объекта и тем, как на него ложится свет. И падающая тень также должна соответствовать форме объекта.
И еще, в упражнениях для затенения используется диагональная штриховка, но я бы советовала пробовать в дальнейшем штриховать по форме объекта, тогда объект будет более объемный. Но штриховка по форме, да и вообще штриховка — тема довольно обширная, я уже начала ее изучать и скажу, что без тренировки рук и ровного быстрого штриха тут никуда, так что даже если делать только то, что я уже выложила, делать регулярно, то рисунки неизбежно будут становиться все лучше.
Дорисовываем и продолжаем 🙂
С данного урока начинается наша программа обучения рисунку. В этом задании рассматривается тема рисования простых геометрических фигур .
Рисование геометрических фигур можно сравнить с изучением алфавита для того, кто осваивает иностранный язык. Геометрические формы – первая стадия построения объекта любой сложности. Это хорошо видно в компьютерном моделировании, где построение трехмерного космического корабля начинается с простого кубика. В рисунке все изображаемые предметы всегда состоят или делятся на простые геометрические формы. Для обучения рисунку это значит ровно одно: научившись правильно изображать геометрические фигуры, научитесь рисовать все остальное.
Построение геометрических фигур.
Начинать построение нужно с анализа модели, образно говоря, проникнуть вглубь конструкции на уровень вершин и линий. Это значит, представить геометрическую фигуру в виде каркаса, состоящего только из линий и вершин (место пересечения линий), путем воображаемого удаления плоскостей. Важным методологическим приемом является изображение невидимых, но существующих линий. Закрепление такого подхода с первых уроков станет полезным приемом для рисования более сложных моделей.
Далее, под руководством педагога наметить на листе расположение линий и вершин, легкими, скользящими движениями, без нажима на карандаш.
Положению рисунка на листе стоит уделить отдельное внимание по нескольким причинам:
- Нахождение центральной оси листа поможет при дальнейшем построении как отправная точка для вертикальных линий конструкции.
- Определение линии горизонта, для правильного изображения перспективы.
- Учет светотеневой моделировки, собственные и падающие тени, чтобы они поместились в пространстве листа и уравновешивали друг друга.
После нанесения основных конструктивных линий следует детальная прорисовка видимых ребер предмета, в случае с объектами вращения (шар, конус) это внешние края формы.
За конструктивной частью следует штриховая моделировка. На мы подробно разбираем правила и технику нанесения штрихов на геометрические предметы.
Профессиональное обучение рисунку легко сравнить с уроками музыки, где сухие правила и точные схемы в конечном итоге приводят будущего композитора к творческим произведениям. Так и в рисунке законы построения форм, правила перспективы, схемы расположения теней помогают художнику создавать уникальные шедевры.
Отчего опытные художники могут быстро наносить сложные рисунки, не тратя много времени на разметку, построение? Потому что вначале крепко заучили правила и каноны, и теперь достаточно ясно представляют строение любой формы. Схематичный рисунок освобождает внимание автора от конструкции и сосредотачивает фокус на композиции, идее, образе своего творения. Существует мнение, что заученные схемы не дадут художнику полностью раскрыться.
Стоит посмотреть, с чего начинали такие креативные мастера как Пикассо и Дали, чтобы понять ошибочность данного суждения. Но лучшей проверкой станет обучение в нашей студии, где вы на практике убедитесь в плюсах академического подхода.
Ждем Вас в нашей художественной студии!
Если вы новичок в изобразительном искусстве и хотите узнать, как создавать лёгкие 3D-рисунки карандашом для начинающих, то наша статья поможет разобраться вам с первыми азами.
3D-картины подняли искусство рисования на совершенно новый уровень. Множество современных художников создаёт умопомрачительные 3D-рисунки, которые буквально вырываются в воздух с поверхности бумаги за счёт наложения теней, безупречной перспективы, а также использования нескольких листов бумаги для создания более сложной композиции.
Вы сможете научиться рисовать так же, как эти мастера, но для начала вам нужно поподробнее узнать об основных принципах и приёмах. В этом мы вам поможем.
Основные принципы
Первый момент, который необходимо освоить при рисовании объёмных изображений, это как правильно штриховкой покрыть на сфере место, наиболее удалённое от света.
Те точки, на которые падает свет, должны быть наиболее светлыми, а поверхность объекта должна становиться всё темнее, чем дальше вы продвигаетесь от источника света.
Если вы планируете сделать снимок своего рисунка, как это делают многие художники, вы должны обратить внимание на фактический источник света в том месте, где вы работаете. Посмотрите, как он влияет на объект, который вы рисуете. Это может усилить впечатление, будто объект на рисунке – на самом деле в комнате.
Не забудьте проработать вопрос о том, как выглядят различные текстуры (камень, кирпич, листья) в зависимости от освещения.
Это не такая уж сложная штука, когда помнишь о её основном правиле: предметы, которые расположены к зрителю ближе, изображаются крупнее, чем те, которые расположены дальше.
Если вы хотите визуально проверить это правило и удостовериться, что оно действительно так работает, просто найдите длинную улицу, встаньте в её конце посередине и посмотрите в противоположную сторону. Ширина дороги будет постепенно уменьшаться к горизонту.
Когда вы будете рисовать свою 3D-картинку, подумайте, как будет располагаться зритель, как он будет на неё смотреть — со стороны или сверху?
Выход за пределы листа . Некоторые художники используют свою руку как добавление к рисунку. Дело в том, что рука взаимодействует с рисунком и добавляет ощущение реальности, дополняет 3D-эффект.
Сначала на некоторых фотографиях видно, что мастер как будто держит своё изображение пальцами… Но только потом мы видим, что это всего лишь иллюзия.
Некоторые умельцы выбирают для взаимодействия с картинкой настоящий бокал или карандаш. Они располагают их каким-то образом рядом с изображёнными объектами или даже на них. И иногда не понятно, где реальность, а где творчество!
Рисование 3D-фигур
Если вы хотите научиться рисовать 3D-картинки карандашом реалистично, то вам следует начать с основных объёмных геометрических форм. Когда вы поймёте принципы изображения многомерных форм, вы сможете применить полученные знания к любым объектам.
В нашем уроке мы разберём, как поэтапно создать карандашом объёмные рисунки таких фигур, как призма, пирамида, куб, цилиндр, сфера и конус.
Обе эти фигуры в своей основе используют треугольники.
При рисовании призмы начните с обычного равнобедренного треугольника и маленькой точки где-то в стороне (точка на горизонте). Не имеет значения, с какой стороны вы её выбрали.
Начните строить две пунктирные линии от вершины треугольника к нашей точке и от угла основания, который к ней ближе. Определите, какой длины будет призма. Помните, что дальнее видимое её ребро будет параллельно стороне треугольника, относительно которой выстраивалась призма.
Чтобы создать пирамиду, нарисуйте равносторонний треугольник, его основание сделайте пунктиром. Из вершины постройте вертикальный отрезок вниз. Он должен опускаться чуть ниже пунктирной линии.
Нижнюю точку отрезка соедините по диагонали с углами у основания треугольника. Ничего, если углы будут не совсем идентичны, это даже добавит реалистичности.
Эту фигуру можно изобразить несколькими способами, ниже вы увидите два из них.
Способ 1. Нарисуйте два квадрата одинакового размера. Один должен частично перекрывать другой, насколько сильно – на ваше усмотрение. Соедините верхние и нижние углы двух квадратов, таким образом образуются рёбра фигуры.
Способ 2. Принцип рисования здесь напоминает подход, который мы применяли при изображении пирамиды. Только на этот раз вам надо сделать три равные параллельные прямые. Две линии по бокам должны располагаться на одном уровне, а та, что посередине, должна быть опущена чуть ниже.
Соедините верхние точки трёх линий диагоналями, сделайте то же самое с нижними точками. Через верхние точки проведите линии, параллельные ближайшим к вам верхним рёбрам куба. На их пересечении образуется точка – дальний угол куба.
Цилиндр
Начните с овала. Не волнуйтесь, если он не получается у вас ровным с первого раза. Тренируйтесь!
Если ваш овал вертикальный, то из крайних его точек сверху и снизу проведите перпендикулярные горизонтальные прямые (если овал горизонтальный, то, соответственно, наоборот). Проводите их до тех пор, сколько вам требуется, смотря какой длины вы хотите получить цилиндр.
Соедините крайние точки нарисованных отрезков изогнутой линией, которая повторяет округлость овала. Для того, чтобы убедиться, что верхняя и нижняя части цилиндра совпадают по форме, попробуйте перевернуть рисунок вверх ногами или на 90 градусов. Это изменит вашу точку зрения, и любые несоответствия будут выделяться.
Есть несколько различных по сложности способов изображения сферы . Но в любом случае рисунок сферы будет начинаться с простой окружности. Нарисуйте её от руки или обведите какой-нибудь предмет, например, стакан.
Чтобы круг стал похож на объёмную сферу, нужно правильно заштриховать её поверхность, определить теневые области. Сначала определяется самое светлое место шара, то, куда падает свет. Затем с противоположной стороны начинается интенсивная штриховка. Там тень будет самой тёмной.
Постепенно продвигайтесь к светлому участку, снижая интенсивность цвета так, чтобы в итоге прийти к самому светлому цвету. Старайтесь, чтобы ваши штрихи повторяли форму шара, не были резкими, перпендикулярными.
Чтобы переходы от тени к светлому месту были минимально заметны, растушёвывайте поверхность сферы пальцем или специальной растушёвкой.
Эта фигура представляет собой нечто среднее между цилиндром и пирамидой. Итак, используем наши знания об обеих фигурах и применим сейчас в рисовании.
При попытке нарисовать какую-либо фигуру в 3D важное значение имеют прямые линии. Для этого, особенно по началу, используйте линейку или какой-то другой плоский предмет из прочного материала (чтобы не прогибался) с прямым краем.
Будьте внимательны к углам и расположению линий. Например, такие фигуры, как куб, имеют прямые углы и параллельные линии в основе. А у конуса углы могут быть разными.
Сравнивайте углы с помощью карандаша. Если вы хотите достичь действительно техничного рисунка, то используйте транспортир. Карандаши и ластики – ваши друзья. Всякий раз, когда только возможно, рисуйте карандашом, чтобы получить правильные углы и линии.
Итак, вы научились поэтапно рисовать карандашом 3D-рисунки для начинающих, основные геометрические формы, которые являются базой для различных предметов. Поэтому полученные знания вы можете применить в рисовании многих объектов.
Как научиться ложить штрих по форме предмета- будем усовершенствовать свое мастерство владения карандашом и учиться создавать рисунок геометрических фигур, создавая их объем. В нашем арсенале есть куб, шар, конус и цилиндр.
Наша работа будет разделяться на две части. Первая часть- мы рисуем по- представлению. Возможно у вас есть макеты этих фигур, если нет, то тогда можете заглянуть на страницу как сделать макет геометрических фигур и, собственно, сделать их, но начнем мы с вами с другого. Мы начнем с понимания, анализа формы сначала без макетов. Вы можете сначала их создать и иногда посматривать на них при рисовании, но главное сейчас- научиться анализировать, логически мыслить, вся ваша работа сейчас заключается в том, что- бы думая, без натуры, научиться передавать форму этих основных фигур. Изначально ведь работа проходит в голове, а не перед глазами. Верно?
Вторая часть- будем рисовать с натуры, но так- же, как и в первом случае, не цепляемся к натуре сильно, а в первую очередь думаем и анализируем сами, и теперь уже проверяем себя с тем, что нам показывает натура.
Итак, первая часть. Можно рисовать на формате А3. Берем ватман, карандаш и рисуем фигуру, также не плохо использовать знания перспективы при построении ее. А потом начинаете «ложить» штрих по форме, вылепливая объем фигуры при помощи своего ума и карандаша.
Мы уже знаем, что светотень распределяется по форме предмета, создавая тональные градации, или зоны. Пока возьмем три основные- свет, полутень и тень. Ограничиваемся только фигурами, не используя все пространство.
Давайте нарисуем куб.
Избегаем ошибок. У меня на рисунке слева сильно передана перспектива , чересчур, так не делайте.
Здесь достаточно совсем немного передать ее, слегка исказив форму. Посмотрите на рисунок справа. Видите разницу между передней стенкой и задней?
Этого достаточно. Не такие у нас большие размеры используются, что- бы мы из малых форм превращали архитектуру.
Поговорим о светопередаче. Свет, тень и полутень показаны.
Но не забудьте о золотом правиле- свет удаляясь по форме предмета темнеет, тень- светлеет. Смотрите: свет, удаляясь в перспективу слегка теряет свою яркость, добавьте туда немного штриховочки. А теперь полутень и тень, та- же картина, но в обратном порядке. Тень удаляясь слабеет, слегка светлеет. Но все равно, общий тон тени никогда не будет светлее общего тона света, и полутень тоже не вырывается из своих тоновых границ. Все на своем месте.
Смотрим еще: как мы проводили обучение с первого нашего урока, см. основы рисунка , о том не забываем и сейчас. Ближние к нам углы и грани выделяем, делаем на них акценты. Ближняя грань и углы у меня акцентированы, чем и берут основное внимание на себя, все остальное плавно уходит в пространство. Но сильно здесь это пространство не нужно передавать, так как расстояния у нас, в принципе, маленькие.
Замечание: как определить общий тон- прищурьте немного глаза. Резкость убавится и вы сможете увидеть все в общем. И еще не надо смотреть на работу «влоб», почаще отдаляйте ее от себя, рассеивайте зрение, не цепляйтесь за детали.
И дальше остальные фигуры. Эти фигуры, в общем, у нас достаточно обтекаемы, заокруглены, так- что замечаем следующее:
Допустим, первым в ряду стоит шар. Акцентом на нем здесь является тень и наиболее сильна она будет в том месте, где шар приближен к нам более всего. По краям у меня акцентов нет, так как там форма ушла в пространство- учитывайте этот момент при рисовании обтекаемой формы.
Так- же дело обстоит и с цилиндром и конусом. Там, где форма начинает заворачиваться и уходит в пространство- акцент делать не стоит. Но где и нужно акцентировать форму, то там, где идет излом формы и там, где это будет ближе всего к нашим глазам.
Обратите внимание на конус- нижняя часть его к нам приближена больше, чем верхушка. Значит, нижняя часть его будет передана сильнее, а поднимаясь к верху слабее- смотрите на тень, внизу она сильнее, в то время как поднимаясь вверх она теряет свою активность. Не делайте ее одинаковой тональности по всей высоте. Величины эти здесь не огромны, но все равно существуют, иначе условное пространство правильно не передать.
Останавливаю ваше внимание на штриховке. Это что- ни- на- есть стопроцентный штрих, который ложится по форме. Несмотря на то, что он несколько однообразен и скучноват, но очень полезен в плане обучения. Он учит дисциплинированности, концентрации внимания, учит делать ровные линии и просто чистоте исполнения. Рекомендую выполнить эту работу с применением именно этого штриха, просто старайтесь «вылепливать» форму геометрической фигуры, прочувствуйте руками и глазами весь ее объем и как ее форма «живет» в пространстве. Написано странно, но стараюсь как можно сочнее передать вам всю прелесть этого упражнения. А о штрихах, которые должны ложиться по форме предмета и какие ими не являются мы с вами дальше еще поговорим.
И непереживайте, если что- то не будет получаться. Никто не застрахован от ошибок, а их может быть много и идеального на свете не существует ничего. Но у каждого из нас есть возможность попробовать еще раз, дабы сделать еще лучше.
Как нарисовать геометрические фигуры
Как нарисовать геометрические фигуры- теперь попробуем нарисовать геометрические фигуры с окружением. Окутаем их воздухом, нарисуем в пространстве. Берем основные:
Первым у нас пусть пойдет цилиндр.
Ставим цилиндр на предметную плоскость- стол, освещение ставим так, что- бы тень от фигуры падала красиво на предметную плоскость,
не была ни сильно растянутой, ни маленькой- была гармоничной и подчеркивала объем фигуры.
Натяните бумагу на
планшет , чтобы создать чистый рисунок.
Берите планшет размером 30-40, для такой работы вполне достаточно.
Теперь нам нужно закомпоновать наш цилиндр в плоскости листа, найдите его гармоничное место в пространстве листа, учитывая и тени, обязательно. Используйте для поиска пропорций глазомер, подкрепляйте его ощущениями линейной перспективы.
Обязательно передайте предметную плоскость. Фигура у нас не «плавает» в пространстве, она находится на предметной плоскости!
При построении фигуры обязательно показывайте и невидимые грани, показывайте как строите- линии построения. Это нужно более вам, чем зрителю. Расставляйте акценты там, где это нужно, показывайте пересечение плоскостей. Не забывайте о перспективе. Если вы заметили, то нижняя плоскость цилиндра нам видна больше, чем верхняя, оно и правильно, так как линия горизонта (по крайней мере у меня, у вас может быть по- другому), дает такой обзор.
Посмотрите как строится тень- ее можно правильно передать, используя линии построений. Образно: от источника света идут лучи, которые разделяются на два вида, одни- освещают фигуру, останавливаются на ней, потому за фигурой дальше света не будет. А лучи света, которые не попадают на фигуру идут дальше, освещая все на своем пути. И эту границу мы с вами можем показать. И еще: тень, удаляясь от фигуры, будет иметь тенденцию к некоторому увеличению, это напоминает обратную перспективу. Понимаете почему? Если направить лучи наоборот, то линии построения тени сойдутся в одной точке- точке, из которой идет свет.
Вот примерно так у вас должно получиться.
Дальше в принципе натура нам уже и не нужна, так как все можно проанализировать самостоятельно. Включить аналитическое мышление и
логически рассуждать. Но, все- же, давайте разбирать дальше:
По фигуре видно, что свет падает со стороны и сверху. Значит, верхняя плоскость цилиндра у нас будет освещена более всего, и свет так- же
будет падать на предметную плоскость, так как она тоже как и плоскость цилиндра- горизонтальна. Вертикальные плоскости- стена и обрыв
предметной плоскости, а так- же, сам объем цилиндра будут получать меньше освещения, так как падающего основного света они не получают.
Дальше: предметную плоскость мы черной не делаем- угол предметной плоскости получает в данном случае достаточно света, что- бы тень не была здесь самой активной. Но выделить ее- предметную плоскость все- таки нужно. Это достигается за счет выделения угла предметной плоскости.
Дальше: наша предметная плоскость получает основной свет, но нам нужно показать, что она горизонтально расположена. И мы знаем, что удаляясь свет гаснет, слабеет. Вот чем дальше от нас предметная плоскость будет уходить, тем слабее ее свет будет- ложим штрих таким образом.
Теперь надо разобраться с той частью цилиндра, что будет находиться в тени. Цилиндр у нас расположен вертикально к предметной плоскости, значит основной свет будет падать на горизонтальную его верхнюю плоскость. Все остальное- в тени, за исключением того участка, где свет скользит по форме, так как свет падает не точно сверху, а немного со стороны- этот участок у меня выделен самым светлым на вертикальной плоскости его. Общая- же тень цилиндра активнее стены, так как цилиндр имеет активную собственную тень и сам к нам ближе, хоть стена также расположена вертикально.
Стена- же будет темнее предметной плоскости, потому как она вертикальна- значит света здесь будет меньше, и потому, что она будет находиться дальше всего, будет на заднем плане. Ложим штрих таким образом.
Падающая тень фигуры будет самой активной, но она так- же лежит на предметной плоскости, а потому- удаляясь на ней будет немного становиться слабее.
Ну и осталось расставить акценты там, где это необходимо- изломы форм, которые будут к нам располагаться ближе- будут акцентированы.
Если по началу рука не слушается, трудно держать
карандаш и трудно ложить штрих по форме, да и четко определить саму форму штрихом трудно, то есть возможность поработать так, как показано на рисунке слева.
Легонько намечаете изломы формы. То- есть: допустим, вы в курсе, как распределяется свет по форме предмета. Вы знаете, что этих зон пять: блик, свет, полутень, тень и рефлекс. Это все точно, но условно. Что- бы передать более качественно объем фигуры, вы можете намечать сколько угодно изломов, и чем их будет больше, тем объем фигуры будет показан мягче. Зрительно разделяете фигуру на эти зоны и ложите обычный прямой штришок, но так, что- бы вылепить объем- используете частоту стежка- штриха или силу нажима карандаша.
Здесь прошу вас не путать два понятия: как распределяется свет по форме предмета и как ложится штрих по форме предмета. В первом случае у нас- 5 зон, во втором- можем намечать столько зон, изломов формы, сколько вам будет нужно. Но не черните, все вспомагательные линии должны быть малозаметными.
Замечание: если вы могли заметить, посмотрев на этот рисунок, то увидели, что с более освещенной стороны
конуса стена на заднем плане темнее, а с другой, менее освещенной стороны конуса- стена светлее.
Дело в том, что стена одинакова и там и там, но так уж видит наш глаз.
Для остроты ощущения действительности, для наилучшего акцента света и тени, для гармоничного осязания нашим глазом рисунка, да и в
конце концов, давайте сделаем нашему глазу приятное! Пусть он видит в рисунке то, что видит в натуре. Это только легкий нюанс,
который только обогатит наш рисунок, можно ненавязчиво передать.
Дополнение: смотрите как строится тень у конуса.
Дальше давайте сделаем рисунок шара.
Построение вы можете увидеть слева.
Заметьте, как строится тень фигуры. С падающей мы уже разобрались, вроде: определяем с помощью глазомера и подкрепляем знаниями перспективы.
Не забывайте, что тень падает на предметную плоскость- это нужно передать и понимать.
А вот как дела обстоят с собственной тенью? Интересно, что если провести линии от точки освещения до центра шара, через который проходит диаметр, который образует круг тени, то этот диаметр будет перпендикулярен линии, проведенной до точки освещения. Если это понять, то и как ложить штрих по форме шара, дабы показать собственную тень- совсем не сложно.
Теперь мне что- то стало скучновато рисовать в одной манере и захотелось поэкспериментировать.
Посмотрите на работу справа. Как вы думаете, она выполнена штриховкой? Не похоже. Она выполнена тональным пятном с использованием
карандашей различой степени мягкости. Если вы возьмете карандаши с цельным грифелем, без деревянной оправы, и будете просто набирать
тон на бумаге, а не штриховать, то у вас тоже получится такой вот рисунок.
А что еще, кроме техники исполнения у нас не так? Свет наместе, тени тоже, значит- все в порядке.
Но все- же рассмотрим детальнее. Самый яркий свет у нас будет на освещенной стороне шара, на плоскости он будет не таким активным и будет слабеть с удалением от нас. Самая темная тень будет падающая, на изломе предметной плоскости будет света немного больше, но тем не менее, акцентируем эту область.
Посмотрите на собственную тень шара- я ставлю акцент на той области его, которая будет ближе к нам, и заворачиваясь по форме, тень
будет терять активность. Помните: шар- форма обтекаемая.
Стена
в полутени, притом на заднем плане- вот пусть там ненавязчиво и остается. Единственное- она будет «играть» с объемом шара.
Со стороны света стена будет казаться несколько темнее, со стороны тени- светлее. Давайте и здесь сделаем нашему глазу приятное;)
Как научиться ложить штрих по форме предмета. Штриховка
Вот тут мы плавно подошли к тому, о чем уже говорили в самом начале этой страницы. Как ложится штрих по форме предмета и какой штрих таковым не является. Дело в том, что у каждого рисовальщика, в процессе работы или учебы вырабатывается свой определенный стиль штриха. Конечно, есть каноны, у различных исторических времен свои собственные каноны рисования и штриха, но совсем не обязательно им придерживаться. По желанию. Я считаю, если с помощью штриха можно передать объем фигуры и само пространство в листе, то абсолютно все равно, что с себя представляет этот штрих. Главное, что- бы было грамотно все сделано и красиво. По простому- не делайте соломы, учитесь рисовать красиво. К штриху это так- же относится. На этой странице мы учились делать штрих, продолжим еще немного.
Вот например вот так, как я рисую кубик, который у нас еще остался не нарисован.
1. Определяем место фигуры в листе
2. Располагаем фигуру на предметной плоскости и находим его конструкцию и его тень, не забывая учитывать перспективу
3. Определяем место света и тени- ложим легкий штрих. Это дает нам возможность сразу определиться с распределением света и тени в нашем рисунке, разделить их
Если вы посмотрите на штрих, которым выполнена работа, то он достаточно необычен, верно? На уроках рисунка к такому штриху лучше не прибегать, не пугайте учителей, у них не такие современные прогрессивные взгляды, как у вас. Но в своих творческих работах такой штрих применять можно, почему бы и нет? Ведь рисунок сделан по всем законам. Передано пространство в листе, показана форма предмета, переданы основные тональные соотношения в нашем рисунке. Но к этому еще мы добавили штрих, который делает работу интересной и воздушной. Ну а дальше опять, разбираем рисунок, анализируем:
Давайте пройдемся по основным
тональным отношениям, для начала по теням:
самая темная тень- падающая, дальше идет собственная тень куба. Излом предметной плоскости занимает третье место, ее мы выделяем,
но не черним, так как там достаточно света. И четвертая- стена, на которую тоже попадает свет, можно сказать, что стена находится
в полутени, но дальше всего. Смотрите как играет полутень стены с формой куба: со стороны освещенной части куба стена темнее, со
стороны тени- светлеет. Эти градации могут быть очень невелеки, но они присутствуют.
Дальше анализируем свет: самая светлая и освещенная часть будет верхняя плоскость куба, вторая по светлоте- предметная плоскость, которая находится перед нами горизонтально и уходя в пространство- теряет свет.
На изломах форм делаем акценты. Ближние грани куба и углы выделяем, это поможет вытащить его из пространства наперед.
И не забываем- свет удаляясь темнеет, гаснет, тень удаляясь теряет свою активность и несколько светлеет, но учитываем золотое правило: самый темный полутон на свету светлее самого светлого полутона в тени.
На последок: если вы решите поэкспериментировать со штриховкой. Так как и варьируется тональность свето- тени, которую мы передаем в пространстве листа, так и штрих может изменять форму- поиграйте с размером штриха. Стена выполнена штрихом среднего стежка, довольно статичная. Куб выполнен мелким и активным штришком, придающим кубу динамику. А предметная плоскость выполнена длинными стежками, довольно тривиальными и малоинтересными. Так что, даже штрих помогает выявить в картине главное действующее лицо- куб, который выполнен наиболее динамичным штрихом, притягивающим внимание, на мой взгляд. А как вам кажется?
Попробуйде сделать что- то свое, поэкспериментируйте, тогда самая простая работа будет выполняться с удовольствием, большим вниманием и огромным интересом. А когда вы сидите, выполняете работу, например- стараетесь ровно положить штрих по форме, да еще у вас и получается, и при этом начинаете замечать, что от концентрации вашего внимания замирает дыхание, вот в эти самые минуты и ощущаешь всю предесть рисунка и получаешь несказанное удовольствие.
Рисование геометрических фигур многим может показаться скучным занятием, но на самом деле это базовое упражнение для всех художников. Именно геометрические фигуры помогут разобраться с перспективой, объемом, правильностью формы и композицией. Так что если вы решили заняться академическим рисунком или изобразительным искусством в целом, вам обязательно надо научиться тому, как нарисовать цилиндр, шар, куб, тетраэдр и другие фигуры.
Базовый рисунок цилиндра
Карандаш — это основной инструмент художника. Так что вначале надо научиться тому, как нарисовать карандашом. Ведь именно карандашный набросок является основой для большинства других техник.
Для удобства наметим вертикальную ось, а также две горизонтальных — для верхнего и нижнего овала. Длина верхнего и нижнего овала должна быть одинаковой. Что до ширины, у нижнего она должна быть больше.
На следующем этапе сотрем оси, оставив только основные линии.
Потом наведем контур маркером. Делать это надо аккуратно, чтобы линии были максимально ровными и плавными.
Теперь займемся светом и тенью. Это самый главный этап, ведь именно за счет света и тени появляется объем. Также важно обозначить падающую тень.
Все, мы справились с задачей. Для того, чтобы лучше разобраться и набраться опыта, можно попытаться изобразить и другие геометрические тела: куб, шар, пирамиду и т. д.
Темный цилиндр с бликом
Классическим вариантом изображения геометрических тел является их построение по осям — вертикальным и горизонтальным. Но можно воспользоваться и другим способом — мы опишем его, когда будем учиться тому, как нарисовать цилиндр поэтапно.
Вначале рисуем два овала — верхний и нижний. Обратите внимание — верхний овал более узкий, чем нижний.
Потом соединяем овалы двумя параллельными линиями.
На следующем этапе надо убрать все вспомогательные линии.
Теперь поработаем с тенями. Важно обозначить блик, света, полутени тени и рефлекс (более светлый участок после самого темного участка). Также добавляем падающую тень в стороне, противоположной по направлению к источнику света.
Два цилиндра с тенью
Для того чтобы понять, насколько важна падающая тень в изображении геометрических фигур, давайте разберемся, как нарисовать цилиндр с тенью — легкой и насыщенной.
Вначале обозначим основную форму двух цилиндров. Они будут достаточно низкими.
Потом наведем контуры более насыщенно — для этого отлично подойдет мягкий карандаш.
Начнем прорабатывать тени на левой фигуре. Штриховка должна быть достаточно легкой.
Затем наметим тени на левой фигуре они здесь будут гораздо глубже, насыщенные. Не стоит давить на карандаш — лучше взять помягче.
Все, теперь наше геометрическое тело готово.
Черно-белый цилиндр
Научиться тому, как нарисовать объемный цилиндр и другие фигуры — это основы, без которых начинающему художнику не обойтись. Так что давайте разберемся с этим вопросом.
Как и раньше, начнем с двух овалов — для основания и вершины. Длина должна быть одинаковой, а ширина — отличаться в пользу нижнего, это связано с их положением относительно линии горизонта.
После этого соединим их боковыми линиями. Они должны быть строго параллельны.
Добавим рисунку объема. Для этого нужно грамотно отметить все теневые части, блик и падающую тень. Так как наша фигура будет белой, тени должны быть очень легкими. Лучше брать твердые карандаши — HB, H, 2H.
Цилиндр в горизонтальном виде
Для того, чтобы лучше попрактиковаться в рисовании геометрических тел, лучше рисовать их с разных ракурсов. Потому сейчас мы разберемся, как нарисовать лежащий цилиндр.
Рисовать, как и раньше, начнем два овала. Но теперь они будут расположены вертикально и не на одной линии: правый должен быть выше левого.
Затем соединим овалы параллельными диагональными линиями.
После этого сотрем невидимую часть внутреннего овала. Делать это надо достаточно аккуратно.
Затем прорабатываем тени. В центральной части будет световая часть, ближе к боковым линиям — теневые.
Все, изображение полностью готово.
Защита в форме виртуальной экскурсии!
Интересно и познавательно прошла аттестация у воспитанников центра цифрового образования «IT-куб». Южноуральские школьники представили на суд экспертной комиссии виртуальные туры по ярким и значимым местам родного города
«Виртуальная экскурсия по АО ЮАИЗ», «Визуализация процесса производства стеклянных изоляторов», «Мир на ладони»… За этими названиями скрывается грандиозная по сложности работа, проведенная ребятами, обучающимися по направлению «VR/AR разработка».
Так, для того чтобы создать пятиминутный тур по «Южноуральскому арматурно-изоляторному заводу», школьниками пришлось несколько раз побывать на предприятии.
«Ребята фотографировали и снимали площадку с разных ракурсов, беседовали со специалистами предприятия, а при недостатке информации обращались к сети интернет. Затем создавали 3D-модели цехов и оборудования, настраивали освещение и текстуры, добавляли анимацию, — рассказал Владимир Быченок, наставник центра цифрового образования «IT-куб», г. Южноуральска по направлению «VR/AR разработка».
Однако виртуальной экскурсией по заводу ребята решили не ограничиваться. Школьники замахнулись на тур по всему миру. Юные виарщики показали, как можно совместить мировые достопримечательности и инновационные технологии, проведя заочную экскурсию по знаменитым местам и кратко рассказав историю архитектурных ценностей.
«Виртуальная экскурсия — это не просто прекрасная возможность получить визуальную информацию о местах, недоступных для посещения, — подвела итог выступлений Елена Токарева, руководитель центра цифрового образования «IT-куб», г. Южноуральска. — Это еще и современное средство познания окружающего мира и изучения нового материала, которое экономит время и деньги».
Поздравляем ребят с успешной защитой и предлагаем продолжить обучение в следующем учебном году. Тем более что запись уже идет!
Фотобокс Falcon Eyes Light Cube 60 LED
Falcon Eyes Light Cube 60 LED — автономная мини-студия для фотографирования небольших и средних объектов, внутренний размер фотобокса 60х60х60 см. Используется в предметной съемке для печатных каталогов, интернет-магазинов и т.д.
Конструкция разворачивается в квадратный легкий фотобокс и оборудована своим собственным источника света с цветовой температурой 5500К. Внутренние серебристые текстурированные стенки равномерно заполняют куб отраженным светом от двух светодиодных линеек (по 44 светодиода на каждой). Яркость света плавно регулируется диммером, входящим в комплект поставки. Светодиодные линейки установлены на верхней крышке фотобокса, их можно легко переместить вдоль крышки благодаря системе липких лент (велкро). Монтаж конструкции осуществляется также с помощью липких лент, расположенных по периметру стенок. В сложенном виде фотобокс занимает мало места, складывается в кейс с ручкой.
Light Cube 60 LED имеет откидную переднюю панель со встроенным съемочным окном 37х48 см и тремя отверстиями диаметром 11 см, а также верхний люк диаметром 12 см для съемки с верхнего ракурса. Фотобокс поставляется с черным, белым и оранжевым пластиковыми фонами для размещения разных цветных предметов.
- Размер фотобокса: 60х60х60 см
- Размер в сложенном состоянии: 63х63х3 см
- Фронтальное окно: 37х48 см + 3 окна диаметром 11 см
- Верхнее окно: Ø12 см
- Источник света: 2 линейки по 44 светодиода, срок службы 50000 ч.
- Регулировка яркости: есть
- Потребляемая мощность: 23 Вт
- Цветовая температура: 5500К ± 200К
- Индекс цветопередачи CRI: ≥ 90
- Количество фонов в комплекте: 3 (черный, белый и оранжевый)
- Материал каркаса/корпуса: сталь/синтетическая ткань
- Вес (без фонов): 3 кг
- Размер упаковки: 690х660х100 мм
- Вес брутто: 5 кг
Комплектация:
- Корпус фотобокса с каркасом
- Светодиодная линейка — 2 шт
- Крепление линейки (велкро) — 4 шт
- Пластиковый фон — 3 шт
- Сетевой адаптер
- Руководство по эксплуатации
- Гарантийный талон
Как нарисовать куб под разными углами. Основы линейной перспективы (часть 1) — Как рисовать
Угадайте, что? Кубики классные!
Нет, серьезно. Если вы знаете, как нарисовать куб, вы также сможете нарисовать любую трехмерную форму. Конечно, в каждом выбранном вами объекте есть свои нюансы. Тем не менее, основные принципы, гайки и болты рисования остаются прежними.
Все они в этой коробке.
Давай выберем их.
Итак, это не одно из тех руководств «1-2-3». В Интернете их тысячи. Моя цель — дать вам набор навыков, позволяющий рисовать что угодно. Такой подход будет полезен, если вы хотите заниматься концепт-артом, промышленным дизайном, фэнтези / мультипликационным артом. Все они требуют рисования вашего воображения. Значит, нужно уметь рисовать любой объект под любым углом. Вы получите эти знания на уроках. И подкрепляйте его домашними заданиями, выдаваемыми после каждого урока
Теперь вы изучите основы линейной перспективы на примере куба.В следующих статьях мы перейдем к гораздо более сложным предметам. Если вы хотите получить от этой статьи как можно больше пользы, пожалуйста, убейте все разрушающие факторы. Возьмите лист бумаги и ручку и поэкспериментируйте с изучаемыми концепциями. Поверьте, простое чтение мало поможет.
Что такое перспектива?
Перспектива — это система отображения трехмерного мира на плоской поверхности.
Не очень сложно, правда?
Итак, вот наиболее логичная и полезная концепция, о которой следует помнить о перспективе.
Куб виден сквозь кусок плоского стекла. Камера направлена прямо на это стекло.
Стекло называется «Картинная плоскость » (ПП). Линия, проведенная от камеры через PP, называется линией обзора (LOS). Хочу подчеркнуть, что LOS всегда перпендикулярна PP.
«Так какого черта ты мне все это рассказываешь?» — спросите вы.
И вот почему.
Нам нужно знать, как наши линии расположены в пространстве относительно чего-то.Положение камеры — наша путеводная звезда. Основная идея заключается в том, что рисунок в перспективе — это представление изображения с определенной точки просмотра. Без зрителя нет изображения.
Рисование квадрата
Что такое куб? По сути, он состоит из 6 соединенных вместе квадратных плоскостей. Чтобы нарисовать куб, нам нужно знать, как позиционировать квадрат в любом случае, с любой возможной точки обзора.
Теперь нам нужно добавить новое занудное слово в наш словарь — Normal Line или просто Normal.
Если положить конец карандаша на поверхность, он будет совпадать с направлением нормальной линии. Нормаль — это линия, перпендикулярная поверхности.
Все просто.
На каждой плоскости есть бесконечное количество этих нормальных линий. Для простоты нарисуем только один.
Нормали помогают нам определить, как мы видим поверхность.
Берем прямоугольник и ставим перед камерой. Если нормаль направлена прямо на картинную плоскость (90 градусов) , то мы видим поверхность без каких-либо искажений.Прямоугольник — как есть.
И вот самая важная часть.
Если мы наклоним наш прямоугольник в любом направлении, нормальная линия больше не будет перпендикулярна PP. Поверхность прямоугольника сжимается.
Как определить направление сжатия? Нормальная линия говорит нам.
Принцип называется Усадка по нормали.
Каждая плоскость сжимается только вдоль своей нормальной линии.
Мы видим, что самолет изменился в пропорциях.Он уже, потому что сжимается по нормали.
Это всегда так.
Другого способа уменьшить самолет невозможно. Только по ходу нормально. Чем больше плоскость отклонена от камеры, тем больше она сжимается по своей нормальной линии. Я буду повторять эту концепцию снова и снова, потому что это очень важно. Когда дело доходит до рисования, об этих простых вещах часто забывают.
Схождение параллельных линий
Еще одно явление.В приведенном выше примере вы могли заметить, что левое и правое поля прямоугольника сужаются к верху (из обзора камеры). Это происходит потому, что это параллельные линии, уходящие в пространстве (относительно картинной плоскости). Линии, параллельные PP, не сходятся.
Звучит сложно? Что ж, так должно быть. Узнавать новое нелегко.
Я помню свои первые шаги в рисовании — это было чертовски адом. Обещаю, со временем станет легче.
В статьях о перспективе мы углубимся в тему. Это поможет вам в кратчайшие сроки улучшить свои навыки рисования. Не у всех читателей есть горячее желание улучшить свои навыки рисования.
Но если да, то пойдем дальше.
Где сходятся параллельные линии? Я уверен, что вы знаете — на линии горизонта. Об этом написано в каждом артбуке. Поколение за поколением. Эта концепция настолько популярна и догматична, что авторы никогда не пересматривают ее объяснение.
Но мы будем.
Что такое линия горизонта на самом деле?
Мы предполагаем, что нижняя часть нашей камеры параллельна плоскости земли.
У нас есть несколько горизонтальных плоскостей в нашей сцене. По мере того, как эти самолеты поднимаются, они постепенно сжимаются.
Нормальная линия горизонтальной плоскости — вертикальная. Вот почему каждая горизонтальная поверхность сжимается по линии вертикальной .
Когда плоскость полностью сжимается, она превращается в единую линию.Из-за вертикального сжатия эта линия горизонтальна.
Это наша линия горизонта.
Если ваша плоскость разрезает камеру прямо по центру, когда вы ее выдвигаете, это означает, что плоскость сжалась до нуля. Это горизонт.
Параллельные линии, расположенные на горизонтальных плоскостях (не важно на какой), сходятся на линии горизонта. Точки схождения называются точками схода (VP).
Вы можете видеть, что каждый набор параллельных линий имеет собственных VP. Типовая конструкция перспективы может иметь центральную (CVP), левую (LVP) и правую (RVP).
Эллипсы
Я не говорил вам, что самолет должен иметь только прямоугольную форму.
Почему я этого не сделал?
Потому что самолет может иметь любую форму.
Вы просто думаете об этом как о плоском листе бумаги. Из него можно вырезать любую форму. Итак, мы можем сделать самолет в виде круга. Потом помещаем в космос и получаем…
Да! Эллипс.
Здесь я делаю вид, что вы читали мою статью об основных принципах работы линии. Если нет, возможно, вы захотите сделать это сейчас. Потому что в нем есть некоторые основы, которые нам понадобятся.
Плоскость в форме круга также имеет нормаль, и эта нормаль также перпендикулярна поверхности плоскости.
Вот трюк с эллипсами.
Нормальная линия плоскости эллипса всегда проходит в том же направлении, что и его малая ось.
Принцип такой же, как и в случае с прямоугольниками.
Но.
Круг имеет одинаковый диаметр на всем протяжении. В результате сжатия (даже самого незначительного) диаметр будет представлен двумя важнейшими линиями: самой длинной и самой короткой.
Самый большой диаметр — это большая ось . Эта леска не меняет своей длины независимо от того, насколько сильно вы наклоняете поверхность.
Наименьший диаметр — это малая ось . Перпендикулярно большой оси. Она имеет то же направление, что и нормальная линия.Больше всего он меняется, когда круг отклоняется от поля зрения камеры.
Степень сжатия эллипса называется градусом эллипса.
Если нормаль поверхности эллипса направлена под углом 90 градусов к картинной плоскости. Затем камера видит полностью открытый круг.
Если нормаль направлена под углом 45 градусов к точке PP, эллипс называется «эллипсом под 45 градусов».
Чем меньше градусов, тем больше компрессия.
Эллипсы — ваши спасатели
Мы будем использовать эллипсы даже в тех случаях, когда на нашем чертеже нет видимых круговых плоскостей.
Почему?
Есть несколько больших преимуществ.
- Эллипс помогает определить направление нормальной линии поверхности.
Таким образом, вы знаете, в каком направлении сжимать самолет, когда он отклоняется от зрителя.
- Эллипс помогает определить наклон плоскости относительно наблюдателя.
Более сильный наклон = более сильная усадка.
Я не говорил вам этого до последнего момента, надеясь, что вы это заметили.Я считаю, что самые глубокие знания получаются на вашем собственном опыте. За это нужно бороться. Надо быть смелым и любознательным. Другого пути нет.
Итак, что я надеялся, что вы угадали?
- Эллипс помогает найти пропорции идеального квадрата.
Круг внутри квадрата касается каждой из четырех границ в средних точках. Круг в перспективе (эллипс) делает то же самое.
Видите ли, каждый эллипс касается границ квадрата в середине.
Это всегда дело.
Куб состоит из полных квадратов. Знание того, как построить квадрат, очень важно для нашей конечной цели — рисования куба.
Эта статья может показаться слишком длинной по сравнению с конечным результатом.
«Рисунок куба? Шутки в сторону? Но это должно быть так просто … Зачем мне тратить время на чтение всей этой чуши? » .
Прически.
Обещаю, что то, что мы изучаем, скоро поможет вам рисовать такие крутые штуки, как танки, драконы, роботы и т. Д.Конечно, если вам это действительно интересно.
Угол 90 градусов
Помимо пропорций квадрата, мы должны убедиться, что квадрат имеет четыре прямых угла (90 градусов). Нужна правильная конструкция хотя бы одного угла. Три других встанут на свои места.
И снова эллипс — ваш рейнджер.
Это поможет вам построить правильный угол 90 ° между двумя линиями на одной плоскости. Нарисуем прямой угол на плоскости земли.
Определите пропорции квадрата с заданной точки обзора, используя свой эллипс.
Поместите нормальную линию (в данном случае вертикальную, потому что плоскость горизонтальна) в нужное положение, в зависимости от того, как следует повернуть угол.
Если вы хотите, чтобы угол был направлен прямо на зрителя, нормаль должна быть проведена прямо через середину эллипса. Затем нарисуйте две касательные к эллипсу от точки на вертикальной линии. Это приведет к одинаковому сжатию левой и правой сторон (обе на 45 °) нашего бокса.
Если вы хотите повернуть угол по часовой стрелке, вы перемещаете нормаль влево.
Чтобы повернуть его против часовой стрелки, используйте тот же принцип.
Какая часть этой нормальной линии должна выходить за пределы эллипса?
Зависит от степени эллипса. Чем больше открывается — тем длиннее линия. Вы получите это лучше с практикой. Просто не забывайте касаться квадрата в середине.
Есть несколько способов завершить построение квадрата в любом возможном положении.Это зависит от уровня желаемой экстремальности перспективы.
Чем ближе линия горизонта к эллипсу (по отношению к его размеру) — чем более крайняя — перспектива. Линии сходятся быстро, что означает, что объект находится близко к зрителю или он большой. Изображение выглядит так, как будто снято широкоугольным объективом.
Если линия горизонта находится на удалении от эллипса на , перспектива будет плоской на . Линии немного сходятся.Объект выглядит маленьким или находится далеко от зрителя.
Это эффект длинных линз.
Здесь вы видите, что вертикальная линия выходит за пределы эллипса на одинаковом расстоянии в обоих случаях. Нижний угол такой же. Разница только в экстремальности перспективы. И снова. Линия горизонта перпендикулярна нормали эллипса (малая ось).
Горизонт представляет собой по существу плоскую плоскость, параллельную этому эллипсу. Этот самолет просто полностью отклонен от поля зрения зрителя.
Рисование куба (наконец)
У куба шесть сторон, одновременно могут быть видны только 3 из них. Итак, для простоты остановимся только на видимых сторонах (пока). Вы уже знаете, как построить горизонтальный квадрат во всех возможных положениях.
Это будет наш верхний самолет.
Что осталось? Остальные две боковые плоскости. Вертикальные края известны. Это нормальные линии к верхней плоскости.
Что неизвестно, так это длина вертикальной линии.Вертикальная линия параллельна PP, поэтому ее нельзя сильно укоротить. Он становится больше, когда продвигается в пространстве (как и любой другой объект) из-за схождения линий. Итак, мы предполагаем, что он немного длиннее, чем большая ось нашего верхнего эллипса, потому что его большая ось также не может быть сокращена в ракурсе.
Есть трюк, чтобы проверить правильность боковых плоскостей.
Вы можете догадаться, что это?
Ага, это эллипс.
Нарисуем эллипс с малой осью, направленной на RVP.Эллипс должен касаться середин краев плоскости. Попробуйте отобразить этот эллипс между линиями, визуализировать его. Затем мы просто закрываем нижний край левой стороны линией, идущей к LVP. Наконец, мы закрываем правую часть линией, идущей к RVP.
Коробка сделана.
Ускорение усадки
Теперь у нас есть куб. Но вы можете задаться вопросом: как его вращать в пространстве, как наклонять? Это хороший вопрос. Мне нравится, когда задают интересные вопросы! 😀
Чтобы решить эту проблему, мы должны знать об ускорении сжатия . Согласно этому принципу усадка плоскости не является линейной. Другими словами, он прогрессирует все быстрее и быстрее.
Ставим куб на плоскость земли так, чтобы обе боковые плоскости были под углом 45 градусов к PP.
Теперь поворачиваем куб по часовой стрелке. Он все еще стоит на земле.
Вы можете видеть, что левая сторона сжимается больше, а правая становится более толстой как в абсолютных, так и в относительных величинах.
Чем больше усадка плоскости (или линии), тем быстрее она усаживается.
Даже небольшой поворот полностью стянутой лески резко меняет ее длину. По мере того, как он открывается все больше и больше, скорость открытия уменьшается.
Обычные строки делают то же самое. Когда они параллельны полипропилену, их трудно уменьшить. По мере того, как они отворачиваются от зрителя, это становится все легче и легче.
Как нарисовать куб под любым углом за 5 шагов?
Время пришло.
Примите мои извинения за такую долгую прелюдию.Все это важно не только для рисования коробки. Вы оцените этот материал, когда перейдете к более сложным темам в моих последующих статьях.
Итак, приступим!
- Опустите эллипс. Он может представлять любую сторону куба. Единственная проблема здесь — это сжатие и направление нормали.
- Отбросьте нормальную линию в соответствии с желаемым положением переднего края куба. Линия горизонта для этого куба на самом деле не будет горизонтальной (ха-ха). Он просто должен быть перпендикулярен нормали к нашей плоскости.Это единственное требование.
- Определитесь с точки зрения экстремальности. Здесь горизонт вне кадра, а перспектива довольно плоская.
- Измерьте правильную длину «вертикального» угла с помощью эллипса или просто посмотрите на него. Проведите линию до RVP, чтобы закрыть нижнюю границу.
- Последняя сторона сама встанет на свои места. Просто постройте правильные параллельные линии тем, которые уже существуют.
Домашнее задание
Пришло время закрепить свои знания.
Сделайте это, даже если думаете, что уже понимаете, как нарисовать куб под любым углом.
Практика ведет к совершенству, а? Но всегда должна быть хорошая база знаний.
Я рекомендую прочитать этот урок еще раз после того, как сделана домашняя работа.
Вот я сделал для вас демо.
Вы можете видеть, что кубы могут перекрывать друг друга.
Не стесняйтесь играть с разными размерами и углами. Попробуйте разнообразную перспективу крайностей. У больших коробок может быть резкое схождение линий.
Увидимся в следующий раз.
Перспектива и куб
В линейной перспективе необходимо понимать концепцию плана изображения e , , который представляет собой фактическую двумерную поверхность вашей бумаги (или холста). Изображение на бумаге — это изображение того, что можно было бы увидеть за поверхностью бумаги. Если бы вы проследили вид из окна на стекло, стекло представляло бы плоскость изображения.
Другая концепция, которую необходимо понять, — это линия горизонта, которая, конечно же, является горизонтом; его еще называют уровнем глаз. Представьте себе кусок картона с вырезанным из него прямоугольником — видоискатель. Если держать видоискатель на уровне глаз, горизонт будет посередине отверстия. Если вы опустите видоискатель, кажется, что горизонт смещается к верхней части отверстия. Если поднять видоискатель, кажется, что горизонт смещается к нижней части отверстия. Таким образом, на рисунке, когда горизонт находится высоко на странице, мы фокусируемся на вещах ниже уровня наших глаз (мы смотрим вниз).Когда горизонт низок на странице, мы фокусируемся на вещах, находящихся выше уровня наших глаз, над головой (мы смотрим вверх).
Представьте, что вы смотрите на ящик уровня. Если вы видите верхнюю часть прямоугольника, значит, он находится ниже уровня ваших глаз, поэтому горизонт находится над прямоугольником. Если вы видите нижнюю часть коробки, она находится выше уровня ваших глаз, поэтому горизонт находится ниже рамки.
T h e pi c ture plane is t he ac tu a ls u rf a c e на w hi c h an im a g e is cr eat e d . T h e i ma ge появиться s будет позади t h e surfac e.
Чтобы создать впечатление смотрящего вниз, горизонт расположен высоко на странице .
Чтобы создать впечатление o Если смотреть вверх, горизонт равен , поместите d Iow на страницу.
Чтобы создать впечатление смотрящего вниз, горизонт расположен высоко на странице. Чтобы создать впечатление смотрящего вверх, горизонт расположен низко на странице.
Одноточечная перспектива и куб
Двумя наиболее распространенными и полезными типами перспективы являются одноточечная и двухточечная перспектива. Простейшая демонстрация одноточечной перспективы — это смотреть вниз по прямой дороге. Мы знаем, что дорога имеет одинаковую ширину по всей длине, и тем не менее, когда мы смотрим на горизонт, дорога становится все более узкой, пока не сужается до точки на горизонте.Это называется v ani s hi ng po i n t , потому что именно там дорога исчезает. На ровной поверхности точка схода всегда находится на горизонте. Поместите куб на эту дорогу так, чтобы стороны куба были параллельны сторонам дороги. Линии, описывающие удаляющиеся края куба, будут сходиться в той же точке схода, что и дорога. Все удаляющиеся параллельные линии будут иметь одну точку схода.
Th e se нарисованы три прямоугольника i n one — точечная перспектива . T Пунктирными линиями обозначены удаляющиеся линии. Все удаляющиеся линии пересекаются в одной точке на линии горизонта , указывая, что , , они параллельны друг другу, , .
В одноточечной перспективе прямая ровная дорога кажется сужается вдалеке, хотя мы знаем, что это не так.Представьте себе коробку, отступающие края которой параллельны краям дороги. Все эти края «исчезают» в одной и той же точке на горизонте.
Одноточечная перспектива также используется, когда вы изображаете коробки или внутренние части, у которых есть скачки или стены, параллельные картинной плоскости. Горизонтальные и вертикальные линии на гранях, параллельные картинной плоскости, нарисованы перпендикулярно друг другу. Все остальные отступающие края или объект сходятся в точке на линии горизонта. В одноточечной перспективе передняя и задняя части куба параллельны картинной плоскости.Они нарисованы в виде квадратов с перпендикулярными углами. Верх, низ и стороны куба в одноточечной перспективе уходят в пространство. Линии, определяющие их удаляющиеся края, будут сходиться в точке где-то за кубом.
Помните: в одноточечной перспективе вертикали и горизонтали перпендикулярны друг другу на поверхностях, параллельных картинной плоскости.
Когда d r Победа детеныша e или коробка в одном — p oi nt за s pect iv e , s tart wit h ap e rfec t квадрат или r e ctangle ( a ll co rn ers 90 ° угол es) . Th i s представляет h e si de , что соответствует параллельному l плану изображения e . (Исчезающая точка обозначает примечание d как V P. )
To e st ablish the top of th e cu b e, dra w li nes from the top кукуруза e rs -й и кв. и — — — баллов — — — й — куб — — й — горизонт — n l i ne .
b ack из cube is est ab lishe d (arb i tr a ril y for no w) от mak i ng a li ne параллельно верхней из fr o n t из t he cube; e widt h of t hi s li ne is de fin ed by the pe r spec ti v e линий r ew f rom t h e cube’s top f ront corner s.
T h e r eced i ng lines o f th e to p теперь нарисованы в , c onne ct дюйм g th e bac k o f куб t o спереди.
Мы имеем v e n ow install li s h e d a cl os e d c ube i n одноточечный p e rspective.
Чтобы открыть переднюю часть куба, нарисуйте отступающие линии из бота t ом из куб от нижних передних углов с до точки схода.Нижние края и параллельны верхним, поэтому у них будет , , одна и та же точка схода .
Вертикальные линии теперь проводятся от задних углов куба к отступающим линиям нижней части куба.
Там, где вертикальные линии задней части куба пересекаются с отступающими линиями низа, проведите линию, параллельную передней нижней линии.
Задние вертикальные мелкие частицы теперь притягиваются к месту, где они встречаются с отступающими линиями нижней части куба.Примечание: мы не можем видеть верхнюю часть куба, поэтому мы не увидим, как эти линии пересекаются с верхними задними углами.
Это открытый куб в одноточечной перспективе.
Двухточечная перспектива и куб
Двухточечная перспектива используется, когда только вертикальные края куба параллельны плоскости изображения. В этом отличие от одноточечной перспективы, в которой все стороны куба параллельны картинной плоскости.
В кубе в двухточечной перспективе только вертикали действительно параллельны друг другу.Все остальные линии будут указывать на одну из двух точек схода. Если куб выровнен, точки схода будут на горизонте. Все прямые, параллельные друг другу, будут иметь одну точку схода. Чем дальше друг от друга расположены две точки схода, тем дальше от объекта будет находиться ваша точка обзора.
В одноточечной перспективе все стороны куба параллельны картинной плоскости, как показано в примере справа. В двухточечной перспективе только вертикальные края куба параллельны плоскости изображения, как в примере справа.
Для рисования a c ube в двух точках по s pe c tive, we st ar t с ver ti ок. l край, ближайший к pi c ture plane . Точки схода расположены слева и справа от линии горизонта.
Строка s от t he top and b o ttom of th e n e ar ed ge нарисованы с до v точка полировки на справа. Это wi l le s tabli sh th e to p и b o t to m края правого s i de из куб .
Аналогичные линии проведены для левой s ide куба.
Вертикальные линии теперь выбраны (пока произвольно) для задних углов куба. Эти линии помещаются между удаляющимися пунктирными линиями.
Теперь нарисованы верхний и нижний края двух сторон.
Чтобы найти задние края вершины куба, проведите линию от левого угла блока до точки схода справа.Проведите еще одну линию от правого заднего угла до точки схода слева.
Задние верхние края прорисованы.
Это замкнутый куб в двухточечной перспективе.
Чтобы изобразить открытый куб в двухточечной перспективе, проведите линию от точки схода слева до правого переднего нижнего угла.
Чтобы определить глубину куба, проведите линию от точки схода справа до заднего левого нижнего угла.Затем проведите вертикальную линию от верхнего заднего угла до места пересечения линий от точек схода.
Нарисуйте линии там, где мы бы их видели, если бы была открыта только правая сторона прямоугольника.
Это открытый куб в двухточечной перспективе.
© Авторские права Билл Мартин 2007-2014 • PO Box 511, Albion, CA 95410 • [email protected]
Определение куба с калькулятором — Math Open Reference
Определение куба с калькулятором — Math Open ReferenceОпределение: Твердое тело с шестью равными квадратными гранями.Правильный шестигранник.
Попробуй это Перетащите в любое место куба ниже, чтобы повернуть его в любом направлении. Обратите внимание на то, что все грани квадратные и одинаковые (совпадающие). Выберите параметры, чтобы изменить внешний вид куба.
Куб — это область пространства, образованная шестью одинаковыми квадратными гранями, соединенными по краям. Три ребра соединяются в каждом углу, образуя вершину. Куб также можно назвать правильным шестигранником. Это один из пяти правильных многогранников, которые также иногда называют Платоновы тела.
Части куба
| Лицо | Также называется фасетами или сторонами. У куба шесть граней, и все они квадратные, Таким образом, каждая грань имеет четыре равные стороны, и все четыре внутренних угла являются прямыми углами. Видеть Определение квадрата. На рисунке выше перетащите ползунок «разнесение», чтобы для наглядности выделить грани. |
| Кромка | Линейный сегмент, образованный на стыке двух краев. У куба 12 ребер.Поскольку все грани квадратные и совпадают друг с другом, все 12 ребер имеют одинаковую длину. |
| Вершина | Точка, образованная на стыке трех ребер. У куба 8 вершин. |
| Диагонали лица | Диагонали лица — это отрезки линий, соединяющие противоположные углы лица. На каждой грани по две, всего в кубе 12. Длина диагоналей лица определяется по формуле где с — длина одной стороны (края).Поскольку грани квадратные, это то же самое, что и диагональ квадрата. |
| Диагонали в пространстве | Космические диагонали — это отрезки линий, соединяющие противоположные углы куба, прорезая его интерьер. Куб имеет 4 диагонали пространства. Длина диагонали пространства определяется формулой где с — длина одной стороны (края). |
Свойства куба
| Объем | Объем s 3 где s — длина одного края.Видеть Объем куба. |
| Площадь | Площадь поверхности куба равна 6s 2 , где s — длина одного ребра. См. Площадь поверхности куба. |
Калькулятор
Используйте калькулятор выше, чтобы вычислить свойства куба.
Введите любое одно значение, и остальные будут рассчитаны. Например, введите длину стороны, и будет рассчитан объем.
Точно так же, если вы введете площадь поверхности, будет рассчитана длина стороны, необходимая для получения этой площади.
Связанные темы
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Как нарисовать трехмерный куб!
Привет, друзья!
В этом уроке рисования я научу вас очень востребованной теме — , как нарисовать трехмерный куб!
Сейчас есть много разных видео / уроков по рисованию куба.
Но…
Я хочу сделать акцент на ПОНИМАНИИ того, как куб выглядит со всех углов, что позволит вам нарисовать его под ЛЮБЫМ углом, который вам нужен .
Звучит круто? Потому что это так.
Первое — смотрите видео. Затем читайте основные советы.
Хорошо, понятно ?! Теперь по основным пунктам:
Что такое куб?
Куб — это трехмерный объект , имеющий 6 сторон одинакового размера. Он также имеет 8 острых углов.
Вот прозрачный куб, изображающий это.
На самом деле мы можем видеть только до 3-х плоскостей куба.
Вот как это выглядит.
Разные углы
Если мы переместим куб, мы увидим меньше одних сторон и больше других.
Это происходит потому, что когда мы смотрим на вещи под углом, они сжимаются. Это называется ракурсом и будет рассмотрено в отдельном посте (=
Так или иначе, вот несколько кубиков под разными углами.
Обратите внимание, как в самом центре куба — мы можем видеть только ОДНУ сторону.
Те, что над ним, наклонены вверх или вниз и позволяют нам видеть ДВЕ стороны.
Остальные наклонены вверх / вниз И вбок. Это позволяет видеть ТРИ стороны.
Вот как это работает (=
Надеюсь, теперь вы можете нарисовать трехмерный куб под ЛЮБЫМ углом, каким пожелаете!
Задайте мне вопросы или что-нибудь еще, что вы можете придумать, и я сделаю все возможное, чтобы помочь!
Также не забудьте ПОДПИСАТЬСЯ на мой блог (СЛЕВА) или через мою страницу Get Awesome Stuff!
Вы получите мою электронную книгу бесплатно + отличные советы и рекомендации по рисованию, которые будут доставлены прямо вам! (=
До следующего раза,
— Liron
Нравится:
Нравится Загрузка…
геометрия — Найдите углы обзора куба по проекции его граней
Для общей перспективной проекции недостаточно знать направления изображений осей координат в некоторой точке изображения (или углы между ними), чтобы восстановить положение камеры. Проблема в том, что их точки схода обычно конечны, поэтому эти углы зависят от местоположения на изображении. Что касается изображения в вашем вопросе, вероятно, можно с уверенностью предположить, что объект находится далеко от камеры и что диапазон глубин в этой части изображения небольшой по сравнению с этим расстоянием.Это позволяет нам аппроксимировать перспективную проекцию ортогональной проекцией, то есть использовать аффинную камеру. (Хартли и Зиссерман обсуждают ошибки в этом приближении в Multiple View Geometry In Computer Vision §6.3.) Хорошая вещь в этом приближении для наших целей состоит в том, что точки схода линий, которые не параллельны направлению проекции, находятся на бесконечности — параллельные линии сопоставляются с параллельными линиями, так что направления изображений координатных осей не зависят от положения на изображении.3 $ из $ \ mathtt R $. Это вектор направления мировой координаты, который указывает от начала координат к камере.
Перевод $ \ mathbf t $ влияет только на последний столбец $ \ mathtt P $, который нам не важен, поэтому мы можем игнорировать его. Если мы предполагаем квадратные пиксели и отсутствие перекоса, то с точностью до несущественного постоянного множителя $ \ mathtt K_ {2 \ times2} = \ mathtt I_ {2 \ times2} $, сводя $ \ mathtt P $ к матрице справа. Первые три столбца матрицы камеры — это координаты изображения точек схода мировых координатных осей, поэтому, если $ \ mathbf x $, $ \ mathbf y $ и $ \ mathbf z $ являются векторами направления, отсчитываемыми от изображения, мы иметь $$ \ mathtt R_2 = \ begin {bmatrix} \ lambda \ mathbf x & \ mu \ mathbf y & \ tau \ mathbf z \ end {bmatrix} $$ для некоторых положительных масштабных коэффициентов $ \ lambda $, $ \ mu $ и $ \ tau $.{3T} \ приблизительно $ (-0,4449, -0,618222, 0,64797), что соответствует азимуту -125,74 ° и полярному углу 49,6113 °, тот же результат, что и в другом ответе.
Необходимо иметь дело с несколькими вырожденными конфигурациями. Если какая-либо из линий изображения совпадает, невозможно получить направление взгляда без дополнительной информации, например известной длины вдоль совпавших осей. Если проекция параллельна одной из осей мировых координат, ее изображение будет представлять собой одну точку, а не линию, поэтому описанный выше метод неприменим.Однако достаточно легко определить соответствующий поворот из оставшихся видимых изображений осей. Интересная вырожденная конфигурация — это когда три вектора расположены на одинаковом расстоянии: соответствующая линейная система имеет только тривиальное решение. Я полагаю, что этот нулевой результат отражает двусмысленность, присущую старой оптической иллюзии «ярусов кубов». Однако, поскольку вы знаете, какое ребро является каким, это можно устранить, но приведенный выше алгоритм бесполезен.
Я не рассматривал, можно ли ослабить ограничения по соотношению сторон или без перекоса, не требуя дополнительных данных от изображения и сцены.
TIP 104 | Как легко нарисовать куб (2-точечная перспектива)
Куб — это 6-сторонняя трехмерная форма , похожая на игральную кость или кубик Рубика.
Художники и промышленные дизайнеры учатся рисовать в перспективе, рисуя серию кубов под любым углом.
Помогает развить навык трехмерной визуализации .
Чтобы они могли научиться рисовать любые изделия с хорошими пропорциями.
Перспектива может напугать многих новичков.
Однако, если мы разложим процесс на простые шаги,
вы сможете очень быстро освоить основы.
Этот видеоурок покажет вам простой способ, , как легко нарисовать куб с двухточечной перспективой.
Вы увидите:
- Пошаговое руководство, как нарисовать куб
- Покадровая съемка куба с 9 основных ракурсов.
Как нарисовать куб в перспективе (2 точки)
Щелкните здесь, чтобы загрузить полный сборник набросков для начинающих (4 руководства)
Статья по теме: Как нарисовать куб с перспективой в одну точку
Словарь двухточечной перспективы
Чтобы легче понять перспективу, мы рисуем простой куб.
Эта двухточечная перспектива состоит всего из 4 элементов:
- ЗЕЛЕНАЯ ЛИНИЯ: линия горизонта
- ЗЕЛЕНЫЕ ТОЧКИ: 2 точки исчезновения
- СИНИЕ ЛИНИИ: 4 сходящиеся линии
- РОЗОВЫЕ ЛИНИИ: 4 вертикальные линии
Когда вы будете рисовать в перспективе, вы должны учитывать это.
Что такое линия горизонта?
ВАЖНО: Линия горизонта также называется: Уровень глаз.
ЛЮБОПЫТНЫЙ ФАКТ: Линия горизонта — это прямая горизонтальная линия, которую вы видите далеко на пляже, когда вода встречается с небом.(По сути, это основная линия, которую вы видите из любого пейзажа очень далеко.)
В зависимости от положения вашего куба (по направлению к линии горизонта) зритель будет воспринимать его по-разному.
Эта позиция будет определять точку обзора куба .
Как нарисовать куб поэтапно
Шаг 0. Типичная ошибка
СОХРАНИТЬ: Распространенная ошибка новичков — когда все сходящиеся линии не связаны с вашими точками схода.
ШАГ1.
Проведите линию горизонта
ШАГ2.
Нарисуйте точки схода
ШАГ 3.
Нарисуйте вертикальную линию
ШАГ 4.
Установите высоту
ШАГ 5.
Соедините каждую точку с обеими точками схода
ШАГ6.
Оцените ширину с обеих сторон
(Проверьте исходный вид)
ШАГ7.
Найдите эти 4 точки и проведите 2 вертикальные линии
ШАГ8.
Нарисуйте заднюю поверхность куба
Точки левых вертикальных линий соединяются с правой точкой схода.
ШАГ9.
Нарисуйте другую заднюю поверхность куба
Точки правых вертикальных линий соединяются с левой точкой схода.
ШАГ 10.
Обратите внимание на две точки позади. Они выровнены по вертикали?
ШАГ 11.Если да, то соедините их с успехом !!
ПОСЛЕДНИЙ ШАГ.
Смелый куб!
КУБИЧЕСКОЕ УПРАЖНЕНИЕ:
НАРИСИТЕ КАЖДЫЙ УГОЛ!
УЗНАТЬ БОЛЬШЕ О CUBE VIEWPOINT
Куб и вертикальное положение
Случай A: Сверху
Когда вы рисуете куб на верхней стороне линии горизонта: это над уровнем ваших глаз . Видна под поверхностью куба.
Случай B: Ниже
Когда вы рисуете куб в нижней части линии горизонта: он находится на ниже уровня ваших глаз. Видна верхняя поверхность куба.
Просто, правда? 🙂
Линия горизонта также называется уровнем глаз
Эксперимент с кубом | Вертикальное положение
Я приглашаю вас поэкспериментировать с этим в реальной жизни .:
- Возьмите коробку, толстую книгу или что-нибудь кубическое.
- Держи его перед собой
- Переместите его вверх и вниз.
- Будьте внимательны к нижней и верхней поверхности вашего объекта.
Оба куба можно нарисовать на одной линии горизонта
Куб и горизонтальное положение
Случай A: Куб посередине
Когда куб нарисован в центре обеих точек схода (2 зеленые точки), левая и правая стороны куба визуально равны.
Случай B: Куб слева
Когда куб находится слева, правая сторона визуально становится на длиннее.
(Это называется визуальный эффект ракурса.)
Эксперимент с кубом | Горизонтальное положение
Представьте, что вы разговариваете с кем-то лицом к лицу. Вертикальная линия носа представляет передний край куба.
Если этот человек находится перед вами, вы видите как левую, так и правую стороны лица.
Но когда этот человек сделает шаг слева от вас, вы увидите больше его правой стороны.
УПРАЖНЕНИЯ:
Нарисуйте много коробок разных размеров!
Теперь вы готовы рисовать множество коробок любых размеров и углов с помощью этого простого пошагового руководства по рисованию куба! : D
3d чертеж коробки с любых ракурсов!
Поздравляем с прохождением учебного курса «Куб и ящики»!
Что дальше?
Давайте повысим уровень игры!
Чтобы получить этот навык рисования куба , пока он не станет интуитивно понятным, мы собираемся немного поднять уровень.🙂
Я покажу вам, как нарисовать сложные трехмерные формы с помощью очень простой техники — все начинается с базового чертежа куба .
Мы увеличим ваше 3D видение, нарисовав i бесконечность форм из ваше собственное воображение!
Получайте удовольствие от рисования неограниченного количества форм, начиная с простой двухточечной перспективы!
Interactivate: поперечные сечения
Наставник: Если вы разрежете кусочек куба, какая форма будет вырезана?
Студент: Квадрат!
Наставник: Это всегда правда? Что, если разрезать куб под углом?
Студент: Ну, тогда две стороны будут длиннее двух других, поэтому я предполагаю, что форма будет прямоугольник.
Наставник: Верно. Что бы произошло, если бы вы разрезали куб под другим углом — скажем, если бы вы просто отрезать самый кончик кубика?
Студент: Тогда … я думаю, это будет треугольник, например:
Наставник: Совершенно верно! Как вы думаете, какие еще формы можно было бы создать, разрезав поперечное сечение квадрат?
Студент: Хм, я уверен, что если вы можете создать треугольник, отрезав только угол куба, тогда вы можете создать пятиугольник, отрезав кусок побольше, например:
Наставник: Это хорошо, так что вы видите, что вы можете создать поперечное сечение с большим количеством сторон, чем у оригинала. форма.Что произойдет, если вы наклоните поперечное сечение еще больше, чтобы верхний угол поперечное сечение тоже было отрезано?
Студент: Тогда у вас будет … шестиугольник!
Наставник: Совершенно верно! Как вы думаете, можно ли построить фигуру с большим количеством сторон, например, семиугольник?
Студент: Я не могу понять, как это сделать, так как я не могу отрезать больше двух из четырех углы.
Наставник: Не волнуйтесь, то, что я просил сделать, на самом деле невозможно! На кубе всего шесть граней, поэтому максимальное количество сторон — шесть.
Студент: В этом есть смысл. Бьюсь об заклад, вы можете сделать это с любой призмой — просто нужно наклонить сечение правильно, чтобы пересечь все грани.
Наставник: Вы совершенно правы, любую призму можно разрезать так, чтобы в поперечном сечении было как можно больше сторон. поскольку у призмы есть грани. Однако не все формы обладают этим же свойством. Вы можете придумать 3-х мерная фигура, стороны которой не может ли все быть рассечено одной и той же плоскостью?
Ученик: Возможно, это икосаэдр, потому что нет плоскости, которая могла бы пересечь все двадцать его сторон:
Наставник: Хорошо, Икосаэдр — это пример многогранника, который не является призмой.Если рассматривать призмы только то, что будет с поперечными сечениями призмы, если количество боковых граней приблизилась к бесконечности?
Студент: Я никогда не слышал о призме с бесконечной гранью …
Наставник: Ну, когда вы пытаетесь визуализировать что-то, чего раньше не видели, попробуйте использовать то, что вы уже знаете. Представьте себе правильный квадрат, затем правильный пятиугольник, затем правильный квадрат. шестиугольник и так далее. По мере увеличения количества сторон, какая еще форма делает фигуру? подход?
Студент: Хм, он начинает больше походить на круг, потому что вы не видите никого из людей. стороны.
Наставник: Совершенно верно. Фактически, математики формально определяют круг как правильный многоугольник с бесконечной количество сторон. Итак, что произойдет, если вы разрежете круговую призму, также известную как цилиндр?
Ученик: Ну, очевидно, вы могли бы сделать круг, если бы разрезать фигуру по горизонтали, и вы могли бы сделать прямоугольник, если вырезать фигуру вертикально. Однако более интересным является тот факт, что вы можете сделайте овал, если разрезать цилиндр под углом:
Наставник: Существует бесконечное количество трехмерных фигур, каждая из которых имеет собственное поперечное сечение.Фактически, любую двумерную форму можно определить как поперечное сечение трехмерного объекта. форма. Это пригодится при обсуждении конических сечений, но также будет полезно, если вы решаете пройти обучение по многомерному исчислению и другие математические классы высокого уровня.
Студент: Зачем определять двумерные формы как поперечные сечения? Почему бы просто не оставить их в двух измерениях?
Наставник: При работе с двухмерными фигурами обычно — это проще, просто оставить их в двух измерениях.Тем не менее, поперечные сечения широко используются для рассчитать объем неправильных фигур. Изучив исчисление, вы научитесь вычислить площадь практически любой двумерной формы. Поскольку трехмерный объект может быть разделенные на большое количество поперечных сечений, площади этих поперечных сечений можно использовать для рассчитать объем трехмерного объекта.
.