Как нарисовать несуществующий объемный треугольник поэтапно • Makusha
Сегодня мы расскажем вам, как легко прослыть художником среди своих друзей или показать девушке, какой ты весь разносторонний (о, они это любят!). Итак начнем!
Нам понадобится: 50 грамм для храбрости, 2 карандаша (один жесткий, другой мягкий), лист бумаги, линейка и ластик. Да начнется магия!
Как нарисовать несуществующий объемный треугольник поэтапно
Шаг 1.
Рисуем обычный треугольник – он не должен являть собой венец геометрической мысли: просто соедини три линии.
Как нарисовать несуществующий объемный треугольник поэтапно
Шаг 2.
Теперь нарисуй внутри линии, прямо как у нас. Старайся сделаить их одной ширины, ты ж не рукожоп, как мы!
Как нарисовать несуществующий объемный треугольник поэтапно
Шаг 3.
Нарисовал? Молодец! Теперь нарисуй еще, как мы показали. Мы знаем, ты устал, но скоро все закончится.
Мы знаем, ты устал, но скоро все закончится.
Как нарисовать несуществующий объемный треугольник поэтапно
Шаг 4.
Спили вершины треугольника как на рисунке.
Как нарисовать несуществующий объемный треугольник поэтапно
Шаг 5.
Теперь обведи все линии, которые выделили мы, жирным карандашом, пером или гелевой ручкой. Или маркером. Или фломастером. Может надо бутерброд забацать?
Как нарисовать несуществующий объемный треугольник поэтапно
Шаг 6.
Сотри все ненужное. Мы близко к цели, видишь?
Как нарисовать несуществующий объемный треугольник поэтапно
Шаг 7.
Тут мы обратились к богам Олимпа и они нарисовали нам тени. Ты рисуй сам.
Как нарисовать несуществующий объемный треугольник поэтапно
Шаг 8.
Теперь можно вырезать наше творение лезвием или ножницами и ломать хрупкие разумы своих друзей. Этот треугольник входит в число фигур, которые геометрически не имеют право на существование или по по-другому “несуществующие фигуры”.
Этот треугольник входит в число фигур, которые геометрически не имеют право на существование или по по-другому “несуществующие фигуры”.
Надеемся, тебе понравилось, ибо мы старались и крали этот урок рисования несуществующего треугольника поэтапно. И теперь тебе лучше нарисовать героев Время приключений.
Как нарисовать несуществующий объемный треугольник поэтапно
Как нарисовать правильный треугольник вписанный в окружность
Popular
Основы черчения
Строительное
Машиностроительное
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг.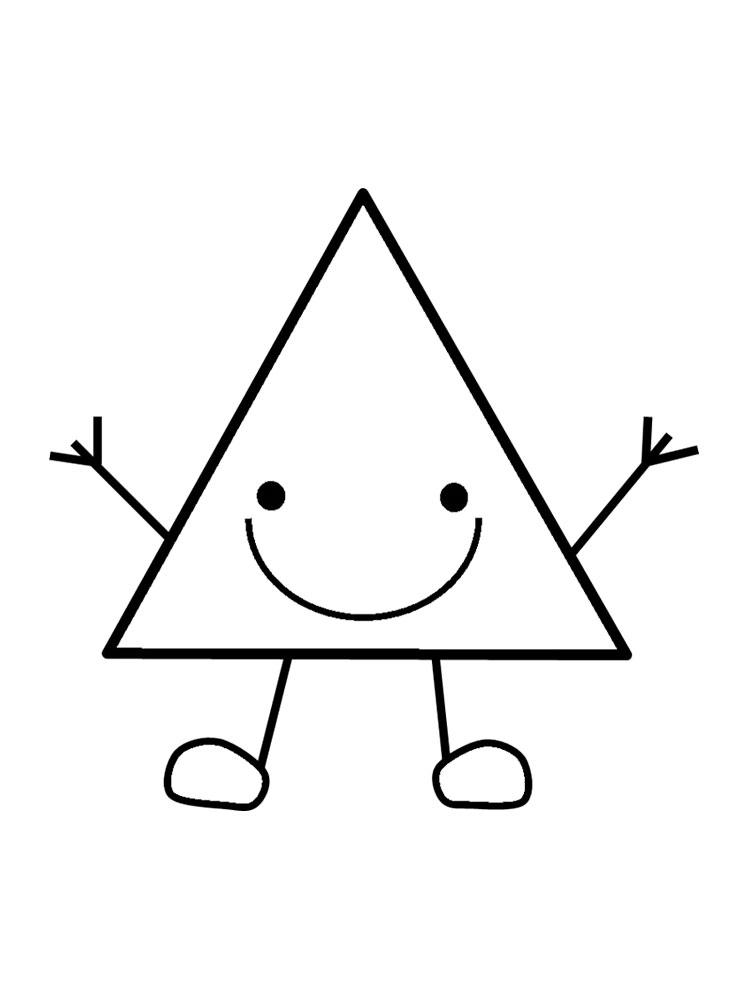 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В.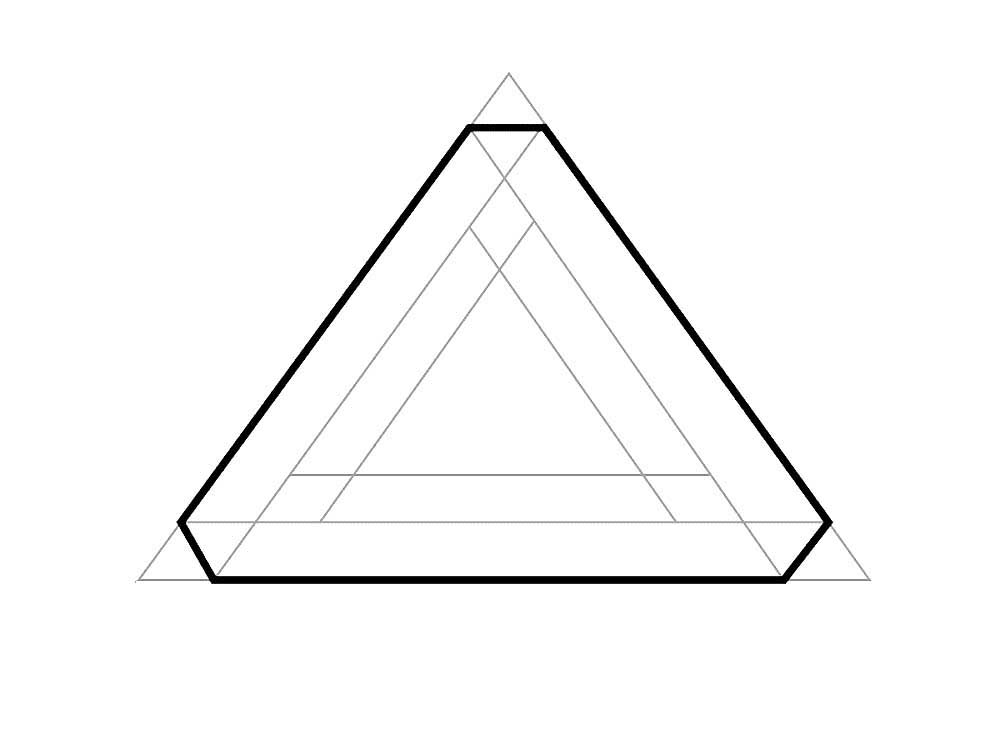 Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.
Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.
Деление окружности на равные части и построение правильных вписанных многоугольников можно выполнить как циркулем, так и с помощью угольников и рейсшины.
Деление окружности на четыре равные части и построение правильного вписанного четырехугольника. Две взаимно перпендикулярные центровые линии делят окружность на четыре равные части (рис. 115, а). Соединив точки пересечения этих линий с окружностью прямыми, получают правильный вписанный четырехугольник.
Деление окружности на восемь равных частей и построение правильного вписанного восьмиугольника. Две взаимно перпендикулярные линии, проведенные под углом 45° к центровым линиям с помощью угольника с углами 45, 45 и 90° и рейсшины (рис. 115, б), вместе с центровыми линиями разделят окружность на восемь равных частей.
Деление окружности на восемь равных частей можно выполнить циркулем. Для этого из точек 1 и 3 (точки пересечения центровых линий с окружностью) произвольным радиусом делаются засечки до взаимного пересечения, тем же радиусом делают две засечки из точек 3 и 5 (рис. 115, в). Через точки пересечения засечек и центр окружности проводят прямые линии до пересечения с окружностью в точках 2, 4, 6, 8.
Если полученные восемь точек соединить последовательно прямыми линиями, то получится правильный вписанный восьмиугольник (рис. 115, в).
Деление окружности на три равные части и построение правильного вписанного треугольника выполняют с помощью циркуля или угольника с углами 30, 60 и 90° и рейсшины.
При делении окружности циркулем на три равные части из любой точки окружности, например из точки Л пересечения центровых линий с окружностью (рис. 116, а и б), проводят дугу радиусом R, равным радиусу данной окружности, получают точки 1 и 2. Третья точка деления (точка 3) будет находиться на противоположном конце диаметра, проходящего через точку Л. Последовательно соединив точки 1, 2 и 3, получают правильный вписанный треугольник. При построении правильного вписанного треугольника, если задана одна из его вершин, например точка 1, находят точку А. Для этого через заданную точку 1 проводят диаметр (рис. 116, в). Точка А будет находиться на противоположном конце этого диаметра. Затем проводят дугу радиусом R равным радиусу данной окружности, получают точки 2 и 3.
При делении окружности на три равные части с помощью угольника и рейсшины через точку 1 под углом 60° проводят две прямые линии до пересечения с окружностью в точках 2 и 3 (рис. 117, а, б), точки 2 и 3 соединяют и получают правильный вписанный треугольник (рис.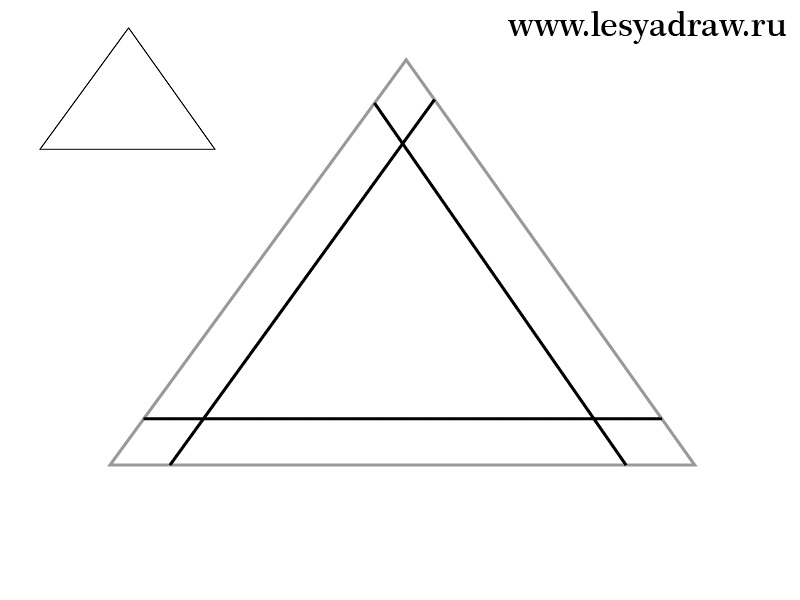 117, в).
117, в).
Деление окружности на шесть равных частей и построение правильного вписанного шестиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля. При делении окружности на шесть равных частей циркулем из двух концов одного диаметра радиусом, равным радиусу данной окружности, проводят дуги до пересечения с окружностью в точках 2, 6 и 3, 5 (рис. 118). Последовательно соединив полученные точки, получают правильный вписанный шестиугольник. Деление окружности на шесть равных час-1ен и построение правильного вписанного шестиугольника с помощью угольника и рейсшины показано на рис. 119 и 120. Деление окружности на двенадцать равных частей и построение правильного вписанного двенадцатиугольника выполняют с помощью угольника с углами 30, 60 и 90° и рейсшины или циркуля.
При делении окружности циркулем из четырех концов двух взаимно перпендикулярных диаметров окружности проводят радиусом, равным радиусу данной окружности, дуги до пересечения с окружностью (рис. 121). Соединив полученные точки, получают двенадцатиугольник.
121). Соединив полученные точки, получают двенадцатиугольник.
При построении двенадцатиугольника с помощью угольника и рейсшины точки деления строят, как показано на рис. 119 и 120.
Деление окружности на пять и десять равных частей и построение правильного вписанного пятиугольника и десятиугольника показано на рис. 122.
Половину любого диаметра (радиус) делят пополам (рис. 122, а), получают точку А. Из точки А, как из центра, проводят дугу радиусом, равным расстоянию от точки А до точки 1, до пересечения со второй половиной этого диаметра, в точке В (рис. 122, б). Отрезок 1В равен хорде, стягивающей дугу, длина которой равна 1 /5 длины окружности. Делая засечки на окружности (рис. 122, в) радиусом R, равным отрезку 1В, делят окружность на пять равных частей. Начальную точку 1 выбирают в зависимости от расположения пятиугольника. Из точки / строят точки 2 и 5 (рис. 122, в), затем из точки 2 строят точку 3, а из точки 5 строят точку 4.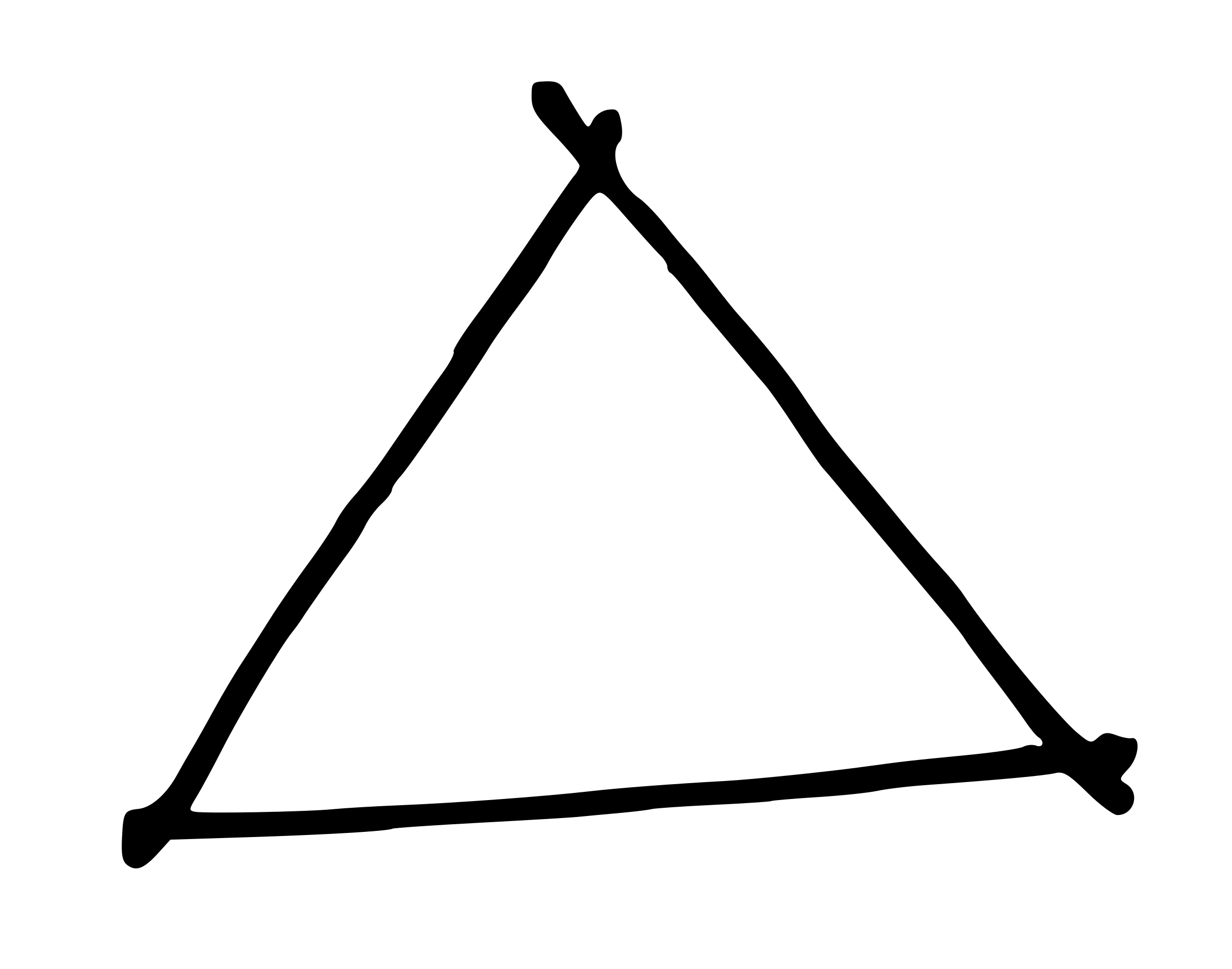 Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Расстояние от точки 3 до точки 4 проверяют циркулем; если расстояние между точками 3 и 4 равно отрезку 1В, то построения были выполнены точно. Нельзя выполнять засечки последовательно, в одну сторону, так как происходит набегание ошибок и последняя сторона пятиугольника получается перекошенной. Последовательно соединив найденные точки, получают пятиугольник (рис. 122, г).
Деление окружности на десять равных частей выполняют аналогично делению окружности на пять равных частей (рис. 122), но сначала делят окружность на пять частей, начиная построение из точки /, а затем из точки 6, находящейся на противоположном конце диаметра (рис. 123, а). Соединив последовательно все точки, получают правильный вписанный десятиугольник (рис. 123, б).
Деление окружности на семь и четырнадцать равных частей и построение правильного вписанного семиугольника и четырнадцатиугольника показано на рис. 124 и 125.
Из любой точки окружности, например точки Л, радиусом заданной окружности проводят дугу (рис. 124, а) до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
124, а) до пересечения с окружностью в точках В и D. Соединим точки В и D прямой. Половина полученного отрезка (в данном случае отрезок ВС) будет равна хорде, которая стягивает дугу, составляющую 1 /7 длины окружности. Радиусом, равным отрезку ВС, делают засечки на окружности в последовательности, показанной на рис. 124, б. Соединив последовательно все точки, получают правильный вписанный семиугольник (рис. 124, в).
Деление окружности на четырнадцать равных частей выполняется делением окружности на семь равных частей два раза от двух точек (рис. 125, а).
Сначала окружность делится на семь равных частей от точки /, затем то же построение выполняется от точки 8. Построенные точки соединяют последовательно прямыми линиями и получают правильный вписанный четырна-дцатиугольник (рис. 125, б).
СОПРЯЖЕНИЯ
Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе. На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.
На чертеже поверхности изображаются линиями, которые также плавно переходят одна в другую.
На рис. 126, а изображена деталь, в которой плавные переходы одних плоскостей в другие представляют собой цилиндрические поверхности. На чертеже (рис. 126, б) эти плоскости изображены прямыми линиями, а цилиндрические поверхности — дугами окружностей. Плавные переходы от одной прямой к другой в этих случаях выполняются дугой заданного радиуса.
Плавный переход одной цилиндрической поверхности в другую может являться цилиндрической поверхностью (рис. 127, а). На чертеже эти цилиндрические поверхности изображены дугами окружностей, (рис. 127, б). В этом случае плавный переход одной дуги окружности в другую осуществляется дугой окружности заданного радиуса.
На рис. 126, а и 127, а рассмотрены простейшие примеры плавных переходов поверхностей. В чертежах более сложных деталей плавные переходы между поверхностями изображаются различными сочетаниями прямых, окружностей и их дуг. Вариантов таких сочетаний может быть много, но их объединяет одно — плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Вариантов таких сочетаний может быть много, но их объединяет одно — плавность перехода. Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением. При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т. е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Задачи на сопряжения условно можно разделить на три группы.
Первая группа задачвключает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.
Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.
Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 128). Точка касания выбирается произвольно. Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O1, О2и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (O1, О2и т. д.) будут находиться на одинаковом расстоянии от заданной прямой, т. е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 128). Назовем эту линию линией центров. Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например точку О. Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
В детали, которая изображена на рис. 129, а, пластина плавно переходит в цилиндр. При выполнении чертежа этой детали необходимо построить плавный переход прямой в окружность.
Задача аналогична предыдущей, но дополнена условием, что точка касания задана, так как задан размер А (рис. 129, б), который определяет величину прямолинейного участка.
Отложив размер Л, находят точку касания (точку /С), затем из точки К восставляют перпендикуляр, на котором откладывают радиус R заданной окружности, и находят центр окружности (точку О). При обводке сначала от точки касания проводится дуга заданного радиуса, а потом — прямая.
Из сказанного следует:
1) центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;
Не нашли то, что искали? Воспользуйтесь поиском:
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии.
 Удостоверьтесь, что достаточно места для рисования всех трех сторон!
Удостоверьтесь, что достаточно места для рисования всех трех сторон! - Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую. Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
- Использование объекта с круглой базой: этот совет подойдет для построения дуги.
 Предложенный метод по сути такой же, как с использованием циркуля.
Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.

- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
Узнаем как правильно нарисовать треугольник: этапы выполнения задания
Как нарисовать треугольник? Этому учат в процессе изучения геометрии в школе. Чтобы задание было выполнено правильно, важно точно знать, какой треугольник необходимо изобразить: равносторонний, равнобедренный или же вписанный. Правилам начертания этих фигур будет посвящена данная статья.
Правилам начертания этих фигур будет посвящена данная статья.
Как рисовать треугольник с равными сторонами?
Как нарисовать треугольник, стороны у которого равны? Для этого можно воспользоваться одним из трех методов.
Такая фигура имеет три одинаковые по длине стороны, связанные тремя углами равной ширины. Это может быть сложным для рисования треугольника вручную. Поэтому можно использовать круглый объект для выделения углов.
Варианты создания фигуры
Обязательно используйте линейку и один из представленных ниже способов:
- Применение циркуля: надо начертить ровную линию. Проведите карандаш вдоль прямого края бумаги. Этот сегмент линии образует одну из сторон. А это означает, что нужно будет чертить вторую и третью линии одинаковой длины, каждая из которых достигает точки под углом 60° от первой линии. Удостоверьтесь, что достаточно места для рисования всех трех сторон!
- Разделите сегмент циркулем. Вставьте карандаш и убедитесь, что он острый! Поместите точку циркуля на один конец сегмента и установите карандаш на другую.
 Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник. - Использование объекта с круглой базой: этот совет подойдет для построения дуги. Предложенный метод по сути такой же, как с использованием циркуля.
Указанные советы помогут выяснить, как нарисовать равносторонний треугольник.
Рекомендации по построению равнобедренного треугольника
Равнобедренный треугольник представляет собой фигуру с двумя равными сторонами и двумя равными углами. Если знаете длину, основание и высоту стороны, это можно сделать только с линейкой и циркулем (или просто циркулем, если заданы размеры).
Как нарисовать равнобедренный треугольник:
- Учитывая все боковые длины. Чтобы использовать этот метод, важно знать длину основания треугольника и длину двух равных сторон.
- Учитывая две равные стороны и угол между ними. Чтобы использовать этот метод, нужно знать длину двух равных сторон и измерение угла между этими двумя сторонами.
- Учитывая базовые и смежные углы – необходимо знать длину базы, градусы двух углов, смежных с основанием. Помните, что два угла, смежные с основанием равнобедренного треугольника, будут равны.
- Основа и высота. Нужно знать длину основания треугольника, а также высоту этой геометрической фигуры.
Вписанный треугольник
Как нарисовать вписанный треугольник? Выберите круглый объект. Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Используйте предмет с круглым основанием. Выбор компакт-диска станет хорошим вариантом. Но можно взять и другой объект нужного размера. Для этого метода свойственно, что длина каждой стороны равносторонней геометрической фигуры с тремя углами будет равна размерам радиуса (половине диаметра) круга.
Как нарисовать треугольник, если используете компакт-диск? Представьте себе равносторонний треугольник, который вписывается в верхнюю правую часть компакт-диска. Надо начертить первую из сторон. Радиус круглого объекта – расстояние на полпути до получения желаемого результата. Удостоверьтесь, что линии нарисованы ровно.
С помощью линейки просто выполните измерения диаметра объекта и нарисуйте линию на половину длины. Если ее нет, поместите круглый объект на бумагу, затем тщательно проведите по окружности карандашом. Удалите объект – должен быть идеальный круг. Используйте прямой край, чтобы нарисовать линию через точный центр круга: точку, которая полностью равноудалена от любой точки по окружности круга.
Используйте круглый объект для создания дуги. Поместите объект по отрезку линии, с краем круга, расположенным на одном конце линии. Для обеспечения точности убедитесь, что линия проходит четко через центр круга. Используйте карандаш, чтобы начертить дугу – это четверть пути по окружности.
Начертите еще одну дугу. Теперь сдвиньте круглый объект так, чтобы край касался другого конца сегмента линии.
Подведем итоги
В статье были предоставлены рекомендации, как нарисовать треугольник равносторонний, равнобедренный и вписанный в окружность.
Как нарисовать треугольники в Adobe Photoshop
Photoshop предлагает практически безграничные возможности для творческой реализации. Однако пользователи, которые только начинают работать с программой могут испытывать сложность в самом элементарном, например, в рисовании геометрических фигур. Чаще всего, сложности происходят как раз, когда нужно нарисовать треугольник. На самом деле здесь всё просто, и мы разберёмся, как это сделать.
Как нарисовать треугольник в Photoshop
Изучив левую панель с инструментами, а особенно инструменты, позволяющие рисовать геометрические фигуры, пользователь не найдёт иконку треугольника. Есть квадраты, эллипсы, многоугольники и т.д., но нет треугольников. А рисование треугольника как раз происходит с помощью инструмента «Многоугольник».
- Выберите соответствующий инструмент в левой панели.
- В верхней части интерфейса рабочей области обратите внимание на значение поля «Стороны». По умолчанию там стоит «6», следовательно, программа и рисует шестиугольники. Для создания треугольника нужно только поставить там цифру «3». По аналогичной схеме вы можете нарисовать квадрат, пятиугольник, семи и так далее угольник.
- Указав нужное количество сторон, выберите цвет заливки в соответствующем пункте. Для примера выберем чёрный цвет заливки.
- Нажмите левой кнопкой мыши по холсту и удерживайте её для рисования треугольника. Тяните контуры и поворачивайте их.
 В программе доступен предпросмотр результата.
В программе доступен предпросмотр результата. - Полученный результат можно настроить под свои нужды. Например, можно менять направление углов, цвет заливки, обводку и некоторые другие параметры. Давайте посмотрим, как это делается с основными параметрами:
- Для смены заливки вам просто нужно нажать на квадратике с цветом, что расположен в верхней части рабочей области, и выбрать там нужный цвет;
- Чтобы сменить направление углов, выберите инструмент выделение узлов, а затем курсором нажмите на нужный угол. После нужно будет просто перетащить его в нужное направление;
- Для изменения или добавления обводки обратите внимание на пункт «Штрих». Там задайте цвет штриха, его толщину и тип обводки. Чтобы увидеть полученный эффект, вы можете отключить заливку.
Также треугольник можно нарисовать с помощью инструмента «Прямолинейное лассо», хотя этот вариант создания геометрических фигур не является таким очевидным. Выполняется следующим образом:
- Выберите инструмент «Прямолинейное лассо».

- Для удобства вы можете задать направляющие. Их не будет видно на рисунке, если вы решите его сохранить на компьютер. Вызовите линейку с помощью сочетания клавиш Ctrl+R.
- Теперь с боковой и верхней стороны перетяните направляющие. Просто зажмите верхнюю (боковую линейку) и тяните.
- Установите пересечение двух направляющих, чтобы получить прямой угол.
- С помощью инструмента «Прямолинейное лассо» нарисуйте треугольник нужного размера и нужной ориентации.
- Пока вы только получили выделение, а не полноценную фигуру. Вам нужно залить её цветом, чтобы получить полноценную геометрическую фигуру. Кликните по области выделения правой кнопкой мыши и из контекстного меню выберите пункт «Выполнить заливку». В некоторых версиях Фотошоп вместо этого пункта может быть «Выполнить обводку».
- Будет открыто окошко для настройки цвета заливки. В блоке «Содержимое» найдите параметр «Использовать» и там выберите вариант «Цвет». В зависимости от ваших целей, может потребоваться выбрать другой вариант.
 Вдруг вы хотите сделать у треугольника градиентную заливку.
Вдруг вы хотите сделать у треугольника градиентную заливку. - Дополнительно можете задать параметры обводки – её ширину, цвет и расположение относительно границы фигуры.
- Вы получили готовый треугольник. Теперь вам осталось только снять с него выделение, что делается с помощью сочетания клавиш Ctrl+D.
Читайте также:
Как вырезать объект в Фотошопе (Photoshop) «Пером» — инструкция
Рисовать онлайн: топ лучших сервисов для детей и взрослых
Инструкция как создать мультяшный эффект в Фотошопе (Photoshop)
Adobe Photoshop: разбор основных функций и возможностей
Как видите, нет ничего сложного в том, чтобы создать треугольник. По аналогичным схемам можно делать другие геометрические фигуры, которые содержат несколько углов. Если данная статья оказалась для вас полезной, поделитесь ей с другими людьми, возможно, она им тоже пригодится.
Как нарисовать треугольник в фотошопе — бесплатный онлайн урок
Существует множество областей, в которых вы могли бы применить знания программы Photoshop. Могу с уверенностью вам сказать, что порой для двух разных областей требуются настолько разные навыки, что просто диву даешься. Дизайнер может даже не представлять, как можно отретушировать портрет. А фотограф и понятия иметь не будет, как работать с линейками. Но есть вещи, которые желательно знать всем. Как, например, создание простейших фигур. Разберемся, как нарисовать треугольник в фотошопе.
Могу с уверенностью вам сказать, что порой для двух разных областей требуются настолько разные навыки, что просто диву даешься. Дизайнер может даже не представлять, как можно отретушировать портрет. А фотограф и понятия иметь не будет, как работать с линейками. Но есть вещи, которые желательно знать всем. Как, например, создание простейших фигур. Разберемся, как нарисовать треугольник в фотошопе.
Способов рисования треугольника в Adobe Photoshop CS 6 несколько. Начнем с инструмента «многоугольник».
Создадим новый документ. Справа отыщем инструмент «многоугольник» и выберем его.
Теперь выбираем цвет будущего треугольника. На той же панели инструментов. Этот способ позволит нам создать треугольник залитый цветом.
А теперь на верхней панели устанавливаем кол-во углов треугольника.
Теперь делаем клик на рабочей области и протягиваем. Треугольник готов!
Давайте разберем еще один способ. Как нарисовать треугольник в фотошопе при помощи пера.
Возвращаемся к той же панели инструментов. Выбираем «перо».
Делаем 2 клика по рабочей области и замыкаем контур.
Это способ позволит нам сделать как треугольник залитый цветом, так и контур треугольника. Начнем с контура.
Кликаем по нарисованному треугольнику левой клавишей мыши. В выпадающем списке выбираем «выполнить обводку контура».
Как видите, выскочило окно, позволяющее выбрать нам два варианта. Обводка кистью или карандашом. Я применю кисть.
Знайте, что обводка контура будет выполнена при помощи настроек, которые были выставлены заблаговременно.
Обводка выполнена. Чтобы убрать контур, выберите инструмент «перо» вновь. Кликните левой клавишей мыши, чтобы вызвать контекстное меню. И выберите команду «удалить контур».
А теперь разберемся, как при помощи пера сделать треугольник заполненный цветом. Возвращаемся к контуру. Кликаем левой клавишей мыши. В выпадающем меню выбираем «образовать выделенную область». И переходим к боковой панели, к уже знакомому нам инструменту выбора цвета. Устанавливаем нужный. На той же панели ищем «заливку».
И переходим к боковой панели, к уже знакомому нам инструменту выбора цвета. Устанавливаем нужный. На той же панели ищем «заливку».
Кликаем по выделенной области.
Снимание выделение при помощи комбинации клавиш ctrl+d. Треугольник, залитый цветом готов!
На первый взгляд может показаться, что второй способ гораздо удобнее, потому как мы можем выбрать любую форму треугольника. Но на деле и первый способ позволяет нам проводить любые манипуляции по измене формы. Но это уже совсем другая история.
Как нарисовать остроугольный треугольник. Как построить равнобедренный треугольник. Построение равностороннего треугольника
Инструкция
Поставьте иглу циркуля в отмеченную точку. Нарисуйте ножкой с грифелем дугу окружности отмеренного радиуса.
В любом месте по окружности нарисованной дуги поставьте точку. Это будет вторая вершина B создаваемого треугольника.
Аналогичным способом поставьте ножку на вторую вершину. Проведите еще одну окружность так, чтобы она пресекалась с первой.
Проведите еще одну окружность так, чтобы она пресекалась с первой.
В точке пересечения обоих проведенных дуг и находится третья вершина C создаваемого треугольника. Отметьте ее на рисунке.
Получив все три вершины, соедините их прямыми линиями с помощью любой ровной поверхности (лучше линейки). Треугольник ABC построен.
Если окружность касается всех трех сторон данного треугольника, а её центр находится внутри треугольника, то ее называют вписанной в треугольник.
Вам понадобится
- линейка, циркуль
Инструкция
Из вершин треугольника (стороны противоположной делимому углу) циркулем проводят дуги окружности произвольного радиуса до пересечения их между собой;
Точку пересечения дуг по линейке соединяют с вершиной делимого угла;
Тоже самое проделывают с любым другим углом;
Радиусом вписанной в треугольник окружности будет отношение площади треугольника и его полупериметра: r=S/p , где S — площадь треугольника, а p=(a+b+c)/2 — полупериметр треугольника.
Радиус вписанной в треугольник окружности равноудален от всех сторон треугольника.
Источники:
- http://www.alleng.ru/d/math/math52.htm
Рассмотрим задачу построения треугольника при условии, что известны три его стороны или одна сторона и два угла.
Вам понадобится
- — циркуль
- — линейка
- — транспортир
Инструкция
Допустим, даны три стороны : a, b и с. Пользуясь , несложно с такими сторонами. Для начала выберем самую длинную из этих сторон, пусть это будет сторона с, и начертим ее. Затем установим раствор циркуля на величину другой стороны, стороны a, и начертим циркулем окружность радиуса a с центром на одном из концов стороны c. Теперь установим раствор циркуля на величину стороны b и начертим окружность с центром на другом конце стороны c. Радиус этой окружности равен b. Соединим точку пересечения окружностей с центрами и получим треугольник с искомыми сторонами.
Чтобы начертить треугольник с заданной стороной и двумя прилегающими углами, возьмите транспортир. Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.
Начертите сторону указанной длины. На краях ее отложите транспортиром углы. На пересечении сторон углов получите третью вершину треугольника.
Видео по теме
Обратите внимание
Для сторон треугольника справедливо следующее утверждение: сумма длин двух любых сторон должна быть больше третьей. Если это не выполняется, то построить такой треугольник невозможно.
Окружности в шаге 1 пересекаются в двух точках. Можно выбрать любую, треугольники будут равными.
Правильный треугольник — тот, у которого все стороны обладают одинаковой длиной. Исходя из этого определения, построение подобной разновидности треугольника является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
С помощью линейки соединить отмеченные на листке точки последовательно, друг за другом так, как это показано на рисунке 2.
Обратите внимание
В правильном (равностороннем) треугольнике все углы равны 60 градусам.
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это означает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Любой правильный треугольник является равнобедренным, в то время как обратное утверждение не верно.
У любого равностороннего треугольника одинаковы не только стороны, но и углы, каждый из которых равен 60 градусам. Однако чертеж такого треугольника, построенный при помощи транспортира, не будет обладать высокой точностью. Поэтому для построения данной фигуры лучше воспользоваться циркулем.
Вам понадобится
- Карандаш, линейка, циркуль
Инструкция
Затем возьмите циркуль, установите его в из концов (будущей вершине треугольника) и проведите окружность с радиусом, равным длине этого отрезка. Можно не проводить окружность целиком, а начертить лишь ее четверть, от противоположного края отрезка.
Теперь переставьте циркуль в другой конец отрезка и снова начертите окружность того же радиуса. Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.
Здесь будет достаточно построить окружности, проходящую от дальнего конца отрезка до пересечения с уже построенной дугой. Полученная точка будет третьей вершиной вашего треугольника.
Чтобы закончить построение, снова возьмите линейку с карандашом и соедините точку пересечения двух окружностей с обоими концами отрезка. Вы получите треугольник, все три стороны которого абсолютно равны, – это можно будет легко проверить с помощью линейки.
Видео по теме
Треугольник – это многоугольник, у которого три стороны. Равносторонним или правильным треугольником называют треугольник, у которого все стороны и углы равны. Рассмотрим, как можно нарисовать правильный треугольник.
Вам понадобится
- Линейка, циркуль.
Инструкция
С помощью циркуля нарисуйте еще одну окружность, центр которой будет в точке В, а радиус равен отрезку ВА.
Окружности будут пересекаться в двух точках. Выберите любую из них. Назовите ее С. Это будет третьей вершиной треугольника.
Это будет третьей вершиной треугольника.
Соедините вершины между собой. Получившийся треугольник будет правильным. Убедитесь в этом, померив его стороны линейкой.
Рассмотрим способ построения правильного треугольника с помощью двух линеек. Начертите отрезок ОК, он будет одной из сторон треугольника, а точки О и К его вершинами.
Не сдвигая линейки после построения отрезка ОК, приложите перпендикулярно к ней еще одну линейку. Проведите прямую m пересекающую отрезок ОК в середине.
С помощью линейки отмерьте отрезок ОЕ, равный отрезку ОК так, чтобы один его конец совпадал с точкой О, а другой находился на прямой m. Точка Е буде третьей вершиной треугольника.
Закончите построение треугольника, соединив точки Е и К. Проверьте правильность построения с помощью линейки.
Обратите внимание
Убедиться в том, что треугольник правильный можете с помощью транспортира, измерив углы.
Полезный совет
Равносторонний треугольник так же можно начертить на листе в клетку с помощью одной линейки. Вместо другой линейки используйте перпендикулярные линии.
Вместо другой линейки используйте перпендикулярные линии.
Источники:
- Классификация треугольников. Равносторонние треугольники
- Что такое треугольник
- построение правильного треугольника
Вписанным называется такой треугольник, все вершины которого находятся на окружности. Построить его можно, если знать хотя бы одну сторону и угол. Окружность называется описанной, и она будет единственной для данного треугольника.
Вам понадобится
- — окружность;
- — сторона и угол треугольника;
- — лист бумаги;
- — циркуль;
- — линейка;
- — транспортир;
- — калькулятор.
Инструкция
От точки А с помощью транспортира отложите заданный угол. Продолжите сторону угла до пересечения с окружностью и поставьте точку С. Соедините точки В и С. У вас получился треугольник АВС. Он может быть любого типа. Центр окружности у остроугольного треугольника него, у тупоугольного — вне, а у прямоугольного — на гипотенузе. Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.
Если вам задан не угол, а, например, три стороны треугольника, вычислите один из углов по радиусу и известной стороне.
Значительно чаще приходится иметь дело с обратным построением, когда задан треугольник и надо вокруг него описать окружность. Вычислите его радиус. Сделать это можно по нескольким формулам, в зависимости от того, что вам дано. Радиус можно найти, например, по стороне и синусу противолежащего угла. В этом случае он равен длине стороны, разделенной на удвоенный синус противолежащего угла. То есть R=a/2sinCAB. Можно его выразить и через произведение сторон, в этом случае R=abc/√(a+b+c)(a+b-c)(a+c-b)(b+c-a).
Определите центр окружности. Разделите все стороны пополам и проведите серединам перпендикуляры. Точка их пересечения и будет центром окружности. Начертите ее так, чтобы она пересекла все вершины углов.
Две короткие стороны прямоугольного треугольника, которые принято называть катетами, по определению должны быть перпендикулярны между собой.![]() Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.
Это свойство фигуры значительно облегчает ее построение. Однако возможность точно определить перпендикулярность есть не всегда. В таких случаях можно рассчитать длины всех сторон — они позволят построить треугольник единственно возможным, а поэтому правильным, способом.
Вам понадобится
- Бумага, карандаш, линейка, транспортир, циркуль, угольник.
Как начертить треугольник?
Построение различных треугольников — обязательный элемент школьного курса геометрии. У многих это задание вызывает страх. Но на самом деле, все довольно просто. Далее в статье описано, как начертить треугольник любого типа с помощью циркуля и линейки.
Треугольники бывают
- разносторонние;
- равнобедренные;
- равносторонние;
- прямоугольные;
- тупоугольные;
- остроугольные;
- вписанные в окружность;
- описанные вокруг окружности.
Построение равностороннего треугольника
Равносторонним называется треугольник, у которого все стороны равны. Из всех видов треугольников, начертить равносторонний проще всего.
Из всех видов треугольников, начертить равносторонний проще всего.
- С помощью линейки начертите одну из сторон, заданной длины.
- Измерьте ее длину с помощью циркуля.
- Поместите острие циркуля в один из концов отрезка и проведите окружность.
- Переставьте острие в другой конец отрезка и проведите окружность.
- У нас получилось 2 точки пересечения окружностей. Соединяя любую из них с краями отрезка, мы получаем равносторонний треугольник.
Построение равнобедренного треугольника
Данный тип треугольников можно построить по основанию и боковым сторонам.
Равнобедренным называется треугольник, у которого две стороны равны. Для того чтобы начертить равнобедренный треугольник по данным параметрам, необходимо выполнить следующие действия:
- С помощью линейки откладываем отрезок, равный по длине основанию. Обозначаем его буквами АС.
- Циркулем измеряем необходимую длину боковой стороны.
- Рисуем из точки А, а затем из точки С, окружности, радиус которых равен длине боковой стороны.

- Получаем две точки пересечения. Соединив одну из них с точками А и С, получаем необходимый треугольник.
Построение прямоугольного треугольника
Треугольник, у которого один угол прямой, называют прямоугольным. Если нам даны катет и гипотенуза, начертить прямоугольный треугольник не составит труда. Его можно построить по катету и гипотенузе.
Построение тупоугольного треугольника по углу и двум прилегающим сторонам
Если один из углов треугольника тупой (больше 90 градусов), его называют тупоугольным. Чтобы начертить по указанным параметрам тупоугольный треугольник необходимо сделать следующее:
- С помощью линейки откладываем отрезок, равный по длине одной из сторон треугольника. Обозначим его буквами А и D.
- Если в задании уже нарисован угол, и вам необходимо начертить такой же, то на его изображении отложить два отрезка, оба конца которых лежат в вершине угла, а длина равняется указанным сторонам. Соедините полученные точки.
 У нас получился искомый треугольник.
У нас получился искомый треугольник. - Чтобы его перенести на свой чертеж, вам необходимо измерить длину третьей стороны.
Построение остроугольного треугольника
Остроугольный треугольник (все углы меньше 90 градусов) строится по тому же принципу.
- Нарисуйте две окружности. Центр одной из них лежит в точке D, а радиус равен длине третьей стороны, а у второй центр находится в точке А, а радиус равен длине указанной в задании стороны.
- Соедините одну из точек пересечения окружности с точками А и D. Искомый треугольник построен.
Вписанный треугольник
Для того чтобы начертить треугольник в окружности, нужно помнить теорему, в которой говорится, что центр описанной окружности лежит на пересечении серединных перпендикуляров:
У тупоугольного треугольника центр описанной окружности лежит за пределами треугольника, а у прямоугольного — на середине гипотенузы.
Чертим описанный треугольник
Описанный треугольник — это треугольник, в центре которого нарисована окружность, касающаяся всех его сторон. Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Центр вписанной окружности лежит на пересечении биссектрис. Для их построения необходимо:
Как построить равнобедренный треугольник? Это легко сделать с помощью линейки, карандаша и клеточек тетради.
Построение равнобедренного треугольника начинаем с основания. Чтобы рисунок получился ровным, количество клеточек в основании должно быть четным числом.
Делим отрезок — основание треугольника — пополам.
Вершину треугольника можно выбрать на любой высоте от основания, но обязательно ровно над срединой.
Как построить остроугольный равнобедренный треугольник?
Углы при основании равнобедренного треугольника могут быть только острыми. Чтобы равнобедренный треугольник получился остроугольным, угол при вершине тоже должен быть острым.
Для этого вершину треугольника выбираем повыше, подальше от основания.
Чем выше вершина, тем меньше угол при вершине. Углы при основании при этом, соответственно, увеличиваются.
Как построить тупоугольный равнобедренный треугольник?
С приближением вершины равнобедренного треугольника к основанию градусная мера угла при вершине увеличивается.
Значит, чтобы построить равнобедренный тупоугольный треугольник, вершину выбираем пониже.
Как построить равнобедренный прямоугольный треугольник?
Чтобы построить равнобедренный прямоугольный треугольник, надо вершину выбрать на расстоянии, равном половине основания (это обусловлено свойствами равнобедренного прямоугольного треугольника).
Например, если длина основания — 6 клеточек, то вершину треугольника располагаем на высоте 3 клеточек над серединой основания. Обратите внимание: при этом каждая клеточка у углов при основании делится по диагонали.
Построение равнобедренного прямоугольного треугольника можно начать с вершины.
Выбираем вершину, от нее под прямым углом откладываем равные отрезки вверх и вправо. Это — боковые стороны треугольника.
Соединим их и получим равнобедренный прямоугольный треугольник.
Построение равнобедренного треугольника с помощью циркуля и линейки без делений рассмотрим в другой теме.
Еще дети дошкольного возраста знают, как выглядит треугольник. А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
А вот с тем, какие они бывают, ребята уже начинают разбираться в школе. Одним из видов является тупоугольный треугольник. Понять, что это такое, проще всего, если увидеть картинку с его изображением. А в теории это так называют «простейший многоугольник» с тремя сторонами и вершинами, одна из которых является
Разбираемся с понятиями
В геометрии различают такие виды фигур с тремя сторонами: остроугольный, прямоугольный и тупоугольный треугольники. При этом свойства этих простейших многоугольников одинаковы для всех. Так, для всех перечисленных видов будет соблюдаться такое неравенство. Сумма длин любых двух сторон обязательно будет больше протяженности третьей стороны.
Но для того чтобы быть уверенным, что речь идет именно о законченной фигуре, а не о наборе отдельных вершин, необходимо проверить, чтобы соблюдалось основное условие: сумма углов тупоугольного треугольника равняется 180 о. Это же верно и для других видов фигур с тремя сторонами. Правда, в тупоугольном треугольнике один из углов будет еще больше 90 о, а два оставшихся обязательно будут острыми.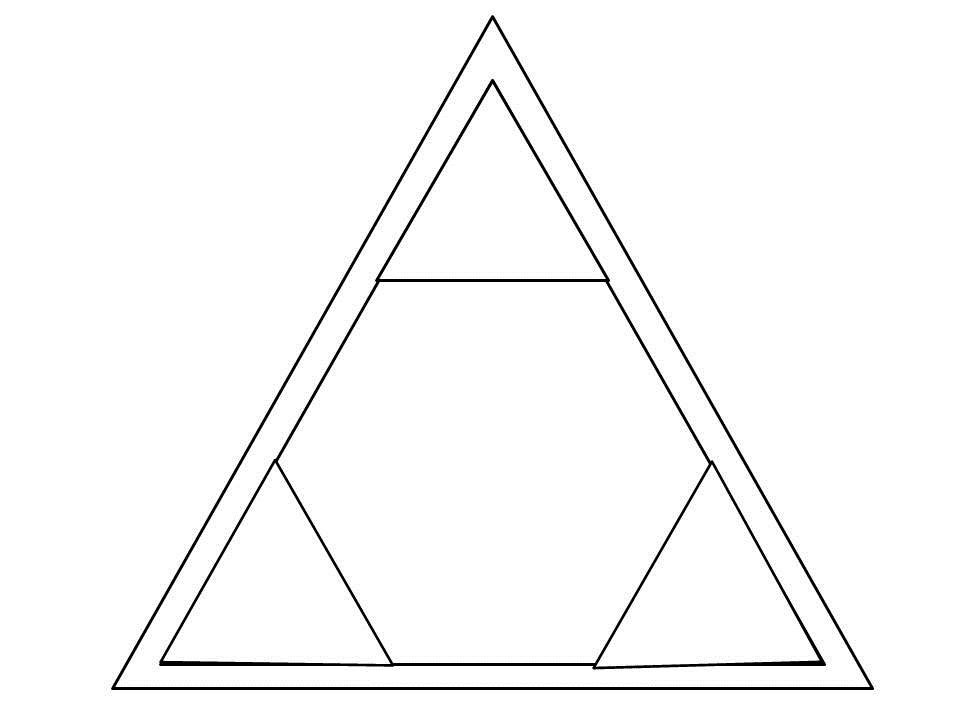 При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
При этом именно наибольший угол будет находиться напротив самой длинной стороны. Правда, это далеко не все свойства тупоугольного треугольника. Но и зная лишь эти особенности, школьники могут решать многие задачи по геометрии.
Для каждого многоугольника с тремя вершинами верно и то, что, продолжая любую из сторон, мы получим угол, размер которого будет равен сумме двух несмежных с ним внутренних вершин. Периметр тупоугольного треугольника рассчитывается так же, как и для других фигур. Он равняется сумме длин всех его сторон. Для определения математиками были выведены различные формулы, в зависимости от того, какие изначально присутствуют данные.
Правильное начертание
Одним из важнейших условий решения задач по геометрии является верный рисунок. Часто учителя математики говорят о том, что он поможет не только наглядно представить, что дано и что от вас требуется, но на 80% приблизиться к правильному ответу. Именно поэтому важно знать, как построить тупоугольный треугольник. Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если вам нужна просто гипотетическая фигура, то вы можете нарисовать любой многоугольник с тремя сторонами так, чтобы один из углов был больше 90 о.
Если даны определенные значения длин сторон или градусы углов, то чертить тупоугольный треугольник необходимо в соответствии с ними. При этом необходимо стараться максимально точно изобразить углы, высчитывая их при помощи транспортира, и пропорционально данным в задании условиям отобразить стороны.
Основные линии
Зачастую школьникам мало знать только то, как должны выглядеть те или иные фигуры. Они не могут ограничиться лишь информацией о том, какой треугольник тупоугольный, а какой прямоугольный. Курсом математики предусмотрено, что их знания об основных особенностях фигур должны быть более полными.
Так, каждому школьнику должно быть понятно определение биссектрисы, медианы, серединного перпендикуляра и высоты. Кроме того, он должен знать и их основные свойства.
Так, биссектрисы делят угол пополам, а противоположную сторону — на отрезки, которые пропорциональны прилегающим сторонам.
Медиана делит любой треугольник на два равных по площади. В точке, в которой они пересекаются, каждая из них разбивается на 2 отрезка в пропорции 2: 1, если смотреть от вершины, из которой она вышла. При этом большая медиана всегда проведена к его наименьшей стороне.
Не меньше внимания уделяется и высоте. Это перпендикуляр к противоположной от угла стороне. Высота тупоугольного треугольника имеет свои особенности. Если она проведена из острой вершины, то она попадает не на сторону этого простейшего многоугольника, а на ее продолжение.
Серединный перпендикуляр — это отрезок, который выходит из центра грани треугольника. При этом он расположен к ней под прямым углом.
Работа с окружностями
В начале изучения геометрии детям достаточно понять, как начертить тупоугольный треугольник, научиться отличать его от остальных видов и запомнить его основные свойства. А вот старшеклассникам этих знаний уже мало. Например, на ЕГЭ часто встречаются вопросы про описанные и вписанные окружности. Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Первая из них касается всех трех вершин треугольника, а вторая имеет по одной общей точке со всеми сторонами.
Построить вписанный или описанный тупоугольный треугольник уже намного сложнее, ведь для этого необходимо для начала выяснить, где должен находиться центр окружности и ее радиус. Кстати, необходимым инструментом станет в этом случае не только карандаш с линейкой, но и циркуль.
Те же сложности возникают при построении вписанных многоугольников с тремя сторонами. Математиками были выведены различные формулы, которые позволяют определить их месторасположение максимально точно.
Вписанные треугольники
Как уже было сказано ранее, если круг проходит через все три вершины, то это называется описанной окружностью. Главным ее свойством является то, что она единственная. Чтобы выяснить, как должна располагаться описанная окружность тупоугольного треугольника, необходимо помнить, что ее центр находится на пересечении трех серединных перпендикуляров, которые идут к сторонам фигуры. Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Если в остроугольном многоугольнике с тремя вершинами эта точка будет находиться внутри него, то в тупоугольном — за его пределами.
Зная, например, что одна из сторон тупоугольного треугольника равна его радиусу, можно найти угол, который лежит напротив известной грани. Его синус будет равен результату от деления длины известной стороны на 2R (где R — это радиус окружности). То есть sin угла будет равен ½. Значит, угол будет равен 150 о.
Если вам необходимо найти радиус описанной окружности тупоугольного треугольника, то вам пригодятся сведения о длине его сторон (c, v, b) и его площади S. Ведь радиус высчитывается так: (c х v х b) : 4 х S. Кстати, неважно, какого именно у вас вида фигура: разносторонний тупоугольный треугольник, равнобедренный, прямо- или остроугольный. В любой ситуации, благодаря приведенной формуле, вы можете узнать площадь заданного многоугольника с тремя сторонами.
Описанные треугольники
Также довольно часто приходится работать со вписанными окружностями.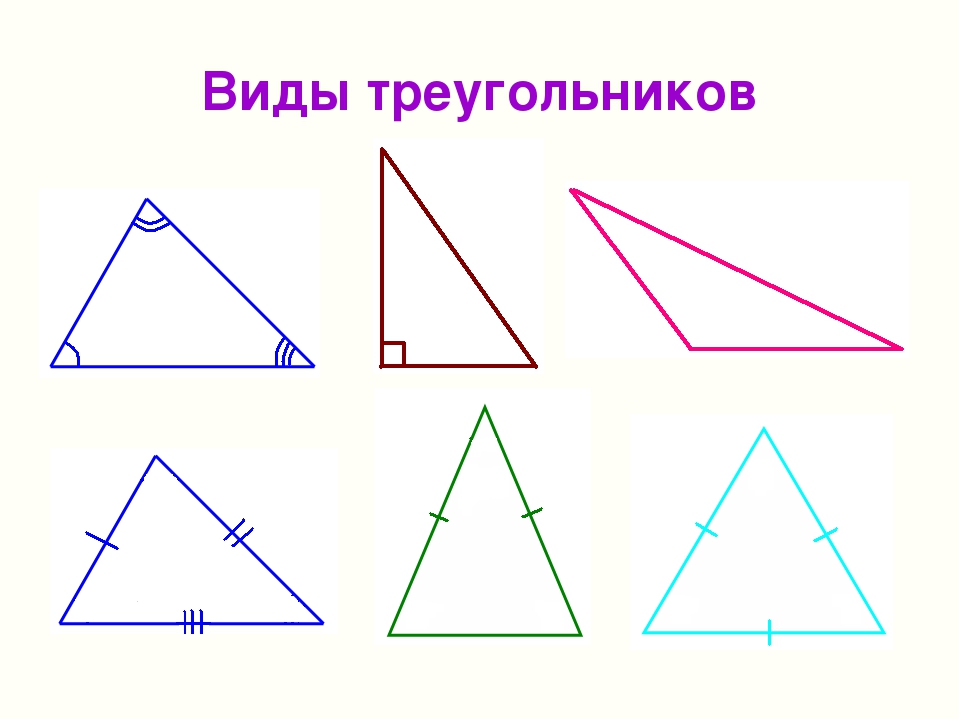 По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
По одной из формул, радиус такой фигуры, умноженный на ½ периметра, будет равняться площади треугольника. Правда, для ее выяснения вам необходимо знать стороны тупоугольного треугольника. Ведь для того чтобы определить ½ периметра, необходимо сложить их длины и разделить на 2.
Чтобы понять, где должен находиться центр круга, вписанного в тупоугольный треугольник, необходимо провести три биссектрисы. Это линии, которые делят углы пополам. Именно на их пересечении и будет находиться центр окружности. При этом он будет равноудален от каждой из сторон.
Радиус такой окружности, вписанной в тупоугольный треугольник, равняется из частного (p-c) х (p-v) х (p-b) : p. При этом p — это полупериметр треугольника, c, v, b — его стороны.
python — Как нарисовать прямоугольный треугольник с помощью tkinter?
Я пытаюсь нарисовать прямоугольный треугольник с помощью tkinter. Я не могу понять, как это сделать, я могу сделать прямоугольник, а затем еще один, но я не могу сделать второй прямоугольник треугольником.
Вот пример того, что я хочу сделать, как далеко я продвинулся, и мой код:
Что я хочу сделать:
Как далеко я продвинулся:
Мой код:
from tkinter import *
root= Tk()
can = Canvas(root, width=200, height=200)
can.pack()
shape1={'bounds': [20, 20, 80, 50], 'kind': 'rect', 'fill': True}
shape2={'bounds': [80, 50, 20, 35], 'kind': 'tri', 'fill': True}
can.create_rectangle(list(shape1.values())[0],fill='black')
can.create_rectangle(list(shape2.values())[0],fill='white')
root.mainloop()
0
Fred Enator 5 Окт 2020 в 17:12
2 ответа
Лучший ответ
Вы можете использовать polygon — функцию, чтобы нарисовать треугольник. Просто укажите list угловых точек вашего треугольника в качестве аргумента.
points = [x1,y1, x2,y2, x3,y3]
can. create_polygon(points, fill='white')
create_polygon(points, fill='white')
Дополнительную информацию см. В документации по tkinter.
4
Aerows 5 Окт 2020 в 14:23
Вы должны использовать create_polygon(), чтобы нарисовать треугольник:
shape2={'bounds': [20, 50, 80, 35, 80, 50], 'kind': 'tri', 'fill': True}
can.create_polygon(list(shape2.values())[0],fill='white',outline='white')
2
acw1668 5 Окт 2020 в 15:13
треугольников
Рисование треугольников
Инструмент «Общий треугольник» позволяет нарисовать любой треугольник.
Щелчок правой кнопкой мыши на одной из сторон треугольника позволит вам настроить стороны и углы треугольника. Вы также можете добавить метки и текст к краю.
Вы также можете добавить метки и текст к краю.
Свойства треугольника динамически определяют, достаточно ли вы ввели информации для определения уникального треугольника.В этом примере мы удалили длину первой стороны, а оставшейся информации недостаточно для определения треугольника. Затем FX Draw позволяет вам вводить другую информацию (например, углы) до тех пор, пока не будет определен уникальный (и действительный) треугольник.
В этом примере мы ввели три стороны, которые не могут образовать треугольник, поэтому FX Draw не заблокировал другие параметры.
Доступные параметры для треугольников
$ площадь
$ aalt
$ balt Высота
$ из расчета
$ периметр
$
$ b Размер уголка
$ c
долл. США
$ сб Длины сторон
$ sc
Инструменты «Равнобедренные треугольники» позволяют по-разному рисовать равнобедренные треугольники.
При использовании инструмента «Первый равнобедренный треугольник» первая линия, которую вы рисуете, является основанием равнобедренного треугольника.
При использовании второго инструмента равнобедренный треугольник первая линия представляет собой одну из двух совпадающих сторон.
Щелчок правой кнопкой мыши на одной из сторон треугольника позволит вам добавить метки и текст к краям треугольника.У вас также есть возможность автоматически отмечать стороны одинаковой длины.
Инструмент «Равносторонний треугольник» позволяет быстро рисовать равносторонние треугольники.
Щелчок правой кнопкой мыши на одной из сторон треугольника позволит вам добавить метки и текст к краям треугольника. У вас также есть возможность автоматически отмечать стороны одинаковой длины.
Инструменты «Правые треугольники» позволяют рисовать прямоугольные треугольники по-разному.
При использовании первого инструмента прямоугольного треугольника первая линия, которую вы рисуете, является одной из более коротких сторон прямоугольного треугольника.
При использовании второго инструмента прямоугольного треугольника первая линия представляет собой гипотенузу.
Щелчок правой кнопкой мыши на одной из сторон треугольника позволит вам добавить метки к середине линии.
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}} *
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}} / 500 {{l10n_strings.TAGS}} {{$ item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$ select.selected.display}}{{article.content_lang.display}}
{{l10n_strings.AUTHOR}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$ select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Калькулятор треугольников
Укажите 3 значения, включая хотя бы одну сторону в следующих 6 полях, и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 2, пи / 4 и т. Д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники обычно описывают на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют равную длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют равную длину, называется равнобедренным.Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Отметки на краю треугольника — это обычное обозначение, которое отражает длину стороны, где одинаковое количество отметок означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых различным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому логично, что равносторонний треугольник имеет три равных внутренних угла и три стороны равной длины.Обратите внимание, что треугольник, представленный в калькуляторе, не показан в масштабе; хотя он выглядит равносторонним (и имеет отметки угла, которые обычно воспринимаются как равные), он не обязательно является равносторонним и представляет собой просто представление треугольника. После ввода фактических значений выходные данные калькулятора будут отражать форму входного треугольника.
Треугольники, классифицируемые на основе их внутренних углов, делятся на две категории: прямые и наклонные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90 °, и обозначается двумя отрезками прямой, образующими квадрат в вершине, составляющей прямой угол.Самый длинный край прямоугольного треугольника, противоположный прямому углу, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как наклонный треугольник и может быть тупым или острым. В тупоугольном треугольнике один из углов треугольника больше 90 °, а в остром треугольнике все углы меньше 90 °, как показано ниже.
Факты, теоремы и законы о треугольнике
- Учитывая длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения.Обратитесь к треугольнику выше, предполагая, что a, b и c — известные значения.
Площадь треугольника
Существует несколько различных уравнений для вычисления площади треугольника в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b , и высоту, h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка линии, проведенного от вершины, противоположной основанию, до точки на основании, образующей перпендикуляр.
Учитывая длину двух сторон и угол между ними, следующую формулу можно использовать для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному на калькуляторе выше. Для a = 9, b = 7 и C = 30 °:
Другой метод вычисления площади треугольника основан на формуле Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат.Однако для этого требуется, чтобы длина трех сторон была известна. Опять же, со ссылкой на треугольник, представленный в калькуляторе, если a = 3, b = 4 и c = 5:
Медиана, внутренний и окружной радиус
Медиана
Медиана треугольника определяется как длина отрезка прямой, который проходит от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек в треугольнике) треугольника.См. Рисунок ниже для пояснения.
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:
Где a, b и c обозначают длину стороны треугольника, как показано на рисунке выше.
В качестве примера, учитывая, что a = 2, b = 3 и c = 4, медиана m a может быть рассчитана следующим образом:
Inradius
Inradius — это радиус наибольшего круга, который может поместиться внутри данного многоугольника, в данном случае треугольника.Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вращения и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром, поскольку центр, по определению, находится на равном расстоянии от каждой стороны треугольника.
В данном калькуляторе внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (ов) треугольника по следующим формулам:
где a, b и c — стороны треугольника
.Круговой радиус
Радиус описанной окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника.Центр этой окружности, где пересекаются все срединные перпендикуляры каждой стороны треугольника, является центром описанной окружности и точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
В данном калькуляторе радиус описанной окружности рассчитывается по следующей формуле:
Где a — сторона треугольника, а A — угол, противоположный стороне a
Хотя используются сторона a и угол A, в формуле можно использовать любую из сторон и их соответствующие противоположные углы.
Нарисуйте треугольник с помощью Arcade в Python
Arcade — это библиотека Python, которая используется для разработки 2D-игр. Arcade требуется поддержка OpenGL 3.3+. В аркаде базовое рисование не требует знаний о том, как определять функции или классы или как создавать циклы, просто у нас есть встроенные функции для рисования примитивов.
Встроенная функция Arcade для рисования треугольника:
1: arcade.draw_traingle_outline (): Эта функция используется для рисования контура треугольника.
Синтаксис: arcade.draw_triangle_outline (x1, y1, x2, y2, x3, y3, color, border_width)
Параметры:
- x1: x значение первой координаты.
- y1: значение y первой координаты.
- x2: x значение второй координаты.
- y2: значение y второй координаты.
- x3: x значение третьей координаты.
- y3: значение y третьей координаты.
- цвет: Цвет контура треугольника.
- border_width: Ширина границы в пикселях. По умолчанию 1.
Давайте посмотрим на примере, чтобы лучше понять его работу.
Python3
|
|
Укрепите свои основы с помощью курса Python Programming Foundation и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS .А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень
Рисование фигур с помощью холста - веб-API
Теперь, когда мы настроили среду холста, мы можем перейти к деталям того, как рисовать на холсте. К концу этой статьи вы научитесь рисовать прямоугольники, треугольники, линии, дуги и кривые, познакомившись с некоторыми из основных фигур. Работа с контурами важна при рисовании объектов на холсте, и мы увидим, как это можно сделать.
Прежде чем мы сможем начать рисовать, нам нужно поговорить о сетке холста или о пространстве координат . Наш скелет HTML с предыдущей страницы имел элемент холста шириной 150 пикселей и высотой 150 пикселей.
Обычно 1 единица сетки соответствует 1 пикселю на холсте. Начало этой сетки расположено в верхнем левом углу в координате (0,0). Все элементы размещаются относительно этого начала координат. Таким образом, положение верхнего левого угла синего квадрата становится x пикселей слева и y пикселей сверху, в координатах (x, y).Позже в этом уроке мы увидим, как мы можем перевести начало координат в другое положение, повернуть сетку и даже масштабировать ее, но пока мы будем придерживаться значения по умолчанию.
В отличие от SVG, поддерживает только две примитивные формы: прямоугольники и пути (списки точек, соединенных линиями). Все остальные формы должны быть созданы путем объединения одного или нескольких контуров. К счастью, у нас есть набор функций рисования контуров, которые позволяют создавать очень сложные формы.
Сначала посмотрим на прямоугольник.Есть три функции, которые рисуют прямоугольники на холсте:
-
fillRect (x, y, ширина, высота) - Рисует прямоугольник с заливкой.
-
strokeRect (x, y, ширина, высота) - Рисует прямоугольный контур.
-
clearRect (x, y, ширина, высота) - Очищает указанную прямоугольную область, делая ее полностью прозрачной.
Каждая из этих трех функций принимает одни и те же параметры. x и y определяют положение на холсте (относительно исходной точки) верхнего левого угла прямоугольника. ширина и высота обеспечивают размер прямоугольника.
Ниже представлена функция draw () с предыдущей страницы, но теперь она использует эти три функции.
Пример прямоугольной формы
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = canvas.getContext ('2d');
ctx.fillRect (25, 25, 100, 100);
ctx.clearRect (45, 45, 60, 60);
ctx.strokeRect (50, 50, 50, 50);
}
} Результат этого примера показан ниже.
| Скриншот | Живой образец |
|---|---|
Функция fillRect () рисует большой черный квадрат 100 пикселей с каждой стороны. Затем функция clearRect () стирает квадрат 60x60 пикселей из центра, а затем вызывается strokeRect () , чтобы создать прямоугольный контур 50x50 пикселей внутри очищенного квадрата.
На следующих страницах мы увидим два альтернативных метода для clearRect () , а также увидим, как изменить цвет и стиль обводки визуализированных фигур.
В отличие от функций контура, которые мы увидим в следующем разделе, все три прямоугольные функции рисуют непосредственно на холсте.
Теперь посмотрим на пути. Путь - это список точек, соединенных отрезками линий разной формы, изогнутыми или нет, разной ширины и разного цвета. Путь или даже подпуть можно закрыть. Чтобы сделать фигуры с помощью контуров, мы предпримем несколько дополнительных шагов:
- Сначала вы создаете путь.
- Затем вы используете команды рисования, чтобы нарисовать контур.
- После того, как путь был создан, вы можете обвести его или заполнить, чтобы отобразить его.
Вот функции, используемые для выполнения этих шагов:
-
beginPath () - Создает новый путь. После создания будущие команды рисования направляются в путь и используются для построения пути.
- Методы пути
- Методы для задания разных путей для объектов.
-
closePath () - Добавляет прямую линию к пути до начала текущего вложенного пути.
-
ход () - Рисует фигуру, обводя ее контур.
-
заполнить () - Рисует сплошную фигуру, заполняя область содержимого контура.
Первым шагом для создания пути является вызов beginPath () . Внутри контуры хранятся в виде списка подпутей (линий, дуг и т. Д.), Которые вместе образуют форму. Каждый раз, когда вызывается этот метод, список сбрасывается, и мы можем начать рисовать новые фигуры.
Примечание: Когда текущий путь пуст, например сразу после вызова beginPath () , или на вновь созданном холсте, первая команда построения пути всегда обрабатывается как moveTo () , независимо от того, что она на самом деле есть.По этой причине вам почти всегда нужно специально устанавливать начальную позицию после сброса пути.
Второй шаг - это вызов методов, которые фактически определяют пути, которые нужно нарисовать. Мы увидим это в ближайшее время.
Третий и необязательный шаг - вызвать closePath () . Этот метод пытается замкнуть фигуру, проведя прямую линию от текущей точки до начала. Если фигура уже закрыта или в списке только одна точка, эта функция ничего не делает.
Примечание: Когда вы вызываете fill () , все открытые фигуры закрываются автоматически, поэтому вам не нужно вызывать closePath () . Это , а не , когда вы вызываете stroke () .
Рисование треугольника
Например, код для рисования треугольника будет выглядеть примерно так:
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = холст.getContext ('2d');
ctx.beginPath ();
ctx.moveTo (75, 50);
ctx.lineTo (100, 75);
ctx.lineTo (100, 25);
ctx.fill ();
}
}
Результат выглядит так:
| Снимок экрана | Живой образец |
|---|---|
Перемещение пера
Одна очень полезная функция, которая фактически ничего не рисует, но становится частью описанного выше списка путей, - это moveTo () функция.Вероятно, вы можете представить себе это как то, что вы поднимаете ручку или карандаш с одного места на листе бумаги и кладете их на другое.
-
moveTo (x, y) - Перемещает перо к координатам, указанным в
xиy.
Когда холст инициализируется или вызывается beginPath () , вы, как правило, захотите использовать функцию moveTo () , чтобы разместить начальную точку в другом месте. Мы также могли бы использовать moveTo () для рисования несвязанных путей.Взгляните на смайлик ниже.
Чтобы попробовать это на себе, вы можете использовать приведенный ниже фрагмент кода. Просто вставьте его в функцию draw () , которую мы видели ранее.
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = canvas.getContext ('2d');
ctx.beginPath ();
ctx.arc (75, 75, 50, 0, Math.PI * 2, истина);
ctx.moveTo (110, 75);
ctx.arc (75, 75, 35, 0, Math.PI, ложь);
ctx.moveTo (65, 65);
ctx.arc (60, 65, 5, 0, Math.PI * 2, истина);
ctx.moveTo (95, 65);
ctx.arc (90, 65, 5, 0, Math.PI * 2, истина);
ctx.stroke ();
}
}
Результат выглядит так:
| Скриншот | Живой образец |
|---|---|
Если вы хотите увидеть соединительные линии, вы можете удалить линии, которые вызывают moveTo () .
Примечание: Чтобы узнать больше о функции arc () , см. Раздел «Дуги» ниже.
Линии
Для рисования прямых линий используйте метод lineTo () .
-
lineTo (x, y) - Рисует линию из текущей позиции рисования в позицию, заданную параметрами
xиy.
Этот метод принимает два аргумента, x и y , которые являются координатами конечной точки линии. Начальная точка зависит от ранее нарисованных путей, где конечная точка предыдущего пути является отправной точкой для следующих и т. Д.Начальную точку также можно изменить с помощью метода moveTo () .
Пример ниже рисует два треугольника: один с заливкой и один с контуром.
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = canvas.getContext ('2d');
ctx.beginPath ();
ctx.moveTo (25, 25);
ctx.lineTo (105, 25);
ctx.lineTo (25, 105);
ctx.fill ();
ctx.beginPath ();
ctx.moveTo (125, 125);
ctx.lineTo (125, 45);
ctx.lineTo (45, 125);
ctx.closePath ();
ctx.stroke ();
}
}
Это начинается с вызова beginPath () , чтобы начать новый контур формы. Затем мы используем метод moveTo () , чтобы переместить начальную точку в желаемое положение. Ниже нарисованы две линии, составляющие две стороны треугольника.
| Скриншот | Живой образец |
|---|---|
Вы заметите разницу между закрашенным и заштрихованным треугольником.Как упоминалось выше, это связано с тем, что фигуры автоматически закрываются при заливке контура, но не при обводке. Если бы мы пропустили closePath () для обведенного треугольника, были бы нарисованы только две линии, а не полный треугольник.
Дуги
Для рисования дуг или окружностей мы используем методы arc () или arcTo () .
-
arc (x, y, radius, startAngle, endAngle, против часовой стрелки) - Рисует дугу с центром в позиции (x, y) с радиусом r , начиная с startAngle и заканчивая endAngle в заданном направлении, обозначенном против часовой стрелки (по умолчанию по часовой стрелке).
-
arcTo (x1, y1, x2, y2, radius) - Рисует дугу с заданными контрольными точками и радиусом, соединенную с предыдущей точкой прямой линией.
Давайте более подробно рассмотрим метод arc , который принимает шесть параметров: x и y - это координаты центра окружности, на которой должна быть нарисована дуга. Радиус не требует пояснений. Параметры startAngle и endAngle определяют начальную и конечную точки дуги в радианах вдоль кривой окружности.Они отсчитываются от оси x. Параметр против часовой стрелки - это логическое значение, которое, когда истинно , рисует дугу против часовой стрелки; в противном случае дуга рисуется по часовой стрелке.
Примечание : Углы в функции arc измеряются в радианах, а не в градусах. Чтобы преобразовать градусы в радианы, вы можете использовать следующее выражение JavaScript: радиан = (Math.PI / 180) * градусов .
Следующий пример немного сложнее, чем те, которые мы видели выше.Он рисует 12 разных дуг с разными углами и заливками.
Две петли для предназначены для прохода по рядам и столбцам дуг. Для каждой дуги мы начинаем новый путь, вызывая beginPath () . В коде каждый из параметров дуги для ясности указан в переменной, но в реальной жизни это не обязательно.
Координаты x и y должны быть достаточно четкими. radius и startAngle фиксированы. endAngle начинается с 180 градусов (полукруга) в первом столбце и увеличивается с шагом в 90 градусов, завершаясь полным кругом в последнем столбце.
Оператор для параметра по часовой стрелке приводит к тому, что первая и третья строки рисуются как дуги по часовой стрелке, а вторая и четвертая строки - как дуги против часовой стрелки. Наконец, оператор if делает верхнюю половину заштрихованной дугой, а нижнюю половину - заполненной дугой.
Примечание: В этом примере требуется холст немного большего размера, чем другие на этой странице: 150 x 200 пикселей.
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = canvas.getContext ('2d');
for (var i = 0; i <4; i ++) {
for (var j = 0; j <3; j ++) {
ctx.beginPath ();
var x = 25 + j * 50;
var y = 25 + i * 50;
var radius = 20;
вар startAngle = 0;
var endAngle = Math.PI + (Math.PI * j) / 2;
var против часовой стрелки = i% 2! == 0;
ctx.arc (x, y, радиус, startAngle, endAngle, против часовой стрелки);
if (i> 1) {
ctx.наполнять();
} еще {
ctx.stroke ();
}
}
}
}
}
| Скриншот | Живой образец |
|---|---|
Кривые Безье и квадратичные кривые
Следующим типом доступных траекторий являются кривые Безье, доступные как в кубическом, так и в квадратичном вариантах. Обычно они используются для рисования сложных органических форм.
-
quadraticCurveTo (cp1x, cp1y, x, y) - Рисует квадратичную кривую Безье от текущего положения пера до конечной точки, указанной параметрами
xиy, используя контрольную точку, указанную параметрамиcp1xиcp1y. -
bezierCurveTo (cp1x, cp1y, cp2x, cp2y, x, y) - Рисует кубическую кривую Безье от текущего положения пера до конечной точки, указанной параметрами
xиy, используя контрольные точки, указанные параметрами (cp1x,cp1y) и (cp2x, cp2y).
Разница между ними заключается в том, что квадратичная кривая Безье имеет начальную и конечную точки (синие точки) и только одну контрольную точку (обозначена красной точкой), в то время как кубическая кривая Безье использует две контрольные точки.
Параметры x и y в обоих этих методах являются координатами конечной точки. cp1x и cp1y - координаты первой контрольной точки, а cp2x и cp2y - координаты второй контрольной точки.
Использование квадратичных и кубических кривых Безье может быть довольно сложной задачей, потому что в отличие от программного обеспечения для векторного рисования, такого как Adobe Illustrator, у нас нет прямой визуальной обратной связи относительно того, что мы делаем.Из-за этого довольно сложно рисовать сложные формы. В следующем примере мы будем рисовать несколько простых органических форм, но если у вас есть время и, самое главное, терпение, можно создать гораздо более сложные формы.
В этих примерах нет ничего сложного. В обоих случаях мы видим последовательность нарисованных кривых, которые в конечном итоге приводят к завершенной форме.
Квадратичные кривые Безье
В этом примере используется несколько квадратичных кривых Безье для визуализации выноски речи.
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = canvas.getContext ('2d');
ctx.beginPath ();
ctx.moveTo (75, 25);
ctx.quadraticCurveTo (25, 25, 25, 62,5);
ctx.quadraticCurveTo (25, 100, 50, 100);
ctx.quadraticCurveTo (50, 120, 30, 125);
ctx.quadraticCurveTo (60, 120, 65, 100);
ctx.quadraticCurveTo (125, 100, 125, 62,5);
ctx.quadraticCurveTo (125, 25, 75, 25);
ctx.stroke ();
}
}
| Скриншот | Живой образец |
|---|---|
Кубические кривые Безье
В этом примере сердце нарисовано с использованием кубических кривых Безье.
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = canvas.getContext ('2d');
ctx.beginPath ();
ctx.moveTo (75, 40);
ctx.bezierCurveTo (75, 37, 70, 25, 50, 25);
ctx.bezierCurveTo (20, 25, 20, 62,5, 20, 62,5);
ctx.bezierCurveTo (20, 80, 40, 102, 75, 120);
ctx.bezierCurveTo (110, 102, 130, 80, 130, 62,5);
ctx.bezierCurveTo (130, 62,5, 130, 25, 100, 25);
ctx.bezierCurveTo (85, 25, 75, 37, 75, 40);
ctx.наполнять();
}
}
| Снимок экрана | Живой образец |
|---|---|
Прямоугольники
В дополнение к трем методам, которые мы видели в Рисование прямоугольников, которые рисуют прямоугольные формы непосредственно на холсте7, есть также прямоугольники 9034 () , который добавляет прямоугольный путь к текущему открытому пути.
-
прямоугольник (x, y, ширина, высота) - Рисует прямоугольник, верхний левый угол которого задан как (
x,y) с указанной шириной
Перед выполнением этого метода автоматически вызывается метод moveTo () с параметрами (x, y). Другими словами, текущее положение пера автоматически сбрасывается до координат по умолчанию.
Создание комбинаций
До сих пор в каждом примере на этой странице использовался только один тип функции контура для каждой формы. Однако нет ограничений на количество или типы путей, которые вы можете использовать для создания формы. Итак, в этом последнем примере давайте объединим все функции пути, чтобы создать набор очень известных игровых персонажей.
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = canvas.getContext ('2d');
округленныйRect (ctx, 12, 12, 150, 150, 15);
округленныйRect (CTX, 19, 19, 150, 150, 9);
Round RoundRect (CTX, 53, 53, 49, 33, 10);
Round RoundRect (CTX, 53, 119, 49, 16, 6);
округленныйRect (ctx, 135, 53, 49, 33, 10);
округленныйRect (ctx, 135, 119, 25, 49, 10);
ctx.beginPath ();
ctx.arc (37, 37, 13, Math.PI / 7, -Math.PI / 7, ложь);
ctx.lineTo (31, 37);
ctx.fill ();
for (var i = 0; i <8; i ++) {
ctx.fillRect (51 + я * 16, 35, 4, 4);
}
for (i = 0; i <6; i ++) {
ctx.fillRect (115, 51 + я * 16, 4, 4);
}
for (i = 0; i <8; i ++) {
ctx.fillRect (51 + я * 16, 99, 4, 4);
}
ctx.beginPath ();
ctx.moveTo (83, 116);
ctx.lineTo (83, 102);
ctx.bezierCurveTo (83, 94, 89, 88, 97, 88);
ctx.bezierCurveTo (105, 88, 111, 94, 111, 102);
ctx.lineTo (111, 116);
ctx.lineTo (106.333, 111.333);
ctx.lineTo (101,666, 116);
ctx.lineTo (97, 111.333);
ctx.lineTo (92.333, 116);
ctx.lineTo (87,666, 111,333);
ctx.lineTo (83, 116);
ctx.fill ();
ctx.fillStyle = 'белый';
ctx.beginPath ();
ctx.moveTo (91, 96);
ctx.bezierCurveTo (88, 96, 87, 99, 87, 101);
ctx.bezierCurveTo (87, 103, 88, 106, 91, 106);
ctx.bezierCurveTo (94, 106, 95, 103, 95, 101);
ctx.bezierCurveTo (95, 99, 94, 96, 91, 96);
ctx.moveTo (103, 96);
ctx.bezierCurveTo (100, 96, 99, 99, 99, 101);
ctx.bezierCurveTo (99, 103, 100, 106, 103, 106);
ctx.bezierCurveTo (106, 106, 107, 103, 107, 101);
ctx.bezierCurveTo (107, 99, 106, 96, 103, 96);
ctx.fill ();
ctx.fillStyle = 'черный';
ctx.beginPath ();
ctx.arc (101, 102, 2, 0, Math.PI * 2, истина);
ctx.fill ();
ctx.beginPath ();
ctx.arc (89, 102, 2, 0, Math.PI * 2, истина);
ctx.fill ();
}
}
function roundedRect (ctx, x, y, width, height, radius) {
ctx.beginPath ();
ctx.moveTo (x, y + радиус);
ctx.lineTo (x, y + height - радиус);
ctx.arcTo (x, y + высота, x + радиус, y + высота, радиус);
ctx.lineTo (x + width - радиус, y + высота);
ctx.arcTo (x + ширина, y + высота, x + ширина, y + высота-радиус, радиус);
ctx.lineTo (x + ширина, y + радиус);
ctx.arcTo (x + width, y, x + width - радиус, y, радиус);
ctx.lineTo (x + радиус, y);
ctx.arcTo (x, y, x, y + радиус, радиус);
ctx.stroke ();
}
Полученное изображение выглядит так:
| Скриншот | Живой образец |
|---|---|
Мы не будем вдаваться в подробности, так как это на самом деле удивительно просто.Наиболее важные моменты, на которые следует обратить внимание, - это использование свойства fillStyle в контексте рисования и использование служебной функции (в данном случае roundedRect () ). Использование служебных функций для фрагментов рисования, которые вы часто выполняете, может быть очень полезным и уменьшить объем необходимого кода, а также его сложность.
Мы еще раз рассмотрим fillStyle более подробно позже в этом руководстве. Здесь все, что мы делаем, это используем его для изменения цвета заливки контуров с черного цвета по умолчанию на белый, а затем обратно.
Как мы видели в последнем примере, может быть серия путей и команд рисования для рисования объектов на вашем холсте. Чтобы упростить код и повысить производительность, объект Path3D , доступный в последних версиях браузеров, позволяет кэшировать или записывать эти команды рисования. Вы можете быстро воспроизвести свои пути.
Давайте посмотрим, как мы можем создать объект Path3D :
-
Path3D () - Конструктор
Path3D ()возвращает новый экземпляр объектаPath3D, необязательно с другим путем в качестве аргумента (создает копию) или, необязательно, со строкой, состоящей из данных пути SVG.
новый Path3D ();
новый Path3D (путь);
новый Path3D (d); Все методы пути, такие как moveTo , rect , arc или quadraticCurveTo и т. Д., О которых мы узнали выше, доступны для объектов Path3D .
API Path3D также добавляет способ объединения путей с помощью метода addPath . Это может быть полезно, например, когда вы хотите построить объекты из нескольких компонентов.
-
Path3D.addPath (путь [, преобразование]) - Добавляет путь к текущему пути с дополнительной матрицей преобразования.
Пример Path3D
В этом примере мы создаем прямоугольник и круг. Оба хранятся как объект Path3D , поэтому они доступны для дальнейшего использования. С новым Path3D API несколько методов были обновлены, чтобы опционально принимать объект Path3D для использования вместо текущего пути.Здесь, например, для рисования обоих объектов на холсте используются обводка , и , заливка с аргументом пути.
function draw () {
var canvas = document.getElementById ('холст');
if (canvas.getContext) {
var ctx = canvas.getContext ('2d');
var rectangle = new Path3D ();
прямоугольник. прямоугольник (10, 10, 50, 50);
var circle = new Path3D ();
circle.arc (100, 35, 25, 0, 2 * Math.PI);
ctx.stroke (прямоугольник);
ctx.fill (кружок);
}
}
| Снимок экрана | Живой образец |
|---|---|
Использование путей SVG
Еще одна мощная функция нового холста Path3D API холста использует данные пути SVG для инициализации пути.Это может позволить вам передавать данные пути и повторно использовать их как в SVG, так и в холсте.
Путь переместится в точку ( M10 10 ), а затем переместится по горизонтали на 80 точек вправо ( h 80 ), затем на 80 точек вниз ( v 80 ), затем на 80 точек влево ( h - 80 ), а затем обратно в начало ( z ). Вы можете увидеть этот пример на странице конструктора Path3D .
var p = new Path3D ('M10 10 h 80 v 80 h -80 Z'); % PDF-1.5 % 1 0 объект >>> эндобдж 2 0 obj > поток 2014-09-24T03: 37: 38 + 05: 302014-09-24T03: 37: 40 + 05: 302014-09-24T03: 37: 40 + 05: 30Adobe InDesign CS5 (7.0)
| <сценарий> | |
| функция init () { | |
| // Получить объект холста из DOM | |
| var canvas = document.getElementById ("myCanvas"); | |
| // Инициализация контекста WebGL | |
| var gl = canvas.getContext ("webgl"); | |
| если (! Gl) { | |
| console.log («Не удалось получить контекст отрисовки для WebGL»); | |
| возврат; | |
| } | |
| // Инициализация шейдеров | |
| var vs = document.getElementById ('shaderVs'). innerHTML; | |
| var fs = document.getElementById ('shaderFs'). InnerHTML; | |
| если (! InitShaders (gl, vs, fs)) { | |
| console.log («Не удалось инициализировать шейдеры.»); | |
| возврат; | |
| } | |
| // Записываем позиции вершин в вершинный шейдер | |
| var n = initVertexBuffers (gl); | |
| , если (n <0) { | |
| консоль.log ('Не удалось установить положение вершин'); | |
| возврат; | |
| } | |
| // Чистый холст | |
| gl.clearColor (0,0, 0,0, 0,0, 1,0); | |
| gl.clear (gl.COLOR_BUFFER_BIT); | |
| // Ничья | |
| гл.drawArrays (gl.TRIANGLES, 0, n); | |
| } | |
| функция initVertexBuffers (gl) { | |
| // вершины | |
| var dim = 3; | |
| var vertices = new Float32Array ([ | |
| 0, 0.5, 0, // Вершина # 1 | |
| -0,5, -0,5, 0, // Вершина # 2 | |
| 0,5, -0,5, 0 // вершина # 3 | |
| ]); | |
| // Создаем буферный объект | |
| var vertexBuffer = gl.createBuffer (); | |
| если (! VertexBuffer) { | |
| консоль.log ('Не удалось создать буферный объект'); | |
| возврат -1; | |
| } | |
| gl.bindBuffer (gl.ARRAY_BUFFER, vertexBuffer); | |
| gl.bufferData (gl.ARRAY_BUFFER, вершины, gl.STATIC_DRAW); | |
| // Присваиваем вершины в объекте буфера переменной a_Position | |
| var a_Position = gl.getAttribLocation (gl.program, 'a_Position'); | |
| , если (a_Position <0) { | |
| console.log ('Не удалось получить место хранения a_Position'); | |
| возврат -1; | |
| } | |
| gl.vertexAttribPointer (a_Position, dim, gl.FLOAT, false, 0, 0); | |
| гл.enableVertexAttribArray (a_Position); | |
| // Возвращаем количество вершин | |
| вернуть vertices.length / dim; | |
| } | |
| функция initShaders (gl, vs_source, fs_source) { | |
| // Компиляция шейдеров | |
| var vertexShader = makeShader (gl, vs_source, gl.VERTEX_SHADER); | |
| var fragmentShader = makeShader (gl, fs_source, gl.FRAGMENT_SHADER); | |
| // Создать программу | |
| var glProgram = gl.createProgram (); | |
| // Присоединяем и связываем шейдеры с программой | |
| гл.attachShader (glProgram, vertexShader); | |
| gl.attachShader (glProgram, fragmentShader); | |
| gl.linkProgram (glProgram); | |
| if (! Gl.getProgramParameter (glProgram, gl.LINK_STATUS)) { | |
| alert («Не удалось инициализировать программу шейдера»); | |
| вернуть ложь; | |
| } | |
| // Используйте программу | |
| гл.useProgram (glProgram); | |
| gl.program = glProgram; | |
| вернуть истину; | |
| } | |
| функция makeShader (gl, src, type) { | |
| var shader = gl.createShader (тип); | |
| gl.shaderSource (шейдер, src); | |
| gl.compileShader (шейдер); | |
| если (! Gl.getShaderParameter (шейдер, gl.COMPILE_STATUS)) { | |
| alert («Ошибка компиляции шейдера:» + gl.getShaderInfoLog (shader)); | |
| возврат; | |
| } | |
| вернуть шейдер; | |
| } | |

 Удостоверьтесь, что достаточно места для рисования всех трех сторон!
Удостоверьтесь, что достаточно места для рисования всех трех сторон! Предложенный метод по сути такой же, как с использованием циркуля.
Предложенный метод по сути такой же, как с использованием циркуля.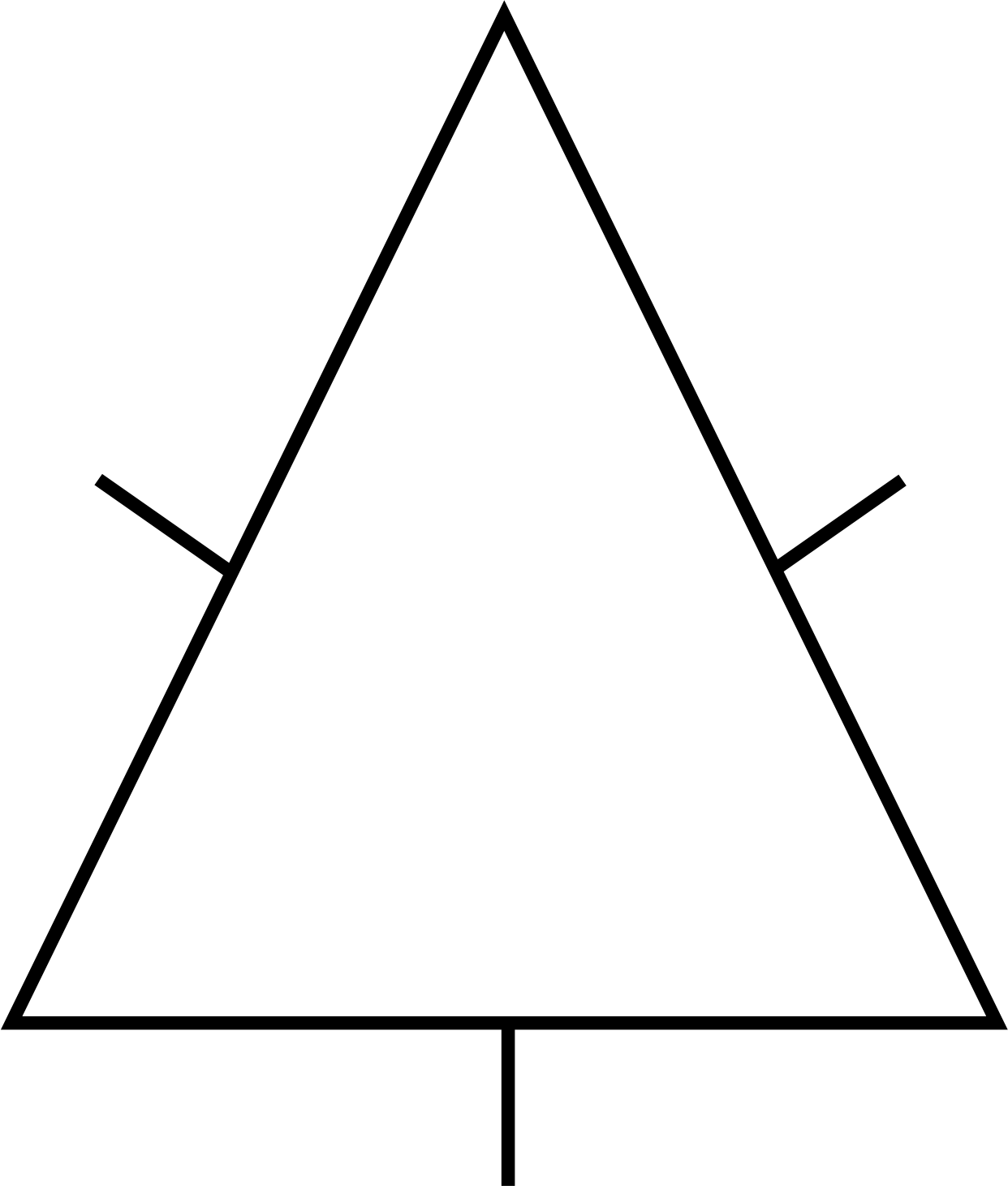
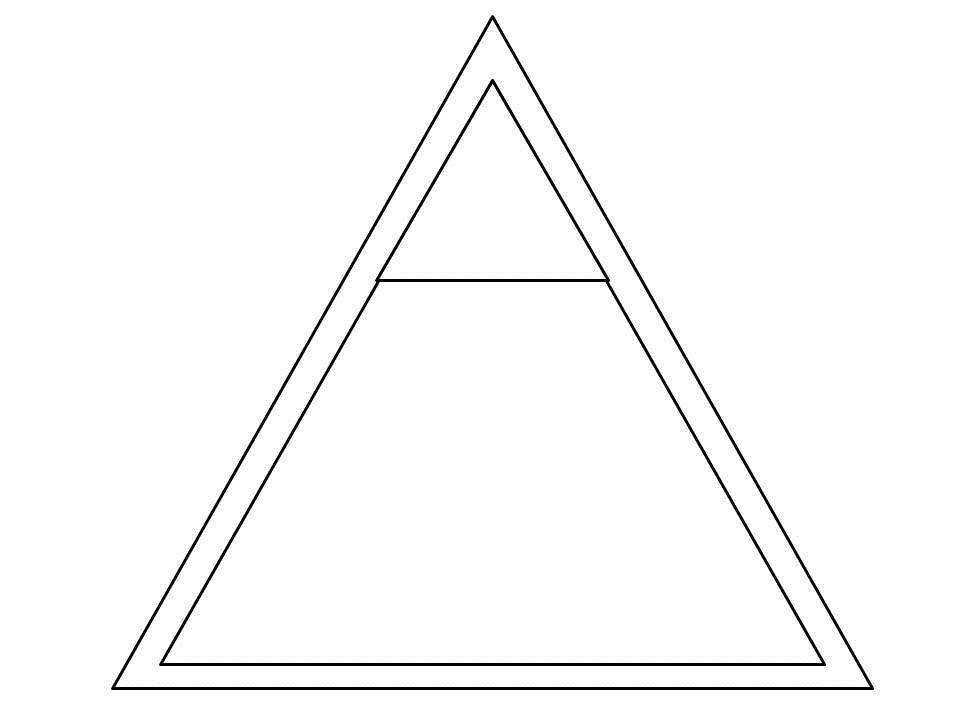 Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
Опишите дугу. Не изменяйте установленную «ширину» инструмента от точки циркуля до точки карандаша. Нарисуйте вторую дугу, чтобы она пересекала первую дугу, которую уже нарисовали. Отметьте точку, в которой пересекаются две дуги. Это вершина (верхняя точка) треугольника. Он должен лежать в точном центре сегмента линии, который нарисовали. Теперь можете сделать две прямые линии, ведущие к этой точке: по одному от каждого конца «нижнего» сегмента линии. Закончите треугольник. Далее с помощью линейки надо нарисовать еще два сегмента прямой линии – это стороны в треугольнике. Подключите каждый конец исходного сегмента линии к точке, в которой пересекаются дуги. Чтобы закончить работу, сотрите дуги, которые нарисовали, так, чтобы остался только треугольник.
 У нас получился искомый треугольник.
У нас получился искомый треугольник. create_polygon(points, fill='white')
create_polygon(points, fill='white')