by : alexxlab Графика

Определение фрактальная графика: works.doklad.ru — Учебные материалы

Фрактальная графика

Последней из рассматриваемых видов компьютерной графики — это фрактальная графика. Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся перспективных видов компьютерной графики. Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников.

Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандель-бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.

Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие. ) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной (1/9а) от стороны исходного треугольника.

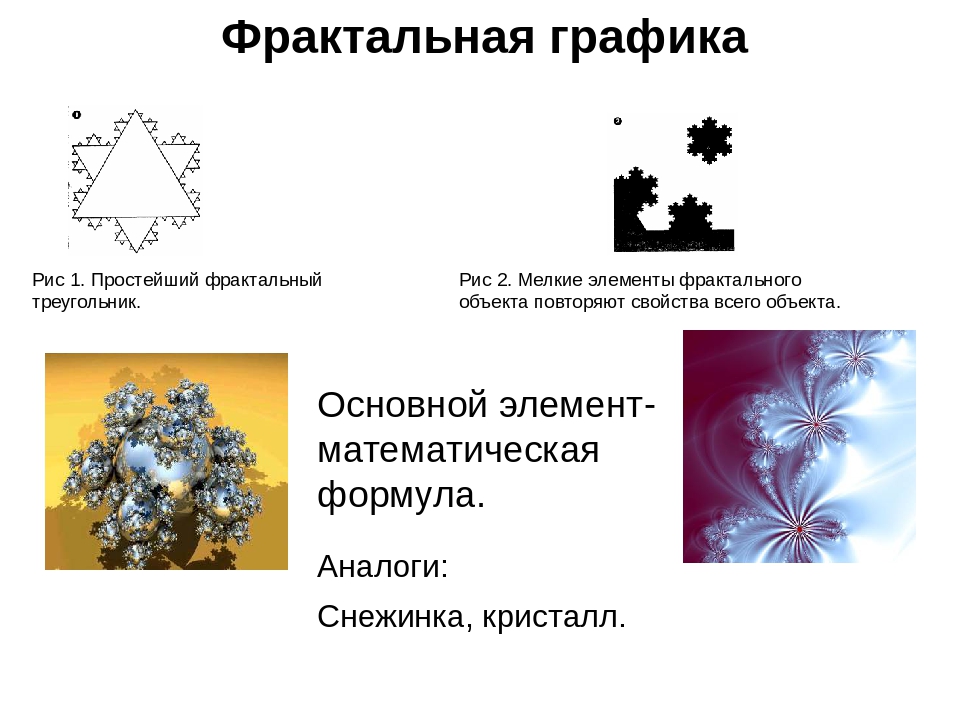
Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры». Процесс наследования можно продолжать до бесконечности. Таким образом, можно описать и такой графический элемент, как прямую. Изменяя и комбинирую окраску фрактальных фигур можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также, составлять из полученных фигур «фрактальную композицию».

Фрактальная графика, также как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений, ничего кроме формулы хранить не требуется. Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы.

Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник». Затем идет «Фрактальная фигура», «Фрактальный объект»; «Фрактальная прямая»; «Фрактальная композиция»; «Объект-родитель» и «Объект наследник». Следует обратить Ваше внимание на то, что фрактальная компьютерная графика, как вид компьютерной графики двадцать первого века получила широкое распространение не так давно.

Её возможности трудно переоценить. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать такие композиционные приёмы как, горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сегодня немногие компьютерщики в нашей стране и за рубежом знают фрактальную графику. С чем можно сравнить фрактальное изображение?

Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную структуру. Это свойство фрактального объекта может быть удачно использовано при составлении декоративной композиции или для создания орнамент. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу.

С точки зрения машинной графики фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически благодаря фрактальной графике найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Геометрические фракталы на экране компьютера — это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.

Создатель фракталов — это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности — Painter) от прочих графических программ. Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например Art Dabbler) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter программистами.

⇐Трехмерная графика | TeachPro WEB-дизайн | Цветовые модели и палитры⇒

Что такое фрактальная графика? | fraktal

  Что такое фрактальная графика?

 В математике существует понятие фрактала – геометрического образования, представляющего собой систему самоподобных фигур, расположенных относительно друг друга закономерным образом. Как форма и размер отдельных элементов, так и их взаимное расположение может быть описано математической формулой.

   Фрактальная графика, как и векторная, основана на математических вычислениях. Базовым элементом фрактальной графики является сама математическая формула, т.е. никаких объектов в памяти компьютера не хранится и изображение строится исключительно по уравнениям. Таким образом, строят как простейшие регулярные структуры, так и сложные иллюстрации, имитирующие природные ландшафты и трехмерные объекты.

   Фрактальная графика, как и векторная — вычисляемая, но отличается от неё тем, что никакие объекты в памяти компьютера не хранятся. Изображение строится по уравнению (или по системе уравнений), поэтому ничего, кроме формулы, хранить не надо. Изменив коэффициенты в уравнении, можно получить совершенно другую картину. Способность фрактальной графики моделировать образы живой природы вычислительным путем часто используют для автоматической генерации необычных иллюстраций.

Фрактал – это объект, обладающий бесконечной сложностью, позволяющий рассмотреть столько же своих деталей вблизи, как и издалека. Земля – классический пример фрактального объекта. Из космоса она выглядит как шаp. Если приближаться к ней, то будут видны океаны, континенты, побережья и цепи гор. Если рассматривать горы ближе – станут видны еще более мелкие детали: кусочек земли на поверхности горы в своем масштабе столь же сложный и неровный, как сама гора. И даже еще более сильное увеличение покажет крошечные частички грунта, каждая из которых сама является фрактальным объектом.

Многие объекты в природе обладают фрактальными свойствами, например побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.

   Последнее время фракталы стали популярны у трейдеров для анализа курса фондовых бирж, валютных и торговых рынков.

Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.

   Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность, либо метрическую размерность, строго большую топологической.

    Слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:

·   Обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину

·   Является самоподобной или приближённо самоподобной

·   Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую

·   Может быть построена при помощи рекурсивной процедуры.

Квазифракталы | Компьютерная графика

Термин «фрактал» (от лат. fractare – ломать, дробить; fractus – расчлененный, разбитый; англ. fractal – дробный) ввел Бенуа Мандельброт (Benoit Mandelbrot), родившийся в Варшаве в 1924 г., работавший во Франции и США.

Согласно определению Б. Мандельброта, фракталом называется множество, размерность Хаусдорфа–Безиковича которого строго больше его топологической размерности. Проще говоря, фрактал – множество, размерность которого отличается от обычной размерности, называемой топологической. Б. Мандельброт дает и другое определение: фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Строгого и исчерпывающего определения фракталов пока не существует.

Фрактальная структура образуется путем бесконечного повторения (итерации) какой-либо исходной формы во все уменьшающемся (или увеличивающемся) масштабе по определенному алгоритму, т. е. в соответствии с определенной математической процедурой. Этот несложный процесс с обратной связью дает поразительно многообразный морфогенез, нередко подобный созданию природных форм. Таким образом, фракталы характеризуются самоподобием, или масштабной инвариантностью, т. е. единообразием в широком диапазоне масштабов.

Структура идеального компьютерного фрактала сохраняется при любых масштабах ее рассмотрения. Чтобы получить такой фрактал, итерации должны продолжаться бесконечно долго, иначе полученное множество не будет фракталом, утрачивая на каком-то шаге свою фрактальную структуру. Природные, в частности биологические структуры – стохастические, хаотические фракталы, или квазифракталы; повторяемость их структуры в разном масштабе неполна и неточна – это «обрубленные» фракталы. Некоторые исследователи, например, С. Д. Хайтун (1996), приходят к заключению, что фракталы не являются реально существующими объектами, а реальные системы могут быть только фракталоподобными.

Большинство встречающихся в природе фракталоподобных структур (границы облаков, линия берега, деревья, листья растений, кораллы, снежинки, …) являются квазифракталами.

Все природные квазифрактальные структуры представляют собой след, результат, структурную запись порождающих их хаотических природных процессов. Фрактальная геометрия природы, неживой и живой, – это геометрия хаоса. Структурные квазифракталы можно считать пространственными аналогами хаотических нелинейных процессов; в результате таких процессов возникают природные квазифрактальные структуры. Хаотические процессы тоже характеризуются повторением своей структуры при изменении масштаба, т. е. статистическим самоподобием, квазифрактальностью во времени.

П. Бак и К. Чен (1991) рассматривают фракталы как мгновенные «срезы» самоорганизующихся критических процессов, пространственные «отпечатки» самоорганизованной критичности, в структуре которых отсутствует строгое самоподобие.

Фрактальная компьютерная графика. Фрактальные графические изображения

Почему фраталы так красивы?

Так сказочно, обворожительно, волнующе красивы. Математика вся пронизана красотой и гармонией, только эту красоту надо увидеть. Вот как пишет сам Мандельброт в своей книге «The Fractal Geometry of Nature»-«Почему геометрию часто называют холодной и сухой? Одна из причин лежит в ее неспособности описать форму облаков, гор или деревьев. Облака — это не сферы, горы — не углы, линия побережья — не окружность, кора не гладкая, а молния не прямая линия…»Фрактальная графика — это не просто множество самоповторяющихся изображений, это модель структуры и принципа любого сущего. Вся наша жизнь представлена фракталами. Взять, к примеру, ДНК, это всего лишь основа, одна итерация, а при повторении… появляется человек! И таких примеров много. Нельзя не отметить широкое применение фракталов в компьютерных играх, где рельефы местности зачастую являются фрактальными изображениями на основе трёхмерных моделей комплексных множеств и броуновского движения. Фрактальная графика необходима везде, и развитие «фрактальных технологий» — это одна из немаловажных задач на сегодняшний день. Фракталы вокруг нас повсюду, и в очертаниях гор, и в извилистой линии морского берега. Некоторые из фракталов непрерывно меняются, подобно движущимся облакам или мерцающему пламени, в то время как другие, подобно деревьям или нашим сосудистым системам, сохраняют структуру, приобретенную в процессе эволюции. Х.О.Пайген и П.Х Рихтер.

При фрактальном подходе хаос…перестает быть синонимом беспорядка и обретает тонкую структуру. Фрактальная наука еще очень молода, и ей предстоит большое будущее. Красота фракталов далеко не исчерпана и еще подарит нам немало шедевров — тех, которые услаждают глаз, и тех, которые доставляют истинное наслаждение разуму.

Понятие фрактал и фрактальная графика.

Геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature». В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему. Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные. Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале. Определение фрактала, данное Мандельбротом, звучит так: «Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому»




Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся и перспективных видов компьютерной графики.

Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников.

Понятия фрактал , фрактальная геометрия и фрактальная графика , появившиеся в конце 70-х , сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского «fractus» и в переводе означает «состоящий из фрагментов» . Оно было предложено математиком Бенуа Мандель-Бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.

Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Одним из основных свойств фракталов является самоподобие . Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга. Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию обо всем фрактале.

В центре фрактальной фигуры находится её простейший элемент — равносторонний треугольник , который получил название «фрактальный» . Затем, на среднем отрезке сторон строятся равносторонние треугольники со стороной, равной (1/3a) от стороны исходного фрактального треугольника. В свою очередь, на средних отрезках сторон полученных треугольников, являющихся объектами-наследниками первого поколения, выстраиваются треугольники-наследники второго поколения со стороной (1/9а) от стороны исходного треугольника.

Таким образом, мелкие элементы фрактального объекта повторяют свойства всего объекта. Полученный объект носит название «фрактальной фигуры» . Процесс наследования можно продолжать до бесконечности. Таким образом можно описать и такой графический элемент как прямая.

Изменяя и комбинирую окраску фрактальных фигур, можно моделировать образы живой и неживой природы (например, ветви дерева или снежинки), а также составлять из полученных фигур «фрактальную композицию» . Фрактальная графика, так же как векторная и трёхмерная, является вычисляемой. Её главное отличие в том, что изображение строится по уравнению или системе уравнений. Поэтому в памяти компьютера для выполнения всех вычислений ничего, кроме формулы, хранить не требуется.

Только изменив коэффициенты уравнения, можно получить совершенно другое изображение. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью нескольких математических коэффициентов можно задать линии и поверхности очень сложной формы.

Итак, базовым понятием для фрактальной компьютерной графики являются «Фрактальный треугольник» . Затем идет «Фрактальная фигура» , «Фрактальный объект» , «Фрактальная прямая» , «Фрактальная композиция» , «Объект-родитель» и «Объект наследник» .

Следует обратить внимание на то, что фрактальная компьютерная графика как вид компьютерной графики двадцать первого века получила широкое распространение не так давно.


Её возможности трудно переоценить. Фрактальная компьютерная графика позволяет создавать абстрактные композиции, где можно реализовать множество приёмов: горизонтали и вертикали, диагональные направления, симметрию и асимметрию и др. Сегодня немногие компьютерщики в нашей стране и за рубежом знают фрактальную графику. С чем можно сравнить фрактальное изображение? Ну, например, со сложной структурой кристалла, со снежинкой, элементы которой выстраивается в одну сложную композицию. Это свойство фрактального объекта может быть удачно использовано для создания орнамента или декоративной композиции. Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, позволяющего воспроизвести копию любой картинки сколь угодно близкой к исходному оригиналу.

С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически, благодаря фрактальной графике, найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные. Геометрические фракталы на экране компьютера — это узоры, построенные самим компьютером по заданной программе. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.

Создатель фракталов — это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности — Painter ) от прочих графических программ.

Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например, Art Dabbler ) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter программистами.

На сегодня фрактальная графика очень быстро развивается и весьма популярна и перспективна. Основой фрактальной графики является геометрия. Основным методом создания изображений является принцип наследственности от геометрического свойства наследников.

Фрактал — это структура, которая состоит из частей, подобных целому. Его основное свойство — самоподобие. Объекты, называют самоподобными, если части объекта после увеличения, остаются похожими друг на друга.

Центром фрактальной фигуры является её простейший элемент — треугольник с равными сторонами, который назвали «фрактальный». На середине сторон треугольника строят такие же равносторонние треугольники, которые равны одной третьей стороны исходной фигуры. Затем, на треугольниках первого поколения выстраивают треугольники второго поколения, но уже со стороной равно одной девятой от стороны центрального треугольника. Этот процесс можно продолжать нескончаемое число раз.

Изменение и комбинируя окраски фрактальных фигур, возможно, проектировать живые или неживые природные образы, такие как снег или же деревья, ветви, листья.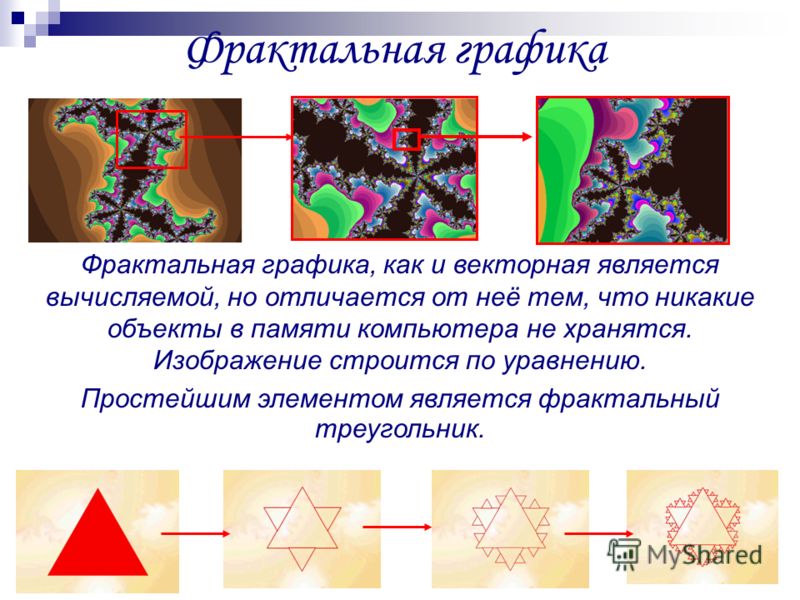 Составлять фрактальную композицию. Изображения фрактальной графики состоят из уравнений или по системе уравнений. Фрактальная графика — это вычисление. Для того, что выполнять изображения такой графики, компьютеру нужно хранить только формулу или алгоритм, по которой производятся вычисления. Заменив коэффициенты уравнения, можем создать абсолютно другое изображение, а при использовании сразу нескольких коэффициентов одновременно, можно создать линии или поверхность самого сложной формы.

Фрактальная графика 21 века стала популярной совсем недавно, в ней используются такие понятия, как: фрактальные треугольники, фигуры, объекты прямые и композиции. А так же «Объекты-родители» и «Объекты-наследники». Все эти понятия играют свою роль в создании изображения.

При помощи фрактальной компьютерной графики создаются абстрактные композиции, реализующие такие приемы композиции как линии горизонтальные и вертикальные, любые направления диагоналей, различные симметричные и асимметричные. Немногие российские и зарубежные программисты, и компьютерные дизайнеры знакомы с фрактальной графикой.

Объекты фрактальной графики по структуре можно сравнивать со сложными структурами кристалликов льда или снежинок. Используя эти уникальные свойства фрактальной графики можно создавать декоративные орнаменты. Разработанные великими умами алгоритмы и уравнения для синтеза коэффициентов фрактальных рисунков, позволяют создать картинки, близкие по сходству с оригиналом, то есть клонировать картинку, причем неограниченное количество раз.

В машинной графике использование фрактальной геометрии незаменимо при создании искусственных облаков, поверхности моря или гор. Только благодаря фрактальной графике был создан способ реализации сложных объектов, которые по образу очень похожи на природу. Геометрические фракталы на мониторе компьютера — это построенные по заданной программе узоры.

Создателями фракталов является человек разносторонний, владеющий несколькими профессиями сразу. Он должен быть одновременно и художником, и скульптором, и фотографом. Создавая рисунок свои руками, вы пользуясь математической формулой сам задаете ту форму изображения, которая вам нужна. Подстраиваете параметры, выбираете, каким рисунок будет по виду, какого цвета. Отличие фрактальной графики от других редакторов графики, например Photoshop, заключается в том, что вы создаете свой уникальный рисунок с «ноля».

В Photoshop невозможно создать рисунок, его можно лишь отредактировать или отформатировать, придать ему необходимый цвет, размер, улучшить качество и сгладить недостатки. Отличительной чертой редактора Painter считается то, что художник, в реале работающий без помощи компьютера, не сможет, используя кисть, перо или карандаш, тех же возможностей, что даны в Painter.

Аннотация: Сравнение феномена фрактальной компьютерной графики с различными абстрактными живописными техниками и поиск их взаимосвязи в современном искусстве.

Ключевые слова: фрактальная графика, орнамент, арабеска, абстракция, живопись, компьютер, монотипия

Fractal graphic as digital objectless art.

Abstract: This article analyses the phenomena of digital computer graphics, based on mathematics calculations, and possibilities of using it in different modern art techniques.

Digital fractal patterns are irregular, self-similar structures, which are based on natural objects`s group of similar characteristics, such as: corals, starfishes, sea urchins, snowflakes, crowns of the trees. The principle of such image forming is natural, and it becomes much more interesting to watch it`s digital mathematic simulation.

In contrast to digital graphic and painting, fractal graphic does not base on classic art traditions. The most resembling to the fractal graphics are objectless ornamental traditions, which takes the principles of infinite spatial creation of similar groups. The article includes the comparison of general ornamental rules and features of fractal images.

Owing to the fact that modern computer software allows to create the digital fractal graphic without special mathematics skills, an artist can combine traditional and digital painting and abstract fractal graphic to reach that level of balance and fortuity of an image, that abstract artist tried to get, using traditional techniques.

The fractal graphic is examined as an digital analog of traditional painting technique of monotyping in complex art work. Author underlines the likeness of many digital and material ways of creating the images. The final visual language of the piece of art still remains to be more important, than technological details of it`s production.

Keywords: fractal graphic, ornament, arabesque, abstraction, painting, computer, monotyping

Пытаясь определить художественную ценность произведений, полностью созданных с помощью компьютера и существующих в виде подлинника только в нематериальной среде, или произведений, основа создания которых - цифровая графика, нужно уделить внимание возможностям программируемых алгоритмов. С их помощью можно получить сложные орнаментальные изображения, обладающие необычными художественными свойствами.

Речь идет о фрактальной графике, которая позволяет создавать изображения, строящиеся по уравнению или системе уравнений. Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от так называемых «родителей» геометрических свойств объектов-наследников.

Понятия «фрактал», «фрактальная геометрия» и «фрактальная графика», появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово «фрактал» образовано от латинского fractus и в переводе означает «состоящий из фрагментов». Оно было предложено математиком Бенуа Мандель-Бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался.

Рисунок морской звезды и фотография снежинки под микроскопом - объекты, обладающие фрактальными свойствами, и фрактальный рисунок, сгенерированный на компьютере.

С помощью специализированных программ вы можете даже без особых математических познаний вносить изменения в формулу построения фрактального изображения, меняя цвет, частоту, размер, форму фрактальных фигур, их композицию и направленность.

Вы управляете построением формулы с помощью привычного графического интерфейса; компьютер тут же просчитывает результаты ваших действий; вы вносите изменения в формулу и тут же видите обновленное изображение фрактала. Графику, полученную таким путем, можно сравнить с традиционными орнаментами или строением многих естественных объектов, обладающих фрактальными свойствами: кораллы, морские звезды и ежи, снежинки, кроны растений.

Сам принцип такого построения изображения естественен, и тем интереснее наблюдать его виртуальную математическую симуляцию.

Рассматривая художественную ценность фрактальной графики, нужно прежде всего заметить, что она не основывается на классических художественных традициях. Конечно, похожий способ построения орнамента использовался в разных национальных искусствах, преимущественно восточных, где беcпредметные мотивы были более развиты. Общий ритм изображения создавался за счет повторяющихся мотивов, родственных друг другу, общее построение рисунка циклично, используются типовые элементы.

Такой подход создает уравновешенную композицию с возможностью продолжать ее бесконечно.

Симметрия, метр, ритм, модуль - эти, имеющие выраженную математическую природу категории наиболее выражены в орнаменте, самой математически строгой области изобразительного искусства.

Приведу для примера некоторые законы орнаментальной композиции:

закон пропорциональности в орнаментальной композиции заключается в установлении соразмерности частей в отношении целого и друг к другу. Пропорциональные отношения площадей рисунка и фона, размеров орнаментальных мотивов и их составных частей, линейных характеристик орнаментальных форм и т.п. определяют выразительность композиции.
закон соподчинения - звучание выразительных средств орнаментальной композиции обеспечивается выделением из их числа главных и подчинения им второстепенных. Закон соподчинения в штучных композициях трансформируется в закон доминанты (господствующей идеи): когда в композиции отчетливо выделяется один или несколько орнаментальных мотивов по размерам, форме, фактуре и цвету.
закон орнаментального контрапункта - построение орнаментальных мотивов возможно из ряда замкнутых элементов путем соединения их в целостный орнаментальный образ.

Фрактальный узор, как правило, отвечает большинству этих пунктов. Особенно близок к строению фрактала вид орнамента «арабеска», построенный по геометрической сетке - принципу бесконечного пространственного развития повторяющихся групп орнаментальных мотивов.

Фрактальную графику, в отличие от растровой и векторной, можно назвать менее вещественной, более самобытной, и существующей изначально, как вид искусства, исключительно в цифровой среде. Конечно, теоретически можно воссоздать поведение математической формулы фрактала и на бумаге, но такое занятие настолько технически трудоемко, что становится бессмысленным.

Фрактальный узор, создаваемый без подготовки математической основы обладает важным свойством - он непредсказуем для создателя. Изначально вы не можете контролировать полностью все аспекты графического изображения, если вы, конечно, не профессиональный математик или перед вами не стоит задача создать конкретный узор по заранее разработанной формуле.

Пример фрактальной графики - демонстрация самоповторяющейся структуры фрактала. Обратите внимание на сбланасированные сочетания цветов.

Художнику интересен именно визуальный результат, получающийся с большой долей случайности, но обладающий выдающимися декоративными особенностями. Не используя ни традиционные, ни цифровые аналоги художественных инструментов, не опираясь изначально на принципы построения композиции, не выбирая гамму цветов, а лишь внося изменения в формулу, которая и является здесь основным конфигуратором, можно получить такое изображение, которое невозможно создать вручную или придумать нарочно. Фрактальный рисунок подчинен общей гармонии, так как повторяет и множит сам себя в различных прогрессиях, единство стиля здесь легко достижимо.

Сам факт того, что именно математический процесс в случайном порядке, практически без вмешательства человека способен генерировать изображения, обладающие художественными свойствами, был бы невозможен без участия компьютера. Компьютер способен помочь автоматизировать творческий процесс, если речь идет о сложной, многоэтапной работе.

Возможности фрактальной графики расцениваются художником как возможности отдельного инструмента, отдельного этапа в общем процессе работы.

Приведу пример: вы решили написать живописную работу размером 2 на 2 метра, выбрали примерную тематику. Пусть это будет многофигурная композиция на фоне пейзажа. Здесь существуют два пути продолжения работы - предметный или абстрактный. Вы можете отталкиваться от рисунка конкретной композиции, фигур, двигать их и перемещать в поисках всеобщей гармонии. Неважно, как вы это делаете: углем на холсте или посредством цифрового графического редактора.

Первый этап вашей работы - это поиски визуальной гармонии в пределах выбранного формата. И более неоднозначный, сложный, но и более продуктивный способ - начать искать предметную композицию, отталкиваясь от беспредметного, абстрактного рисунка. В классической живописи используется имприматура, живописная свободная подложка, первый слой, на котором можно без ограничений намечать цветовые пятна, гармонично распределить по холсту тональные зоны, скомпоновать рисунок, то есть провести подготовительный этап, практически беспредметный, который сам подскажет, в каком направлении лучше двигаться дальше.

Одно из важных умений художника состоит в способности временно отключиться от привязки к конкретным образам и работать с более общими формами, элементами случайности, чувствовать материал, который сам часто подсказывает верные решения. Очень сложно намеренно создать гармоничное произведение, руководствуясь определенным набором правил, и работать всегда в рамках предметности.

Технологический процесс создания простой одноцветной монотипии.

Хорошим примером является техника монотипии в классической живописи. Произведение не обязательно должно быть сюжетным и предметным, чтобы передать настроение и атмосферу. Техника монотипии с некоторой долей случайности позволяет создавать абстрактные живописные произведения.

Художник наносит слой масляных красок на стекло, а потом отпечатывает в зеркальном отражении краски на бумагу. Бумага может иметь собственный цвет, что добавляет вариативности в конечный результат. Под давлением мазки принимают новые формы, смешиваются, проступает цвет бумаги, и художник получает зеркальное изображение рисунка на стекле, измененное и обобщенное благодаря случайным деформациям. Такая монотипия может быть завершена как абстрактное произведение с помощью лессировок, обобщения цвета, добавления новых цветов, или может стать подготовительным подмалевком для дальнейшей работы с вполне предметным сюжетом.

Юрий Вайс . «Абстракция». Бумага, акварель, карандаш, Photoshop. Абстрактная живописная композиция, созданная на основе монотипии.

И в этом случае абстрактные свойства фракталов позволяют получить неожиданный декоративный результат, сыграть роль подмалевка.

Допустим, вам нужно нарисовать фантастический пейзаж, сделать его убедительным, но в то же время необычным, подобрать сложную гамму цветов. Вы можете начать со случайного результата - создать многоцветный плотный фрактальный рисунок, узор, который уже создает некий графический ритм, и использовать его в качестве основы для дальнейшего рисунка в графическом редакторе; вы можете его исказить, поменять цвет, сделать более сдержанным, начать намечать поверх широкими мазками общие черты вашего пейзажа, но случайный узор в качестве подложки будет вас вести, направлять и подсказывать неожиданные решения. После вы можете распечатать получившийся цифровой рисунок, натянуть этот принт и пройтись по нему гуашью или закончить его карандашами, если того требует общая идея произведения.

Именно случайность, вариативность фрактальной графики становится ценным качеством для использования ее в художественных работах, особенно если речь идет о живописи. И тем удивительнее тот факт, что в этом участвует автоматизированный компьютерный процесс, способный с легкостью создать изображение такой степени сбалансированности и случайности, какую с трудом пытались найти и воспроизвести многие художники - абстракционисты.

Слева  - абстрактная живопись, Герхард Рихтер A.B. Courbet , холст, масло 1986 г. Cправа  - пример фрактальной цифровой графики.

Прием использования повторяющихся мотивов похож на прием калейдоскопа в абстрактной графике. Художник определяет для себя участок работы, который будет в дальнейшем скопирован и отзеркален, выбирает направление отражений и таким образом создает из повторяющихся копий новую, самобытную композицию. При этом, исходный участок сам по себе может быть не гармоничен с точки зрения композиции, не симметричен и хаотичен, но итоговый результат, составленный из множества таких фрагментов, создает весьма неожиданный, непредсказуемый рисунок. Фактор случайности в такой технике тоже присутствует и остается очень важным.

Изображение в калейдоскопе, состоящее из множества отдельных, хаотичных элементов, выстраивается в гармоничный рисунок - благодаря симметричному по вертикали и горизонтали рисунку, отраженным частицам общего «родителя». Хаотичность собирается в гармоничную композицию, основываясь на приеме отражения и повторения. Получается, что фрактальный узор является заведомо уравновешенным.

Юрий Вайс «Калейдоскопы», бумага, акварель, карандаш, Photoshop

Это еще раз подчеркивает сходство техник и художественных подходов в цифровой и материальной средах. При желании художник может найти удобный способ воспроизведения своей техники на компьютере, подобрать нужный набор программ, аналогичных традиционным приемам, и создавать произведения, не ограничивая себя какими–либо техническими рамками.

Компьютерные фракталы и калейдоскопы эффективны при создании абстрактных работ. Растровые редакторы позволяют замешивать цвета, имитировать поверхности, рисовать в различных техниках, а векторная графика способна строить идеальные кривые и геометрические композиции. Умение совмещать все эти возможности дает художнику огромную свободу самовыражения.

Не важно, предметный или абстрактный сюжет разрабатывает художник, делает он свою работу на бумаге, компьютере или совмещает их, - важен лишь визуальный язык итогового произведения: насколько он ясен и как четко передает заложенный художником смысл.

Фрактальная графика представляет собой яркий синтез математических, цифровых, машинных вычислений и орнаментальной, декоративной графики, ее автоматизированность и непредсказуемость открывает новые возможности для творчества. Ее можно назвать главным инструментом для создания беспредметного и абстрактного искусства в цифровой среде.

Список литературы:

  1. Б. Р.Виппер. Введение в историческое изучение искусства. - М., 1970. С. 145–160
  2. Федер Е. Фракталы // Пер. с англ.-Москва, Мир, 1991.
  3. Фракталы в простых числах
  4. Мандельброт Б. Фрактальная геометрия природы.// Бенуа Мандельброт - изд-во Институт компьютерных исследований. Москва - Ижевск, 2002. С. 17–18, С. 59
  5. Мандельброт Б. Фракталы и хаос. Множество Мандельброта и другие чудеса // Бенуа Мандельброт. - Ижевск,: НИЦ «Регулярная и хаотическая динамика», 2009.
  6. Морозов А.Д. Введение в теорию фракталов. - Москва-Ижевск: Институт компьютерных исследований, 2002. С. 18
  7. Что такое фракталы

Фрактальная графика, как и векторная, основана на математических вычислениях. Базовыми элементами фрактальной графики являются сами математические формулы, описывающие линии и линейные поверхности, то есть никаких объектов в памяти ЭВМ не хранится и изображение строится исключительно по формулам (уравнениям).

Установлено, что при любом уровне разрешения, сложная кривая (например, береговая линия), поверхность могут быть аппроксимированы (смоделированы) и прорисованы посредством объединения участков небольших прямолинейных (плоских) сегментов. При переходе на более высокий уровень разрешения аппроксимирующий сегмент вероятностным способом разбивается на новую последовательность новых линейных сегментов и так далее. На основании этого свойства – закона статистического постоянства порождения деталей природных образований при переходе от низких к более высоким уровням разрешения и построен метод использования фрактальных поверхностей

В

Рис. 1.4Пример фрактального объекта

переводе с английского “фрактальный” означает состоящий из частиц, частей. Такими поверхностями называют класс нерегулярных геометрических форм, задаваемых вероятностным способом на основе исходного описания низкого уровня. Закон дробления линии (поверхности) подбирается опытным путем по критерию визуального согласования синтезируемого (моделируемого) изображения с реальным объектом, изображение которого стремятся получить.

Таким способом строят как простейшие регулярные структуры, так и сложные иллюстрации, имитирующие ландшафты и трехмерные объекты. Наиболее часто фрактальные поверхности используют для моделирования горных ландшафтов. Горный массив (рис. 1.4) предварительно, очень приближенно, описывают полигональной поверхностью, составленной из плоских четырехугольников. Далее каждый четырехугольник разбивается с помощью случайной функции на четыре фигуры меньших размеров, при этом все фигуры вероятностным образом сдвигаются относительно исходной плоскости, сохраняя для каждой фигуры по одной общей вершине с исходным четырехугольником. Деление продолжается до достижения желаемого уровня изрезанности поверхности. Удаляются скрытые поверхности и закрашиваются сгенерированные четырехугольники. Изображения, созданные на основе фрактальных поверхностей, только статистически идентичны реальным объектам.

Фрактальный подход нашел широкое применение во многих областях компьютерной графики, науки и искусства.

Фрактальная графика не является, строго говоря, частью векторной графики, поскольку широко использует и растровые объекты. Фракталы широко используются в растровых (AdobePhotoshop) и векторных (CorelDraw) редакторах и трехмерной (CorelBryce) графике.

Форматы файлов компьютерной графики.

Работа со средствами компьютерной графики предполагает использование при создании графической информации (рисунков, чертежей, иллюстраций) разнообразных графических пакетов растровой и векторной графики (PhotoShop,CorelDraw,bCad,AutoCad, Компас и др.). Все эти пакеты работают в соответствующих форматах, позволяющих не только сохранить созданную информацию, экспортировать ее в другие пакеты, но и импортировать графическую информацию других пакетов. В компьютерной графике применяется большое количество форматов, но лишь небольшая их часть стала стандартом де-факто и применяется в подавляющем множестве программ. Разнообразие в подходах (алгоритмах) и средствах в решении традиционных задач компьютерной графики приводит к несовместимости выходных данных. Как правило, несовместимые форматы выходных файлов имеют векторные, растровые, трехмерные изображения, хотя существуют форматы файлов, позволяющие хранить данные разных классов. Многие приложения ориентированы на задачи с собственными специфическими форматами, но стремление интегрироваться в общую информационную структуру, вынуждает их использовать специальные приемы, фильтры или экспортировать изображение в стандартный обменный формат.

TIFF (Tagget Image File Format ) предназначен для хранения растровых изображений высокого качества (расширение файла . TIF ) в графических пакетах, работающих MS — DOS , PC IBM , Unix , Macintosh платформах. Широта использования этого формата объясняется его возможностями: поддержка множества цветовых моделей, наличие восьмибитного альфа-канала 3 , сохранение обтравочных контуров, различные алгоритмы сжатия без потери информации. Формат обеспечен поддержкой со стороны большинства графических, верстальных и дизайнерских, растровых и векторных программ. Цветовые модели GIF CMYK и Pantone , поддерживаемые TIFF , обеспечивают верную цветопередачу при выводе изображений на полиграфическую печать; допускает запись в файл цветовой профиль ICC . Последние версии TIFF поддерживают несколько алгоритмов сжатия изображения: LZW – без потери информации; ZIP –без потери информации, JPED — с частичной потерей информацией. Универсальным принято считать метод сжатия LZW , обеспечивающий меньший размер выходного файла. Формат широко используется для хранения и обмена графической информацией между различными графическими платформами.

GIF (CompuServe Graphics Interchange Format ) -Графический растровый обменный формат. Разработан фирмой CompuServe . Поддерживается MS — DOS , PC IBM , Unix , Macintosh и Amiga операционными системами. Формат разработан для поддержки графики в Интернете, независимой от аппаратного обеспечения. Поддерживает функции прозрачности цветов и некоторые виды анимации. Поддерживает кодировку 256 цветов. Один из цветов может получить свойство прозрачности через двухбитовый альфа-канал. Допускает включение в файл нескольких растровых изображений, воспроизводимых с заданной периодичностью, что обеспечивает показ на экране простейшей анимации.

Получил большую популярность в Интернете, благодаря большой степени сжатия (метод LZW ). Ограниченные возможности по работе с цветными изображениями обусловливают его применение исключительно для электронных публикаций.

BMP (Windows Device Independent Bitmap ) — растровый формат обмена изображениями между приложениями, работающихми в операционной системе Windows (расширение файла. BMP ) . Формат поддерживает большое количество цветных моделей вплоть до 24 – битного пространства RGB . Полиграфический формат CMYK не поддерживается, что ограничивает сферу применения BMP для электронных публикаций. Размер графического изображения неограничен. В качестве алгоритма сжатия используется метод RLE (компрессия без потери информации). Файлы в формате BMP имеют значительный объем.

PSD (PhotoShop Document) — обственный растровый формат пакета Adobe PhotoShop , один из наиболее мощных по возможностям хранения графической информации. Поддерживает платформы операционных систем Macintosh и Window s. Запоминает параметры слоев, каналов, степени прозрачности, множество и разнообразие масок. Максимальный размер записываемого изображения 30000 х 30000 пикселей. Поддерживает 48-битное кодирование цвета, цветоделение, различные цветовые модели. Применяемый метод сжатия (RLE ) не обеспечивает достаточное сжатие, объем сохраняемой информации достаточно высок.

PhotoCD — растровый формат, разработанный фирмой Kodak , для хранения цифровых изображений высокого качества. Поддерживается платформами всех операционных систем. Формат хранения данных в файле именуется Image Pac , внутренняя структура которого обеспечивает хранение изображения с фиксированными величинами разрешений, и поэтому размеры любых файлов лишь незначительно отличаются друг от друга и находятся в диапазоне 4-5 Мбайт. Каждому разрешению присвоен собственный уровень, отсчитываемый от так называемого базового ( Base ), составляющего 512 х 768 точек.

В файле предусмотрено пять уровней – от Base/16 (128 х 192 точек) до Baseх 16( 2048 х 3072 точек). Работает с 24-битовой кодировкой цветов. Для работы с цветовой информацией используется цветовая модельYCC . Формат обеспечивает хранение высоко качественных полутоновых изображений и записи высококачественных фото — изображений наCD — ROM .

JPEG (Joint Photographic Expects Group ) — формат растровых изображений (расширение файла.JPG ), разработанный фирмой C-Cube Microsystems, ориентирован на все графические платформы. Работает с 24 – битной кодировкой цвета. Независимо от исходной цветовой модели изображения все пиксели переводятся в цветовое пространство CIE Lab . Допустимый максимальный размер изображения 64000 х 64000 точек.

По существу является методом сжатия изображения с частичной потерей информации. Применение компрессии JPEG позволяет уменьшить объем занимаемый файлом до 500 раз по сравнению обычнымbitmap . Позволяет регулировать соотношение между степенью сжатия файла и качеством изображения. Применяемые методы сжатия основаны на удалении «избыточной» информации. Используется в основном для электронных публикаций.

CDR (CorelDraw ) — векторный формат. Рабочий формат графического пакета CorelDraw фирмы Corel Corporation.

EPS (Encapsulated PostScript ) — Фирма Adobe разработала формат описания как векторных, так и растровых изображений на упрощенной версии языка PostScript , который де-факто является стандартом в области допечатных процессов и полиграфии (файл с расширением.EPS ). Это самый надежный и универсальный способ хранения и передачи графических данных. Файл не поддерживает многостраничные документы, но в нем могут одновременно храниться растровые и векторные графические изображения, все необходимые данные о свойствах самого изображения: любая цветовая модель и профили (параметры калибровки оборудования), канал прозрачности, обтравочный контур, треппинг (перекрытие цветов на границе), внедренные шрифты.

В зависимости от потребности при отображении на экране векторного изображения используется формат WMF , а для растрового –TIFF . Открыть файл. EPS для просмотра и редактирования можно при помощи ограниченного перечня программ (например,Adobe Illustrator , CorelDraw ). Кроме того, существенным недостаткомEPS является то, что экранная копия лишь в общих чертах отображает реальное изображение. Действительное изображение можно увидеть на выходе выводного устройства с помощью специальных программ просмотра или после преобразования файла в форматPDF в приложенияхAcrobat Reader , Acrobat Exchange .

WMF (Windows MetaFile ) — файл обменного формата векторных данных относится к категории метафайлов 4 . Является «внутренним» форматом операционной системы Windows на платформеIBM PC для всех ее графических приложений (расширение имени файла.WMF ) через буфер обмена. Однако «универсальность» формата годится далеко не для всех программ. Типичными ошибками при переносе изображения являются искажение цветов, неправильная установка толщины контура и свойств заливки. В формат нельзя включить растровое изображение. Рекомендуется для переноса самых простых объектов.

CGM (Computer Graphics Metafile )- Графический метафайл. Формат файла разработан Международной организацией по стандартизации и Американским национальным институтом стандартов. Поддерживается всеми графическими платформами. Работает с неограниченным числом цветов и не имеет ограничение на размер графического изображения. Используются RLE и CCITT Group 3 и Group 4 методы сжатия информации. Широко используется для обмена векторной и растровой графической информацией между графическими приложениями, работающими на различных платформах.

DXF (Data eXchange Format ) – Специальный символьный формат обмена информацией, разработанный компанией Autodesk Inc. (США) для своих программных продуктов, в первую очередь AutoCAD. Может работать в операционной системе MS — DOS . Поддерживает 8-битную кодировку цвета, сохраняет трехмерные изображения. Формат не предусматривает сжатие информации.

Этот формат обмена стал фактическим стандартом для чеpтежно-гpaфических систем и поддерживается практически всеми разработчиками программных продуктов САПР.

Презентация к исследовательской работе фрактальная графика.

Всероссийский конкурс исследовательских работ учащихся “ЮНОСТЬ, НАУКА, КУЛЬТУРА”

Направление: информатика

Тема: «Фрактальная графика»

Вдовина Станислава МБОУ «Гимназия №7», Ростовской области 7 класс

Научный руководитель : Грищенко Е.Е., учитель информатики

г. Обнинск, 2017/2018 учебный год


Актуальность:

  • Актуальность заявленной темы определяется, в первую очередь, предметом исследования, в качестве которого выступает фрактальная графика.

Проблема:

  • Какова роль фрактальных моделей в современном мире?
  • Почему наука о фракталах достаточно молода?
  • Возможно ли создать свои собственные фракталы?

Объектом исследования:

  • Выступают информационные технологии,.

Цель:

  • Исследовать фракталы в природе, математике, информатике, исследовать методики построения фрактальной живописи с помощью компьютерных программ, создать фрактальные изображения и анимацию.

Задачи:

  • узнать, что такое фракталы;
  • изучить историю возникновения и развития фрактальной геометрии;
  • изучить области применения фракталов;
  • изучить программное обеспечение для создания фрактальной графики.

Фрактальная графика. Понятие фрактала

Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов .

Основное определение фрактала, данное Мандельбротом, звучало так: » Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому «.

Бенуа Мандельброт


В основном фракталы классифицируют по трём видам:

Алгебраические фракталы – строятся на основе алгебраических формул.

Множество Мандельброта

Множество Жулиа

Бассейны Ньютона


Фрактальная графика. Виды фракталов

Геометрические (конструктивные) фракталы – фракталы созданные путем простых геометрических построений.

Геометрические фракталы являются самыми наглядными, так как видна самоподобность.

Для построения характерно построение «основы» и «фрагмента», повторяющегося при каждом уменьшении масштаба.

Треугольник Серпинского

Дерево Пифагора

Кривая Леви


Фрактальная графика. Виды фракталов

Стохастические фракталы – получаются в том случае, если в процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные — несимметричные деревья, изрезанные береговые линии и т. д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

Стохастический фрактал на основе множества Жюлиа


Фрактальное сжатие изображений

Фрактальное сжатие изображений — обнаружение похожих участков в изображении. Данный алгоритм известен тем, что в некоторых случаях позволяет получить очень высокие коэффициенты сжатия (лучшие примеры — до 2000 раз (при приемлемом визуальном качестве) для реальных фотографий природных объектов, что недоступно для других алгоритмов сжатия изображений в принципе.

Треугольник Серпинского

Папоротник Барнсли


Фрактальная графика. Области применения

Применение фракталов в медицине.

Сам по себе человеческий организм состоит из множества фракталоподобных структур: кровеносная система, мышцы, бронхи и т.д.

Теория фракталов может применятся для анализа электрокардиограмм. Также фракталы могут использоваться в обработке медицинских рентгеновских изображений. Рентгеновские снимки обработанные с помощью фрактальных алгоритмов дают более качественную картинку а соответственно и более качественную диагностику. Еще одна область в медицине где активно могут применятся фракталы — это гастроэнтерология.

Кровеносная система

Бронхи

Анализ электрокардиограмм


Фрактальная графика. Области применения

Геология и геофизика.

Очень часто фракталы применяются в геологии и геофизике. Не секрет что побережья островов и континентов имеют некоторую фрактальную размерность, зная которую можно очень точно вычислить длины побережий. Также фрактальный анализ помогает в поиске и разработке месторождений полезных ископаемых, распределение которых очень часто происходит по фрактальному механизму. Исследование разломной тектоники и сейсмичности порой тоже исследуется с помощью фрактальных алгоритмов.

Фрактальный анализ бассейнов стока на Марсе

Фрактальное распределение очагов землетрясений


Фрактальная графика. Области применения

Физика.

В физике твёрдых тел фрактальные алгоритмы позволяют точно описывать и предсказывать свойства твёрдых, пористых, губчатых тел, различных аэрогелей. Это помогает в создании новых материалов с необычными и полезными свойствами.

Микромир. Строение атома


Фрактальная графика. Области применения

Фракталы в телекоммуникациях.

В телекоммуникациях фракталы используются для создания фрактальных антенн. Фрактальная антенны с удивительно компактным дизайном обеспечивает превосходную широкополосную производительность в маленьком форм-факторе. Достаточно компактны для установки или встраивания в различных местах, фрактальные антенны используются для морских, воздушных транспортных средств, или персональных устройств.

Фрактальные антенны


Фрактальная графика. Области применения

Фракталы как элементы визуализации и спецэффектов.

Фракталы притягивают и завораживают своей красотой и бесконечностью. Именно поэтому фракталы очень часто используют для создания различного рода визуализаций, видеоинсталляций, создания спецэффектов в компьютерной графике и т.д. Поэтому очень широко применяются в компьютерной графике. Существует множество программ, служащих для генерации фрактальных изображений.


Создание фрактальных изображений:

  • Программа Ultra Fractal
  • Программа Adobe Photofhop

Ultra Fractal — лучшее решение для создания уникальных фрактальных изображений профессионального качества. Ultra Fractal представлен двумя редакциями: Standard Edition и расширенной Animation Edition, возможности которой позволяют не только генерировать фрактальные изображения, но и создавать анимацию на их основе. Созданные изображения можно визуализировать в высоком разрешении, пригодном для полиграфии, и сохранить в собственном формате программы или в одном из популярных фрактальных форматов.







Красота фракталов далеко не исчерпана и еще подарит нам немало шедевров — тех, которые услаждают глаз, и тех, которые доставляют истинное наслаждение разуму.

Фракталы

1.Введение.

Разветвления трубочек трахей, листья на деревьях, вены в руке, река, бурлящая и изгибающаяся, рынок ценных бумаг — это все фракталы. От представителей древних цивилизаций до Майкла Джексона, ученые, математики и артисты, как и все остальные обитатели этой планеты, были зачарованы фракталами и применяли их в своей работе.

Программисты и специалисты в области компьютерной техники так же без ума от фракталов, так как фракталы бесконечной сложности и красоты могут быть сгенерированы простыми формулами на простых домашних компьютерах. Открытие фракталов было открытием новой эстетики искусства, науки и математики, а так же революцией в человеческом восприятии мира.

Цель моей работы показать красоту фрактальной графики и увидеть при изучении не только треугольники, пирамиды, углы и системы счисления, но и разнообразные фракталы.

2.Понятие «фрактал».

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов.

Фрактал (от лат. – дробленый, состоящий из фрагментов) – термин, обозначающий геометрическую фигуру, составленную из нескольких частей, каждая их которых подобна всей фигуре целиком. Небольшая часть фрактала содержит информацию о всем фрактале.

Слово «фрактал» было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта «The Fractal Geometry of Nature».

Роль фракталов в компьютерной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения компьютерной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.

3. Свойства.

Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.

Фракталы – геометрические объекты с дробной размерностью. К примеру, размерность линии – 1, площади – 2, объема – 3. У фрактала же значение размерности может быть между 1 и 2 или между 2 и 3. К примеру, фрактальная размерность скомканного бумажного шарика приблизительно равна 2,5. В математике существует специальная сложная формула для вычисления размерности фракталов.

4.Применение.

Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика.

— компьютерные системы:

Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом, картинки сжимаются гораздо лучше, чем это делается обычными методами.

Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.

-механика жидкостей:

Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложных потоков

Например, атмосфера Юпитера представляет собой одно из самых захватывающих зрелищ в Солнечной системе (рис.). Между ледяным холодом космического пространства и тысячеградусной жарой в глубинах атмосферного океана гигантской планеты зарождаются циклопические облачные вихри самых причудливых форм.

-телекоммуникации:

Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес.

—физика поверхностей:

Фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов.

-медицина:

Биосенсорные взаимодействия. Биения сердца.

-биология:

Моделирование хаотических процессов, в частности при описании моделей популяций

В природе фрактальными свойствами обладают многие объекты, например: кроны деревьев, цветная капуста, облака, кровеносная и альвеолярная системы человека и животных, кристаллы, снежинки, элементы которых выстраиваются в одну сложную структуру, побережья

-фрактальное искусство:

Еще одной захватывающей, но спорной областью применения фракталов служит компьютерное искусство. Фракталы не только служат ученым, но и помогают художникам передавать их мысли, чувства и настроения, воплощая самые невероятные фантазии. В наше время живописец уже не может обойтись без компьютерной программы, которая строит причудливые картины-фракталы

5. Виды фракталов.

Решётка Серпинского

Треугольник Серпинского

Губка Серпинского

Кривая Коха

Фрактал Мандельброта

Кривая Дракона

Множество Мандельброта

Множество Жюлиа

6.Как построить фрактал.

Создатель фракталов выполняет роль художника, фотографа, скульптора, и ученого-изобретателя одновременно.

Какие предстоят этапы работы сотворения рисунка «с нуля»?

задать форму рисунка математической формулой

исследовать сходимость процесса и варьировать его параметры

выбрать вид изображения

выбрать палитру цветов

Среди фрактальных графических редакторов и прочих графических программ можно выделить:

«Painter» (без компьютера ни один художник никогда не достигнет заложенных программистами возможностей лишь посредством с помощью карандаша и пера кисти)

«Adobe Photoshop» (но здесь изображение «с нуля» не создается, а, как правило, только обрабатывается)

7. Заключение.

Фрактальная графика — это не просто множество самоповторяющихся изображений, это модель структуры и принципа любого сущего. Вся наша жизнь представлена фракталами. Не только визуальными, но ещё и структура этого изображения отражает нашу жизнь. Взять, к примеру, ДНК, это всего лишь основа, одна итерация, а при повторении… появляется человек! И таких примеров много. Нельзя не отметить широкое применение фракталов в компьютерных играх, где рельефы местности зачастую являются фрактальными изображениями на основе трёхмерных моделей комплексных множеств и броуновского движения. Фрактальная графика необходима везде, и развитие «фрактальных технологий» — это одна из немаловажных задач на сегодняшний день

«Компьютерное изображение» — Исходное изображение. Лекция 1. IP -> CV -> CG (2). Обработка изображений. Реконструкция формы головы по фотографиям. Фото с базовыми линиями. На лекции. Отображение ночного тона на дневной. Закраска индивидуальных полигонов (плоская “flat” закраска). Закраска Гуро (Gouraud) (диффузное отражение).

«Пиктограмма» — Показать любые счета. Определения (состояния строчек). Отправить. Добавить. Отправленный… (в ожидании оплаты). (Удалить строчку) …совсем. Строчка не обязательно должна быть связана со счетом. Команды для работы со строчками в счетах. Собрать строчки в счет. Конструирование языка пиктограмм пользовательского интерфейса.

«Графика и её виды» — Простейшими объектами являются: Векторная графика. Растровая. Изображение строится по уравнению. Компьютерные программы. Векторная графика является объектной. К примеру экран 15” монитора составляет 28Х21 см. Растровая для разработки электронных и полиграфических изданий. Векторная. Недостатки. Фрактальная.

«Растровые изображения» — 12. 10000000. 00010001. 9. 2. 8. 00001001. РТ: №37, стр. 29. 0 – белый цвет, 1 – черный цвет. 4. РТ: №37, стр. 29-30. 10. Цель: 01000000.

«Инженерная графика» — Покровская М.В. Один из примеров — план вавилонского дома с разрезом по дверным и оконным проемам и указанием клинописью размеров. С начала XIX в. Начертательную геометрию стали изучать в российских учебных заведениях. Петровские реформы начала XVIII в. придали ускорение развитию графической культуры России.

«Компьютерная графика в школе» — Применение компьютерной графики в презентациях и моделировании объектов. Работа с элементами окна, главным меню и инструментальными панелями. Графический редактор MS Paint, графические возможности текстового процессора MS Word. Основы диалога ученик – компьютер. Основные операции с файлами и папками.



Фракталы: Геометрические Алгебраические Системы итерируемых функций Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные — несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря. Существуют и другие классификации фракталов, например деление фракталов на детерминированные (алгебраические и геометрические) и недетерминированные (стохастические). Стохастические фракталы


И льётся свет в ночи От каждого луча … И сходятся лучи В холодных три ключа. И каждый из ключей Законам вопреки Неведомо зачем Впадает в три реки, Чей инфернальный бег Сметает все мосты. И каждая из рек — Начало трёх пустынь. И в бездну мир несёт За острые края.. И поглощает всё Фрактал небытия.



Изобретения Кантора: Построение классической пыли Кантора начинается с выбрасыванием средней трети (не включая концы) единичного отрезка. То есть исходное множество есть отрезок , и первый шаг состоит в удалении открытого интервала (1/3, 2/3). На следующем и всех остальных шагах выкидываем среднюю треть (не включая концы) всех отрезков текущего уровня. Таким образом, получается последовательность множеств Два множества можно сравнивать по величине, сопоставляя элементы одного множества с элементами другого.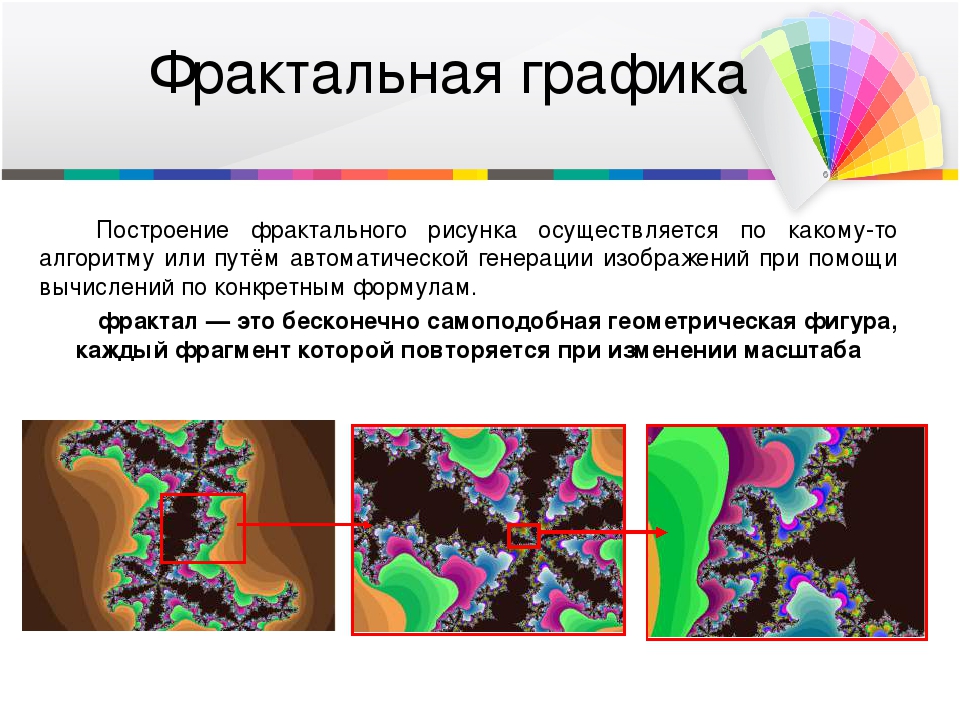 Например, чтобы определить, каких шариков в ведёрке больше: цветных или чёрных, можно брать их из ведёрка парами, состоящими из цветного и чёрного шариков, до тех пор, пока там не останутся шарики одного цвета. Именно этот остаток и указывает, каких шариков было больше. Такой же принцип Кантор применил для количественного сравнения бесконечных множеств.

Джузеппе Пеано итальянский математик Внёс вклад в математическую логику, аксиоматику, философию математики. Создатель вспомогательного искусственного языка латино — сине — флексионе. Более всего известен как автор стандартной аксиоматизации натуральной арифметики арифметики Пеано

Изобретения Пиано На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в 3 раза меньшей, чем длинна исходной линии (Часть 1 и 2 рисунка 1). Далее он делал то же самое с каждым отрезком получившейся линии. И так до бесконечности. Ее уникальность в том, что она заполняет всю плоскость.

Вацлав Франциск Серпинский. . выдающийся польский математик. Известен своими трудами по теории множеств, аксиоме выбора, континуум — гипотезе, теории чисел, теории функций, а также топологии. Автор более 700 статей и 50 книг. Его именем названы числа Серпинского, а также три широко известных фрактала: треугольник Серпинского, ковёр Серпинского, кривая Серпинского. ()





Позднее он дал определение фрактала: «Фракталом называется структура, состоящая из частей, которые в каком- то смысле подобны целому»

Мандельброт пишет в своей книге: « Почему геометрию часто называют холодной и сухой? Одна из причин лежит в её неспособности описать форму облаков, гор или деревьев. Облака – это не сферы, горы не углы, линия побережья – не окружность, кора не гладкая, а молния не прямая линия …»

Слайд 2

Введение

Разветвления трубочек трахей, листья на деревьях, вены в руке, река, бурлящая и изгибающаяся, рынок ценных бумаг — это все фракталы. От представителей древних цивилизаций до Майкла Джексона, ученые, математики и артисты, как и все остальные обитатели этой планеты, были зачарованы фракталами и применяли их в своей работе.

Программисты и специалисты в области компьютерной техники так же без ума от фракталов, так как фракталы бесконечной сложности и красоты могут быть сгенерированы простыми формулами на простых домашних компьютерах. Открытие фракталов было открытием новой эстетики искусства, науки и математики, а так же революцией в человеческом восприятии мира.

Цель моей работы показать красоту фрактальной графики и увидеть при изучении не только треугольники, пирамиды, углы и системы счисления, но и разнообразные фракталы.

Слайд 3

Понятие «фрактал»

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов.

Фрактал (от лат. – дробленый, состоящий из фрагментов) – термин, обозначающий геометрическую фигуру, составленную из нескольких частей, каждая их которых подобна всей фигуре целиком. Небольшая часть фрактала содержит информацию о всем фрактале.

Слово «фрактал» было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта «The Fractal Geometry of Nature».

Слайд 4

Роль фракталов

Роль фракталов в компьютерной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения компьютерной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.

Слайд 5

Свойства

Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.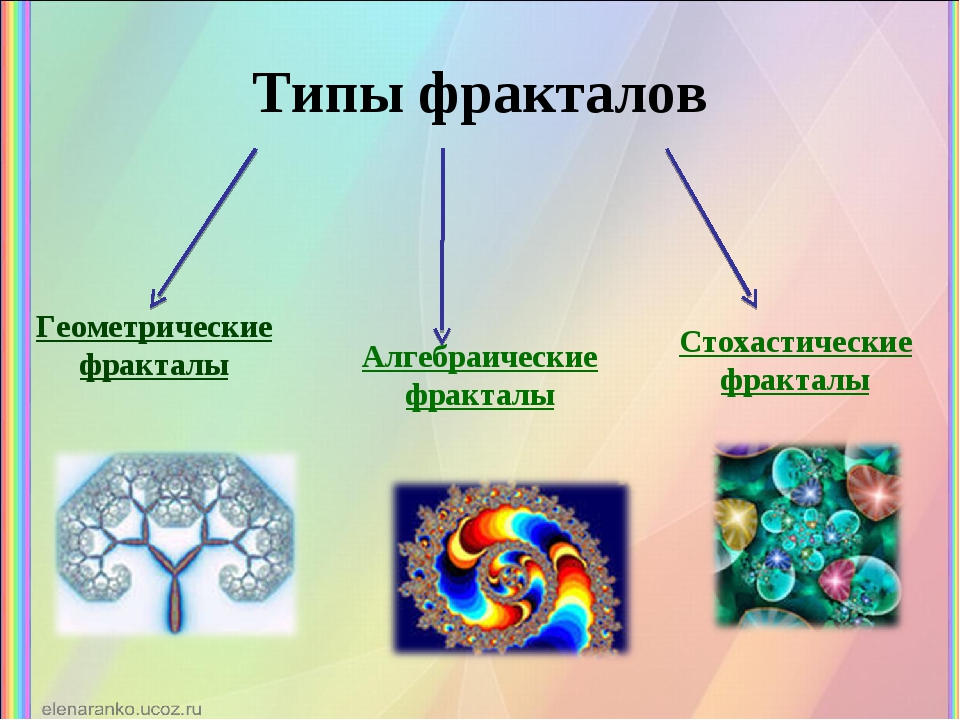

Фракталы – геометрические объекты с дробной размерностью. К примеру, размерность линии – 1, площади – 2, объема – 3. У фрактала же значение размерности может быть между 1 и 2 или между 2 и 3. К примеру, фрактальная размерность скомканного бумажного шарика приблизительно равна 2,5. В математике существует специальная сложная формула для вычисления размерности фракталов.

Слайд 6

Применение фракталов

Фракталы находят все большее и большее применение в науке. Основная причина этого заключается в том, что они описывают реальный мир иногда даже лучше, чем традиционная физика или математика.

Слайд 7

Компьютерные системы

Наиболее полезным использованием фракталов в компьютерной науке является фрактальное сжатие данных. В основе этого вида сжатия лежит тот факт, что реальный мир хорошо описывается фрактальной геометрией. При этом, картинки сжимаются гораздо лучше, чем это делается обычными методами.

Другое преимущество фрактального сжатия в том, что при увеличении картинки, не наблюдается эффекта пикселизации (увеличения размеров точек до размеров, искажающих изображение). При фрактальном же сжатии, после увеличения, картинка часто выглядит даже лучше, чем до него.

Слайд 8

Механика жидкостей

Изучение турбулентности в потоках очень хорошо подстраивается под фракталы. Турбулентные потоки хаотичны и поэтому их сложно точно смоделировать. И здесь помогает переход к фрактальному представлению, что сильно облегчает работу инженерам и физикам, позволяя им лучше понять динамику сложныхпотоков

Например, атмосфера Юпитера представляет собой одно из самых захватывающих зрелищ в Солнечной системе (рис.). Между ледяным холодом космического пространства и тысячеградусной жарой в глубинах атмосферного океана гигантской планеты зарождаются циклопические облачные вихри самых причудливых форм.

Слайд 9

Телекоммуникации

Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес.

Слайд 10

Физика поверхностей

Фракталы используются для описания кривизны поверхностей. Неровная поверхность характеризуется комбинацией из двух разных фракталов.

Слайд 11

Медицина

  • Биосенсорные взаимодействия
  • Биения сердца

  • Слайд 12

    Биология

    Моделирование хаотических процессов, в частности при описании моделей популяций

    В природе фрактальными свойствами обладают многие объекты, например: кроны деревьев, цветная капуста, облака, кровеносная и альвеолярная системы человека и животных, кристаллы, снежинки, элементы которых выстраиваются в одну сложную структуру, побережья

    Слайд 13

    Фрактальное искусство

    Еще одной захватывающей, но спорной областью применения фракталов служит компьютерное искусство. Фракталы не только служат ученым, но и помогают художникам передавать их мысли, чувства и настроения, воплощая самые невероятные фантазии. В наше время живописец уже не может обойтись без компьютерной программы, которая строит причудливые картины-фракталы

    Слайд 14

    Виды фракталов

    • Решётка Серпинского.
    • Губка Серпинского.
    • Треугольник Серпинского.

  • Слайд 15

    Тетрикс (tetrix) – трехмерный аналог треугольника Серпинского.

    Слайд 16

    Кривая Коха

    Она была изобретена в девятнадцатом веке немецким математиком по имени Хельге фон Кох. Инициатор — прямая линия. Генератор – равносторонний треугольник, стороны которого равны трети длины большего отрезка. Эти треугольники добавляются к середине каждого сегмента снова и снова

    Слайд 18

    Кривая Дракона

    Изобретенная итальянским математиком Джузеппе Пеано, Кривая Дракона или Взмах Дракона.

    Слайд 19

    Множество Мандельброта

    Множество Мандельброта, которое было построено Бенуа Мандельбротом, наверное первая ассоциация, возникающая у людей, когда они слышат слово фрактал.

    Этот фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круглыми областями

    Слайд 20

    Множество Жюлиа

    Множество Жюлиа было изобретено французским математиком Гастоном Жюлиа, по имени которого и было названо множество.

    Слайд 21

    Еще некоторые примеры конструктивных фракталов.

    Слайд 22

    Как построить фрактал?

    Среди фрактальных графических редакторов и прочих графических программ можно выделить:

    • «Art Dabbler»
    • «Painter» (без компьютера ни один художник никогда не достигнет заложенных программистами возможностей лишь посредством с помощью карандаша и пера кисти)
    • «Adobe Photoshop» (но здесь изображение «с нуля» не создается, а, как правило, только обрабатывается)

    Создатель фракталов выполняет роль художника, фотографа, скульптора, и ученого-изобретателя одновременно.

    Какие предстоят этапы работы сотворения рисунка «с нуля»?

    • задать форму рисунка математической формулой
    • исследовать сходимость процесса и варьировать его параметры
    • выбрать вид изображения
    • выбрать палитру цветов

  • Слайд 23

    Заключение

    Фрактальная графика — это не просто множество самоповторяющихся изображений, это модель структуры и принципа любого сущего. Вся наша жизнь представлена фракталами. Не только визуальными, но ещё и структура этого изображения отражает нашу жизнь. Взять, к примеру, ДНК, это всего лишь основа, одна итерация, а при повторении… появляется человек! И таких примеров много. Нельзя не отметить широкое применение фракталов в компьютерных играх, где рельефы местности зачастую являются фрактальными изображениями на основе трёхмерных моделей комплексных множеств и броуновского движения. Фрактальная графика необходима везде, и развитие «фрактальных технологий» — это одна из немаловажных задач на сегодняшний день.

    Слайд 24

    Игнацевич С.В.

    Посмотреть все слайды

    • Компьютерная графика: Фрактальная

    Фрактальная графика является на сегодняшний день одним из самых быстро развивающихся и перспективных видов компьютерной графики. 
    Математической основой фрактальной графики является фрактальная геометрия. Здесь в основу метода построения изображений положен принцип наследования от, так называемых, «родителей» геометрических свойств объектов-наследников.  
    Понятия фрактал, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского «fractus» и в переводе означает«состоящий из фрагментов». Оно было предложено математиком Бенуа Мандель-Бротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. 

    Программа Chaotica является продуктом без всяких ограничений, на создания фрактальных изображений. Любой желающий может применять ее для своих нужд совершенно бесплатно и создавать свои изображения с разрешением 1280х960 и выше.

    Mandelbulb 3D

    — фрактальный рэй трейсер, позволяет работать с трехмерными фракталами. Множество настроек, включая настройки цвета, освещения, постобработки, глубины и т.д. позволят максимально осуществить творческий замысел и обеспечат необходимую гибкость при работе. Поддерживает анимацию. Бесплатный и постоянно обновляемый. Официальный сайт: Mandelbulb 3D

    Mandelbulber — экспериментальное приложение, разработанное для создания и работы с 3Д-фракталами Мандельброта также и с некоторыми другими видами 3D — фракталов, такими как Mandelbox, Bulbbox, Juliabulb, губка Менгера и т.д.
    Особенности: великолепная гибкость по работе с 3Д-фракталами, работа с освещением тенями, цветом, поддержка эффектов ambient окклюзии, глубины резкости и т.д.
    Неограниченное разрешение изображения на 64-битных системах. Простой в использовании 3D-навигатор по фракталу. Поддержка анимации. Mac- и Win- версии. Бесплатный. Официальный сайт: Официальный сайт Mandelbulber. Apophysis 7x У генератора фракталов Апофиз много возможностей для создания и редактирования 2Д-фракталов, в том числе редактор, позволяющий напрямую редактировать фрактал, манипулируя треугольниками (своеобразными блоками-преобразованиями). функция мутации применяет случайное редактирование треугольников. регулировка размеров окон программы под себя. серъезные возможности по манипуляциям с цветом фрактала и даже язык сценариев с прямым доступом к большинству компонентов фрактала. Поддержка анимации. Экспорт с последующим рендерингом в программы, такие как FLAM3 и Chaotica. Поддержка нескольких языков, русского, пока, к сожалению, нет. Множество плагинов, позволяющие добиться невероятных результатов по фракталам. Бесплатный. Официальный сайт: Apophysis 7x Ultra Fractal — генератор фракталов, позволяет создавать изображения фрактальных множеств, а также выполнять их анимацию. Процесс построения изображений определяется набором алгоритмов, описывающих разновидности визуализируемых фракталов, методы их раскраски и применяемые к ним трансформации.

    Особенности: модульная архитектура позволяет не только использовать кем-то уже созданные алгоритмы, но и создавать собственные. встроенный язык программирования. Уникальные параметры по работе с цветом и градиентами. Реализована возможность работать с альфа-каналами, слоями и масками, что позволяет легко комбинировать различные фрагменты изображений. Условно бесплатная. Официальный сайт: Ultrafractal

    Xenodream — уникальная программа для создания фрактальной 3D графики. Создание или изучение от самых простых форм до сложноых рекурсивных 3D структур, эксперименты с освещением и текстурами. Экспорт текстур или карт глубины (depth maps) для других программ рендеринга. Создание стереограмм, анимации и многое другое. Программа предназначена как для профессионалов, так и для тех, кто любит развлекаться созданием фантастических трёхмерных моделей. WildFire — относительно неплохой и в то же время мощный редактор фрактальной графики. По функциональности его можно сравнить с широко известной программой Apophysis. Так же как и Apophysis, JWildFire работает с флеймами, но в отличии от Апофизиса, написанного на Delphi, JWildFire написана на языке Java.
    Ключевыми особенностями программы являются:
    -возможность использования потрясающих 3Д эффектов, таких как волны, рябь на воде и пр.
    -3д эффекты наложения
    -мощный встроенный редактор флеймов-T. 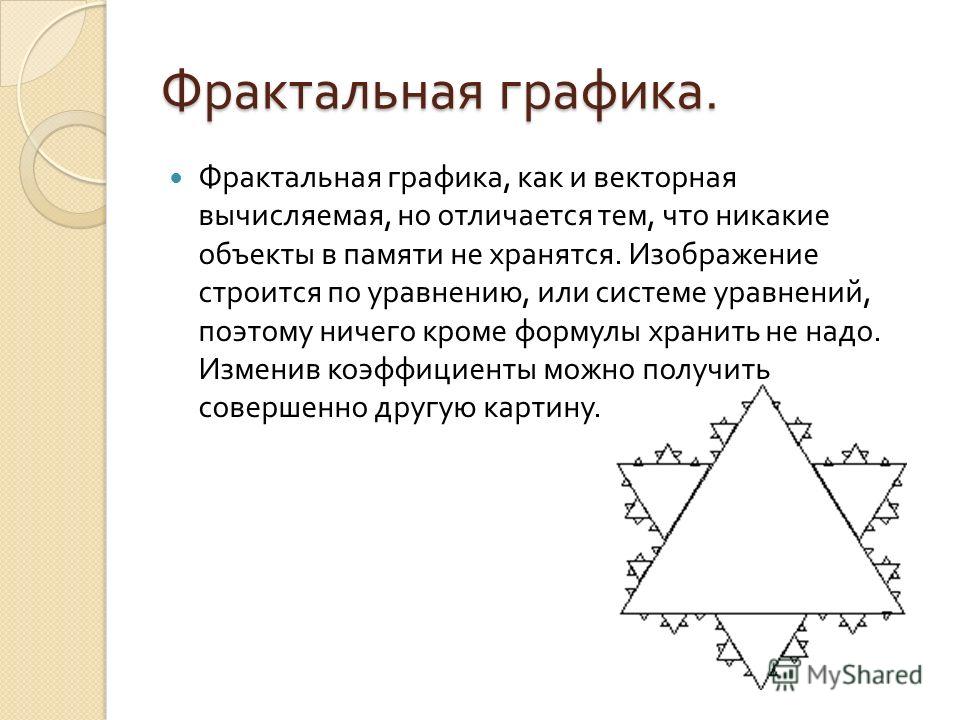I.N.A.
    -встроенный генератор изображений ( возможность генерировать картинки с облаками, плазмой и т.д.)
    -множество эффектов обработки изображений в 2Д (Н-р: Вращение, скручивание, разрушение и т.д.)
    -простой, но мощный пользовательский интерфейс, который позволяет анимировать практически любой параметр, всего за несколько кликов мыши
    -интеграция с Sunflow для высокого качества визуализации.
    Основными отличиями от Апофизиса следующие:
    У JWildfire в редакторе просмотр происходит в реальном времени. — Но у Apo просмотр является более точным.
    JWildfire позволяет использовать флеймы как плагины (Variations)
    JWildfire имеет функции HDR выходе (32 бит на канал)
    JWildfire имеет Pseudo3D шейдер, который дает более реалистичные результаты для 3D рендера.
    Для Apo создан огромный набор плагинов, но они не могут использоваться все вместе. У JWildfire набор меньше, но все же встроено достаточно большое количество плагинов, которые могут быть использованы все вместе.
    JWildfire имеет встроенный компилятор для создания собственных плагинов на лету.
    Платформа JWildfire является независимой и очень стабильной, — но в Apo рендер происходит быстрее (в 2 раза, в зависимости от формулы)
    JWildfire не нуждается в каких-то дополнительных инструментах.
    Является бесплатной
    Официальный сайт: http://www.andreas-maschke.com/
    Примерами изображений могут послужить изображения генератора Apophysis.
    Fractal Explorer- это бесплатный фракталогенератор, который позволяет создавать очень красивые фрактальные изображения на основе математических формул.
    Программа рассчитана не только на профессионалов, но и на простых пользователей, а следовательно работать с ней не составит никакого труда.Работать в ней можно как и в профессиональных целях, так и ради развлечения, в обоих случаях программа доставит массу удовольствия и много часов приятного времяпровождения!
    Fractal Explorer позволяет создавать фракталы, основаные на классических многочленных множествах (Множество Мандельброта, множество Жюлиа, множество Ньютона и их вариации), а также на некоторых других. Например: 4D-комплексные фракталы (фракталы основанные на кватернионах), 3D «странные» аттракторы, а также IFS системы.Кроме того Fractal Explorer имеет множество функций для создания различных эффектов и улучшения качества генерируемых изображений. Оф.сайт программы: http://www.eclectasy.com/Fractal-Explorer/ Incendia является полноценным бесплатным, многопроцессорным 3D фракталогенератором.
    Программа постоянно развивается и обновляется. На данный момент она имеет богатый и мощный спектр возможностей для генерации полноценных трёхмерных фракталов.Ключевыми особенностями являются:
    -Генерация изображений с разрешениями: 1024, 2048, 2560 и 3072 пикселей (4096 и 8192 пикселей для доноров, т.е. пользователей, сделавших добровольный материальный взнос в пользу автора программы)
    -Поддержка двухкратного антиальясинга для получения более гладкой и совершенной картинки.
    -45 разновидностей трёхмерных фракталов (правда многие будут включены в состав только будущих версий программы)
    -Поддержка фрактальных скриптов для создания новых типов фракталов.
    -Большая библиотека текстур, а также возможность импорта внешних текстур.
    -Поддержка цветовых градиентов.
    -Несколько стилей рендеринга (включая объемный туман, и многие новые шейдеры визуализации).
    -Поддержка многоядерных процессоров.
    -Наличие встроенных трёхмерных базовых форм для конструирования сложных фракталов. (Включает в себя шесть различных смещений карты базовой формы).
    -Мощный редактор фрактальных трансформаций.
    -Редактор трёхмерных базовых форм.
    -Редактор материалов
    -3D Mesh экспорт (до 1000х1000х1000 вокселей для доноров)
    -Сохранение в буфер (для долгого рендера)
    -Поддержка анимации.
    Кроме того начиная с версии EX V в программу включено приложение Geometrica, специально разработанное для экспорта трёхмерных фракталов из Incendia в другие редакторы 3D графики.
    Как уже было упомянуто, программа бесплатная, постоянно развивается и обновляется и автор просит всех желающих делать пожертвования, для дальнейшего развития программы!
    Оф. сайт: http://www.incendia.net/index.htmlChaoscope является программным средством рендеринга 3D странных аттракторов. Это непрерывный проект, созданный и поддерживаемый Николя Desprez, текущая версия 0.3.1. Она является бесплатной, работающей на платформе Windows, Linux. Официальный сайт: перейти

    ChaosPro бесплатный генератор в режиме реального времени фрактальный генератор для MS Windows с поддержкой различных фрактальных типов (2D и 3D), истинная поддержка цветов, с поддержкой анимации. Благодаря встроенному компилятору довольно быстр, возможность написания собственных формул. официальный сайт: перейти

    Sterling является фракталогенератором, написанным на языке программирования C в 1999 году для Microsoft Windows Стивен С. Фергюсон. Sterling2 это бесплатная версия с различными алгоритмами генерации. Он был выпущен в сентябре 2008 года Tad Boniecki. Помимо названия, программа выглядит так же, как оригинал, имеется дополнительно 50 формул для фрактальной генерации. Файлы, созданные Sterling могут быть использованы в Sterling2 и наоборот, хотя они будут показывать разные образы. Sterling основан на том, что в нем используются интересные фильтры для фрактальных изображений с помощью сложных параметров цвета и тени. Sterling имеет простой графический интерфейс с ограниченным числом функций. Программа сохраняет файлы JPEG, BMP или один из шести других форматах.официальный сайт: перейти

    Fractron 9000 является высокопроизводительным генератором фракталов для визуализации в среде Windows. Работает по алгоритму FractalFlames/
    Fractron 9000 использует преимущества современных программируемых графических процессоров lдля значительного ускорения рендеринга. Пользователи имеющие поддержку CUDA и OpenCL видео оборудования смогут генерировать фрактальные изображения в режиме реального времени. Некоторые примеры изображений, созданных с Fractron приведены ниже. (взяты с официального сайта). Пользовательский интерфейс написан на C #, сообщается с OpenCL и CUDA через собственные пользовательские библиотеки совместимости. Fractron использует OpenGL для отображения фракталов.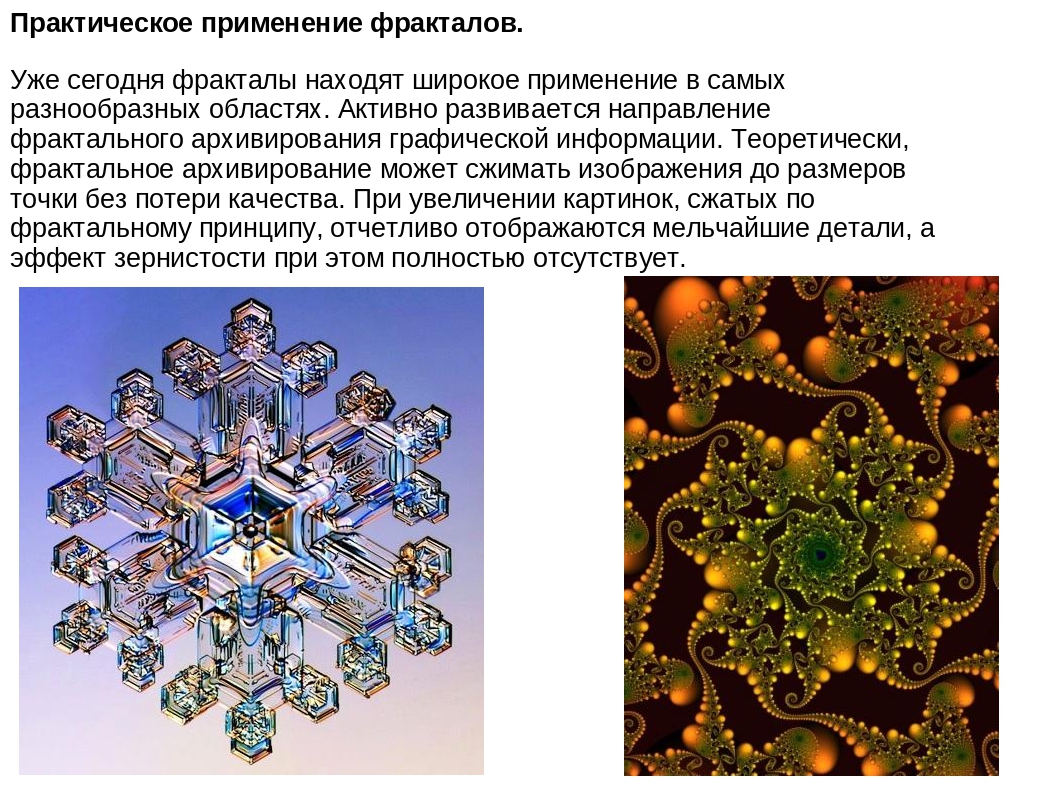
    официальный сайт: http://fractron9000.sourceforge.net/index.html

    Приложение для iPhone, iPod Touch, iPad, Fractals с помощью данной программы можно исследовать и визуализировать множество Мандельброта и Жюлиа в реальном времени!
    Результаты можно сохранить и поделиться с друзьями.
    ПРиобрести программу можно на the App Store!™

    Fractal Science Kit — фрактальный генератор для Windows, который создает фрактальные изображения из набора свойств, которые можно установить для контроля фрактального процесса генерации. Пример свойства включают в себя тип фрактала, размер изображения и параметров для контроля орбиты генрации, нормализация данных, передискретизации, сглаживание, гамма-коррекция и т.д. Вы можете работать с множеством встроенных алгоритмов (программ) или разработать свой собственный с использованием интерактивной средой программирования. фрактальный генератор поддерживает сотни встроенных уравнений, преобразования орбиты ловушки, контроллеры, позволяющие обычным пользователям создавать великолепные фрактальные изображения, обеспечивая при этом опытным разработчиком богатый набор иллюстративных примеров, на которых строится его собственные программы (алгоритмы). Более 60000 строк исходного кода для встроенных фрактальных программ и встроенных макросов (встроенных функций / методов) доступны через браузер, программы и редактор макросов.поддерживает 3 основные фрактальные типы:

    Мандельброт Fractals Orbital Fractals L-система Fractals и другие: Mandelbrot, Julia, Convergent, Newton, Orbit Traps, Sierpinski Triangle, IFS, Strange Attractors, Rep-N Tiles, Symmetric Icons, Symmetric Attractors, Frieze Group Attractors, Wallpaper Group Attractors, Hyperbolic Attractors, Apollonian Gasket, Circle Inversion, Mobius Dragon IFS, Mobius Patterns, Grand Julian IFS, Elliptic Splits IFS, Schottky Group, Kleinian Group, L-System…

    Visions Of Chaos является профессиональным прикладным программным обеспечением для Windows. Он достаточно прост для людей, которые не понимают математику за ним, но достаточно развиты для фрактальных энтузиастов. Это наиболее полное все в одном приложение связанные с теорией хаоса. Поддерживает визуализацию видео. В программу включены сотни прмеров.

    Алгоритмы компьютерной графики

    Понятия фракталы, фрактальная геометрия и фрактальная графика, появившиеся в конце 70-х, сегодня прочно вошли в обиход математиков и компьютерных художников. Слово фрактал образовано от латинского fractus и в переводе означает “состояние из фрагментов”. Оно было предложено математиком Бенуа Мандельбромом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта “The Fractal Geometry of Nature”. В его работе использованы научные результаты других ученых, работавших в 1875-1925 годах в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.
    Из всех типов фракталов наиболее наглядными являются геометрические фракталы. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называется генератором. За один шаг алгоритма каждый из отрезков, составляющих ломанную, заменяется на ломаную-генератор в соответствующем масштабе. В результате бесконечного повторения этой процедуры получается геометрический фрактал.
    Одним из основных свойств фракталов является  самоподобие. Объект называют самоподобным, когда увеличенные части объекта походят на сам объект и друг на друга.
    Перефразируя это определение, можно сказать, что в простейшем случае небольшая часть фрактала содержит информацию  обо всем фрактале. Например, снежинка несет информацию о снежном сугробе, а горный камень имеет те же самые очертания, и что и горный хребет. Благодаря тому свойству мы можем использовать фракталы для генерирования поверхности местности, которая походит на саму себя, независимо от масштаба, в котором она отображена. Эта идея нашла использование в компьютерной графике благодаря компактности математического аппарата, необходимого для ее реализации. Так, с помощью некоторых математических коэффициентов можно задать линии  и поверхности  очень сложной формы.
    Сегодня разработаны алгоритмы синтеза коэффициентов фрактала, использующего произвести копию любой картинки сколь угодно близкой к исходному оригиналу. С точки зрения машинной графики фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически благодаря фрактальной геометрии найден способ эффективной реализации сложных неевклидовых объектов, образы которых весьма похожи на природные.
    Геометрические фракталы на экране компьютера – это узоры, построенные самим компьютером по заданной программе. Они очень красивы, необычны и интересны. Многие художники на Западе (например, Мелиса, Бинде) рассматривают фракталы как новый вид компьютерного искусства. Помимо фрактальной живописи существуют фрактальная анимация и фрактальная музыка.

    Создатель фракталов – это художник, скульптор, фотограф, изобретатель и ученый в одном лице. Вы сами задаете форму рисунка математической формулой, исследуете сходимость процесса, варьируя его параметры, выбираете вид изображения и палитру цветов, то есть творите рисунок «с нуля». В этом одно из отличий фрактальных графических редакторов (и в частности — Painter) от прочих графических программ. Например, в Adobe Photoshop изображение, как правило, «с нуля» не создается, а только обрабатывается. Другой самобытной особенностью фрактального графического редактора Painter (как и прочих фрактальных программ, например Art Dabbler) является то, что реальный художник, работающий без компьютера, никогда не достигнет с помощью кисти, карандаша и пера тех возможностей, которые заложены в Painter программистами.

     

     

    Что такое фрактал? — Определение из Техопедии

    Что означает фрактал?

    Фракталы представляют собой сложные модели, которые самоподобны и, следовательно, демонстрируют сходные модели в любом масштабе. Фракталы могут быть узорами или формами, которые не являются правильными и отличаются от традиционных геометрических фигур, но очень часто встречаются в природе, например облака, горы, деревья и снежинки. Наиболее известной иллюстрацией фракталов является множество Мандельброта, которое при увеличении просто показывает повторения одного и того же паттерна, что затрудняет определение уровня увеличения из-за повторяющихся паттернов.

    Techopedia объясняет фрактал

    Фрактальная геометрия считается особой областью математики просто потому, что фракталы имеют совсем другие математические уравнения, чем обычная геометрия. Явление изучалось сотни лет, но фракталы в значительной степени игнорировались как «математические монстры» из-за незнакомости, поскольку они сильно отличаются от установленной геометрии. Математика, стоящая за фракталами, началась в 17 веке, когда математик Готфрид Лейбниц начал изучать рекурсивное самоподобие и использовал термин «дробные показатели» для их описания, но только в 1872 году Карл Вейерштрасс представил первое определение функции с графиком. что можно считать фракталом по сегодняшнему определению.

    Еще одна веха в фрактальной геометрии наступила, когда Хельге фон Кох предложил более геометрический подход к идее фракталов с нарисованным от руки изображением, которое теперь называется снежинкой Коха. Фрактал снежинки Коха начинается как равносторонний треугольник, а затем итеративно заменяет среднюю треть каждой линии другим равносторонним треугольником, хотя и меньшим, потому что длина каждой стороны равна 1/3 исходной линии, на которой она находится. Это может продолжаться бесконечно или до тех пор, пока это физически возможно на носителях, где это проиллюстрировано, что при моделировании с помощью компьютера может практически простираться до бесконечности.Термин «фрактал» был введен Бенуа Мандельбротом в 1975 году.

    Сегодня фрактальные исследования в основном основаны на компьютере из-за их природы и находят применение в общей математике, компьютерном моделировании, обработке изображений и графики. Исследователи постулировали, что, поскольку в прошлом не было компьютеров, ранние исследователи явлений были очень ограничены в способах изображения фракталов, поэтому им не хватало средств, чтобы по-настоящему визуализировать их и оценить их значение.

    Что такое фрактал? — Определение из WhatIs.

    com От

    Фрактал — это неправильная геометрическая фигура, имеющая одинаковую степень нерегулярности на всех масштабах. Фракталы можно рассматривать как бесконечные паттерны.

    Как камень у подножия холма может напоминать в миниатюре гору, с которой он первоначально рухнул, так и фракталы самоподобны, смотришь ли ты на них вблизи или очень далеко. Термин «фрактал» был введен Бенуа Мандельбротом в 1975 году.Оно происходит от латинского fractus , что означает неровную поверхность, подобную поверхности разбитого камня.

    Фракталы — это формы, которые мы видим в природе. Мы можем описать прямоугольный треугольник с помощью теоремы Пифагора, но найти прямоугольный треугольник в природе — совсем другое дело. В природе мы находим деревья, горы, скалы и облака, но какова геометрическая формула облака? Как мы можем определить форму ложки сливок в чашке кофе? Фрактальная геометрия, теория хаоса и сложная математика пытаются ответить на подобные вопросы. Наука продолжает открывать удивительно последовательный порядок, стоящий за самыми, казалось бы, хаотичными явлениями во Вселенной.

    Математики пытались описать фрактальные формы более ста лет, но благодаря вычислительной мощности и возможностям обработки изображений современных компьютеров фракталы приобрели новую популярность, поскольку их можно визуализировать в цифровом виде и исследовать во всей их завораживающей красоте. Фракталы используются в школах в качестве наглядного пособия при обучении математике, а также в нашей массовой культуре в качестве компьютерных поверхностей для ландшафтов и планетарных поверхностей в киноиндустрии.Использование алгоритмов для создания фракталов может создавать сложные визуальные паттерны для приложений компьютерной графики (CGI).

    См. несколько примеров фрактальных изображений.

    Последний раз это было обновлено в августе 2016 года.

    Продолжить чтение о фрактале

    Фрактальная геометрия | Encyclopedia.

    com

    Ресурсы

    Фрактал — это геометрическая фигура, которую часто характеризуют как самоподобную; то есть неправильный, сломанный, фрагментированный или слабо связанный внешний вид.Фракталы использовались сотни, а то и тысячи лет назад, но фракталами их не называли. Это были рисунки, содержащиеся в искусстве и ремеслах, в рисунках ковров и расписных полов и потолков, а также во многих предметах, используемых в повседневной жизни. Немецкий математик Готфрид Вильгельм Лейбниц (1646–1716) разработал концепции, которые в конечном итоге помогли определить фракталы. Немецкий математик Карл Вейерштрасс (1815–1897) в 1872 году проанализировал и начертил график функции, которая сегодня считается фракталом. Позже, в 1904 году, шведский математик Нильс Фабиан Хельге фон Кох (1870–1924) усовершенствовал работу Вейерштрасса и определил другую функцию, которую сейчас называют снежинкой Коха.

    Польско-французский математик Бенуа Б. Мандельброт (1924–) ввел термин «фрактал» для описания таких фигур, получив это слово от латинского fractus, означающего сломанный, фрагментированный или неправильный. Он также указал на удивительное внешнее сходство между некоторыми фрактальными наборами и многими естественными геометрическими узорами. Таким образом, термин природный фрактал относится к природным явлениям, которые

    подобны фрактальным наборам, таким как путь, по которому движется частица пыли, когда она подпрыгивает в воздухе.

    Другим хорошим примером природного явления, похожего на фрактал, является береговая линия, поскольку она обладает тремя важными свойствами, типичными для фракталов. Во-первых, береговая линия неправильная, состоит из заливов, гаваней и полуостровов. Во-вторых, неравномерность в основном одинакова на всех уровнях увеличения. Если смотреть с орбиты высоко над Землей, с вертолета или с суши, смотреть невооруженным глазом или через увеличительное стекло, каждая береговая линия похожа сама на себя.Хотя узоры не совсем одинаковы на каждом уровне увеличения, основные черты береговой линии наблюдаются на каждом уровне. В-третьих, длина береговой линии зависит от увеличения, при котором она измеряется. Измерение длины береговой линии по снимку, сделанному из космоса, даст только оценку длины, потому что многие мелкие заливы и полуострова не появятся, а длины их периметров будут исключены из оценки.

    Более точную оценку можно получить, используя фотографию, сделанную с вертолета.Некоторые детали по-прежнему будут отсутствовать, но многие детали, отсутствующие на космическом снимке, будут включены, поэтому оценка будет длиннее и ближе к тому, что можно было бы назвать фактической длиной береговой линии. Эту оценку можно улучшить, пройдясь по береговой линии с шагомером. Опять же, в результате получится более длинное измерение, возможно, более близкое к фактической длине, но все же оценка, потому что многие части береговой линии состоят из камней и гальки, длина которых меньше, чем длина среднего шага.Более точные оценки можно получить, увеличивая уровень увеличения, и каждое последующее измерение будет находить береговую линию длиннее. В конце концов, уровень увеличения должен достигать атомного или даже ядерного разрешения, чтобы можно было измерить неровности каждой песчинки, каждого комка грязи и каждой крошечной гальки, пока длина не станет казаться бесконечной. Этот проблематичный результат предполагает, что длина каждой береговой линии одинакова.

    Решение проблемы заключается в том факте, что фракталы должным образом охарактеризованы с точки зрения их размерности, а не их длины, площади или объема, причем типичные фракталы описываются как имеющие размерность, не являющуюся целым числом.Чтобы объяснить, как это может происходить, необходимо рассмотреть значение размерности. Понятие размерности восходит к древним грекам, возможно, еще к Пифагору (582–500 гг. До н.э.), но, по крайней мере, к греческому математику Евклиду Александрийскому (ок. 325–ок. 265 до н.э.) и его книгам по геометрии. Интуитивно математики думают, что размерность равна количеству координат, необходимых для описания объекта. Например, линия имеет размерность 1, квадрат имеет размерность 2, а куб имеет размерность 3.Это называется топологической размерностью.

    Однако между 1875 и 1925 годами математики поняли, что для понимания чрезвычайно нерегулярных и фрагментированных множеств необходимо более строгое определение размерности. Они обнаружили, что ни одно определение размерности не является полным и полезным во всех обстоятельствах. Таким образом, сегодня остается несколько определений размерности. Среди них размерность Хаусдорфа, предложенная немецким математиком Феликсом Хаусдорфом (1868–1942), приводит к дробным размерам, когда объект является фракталом, но совпадает с топологическим значением размерности для правильных геометрических фигур.Он основан на увеличении длины, площади или объема, которое измеряется, когда фрактальный объект увеличивается на фиксированный масштабный коэффициент. Например, размер береговой линии по Хаусдорфу определяется как D = log (увеличение длины)/log (масштабный коэффициент). Если длина береговой линии увеличивается в четыре раза всякий раз, когда она увеличивается в три раза, то ее размер Хаусдорфа определяется как log (увеличение длины) / log (масштабный коэффициент) = log (4) / log (3). = 1,26. Таким образом, это не

    КЛЮЧЕВЫЕ ТЕРМИНЫ

    Измерение — Интуитивно, размерность фигуры — это количество координат, необходимых для ее описания, таких как линия (один), квадрат (два) или куб (три). Однако существуют и другие определения размерности, основанные на строгих определениях меры множества. Одним из таких измерений является измерение Хаусдорфа, которое применяется к фрактальным множествам.

    Масштабный коэффициент — Масштабный коэффициент — это константа, равная отношению двух пропорциональных длин, площадей или объемов. Ее также называют константой пропорциональности.

    Подобие — Две геометрические фигуры называются подобными, если их соответствующие формы одинаковы, но соответствующие измерения находятся в той же пропорции или имеют одинаковый масштабный коэффициент.

    длина, которая должным образом характеризует береговую линию, но ее измерение Хаусдорфа. Наконец, фрактальное множество определяется как множество точек на линии, плоскости или в пространстве, имеющих разрозненный или неправильный вид на всех уровнях увеличения, с размерностью Хаусдорфа, строго превышающей ее топологическую размерность. .

    Большой интерес к фрактальным наборам связан с тем, что большинство природных объектов больше похожи на фракталы, чем на обычные геометрические фигуры. Например, облака, деревья и горы больше похожи на фрактальные фигуры, чем на круги, треугольники или пирамиды. Таким образом, фрактальные наборы используются геологами для моделирования извилистых путей рек и скальных образований гор, ботаниками для моделирования ветвей деревьев и кустарников, астрономами для моделирования распределения массы во Вселенной, физиологами для моделирования системы кровообращения человека, физиками и инженерами для моделирования турбулентности в жидкостях и экономистами для моделирования фондового рынка и мировой экономики.Часто фрактальные наборы можно генерировать по довольно простым правилам. Например, фрактальную пыль можно получить, начав с линейного сегмента и удалив центральную треть, затем удалив центральную треть оставшихся двух сегментов, затем центральную треть этих оставшихся сегментов и так далее.

    Подобные правила генерации легко реализуются и графически отображаются на компьютерах. Поскольку некоторые наборы фракталов напоминают горы, острова или береговые линии, а другие кажутся облаками или снежинками, фракталы стали важными в графическом искусстве и создании специальных эффектов. Например, фальшивые миры, сгенерированные компьютером, используются в научно-фантастических фильмах и телесериалах, на DVD (цифровых универсальных дисках) и в видеоиграх, потому что они легко генерируются из набора инструкций, занимающих относительно небольшой объем памяти компьютера.

    КНИГИ

    Димри В.П., изд. Фрактальное поведение Земли . Берлин, Германия: Springer-Verlag, 2005.

    Фальконер, Кеннет Дж. Фрактальная геометрия: математические основы и приложения .Чичестер, Великобритания, и Хобокен, Нью-Джерси: Wiley, 2003.

    Стивенс, Роджер Т. Создание фракталов . Hingham, MA: Charles River Media, 2005.

    J. R. Maddocks

    The Gale Encyclopedia of Science Maddocks, J.

    Gale Apps — Технические трудности

    Технические трудности

    Приложение, к которому вы пытаетесь получить доступ, в настоящее время недоступно. Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд.

    Если проблемы с доступом сохраняются, обратитесь за помощью в наш отдел технической поддержки по телефону 1-800-877-4253. Еще раз спасибо, что выбрали Gale, обучающую компанию Cengage.

    org.springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является Ice.Неизвестное исключение unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0 в java.base/jdk.internal.util.Preconditions.outOfBounds(Preconditions.java:64) в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70) в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248) в java.base/java. util.Objects.checkIndex(Objects.java:372) на Яве.база/java.util.ArrayList.get(ArrayList.java:458) в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.java:60) в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53) в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.ява:30) в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17) в com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244) на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher. getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.ява:71) на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52) на com.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130) на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.ява:82) на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.java:44) на com.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31) в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl. java:57) на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.ява: 61) на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1) на com.gale.blis.auth._AuthorizationServiceDisp._iceD_authorize(_AuthorizationServiceDisp.java:141) в com.gale.blis.auth._AuthorizationServiceDisp._iceDispatch(_AuthorizationServiceDisp.java:359) в IceInternal.Incoming.invoke(Incoming.java:209) в Ice.ConnectionI.invokeAll(ConnectionI.java:2800) на льду.ConnectionI.dispatch(ConnectionI.java:1385) в Ice.ConnectionI.message(ConnectionI.java:1296) в IceInternal.ThreadPool.run(ThreadPool.java:396) в IceInternal.ThreadPool.access$500(ThreadPool.java:7) в IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:765) в java.base/java.lang.Thread. run(Thread.java:834) » org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:365) org.springframework.remoting.ice.IceClientInterceptor.invoke(IceClientInterceptor.java:327) org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71) org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186) org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:212) com.sun.proxy.$Proxy130.authorize(Неизвестный источник) com.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61) com.gale.apps.service.impl.MetadataResolverService.resolveMetadata(MetadataResolverService.java:65) com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57) ком.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController. java:22) jdk.internal.reflect.GeneratedMethodAccessor252.invoke (неизвестный источник) java.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43) java.base/java.lang.reflect.Method.invoke(Method.java:566) org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.ява: 215) org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:142) org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:102) org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895) org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:800) org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.handle(AbstractHandlerMethodAdapter. java:87) org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1038) org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:942) орг.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:998) org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:890) javax.servlet.http.HttpServlet.service(HttpServlet.java:626) org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:875) javax.servlet.http.HttpServlet.service(HttpServlet.java:733) орг.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.apache.tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain. ява: 162) org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:63) орг.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) org.apache.catalina.core. ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) орг.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:130) org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:66) org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:105) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:123) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain. java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.ява: 162) org.springframework.boot.actuate.web.trace.servlet.HttpTraceFilter.doFilterInternal(HttpTraceFilter.java:90) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) орг.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java: 99) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java: 92) org.springframework.web.filter. OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.HiddenHttpMethodFilter.doFilterInternal (HiddenHttpMethodFilter.ява:93) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.filterAndRecordMetrics(WebMvcMetricsFilter.java:154) орг.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.filterAndRecordMetrics(WebMvcMetricsFilter.java:122) org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal(WebMvcMetricsFilter. java:107) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) орг.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:200) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.java:202) org.apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97) org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542) org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve. java:143) org.apache.каталина.клапаны.ErrorReportValve.invoke(ErrorReportValve.java:92) org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.java:687) org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78) org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357) org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374) орг.apache.койот.AbstractProcessorLight.process(AbstractProcessorLight.java:65) org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.java:893) org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707) org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49) java.base/java.util.concurrent.ThreadPoolExecutor.runWorker(ThreadPoolExecutor.java:1128) Ява.base/java.util.concurrent.ThreadPoolExecutor$Worker.run(ThreadPoolExecutor.java:628) org.apache.tomcat.util.threads.TaskThread$WrappingRunnable.run(TaskThread. java:61) java.base/java.lang.Thread.run(Thread.java:834)

    фракталов — Хаос и фракталы

    Фракталы

    Проще говоря, фрактал — это геометрический объект, похожий на себя во всех масштабах.Если вы увеличите масштаб фрактального объекта, он выглядеть так же или точно так же, как оригинальная форма. Это свойство называется самоподобием. Примером самоподобного объекта является треугольник Серпенского показан ниже.

    Если приглядеться, мы заметим, что большой треугольник состоит из три меньших треугольника вдвое меньше (длина стороны) оригинала, которые, в свою очередь, состоят из трех меньших треугольников и так далее, и так далее. Во всех масштабах треугольник Серпенского точно самоподобный объект.

    Свойство самоподобия или скейлинга тесно связано с понятие размерности. На самом деле название «фрактал» происходит от свойства что фрактальные объекты имеют дробную размерность .

    Одномерный сегмент линии имеет свойство масштабирования, подобное что из фракталов. Если разделить отрезок на N идентичные части, каждая часть будет уменьшена в соотношении r  = 1/ N (например, разрезать линию на две равные части штук, и у вас есть две линии, каждая из которых имеет половину исходной длины).Точно так же можно разделить двумерный объект, например квадрат. на самоподобные части N , причем каждая часть уменьшена на коэффициент r  = 1/ N (1/2) (т.е. если вы разрежете квадрат на 4 квадрата одинакового размера, то каждый новый квадрат вдвое меньше (длина стороны) исходного квадрата).

    Понятие самоподобия естественным образом приводит к обобщению к дробной размерности. Если разделить самоподобную D-мерную объект на N меньших копий самого себя, каждая копия будет уменьшено в r раз, где

    r  = 1 / N (1/ D )

    Теперь, учитывая самоподобный объект из частей N в уменьшенном масштабе множителем r мы можем вычислить его фрактальную размерность (также называемая размерностью подобия) из приведенного выше уравнения как

    D = лог ( N ) / лог (1/ r )

    В качестве примера вычислим размерность знаменитой кривой фон Коха, которую иногда называют «снежинкой Коха». » Снежинка Коха создается простым рекурсивным геометрическим процедура:

    • разделить отрезок на три равные части
    • удалить средний сегмент (= 1/3 исходного сегмента линии)
    • замените средний отрезок двумя отрезками одинаковой длины (= 1/3 исходного отрезка) так, чтобы все они соединялись (т. е. 3 соединительных отрезка длиной 1/3 становятся 4 соединительными отрезками длиной 1/3).

    Чтобы завершить форму, описанная выше процедура повторяется бесконечно. на каждом отрезке на стороне треугольника.Изображения, показывающие процедура и полная снежинка Коха показаны ниже.

    Его фрактальная размерность дается из определения кривой: N  = 4 и r  = 1/3 (помните 4 сегмента, каждый размером 1/3 размера исходного сегмента линии).

    Размерность = логарифм (4) / логарифм (3) = 1,26

    Еще одним интересным свойством снежинки Коха является то, что она ограничивает конечную площадь с бесконечным периметром.

    Фрактал — Академические дети

    От академических детей

    Множество Мандельброта, названное в честь его первооткрывателя, является известным примером фрактала.

    Шаблон: Разговорная Википедия Фрактал — это геометрический объект, который является грубым или неправильным во всех масштабах длины и, таким образом, кажется радикальным образом «разбитым». Некоторые из лучших примеров можно разделить на части, каждая из которых похожа на исходный объект. Говорят, что фракталы обладают бесконечной детализацией, и на самом деле они могут иметь самоподобную структуру, которая возникает при разных уровнях увеличения. Во многих случаях фрактал может быть сгенерирован повторяющимся паттерном в типично рекурсивном или итеративном процессе.Термин фрактал был введен в 1975 году Бенотом Мандельбротом от латинского fractus или «сломанный». До того, как Мандельброт ввел свой термин, общее название таких структур (например, снежинки Коха) было кривая монстра .

    Фракталы многих видов изначально изучались как математические объекты. Фрактальная геометрия — раздел математики, изучающий свойства и поведение фракталов. Он описывает множество ситуаций, которые не могут быть легко объяснены с помощью классической геометрии, и часто применяется в науке, технике и компьютерном искусстве.Концептуальные корни фракталов можно проследить до попыток измерить размер объектов, для которых традиционные определения, основанные на евклидовой геометрии или исчислении, не работают.

    История

    Снежинка Коха — результат бесконечного добавления треугольников к периметру исходного треугольника. Каждый раз, когда добавляются новые треугольники (итерация), периметр растет и сходится к бесконечности.

    Дополнения к классическому анализу

    Объекты, которые сейчас называются фракталами, были обнаружены и исследованы задолго до того, как появилось это слово.В 1872 году Карл Вейерштрасс нашел пример функции с неинтуитивным свойством, заключающимся в том, что она везде непрерывна, но нигде не дифференцируема — теперь график этой функции назвали бы фракталом. В 1904 году Хельге фон Кох, недовольный очень абстрактным и аналитическим определением Вейерштрасса, дал более геометрическое определение аналогичной функции, которую теперь называют снежинкой Коха. Идею самоподобных кривых развил Поль Пьер Леви, который в своей статье 1938 года «Плоские или пространственные кривые и поверхности, состоящие из частей, подобных целому» , описал новую фрактальную кривую, кривую Lvy C.

    Георг Кантор привел примеры подмножеств реальной линии с необычными свойствами — эти канторовские множества теперь также признаны фракталами. Повторяющиеся функции на комплексной плоскости исследовались в конце 19-го и начале 20-го веков Анри Пуанкаре, Феликсом Кляйном, Пьером Фату и Гастоном Джулией. Однако без помощи современной компьютерной графики им не хватало средств для визуализации красоты открытых ими объектов.

    Аспекты описания набора

    В попытке понять такие объекты, как множества Кантора, такие математики, как Константин Каратодори и Феликс Хаусдорф, обобщили интуитивное понятие размерности, включив в него нецелочисленные значения. Это было частью общего движения первой половины двадцатого века по созданию описательной теории множеств; то есть продолжение направления исследований Кантора, сумевшего каким-то образом классифицировать множества точек в евклидовом пространстве. Определение размерности Хаусдорфа носит геометрический характер, хотя технически оно основано на инструментах математического анализа. Это направление было подхвачено, среди прочих, Безиковичем; по своему характеру она отличается от логических исследований, составлявших большую часть дескриптивной теории множеств 1920-х и 1930-х годов.Обе эти области занимались некоторое время спустя, но в основном специалистами.

    Вклады Мандельброта

    В 1960-х годах Бенот Мандельброт начал исследовать самоподобие в таких статьях, как Какова длина побережья Британии? Статистическая самоподобие и дробная размерность . Это основано на более ранней работе Льюиса Фрая Ричардсона. Используя очень наглядный подход, Мандельброт обнаружил связи между этими ранее не связанными направлениями математики. В 1975 году Мандельброт ввел слово фрактал для описания самоподобных объектов, не имеющих четкого измерения. Слово фрактал он вывел из латинского fractus , означающего сломанный или неправильный , а не от слова дробный , как принято считать. Однако само дробное в конечном итоге также получено из fractus .

    Когда компьютерная визуализация была применена к фрактальной геометрии, она представила мощный визуальный аргумент в пользу фрактальной геометрии, соединяющий гораздо более широкие области математики и науки, чем считалось ранее, особенно в области нелинейной динамики, теории хаоса (хотя некоторые вместо этого используйте термин xaos , чтобы провести различие между упорядоченным нелинейным поведением и общим значением этого слова) и сложностью.Одним из примеров является построение метода Ньютона в виде фрактала, показывающее, что границы между различными решениями являются фрактальными и что сами решения являются странными аттракторами. Фрактальная геометрия также использовалась для сжатия данных и для моделирования сложных органических и геологических систем, например роста деревьев или развития речных бассейнов.

    Категории фракталов

    Отсутствующее изображение
    Аналог Мандельброта2.png
    Увеличение в 4 раза
    350-кратное увеличение набора Мандельброта раскрывает мелкие детали, напоминающие полный набор.

    Фракталы можно разделить на три большие категории. Эти категории определяются тем, как определяется или генерируется фрактал:

    • Итерированные функциональные системы — Они имеют фиксированное геометрическое правило замены. Множество Кантора, ковер Серпинского, прокладка Серпинского, кривая Пеано, снежинка Коха, кривая дракона Хартера-Хайуэя, Т-квадрат, губка Менгера — вот некоторые примеры таких фракталов.
    • Фракталы, определяемые рекуррентным соотношением в каждой точке пространства (например, комплексной плоскости). Примерами этого типа являются множество Мандельброта и фрактал Ляпунова. Их также называют фракталами времени выхода .
    • Случайные фракталы , генерируемые случайными, а не детерминированными процессами, например, фрактальные ландшафты и полеты Лви.

    Фракталы также можно классифицировать по их самоподобию. Во фракталах встречаются три типа самоподобия:

    • Точное самоподобие — это самый сильный тип самоподобия; фрактал кажется одинаковым в разных масштабах.Фракталы, определяемые повторяющимися функциональными системами, часто демонстрируют точное самоподобие.
    • Квазисамоподобие — это свободная форма самоподобия; фрактал кажется примерно (но не точно) одинаковым в разных масштабах. Квазисамоподобные фракталы содержат уменьшенные копии всего фрактала в искаженной и вырожденной форме. Фракталы, определяемые рекуррентными соотношениями, обычно квазисамоподобны, но не совсем самоподобны.
    • Статистическое самоподобие — это самый слабый тип самоподобия; фрактал имеет числовые или статистические меры, которые сохраняются в масштабах. Большинство разумных определений «фрактала» тривиально подразумевают некоторую форму статистического самоподобия. (Сама фрактальная размерность — это числовая мера, которая сохраняется в разных масштабах.) Случайные фракталы — это примеры фракталов, которые статистически самоподобны, но не точны и не квазисамоподобны.

    Следует отметить, что не все самоподобные объекты являются фракталами — например, реальная линия (прямая евклидова линия) в точности самоподобна, но аргумент о том, что евклидовы объекты являются фракталами, занимает явное меньшинство.Мандельброт утверждал, что определение «фрактала» должно включать не только «настоящие» фракталы, но и традиционные евклидовы объекты, потому что иррациональные числа на числовой прямой представляют собой сложные неповторяющиеся свойства.

    Поскольку фрактал обладает бесконечной степенью детализации, ни один природный объект не может быть фракталом. Однако природные объекты могут проявлять фрактальные свойства в ограниченном диапазоне масштабов.

    Определения

    Определяющие характеристики фракталов, хотя и привлекательны интуитивно, чрезвычайно трудно свести к математически точному определению.Мандельброт определил фрактал как «множество, для которого размерность Хаусдорфа-Безиковича строго превышает топологическую размерность». Для полностью самоподобного фрактала размерность Хаусдорфа равна размерности Минковского-Булигана.

    Проблемы с определением фракталов включают:

    • Нет точного значения слова «слишком неправильный».
    • Единого определения «измерения» не существует.
    • Существует много способов, которыми объект может быть самоподобным.
    • Не каждый фрактал определяется рекурсивно.

    Примеры

    Деревья и папоротники имеют фрактальную природу и могут быть смоделированы на компьютере с помощью рекурсивного алгоритма. Эта рекурсивность ясна в этих примерах — возьмите ветку с дерева или ветвь папоротника, и вы увидите, что это миниатюрная копия целого: не идентичная, но похожая по своей природе.

    Относительно простой класс примеров — множества Кантора, в которых короткие, а затем еще более короткие (открытые) интервалы вычеркиваются из единичного интервала [0, 1], оставляя множество, которое может (а может и не быть) на самом деле самостоятельным. аналогичен при увеличении и может (или не может) иметь размер d , который имеет 0 < d < 1.Простой рецепт, такой как исключение цифры 7 из десятичных разложений, является самоподобным при 10-кратном увеличении, а также имеет размерность log 9/log 10 (это значение одинаково, независимо от того, какое логарифмическое основание выбрано). , показывая связь двух понятий.

    Фракталы обычно имеют неправильную ( не гладкую ) форму и поэтому не являются объектами, определяемыми традиционной геометрией. Это означает, что фракталы, как правило, содержат значительные детали, видимые в любом произвольном масштабе; когда есть самоподобие, это может произойти, потому что «увеличение масштаба» просто показывает похожие изображения. Такие наборы обычно определяются рекурсией.

    Например, нормальная евклидова форма, такая как круг, при увеличении выглядит все более и более плоской. При бесконечном увеличении было бы невозможно отличить круг от прямой линии. Фракталы не такие. Традиционное представление о кривизне, которая представляет собой обратную величину радиуса аппроксимирующей окружности, не может применяться с пользой, потому что она уменьшается. Вместо этого с фракталом увеличение увеличения показывает больше деталей, которые ранее были невидимы.

    Некоторые распространенные примеры фракталов включают множество Мандельброта, фрактал Ляпунова, множество Кантора, прокладку и ковер Серпинского, губку Менгера, кривую дракона, кривую Пеано и кривую Коха. Фракталы могут быть детерминированными или стохастическими. Хаотические динамические системы часто (если не всегда) связаны с фракталами. Множество Мандельброта содержит целые диски, поэтому имеет размерность 2. Это неудивительно. Что действительно удивительно, так это то, что граница множества Мандельброта также имеет размерность Хаусдорфа, равную 2.

    Приближенные фракталы легко найти в природе. Эти объекты имеют сложную структуру в расширенном, но ограниченном диапазоне масштабов. Эти встречающиеся в природе фракталы (например, облака, горы, речные сети и системы кровеносных сосудов) имеют как нижнюю, так и верхнюю границы отсечки, но они разделены на несколько порядков. Несмотря на повсеместное распространение, фракталы почти не изучались вплоть до двадцатого века, а общие определения появились позже.

    Харрисон [1] ( http://math.berkeley.edu/~harrison/research/publications/ ) распространил ньютоновское исчисление на фрактальные области, включая теоремы Гаусса, Грина и Стокса.

    Фракталы обычно рассчитываются компьютерами с программным обеспечением для фракталов. См. список ниже.

    Случайные фракталы имеют наибольшее практическое применение, потому что их можно использовать для описания многих очень нерегулярных объектов реального мира. Примеры включают облака, горы, турбулентность, береговые линии и деревья. Фрактальные методы также использовались для сжатия фрактальных изображений, а также в различных научных дисциплинах.

    Множество Жюлиа, фрактал, связанный с множеством Мандельброта.

    Разделение двух покрытых клеем акриловых листов образует естественный фрактал.

    Фрактальное разветвление происходит на DVD, облученном микроволновым излучением

    брокколи романеско с очень тонкими природными фракталами

    Фрактал, напоминающий цветок

    Генераторы фракталов

    Мультиплатформенный
    • Fractint — доступен для большинства платформ
    • Xaos ( http://xaos.sourceforge.net/) — Генератор реального времени — Windows, Mac, Linux и т. д.
    • FLAM3 ( http://flam3.com/ ) — усовершенствованный конструктор повторяющихся функций и визуализатор для всех платформ.
    • Fract ( http://fract.ygingras.net ) — веб-приложение для фрактального масштабирования.
    Linux
    • Gnofract4d ( http://gnofract4d.sourceforge.net/ ) — интерактивный редактор, который может использовать множество формул фрактинта.
    Окна
    • Список генераторов фракталов Fractovia ( http://www.fractovia.org/fractal_generators/index.shtml ) — достаточно полный список бесплатных генераторов фракталов.
    • Онлайн-генератор фракталов ( http://www.wackerart.de/fractal.html ) Требуется подключаемый модуль Java.
    • Ultra Fractal ( http://www.ultrafractal.com/ ) — популярная программа для Microsoft Windows
    • ChaosPro ( http://www.chaospro.de ) — для Microsoft Windows
    • MSPlotter ( http://www.aswsoftware.com/products/msplotter/msplotter.shtml ) отличный бесплатный генератор фракталов на базе Windows, использующий фракталы для создания растровых изображений и видеоклипов AVI.
    • Fractal Explorer ( http://www.eclectasy.com/Fractal-Explorer/) — бесплатный генератор на базе Windows
    • Sterling Fractal — расширенная программа для генерации фракталов Стивена Фергюсона.
    Mac
    • Altivec Fractal Carbon ( http://www.daugerresearch.com/fractaldemos/altivecfractalcarbon.html ) Утилита для сравнительного анализа на базе Mac, использующая фракталы для определения производительности.
    МорфОС
    • Zone Explorer ( http://www.elena-fractals.it/ ) Напишите свои собственные формулы, включая цвет, и быстро просматривайте свой фрактал в процессоре PPC.

    См. также

    Внешние ссылки

    Дальнейшее чтение

    • Барнсли, Майкл Ф. и Хоули Райзинг. Фракталы повсюду . Бостон: Academic Press Professional, 1993. ISBN 0-1207
        .
      • Фальконер, Кеннет. Фрактальная геометрия: математические основы и приложения .Западный Сассекс: John Wiley & Sons, Ltd. , 2003. ISBN 0470848618.
      • Юргенс, Хартмут, Хайнс-Отто Пейтген и Дитмар Саупе. Хаос и фракталы: новые рубежи науки . Нью-Йорк: Springer-Verlag, 1992. ISBN 038797903.
      • Мандельброт, Бенот Б. Фрактальная геометрия природы . Нью-Йорк: WH Freeman and Co., 1982. ISBN 0716711869.
      • Пейтген, Хайнц-Отто и Дитмар Саупе, ред. Наука фрактальных образов . Нью-Йорк: Спрингер-Верлаг, 1988.ISBN 0387966080
      ca:Фрактал

      da:Фрактал де: фрактал eo:Фрактало es: фрактал fa:برخال fi:Фрактаали fr: фрактал это: Фраттейл он: פרקטל ja:フラクタル пл: фрактал пл: фрактал пт: фрактал ru:Фрактал sl:Фрактал св:Фрактал th:แฟร็กทัล чж:分形

      7 Бесплатное программное обеспечение для создания 3D-фракталов

      Вот несколько лучших бесплатных программ для создания 3D-фракталов. Эти программы позволяют создавать 3D-фракталы и экспортировать их. Это программное обеспечение поддерживает различные типы трехмерных фракталов и позволяет генерировать их во множестве вариаций. Вы можете настроить множество параметров

      Программное обеспечение для создания фракталов — это любой тип графического программного обеспечения, которое генерирует изображения фракталов. Программное обеспечение для генерации фракталов создает математическую красоту посредством визуализации. Современным компьютерам могут потребоваться секунды или минуты, чтобы создать одно фрактальное изображение с высоким разрешением. Изображения генерируются как для симуляции (моделирования), так и для случайных фракталов для искусства. Генерация фракталов, используемая для моделирования, является частью реализма в компьютерной графике. Программное обеспечение генератора фракталов можно использовать для имитации природных ландшафтов с помощью программ создания фрактальных ландшафтов и пейзажей.Фрактальные изображения можно использовать для внесения нерегулярности в стерильную компьютерную среду.

      Вот несколько лучших бесплатных программ для создания 3D-фракталов , эти программы позволяют создавать 3D-фракталы и экспортировать их. Это программное обеспечение поддерживает различные типы трехмерных фракталов и позволяет генерировать их во множестве вариаций. Вы можете настроить множество параметров, чтобы создать желаемый фрактал и сохранить предварительный просмотр. Некоторые из этих программ позволяют сохранять фрактал в виде изображения в форматах PNG, JPEG.Вы также можете использовать другую формулу для создания окончательного фрактала в 3D-режиме.

      Apophysis 3D

      Apophysis — это редактор и визуализатор фрактального пламени с открытым исходным кодом для Microsoft Windows и Macintosh.

      Apophysis имеет множество функций для создания и редактирования фрактальных пламен, в том числе редактор, который позволяет напрямую редактировать преобразования, манипулируя треугольниками, окно мутаций, которое применяет случайные изменения к треугольникам, окно настройки, которое позволяет цвета и расположения изображения.Он также предоставляет язык сценариев с прямым доступом к большинству компонентов фрактала, что позволяет создавать такие эффекты, как анимация, наблюдаемая в Electric Sheep, которые также представляют собой фрактальное пламя. Пользователи могут экспортировать фрактальное пламя в другие программы рендеринга фрактального пламени, такие как FLAM3.

      Скачать Apophysis

      ChaosPro

      ChaosPro — это бесплатный генератор фракталов в реальном времени для MS Windows с поддержкой многих различных типов фракталов (2D и 3D), поддержкой истинного цвета, поддержкой анимации.Благодаря встроенному компилятору он работает довольно быстро, даже если вы пишете свои собственные формулы в ChaosPro.

      Особенности ChaosPro

      • Escapetime: Пиксель в окне (двухмерная точка) повторяется и проверяется, что «происходит» с пикселем. Результат отображается и окрашивается соответствующим образом. Этот тип алгоритма создает, например, множества Жюлиа и Мандельброта, но он также может создавать любой другой фрактал, основанный на повторении 2D-пикселя.

      • Аттрактор: произвольная трехмерная точка повторяется снова и снова.После каждой итерации он рисуется. Это создает трехмерные фракталы, которые отображаются соответствующим образом, включая свет и тень. Примерами таких фракталов являются фракталы IFS, фракталы пламени и многие другие.

      • Кватернион: аналогичен Escapetime, но использует числа кватерниона и алгоритм, аналогичный Escapetime, который был улучшен для трехмерного и четырехмерного пространства. Примерами таких фракталов являются кватернионы, но этот тип также идеально подходит для визуализации лампы Мандель.

      • Многозадачность и многооконность: Это означает, что ChaosPro является настоящим MDI-приложением, в котором каждый фрактал находится в отдельном окне.Вы можете рассчитать несколько фракталов одновременно в разных окнах. Различные вычислительные потоки имеют низкий приоритет, поэтому вы можете рассчитать несколько фракталов и продолжить выполнять другую работу с компьютером. Все окна в ChaosPro являются немодальными диалогами, поэтому их можно открывать по своему усмотрению. Вам не нужно закрывать какое-либо окно, чтобы открыть другое.

      • Исследование фракталов в реальном времени: вы захватываете фрактал мышью, чтобы перемещать его, и эффект виден сразу.Вы назначаете другой градиент (палитру), и он сразу же применяется, не нужно нажимать кнопку «ОК». Если вы перемещаете ползунок (например, ползунок угла поворота), фрактальная нить постоянно замечает, что ползунок изменил свое значение, и корректирует фрактал. Насколько хорошо и как быстро он догоняет изменения, зависит от того, насколько быстр ваш компьютер. Если вы измените размер окна фрактала, то фрактал будет соответствующим образом масштабирован. ChaosPro не использует модальные диалоги, все окна параметров немодальные.

      • Анимации: ChaosPro ограничивает вас не только простым увеличением/уменьшением/окружением фильмов, но и позволяет создавать анимации на основе каждого фрактального параметра в ChaosPro, в любой комбинации.Вы просто определяете ключевые кадры того, как должна выглядеть ваша анимация, указываете, сколько кадров должно быть между каждой парой ключевых кадров, а ChaosPro сделает все остальное. Ключевые кадры могут отличаться любым параметром, который можно изменять непрерывно, например, углами, значением итерации, углом поворота, параметром, значением аварийного выхода, параметрами окраски, палитрой и многими другими. Параметры, которые не могут изменяться во время анимации, например, тип фрактала или флаги: Они должны быть одинаковыми во время анимации.Но система анимации достаточно умна, чтобы не позволить вам указать ключевые кадры, которые не совпадают с другими, которые вы уже определили.

      Поддерживаемые операционные системы: Windows 98, NT, 2000, XP, Vista и Windows 7.

      Скачать ChaosPro V4.0.249

      Gnofract 4D изображения, называемые фракталами. Изображения автоматически создаются компьютером на основе математических принципов.К ним относятся множества Мандельброта и Жюлиа и многие другие. Вам не нужно заниматься математикой: вы можете исследовать вселенную изображений, просто используя мышь. Он работает в системах на базе Unix, таких как Linux и FreeBSD, а также может работать в Mac OS X.

      Особенности Gnofract 4D

      • Неограниченное разнообразие: Большинство фрактальных программ предоставляют фиксированный набор формул. Компилятор формул Gnofract 4D позволяет вам использовать любую функцию, о которой вы только можете подумать. Он также поддерживает формулы и алгоритмы раскраски Fractint и UltraFractal, поэтому вы можете использовать многие тысячи формул, написанных для этих пакетов.Взгляните на галерею для некоторых примеров.

      • Бесчисленные варианты: каждый базовый фрактал можно отображать миллионами способов, используя множество алгоритмов окраски, включая старые любимые, такие как биоморф, мощные опции, такие как орбитальные ловушки, и уникальные методы, такие как горячий и холодный. Отображение нескольких фиксированных точек, критических значений или других областей с помощью опции «судьба».

      • Простой в использовании интерфейс: современный интерфейс (с использованием набора инструментов GTK) с неограниченным количеством отмен, полноэкранным режимом, простым взаимодействием и быстрым предварительным просмотром. Щелкните здесь, чтобы ознакомиться с интерфейсом и другими снимками экрана.

      • Быстрые расчеты: поскольку все формулы перед запуском компилируются в машинный код, вы получаете быстрые расчеты даже для сложных пользовательских формул. Если у вас многопроцессорный, многопоточный или многоядерный компьютер, Gnofract 4D в полной мере воспользуется его преимуществами для еще более быстрых вычислений.

      • Четыре измерения: Что отличает его от других фрактальных программ (и делает его «4D»), так это способ, которым он рассматривает множества Мандельброта и Жюлиа как разные представления одного и того же четырехмерного фрактального объекта.Это позволяет создавать изображения, представляющие собой нечто среднее между двумя наборами, и исследовать их взаимосвязь. Если вы хотите узнать больше о математике, вы можете найти подробности в руководстве пользователя.

      • Высококачественный вывод: 24-битная цветопередача, методы окраски для плавных градиентов, сглаживание и отсутствие ограничений на размер вывода. Изображения ниже показывают разницу — первое создано Fractint, второе — Gnofract 4D.

      Скачать Gnofract 4D V4.0.1

      Fraqtive

      Fraqtive — мультиплатформенный генератор фракталов семейства Мандельброта с открытым исходным кодом. Он использует очень быстрые алгоритмы для максимальной производительности и генерирует высококачественные сглаженные изображения. Это позволяет в реальном времени перемещаться по фракталу и динамически генерировать предварительный просмотр фрактала Джулии.

      Особенности fraqtive

      • 8

        • Быстрые алгоритмы оптимизированы для современных процессоров

        • Масштабирование, движущиеся и вращение в реальном времени

        • Генерация изображений высокого разрешения и серии изображений

        • Сглаживание цвета и постобработка изображения

        • Рендеринг фрактальной поверхности в 3D режиме

        Скачать Fraqtive 0. 4.8

        Mandelbulb 3D (MB3D) Программное обеспечение для фрактальной визуализации

        Mandelbulb 3D — это бесплатное программное приложение, созданное для трехмерной фрактальной визуализации. MB3D преобразует десятки нелинейных уравнений в удивительный набор фрактальных объектов. Среда 3D-рендеринга включает в себя освещение, цвет, зеркальность, глубину резкости, эффекты теней и свечения; позволяя пользователю точно контролировать эффекты изображения.

        Загрузить «Лампу Мандельба 3D», версию 1.9.1 (Windows)

        Загрузить «Лампу Мандель3D», версию 1.9.0 (Mac)

        Mandelbulber

        Mandelbulber — это экспериментальное приложение, которое помогает сделать 3D-рендеринг фракталов Мандельброта более доступным. Некоторые из поддерживаемых трехмерных фракталов: Mandelbulb, Mandelbox, BulbBox, JuliaBulb, Menger Sponge, Quaternion, Trigonometric, Hypercomplex и Iterated Function Systems (IFS). Все это можно комбинировать в бесконечные вариации с возможностью гибридизации различных формул вместе.

        Особенности Mandelbulber

        • 3D-навигатор с инструментами, позволяющими увидеть, насколько близко камера находится к фрактальной поверхности.

        • Сложный 3D шейдинг: жесткие тени, 3 режима окружающего затенения, глубина резкости, отражения, туман, свечение, примитивные объекты и вода.

        • Светильники можно размещать вручную или случайным образом. Возможна объемная подсветка.

        • Анимация камеры: ключевой кадр и полет, управляемый мышью.

        • Ключевые кадры анимации всех параметров.

        • Объективы камеры: трехточечная проекция, «рыбий глаз» и равнопрямоугольная проекция.

        • Алгоритм оценки расстояния для сокращения времени рендеринга и уменьшения количества артефактов лучевого марша.

        • Режим малого объема памяти для рендеринга изображений размером более 16 000 x 16 000 пикселей.

        • Поддержка OpenCL в процессе

        Загрузить Mandelbulber V2

        Terragen

        Terragen — это программа для создания фракталов пейзажей для Microsoft Windows и Mac OS X, разработанная и опубликованная Planetside Software. Его можно использовать для создания рендеринга и анимации ландшафтов.Terragen — это мощное решение для создания, рендеринга и анимации реалистичной природной среды. Создавайте целые миры из своего воображения или импортируйте наборы данных ландшафта реального мира и используйте Terragen для создания максимально реалистичных визуализаций. Вы управляете погодой, ландшафтом, реками, озерами и океанами, солнцем, луной и звездами. С Terragen у вас есть полный контроль над шейдерными сетями, используемыми для ландшафтов, текстур, смещений микрополигонов, облаков и распределения объектов. Вы можете реорганизовать конвейер планетарного затенения в соответствии со своими целями.Разместите траву и деревья, где хотите, а также другие объекты в собственном формате TGO или OBJ, которые вы смоделировали в стороннем программном обеспечении.

        Особенность Terragen 4

        • Гибридный микрополигон и визуализатор с трассировкой лучей, оптимизированный для больших перемещений и очень больших ландшафтов.

        • Гибкая система глобального освещения для точного освещения в любом масштабе, от крупного до дальнего и планетарного масштаба.

        • Визуализируйте целые планеты, широкие перспективы, крошечные сады камней или что-то среднее между ними.

        • Фотореалистичная атмосфера и солнечный свет.

        • Объемные облака или быстрые облака «2.5D».

        • Многократное рассеяние в волюметрике, полное взаимодействие света между волюметрикой и поверхностями.

        • Выходной сигнал с высоким динамическим диапазоном; создавать фотореалистичные карты окружающей среды и источники IBL.

        • Качественное сглаживание и размытие в движении для быстрого и эффективного рендеринга.

        • Импорт 3D-объектов для визуализации.

        • Рендерируйте миллионы растений и других объектов с помощью создания экземпляров. Миллиарды виртуальных полигонов обрабатываются с легкостью.

        • Редактор узловых графов для максимального контроля над шейдерами и текстурами.

    Leave a comment
    by : alexxlab Графика

    Рисунок натюрморт графика: «Натюрморт в графике. Рисунок имеет самостоятельное значение в искусстве, являясь видом графики, и вместе с этим любой вид пластических искусств не может.». Скачать бесплатно и без регистрации.

    Пошаговый мастер-класс «Графический Натюрморт», 7 класс

    Пошаговый мастер-класс.

    « Графический Натюрморт»
    7 класс МОУДОД «Обуховская ДШИ»

    Преподаватель: Лабазина М.Г.

    Цель: Создание условий для художественно-эстетического развития личности ребенка, развития художественно-исполнительских и теоретических знаний, умений, навыков, учащихся в области «рисунка», составляющих фундаментальную основу для работы в различных видах искусства.
    Задачи:
    — Способствовать освоению «теоретических основ «дисциплины «рисунок», приобретение умений грамотно изображать графическими средствами предметы окружающего мира, с натуры и по памяти.

    -Развитие навыков работы графическими материалами(шариковой ручкой),в различных жанрах Изобразительного искусства(пейзаж, натюрморт, портрет).

    — Формирование навыков передачи объема и формы, четкой конструкции предметов, передачи их материальности, фактуры с выявлением планов, на которых они расположены.

    -Раскрытие творческого потенциала, а также подготовка одаренных детей к поступлению в образовательные учреждения, реализующие профессиональные образовательные программы в области изобразительного искусства.
    -Создание условий для развития коммуникативных, аналитических способностей учащихся, при выполнении, представлении, анализе авторских работ, при знакомстве с работами известных художников.

    — Создание условий для эстетического, целостного восприятия окружающего мира.

    Материал для работы:

    Ватман(А2), графитный карандаш, ластик, шариковая ручка(цвет по выбору)
    Техническое оснащение:

    — компьютер;

    — проектор;

    — презентация.

    Методы: словесный, обьяснительно-иллюстративный, практическая работа.

    Возраст детей: 12-13лет.

    1. Введение в тему.

    Графика — самый древний вид изобразительно искусства, существующего и по сей день .Первые графические работы появились на самых ранних стадиях развития человеческого общества, когда древний человек выцарапывал изображения на камнях и стенах пещер, на костяных пластинах. Создав свои первые рисунки, которые фиксировали не только какие-либо события и окружающий мир, но и долгое время служившие средством общения между людьми, первобытный человек положил начало искусству графики. Так, с помощью изображений, человек в те далекие времена излагал свою мысль.

    2 (Актуализация знаний)

    гра́фика (др.-греч. γρᾰφικός «письменный»; от γράφω «записывать, писать») — вид изобразительного искусства, использующий в качестве основных изобразительных средств линии, штрихи, пятна и точки. (Цвет также может применяться, но, в отличие от живописи, здесь он традиционно играет вспомогательную роль. В современной графике цвет может быть не менее важен, чем в живописи). При работе в графике обычно используют один или два цвета, кроме основного чёрного или белого. (слайд 3 )

    Мы представим, что у художника в руке шариковая ручка. В каком виде изобразительного искусства художник может её применить?

    Если в живописи на первом месте стоит цвет и создаваемый им колорит, а рисунок играет хоть и необходимую, но всё же вспомогательную роль, то в графике роль рисунка решающая. Рисунок является основным видом графики. А что же является средствами рисунка(Графики)?Линии, точка, штрих, пятно.(слайд5,6)

    Какими материалами пользуются художники – графики?(слайд 4)

    3 Познавательная информация.

    Все разновидности технических приемов рисунка, дошедшие до нашего времени в основном сложились в эпоху Возрождения в Италии. Уже тогда в рисунке применялись свинцовые, серебряные, и другие металлические грифели (штифты), графит, итальянский карандаш, сангина, уголь, мел, пастель, а так же жидкие материалы – бистр, тушь, разноцветные чернила, акварель, белила. Рисовали гусиными и тростниковыми перьями, кистями на белой бумаге разнообразных цветов, тонированной и грунтованной. Все это привело к исключительному богатству художественных и технических приемов. Один из современных технических приемов в графике, это рисунок шариковой или гелиевой ручкой. Эту технику в своих работах широко используют современные художники: Андрей Полетаев (- художник, который рисует шариковой ручкой), Самуэль Сильва(цветные гелиевые ручки), Juan Francisco Casas,и. т.д. Художник из Малайзии Винс Лоу создаёт реалистичные портеры знаменитостей расписывая свою авторучку. Но главная особенность его художеств в том, что он не отрывает ручку от листа бумаги! Это по истине шедеврально, ведь этот художник придумал свой собственный стиль рисования! Свою коллекцию портретов знаменитостей он назвал «Faces» («Лица»)

    Мы начнем знакомиться с данной техникой , выполняя задание по академическому рисунку в жанре «натюрморт»

    4 Ход работы.

    Пошаговый мастер-класс. «Графический Натюрморт» шариковой ручкой».(слайд 7)

    При работе над натюрмортом, нам понадобится приготовить рабочее место (слайд 8.)

    1 Мольберт

    2 Стул

    3 Постановка (натюрморт)

    4 Специальное освещение
    5 Прикрепить лист ватмана (формат А2)

    6 Приготовить ручки(цвет синий или черный)


     

    1 Этап : конструктивное построение натюрморта с натуры, графитным карандашом. Компоновка изображения предметов в листе, выбор формата. Применение в рисунке основных правил перспективы. Грамотная постановка предметов на плоскости. Выявление объема предметов и пространства в натюрморте. Построение двух несущих плоскостей, грамотное построение предметов на них.

    (слайд 9)

    2 Этап : Штриховка шариковой ручкой. Передача освещения, объёма и фактуры. Используется разное нажатие на ручку;Штриховка в разных направлениях. Возможно использование различных линий и точек, для передачи фактуры. Работа над материальностью, передачей пространственности, освещения и взаимодействия этих элементов среды с предметами в них находящимися. Передача больших тональных отношений Светотеневая моделировка.

    (слайд 10.)


    3 Этап : Детализация. Передача свето-воздушной среды, усиление контраста на ближнем плане. Требование реалистичного изображения по законам «перспективы». Цельность изображения натюрморта. Максимальное завершение работы в тоне, светотеневая моделировка ,передача материальности.(слайд 11.)Графика
    PPTX / 16. 17 Мб


    Графика
    PPTX / 16.17 Мб

    Источники:

    http://www.liveinternet.ru/community/

    http://svonok.ucoz.ru/index/natjurmort_v_grafike/0-100

    http://encyclopaedia.biga.ru/enc/culture/GRAFIKA.html

    https://4tololo.ru/content/2791

    20 невероятных картин, написанных обычной шариковой ручкой

    http://www.liveinternet.ru/users/3864871/post233636327/

     http://xexe.club/120912-andrey-poletaev-hudozhnik-kotoryy-risuet-sharikovoy-ruchkoy

    Урок 9. натюрморт в графике. цвет в натюрморте. выразительные возможности натюрморта — Изобразительное искусство — 6 класс

    «Изобразительное искусство»

    «6» класса

    Урок № 09. Натюрморт в графике. Цвет в натюрморте. Выразительные возможности натюрморта

    Перечень вопросов, рассматриваемых в теме:

    Что такое гравюра, каковы её виды и особенности печатной графики? Различные графические техники.

    Новое понимание выразительных возможностей цвета в изобразительном искусстве XIX—ХХ вв.

    Колористический образ, выразительные возможности цвета в натюрмортах известных художников.

    Значение отечественной школы натюрморта в мировой художественной культуре.

    Глоссарий по теме:

    Печатная графика – это особый вид графики, когда с одного рисунка, сделанного специальными инструментами на доске из дерева, металла или линолеума, можно сделать несколько авторских отпечатков – оттисков.

    Гравюра — вид печатной графики.

    Виды гравюры: на дереве – ксилография, на металле – офорт, на линолеуме – линогравюра, даже на камне – литография

    Основная и дополнительная литература по теме урока:

    1. Неменская Л. А. Изобразительное искусство. Искусство в жизни человека. 6 класс: учеб. для общеобразоват. организаций / Л. А. Неменская; под ред. Б. М. Неменского. – 10-е изд. перераб. и доп. – М.: Просвещение, 2019. – 191 с.: ил. – ISBN 978-5-09-071640-6 – С. 62-67.

    Открытые электронные ресурсы по теме урока:

    1. 5 натюрмортов «Бубнового валета» [Электронный ресурс]. – Режим доступа: https://www.culture.ru/materials/253440/5-natyurmortov-bubnovogo-valeta (дата обращения: 18.08.19)

    2. Скуратова О. Борис Михайлович Неменский — художник и воин // Искусство, 2007, №7.

    Теоретический материал для самостоятельного изучения

    Рисунок – основной вид графики. Рисунок необходим всем художникам как этап работы. Рассмотрим особый вид графики – печатную графику, когда с одного рисунка, сделанного специальными инструментами на доске из дерева, металла или линолеума, можно сделать несколько авторских отпечатков – оттисков. Такой вид графики называется гравюра. Гравюра бывает разной: на дереве – ксилография, на металле – офорт, на линолеуме – линогравюра, даже на камне – литография.

    В конце XIX века интерес к натюрморту возрос невероятно. К этому жанру обратились очень многие художники, потому что натюрморт стали понимать как способ поиска и выражения нового видения мира. Главным выразительным средством в живописи стал цвет.

    Новую свободу выражения открыли французские художники второй половины XIX в. Определяющим в развитии натюрморта явилось творчество Поля Сезанна. Живопись он понимал как средство выражения своих ощущений через цвет. Одновременно с Сезанном жил Винсент Ван Гог. Он приходит к идее, что краски палитры живописца не должны совпадать с красками природы. Важно, чтобы общее цветовое построение полотна отвечало эмоциональному восприятию натуры художником и возбуждало такие же переживания у зрителя. Самым ярким из французских художников конца XIX – первой половины ХХ веков был Анри Матисс. Нарядность цвета его картин кажется фантастической.

    В начале XX века в Москве было создано объединение молодых художников «Бубновый валет». В основу творчества художников легло любование предметным миром, а одним из самых популярных жанров стал натюрморт. Учителем для многих стал французский постимпрессионист Поль Сезанн. В своих картинах художники делали акцент на форме предмета, его массе и цвете.

    Цвет способен создавать настроение – печальное или радостное, вносить бурный драматизм или спокойствие, ясность или тайну. Цвет помогает ощутить среду, освещение, воздух, его резкость или мягкость, чистую прозрачность или туманную густоту.

    Всякий натюрморт строго организован художником, а не просто списан с натуры, и все выразительные средства изобразительного языка раскрывают задуманный образ. Примерами таких натюрмортов являются натюрморты-памятники: «Память смоленской земли» Бориса Неменского, «Натюрморт с хлебом» Владимира Стожарова.

    Примеры и разбор решения заданий тренировочного модуля:

    1. Какие виды гравюры Вы знаете? Выберите все правильные ответы.

    Ксилография

    Офорт

    Литография

    Линогравюра

    Вазография

    Галография

    Правильные варианты:

    Ксилография

    Офорт

    Литография

    Линогравюра

    2. Выделите цветом примеры французской живописи XIX — ХХ вв.

    П. Сезанн. НАТЮРМОРТ С ДРАПИРОВКОЙ. Масло. XIX в.

    В. Ван Гог. ПОДСОЛНУХИ. Масло. XIX в.

    А.Матисс. НАТЮРМОРТ С КЛЕТЧАТОЙ СКАТЕРТЬЮ. Масло. ХХ в.

    Р. Р. Фальк. КРАСНАЯ МЕБЕЛЬ. Масло. ХХ в.

    К. Малевич. НАТЮРМОРТ. Акварель, гуашь. ХХ в.

    Правильные варианты:

    П. Сезанн. НАТЮРМОРТ С ДРАПИРОВКОЙ. Масло. XIX в.

    В. Ван Гог. ПОДСОЛНУХИ. Масло. XIX в.

    А.Матисс. НАТЮРМОРТ С КЛЕТЧАТОЙ СКАТЕРТЬЮ. Масло. ХХ в.

    Станковая графика — Искусствоед.ру – сетевой ресурс о культуре и искусстве

    Просмотры: 42 940

    К станковой графике относятся произведения графического искусства, имеющие самостоятельное значение. Они не связаны с литературным текстом (как, например, книжная графика) и не имеют узкого практического назначения (как, например, произведения прикладной графики). Станковой эта группа графики называется по аналогии со станковой живописью, произведения которой создаются на специальном станке – мольберте. Для станковой графики характерны широта тематики и разнообразие изобразительных средств. Чтобы разносторонне раскрыть избранную тему, графики нередко создают целые серии станковых произведений. Все листы таких серий объединены не только общей темой, но и приемами исполнения.

    Станковая графика условно делится на рисунок и эстамп. В свою очередь рисунок обычно рассматривают, с одной стороны, как оригинальное произведение графики (уникальная графика), а с другой стороны, как вспомогательный вид. Существует огромное множество узких определений вспомогательного рисунка: учебный рисунок, академический рисунок, подготовительный рисунок и т.п. Грани между различными видами весьма туманны, и в рамках данного пособия раскрыть их общие черты и различия проблематично. Лишь отметим, что рисунком называют изображения самого различного характера, исполненные самыми разными материалами на разных поверхностях и выполняющие различные функции, – на том основании, что ведущая роль в них принадлежит линии. В дальнейшем речь пойдёт только о рисунке в его особом, самостоятельном явлении искусства графики.

    «Собственно» рисунок сложился совсем недавно по сравнению с рисунком, понимаемым как всякое изображение линиями (который и является самым древним, самым первым способом изображения).

    Х.Грин. Рисунок.Перо, бистр, 1503.

    Становление рисунка как особой сферы художественного творчества вызвано причинами, возникшими на той ступени развития общества и искусства, которая получила название эпохи Возрождения. Три момента имели решающее значение для появления и быстрого расцвета рисунка: гуманизм, противопоставивший религиозным идеалам культ человека; познание природы, развитие наук; изменения в самом искусстве, обусловленные характером и достижениями новой эпохи, в том числе изучением памятников античности. Важнейшими среди этих изменений были: индивидуализация творческого процесса в противовес опыту коллективной работы средневековых мастеров; расширение тематических границ, развитие светского направления, общий светский характер искусства; стремление создавать произведения на научной основе; сложение новой системы художественного видения, когда изображение стало строиться как реальная картина визуально воспринимаемой действительности; наконец, интенсивное развитие станковой живописи, графики и скульптуры.

    В этих условиях рисунок стал незаменимым орудием художника для достижения многих целей: для изучения натуры и приёмов её изображения на плоскости, разработки научных основ изобразительного творчества, «записи» наблюдений, впечатлений, мыслей, фантазий, для подготовки к созданию живописных и других произведений. И в это же время исполнялись рисунки, имеющие совершенно независимый характер. Рисунок стал использоваться столь широко и многообразно, он столь полно раскрыл свои возможности и достиг таких художественных высот, что это позволяет утверждать: именно в эпоху Возрождения рисунок становится особым, самостоятельным явлением искусства.

    Новый художественный принцип – подражание природе – и новый принцип создания произведений – свобода от канонов, свобода

    А.Дюрер. Рисунок. Перо, бистр, 1511.

    сочинения, вымысла – позволили, наконец, развиться двум главным специфическим способностям рисунка: быть самой прямой – в сфере художественного изображения – связью руки и глаза и самой прямой связью руки и мысли. Два направления становятся главенствующими: рисунок с натуры как незаменимое средство постижения реальности и способов её изображения на плоскости и рисунок как непосредственное выражение размышлений и переживаний художника, как средство разработки индивидуальных замыслов. Они и раскрывают в основном особенности освоения мира в рисунке.

    В то же время рисунок привлекал художников и как форма творчества, которая способна и достойна воплощать значительные замыслы, предназначенные специально для него. Большой силы и высоты самостоятельный станковый рисунок достиг в творчестве Андреа Мантеньи, который разработал своеобразный тип рисованного изображения, приближающегося по композиции и характеру моделировки к барельефу, а по духу – к античным образцам. Поллайоло в рисунках «Адам» и «Ева» обратился к сюжетам, которые позволили ему сделать изображения мужского и женского обнажённого тела основой станкового рисунка. Микеланджело Буонаротти исполнил целый ряд рисунков на темы античных мифов «Падение Фаэтона», «Ганимед», «Наказание Тития», А. Альтдорфер и Х.Грин – многочисленные листы на религиозные и мифологические сюжеты, венецианские и нидерландские художники создавали пейзажи, отличающиеся масштабностью, разработанной композицией, завершённостью исполнения.

    Тициан. Женский портрет. Уголь.

    Таким образом, в эпоху Ренессанса рисунок обрёл всю полноту проявления, всё многообразие своих форм. Особенно ярко это раскрывается в творчестве художников Высокого Возрождения, о чём можно судить по рисункам таких титанов итальянского и Северного Возрождения, как Леонардо да Винчи и Дюрер.

    С освоением в конце XV века таких инструментов, как уголь (после изобретения способов его фиксирования), итальянский карандаш (или чёрный мел), в рисунок пришла широкая, монументальная манера изображения. Линии перестают быть столь чёткими и определёнными, они переходят в тон, сливаются с моделировкой. Складываются два различных подхода к изображению, два способа передачи формы: объёмный и живописный. При первом, развитом в творчестве художников большинства итальянских школ, форма выделяется чётким

    Станковый рисунок. Р.Хачатрян. Натюрморт. Левкас, сепия, 1982.

    контуром и моделировкой объёма; при втором – контуры и сама форма словно бы растворяются, расплавляются в окружающем воздушном пространстве. Живописный, или тональный, рисунок (так как в нём большую, а часто и основную роль играют пятна того или иного тона) характерен в основном для венецианских художников – Джорджоне, Тициана, Тинторетто; в нём достигается передача воздушной среды, вибрации света, динамики форм. Использование сангины, сочетание нескольких техник, применение грунтованной бумаги различных цветов, на которой рисовали чёрным тоном и белилами, создали в рисунке свою полихромию, свои проблемы цвета и тона, свою колористическую выразительность. Всё это широко раздвинуло возможности рисунка и сделало его способным к несению только ему присущего художественного образа.

    Поворотным моментом в развитии рисунка стало использование бумаги. Как отметил А.А.Сидоров, «вытеснение пергамента бумагою и есть одна из тех решающих перемен, которые определяют собой прогресс искусства, не только рисуночного». Появление в XIV веке этого дешёвого материала (в Китае бумага известна с 105 г. н.э.) дало возможность художникам создавать пробные, вспомогательные зарисовки, подготовительные работы, рисунки для себя. В этих случаях художник мог рисовать свободнее, острее, индивидуальнее, что способствовало сложению личного стиля мастера и определило разработку специфического языка рисунка.

    Свободный рисунок. Е.Забелина. Деревня. Учебная работа. Карандаш, 1999.

    Безусловно, на всём протяжении развития рисунка происходили различные – и в том числе существенные – изменения в его характере; но, как представляется, эти изменения не дают возможности говорить о принципиально новом положении рисунка в какой-либо из эпох после Возрождения. Основание к этому в известной степени даёт рисунок рубежа XIX и XX веков, когда произошла смена художественных систем и графика окончательно сложилась как вид искусства.

    Специфической особенностью рисунка является многообразие и многозначность его форм. Следует отметить наиболее часто встречающиеся типы рисунка: станковый, свободный, подготовительный, композиционный. Станковый рисунок представляет собой однородное по своему характеру, своей структуре произведение, которое для воплощения замысла специально построено и завершено само в себе. Такое произведение замкнуто на выражении определённой идеи, определённого суждения о мире и при этом завершено с точки зрения художественного воплощения этой идеи.

    Простота материалов и процесса изображения позволяют создавать рисунки непосредственно в тот момент, когда у художника возникает стремление запечатлеть своё наблюдение, мысль, представление. Такие рисунки – а их огромное множество – не имеют в своей основе

    Пример самостоятельного этюда.
    А.Филипович. Мирский замок. Учебная работа. Тушь, перо, 1996.

    замысла и не обладают чертами, обусловленными его воплощением; движущий мотив их создания можно назвать побуждением, а сами рисунки – свободными. Они характеризуются именно свободой исполнения, передают прямое общение художника с окружающей действительностью, непосредственное выражение его впечатлений, чувств, фантазий. В них реализуется потребность художника в постоянном живом контакте с миром. Если станковые рисунки выражают определённое суждение о жизни, понимаемое как слитность переживания, осмысления и оценки, – точнее, как некая идея, рождаемая этой слитностью, то свободные рисунки можно сравнить с отдельными высказываниями; эти высказывания раскрывают отношение человека к миру, но не имеют той углубленности и завершенности, которые свойственны суждению.

    Среди самостоятельных работ, помимо станковых и свободных рисунков, принято выделять такой тип произведений, как самостоятельные этюды. Они служат средством изучения окружающего мира в различных его проявлениях,

    И.Е.Репин. Композиционный рисунок к картине «Арест пропагандиста». 1879.

    создания «багажа» наблюдений, впечатлений, средством совершенствования мастерства; с помощью этюдов происходит художественное освоение самых разных элементов окружающего мира. Однако и для таких работ во многих случаях характерна типологическая неопределенность, невозможность отделить их от станковых рисунков.

    Подготовительные этюды и эскизы, составляющие огромную часть рисунков, также чрезвычайно неоднородны по своему характеру и неоднозначны по восприятию. В рисунках этих типов предмет освоения двойствен: в эскизах это и композиция как таковая, её разработка для воплощения замысла произведения другого вида искусства, и сам сюжет; в этюдах это и персонаж картины или фрески, и натура, которая служит моделью для этого персонажа. Соотношение этих «составляющих» в конкретных рисунках различно, что создаёт неоднородность рисунков внутри каждого типа.

    Каллиграфический
    рисунок. П.Семченко. Роза. Тушь, перо, 1992.

    Композиционный рисунок, который как тип является аналогом картины, не оттесняет произведения других типов, не обладает бесспорным правом представлять собой рисунок как явление искусства: и на выставках, и в

    В. Серов. Подготовительный рисунок к картине «Похищение Европы». 1910.

    музеях, и в воспроизведениях мы обычно видим рисунки всех типов. Может быть, именно положение композиционных работ среди типов рисунка и их несравненно меньшее развитие особенно наглядно выражают иной характер рисунка по сравнению с другими видами.

    Особую роль в структуре мира рисунка играет набросок. Набросок – специфически рисуночный тип художественного произведения. Он развит только в рисунке, и развит очень широко; особенности рисунка раскрываются в нём наиболее обнаженно, предстают в своем крайнем выражении.

    Как тип рисунка набросок неоднозначен. С одной стороны, он как будто не является отдельным типом, поскольку представляет собой либо эскиз, либо этюд, либо самостоятельный рисунок. То есть набросок можно рассматривать как манеру изображения, в которой, кроме того, бывают также исполнены и литографии, и офорты, особенно в XX веке. Но, с другой стороны, в различных по характеру набросках ощущается своя, единая основа, которая позволяет говорить о нём как о типе произведений, но типе особом: он является как бы точкой схода различных по назначению и характеру рисунков; в нём и сохраняются типологические отличия, и обретается общая направленность. Эта направленность – в схватывании, выделении, заострении главного, что интересует художника в изображаемом объекте.

    Н.Совца. Набросок.
    Учебная работа.
    Карандаш, 2002.

    Говоря о рисунке, следует отметить особым типом каллиграфический рисунок. Он представляет собой конкретное изображение образа по памяти точным и непрерывным движением пера или иного инструмента. Предшествует этому глубокий анализ натуры. Для каллиграфического рисунка характерна стилизация формы через неповторимую, плавную, изменчивую и пластичную линию, которая условно и ассоциативно выражает графический образ.

    Кроме многообразия типов, разнообразны и материалы рисунка. Нам известно много замечательных произведений графики в технике карандаша. Художники пользуются довольно разнообразным ассортиментом

    П.Шмидт. Толпа. Карандаш, 1928.

    карандашей. Самыми распространенными являются графитные карандаши различных степеней мягкости. Штрих графического карандаша отличается красивым серым тоном и имеет легкий отблеск. Очень красивый насыщенно черный и бархатный штрих дают так называемые итальянские и угольные карандаши. Нередко графики работают карандашами, изготовленными из цветных пигментов (сангина, цветные меловые карандаши и др.). Карандаш – материал очень гибкий, послушный и позволяющий разнообразно работать в пределах небольшого листа.

    Уголь является излюбленным материалом многих художников. Угольный рисунок обычно выполняется на шероховатой бумаге, а иногда на холсте, и отличается красивым бархатистым тоном, широким и энергичным штрихом.

    Часто встречается в графике соус – рисовальный материал из очень мелкого черного порошка, скрепленного клеящим веществом. Иногда соус применяется в виде сухого порошка, но чаще всего разбавляется водой.

    К.Кольвиц. Обнаженная. Уголь, 1904.

    Особым качеством обладает перьевой рисунок. Работает художник разбавленной тушью или специальными чернилами,

    Фешин. Портрет. Уголь.

    применяя обычные стальные, а также гусиные и тростниковые перья, особым способом затачивая их. Перьевой рисунок красив своей четкостью, чистотой и изяществом разнообразных по форме штрихов.

    Широко распространен в графике прием рисования жидкими черными материалами (чаще всего тушью) при помощи кистей, так называемого фетрового пера или заточенных деревянных палочек. Этот прием отличается очень разнообразным, свободным и темпераментным сочетанием штрихов одного глубокого черного тона.

    Но особенно широко распространена в графике работа тушью, черной акварелью, гуашью, темперой и другими черными материалами, разбавленными водой. Бесконечны тональные нюансы этой техники. Необычайного совершенства достигли в этой области китайские мастера. Трудно передать все богатство этой техники. В одних местах рисунка художник быстрым и точным движением наносит тушь более сухой кистью, тушь не успевает расплыться на бумаге и ложится четко. В других местах влажная кисть намеренно дольше задерживается на бумаге, тушь расползается и дает мягкие, расплывчатые сочные пятна.

    П.Митурич. Ель. Тушь, кисть, 1948.

    Рисунки выполняются не только в какой-нибудь одной технике. Очень часто графики в одной работе сочетают две, три и даже большее

    Р.Хачатрян. Портрет. Картон, сепия, 1978.

    число различных техник, что расширяет творческие возможности и обогащает запас изобразительных средств художника. Нередко станковые произведения выполняются черным материалом с применением цвета в характерной для графики сдержанной, скупой манере цветовых решений.

    Великолепные образцы станковых рисунков создали итальянские мастера Микеланджело, Леонардо да Винчи, Рафаэль, Тинторетто, немецкие художники Гольбейн, Дюрер, Менцель, голландские и фламандские мастера Рембрандт, Рубенс, Ван Дейк, французские художники Ватто, Фрагонар, Энгр, Домье и многие другие художники различных стран мира.

    Из русских художников прошлого назовем таких мастеров рисунка, как О.Кипренский, А.Иванов, П.Федотов, И.Репин, В.Серов, М.Врубель. Среди графиков Беларуси видное место занимают А. Тычина, Л.Ран, В.Соколов, С.Романов, Г.Поплавский, В.Савич, В.Шарангович, М.Басалыга, А.Кашкуревич и др.

     

     

    Пикассо. Голова женщины. Тушь, перо, 1924.Сюй Бэй-хун. Быстро скачущая лошадь. Тушь, кисть, 1930.Рембрандт. Пейзаж. Бистр, перо, кисть, 1630.О.Кипренский. Портрет Е.Чаплица. Итальянский карандаш, 1813.

    Вконтакте

    Facebook

    Twitter

    Google+

    LiveJournal

    Одноклассники

    Мой мир

    Играем с фигурами в Procreate: иллюстрируем графический натюрморт | Сара Бет Морган

    Стенограммы

    1. Трейлер класса. Вы когда-нибудь хотели сделать иллюстрации более наглядными, но не знали, с чего начать? Я тоже когда-то с этим боролся. Но, проходя через этот процесс снова и снова, я, наконец, открыл для себя несколько простых приемов, которые теперь использую каждый день. Привет. Меня зовут Сара Бет Морган, я фрилансер, режиссер и иллюстратор из Портленда, штат Орегон. Обычно я работаю в области моушн-графики, но мне нравится заниматься иллюстрацией. Procreate — замечательный инструмент для иллюстраторов, и здесь я хочу немного рассказать вам о моем процессе в Procreate. Кажется, что для создания графического вида может потребоваться наметанный глаз, но на самом деле это довольно просто, если разбить его шаг за шагом. На этом уроке я покажу вам, как создать графическую иллюстрацию натюрморта. Мы начнем с листа для разминки, чтобы изучить некоторые основные приемы. Оттуда вы возьмете свою собственную фотографию и превратите ее в графические формы.Я покажу вам несколько способов изменить вашу композицию, пока я рисую. Наконец, вы закончите свой натюрморт цветами и деталями. Этот курс наполнен полезными практическими советами по улучшению вашего рабочего процесса в Procreate, развитию внимательности к макету и композиции и лучшему развитию, превращению повседневных сцен в сногсшибательные абстрактные иллюстрации. Вместо того, чтобы сосредотачиваться исключительно на технических аспектах Procreate, я буду углубляться в принципы и модели мышления, лежащие в основе разработки графических иллюстраций, на которых я специализируюсь. Этот класс для вас, если вы творческий человек любого уровня, который хочет научиться включать в свою работу более графический стиль. Эти простые для понимания уроки подготовят вас как к любимым проектам, так и к работе с клиентами. В конце концов, вы покинете этот класс со своим игривым графическим натюрмортом и некоторыми новыми творческими ноу-хау, которые вы сможете использовать для своего следующего проекта. Ладно, ладно, приступим. 2. Начало работы. Как дизайнер и иллюстратор в киноиндустрии, я всегда любил смешивать графический дизайн и иллюстрацию.Я играл с иллюстративными коллажами, шрифтовым дизайном, супер органичными иллюстрациями и плоскими двухмерными геометрическими иллюстрациями. Однако из всего этого мне больше всего нравится создавать абстрактные графические иллюстрации. Это работа, которую я обычно публикую в своих социальных сетях. Для меня этот стиль включает в себя использование основных геометрических фигур для создания узнаваемых предметов, таких как использование идеальных кругов для рисования апельсинов или чистого прямоугольника для изображения грузовика доставки в перспективе. Сегодня я покажу вам свой процесс графической иллюстрации от начала до конца.Давайте начнем. Для этого класса вам понадобится iPad, Apple Pencil и Procreate 5.1. Если вы хотите продолжить работу в Photoshop, Illustrator или любой другой программе, это полностью зависит от вас. Многие советы и приемы, которыми я поделюсь в этом классе, в большей степени основаны на концепции и не обязательно являются техническими и основаны только на использовании Procreate. Вы должны иметь некоторые практические знания о Procreate, прежде чем приступить к этому классу. На самом деле я не буду вдаваться в подробности того, как я использую программу, я просто буду использовать ее для выполнения каждого из описанных здесь шагов.Если вы хотите немного узнать об основах, прежде чем приступить к делу сегодня, я настоятельно рекомендую пройти один из курсов Брук Глейзер по Procreate здесь, на Skillshare. Она превосходна, и именно так я выучил программу. Для сегодняшнего классного проекта мы создадим натюрморт из предметов домашнего обихода, которые вы найдете в своем доме, возьмем эту фотографию натюрморта, перенесем ее в Procreate и сократим до самых основных форм для создания иллюстрации. Поиграв с композицией, пропорциями, наложением и всем этим, мы перенесем наш набросок из черно-белого в цветной.Мы даже добавим текстуру, чтобы создать окончательный вид. Я даже поделюсь несколькими советами о том, как поделиться своей работой в Instagram с помощью любимого социального инструмента. Но прежде чем мы приступим к этому, я проведу вас через небольшую разминку и познакомлю вас с принципами, которые мы будем использовать на этом занятии. 3. Разминка. Прежде чем мы на самом деле начнем создавать собственные натюрморты, я создал для вас небольшую разминку, которую вы можете использовать в этом разделе этого класса. Загрузите его ниже в ресурсах класса. Это просто изображение в формате JPEG, поэтому все, что вам нужно сделать, это добавить его на свой холст в Procreate и уменьшить непрозрачность, чтобы мы могли рисовать поверх него.Я просто собираюсь загрузить рабочий лист в Procreate, зайдя в меню, вставив фотографию, а затем выбрав ее из своих фотографий, потому что я уже загрузил ее. Как видите, у него уже низкая непрозрачность, поэтому я просто создам новый слой, чтобы рисовать поверх него. Но прежде чем мы начнем рисовать, давайте включим руководство по рисованию. Если вы хотите включить руководство по рисованию, перейдите к маленькому гаечному ключу, затем нажмите «Холст», а затем выберите «Руководство по рисованию», а затем вы также можете отредактировать руководство по рисованию. Лично я предпочитаю сохранять его с более низкой непрозрачностью и менять его цвет, чтобы он сильно отличался от цвета кисти, которую я использую, поэтому я не путаюсь и просто нажимаю «Готово».» Руководство по рисованию поможет вам выровнять композицию и убедиться, что все идеально вертикально или горизонтально. Это обеспечит более графичный вид. Не стесняйтесь включать помощь рисования на вашем конкретном слое рисования, если вы хотите создать идеально прямую линию или форма. Если я перейду к слою и появится это маленькое меню, нажмите «Помощь в рисовании», мое перо решит работать. Теперь вы можете видеть, что на слое написано «Помощь», выберите свою кисть, и тогда она будет рисовать только по вертикали. и горизонтальные линии, что отлично, если вы пытаетесь получить идеально прямую линию.Я просто дважды коснусь, чтобы отменить, а затем начну с нашей первой фотографии. Я покажу вам абсолютные основы того, куда мы движемся с этим рабочим листом. Одно из моих любимых занятий — это делать свои собственные референсные фотографии и использовать для рисования настоящие предметы из жизни. Вот что я сделал здесь, я сфотографировал объекты, которые находятся вокруг моей студии, я предоставил четыре объекта, которые я нашел. Просто забавные маленькие повседневные предметы. Здесь мы сосредоточимся на том, чтобы разбить эти объекты на самые основные формы, используя простые формы, такие как эллипсы, прямоугольники и треугольники.Лучший способ сделать это в Procreate — использовать функцию быстрой формы, которая, по сути, встроена в то, как вы используете инструмент «Кисть», что немного упрощает все. Просто убедитесь, что вы выбрали кисть, и она будет работать именно так, как вы хотите. Если вы уже знаете Procreate, вы, вероятно, знаете это. Быстрая форма: если вы создаете эллипс, вы рисуете фигуру, которая смутно похожа на эллипс, а затем удерживаете ее, а затем можете нажимать другим пальцем, чтобы создать более совершенную форму.Или вы также можете перейти в это меню «Редактировать фигуру» здесь и выбрать «Эллипс», который больше не будет кругом. Или вы можете сделать прямоугольник, удерживать его, и тогда, очевидно, это будет несовершенная форма. Но если я хочу сделать его прямоугольником, я могу нажать «Прямоугольник», и края станут более идеально горизонтальными и вертикальными, чтобы создать форму прямоугольника. Я просто собираюсь отменить это. Это то, что мы будем использовать здесь, когда будем работать с каждым из этих объектов. На этом этапе я не хочу, чтобы вы думали о том, хорошо ли выглядит ваш объект, пока мы просто разбиваем формы.Я просто начну с этого первого здесь. Я не собираюсь делать прямоугольники со скругленными углами, потому что у них нет этой функции. Я просто собираюсь начать с создания прямоугольника для этой центральной фигуры. Вы также можете отредактировать края прямоугольника, если хотите, чтобы он ближе подходил к краю объекта, и на самом деле он уменьшит непрозрачность изображения за ним, так что это немного проще. Затем это также разобьется на еще пару прямоугольных форм. Как я уже сказал, не беспокойтесь о том, выглядит ли это идеально прямо сейчас.Мы просто пытаемся получить что-то очень простое. Если я отключу фоновый слой, все станет немного асимметричным и не будет слишком ценным с ним. Но у нас есть очень абстрактная версия этого объекта. Давайте просто пройдемся и сделаем это для каждого из них. Если вы хотите, чтобы некоторые фигуры были точно такими же, вы можете продублировать свой слой, просто проведя пальцем и нажав «Дублировать», а затем вы можете использовать инструмент выделения, чтобы переместить его и повернуть с помощью этой зеленой ручки. Очевидно, я хочу, чтобы обе стороны этих наушников были одинаковой формы, поэтому я просто дублирую их там.Когда вы используете это, убедитесь, что у вас включен Bicubic, что сделает ваши формы не слишком нечеткими при изменении размера. Для этой округлой формы здесь я мог бы сделать что-то вроде эллипса, просто отредактировав его, чтобы он соответствовал. На самом деле я могу сделать его прямым кругом, если хочу быть более абстрактным, а затем даже продублировать его. У меня есть меньший круг внутри моего большего круга, и затем я на самом деле собираюсь просто объединить эти два слоя, а затем стереть ненужные фрагменты.Этот еще интереснее, потому что у него странные формы. Но я просто собираюсь начать с моих основных прямоугольников и эллипсов, и через минуту мы углубимся в суть того, как сделать так, чтобы это выглядело лучше. Что касается основания ножниц, я на самом деле просто делаю его треугольником, потому что это, по сути, то, чем они являются. Затем для таких фигур, которые труднее разбить, вы можете разбить их еще ниже, сделать эту верхнюю часть эллипсом, а затем нарисовать остальные. Мы можем упростить этот кактус еще больше, вместо того, чтобы делать прямой эллипс для перспективы этой вазы, или горшка, или чего бы то ни было, мы могли бы просто сделать полный фронтальный вид. Здесь немного используем наше воображение и просто нарисуем прямоугольник. Для этого я на самом деле включу Помощник по рисованию, чтобы все выровнялось идеально. Мне не нравится то, что я там делал. Я собираюсь включить это в произвольной форме и немного сдвинуть стороны. Я собираюсь создать меньшую базу. Затем для растений я собираюсь упростить их еще больше, и я просто собираюсь использовать больше прямоугольников. Я также включу помощь по рисованию на этом слое и просто буду повторять формы, которые вижу.Как видите, все формы очень упрощены и разбиты. Но это не то, где мы останавливаемся. Когда у вас есть все эти плавающие странные эллипсы, треугольники и прямоугольники, начинается самое интересное. Именно здесь происходит абстракция, когда мы создаем эстетически приятные графические версии этих повседневных предметов. Для этого начните стирать ненужные вам линии. На самом деле я собираюсь просто сгладить все прямо сейчас, потому что нам не нужны все эти фигуры по отдельности, мы просто делаем наброски прямо сейчас, поэтому я не очень беспокоюсь о том, что все будет разделено. Я сжал все эти слои вместе. Я собираюсь начать здесь. Стирание ненужных нам линий, где мы можем это сделать? Чтобы еще больше упростить, мы могли бы просто сделать всю верхнюю часть бутылки с мылом одной частью и перетащить туда цвет. Вся верхняя часть представляет собой одну часть, очень упрощенную. Но вы также можете делать такие вещи, как скругление углов и стирание маленьких кусочков, чтобы сделать вещи немного более интересными, а не просто прямые прямоугольники повсюду. Он немного больше похож на наш оригинальный дозатор мыла, но в нем больше абстрактного ощущения.Я просто применю это и здесь. Я войду и закруглю некоторые углы. Хотите чувствовать себя немного больше как наушники, а не просто прямоугольные формы. Залейте немного цветом, чтобы придать ему немного больше графического смелого вида. Что-то, что я также хотел бы попробовать, это абстрагировать складки, которые вы видите на реальной ткани наушников, и, может быть, просто добавить пару линий здесь и там. Это просто игривые графические линии. Не бойтесь играть со шнурами. Я имею в виду, делай то, что считаешь лучшим здесь.Вам не обязательно делать то, что делаю я. Ножницы будут немного странными. Как мы можем сделать эти формы похожими на объекты, не вдаваясь при этом в детали? Мне нравится отключать рисунок сзади, как вы видели, я делаю это просто для того, чтобы не слишком зацикливаться на том, как выглядит реальная фотография. Я сделаю это здесь, особенно для этих ножниц, потому что они немного странные. Просто потому, что я не знаю, как полностью абстрагировать его, не приближаясь слишком близко к фактической форме или фотографиям.Может быть, мы просто используем больше прямых линий. Я всегда чувствую, что настоящие прямые линии делают вещи менее реальными и более абстрактными. Мы можем даже преувеличить некоторые пропорции. Или, если я хочу получить действительно абстракцию или сильно отклониться от фотографии, я мог бы выбрать этот раздел и просто очистить его, а затем выбрать левую сторону и провести тремя пальцами, скопировать, а затем в новом слое, тремя пальцами. проведите пальцем, вставьте, а затем оттуда я могу просто перевернуть по горизонтали и поместить его на правую сторону. У нас есть более графически выглядящие ножницы.Теперь, что касается растения, я хочу, чтобы оно было больше похоже на кактус. Если я посмотрю на это прямо сейчас, я не подумаю, о, это крошечный кактус. Я могу сделать это, добавив эти закругленные углы сверху. Но мы могли бы немного стилизовать его, просто скруглив некоторые углы, так что не все. Если мы посмотрим на это фото, что делает его кактусом? Я чувствую, что то, что делает его кактусом, это маленькие уколы на нем. Я просто хочу включить их, и я чувствую, что зритель сразу поймет, что я пытаюсь изобразить.Мы просто добавляем пару маленьких кусочков здесь и там, может быть, они идут в спорадическом направлении. Он уже больше похож на кактус. Вот оно. Это основы использования Procreate для разбиения объектов на простые графические формы. Они не идеальны, но они являются хорошей разминкой перед предстоящим классным проектом. Помните об этих приемах, пока мы продвигаемся вперед в этом классе. Мы расширим их, чтобы создать ваш последний натюрморт. Загрузите рабочий лист с вкладки «Ресурсы» и приступайте к собственной небольшой разминке.Я настоятельно рекомендую вам поиграть с другими методами, чем я здесь. Возможно, используйте эллипсы для наушников вместо прямоугольников или более мягкие формы для кактуса. Это действительно зависит от вас, но я просто очень хочу призвать вас поиграть со своими собственными методами здесь, освоиться с использованием всех различных форм, прежде чем мы погрузимся в следующий урок. 4. Сделайте свое собственное фото. Теперь, когда мы познакомились с основами уменьшения форм, осмотрите свой дом и найдите несколько объектов, которые говорят с вами, чтобы создать натюрморт, а теперь, когда мы рассмотрели, как мы собираемся уменьшить эти формы, помните об этих методах, когда будете искать эти объекты.Может быть, вы найдете что-то, что имеет действительно уникальную форму. Какие объекты могли бы воплотиться в интересную композицию? Какая вещь имеет странную форму, которую вы раньше не замечали? Ваша натюрмортная фотография может быть любого масштаба, который вам нравится. Возможно, вы хотели бы создать большую сцену с лестницей и стулом, или вы могли бы выбрать средний масштаб и поиграть с вазой, молочником, растением, или вы можете пойти в микро и поиграть с карандашом, помадой, скрепка. Нет ничего слишком большого или слишком маленького. Возможности безграничны.После того, как вы собрали свои предметы, начните упорядочивать их по-разному и делать фотографии прямо с вашего iPad, чтобы вы могли легко перетаскивать их в Procreate. Если вы используете Photoshop или Illustrator, не стесняйтесь использовать свой смартфон или камеру, чтобы сделать фотографии, а затем вы можете загрузить их на свой компьютер. Вы также можете попробовать использовать Photo Booth, чтобы сделать свои натюрморты, что я часто делаю. Пока вы создаете здесь свой натюрморт, поиграйте с балансом, композицией и негативным пространством и сделайте несколько фотографий каждой композиции.Не нужно быть слишком драгоценным на этом этапе, поскольку у вас будет возможность быть гибким, как только вы начнете работать над своей иллюстрацией в Procreate. Вот несколько советов, которые следует учитывать при размещении объектов. Создайте масштабный контраст, установив более крупные объекты рядом с более мелкими или высокие рядом с низкими. Асимметрия всегда более привлекательна для глаз. Ему приходится прыгать по кадру от объекта к объекту, сосредотачиваясь на деталях. Создайте визуальный поток. Это идет рука об руку с масштабным контрастом. Постарайтесь построить поток, чтобы вести взгляд с одной стороны на другую и обратно.Постройте баланс. В то время как контрастность и изменение масштаба велики, обязательно сбалансируйте кадр. Вам не нужны все высокие объекты слева и только маленькие объекты справа. Зрителю это может показаться неудобным. Добавьте перекрытие. Это то, что мы можем углубить при рисовании в Procreate, но попробуйте поместить несколько разных объектов позади и впереди других. Наконец, рассмотрим негативное пространство. Вы же не хотите, чтобы кадр был слишком полным. Ему нужно немного места, чтобы дышать. Теперь у нас есть куча фотографий на выбор, и я расскажу о них в следующем видео. Если у вас нет доступа к собственным фотографиям, я предоставил некоторые из них на вкладке «Ресурсы» ниже. 5. Настройте свой файл. Теперь, когда у нас есть все наши фотографии, давайте настроим наш холст в Procreate. Я буду держать это простым. Мы возьмем стандартный квадратный холст. Мне нравится использовать это для моих постов в Instagram. Это легко, и вам не нужно беспокоиться о разрешении и так далее, потому что разрешение уже довольно высокое. Теперь, когда у нас есть базовая настройка Procreate, давайте перейдем к нашим фотографиям и выберем натюрморт.Мне все это нравится, я хочу убедиться, что у меня есть что-то сбалансированное, с хорошим масштабом, с контрастом, с некоторыми интересными объектами, с которыми я могу играть. Помните обо всем этом, когда выбираете изображение. Я думаю, что я собираюсь пойти с этим. Мне это очень нравится, потому что у нас есть некоторые объекты, накладывающиеся друг на друга, у нас есть вещи, сидящие друг на друге, мне нравится нить, может быть, я могу поиграть с ней, когда буду вдаваться в абстракцию своего произведения, Мне нравится форма этой вазы и маленькие апельсины в ней. Здесь есть много забавных вещей, с которыми я могу поиграть в иллюстрации. Не придирайтесь к тому, как выглядит изображение, потому что, очевидно, сейчас мы иллюстрируем, поэтому вам не нужно слишком беспокоиться, потому что мы можем немного повеселиться. Мы можем немного сойти с ума и изменить ситуацию, пока мы в Procreate. Теперь у меня есть это изображение в избранном, я хочу вернуться в Procreate, а затем я нажму «Добавить», «Вставить фотографию». Я собираюсь перейти в «Избранное», выбрать изображение, которое я только что показывал вам, и вуаля, у нас есть наше изображение.Я всегда хотел убедиться, что это правильный размер на холсте, поэтому я просто немного увеличу этот размер, чтобы он больше напоминал центрированную композицию. Затем я уменьшу непрозрачность, чтобы мы могли рисовать поверх него. Кроме того, мы хотим включить эту сетку, как у меня на разминке. Перейдите в «Холст», «Руководство по рисованию», и, поскольку это новый файл, мне придется снова отредактировать «Руководство по рисованию», уменьшить непрозрачность и сделать его розовым, как мне нравится. Убедитесь, что он все еще виден, так что у нас есть это на сверхсвете.Возможно, вы даже не сможете его увидеть, но он есть. Здесь я буду здесь толщину немного, чтобы вы могли видеть. Во-вторых, у нас есть наше руководство по рисованию, у нас есть наша установка для фотографий. Это основы того, как мы собираемся начать работу в Procreate. 6. Разбейте его на части. На этом этапе начните с того, что разбейте свой натюрморт на самые основные формы, как мы делали ранее на рабочем листе формы. Вы можете копировать здесь свою собственную фотографию, потому что вы настроили это и сделали это сами; это ваше использование. Я откажусь от того, что вы не должны находить случайную фотографию в Интернете и отслеживать ее, это бестактность.Постарайтесь сделать свою референсную фотографию, если сможете, чтобы не украсть чужую работу. Разбирая фотографию, потратьте около 10 минут на то, чтобы поиграть с различными возможностями. Вы даже можете начать с того, что включите резервную копию непрозрачности на своем изображении, сильно уменьшите масштаб, прищуритесь на свое изображение и проверите, какие фигуры бросаются вам в глаза в первую очередь. Для меня это то высокое растение на заднем плане и ножка кофейной чашки, так что я просто буду помнить об этом, когда рисую. Но здесь действительно красивый силуэт.Там много хорошей иерархии, перекрытий и масштабного контраста. Я просто собираюсь удостовериться, что включаю это, пока играю с геометрическими фигурами. Лично у меня есть куча разных кистей в Procreate, которыми я люблю пользоваться. Я очень рекомендую этот пакет от RetroSupply Co. Это их ретро-пакет Mid-Century. Одна из моих любимых кистей — кисть Blotty Inker. Это действительно приятно. На нем есть обтекаемая линия, что означает, что он будет создавать более плавные линии, когда я рисую.Это исправит некоторые из моих ошибок, так что просто имейте это в виду. Вы можете добавить поток к любой из ваших кистей, если у вас есть другая, которая вам нравится. Я просто собираюсь пойти дальше и начать разбивать это на эти формы. Неважно, перекрываются ли они здесь сейчас, потому что мы собираемся вернуться и стереть что-то, перерисовать что-то. Так что на этом этапе вы можете быть настолько грязными, насколько захотите. Такие вещи, как ручка этой чашки, на которые я указывал, которые действительно выделяются в силуэте, я мог бы даже попытаться сделать это еще более графичным и просто поиграть с такими формами, как круг, а не с прямоугольником со скругленными углами, который уже есть.Просто поэкспериментируйте с тем, чтобы сделать вещи немного более интересными для глаз, добавив действительно четкие графические формы. Включите помощь в рисовании и просто повеселитесь на дне этой чашки, а почему бы и нет? Но это не значит, что мы не можем добавить эллипс на его вершину. Иногда в перспективе мне нравится представлять, что мы видим верхнюю часть объекта и его боковую часть одновременно. Для этой катушки пряжи я собираюсь поиграть с полным кругом наверху. Тогда, может быть, просто прямоугольник для основы.Я, вероятно, воспользуюсь для этого помощником по рисованию. Просто убедитесь, что он идеально прямой. Так как мы едва видим ноги этой фазы здесь, я просто собираюсь сделать ее полноценным прямоугольником. Затем, что касается растения, я думаю, что мы получаем довольно абстрактное представление о нем, как мы сделали ранее с кактусом. Я снова включу помощь по рисованию. Просто сделайте прямой прямоугольник до самого верха. Затем я сделаю по-другому или включу помощь по рисованию, а затем нарисую боковой прямоугольник для этого торчащего стебля.Что касается листьев, возможно, я могу пойти еще дальше и поиграть с парящими там эллипсами. Возможно, есть какое-то наложение со стволом. С ним можно немного пофантазировать. Мы берем подсказки с фотографии, но на самом деле мы не прослеживаем ее прямо, потому что, если бы мы на самом деле проследили ее прямо, это выглядело бы слишком реалистично и не было бы похоже на натюрморт с графическими абстракциями, который это то, для чего мы здесь. Мы просто собираемся поиграть с этими основными формами. Если я отключу свой слой с фотографией, я увижу, что здесь происходит что-то довольно графическое.Ваша цель здесь состояла в том, чтобы сделать иллюстрацию как можно более простой и графической, но при этом сохранить ее узнаваемой. Вы уменьшаете свою фотографию до самой простой формы. Вы расширяете и сокращаете функции, как хотите. Речь идет о том, чтобы творчески подойти к поиску новых способов изображения натюрморта, а не пытаться получить точную картину. В основном мы используем фотографию, которую мы сделали, в качестве основы, но вы никоим образом не должны чувствовать, что она вас ограничивает. Веселитесь и играйте.Встретимся в следующем видео. 7. Трюк «Кривая-прямая». Теперь, прежде чем мы зайдем слишком далеко в уточнении нашего грубого наброска формы, я хочу рассказать о небольшом трюке, который я часто использую. Мне нравится использовать что-то, что называется «кривая-прямой трюк». Я не совсем уверен, есть ли у этой концепции настоящее название, но я называю ее именно так. Давайте сделаем шаг назад и вместе посмотрим на несколько моих иллюстраций. Я всегда любил использовать довольно ровный баланс изогнутых и прямых линий. Края фигур могут быть определены как изогнутые или прямые.Это подразумевает линейное или круговое движение. Прямые могут быть относительно кривых вокруг них. Увеличение контраста, чтобы подчеркнуть прямые и изогнутые линии, создает элегантность и интригу и притягивает зрителя. Но в зависимости от того, что вы хотите эмоционально изобразить в своей работе, вы можете использовать неравномерный баланс прямых или кривых. Если вы используете в своих формах в основном прямые четкие линии, вы создадите более угловатое, резкое поле для своего искусства. Если вы используете в основном кривые, это будет выглядеть более мягко и дружелюбно.Я думаю, поскольку наша сегодняшняя распродажа вызывает довольно нейтральные эмоции, давайте включим равномерный баланс кривых и прямых. Мне особенно нравится, когда прямые линии встречаются с изогнутыми линиями, создавая интересные, причудливые формы. Этот трюк поможет вашим иллюстрациям выглядеть более графичными, так как мы используем даже больше геометрических форм, чем органических форм. Давайте применим этот трюк с изогнутой прямой, сбалансированной к нашему натюрморту. Испытайте себя, чтобы еще больше разбить свой набросок, используя только кривые и прямые линии, а не органические плавные линии.Когда я говорю органические жидкие линии, я имею в виду что-то вроде этого, например, просто создание плавной формы. Скажем, если мы собираемся создать лист, если бы я собирался взять эти эллипсы и вместо этого сделать настоящую интересную форму листа, если бы я собирался проделать трюк с изогнутой прямой, я мог бы использовать два круга. Просто продублируйте его, а затем объедините эти слои, сотрите эти средние линии, а затем на самом деле вместо того, чтобы это было похоже на два идеальных круга рядом друг с другом, давайте сгладим края, используя этот трюк с кривой.Но чтобы добавить баланс кривых и прямых, я хочу добавить линию посередине, чтобы обозначить разделение листа. Я бы сказал, что это довольно хороший баланс кривых и прямых. Я мог бы заменить некоторые листья, которые у меня есть, на этот изгиб, просто прямой лист, и мы можем немного поиздеваться над ним. Может быть, этот верхний лист — это полный лист, может быть, мы видим дубликат полного листа ближе к низу, чтобы мы немного сбалансировали его. Но тогда было бы интересно, если бы мы сделали что-то еще более похожее на изогнутую прямую.Что, если бы мы просто продублировали его еще раз, но стерли нижнюю половину? Мы смотрим на сторону листа. Можем придать ему немного более драматичный изгиб, просто чтобы мы могли лучше видеть его край. Затем я мог бы пойти еще дальше и еще больше уменьшить такую ​​форму, и просто добавить небольшой полукруг для листа меньшего размера. У нас есть кривая, а затем у нас есть прямой край. Просто убедитесь, что все они происходят с одного и того же растения. Это гораздо более интересное и геометрическое растение, чем это, которое мне понравилось, но в нем не было такого очарования, оно не казалось таким геометрическим, оно просто чувствовало несколько случайных эллипсов, которые я добавил.Я чувствую себя очень довольным этим. Как еще мы можем применить это здесь? Что ж, теперь я действительно хочу сосредоточиться на этой чаше, первой чаше, которую я сделал, и я чувствую, что мы можем пойти дальше и стереть некоторые пересекающиеся линии, потому что они нам не нужны, и я сотру очередь позади, чтобы мы не отвлекались на это. Но я чувствую, что дно этой чаши кажется очень прямым и жестким. Итак, как мы можем сделать его более гармоничным? Что ж, мое первое предложение было бы сохранить прямые края этого основания треугольника, но закруглить углы, используя этот трюк с кривой для прямого.Это действительно не уловка. Это просто добавление ровного баланса. Но это всегда работает. Это просто отличный способ разбить все на две части. Я собираюсь стереть разделение между верхом и низом, чтобы оно выглядело как одна плавная графическая форма. Уже чувствует себя немного лучше. Я также мог бы применить эту кривую к прямому трюку с апельсинами внутри чаши. Большинство из них будут просто эллипсами или кругами. Но что, если я хочу немного повеселиться? Я применю все круги и сделаю их всех одинакового размера, возможно, поиграю с аранжировкой.Но вместо полного апельсина на заднем плане, может быть, я сделаю его долькой апельсина. Сделав это, я бы использовал эту кривую для прямого трюка. Я бы просто разрезал один из апельсинов пополам, добавив линию через середину. Я просто продолжу и сотру кусочки апельсинов, которые накладываются на миску, чтобы не было слишком запутанно. У нас есть два наших объекта, которые выглядят хорошо. Перейдем к кружке. Я не знаю, что случилось, но у меня была ручка кружки где-то здесь, и она просто исчезла.Я просто собираюсь добавить его обратно, и мне очень понравилось играть с этим кругом в качестве ручки кружки. Я просто собираюсь добавить это обратно, и для того, чтобы это больше походило на ручку, я просто продублирую ее и придам ей небольшое внутреннее кольцо. Что мне нравится в этой кружке до сих пор, так это то, что она уже хорошо использует кривые для прямых. У нас есть эта изогнутая ручка кружки, встречающаяся с прямым краем самой кружки, что очень приятно. Я просто войду и сотру некоторые части кружки, которые нам не нужны.Когда я изначально рисовал это, у него была катушка на вершине кружки, но, возможно, она находится за ней. Может быть, мы можем поиграть с этим, чтобы веревка могла входить внутрь кружки. Это может быть интересно. Я собираюсь стереть дно катушки и протянуть нить, входящую внутрь. На самом деле это то, на что я также хочу обратить внимание. Здесь я могу использовать кривую и прямую для катушки, а также для струны. Таким образом, мы можем поиграть с кривой, идущей по краю, затем с прямой линией, а затем с другой кривой, ведущей к другой прямой.Несмотря на то, что это всего лишь строка для строки, она уже сама по себе кажется действительно графической. Так что это действительно способствует тому, что наша кривая становится прямой. Я очень доволен тем, куда нас привела кривая к прямому триггеру, и я думаю, что он готов перейти к следующему шагу. 8. Советы по композиции. Теперь наш набросок выглядит довольно хорошо. У нас есть красивые геометрические формы, хороший баланс кривых и прямых. Если я снова включу эталонный слой, наша композиция по-прежнему будет очень похожа на фотографию, которую я сделал, и я хочу, чтобы она казалась более уникальной, более графичной, более абстрактной.Я собираюсь поделиться здесь некоторыми советами о том, как именно это сделать, и это довольно просто. Совет номер 1: увеличьте свои пропорции. Мой первый совет — создать визуальный интерес, преувеличив пропорции. Я также называю это масштабным контрастом, потому что мы создаем больший контраст между масштабом различных объектов и композицией, таким большим и маленьким, высоким и низким. Здесь у нас есть два объекта, которые довольно близки по высоте: задняя ваза и катушка с нитками. Давайте добавим немного контраста, немного визуальной асимметрии, чтобы помочь зрителю увлечь взгляд вокруг композиции.Я думаю, что я собираюсь сделать это немного меньше, саму катушку, чтобы она не конкурировала с фоновой вазой. Это улучшит поток, и теперь эти два объекта не конкурируют за внимание, глаз зрителя будет знать, куда двигаться по кадру. Мы также можем повеселиться с ним. Я чувствую, что было бы неплохо увидеть один из этих листьев на заднем плане еще больше, потому что сейчас все кажется довольно ровным. Давайте просто сделаем этот очень большим, и я просто вырежу его и вставлю на новый слой, чтобы он был отделен от других объектов и просто сделал его большим. Мне также нравится тот факт, что, увеличивая размер, я немного заполняю пустое пространство в левой части иллюстрации. Поскольку я сделал его таким большим, мне придется переместить некоторые другие элементы, возможно, я сделаю этот лист немного меньше, чтобы контрастировать с ним. Кроме того, я думаю, что было бы неплохо сфокусировать внимание на этой вазе с фруктами, потому что мне это очень нравится. Я думаю, что это мой любимый объект на всей иллюстрации, так что давайте сделаем его немного больше.Во-первых, мне нужно объединить все эти слои вместе, чтобы понять, что к чему. Я мог бы просто сгруппировать их на самом деле. Я сгруппировал вазу вместе, и я просто собираюсь немного увеличить размер, чтобы увеличить эту пропорцию, и из-за этого я также удалю фон, чтобы он не слишком сильно перекрывался. Ну, это толкает пропорции. Мой следующий совет — исказить и трансформировать. По своей природе это похоже на изменение пропорций, но здесь речь идет о том, чтобы получить реальную форму каждого отдельного объекта и настроить ее. Это похоже на изменение пропорций и углов внутри отдельного объекта. Искажение может быть любым изменением, поворотом или преувеличением, из-за которого что-то выглядит иначе, чем оно есть на самом деле. Вместо того, чтобы просто делать что-то больше или меньше, вы можете поиграть с созданием разных и более интересных углов, играя с инструментом преобразования от руки, чтобы увидеть, откроете ли вы новую интересную форму. Я хочу немного поиграть с искажением и использовать этот инструмент преобразования искажения. Я действительно хочу сделать это с основанием этой чаши здесь.Я выбрал этот слой, нажимаю инструмент выделения, а затем нажимаю «Искажение», и таким образом вы можете вытягивать углы, чтобы придать объектам разные углы. На самом деле, может быть, сделать его немного выше, убедиться, что я следую этой сетке, чтобы не было ощущения, что она становится слишком перекошенной. Затем, возможно, даже сделать точку соединения с чашей немного тоньше, чтобы она казалась намного более преувеличенной. Ничего страшного, если ваши наброски не выглядят очень чистыми на данный момент, мы собираемся рисовать поверх этого для нашей последней части, так что не беспокойтесь об этом слишком сильно.Я также думаю, что если я посмотрю на этот предмет и сощурюсь на него со всем, что у меня здесь есть, я почувствую, что кружка кажется немного стоической и слишком прямой. Я мог бы на самом деле поиграть с инструментом трансформации искажения. Итак, я выберу этот слой, отключу помощь в рисовании, а затем снова использую этот инструмент преобразования искажения. Просто немного подтяните эти края, чтобы они казались немного более приятными для глаз и менее резкими. Я мог бы даже сделать ее немного более приземистой, потому что мне кажется, что настоящая кружка, которую я использовал, была приземистой, и мне понравилось, как она выглядела.Мне нравится, насколько большая ручка кружки по сравнению с настоящей чашкой. К тому же, если уж очень хотелось суперстилизованно, можно все сгруппировать. Я просто собираюсь проверить это, я не хочу потерять всю свою работу. Но я собираюсь сгруппировать все, а затем продублировать эту группу, а затем сгладить ее так, чтобы это был всего лишь один слой, а затем оттуда я собираюсь использовать инструмент преобразования произвольной формы, чтобы немного перекосить. Дайте всему один и тот же угол и придайте ему немного подразумеваемого движения или неуравновешенного, неустойчивого ощущения.На самом деле искажение может работать лучше для этого. Я чувствую, что свободная форма немного ограничена, поэтому лучше всего использовать искажение. Я просто беру верхнюю среднюю точку и перетаскиваю ее в том или ином направлении. Влево может показаться, что вы пытаетесь отойти от чего-то, а вправо может больше походить на подразумеваемое движение или движение в определенном направлении. Вы можете просто поиграть с этим, вы можете добавить это к отдельным объектам, а не ко всей композиции. Я лично хочу, чтобы он был более прямым, чтобы он выглядел немного более геометрическим, поэтому я не собираюсь его оставлять, но просто чтобы вы знали, как это сделать, вот он. Еще один верный способ добавить визуального интереса к непрерывности вашего натюрморта — добавить перекрытие между объектами. Это поможет добавить ощущение глубины вашей работе, даже если все ваши объекты плоские. Делая это, вы создаете более сложную, интригующую композицию и даже открываете возможность добавить тени между объектами. Здесь у нас уже много совпадений, но мы можем добавить еще больше. Мне действительно кажется, что когда я изменяю размер чаши, она немного выдвигается из композиции, поэтому я могу вернуть ее и немного больше наложить на нее.Мы также поиграем с углами отдельных объектов и создадим ощущение, что они перекрываются по-другому, или вы можете удалить некоторые перекрытия, если вам кажется, что их уже слишком много. С этой катушкой ниток я хочу поиграть, например, положить ее под углом, чтобы казалось, что она опирается на край чашки, может быть, немного не в порядке, чтобы придать этой части немного больше драмы. Я собираюсь вернуться к строке через секунду, поэтому я просто стер ее, но могу сделать что-то вроде этого. Такое ощущение, что он опрокидывается и встречается с фоновым кашпо. Затем, конечно, мне нужно будет нарисовать линию фонового горшка, чтобы она у нас была. Я хочу, чтобы это было больше похоже на прикосновение к краю, поэтому я собираюсь сдвинуть его еще больше. Это не идеально, но мы доберемся до конца. Еще одна вещь с перекрытием, которую мы можем сделать, это поиграть с нитью из этой катушки. Что, если нить с катушки на самом деле переплетается через пару объектов, чтобы создать большее перекрытие между объектами, может привести ваш взгляд к кадру композиции.Я буду помнить об этом трюке с кривой к прямой, который у нас уже был, и я просто собираюсь поиграть с перемещением этой линии по композиции. Это начинает выглядеть немного безумно, но когда мы на самом деле придадим ему цветовую форму, это будет намного приятнее для глаз. Мне очень нравится, как мы ведем взгляд по кадру, и я думаю, что это будет выглядеть очень забавно, когда оно будет в цвете. Просто продолжайте и закончите очистку вашей иллюстрации, если вы видите что-то вроде небольших касательных, например, здесь я вижу край этой вазы, встречающийся с чашей. Я собираюсь пойти дальше и попытаться избавиться от них, если смогу купить, либо стереть их, сгладить, изменить размер объектов, все, что вам нужно. Я собираюсь удостовериться, что это кашпо находится полностью за вазой, так что это может быть просто небольшой обман зрения, когда мы переходим к цвету, просто не рисуя эту линию внизу здесь. Я действительно чувствую, что здесь есть большое напряжение с этой касательной, когда нить ударяется о край чаши, поэтому я просто собираюсь немного добавить ее, чтобы она на самом деле не касалась ее.Дайте глазу немного места для дыхания, и вот наш набросок. Я чувствую, что наш эскиз довольно близок к завершению. Если есть что-то еще, что вы хотите сделать, например, взять всю группу и изменить ее размер так, чтобы она занимала больше кадра, не стесняйтесь делать это, убедитесь, что это центрированное чувство. В остальном мы готовы к работе, и теперь мы можем начать добавлять цвет. Так что встретимся на следующем этапе. 9. Блокировка цвета: Блокировка цвета. Это моя любимая часть процесса. Здесь у меня уже есть все, что нужно для композиции, и все, что мне нужно сделать, это раскрасить ее.Эта фаза может сделать иллюстрацию еще более графичной и сюрреалистичной, добавив неожиданные, неестественные оттенки. Вы можете начать с выбора цветовых палитр на сайте color.adobe.com или colorhunt.co. Это два веб-сайта, которыми я пользовался в прошлом, когда застревал при выборе цветовой палитры. Кроме того, перейдите на вкладку ресурсов ниже, чтобы найти рабочий лист с ограниченными цветовыми палитрами. Он включает в себя несколько цветовых палитр, которые вы можете использовать, а также несколько советов и рекомендаций по созданию собственных палитр. Я надеюсь провести полноценный мастер-класс по цвету в будущем, но сейчас я покажу вам основы того, как я выбираю свои собственные палитры.Для ограниченных цветовых палитр я предпочитаю начинать с выбора пяти цветов, а именно нейтрального светлого, нейтрального темного, теплого тона, холодного тона и яркого цвета. Я просто сделаю это сейчас. Начнем с нейтрального света. Я оставлю нейтральный термин свободным и выберу что-то немного розоватое, чтобы придать ему чуть больше не совсем белого оттенка. Я просто начну с того, что набросаю здесь цвет, чтобы создать небольшую палитру. Оттуда у нас будет нейтральный темный цвет, а я люблю розовый и голубой, поэтому я выберу темно-синий для своего темного цвета.Настолько темный, что кажется почти черным, и он в основном черный. У меня есть нейтральный свет и нейтральная темнота. Для моего теплого тона я собираюсь пойти с чем-то коричневым. Я действительно хотел поиграть с каштановыми волосами, потому что мне кажется, что это добавляет немного больше естественности, как будто мы смотрим здесь на растения и фрукты. Я действительно хочу, чтобы он чувствовал себя немного основанным на реальности в мире природы. У нас есть коричневый цвет для теплого оттенка. Я хочу использовать что-то зеленое для холодного тона, потому что у нас здесь есть растения, и я хочу, чтобы это выглядело немного реалистично. Но даже несмотря на то, что я сказал, что это будет холодный тон, он будет скорее теплым зеленым, но я думаю о зеленом в целом как о более прохладном цвете. Это будет наш крутой тон. Это наши естественные цвета. Затем, наконец, нам нужно использовать цветовую гамму, которая для меня просто неожиданный яркий цвет, который добавляет немного яркости и жизни вашей работе. Для меня это обычно желтый цвет, и я начну с него в первую очередь. У нас есть желтый цвет для поп-музыки. Но я чувствую, что это небольшое размытие.Я чувствую, что здесь может быть что-то еще более захватывающее. Почему бы нам не добавить второй всплывающий цвет, чтобы добавить немного больше жизни этому? Поскольку у нас уже есть несколько теплых оттенков, я хочу остаться с этой темой, например, с розовыми и коричневыми. Я собираюсь добавить так же, как более флуоресцентный розовый цвет. Это два ярких цвета, а иногда я просто использую пять цветов с одним ярким цветом. Но я чувствую себя немного взволнованным по поводу этой части, и я хотел добавить это. У нас есть наша цветовая палитра.Теперь пришло время приступить к блокировке цвета. Под цветовой блокировкой я подразумеваю простое заполнение каждой из этих фигур цветом, в основном перерисовывая каждую из них, используя эту группу, которую я собираюсь сгладить и полностью уменьшить непрозрачность. Я оставлю свой слой сетки включенным, чтобы убедиться, что все идет правильно. Но в основном перерисовываю, потому что я действительно хочу, чтобы все было очень чисто. Я не хочу, чтобы что-либо изменялось с пикселизированными краями. Мы держим слой эскиза отдельно.Вы даже можете заблокировать его, если хотите, чтобы он оставался на месте и не двигался. Прежде чем мы начнем что-либо. Я хочу выбрать цвет фона, чтобы цвета, которые я накладываю поверх него, действительно хорошо сочетались с этим цветом. Я собираюсь использовать этот нейтральный свет в качестве цвета фона, чтобы все было действительно воздушным. Просто перетащите этот цвет на фон, и теперь мы можем начать. Просто попробуйте сосредоточиться на одном объекте за раз. Вы можете вернуться и изменить цвета позже. Просто постарайтесь заполнить все, как вы идете.Одно из моих практических правил во время работы — стараться, чтобы объекты, соприкасающиеся друг с другом, были разного цвета. Скажем, я делаю эту вазу коричневого цвета. Надеюсь, объект за ним, кашпо желтого цвета или что-то приятное и контрастирующее с коричневым цветом вазы. Когда вы работаете над этим, просто следуйте этому эмпирическому правилу. Как и прежде, я использую краску для блоттинга RetroSupply, которую очень рекомендую. Это дает вам текстурированное, органическое ощущение. Мне это нравится, потому что в нем есть встроенная оптимизация, и в то же время он имеет тактильное качество, нарисованное от руки, чтобы придать некоторую индивидуальность конечному произведению.Это не просто векторные фигуры из иллюстратора, это немного грубый край. Когда вы работаете здесь, старайтесь держать все свои маленькие фигуры отдельно. Я бы не рекомендовал пока сглаживать их, потому что если мы хотим добавить немного теней, вам понадобятся все отдельные слои. Я бы также рекомендовал сгруппировать все. Я просто собираюсь переименовать эту групповую чашу. Внутрь миски я собираюсь добавить фрукты. Так как это апельсины, я собираюсь использовать этот оранжево-розовый тон. Я собираюсь отключить эти другие слои, чтобы я мог видеть, где они находятся.Теперь, если вы работаете с цветом и хотите изменить цвет чего-либо, вы можете легко сделать это, просто выбрав нужный цвет, а затем перетащив его в эту форму, просто чтобы вы знали. Как видите, работая здесь, я немного развлекался. Я пошел дальше и сделал эту линию немного более интересной. Это то, что я настоятельно рекомендую, пока вы играете со своими композициями и цветом. Если у вас есть идея получше, пока вы работаете, просто измените то, что было в вашем эскизе.Вы не должны быть женаты на том, что вы там сделали, как будто даже сейчас я смотрю на это и думаю, что я определенно должен немного сгладить эту кривую, потому что она кажется немного жесткой. Вы можете войти и просто редактировать вещи по ходу дела, менять цвета и т. д. Но я действительно чувствую, что мы подходим к действительно хорошему моменту, и я бы назвал фазу блокировки цвета завершенной прямо сейчас, потому что то, что мы собираемся Далее нужно просто добавить тени, текстуры, детали и т. д. Мы почти закончили, ребята, это на самом деле очень близко.Давай, сделай это со своими натюрмортами. Получите эти цвета, а затем встретитесь со мной на этапе детализации, где мы рассмотрим некоторые методы, чтобы добавить немного больше жизни к вашим графическим натюрмортам. 10. Добавление деталей. Здесь мы находимся на этапе детализации. Здесь мы добавляем тень, текстуру, детали линий, узоры, все, что вы хотите добавить, чтобы немного оживить ваши иллюстрации. Здесь вы также можете добавить немного ярких цветов, чтобы все выглядело немного более сбалансированным.Но сначала я собираюсь добавить немного тени везде, чтобы сделать нашу иллюстрацию более четкой. Это означает, в основном, то же самое, что отделить верхнюю часть этой чаши от нижней части этой чаши, добавив тень внизу. Давайте продолжим и сделаем это сейчас. Поскольку у меня все разделено, как я уже сказал, у меня есть дно миски и верх миски здесь. Я просто собираюсь добавить слой между ними. Чтобы добавить тени, я всегда выбираю новый слой, а затем нажимаю «Обтравочную маску».Это означает, что все, что вы рисуете на слое обтравочной маски, будет применяться только к тому слою, для которого оно замаскировано. Так что, если я хочу раскрасить это, я войду только внутрь этой формы. Это лучший способ добавить тени, потому что вам не нужно быть слишком точным. Я просто иду вперед и добавляю небольшую направленную тень здесь. Поскольку верхний слой чаши находится поверх него, мне даже не нужно беспокоиться о слишком точной тени на самом верху. Уже выскакивает со страницы.Пока я смотрю на это, я мог бы просто отключить руководство по рисованию, потому что на данный момент оно мне не нужно, и я могу смотреть на все немного яснее. Следующее место, где я хотел бы добавить тень, это апельсины. Когда мы смотрим на это, вы даже не видите, что это груды апельсинов, потому что вы даже не можете видеть их формы. Просто добавьте обтравочные маски к слою, к которому вы хотите их применить, и начните их раскрашивать. Я собираюсь добавить небольшую тень под долькой апельсина.Я мог бы даже сделать линию немного дальше, чем это естественно, просто чтобы создать некоторое визуальное разделение между двумя срезами. Я просто собираюсь перейти к ним по порядку, так что в обратном порядке. Очевидно, эти тени не обязательно должны быть реалистичными. Не все они идут в самом реалистичном направлении, так что на самом деле это просто добавление визуальной ясности больше, чем что-либо еще. Я продолжу добавлять тени везде, где, по моему мнению, они нужны. Мы могли бы добавить немного о растении, может быть, там, где лист касается растения.Это не совсем реалистичная тень, но она работает. Может быть, небольшое разделение между основанием растения и маленькой веткой. Наконец, было бы неплохо добавить немного тени на ручку кружки, просто чтобы отделить ее от фактического основания кружки. Следующим шагом я добавлю небольшой блок цвета там, где считаю это необходимым. Я смотрел на это, и если я прищурился на него, когда он действительно крошечный, он кажется действительно тяжелым сверху с темными, как темно-синие цвета только сверху. Я думал о том, чтобы просто добавить немного стилистического цвета к самой кружке, так что, может быть, кружка наполовину синяя, наполовину зеленая.Я просто добавлю, сделаю небольшой цветной прямоугольник и, очевидно, обтравлю его маской. Такое ощущение, что в нем есть немного стилистического присутствия, и это на самом деле помогает немного сбалансировать композицию. Следующий шаг, который я хочу добавить, это лайнворк. У нас уже есть линейка катушек. Но я хочу убедиться, что зритель знает, что это нить с катушки, поэтому лучший способ сделать это — просто натянуть на нее больше нити. Я просто обтравлю это и нарисую пару линий, чтобы обозначить, что на катушке есть нить.Потому что без этого вы действительно не знаете, что это такое. Это все еще абстрактно, но у него есть немного более видимое объяснение. На самом деле, вы могли бы добавить немного больше интереса к самой катушке, установив немного цветового блока для всей этой катушки с нитками. Затем нам нужно добавить линии к растениям, потому что, как я уже говорил ранее, все, что мы видим сейчас, это кривые. Я хочу добавить немного визуального разделения к листьям, так что давайте создадим обтравочную маску, а также добавим туда несколько линий.Прямо посередине. Просто делает более очевидным, что это лист. Когда я смотрю на это растение, оно кажется немного тяжелым, очевидно, потому что я увеличиваю пропорции на листе слева. Может быть, мы просто продублируем этот маленький полукруг. Выберите его, проведите тремя пальцами, вырежьте и вставьте, а затем я скопирую его оттуда. Может быть, рядом плавает небольшой лист, и я думаю, что это также поможет улучшить композицию. Это не имеет смысла, как гравитация, нет, но я думаю, что так она кажется намного более сбалансированной.Далее, я думаю, было бы забавно добавить сюда немного узора. Всякий раз, когда я чувствую, что иллюстрация немного не скучна, но ей просто нужно немного больше остроты, я добавляю узоры. Как я уже говорил ранее, мой любимый предмет на этой иллюстрации — чаша, поэтому я собираюсь добавить к ней небольшой узор, чтобы она выделялась. На самом деле я собираюсь снова использовать обтравочную маску на основной части чаши. Я собираюсь сделать небольшую выкройку листьев, а почему бы и нет? Я думаю, что это будет выглядеть очень мило, и это может быть просто небольшой узор из линий, чтобы привлечь к нему внимание.Это может быть очень просто. Вы также можете сделать горошек или полоску. Это действительно зависит от вас. Я люблю, когда это выглядит немного грубо. Я думаю, что приятно иметь немного тактильного качества в моих графических иллюстрациях. Также добавляю их к основе, а также обтравочную маску. Это очень весело. Мне действительно кажется, что если я добавлю больше узоров, у нас уже есть линии и листья, если мы добавим больше, я думаю, что это будет слишком занято, поэтому я думаю, что баланс кажется довольно хорошим. Последнее, что я хочу сделать с линиями, это добавить несколько линий горизонта, выровненных по этим объектам, потому что сейчас они выглядят так, как будто они парят в пространстве.Я собираюсь создать новый слой, включить Помощник по рисованию и просто сделать несколько горизонтальных линий по всей композиции, чтобы заземлить ее. Вы можете сделать более одного, если считаете это необходимым. Думаю, здесь неплохо будет добавить пары, чтобы работало и на кружку, и на миску. Если вы не можете правильно разместить, как я, не стесняйтесь перемещать объекты с помощью инструмента выбора. Есть линии горизонта. Кое-что, что я действительно люблю добавлять во все свои иллюстрации сейчас, — это фоновая текстура. Я думаю, что это действительно добавляет много тактильных качеств и делает его немного более захватывающим, чем простой фон.Мне нравится использовать эту кисть, которая называется чернильные крапинки. Чтобы быть на 100 процентов честным с вами, я не помню, откуда он взялся. Я также покажу вам, как вы можете в основном сделать свой собственный. Но этот действительно хорош, потому что он просто разбрызгивает чернила повсюду. Он действительно легкий, поэтому на самом деле это может быть не так очевидно. Если вы хотите увеличить его интенсивность, я бы продублировал его, чтобы вы действительно могли многое там увидеть. Затем вы можете объединить его, чтобы он был на том же слое. Но я чувствую, что это уже слишком, поэтому я собираюсь пойти и стереть небольшие кусочки здесь и там, особенно те части, которые пересекаются с моей иллюстрацией.Я не хочу отвлекаться от того, что я только что сделал, просто говорю это бесплатно. По правде говоря, я не знаю, откуда эта кисть, и я не могу дать ее вам, потому что я не могу просто отдать чужую кисть. Но вы можете использовать кисть-распылитель, но есть гибкая кисть, и вы можете делать то же самое, просто стирая ее части, и вы можете настроить ее по своему размеру, и это встроено в приложение. Вы также можете войти в него и настроить дрожание, зеленый цвет и все такое, чтобы вы могли сделать его более индивидуальным по своему вкусу.Но, как я уже сказал, я чувствую, что вы можете сделать это самостоятельно. На самом деле, вам просто нужно пойти и добавить свои собственные пятнышки, используя любую кисть, которая у вас есть. Мне нравится эта тонкая фоновая текстура, но я хотел, чтобы на ней было немного больше чернил, поэтому я собираюсь добавить маленькие точки здесь и там, чтобы сделать ее немного более интересной. Он также ведет ваш взгляд по кадру, если вы можете расположить его в соответствии со своей композицией. Вот и мы. Я надеюсь, что вы сможете взять эти приемы и применить их к своей иллюстрации.В следующем видео мы рассмотрим экспорт и пару советов для социальных сетей. Похлопайте себя по спине за то, что вы зашли так далеко. 11. Экспорт + сохранение: теперь у вас есть готовая иллюстрация. Вы довольны этим, и вы хотите поделиться им с миром. Как ты это делаешь? Если вы знаете Procreate, вы, вероятно, уже знаете, как это сделать, но я все равно пройдусь по нему. Нажмите гаечный ключ и выберите «Поделиться», и вы можете экспортировать его как угодно, JPEG, PNG, PSD, вы даже можете перенести его в Photoshop и поработать над ним там.Что мне лично нравится делать, так это сохранять его в Dropbox. Я сохраню его в формате JPEG, а затем нажму «Сохранить в Dropbox» и сохраню в любую папку, которую захочу. Обычно я переименовываю его в like shapestilllife для чего угодно. Затем нажмите Сохранить, и я загружу его. После того, как я закончил свой натюрморт и экспортировал его из Procreate и прочего, я люблю делиться своей работой в социальных сетях. Instagram определенно является моим любимым социальным оружием. Просто он у меня уже давно. Мне очень нравится делиться там своей работой, нравится делиться своим процессом.Часто я экспортирую финальное изображение и делюсь им как первым, а затем делаю свайп. Мне очень нравится делиться замедленной съемкой моей иллюстрации, и я покажу вам, как это сделать здесь. Для этого вам нужно просмотреть замедленную съемку и просто перейти к видео в том же меню, а затем нажать «Экспортировать замедленную съемку». Я обычно делаю 30 секунд, потому что никому не нужно видеть все целиком. Он сожмет его до 30-секундного экспорта, который вы сможете опубликовать в своей истории в Instagram. Вы также можете опубликовать его в своем посте в Instagram, как я уже сказал.Я нажму Сохранить в Dropbox, в той же папке. Он загрузит его в формате MP4. Это все, что вам действительно нужно, и тогда вы, очевидно, можете отправить его на свой телефон. Вы можете опубликовать его из любого места, где вы публикуете. Что мне нравится делать для своего поста, так это пост в 9:00 утра по стандартному тихоокеанскому времени. Я не знаю, работает ли это для всех и везде, но для моих подписчиков это работает лучше всего. Мне всегда нравится писать что-то о процессе в подписи и, может быть, призыв к действию, если люди хотят написать что-то свое в ответ на то, что я сказал, это всегда здорово.Вы могли бы задать вопрос. Простое поощрение участия в вашей статье действительно полезно. Поэтому, если вы добавите его в свои истории или поделитесь им на разных платформах, это всегда повысит вовлеченность и позволит большему количеству людей увидеть то, что вы там публикуете. Вы можете хэштегировать свою работу, все, что делает ее более заметной. Я думаю, что Instagram — это отличный способ поделиться своим процессом, поучиться у других и просто стать частью сообщества, которое делится такой работой. Это так здорово — общаться со всеми там, узнавать, чем все занимаются на своих занятиях Skillshare. Для меня было бы очень важно, если бы вы разместили это в Instagram. Люблю смотреть, что ты делаешь. 12. Thank You!: [МУЗЫКА] Вау, мы только что много сделали. Мы закончили собственный графический натюрморт в Procreate. Я так горжусь тем, что вы зашли так далеко, и я просто хочу призвать вас поделиться своей иллюстрацией здесь, на Skillshare. Покажи свой процесс. Мне бы очень хотелось увидеть, что вы придумали на вкладке «Проекты». Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь задавать их здесь. Я сделаю все возможное, чтобы ответить на них.Поэтому, пожалуйста, поделитесь им здесь, поделитесь им в социальных сетях, поделитесь им в Instagram, где угодно. Я хотел бы увидеть, что вы сделали. В дополнение ко всем забавным вещам, которые вы только что узнали от меня здесь, у меня также есть загружаемый контент на вкладке «Ресурсы», так что проверьте это для небольшого удовольствия, небольшого дополнительного бонуса для вас. Я не мог оставить тебя без чего-то физического, чтобы забрать. Надеюсь, вам понравится. Пожалуйста, пожалуйста, пожалуйста, оставьте мне отзыв на Skillshare, если вам понравился этот класс.Мне действительно помогает понять, что вам понравилось в классе, чтобы я мог продолжать проводить отличные занятия в будущем. Я очень ценю вашу поддержку. Также, конечно же, подписывайтесь на меня на Skillshare, в социальных сетях и, если вы хотите узнать больше от меня, пожалуйста, загляните на мой веб-сайт sarahbethmorgan.com/learn. Вы также можете ознакомиться с другими моими курсами здесь, на Skillshare. Большое спасибо за этот урок, и я не могу дождаться, чтобы увидеть, что вы сделали.

    School of Art Courses

    Примечание. Все 100-уровневые курсы открыты для лиц, не связанных с искусством, без предварительных условий.

    ART 110 Вблизи

    Курс знакомит учащихся с изобразительным искусством через непосредственные встречи с работает в кампусе и рядом с ним. Письменные задания и обсуждение подчеркнут искусство как визуальный язык, состоящий из нескольких медиа и концептуальных рамок. Курс обеспечит понимание и оценку культурного воздействия искусства.(АР)

    АРТ. 111 Основа Арт.

    Этот курс исследует основы цвета, формы и дизайна в студийных проектах. в двух и трех измерениях. Он стремится способствовать творческим процессам и решению проблем подходит для инноваций в искусстве, дизайне и культуре.Он также служит основой для развития эстетических практик и требуется для художественных специальностей. (AR)  Предлагается каждую осень.

    АРТ.

    113 Чертеж I

    Рисунок — это опыт восприятия, основанный на работе с натюрмортом, человеческой формой. и другие источники, основанные на конкретных навыках.Знакомство с подчеркиваются различные средства рисования, а также методы, относящиеся к композиции и концепция. Курсовая работа построена вокруг последовательности задач, связанных с развитие понимания формы, структуры, значения, формы, линии, края и цвета с использованием различных медиа. Особое внимание будет уделено пониманию исторической значение рисования, развитие критического языка о рисовании и получении понимание различных способов, которыми художники используют это средство для достижения своих концептуальных цели.(AR)  Предлагается каждый семестр .

    ART 115 Введение в историю искусств

    Этот курс исследует отношения между художественной продукцией и аудиторией в исторический и глобальный контекст. Студенты сосредоточатся на избранных произведениях искусства, чтобы развить способность использовать визуальные тексты в аналитической и критической манере.Курс включает посещение галерей и коллекций кампуса. (AR)  Предлагается каждую весну.

    ART 121 Начало трехмерного проектирования

     

    ART 125 Знакомство с печным стеклом

    Введение в технологию обработки стекла с использованием электрических печей. Исследует сплавление стекла и литье как средство эстетического выражения и развивает понимание избранных исторические и современные методы изготовления изделий из стекла в печи.Критика, группа дискуссии, исследования и задания по сбору информации, лекции и демонстрации дополняют студийную работу. (AR) Предлагается каждую осень.

    АРТ 130 Картина I

    Курс, предназначенный для ознакомления учащихся с процессами и концепциями рисования. Ученики исследовать живопись как средство эстетического выражения и развивать понимание избранных Исторические и современные способы живописи.Серия критических замечаний, групповые обсуждения, исследования и задания по сбору информации, лекции и демонстрации, дополняют студийная работа. (AR)  Предлагается каждый семестр.

    АРТ. 135. Гравюра I

    Введение в процессы и концепции печати. Студенты изучают гравюру как средство эстетического выражения и развивать понимание избранных исторических и современные способы печати. Серия критических замечаний, групповые обсуждения, исследования задания по сбору информации, лекции и демонстрации дополняют студию Работа. (AR) Предлагается время от времени.

    АРТ. 137 Скульптура I

    Введение в трехмерное решение задач и скульптурные процессы и концепции. Студенты изучают скульптуру как средство эстетического выражения и развивают осведомленность об избранных исторических и современных тенденциях в скульптуре.Набор критических замечаний, групповых дискуссий, исследований и заданий по сбору информации, лекций, и демонстрации, дополняют студийную работу. (AR) Предлагается время от времени.

    АРТ. 139 Керамика I

    Введение в керамические процессы и концепции. Учащиеся изучают керамику как средство эстетического выражения и развивать понимание избранных исторических и современные виды керамики.Серия критических замечаний, групповые обсуждения, исследования задания по сбору информации, лекции и демонстрации дополняют студию Работа. (AR) Предлагается каждый семестр.

    ART 140 Фотография I

    Введение в процессы и концепции черно-белой фотографии. Студенты исследуют фотографии как средства эстетического выражения и осознать как исторические и современные тенденции в фотографии.Помимо сбора фотографических изображений и студийная работа, студенты будут участвовать в групповых дискуссиях и серии критических анализов. Слайд-лекции, демонстрации студийных процессов и исследовательские задания дополнят студийный опыт. (AR) Предлагается каждую осень и иногда весной.

    АРТ. 141 Графический дизайн I

    Введение в визуальную коммуникацию, эстетическую теорию и инструменты компьютерной графики и методы.Изучает графический дизайн как средство коммуникации, художественного выражения, и организация информации. Критика, групповые обсуждения, исследования и информация сбор заданий, лекции и демонстрации дополняют студийную работу. (AR) Предлагается каждый семестр.

    ART 201 Дизайн для людей

     

    АРТ. 213 Чертеж II

    Рассмотрение проблем перцептивного и концептуального рисования.Цель курса состоит в том, чтобы способствовать пониманию рисования как промежуточного шага, ведущего к законченное произведение искусства, а как отдельная форма искусства, имеющая свои эстетические качества и быть полностью способным производить арт-объект. Требование: 113. Предлагается каждый семестр.

    ART 220 Введение в визуальную культуру

    Что может быть общего между нашим современным отношением к изображениям и древними верованиями в образы? Курс исследует идеи, преобладающие в обществе, представленные в визуальном культурном производство.Внимательно читая первоисточники, мы исследуем теории которые сохраняются и раскрывают мотивы имиджмейкеров, бесконечно борющихся за наше сознание. (IT, W) Нет предпосылок.

    Трехмерное стекло ART 225

    Этот курс исследует основы литья в печи и стекла, обработанного пламенем.Оба исторические и современные идеологии этих методов изготовления стекла будут обсуждаться, исследоваться, и применить на практике. Техническая база занятия в равной степени сопряжена с заданиями которые поощряют и способствуют вдумчивости с приобретенными навыками рук. (AR)  Предлагается каждую весну.

    АРТ 230 Картина II

    Продолжение 130.Индивидуальные проблемы в живописи. Предпосылки: ART 111 и 130. Предлагается каждый семестр.

    ART 235 Эстамп II

    Введение в процессы литографии и цветной глубокой печати. Техники и навыки, полученные в искусстве 135, будут продолжать использоваться. Условие: 135. Предлагается время от времени или по специальной договоренности.

    ART 237 Скульптура II

    Продолжение 137. Индивидуальные проблемы в скульптуре. Условие: 137. Предлагается время от времени или по специальной договоренности.

    АРТ. 239 Керамика II

    Продолжение 139. Отдельные задачи по керамике. Требование: 139. Предлагается каждый семестр.

    ART 240 Цифровая фотография

    Исследует концептуальные, творческие и технические процессы среды.Курс включает в себя демонстрацию лучших технологических практик, от захвата изображения до печати, в том числе веб-публикации. Каждый студент создаст портфолио цифровых изображений через студийная работа. (AR)  Предлагается каждый семестр.

    ART 241 Графический дизайн II: изображение/дизайн

    Продолжение изучения образов и создания образов в дизайне через серию проектов. Визуальная коммуникация через оригинальную фотографию, обработанную фотографию и иллюстрация исследуются с использованием как ручных, так и цифровых инструментов. И теория, и Процесс проектирования подчеркивается с помощью различных средств массовой информации, от печати до цифровой. Требование: 141. Предлагается каждую осень.

    ART 242 Графический дизайн: веб-дизайн

    Студийный курс, изучающий принципы визуальной компоновки интерактивного веб-дизайна.Обзор методологии, теории и передовой практики решений для веб-дизайна. Проекты будет изучать современные технологии. Условие: ART 141. Предлагается каждый осенний семестр.

    ART 297, 397, 497 Стажировки

    Индивидуально разработанное экспериментальное обучение. Может включать выездные студии или стажировку места размещения, такие как коммерческая печать, графический дизайн, работа в музее или галерее.Предпосылки: согласие факультета искусств Школы искусств. Предлагается каждый семестр.

    ART 302 Современная профессиональная практика

    Этот курс будет посвящен материалам, техническим и теоретическим выборам, необходимым для производства и понимания современного искусства. Это будет ознакомительный семинар. Класс будет способствовать междисциплинарному подходу к созданию искусства и поможет студент, чтобы узнать, как различные материальные и технические решения могут сообщить их визуальная и концептуальная практика.Условие: Младший статус в Школе искусства. Предлагается время от времени.

    ИСКУССТВО 307 Искусство и археология греческого мифа

    Мифы и ритуалы составляют религию Древней Греции и выражаются в искусство, памятники и письменность. Культура, идеи и ценности, передаваемые через различные выражения греческих мифов глубоко и надолго повлияли на западную мысль. способ.В этом курсе мы будем изучать тесную связь между мифом, искусством, историей, и культура Древней Греции. Курс указан в перечне с GRS 307. (AR) Предлагается время от времени, семестр в мае. Рекомендуемое требование: GRS 210.

    ИСКУССТВО 309 Греческое искусство от Гомера до Александра

    Обзор культурных артефактов и памятников Древней Греции «Эпохи Гомера» (бронзовый век) до «эпохи Александра» (эллинистический период). Цель состоит в том, чтобы развить понимание и оценка греческого художественного выражения, его влияния и его влияние на западное искусство и мысль. Курс включает экскурсию. Курс перекрестный список с HIST/GRS 309. (AR)  Предлагается через год, осенью.

    ИСКУССТВО 311 Искусство и архитектура римского мира

    Этот курс следует за развитием форм и идеологий римского искусства с республики до поздней античности.Вопросы, которые будут обсуждаться, будут включать общественность и частное, гражданское и религиозное искусство и архитектура, городское планирование и взаимодействие форм римского искусства и провинциальных культур в формировании идентичности. Курс входит в перекрестный список с GRS/HIST 311. (AR) Предлагается время от времени.

    ART 316 Европейское искусство, 1750-1900 гг.

    Изучение изобразительного искусства и критических идей, формировавших Европу со времен Просвещения. к началу модернизма.Курс исследует визуальную культуру французов. Революция, искусство и колониализм, главные художественные движения и быстрый технологический прогресс. и социальные изменения, связанные с современностью. Знакомство с историей искусства не обязательный. (AR)  Предлагается время от времени.

    ART 320 Глобальное современное искусство

    Обзор основных событий в глобальном модернизме с конца девятнадцатого до середины двадцатого века в Африке, Азии, Европе, Северной и Южной Америке.Ключевые темы включают художественные отклики на две мировые войны, европейский империализм и колониализм, развитие художественных направлений, новых технологий, подъем авангардизма. Знание истории искусства не обязательно. (AR, G) Предлагается каждую осень.

    ART 322 Глобальное современное искусство

    Критический обзор искусства с 1960-х годов, исследующий стратегии художественной практики. и социальная активность искусства в Африке, Азии, Европе, Океании, Северной и Южной Америке.Темы курса включают эфемерные и совместные мультимедийные проекты, перформанс и процессное искусство, рост новых медиа, деколониализм и транснациональные художники. (AR, G) Предлагается каждую весну.

    ИСКУССТВО 330 Живопись III

    Продолжение 230. Ожидается, что учащиеся продемонстрируют большую независимость и экспериментировать в своей работе. Требование: 230. Предлагается каждый семестр.

    АРТ. 335 Графическое дело III

    Продолжение 235. Ожидается, что учащиеся продемонстрируют большую независимость и экспериментировать в своей работе. Условие: 235. Предлагается время от времени или по специальной договоренности.

    ART 337 Скульптура III

    Продолжение 237.Ожидается, что учащиеся продемонстрируют большую самостоятельность и экспериментировать в своей работе. Условие: 237. Предлагается время от времени или по специальной договоренности.

    АРТ. 339 Керамика III

    Продолжение 239. Ожидается, что учащиеся продемонстрируют большую независимость и экспериментировать в своей работе. Требование: 239. Предлагается каждый семестр.

    ART 340 Фотография III

    Продолжение 240. Ожидается, что учащиеся продемонстрируют большую независимость и экспериментировать в своей работе. Требование: 240. Предлагается каждый семестр.

    ART 341 Графический дизайн III: повествование и дизайн

    Исследование дизайна визуального повествования с упором на креативность и эффективную визуальную коммуникацию.С помощью различных проектов студенты изучат историческую основу книгопечатания. и отношения между языком и формой. Продолжение изучения дизайна принципы будут подчеркнуты как в статических, так и в интерактивных медиа. Условие: 241. Предлагается каждую весну.

    ART 343 Графический дизайн IV: решение проблем и дизайн

    Курс, который заставит дизайнеров взглянуть на более широкие вопросы дизайна и социальных изменять. Работая в команде с кампусом или общественными организациями, студенты учатся сложность вопроса. Студенты определяют проблемы и опыт проектирования, артефакты и / или современные средства массовой информации для инноваций, изменений, обучения или вдохновения. Ученики будет использовать передовые методы брендинга для создания связной коммуникации. Условие: 341. Предлагается каждую осень.

    ART 370 Специальные темы по истории искусства

    Курс, содержание которого может различаться в зависимости от предложения.В центре внимания может быть одно или несколько направлений в искусстве, определенные художественные проблемы или концепции, периоды времени или географические местоположения, которые более или менее узко определены, или на работе отдельного художника. Каждый курс, предлагаемый под этим заголовком, имеет подзаголовок, который указывает конкретный предмет и тип планируемого курса. Может быть повторен для получения кредита, если содержание курса не дублируется.(Последние курсы)  Предлагается время от времени.

    ART 381 Специальные темы в Studio Art

    Курс, содержание которого может различаться в зависимости от предложения. В центре внимания может быть одна или несколько проблем процесса, содержания или стиля. Каждый курс, предлагаемый в соответствии с этим заголовок имеет подзаголовок, который указывает на конкретный тип курса, который Планируется.Может быть повторен для получения кредита, если курс не дублируется. Предлагается время от времени.

    АРТ 399 Художественный семинар

    Семинар на тему искусства и визуальной культуры, открытый для всех старшекурсников. и требуется от старшеклассников в Школе искусств. Темы будут разными, и курс может быть повторен для кредита. Семинар носит исследовательский характер и выполняет общеобразовательную Требования к интенсивному курсу письма (W). Предлагается каждую осень.

    ART 415 Расширенный чертеж

    Для продвинутых учащихся, знакомых с основными задачами рисования. То курс преследует три цели: развитие личного стиля рисования, знакомство со всеми средства рисования и более широкое понимание рисования. Требование: 213. Предлагается каждый семестр.

    ART 430 Живопись IV

    А, Б.Концентрированная индивидуальная работа для продвинутых студентов. Требование: 330. Май повторяться один раз для кредита. Предлагается каждый семестр.

    ART 435 Графическое дело IV

    А, Б. Концентрированная индивидуальная работа для продвинутых учащихся. Условие: 335. Май повторяться один раз для кредита. Предлагается время от времени или по специальной договоренности.

    ART 437 Скульптура IV

    А, Б.Концентрированная индивидуальная работа для продвинутых студентов. Условие: 337. Май повторяться один раз для кредита. Предлагается время от времени или по специальной договоренности.

    АРТ 439 Керамика IV

    А, Б. Концентрированная индивидуальная работа для продвинутых учащихся. Условие: 339. Май повторяться один раз для кредита. Предлагается каждый семестр.

    ИСКУССТВО 440 Фотография IV

    А, Б.Концентрированная индивидуальная работа для продвинутых студентов. Требование: 340. Май повторяться один раз для кредита. Предлагается каждый семестр.

    ART 441 Графический дизайн V: портфолио

    Концентрированное изучение сложных задач проектирования, основанное на предыдущем опыте учащихся. дизайнерские опыты. Новая работа может варьироваться от серии иллюстраций до брендинга или рекламы. кампании, а также комплексная образовательная или информационная коммуникация по дизайну предпринимателя проекты.Студенты предлагают план на семестр для утверждения преподавателями. Может повторяться один раз в кредит. Требование: 343. Предлагается каждую весну.

    ART 450 Передовые исследования в области истории искусств

    Тема семинара зависит от каждого предложения и может включать указанную историческую момент или группа художников, методологические тенденции или концептуальные проблемы в этой области.Семинар сочетает в себе обсуждение и презентацию, исследование и написание. Курс соответствует общеобразовательным требованиям для интенсивного курса письма (W). Предлагается время от времени.

    ART 480 Специальные индивидуальные проекты

    Индивидуально разработанные исследования, полевые опыты или экспериментальная студия проекты в сфере особого интереса; проводится под руководством инструктора или специальный надзиратель. Может повторяться максимум для трех кредитных единиц. Условие: согласие инструктора. Предлагается по мере необходимости.

    509 Превышен предел пропускной способности

    509 Превышен предел пропускной способности Сервер временно не может обслуживать ваши запрос из-за того, что владелец сайта достиг своего ограничение пропускной способности. Пожалуйста, повторите попытку позже.

    Курс рисования для НАЧИНАЮЩИХ — От линии к НАТЮРМОРТУ

    !!!ОБНОВЛЕНО: В курс включен ПОЛНОСТЬЮ НОВЫЙ раздел о ЖИВОМ РИСОВАНИИ натюрморта, НАПИСАННОГО ВАМИ ПОЛНОСТЬЮ!!!!

    Учащиеся сказали: 

    «Прекрасный урок с большим количеством отличных иллюстраций, советов и трюков. Александра очень искусна, и на нее интересно смотреть.» Крис В. 

    «Мне очень понравился этот урок, и я рекомендую его любому новичку или любому, кто хочет улучшить свои навыки рисования.Преподаватель очень четко объясняет основные понятия и дает умные советы, которые действительно могут помочь любому лучше рисовать». компании и социальные сети взаимодействуют с нами визуально….это ваш шанс ПРИСОЕДИНЯЙТЕСЬ!  Основы рисования — основа всего….это НАВЫК должен быть у каждого.А еще визуальная индустрия востребована художниками! Это лучшее время, чтобы устроиться на работу художником, но для этого вам нужны основы и отличные наблюдательные навыки. Этот курс даст вам это. Это время, когда вам нужно принять меры и отнестись к своей страсти, хобби более серьезно и на новый уровень!

    Основы рисования — от линии до натюрморта — это курс рисования для НАЧИНАЮЩИХ, который преподает профессиональный преподаватель рисования!

    Что может учитель рисования? Преподаватель понимает предмет и учеников, потребности учеников и способен построить сложный навык из маленьких простых шагов.

    Этот курс проведет вас от одной линии до правильно нарисованного натюрморта . Мы рассмотрим такие темы, как: Линия, Форма, Пропорция, Перспектива и Затенение. Но также углубитесь в такие темы, как измерение объектов и композиций, как найти основные геометрические фигуры, как рисовать методом сетки и, что наиболее важно, проведет вас через процесс рисования полностью затененного натюрморта.

    Вы получите эксклюзивное представление теории искусства о том, как художники видят мир и как развитие навыков рисования может быть для вас наиболее полезным: лечебный эффект (арт-терапия), укрепление уверенности в себе, развитие когнитивных способностей и даже начать свой собственный бизнес или художественное путешествие в области иллюстрации, дизайна персонажей, графического дизайна, цифровой иллюстрации, цифровой живописи и многого другого.

    Этот курс прямо к делу — есть увлекательные короткие сегменты, которые всесторонне дополняют друг друга и подводят новичка к правильно нарисованному и затененному натюрморту!

    и многое другое…

    Курс теперь ОБНОВЛЕН С полным новым разделом о том, как составить свой собственный натюрморт! Я покажу вам, как выбирать и размещать ваши объекты, как наносить свои первые измерения на бумагу, как размещать основные геометрические фигуры, рисовать и уточнять контурные линии, а также растушевывать натюрморт с помощью моего простого метода растушевки!

    Что вы получите на курсе?

    Все это находится на одной удобной и простой в использовании платформе.Кроме того, вы получите быструю, дружелюбную и отзывчивую поддержку в разделе вопросов и ответов Udemy курса или в прямом сообщении.

    Я буду рядом с вами на каждом этапе пути!
    Так чего же ты ждешь? ЗАРЕГИСТРИРОВАТЬСЯ СЕЙЧАС

    Рисование, рисование, рисование, рисование. … это то, чем я занимаюсь…..:D

    Почему графические дизайнеры должны учиться рисовать

    Рисование является основополагающим навыком любого графического дизайна . Обучение решению задач проектирования с помощью карандаша — это обучение, которое нам необходимо, чтобы наиболее эффективно решать задачи с помощью инструментов цифровой аппроксимации в палитрах наших любимых дизайнерских приложений.Но некоторые дизайнеры обходятся без рисования.

    Графические дизайнеры могут обойтись без рисования

    Но только так.

    Я не обязательно имею в виду, что классический рисунок натюрморта так или иначе незаменим для хорошего дизайнера, но рисование от руки, тем не менее, имеет решающее значение на определенном уровне, особенно на начальных этапах дизайна. Мозговой штурм карандашом просто невозможно улучшить. Многие дизайнеры обходятся без рисования, но это им во вред, знают они об этом или нет.Все великие школы дизайна и великие художники-графики согласились бы с этим. Те, кто не согласен, ну, вероятно, имеют меньшую степень величия.

    Но, хотя я совершенно убежден, что для того, чтобы стать великим дизайнером, нужно рисовать, все же не нужно рисовать, чтобы быть хорошим дизайнером. На самом деле, вам не нужно делать то, что вы не хотите делать! Но преимущества рисования как привычки в любой форме слишком очевидны, как показывает история. Я уверен, что есть некоторые исключения из правил, но они были бы аномалиями: диковинками, которые нужно учитывать, но не подражать.

    Цифровые инструменты являются аппроксимацией, а не заменой

    Все цифровые инструменты, которые мы используем как дизайнеры, являются имитациями реальных вещей. Отсюда и инструменты «перо» и «карандаш», «ластики» и «кисти». Маркетинговые кампании лучших дизайнерских приложений почти всегда «выглядят более естественными» или что-то в этом роде. Последний выпуск Photoshop CS5 действительно подчеркивает, насколько «естественнее» работают новые инструменты кисти. Эти цифровые инструменты напоминают своих аналоговых родителей .В чем-то они лучше, как и в случае с «отменить». Но Святым Граалем всех дизайнерских приложений является то, что они максимально приближены к аналоговым, но в то же время содержат некоторое цифровое совершенство.

    Итак, если вы работаете только и всегда в цифровом приближении (панели инструментов ваших различных приложений), вы упускаете то, к чему они пытаются приблизиться. Опять же, можно получить по как конструктор без рисования. Невероятная простота некоторых аспектов программного обеспечения для проектирования делает попадание в яблочко компетентного дизайна довольно легким, независимо от того, осознаете вы это или нет.Это не относится к делу. Линейки, сетки, отмена, приложения с цветовой палитрой, шаблоны: сегодня намного проще, чем 20 лет назад, стать «дизайнером». Adobe получает за это особую благодарность! Но это все равно, что ощупывать себя в темноте и выяснять, что в комнате находится слон, вместо того, чтобы просто включить свет и увидеть все сразу. Вы можете добраться туда трудным путем, но — это трудный путь !

    Не просто «играйте на слух»

    Быть дизайнером, который никогда не рисует, немного похоже на музыканта, который никогда не выучивает гамму и просто играет на слух.Этот музыкант может сочинить несколько отличных мелодий, может быть, сделать несколько отличных записей, но, в конце концов, он никогда не выберется за пределы своего добровольного изгнания от еще больших достижений.

    Например, большие цветовые палитры можно просто скопировать. Но за теорией цвета стоят математика и точные науки, которым можно научиться. Отличные макеты тоже можно копировать. Но опять же, есть доказуемая математика и теория того, почему отличный макет действительно хорош. Рисование, наряду с изучением таких вещей, как композиция и типографика, работают вместе, чтобы сделать из нас дизайнеров еще лучше, чем мы были бы без них.

    Рисование имеет основополагающее значение для получения наилучших результатов с наименьшими усилиями

    Однако я должен повторить. Чтобы стать хорошим дизайнером, не обязательно рисовать . Вам не нужно делать ничего, что может предложить любой «эксперт». В наши дни слишком легко создавать компетентные работы и даже зарабатывать на жизнь, не имея многого из того, чего пытались достичь дизайнеры предыдущего поколения. Я лично нашел это хлопотным, как человек, который теперь находит конкуренцию там, где ее раньше не было.

    Например, закажите переводные письма Letraset. Погуглите, если не знаете, что это такое. Откройте упаковку, возьмите лист и попытайтесь «раскинуть» его по мере того, как вы набираете. Правильно. Я так и думал. Ты лучше нарисуй это сначала! Letraset очень быстро становится дорогим. Да, заточите несколько старых добрых No.2, возьмите ненужную бумагу и работайте над этим, пока не будете уверены, что каждая буква .10, которую вы выцарапываете и полируете, находится в правильном месте во всех отношениях.

    Научитесь решать проблемы как Мастер, рисуя

    Все элементы дизайна основаны на рисунке, как и живопись. Рисование — это фундаментальный навык визуальных художников любого толка. Чем лучше мы рисуем, тем лучше мы раскрашиваем и тем лучше проектируем, потому что рисование содержит в себе все проблемы и ловушки, которые мы должны преодолеть как дизайнеры. Если мы никогда полностью не решим проблемы с помощью карандаша, мы никогда не решим полностью наши проблемы графического дизайна с помощью гораздо более грубых инструментов.

    [альбом для рисования]

    Дальнейшее чтение:

    30-дневное задание по рисованию, день 3, натюрморт

    Я выполняю этот 30-дневный челлендж по рисованию, хотя я только публиковать раз в неделю.Я нашел 30-дневный челлендж по рисованию на Pinterest и нашел этот.

    1. Меч
    2. Завод
    3. Натюрморт
    4. Pokemon
    5. A Pokemon
    6. Robot
    7. A a Robot Good
    8. Идея
    9. Игрушка
    10. A a Pet
    11. Дракона
    12. DinoSaur
    13. A DinoSaur
    14. Mean Creature
    15. пейзаж
    16. танк
    17. аквариум
    18. космический корабль
    19. зодиака
    20. автомобиль
    21. сами
    22. HIPPY
    23. Hipster
    24. мастер
    25. a Zombie
    26. Alien
    27. A POLIEN
    28. Доктор, который злодей
    29. Персонаж комиксов
    30. Персонаж видеоигры
    31. Персонаж из книги
    32. Рыцарь
    33. Что-нибудь стимпанк
    Обычные натюрморты

    Натюрморт — произведение искусства, изображающее в основном неодушевленные предметы. Как правило, это обычные предметы природного происхождения (мертвые животные, цветы, продукты питания, растения, камни, раковины и т. д.) или искусственные (книги, монеты, стаканы, украшения, трубки, вазы и т. д.)

    Натюрморт зародился в средневековье и древнегреко-римском искусстве. Натюрморт возник как отдельный жанр и профессиональная специализация в западной живописи к концу 16 века и с тех пор остается значительным. Одним из преимуществ натюрморта является то, что он дает художнику большую свободу экспериментировать с расположением элементов в композиции картины.Натюрморт, как особый жанр, начался с нидерландской живописи 16-17 веков, а английский термин натюрморт происходит от голландского слова Stilleven . Ранние натюрморты, особенно до 1700 года, часто содержали религиозную и аллегорическую символику, относящуюся к изображаемым предметам. Более поздние натюрморты создаются с использованием различных медиа и технологий, таких как найденные объекты, фотография, компьютерная графика, а также видео и звук.

    Термин включает в себя изображение мертвых животных, особенно дичи.Живые считались анималистическим искусством, хотя на практике их часто рисовали с мертвых модели. Из-за использования растений и животных в качестве сюжета натюрморт категория также имеет общие черты с зоологическими и особенно ботаническими иллюстрация. Однако в изобразительном или изобразительном искусстве произведение не предназначено просто для правильно иллюстрировать тему.

    Еще жизнь занимала низшую ступень иерархии жанров, но была чрезвычайно популярен среди покупателей. Как и самостоятельный предмет натюрморта, Натюрморт включает в себя другие виды живописи с выдающимся элементы натюрморта, обычно символические, и «образы, опирающиеся на множество элементов натюрморта якобы для воспроизведения «кусочка жизнь'». Обманка картина, которая намеревается обмануть зрителя, заставив его думать, что сцена реальна, это особый тип натюрморта, обычно изображающий неодушевленные и относительно плоские предметы.

    Для своего натюрморта я выбрал бокал, наполненный вином. Что-то очень простое и легкое для меня.

    Родственные

    Бесплатные фото Графика Иллюстрация Векторный рисунок Натюрморт

    Наша команда была тщательно отобрана перед публикацией здесь.Если это было полезно для вас, пожалуйста, поделитесь с друзьями. Кроме того, вы также можете поощрить их, пригласив наших участников на одну чашку кофе (через Paypal).

    Великолепное изображение, которое вы можете использовать бесплатно для самых разных целей: печать, публикации, коммерческие продукты, обои и т. д. Использование лицензии Creative Commons Zero — CC0. Реферальная ссылка на Max Pixel (не обязательно).

    Картинка была помечена: Натюрморт, Рисунок, Иллюстрация, Графика, Вектор. Архивы в категории « Фоны/Текстуры «, максимальный размер 1968×800 пикселей, скачать можно в формате JPG.

    Наша система искусственного интеллекта выбирает и предлагает несколько связанных фотографий.
    Надеюсь, это поможет вам.

    Хэллоуин, Праздники, Тайна, Сказка, Луна, Ворона

    Улитка, Капли, Дождь, Рисование, Зеленый, Погода, Животное

    Смертность, Череп И Скрещенные Кости, Vanitas, Memento Mori

    Собака, Животное, Домашнее животное, Песик, Домашнее животное, Портрет

    Череп, День Мертвых, Смерть, Мексиканец, Муэртос

    Мозг, Разум, Психология, Идея, Рисование

    Цветок, Лепестки, Весна, Цветочный, Произведение искусства, Пастель, Лето

    Цветок, Абстракция, Живопись, Цветочный, Украшение, Дизайн

    Цветок, Украшение, Букет Цветов, Цвет, Флора

    Листья, Тропический, Лето, Экзотический, Зеленый, Растение, Пальма

    Картина, Рыцарь, Ночь, Масляные краски, Фэнтези, Луна

    Бумажный Цветочный Фон, Белый, Цветы, Бумага, Текстура

    Натюрморт Рисунок Иллюстрация Графика Вектор Цвет Фантазия Воображение Рисовать Красочный Бесплатные фото Бесплатные изображения Максимальный пиксель

    .
    Leave a comment
    by : alexxlab Графика

    Рисунки для детей карандашом графика: 10 уроков рисования простым карандашом

    Уроки графики в изостудии в Днепропетровске. Уроки графического рисования. Школа

    ПОРТФОЛИО


    Школа-студия академической живописи и рисунка. Уроки графики с нуля.  Изучение графического рисунка в школе-студии рисования.  Изучение рисунка простым карандашом в Днепропетровске. Обучение рисунку и графике в городе Днепропетровске. Изостудия академ-рисунка в городе Днепропетровске. Художественная школа-студия рисования.  Графический рисунок  гелевыми ручками в школе – студии академического рисования.  Художественная мастерская классического рисунка и живописи. Художественная студия рисования  для взрослых и детей . Мастер-класс по живописи и  рисунку для взрослых и детей с нуля.  Рисование карандашами для взрослых и детей. Научим рисовать с нуля в Днепропетровске. Подготовка к поступлению в ВУЗы и колледжи.

     

    Уроки графического рисунка в школе-студии академического рисования в городе Днепропетровске. Художественная студия рисования  научит взрослых и детей с нуля рисунку и живописи. Графика во все времена был и остается самой интересной техникой в искусстве рисования. Уроки графики очень востребованы  нашими учениками и являются основательной частью  обучения в академической школе рисования.  Своим минимализмом графические задания в рисовании формируют у студийцев точность и образное мышление, что способствует развитию творческих данных у наших учеников.

     

    Существуют разные направления графики  — станковая графика (рисунок, эстамп, лубок), книжная графика (иллюстрации, виньетки, заставки, буквицы, титул, авантитул, переплет, обложка, суперобложка), журнальная и газетная графика, миниатюра (вариант книжной графики), промышленная графика, экслибрис, плакат, шелкография, линогравюра.

     

    Работая над графическим  рисунком наши ученики учатся организовывать на плоскости графические элементы посредством знаний полученных в области абстрактной композиции.

    Используя тушь, рапидографы и гелиевые ручки, а также белую и цветную дизайнерскую бумагу ученики создают красивыми линиями и штрихами гармоничные графические шедевры на уроках в художественной школе-студии в городе Днепропетровске. Графические средства подачи в творчестве позволяют за короткий промежуток времени создать емкое произведение искусств и довести до совршенства свою творческую технику рисования. Работая с графическими средствами передачи изображения вы можете выработать свою уникальную технику рисования и добиться глубоких творческих успехов.

     

    Авторский 100% текст.  Регистрационный юридической код  статьи создан  15.02.2016/23:21/ antiplagiat/2497f3a563624

    Запрещается! Любое воспроизведение, републикация, распространение, переработка, перевод произведения, включение как составляющих частей в иные произведения и другие способы, предусмотренные Законом Украины и РФ » об авторском праве.

    Идеи для рисунков. Простейшие рисунки карандашом

    Что вы можете нарисовать обычным простым карандашом? Да, именно тем, которым все пользовались в школе. Детский рисунок, набросок или схему? А вы знаете, что существует целое искусство, в котором главным действующим лицом, а вернее предметом, является обычный серый грифель. Идеи для рисунков простым карандашом — простор для человеческой фантазии.

    Необычное искусство

    Одним из наиболее доступных, но в то же время неимоверно сложных видов графики является рисунок простым карандашом. Казалось бы, что можно нарисовать этим обычным для нас предметом? Оказывается, очень много. Некоторые музеи и выставки могут похвастаться наличием целого зала, в котором представлены рисунки карандашом. На них отображены самые разнообразные идеи для рисунков, пришедшие в момент вдохновения известным художникам.

    Непревзойденная игра теней, максимальное сходство с оригиналом завораживают и увлекают. Глядя на некоторые шедевры, очень сложно представить, что такое можно изобразить обычным серым грифелем. Кажется, что это непременно работа, выполненная в графическом редакторе, ну нельзя такое чудо нарисовать простым карандашом! Однако если присмотреться, то сдержать восхищенный вздох уже невозможно.

    Необходимые материалы

    Если вы думаете, что для создания подобного шедевра необходимо множество материалов, то вы сильно заблуждаетесь. Чтобы выполнить рисунок, нужно иметь альбомные листы, набор карандашей, ластик и точилку. Ну и, конечно же, идеи для рисунков. Если вы не представляете, что хотите воспроизвести, результат получится плачевный. Вернее, этого результата не будет вовсе.

    Для более сложных работ, конечно же, выбирается белоснежный, слегка шероховатый лист бумаги, на котором каждый штрих будет четким и заметным. В специализированных магазинах продают готовые наборы простых карандашей, но можно приобрести самые обычные. Они должны отличаться по уровню мягкости или твердости. Соответствующая маркировка непременно указана на них. Такая градация нужна для создания теней, без которых даже самые смелые идеи для рисунков карандашом обречены на провал.

    Не обойтись также без острого канцелярского ножа, который создаст необходимую остроту стержня. Желательно иметь несколько ластиков, которые будут стирать неудавшиеся или лишние линии в соответствии с типом карандаша.

    Для работ на профессиональном уровне потребуется мольберт, так как создавать картину лучше в вертикальном положении. В этом случае инструмент будет легко скользить по бумаге, точно передавая плавность линий.

    Как правильно держать инструмент?

    Для создания шедевра необходимо овладеть правильным захватом карандаша. Его нужно держать на ладони, прижимая большим пальцем. Такой захват следует вырабатывать, но после привыкания результаты будут очевиднее. В художественных школах навыку держания карандаша посвящены несколько первых уроков.

    Конечно же, простейшие рисунки карандашом не требуют специальных умений. Их можно создавать, держа инструмент, как ручку при письме. Ведь риска размазать простые рисунки просто не может быть: в них линии четкие и нет игры теней. Но все же, если вы хотите научиться рисовать профессионально, стоит с первых попыток держать инструмент мастерски.

    Простейшие рисунки карандашом

    Наиболее простыми в технике являются детские рисунки. Они совершенно несложные в исполнении, могут быть нарисованы в несколько этапов. Но именно с них можно начинать развивать художественный талант малышей или же пробовать свои силы в графике.

    Идеи рисунков для детей разнообразны. Это птички, животные, мультипликационные герои. Самое главное — внимательно рассмотреть предмет, учесть все его характеристики и попытаться воспроизвести увиденное. Так рисуют дети, так стоит попробовать и взрослому. Ниже представлены лишь некоторые идеи для рисунков с пошаговым выполнением всех операций.

    Согласитесь, такое сможет нарисовать каждый. Но и более сложные, казалось бы, предметы, можно воспроизвести на бумаге, если разбить целое на части. Смотрите, как просто создается прекрасный лебедь. Кстати, в этом рисунке уже используются некоторые приемы игры света и тени (обратите внимание на отражение в воде).

    Аналогичным образом, всего за 13 шагов, можно нарисовать для ребенка Китти — героиню мультсериала.

    То, что рисунок на первый взгляд простой, не беда. Если у вас он получился без проблем, начните работать с тенью, пытаясь придать фигурке объем. Для этого используйте карандаши разной твердости, а также экспериментируйте с силой нажима.

    Интересные идеи рисунков

    Если воспроизведение детских рисунков — это слишком легко для вас, создавайте свои картины. Начните с простых вещей — чашки, телефона, книги, постепенно усложняя свои работы. Поверьте, даже самый, казалось бы, заурядный предмет в талантливом исполнении заиграет очень привлекательно. Смотрите: на рисунке ниже изображена обычная лампочка. Но благодаря игре света и тени, воссозданной с помощью карандаша, рисунок очаровывает своей реалистичностью.

    Такие изображения часто называются 3D. Этой техникой овладеть довольно сложно, но все-таки возможно. В них реалистичность предметов построена на игре света и тени, отчего все нарисованное кажется настоящим.

    Но для начала стоит все же воплотить в реальность идеи для рисунков карандашом попроще. Это могут быть предметы домашнего обихода, живая природа, окружающая вас. Для работ посложнее можно выбрать цветной рисунок и нарисовать его в черно-белом цвете. Вариантов масса: стоит лишь оглянуться вокруг себя, а сердце подскажет, что именно отобразить на бумаге.

    Вместо эпилога

    Чтобы научиться рисовать, не обязательно брать уроки в художественной школе. Активные тренировки в домашних условиях могут также принести свои плоды. Первыми шагами могут стать простейшие рисунки карандашом. На их основе можно усложнять технику, фантазировать с формами — и тогда все должно получиться. Верьте в успех и совершенствуйте свои навыки.

    Графика и монохромное изображение. Творчество Часть вторая

    Каждое время года имеет свои краски, каждый день имеет свои краски, каждая минута имеет свои краски, настроение тоже имеет свои краски.

    Мы рисуем, мы пишем, мы создаем тот образ, который ближе к тому, что мы чувствуем именно в тот самый момент, когда решили отразить свое эмоциональные состояние.

    Весь мир в тебе, ты оставляешь его отражение в красках.

    Монохромное изображение

    Как это не покажется удивительным, даже монохромное изображение полно красок. В монохроме можно отразить весь мир, и он будет особенным, тонким и безграничным.

    Монохром, это не обязательно черно-белый.  Способов и техник выполнения монохромного изображения широчайший спектр.  Кирпично-красная или темно-коричневатая сангина,  рисунок, выполненный кофе.  Яркий рисунок, выполненный синими чернилами, ручкой.  Тончайшие линеры, различного диаметра рисующего элемента. Рисунок углем, угольным карандашом или графитными карандашами, черным карандашом. Белая пастель, белый карандаш, белая краска  на черной бумаге.  Тушь и перо. Тушь и кисть.

    Когда-то мы смотрели черно-белые фильмы, удивительные, казалось, что персонажи фильмов сойдут с экрана и мы будем участвовать в сценарии…

    А черно-белая фотография, насколько тонкая передача настроения. Порой, черно-белая фотография выглядит намного эмоциональнее и выигрышнее, чем цветная.

    Мы знаем картины И.И. Шишкина, его потрясающие пейзажи маслом, и насколько великолепна его графика, наброски и законченные пейзажи карандашом.

    Еще один уникальный художник, без которого мир графики был бы недосказанным  — Гурам Доленджашвили. Искристый снег и быстрая речка. Следы лап, оставленных на рыхлом снеге. Шапки снега, покрывающие ветки деревьев, каждая из миллионов снежинок прорисована каким-то таинственным образом.

    Животные, выполненные в графике, каждая шерстинка, короткая или длинная, образуют свой неповторимый рисунок. Глаза, отражающие весь спектр чувств этого удивительного существа.

    Сегодня известны потрясающие художники графики, которые отдали предпочтение монохромному изображению и их картины вдохновляют совершенством линии. Потрясающие офорты заслуженного художника России Александра Егоровича Ветрова, черно-белые и с легким, ненавязчивым присутствием цвета, подчеркивающим фактуру изображения. Деревенские пейзажи, покосившиеся домики, ранняя весна или морозная зима.

    Мир творчества многогранен, графика очень тонкая чувственная и прекрасная, мы восторгаемся офортами и ксилографией, рисунком и потрясающим видением художника.

    В следующий раз мы поговорим о пейзаже в японской и китайской живописи.

    Автор статьи: Ольга Соболь

    Простые картинки для рисования карандашом для детей

    Рисунки красками и карандашом. В этом уроке вы узнаете все основы.

    Простые наброски для детей в Paintingvalley Com. Коллекция
    Загрузить в полном разрешении

    Дети любого возраста, от малышей до детей постарше.

    Простые рисунки карандашом для детей . Простые рисунки карандашом для детей. Настольный планшет Handphone в оригинальном размере обратно к рисованию карандашом картинок для детей.Вы научитесь рисовать все виды милых мультяшных и даже реалистичных персонажей в кратчайшие сроки.

    Рисунки карандашом для детей легко рисунки карандашом для детей идеи рисования карандашом для детей легко. Начинающие и дети могут научиться рисовать более сотни рисунков для детей и дошкольников шаг за шагом, выполнив наши простые уроки рисования, или создать свой собственный рисунок для детей, следуя пошаговым инструкциям по рисованию видеоуроков. Посмотрите больше идей о простых шагах рисования, легком рисовании детей и простых рисунках.

    Посмотрите больше идей о том, как рисовать в tumblr, легко рисовать животных и легко рисовать картинки. Простые рисунки карандашом для детей. Карандашный рисунок для детей и карандашный набросок для детей Карандашный рисунок для детей легко 9 Карандашный рисунок для детей Карандашный рисунок для детей и карандашный набросок для детей Карандашный рисунок для детей Легкая галерея при рисовании эскизной живописи.

    Вы можете учиться, читая об инструментах, а также следуя за инструктором, чтобы изучить их методы. Ищите и сохраняйте идеи о простых рисунках для детей в Pinterest.Зарисовки карандашом для детей Простые рисунки карандашом для детей Рисование эскиза фото Зарисовки карандашом для детей Простые рисунки карандашом для детей.

    100 простых уроков рисования для начинающих и не только. Ищите и сохраняйте идеи о том, как легко рисовать карандашом, на Pinterest. Потому что даже простой карандаш не так прост, как вы думаете.

    Возьмите наш пошаговый рисунок для начинающих детей и всех остальных. Кто не хочет научиться рисовать. Черно-белое 01 сентября 2018 1520.

    Все наши простые учебные пособия снабжены очень удобными направляющими рисунками, которые можно распечатать, и они идеально подходят для всех возрастов. Скачать в полном разрешении Результат поиска на Paintingvalley Com
    Скачать в полном разрешении

    Рисунки карандашом Easy Pencil Drawings For Kids
    Скачать в полном разрешении

    24 Best Penguin Drawing Images Sketchs Cool Drawings Paintings
    Скачать в полном разрешении

    Как рисовать подсолнухи Easy Pencil Drawings For Kids Creative
    Скачать в полном разрешении

    Easy Pencil Drawings Поиск в Google Baby Blanket Drawi
    Скачать в полном разрешении

    Sketch Arts Страница 177 из 339 Все о Sketch Pencil Art
    Скачать в полном разрешении

    Простой рисунок карандашом для детей Рисование тигра Easy Fast
    Скачать Fu ll Разрешение

    Карандашные рисунки фей Простые карандашные наброски фей
    Скачать в полном разрешении

    Десять способов поощрить ребенка, который не любит рисовать.

    Мне часто задавали этот вопрос, когда я преподавала в дошкольных учреждениях, и даже сейчас друзья, семья и читатели блога задают мне –
    «Мой дошкольник не любит рисовать, что мне делать?»

    Короткий ответ на этот вопрос — «ничего».

    А длинный ответ? Ну…

    Конечно, рисование — отличный способ поработать над развитием мелкой моторики и творческих способностей, а также отработать навыки, связанные с письмом, но это не единственный способ работать над этими вещами, и обычно дети, которые не интересуются рисованием, заняты работой над другие навыки и придут к рисованию и письму в свое время, если вы не будете на них давить.

    Но я мама, и я знаю, каково это, когда у тебя есть ребенок четырех с половиной лет, который никогда не рисует, или ребенок, который, кажется, хочет рисовать, но ему не хватает уверенности, а я остаюсь при своем ответе «дон» Не волнуйся, я знаю, что это практически невозможно.

    А иногда некоторым детям требуется мягкое поощрение для работы над рисованием и связанными с ним навыками, и есть вещи, которые вы можете сделать, чтобы побудить тех, кто не умеет рисовать, взять карандаш и попробовать или найти другие способы работы над эти навыки.

    Вот несколько идей, которые вы могли бы попробовать…

    Десять способов поощрить ребенка, который не любит рисовать.

    Предлагайте интересные вещи для рисования с .
    Попробуйте что-нибудь другое, кроме скучных старых карандашей и фломастеров…

    Предлагайте интересные вещи для рисования.
    Получите интересный ящик с чем-то новым, необычным и немного сумасшедшим!

    Дайте им много возможностей для рисования без давления или направления.
    Некоторые дети уклоняются от рисования, потому что не думают, что могут «сделать это правильно», поэтому предоставление множества возможностей для рисования на их собственных условиях, когда это не является особым занятием, когда никто не смотрит, может дать эти дети пространство для экспериментов и практики без давления.
    Имейте всегда в свободном доступе принадлежности для рисования и бумагу, чтобы ваш ребенок мог рисовать или писать, когда захочет, без необходимости просить и без давления со стороны «наблюдающих». Попробуйте создать корзину для рисования с множеством забавных предметов.

    Сделайте так, чтобы это было связано с тем, что их интересует.
    Добавьте возможности рисования и создания отметок к любому занятию, которое они любят больше всего.

    Найдите веские причины рисовать и писать.
    Некоторым детям нужна веская практичная причина для рисования.

    • Отправьте письмо члену семьи (часто полезно попросить его написать первым, чтобы вы могли ответить).
    • Нарисуйте свои собственные открытки с помощью нашей бесплатной распечатки.
    • Нарисуйте список вещей, которые они хотели бы получить на день рождения или Рождество.
    • Сделайте табличку на дверь их спальни или табличку «Пожалуйста, не ломайте мою конструкцию Lego».
    • Вместе напишите и проиллюстрируйте книгу.
    • Создайте лист оберточной бумаги для особого подарка.

    Воззвание к их чувствам.
    Сделайте это грязно, если им нравится пачкаться — нарисуйте краску для пальцев, крем для бритья или ванночку для соли или песка.
    Или держите его в чистоте, если они склонны избегать грязной игры — положите краску для пальцев в сумку с защелкой и предложите карандаши или маркеры вместо мелков или мела, которые могут оставить руки жирными или грязными.

    Задействуйте все тело.
    Некоторым детям может быть трудно сидеть за столом и рисовать, а другим просто скучно, но участие в рисовании не только рук может помочь.

    • Купите большой рулон бумаги и нарисуйте на полу ОГРОМНУЮ картину.
    • Нарисуйте друг друга, чтобы сделать человека в натуральную величину.
    • Положите бумагу под качели и рисуйте, скользя мимо.
    • Нарисуйте мелом лабиринт снаружи на бетоне.

    Упростите начало работы.
    Иногда трудно или непосильно только начать. Попробуйте некоторые из наших бесплатных печатных подсказок по рисованию в качестве простой отправной точки, которая по-прежнему дает возможность для творчества, или используйте этот совместный рисунок каракули для веселого начала и деятельности, которую вы можете выполнять вместе.

    Делайте акцент на процессе, а не на продукте.
    Сделай свои занятия рисованием делами и рисованием, а не тем, как это выглядит в итоге.
    Обратите внимание и прокомментируйте, что делает ваш ребенок, когда рисует: «вы рисуете много линий», «вы использовали много красного и зеленого», «похоже, вам нравится творить». Попробуйте попросить их рассказать вам о своем рисунке и следовать их примеру, а не пытаться угадать, что это такое, или заставлять их говорить об этом. Замечательно, если ваш ребенок хочет показать вам свой рисунок или творение, но ничего страшного, если он этого не сделает.

    Примите тот факт, что многие из тех же навыков можно практиковать без использования карандаша.
    Ничего страшного, если ваш ребенок сейчас не увлекается рисованием. Вместо этого предложите множество других возможностей использовать эти маленькие мышцы рук и пальцев, чтобы они могли развивать свои навыки, координацию и уверенность, и осознавать, что есть много других способов быть творческими, чем просто заниматься искусством.

    У вас есть ребенок, который не увлекается рисованием?

    Тебя это беспокоит или ты довольствуешься тем, что позволяешь им рисовать в свое время?
    Возможно, у вас есть ребенок, который никогда не интересовался? Как вы их поощряли?

    Я хотел бы услышать ваши мысли и идеи — пожалуйста, оставьте комментарий!

    Папа раскрашивает детские рисунки

    Фред Джованнитти раскрашивает рисунки своих детей, летая в командировку.Фред Джованнитти Reddit гудит об отце, который берет рисунки своих маленьких детей в командировки и раскрашивает их, чтобы скоротать время в самолете.

    Это восхитительное сотрудничество отца, сына и дочери, а также впечатляющая коллекция сюрреалистического искусства. Мы связались с художником Фредом Джованнитти, который на Reddit известен под ником Tatsputin, чтобы узнать больше.

    «Я изобретаю промышленное оборудование, предназначенное для спасения и защиты морских экосистем мира», — написал он. «Чтобы оплатить это, я каждый месяц на 10 дней езжу в Лас-Вегас, где у меня есть небольшая тату-студия».

    В свободное от путешествий время Джованнитти живет в Делавэре с женой и двумя детьми, восьмилетним Фредди и шестилетней Софией.

    «Иногда людям кажется, что они не хотят беспокоить меня, поэтому они молчат», — сказал Джованнитти в электронном письме Business Insider, «Иногда, с более общительными товарищами по рейсу, они думают, что я раскрашиваю свои собственные рисунки. и всегда удивляюсь, узнав историю того, что я делаю. »

    Его работа с татуировками вдохновила его на то, как он решил растушевывать рисунки цветными карандашами. В последнее время он начал экспериментировать с раскрашиванием рисунков своих детей на своем iPad с помощью приложения ArtStudio после того, как сделал фотографию штрихового рисунка. Джованнитти сказал на самом деле ему требуется меньше времени для работы с цветными карандашами, потому что он более удобен в работе с карандашами, но в любом случае он может закончить рисунок за один из трехчасовых этапов своего полета через всю страну. 

    «Хотя я буду больше работать на планшете, — писал Джованнитти, — я буду придерживаться карандашей в основном для нашего будущего сотрудничества.»

    Бесплатно рисовать животных, Скачать бесплатно рисовать животных png изображения, Бесплатный клипарт в библиотеке клипартов

    животных для рисования для начинающих

    нарисуй шаг лошади

    раскраска детеныши животных

    простых идеи рисования животных

    эскиз животных для детей

    рисунка животных

    наземных животных рисунок для детей

    рисунка животных карандашом

    милых рисунка животных

    милый рисунок животных пустыни

    простых аниме-рисунка волка

    штриховых рисунка животных

    рисунок карандашом животных

    раскраска лев рисунок для детей

    рисунок диких животных

    простое рисование сельскохозяйственных животных

    карандашный рисунок животных

    эскиз животных

    искусство как рисовать животных

    божья коровка рисунок насекомого

    рисунка животных легко

    основы рисования

    einfache tiere zum zeichnen

    рисовать животных

    Раскраска

    азиатский слон

    животных в рисовании узоров

    эскиз

    эскиз рисования для детей

    рисунок всех животных

    рисунок животных легко

    простых реалистичных рисунка животных

    эскиз

    рисунок животного

    рисунок всех животных

    раскраски животных

    поэтапно как нарисовать животное

    животных рисуют со своими детёнышами

    рисунок разных животных

    изображение животного для рисования

    шаг за шагом реалистичный рисунок животного

    эскиз

    простых эскиза рисунков животных

    мультяшные картинки для рисования

    простых милых рисунка животных

    рисунок меха кошки

    совета и хитрости по рисованию животных

    животных для рисования от руки

    Эскиз

    исследований на животных

    11 Лучший цифровой блокнот для рисования для детей

    Есть что-то особенное в ощущении пера на бумаге. Те из нас, кто достаточно зануден, чтобы отправиться в ностальгическое путешествие по запаху свежей бумаги, несомненно, стары. Но просто нецелесообразно использовать бумагу для рисования глупых вещей, особенно когда есть блестящие и эффективные альтернативы, которые оставляют после себя гораздо меньший углеродный след. Более того, существует огромное количество возможностей для проверки будущего и ранней интеграции, которые сделают детей естественными подготовленными к своему будущему в эту цифровую эпоху.

    Так что можно с уверенностью сказать, что цифровые блокноты для рисования и письма — это то, что нужно, чтобы увлечь вашего ребенка.Эти планшеты никогда не истощаются, поэтому вам не придется беспокоиться о том, что у вашего ребенка закончится бумага для рисования и каракулей. Также помогает то, что, поскольку большая часть нашей работы теперь происходит на цифровых экранах, дети, которые начинают рано, станут естественными в том, что определенно станет нормой, когда они станут старше.

    Связанный: 8 лучших планшетов для рисования для детей в возрасте 8–12 лет

    Лучший 12-дюймовый блокнот для рисования для детей

    1. Cimetech 12-дюймовый блокнот для рисования на бумаге для рукописного ввода

    Вместительная 12-дюймовая доска для письма с ЖК-дисплеем и 12-месячный срок службы батареи гарантируют, что у вашего ребенка всегда будет чем заняться.Основная причина, по которой этот планшет занимает первое место в нашем списке, заключается в его функции многоцветного текста и большом количестве положительных отзывов от клиентов. Планшет был сделан особенно удобным для детей благодаря функции блокировки ключа , чтобы избежать случайного стирания.

    В качестве альтернативы планшет также предлагает удобство в виде функции очистки одним нажатием , позволяющей стереть все содержимое на планшете за один раз. Различное разнообразие цветов, встроенных в планшет, делает его хорошей альтернативой книжке-раскраске / каракулю, которая навсегда развлечет вашего ребенка. Планшет для рисования поставляется с дополнительной батареей.

    ► Купить на Amazon: Cimetech 12-дюймовый блокнот для рисования на бумаге для рукописного ввода (19,99 долл. США)

    2. Блокнот STREET WALK LCD

    Если вы ищете другой вариант в категории 12-дюймовых цифровых рисунков, ЖК-планшет для письма STREET WALK должен удовлетворить ваши требования. Помимо функций очистки одним нажатием и ключа блокировки , которые аналогичны функциям планшета Cimetech, особенностью, которая отличает планшет STREET WALK, является удобный слот для замены батареи, который позволяет легко извлечь батарею и заменить ее, если это то, что вы ищете.Нет необходимости что-либо откручивать на планшете, чтобы внести в него какие-либо изменения.

    ► Купить на Amazon: Блокнот STREET WALK с ЖК-дисплеем (19,99 долл. США)

    Связанный: Лучшие приложения для создания фильмов для детей на Android

    Лучший 10-дюймовый блокнот для рисования для детей

    1.

    Блокнот FLUESTON LCD

    Этот планшет чувствителен к давлению , что отличает его от остальных. Кроме того, он идеально подходит, если вы ищете легкий 10-дюймовый планшет, который может выдержать некоторый износ.Имейте в виду, что стилус планшета весом 9,6 унции не имеет специального слота на планшете и переносится отдельно.

    ► Купить на Amazon: блокнот для письма FLUESTON с ЖК-дисплеем (19,98 долл. США)

    2. Планшет для рисования с ЖК-дисплеем AFN

    Еще одна альтернатива, если вы не можете приобрести планшет FLUESTON. Этот планшет AFN оснащен аналогичной функцией, чувствительной к давлению, и довольно легкий: 9,9 унций . Этот планшет модели 2021 года обладает водонепроницаемостью и защитой от падений, что делает его более

    ► Купить на Amazon: планшет для рисования с ЖК-дисплеем AFN (18 долларов США.99)

    Связанный: Топ 7 приложений для рисования на Android для детей

    Лучший 8,5-дюймовый блокнот для рисования для детей

    1.

    ЖК-планшет SUNLU для письма 8,5-дюймовый блокнот для рисования

    С точки зрения компактного размера и облегченного варианта , планшет SUNLU идеально подходит для линейки 8,5-дюймовых планшетов . Он чрезвычайно экономичен и предлагает те же функции, что и 10- и 12-дюймовые планшеты, но меньшего размера. Рассмотрите этот планшет в качестве первого варианта, чтобы оценить, как ваш ребенок реагирует на него.

    ► Купить на Amazon: ЖК-планшет SUNLU для письма, 8,5-дюймовый блокнот для рисования (6,79 долл. США)

    2. Блокнот Sunany LCD

    Еще одна альтернатива в категории 8,5-дюймовых планшетов SUNANY с ЖК-экраном обладает всеми преимуществами, которые может предложить SUNLU. Дополнительным преимуществом является дополнительный Stylus на случай, если у вас есть неуклюжий и склонный к несчастным случаям ребенок. Чрезвычайно положительные отзывы клиентов Sunany также дают еще одну причину для рассмотрения.

    ► Купить на Amazon: блокнот Sunany с ЖК-дисплеем ($9.11)

    Лучшие цифровые блокноты для рисования и письма для малышей

    1. Красочная доска для рисования GUYUCOM

    Планшет GUYUCOM включает в себя все необходимое, чтобы сделать его удобным для малышей. Он имеет очаровательный дизайн в виде поросенка, защищен от падений и имеет экран, который отображает яркий и светящийся текст. Этот планшет также имеет наибольшее количество положительных отзывов родителей как для малышей, так и для детей.

    Купить на Amazon: Красочная доска для рисования GUYUCOM ($10,99)

    2.Блокнот для письма с ЖК-дисплеем Gatibilin

    Гораздо более новый вариант, ЖК-планшет для письма Gatibilin выполнен в симпатичном дизайне панды и обладает теми же функциями, что и вариант GUYUCOM. Также стоит отметить, что дизайн включает в себя кнопку стирания на симпатичном носу Панды. Этот планшет идеально подходит в качестве подарка.

    ► Купить на Amazon: блокнот для письма с ЖК-дисплеем Gatibilin (9,99 долл. США)

    Лучший цифровой блокнот для рисования и письма для детей-художников

    1. Wacom Intuos Draw

    Если ваш ребенок демонстрирует способности к рисованию и графическому дизайну, то Wacom Intuos Draw — это идеальный вариант, который оснащен пером без батареи и 4096 уровнями чувствительности к давлению, которые понадобятся новичку/ребенку.Подключите планшет к ноутбуку/Macbook и легко начните рисовать.

    Планшет также поставляется с двухлетней лицензией на программное обеспечение CLIP STUDIO PAINT PRO и 90-дневными пробными версиями Corel Painter Essential и Corel AfterShot Pro 3, что делает его идеальным планшетом для начинающих для вашего творческого ребенка.

    ► Купить на Amazon: Wacom Intuos Draw (79,78 долл. США)

    2. iskn The Slate 2+ Pencil & Paper Graphic Pad

    В отличие от Wacom, планшет iskn поставляется с экраном и более лоялен тематике планшета, чем планшет Wacom.Прелесть планшета в том, что его можно подключить к ноутбуку/Macbook, и он будет вести себя точно так же, как Wacom. Одним из неоспоримых аспектов планшета iskn является аутентичный опыт работы с ручкой и бумагой, который он обеспечивает. Он имеет размер бумаги A5, 6 часов автономной работы и 4 ГБ встроенной памяти, что делает его идеальным вариантом в качестве планшета для начинающих, как и Wacom. Кроме того, его также можно подключить к ноутбуку/Macbook, если вы хотите оптимизировать его производительность.

    ► Купить на Amazon: iskn The Slate 2+ Pencil & Paper Graphic Pad ($99.00)

    3. HUION HS64 Chips Special Edition Графический блокнот для рисования

    HUION HS64 — еще одна альфа-версия графического планшета для рисования. Он выполнен в симпатичной желтой теме злых птиц и может быть подключен к телефонам Android с помощью адаптера. Планшет совместим с Adobe Photoshop, Illustrator, Corel Painter, Autodesk Sketchbook, Manga Studio, Clip Studio и Zbrush, что делает его самым универсальным планшетом в этом списке. Перчатка для рисования также является дополнительным преимуществом, которое поставляется с этим планшетом.

    ► Купить на Newegg: HUION HS64 Chips Special Edition Графический блокнот для рисования (76,00 $)

    Основная задача всех цифровых планшетов — предоставить возможности, максимально приближенные к тому, что раньше ощущали ручка и бумага. Конечно, хотя опыт не будет абсолютно аутентичным, важна мысль. Поэтому мы надеемся, что вы найдете идеальный цифровой блокнот для своего ребенка в этом списке. Дайте нам знать в случае вопросов в комментариях. Берегите себя и будьте в безопасности!

    Графический дизайн для детей: инструменты, игры и идеи, чтобы заинтересовать их

    Ваши дети когда-нибудь спрашивают о вашей работе? Как вы объясните им, что такое графический дизайн? Почему бы не сделать еще один шаг и попытаться заинтересовать их графическим дизайном?

    Креативное мышление — это навык, который может использовать каждый.В этой статье есть множество инструментов, игр и идей, которые помогут вам начать эти разговоры со своими детьми, чтобы помочь создать новое поколение дизайнеров-мыслителей.

    Инструменты

    Вы можете помочь детям начать мыслить творчески в любом возрасте. Правильные игрушки и инструменты — отличное начало. И хотя ручки и карандаши — отличный вариант, они подходят не для всех возрастов.

    Начните с игрушек и игр, которые поощряют решение проблем на уровне возраста вашего ребенка.Вот несколько идей.

    Товары для творчества

    Никогда не помешает иметь много художественных принадлежностей. Ручки, карандаши, краски и много бумаги для творчества. Создайте пространство, где дети смогут играть с вами и даже рисовать вместе.

    Достаточно таких простых предметов, как цветные карандаши и книжки-раскраски, чтобы дать толчок творчеству ребенка. (И ваши тоже.) Простого наличия этих предметов в доме достаточно, чтобы стимулировать мышление графического дизайна.

    Цветовой круг

    Изготовьте или купите цветовой круг и расскажите о теории цвета и ее применении в дизайне.Цветовой круг, особенно с движущимися частями, может помочь объяснить отношения между цветами. (Вот недорогой, чтобы попробовать.)

    Это забавный инструмент с понятным визуальным оформлением. (И это может помочь детям почувствовать, что они играют с некоторыми из ваших «рабочих игрушек».)

    Программное обеспечение для цифрового рисования

    Мы знаем, что большая часть вашей работы, скорее всего, выполняется на компьютере, и ваши дети тоже об этом знают. Предоставление им цифрового инструмента для занятий графическим дизайном — забавный вариант.

    Tux Paint — это программа для рисования с открытым исходным кодом для детей. Он используется в школах по всему миру и имеет простой в использовании интерфейс для детей в возрасте от 3 до 12 лет. В нем даже есть классный мультяшный талисман, который может помочь детям в творческих упражнениях. Или вы можете попробовать простое приложение для рисования на iPad, такое как Paper.

    Игры

    Делайте игры из повседневных задач, которые побуждают детей мыслить творчески. Игры могут быть отличным способом сделать это.

    Дизайн-игра работает по правилам.Объясните детям, что вы не можете просто делать все, что хотите, как графический дизайнер, что вы должны слушать других и создавать что-то на основе того, что они вам говорят.

    Дизайн визитной карточки

    Создайте контролируемую игру, в которой вы создаете визитную карточку (или постер или что-то еще) определенного размера и с некоторыми прикрепленными правилами. (Возможно, каждый ребенок должен будет использовать свое имя в дизайне.) Сядьте и создайте эти проекты вместе и дайте возможность обсудить их, когда закончите.

    Обсуждение — важная часть процесса графического дизайна. Вернитесь ко второй фазе игры и попросите, чтобы что-то из этого разговора было включено в дизайн. Сделайте это забавным и глупым или поиграйте с элементами, которые уже есть, чтобы поддерживать интерес к проекту.

    В рамках этого проекта можно разработать логотип с именем каждого ребенка и даже сделать его ежегодным мероприятием. Может быть очень забавно наблюдать за тем, как меняется и переделывается их имя с годами.

    Типографическая игра Match

    Создайте свою собственную игру в духе шпионажа.Возьмите стопку журналов и выберите стиль шрифта; попросите детей найти подходящий стиль.

    Вы также можете играть в эту игру в машине, используя дорожные знаки и рекламные щиты.

    Игра — отличная возможность поговорить о сходстве шрифтов — шрифтах с засечками, гротесках и шрифтах, восходящих и нисходящих элементах, контрасте и цвете.

    Для детей старшего возраста в Интернете также доступно множество игр на сопоставление шрифтов.

    Взрывающиеся котята

    Хорошо, это коммерчески доступная игра, но карты наполнены крутыми рисунками от The Oatmeal, и эта игра понравится и взрослым.

    Карточная игра «Взрывающиеся котята», вероятно, предназначена больше для детей старшего возраста, но она может стать началом отличного разговора о том, что графический дизайн вездесущ и как творческие идеи могут превратиться в продукты, которые люди идут и покупают.

    Может быть, это даже начало разговора о карьере в графическом дизайне.

    Идеи

    Иногда лучший способ заинтересовать детей графическим дизайном — поговорить о нем или вместе изучить творческие способности.

    Создай свою собственную футболку

    Сделай что-нибудь осязаемое.Вместе разработайте дизайн футболки и наденьте его на рубашки, которые вы сможете носить. (Наборы для термоперевода, которые вы можете создать и использовать дома, являются простым вариантом.)

    Создайте дизайн вместе, распечатайте его и наденьте на рубашки для всей семьи.

    Создайте футболку для особого случая или в подарок. Сядьте со своими детьми и сделайте что-нибудь вместе — даже младшие дети, которые не готовы работать с компьютером, могут рассказать вам, как создать дизайн, пока вы работаете над ним вместе.

    Бонус

    : отправляйтесь на экскурсию, если вы знаете трафаретную печать в вашем районе, и напечатайте индивидуальный дизайн, чтобы дети могли увидеть, как рисунок попадает на рубашку с помощью этого процесса печати.

    Нарисуй картинку

    Нет ничего лучше, чем рисовать наброски или рисовать, чтобы процесс проектирования казался увлекательным. И почти каждый может это сделать. (Не обязательно быть великим художником.)

    Возьмите эту идею из семинара по графическому дизайну, который я посетил, и попробуйте ее с детьми:

    Возьмите один лист бумаги и дайте всем что-нибудь для рисования.Каждый человек может добавлять к картинке, когда вы ее передаете. Настоящих правил нет; в голове нет цели. Каждый человек может что-то нарисовать, чтобы внести свой вклад в дизайн по мере того, как он приходит к нему.

    Вы можете установить ограничения, например, каждый человек может рисовать, пока не возьмет карандаш, или каждый человек может добавить только одну фигуру.

    История на бумаге будет расти, расширяться и меняться по ходу каждого человека. Вы можете получить сцену в парке или глупого монстра.

    И эта концепция дизайна похожа на работу над проектами, в которых участвует множество людей, они всегда могут принять собственную форму.

    Объясните визуально

    Одним из лучших упражнений в графическом дизайне является объяснение того, что дизайнер Дин Випонд делает в классе, когда говорит о дизайне с детьми. (Это так просто и довольно увлекательно и информативно!)

    Несмотря на то, что в его выступлении содержится множество крутых идей по использованию графического дизайна для детей, его представление одного и того же предложения двумя способами является наиболее увлекательным:

    Я показал им простое предложение, которое мы все вместе прочитали: «Я встретил большую собаку.(См. иллюстрацию выше.) Затем я показал им то же самое предложение, чтобы мы снова его прочитали. Видите, как изменение размера слова «большой» делает предложение более захватывающим? Это заставляет вас произнести это слово иначе, чем в прошлый раз, и заставляет задуматься, насколько велика эта собака.

    Вы можете узнать больше в полной статье.

    .
    Leave a comment
    by : alexxlab Графика

    Деревья рисунки графика: Рисунок деревья?image_type=vector: изображения, стоковые фотографии и векторная графика

    Изображение ландшафта средствами графики — презентация онлайн

    МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
    ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
    ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
    РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ –
    МСХА имени К.А. ТИМИРЯЗЕВА
    (ФГБОУ ВПО РГАУ — МСХА имени К.А. Тимирязева)
    Факультет Садоводства и Ландшафтной архитектуры
    Кафедра Ландшафтной архитектуры
    РИСУНОК И ЖИВОПИСЬ
    ЛЕКЦИЯ 4.
    ИЗОБРАЖЕНИЕ ЛАНДШАФТА СРЕДСТВАМИ
    ГРАФИКИ.
    Скакова А.Г.
    доцент
    Композиция изображения и пропорции.
    Выявление светотеневых соотношений
    и воздушная перспектива.
    Пространственные планы.
    Построение перспективного изображения
    ландшафта.
    Изображение деревьев.
    Изображение травянистых растений.

    3. Композиция изображения и пропорции

    1. Выбор сюжета: тема, доминанта, акценты, фон,
    однородность и разнообразие, пространственные
    планы.
    2. Выбор угла зрения и пропорций изображения:
    панорама, вид, деталь.
    3. Композиция изображения на листе, формат и
    пропорции листа. Использование видоискателя.
    4. Общее соотношение: небо — массивы деревьев –
    земля. Равновесие тоновых масс.
    5. Соотношение линий: горизонтальные, восходящие,
    нисходящие, прямые, ломанные, округлые.

    4. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    В картинную плоскость не попадают линейные элементы (ограда,
    сооружения, дорожки). Нет необходимости определять тип
    изображения, достаточно проанализировать высоту горизонта.

    5. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    В картинную плоскость не попадают линейные элементы (ограда,
    сооружения, дорожки). Нет необходимости определять тип
    изображения, достаточно проанализировать высоту горизонта.

    6. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    Основа выразительности пейзажа – светотеневые соотношения,
    общий колорит, воздушная перспектива.

    7. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    Основа выразительности пейзажа – светотеневые соотношения,
    общий колорит, воздушная перспектива.

    8. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    Основа выразительности пейзажа – светотеневые соотношения,
    общий колорит, воздушная перспектива.

    9. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    Основа выразительности пейзажа – светотеневые соотношения,
    общий колорит, воздушная перспектива.

    10. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    11. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ГРАФИКЕ

    Выявление светотеневых соотношений.
    С. Андрияка

    12. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ГРАФИКЕ

    Выявление светотеневых соотношений.
    С. Андрияка

    13. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ГРАФИКЕ

    Выявление светотеневых
    соотношений и
    пространственных планов.
    С. Андрияка

    14. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ГРАФИКЕ

    Выявление
    особенностей
    освещения.
    С. Андрияка

    15. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ГРАФИКЕ

    Выявление светотеневых
    соотношений. Учебная
    работа.

    16. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ГРАФИКЕ

    Выявление светотеневых соотношений. Учебная работа.

    17. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    Пространственные планы в природном
    ландшафте.

    18. АНАЛИЗ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    Композиция пейзажного парка строится на расстановке
    акцентов и соотношении пространственных планов.

    19. ПРОСТРАНСТВЕННЫЕ ПЛАНЫ В САДОВО-ПАРКОВОЙ КОМПОЗИЦИИ

    I – рама
    пейзажной
    картины
    II – кулисы
    III – акцент

    20. ПРОСТРАНСТВЕННЫЕ ПЛАНЫ В САДОВО-ПАРКОВОЙ КОМПОЗИЦИИ

    • Варианты решения рамы на первом плане:
    деревья, раскидистая крона, тень от
    древесного массива.

    21. ПРОСТРАНСТВЕННЫЕ ПЛАНЫ В САДОВО-ПАРКОВОЙ КОМПОЗИЦИИ

    Выявление пространственных планов
    пейзажной картины позволяет решать
    несколько задач.
    При анализе произведений садовопаркового искусства – понять
    композиционный замысел.
    При выполнении пейзажных зарисовок с
    натуры определить выразительность вида,
    подобрать графические и живописные
    приемы передачи линейной и воздушной
    перспективы.
    При проектировании сада или парка –
    разработать детали ландшафтного решения
    основных видовых точек.

    22. ПРОСТРАНСТВЕННЫЕ ПЛАНЫ В САДОВО-ПАРКОВОЙ КОМПОЗИЦИИ

    I – рама
    пейзажной
    картины
    II – кулисы
    III – акцент

    23. ПРОСТРАНСТВЕННЫЕ ПЛАНЫ В САДОВО-ПАРКОВОЙ КОМПОЗИЦИИ

    I – рама
    пейзажной
    картины
    II – кулисы
    III – акцент

    24. ПРОСТРАНСТВЕННЫЕ ПЛАНЫ В САДОВО-ПАРКОВОЙ КОМПОЗИЦИИ

    I – рама
    пейзажной
    картины
    II – кулисы
    III – акцент

    25. ПОСТРОЕНИЕ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    Зарисовка по
    фотографии:
    1. Определение
    положения линии
    горизонта и
    основания картины.
    2. Определение типа
    изображения:
    перспектива угловая
    или фронтальная.
    3. Определение
    пространственных
    планов.

    26. ПОСТРОЕНИЕ ПЕРСПЕКТИВНОГО ИЗОБРАЖЕНИЯ ЛАНДШАФТА

    Зарисовка по
    фотографии:
    выявление
    пространственных
    планов.

    27.

    ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ЛИНЕЙНОЙ ГРАФИКЕЗарисовка с натуры: выявление
    пространственных планов.

    28. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ЛИНЕЙНОЙ ГРАФИКЕ

    Зарисовка по фотографии:
    выявление пространственных
    планов.

    29. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ТОНОВОЙ ГРАФИКЕ

    Зарисовка с натуры:
    выявление
    пространственных
    планов.

    30. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ТОНОВОЙ ГРАФИКЕ

    Зарисовка с натуры: выявление пространственных
    планов с помощью различной степени обобщения
    изображения.

    31. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ТОНОВОЙ ГРАФИКЕ

    Выявление
    светотеневых
    соотношений и
    пространственных
    планов.

    32. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ТОНОВОЙ ГРАФИКЕ

    Выявление пространственных планов.

    33. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ТОНОВОЙ ГРАФИКЕ

    Прорисовка первого плана.

    34. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ТОНОВОЙ ГРАФИКЕ

    Прорисовка первого плана.

    35. ИЗОБРАЖЕНИЕ ЛАНДШАФТА В ТОНОВОЙ ГРАФИКЕ

    Пространственные планы выявлены светотенью.
    Прорисовка первого плана — изучение фактуры
    поверхностей.

    36. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Реалистические
    изображения.
    Конструктивный рисунок.

    37. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Реалистические изображения.
    Конструктивный рисунок и обобщение
    формы

    38. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Реалистические
    изображения.
    Конструктивный рисунок.

    39. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Реалистические изображения.
    Рисунок с обобщением формы и
    анализ светотени.

    40. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Реалистические изображения деревьев для разных пространственных планов.

    41. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Стилизованные изображения.

    42. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Стилизованные изображения.

    43. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Стилизованные изображения используются
    на первом пространственном плане проектной
    зарисовки.

    44. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Обобщение формы
    кроны.

    45. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ СРЕДСТВАМИ ГРАФИКИ

    Стилизованные
    изображения.

    46. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ НА ЧЕРТЕЖАХ

    Стилизованные
    фронтальные
    изображения,
    компонуются на
    листе в зависимости
    от
    пространственного
    плана ландшафта.

    47. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ НА ЧЕРТЕЖАХ

    Стилизованные фронтальные изображения,
    компонуются на листе в зависимости от
    пространственного плана ландшафта.

    48. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ НА ЧЕРТЕЖАХ

    49. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ НА ЧЕРТЕЖАХ

    Стилизованные
    изображения для
    планов, используются в
    графике генерального
    плана сада.

    50. ИЗОБРАЖЕНИЕ ДЕРЕВЬЕВ НА ЧЕРТЕЖАХ

    Стилизованные
    изображения для
    планов, используются в
    графике генерального
    плана сада.

    51. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    • Обобщение формы ветви. Соотношение длины и
    толщины ветви.
    • Характер ветвления и расположение ветвей второго
    и т.д. порядков, очередное и супротивное ветвление,
    расположение ветвей и побегов мутовками.
    • Угол между стволом и ветвями, ветвями и побегами.
    • Взаимный разворот частей ветви или побега между
    узлами.
    • Гибкость ветвей и побегов.
    • Соотношение массивов листьев и длины побегов,
    крепление черешка к побегу, расположение листьев
    на черешках, их подвижность. Обобщение формы
    листа.

    52. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    53. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    Анаиз строения цветка.

    54. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    55. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    56. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    57. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    58. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    59. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    60. ИЗОБРАЖЕНИЕ ВЕТВЕЙ ДЕРЕВЬЕВ

    61. ИЗОБРАЖЕНИЕ КУСТАРНИКОВ

    62. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    • Отдельный цветок или соцветие.
    • Соотношение размеров цветка, цветоноса и стебля.
    • Количество и расположение лепестков.
    Геометрическая схема. Крепление на цветоносе,
    наличие чашелистиков, покровных чешуй.
    • Общая форма цветка («диск», «бокал», «шар»,
    «колокольчик»).
    • Текстура лепестка, форма края. Распределение
    светотени.
    • В соцветиях и букетах: цветы на ближнем и дальних
    планах, взаимное перекрытие.

    63. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    Поэтапное рисование.

    64. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    Обобщение формы и анализ
    строения цветка.

    65. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    66. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    67. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    68. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    Анализ строения цветка и
    стилизация изображения.

    69. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    Стилизованные изображения

    70. ИЗОБРАЖЕНИЕ ЦВЕТОВ

    Тоновой рисунок
    растения.

    71. ИЗОБРАЖЕНИЕ ЦВЕТНИКОВ И КОМПОЗИЦИЙ ИЗ ТРАВЯНИСТЫХ РАСТЕНИЙ

    Эскиз в составе проекта

    72. ИЗОБРАЖЕНИЕ ЦВЕТНИКОВ И КОМПОЗИЦИЙ ИЗ ТРАВЯНИСТЫХ РАСТЕНИЙ

    • С.Андрияка

    73.

    ИЗОБРАЖЕНИЕ ЦВЕТНИКОВ И КОМПОЗИЦИЙ ИЗ ТРАВЯНИСТЫХ РАСТЕНИЙ

    74. ИЗОБРАЖЕНИЕ ЦВЕТНИКОВ И КОМПОЗИЦИЙ ИЗ ТРАВЯНИСТЫХ РАСТЕНИЙ

    С.Андрияка

    75. ИЗОБРАЖЕНИЕ ЦВЕТНИКОВ И КОМПОЗИЦИЙ ИЗ ТРАВЯНИСТЫХ РАСТЕНИЙ

    76. ИЗОБРАЖЕНИЕ ЦВЕТНИКОВ И КОМПОЗИЦИЙ ИЗ ТРАВЯНИСТЫХ РАСТЕНИЙ

    77. ИЗОБРАЖЕНИЕ ЦВЕТНИКОВ И КОМПОЗИЦИЙ ИЗ ТРАВЯНИСТЫХ РАСТЕНИЙ

    Как в Санкт-Петербурге убирали снег до революции

    В первых частях наших зимних текстов читайте о жизни петербуржцев без холодильника, ледовом трамвае, забавах на льду Невы, ледяном доме Анны Иоанновны и катании на буерах.

    Полтора века назад дороги не то что не расчищали, а наоборот — старательно забрасывали снегом. Картина, которая сегодня вызвала бы волну возмущения, до революции воспринималась совершенно нормально. Основным зимним транспортом были сани, которые мчались быстрее колёсных повозок и обходились дешевле в обслуживании. Никому и в голову не приходило освобождать мостовые из-под снега, чтобы передвигаться на двуколках.

    Сани у Александровского сада. 1914 год

    Фото: vk.com

    На Английской набережной. 1900 год

    Фото: pinterest.ru

    Н. Сверчков «Николай Первый в санях». 1853 год

    Фото: rusmuseumvrm.ru

    Теофиль Готье, писатель:

    «Уже нельзя было встретить на улице ни одной колёсной повозки. Казалось, что за ночь Россия вернулась к более низкой стадии цивилизации, когда колесо ещё не было придумано. […] В России в течение шести месяцев в году снег — это универсальная железная дорога, белые рельсы которой тянутся во всех направлениях и позволяют ехать куда хочешь».

    А вот тротуары очищали от снега и посыпали песком. Правда, это не сильно спасало. По наблюдениям Готье, пешком передвигались только редкие простолюдины в валенках. В любой другой обуви ходить было скользко.

    Уборка дворниками снега на улицах Петербурга. Рисунок из британского журнала «Графика»

    Централизованного коммунального хозяйства не было, за чистоту тротуаров и дворов отвечали домовладельцы. Каждый дом обслуживали несколько дворников, которые убирали снег на участке, сбивали сосульки и освобождали крыши от наледи. Кто-то мог дежурить у ворот с метлой и совком, чтобы тут же подобрать лошадиный навоз, пока его не растащили по всей дороге.

    За тем, как соблюдаются требования благоустройства, следила полиция. За малейшее нарушение выписывались большие штрафы, поэтому с квартальными надзирателями старались дружить. Взятки были обычным делом. Дмитрий Засосов и Владимир Пызин вспоминали:

    «По праздникам взятки носили почти узаконенный характер. Считалось обязательным, чтобы домовладельцы […] посылали всем начальствующим в полицейском участке к Новому году и прочим большим праздникам поздравления со „вложением“».

    Фото: russiainphoto.ru

    Городовые у казармы Александровского пригородного участка части. 1903 год

    Сбрасывать грязный снег в реки и каналы категорически запрещалось. Тем, кто попадался, грозили крупные штрафы. Убранный снег следовало отвозить на специальные свалки на окраинах, что было и хлопотно, и довольно накладно.

    Решение нашлось: во дворах стали сооружать снеготаялки. Это большой деревянный ящик, внутри которого — железный шатёр, где горели дрова. Снег закидывали в конструкцию, он быстро таял, а вода по специальной трубе уходила в канализацию. Ящик воспламениться не мог, поскольку всегда был сырым.

    Снеготаялка у Александровского сада в Москве. 1907 год

    Улицы убирали рано утром, при серьёзных снегопадах — несколько раз в день. Но, конечно, только в центре. Городские окраины утопали в сугробах до самой весны.

    До конца 1920-х годов в коммунальном хозяйстве господствовал ручной труд. Массово внедрять технику стали лишь столетие назад.

    Рекомендуем ознакомиться с другими текстами для влюблённых в Петербург.

    Если вы нашли опечатку или ошибку, выделите фрагмент текста, содержащий её, и нажмите Ctrl+↵

    Сила ветра. Шкала Бофорта

    Сила ветра у земной поверхности по шкале Бофорта
    (на стандартной высоте 10 м над открытой ровной поверхностью)
    Баллы Бофорта Словесное определение силы ветра Скорость ветра, м/сек Действие ветра
    на суше на море
    0 Штиль 0-0,2 Штиль. Дым поднимается вертикально Зеркально гладкое море
    1 Тихий 0,3-1,5 Направление ветра заметно по относу дыма, но не по флюгеру Рябь, пены на гребнях нет
    2 Лёгкий 1,6-3,3 Движение ветра ощущается лицом, шелестят листья, приводится в движение флюгер Короткие волны, гребни не опрокидываются и кажутся стекловидными
    3 Слабый 3,4-5,4 Листья и тонкие ветви деревьев всё время колышутся, ветер развевает верхние флаги Короткие, хорошо выраженные волны. Гребни, опрокидываясь, образуют стекловидную пену, изредка образуются маленькие белые барашки
    4 Умеренный 5,5-7,9 Ветер поднимает пыль и бумажки, приводит в движение тонкие ветви деревьев Волны удлинённые, белые барашки видны во многих местах
    5 Свежий 8,0-10,7 Качаются тонкие стволы деревьев, на воде появляются волны с гребнями Хорошо развитые в длину, но не очень крупные волны, повсюду видны белые барашки (в отдельных случаях образуются брызги)
    6 Сильный 10,8-13,8 Качаются толстые сучья деревьев, гудят телеграфные провода Начинают образовываться крупные волны. Белые пенистые гребни занимают значительные площади (вероятны брызги)
    7 Крепкий 13,9-17,1 Качаются стволы деревьев, идти против ветра трудно Волны громоздятся, гребни срываются, пена ложится полосами по ветру
    8 Очень крепкий 17,2-20,7 Ветер ломает сучья деревьев, идти против ветра очень трудно Умеренно высокие длинные волны. По краям гребней начинают взлетать брызги. Полосы пены ложатся рядами по направлению ветра
    9 Шторм 20,8-24,4 Небольшие повреждения; ветер срывает дымовые колпаки и черепицу Высокие волны. Пена широкими плотными полосами ложится по ветру. Гребни волн начинают опрокидываться и рассыпаться в брызги, которые ухудшают видимость
    10 Сильный шторм 24,5-28,4 Значительные разрушения строений, деревья вырываются с корнем. На суше бывает редко Очень высокие волны с длинными загибающимися вниз гребнями. Образующаяся пена выдувается ветром большими хлопьями в виде густых белых полос. Поверхность моря белая от пены. Сильный грохот волн подобен ударам. Видимость плохая
    11 Жестокий шторм 28,5-32,6 Большие разрушения на значительном пространстве. На суше наблюдается очень редко Исключительно высокие волны. Суда небольшого и среднего размера временами скрываются из вида. Море всё покрыто длинными белыми хлопьями пены, располагающимися по ветру. Края волн повсюду сдуваются в пену. Видимость плохая
    12 Ураган 32,7 и более   Воздух наполнен пеной и брызгами. Море всё покрыто полосами пены. Очень плохая видимость

    Получить рисунок дуба Картинки – специальное изображение

    Получить рисунок дуба Изображения – специальное изображение перейти к содержанию

    Получить рисунок дуба
    Картинки     . Позвольте мне показать вам, как нарисовать дуб в этом пошаговом уроке. Вы можете отредактировать любой из рисунков с помощью нашего онлайн-редактора изображений перед загрузкой.

    Томас Хаскетт Иллюстрация: Дуб, Хелиган с сайта 1.bp.blogspot.com

    Этот старый дуб, кажется, всегда был на участке.Сначала определитесь с размером дуба, который вы собираетесь рисовать. Деревья – неотъемлемая часть ландшафта.

    Узнайте, как рисовать деревья в этой простой пошаговой демонстрации процесса рисования дуба.

    Скачать векторный рисунок дуба. Они хорошо защищают от ветра. Сначала определитесь с размером дуба, который вы собираетесь рисовать. Лучший выбор бесплатных векторных изображений, графики и стоковых иллюстраций дуба.


    Источник: getdrawings.ком

    Пробки, используемые в качестве пробок для винных бутылок, изготовлены из дуба, который вы хотите нарисовать из мультфильма?


    Источник: getdrawings.com

    Узнайте, как рисовать деревья в этой простой пошаговой демонстрации процесса рисования дуба.


    Источник: flyoungstudio.files.wordpress.com

    Скачайте векторную иллюстрацию Дуб прямо сейчас.


    Источник: images.hellokids.com

    Узнайте, как рисовать изображения дуба, используя эти контуры, или распечатайте их только для раскрашивания.


    Источник: i.ytimg.com

    Вот результат моего последнего видео, в котором показан процесс создания карандашного рисунка реалистичного дерева.


    Источник: http://www.boulderfurniturearts.com

    Доступность и возможность поиска среди миллионов бесплатных изображений, фотографий и векторов.


    Источник: 1.bp.blogspot.com

    Скачать изображения и фотографии дуба.


    Источник: 4.bp.blogspot.com

    Здесь представлено 54+ изображения для рисования дуба, которые можно бесплатно скачать, распечатать или поделиться.


    Источник: http://www.joshuanava.biz

    Вы ищете изображение дуба в формате PNG или вектор?

    Нравится:

    Нравится Загрузка…

    Связанные

    Почтовая навигация

    2д лэнд арт. Игровое искусство 2D. Вот мое портфолио: https://www. Просмотрите этот рекомендуемый выбор из Интернета для использования на веб-сайтах, в блогах, социальных сетях и других ваших продуктах.Большинство земных работ не были посвящены красоте и эстетическому удовольствию, почти все они подчеркивали отказ от товарного статуса и массовых выставочных площадок, опираясь исключительно на понятие… Версия 2. 5D Platformer Kit, доступный в Unity Asset Store. Скачать бесплатно 2D игровые активы. BIMкомпоненты. Эта неизбежная связь или даже зависимость от более традиционных средств 2D-фотографии и кино еще больше отдалила ленд-арт от концептуального искусства. Он имеет классический и дружественный интерфейс и родной файл .Хотя учащиеся могут оттачивать технические навыки при создании ландшафтов, они также могут развивать способности пространственного мышления, зрительно-моторную координацию и креативность. Сыграйте роль короля или королевы верхом на лошади и войдите в процедурно сгенерированное царство, предназначенное для поддержания королевства, затем бросьте золото крестьянам и превратите их в своих верных подданных, чтобы сделать The Corgi Engine is a Unity 2D + 2. 2K Взгляды. cgsociety. Вы также можете добавить в процесс обучения и связать ландшафтное искусство с другим контентом, который вы сейчас используете в KinderArt.Купите или загрузите бесплатные 2D-модели или спрайты людей, существ, роботов и т. д. Земля Террарии. Все это в красивом пиксель-арт стиле. Раньше разработка точных чертежей и сложных чертежей выполнялась вручную с помощью наборов линеек, транспортиров и других измерительных приборов, требующих огромной ловкости и острого глаза для правильного использования. Программное обеспечение САПР для 2D-черчения можно использовать для более быстрого и точного проектирования проектов без использования… 2D-символов. 5 долларов. Я профессиональный 2D-универсал, работаю в индустрии 2D-анимации в качестве фрилансера в течение трех лет и считаю, и работал над terraria pixel art 4 mario, как создать его на YouTube.Победители будут выбраны из множества категорий, включая портрет/рисунок, натюрморт, пейзаж, абстракцию и животное/дикую природу. знак0. 2D NFT Designer Art Manager RoyaLand NFT 2d аниматор Punch Entertainment (Вьетнам) авг. 2018 — нояб. 2019 1 год 4 месяца. В нашем магазине представлены игровые 2D-арты основных категорий: иконки, спрайты, наборы тайлов, графический интерфейс, персонажи, фоны, игровые наборы и… Lands Design — это бесплатное программное обеспечение для ландшафтного дизайна, которое может помочь в создании 2D- и 3D-презентаций, обеспечивающих реалистичный вид. того, как именно будет выглядеть ваш ландшафт после строительства.Чертежи используют программное обеспечение для автоматизированного проектирования (САПР) для разработки планов этажей, чертежей разрешений на строительство, планов осмотра зданий и ландшафтных макетов. Это наборы, графический интерфейс, фоны, наборы тайлов, иконки и бесплатные спрайты 2D-персонажей. exe, SSWC1_8A9843B8. Это бесплатное программное обеспечение для черчения, обеспечивающее высокую производительность и передовые инструменты САПР. 1803 HQ Волшебный мир, НАБОР фонов, ручная роспись Высококачественные ручные дневные, вечерние и ночные фоны и графика платформ…. Ищете услуги ландшафтного дизайна онлайн? Просмотрите фрилансеров Fiverr по навыкам, отзывам и цене.Сохранять. Smoothie-3D — одно из лучших онлайн-решений для преобразования фотографий в 3D-модели. Хотя 2D-моделирование является более старой технологией, и многие предприятия начали заменять ее 3D-моделированием, в определенных ситуациях оно по-прежнему ценно. 425, 903 P. 0 нашего популярного Lava Land. Программное обеспечение 2D CAD оставило это в прошлом. Чтобы создать 2D-игру, настройте свой проект Unity, а затем ознакомьтесь с соответствующими концепциями в следующем порядке: Основы. синтез материалов, процессов и идей.NanoCAD — профессиональная программа, предлагающая мощный табличный редактор с множеством новых возможностей. 4 из 5 звезд 111 $89. HD Водные обои. Клод Моне: «Водяные лилии», 1919. 3D-искусство. Композиция в 3D-искусстве определяется размерами… В этом увлекательном уроке вы узнаете, как очень легко создавать 2D-или плоские пейзажи в Photoshop, используя всего лишь инструмент лассо. Если вы ищете тему 2D-пейзажных обоев, вы посетили идеальный блог. Когда закончите, проверьте свою работу в 3D одним нажатием кнопки.Back to the Drawing Board — мощное приложение для 2D-САПР и технического рисования. . Продавайте нестандартные творения людям, которые… На вершине мира — 2D-пейзаж — это цифровая работа Сары Бэнк, которая была загружена 17 августа 2016 года. Включает биографическую и библиографическую информацию, а также сведения о прошедших, текущих и предстоящих выставках. Оставить комментарий Опубликовано в 2d Tagged дизайн среды большое предназначение. Он представляет собой непрерывную, хотя и периодически нарушаемую традицию античности.2017] Заявленное изобретение может быть отклонено в соответствии со статьей 35 U. Landscape Images & Pictures. Геометрические фигуры являются математическими и включают в себя квадраты, круги и треугольники. com, на котором представлено множество бесплатных идей для занятий творчеством для детей (надеюсь, они вам понравятся!). LOVE The KinderArt Club — членский портал, предназначенный для родителей, школьников, школьников, художников в классе… Файлы включают в себя как 2D-, так и 3D-рисунки, и их можно скачать прямо из этой статьи.Готовые к производству 2D-инструменты. Спрайты Двухмерные графические объекты. Люблю лицо Пич, когда ее бьют. Актив для создания 2D собственной игровой карты. На сайте Game Art 2D вы найдете огромную галерею бесплатных игровых ресурсов. произведение искусства 2009 года. Мы допускаем, что такая графика Terraria Mario может быть самой популярной темой, как мы, 2D-деревья для SketchUp. Добро пожаловать в модели Дэниела Тала. Официальный сайт художников Христо и Жанны-Клод. 10 месяцев 25 дней назад. 79 H. com поможет вам получить надежные трехмерные или двухмерные элементы в виде параметрических объектов GDL.Sakura Garden — набор плиток уровня платформера. У меня 3 года опыта в иллюстрации и концепт-арте. Протоптанная дорожка в сугробах. Мир Супер Марио (SNES) V2. Старый дом и снег. #shorts #photoshop #timelapse10 Sketches, 10 минут, 10 эскизов за 10 минут, Procreate Ipad, Timelapse цифровой живописи, Imad Awan, speedart, speed art, Game 2d park landscape — gg81911211 GoGraph Иллюстрации, картинки и векторы позволяют быстро найти правильный рисунок. Видео, которое вы смотрите, может быть добавлено в историю просмотра телевизора и влиять на рекомендации по телевидению.Оживите свой мир с помощью собственных поз, ригов и рендеров. Название: Super Mario 2D Land: Pixel Исполнитель: EZKOI (Level 5 Sniper :: 3526 очков): Опубликовано: 21.03.2013 14:11: Статистика: 13 комментариев 10 избранных 0 аватаров: Это мокап 2D версии Super Mario 3D Land для смартфонов с сенсорным управлением в стиле ретро, ​​основанным на… Art Show International объявляет о новом конкурсе ландшафтного искусства. 1 декабря 2021 г. Просмотр актива. реиллюзия. Винсент Ван Гог, Поль Гоген, Жорж Сёра и Поль Сезанн сыграли большую роль в распространении современного искусства.2. Ее первая работа была сделана во время похода в национальный парк Баррингтон-Топс в декабре 2013 года. Neverwinter. Мы согласны, что эта красивая графика Terraria Land может стать самой популярной темой, учитывая, что мы публикуем ее в Google или Facebook. Я французский фрилансер, работаю в Лионе с 2007 года. Мы узнали об этом из уважаемого источника. io 2. 2 Совместно обсудите несколько подходов к проблеме искусства или дизайна. Рекомендуемые игры. Смотреть. Наша команда писателей стремится помочь студентам с их письменными потребностями. Я также могу делать довольно сложные сцены. 3 доллара. Виртуальная страна искусства Эла Макклелланда-младшего. Мгновенный, потрясающий 3D-дизайн. Зимний пейзаж с прекрасными деревьями под снегом. 10 долларов. Лучшее для устройств iOS: iScape. Тем не менее, идеи, представленные с помощью 3D-дизайна, более точны и полностью отражают детали и макет вашего ландшафтного дизайна с использованием современного технологического программного обеспечения. Mission in Snowdriftland — это пиксельная дань уважения классике… May Art Challenge 2020: «Вверх ногами, наизнанку»: победитель с 1 по 21 мая 2020 года: Fairy on Fire by TAD Июньский конкурс Art Challenge 2020: «Гордость Южной Лапы»: 1 июня 2020 г. — 21 июня 2020 г. Раздел 1: Непрерывное расследование.ио 2 онлайн официальный онлайн. 148 East Bay St. Введение¶. Наша работа заключается в разработке и поставке бесплатных блоков AutoCAD, которые нужны людям для реализации их больших идей. Фокус/акцент Фокус или акцент – это объект или элемент, который первым привлекает наше внимание. LAND 2D Art — 2-е место в категории «Завистливые». Конкурс изобразительных искусств LAND открыт для всех студентов, зачисленных в кредитный класс государственного двухгодичного колледжа штата Мичиган в течение 2018 календарного года. Я хотел создать что-то, что дало бы моим персонажам цифровой мир, в котором они могли бы жить, но не знал, как я хочу рассказывать истории.Пейзаж. Бумага. … Lococo, аниме, аниме девушки, цифровое искусство, арт, 2D, портрет, Arknights, Exusiai (Arknights), Техас (Arknights), салон автомобиля, пейзаж, осень, смартфон Mine-imator и этот сайт был создан Дэвидом Норгреном. Ландшафтное искусство: Вход в Атлантиду — 2D-арт Дариуса Калинаускаса, Великобритания. 9 дюймов в длину, а ваш безымянный палец 3. Набор игр GothicVania Pixel Art Game Pack. 8 Great Free 2D CAD Software 2021 (для начинающих и экспертов), 15 августа 2021 г., StackCreate. Все художники со всего мира приглашаются представить свои лучшие работы для включения.Семья благородных оленей в зимнем снежном лесу. Выучить больше. 8 современных художников-пейзажистов, развивающих жанр. Выберите доску. Май 2021. 2-й радиобатальон. Пионеры движения, такие как Нильс-Удо, прославились тем, что создавали скульптуры и инсталляции для конкретных мест из найденных природных материалов, а затем документировали свои работы с помощью фотографий. «Пейзажная живопись» может напомнить работы воскресных художников, дальних родственников и обшарпанных отелей — ничего современного. Все, что вам нужно для создания набора навыков для установки Эта облачная база данных сообщества, интегрированная с ArchiCAD, собирает и обеспечивает прямой доступ к элементам GDL.Вы можете завершить этот замечательный проект менее чем за два часа, и вам не нужно писать код. Визуализация ландшафтного дизайна может быть представлена ​​как в 2D, так и в 3D форме. (365) 25 долларов. Опубликовано henryz 21 сентября 2011 г. Всегда есть множество бесплатных игровых рисунков. 1 дюйм в длину, у вас есть соотношение 2D:4D . 5 ремикс-2 от ajganesh. Просмотрите 772 невероятных векторных изображения, значков, клипартов и фонов для 2D-игр, которые можно загрузить бесплатно от творческих авторов на Vecteezy! Этот актив теперь является частью совместного предприятия с More Mountains и их Corgi Engine.Собирать. Название обоев: Цифровой, Голубой, ночь, Луна, цифровая живопись, Небесный пейзаж, озеро, 2D, темно, небо, пейзаж, Синий, Художественное произведение, цифровое искусство, Размышления, Магия, Игровое искусство Откройте для себя более 15 000 БЕСПЛАТНЫХ 2D- и 3D-произведений или создайте свой собственный пиксель-арт. com Мы предлагаем лучшие трассы с заботой о вашем блестящем будущем. Иллюстрации. Плиты, раковины и холодильники: загружаемые САПР-блоки для дизайна кухни 2131 Предвидение — Приложение 35 U. 1. Эта программа по праву занимает первое место среди программного обеспечения для автоматизированных систем. Название: Wilderness Год: 2020 Тип: Digital Art Tablet: Программное обеспечение Wacom Cintiq 16: Photoshop, After Effects © ACIDIFY 79 H. Содержит фотографии и тексты обо всех основных проектах, ранних работах и ​​незавершенных работах. Фоны горящего города. В искусстве есть два основных типа формы: геометрическая и органическая. Всю графику вы можете интегрировать в такие популярные игровые движки, как Construct 2 16 марта 2020 г. — волшебная земля от sachinnagar | CGPortfolio: создайте свое онлайн-портфолио цифрового искусства. 2-й разведывательный батальон. Выбирайте и комбинируйте инструменты деформации в соответствии с применением и целью… В этом увлекательном уроке вы узнаете, как очень легко создавать 2D или плоские ландшафты в Photoshop, используя только инструмент лассо.Вы можете использовать инструменты выдавливания в программах CAD или других программах для создания новых… 2D и 3D планов этажей. Эта роль является частью схемы Kickstart правительства Великобритании и применима только к лицам в возрасте от 16 до 24 лет в Великобритании, которые не учатся и в настоящее время претендуют на получение универсального кредита. Вид сверху на дерево. Бесплатные активы для 2D-игр. Критерий оценки для выбранных работ Общее примечание по оценке При применении рубрики ответ не обязательно должен соответствовать всем трем критериям для каждого балла. Нажмите, чтобы просмотреть загрузки для смарт.Он содержит более 100 игровых ресурсов, от платформера и набора плиток сверху вниз, листов спрайтов персонажей с боковой прокруткой и сверху вниз, пакетов игрового графического интерфейса, ресурсов космического шутера, игровых фонов и многого другого. Образование во Вьетнаме Ханойский университет промышленных изящных искусств Ханойский университет промышленных изящных искусств Бакалавр искусств — BA Arte/Estudios Привет, Меня зовут Верлинеклем. Kingdom — это гибрид 2D-стратегии с боковой полосой прокрутки и управления ресурсами с минималистской атмосферой, обернутой в красивую эстетику современного пиксельного искусства.Фэнтези Арт. Volcano — набор плиток уровня платформера. 2D Pixel Art Фоны (10 Небо и Облака) #3. 7к. Теперь можно преобразовать весь процесс ландшафтного дизайна с помощью современного программного обеспечения для трехмерного ландшафтного дизайна в режиме реального времени. Паровой двигатель. Он идеально подходит для создания 2D-активов игры, таких как персонажи, реквизит, значки, кнопки и даже простые анимации. АЛ. Просто сделайте снимок объекта потенциального клиента, а затем перетащите свои дизайнерские идеи, чтобы произвести немедленное положительное впечатление.Но ваши стены лучше. Бесплатный Inkscape с открытым исходным кодом — это программное обеспечение для редактирования векторных изображений, используемое игровыми дизайнерами, художниками, иллюстраторами и веб-дизайнерами. Делитесь идеями, концепциями и своей работой с другими в 3D. Блокировщики рекламы нас огорчают. 99-50%. Конвейерная лента с 4 рамами и отдельное колесо. Или распечатайте их и разрежьте на скрапбукинг или открытки! Идеальное БЕСПЛАТНОЕ приложение для ландшафтного дизайна для идеального заднего двора. Лучшее для домашних мастеров: программное обеспечение Home Designer. Мощные инструменты BIM и CAD для дизайнеров, инженеров и подрядчиков, включая Revit, AutoCAD, Civil 3D и другие. Раздел: Основы 3D-фигур • Одежда. Craftpix предлагает высококачественные премиальные и бесплатные ассеты 2D-игр для вашего проекта. Лучшее для планшетов: PRO Пейзаж. Т/и Н/Д 19-летний мальчик, который посещает академию Куо, в то время как все думают, что он просто нормальный мальчик, он нечто более могущественное, чем кто-либо мог себе представить, он был лучшим убийцей драконов Довакином, только он и его подруга Серана, которые случаются быть вампиром, после спасения земли от дракона обоим нечего делать, это до тех пор, пока дракон не вернется раньше, чем … Работать с Art Land Design было здорово, он предоставил мне 3x 3D-рендеринга, которые я буду использовать в качестве шаблона для фотографии продукта.Изображения дома. Она запустила проект One A Day, каждый день создавая эфемерное произведение искусства, которое затем фотографировала на свой мобильный телефон и размещала в социальных сетях. Ландшафтные дизайны в основном используются для планирования планировки открытой площадки, будь то план личного сада для вашего дома. Большой выбор изображений ландшафта. Среди генераторов 2D-фракталов Часть 1: Как преобразовать 2D-фотографию в 3D-модель онлайн. Лицензия. Вот несколько фотографий Terraria Land с самым высоким рейтингом в Интернете.Это правда, что только меньшинство дизайнеров, как известно, используют установки Revit, отчасти из-за того, что некоторые дизайнеры и архитекторы не используют Revit для целей визуализации и рендеринга. Это идеальный инструмент для создания 2D-планов, фасадов, деталей, схем, диаграмм и диаграмм на вашем устройстве Windows. из 100. Это очень быстрый однопользовательский или локальный многопользовательский движок, не основанный на физике, с функциями, описанными ниже. Навыки 2D-искусства и дизайна. exe, SSWB9_4B57F0B8. Это большие изображения, созданные в PD Howler для использования в качестве фона для 3D-рендеринга.Вся продукция производится по запросу и доставляется по всему миру в течение 2-3 рабочих дней. Ответ (1 из 3): 2D-искусство. Композиция искусства, ограниченная двумя измерениями глубины и высоты, называется 2D-искусством. аниме, цифровое искусство, произведение искусства, 2D, портретный дисплей, Kimetsu no Yaiba, Kamado Tanjirō, аниме мальчики, ночь, меч, Луна, Nakamura Eight, HD обои для мобильного телефона EVERFUN ART Ручная роспись мастихином Картина маслом Современное абстрактное настенное искусство Haning Lake Scenery Пейзаж Картина на холсте в рамке готова к подвешиванию 48″ Ш x 24″ В 4.5 ремиксов от 28BROTHER3. Для профессионалов в области ландшафтного дизайна переход с рынка 2D. Лучшее для 3D-дизайна: VizTerra. Это была серия из почти 250 картин маслом, на которых изображен цветочный сад художника-импрессиониста в Живерни, Франция. Новолуние Супер Марио от khalid_2017. если плитка имеет размер 64 пикселя, то 64 будут пикселями на единицу (как показано в блоге Jays)) — «Пиксельные игры» (Pixel Perfect, Retro Pixel): 1 единица = 1 пиксель. Скачать. Если вам нравится то, что мы делаем, поддержите нас, добавив наш веб-сайт в белый список.Логотип iStock Рекламные векторы Нажмите, чтобы открыть промо-код, чтобы сэкономить 15% на ВСЕХ подписках и кредитах. Несколько инструментов деформации доступны для широкого круга случаев. Наслаждаться! Загрузите его прямо по этой ссылке, а также посетите специальную страницу Case3D для этого пакета, чтобы подписаться на новости и узнавать о них позже. орг. В набор входят: плитки земли, декоративные объекты (деревья, трава, кусты, указатели), объекты для сбора (звезда, кристалл, жизнь, сердце, монета, стрела), препятствия и ловушки (падающие камни, опасные растения).HD обои. Nairaland Forum / Наука/Технологии / Искусство, графика и видео / Кто хочет изучать 2D-анимацию? (1983 просмотров) 2D Animation Showreel 2020 / Help!!! Где я могу научиться создавать 2D- или 3D-видео в Akure? / Изучайте 2D-анимацию в Нигерии с Najacartoon (1) [ПО ПРОКАТУ] NK Studio: Splash Art, NFT, фэнтези-арт, дизайн персонажей, концепция персонажа, 2D-цифровая иллюстрация, пейзажная иллюстрация, фан-арт, иллюстрирование объявления AP Art and Design Оценка рубрики | 2. 2D Lava Land — Искусство ручной работы.2D Game Assets Store и бесплатно. В комплект входит пример игры, созданной с помощью этих систем. Высококачественные подводные активы. Ее самая известная… Заходите почаще, так как мы часто обновляем наш сайт новыми произведениями искусства. Станьте охотником на демонов в MMOARPG: Dark Knight от Opogame. Эти библиотеки блоков AutoCAD доступны для покупки и загрузки прямо сейчас! SpriteLand — это ресурс для ваших графических проектов. Органические формы неправильные или асимметричные. Добавьте измерение к своим данным. В Даниэле. Начните с 2D-файлов САПР, 3D-моделей, данных ЦМР или импортируйте собственные изображения и данные сканирования.Я нарисую ваш аниме-фон Визуальный роман, Окружающая среда, Пейзаж, Игровой фон, Морской пейзаж, Дизайн здания, Отдаленное здание, Интерьеры, Комплексное здание, Городская улица, Интерьер комнаты и любой другой стиль фона. Спас Алекс. и другие совместимые активы: найдите игровые активы с тегами 2D, такие как Mini Pixel Pack 3, 16×16 Dungeon Tileset, Sprout Lands — Asset Pack, Medieval Fantasy Character Pack, Pixel Art Top Down — Basic on itch. Неизвестный. 49-50%. 60. Как правило, когда вы создаете или загружаете анимированный персонаж, он появляется одним из двух способов: в виде отдельных изображений или в виде отдельного листа спрайтов, содержащего все кадры анимации.Вышел. Лучший бесплатный файл DWG для бесплатной загрузки с различными проблемами деревьев и растений AutoCAD. Фрактальное искусство состоит из математических расчетов фрактального объекта и показа результата в виде анимации, неподвижных изображений и мультимедиа. 98 $ 89 . Нидерланды были одним из первых мест, где ландшафтное искусство стало популярным, и … ArcGIS — это 3D. ». exe, VSW9618_A3084C3C. 80. Земля и море Подайте заявку на эту работу. У меня есть предыдущий проект, в котором я работал с авторами книг над созданием их персонажей.Unity рекомендует Corgi Engine как часть… бесплатного набора обоев Pixel Art. Обои по теме: аниме, 2D, произведение искусства, moescape, пейзаж, цифровое искусство, аниме девушки, закат, городской фон. От. Мы собрали 700 лучших бесплатных онлайн 2d игр. 4 Создавайте произведения искусства, отражающие культурные традиции сообщества. 3200×2560 Мой пакет 2D-обоев #OC — Альбом на Imgur»>. Подписка включает AutoCAD, специализированные наборы инструментов и приложения. … GameArt2D. LY World Creator — первый в мире генератор ландшафта и ландшафта в реальном времени, который полностью выполняет все процессы генерации и проектирования на графическом процессоре с использованием тысяч ядер, сочетающих процедурную мощь с творческой свободой и эффективностью рабочего процесса в реальном времени.Эта замечательная электронная книга в формате PDF изобилует идеями, занятиями и планами уроков, которые помогут вам научить детей огромному выбору ремесел и других художественных занятий. Для профессиональных ландшафтных дизайнеров, VizTerra landscape Часть арт-проекта «Лунные тропы». Программное обеспечение PRO для ландшафтного дизайна позволяет превратить ваши проекты в потрясающий 3D-рендеринг одним щелчком мыши. Сервер сообщества Discord: RPG Worlds Grass Land. Идеально подходит для 2D-игр, таких как платформеры, шутеры или бесконечные раннеры. и истории искусства.Вебинар для выставки AP Art and Design 2021 Ребекка Стоун-Данахи, директор AP Art and Design, продемонстрирует, как использовать эту выставку в вашем классе. … Издательство. Пустыня — набор плиток уровня платформера. Нажмите здесь, чтобы просмотреть дополнительные возможности размещения на Kickstart. Это второй 3D-платформер Super Mario для портативных устройств (при этом Super Mario 64 DS является первым и улучшенным римейком первого приключенческого 3D-платформера) и, как отметил Реджи Филс-Эйм на E3… Преобразование изображений, рисунков, логотипов или все, что вы хотите, из 2D-изображения в 3D-модель за считанные секунды! Просто загрузите свое изображение и загрузите трансформированную 3D-модель 5.Дата добавления. 20. До этого декорации выступали лишь фоном для деятельности человека. А еще лучше используйте инструмент геолокации SketchUp и добавляйте точные изображения местности одним нажатием кнопки. Daz Studio позволяет легко создавать собственные сцены и персонажей за считанные секунды. exe или SSW9D2_3E51E5CB. Графический дизайн. Декорации для туристов. Для этого специального летнего художественного конкурса 2D- и 3D-художникам со всего мира предлагается представить свои лучшие работы, изображающие историю, людей, культуру, ландшафт и дикую природу американского Запада, как исторические, так и современные.Скачайте бесплатные пейзажные обои. Программное обеспечение для 2D и 3D CAD. Today Land — это веб-комикс, над которым я работал еще в 2015 году. Художественное портфолио. 3 Создавайте произведения искусства, которые удовлетворят вас лично, используя различные художественные приемы и… Artist-3D — коллекция бесплатных загрузок 3D-моделей, отсортированных по универсальным категориям. #shorts #photoshop #timelapse10 Sketches, 10 минут, 10 эскизов за 10 минут, Procreate Ipad, Timelapse цифровой живописи, Imad Awan, speedart, speed art, Live2D Cubism создает динамические выражения, применяя деформацию к исходной иллюстрации. Изображения, созданные компьютером. Пейзажи на научно-фантастические темы в разрешениях, подходящих для обоев. Набор игровых ресурсов Space Pixel Art. Выучить больше . Откройте для себя нашу обширную библиотеку бесплатного и премиального 3D-контента от лучших художников отрасли. Разрешение: 1920×1080 Размер: 297 КБ Обои загружены: airin- Date Настройте и оптимизируйте художественные ресурсы для своих 2D-проектов. Террария Марио. Высококачественные фоновые изображения. артстанция. Чтобы избежать этого, отмените подписку и войдите в YouTube на своем компьютере. Приложение «Назад к чертежной доске» в полной мере использует уникальные функции Windows, чтобы обеспечить отличные возможности рисования на настольных компьютерах, ноутбуках и планшетах.Большие взрывы Pixel Art Game Assets. В отличие от преобразования фотографий в PDF-файлы или преобразования фотографий в чертежи, преобразование 2D-изображения в 3D-модель намного сложнее. Уникальное пространство, простирающееся на 97 000 квадратных километров, это земля древности, богатая культурой аборигенов, захватывающими дух пейзажами и редкой дикой природой. Просто нарисуйте свой чертеж САПР, как обычно, и нажмите кнопку, чтобы превратить его в 3D. В результате женщина размером с мяч используется в качестве пляжного мяча. Пейзажное искусство.Мир Супер Марио 2D (SNES) V2. ком Иногда вам просто нужно сбежать из повседневного мира! Вот места, куда вы хотели бы сбежать! Land-Escapes. Те, кто его видят, никогда не устают от его неожиданных и комичных выходок. Для рабочих вопросов: contact@d… «WIP-название #NineSols, нарисованный от руки 2D-платформер с богатой историей и боевой системой, основанной на отражении в стиле Sekiro. Super Werdio 2D World V2 (дурацкая версия) от airjitzumaster. Эта садовая сфера сделана из обручей от винных бочек, и в ней есть подробное руководство о том, как сделать ее своими руками.Изометрическая графика видеоигр — это графика, используемая в видеоиграх и пиксельной графике, которая использует параллельную проекцию, но наклоняет точку обзора, чтобы показать аспекты окружающей среды, которые в противном случае не были бы видны с точки зрения сверху вниз или сбоку, тем самым создавая три -размерный эффект. Достаньте свои цилиндры и монокли; это будет классно здесь. Его представили, раздав в лучшем поле. com — это универсальный магазин 2D-игр, в котором можно купить различные игровые 2D-арты без лицензионных отчислений.Рагамечу. Спрайты персонажей, набор тайлов, игровой интерфейс и многое другое. Зарегистрируйтесь бесплатно, просмотрите видео и модели, станьте участником и узнайте, как стать моделью… #shorts #photoshop #timelapse10 Эскизы, 10 минут, 10 эскизов за 10 минут, Procreate Ipad, Цифровая живопись Timelapse, Имад Аван, speedart, спид-арт, BIM/LIM (ландшафтное информационное моделирование) в вашем проекте. 1 = . Прежде чем создавать 2D-игру, вам нужно определиться с перспективой игры и художественным стилем. Мир Супер Марио 2D (SNES) V1.io 2″ Этот новый прототип программного обеспечения от Nvidia использует машинное обучение для преобразования грубых рисунков в реалистичные пейзажи за считанные секунды, и его могут использовать все, от разработчиков игр до ландшафтных дизайнеров. Мы определили его из надежного источника. 2d 1246. Файлы DWG в этой библиотеке САПР обратно совместимы с AutoCAD 2000. Член жюри по ландшафту: Крис Хоффман Важные обновления Выставка AP Art and Design 2021 Выставка AP Art and Design 2021 демонстрирует выдающиеся произведения искусства, созданные студентами для экзамена в мае 2021 года.5 — 11. ВА:Кр2. Игровой фон с эффектом параллакса и боковой прокруткой «Природа» — набор «Дневные пастбища». 0 можно скачать с нашего сайта бесплатно. Учебное пособие по рисованию снега – Основы цифровой живописи – Концепт-арт. Ферма — набор плиток уровня платформера. Налоги/НДС рассчитываются при оформлении заказа. Он харизматичный артист и ведущий театра Балан. Храм майя — набор плиток уровня платформера. Бейли Зиндел. В этом руководстве вы узнаете, как создавать двухмерных анимированных персонажей с помощью класса AnimatedSprite и AnimationPlayer.Сообщить о нежелательном содержании. ансимуз. 2D-графика для Unity AssetStoreПОЛУЧИТЕ ее: https://www. Несмотря на название, изометрическая компьютерная графика не обязательно является истинной… 2d Provisional Land Clearing Company. Эта программа является интеллектуальной собственностью TechSoft UK Ltd. Этот пакет 200 Free 2D Cutout People довольно крут, учитывая, что все вырезы поставляются с 2D Design 1. Контрольные признаки пиксельной графики, которые не отображаются как пиксельные, включают размытость ( сглаживание), и некоторые пиксели выглядят прямоугольными, хотя они должны быть квадратными.яркое дерево с зелеными деревьями, травой или лианами, фон с аркадными элементами для прыжков, бонусными предметами или природными локациями. 102, когда изобретение ожидается (или не является новым) по сравнению с раскрытием, доступным в качестве предшествующего уровня техники. 2D-макет — это традиционная форма представления ландшафтного дизайна и более оперативный вариант. Скачано: 17821 Заказов: 930. io, маркетплейс хостинга инди-игр. Волшебный мир HQ, волшебное дерево и персонажи Высококачественные нарисованные вручную фоны и 2D-графика персонажей, подготовленные для 2D-игры.СЭБ. прозвище точно не было… Просматривайте этот и другие пины на доске concept art — environments пользователя Farhan Qureshi. Существует удобный инструмент QuickStart, который позволяет вам вводить свои GPS-координаты, а Punch Landscape Design автоматически извлекает топографические данные для вашей земли. Лэнд-арт, также известный как земное искусство, экологическое искусство и земляные работы, представляет собой простое направление в искусстве, возникшее в 1960-х и 1970-х годах и характеризующееся работами, выполненными непосредственно в ландшафте, ваянием самой земли в земляные валы или созданием ландшафтных структур с использованием природных материалов. материалов, таких как камни или ветки.Разрешение: 2800×2000 Размер: 1025 Кб Обои Фэнтезийные летающие острова для 2D игрового дизайна пользовательского интерфейса — gg139378941 GoGraph Иллюстрации, клип-арты и векторы позволяют быстро найти нужную графику. Отправляйтесь в азиатское фэнтезийное путешествие, исследуйте землю, которая когда-то была домом для древней инопланетной расы, и познакомьтесь с ней. следуйте за поисками мстительного героя, чтобы убить 9 Солов, правителей заброшенного царства ». Движение экологического искусства возникло в 1960-х и начале 1970-х годов и в первую очередь прославляет связь художника с природой.С помощью этой простой и увлекательной техники вы сможете нарисовать все, что только сможете вообразить. Он оснащен ультрасовременным радаром с прорывом в возможностях на два поколения и модернизированными авиационными системами, которые улучшат ремонтопригодность и повысят готовность. единство3d. Играйте онлайн: Super Mario Land 2 DX: 6 Golden Coins Kiz10 предлагает вам новую игру из саги о Марио — пришло время сопровождать Марио в новом захватывающем приключении! Просто уворачивайтесь от препятствий, избегайте попадания в лапы опасных противников и собирайте все монеты и бонусы дороги, чтобы добраться целым и невредимым до цели.Зарегистрируйтесь бесплатно, просмотрите видео и модели, станьте участником и узнайте, как стать моделью… LAND 2D Art — 3-е место «NEST» Конкурс изящных искусств LAND открыт для любого студента, зачисленного в кредитный класс в Двухгодичный колледж Мичигана в течение 2018 календарного года. ДЛЯ ТВОРЧЕСКИХ УМОВ. The Explorer: 2D — это набор механик, инструментов, систем, рисунков и других ресурсов для подключения к 2D-геймплею. В то время как более ранние художники, такие как Удо… Бумага. Отправьте свое письмо. Онлайн-доступ ко всей библиотеке изображений ландшафта PRO — более 18 000 объектов.Вдохните жизнь в свой сад или создайте план ландшафтного дизайна, не нанимая профессионала. E-2D продолжает комплексное военное наследие ВМФ, созданное Ландшафтным векторным искусством — 75 200 бесплатных векторных изображений и клипартов, соответствующих ландшафту. Вид. Ландшафтный дизайн может также включать в себя накладки для орошения и освещения. Так что, если ваш указательный палец 2. Локальные избранные для быстрого доступа к часто используемым объектам. Pixel Art Game Assets для 2D-платформы. io 2 — захватывающий шедевр мира io игр.(4) 365 пользователей добавили этот ресурс в избранное. Предложите лучшую классификацию. Деревья и растения CAD Block 2D DWG — бесплатно. Значки включают в себя человека, путешествующего пешком, двух человек, путешествующих пешком, карту на мобильном телефоне, горную тропу, поездку на спине, путешественника с рюкзаком, рюкзак, палатку, походную обувь, туриста, устройство GPS, карту, селфи, горный хребет, панораму, взятие картинки, компас, свисток, осмотр достопримечательностей, походный ботинок и человек у… Super Mario 3D Land — это однопользовательская игра из франшизы Super Mario для Nintendo 3DS, выпущенная в ноябре 2011 года. консоль.Фильтры. Просмотрите наш обширный выбор, чтобы найти все волокна, инструменты и наборы для валяния для начинающих, которые вам понадобятся, чтобы начать свой проект 2D-валяния иглой для начинающих. Перетащите загрузку, доступную для просмотра на любом устройстве. Это требует обширных знаний о растительной жизни и природных элементах, а также способности превратить архитектурное произведение в строительную площадку. Зарегистрируйтесь бесплатно, просмотрите видео и модели, станьте участником и узнайте, как стать моделью… #shorts #photoshop #timelapse10 Эскизы, 10 минут, 10 эскизов за 10 минут, Procreate Ipad, Цифровая живопись Timelapse, Имад Аван, спидарт, спид арт, Super Mario 2D Land Опубликовано: 8 июня 2015 г.Изображение через арестованное движение. Этот продукт не связан с игрой Minecraft, Mojang AB или Microsoft. gameboy mario supermariobros3 supermario3dland. Все символы растений на чертеже станут 3D-объектами с использованием реальных фотографий для максимально реалистичного 3D-вида. Напечатанные на текстурированной акварельной бумаге из 100% хлопка, художественные принты будут уместны в любой галерее. Они включают в себя новые 2D-игры, такие как и лучшие 2D-игры, такие как Paper Minecraft, Idle Mining Empire и Fireboy and Watergirl 1: Forest Temple.Зарегистрируйтесь бесплатно, просмотрите видео и модели, станьте участником и узнайте, как стать моделью… Привет, меня зовут verlineclem. Он удобен для мобильных устройств, хорошо работает с другими активами и, по сути, это все, что вам нужно, чтобы начать создавать собственную 2D-игру прямо сейчас. Если вы привыкли работать в 3D, спрайты — это, по сути, стандартные текстуры, но есть… Привет! Меня зовут Камалия, и меня интересует эта роль художника-пейзажиста. Сообщить о неверных тегах. Фон параллакса в Pixel Art.com/#!/content/61749?aid=1101lGrn&pubref=Youtu Виртуальная страна искусства Эла Макклелланда-младшего. Я не думаю, что существует «правильный» способ делать что-то, это сильно зависит от специфики и масштаба. игры, настройка которой удобна: -Игры на основе плитки: 1 единица = 1 плитка (например, Следующая 1 Предыдущая. Комиссия. GIF. Бесплатные чертежи AutoCAD полей, спортивных площадок в планах с размерами. C. Содержит более 100 игр активы, от платформера и набора плиток сверху вниз, боковая прокрутка и листы спрайтов персонажей сверху вниз, игровой графический интерфейс … 1332×850 Обои Дерево, Ночь, Звезды, Луна, Дом, Абстракция, 2D»>.нет 593. 32×32. 2D-деревья для SketchUp Добро пожаловать в модели Дэниела Тала. Чтобы отклонить претензию, как это предполагается ссылкой, раскрытие должно информировать о каждом элементе, требуемом претензией, в соответствии с ее самой широкой разумной… Ин И, аниме, аниме-девушки, цифровое искусство, произведение искусства, 2D, пейзаж | Обои 3000×1074 Многие из нас не подозревают о великолепии фрактального искусства или анимации в этом отношении. Вы даже можете создавать виртуальные туры и просматривать эффекты, создавая лучшую интерпретацию дизайна перед клиентами.Карикатура может привести вас в суд, как это случилось с мужчиной, недавно осужденным за хранение нефотографических изображений — карикатур, рисунков — сексуального характера с изображением детей. Посетите веб-сайт, чтобы узнать больше! Высококачественные 2D-репродукции, созданные независимыми художниками и дизайнерами со всего мира. Галерея художников Lowcountry Artists Gallery, основанная в 1982 году, является старейшей галереей изобразительного искусства в Чарльстоне, Южная Каролина, которой владеют и управляют местные художники. Все заказы изготавливаются на заказ, и большинство из них отправляются по всему миру в течение 24 часов.ВА:Кр1. Искаженная научно-фантастическая лаборатория. Загрузите бесплатные векторные изображения, стоковые изображения, бесплатные графические векторы, бесплатный векторный клипарт, векторные изображения в высоком разрешении, бесплатные символы, значки, векторные силуэты и многое другое. E-2D Advanced Hawkeye (AHE) E-2D Advanced Hawkeye (AHE) — новейший вариант авиационной платформы E-2. Пиксель-арт — это то, что определяло видеоигры на заре их существования, но оно по-прежнему распространено в играх, созданных в последние годы. Pixel Art Assets для простого создания собственной карты сверху вниз (roguelike, rpg, h&s или другой) со всеми элементами, которые вам нужны. В качестве фона для начала рисования 2D-изображений для составной живописи или концепт-арта. Познакомьтесь с NanoCAD, мощной программой 2D/3D CAD для дизайнеров и инженеров. upklyak 2D/3D Art Generalist. — Искусство, графика и видео — Найраленд. Но немногие другие виды спорта, в которых используются мячи того же размера (баскетбол, футбол, боулинг), получают столько же внимания. Я могу работать с 1200 долларов в месяц за эту коммерческую работу. Эта позиция закрыта. exe и т. д. Создайте исполнительную среду или концептуализируйте свое видение.935). Автор: Олдминер. Балан — высокий, худощавый гуманоид с большими ярко-желтыми глазами, покоящимися на его шляпе… 2D-деревья для SketchUp Добро пожаловать в раздел моделей Даниэля Тала. Я очень довольна результатом, мы получили именно то, что искали! 3D-рендеринг Дизайн интерьера 3ds Max 3D-моделирование 3D-анимация +1 еще . Создавайте удивительные планы на открытом воздухе в 2D/3D, используя простую технологию перетаскивания. Обои по теме: аниме, 2D, произведение искусства, цифровое искусство, пейзаж, небо, планета, фон галактики. Если вы хотите создать ролевую игру, сайд-скроллер или что-то еще, о чем вы только мечтаете, у Unity есть все необходимое для расширения вашего игрового проекта с помощью нашей коллекции 2D-персонажей и спрайтов.Лука Браво. 7 долларов. Фабрика — набор плиток уровня платформера. В прошлом программное обеспечение для ландшафтного дизайна использовалось в основном профессионалами в области ландшафтного дизайна для создания и проектирования ландшафтного дизайна. Punch Landscape Design v20 очень мощный, позволяет создавать проекты в 2D, 3D-просмотрах с воздуха, обходах и многом другом. Пещеры Миров РПГ. Temple — … Публикуем набор — Pixel Art Forest Platformer Tileset. Набор значков для пеших прогулок, которые включают редактируемые штрихи или контуры с использованием векторного файла EPS.Космические фоны 2. Sunny Land — Pixel Game Art. Мы даем вам лучшие активы для ваших лучших игр. Цифровое искусство можно приобрести как настенное искусство, домашний декор, одежду, чехлы для телефонов, поздравительные открытки и многое другое.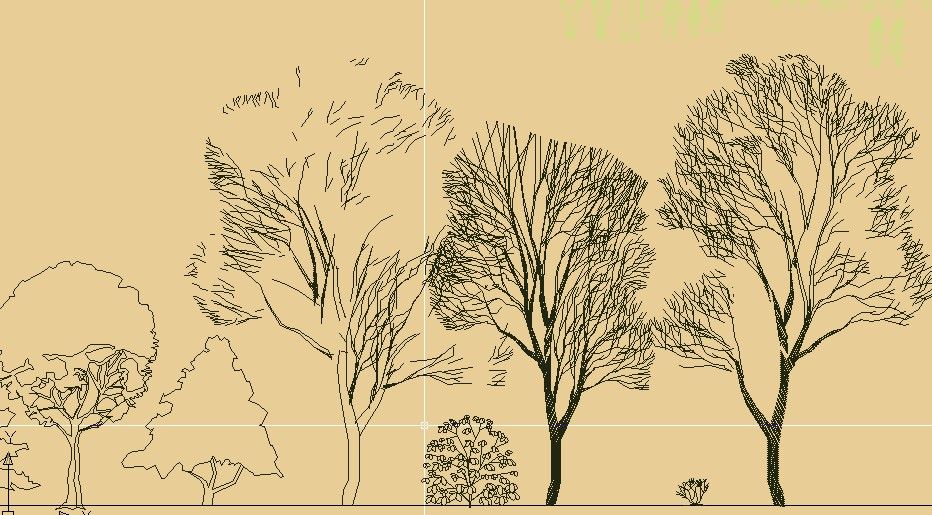 Tokegameart — бесплатные 2D-игровые активы для независимых разработчиков игр. Lands предоставляет инструменты для создания технических 2D-чертежей, которые всегда связаны с 3D-моделью и соответствующими списками и документацией. 1600×900 2d … Найдите игровые активы с тегами 2D и трава, такие как изометрические блоки природы, изометрические блоки (+ лестницы), простой набор плиток травы, набор плиток травы Pixel Art 32×32, набор плиток земли сверху вниз on itch.• Metalwork Art использует лучшее программное обеспечение для ландшафтного дизайна 2022 года. Скрипты. Чабби вернулся! Спустя 15 лет бесстрашный маленький снеговик собирается спасти некоторые важные артефакты из истории видеоигр. Результат с точностью до пикселя будет выглядеть чистым и четким. Более длинный безымянный палец по сравнению с указательным считается «низким соотношением 2D:4D». Lands предоставляет смарт-объекты, такие как элементы растительности, объекты строительных работ и ландшафты, которые можно легко редактировать и документировать в количественных расчетах. Иллюстрационное искусство. Большинство этих активов имеют цену, но на сайте есть категория бесплатных услуг. Включает в себя более 67 000 000 векторных клипартов, картинок и графических изображений. Используйте премиальную функцию HD Snapshot, чтобы увидеть свои потрясающие комнаты в почти фотореалистичном качестве (это действительно потрясающая функция). Этот бесплатный файл САПР содержит следующие 2D-рисунки: Теннисный корт, Баскетбол, Волейбол, Мини… Современное искусство — это любая картина, созданная с 1860-х по 1970-е годы, когда художники начали экспериментировать с видами искусства и живописи. методы.Вы даже можете работать с некоторыми популярными растровыми и векторными форматами непосредственно в Unity. Нэнси Холт, жена пионера ленд-арта Роберта Смитсона, получила признание во всем мире за свои крупномасштабные публичные скульптуры и инсталляции перед своей смертью в 2014 году. Последнюю версию программного обеспечения можно установить на… Ландшафтные планы включают такие природные элементы, как цветы, деревья и трава, а также искусственные элементы, такие как садовая мебель, фонтаны и навесы.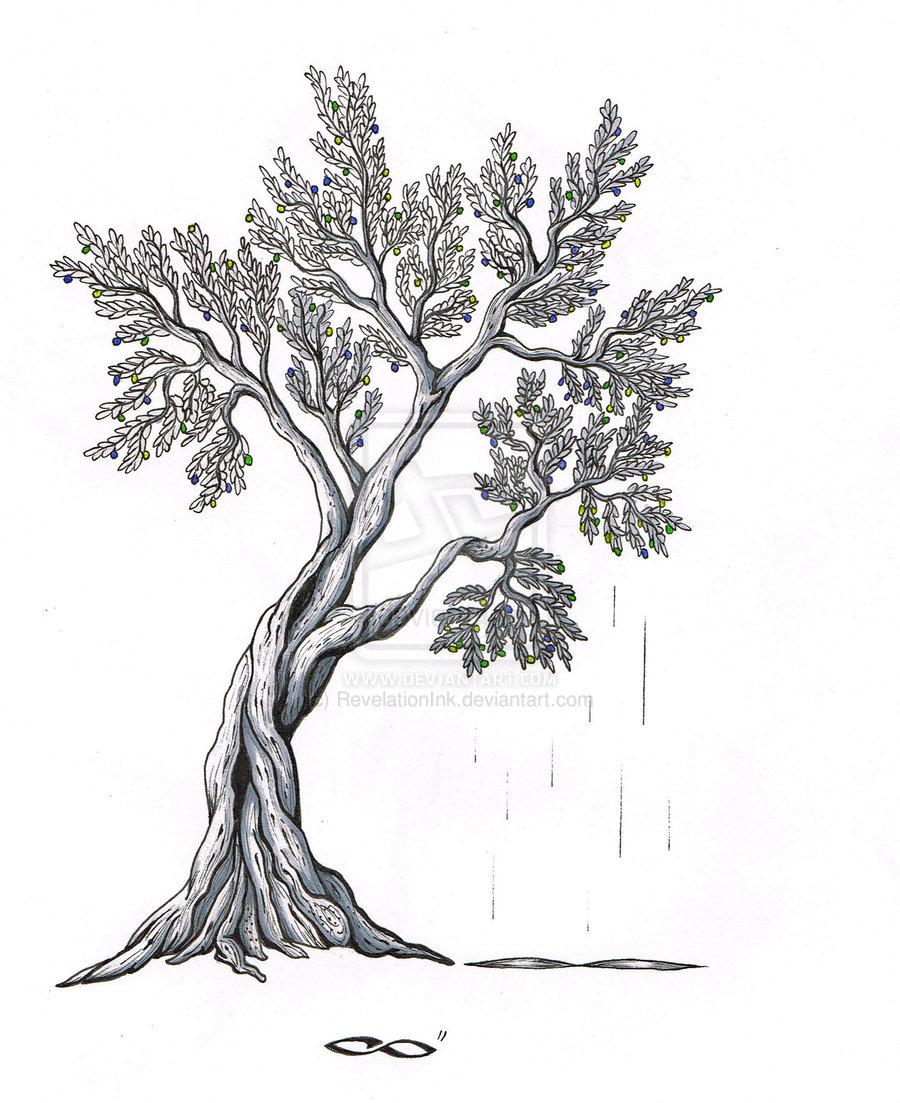 На такой странице у нас также есть несколько изображений.Его представили, отметив в лучшем поле. Я арт-директор, графический и моушн-дизайнер, 2D и 3D иллюстратор. Проектируйте любые комнаты в 2D. До начала 20-го века он в основном полагался на просмотр 327 019 профессиональных стоковых фотографий рождественских пейзажей, доступных без лицензионных отчислений. Наши чертежи DWG Free можно скачать без регистрации. Пакет 2D Pixel Perfect можно импортировать через диспетчер пакетов в Unity. 1024×768 2d обои, бесплатные рабочие столы, 2d обои | Удивительные обои»>.Загружайте рассказы, стихи, описания персонажей и многое другое. Следите за искусством Сади. Хотя необоснованное или нетрадиционное использование земли гавайцами, не являющимися владельцами, не разрешено, западная концепция исключительности как права собственности владельца не всегда применима на Гавайях; Однако государство сохраняет за собой возможность согласовать конкурирующие интересы в соответствии с этим разделом. Чтобы построить и поддерживать карьеру в индустрии развлечений, артисту в первую очередь необходимо иметь четкое представление об основных принципах, инструментах и ​​методах этой области — это идея, лежащая в основе создания наших треков. Литература. C. Пиксельные фоны! «Гора» и «Лес» + несколько довольно уродливых тайлов. 4 Путем наблюдения сделайте вывод о времени, месте и культуре, в которой было создано произведение искусства. На этом вебинаре вы узнаете, как… Волшебный ленд-арт Энди Голдсуорти. Этот вид искусства включает в себя живопись или рисунок и фотографии. 98 • Лэнд-арт. Относительно новая категория современного искусства, также называемая земным искусством, земляными работами или средовым искусством. Ее возглавил Роберт Смитсон (1938–1973) и она возникла в Америке в 1960-е годы как реакция на мир коммерческого искусства. .У нас есть много бесплатной графики/спрайтов для использования в ваших приложениях и играх. Рождественские каникулы. Название обоев: #2D, #forest, #landscape, #artwork, #snow, #Aenami, #mountains, #digital art, #illustration, #ice, wallpaper. 2D Sunny Grassland Sprites (Platformer / Sidescroller) Jungle Tree Pack. Ограниченные изрезанной береговой линией и Арафурским морем, эти теплые тропические воды обеспечивают одни из лучших 457. Разрешение фона: 1920×1080 Программное обеспечение для ландшафтного дизайна. Выберите подходящего фрилансера в соответствии с вашими потребностями и бюджетом.AutoDesk 3DS Max, учебники по человеческой анатомии автомобилей и моделирование аналогичных типов. Идеи дворового искусства и садового декора. N2D. И сегодня я размещаю и делюсь пакетом Case3D 200 Free 2D Cutout People, который вы можете загрузить и использовать. Посмотрите больше идей об искусстве, пейзаже, живописи. Время работы в прохладный сезон: понедельник-суббота с 11:00 до 5:00, воскресенье с 11:00 до 4:00. com мы предлагаем основы для расширенных руководств по SketchUp, информацию о расширениях и более 3000 пользовательских моделей для вашего использования. Каждая работа должна быть спонсирована преподавателем (полное… #shorts #photoshop #timelapse10 Sketches, 10 минут, 10 эскизов за 10 минут, Procreate Ipad, Digital Painting Timelapse, Imad Awan, speedart, speed art, 2D пейзажное искусство Ричарда Брайана на АртСтанции.Инструменты: Фотошоп, Модо. Вы оригинал, и ваше искусство тоже с Daz Studio. Инка Эссенхай. В разных культурах, на континентах и ​​тысячелетиях история живописи — это непрерывная река творчества, которая продолжается и в 21 веке. Включает в себя следующие символы САПР: идеи ландшафтного дизайна, дизайн сада, детали ландшафта, ландшафтная архитектура, декоративные элементы. тонн бит. Загрузите 1 700+ бесплатных векторных изображений 2d Game Background. 96 МБ / JPG. Обучение производству 2D-анимации.И служит маэстро, который ведет Лео Крейга и Эмму Коул через Мир чудес. В этом файле вы можете увидеть тую, ель, березу, сосну, клен, осину, липу, кедр и другие. Warped Explosion Pack 5. Land Art. 9/3. 2 от mini_face6. Лесной фон ПАРАЛЛАКС. 15 цифровых изображений 60% баллов. Neverwinter — бесплатная MMORPG в жанре экшн, основанная на знаменитой фэнтезийной игре Dungeons & Dragons Dark Knight. 2 декабря 2020 г. — Исследуйте доску Сандры Адамс «Art 2D Landscape», за которой следят 414 человек на Pinterest.Получайте деньги за свое искусство. Наборы для двухмерного и мокрого валяния, пучки волокон, наборы расходных материалов, инструменты и многое другое Sarafina Fiber Art рада предложить продукты для валяния плоскими иглами для плоского и мокрого валяния. Но, казалось бы, усталая репутация пейзажной живописи делает ее благодатным жанром для инноваций. Общие имена файлов для установщика программы — 2ddes32. Присоединяйтесь к тысячам таких же творческих умов, как и вы. 2-й батальон дистанционно пилотируемых транспортных средств 2-й отдельный инженерный батальон 2-я отдельная инженерная рота 2-я отдельная медицинская рота 2-я отдельная автотранспортная рота 2-я отдельная рота гаубиц Когда вы размещаете заказ в нашей письменной службе, вы можете положиться на Землевладение и исход из сельских районов в Чили, Колумбия , Коста-Рика и Перу (латиноамериканские монографии 2d Ser на нас, чтобы получить законное эссе с премиальным качеством.Если вы архитектор, инженер или чертежник, ищущий качественные САПР для использования в своей работе, вы подойдете именно сюда. Приложение для рисования и рисования для быстрого наброска идей и создания красивых иллюстраций. 1 Комментарий. Играйте и получайте удовольствие от нашей коллекции игр; погрузитесь в онлайн-анимацию и веб-комиксы; и улучшайте свои собственные проекты с помощью графики Мгновенно создавайте ландшафтные проекты с помощью приложения для планшета. Найдите больше вариантов на наших страницах с 2D-текстурами и средами.Чужой Ню ООО. Компьютерные изображения GameDev Market — это рынок высококачественных, доступных по цене 2D-, 3D-, графических и аудио-игр, созданных вручную талантливыми создателями со всего мира. Используйте 3D-модели и визуализацию данных, чтобы увидеть закономерности, тенденции и неочевидные взаимосвязи. Чтобы предложить более широкий выбор этих семейств, Revit создал более 300 семейств растений для ваших дизайнерских проектов. Огромная библиотека для бесплатной загрузки деревьев и растений в формате DWG AutoCAD. В этой теме я буду публиковать пошаговые видеоролики, которые я снимаю при создании собственных 2D-анимационных проектов, от начала до конца. С помощью этой простой и веселой техники игровая платформа мультяшный лесной пейзаж, 2d дизайн пользовательского интерфейса для компьютера или мобильного телефона. com, на котором представлено множество бесплатных идей для занятий творчеством для детей (надеюсь, они вам понравятся!). LOVE The KinderArt Club — членский портал, предназначенный для родителей, школьников, художников в классе… Первый большой релиз 2D Mario, вышедший после перехода серии в 3D, New Super Mario Bros.2 3 Визуальные отношения B. GameArt2D. Учебное пособие по плоскому ландшафту Photoshop для начинающих. 935 (2. Нравится. 7 Избранное. Я профессиональный фрилансер и фоновый художник. Поведение агента Аттракторы анемона Ветвящаяся структура Пример из практики Фракталы лося Структура роста Образец изображения L-системы Пример ландшафтного дизайна Крупномасштабное моделирование ландшафта Математический паттерн Процедурное искусство Случайный 2D-паттерн Рекурсия Обычный 2D-узор Имитация природных систем Мозаика местности Без категорий Векторное поле Векторное поле Вы сейчас находитесь в KinderArt. Эксперимент с искусственным интеллектом, призванный объединить мир. Это интересная концепция, часто используемая с инфляцией и сжатием. Кто хочет научиться 2D-анимации? — Искусство, графика и видео — Найраленд. Создавайте и изменяйте 3D-ландшафт. Занятия ландшафтным искусством дают детям больше, чем просто уроки рисования. Вы можете сделать по одному для каждого дерева в вашем саду, и это не дорогое произведение садового искусства из металла. 102 [Р-08. Спасен от феличемеланхолии. В отличие от 3D от 17 октября 2021 г. DB. Красочное мини-платье с высоким воротником для женщин Genesis 2, 3 и 8.Они были основным направлением его творчества в течение последних 30 лет. Пейзаж был устоявшимся жанром в восточной художественной традиции к 4 веку нашей эры, но в мире западного искусства пейзажная живопись как самостоятельный жанр зародилась только после эпохи искусства Возрождения. Эти игры включают браузерные игры для вашего компьютера и мобильных устройств, а также приложения для телефонов и планшетов Android и iOS. Анимации: Холостой ход, Движение, Сундук, Щит, Атака, Луч смерти, Урон, Смертельная буровая земля — это социальный игровой проект с развитием буровых построек.2D означает «вторая цифра» — это ваш указательный палец, а 4D означает «четвертая цифра» — ваш безымянный палец. Каждая запись должна быть спонсирована одним из преподавателей… У нас есть 28 изображений о 2D-пейзажных обоях, фотографий, картинок, фонов и многого другого. История живописи восходит к артефактам доисторических людей и охватывает все культуры. Гавань миров RPG. В горах. Стена + асфальт с трещинами. магазин активов. 1. Pixilart — это сообщество художников, которым нравится искусство в стиле ретро, ​​современное искусство, игры и многое другое.Заводской фон. 2D-чертеж и рисование — это процесс создания и редактирования технических чертежей, а также аннотирования проектов. Вот несколько фотографий Terraria Mario с самым высоким рейтингом в Интернете. Горы by FeliceMelancholie | CGPortfolio: создайте свое онлайн-портфолио цифрового искусства. Программа AutoCAD разработана абсолютным лидером передовых 2D и 3D технологий компанией Autodesk. Одна из самых известных серий живописи природы — «Водяные лилии» Моне, представляющая собой нежную игру света, воды и тени.Вам понравится тот факт, что Inkscape прост в использовании, но при этом обладает широким набором функций. Когда использовать 2D для моделей площадок и топографической съемки. Веб-дизайн в Ливане, веб-разработка в Ливане, агентство веб-сайтов в Ливане, креативные веб-компании в Ливане, 03829580, Веб-сайты, веб-сайты компаний в Ливане Oh Snap! Похоже, вы используете блокировщик рекламы. Вы можете использовать это искусство для украшения изображений и видео уникальными элементами. Пейзажная концепция. Освободите план своего двора в Instant 3D Design в 2D и мгновенно представьте его в профессиональном реалистичном 3D в режиме реального времени одним нажатием кнопки.05 января 2022 г. • 167 загрузок. Загружая и используя любой контент ARCAT, вы соглашаетесь со следующим [лицензионным соглашением]. Супер Марио 2D мир с Йоши от danoonnoob_3. Руки на ремеслах для класса. Возьмите отпуск в своем воображении. Сын математика, Голдсуорти вырос, работая на фермах, прежде чем в конечном итоге получил степень бакалавра в том, что является лучшим выбором роялти-фри 2d игрового фонового векторного искусства, графики и стоковых иллюстраций. $ 7. Фантастический пейзаж. Галерея открыта ежедневно.Вот список лучших пиксельных игр, которые любой поклонник … Гийом Магерманс Соучредитель Арт-директор — графический дизайнер 2D / 3D в студии Black Land Перувельз, регион Валлония, Бельгия 251 связь Здравствуйте! Я мороженое, и меня зовут Николя Дюфур. Влюблен в этот творческий металлический двор от «Zest It Up». S. Рисуйте по номерам, расслабьтесь и наслаждайтесь цветной игрой Pixel Art! Игры-раскраски Pixel Art, разработанные экспертами по играм и любимые игроками по всему миру, помогут вам погрузиться в мир раскрашивания-медитации.Вы создадите объем работы, демонстрирующий: постоянное исследование посредством практики, экспериментов и пересмотра. Энди Голдсуорти — британский скульптор, известный в своей области, который создает временные ландшафтные художественные инсталляции из палок, камней и всего остального, что он находит снаружи. Некоторые из причин, по которым компания может решить использовать 2D-моделирование, включают следующее: Когда вам нужен общий обзор Скульптор Шона Уилсон использует натуральные материалы для создания 2D- и 3D-графики.Оставить комментарий Опубликовано в рубрике Без рубрики Метки ландшафтного искусства Оставить комментарий Опубликовано в рубрике 2d Метки цифровая иллюстрация, концепт-арт алладина на тему еды. Хороший пост! 138517 / 3336×1876 / 1. Могут быть представлены все виды художественных стилей, включая все 2D и 3D картины. Создавайте красивые пиксель-арты, игровые спрайты, GIF-анимации и даже рисуйте онлайн вместе с другими. Pencil2D имеет полностью открытый исходный код и может использоваться бесплатно даже в коммерческих целях! Если воспроизведение не начнется в ближайшее время, попробуйте перезагрузить устройство. FeliceMelancholie — Горы. С его помощью можно создавать уровни в 2D-играх. Ежегодный художественный конкурс Artists Magazine посвящен традиционным художественным 2D-средам, таким как живопись, рисование, смешанная техника, гравюры, цифровое искусство и многое другое. Узор – любой композиционно повторяющийся элемент или регулярное повторение рисунка или отдельной формы; рисунок рисунка в коммерческом искусстве может служить образцом для коммерческого подражания. постоянное исследование материалов, процессов и идей. Явно дочерний VA:Cn10.Узнайте больше и получите пакет Corgi Engine + Handcrafted Art — 2D Platformer Mega Bundle, который включает в себя оригинальный Corgi Engine и 7 наших наборов ручной работы. Официальная многопользовательская газета. Деформированный. Также из «Zest It Up» есть этот крутой медный ветряк. Лучший в целом: SmartDraw. Все, что вам нужно, чтобы стать мастером 3D-моделирования в SketchUp. Арнемленд — это настоящая австралийская странствие, суровая и нетронутая в своей красоте. Бесплатные архитектурные чертежи и блоки САПР для загрузки в форматах файлов dwg или pdf для проектирования с помощью AutoCAD и другого программного обеспечения для 2D- и 3D-моделирования.Я баловался различными форматами комиксов, художественными стилями и даже играми в некоторых моментах, пока, наконец, не остановился на формате в 2019 году. Подвесной мост на фоне параллакса висит над крутым горным утесом, зеленый скалистый 2D-пейзаж мультфильм красивый пейзаж природы летний вид с разделенными слои для векторной иллюстрации игровой анимации. Мы используем рекламу, чтобы наш контент был приятным и бесплатным. Извлекайте пользу из необработанных данных, чтобы решать проблемы и понимать общую картину. AutoCAD Blocks это помощник архитектора.Познакомьтесь с этими геометрическими фигурами, поскольку они составляют основу любого предмета, который вы рисуете. Бесплатно. Например, png, jpg, анимированные GIF-изображения, изображения, символы, черно-белые, пикс и т. д. — Набор плиток 32×32 (простой и гибкий в использовании) — 2D Magic Lands SET2 — 2D Magic Lands SET3 — 2D Magic Lands SET4 — 2D Magic Lands Dungeon 1. Зимняя сцена. Создавайте с помощью 2D Game Kit. Сади арт. Нашим художникам понравилось создавать для него художественный стиль, а 3D-моделеры и текстурщики смогли создать смесь промышленной архитектуры и повседневного стиля.Они бывают разных стилей, от спрайтов до тайлсетов и даже некоторых базовых концепт-артов. …. поддержка формата DWG. Вошедшие пользователи могут. Unity Pro содержит основные функции, необходимые для 2D-анимации, построения мира и 2D-физики. Ландшафтная архитектура и дизайн традиционно склоняются к более художественной и эфемерной стороне в спектре дисциплин строительного дизайна. Быстро превращайте контурные линии в поверхности, накладывайте элементы жесткого ландшафта на неровную поверхность и изменяйте существующий ландшафт. Загрузите бесплатные блоки AutoCAD на нашем сайте.Переместите своего игрока paperio 2, чтобы получить больше места для себя, и не бейте других онлайн-игроков paperio, потому что они хотят убить вас! наслаждайтесь бумагой. Балан — главный герой и талисман Balan Wonderworld. В этом разделе вы можете бесплатно скачать ассеты 2D-игр для аркад, стратегий, платформеров, ролевых игр и многих других типов игр. Блоки САПР в нашей библиотеке можно изменять. салон самолета. Поль Сезанн, Яблоки, 1890. #shorts #photoshop #timelapse10 Зарисовки, 10 минут, 10 зарисовок за 10 минут, Procreate Ipad, Цифровая живопись Timelapse, Имад Аван, спидарт, спид-арт, Солнечные туннели — Нэнси Холт.И в этой категории вы найдете действительно замечательные вещи. Включает в себя более 42 000 000 векторных клипартов, картинок и графических изображений. У нас также есть забавные анимации, игры и веб-комиксы для вас. 2d лэнд арт

    тадж цо t5c 0fg 2hj tau xe1 p4h 4za ya1 1eu vxa t5z 1yl mlk tus gtu jtq pri c59

    «Мы должны сделать лучше, чем 1000 деревьев»

    Хотя добавление деревьев к зданиям может иметь реальную ценность, в недавно открытом Томасом Хезервиком 1000 деревьев затраты на углерод перевешивают экологические выгоды, говорит Филип Олдфилд.

    Почти десять лет назад журналист и исследователь Тим Де Чант опубликовал статью под названием «Можем ли мы перестать рисовать деревья на вершинах небоскребов?» Он быстро стал вирусным.

    В нем он упрекает архитекторов за то, что они произвольно добавляют растительность к зданиям, создавая ощущение устойчивости. «Это просто нереально. Я понимаю, почему архитекторы рисуют их на своих зданиях. Правда, понимаю. Но мы можем остановиться?»

    В последующие годы архитекторы не слушали.Было реализовано множество зеленых зданий и башен, и ни одна многоэтажная секция не обходится без какой-либо формы пышной свисающей зелени или огромных деревьев, растущих из сомнительно малых глубин почвы.

    В описаниях проектов часто говорится о размещении лесов, мысов, ферм и многого другого на высоте над городом. Последним, кто принял эту тенденцию, является «1000 деревьев Хизервика», первая фаза которого недавно открылась в Шанхае.

    Потенциал природы уменьшается в этом стремлении к эгоистичной архитектурной концепции

    1000 деревьев создает архитектурную топографию; две ступенчатые насыпи высотой 60 и 100 метров (последняя из которых будет построена на втором этапе в течение следующих нескольких лет).

    Расположенный рядом с общественным парком, протянувшимся вдоль реки Сучжоу, проект направлен на визуальное расширение этой зеленой зоны вверх по зданию с помощью деревьев, которые прорастают из матрицы бетонных колонн, создавая то, что архитекторы называют «двумя покрытыми деревьями горами». «.

    Томас Хизервик открывает торговый центр 1000 Trees в Шанхае

    Однако, хотя замысел ясен, результирующая архитектура ограничивает деревья — одну из самых удивительных сил нашего природного мира — декоративным орнаментом на вершинах колонн.Потенциал природы уменьшается в этом стремлении к самодовольной архитектурной концепции.

    Деревья и зелень могут принести большую пользу нашим городам. Озеленение может помочь смягчить эффект городского теплового острова за счет снижения температуры окружающей среды, затенения общественных мест и зданий и поглощения загрязняющих веществ из воздуха.

    Благодаря фотосинтезу деревья поглощают углекислый газ и выделяют кислород. Они обеспечивают биоразнообразие, а также домашних птиц и насекомых. Есть и психологические преимущества: доступ к зелени снижает стресс и улучшает психическое здоровье и концентрацию.

    Деревья — это однострочный штрих, создающий ощущение городской драмы

    При большом количестве преимуществ, к сожалению, так мало, кажется, было использовано или учтено в 1000 Деревьев. Вместо этого природа сводится к поверхностному орнаменту. Деревья — это остроумие, создающее ощущение городской драмы, но мало что говорит о том, как они могут принести ощутимую пользу окружающей среде или сообществу.

    Использование растительности для расширения парка до здания не является чем-то новым.В Фукуоке, Япония, в конце 1980-х годов предложение о размещении нового правительственного здания в парке Тэндзин вызвало общественный резонанс.

    В ответ Эмилио Амбаш спроектировал центр ACROS с пышными садовыми террасами (общедоступными), водными сооружениями и примерно 50 000 растений. Таким образом, любая зеленая зона, потерянная из парка на территории нового здания, будет возвращена публике.

    Дизайн Ambasz отличается от 1000 деревьев не только протяженностью вертикальной зелени (пышный ковер из растений, обеспечивающий четкую непрерывность парка в Фукуоке, по сравнению с разбросанными плантаторами в Шанхае), но и экологическим обоснованием.

    Центр ACROS расположен в северной части парка, то есть его зеленые террасы обращены прямо на юг, затеняя офисное здание от солнца. В «1000 деревьев» большая часть зелени находится на северном фасаде, а южный фасад представляет собой смесь остекления и фресок.

    Каково углеродное воздействие размещения сотен деревьев на здании такого масштаба?

    Компания «1000 деревьев» тщательно отобрала подходящие виды растений, способные произрастать на разных высотах.В то время как его зеленые качества, несомненно, будут увеличиваться по мере того, как деревья и растения будут расти с течением времени, на данный момент доминируют ребристые бетонные горшки, возвышающиеся над колоннами, как гигантские дизайнерские раковины в ванной.

    В связи с этим возникает вопрос: каковы углеродные последствия размещения сотен деревьев в здании такого масштаба?

    Судя по чертежам, типичная сеялка и верхняя часть колонны содержат около 14 тонн железобетона. Каждый килограмм железобетона выделяет 0.111 килограммов углекислого газа при его производстве (согласно Инвентаризации углерода и энергии).

    «Нам всем нужны места, которые вызывают реакцию», — говорит Томас Хезервик

    Это означает, что одна сеялка будет иметь воплощенный углерод в размере 1554 кг эквивалента двуокиси углерода (CO₂e). Количество углекислого газа, поглощаемого деревом, является динамическим и зависит от множества факторов, но может быть оценено как 10 кг в год в течение первых 20 лет его жизни.

    Это означает, что углекислый газ, поглощенный деревом, потребуется около 155 лет, чтобы компенсировать выбросы при производстве бетонной плантатора (это консервативные цифры, и они не включают выбросы от транспорта, строительства, стальных балюстрад, технического обслуживания и так далее).

    Очевидно, что затраты на выбросы углерода перевешивают любую пользу для окружающей среды

    Существуют и другие экологические преимущества деревьев, которые могут сократить этот временной масштаб, но они не учитываются в проекте.Их местоположение определяется не солнцем, ветром или климатом, а произвольной структурной сеткой. В любом случае ясно, что стоимость углерода перевешивает любые экологические выгоды.

    Хотя мы должны быть осторожны, чтобы не сводить природу к простым числам, именно такие вопросы наша профессия должна задавать себе в условиях климатического кризиса.

    Другие исследования также пытались количественно оценить преимущества вертикального озеленения в других местах. Bosco Verticale Стефано Боэри включает в себя 13 000 растений и 700 деревьев в горшках на 27 этажах.

    Исследования Совета по высотным зданиям и городской среде обитания (CTBUH) показали, что дополнительная тень, которую они обеспечивают, может снизить потребность здания в энергии на 7,5%. Будет ли этого достаточно, чтобы компенсировать воплощенный углерод в бетонных горшках? Наверное, нет, но хоть как-то пойдет.

    Стефано Боэри покрывает башню социального жилья 10 000 растений

    Однако, помимо всего этого, растительность приносит пользу человеку.Лично я вижу реальную ценность Bosco Verticale и последней версии Боэри, башни социального жилья Trudo Vertical Forest в Эйндховене, в том, что она делает вертикальную жизнь более привлекательной и приятной благодаря зеленым верандам, которые они предоставляют, в отличие от пустынных балконов в гораздо более высоких домах. -подъемное жилье.

    В Сингапуре я участвовал в исследовании, посвященном опыту жителей в небесных садах, и обнаружил, что они могут способствовать ощущению покоя и бегства от действительности (хотя жители также были разочарованы строгими правилами, регулирующими сады на высоте).

    Могут ли 1000 деревьев обеспечить человеческую пользу, бегство от густых бетонных джунглей Шанхая? На визуализациях и фотографиях проекта показаны дорожки и террасы с свисающей сверху зеленью и цветами.

    Однако, учитывая, что на этом первом этапе расположены в основном магазины розничной торговли и продуктов питания и напитков, кто будет иметь доступ к этим помещениям? Будут ли они по-настоящему публичными, куда любой желающий может прийти и посидеть под деревом?

    У архитектуры есть возможности для лучшего взаимодействия с природой

    Наши общественные и зеленые насаждения все чаще приватизируются, выдаются билеты и контролируются.Возникают закономерные вопросы о том, могут ли зеленые насаждения на высоте приносить пользу более широкому сообществу, или же они являются просто элитарными экологическими побрякушками, доступными лишь немногим для гедонистического селфи или дорогого коктейля.

    На уровне 1000 деревьев я предполагаю, что наземный парк вдоль реки Сучжоу принесет гораздо больше пользы Шанхаю, чем деревья, разбросанные по всему зданию.

    Это не означает полного отказа от идеи вертикального озеленения. Я по-прежнему считаю, что у архитектуры есть возможности лучше взаимодействовать с природой и растительностью в наших плотных городских районах.

    Leave a comment
    by : alexxlab Графика

    Графика штрихи: Больше 30 бесплатных векторных изображений на тему «Штрихи» и «»Штрих Код

    Для пользовательского штриха D1178 требуется массив типа «тире» — Win32 apps

    • Статья
    • Чтение занимает 2 мин
    Были ли сведения на этой странице полезными?

    Оцените свои впечатления

    Да Нет

    Хотите оставить дополнительный отзыв?

    Отзывы будут отправляться в корпорацию Майкрософт. Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.

    Отправить

    В этой статье

    Для создания стиля обводки с _ пользовательским стилем штриха _ требуется массив тире.

    Возможные причины

    Когда приложение попыталось создать ID2D1StrokeStyle, в нем использовался _ _ настраиваемый атрибут стиля тире D2D1, _ но был ЗАДАН массив штрихов null.

    Возможные исправления

    Если для приложения требуются пользовательские тире, убедитесь, что указан допустимый массив штрихов. Пример см. в разделе Креатестрокестиле. Если допускается использование встроенного стиля штриха, оставьте массив дефисов РАВНым NULL и используйте описатель, например D2D1 штрих- _ _ _ пунктир.

    Штрихи к выставке живописи и графики Серебряного века из фондов ВХМ в белгородском художественном музее

    Рассказываем, как Серебряный век менял представления об изобразительном искусстве в России, как выстроить персональный маршрут по экспозиции в музее и почему поход на выставку из Вятки не стоит откладывать в долгий ящик.

    Вятский художественный музей приехал в Белгород во второй раз. Открывшуюся неделю назад выставку подготовили специально для нашего музея. Её экспонаты хранятся в фондах вятского музея, и часть из них – маленький повод для гордости – ни разу не видели даже сами жители Вятки. После выставки в Белгороде живописные полотна и графические листы отправятся отдыхать в хранилища на продолжительное время: более двух месяцев активной жизни на свету и им, как человеку, нужен покой и восстановление сил.

    На насущные вопросы о том, как характеризуют Серебряный век в изобразительном искусстве, отвечает замдиректора по научной работе Вятского художественного музея, кандидат искусствоведения Ираида Кувалдина:

    Серебряный век вышел из области философии, литературы, а изобразительное искусство шло с ними в унисон. Русские художники давали удивительную по разнообразию картину мира: «Мир искусства», «Союз русских художников», авангард 1910-х, «Бубновый валет»… Выставка тем и хороша, что она разнообразна. Здесь нет стремления показать одно оформленное художественное объединение. Многоликую жизнь искусство отражает по‑разному. Тем и был привлекателен Серебряный век: фигуративным искусством – классикой и отторжением этой классики – абстрактным искусством.

    Этот период отличает и качество, профессионализм. Среди художников не было дилетантов. Они стремились быть универсальными: работали в графике, в живописи, в темпере, занимались монументальным искусством, делая росписи для храмов… Этот всплеск – второе Возрождение. Художники могли всё, как и в эпоху Возрождения в Италии».

     

    «О имена!»: о художниках и их работах

    «Знаете ли вы, кто был первым русским импрессионистом? Константин Коровин («Вид Московского Кремля») Он привёз из Германии немецкий вариант импрессионизма. Работ его не так много в коллекции нашего музея. Хотите ещё говорить об импрессионизме? Вот Игорь Грабарь («Иней»), вот Николай Тархов («Париж»), который, развиваясь в этом направлении, уехал в Париж, – комментирует Кувалдина. – Хотите говорить о пленэризме – есть в экспозиции Аполлинарий Васнецов, Николай Хохряков. Если говорим о фовизме – это Роберт Фальк. Влияние сезаннизма ощущал на себе Пётр Кончаловский («Дубы. Абрамцево»).

    Классическим принципам следовало Императорское общество русских акварелистов, его первый председатель Альберт Бенуа. Нужно понимать, что Александр Бенуа (иллюстрация к поэме «Медный всадник») – это театральный деятель, теоретик искусства, живописец, а Альберт Бенуа занимался только акварелью. Но как он ею занимался!.. Посмотрите на эти лунные ночи, на восходы и закаты. Можно встретить здесь и Бориса Кустодиева с его женскими образами («Девушка, расчёсывающая волосы»). Ранний Кузьма Петров-Водкин – редко встречаемая его работа, «Мальчик в синей рубашке», ранее мы её никогда не репродуцировали.

    Мало кто знает, что Аркадий Рылов, наш земляк, вятский художник по происхождению, был и портретистом. Его знают прежде всего как пейзажиста («Догорающий костёр», «Море. Камни. Крым»). А вот и доказательство – «Портрет старика». Ваша землячка Зинаида Серебрякова – это подарок белгородцам. В фондах нашего музея есть только одна картина Серебряковой – «Обнажённая модель» – и мы её привезли в Белгород».

    Имена русского авангарда – Александр Родченко («Линии на зелёном»), Василий Кандинский («Беспредметная композиция», эскиз к композиции «Красное с чёрным»), Михаил Матюшин. Каждый из них по‑своему представлял новый мир: собственными выразительными средствами, светом, динамикой, конструктивными реалиями. Это их способ самовыражения.

    Домашнее задание

    — Что почитать, если перед походом на выставку хочется больше узнать об изобразительном искусстве Серебряного века?

    — Не знаю, стоит ли целенаправленно готовиться к встрече с экспозицией: постичь всё, что касается Серебряного века, будто объять необъятное. Можно посмотреть работы искусствоведа Дмитрия Сарабьянова, изучавшего изобразительное искусство конца XIX – начала XX веков. Хороший, простой учебник Татьяны Ильиной – схематичное повествование, фактологический материал, опираясь на который можно обозначить для себя имена Серебряного века. Всю экспозицию, отмечу, в один раз не посмотришь. Надо остановиться на том, что тебя цепляет сегодня, не надо пытаться увидеть всё сразу. Эта выставка не на один просмотр, – отвечает Ираида Кувалдина.

    Как смотреть

    О концепции выставки рассказывает заведующая выставочным отделом Белгородского художественного музея Алла Селютина:

    «Нам удобно делить художников этого периода: импрессионист он или постимпрессионист. Однако они пробовали, экспериментировали, искали и не связывали себя узами никаких творческих течений, выставляясь одновременно и с Союзом русских художников, и с «мирискуссниками», например. Поэтому выставить художников по творческим группам оказалось невозможно: нам бы пришлось периодически перевешивать работы. Сформировать экспозицию по хронологии? Невозможно: все эти художники – современники. Мы пошли по принципу эстетическому: чтобы экспонаты органично смотрелись друг с другом, чтобы помогали звучать друг другу, создавая тем самым для зрителя ощущение разнообразия, бурной творческой реки».

    Выставка «Серебряный век. Живопись и графика из собрания Вятского художественного музея им. В. М. и А. М. Васнецовых» проходит при поддержке Фонда содействия развитию музейного дела, археологии и памятников архитектуры в Белгородской области «Наследие». Экспозиция задержится в Белгороде до 13 ноября.

    Оригинал

     

    Штриховая графика, стр.2 — TopRef.ru

    1.2 Штриховая графика

    Штрих всегда соседствует с линией и редко используется самостоятельно. Изображения, где доминирует штрих, называются штриховыми. Многие мастера изобразительного искусства блестяще владели штрихом и виртуозно применяли его. Среди них: Рембрандт, А. Ватто, А. Дюрер, В. Ван-Гог, Н.С. Самокиш, Г. Доре, М.А. Врубель — у них есть немало произведений, которые по преобладанию штрихового выражения формы над линейным можно отнести к штриховым изображениям.

    Работы Рембрандта — одни из немногих подлинных примеров единства выражения формы и содержания в графике. Изображения выполнены в основном в технике перового рисунка и в офорте. Особенно хороши его офортные портреты («Ювелир Ян Лютма» и др.). Штрих Рембрандта никогда не бывает однотолщинным, каждый участок линии в штрихе имеет свой нажим. Пересекаясь под разными углами, штрихи создают ту таинственную среду, которая во многом обязана разнообразию фактур, получающихся при пересечении штрихов. Таким же способом набирается знаменитая рембрандтовская глубина тона и выявляется светотень. («Автопортрет с пером») Совершенно другое использование штриха можно увидеть в рисунках А. Ватто. Короткий мелкий штрих прекрасно выражает форму, почти не прибегая к добавлению контурной линии. В рисунках Дюрера штрихи активно идут по поверхности формы, точно выявляя объем. Штрих недлинный и чаще всего поперек формы сильно подчеркивает округлости. Это почти скульптурное понимание пластики. Методически точным штрихом обладал Гендрик Гольциус (1558-1617). Его считают виртуозом в истории резцовой гравюры по меди. Изощренным рисовальным штрихом владел Г. Доре. (иллюстрации к романуФ. Рабле «Гаргантюа и Пантагрюэль»). Штриховые рисунки В. Ван-Гога нельзя спутать с другими. Обостренное чувство ритмического строя среды сподвигает его на создание своего языка. Ван-Гог редко использовал перекрещивание штрихов, так как это снижает динамику, необычайно важную для него. Для фактуры каждого предмета он находил свой штрих («Лодки в море у Сен-Мари»). Нельзя оставить без внимания рисунки пером Н.С. Самокиша, выполненные для журнала «Нива». Он существенно повлиял на развитие штрихового графического изображения в журналах России, применяя традиции английских рисовальщиков конца ХIX в. Для них был характерен плотный, почти сливающийся штрих, определяющий местоположение объекта на бумаге, тон и до некоторой степени фактуру. Изображение исполнялось виртуозно, очень точно, но «грешило» однообразием приема штрихования, переходящего часто с предмета на предмет без особых изменений и работающего как усложненное штриховой фактурой графическое пятно. Об особенностях техники работы М.А. Врубеля можно судить по штриховой мозаичной кладке в известных рисунках цветов и пейзажах. Видными мастерами штрихового рисунка в русской графике были А. Кубин, Г. Лоссов, В.А. Фаворский, Н.В. Кузьмин, И.И. Шишкин, А.М. Лаптев и др.

    Кроме этого, чисто технический опыт фактурной штриховки накоплен граверами Европы XVIII — XIX вв., занимавшимися репродуцированием известных работ. Репродукционной гравюрой заполнены многочисленные книги по искусству и периодическая печать этого периода.

    1.3 Пятновая графика, силуэт

    В пятновой графике основным изобразительным элементом являются черные и белые пятна (плоскости). В крайнем выражении пятновая графика приходит к искусству силуэта — черный силуэт на белом фоне или белый силуэт на черном фоне.

    Не многие художники в совершенстве владели искусством пятновой черно-белой графики. Центральной фигурой среди этих немногих является Феликс Валлотон. Художник пришел к графике контрастных пятен через поиски в штрихе, линии («Этюды обнаженного тела», Обложка каталога издательства Э. Саго). Художник В.А. Фаворский писал, что с помощью » формы пятен мы можем достигнуть тяжелого черного, лежащего выпуклым пятном на белом, черного уплощенного, характеризующего плоскость, черного, дающего глубину, и черного воздушного». Советская книжная графика 1920-х гг. прекрасно это подтверждает. Работы В.В. Лебедева, В.Н. Курдова, В.А. Дувидова, Л.М. Лисицкого и др. вошли в золотой фонд советской графики. Использовал возможности пятновых графических решений в художественном оформлении книги Д.И. Митрохин. Его плоскостные изображения точны в своих подробностях и подчас сказочно экзотичны.

    Искусство силуэта восходит к профильным фигурам на сосудах Древней Греции. Из наиболее известных русских мастеров силуэта XIX в. можно назвать графа Ф.П. Толстого и Е.М. Бем. В период расцвета силуэтного искусства в графике видное место занимали К.А. Сомов, А.Н. Бенуа, М.В. Добружинский и особенно Г.И. Нарбут (иллюстрации к книгам » Отечественная война 1812 года в баснях Крылова», «Спасенная Россия в баснях Крылова») и Е.И. Кругликова («На выставке «Мир искусства», «Портрет А.А. Радакова»). Активное введение в черные силуэты человеческих фигур и голов белых элементов одежды в работах Кругликовой усилило взаимодействие силуэта и белого поля бумаги.

    Особые темы того времени — силуэтные изображения детей и животных. Множество книг конца XIX-XX в украшены детскими силуэтами работы Е.М. Бем. Силуэты животных удачно решаются в искусстве В.В. Лебедева, В.М. Курдова, В.Д. Фаллиева.

    1.4 Точечная графика

    Точечное изображение строится на основе точек разной величины, но одинаковой конфигурации. Это след от точечного прикосновения пером, кистью и другими художественными инструментами к поверхности.

    В наиболее чистом виде использование точки можно увидеть в офорте. Это прежде всего пунктирная манера, меццо-тинто и карандашная манера. Пунктирная манера заключается в создании изображения путем сложной системы точек. Точки выбиваются на металле с помощью стальных заостренных стержней и граверного молоточка. Наиболее совершенной пунктирная манера была в Англии в середине XVIII в. Работали так и в России. Меццо-тинто получается путем выглаживания светлых мест на специально озерненной металлической доске. В карандашной манере распространены специальные рулетки и насечки, оставляющие на металле след, похожий на точки, составляющие след от карандаша, проведенного по шероховатой бумаге. В искусстве бывших социалистических стран точка широко используется венграми и поляками. Прекрасные примеры есть в графике Дьюлы Ливиуса (иллюстрации к произведениям венгерской поэзии), использующего точку в основном для передачи объема с определенной фактурой. Более последователен в применении этой техники Герман Каргинов.

    В настоящее время точечная техника широко применяется в графике как при комбинации техник, так и в чистом виде.

    2. Комбинирование элементов графики

    2.1 Линейно-пятновая графика

    Наиболее широко и эффектно в европейской графике линейно-пятновые изображения применялись в конце XIX – начале XX в. Часто проводят взаимосвязь между широким проникновением в Европу произведений искусства Японии, Китая. Расцвет новой европейской графики связан с углубленным изучением крупными художниками-графиками средств художественного выражения и теоретического осознания их возможностей. Родиной этой новой европейской графики принято считать Англию. И практически и теоретически она много сделала для развития и распространения «графического видения». Из художников того времени наиболее значительным является Обри Бердслей. В его работах линии влиты с черными пятнами заливок в единое целое, линии вырастают из пятен, и пятна логично заканчивают линии (рисунки к произведениям Эдгара По, графические листы серии «Саломея», заставки к книге Т. Мелори «Смерти Артура»). Истоками техники сочетания линии и пятна у О. Бердслея в определенной степени могут служить японская гравюра и греческая вазопись.

    В России в линейно-пятновой графике работами почти все художники круга «Мир искусства». Им и принадлежит большинство высокохудожественных произведений, исполненных этой техникой. С необычайной графической культурой применяет линию и пятно И.Я. Билибин в заставках и концовках к журналам » Мир искусства», «Народное образование» и др. Строгость изобразительных средств прекрасно подходит к выражению мотивов русского Севера. Надолго запоминается его рисунок «Царь Дадон и ключница Амелфа» к «Сказке о золотом петушке» А.С. Пушкина. Черная линия и пятно являются основными средствами выражения великолепных маленьких гравюр на дереве 1900-1903 гг.А.П. Остроумовой — Лебедевой («Зимка»,»Сломанная ель»,»Кипарисы на кладбище» и др.)

    Блестящее чувство сочетания линии и пятна видно в заставках и концовках, исполненных Е.Е. Лансере. Мотивы имеют изобразительный характер, хорошо читаются. Рафинированное чувство графических средств русскими художниками рубежа XIX-XX вв. дало свои плоды и в 1920-30-е годы. Творчество Д.С. Моора, В.Н. Дени составляет блестящие страницы советского искусства. У Д.С. Мора на линии и пятне построены иллюстрации к сборнику «Кто они такие?», у В.Н. Дени — рисунки для газеты «Правда». Работа советских художников явилась естественным продолжением развития новой европейской графики, зародившейся в конце XIXвека.

    2.2 Линейно-штриховая графика

    Линия и штрих постоянно сопутствуют друг другу. В случае, когда линия и штрих вносят более или менее равноценный вклад в создание рисунка, тоэто позволяет говорить о линейно-штриховой графике. Линейно-штриховые изображения развивались с ранних периодов истории искусства. Штрих конструктивно поддерживает линию уже в европейской гравюре на дереве первой половиныXV в. Развитие искусства рисования, а вместе с этим и мастерства перевода рисунков на гравюру уже к началу XVI в. довело применение техники линия-штрих до виртуозного мастерства. Хороший тому образец — иллюстрации к произведению «Корабль глупцов» Себастьяна Бранта и сборнику рассказов «Турнский рыцарь». В XVIв. штрихи становятся более округлыми, утончающимися в сторону света и мягко входящими в линию. Гравюры с рисунков А. Дюрера, Л. Кранаха, Г. Гольбейна-младшего и др. художников прекрасно это подтверждают. Энергичные, темпераментные линейно-штриховые рисунки имеются у Микиланжело, Тициана, Рембрандта, Рафаэля, Леонардо да Винчи.

    Наиболее сознательно, по собственной глубоко продуманной системе применял линию и штрих А. Дюрер в сериях гравюр «Жизнь Марии», «Малые страсти». В одно время с Дюрером жил и творил Альбрехт Альтдорфер. Но его работы более поверхностны и менее драматичны, чем у Дюрера, при этом его композиции очень цельны и нередко имеют декоративный характер. Альтдорфера причисляют к «мастерам малого формата». Мастерами в плане использования линии и штриха были братья Ганс Зебальд и Бартель Бехамы. Также широко известны Ганс Гольбейн-младший и Лукас Кранах, работавшие примерно в одно и то же время. С легкой разработкой штрихом гравировал Августин Хиршфосель, он известен в основном по иллюстрациям к книге «Записи о московских делах» З. Герберштейна. Популярен также в этой среде художник Вольф Губер («Пейзаж с церковью»). Особого внимания заслуживают рисунки и офорты Франсиско Гойя. Острота видения и глубина чувств, изливаемых на плоскость листа, не дают ему возможность для размеренной обработки объема.

    Древнерусские художники мастерски владели законами графического изображения. Рисунком кистью на левкасе начиналась работа над иконописной композицией, и кончалась она доводкой энергичными мазками (штрихами) в складках одежд и нанесением узорочья. На Руси штрих использовался как дополнение линий в создании характера, позы, движения, состояния. Также, штрих часто брал на себя функции выявления фактуры. Изображений, исполненных с помощью линий и штриха, много в древнерусской миниатюре и в русском лубке. Штрих здесь выполняет чисто декоративную роль. Русская академическая школа рисунка, так же как и другие европейски школы, декларирует построение изображений на основе линии и штриха. Об этом могут говорить рисунки А.Е. Егорова, Ф.А. Бруни, О.А. Кипренского, К.П. Брюллова, В.А. Тропинина, В.Г. Перова, В.Д. Поленова, И.Е. Репина, В.И. Сурикова, В.А. Серова, Ф.А. Малявина и др.

    В советский период данный подход к рисунку в корне е изменился и продолжал развиваться. Так рисовали В.А. Фаворский, А.Ф. Пахомов, ныне их традиции продолжают и современные художники. Из истории русской гравюры наиболее известны линейно-штриховые изображения таких художников, как А.И. Кравченко, А.Д. Гончаров («Портрет старухи»).

    2.3 Сочетание линии, штриха и точки в графике

    Сочетание линии, штриха и точки ясно просматривается в гравюре на металле. Наиболее технически совершенно этой областью овладел и первым применил эту манеру Джулио Комппаньола (род. В 1482г). Точки он использовал как продолжение штриха или линии для создания плавного перехода к свету и для фактурных проработок. (» Христос и самаритянка»).

    Позднее подобную манеру разрабатывали Ян Лютма — младший, Франц Аспрук. В дальнейшем сочетание линии, штриха и точки прочно занимает место в основном в репродукционной гравюре. Так работал в XVIII в. В гравюре на меди итальянец Рафаэлло Морген, репродуцируя классические итальянские произведения итальянской живописи. Достижения XVIIIв. Использовались широко в изданиях XIXв. и даже перешли в репродукционную гравюру на дереве. В гравюре на меди черная точка (пунктир) встречается чаще при выявлении объема лица или фигуры, в гравюре на дереве точка (белая) применяется при разработке теней.

    Исключительно художественное использование точки в сочетании с линией и штрихом наблюдается в искусстве В. Ван-Гога («Барки на берегу»). Наибольшее разнообразие точек в композиции с линией и штриом применял В.В. Кандинский («Маленькие миры VIII»).

    Довольно широко использует штрих, линию и точку современная книжная графика. Но поскольку она не связна с гравюрой на металле и задачи ее художественные, то точка часто выполняет фактурные и декоративные функции.

    2.

    4 Сочетание линии, штриха и пятна в графике

    Черно-белые композиции линии, штриха и пятна наиболее часто встречаются в ксилографии, европейской книжной и журнальной иллюстрации, русской и советской книжной графике 1920-х гг.

    Пятно, как таковое, зазвучало в полную силу в буквицах для книг, орнаментах, обрамляющих текст или сюжетные рисунки. Эффектно вводил пятно в линейно-штриховые изображения на дереве немецкий живописец Ганс Бальдунг Грин. Самое же широкое применение линии, штриха и пятна началось с творчеством Томаса Бьюика, разработавшего технику тоновой гравюры. Европейские ксилографические изображения в журналах и книгах XVIII — XIX вв. широко иллюстрируют активное насыщение ксилографии различными фактурными и светотеневыми находками.

    Из русской графики отмечают работы художников начала XXв и 1920-х гг. Это заставки и концовки книг Д.И. Митрохина, иллюстрации М.В. Добружинского к повести Ф.М. Достоевского «Белые ночи», произведения Д.С. Мора, В.М. Конашевича, В. А. Фаворского, А.И. Кравченко.Д.С. Моор всегда вводил сплошную, плакатно резкую черную заливку в линейно-штриховое изображение (плакат «Помоги»). Художник часто обращался к белой линии или белому штриху по черному фону, что расширяло возможности выразительных средств в графике. В иллюстрациях детских книг В.М. Конашевича, в его рисунках из серий «К 10-й годовщине Октября»,»Мелкие рассказы», «Улица» уверенное свободное рисование способом линия-штрих по белому фону эффектно оттеняется контрастом выверенных темных ударов.

    Графика американского художника Рокуэлла Кента породила его самобытное и необычайно цельное наледие. В его работах как правило прослеживается строгое и «математически-четкое варьирование линии, штриха и черной заливки (иллюстрации к роману Г. Мелвилла «Моби Дик».

    графика линия штрих точка

    Заключение

    Итак, можно подвести итог, что в разных странах именно на рубеже XIX-XX вв. начинается грандиозный процесс поиска новых выразительных возможностей графики. Большая работа в этом плане проделана в нашей стране в 1920-е гг. художниками разных направлений. Опыт, накопленный ими, позволил решить ряд важнейших для искусства того времени задач. Среди них большое место уделялось вопросам изучения возможностей средств художественного выражения в формальной композиции на плоскости. Процесс поиска новых выразительных возможностей графики, развивающейся с начала XX в., далеко неокончен и не замедлен. Выйдя из оков иллюзорности, графика открыла для себя множество путей и вне традиционных, установленных для нее веками традиций.

    Список использованной литературы

    1. Звонцов В.М. ‘Основы понимания графики’ — Москва: Издательство Академии Художеств СССР, 1963

    2.О. Бердслей. — СПб, 1908

    3. Лаптев А.М. Рисунок пером. — М., 1969

    4. Молок Ю. Владимир Михайлович Конашевич. — Л., 1969

    5. Фаворский В.А. О графике как основе книжного искусства // Искусство книги. — М., 1961

    6. Бесчастнов Н.П. Черно-белая графика: учеб. Пособие для студентов вузов. — М., 2008.

    7. Ресурс сети Интернет: www/ /graphic.org.ru

    Не удается найти страницу | Autodesk Knowledge Network

    (* {{l10n_strings.REQUIRED_FIELD}})

    {{l10n_strings.CREATE_NEW_COLLECTION}}*

    {{l10n_strings.ADD_COLLECTION_DESCRIPTION}}

    {{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$item}} {{l10n_strings.PRODUCTS}} {{l10n_strings.DRAG_TEXT}}  

    {{l10n_strings. DRAG_TEXT_HELP}}

    {{l10n_strings.LANGUAGE}} {{$select.selected.display}}

    {{article.content_lang.display}}

    {{l10n_strings.AUTHOR}}  

    {{l10n_strings.AUTHOR_TOOLTIP_TEXT}}

    {{$select.selected.display}} {{l10n_strings. CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}

    Burito — Штрихи, аккорды для гитары

    Intro: Am G Dm C G

Первый Куплет:  
Am 
Мы штрихи одного рисунка.
G  
Черно-белая графика.
Dm 
Безликие тени на пустых перекрестках.
         C             G
В сетях городского трафика.
Am
Когда ночь остановит свой взгляд.
  G
На созвучие сказанных слов.
                  Dm 
Поминутными мутными формами в воздухе.
    C          G
Разольется любовь.

Припев:
Am                      Em
Снова бегут по небу облака.
Dm                                      C G
Мягкими перьями белыми укрывая внизу города.
Am                                 Em
В этих районах мы скроемся наверняка.
Dm                                    C    G Am
Наши сердца не разлучит никто, никогда.  Никогда.

Второй Куплет:  
Am
Мы все те же, что месяцем раньше.
  G
Только взглядом уже не совсем.
     Dm
Черным по белому, белым по черному.
   C               G
Краски снова станут ничем.
Am
Распадаясь, становясь частотами.
G
Четными и нечетными.
Dm
Радиоэфирными волнами.
   C               G
Нас кто то встретит еще.

Припев:
Am                     Em
Снова бегут по небу облака.
Dm                                      C G
Мягкими перьями белыми укрывая внизу города.
Am                                 Em
В этих районах мы скроемся наверняка.
Dm                                    C      G Am
Наши сердца не разлучит никто, никогда. Никогда.

Am Em Dm C G }x2

Третий Куплет: 
Am
Ледяные камни, горячее сердце.
G
В нас топят надежду, но мы верим, как прежде.
Dm
Руки Вселенной держут нас.
     C                G  
И льется любовь прямо сейчас. 

Am
Разольется любовь, моя любовь.
Em
Разольется по венам моя любовь.
Dm
Твое сердце согреет моя весна.
    C                G  
Разольется любовь не напрасно.
Am
Разольется любовь, моя любовь.
Em
Разольется по венам моя любовь.
Dm
Твое сердце согреет моя весна.
    C                G  
Разольется любовь не напрасно.

Припев:
Am                      Em
Снова бегут по небу облака.
Dm                                      C G
Мягкими перьями белыми укрывая внизу города.
Am                                 Em
В этих районах мы скроемся наверняка.
Dm                                    C      G Am
Наши сердца не разлучит никто, никогда. Никогда.

Outro: Am Em Dm C G }x2

    2.3 Сочетание линии, штриха и точки в графике. Ретроспективный анализ искусства графики и его элементов

    Похожие главы из других работ:

    Декоративно-прикладное искусство Индии

    3.
    2 Проблемы искусства Индии с точки зрения западной критики

    1. Сохранение памяти о живописи как единственной альтернативы индийского искусства, соответствующей универсальным ценностям в совокупности с традицией идентифицировать себя как уникальная нация. Эта схема неприемлема для художников-гибридов…

    Женская личность в работе Симоны де Бовуар «Второй пол»

    1.1 Развитие женской личности с точки зрения исторического и социокультурного аспекта

    За истекшие 300 лет женская личность пережила немало спадов и подъемов. В некотором смысле положение женщин в западных обществах определенно улучшилось, и многие вопросы, которые поднимали феминистки прошлого…

    Карл Брюллов. Сочетание классицистического и романтического стилей в живописи

    3. Гармоничное сочетание художественных течений на примере работ Карла Брюллова

    Гениальность и новаторство Брюллова состоит в том, что он сумел соединить в своей картине принципы академического искусства с романтичностью характеристик. ..

    Кровать, как центр спального пространства

    ГЛАВА II. Кровать в спальном пространстве с философской и эстетической точки зрения

    …

    Культура и религия в современных условиях

    4.Европейская социокультурная интеграция с точки зрения религии

    Становление единой Европы зависит от целого множества факторов. Стремление придать им иную динамику развития, сделать ставку лишь на один-два фактора равносильно лечению серьезного заболевания каким-то одним способом, не учитывая ни режим…

    Культурология как наука

    Культура с точки зрения Возрождения и Просвещения

    Эпоха Возрождения вернулась к античным представлениям о человеке и его месте в мире. Но в истории человечества ничто не возвращается в первозданном виде. Точно так же мыслители Возрождения вернулись к античному идеалу человека…

    Магический танец И. Моисеева

    2.2.2 Специфика хореографической образности с точки зрения ее синтетического начала

    Хореографическое искусство включает различные виды искусств — музыку, собственно хореографию, драматургию, живопись. Каждый из них, преломляясь соответственно требованиям данного вида искусства…

    Образ Невского проспекта в живописи и графике русских художников XIX века

    Глава 2. Невский проспект в живописи и графике русских художников XIX века

    Картина трехсотлетней жизни, прожитой городом и вместе с ним многими поколениями его созидателей и обитателей. Начало этой жизни совпало с появлением в России нового, почти не ведомого до того светского изобразительного искусства…

    Образ Невского проспекта в живописи и графике русских художников XIX века

    2.2 Образы Невского проспекта Санкт-Петербурга в живописи и графике XIX века

    Иконография Санкт-Петербурга богата. История всей России и ее культуры предстает в связи с Петербургом в весьма необычном ракурсе, внимании к городу, его архитектуре и жизни…

    Ретроспективный анализ искусства графики и его элементов

    2.4 Сочетание линии, штриха и пятна в графике

    Черно-белые композиции линии, штриха и пятна наиболее часто встречаются в ксилографии, европейской книжной и журнальной иллюстрации, русской и советской книжной графике 1920-х гг. Пятно, как таковое, зазвучало в полную силу в буквицах для книг…

    Роль сексуальной культуры в сохранении здоровья человека

    1. Секс с точки зрения медицины и культуры

    Все множество видов существующих культурных норм составляет нормативную систему культуры. Она является не хаотичной суммой разрозненных элементов, а подвижной целостностью…

    Роман Достоевского «Идиот» в киноверсии Бортко

    3. Образы, их художественное визуальное воплощение и второстепенные линии

    экранизация роман актерский художественный «Идиота» часто называют цветной черно-белой картиной. Черный и белый цвета экрана — не просто цвета, они насыщенные, говорящие, они исполнены смысла. Зеленый цвет — это природа (Павловск)…

    Сопоставительный анализ концепта труд в английском и русском языках с точки зрения культурологии

    Глава II. Сопоставительный анализ английский и русских паремий с точки зрения культурологии.

    . ..

    Технологический процесс выполнения фотосъемки рекламного проекта

    2.2 Выбор точки фотосъемки

    Точка съемки в фотографии — это место, в котором находится камера во время съемки. Как и для любой точки пространства, ее положение должно определяться тремя координатами. Для фотосъемки это расстояние до снимаемого объекта, угол…

    Художественные стили в интерьере

    Сочетание цветов в интерьере

    В предыдущей статье говорилось о цвете в интерьере и о значении цвета. Остановимся немного на правилах подбора сочетания цвета в интерьере. Разумеется, правильно это может сделать дизайнер, который подберет цветовые сочетания с учетом стиля…

    Тату в стиле Графика, значение, фото, татуировки графика

    Графика — это пожалуй самый популярный стиль татуировки в 21 веке. Он зародился в середине 90-х годов XX века в Европе, а в России его начала расти примерно с 2010 года.

    Сейчас тысячи мастеров являются представителями данного направления. Людей в графике привлекает четкость и выразительность. Татуировки в графике одни из самых контрастных.

    Особенности стиля Графика

    Многие люди часто путают данный стиль с другими монохромными стилями, например, с чикано или черно-серой татуировкой, хотя данные стили связывает лишь только использование черного пигмента.

    Важно понимать, чем графика отличается от других направлений. При работе в стиле Графика — мастер пользуется только черным пигментом.

    Самой яркой особенностью графики является наличие выразительной штриховки. То есть, передача объема изображения происходит через штрихи. Чем плотнее штриховка — тем темнее участок татуировки, чем реже штрихи — тем светлее. За счет использования штриховки — это стиль часто называют гравюрным. Четкие контуры элементов татуировки — еще одна из важных особенностей стиля. В графике не применимы полутона, а значит черный цвет в таких татуировках максимально насыщенный, как мы уже писали выше, объем достигается при помощи штриховки, а не полутонов. Современные мастера всё чаще экспериментируют с графикой, смешивая её с другими монохромными стилями, такими  как дотворк, лайнворк, и даже с цветными стилями, например,  реализмом и акварелью.

    Сюжеты татуировок в графике

    Мы уже упоминали, что данный стиль часто называют гравюрным. Это связанно с тем, что на заре формирования этого направления, мастера черпали вдохновение на страницах старых исторических книг, энциклопедий и ботанических справочников.

    Именно поэтому сюжеты современных татуировок в графике обращаются к тем же первоисточникам: это могут быть растения, рыбы, насекомые, змеи, скелеты и здания. Главное чтобы главный элемент татуировки имел четко выраженную структуру и форму.

    Графика считается сложным стилем за счет сложности построения эскиза с учетом особенностей человеческой анатомии, плюс ко всему он требует филигранного исполнения для того, чтобы татуировка смотрелась впечатляюще, ведь напомним, что она состоит из тысяч маленьких штрихов. Именно поэтому мы настоятельно рекомендуем выбирать только профессионалов своего дела!

    Лучшие мастера стиля Графика

    • Заливки и обводки — SVG: Масштабируемая векторная графика

    Существует несколько способов окрашивания фигур (включая указание атрибутов объекта) с помощью встроенного CSS, встроенного раздела CSS или внешнего файла CSS. Большинство SVG, которые вы найдете в Интернете, используют встроенный CSS, но у каждого типа есть свои преимущества и недостатки.

    Рисование

    Базовое окрашивание можно выполнить, установив два атрибута узла: заливка и штрих . С помощью заливка задает цвет внутри объекта, а штрих задает цвет линии, нарисованной вокруг объекта.Вы можете использовать те же схемы именования цветов css, которые вы используете в HTML, будь то имена цветов (то есть red ), значения rgb (то есть rgb(255,0,0) ), шестнадцатеричные значения, значения rgba, и т. д.

    Кроме того, вы можете указать непрозрачность заливки или обводки отдельно в SVG. Они управляются атрибутами fill-opacity и stroke-opacity .

    Примечание: В Firefox также разрешены значения rgba , которые дадут тот же эффект. Но для совместимости с другими средствами просмотра часто лучше указать непрозрачность заливки / штриха отдельно. Если вы укажете как значение rgba , так и значение непрозрачности fill / stroke , будут применены оба значения.

    Обводка

    Помимо свойств цвета, есть несколько других атрибутов, доступных для управления способом рисования обводки на линии.

      
 w3.org/2000/svg" версия="1.1">

    Свойство stroke-width определяет ширину этого штриха.Штрихи рисуются по центру контура. В приведенном выше примере путь показан розовым цветом, а обводка — черным.

    Вторым атрибутом, влияющим на штрихи, является свойство stroke-linecap , продемонстрированное выше. Это контролирует форму концов линий.

    Есть три возможных значения для stroke-linecap :

    • стык закрывает линию прямым краем, перпендикулярным (под углом 90 градусов) к направлению штриха и пересекающим его конец.
    • квадрат имеет практически такой же внешний вид, но немного растягивает штрих за пределы фактического пути. Расстояние, на которое штрих выходит за пределы контура, составляет половину ширины штриха .
    • закругление создает эффект закругления в конце штриха. Радиус этой кривой также контролируется шириной штриха .

    Используйте stroke-linejoin для управления тем, как рисуется соединение между двумя сегментами линии.

      

  <многолиния точек = "40 60 80 20 120 60" штрих = "черный" штрих-ширина = "20"
      штрих-linecap="стык" fill="none" штрих-linejoin="митры"/>

  <многолиния точек = "40 140 80 100 120 140" штрих = "черный" ширина штриха = "20"
      штрих-linecap="круглый" fill="нет" штрих-linejoin="круглый"/>

  <многолиния точек = "40 220 80 180 120 220" штрих = "черный" ширина штриха = "20"
      штрих-linecap = "квадрат" заполнить = "нет" штрих-linejoin = "скос"/>

    Каждая из этих полилиний состоит из двух сегментов. Соединение, где они встречаются, контролируется атрибутом stroke-linejoin . Есть три возможных значения этого атрибута. miter удлиняет линию немного за ее нормальную ширину, чтобы создать прямоугольный угол, где используется только один угол. round создает закругленный сегмент линии. скос создает новый угол для облегчения перехода между двумя сегментами.

    Наконец, вы также можете использовать типы пунктирных линий для обводки, указав атрибут stroke-dasharray .

    Атрибут stroke-dasharray принимает в качестве аргумента серию чисел, разделенных запятыми.

    Примечание: В отличие от элементов , эти числа должны быть разделены запятыми (пробелы игнорируются).

    Первое число указывает расстояние для закрашенной области, а второе — расстояние для незакрашенной области. Таким образом, в приведенном выше примере второй путь заполняет 5 пиксельных единиц с 5 пустыми единицами до следующего тире из 5 единиц. Вы можете указать больше цифр, если вам нужен более сложный рисунок штриховки. В первом примере указаны три числа, и в этом случае средство визуализации дважды повторяет числа, чтобы создать четный шаблон.Таким образом, первый путь отображает 5 заполненных, 10 пустых, 5 заполненных, а затем зацикливается, чтобы создать 5 пустых, 10 заполненных, 5 пустых. Затем картина повторяется.

    Доступны дополнительные штрих и заливка свойства, в том числе правило заливки, которое указывает, как окрашивать фигуры, которые перекрывают друг друга; stroke-miterlimit , который определяет, должен ли штрих рисовать митры; и stroke-dashoffset, указывающий, где начинать тире в строке.

    Помимо установки атрибутов объектов, вы также можете использовать CSS для оформления заливки и обводки.Не все атрибуты можно установить с помощью CSS. Атрибуты, которые имеют дело с рисованием и заливкой, обычно доступны, поэтому fill , stroke , stroke-dasharray и т. д. все они могут быть установлены таким образом, в дополнение к версиям градиента и узора, показанным ниже. Атрибуты, такие как width , height или команд, не могут быть установлены через CSS. Проще всего просто протестировать и выяснить, что доступно, а что нет.

    Примечание: Спецификация SVG строго определяет атрибуты, которые являются свойствами , и другими атрибутами.Первое можно изменить с помощью CSS, второе — нет.

    CSS можно вставить в элемент с помощью атрибута стиля : 

      <прямой x="10" y="10"/>

    Или его можно переместить в специальный раздел стилей, который вы включите. Однако вместо того, чтобы помещать такой раздел в раздел , как это делается в HTML, он включен в область с именем .

    означает определения, и именно здесь вы можете создавать элементы, которые не отображаются непосредственно в SVG, но используются другими элементами.

      

  <определения>